Next Article in Journal
A Sightseeing Spot Recommendation System That Takes into Account the Change in Circumstances of Users
Previous Article in Journal
Analyzing Refugee Migration Patterns Using Geo-tagged Tweets
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
IJGI
Volume 6
Issue 10
10.3390/ijgi6100289
ijgi-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Determination of Areas Susceptible to Landsliding Using Spatial Patterns of Rainfall from Tropical Rainfall Measuring Mission Data, Rio de Janeiro, Brazil

by
Renato Fontes Guimarães
1,*,
Wátila Portela Machado
1,
Osmar Abílio De Carvalho, Júnior
1,
David R. Montgomery
2,
Roberto Arnaldo Trancoso Gomes
1,
Harvey M. Greenberg
2,
Márcio Cataldi
3 and
Pedro Coutinho Mendonça
1
1
Department of Geography, University of Brasília, Federal District, Brasília 70910-900, Brazil
2
Department of Earth and Space Sciences, University of Washington, Seattle, WA 98195, USA
3
Department of Agricultural and Environmental Engineering, Fluminense Federal University, Niterói 24210-510, Brazil
*
Author to whom correspondence should be addressed.
ISPRS Int. J. Geo-Inf. 2017, 6(10), 289; https://doi.org/10.3390/ijgi6100289
Submission received: 31 July 2017 / Revised: 5 September 2017 / Accepted: 11 September 2017 / Published: 6 October 2017
Browse Figures
Versions Notes

Abstract

:
Spatial patterns of shallow landslide initiation reflect both spatial patterns of heavy rainfall and areas susceptible to mass movements. We determine the areas most susceptible to shallow landslide occurrence through the calculation of critical soil cohesion and spatial patterns of rainfall derived from TRMM (Tropical Rainfall Measuring Mission) data for Paraty County, State of Rio de Janeiro, Brazil. Our methodology involved: (a) creating the digital elevation model (DEM) and deriving attributes such as slope and contributing area; (b) incorporating spatial patterns of rainfall derived from TRMM into the shallow slope stability model SHALSTAB; and (c) quantitative assessment of the correspondence of mapped landslide scars to areas predicted to be most prone to shallow landsliding. We found that around 70% of the landslide scars occurred in less than 10% of the study area identified as potentially unstable. The greatest concentration of landslides occurred in areas where the root strength of vegetation is an important contribution to slope stability in regions of orographically-enhanced rainfall on the coastal topographic flank. This approach helps quantify landslide hazards in areas with similar geomorphological characteristics, but different spatial patterns of rainfall.

1. Introduction

Mass movements occur at a variety of spatial and temporal scales, influencing hillslope evolution in high-relief areas [1], and posing a significant hazard in upland regions. Relatively little work on landslide prediction has been done to date in the humid tropics [2,3,4]. Particularly dangerous are rapid slope failures occurring along well-defined shear zones due to infiltration of high-intensity rainfall that fills the voids between soil particles, raising the pore-water pressure that acts in opposition to the normal stress, thereby reducing the material strength and triggering instability [5,6,7]. Precipitation and slope steepness influence shallow slope failures within the weathering mantle that generally fails to a depth conditioned by the soil and saprolite/rock strength and root reinforcement. Such translational landslides in the highlands of the state of Rio de Janeiro are common and have caused numerous fatalities in recent years. The combination of heavy summer rains and the lack of urban planning creates high landslide disaster potential in the region where growing cities face possible loss of life and material damage.
Normally, the landscape-scale prediction of landslide hazards considers the geostatistical relationships of previous events. Studies around the world focus on mapping landslide susceptibility based on combining landslide inventories with probabilistic, deterministic, and statistical approaches [8,9,10,11,12,13]. Physically-based (deterministic) models are widely used and have shown good results for shallow slope stability around the world. This type of model does not require a long-term landslide inventory, which is a significant advantage [14]. Examples of this approach include the following methods: Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Model (TRIGRS) [15]; Shallow Slope Stability Model (SHALSTAB) [16]; Stability Index Mapping (SINMAP) [17]; and Shallow Landslides Instability Prediction (SLIP) [18]. These models exhibit different degrees of complexity and hydrological models, yet present similar results when compared to spatial patterns of landslides scars [19]. SHALSTAB is one approach to landslide hazard assessment that uses topographic characteristics to model the spatial distribution of landslide hazards based on combining a simple hydrological model with a slope stability model and digital elevation models [16]. Several studies have tested and applied SHALSTAB in Brazil. Fernandes et al. [20] evaluated the spatial relationships between landslides and morphological factors. Guimarães et al. [21] analyzed the parameterization of soil properties in two basins in Rio de Janeiro after a strong rainstorm. Gomes et al. [22] verified the model’s behavior at different cartographic scales.
Recent research has investigated relationships between landslides and rainfall events [23,24,25]. A variety of landslide models use rainfall data, such as simple 1D numerical approach [26], object-oriented methods [27], logistic regression [28], and distributed hydrological-geotechnical models [29]. Remotely-sensed rainfall data [30] generate spatial patterns at a scale of kilometers to tens of kilometers that can be used to explore the effects of storm events and orographic effects on hazard generation and thereby estimate shallow landslide susceptibility over large areas [31]. For example, Minder et al. [32] used spatial patterns of rainfall using radar (MM5) estimates of the rainfall rate with the SHALSTAB model to predict shallow landslide susceptibility in the Northwestern United States. In this study, we incorporate rainfall from Tropical Rainfall Measuring Mission (TRMM) into landform analysis (SHALSTAB) to test a regional-scale method for assessing landslide hazards and establish critical cohesion indexes for triggering landslides in Rio de Janeiro, Brazil.

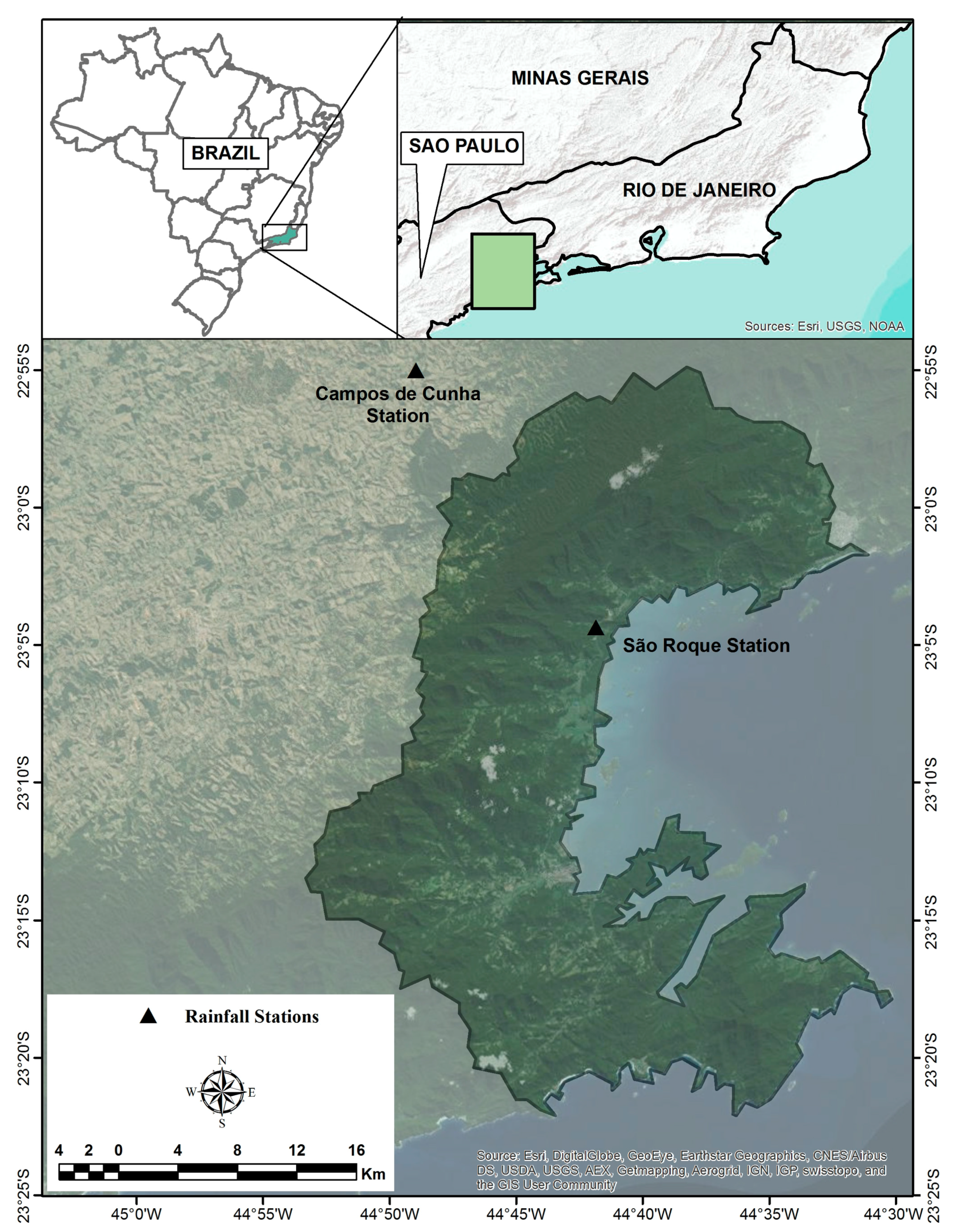
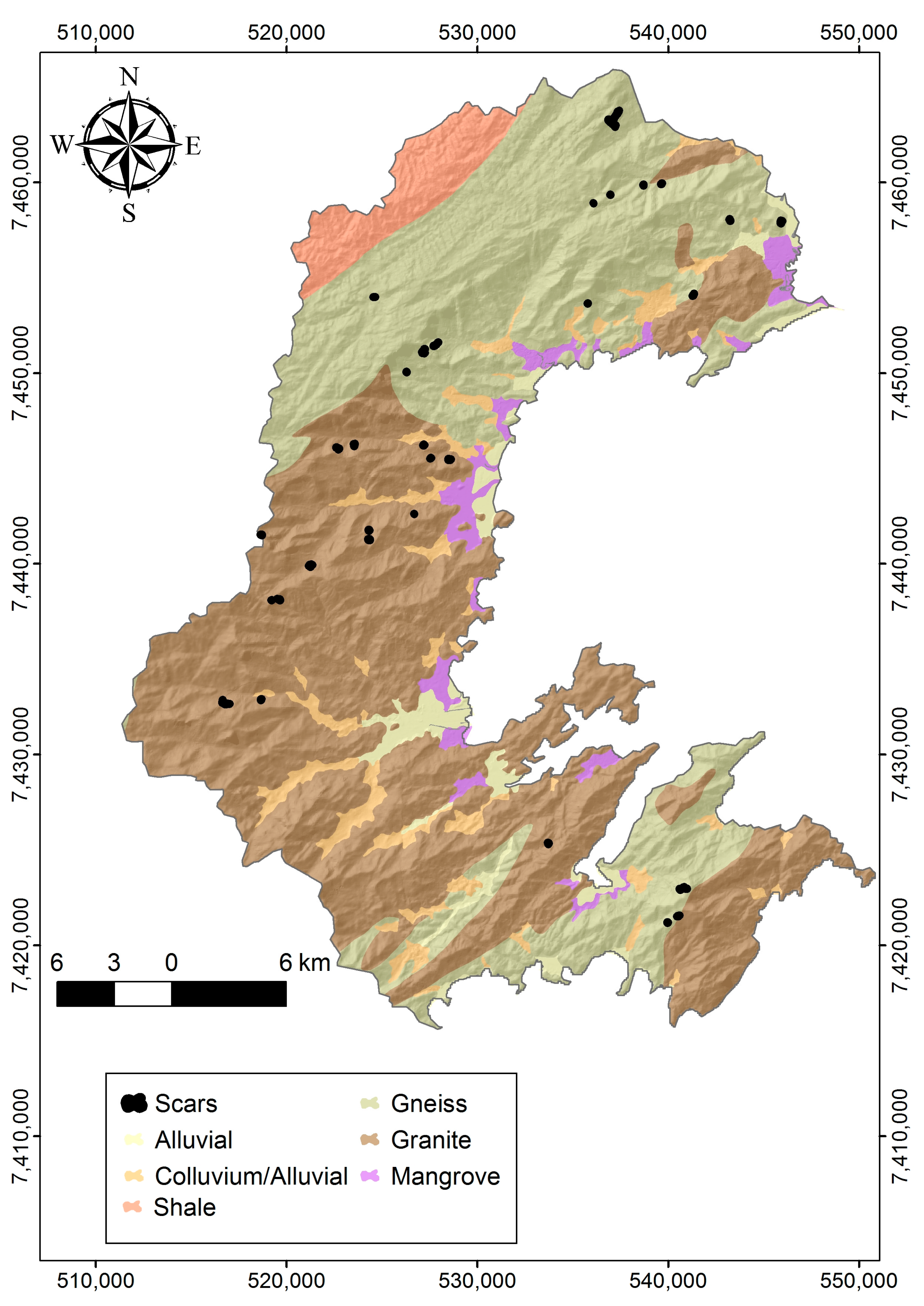
2. Study Area

Paraty is a municipality in the southern portion of the state of Rio de Janeiro, with historical, political, economic, and social importance (Figure 1). The region presents a climatic zoning strongly influenced by large topographical variation and strongly orographic rainfall [33,34]. Average monthly temperatures in the region range from 18 °C in the coldest months to 25 °C in the hottest months. The rainfall stations at São Roque (coast) and Campos de Cunha (behind the mountain) (Figure 1) display distinct behavior over the past 10 years (Table 1). Annual average rainfall at the coastal gauge (São Roque) is 2384 mm, not quite twice that of the Campos de Cunha station, which averages 1345 mm of rainfall annually. According to Soares et al. [35], this region is strongly influenced by the topography of the Serra do Mar, with the most intense rainfall occurring on the steep slopes of the escarpment.
The Bocaina Plateau is the highest area (>2000 m of altitude) of the Serra do Mar (1000 km of extension) situated on the eastern flank of the continental rift border of Southeastern Brazil [36]. The main lithologies of Serra da Bocaina are medium to high-grade orthogneisses and paragneisses, dominated by regional NE-SW trending ductile shear zones that dip steeply (~60°) to the northwest or southeast [37] (Figure 2).
Precambrian deformation was dominated by Neoproterozoic Brasiliano/Pan African Cycle structures during consolidation of the South American Platform [38,39,40]. Over geologic time, the Neoproterozoic shear zones have been consistent zones of weakness during reactivation events [41]. In the Mesozoic, the Late Jurassic separation of the Gondwana supercontinent culminated in the Early Cretaceous opening of the South Atlantic Ocean, which reactivated older discontinuities in pulses from the Cretaceous to Tertiary [41]. Tholeiitic basalt flows and dike swarms preceded this continental breakup [36,42]. The crustal discontinuities also controlled Mesozoic and Cenozoic alkaline magmatism [43]. During the Paleogene, normal faults reactivated Neoproterozoic shear zones, generating a continental rift in Southeastern Brazil parallel to the current coastline [44]. Lastly, late Pleistocene to Holocene neotectonic reactivation caused significant altitude differences between the Bocaina Plateau and adjacent rift valley, determining the local geomorphologic features with abrupt escarpments, a drainage network pattern controlled by the fault zones, and alluvial fan deposits at the base of mountains [44,45].
The soils are thin in the steepest areas over granite, thicker over gneiss in the plateau, and thickest in the coastal plain over sediments. Cambisols are the predominant soil type in the plateau and upland areas where Latosols and Arcisols also occur. Spodosols and Neosols occur in the floodplains (Figure 3).

3. Materials and Methods

3.1. Shallow Landslide Model

SHALSTAB is a physically-based model for the topographic controls of a shallow landslide that couples a slope-stability model based on Mohr-Coulomb criterion with a hydrological model to quantify susceptibility to translational shallow landslide along a well-defined shear plane [46]. We can express the stability of a slope through the ratio of the shear stresses driving slope failure (τ) to those forces tending to resist these driving stresses [11,47]. We adopt the approach known as the infinite-slope stability model, which ignores the effects caused by friction on the sides and ends of a block of soil. It is most applicable for translational slip where the length of the scar greatly exceeds the thickness of the soil. This analysis is based on the condition at slope failure where the shear stress (τ = ρsgzsinθ, where ρs is the soil bulk density, g is the gravitational acceleration, z is the soil thickness, and θ is the ground slope) equals the shear strength (SS) of a slope-forming material, which is given by:
SS = C’ + (σ − μ)tanφ
where C’ is the effective cohesion of the slope-forming material, σ is the normal stress (ρsgzcosθ), μ is the pore-water pressure, and φ is the angle of internal friction.
Assuming hydrostatic conditions and expressing the pore pressure as the relative saturation of the soil, the critical saturation level for slope failure (when τ = SS) may be expressed as:
h z = C ′ ρ w g z cos 2 θ tan φ + ρ s ρ w ( 1 − tan θ tan φ )
where ρw is the density of water and h is the thickness of saturated zone within the soil with a total thickness z.
With respect to the hydrological model, SHALSTAB adopts O’Loughlin’s [48] formulation that assumes infiltrating water penetrates to a lower conductivity layer at the base of the soil, and then follows topographically-determined flow paths. For a steady-state rainfall, the degree of relative saturation is then defined by the relative moisture content (h/z), and may be expressed as:
h z = Q T a b s i n θ
where Q is steady-state precipitation rate, a represents upslope contributing area (m2), b is the length of pixel side (m), θ is the slope (in degrees), and T is the soil transmissivity (m2/day). Since tree roots may be important for soil reinforcement on the steep slopes of the escarpment, we substituted Equation (3) into Equation (2) and solved for the critical cohesion value necessary to resist slope failure as a function of soil properties, topography, and rainfall [49]:
C c r i t i c a l = ρ w g z cos 2 θ tan φ [ a Q b T sin θ − ρ s ρ w ( 1 − tan θ tan φ ) ]
We categorize critical cohesion values into five classes, expressed in kPa, with varying degrees of potential instability, from those where high cohesion is required to maintain slope stability to those where the slope is stable even when the soil is completely saturated (i.e., h = z).
Our procedure for applying SHALSTAB considered the spatial patterns of rainfall to determine the critical cohesion levels through: (a) obtaining a digital elevation model (DEM) and terrain attributes, (b) acquiring rainfall data, (c) parameterizing soil properties, and (d) evaluating model performance through mapping landslides.

3.2. Digital Elevation Model and Terrain Attributes

The topographical attributes of slope and drainage area are commonly incorporated into models for prediction and definition of potentially unstable areas [50,51,52,53]. We built a 20 meter-grid DEM from digital contours from a 1:25,000 scale topographic map and interpolated with “topo to raster” module of ArcGIS software v. 10.4.1 (Environmental Systems Research Institute - ESRI, Redlands, CA, USA, 2016). Slope (θ) and specific catchment area (a/b) were estimated directly from the DEM.

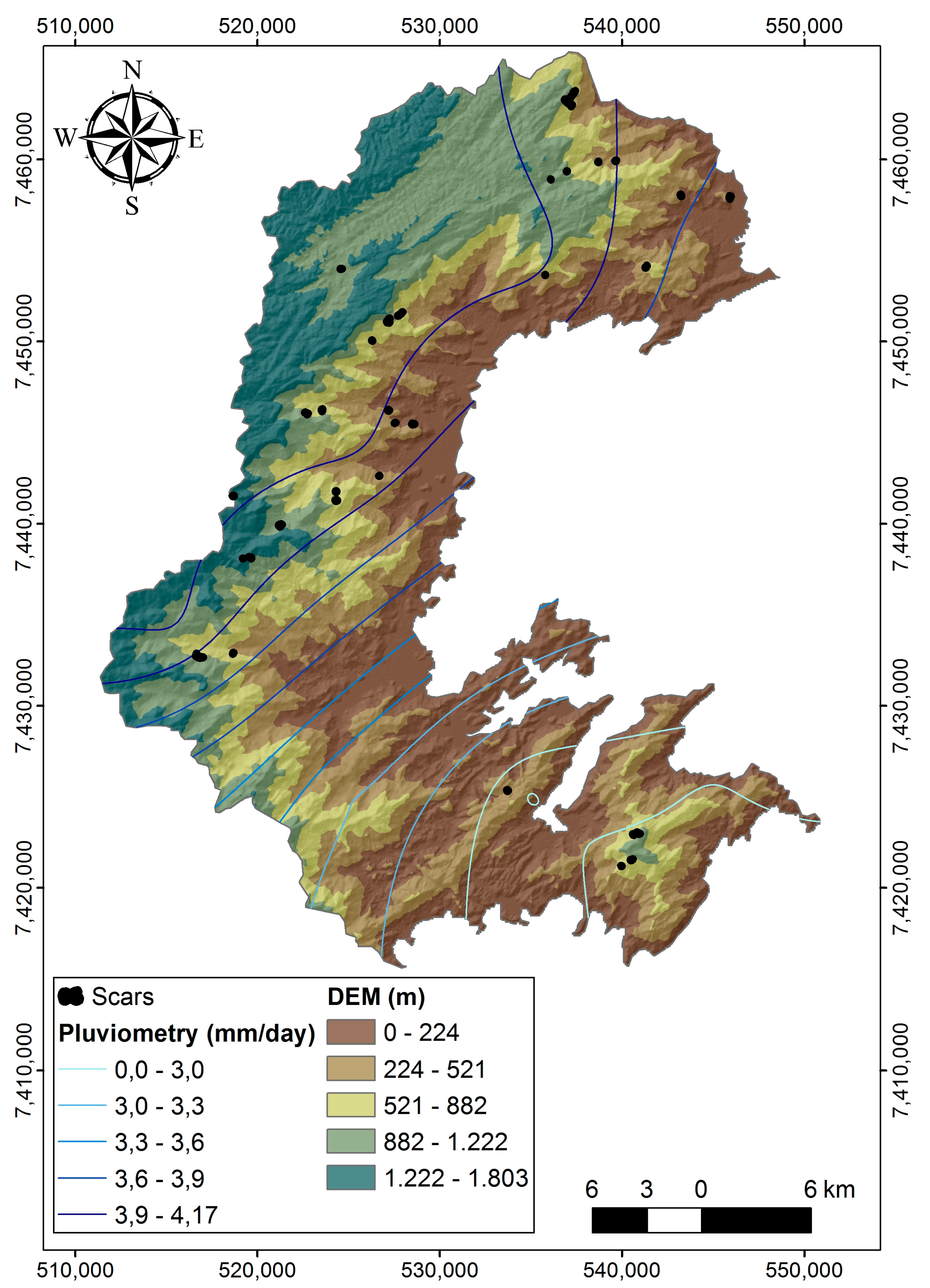
3.3. Acquisition of Rainfall Data

In rainfall data acquisition, the low density of meteorological observations in some regions compromises the applicability of studies related to orographic weather systems that directly influence the precipitation regime [54]. Many studies have used estimation techniques based on precipitation obtained from satellites to estimate the rainfall distribution and relate it to landslide locations [32,55,56]. In addition, some researchers consider rainfall intensity and wind effects in their landslides prediction models. Liu and Shih [57] took into account the effects of wind-driven rainfall as a significant factor in landslides that occurred in Taiwan during Typhoon Mindulle. Similarly, Rogers et al. [58] developed another approach to consider oblique rainfall-aspect in Himalayan Mountains of Northern Pakistan based on directional monsoon effects. While these GIS models consider wind as a landslide-triggering parameter [59], very strong winds are not the case in Southwestern Brazil, and our approach disregards wind intensity.
The Tropical Rainfall Measuring Mission (TRMM), launched in November 1997, provided the first space-based precipitation radar data used for climate studies. TRMM was conceived as an experimental satellite derived from a partnership between NASA and the Aerospace Exploration Agency of Japan (JAXA). The TRMM rainfall product (3B42) provides the most accurate estimates of globally integrated data from CAMS (Climate Assessment and Monitoring System) and GPCC (Global Precipitation Climatology Center) based on TMI (microwave imager) and VIRS (visible and infrared scanner) data. This product provides a global coverage of precipitation in the latitude band 50° N–S at 0.25° × 0.25° (lat/long) resolution and rainfall rates at three-hourly intervals [60]. The quality of rainfall estimates from TRMM 3B43 data have been evaluated using rain gauges in Africa [61,62], Asia [63,64,65], New Mexico [66], and Southern Brazil [67]. These studies conclude that TRMM data show great potential as input data for hydrological models. For this study, we assessed spatial variation in rainfall intensity using the mean values of time series datasets of annual rainfall for 2000–2007, converted to millimeters per day.

3.4. Parameterization of Soil Properties

In studies of natural hillslopes, soil property parameters are essential for quantitative stability analysis [47]. However, the use of models that consider soil spatial variability remains challenging, given the importance of the basal stratigraphic boundary uncertainty (i.e., soil thickness) that affects slope stability [68]. Recent methods of spatial variability of soil properties have been developed to be used in slope reliability analysis. These works are developed using mainly random field theory in small areas, such as a single slope [69,70], a single landslide [71], or even in an artificial hillslope [72]. The complexity of addressing spatial variability in soil properties increases with the area under consideration. In drainage basin studies, soil property values are obtained from laboratory analyses of samples collected in situ [73,74], or based on standard parameters reported in adjacent basins with similar geological and geomorphological characteristics [21,75].
Limited data are available on measured soil properties along the Serra do Mar. De Campos et al. [76] obtained laboratory values of soil friction angle (φ) ranging between 28 and 32 degrees in wet soils and between 35 and 44 degrees in dry soil. In Nova Friburgo (RJ), De Campos et al. [77] took values of 32.4° for the friction angle and 1.5 kPa for cohesion as representative conditions for saturated soil. Costa Nunes [78] found values of 25–40° for the friction angle in the Tijuca Massif. De Ploey and Cruz [79] in Caraguatatuba (SP) conducted field measurements for regolith developed on gneiss and found friction angles varied between 21 and 35 degrees and bulk densities ranged from 1.5 to 2 g/cm3. In this simulation, we choose values within the range of field-measured parameters reported by De Ploey and Cruz [79] from nearby areas and values used by Minder et al. [32] and Montgomery et al. [80] (Table 2).

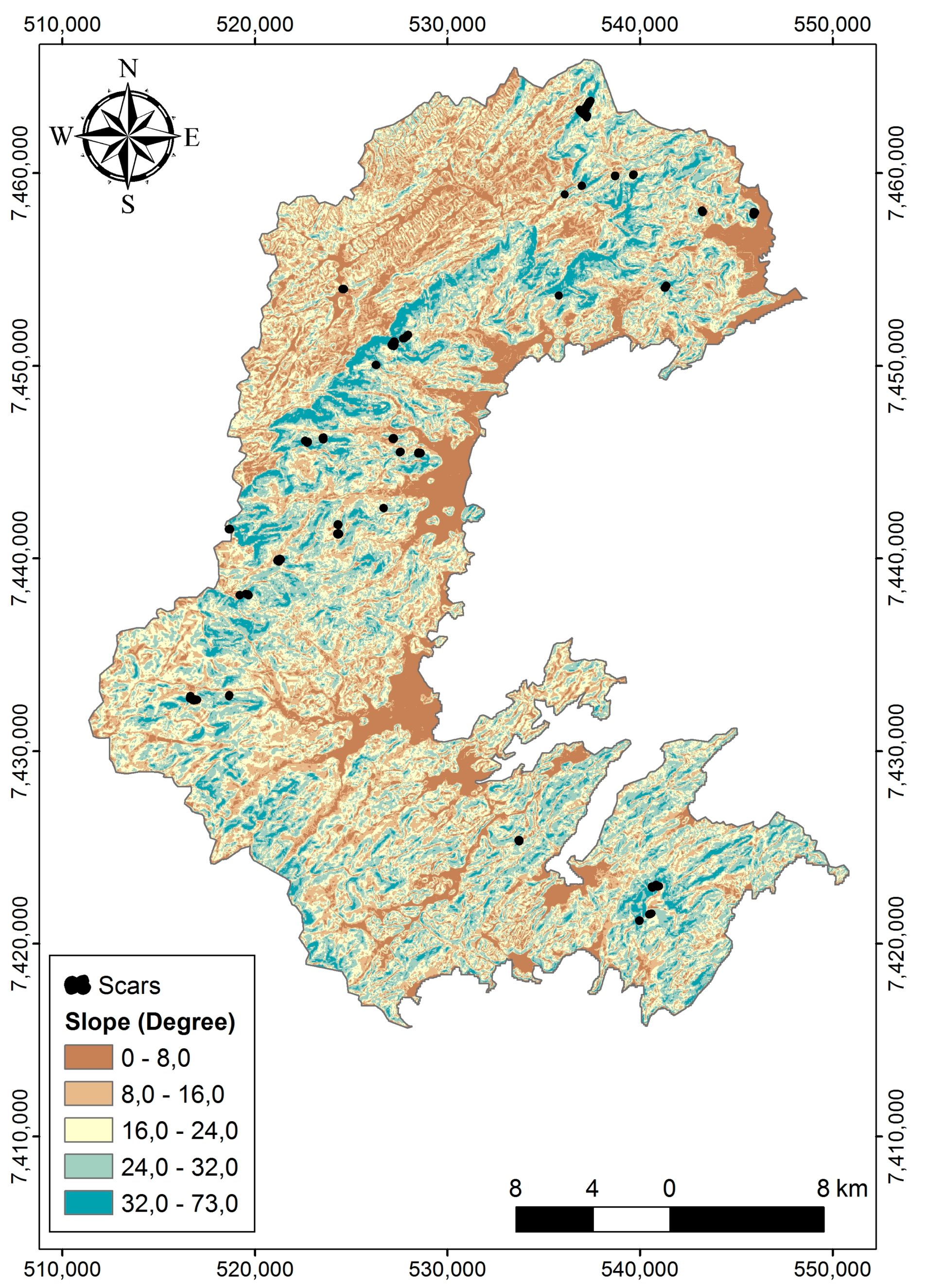
3.5. Landslide Mapping

We assessed the accuracy of the predicted distributions of landslide-prone slopes using SHALSTAB by comparing them to mapped landslide scars. Landslide scars were mapped delineating a defined head (source areas), body (runout tracks), and base (deposits). In this study, we identified landslide scars on georeferenced and orthorectified digital photography acquired in 2006, with a 1-meter spatial resolution. Model performance was evaluated by the percentage of the scars that fell in potentially unstable areas identified by the model.

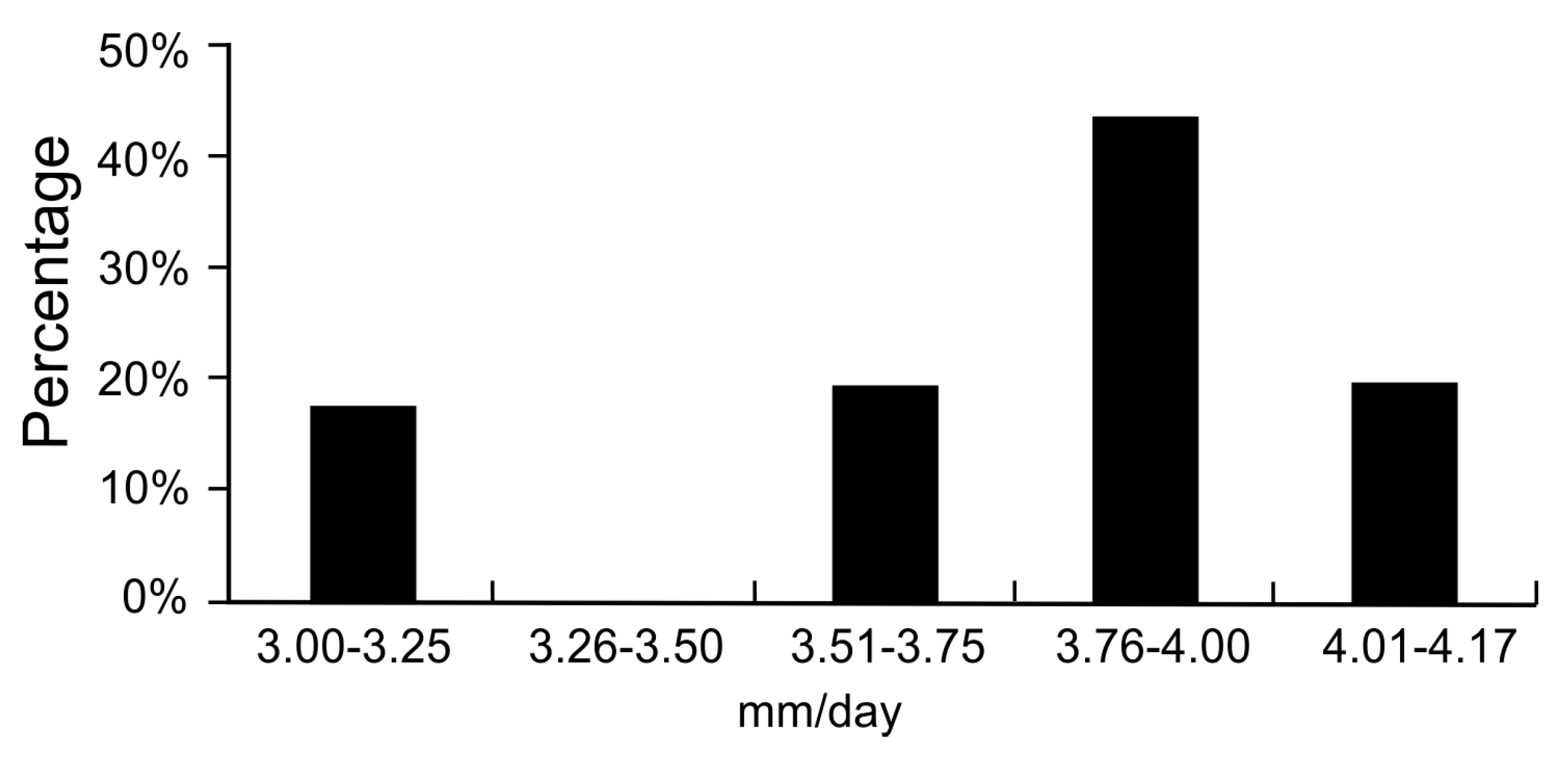
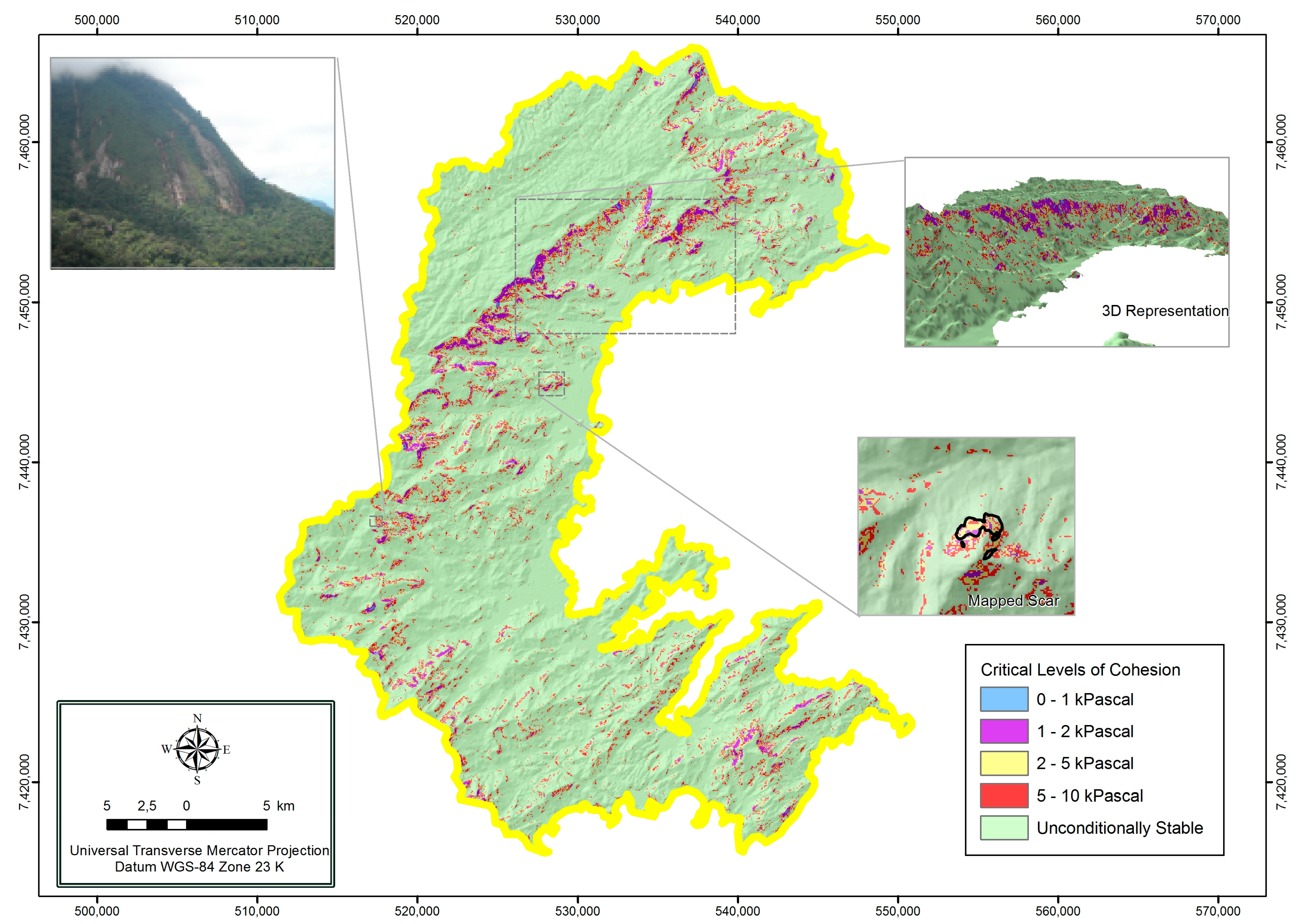
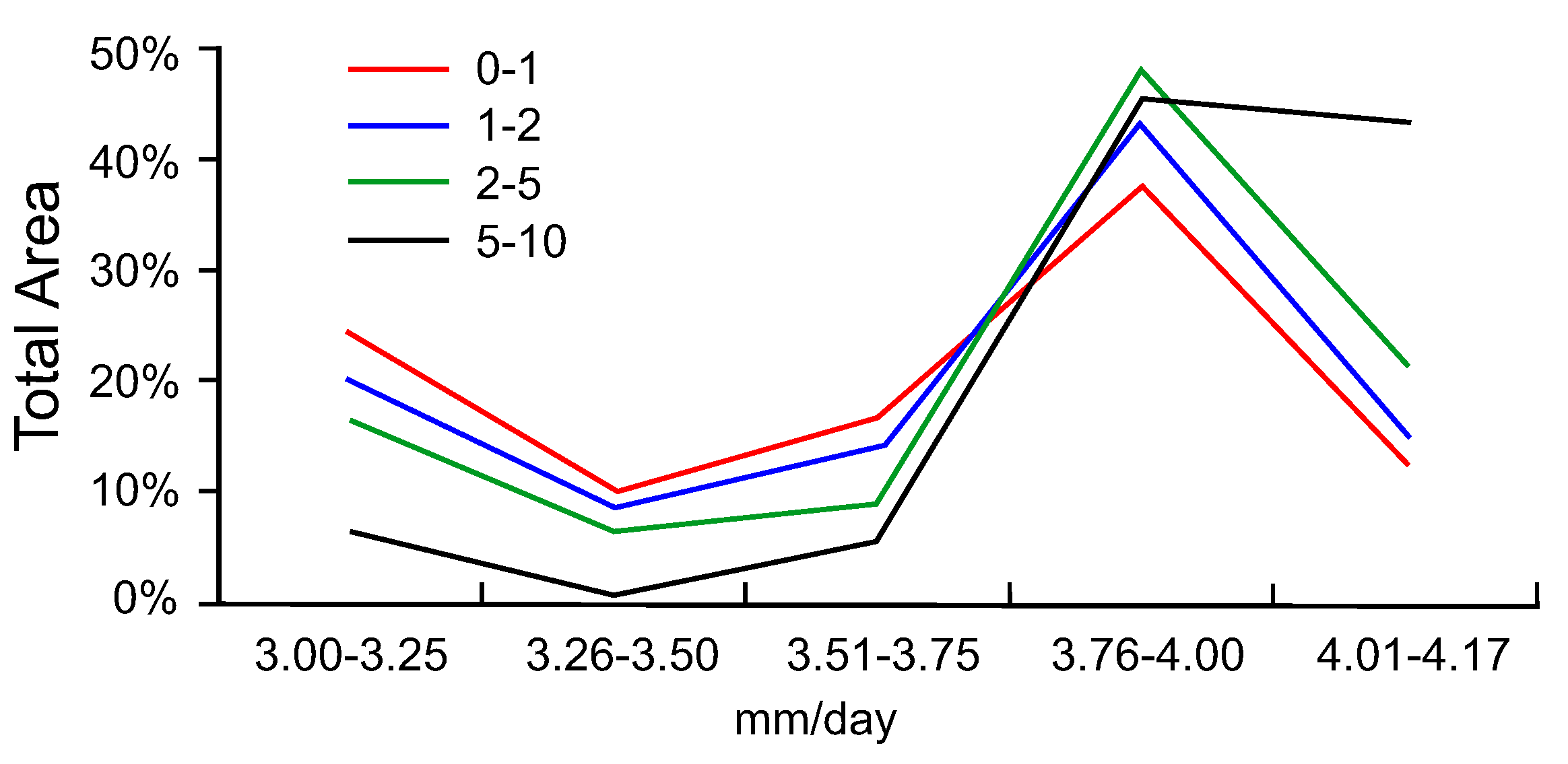
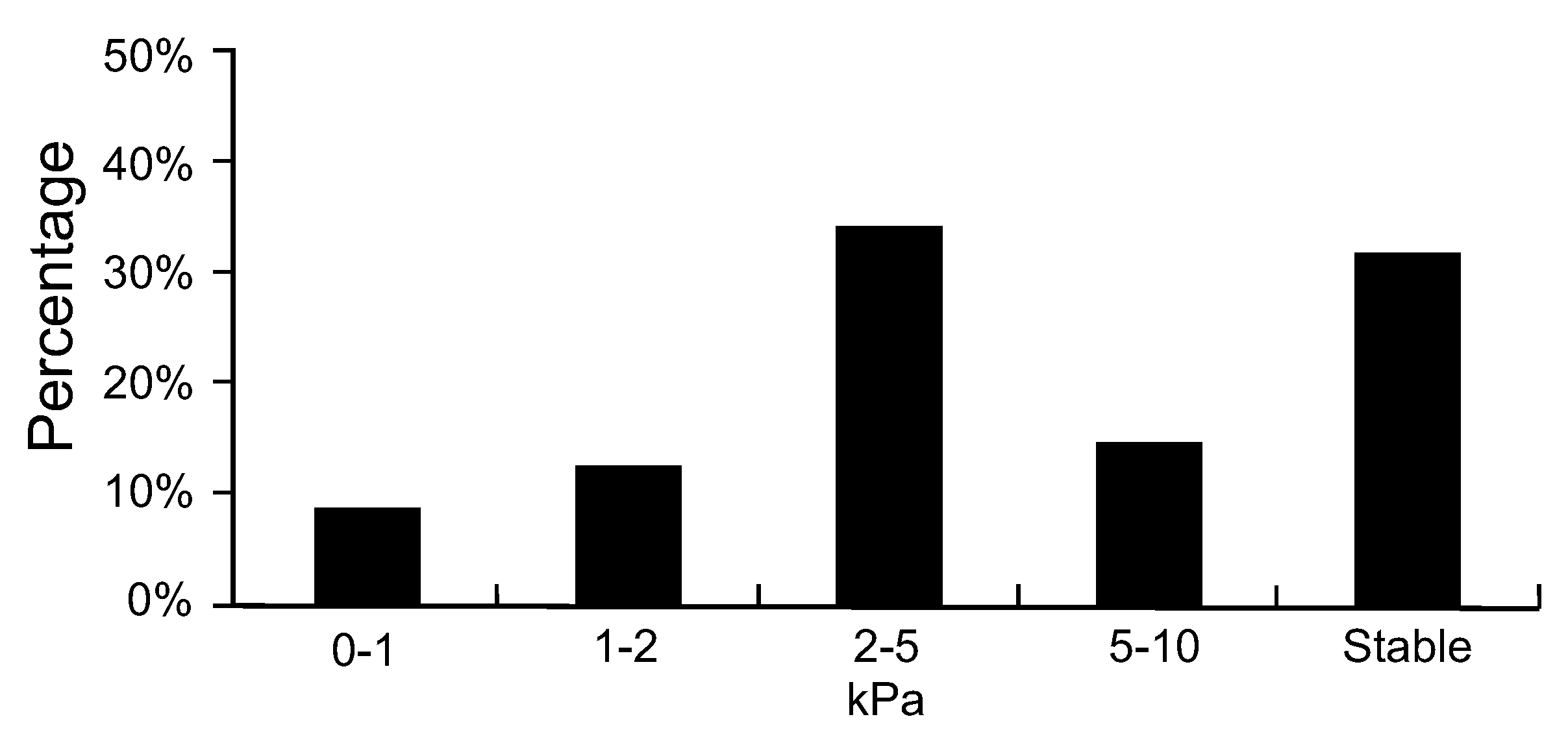
4. Results

The DEM of the study area shows steep and rugged relief in the headwaters (Figure 4), with elevations ranging from sea level to over 1805 m. TRMM data express the daily average rainfall for a series of eight years (2000–2007). The results reinforce the relationship between elevation and average rainfall rate, in which both rise from east to west and south to north (Figure 4). We divided the daily average rainfall rate into five classes, ranging from 3 mm/day to >4 mm/day. We identified from orthophotos 46 landslide scars, most of which occur on the escarpment, and which all together occupy 18 ha, corresponding to 0.02% of the total area. The locations of 80% of the mapped features have daily average rainfall rates over 3.5 mm/day (Figure 5). Slope steepness in the region ranges up to 73 degrees (Figure 6), with the highest values on the escarpment and the lowest values near the coast; the largest contributing areas drain to the coast and define the principal rivers in the county.
Landslide susceptibility maps delineate areas of potential failure based on the five classes of critical cohesion (Table 3). The lowest critical cohesion class (0–1 kPa) occupies 4% of the total area of the county and its spatial distribution is directly related to the escarpment of the Serra of Bocaina and steepest slopes (Figure 7). As the escarpment and steepest slopes are distributed throughout the county, more than half of the locations in this critical cohesion class are in high rain rate areas, and about 24% in the 3–3.25 mm/day class (Figure 8). A relatively small proportion of the landscape accounts for the zone of greatest potential for slope instability, as indicated by the highest critical cohesion categories (i.e., >2 kPa). In the higher rainfall zones, the higher critical cohesion classes occupy more area than lower classes. This is the opposite to the case in the lower rainfall rate areas, where low critical cohesion classes occupy less of the land areas. Thus, the root strength of vegetation plays a greater role in reinforcing slope strength in a wetter zone along the escarpment than in drier coastal zone. Most of the region (91%) is predicted to have little risk of slope failure and be unconditionally stable.
More than 70% of total area of landslide scars occurred in areas predicted to be potentially unstable, which together occupied just 9% of the total area (Figure 9). Almost half (46%) of the landslides occurred in the 2–5 kPa and 5–10 kPa critical cohesion classes, which together cover about 3% of the study area. This suggests an important role for vegetation as an influence on slope stability portions of the region. About a quarter of the landslides occurred in the low critical cohesion classes, and the remaining quarter occurred in areas predicted to be unconditionally stable. The highest landslide frequency occurs in areas with a combination of critical cohesion of 2–5 kPa and high rainfall quantity located in the middle and upper quadrant, which together create conditions favorable to triggering landslides (Table 4). The results indicate that the model predicts areas at higher risk of slope failure and that the combination of greater annual rainfall and slope morphology offers a better assessment of the spatial pattern of landslide risk than does either parameter alone.

5. Discussion

Many challenges are inherent in landslide susceptibility mapping in tropical areas, where there is a continuous increase in the exposure of people to their effects. In this study, we ran the SHALSTAB model in an area representative of steep escarpments with orographic rainfall. We solved the model equation for critical soil cohesion as a measure of slope instability [32]. This allows including precipitation grid values in addition to physical and topographic parameters. The study area has only two precipitation gauges, making the use of TRMM data fundamental for information consistency and mapping improvement in comparison with the landslides’ scar maps. The results show that embedding TRMM data in the SHALSTAB model is relevant to landslide prediction in localities lacking precipitation gauges.
Many researchers use meteorological satellite data to determine landslide-susceptible areas, both in regional areas [81] and global areas [30]. Maggioni et al. [82] performed an extensive review on the comparison of TRMM and gauges around the world. They verified that relief, climate, and seasonality contribute to satellite precipitation products performance. They also attested that TRMM3B42, used in this work, presented the best correlation with gauge observations in tropical regions. Due to its simplicity and flexibility, SHALSTAB has been applied in different ways, through solving for different variables (e.g., Q or Q/T). Solving for the critical soil cohesion as a measure of slope instability using TRMM data offers a way to integrate spatial patterns in rainfall into landslide hazard assessment.
Our analysis shows that particularly landslide-prone areas occur along the escarpment where average daily rainfall is above 3.75 mm/day in locations with a critical cohesion between 2–5 kPa. Given these values, and as Atlantic forest covers almost the entirety of the Serra da Bocaina, forestry practices that decrease root strength would appear to promote instability [32].

6. Conclusions

Strongly orographic rainfall is a major influence on landslide initiation along the passive margin escarpment of Southeastern Brazil. In the summer, cold fronts arriving from the south polar regions of the South Atlantic Ocean deliver heavy, landslide-triggering rainfall along the landslide-prone Serra da Bocaina escarpment, where orographic precipitation increases the landslide hazard. Due to the lack of rain gauges in the area, TRMM-derived estimates are useful for mapping precipitation patterns. Landslide mapping showed that around 70% of all scars occurred in the areas predicted to be potentially unstable, which corresponds to less than 10% of the total area. We find that the highest risk of landslide occurrence is for 2–5 kPa critical cohesion and an average daily rainfall of 3.75–4 mm. Spatial correlation of steeper slopes along the escarpment with greater rainfall delivery means that the cohesion provided by vegetation is particularly important for slope stability along the escarpment. However, the occurrence of about a quarter of the mapped landslides in areas predicted to be unconditionally stable indicates that a significant number of landslides happen in gentle relief. Taken together, our results demonstrate that this method has potential applications in both local and regional planning and disaster prevention. Improvements in resolution and quality datasets for mountain rainfall rates, and in combining gauge networks and high-resolution atmospheric model output would further contribute to better performance for slope stability mapping. In addition, complementary studies should be conducted, correlating the different types of mass movement with the rain intensities.

Acknowledgments

This study was funded through a project grant from the Conselho Nacional de Desenvolvimento Científico e Tecnológico (CNPq). The authors are grateful for financial support from CNPq fellowship (Osmar Abílio de Carvalho Júnior, Renato Fontes Guimarães, Roberto Arnaldo Trancoso Gomes) and Financiadora de Estudos e Projetos (FINEP). The authors acknowledge the contribution from anonymous reviewers.

Author Contributions

Renato Fontes Guimarães, David R. Montgomery, and Osmar Abílio de Carvalho Júnior wrote the manuscript and was responsible for the research design, mathematical model, data preparation and analysis. Wátila Portela Machado, Roberto Arnaldo Trancoso Gomes, and Pedro Coutinho Mendonça provided the data, conducted the field-works and gave relevant technical support. Harvey M. Greenberg provided significant input to the numerical analysis and computational optimization. Márcio Cataldi contributed to the climate data processing. All authors contributed in editing and reviewing the manuscript.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Innes, J.L. Lichenometric dating of debris-flow deposits in the Scottish Highlands. Earth Surf. Process. Landf. 1983, 8, 579–588. [Google Scholar] [CrossRef]
  2. Guimarães, R.F.; Gomes, R.A.T.; Carvalho Júnior, O.A.; Martins, E.S.; Fernandes, N.F. Análise temporal das áreas susceptíveis a escorregamentos rasos no Parque Nacional da Serra dos Órgãos (RJ) a partir de dados pluviométricos. Rev. Bras. Geociênc. 2009, 39, 190–198. [Google Scholar]
  3. Gomes, R.A.T.; Guimarães, R.F.; Carvalho Júnior, O.A.; Fernandes, N.F.; Amaral Júnior, E.V. Combining spatial models for shallow landslides and debris-flows prediction. Remote Sens. 2013, 5, 2219–2237. [Google Scholar] [CrossRef] [Green Version]
  4. Gomes, R.A.T.; Guimarães, R.F.; Carvalho Júnior, O.A.; Fernandes, N.F.; Amaral Júnior, E.V.; Martins, E.S. Identification of the affected areas by mass movement through a physically based model of landslide hazard combined with an empirical model of debris flow. Nat. Hazards 2008, 45, 197–209. [Google Scholar] [CrossRef]
  5. Borga, M.; Dalla Fontana, G.; Da Ros, D.; Marchi, L. Shallow landslide hazard assessment using a physically based model and digital elevation data. Environ. Geol. 1998, 35, 81–88. [Google Scholar] [CrossRef]
  6. Caine, N. The Rainfall Intensity: Duration Control of Shallow Landslides and Debris Flows. Geogr. Ann. Ser. A Phys. Geogr. 1980, 62, 23–27. [Google Scholar] [CrossRef]
  7. Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity-duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
  8. Barredo, J.; Benavides, A.; Hervás, J.; van Westen, C.J. Comparing heuristic landslide hazard assessment techniques using GIS in the Tirajana basin, Gran Canaria Island, Spain. Int. J. Appl. Earth Obs. Geoinf. 2000, 2, 9–23. [Google Scholar] [CrossRef]
  9. Gupta, R.P.; Kanungo, D.P.; Arora, M.K.; Sarkar, S. Approaches for comparative evaluation of raster GIS-based landslide susceptibility zonation maps. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 330–341. [Google Scholar] [CrossRef]
  10. Malamud, B.D.; Turcotte, D.L.; Guzzetti, F.; Reichenbach, P. Landslide inventories and their statistical properties. Earth Surf. Process. Landf. 2004, 29, 687–711. [Google Scholar] [CrossRef]
  11. Mancini, F.; Ceppi, C.; Ritrovato, G. GIS and statistical analysis for landslide susceptibility mapping in the Daunia area, Italy. Nat. Hazards Earth Syst. Sci. 2010, 10, 1851–1864. [Google Scholar] [CrossRef] [Green Version]
  12. Rautela, P.; Lakhera, R.C. Landslide risk analysis between Giri and Tons Rivers in Himachal Himalaya (India). Int. J. Appl. Earth Obs. Geoinf. 2000, 2, 153–160. [Google Scholar] [CrossRef]
  13. Safaei, M.; Omar, H.; Ghiasi, V.; Yousof, Z.B.M. Applying geospatial technology to landslide susceptibility assessment. Electron. J. Geotech. Eng. 2010, 15, 677–696. [Google Scholar]
  14. Pardeshi, S.D.; Autade, S.E.; Pardeshi, S.D. Landslide hazard assessment: Recent trends and techniques. Springerplus 2013, 2, 1–11. [Google Scholar] [CrossRef] [PubMed]
  15. Baum, R.L.; Savage, W.Z.; Godt, J.W. TRIGRS—A Fortran Program for Transient Rainfall Infiltration and Grid-Based Regional Slope-Stability Analysis, Version 2.0; Open-File Report; U.S. Geological Survey: Reston, VA, USA, 2008; 75p.
  16. Montgomery, D.R.; Dietrich, W.E. A physically based model for the topographical control on shallow landsliding. Water Resour. Res. 1994, 30, 1153–1171. [Google Scholar] [CrossRef]
  17. Pack, R.T. The SINMAP Approach to Terrain Stability Mapping. In Proceedings of the 8th International Congress, International Association for Engineering Geology and the Environments, Vancouver, BC, Canada, 21–25 September 1998; p. 8. [Google Scholar]
  18. Montrasio, L.; Valentino, R. A model for triggering mechanisms of shallow landslides. Nat. Hazards Earth Syst. Sci. 2008, 8, 1149–1159. [Google Scholar] [CrossRef]
  19. Zizioli, D.; Meisina, C.; Valentino, R.; Montrasio, L. Comparison between different approaches to modeling shallow landslide susceptibility: A case history in Oltrepo Pavese, Northern Italy. Nat. Hazards Earth Syst. Sci. 2013, 13, 559–573. [Google Scholar] [CrossRef]
  20. Fernandes, N.F.; Guimarães, R.F.; Gomes, R.A.T.; Vieira, B.C.; Montgomery, D.R. Condicionantes Geomorfológicos dos Deslizamentos nas Encostas: Avaliação de Metodologias e Aplicação de Modelo de Previsão de Áreas Susceptíveis. Rev. Bras. Geomorfol. 2001, 2, 51–71. [Google Scholar] [CrossRef]
  21. Guimaraes, R.F.; Montgomery, D.R.; Greenberg, H.M.; Fernandes, N.F.; Gomes, R.A.T.; Carvalho Júnior, O.A. Parameterization of soil properties for a model of topographic controls on shallow landsliding: Application to Rio de Janeiro. Eng. Geol. 2003, 69, 98–108. [Google Scholar] [CrossRef]
  22. Gomes, R.A.T.; Guimarães, R.F.; Carvalho Júnior, O.A.; Fernandes, N.F. Análise de um Modelo de Previsão de Deslizamentos ( Shalstab ) em Diferentes Escalas Cartográficas. Solos Rochas 2005, 28, 85–97. [Google Scholar]
  23. Pike, R.J.; Sobieszczyk, S. Soil slip/debris flow localized by site attributes and wind-driven rain in the San Francisco Bay region storm of January 1982. Geomorphology 2008, 94, 290–313. [Google Scholar] [CrossRef]
  24. Chang, K.T.; Chiang, S.H.; Lei, F. Analysing the relationship between typhoon-triggered landslides and critical rainfall conditions. Earth Surf. Process. Landf. 2008, 33, 1261–1271. [Google Scholar] [CrossRef]
  25. Frattini, P.; Crosta, G.; Sosio, R. Approaches for defining thresholds and return periods for rainfall-triggered shallow landslides. Hydrol. Process. 2009, 23, 1444–1460. [Google Scholar] [CrossRef]
  26. Pagano, L.; Picarelli, L.; Rianna, G.; Urciuoli, G. A simple numerical procedure for timely prediction of precipitation-induced landslides in unsaturated pyroclastic soils. Landslides 2010, 7, 273–289. [Google Scholar] [CrossRef]
  27. Martha, T.R.; Kerle, N.; Jetten, V.; van Westen, C.J.; Kumar, K.V. Characterising spectral, spatial and morphometric properties of landslides for semi-automatic detection using object-oriented methods. Geomorphology 2010, 116, 24–36. [Google Scholar] [CrossRef]
  28. Dominguez-Cuesta, M.J.; Jimenez-Sanchez, M.; Colubi, A.; González-Rodríguez, G. Modelling shallow landslide susceptibility: A new approach in logistic regression by using favourability assessment. Int. J. Earth Sci. 2010, 99, 661–674. [Google Scholar] [CrossRef]
  29. Apip; Takara, K.; Yamashiki, Y.; Sassa, K.; Ibrahim, A.B.; Fukuoka, H. A distributed hydrological-geotechnical model using satellite-derived rainfall estimates for shallow landslide prediction system at a catchment scale. Landslides 2010, 7, 237–258. [Google Scholar] [CrossRef]
  30. Kirschbaum, D.; Stanley, T.; Zhou, Y. Spatial and temporal analysis of a global landslide catalog. Geomorphology 2015, 249, 4–15. [Google Scholar] [CrossRef]
  31. Hong, Y.; Adler, R.F. Predicting global landslide spatiotemporal distribution: Integrating landslide susceptibility zoning techniques and real-time satellite rainfall estimates. Int. J. Sediment Res. 2008, 23, 249–257. [Google Scholar] [CrossRef]
  32. Minder, J.R.; Roe, G.H.; Montgomery, D.R. Spatial patterns of rainfall and shallow landslide susceptibility. Water Resour. Res. 2009, 45, 1–11. [Google Scholar] [CrossRef]
  33. Smith, R.B.; Jiang, Q.; Fearon, M.G.; Tabary, P.; Dorninger, M.; Doyle, J.D.; Benoit, R. Orographic precipitation and air mass transformation: An Alpine example. Q. J. Meteorol. Soc. 2003, 129, 433–454. [Google Scholar] [CrossRef]
  34. Roe, G.H. Orographic Precipitation. Annu. Rev. Earth Planet. Sci. 2005, 33, 645–671. [Google Scholar] [CrossRef]
  35. Soares, F.S.; Francisco, C.N.; Carneiro, M.; Senna, A. Distribuição espaço-temporal da precipitação da região hidrográfica da Baía da Ilha Grande—RJ. Rev. Bras. Meteorol. 2014, 29, 125–138. [Google Scholar] [CrossRef]
  36. Hiruma, S.T.; Riccomini, C.; Modenesi-Gauttieri, M.C.; Hackspacher, P.C.; Neto, J.C.H.; Franco-Magalhães, A.O.B. Denudation history of the Bocaina Plateau, Serra do Mar, southeastern Brazil: Relationships to Gondwana breakup and passive margin development. Gondwana Res. 2010, 18, 674–687. [Google Scholar] [CrossRef]
  37. Eirado, L.G.; Heilbron, M.; Almeida, J.C.H. Os Terrenos Tectônicos Da Faixa Ribeira Na Serra Da Bocaina E Na Baía Da Ilha Grande, Sudeste Do Brasil. Rev. Bras. Geociênc. 2006, 36, 426–436. [Google Scholar]
  38. Schmitt, R.S.; Frimmel, H.E.; Fairchild, T.R. Neoproterozoic-Early Paleozoic events in Southwest Gondwana: Introduction. Gondwana Res. 2008, 13, 435–436. [Google Scholar] [CrossRef]
  39. Bueno, J.F.; Oliveira, E.P.; McNaughton, N.J.; Laux, J.H. U-Pb dating of granites in the Neoproterozoic Sergipano Belt, NE-Brazil: Implications for the timing and duration of continental collision and extrusion tectonics in the Borborema Province. Gondwana Res. 2009, 15, 86–97. [Google Scholar] [CrossRef]
  40. Cordani, U.G.; Teixeira, W.; D’Agrella-Filho, M.S.; Trindade, R.I. The position of the Amazonian Craton in supercontinents. Gondwana Res. 2009, 15, 396–407. [Google Scholar] [CrossRef]
  41. Flávio, F.; De Almeida, M.; Dal, C.; Carneiro, R. Origem E Evolução Da Serra Do Mar. Rev. Bras. Geociênc. 1998, 28, 135–150. [Google Scholar]
  42. Marques, L.S.; Ernesto, M. O magmatismo toleítico da Bacia do Paraná. In Geologia do Continente Sul-Americano: Evolução da Obra de Fernando Flávio Marques de Almeida; Mantesso-Neto, V., Bartorelli, A., Carneiro, C.D.R., Neves, B.B.B., Eds.; Beca: São Paulo, Brazil, 2004; pp. 245–263. [Google Scholar]
  43. Riccomini, C.; Velázquez, V.; Gomes, C.B. Tectonic controls of the Mesozoic and Cenozoic alkaline magmatism in central-southeastern Brazilian platform. In Mesozoic to Cenozoic Alkaline Magmatism in the Brazilian Platform; Gomes, C.B., Comin-Chiaramonti, P., Eds.; EDUSP-FAPESP: São Paulo, Brazil, 2005; pp. 31–55. [Google Scholar]
  44. Riccomini, C.; Sant’Anna, L.G.; Ferrari, A.L. Evolução geológica do rift continental do Sudeste do Brasil. In Geologia do Continente Sul-Americano: Evolução da Obra de Fernando Flávio Marques de Almeida; Mantesso Neto, V., Bartorelli, A., Carneiro, C.D.R., Neves, B.B.B., Eds.; Beca: São Paulo, Brazil, 2004; pp. 383–405. [Google Scholar]
  45. Almeida, F.F.M. The system of continental rifts bordering the Santos basin, Brazil. An. Acad. Bras. Cienc. 1976, 48, 15–26. [Google Scholar]
  46. Summerfield, M.A. Global Geomorphology; Longman Group, Ed.; Burnt Mill: Harlow, UK, 1991. [Google Scholar]
  47. Selby, M.J. Hillslope Materials and Processes; Oxford University Press: Oxford, UK, 1982. [Google Scholar]
  48. O’Loughlin, E.M. Prediction of Surface Saturation Zones in Natural Catchments by Topographic Analysis. Water Resour. Res. 1986, 22, 794–804. [Google Scholar] [CrossRef]
  49. Montgomery, D.R.; Schmidt, K.M.; Greenberg, H.M.; Dietrich, W.E. Forest clearing and regional landsliding. Geology 2000, 28, 311–314. [Google Scholar] [CrossRef]
  50. Dietrich, W.E.; Reiss, R.; Hsu, M.L.; Montgomery, D.R. A process-based model for colluvial soil depth and shallow landsliding using digital elevation data. Hydrol. Process. 1995, 9, 383–400. [Google Scholar] [CrossRef]
  51. Nefeslioglu, H.A.; San, B.T.; Gokceoglu, C.; Duman, T.Y. An assessment on the use of terra ASTER L3A data in landslide susceptibility mapping. Int. J. Appl. Earth Obs. Geoinf. 2012, 14, 40–60. [Google Scholar] [CrossRef]
  52. San, B.T. An evaluation of SVM using polygon-based random sampling inlandslide susceptibility mapping: The Candir catchment area(western Antalya, Turkey). Int. J. Appl. Earth Obs. Geoinf. 2014, 26, 399–412. [Google Scholar] [CrossRef]
  53. Santini, M.; Grimaldi, S.; Nardi, F.; Petroselli, A.; Rulli, M.C. Pre-processing algorithms and landslide modelling on remotely sensed DEMs. Geomorphology 2009, 113, 110–125. [Google Scholar] [CrossRef]
  54. Rozante, J.R.; Moreira, D.S.; de Goncalves, L.G.G.; Vila, D.A. Combining TRMM and Surface Observations of Precipitation: Technique and Validation over South America. Weather Forecast. 2010, 25, 885–894. [Google Scholar] [CrossRef]
  55. Wieczorek, G. Effect of rainfall intensity and duration on debris flows in central Santa Cruz Mountains, California. In Debris Flows/Avalanches: Process, Recognition, and Mitigation; Costa, J.E., Wieczorek, G.F.E., Eds.; Geological Society of America: Boulder, CO, USA, 1987; Volume 7, pp. 93–104. [Google Scholar]
  56. Vrieling, A.; de Jong, S.M.; Sterk, G.; Rodrigues, S.C. Timing of erosion and satellite data: A multi-resolution approach to soil erosion risk mapping. Int. J. Appl. Earth Obs. Geoinf. 2008, 10, 267–281. [Google Scholar] [CrossRef]
  57. Liu, J.K.; Shih, P.T.Y. Topographic correction of Wind-Driven rainfall for landslide analysis in central Taiwan with validation from Aerial and satellite optical images. Remote Sens. 2013, 5, 2571–2589. [Google Scholar] [CrossRef]
  58. Rogers, J.D.; Ahmed, M.F.; Ismail, E.H. Landslide Susceptibility Screening Using Wind-Driven Rainfall. Assoc. Environ. Eng. Geosci. 2016, 22, 297–318. [Google Scholar] [CrossRef]
  59. Ismail, E.H.; Rogers, J.D.; Ahmed, M.F.; Usery, E.L.; Abdelsalam, M.G. Landslide susceptibility mapping of Blue Nile and Tekeze River Basins using oblique rainfall-aspect rasters. Bull. Eng. Geol. Environ. 2017, 1–19. [Google Scholar] [CrossRef]
  60. Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM Multisatellite Precipitation Analysis (TMPA): Quasi-Global, Multiyear, Combined-Sensor Precipitation Estimates at Fine Scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
  61. Dinku, T.; Ceccato, P.; Grover-Kopec, E.; Lemma, M.; Connor, S.J.; Ropelewski, C.F. Validation of satellite rainfall products over East Africa’s complex topography. Int. J. Remote Sens. 2007, 28, 1503–1526. [Google Scholar] [CrossRef]
  62. Haile, A.T.; Rientjes, T.; Gieske, A.; Gebremichael, M. Multispectral remote sensing for rainfall detection and estimation at the source of the Blue Nile River. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 76–82. [Google Scholar] [CrossRef]
  63. Duncan, J.M.A.; Biggs, E.M. Assessing the accuracy and applied use of satellite-derived precipitation estimates over Nepal. Appl. Geogr. 2012, 34, 626–638. [Google Scholar] [CrossRef]
  64. Yong, B.; Chen, B.; Gourley, J.J.; Ren, L.; Hong, Y.; Chen, X.; Wang, W.; Chen, S.; Gong, L. Intercomparison of the Version-6 and Version-7 TMPA precipitation products over high and low latitudes basins with independent gauge networks: Is the newer version better in both real-time and post-real-time analysis for water resources and hydrologic ext. J. Hydrol. 2014, 508, 77–87. [Google Scholar] [CrossRef]
  65. Qiu, J.; Gao, Q.; Wang, S.; Su, Z. Comparison of temporal trends from multiple soil moisture data sets and precipitation: The implication of irrigation on regional soil moisture trend. Int. J. Appl. Earth Obs. Geoinf. 2016, 48, 17–27. [Google Scholar] [CrossRef]
  66. Chiu, L.S.; Liu, Z.; Vongsaard, J.; Morain, S.; Budge, A.; Neville, P.; Bales, C. Comparison of TRMM and water district rain rates over New Mexico. Adv. Atmos. Sci. 2006, 23, 1–13. [Google Scholar] [CrossRef]
  67. Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.L.; Schönhuber, M. Raindrop Size Distribution in Different Climatic Regimes from Disdrometer and Dual-Polarized Radar Analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
  68. Liu, L.L.; Cheng, Y.M.; Wang, X.M.; Zhang, S.H.; Wu, Z.H. System reliability analysis and risk assessment of a layered slope in spatially variable soils considering stratigraphic boundary uncertainty. Comput. Geotech. 2017, 89, 213–225. [Google Scholar] [CrossRef]
  69. Jiang, S.H.; Huang, J.; Yao, C.; Yang, J. Quantitative risk assessment of slope failure in 2-D spatially variable soils by limit equilibrium method. Appl. Math. Model. 2017, 47, 710–725. [Google Scholar] [CrossRef]
  70. Li, D.Q.; Jiang, S.H.; Cao, Z.J.; Zhou, W.; Zhou, C.B.; Zhang, L.M. A multiple response-surface method for slope reliability analysis considering spatial variability of soil properties. Eng. Geol. 2015, 187, 60–72. [Google Scholar] [CrossRef]
  71. Zhao, H.F.; Zhang, L.; Xu, Y.; Chang, D.S. Variability of geotechnical properties of a fresh landslide soil deposit. Eng. Geol. 2013, 166, 1–10. [Google Scholar] [CrossRef]
  72. Lora, M.; Camporese, M.; Troch, P.A.; Salandin, P. Rainfall-triggered shallow landslides: Infiltration dynamics in a physical hillslope model. Hydrol. Process. 2016, 3251, 3239–3251. [Google Scholar] [CrossRef]
  73. Michel, G.P.; Kobiyama, M.; Goerl, R.F. Comparative analysis of SHALSTAB and SINMAP for landslide susceptibility mapping in the Cunha River basin, southern Brazil. J. Soils Sediments 2014, 14, 1266–1277. [Google Scholar] [CrossRef]
  74. D’Amato Avanzi, G.; Falaschi, F.; Giannecchini, R.; Puccinelli, A. Soil slip susceptibility assessment using mechanical-hydrological approach and GIS techniques: An application in the Apuan Alps (Italy). Nat. Hazards 2009, 50, 591–603. [Google Scholar] [CrossRef]
  75. Aristizábal, E.; García, E.; Martínez, C. Susceptibility assessment of shallow landslides triggered by rainfall in tropical basins and mountainous terrains. Nat. Hazards 2015, 78, 621–634. [Google Scholar] [CrossRef]
  76. De Campos, T.M.P.; Andrade, M.H.N.; Vargas, E.A., Jr. Unsaturated Colluvium Over Roch Slide in a Forest Site in Rio de Janeiro. In Proceedings of the Sixth International Symposium on Landslides, Christchurch, New Zealand, 10–14 February 1992; Balkema A.A.: Rotterdam, The Netherlands, 1992–1995; pp. 1357–1364. [Google Scholar]
  77. De Campos, T.M.P.; Vargas, E.A., Jr.; Amaral, C.P.; Dell Avanzi, E. Instabilization factors of the residual soil slope in Nova Friburgo, Rio de Janeiro. In Proceedings of the II Conferência Brasileira sobre Estabilidade de Encostas, Rio de Janeiro, Brazil, 10–14 November 1997; pp. 967–975. [Google Scholar]
  78. Costa Nunes, A.J. Landslides in Soils of Decomposed Rock due to Intense Rainstorms. In Proceedings of the 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, Mexico, 25–29 August 1969; Sociedad Mexicana de Mecanica de Suelos: Mexico City, Mexico, 1969; pp. 547–554. [Google Scholar]
  79. De Ploey, J.; Cruz, O. Landslides in the Serra do Mar, Brazil. Catena 1979, 6, 111–122. [Google Scholar] [CrossRef]
  80. Montgomery, D.R.; Sullivan, K.; Greenberg, H.M. Regional test of a model for shallow landsliding. Hydrol. Process. 1998, 12, 943–955. [Google Scholar] [CrossRef]
  81. Gaprindashvili, G.; Westen, C.J. Van Generation of a national landslide hazard and riskmap for Georgia. Nat. Hazards 2015, 80, 1–35. [Google Scholar]
  82. Maggioni, V.; Meyers, P.C.; Robinson, M.D.; Maggioni, V.; Meyers, P.C.; Robinson, M.D. A Review of Merged High-Resolution Satellite Precipitation Product Accuracy during the Tropical Rainfall Measuring Mission (TRMM) Era. J. Hydrometeorol. 2016, 17, 1101–1117. [Google Scholar] [CrossRef]
Ijgi 06 00289 g001 550
Figure 1. Study area showing location of rain gauges at Campos de Cunha and São Roque.
Figure 1. Study area showing location of rain gauges at Campos de Cunha and São Roque.
Ijgi 06 00289 g001
Ijgi 06 00289 g002 550
Figure 2. Geological map of the Paraty municipality.
Figure 2. Geological map of the Paraty municipality.
Ijgi 06 00289 g002
Ijgi 06 00289 g003 550
Figure 3. Soil map of the Paraty municipality.
Figure 3. Soil map of the Paraty municipality.
Ijgi 06 00289 g003
Ijgi 06 00289 g004 550
Figure 4. Maps of elevation with TRMM rainfall contour line-derived average daily rainfall for 2000–2007.
Figure 4. Maps of elevation with TRMM rainfall contour line-derived average daily rainfall for 2000–2007.
Ijgi 06 00289 g004
Ijgi 06 00289 g005 550
Figure 5. Scar distribution according to the average rainfall rate.
Figure 5. Scar distribution according to the average rainfall rate.
Ijgi 06 00289 g005
Ijgi 06 00289 g006 550
Figure 6. Slope map of the Paraty municipality.
Figure 6. Slope map of the Paraty municipality.
Ijgi 06 00289 g006
Ijgi 06 00289 g007 550
Figure 7. Critical cohesion based on the SHALSTAB model, using T = 65 m2/day, soil depth = 1 m, bulk density = 2.0 g/cm3, and phi = 33 degrees.
Figure 7. Critical cohesion based on the SHALSTAB model, using T = 65 m2/day, soil depth = 1 m, bulk density = 2.0 g/cm3, and phi = 33 degrees.
Ijgi 06 00289 g007
Ijgi 06 00289 g008 550
Figure 8. Percentage area of rain rate average. The color lines represent critical cohesion predicted by SHALSTAB using TRMM rainfall along the rainfall classes.
Figure 8. Percentage area of rain rate average. The color lines represent critical cohesion predicted by SHALSTAB using TRMM rainfall along the rainfall classes.
Ijgi 06 00289 g008
Ijgi 06 00289 g009 550
Figure 9. Percentage of the total area of the 46 mapped landslide scars by cohesion class.
Figure 9. Percentage of the total area of the 46 mapped landslide scars by cohesion class.
Ijgi 06 00289 g009
Table
Table 1. Annual rainfall (mm) for São Roque and Campos de Cunha rainfall stations.
Table 1. Annual rainfall (mm) for São Roque and Campos de Cunha rainfall stations.
YearCampos de Cunha StationSão Roque Station
200013921822
200111971853
200212862339
200311952441
200414572484
200510672756
200611592489
200712271918
200815092818
200916692934
201016392366
Table
Table 2. Soil parameter values used in this study.
Table 2. Soil parameter values used in this study.
ParameterValue/Unit
Transmissivity (T)65 m2/day
Soil depth (z)1 m
Angle of internal friction (φ)33°
Bulk density (ρs)2 (g/cm3)
Table
Table 3. Critical levels of cohesion class areas.
Table 3. Critical levels of cohesion class areas.
Critical Levels of Cohesion ClassArea (ha)Percentage (%)
5–10 kPa74<1
2–5 kPa21532
1–2 kPa21932
0–1 kPa37584
Unconditionally Stable83,18491
Table
Table 4. Correlation matrix for landslide frequency in terms of critical cohesion and average rainfall.
Table 4. Correlation matrix for landslide frequency in terms of critical cohesion and average rainfall.
Critical Cohesion (kPa)3.00–3.25 (mm/day)3.26–3.50 (mm/day)3.51–3.75 (mm/day)3.76–4.00 (mm/day)4.01–4.17 (mm/day)
0–100040
1–230131
2–520553
5–1000114
Stable30271

Share and Cite

MDPI and ACS Style

Guimarães, R.F.; Machado, W.P.; De Carvalho, O.A., Júnior; Montgomery, D.R.; Gomes, R.A.T.; Greenberg, H.M.; Cataldi, M.; Mendonça, P.C. Determination of Areas Susceptible to Landsliding Using Spatial Patterns of Rainfall from Tropical Rainfall Measuring Mission Data, Rio de Janeiro, Brazil. ISPRS Int. J. Geo-Inf. 2017, 6, 289. https://doi.org/10.3390/ijgi6100289

AMA Style

Guimarães RF, Machado WP, De Carvalho OA Júnior, Montgomery DR, Gomes RAT, Greenberg HM, Cataldi M, Mendonça PC. Determination of Areas Susceptible to Landsliding Using Spatial Patterns of Rainfall from Tropical Rainfall Measuring Mission Data, Rio de Janeiro, Brazil. ISPRS International Journal of Geo-Information. 2017; 6(10):289. https://doi.org/10.3390/ijgi6100289

Chicago/Turabian Style

Guimarães, Renato Fontes, Wátila Portela Machado, Osmar Abílio De Carvalho, Júnior, David R. Montgomery, Roberto Arnaldo Trancoso Gomes, Harvey M. Greenberg, Márcio Cataldi, and Pedro Coutinho Mendonça. 2017. "Determination of Areas Susceptible to Landsliding Using Spatial Patterns of Rainfall from Tropical Rainfall Measuring Mission Data, Rio de Janeiro, Brazil" ISPRS International Journal of Geo-Information 6, no. 10: 289. https://doi.org/10.3390/ijgi6100289

APA Style

Guimarães, R. F., Machado, W. P., De Carvalho, O. A., Júnior, Montgomery, D. R., Gomes, R. A. T., Greenberg, H. M., Cataldi, M., & Mendonça, P. C. (2017). Determination of Areas Susceptible to Landsliding Using Spatial Patterns of Rainfall from Tropical Rainfall Measuring Mission Data, Rio de Janeiro, Brazil. ISPRS International Journal of Geo-Information, 6(10), 289. https://doi.org/10.3390/ijgi6100289

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop