Kinematic Precise Point Positioning Using Multi-Constellation Global Navigation Satellite System (GNSS) Observations
Abstract
:1. Introduction
2. Multi-Constellation PPP Model
2.1. Multi-Constellation PPP
2.2. Kalman Filter Model
2.3. Stochastic Models
3. Multi-Constellation Kinematic PPP Data Processing Strategy
4. Performance Analysis of Multi-Constellation Kinematic PPP
4.1. Experimental Data Description
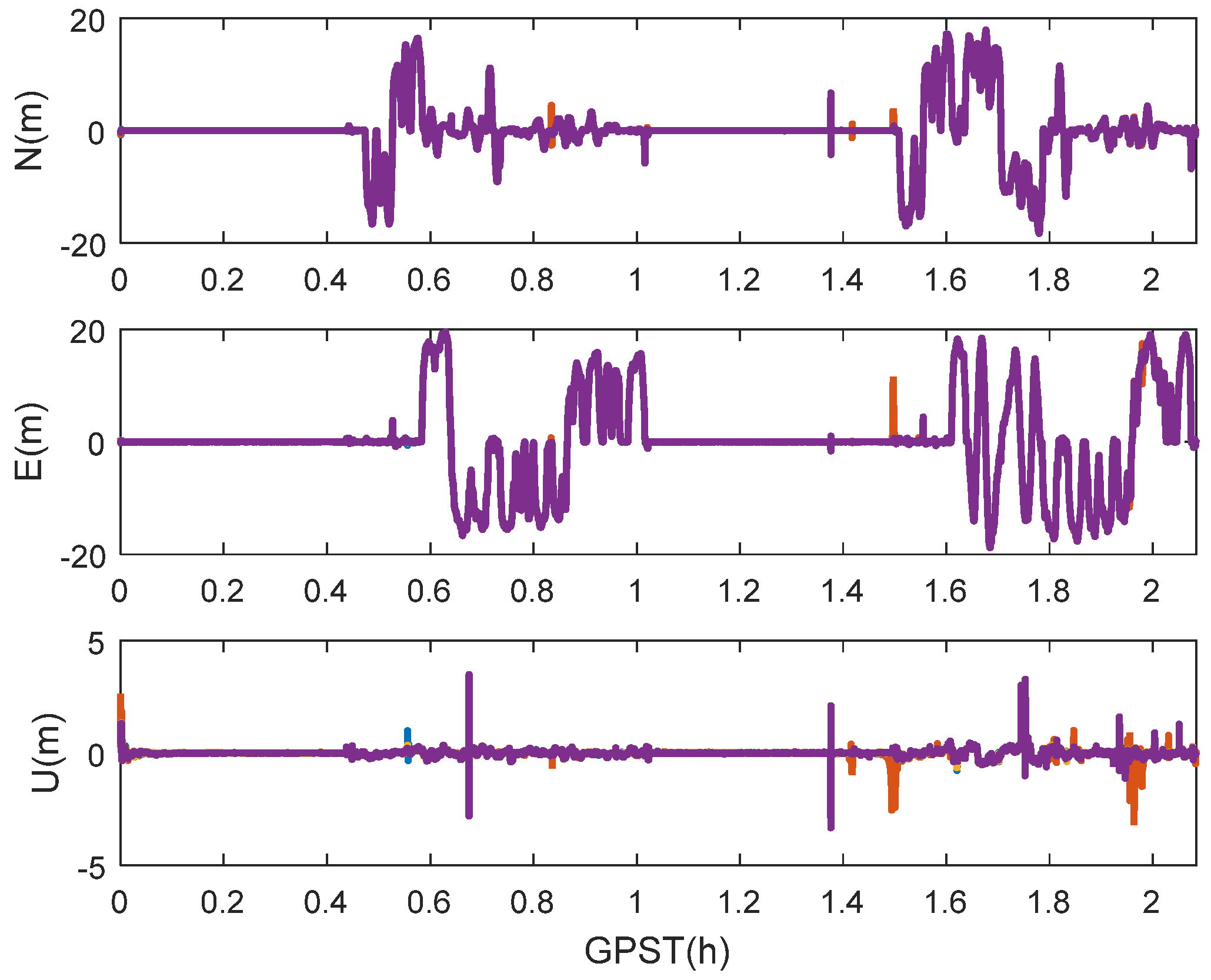
4.2. Results and Analysis
4.2.1. Availability of Multi-Constellation Kinematic PPP
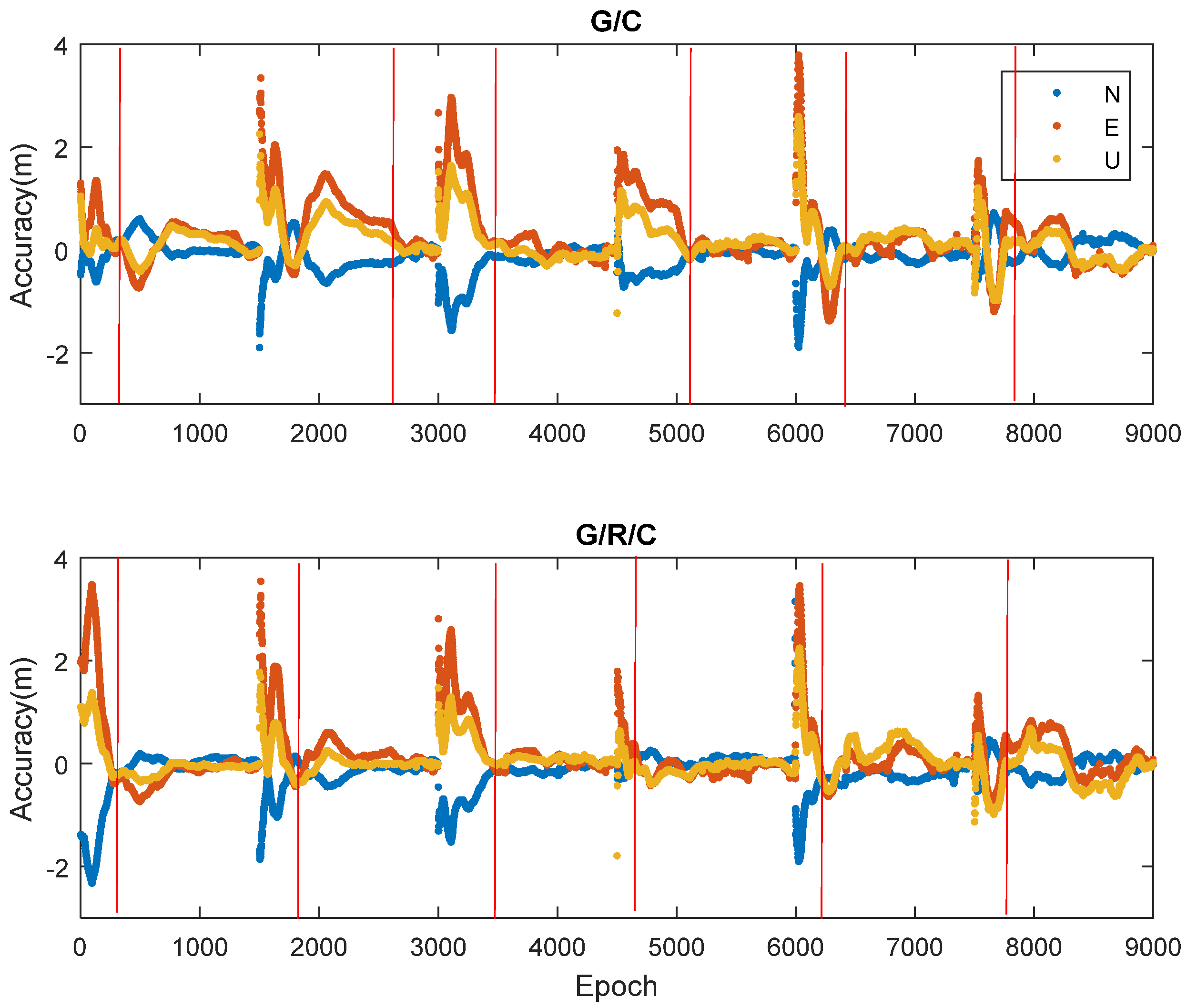
4.2.2. Positioning Accuracy and the RMS of the Kalman Filter
4.2.3. Convergence Time
5. Conclusions
- The availability of multi-constellation kinematic PPP was significantly better than that of GPS-only PPP because more satellites were observable and because the PDOP was better.
- The accuracy of multi-constellation kinematic PPP was greater than that of GPS-only, GPS/BDS and GPS/GLONASS PPP. The positioning accuracy of GPS/GLONASS PPP was slightly lower than that of GPS/BDS PPP.
- The convergence performance of GPS/GLONASS/BDS kinematic PPP was the best for all three coordinate components, particularly in the East direction.
- Multi-constellation kinematic PPP can provide a positioning service with centimetre-level accuracy for dynamic users.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zumberge, J.F.; Heflin, M.B.; Jefferson, D.C.; Watkins, M.M.; Webb, F.H. Precise point positioning for the efficient and robust analysis of GPS data from large networks. J. Geophys. Res. 1997, 102, 5005–5017. [Google Scholar] [CrossRef]
- Dow, J.M.; Neilan, R.E.; Rizos, C. The international GNSS service in a changing landscape of global navigation satellite systems. J. Geod. 2009, 83, 191–198. [Google Scholar] [CrossRef]
- Li, M.; Wickert, M. A novel real-time precise positioning service system: Global precise point positioning with regional augmentation. J. Glob. Position. Syst. 2012, 11, 29. [Google Scholar]
- Li, X.; Ge, M.; Douša, J.; Wickert, J. Real-time precise point positioning regional augmentation for large GPS reference networks. GPS Solut. 2014, 18, 61–71. [Google Scholar] [CrossRef]
- Bisnath, S.; Gao, Y. Current state of precise point positioning and future prospects and limitations. In Observing Our Changing Earth; Springer: Berlin, Germany, 2009; pp. 615–623. [Google Scholar]
- Loyer, S.; Perosanz, F.; Mercier, F.; Capdeville, H.; Marty, J.-C. Zero-difference GPS ambiguity resolution at CNES–CLS IGS analysis Center. J. Geod. 2012, 86, 991–1003. [Google Scholar] [CrossRef]
- Li, T.; Wang, J.; Laurichesse, D. Modeling and quality control for reliable precise point positioning integer ambiguity resolution with GNSS modernization. GPS Solut. 2014, 18, 429–442. [Google Scholar] [CrossRef]
- Laurichesse, D.; Mercier, F.; Berthias, J.-P.; Broca, P.; Cerri, L. Integer ambiguity resolution on undifferenced GPS phase measurements and its application to PPP and satellite precise orbit determination. Navigation 2009, 56, 135–149. [Google Scholar] [CrossRef]
- Ge, M.; Gendt, G.; Rothacher, M.; Shi, C.; Liu, J. Resolution of GPS carrier-phase ambiguities in precise point positioning (PPP) with daily observations. J. Geod. 2008, 82, 389–399. [Google Scholar] [CrossRef]
- O’Keefe, K. Availability and reliability advantages of GPS/Galileo integration. In Proceedings of the 14th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GPS-2001), Salt Lake City, UT, USA, 11–14 September 2001.
- Hewitson, S.; Wang, J. GPS/GLONASS/GALILEO Integration: Separation of Outliers; School of Surveying and Spatial Information Systems, The University of New South Wales: Sydney, Australia, 2003. [Google Scholar]
- Ji, S.; Chen, W.; Ding, X.; Chen, Y.; Zhao, C.; Hu, C. Potential benefits of GPS/GLONASS/GALILEO integration in an urban canyon–Hong Kong. J. Navig. 2010, 63, 681–693. [Google Scholar] [CrossRef]
- Li, X.; Ge, M.; Dai, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Accuracy and reliability of multi-GNSS real-time precise positioning: GPS, GLONASS, BeiDou, and Galileo. J. Geod. 2015, 89, 607–635. [Google Scholar] [CrossRef]
- Li, X.; Zhang, X.; Ren, X.; Fritsche, M.; Wickert, J.; Schuh, H. Precise positioning with current multi-constellation global navigation satellite systems: GPS, GLONASS, Galileo and BeiDou. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Cai, C.; Gao, Y.; Pan, L.; Dai, W. An analysis on combined GPS/COMPASS data quality and its effect on single point positioning accuracy under different observing conditions. Adv. Space Res. 2013, 54, 818–829. [Google Scholar] [CrossRef]
- Yigit, C.O.; Gikas, V.; Alcay, S.; Ceylan, A. Performance evaluation of short to long term GPS, GLONASS and GPS/GLONASS post-processed PPP. Surv. Rev. 2014, 46, 155–166. [Google Scholar] [CrossRef]
- Li, P.; Zhang, X. Integrating GPS and GLONASS to accelerate convergence and initialization times of precise point positioning. GPS Solut. 2014, 18, 461–471. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y. Modeling and assessment of combined GPS/GLONASS precise point positioning. GPS Solut. 2013, 17, 223–236. [Google Scholar] [CrossRef]
- Yang, Y.; Li, J.; Xu, J.; Tang, J.; Guo, H.; He, H. Contribution of the compass satellite navigation system to global PNT users. Chin. Sci. Bull. 2011, 56, 2813–2819. [Google Scholar] [CrossRef]
- Qu, L.; Zhao, Q.; Li, M.; Guo, J.; Su, X.; Liu, J. Precise point positioning using combined BeiDou and GPS observations. In China Satellite Navigation Conference (CSNC) 2013 Proceedings; Springer: Berlin, Germany, 2013; pp. 241–252. [Google Scholar]
- Li, M.; Qu, L.; Zhao, Q.; Guo, J.; Su, X.; Li, X. Precise point positioning with the BeiDou navigation satellite system. Sensors 2014, 14, 927–943. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Teunissen, P.; Zhang, B.; Verhagen, S. Precise point positioning using GPS and Compass observations. In China Satellite Navigation Conference (CSNC) 2013 Proceedings; Springer: Berlin, Germany, 2013; pp. 367–378. [Google Scholar]
- Rizos, C.; Montenbruck, O.; Weber, R.; Weber, G.; Neilan, R.; Hugentobler, U. The IGS MGEX experiment as a milestone for a comprehensive multi-GNSS service. In Proceedings of the ION 2013 Pacific PNT Meeting, Honolulu, HI, USA, 23–25 April 2013.
- Tegedor, J.; Øvstedal, O.; Vigen, E. Precise orbit determination and point positioning using GPS, Glonass, Galileo and BeiDou. J. Geod. Sci. 2014, 4. [Google Scholar] [CrossRef]
- Cai, C.; Gao, Y.; Pan, L.; Zhu, J. Precise point positioning with quad-constellations: GPS, BeiDou, GLONASS and Galileo. Adv. Space Res. 2015, 56, 133–143. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Liu, C. Heading estimation with real-time compensation based on kalman filter algorithm for an indoor positioning system. ISPRS Int. J. Geo-Inf. 2016, 5. [Google Scholar] [CrossRef]
- Li, X.; Wang, J.; Liu, C.; Zhang, L.; Li, Z.; Integrated, W. Fi/PDR/Smartphone using an adaptive system noise extended kalman filter algorithm for indoor localization. ISPRS Int. J. Geo-Inf. 2016, 5. [Google Scholar] [CrossRef]
- Wang, J.; Stewart, M.P.; Tsakiri, M. Stochastic modeling for static GPS baseline data processing. J. Surv. Eng. 1998, 124, 171–181. [Google Scholar] [CrossRef]
- Gao, C.; Wu, F.; Chen, W.; Wang, W. An improved weight stochastic model in GPS Precise Point positioning. In Proceedings of the 2011 International Conference On Transportation, Mechanical, and Electrical Engineering (TMEE), Changchun, China, 16–18 December 2011.
- Xu, Y.; Ji, S. Data quality assessment and the positioning performance analysis of BeiDou in Hong Kong. Surv. Rev. 2015, 47, 446–457. [Google Scholar] [CrossRef]
- Xu, Y.; Ji, S.; Chen, W.; Weng, D. A new ionosphere-free ambiguity resolution method for long-range baseline with GNSS triple-frequency signals. Adv. Space Res. 2015, 56, 1600–1612. [Google Scholar] [CrossRef]
- Collins, J.P.; Langley, R.B. A Tropospheric Delay Model for the User of the Wide Area Augmentation System; Department of Geodesy and Geomatics Engineering, University of New Brunswick: Fredericton, NB, Canada, 1997. [Google Scholar]
- Wu, S.C.; Yunck, T.P.; Thornton, C.L. Reduced-dynamic technique for precise orbit determination of low Earth satellites. J. Guid. Contr. Dyn. 1991, 14, 24–30. [Google Scholar] [CrossRef]
- Kouba, J.; Héroux, P. Precise point positioning using IGS orbit and clock products. GPS Solut. 2001, 5, 12–28. [Google Scholar] [CrossRef]
- Niell, A.E. Improved atmospheric mapping functions for VLBI and GPS. Earth Planets Space 2000, 52, 699–702. [Google Scholar] [CrossRef]




| Common Name | Int. Satellite ID | Pseudo Random Noise (PRN) | Notes |
|---|---|---|---|
| BEIDOU M1 | 2007-011A | C30 | Not in operation |
| BEIDOU G2 | 2009-018A | C02 | Not in operation |
| BEIDOU G1 | 2010-001A | C01 | GEO 140.0°E |
| BEIDOU G3 | 2010-024A | C03 | GEO 110.5°E |
| BEIDOU G4 | 2010-057A | C04 | GEO 160.0°E |
| BEIDOU IGSO 1 | 2010-036A | C06 | IGSO 120°E |
| BEIDOU IGSO 2 | 2010-068A | C07 | IGSO 120°E |
| BEIDOU IGSO 3 | 2011-013A | C08 | IGSO 120°E |
| BEIDOU IGSO 4 | 2011-038A | C09 | IGSO 95°E |
| BEIDOU IGSO 5 | 2011-073A | C10 | IGSO 95°E |
| BEIDOU G5 | 2012-008A | C05 | GEO 58.75°E |
| BEIDOU M3 | 2012-018A | C11 | MEO |
| BEIDOU M4 | 2012-018B | C12 | MEO |
| BEIDOU M5 | 2012-050A | C13 | Not in operation |
| BEIDOU M6 | 2012-050B | C14 | MEO |
| BEIDOU G6 | 2012-059A | C02 | GEO 80.3°E |
| BEIDOU I1-S | 2015 | C31 | IGSO |
| BDS M1-S | 2015 | C34 | MEO |
| BDS M2-S | 2015 | C33 | MEO |
| BDS I2-S | 2015 | C32 | IGSO |
| BDS M3-S | 2016 | C35 | MEO |
| BEIDOU IGSO 6 | 2016 | C15 | IGSO |
| BEIDOU G7 | 2016 | C17 | GEO |
| Parameters | Model and Mitigation Methods |
|---|---|
| Ionospheric delay | Ionosphere-free combined observables |
| Tropospheric delay(dry part) | UNB3m model [32] |
| Receiver antenna PCO and PCV | IGS ANTEX |
| Satellite antenna PCO and PCV | IGS ANTEX |
| Solid earth tides | IERS2010 |
| Ocean loading | IERS2010 |
| Polar tides | IERS2010 |
| Phase wind-up effect | Wu model [33,34] |
| Receiver clock errors | Estimation, white noise |
| STD | ||
|---|---|---|
| N | E | |
| GPS | 0.045 | 0.085 |
| GPS/GLONASS | 0.040 | 0.080 |
| GPS/BDS | 0.013 | 0.050 |
| GPS/GLONASS/BDS | 0.009 | 0.022 |
| N | E | |
|---|---|---|
| GPS | 0.067 | 0.091 |
| GPS/GLONASS | 0.062 | 0.081 |
| GPS/BDS | 0.056 | 0.073 |
| GPS/GLONASS/BDS | 0.042 | 0.060 |
| GPS | GPS/BDS | GPS/GLONASS | GPS/GLONASS/BDS | |
|---|---|---|---|---|
| Mean convergence time (min) | 64.2 | 50.9 | 52.4 | 47.5 |
© 2017 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, X.; Gao, J. Kinematic Precise Point Positioning Using Multi-Constellation Global Navigation Satellite System (GNSS) Observations. ISPRS Int. J. Geo-Inf. 2017, 6, 6. https://doi.org/10.3390/ijgi6010006
Yu X, Gao J. Kinematic Precise Point Positioning Using Multi-Constellation Global Navigation Satellite System (GNSS) Observations. ISPRS International Journal of Geo-Information. 2017; 6(1):6. https://doi.org/10.3390/ijgi6010006
Chicago/Turabian StyleYu, Xidong, and Jingxiang Gao. 2017. "Kinematic Precise Point Positioning Using Multi-Constellation Global Navigation Satellite System (GNSS) Observations" ISPRS International Journal of Geo-Information 6, no. 1: 6. https://doi.org/10.3390/ijgi6010006
APA StyleYu, X., & Gao, J. (2017). Kinematic Precise Point Positioning Using Multi-Constellation Global Navigation Satellite System (GNSS) Observations. ISPRS International Journal of Geo-Information, 6(1), 6. https://doi.org/10.3390/ijgi6010006





