A Subdivision Method to Unify the Existing Latitude and Longitude Grids
Abstract
:1. Introduction
2. Latitude and Longitude Global Subdivision Grids
2.1. Classification of Latitude and Longitude Global Subdivision Grids
2.1.1. Equal Latitude and Longitude Global Grid System
- (a)
- The complexity of statistical analysis due to the difference in grid cell areas.
- (b)
- The system includes grid cell area deformation, shape deformation, and interior point positional errors incremented from equator to the poles.
- (c)
- The cell shape at the top and bottom of the grid system is triangular rather than rectangular.
2.1.2. Variable Latitude and Longitude Global Grid Systems
2.2. Industrial Applications of Latitude and Longitude Global Subdivision Grids
2.2.1. United States National Grid (USNG) and Its Application
2.2.2. World Geographic Reference System (Georef) and Its Application
2.2.3. Global Area Reference System (GARS) and Its Applications
2.2.4. Application of Location Identification
2.2.5. Navigation and Positioning Applications
3. Unifying Latitude and Longitude Global Regular Hierarchical Grids
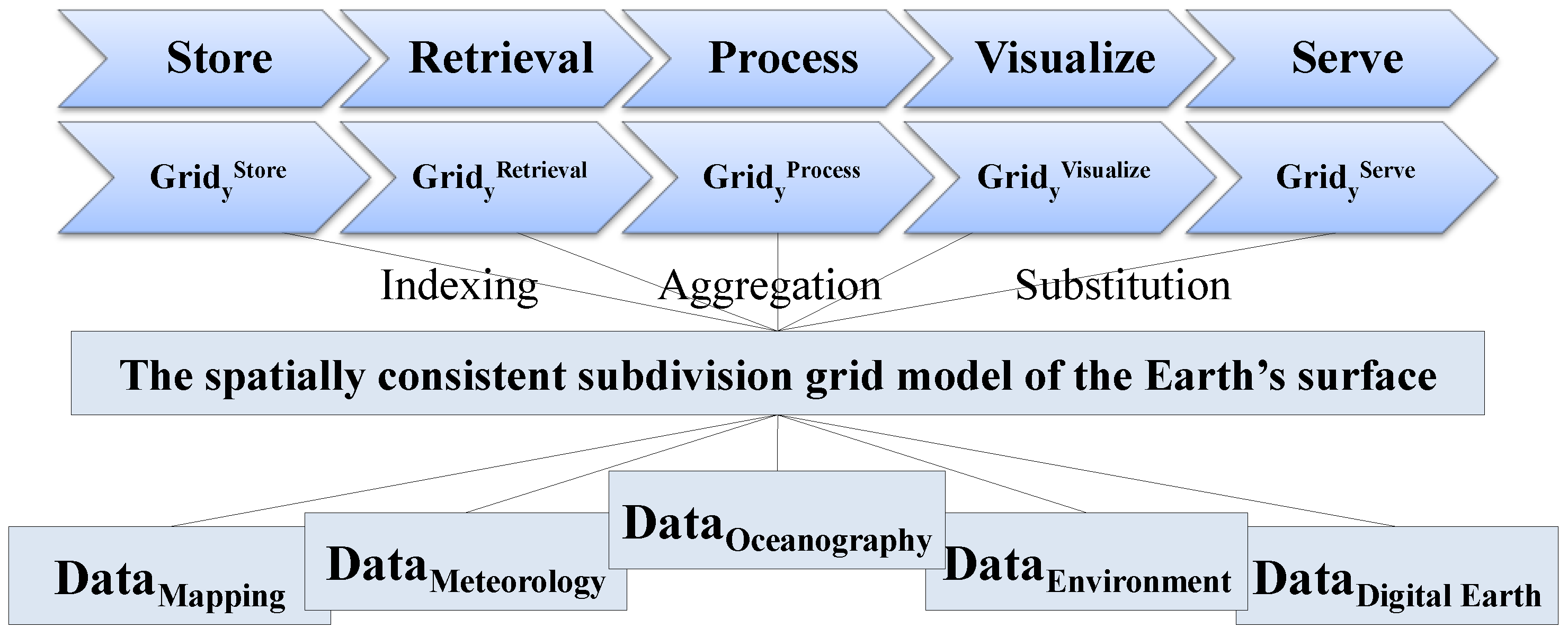
3.1. The Aim of Unifying the Current Latitude and Longitude Grids
3.1.1. Application Problems for Cross-Industry Grids
3.1.2. Application Problems for Cross Business Process Grids
3.2. Constraint Analysis of the Consistency of Latitude and Longitude Grid Model Designs
3.2.1. Definition and Characteristics of Latitude and Longitude Grid Models
3.2.2. Constraints for Constructing Consistent Latitude and Longitude Grid Models
- (1)
- use CGCS2000 as the basis for geospace;
- (2)
- inherit historical data where possible;
- (3)
- grid codes must be suitable for computer processing and convenient for human identification;
- (4)
- apply geodetic theory and technological systems comprehensively to spatial information organization and geographic object orientation;
- (5)
- include the eight basic grids, 4°, 2°, 1°, 2′, 1′, 2″, 1″ and 0.5″; and
- (6)
- the existing grids based on latitude and longitudes.
4. Geographical Coordinate Global Subdividing Grid with One Dimension Integer Coding on a 2n Tree (GeoSOT)
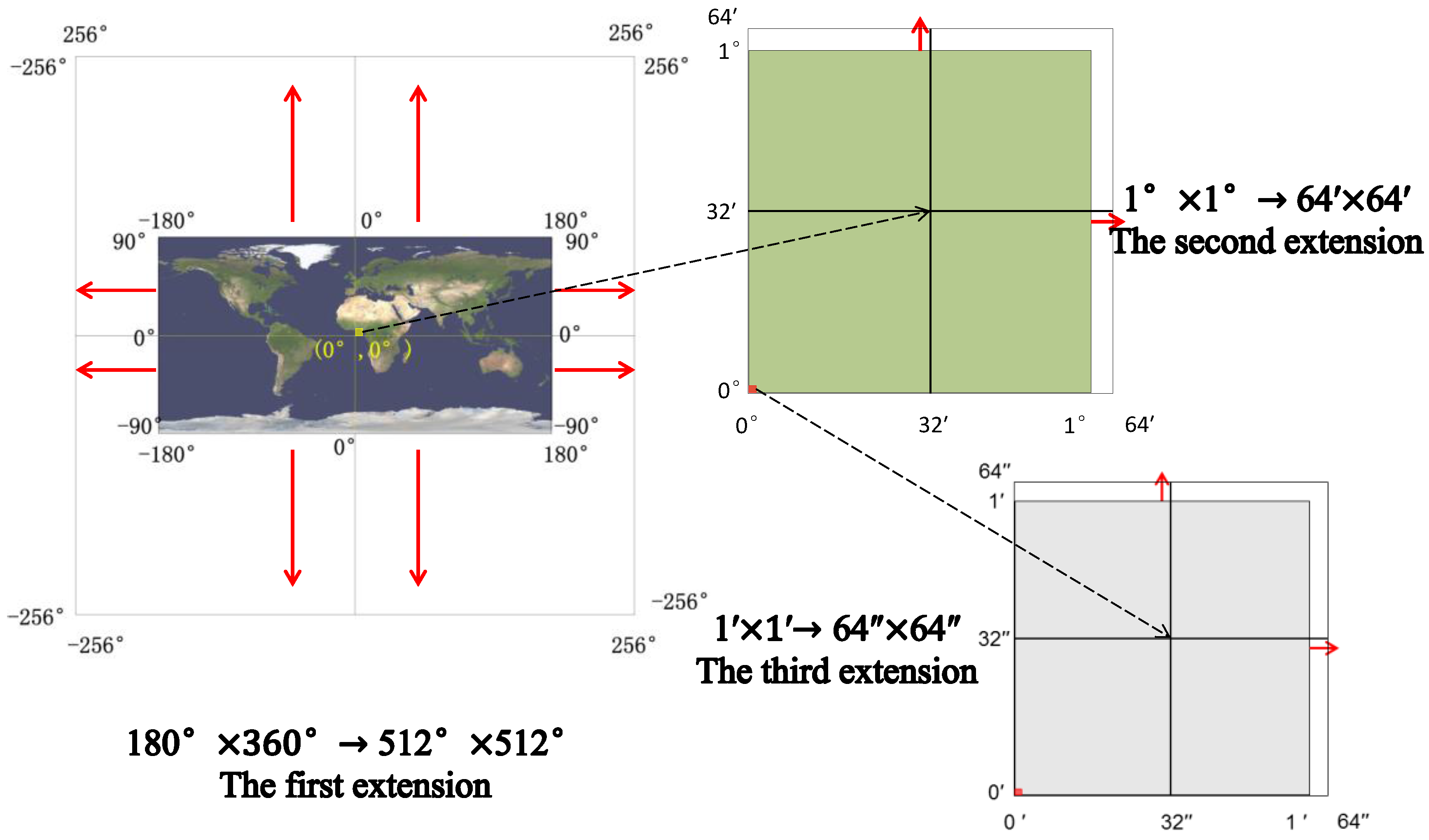
4.1. GeoSOT Subdivision
- (1)
- Divide the polar circles into two parts according to the hypothetical extension rule: on reaching the 1° level, extend from 1° to 64′ before dividing the polar circles.
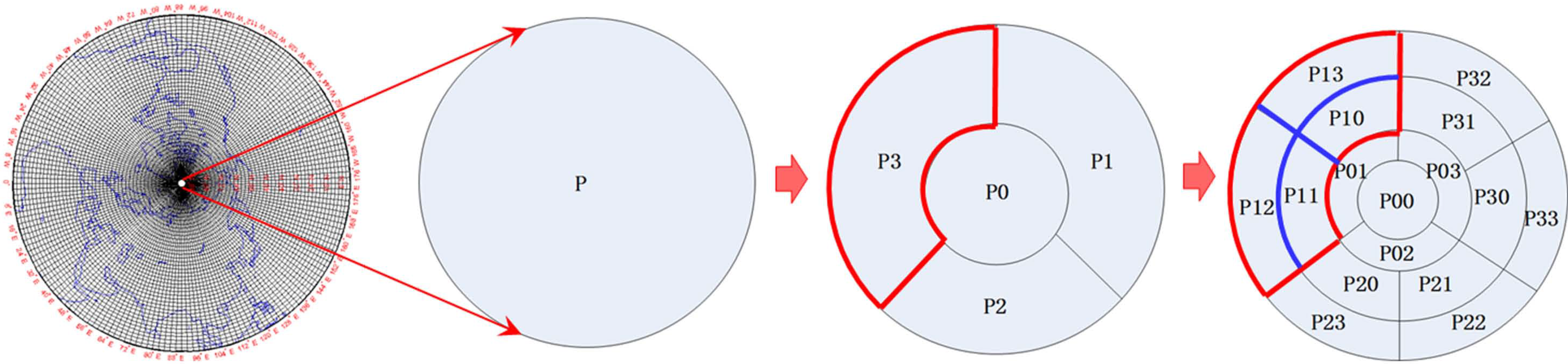
- (2)
- Define the inner circle where the poles are located as P0, and divide the outer circle into three parts along the prime meridian, longitude 120°E, and longitude 120°W. These parts are P1, P2 and P3, respectively, and form four cells together with P0. These four cells are almost equal in size.
- (3)
- From P1, P2 and P3, continue quadtree division, using a similar rule as for the GeoSOT: dividing after extending from 120° to 128°.
4.2. GeoSOT Grid and the Shape on a Sphere
5. Analysis of the Consistency between GeoSOT and Existing Latitude and Longitude Grids
5.1. The Principle behind Consistency between GeoSOT and the Latitude and Longitude Grids
5.2. Analysis of the Isomorphism of GeoSOT with Latitude and Longitude Grids with Absolute Degrees, Minutes, and Seconds
5.3. Analysis of the Isomorphism between GeoSOT and Traditional Map Sheet Grids
- (1)
- Equation (15-1): → . To satisfy , must be true. For the lowest level, , where ;
- (2)
- Equation (15-2): To satisfy , must be true. For the lowest level, , where ;
- (3)
- Equation (15-3): . To satisfy , must be true. For the lowest level, ;
- (4)
- Equation (15-4): → To satisfy , must be true. For the lowest level, , where .
5.4. Analysis of the Isomorphism between GeoSOT and Existing Digital Earth Grids
- (1)
- Equation (18-1): →. To satisfy , must be true. For the lowest level, , where ;
- (2)
- Equation (18-2): →. To satisfy must be true. For the lowest level, , where ;
- (3)
- Equation (18-3): →. To satisfy , must be true. For the lowest level,, where .
5.5. Analysis of Weak Isomorphism between Existing Digital Earth Grids and Traditional Map Sheet Grids
6. Conclusions and Future Work
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhou, C.; Yang, O.U.; Ting, M.A. Progresses of Geographical grid systems researches. Prog. Geogr. 2009, 28, 657–662. [Google Scholar]
- Cheng, C. The global subdivision grid based on extended mapping division and its address coding. Acta Geod. Cartogr. Sin. 2010, 39, 295–302. [Google Scholar]
- Du, Y. Study the Key Technologies of Global Multi-Resolution Virtual Terrain; Zhengzhou Institute of Surveying & Mapping: Zhengzhou, China, 2005. [Google Scholar]
- Geng, X.H.; Cheng, C.Q.; Song, S.H.; Li, D.P. Global subdivision systems based on map kilo-grids. Geogr. Geo-Inf. Sci. 2010, 26, 15–18. [Google Scholar]
- Li, L.; Zhu, X.; Cao, W. Geographic Grid; GB/T 12409–2009; Standards Press of China: Beijing, China, 2009. [Google Scholar]
- Goodchild, M.F. Discrete Global Grids for Digital Earth. Available online: http://www.ncgia.ucsb.edu/globalgrids/papers/goodchild.pdf (accessed on 13 June 2010).
- Sahr, K. Icosahedral Modified Generalized Balanced Ternary and Aperture 3 Hexagon Tree. U.S. Patent #07,876,967, 25 January 2011. [Google Scholar]
- Tong, X.; Ben, J.; Wang, Y.; Zhang, Y. Efficient encoding and spatial operation scheme for aperture 4 hexagonal discrete global grid system. Int. J. Geogr. Inf. Sci. 2013, 27, 898–921. [Google Scholar] [CrossRef]
- Mahdavi-Amiri, A.; Samavati, F.; Peterson, P. Categorization and conversions for indexing methods of discrete global grid systems. ISPRS Int. J. Geo-Inf. 2015, 4, 320–336. [Google Scholar] [CrossRef]
- Lukatela, H.; Lukatela, H. Hipparchus geopositioning model: An overview. In Proceedings of the Eighth International Symposium on Computer-Assisted Cartography, Baltimore, MD, USA, 29 March–3 April 1987.
- Mahdavi-Amiri, A.; Harrison, E.; Samavati, F. Hexagonal connectivity maps for digital earth. Int. J. Digit. Earth 2014, 8, 1–20. [Google Scholar] [CrossRef]
- Sahr, K. Location coding on icosahedral aperture 3 hexagon discrete global grids. Comput. Environ. Urban Syst. 2008, 32, 174–187. [Google Scholar] [CrossRef]
- Dutton, G.H. A Hierarchical Coordinate System for Geoprocessing and Cartography; Springer: Berlin, Germany, 1999. [Google Scholar]
- Mahdavi-Amiri, A.; Harrison, E.; Samavati, F. Hierarchical grid conversion. Comput. Aided Des. 2016, 79, 12–26. [Google Scholar] [CrossRef]
- National Aeronautics and Space Administration (NASA). World Wind. Available online: http://worldwind.arc.nasa.gov (accessed on 18 July 2011).
- Koller, D.; Lindstrom, P.; Ribarsky, W.; Hodges, L.F.; Faust, N.; Turner, G. Virtual GIS: A real-time 3D geographic information system. In Proceedings of the IEEE Conference on Visualization, Atlanta, GA, USA, 29 October–3 November 2011.
- Falby, J.S.; Zyda, M.J.; Pratt, D.R.; Mackey, R.L. NPSNET: Hierarchical data structures for real-time three-dimensional visual simulation. Comput. Graph. 2010, 17, 65–69. [Google Scholar] [CrossRef]
- Mahdavi-Amiri, A.; Alderson, T.; Samavati, F. A survey of digital earth. Comput. Graph. 2015, 53, 95–117. [Google Scholar] [CrossRef]
- Reddy, M.; Eriksen, M.; Leclerc, Y.; Brecht, J.; Colleen, D.; Reddy, M. SRI’s Digital Earth Project; Technical Note 560; SRI International: Menlo Park, CA, USA, 2002. [Google Scholar]
- Ottoson, P.; Hauska, H. Ellipsoidal quadtrees for indexing of global geographical data. Int. J. Geogr. Inf. Sci. 2002, 16, 213–226. [Google Scholar] [CrossRef]
- Gong, J. Advances in Data Processing and Analysis of Earth Observation; Wuhan University Press: Wuhan, China, 2007. [Google Scholar]
- Federation of American Scientists (FAS). Digital Terrain Elevation Data. Available online: http://fas.org/irp/program/core/dted.htm (accessed on 24 January 2008).
- Bjørke, J.T.; Grytten, J.K.; Hager, M.; Nilsen, S. A global grid model based on “constant area” quadrilaterals. In Proceedings of the Scangis’2003—The Scandinavian Research Conference on Geographical Information Science, Espoo, Finland, 4–6 June 2003.
- Purse, M.; Oliver, S.; Lewis, A.; Minchin, S.; Wyborn, L.; Gibb, R.; Fraser, A.; Evans, B. Specification of a global nested grid system for use by Australia and New Zealand. In Proceedings of the 7th eResearch Australasia Conference, Brisbane, Australia, 20–25 October 2013.
- Mahdavi-Amiri, A.; Bhojani, F.; Samavati, F. One-to-two digital earth. Adv. Vis. Comput. 2013, 8034, 681–692. [Google Scholar]
- Gorski, K.M.; Hivon, E.; Banday, A.J.; Wandelt, B.D.; Hansen, F.K.; Reinecke, M.; Bartelman, M. HEALPix—A framework for high resolution discretization, and fast analysis of data distributed on the sphere. Astrophys. J. 2005, 622, 759–771. [Google Scholar] [CrossRef]
- Zhou, M.; Chen, J.; Gong, J. A pole-oriented discrete global grid system: Quaternary quadrangle mesh. Comput. Geosci. 2013, 61, 133–143. [Google Scholar] [CrossRef]
- International Satellite Cloud Climatology Project (ISCCP). ISCCP Map Grid Information. Available online: http://isccp.giss.nasa.gov/docs/mapgridinfo.html (accessed on 23 July 2014).
- Network Control Language (NCL). POP Grid. Available online: http://www.ncl.ucar.edu/Applications/popgrid.shtml (accessed on 18 March 2015).
- Network Control Language (NCL). ORCA Grid. Available online: http://www.ncl.ucar.edu/Applications/orca.shtml (accessed on 18 March 2015).
- United States National Guard (USNG). U.S. National Grid Information Center. Available online: http://www.usngcenter.org (accessed on 3 September 2016).
- The Department of the Army (DA). Map Reading and Land Navigation: FM 3-25.26. Available online: https://www.amazon.com/Map-Reading-Land-Navigation-3-25-26/dp/1460970837 (accessed on 6 September 2016).
- National Graphical Association (NGA). GARS. Available online: http://earth-info.nga.mil/GandG/coordsys/grids/gars.html (accessed on 15 September 2014).
- Lu, N. Research on Navigation Grid Code; Peking University: Beijing, China, 2013. [Google Scholar]
- Lu, Y.; Liu, X.; Guo, Y. Subdivision and Numbering for the National Primary Scale Topographic Maps; GB/T 13989–2012; Standards Press of China: Beijing, China, 2012. [Google Scholar]

| Scale | Size of Grid | Frequency of Longitude (m) | Frequency of Latitude (m) | Aperture | RBasic | |
|---|---|---|---|---|---|---|
| Global | 360° × 180° * | 60 | 45 | 2700 | - | - |
| 1:1,000,000 | 6° × 4° | 2 | 2 | 4 | 2° × 2° | (3, 2) |
| 1:500,000 | 3° × 2° | 2 | 2 | 4 | 1° × 1° | (3, 2) |
| 1:250,000 | 1°30′ × 1° | 3 | 3 | 9 | 30′ × 30′ | (3, 2) |
| 1:100,000 | 30′ × 20′ | 2 | 2 | 4 | 10′ × 10′ | (3, 2) |
| 1:50,000 | 15′ × 10′ | 2 | 2 | 4 | 5′ × 5′ | (3, 2) |
| 1:25,000 | 7′30″ × 5′ | 2 | 2 | 4 | 30″ × 30″ | (15, 10) |
| 1:10,000 | 3′45″ × 2′30″ | 2 | 2 | 4 | 5″ × 5″ | (45, 30) |
| 1:5,000 | 1′52.5″ × 1′15″ | - | - | - | 0.5″ × 0.5″ | (225, 150) |
| National Basic Scale Map Range | Standard Scale | Inclusion Condition for Basic Grids | ||
|---|---|---|---|---|
| Exclusion condition for combined map | Difference in longitude | Difference in latitude | ||
| 6° | 4° | 1:1,000,000 | 3 × 2 = 6 2° grids | |
| 3° | 2° | 1:500,000 | 3 × 2 = 6 1° grids | |
| 1°30′ | 1° | 1:250,000 | 45 × 30 = 1350 2′ grids | |
| 30′ | 20′ | 1:100,000 | 15 × 10 = 150 2′ grids | |
| 15′ | 10′ | 1:50,000 | 15 × 10 = 150 1′ grids | |
| 7′30″ | 5′ | 1:25,000 | 225 × 150 = 33,750 2″ grids | |
| 3′45″ | 2′30″ | 1:10,000 | 225 × 150 = 33,750 1″ grids | |
| 1′52.5″ | 1′15″ | 1:5,000 | 225 × 150 = 33,750 0.5″ grids | |
| Level | Size of Grid | Frequency of Longitude (m) | Frequency of Latitude (m) | Aperture | RBasic | |
|---|---|---|---|---|---|---|
| 0 | 360° × 180° | 36 | 18 | 648 | - | - |
| 1 | 10° × 10° | 10 | 10 | 100 | 10° × 10° | (1, 1) |
| 2 | 1° × 1° | 6 | 6 | 36 | 1° × 1° | (1, 1) |
| 3 | 10′ × 10′ | 10 | 10 | 100 | 10′ × 10′ | (1, 1) |
| 4 | 1′ × 1′ | 6 | 6 | 36 | 1′ × 1′ | (1, 1) |
| 5 | 10″ × 10″ | 10 | 10 | 100 | 10″ × 10″ | (1, 1) |
| 6 | 1″ × 1″ | - | - | - | 1″ × 1″ | (1, 1) |
| National Geographic Grid | Inclusion Condition for Basic Grids | |
|---|---|---|
| Difference in Latitude | Difference in Longitude | |
| 10° | 10° | 5 × 5 = 25 2° grids |
| 1° | 1° | 1 × 1 = 1 1° grids |
| 10′ | 10′ | 5 × 5 = 25 2′ grids |
| 1′ | 1′ | 1 × 1 = 1 1′ grids |
| 10″ | 10″ | 5 × 5 = 25 2″ grids |
| 1″ | 1″ | 1 × 1 = 1 of 1″ grids |
| Level | Size of Grids | Possible Grid Shapes of the GeoSOT Subdivision Grid on a Spherical Surface | Level | Size of Grids | Possible Grid Shapes of the GeoSOT Subdivision Grid on a Spherical Surface |
|---|---|---|---|---|---|
| G | 512° grid | 180° × 360° | |||
| 1 | 256° grid | 90° × 180° | 17 | 16″ grid | 16″ × 16″, 12″ × 16″, 16″ × 12″, 12″ × 12″ |
| 2 | 128° grid | 90° × 128°, 90° × 52° | 18 | 8″ grid | 8″ × 8″, 4″ × 8″, 8″ × 4″, 4″ × 4″ |
| 3 | 64° grid | 64° × 64°, 26° × 64°, 64° × 52°, 26° × 52° | 19 | 4″ grid | 4″ × 4″ |
| 4 | 32° grid | 32° × 32°, 26° × 32°, 32° × 20°, 26° × 20° | 20 | 2″ grid | 2″ × 2″ |
| 5 | 16° grid | 16° × 16°, 10° × 16°, 16° × 4°, 10° × 4° | 21 | 1″ grid | 1″ × 1″ |
| 6 | 8° grid | 8° × 8°, 8° × 4° | 22 | 1/2″ grid | 1/2″ × 1/2″ |
| 7 | 4° grid | 4° × 4° | 23 | 1/4″ grid | 1/4″ × 1/4″ |
| 8 | 2° grid | 2° × 2° | 24 | 1/8″ grid | 1/8″ × 1/8″ |
| 9 | 1° grid | 1° × 1° | 25 | 1/16″ grid | 1/16″ × 1/16″ |
| 10 | 32′ grid | 32′ × 32′, 28′ × 32′, 32′ × 28′, 28′ × 28′ | 26 | 1/32″ grid | 1/32″ × 1/32″ |
| 11 | 16′ grid | 16′ × 16′, 12′ × 16′, 16′ × 12′, 12′ × 12′ | 27 | 1/64″ grid | 1/64″ × 1/64″ |
| 12 | 8′ grid | 8′ × 8′, 4′ × 8′, 8′ × 4′, 4′ × 4′ | 28 | 1/128″ grid | 1/128″ × 1/128″ |
| 13 | 4′ grid | 4′ × 4′ | 29 | 1/256″ grid | 1/256″ × 1/256″ |
| 14 | 2′ grid | 2′ × 2′ | 30 | 1/512″ grid | 1/512″ × 1/512″ |
| 15 | 1′ grid | 1′ × 1′ | 31 | 1/1024″ grid | 1/1024″ × 1/1024″ |
| 16 | 32″ grid | 32″ × 32″, 28″ × 32″, 32″ × 28″, 28″ × 28″ | 32 | 1/2048″ grid | 1/2048″ × 1/2048″ |
| Level | Size of Grid | Possible Grid Shapes of the Subdivision Grid on a Sphere (Except for the Polar Point Cells) |
|---|---|---|
| 8 | 128° × 1° | 120° × 1° |
| 9 | 64° × 32′ | 64° × 32′, 56° × 32′, 64° × 28′, 56° × 28′ |
| 10 | 32° × 16′ | 32° × 16′, 24° × 16′, 32° × 12′, 24° × 12′ |
| 11 | 16° × 8′ | 16° × 8′, 16° × 4′, 8° × 8′, 8° × 4′ |
| 12 | 8° × 4′ | 8° × 4′ |
| 13 | 4° × 2′ | 4° × 2′ |
| 14 | 2° × 1′ | 2° × 1′ |
| 15 | 1° × 32″ | 1° × 32″, 1° × 28″ |
| 16 | Below this level, rules are as for the GeoSOT grid. | |
| Level | Grid Size | Approximate Dimension Near the Equator | Quantity | Level | Grid Size | Approximate Dimension Near the Equator | Quantity |
|---|---|---|---|---|---|---|---|
| G | 512° specification | Global region | 1 | ||||
| 1 | 256° specification | 1/4 global region | 4 | 17 | 16″ specification | 512 m specification | 3,649,536,000 |
| 2 | 128° specification | 8 | 18 | 8″ specification | 256 m specification | 14,598,144,000 | |
| 3 | 64° specification | 24 | 19 | 4″ specification | 128 m specification | 51,321,600,000 | |
| 4 | 32° specification | 72 | 20 | 2″ specification | 64 m specification | 205,286,400,000 | |
| 5 | 16° specification | 288 | 21 | 1″ specification | 32 m specification | 821,145,600,000 | |
| 6 | 8° specification | 1024 km specification | 1012 | 22 | 1/2″ specification | 16 m specification | 3,284,582,400,000 |
| 7 | 4° specification | 512 km specification | 3960 | 23 | 1/4″ specification | 8 m specification | 13,138,329,600,000 |
| 8 | 2° specification | 256 km specification | 15,840 | 24 | 1/8″ specification | 4 m specification | 52,553,318,400,000 |
| 9 | 1° specification | 128 km specification | 63,360 | 25 | 1/16″ specification | 2 m specification | 210,213,273,600,000 |
| 10 | 32′ specification | 64 km specification | 253,440 | 26 | 1/32″ specification | 1 m specification | 840,853,094,400,000 |
| 11 | 16′ specification | 32 km specification | 1013,760 | 27 | 1/64″ specification | 0.5 m specification | 3,363,412,377,600,000 |
| 12 | 8′ specification | 16 km specification | 4,055,040 | 28 | 1/128″ specification | 25 cm specification | 13,453,649,510,400,000 |
| 13 | 4′ specification | 8 km specification | 14,256,000 | 29 | 1/256″ specification | 12.5 cm specification | 53,814,598,041,600,000 |
| 14 | 2′ specification | 4 km specification | 57,024,000 | 30 | 1/512″ specification | 6.2 cm specification | 215,258,392,166,400,000 |
| 15 | 1′ specification | 2 km specification | 228,096,000 | 31 | 1/1024″ specification | 3.1 cm specification | 861,033,568,665,600,000 |
| 16 | 32″ specification | 1 km specification | 912,384,000 | 32 | 1/2048″ specification | 1.5 cm specification | 3,444,134,274,662,400,000 |
| k | k1 | X | k2 | Y | k0 |
|---|---|---|---|---|---|
| 1 | 8 | 3 | 8 | 2 | 8 |
| 2 | 9 | 3 | 9 | 2 | 9 |
| 3 | 14 | 45 | 14 | 30 | 14 |
| 4 | 14 | 15 | 14 | 10 | 14 |
| 5 | 15 | 15 | 15 | 10 | 15 |
| 6 | 20 | 225 | 20 | 150 | 20 |
| 7 | 21 | 225 | 21 | 150 | 21 |
| 8 | 22 | 225 | 22 | 150 | 22 |
| Level | Grid Size | Grid Number |
|---|---|---|
| 0 | 360° × 180° | 1 |
| 1 | 36° × 36° | 10 × 5 |
| 2 | 18° × 18° | 20 × 10 |
| 3 | 9° × 9° | 40 × 20 |
| 4 | 4°30’ × 4°30’ | 80 × 40 |
| 5 | 2°15’ × 2°15’ | 160 × 80 |
| 6 | 1°7’30’’ × 1°7’30’’ | 320 × 160 |
| 7 | 33’45’’ × 33’45’’ | 640 × 320 |
| 8 | 16’52.5’’ × 16’52.5’’ | 1280 × 640 |
| 9 | 8’26.25’’ × 8’26.25’’ | 2560 × 1280 |
| … | … | … |
| k | k1 | X | k2 | Y | k0 |
|---|---|---|---|---|---|
| 1 | 7 | 9 | 7 | 9 | 9 |
| 2 | 8 | 9 | 8 | 9 | 9 |
| 3 | 9 | 9 | 9 | 9 | 9 |
| 4 | 14 | 135 | 14 | 135 | 135 |
| 5 | 15 | 135 | 15 | 135 | 135 |
| 6 | 20 | 2025 | 20 | 2025 | 2025 |
| 7 | 21 | 2025 | 21 | 2025 | 2025 |
| 8 | 22 | 2025 | 22 | 2025 | 2025 |
| 9 | 23 | 2025 | 23 | 2025 | 2025 |
| … | … | … | … | … | … |
| Scale | Map Range | Aggregation of nth Level | The Grid Range of the nth Level for GeoSOT | Aggregation Number | Approximation Error |
|---|---|---|---|---|---|
| 1:1,000,000 | 6° × 4° | after 8th Level | 2° × 2° | 3 × 2 | 0% |
| 1:500,000 | 3° × 2° | after 9th Level | 1° × 1° | 3 × 2 | 0% |
| 1:250,000 | 1°30’ × 1° | after 14th Level | 2’ × 2’ | 45 × 30 | 0% |
| 1:100,000 | 30’ × 20’ | after 14th Level | 2’ × 2’ | 15 × 10 | 0% |
| 1:50,000 | 15’ × 10’ | after 15th Level | 1’ × 1’ | 15 × 10 | 0% |
| 1:25,000 | 7’30’’ × 5’ | after 20th Level | 2’’ × 2’’ | 225 × 150 | 0% |
| 1:10,000 | 3’45’’ × 2’30’’ | after 21th Level | 1’’ × 1’’ | 225 × 150 | 0% |
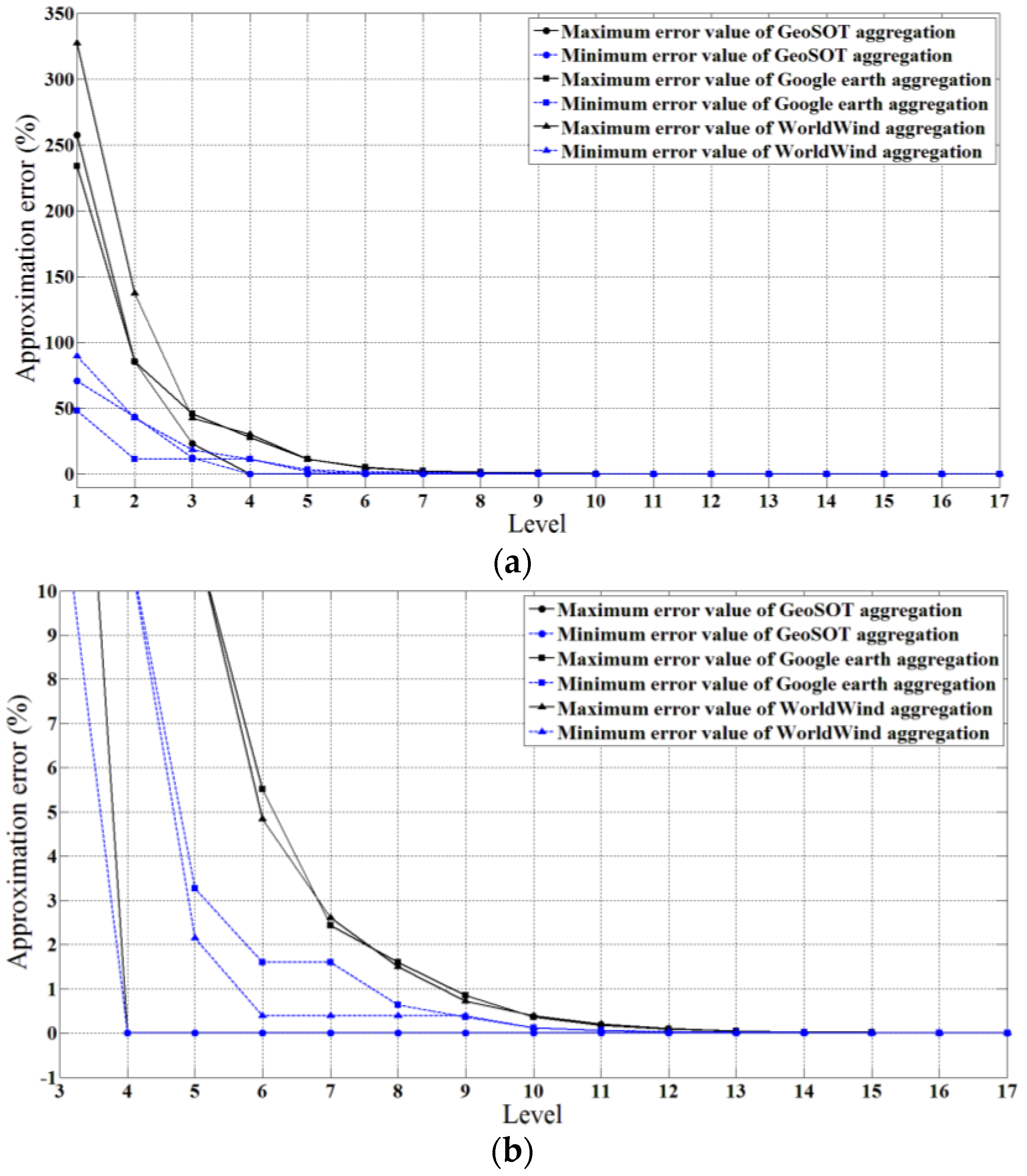
| Scale | Map Range | Aggregation of nth Level | The Grid Range of the nth Level for World Wind | Aggregation Number | Approximation Error |
|---|---|---|---|---|---|
| 1:1,000,000 | 6° × 4° | 4 | 4°30’ × 4°30’ | 2, 4 | 68.75%~237.5% |
| 1:1,000,000 | 6° × 4° | 5 | 2°15’ × 2°15’ | 6, 8, 9, 12 | 26.56%~153.13% |
| 1:1,000,000 | 6° × 4° | 6 | 1°7’30’’ × 1°7’30’’ | 24, 30 | 26.56%~58.20% |
| 1:1,000,000 | 6° × 4° | 7 | 33’45’’ × 33’45’’ | 88, 96 | 16.02%~26.56% |
| 1:1,000,000 | 6° × 4° | 8 | 16’52.5’’ × 16’52.5’’ | 330, 352 | 8.76%~16.02% |
| 1:1,000,000 | 6° × 4° | 9 | 8’26.25’’ × 8’26.25’’ | 1247, 1276, 1290, 1320 | 2.75%~8.76% |
| 1:500,000 | 3° × 2° | 5 | 2°15’ × 2°15’ | 2, 4 | 68.75%~237.5% |
| 1:500,000 | 3° × 2° | 6 | 1°7’30’’ × 1°7’30’’ | 6, 8, 9, 12 | 26.56%~153.13% |
| 1:500,000 | 3° × 2° | 7 | 33’45’’ × 33’45’’ | 24, 30 | 26.56%~58.20% |
| 1:500,000 | 3° × 2° | 8 | 16’52.5’’ × 16’52.5’’ | 88, 96 | 16.02%~26.56% |
| 1:500,000 | 3° × 2° | 9 | 8’26.25’’ × 8’26.25’’ | 330, 352 | 8.76%~16.02% |
| 1:500,000 | 3° × 2° | 10 | 4’13.125’’ × 4’13.125’’ | 1247, 1276, 1290, 1320 | 2.75%~8.76% |
| 1:250,000 | 1°30’ × 1° | 6 | 1°7’30’’ × 1°7’30’’ | 2, 4 | 68.75%~237.5% |
| 1:250,000 | 1°30’ × 1° | 7 | 33’45’’ × 33’45’’ | 6, 8, 9, 12 | 26.56%~153.13% |
| 1:250,000 | 1°30’ × 1° | 8 | 16’52.5’’ × 16’52.5’’ | 24, 30 | 26.56%~58.20% |
| 1:250,000 | 1°30’ × 1° | 9 | 8’26.25’’ × 8’26.25’’ | 88, 96 | 16.02%~26.56% |
| 1:250,000 | 1°30’ × 1° | 10 | 4’13.125’’ × 4’13.125’’ | 330, 352 | 8.76%~16.02% |
| 1:250,000 | 1°30’ × 1° | 11 | 2’6.5625’’ × 2’6.5625’’ | 1247, 1276, 1290, 1320 | 2.75%~8.76% |
| 1:100,000 | 30’ × 20’ | 8 | 16’52.5’’ × 16’52.5’’ | 4, 6, 9 | 89.84%~327.15% |
| 1:100,000 | 30’ × 20’ | 9 | 8’26.25’’ × 8’26.25’’ | 12, 15, 16, 20 | 42.38%~137.3% |
| 1:100,000 | 30’ × 20’ | 10 | 4’13.125’’ × 4’13.125’’ | 40, 48 | 18.65%~42.38% |
| 1:100,000 | 30’ × 20’ | 11 | 2’6.5625’’ × 2’6.5625’’ | 150, 160, 165, 176 | 11.24%~30.52% |
| 1:100,000 | 30’ × 20’ | 12 | 1’3.28125’’ × 1’3.28125’’ | 551, 570, 580, 600 | 2.15%~11.24% |
| 1:100,000 | 30’ × 20’ | 13 | 31.640625’’ × 31.640625’’ | 2166, 2204, 2223, 2262 | 0.39%~4.48% |
| 1:50,000 | 15’ × 10’ | 9 | 8’26.25’’ × 8’26.25’’ | 4, 6, 9 | 89.84%~327.15% |
| 1:50,000 | 15’ × 10’ | 10 | 4’13.125’’ × 4’13.125’’ | 12, 15, 16, 20 | 42.38%~137.3% |
| 1:50,000 | 15’ × 10’ | 11 | 2’6.5625’’ × 2’6.5625’’ | 40, 48 | 18.65%~42.38% |
| 1:50,000 | 15’ × 10’ | 12 | 1’3.28125’’ × 1’3.28125’’ | 150, 160, 165, 176 | 11.24%~30.52% |
| 1:50,000 | 15’ × 10’ | 13 | 31.640625’’ × 31.640625’’ | 551, 570, 580, 600 | 2.15%~11.24% |
| 1:50,000 | 15’ × 10’ | 14 | 15.8203125’’ × 15.8203125’’ | 2166, 2204, 2223, 2262 | 0.39%~4.48% |
| 1:25,000 | 7’30’’ × 5’ | 10 | 4’13.125’’ × 4’13.125’’ | 4, 6, 9 | 89.84%~327.15% |
| 1:25,000 | 7’30’’ × 5’ | 11 | 2’6.5625’’ × 2’6.5625’’ | 12, 15, 16, 20 | 42.38%~137.3% |
| 1:25,000 | 7’30’’ × 5’ | 12 | 1’3.28125’’ × 1’3.28125’’ | 40, 48 | 18.65%~42.38% |
| 1:25,000 | 7’30’’ × 5’ | 13 | 31.640625’’ × 31.640625’’ | 150, 160, 165, 176 | 11.24%~30.52% |
| 1:25,000 | 7’30’’ × 5’ | 14 | 15.8203125’’ × 15.8203125’’ | 551, 570, 580, 600 | 2.15%~11.24% |
| 1:25,000 | 7’30’’ × 5’ | 15 | 7.91015625’’ × 7.91015625’’ | 2166, 2204, 2223, 2262 | 0.39%~4.48% |
| 1:10,000 | 3’45’’ × 2’30’’ | 11 | 2’6.5625’’ × 2’6.5625’’ | 4, 6, 9 | 89.84%~327.15% |
| 1:10,000 | 3’45’’ × 2’30’’ | 12 | 1’3.28125’’ × 1’3.28125’’ | 12, 15, 16, 20 | 42.38%~137.3% |
| 1:10,000 | 3’45’’ × 2’30’’ | 13 | 31.640625’’ × 31.640625’’ | 40, 48 | 18.65%~42.38% |
| 1:10,000 | 3’45’’ × 2’30’’ | 14 | 15.8203125’’ × 15.8203125’’ | 150, 160, 165, 176 | 11.24%~30.52% |
| 1:10,000 | 3’45’’ × 2’30’’ | 15 | 7.91015625’’ × 7.91015625’’ | 551, 570, 580, 600 | 2.15%~11.24% |
| 1:10,000 | 3’45’’ × 2’30’’ | 16 | 3.955078125’’ × 3.955078125’’ | 2166, 2204, 2223, 2262 | 0.39%~4.48% |
| Scale | Map Range | Aggregation of nth Level | The Grid Range of the nth Level for Google Earth | Aggregation Number | Approximation Error |
|---|---|---|---|---|---|
| 1:1,000,000 | 6° × 4° | 6 | 5°37’30’’ × 2°48’45’’ | 4, 6 | 163.67%~295.51% |
| 1:1,000,000 | 6° × 4° | 7 | 2°48’45’’ × 1°24’22.5’’ | 9, 12, 16 | 48.32%~163.67% |
| 1:1,000,000 | 6° × 4° | 8 | 1°24’22.5’’ × 42’11.25’’ | 30, 35, 36, 42 | 23.60%~73.03% |
| 1:1,000,000 | 6° × 4° | 9 | 42’11.25’’ × 21’5.625’’ | 108, 117, 120, 130 | 11.24%~33.90% |
| 1:1,000,000 | 6° × 4° | 10 | 21’5.625’’ × 10’32.8125’’ | 414, 432 | 6.60%~11.24% |
| 1:1,000,000 | 6° × 4° | 11 | 10’32.8125’’ × 5’16.40625’’ | 1610, 1645, 1656, 1692 | 3.64%~8.92% |
| 1:500,000 | 3° × 2° | 7 | 2°48’45’’ × 1°24’22.5’’ | 4, 6 | 163.67%~295.51% |
| 1:500,000 | 3° × 2° | 8 | 1°24’22.5’’ × 42’11.25’’ | 9, 12, 16 | 48.32%~163.67% |
| 1:500,000 | 3° × 2° | 9 | 42’11.25’’ × 21’5.625’’ | 30, 35, 36, 42 | 23.60%~73.03% |
| 1:500,000 | 3° × 2° | 10 | 21’5.625’’ × 10’32.8125’’ | 108, 117, 120, 130 | 11.24%~33.90% |
| 1:500,000 | 3° × 2° | 11 | 10’32.8125’’ × 5’16.40625’’ | 414, 432 | 6.60%~11.24% |
| 1:500,000 | 3° × 2° | 12 | 5’16.40625’’ × 2’38.203125’’ | 1610, 1645, 1656, 1692 | 3.64%~8.92% |
| 1:250,000 | 1°30’ × 1° | 8 | 1°24’22.5’’ × 42’11.25’’ | 4, 6 | 163.67%~295.51% |
| 1:250,000 | 1°30’ × 1° | 9 | 42’11.25’’ × 21’5.625’’ | 9, 12, 16 | 48.32%~163.67% |
| 1:250,000 | 1°30’ × 1° | 10 | 21’5.625’’ × 10’32.8125’’ | 30, 35, 36, 42 | 23.60%~73.03% |
| 1:250,000 | 1°30’ × 1° | 11 | 10’32.8125’’ × 5’16.40625’’ | 108, 117, 120, 130 | 11.24%~33.90% |
| 1:250,000 | 1°30’ × 1° | 12 | 5’16.40625’’ × 2’38.203125’’ | 414, 432 | 6.60%~11.24% |
| 1:250,000 | 1°30’ × 1° | 13 | 2’38.203125’’ × 1’19.1015625’’ | 1610, 1645, 1656, 1692 | 3.64%~8.92% |
| 1:100,000 | 30’ × 20’ | 10 | 21’5.625’’ × 10’32.8125’’ | 4, 6, 9 | 48.32%~233.71% |
| 1:100,000 | 30’ × 20’ | 11 | 10’32.8125’’ × 5’16.40625’’ | 12, 15, 16, 20 | 11.24%~85.39% |
| 1:100,000 | 30’ × 20’ | 12 | 5’16.40625’’ × 2’38.203125’’ | 48, 54, 56, 63 | 11.24%~46% |
| 1:100,000 | 30’ × 20’ | 13 | 2’38.203125’’ × 1’19.1015625’’ | 192, 204, 208, 221 | 11.24%~28.04% |
| 1:100,000 | 30’ × 20’ | 14 | 1’19.1015625’’ × 39.55078125’’ | 713, 736, 744, 768 | 3.27%~11.24% |
| 1:100,000 | 30’ × 20’ | 15 | 39.55078125’’ × 19.775390625’’ | 2806, 2852, 2867, 2914 | 1.6%~5.52% |
| 1:50,000 | 15’ × 10’ | 11 | 10’32.8125’’ × 5’16.40625’’ | 4, 6, 9 | 48.32%~233.71% |
| 1:50,000 | 15’ × 10’ | 12 | 5’16.40625’’ × 2’38.203125’’ | 12, 15, 16, 20 | 11.24%~85.39% |
| 1:50,000 | 15’ × 10’ | 13 | 2’38.203125’’ × 1’19.1015625’’ | 48, 54, 56, 63 | 11.24%~46% |
| 1:50,000 | 15’ × 10’ | 14 | 1’19.1015625’’ × 39.55078125’’ | 192, 204, 208, 221 | 11.24%~28.04% |
| 1:50,000 | 15’ × 10’ | 15 | 39.55078125’’ × 19.775390625’’ | 713, 736, 744, 768 | 3.27%~11.24% |
| 1:50,000 | 15’ × 10’ | 16 | 19.775390625’’ × 9.8876953125’’ | 2806, 2852, 2867, 2914 | 1.6%~5.52% |
| 1:25,000 | 7’30’’ × 5’ | 12 | 5’16.40625’’ × 2’38.203125’’ | 4, 6, 9 | 48.32%~233.71% |
| 1:25,000 | 7’30’’ × 5’ | 13 | 2’38.203125’’ × 1’19.1015625’’ | 12, 15, 16, 20 | 11.24%~85.39% |
| 1:25,000 | 7’30’’ × 5’ | 14 | 1’19.1015625’’ × 39.55078125’’ | 48, 54, 56, 63 | 11.24%~46% |
| 1:25,000 | 7’30’’ × 5’ | 15 | 39.55078125’’ × 19.775390625’’ | 192, 204, 208, 221 | 11.24%~28.04% |
| 1:25,000 | 7’30’’ × 5’ | 16 | 19.775390625’’ × 9.8876953125’’ | 713, 736, 744, 768 | 3.27%~11.24% |
| 1:25,000 | 7’30’’ × 5’ | 17 | 9.8876953125’’ × 4.94384765625’’ | 2806, 2852, 2867, 2914 | 1.6%~5.52% |
| 1:10,000 | 3’45’’ × 2’30’’ | 13 | 2’38.203125’’ × 1’19.1015625’’ | 4, 6, 9 | 48.32%~233.71% |
| 1:10,000 | 3’45’’ × 2’30’’ | 14 | 1’19.1015625’’ × 39.55078125’’ | 12, 15, 16, 20 | 11.24%~85.39% |
| 1:10,000 | 3’45’’ × 2’30’’ | 15 | 39.55078125’’ × 19.775390625’’ | 48, 54, 56, 63 | 11.24%~46% |
| 1:10,000 | 3’45’’ × 2’30’’ | 16 | 19.775390625’’ × 9.8876953125’’ | 192, 204, 208, 221 | 11.24%~28.04% |
| 1:10,000 | 3’45’’ × 2’30’’ | 17 | 9.8876953125’’ × 4.94384765625’’ | 713, 736, 744, 768 | 3.27%~11.24% |
| 1:10,000 | 3’45’’ × 2’30’’ | 18 | 4.94384765625’’ × 2.471923828125’’ | 2806, 2852, 2867, 2914 | 1.6%~5.52% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, C.; Tong, X.; Chen, B.; Zhai, W. A Subdivision Method to Unify the Existing Latitude and Longitude Grids. ISPRS Int. J. Geo-Inf. 2016, 5, 161. https://doi.org/10.3390/ijgi5090161
Cheng C, Tong X, Chen B, Zhai W. A Subdivision Method to Unify the Existing Latitude and Longitude Grids. ISPRS International Journal of Geo-Information. 2016; 5(9):161. https://doi.org/10.3390/ijgi5090161
Chicago/Turabian StyleCheng, Chengqi, Xiaochong Tong, Bo Chen, and Weixin Zhai. 2016. "A Subdivision Method to Unify the Existing Latitude and Longitude Grids" ISPRS International Journal of Geo-Information 5, no. 9: 161. https://doi.org/10.3390/ijgi5090161
APA StyleCheng, C., Tong, X., Chen, B., & Zhai, W. (2016). A Subdivision Method to Unify the Existing Latitude and Longitude Grids. ISPRS International Journal of Geo-Information, 5(9), 161. https://doi.org/10.3390/ijgi5090161





