Automatic and Accurate Conflation of Different Road-Network Vector Data towards Multi-Modal Navigation
Abstract
:1. Introduction
2. Related Work
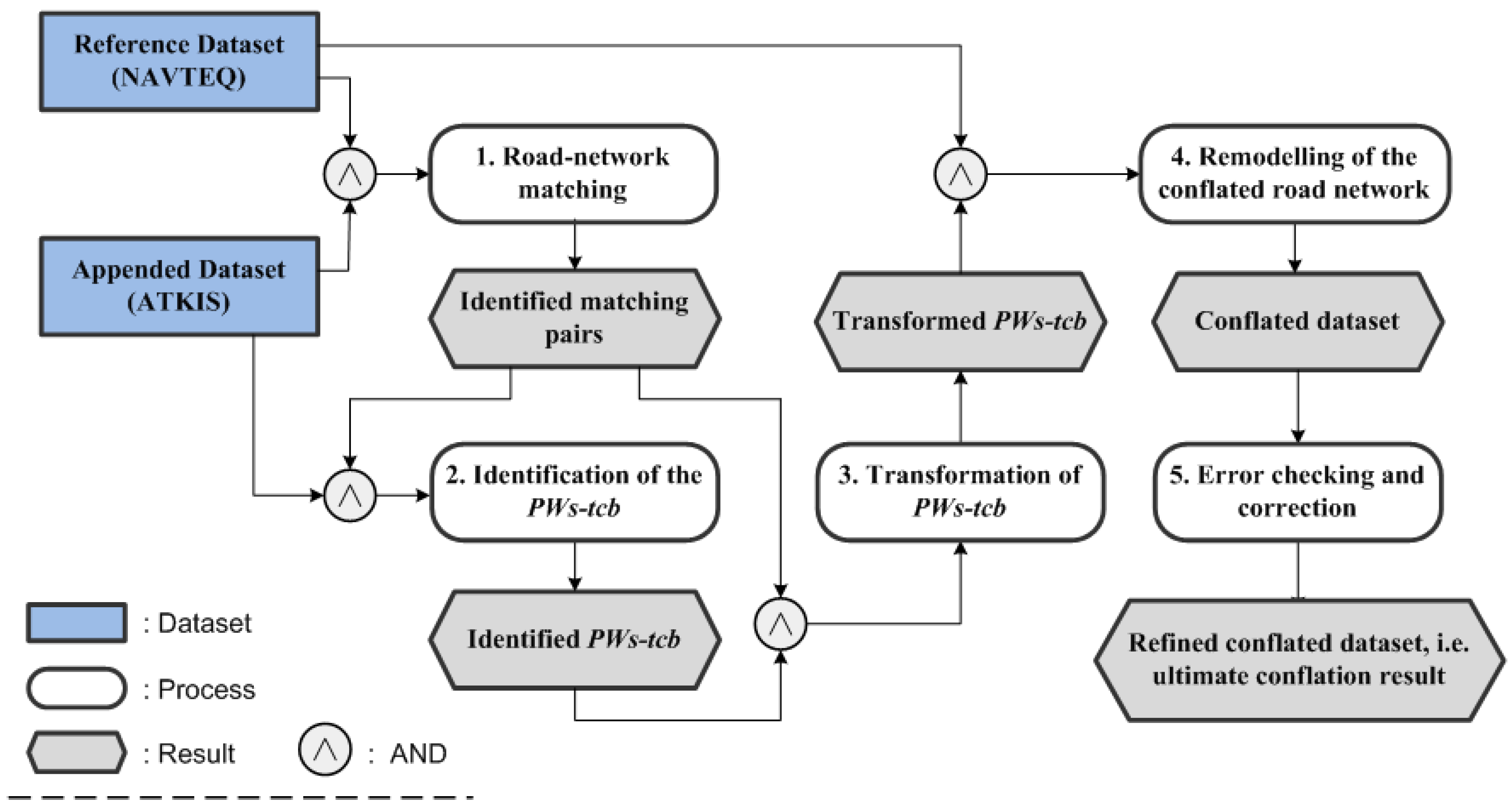
3. Strategy
3.1. Road-Network Matching between Participating Datasets
3.2. Identification of the PWs-Tbc in ATKIS
3.3. Transformation of PWs-tbc to Eliminate Geometric Inconsistency
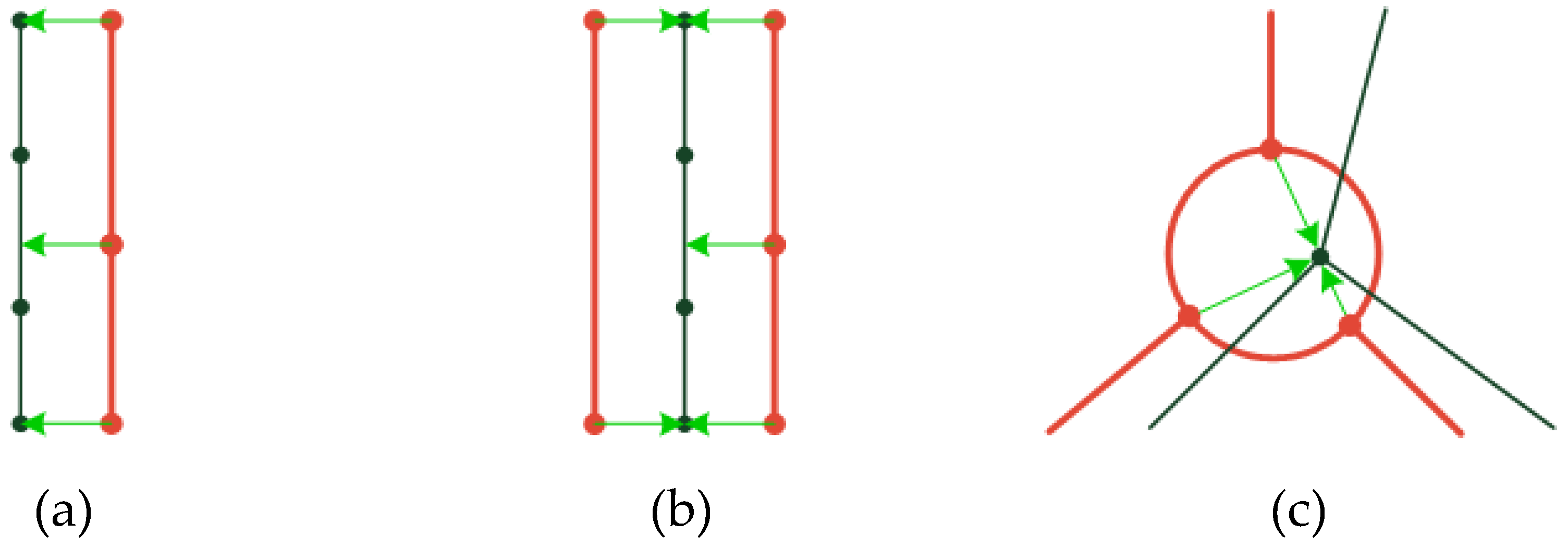
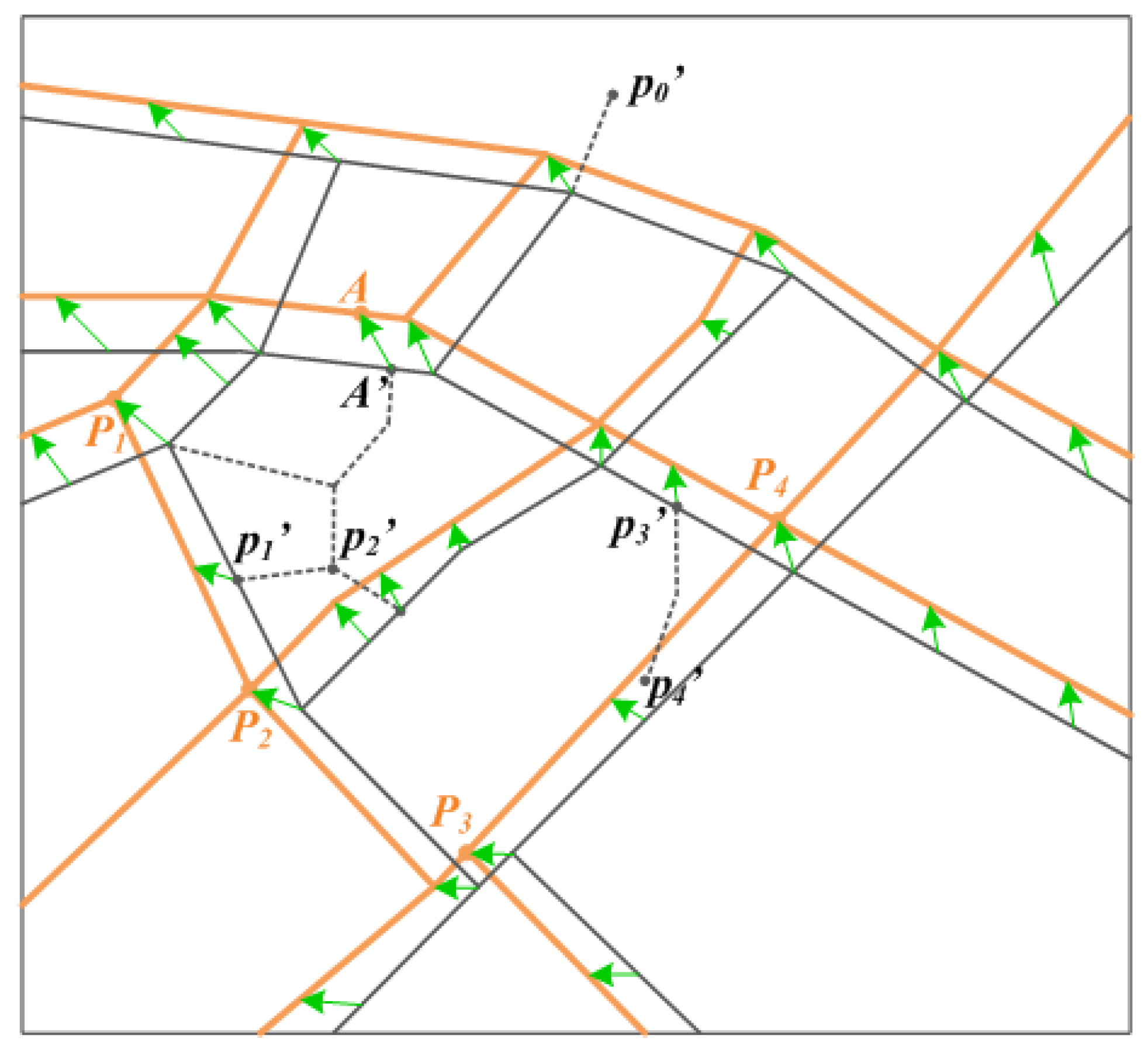
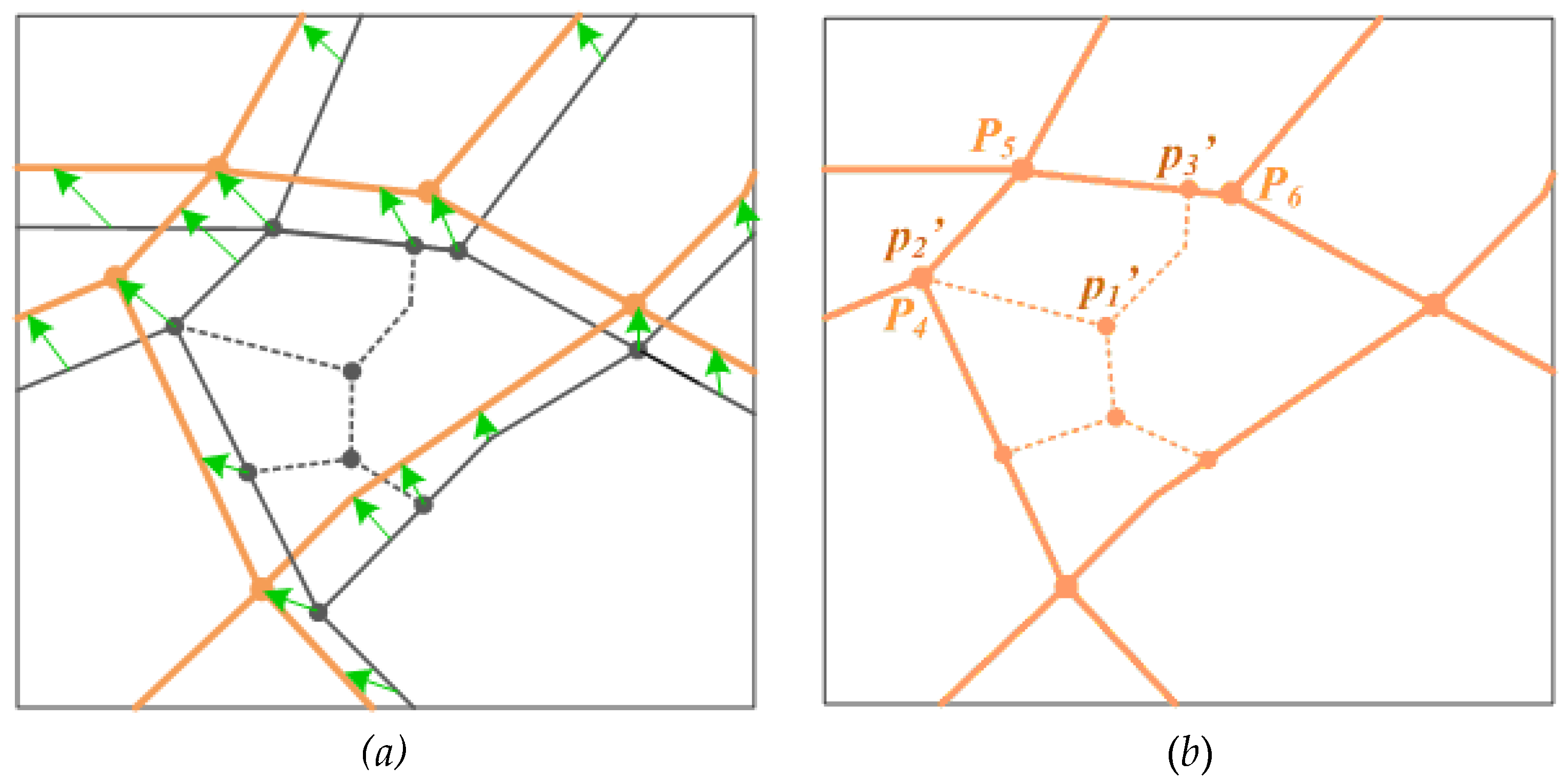
Step 1: Establishment of the control point pairs
Step 2: Alignment based on control point pairs
- (a) Turning points which are duplicated to the fromPoints of CPPs
- (b) Road crossings or dead ends which are not duplicated to the fromPoint of any CPP
- m—number of the neighbors of pi;
- n—number of the CPPs;
- α, β—two experimental coefficients larger than 0.
- (c) Other Turning points of the PWs-tbc.
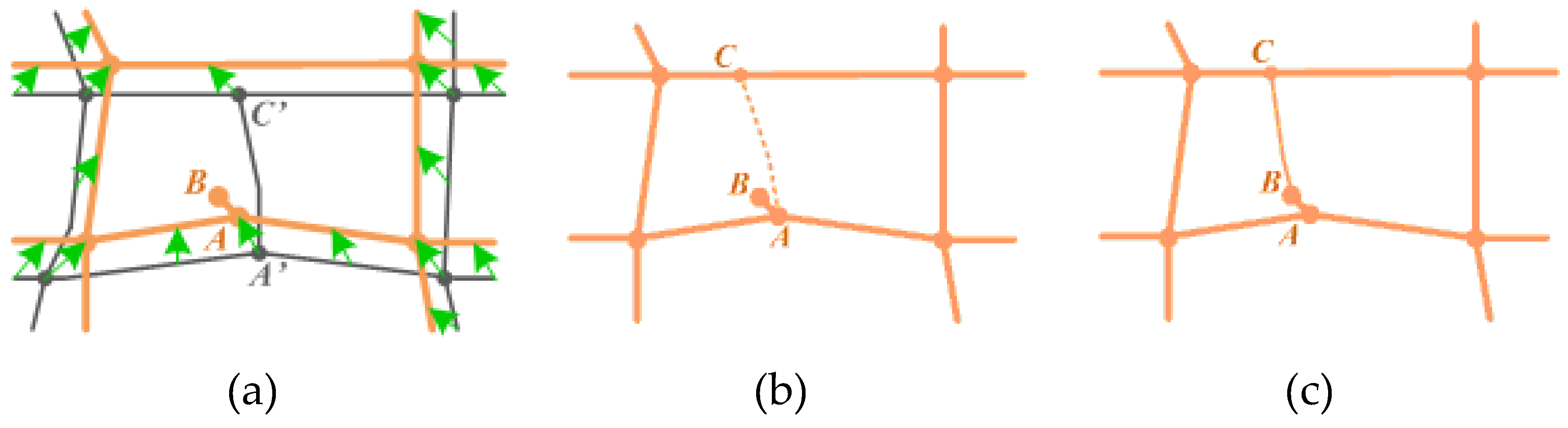
3.4. Remodelling of the Conflated Dataset
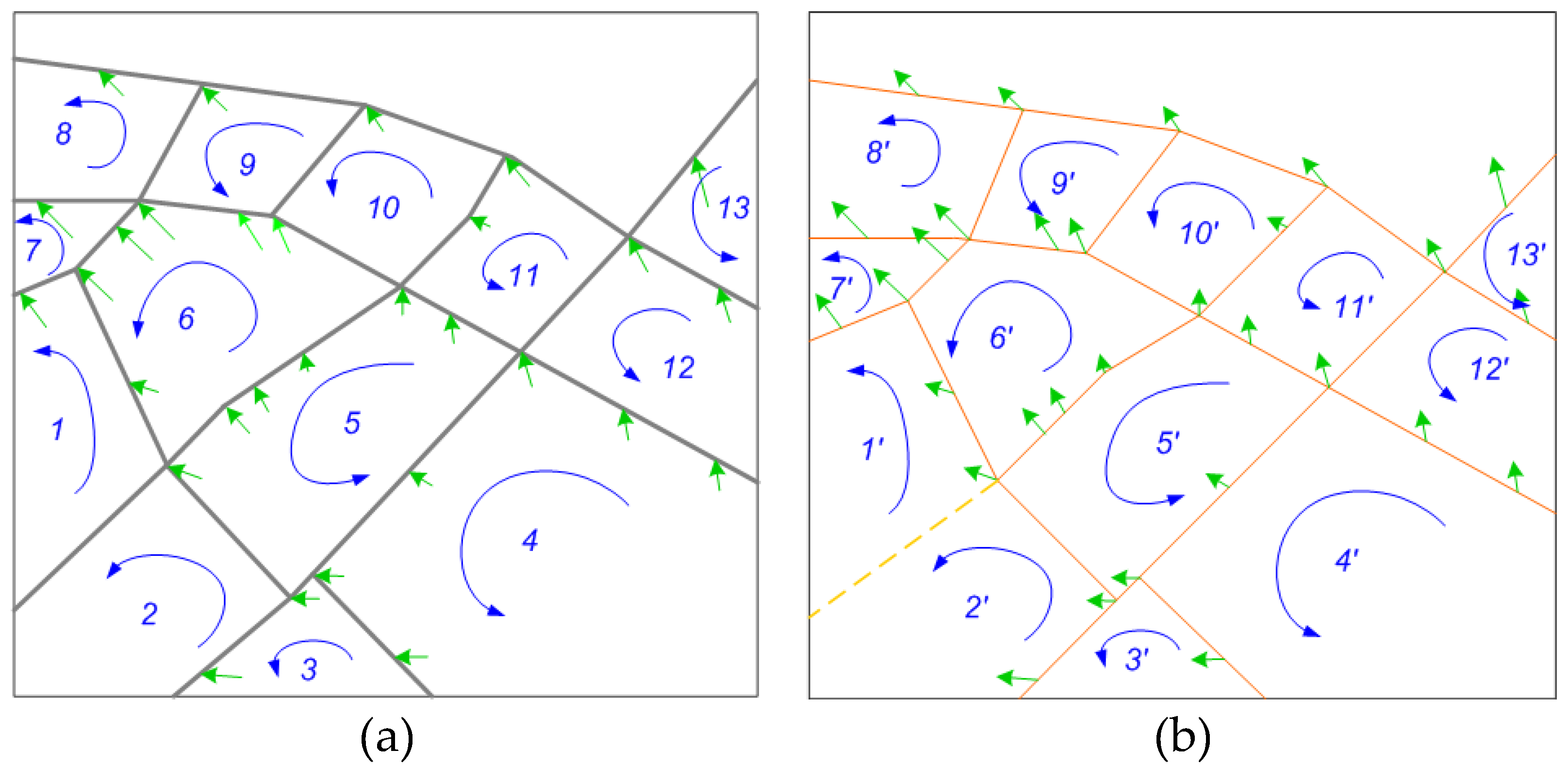
3.4.1. Creating New Intersections (Nodes)
3.4.2. Decomposition and Transferring of Semantic Information
3.4.3. Entity ID Issues
3.5. Error Detection and Correction
Category 1: Duplicated conflated pedestrian ways.
Category 2: Partial duplications.
Category 3: Conflated pedestrian ways that are possibly wrong.
Category 4: Reliable conflated pedestrian ways.
4. Discussion of Conflation Results
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Saalfeld, A. Conflation: Automated map compilation. Int. J. Geogr. Inf. Syst. 1988, 2, 217–228. [Google Scholar] [CrossRef]
- Chen, C.-C. Automatically and Accurately Conflating Road Vector Data, Street Maps and Orthoimagery. Ph.D. Thesis, University of Southern California, Los Angeles, CA, USA, 2005. [Google Scholar]
- Lozano, A.; Storchi, G. Shortest viable hyperpath in multimodal networks. Transp. Res. B Methodol. 2002, 36, 853–874. [Google Scholar] [CrossRef]
- Liu, L.; Meng, L. Algorithms of multi-modal route planning based on the concept of switch point. Photogramm. Fernerkund. Geoinform. 2009, 5, 431–444. [Google Scholar] [CrossRef]
- Ruiz, J.J.; Ariza, F.J.; Ureña, M.A.; Blázquez, E.B. Digital map conflation: a review of the process and a proposal for classification. Int. J. Geogr. Inf. Sci. 2011, 25, 1439–1466. [Google Scholar] [CrossRef]
- Gabay, Y.; Doytsher, Y. Automatic adjustment of line maps. In Proceedings of the GIS/LIS’94 Annual Convention, Phoenix, Arizona, USA, 25–27 October 1994; pp. 333–341.
- Gabay, Y.; Doytsher, Y. Automatic feature correction in merging of line maps. In Proceedings of the 1995 ACSM-ASPRS Annual Convention 2, Charlotte, North Carolina, 27 February–2 March 1995; pp. 404–410.
- Walter, V.; Fritsch, D. Matching spatial data sets: A statistical approach. Int. J. Geogr. Inf. Sci. 1999, 13, 445–473. [Google Scholar] [CrossRef]
- Kang, H. Spatial Data Integration: A Case Study of Map Conflation with Census Bureau and Local Government Data; The Ohio State University: Columbus, OH, USA, 2001. [Google Scholar]
- Zhang, M.; Meng, L. An iterative road-matching approach for the integration of postal data. Comput. Environ. Urban Syst. 2007, 31, 598–616. [Google Scholar] [CrossRef]
- Zhang, Q.; Griffiths, S.; Wollersheim, M.; Tighe, M.L.; Xu, C. Conflation of national bridge inventory database with tiger based road vectors. In Proceedings of the XXII ISPRS Congress: ISPRS Annals of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Melbourne, Australia, 25 August–1 September 2012.
- He, D. A Study on Theory and method of spatial vector data conflation. Res. J. Appl. Sci. Eng. Technol. 2013, 5, 563–567. [Google Scholar]
- Zhang, M.; Yao, W.; Meng, L. Enrichment of topographic road database for the purpose of routing and navigation. Int. J. Digit. Earth 2014, 7, 411–431. [Google Scholar] [CrossRef]
- Casado, M.L. Some basic mathematical constraints for the geometric conflation problem. In Proceedings of the 7th International Symposium on Spatial Accuracy Assessment in Natural Resources and Environmental Sciences, Lisbon, Portugal, 5–7 July 2006.
- Parent, C.; Spaccapietra, S. Database Integration: The Key to Data Interoperability, Advances in Object-Oriented Data Modeling; Papazoglou, M.P., Spaccapietra, S., Tari, Z., Eds.; The MIT Press: Cambridge, MA, USA, 2000. [Google Scholar]
- Li, L.; Goodchild, M.F. An optimisation model for linear feature matching in geographical data conflation. Int. J. Image Data Fusion 2011, 2, 309–328. [Google Scholar] [CrossRef]
- Volz, S. An iterative approach for matching multiple representations of street data. In Proceedings of the ISPRS Workshop on Multiple Representation and Interoperability of Spatial Data, Hannover, Germany, 22–24 February 2006.
- Yang, B.; Zhang, Y.; Luan, X. A probabilistic relaxation approach for matching road networks. Int. J. Geogr. Inf. Sci. 2013, 27, 319–338. [Google Scholar] [CrossRef]
- Zhang, M.; Meng, L. Delimited stroke oriented algorithm—Working principle and implementation for the matching of road networks. J. Geogr. Inf. Sci. 2008, 14, 44–53. [Google Scholar] [CrossRef]
- Zhang, M.; Meng, L.; Bobrich, J. A road-network matching approach guided by “structure”. Ann. Geogr. Inf. Syst. 2010, 16, 165–176. [Google Scholar] [CrossRef]
- Chen, J.; Hu, Y.; Li, Z.; Zhao, R.; Meng, L. Selective omission of road features based on mesh density for automatic map generalization. Int. J. Geogr. Inf. Sci. 2009, 23, 1013–1032. [Google Scholar] [CrossRef]

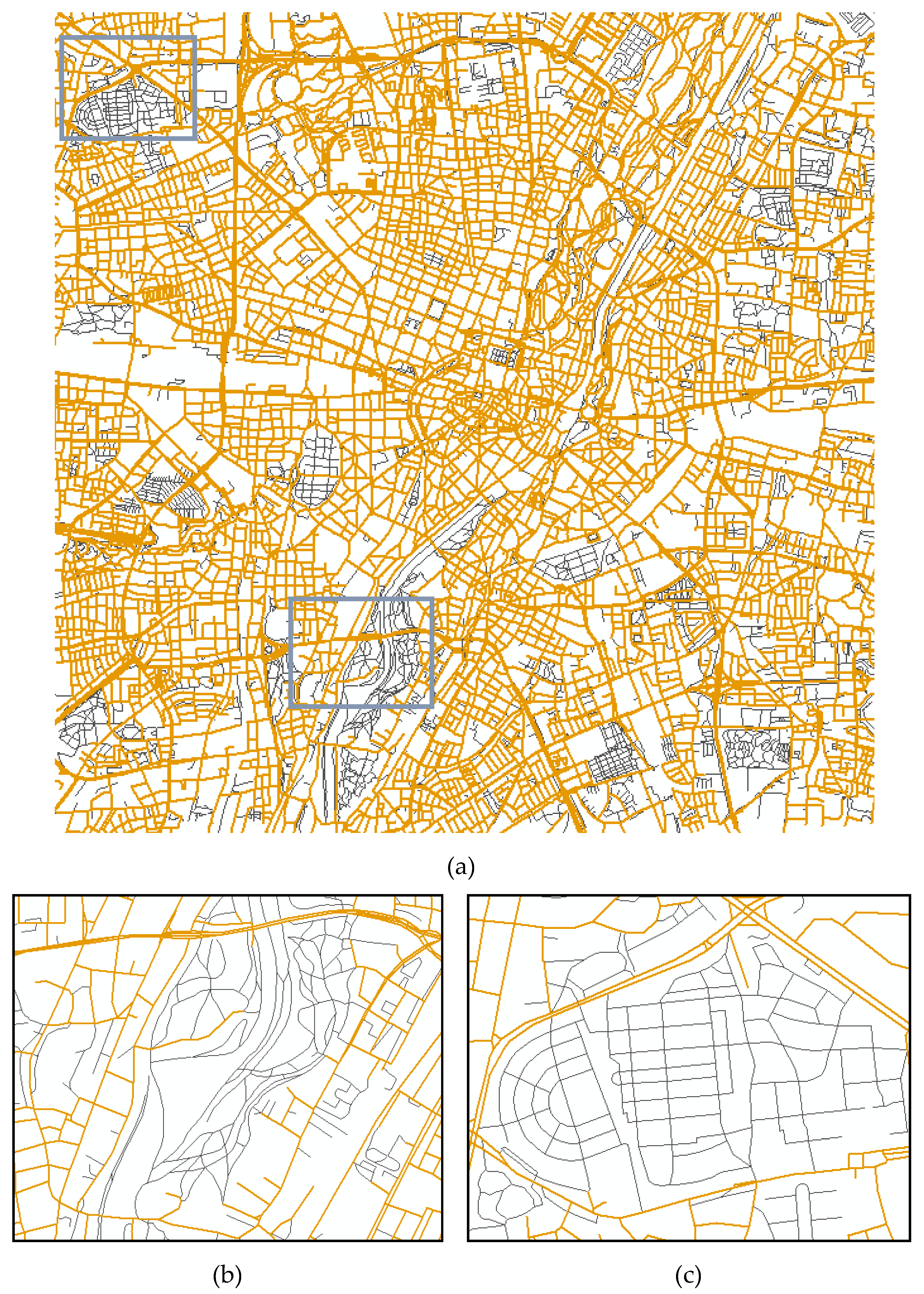
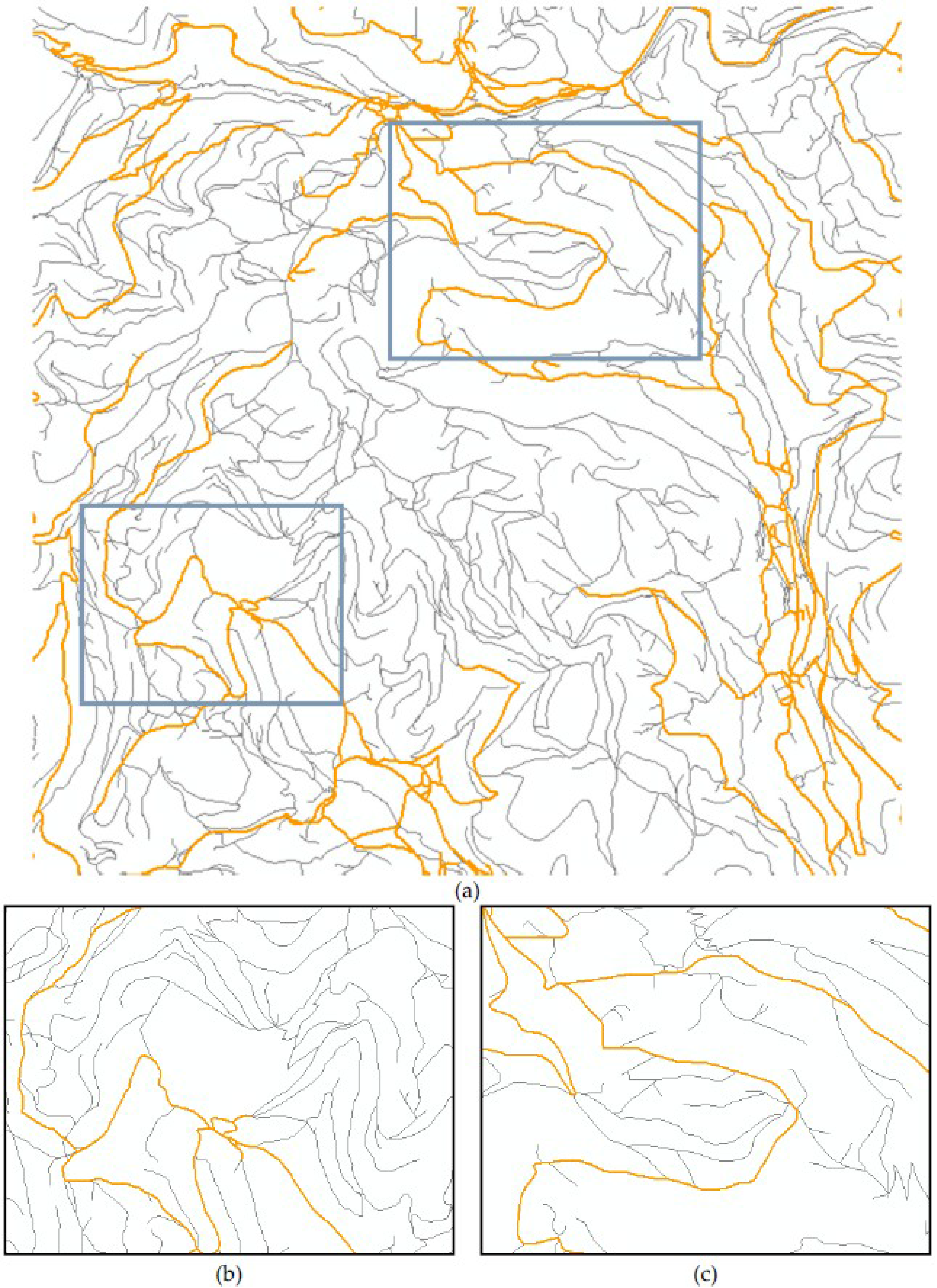
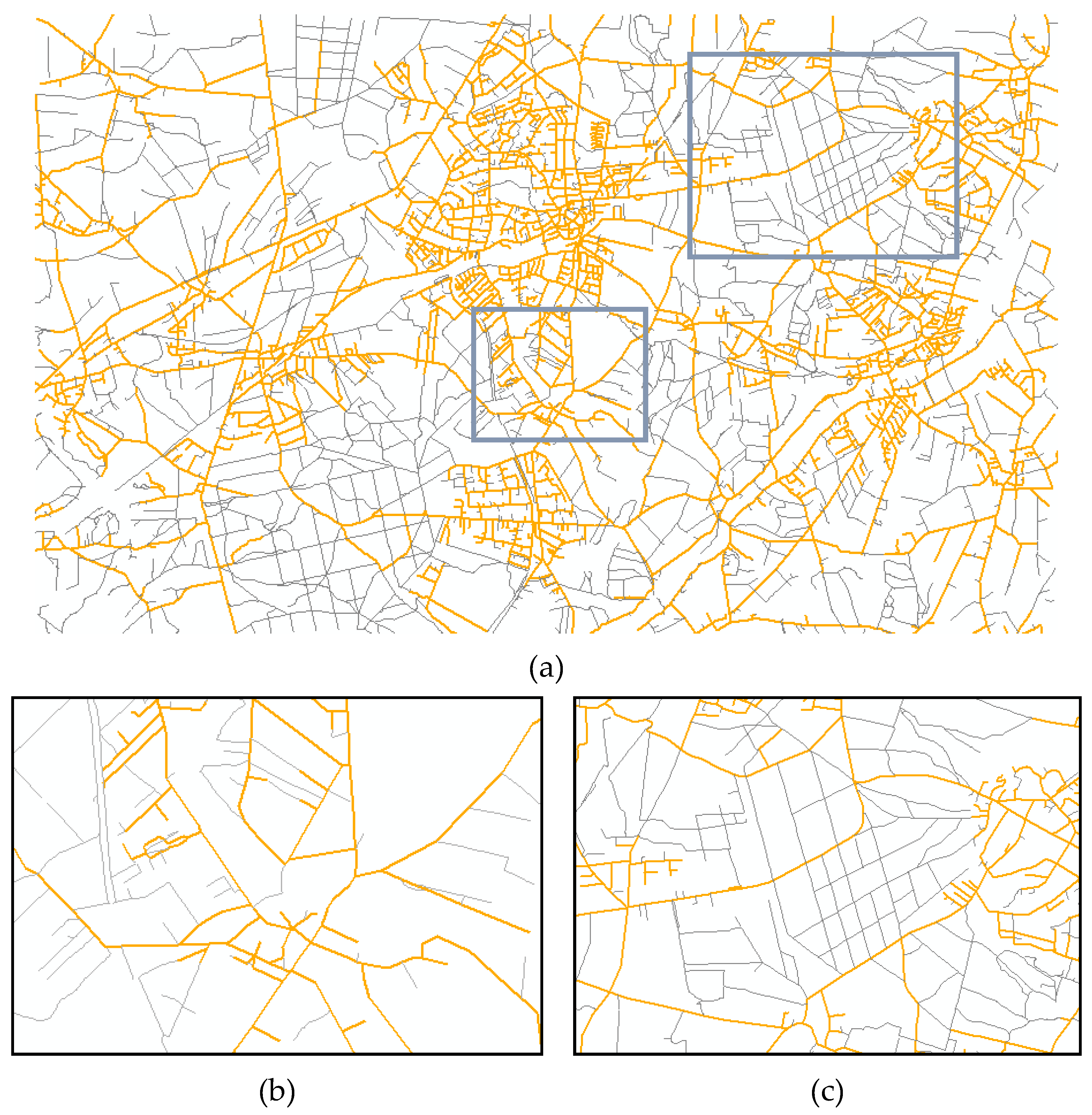
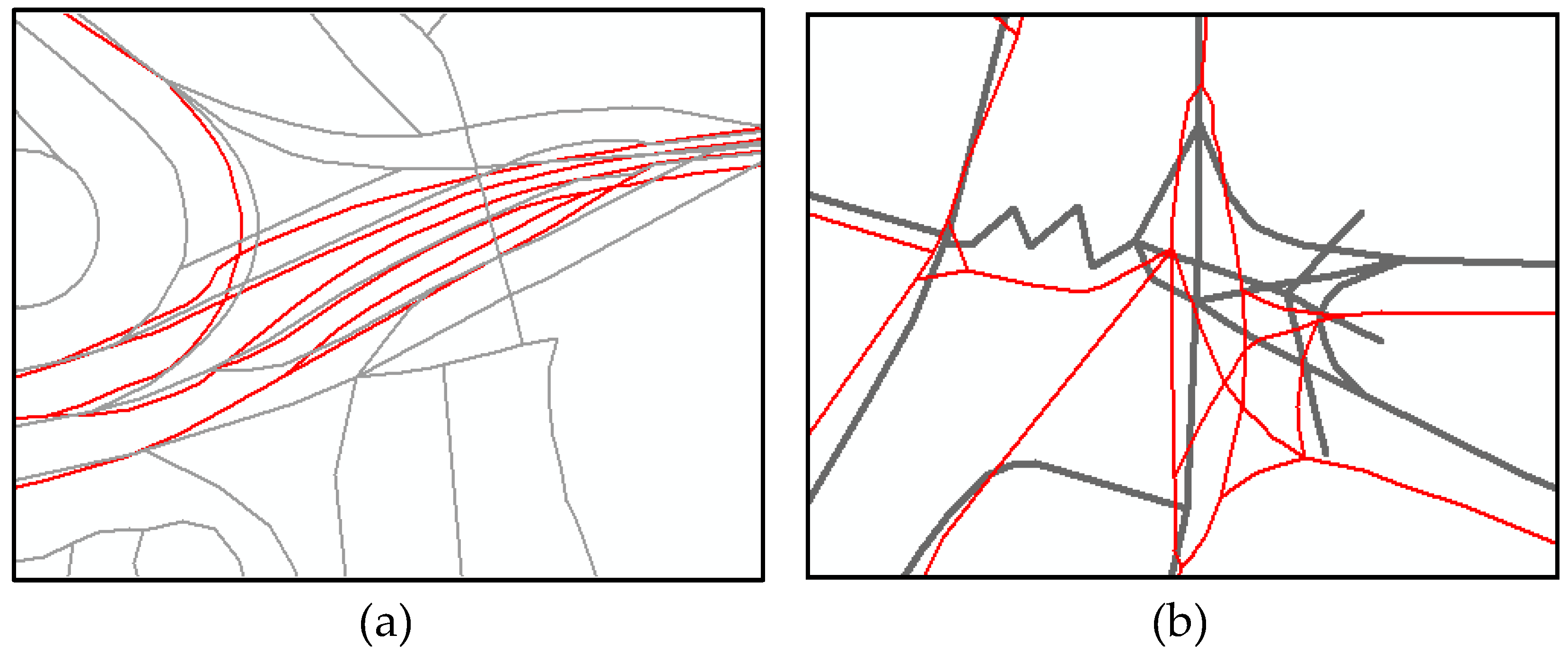
| Test Area (km2) | Area 1 (100 km2) | Area 2 (49 km2) | Area 3 (150 km2) | Total |
|---|---|---|---|---|
| NAVTEQ Features (NF) | 14,960 | 2214 | 3111 | 20,285 |
| ATKIS Features (AF) | 19,516 | 5196 | 6400 | 31,112 |
| Conflated Features (CF) | 5177 | 2246 | 2599 | 10,022 |
| Unfavorable Conflated Features (UCF) | 42 | 11 | 12 | 65 |
| Computing Time (second) (incl. data reading and writing) | 25 s | 6 s | 8 s | 39 s |
| Configuration of the Computer | Intel Core i7 2.80 GHz | |||
| Correctness | ||||
| Overall Correctness = (AF − UCF)/AF × 100% | 99.78% | 99.79% | 99.81% | 99.79% |
| Conflation Correctness = (CF − UCF)/CF × 100% | 99.19% | 99.51% | 99.54% | 99.35% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Yao, W.; Meng, L. Automatic and Accurate Conflation of Different Road-Network Vector Data towards Multi-Modal Navigation. ISPRS Int. J. Geo-Inf. 2016, 5, 68. https://doi.org/10.3390/ijgi5050068
Zhang M, Yao W, Meng L. Automatic and Accurate Conflation of Different Road-Network Vector Data towards Multi-Modal Navigation. ISPRS International Journal of Geo-Information. 2016; 5(5):68. https://doi.org/10.3390/ijgi5050068
Chicago/Turabian StyleZhang, Meng, Wei Yao, and Liqiu Meng. 2016. "Automatic and Accurate Conflation of Different Road-Network Vector Data towards Multi-Modal Navigation" ISPRS International Journal of Geo-Information 5, no. 5: 68. https://doi.org/10.3390/ijgi5050068
APA StyleZhang, M., Yao, W., & Meng, L. (2016). Automatic and Accurate Conflation of Different Road-Network Vector Data towards Multi-Modal Navigation. ISPRS International Journal of Geo-Information, 5(5), 68. https://doi.org/10.3390/ijgi5050068






