A Geosimulation Approach for Data Scarce Environments: Modeling Dynamics of Forest Insect Infestation across Different Landscapes
Abstract
:1. Introduction
2. Complex Systems Theory for Modeling Insect Infestation
3. Methods
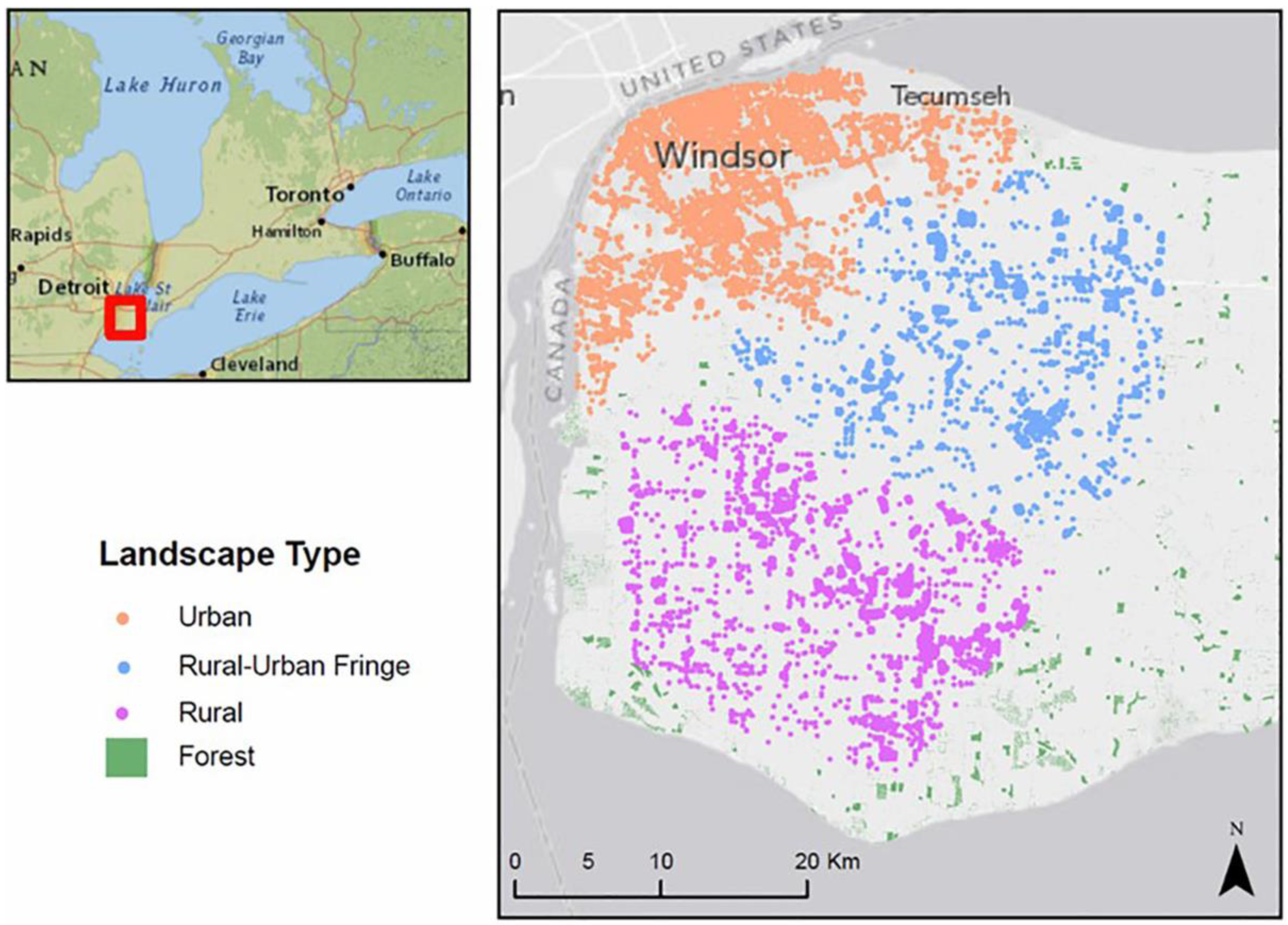
3.1. Study Site and Datasets
- (1)
- GIS data layer providing an initial location of EAB infestation in the City of Windsor in 2002. Additional data from the literature provides information on the average rate of spread where the first North American outbreak of EAB in Michigan. The US had a rate of spread of 12–13 km/year during this time through natural and long distance dispersal [11].
- (2)
- GIS raster files of 10 m spatial resolution were generated to represent three different hypothetical landscape types for forest in urban, rural-urban fringe, and rural settings in and surrounding the City of Windsor. The raster data layers were created using vector land use data acquired from Land Information Ontario (LIO) [39]. The acquired LIO land use data have determined the actual distribution of trees in each of the three landscape types; however, due to the unavailability of tree inventory data for this region, the exact location of individual ash trees is unknown. In addition, the biological characteristics of the ash trees such as age and size were derived from the literature to generate the realistic biological characteristics of ash trees within three landscape types.
- (3)
- Weather and meteorological data for twelve stations distributed by the Government of Canada [40]. This data includes average wind direction and monthly temperature data for a period of two years.
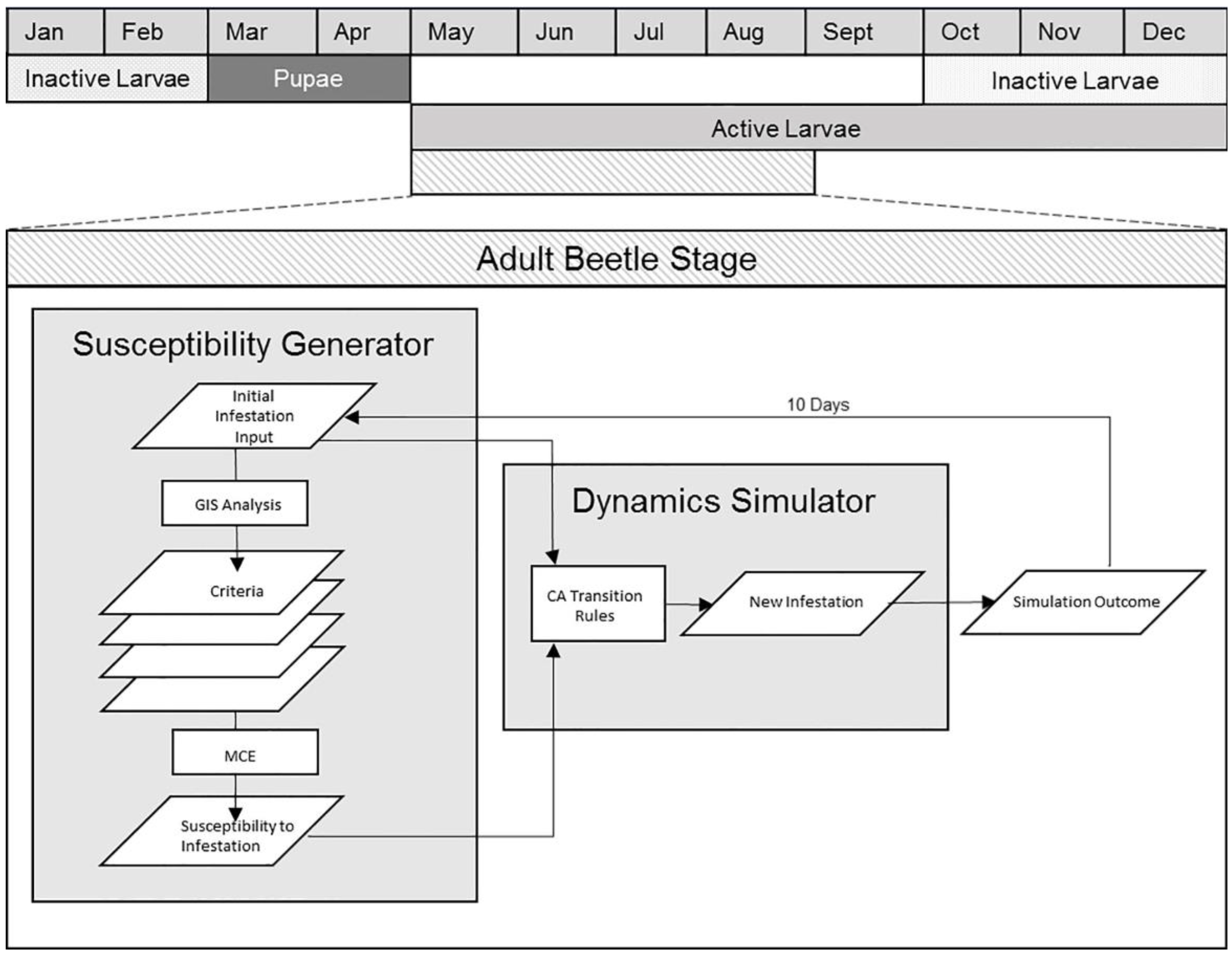
3.2. Model Structure
3.2.1. Model Component 1: Tree Susceptibility
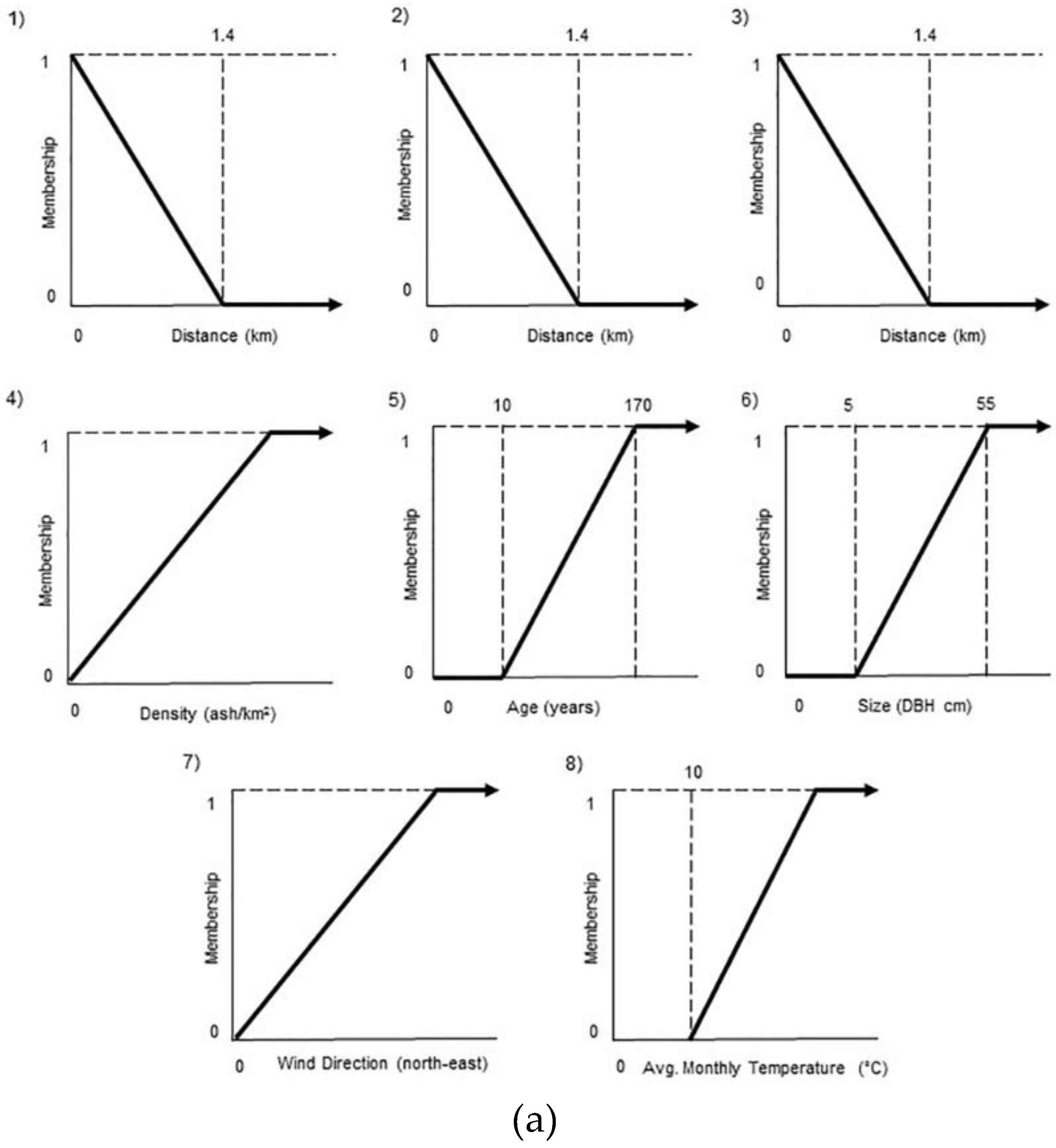
| Category | Priority | Rank | |
|---|---|---|---|
| 1 | Distance | 54.2 | 1 |
| 2 | Age and Size | 23.9 | 2 |
| 3 | Highways | 13.9 | 3 |
| 4 | Roads | 6.2 | 4 |
| 5 | Density | 3.7 | 5 |
| Consistency | 7.80% | ||
| (a) | |||
| Category | Priority | Rank | |
| 1 | Distance | 40.9 | 1 |
| 2 | Wind or Temperature | 32.3 | 2 |
| 3 | Age and Size | 13.9 | 3 |
| 4 | Highways | 6.4 | 4 |
| 5 | Roads | 3.8 | 5 |
| 6 | Density | 2.6 | 6 |
| Consistency | 7.10% | ||
| (b) | |||
| Category | Priority | Rank | |
| 1 | Distance | 37.6 | 1 |
| 2 | Wind | 22.1 | 2 |
| 3 | Temperature | 22.1 | 3 |
| 4 | Age and Size | 8.1 | 4 |
| 5 | Highways | 4.7 | 5 |
| 6 | Roads | 3.2 | 6 |
| 7 | Density | 2.1 | 7 |
| Consistency | 6.00% | ||
3.2.2. Model Component II: Spatial Dynamics Simulator
3.3. Scenarios
3.3.1. Landscape Scenarios
3.3.2. Climate Scenarios
3.4. Model Calibration
4. Results
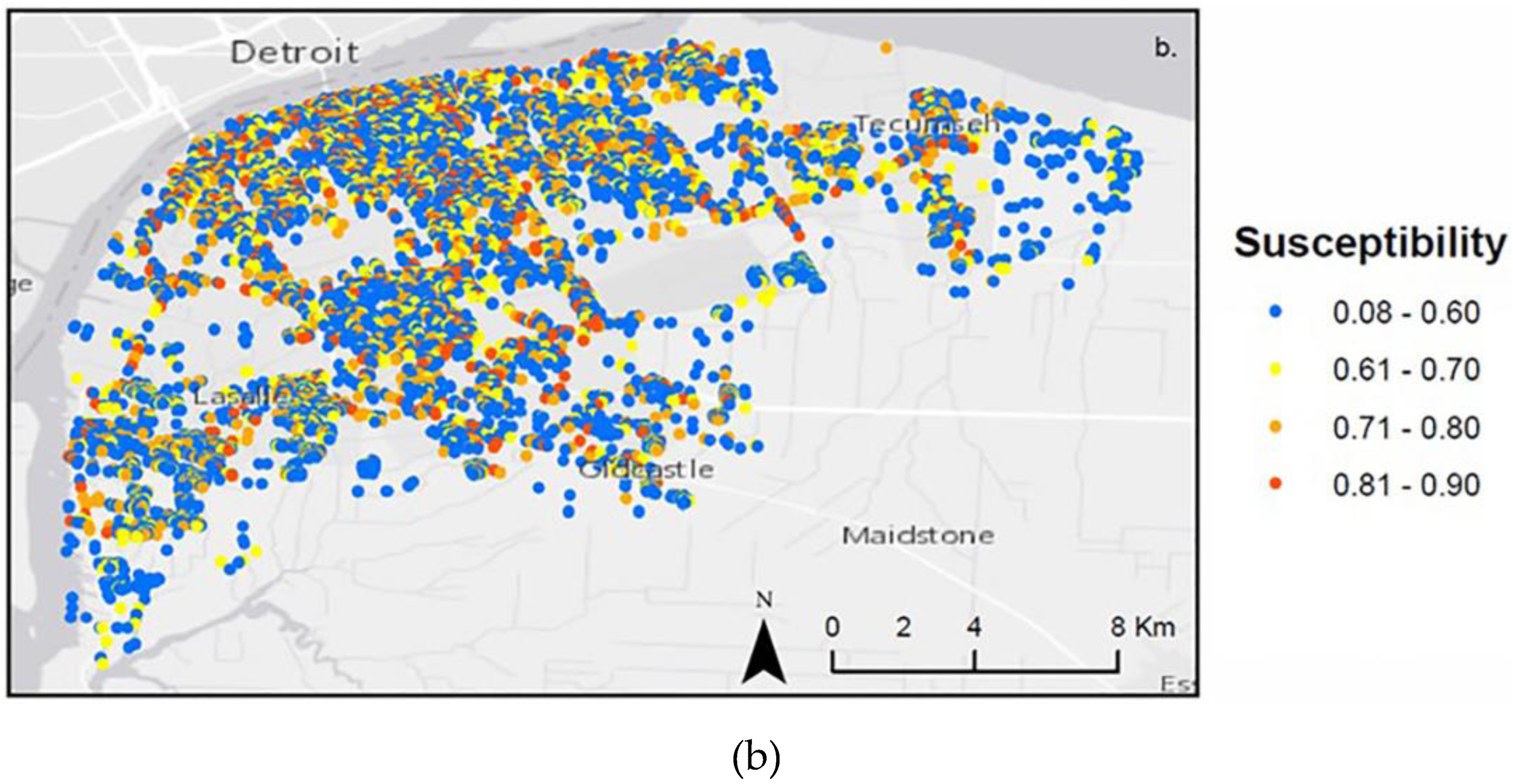
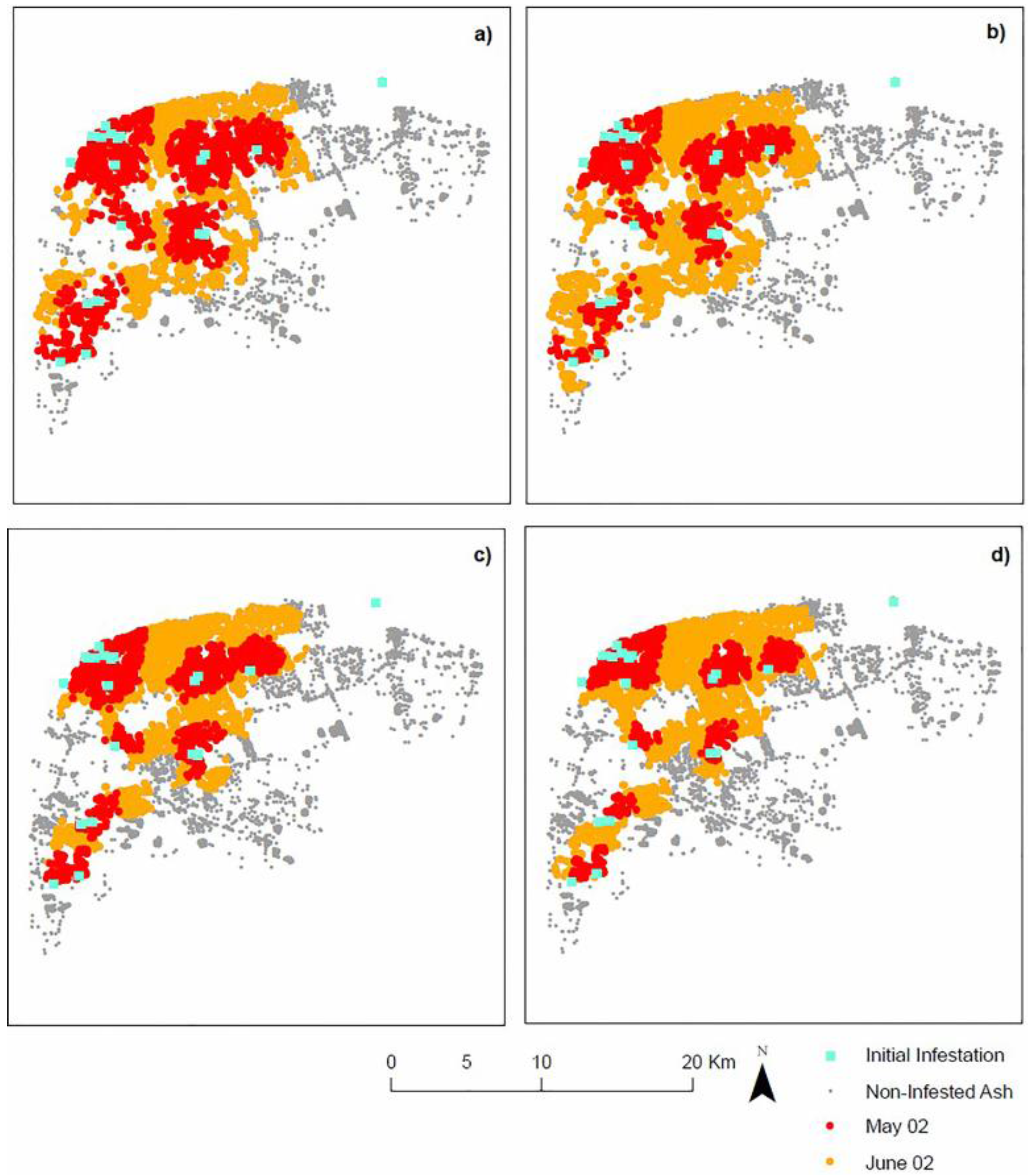
4.1. Landscape Scenarios
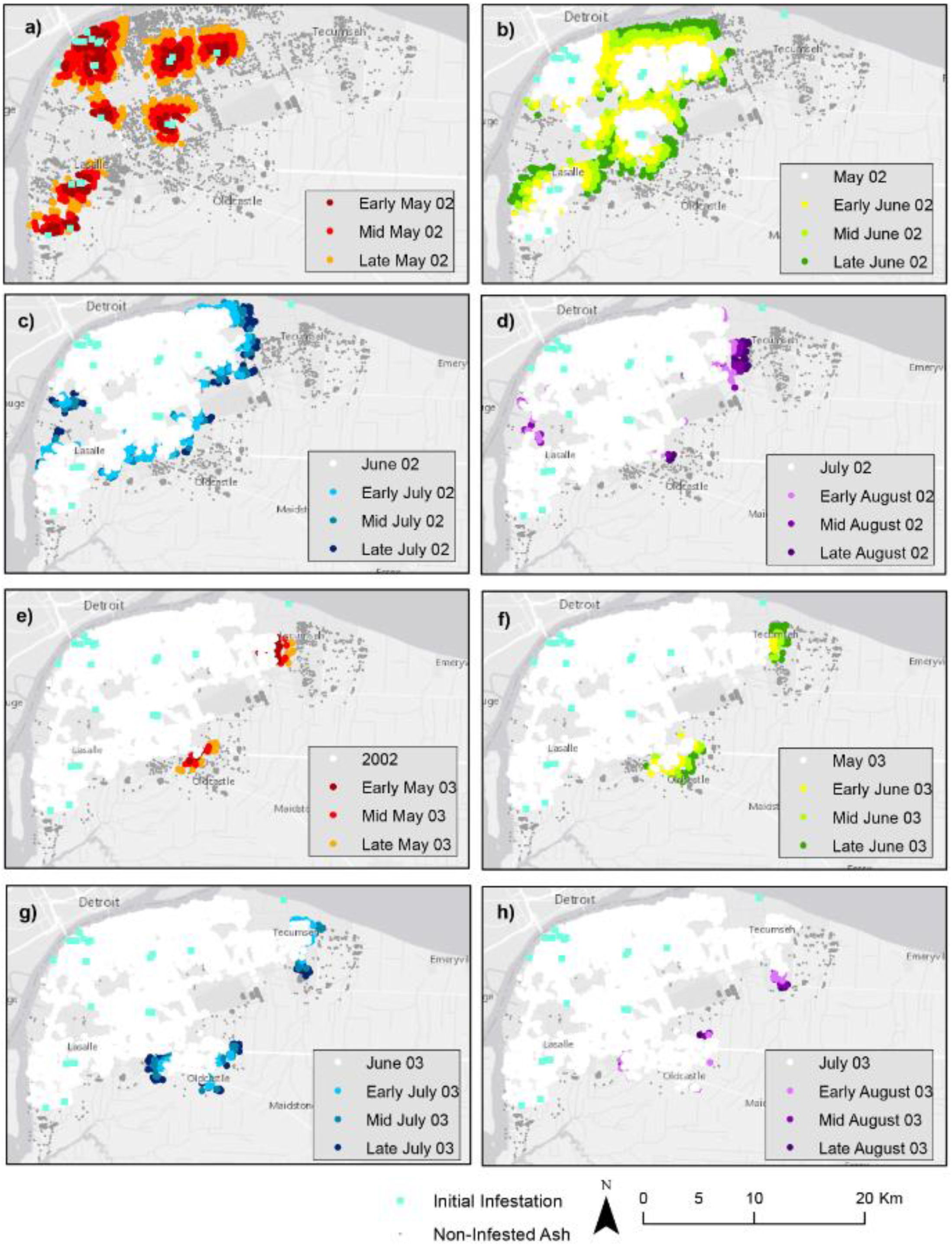
4.2. Climate Scenarios

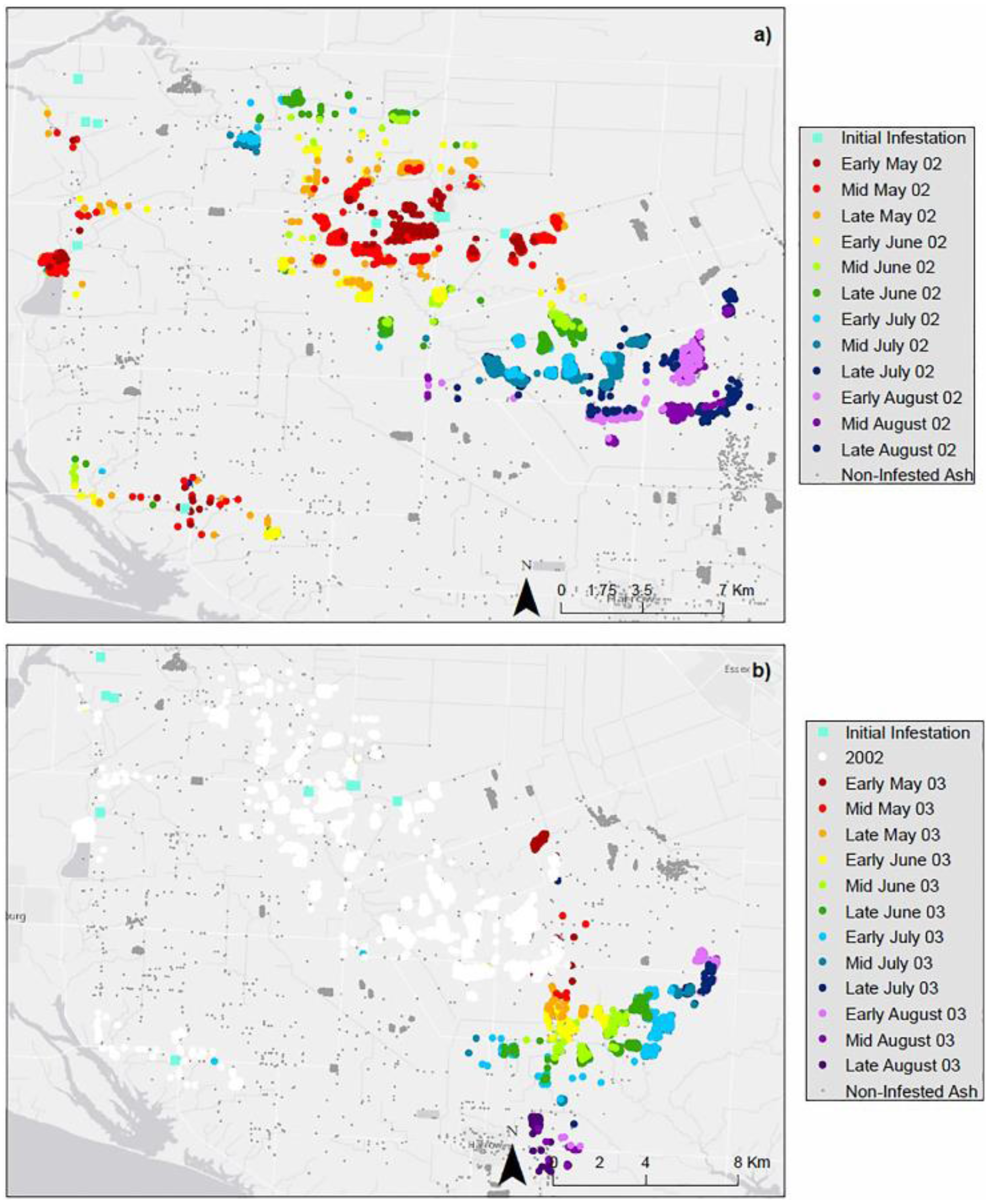
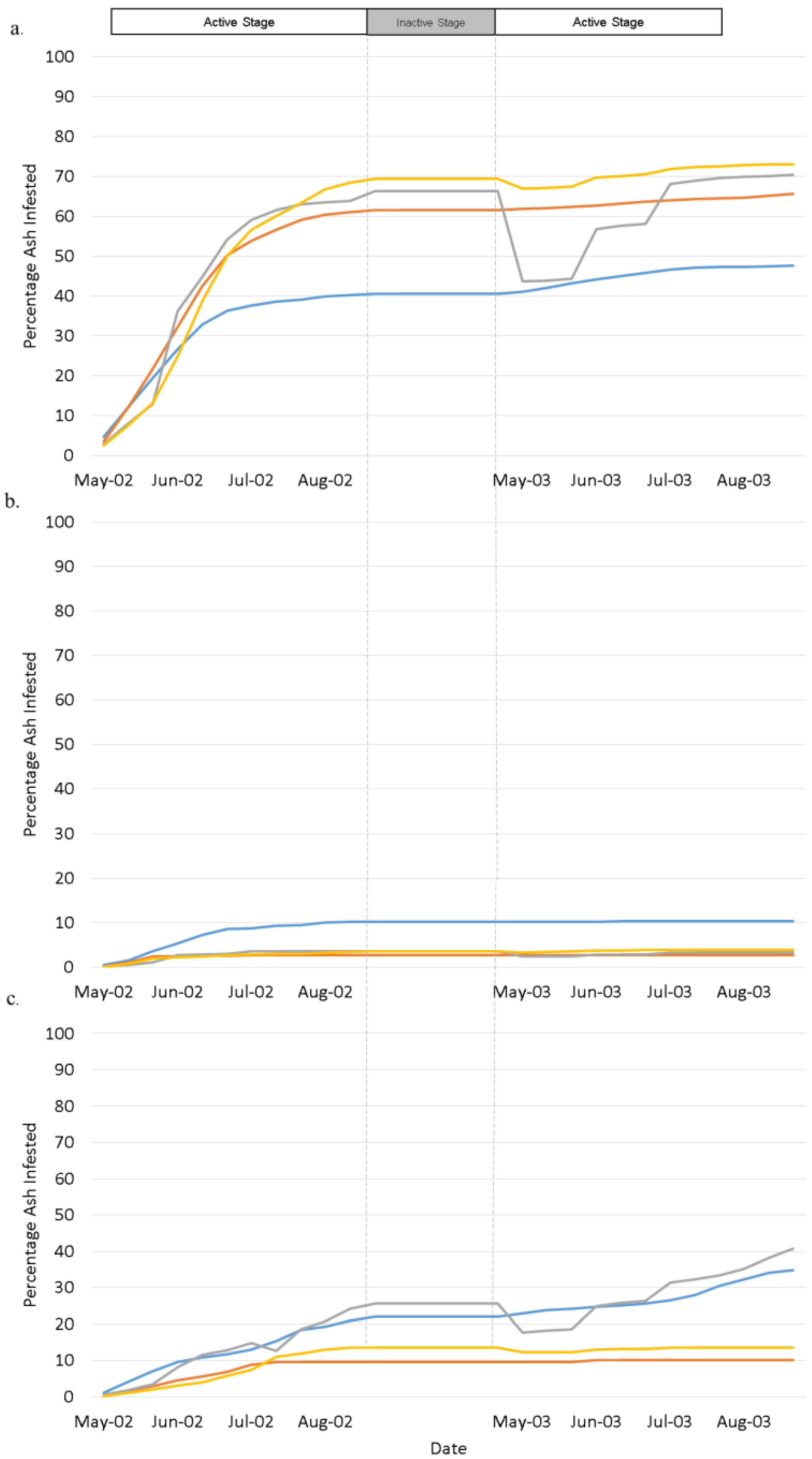
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Latombe, G.; Parrott, L.; Fortin, D. Levels of emergence in individual based models: Coping with scarcity of data and pattern redundancy. Ecol. Model. 2011, 222, 1557–1568. [Google Scholar] [CrossRef]
- Liebhold, A. Use and abuse of insect and disease models in forest pest management: Past, present, and future. In Sustainable Ecological Systems: Implementing an Ecological Approach to Land Management; Tech.Rep.RM-247; US Department of Agriculture, Forest Service: Morgantown, VA, USA, 1994; pp. 204–210. [Google Scholar]
- Parunak, H.V.D.; Savit, R.; Riolo, R.L. Agent-based modeling vs. equation-based modeling: A case study and users’ guide. In Multi-Agent Systems and Agent-Based Simulation; Springer: Paris, France, 1998; pp. 10–25. [Google Scholar]
- Fussmann, G.F. Chaotic dynamics in food web systems. In Complex Population Dynamics: Nonlinear Modeling in Ecology, Epidemiology and Genetics; World Scientific Publishing Company: Singapore, 2007; pp. 1–20. [Google Scholar]
- Goodchild, M.F.; Glennon, A. Representation and computation of geographic dynamics. In Understanding Dynamics of Geographic Domains; CRC Press: Boca Raton, FL, USA, 2008; pp. 13–30. [Google Scholar]
- O’Sullivan, D.; Perry, G.L. Spatial Simulation: Exploring Pattern and Process; John Wiley & Sons: Auckland, New Zealand, 2013. [Google Scholar]
- BenDor, T.K.; Metcalf, S.S.; Fontenot, L.E.; Sangunett, B.; Hannon, B. Modeling the spread of the emerald ash borer. Ecol. Model. 2006, 197, 221–236. [Google Scholar] [CrossRef]
- DeSantis, R.D.; Moser, W.K.; Gormanson, D.D.; Bartlett, M.G.; Vermunt, B. Effects of climate on emerald ash borer mortality and the potential for ash survival in North America. Agric. For. Meteorol. 2013, 178, 120–128. [Google Scholar] [CrossRef]
- Canadian Food Inspection Agency. Emerald Ash Borer Latest Information. Available online: http://www.inspection.gc.ca/plants/plant-protection/insects/emerald-ash-borer/latest-information/eng/1337287614593/1337287715022 (accessed on 26 July 2015).
- McCullough, D.G.; Poland, T.M.; Anulewicz, A.C.; Cappaert, D. Emerald ash borer (Coleoptera: Buprestidae) attraction to stressed or baited ash trees. Environ. Entomol. 2009, 38, 1668–1679. [Google Scholar] [CrossRef] [PubMed]
- Siegert, N.W.; McCullough, D.G.; Liebhold, A.M.; Telewski, F.W. Dendrochronological reconstruction of the epicentre and early spread of emerald ash borer in North America. Divers. Distrib. 2014, 20, 847–858. [Google Scholar] [CrossRef]
- McCullough, D.; Roberts, S. Emerald ash borer; Pest Alert NA-PR-07-02; USDA Forest Service State and Private Forestry, Northeastern Area: Newtown Square, PA, USA, 2002.
- Krcmar-Nozic, E.; Arthur, L.M.; Wilson, B. The Potential Impacts of Exotic Forest Pests in North America: A Synthesis of Research; Pacific Forestry Centre: Saanich, Vic, Canada, 2000. [Google Scholar]
- Kovacs, K.F.; Haight, R.G.; McCullough, D.G.; Mercader, R.J.; Siegert, N.W.; Liebhold, A.M. Cost of potential emerald ash borer damage in US communities, 2009–2019. Ecol. Econ. 2010, 69, 569–578. [Google Scholar] [CrossRef]
- Aukema, J.E.; McCullough, D.G.; Von Holle, B.; Liebhold, A.M.; Britton, K.; Frankel, S.J. Historical accumulation of nonindigenous forest pests in the continental United States. Bioscience 2010, 60, 886–897. [Google Scholar] [CrossRef]
- City of Peterborough. Emerald Ash Borer Management Plan. Available online: http://www.peterborough.ca/Assets/City+Assets/Planning/Documents/Ongoing+Planning+Studies/Emerald+Ash+Borer+Management+Plan.pdf (accessed on 26 July 2015).
- Burr, S.J.; McCullough, D.G. Condition of green ash (Fraxinus pennsylvanica) overstory and regeneration at three stages of the emerald ash borer invasion wave. Can. J. For. Res. 2014, 44, 768–776. [Google Scholar] [CrossRef]
- Muirhead, J.R.; Leung, B.; Overdijk, C.; Kelly, D.W.; Nandakumar, K.; Marchant, K.R.; MacIsaac, H.J. Modelling local and long-distance dispersal of invasive emerald ash borer Agrilus planipennis (Coleoptera) in North America. Divers. Distrib. 2006, 12, 71–79. [Google Scholar] [CrossRef]
- Barlow, L.; Cecile, J.; Bauch, C.T.; Anand, M. Modelling interactions between forest pest invasions and human decisions regarding firewood transport restrictions. PLoS ONE 2014, 9, e90511. [Google Scholar]
- Vermunt, B.; Cuddington, K.; Sobek-Swant, S.; Crosthwaite, J. Cold temperature and emerald ash borer: Modelling the minimum under-bark temperature of ash trees in Canada. Ecol. Model. 2012, 235, 19–25. [Google Scholar] [CrossRef]
- McKenney, D.W.; Pedlar, J.H.; Yemshanov, D.; Barry Lyons, D.; Campbell, K.L.; Lawrence, K. Estimates of the potential cost of emerald ash borer (Agrilus planipennis Fairmaire) in Canadian municipalities. Arboricult. Urban For. 2012, 38, 81–91. [Google Scholar]
- Pontius, J.; Martin, M.; Plourde, L.; Hallett, R. Ash decline assessment in emerald ash borer-infested regions: A test of tree-level, hyperspectral technologies. Remote Sens. Environ. 2008, 112, 2665–2676. [Google Scholar] [CrossRef]
- San Souci, J.; Hanou, I.; Puchalski, D. High-resolution remote sensing image analysis for early detection and response planning for emerald ash borer. Photogramm. Eng. Remote Sens. 2009, 75, 905–909. [Google Scholar]
- Wu, J.; Marceau, D. Modeling complex ecological systems: An introduction. Ecol. Model. 2002, 153, 1–6. [Google Scholar] [CrossRef]
- DeAngelis, D.L.; Mooij, W.M. Individual-based modeling of ecological and evolutionary processes. Annu. Rev. Ecol. Evol. Syst. 2005, 36, 147–168. [Google Scholar] [CrossRef]
- Grimm, V.; Railsback, S.F. Individual-Based Modeling and Ecology; Princeton University Press: Princeton, NJ, USA, 2013. [Google Scholar]
- Batty, M.; Torrens, P.M. Modelling and prediction in a complex world. Futures 2005, 37, 745–766. [Google Scholar] [CrossRef]
- White, R.; Engelen, G. High-resolution integrated modelling of the spatial dynamics of urban and regional systems. Comput. Environ. Urban Syst. 2000, 24, 383–400. [Google Scholar] [CrossRef]
- Torrens, P.M.; Benenson, I. Geographic automata systems. Int. J. Geogr. Inf. Sci. 2005, 19, 385–412. [Google Scholar] [CrossRef]
- Hogeweg, P. Cellular automata as a paradigm for ecological modeling. Appl. Math. Comput. 1988, 27, 81–100. [Google Scholar] [CrossRef]
- Dytham, C. The effect of habitat destruction pattern on species persistence: A cellular model. Oikos 1995, 340–344. [Google Scholar] [CrossRef]
- Balzter, H.; Braun, P.W.; Köhler, W. Cellular automata models for vegetation dynamics. Ecol. Model. 1998, 107, 113–125. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Z.; Yang, D.; Yang, Q.; Yan, J.; He, M. Ecological risk assessment of genetically modified crops based on cellular automata modeling. Biotechnol. Adv. 2009, 27, 1132–1136. [Google Scholar] [CrossRef] [PubMed]
- Dragicevic, S. Modeling the dynamics of coplex systems using cellular, fuzzy sets and GIS: Invasive species propagation. Geogr. Compass 2010, 4, 599–615. [Google Scholar] [CrossRef]
- Bone, C.; Dragicevic, S.; Roberts, A. A fuzzy-constrained cellular automata model of forest insect infestations. Ecol. Model. 2006, 192, 107–125. [Google Scholar] [CrossRef]
- Perez, L.; Dragicevic, S. Landscape-level simulation of forest insect disturbance: Coupling swarm intelligent agents with GIS-based cellular automata model. Ecol. Model. 2012, 231, 53–64. [Google Scholar] [CrossRef]
- Mathey, A.; Krcmar, E.; Dragicevic, S.; Vertinsky, I. An object-oriented cellular automata model for forest planning problems. Ecol. Model. 2008, 212, 359–371. [Google Scholar] [CrossRef]
- Perez, L.; Dragicevic, S. Modeling mountain pine beetle infestation with an agent-based approach at two spatial scales. Environ. Model. Softw. 2010, 25, 223–236. [Google Scholar] [CrossRef]
- Land Information Ontario. Ontario Land Use Dataset. Available online: https://www.ontario.ca/page/land-information-ontario/ (accessed on 26 July 2015).
- Government of Canada. Temperatures Dataset. Available online: http://climate.weather.gc.ca (accessed on 26 July 2015).
- Prasad, A.M.; Iverson, L.R.; Peters, M.P.; Bossenbroek, J.M.; Matthews, S.N.; Sydnor, T.D.; Schwartz, M.W. Modeling the invasive emerald ash borer risk of spread using a spatially explicit cellular model. Landsc. Ecol. 2010, 25, 353–369. [Google Scholar] [CrossRef]
- Mercader, R.J.; Siegert, N.W.; Liebhold, A.M.; McCullough, D.G. Simulating the effectiveness of three potential management options to slow the spread of emerald ash borer (Agrilus planipennis) populations in localized outlier sites. Can. J. For. Res. 2011, 41, 254–264. [Google Scholar] [CrossRef]
- Robertson & Andow. Human-Mediated Dispersal of Emerald Ash Borer: Significance of the Firewood Pathway. Available online: http://www.entomology.umn.edu/prod/groups/cfans/@pub/@cfans/@ento/documents/asset/cfans_asset_139871.pdf (accessed on 27 October 2014).
- Buck, J.; Marshall, J. Hitchhiking as a secondary dispersal pathway for emerald ash borer, Agrilus planipennis. Gt Lakes Entomol. 2008, 41, 197–199. [Google Scholar]
- Ryall, K.L.; Silk, P.J.; Mayo, P.; Crook, D.; Khrimian, A.; Cossé, A.A.; Sweeney, J.; Scarr, T. Attraction of Agrilus planipennis (Coleoptera: Buprestidae) to a volatile pheromone: Effects of release rate, host volatile, and trap placement. Environ. Entomol. 2012, 41, 648–656. [Google Scholar] [CrossRef] [PubMed]
- Pasek, J.E. 30. Influence of wind and windbreaks on local dispersal of insects. Agric. Ecosyst. Environ. 1988, 22, 539–554. [Google Scholar] [CrossRef]
- Huset, R. A GIS-based Analysis of the Environmental Predictors of Dispersal of the Emerald Ash Borer in New York. Master’s Thesis, Syracuse University, Syracuse, NY, USA, May 2013. [Google Scholar]
- Straw, N.A.; Williams, D.T.; Kulinich, O.; Gninenko, Y.I. Distribution, impact and rate of spread of emerald ash borer Agrilus planipennis (Coleoptera: Buprestidae) in the Moscow region of Russia. Forestry 2013, 86, 515–522. [Google Scholar] [CrossRef]
- Saaty, T. The Analytic Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Environmental Systems Research Institute. ArcGIS Desktop: Release 10.1; Environmental Systems Research Institute: Redlands, CA, USA, 2015. [Google Scholar]
- Eastman, J. IDRISI Selva; Clark University: Worchester, MA, USA, 2012. [Google Scholar]
- MacFarlane, D.W.; Meyer, S.P. Characteristics and distribution of potential ash tree hosts for emerald ash borer. For. Ecol. Manag. 2005, 213, 15–24. [Google Scholar] [CrossRef]
- Poland, T.M.; McCullough, D.G. Emerald ash borer: Invasion of the urban forest and the threat to North America’s ash resource. J. For. 2006, 104, 118–124. [Google Scholar]
- Davidson, A. Summer in the City: NASA Turns Technology toward the Earth To Determine What, Exactly, Makes Cities so Hot. Atrodams. 1998. Available online: http://www.metropolismag.com/new/content/tech/aug98sum.htm (accessed on 20 August 2014).
- Tscharntke, T.; Brandl, R. Plant-insect interactions in fragmented landscapes. Annu. Rev. Entomol. 2004, 49, 405–430. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.Y.; Yang, Z.Q.; Gould, J.R.; Zhang, Y.N.; Liu, G.J.; Liu, E.S. The biology and ecology of the emerald ash borer, Agrilus planipennis, in China. J. Insect Sci. 2010, 10. [Google Scholar] [CrossRef] [PubMed]
- Anderson, T.; Dragicevic, S. An agent-based modeling approach to represent infestation dynamics of the emerald ash borer beetle. Ecol. Inform. 2015, 30, 97–109. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons by Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anderson, T.; Dragicevic, S. A Geosimulation Approach for Data Scarce Environments: Modeling Dynamics of Forest Insect Infestation across Different Landscapes. ISPRS Int. J. Geo-Inf. 2016, 5, 9. https://doi.org/10.3390/ijgi5020009
Anderson T, Dragicevic S. A Geosimulation Approach for Data Scarce Environments: Modeling Dynamics of Forest Insect Infestation across Different Landscapes. ISPRS International Journal of Geo-Information. 2016; 5(2):9. https://doi.org/10.3390/ijgi5020009
Chicago/Turabian StyleAnderson, Taylor, and Suzana Dragicevic. 2016. "A Geosimulation Approach for Data Scarce Environments: Modeling Dynamics of Forest Insect Infestation across Different Landscapes" ISPRS International Journal of Geo-Information 5, no. 2: 9. https://doi.org/10.3390/ijgi5020009
APA StyleAnderson, T., & Dragicevic, S. (2016). A Geosimulation Approach for Data Scarce Environments: Modeling Dynamics of Forest Insect Infestation across Different Landscapes. ISPRS International Journal of Geo-Information, 5(2), 9. https://doi.org/10.3390/ijgi5020009







