Urban Link Travel Time Prediction Based on a Gradient Boosting Method Considering Spatiotemporal Correlations
Abstract
:1. Introduction
2. Methodology
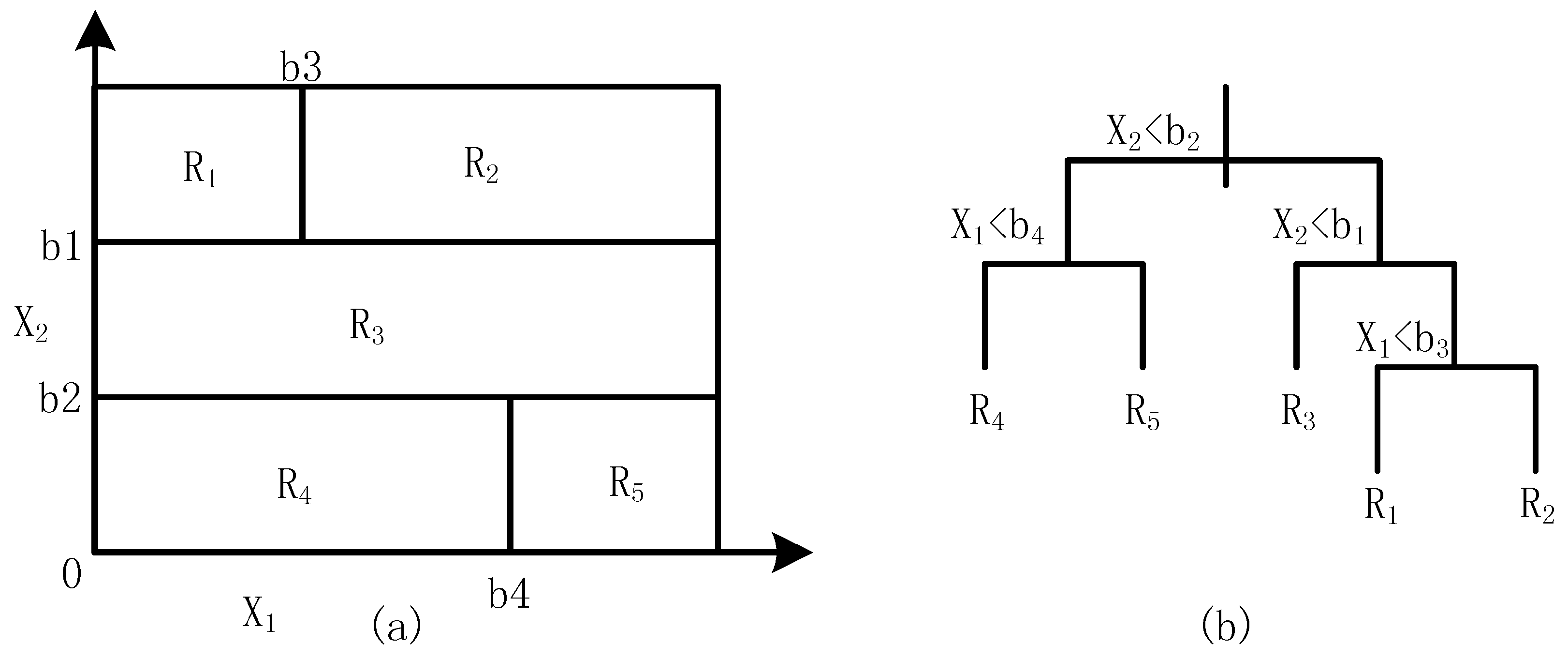
2.1. Single Regression Tree
2.2. Gradient–Boosted Regression Tree
3. Measurement and Correlation in Space and Time
3.1. Spatial Correlation
3.2. Temporal Correlation
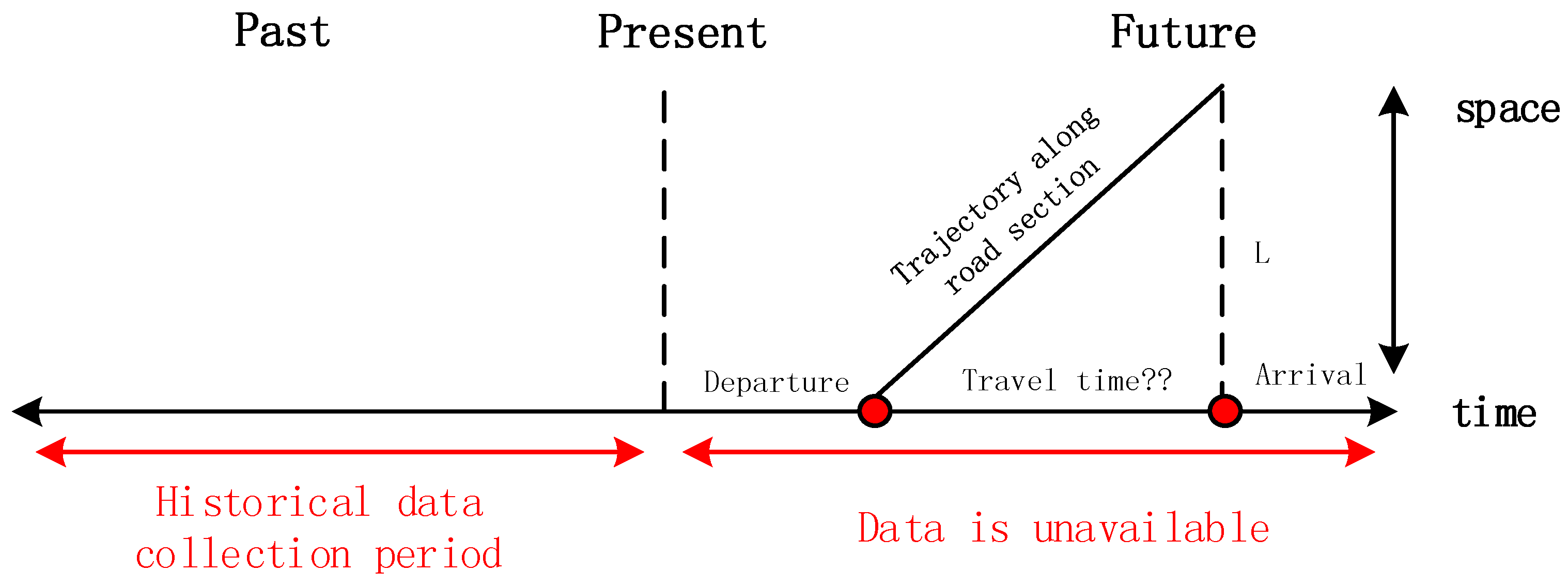
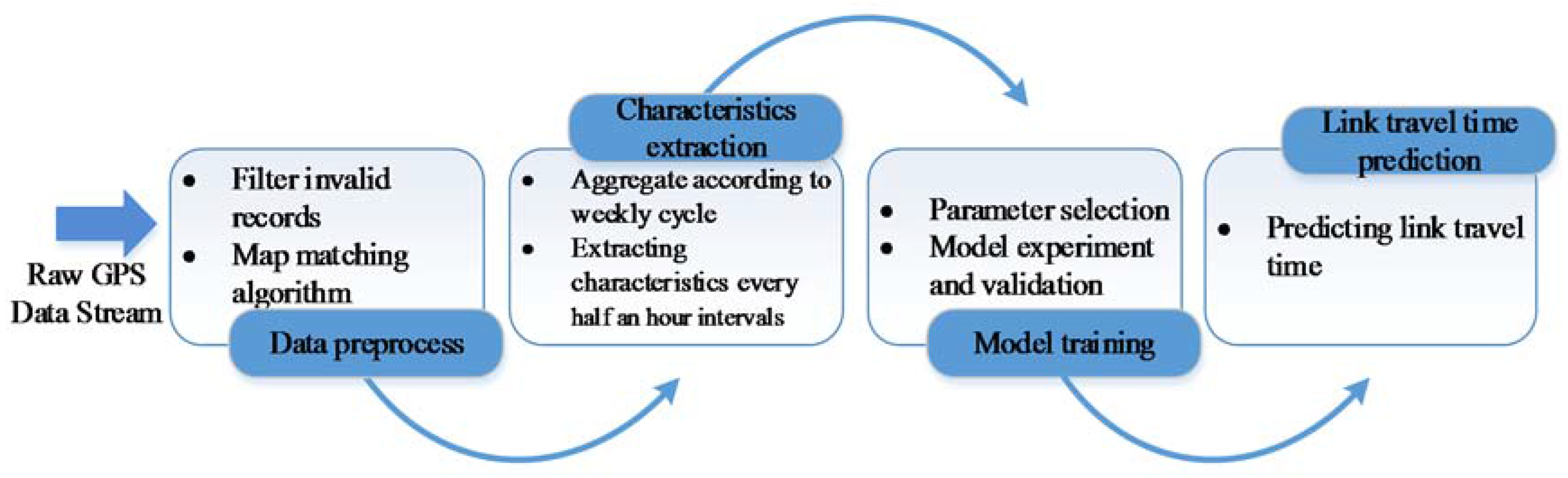
4. The Experiment
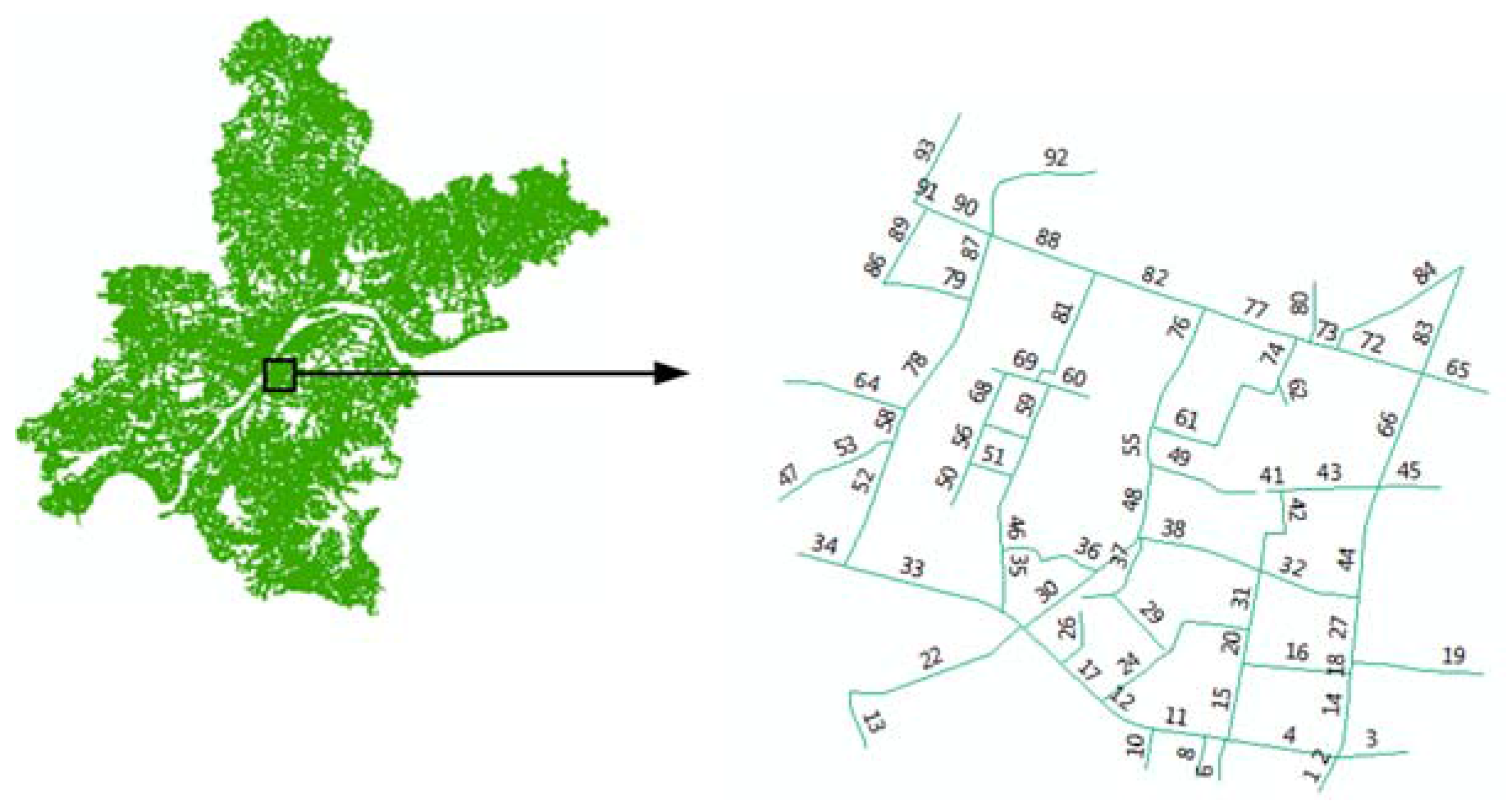
4.1. Data Description and Preparation
4.2. Model Application
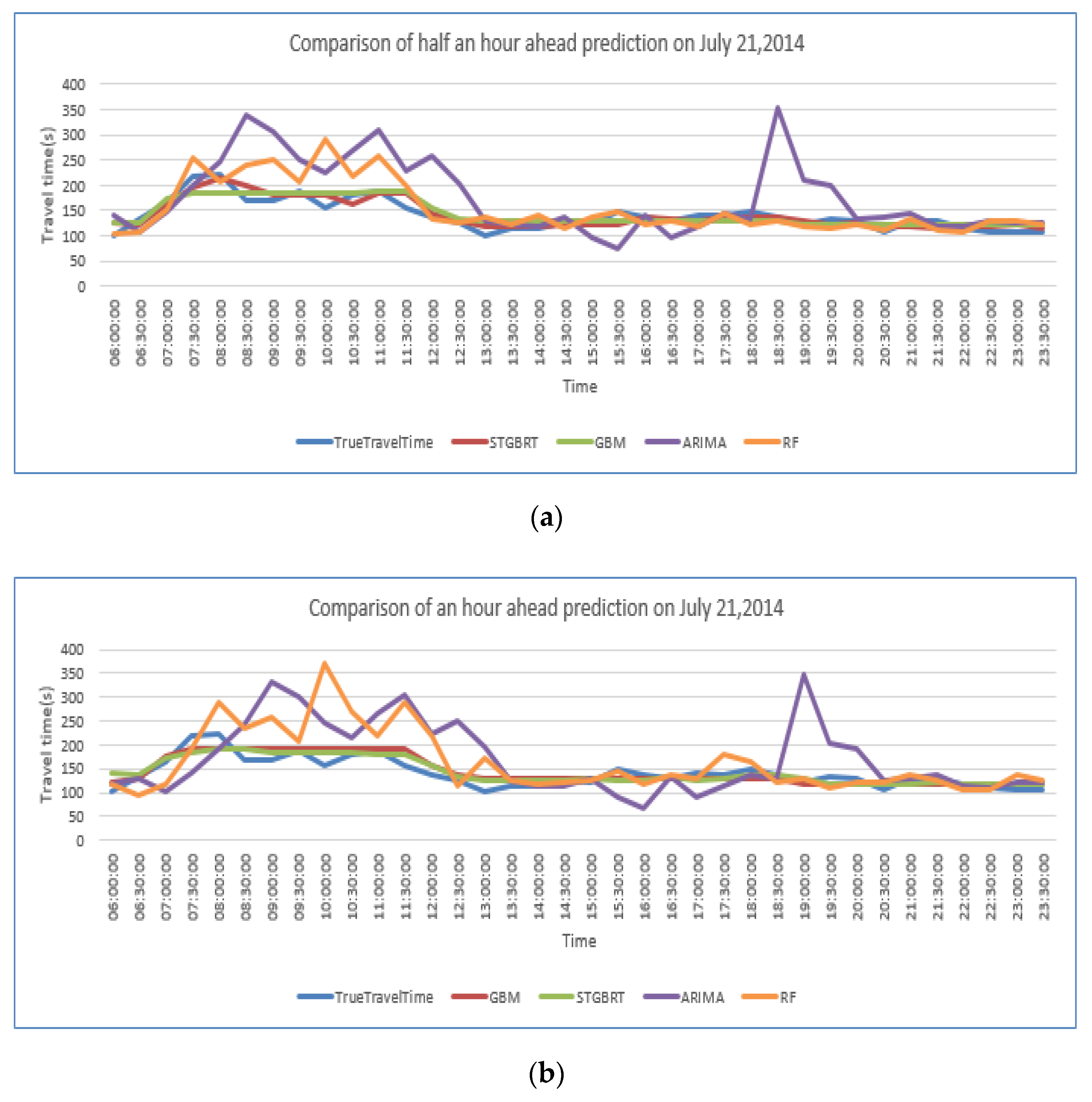
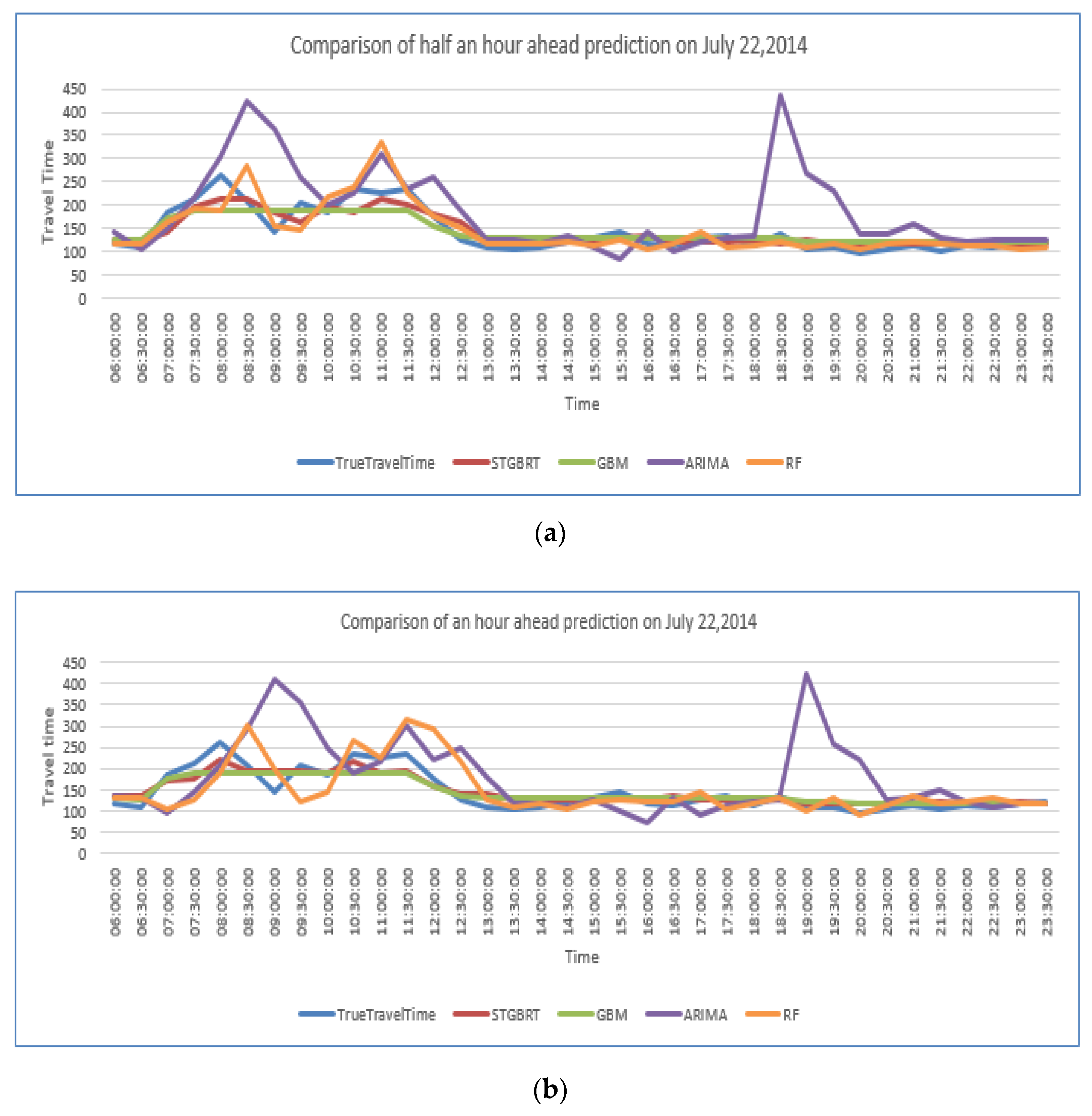
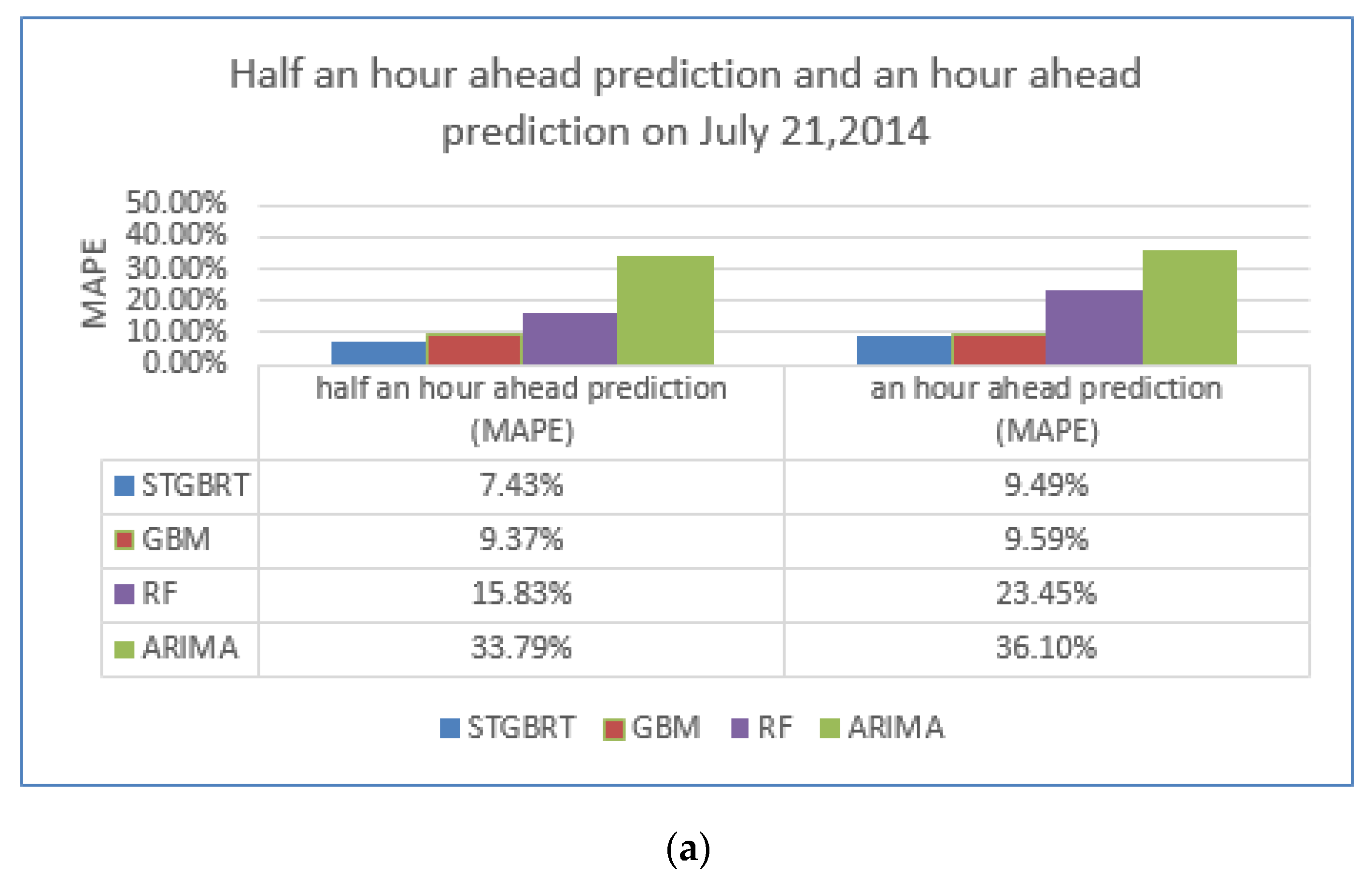
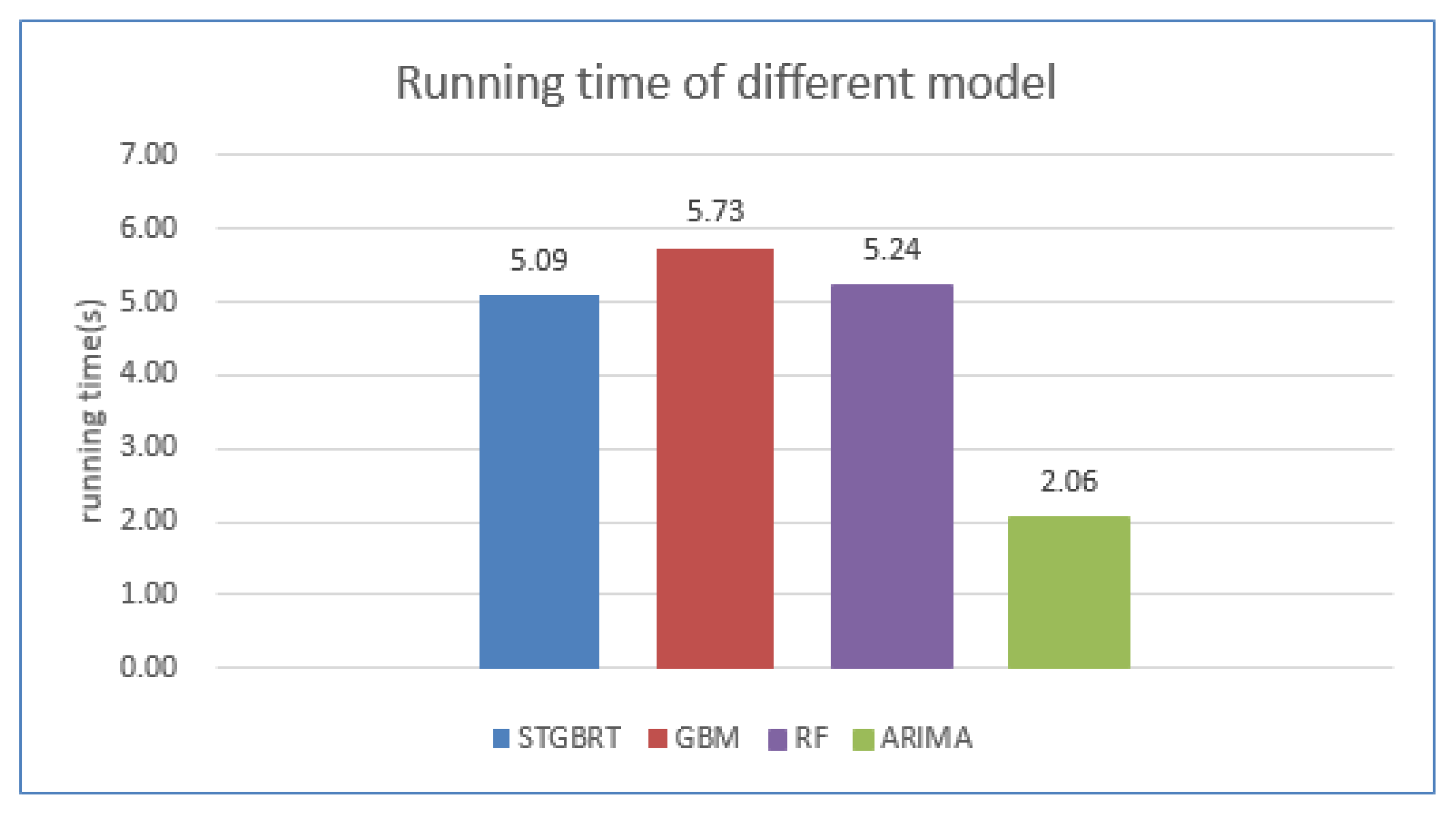
4.3. Model Comparisons
5. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Liu, K.; Yamamoto, T.; Morikawa, T. Feasibility of using taxi dispatch system as probes for collecting traffic information. J. Intell. Transp. Syst. Technol. Plan. Oper. 2009, 13, 16–27. [Google Scholar] [CrossRef]
- Wang, Y.; Zheng, Y.; Xue, Y. Travel time estimation of a path using sparse trajectories. In Proceedings of the 20th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 24–27 August 2014.
- Li, J. Estimation and Prediction of Link Travel Time for Urban Trunk and Secondary Street. Ph.D. Thesis, Jilin University, Jilin, China, 2012. [Google Scholar]
- Yao, E.J.; Zuo, T. Real-time map matching algorithm based on low-sampling-rate probe vehicle data. Beijing J. Beijing Univ. Tech. 2012, 39, 909–913. [Google Scholar]
- Zheng, Y.; Liu, Y.; Yuan, J.; Xie, X. Urban computing with taxicabs. In Proceedings of the 13th International Conference on Ubiquitous Computing, Beijing, China, 17–21 September 2011.
- Zheng, Y.; Liu, F.; Hsieh, H.P. U-Air: When urban air quality inference meets big data. In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2013.
- Min, W.; Wynter, L. Real-time road traffic prediction with spatio-temporal correlations. Transp. Res. Part C Emerg. Technol. 2011, 19, 606–616. [Google Scholar] [CrossRef]
- Fei, X.; Lu, C.C.; Liu, K. A Bayesian dynamic linear model approach for real-time short-term freeway travel time prediction. Transp. Res. Part C Emerg. Technol. 2011, 19, 1306–1318. [Google Scholar] [CrossRef]
- Li, L.; Li, Y.; Li, Z. Efficient missing data imputing for traffic flow by considering temporal and spatial dependence. Transp. Res. Part C Emerg. Technol. 2013, 34, 108–120. [Google Scholar] [CrossRef]
- Haghani, A.; Hamedi, M.; Sadabadi, K.F. Freeway travel time ground truth data collection using bluetooth sensors. J. Transp. Res. Board 2010, 2160, 60–68. [Google Scholar] [CrossRef]
- Williams, B.; Durvasula, P.; Brown, D. Urban freeway traffic flow prediction: Application of seasonal autoregressive integrated moving average and exponential smoothing models. Transp. Res. Rec. J. Transp. Res. Board 1998, 1644, 132–141. [Google Scholar] [CrossRef]
- Smith, B.; Demetsky, M. Traffic flow forecasting: Comparison of modeling approaches. J. Transp. Eng. 1997, 123, 261–266. [Google Scholar] [CrossRef]
- Wang, J.; Shi, Q. Short-term traffic speed forecasting hybrid model based on Chaos-wavelet analysis-support vector machine theory. Transp. Res. Part C Emerg. Technol. 2012, 27, 219–232. [Google Scholar] [CrossRef]
- Wei, Y.; Chen, M.C. Forecasting the short-term metro passenger flow with empirical mode decomposition and neural networks. Transp. Res. Part C Emerg. Technol. 2012, 21, 148–162. [Google Scholar] [CrossRef]
- Li, L.; Chen, X.; Li, Z.; Zhang, L. Freeway travel-time estimation based on temporal–spatial queueing model. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1536–1541. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, Y.; Haghani, A. A hybrid short-term traffic flow forecasting method based on spectral analysis and statistical volatility model. Transp. Res. Part C Emerg. Technol. 2014, 43, 65–78. [Google Scholar] [CrossRef]
- Montgomery, D.C.; Jennings, C.L.; Kulahci, M. Introduction to Time Series Analysis and Forecasting; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hong, W.C. Traffic flow forecasting by seasonal SVR with chaotic simulated annealing algorithm. Neurocomputing 2011, 74, 2096–2107. [Google Scholar] [CrossRef]
- Van Hinsbergen, C.; Van Lint, J.; Van Zuylen, H. Bayesian committee of neural networks to predict travel times with confidence intervals. Transp. Res. Part C Emerg. Technol. 2009, 17, 498–509. [Google Scholar] [CrossRef]
- Antoniou, C.; Koutsopoulos, H.N.; Yannis, G. Dynamic data-driven local traffic state estimation and prediction. Transp. Res. Part C Emerg. Technol. 2013, 34, 89–107. [Google Scholar] [CrossRef]
- Vlahogianni, E.I.; Karlaftis, M.G.; Golias, J.C. Short-term traffic forecasting: Where we are and where we’re going. Transp. Res. Part C Emerg. Technol. 2014, 43, 3–19. [Google Scholar] [CrossRef]
- Zhou, Z.H. Ensemble Methods: Foundations and Algorithms; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Hamner, B. Predicting travel times with context-dependent random forests by modeling local and aggregate traffic flow. In Proceedings of the ICDMW 2010, Sydney, Australia, 14–17 December 2010.
- Wang, Y. Prediction of weather impacted airport capacity using ensemble learning. In Proceedings of the Digital Avionics Systems Conference (DASC) 2011, Sacramento, CA, USA, 25–29 September 2011.
- Ahmed, M.M.; Abdel-Aty, M. Application of stochastic gradient boosting technique to enhance reliability of real-time risk assessment. Transp. Res. Rec. J. Transp. Res. Board 2013, 2386, 26–34. [Google Scholar] [CrossRef]
- Chung, Y.S. Factor complexity of crash occurrence: An empirical demonstration using boosted regression trees. Accid. Anal. Prev. 2013, 61, 107–118. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Haghani, A. A gradient boosting method to improve travel time prediction. Transp. Res. Part C Emerg. Technol. 2015. [Google Scholar] [CrossRef]
- Polikar, R. Ensemble based systems in decision making. IEEE Circ. Syst. Mag. 2006, 6, 21–45. [Google Scholar] [CrossRef]
- Leistner, C.; Saffari, A.; Santner, J.; Bischof, H. Semi-supervised random forests. In Proceedings of the IEEE 12th International Conference on Computer Vision, Porto, Portugal, 27 February–1 March 2009.
- Strobl, C.; Malley, J.; Tutz, G. An introduction to recursive partitioning: Rationale, application, and characteristics of classification and regression trees, bagging, and random forests. Psychol. Method. 2009, 14, 323–348. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R.; Friedman, J. Unsupervised learning. In The Elements of Statistical Learning; Springer: Berlin/Hamburg, Germany, 2009; pp. 485–585. [Google Scholar]
- Quinlan, J.R. Induction of decision trees. Mach. Learn. 1986, 1, 81–106. [Google Scholar] [CrossRef]
- Ruiz, R.; Stützle, T. A simple and effective iterated greedy algorithm for the permutation flowshop scheduling problem. Eur. J. Operat. Res. 2007, 177, 2033–2049. [Google Scholar] [CrossRef]
- Breiman, L. Arcing the Edge. Technical Report 486; Statistics Department, University of California at Berkeley: Berkeley, CA, USA, 1997. [Google Scholar]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Annal. Stat. 2001, 1189–1232. [Google Scholar] [CrossRef]
- Friedman, J.H. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Mason, L.; Baxter, J.; Bartlett, P.L.; Frean, M. Boosting algorithms as gradient descent in function space. In Proceedings of the NIPS 1999, Denver, CO, USA, 29 November–4 December 1999.
- Natekin, A.; Knoll, A. Gradient boosting machines, a tutorial. Front. Neurorobot. 2013. [Google Scholar] [CrossRef] [PubMed]
- Soper, H.E.; Young, A.W.; Cave, B.M.; Lee, A.; Pearson, K. On the distribution of the correlation coefficient in small samples. Appendix II to the papers of" Student" and RA Fisher. Biometrika 1917, 11, 328–413. [Google Scholar]
- Box, G.; Jenkins, G. Time Series Analysis: Forecasting and Control; Holden-Day: San Francisco, CA, USA, 1970. [Google Scholar]
- Mori, U.; Mendiburu, A.; Álvarez, M.; Lozano, J.A. A review of travel time estimation and forecasting for advanced traveller information systems. Transp. A Transp. Sci. 2015, 11, 119–157. [Google Scholar] [CrossRef]
- Fouque, C.; Bonnifait, P. Matching raw GPS measurements on a navigable map without computing a global position. IEEE Trans. Intell. Transp. Syst. 2012, 13, 887–898. [Google Scholar] [CrossRef]
- Chen, B.Y.; Yuan, H.; Li, Q.; Lam, W.H.; Shaw, S.L.; Yan, K. Map-matching algorithm for large-scale low-frequency floating car data. Int. J. Geogr. Inf. Sci. 2014, 28, 22–38. [Google Scholar] [CrossRef]
- Yuan, J.; Zheng, Y.; Zhang, C.; Xie, X.; Sun, G.Z. An interactive-voting based map matching algorithm. In Proceedings of the Eleventh International Conference on Mobile Data Management, Kansas City, MI, USA, 23–26 May 2010.
- Zhang, Y.; Yang, B.; Luan, X. Automated matching urban road networks using probabilistic relaxation. Acta Geod. Catogr. Sin. 2012, 41, 933–939. [Google Scholar]
- Li, Q.; Hu, B.; Yue, Y. Flowing car data map-matching based on constrained shortest path algorithm. Geomat. Inf. Sci. Wuhan Univ. 2013, 7, 805–808. [Google Scholar]
- Yu, D.X.; Gao, X.Y.; Yang, Z.S. Individual vehicle travel-time estimation based on GPS data and analysis of vehicle running characteristics. J. Jilin Univ. 2010, 40, 965–970. (in Chinese). [Google Scholar]
- Dong, H.; Wu, F. Estimation of average link travel time using fuzzy C-mean. Bull. Sci. Technol. 2011, 27, 426–430. [Google Scholar]
- Jiang, G.; Chang, A.; Zhang, W. Comparison of link travel-time estimation methods based on GPS equipped floating car. J. Jilin Univ. 2009, 39, 182–186. (in Chinese). [Google Scholar]
- Liu, Y.; Kang, C.; Gao, S.; Xiao, Y.; Tian, Y. Understanding intra-urban trip patterns from taxi trajectory data. J. Geogr. Syst. 2012, 14, 463–483. [Google Scholar] [CrossRef]
- Liu, X.; Gong, L.; Gong, Y.; Liu, Y. Revealing travel patterns and city structure with taxi trip data. J. Transp. Geogr. 2013, 43, 78–90. [Google Scholar] [CrossRef]
- Zhang, F.; Zhu, X.; Guo, W.; Ye, X.; Hu, T.; Huang, L. Analyzing urban human mobility patterns through a thematic model at a finer scale. ISPRS Int. J. Geo-Inf. 2016. [Google Scholar] [CrossRef]
- Fang, Z.; Li, Q.; Shaw, S.L. What about people in pedestrian navigation? Geo-spat. Inf. Sci. 2015, 18, 135–150. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Machine Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Tsay, R.S. Analysis of Financial Time Series; John Wiley & Sons: New York, NY, USA, 2005. [Google Scholar]
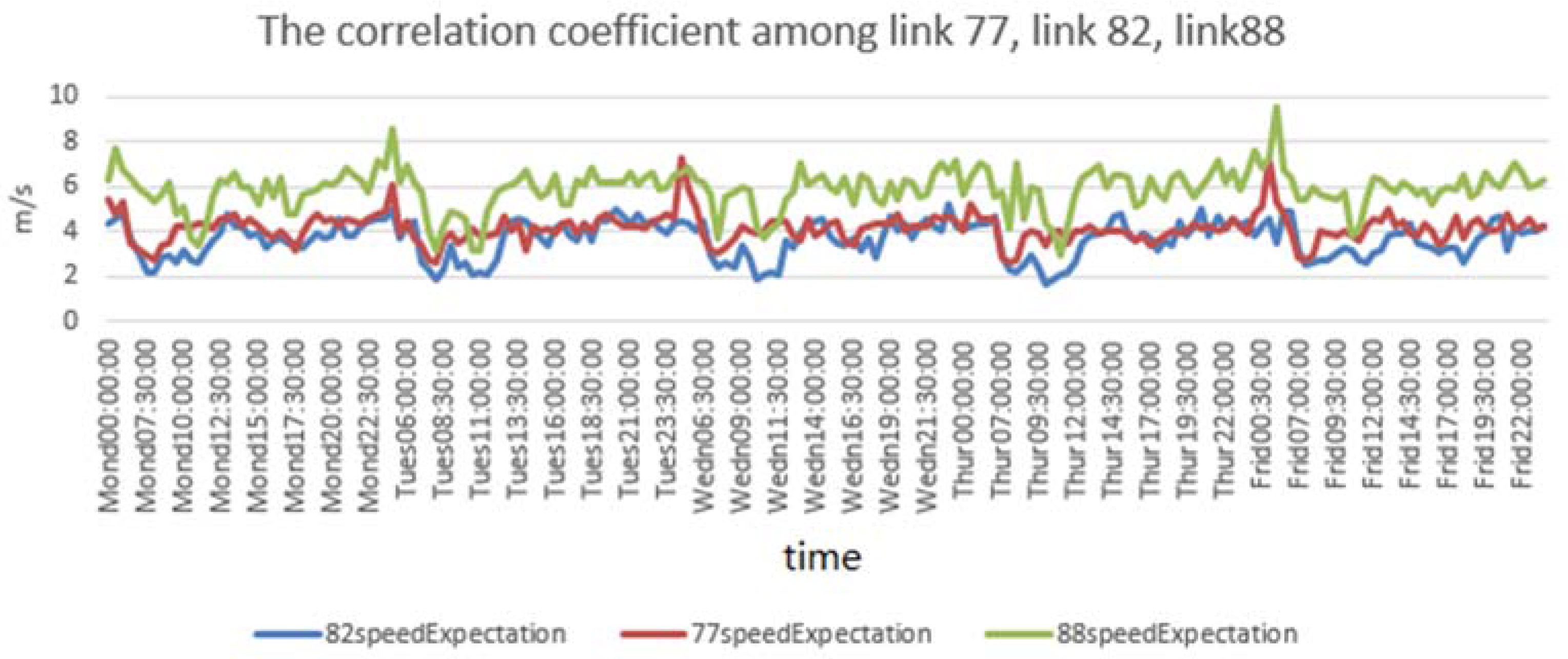


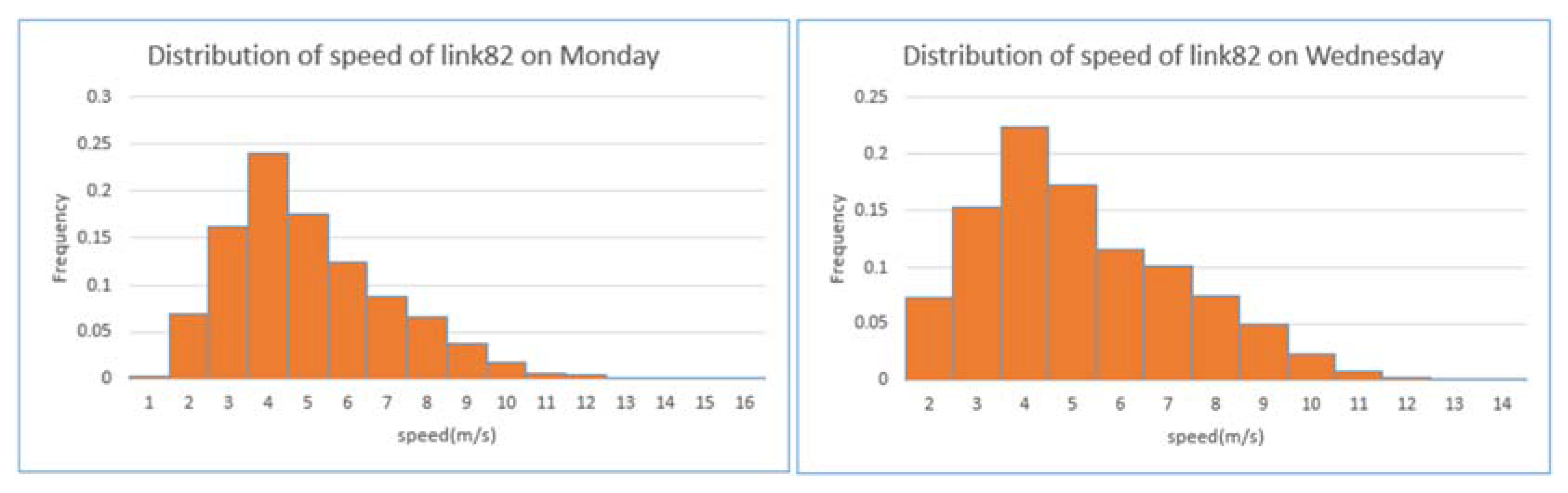
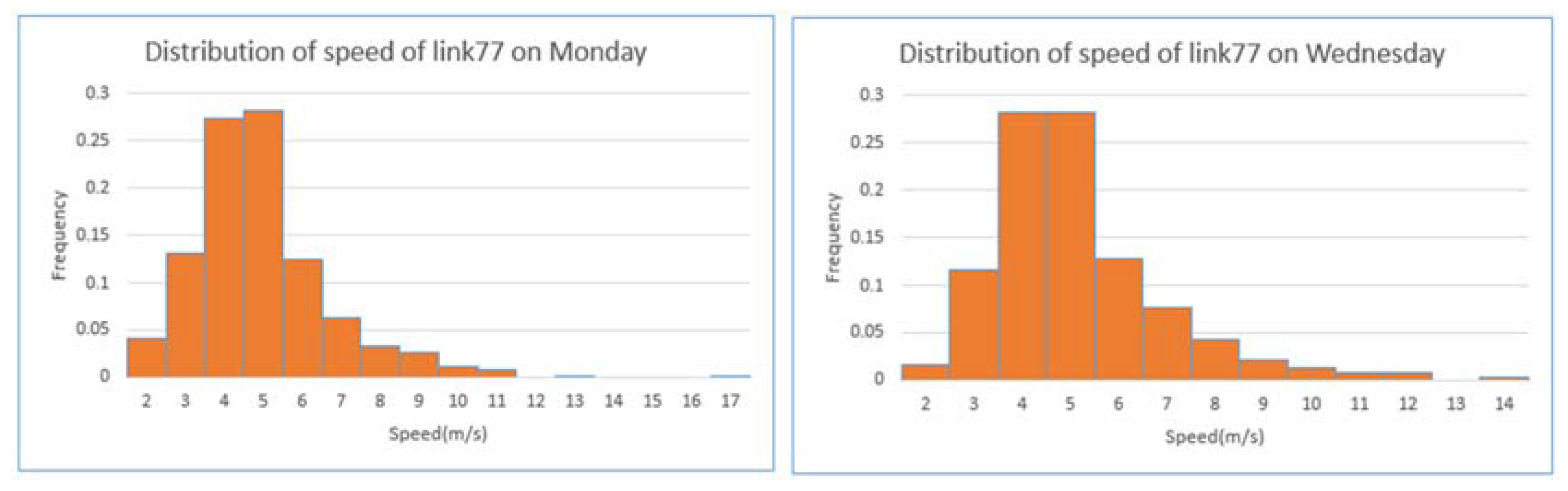
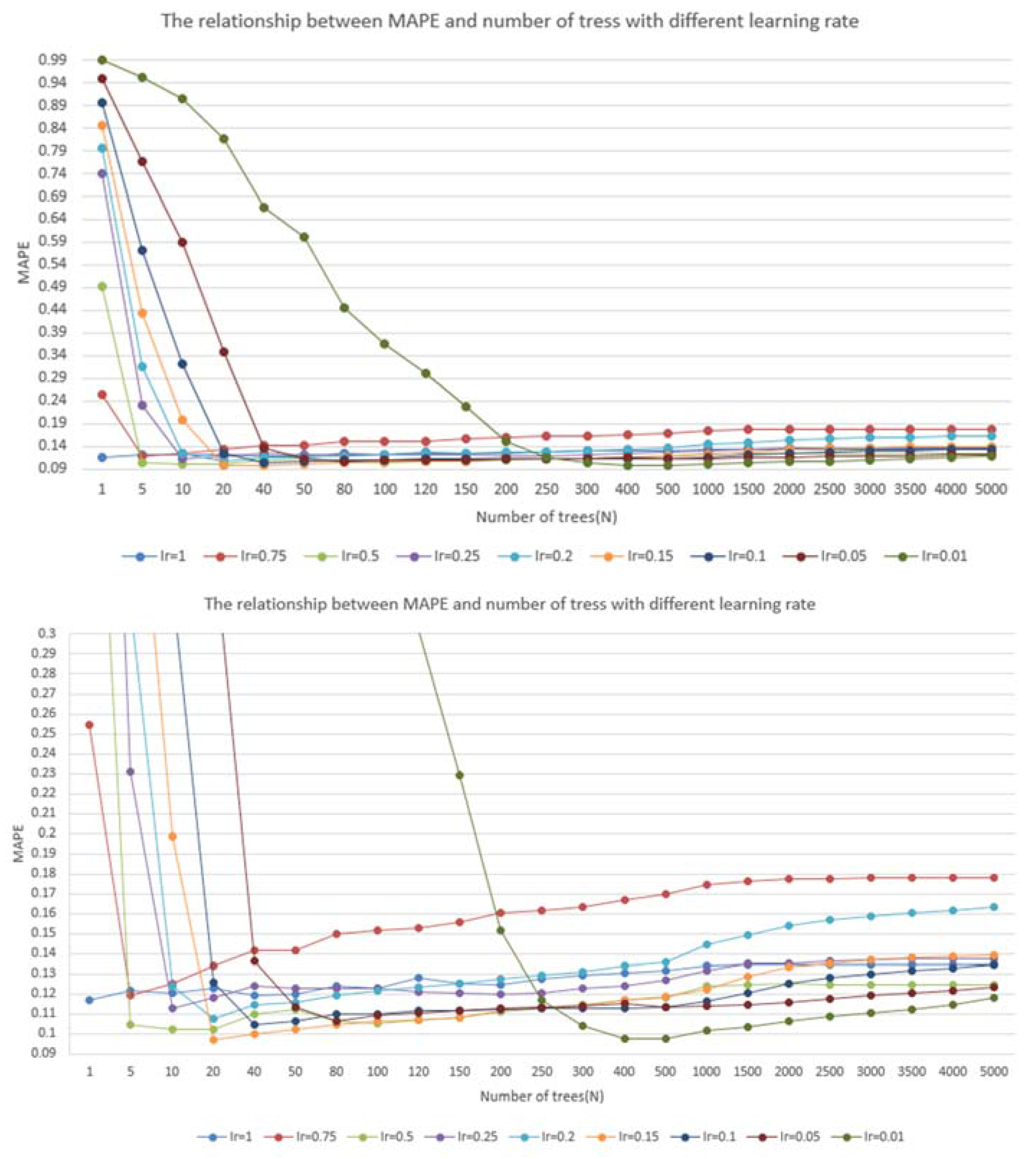
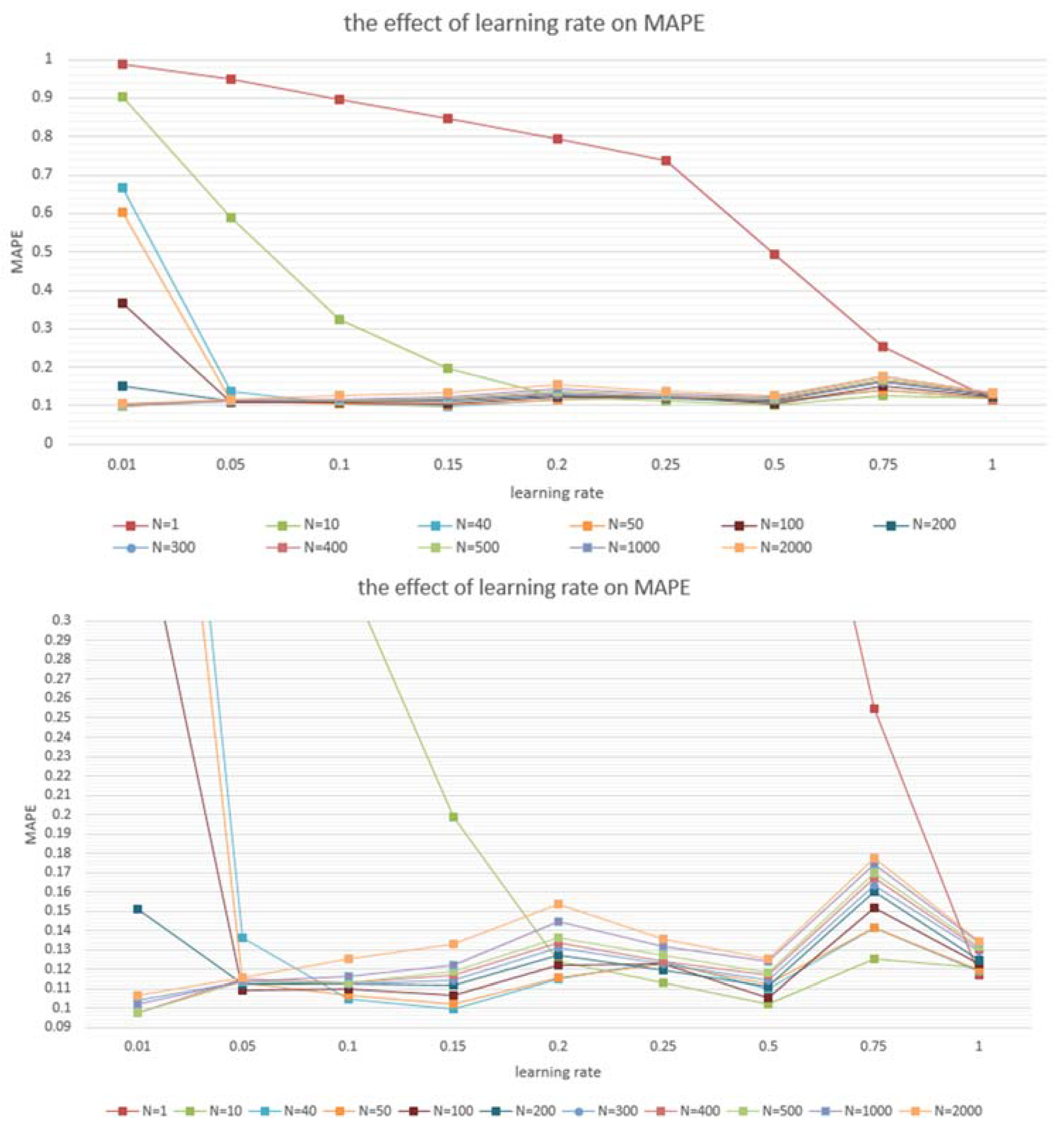
| Link | Monday | Tuesday | Wednesday | Thursday | Friday |
|---|---|---|---|---|---|
| Link 77, link 82 in −1 traffic flow direction | 0.755327 ** | 0.599857 ** | 0.451914 ** | 0.575618 ** | 0.558733 ** |
| Link 88, link 82 in −1 traffic flow direction | 0.719256 ** | 0.837093 ** | 0.762925 ** | 0.715509 ** | 0.605603 ** |
| t | t+1 | t+2 | t+3 | t+4 | t+5 | t+6 | t+7 | t+8 | t+9 | |
|---|---|---|---|---|---|---|---|---|---|---|
| t | 1 | 0.774 ** | 0.557 ** | 0.365 * | 0.224 | 0.169 | 0.189 | 0.114 ** | −0.014 ** | −0.104 * |
| t+1 | 0.774 ** | 1 | 0.741 ** | 0.542 ** | 0.377 ** | 0.236 | 0.168 | 0.202 | 0.139 | 0.040 |
| t+2 | 0.557 ** | 0.741 ** | 1 | 0.734 ** | 0.516 ** | 0.363 * | 0.225 | 0.128 | 0.201 | 0.142 |
| t+3 | 0.365 * | 0.542 ** | 0.734 ** | 1 | 0.724 ** | 0.511 ** | 0.358 * | 0.205 | 0.132 | 0.211 |
| t+4 | 0.224 | 0.377 ** | 0.516 ** | 0.724 ** | 1 | 0.727 ** | 0.508 ** | 0.350 * | 0.223 | 0.169 |
| t+5 | 0.169 | 0.236 | 0.363 * | 0.511 ** | 0.727 ** | 1 | 0.725 ** | 0.511 ** | 0.360 * | 0.244 |
| t+6 | 0.189 | 0.168 | 0.225 | 0.358 * | 0.508 ** | 0.725 ** | 1 | 0.725 ** | 0.514 ** | 0.366 * |
| t+7 | 0.114 | 0.202 | 0.128 | 0.205 | 0.350 * | 0.511 ** | 0.725 ** | 1 | 0.749 ** | 0.554 ** |
| t+8 | −0.014 | 0.139 | 0.201 | 0.132 | 0.223 | 0.360 * | 0.514 ** | 0.749 ** | 1 | 0.753 ** |
| t+9 | −0.104 | 0.040 | 0.142 | 0.211 | 0.169 | 0.244 | 0.366 * | 0.554 ** | 0.753 ** | 1 |
| Section ID | Start Coordinate | End Coordinate | Length (Meter) | ||
|---|---|---|---|---|---|
| Latitude | Longitude | Latitude | Longitude | ||
| 88 | 30.535 | 114.329 | 30.533 | 114.334 | 475.69 |
| 82 | 30.533 | 114.334 | 30.532 | 114.338 | 489.10 |
| 77 | 30.532 | 114.338 | 30.530 | 114.342 | 411.43 |
| Link ID | Enter Endpoint ID | Exit Endpoint ID | Probe vehicle ID | Time Instant | Travel Time (s) | Average Speed (m/s) |
|---|---|---|---|---|---|---|
| 82 | 35 | 48 | 23501 | 2014–06–03 03:17:11 | 100.0 | 4.89 |
| 82 | 35 | 48 | 22608 | 2014–06–02 00:00:50 | 85.0 | 5.75 |
| 82 | 48 | 35 | 29444 | 2014–06–02 00:12:03 | 101.0 | 4.84 |
| Workday | Mean | SD | 25th | 50th | 75th | Min | Max |
|---|---|---|---|---|---|---|---|
| Monday | 6.55 | 2.22 | 5.23 | 6.61 | 7.8 | 1.03 | 26.43 |
| Tuesday | 6.56 | 2.19 | 5.17 | 6.61 | 7.8 | 1.15 | 15.35 |
| Wednesday | 6.64 | 1.95 | 5.41 | 6.61 | 7.8 | 1.46 | 16.4 |
| Thursday | 6.68 | 2.23 | 5.52 | 6.7 | 7.8 | 1.43 | 18.3 |
| Friday | 6.42 | 2.10 | 5.23 | 6.34 | 7.55 | 1.2 | 15.86 |
| Workday | Mean | SD | 25th | 50th | 75th | Min | Max |
|---|---|---|---|---|---|---|---|
| Monday | 4.83 | 2.15 | 3.27 | 4.33 | 6.04 | 0.94 | 15.78 |
| Tuesday | 4.82 | 2.08 | 3.26 | 4.41 | 6.09 | 1.06 | 13.97 |
| Wednesday | 4.73 | 2.09 | 3.12 | 4.25 | 6.19 | 1.04 | 13.59 |
| Thursday | 4.77 | 2.18 | 3.14 | 4.33 | 6.25 | 0.93 | 13.22 |
| Friday | 4.97 | 2.20 | 3.37 | 4.61 | 6.04 | 1.11 | 17.47 |
| Workday | Mean | SD | 25th | 50th | 75th | Min | Max |
|---|---|---|---|---|---|---|---|
| Monday | 4.42 | 1.77 | 3.27 | 4.16 | 5.08 | 1.2 | 16.46 |
| Tuesday | 4.16 | 1.61 | 3.21 | 3.92 | 4.84 | 1.12 | 13.72 |
| Wednesday | 4.61 | 1.81 | 3.37 | 4.29 | 5.14 | 1.32 | 13.72 |
| Thursday | 4.18 | 1.52 | 3.14 | 4.03 | 4.84 | 1.04 | 11.76 |
| Friday | 4.47 | 1.82 | 3.37 | 4.24 | 5.02 | 1.24 | 18.7 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Weekday | Period of day | tarHTTt−1 | tarHTTt−2 | ΔtarHTT t−1 | tarRTTt−1 | tarRTTt−2 | ΔtarRTT t−1 | UpHTTt−1 | UpHTTt−2 | ΔUpHTT t−1 | UpRTTt−1 | UpRTTt−2 | ΔUpRTT t−1 | DoHTTt−1 | DoHTTt−2 | ΔDoHTT t−1 | tarRTTt |
| 1 | 13.0 | 111.16 | 114.01 | −2.85 | 49.0 | 110.0 | −61.0 | 85.56 | 85.56 | 0.0 | 85.56 | 85.56 | 0.0 | 86.26 | 86.26 | 0.0 | 105.82 |
| 2 | 20.0 | 143.01 | 209.02 | −66.01 | 153.83 | 111.14 | 42.69 | 96.49 | 110.89 | −14.4 | 71.0 | 110.89 | −39.89 | 103.91 | 114.3 | −10.39 | 239.41 |
| 3 | 30.0 | 109.18 | 113.22 | −4.04 | 102.97 | 175.2 | −72.23 | 75.87 | 78.24 | −2.37 | 160.0 | 58.0 | 102.0 | 106.32 | 89.06 | 17.26 | 144.19 |
| 4 | 36.0 | 132.91 | 125.41 | 7.5 | 286.39 | 237.0 | 49.39 | 74.68 | 89.75 | −15.07 | 162.99 | 89.75 | 73.24 | 121.74 | 109.14 | 12.6 | 88.0 |
| 5 | 15.0 | 98.81 | 98.81 | 0.0 | 47.97 | 106.0 | −58.03 | 73.87 | 70.79 | 3.08 | 73.0 | 70.79 | 2.21 | 101.6 | 85.72 | 15.88 | 130.47 |
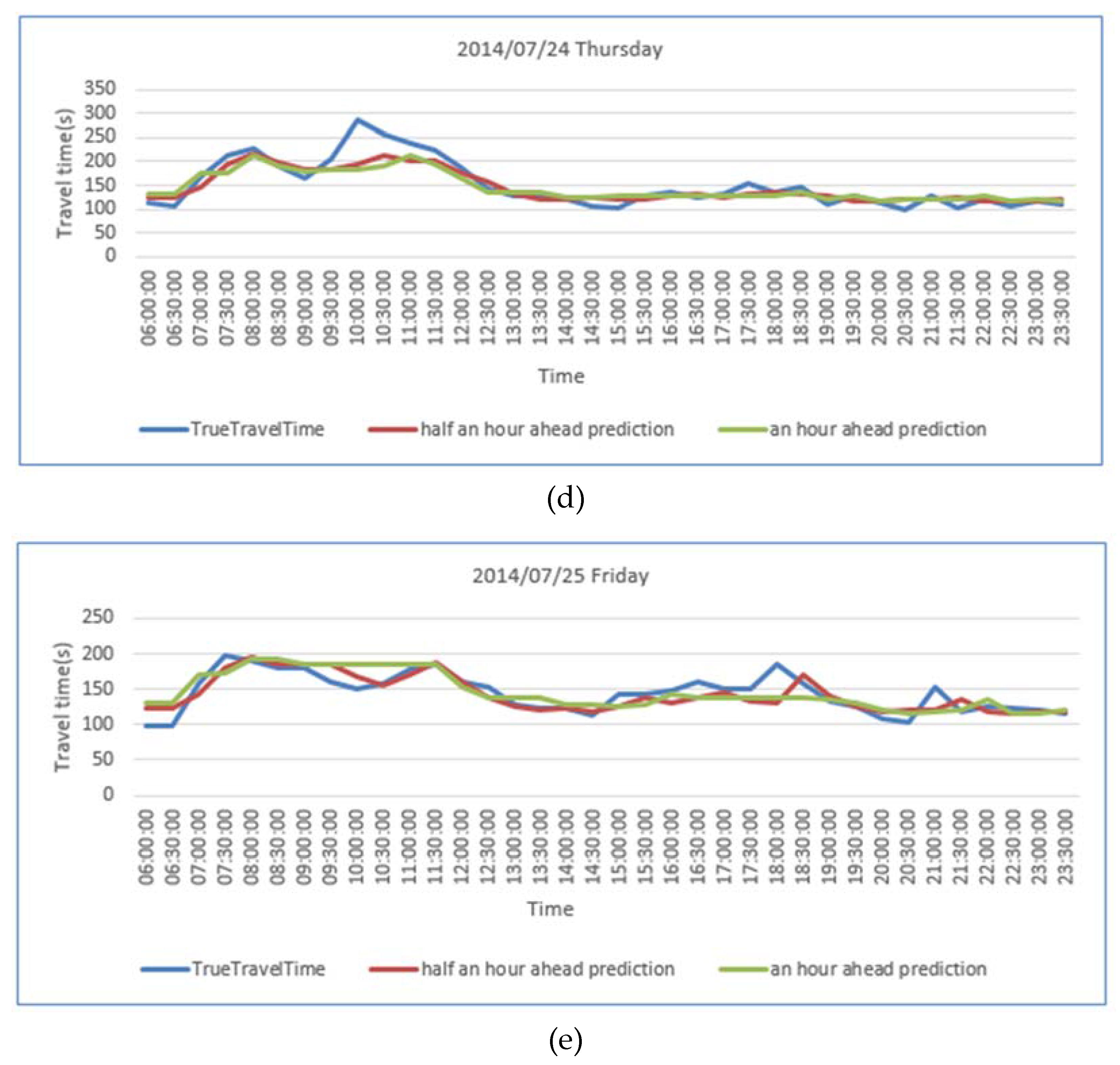
| Ate | 21 July 2014 | 22 July 2014 | 23 July 2014 | 24 July 2014 | 25 July 2014 |
|---|---|---|---|---|---|
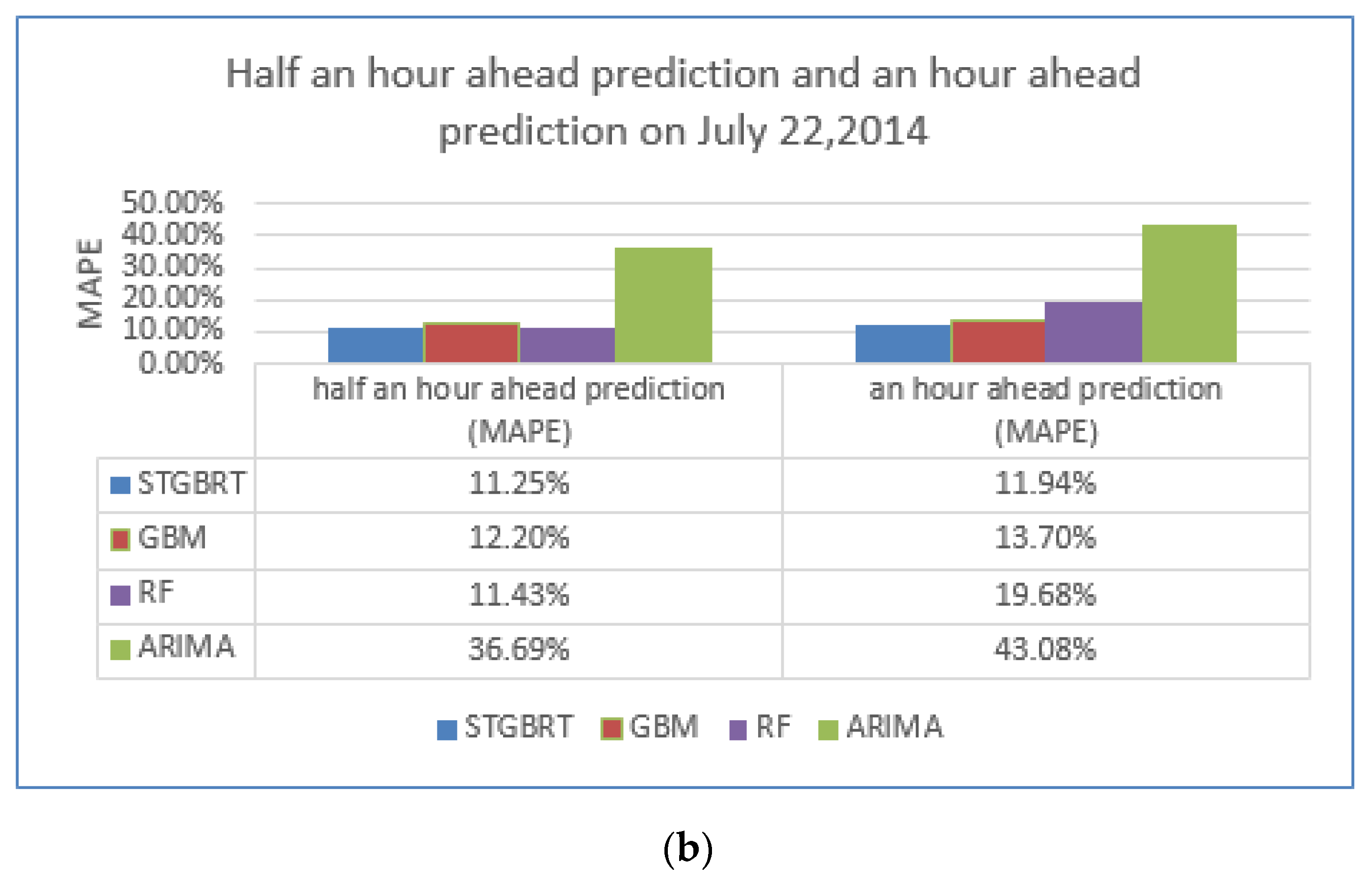
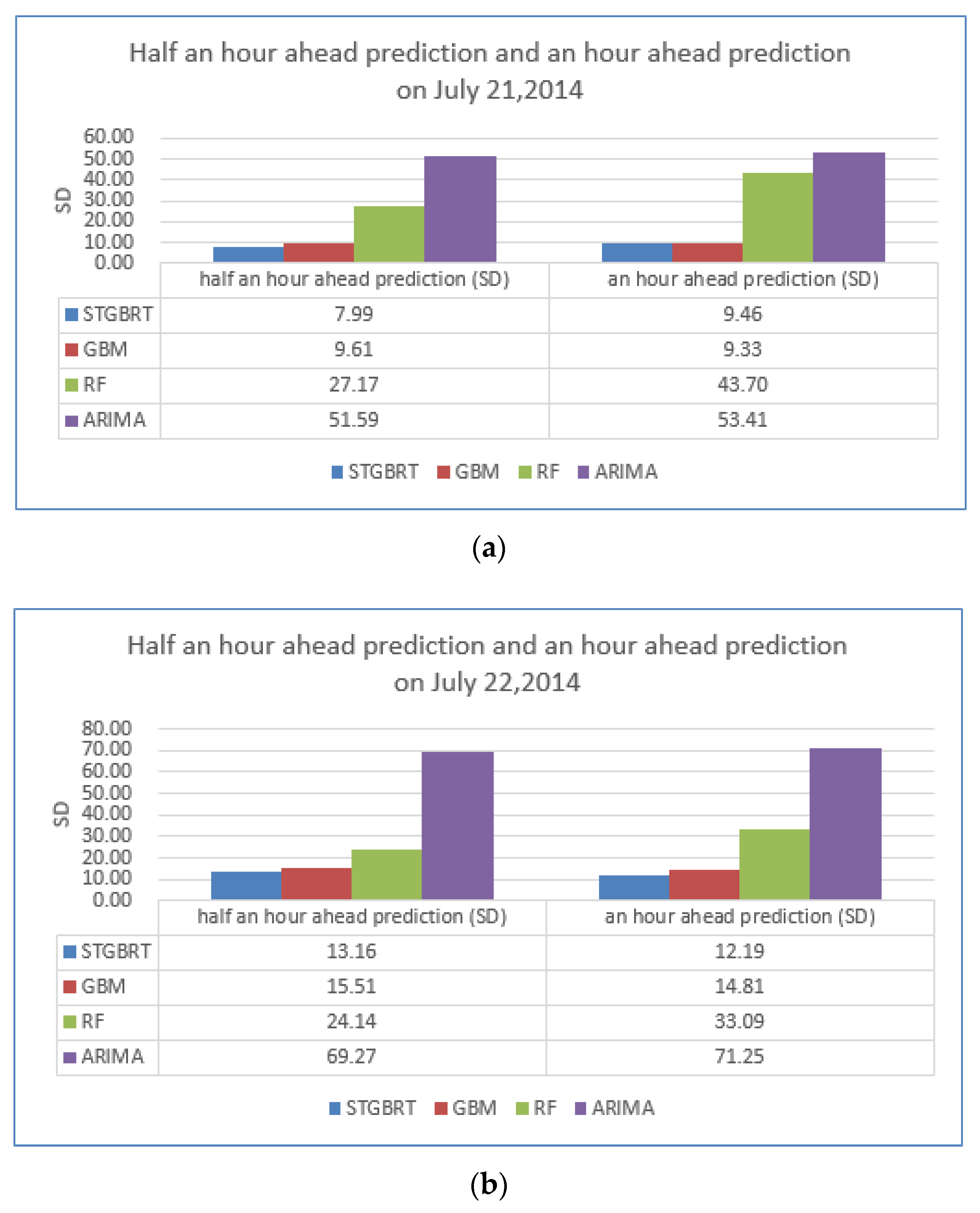
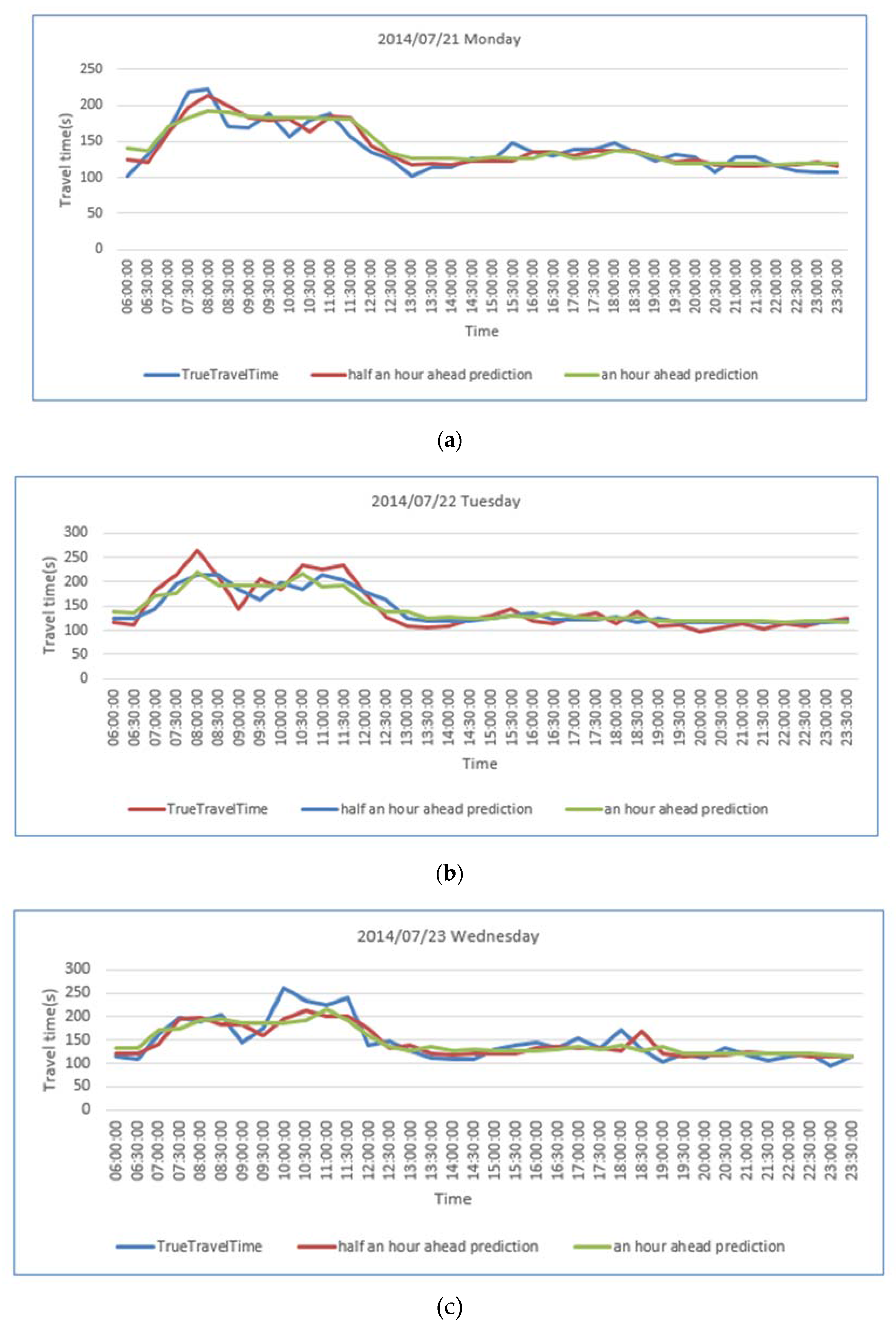
| MAPE of predictions made 30 min ahead | 7.43% | 11.25% | 11.23% | 10.26% | 7.89% |
| MAPE of predictions made an hour ahead | 9.49% | 11.94% | 10.98% | 10.31% | 9.77% |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, F.; Zhu, X.; Hu, T.; Guo, W.; Chen, C.; Liu, L. Urban Link Travel Time Prediction Based on a Gradient Boosting Method Considering Spatiotemporal Correlations. ISPRS Int. J. Geo-Inf. 2016, 5, 201. https://doi.org/10.3390/ijgi5110201
Zhang F, Zhu X, Hu T, Guo W, Chen C, Liu L. Urban Link Travel Time Prediction Based on a Gradient Boosting Method Considering Spatiotemporal Correlations. ISPRS International Journal of Geo-Information. 2016; 5(11):201. https://doi.org/10.3390/ijgi5110201
Chicago/Turabian StyleZhang, Faming, Xinyan Zhu, Tao Hu, Wei Guo, Chen Chen, and Lingjia Liu. 2016. "Urban Link Travel Time Prediction Based on a Gradient Boosting Method Considering Spatiotemporal Correlations" ISPRS International Journal of Geo-Information 5, no. 11: 201. https://doi.org/10.3390/ijgi5110201
APA StyleZhang, F., Zhu, X., Hu, T., Guo, W., Chen, C., & Liu, L. (2016). Urban Link Travel Time Prediction Based on a Gradient Boosting Method Considering Spatiotemporal Correlations. ISPRS International Journal of Geo-Information, 5(11), 201. https://doi.org/10.3390/ijgi5110201





