1. Introduction
Maps are widely used in scientific research. Their accuracy can, however, be critical, with the effect of map error being dramatic in a range of applications (e.g., [
1]). For example, the estimated value of ecosystem services for the conterminous USA determined using the National Land Cover Database (2006) changes from $1118 billion/y to $600 billion/y after adjustment for the known error in the maps used [
2]. It is essential, therefore, that maps be as accurate as possible and the accuracy information is conveyed usefully to map users.
One initial source of error in mapping is the reference data used to construct the map. It is, for example, normally assumed that the reference dataset used is from an authoritative source and can be treated as a gold standard. This is, however, often unlikely to be true. In addition, there may be other concerns about the reference data. These data may, for example, have been generated from samples that are small, biased, and unrepresentative. Moreover, in some large international databases the sampling issues may vary from region to region (e.g., due to different national data acquisition policies). The databases may also contain errors of varying nature and magnitude such as mislabelling arising from confusion between classes [
3], which may also vary regionally if, for example, the skills and expertise of data collectors vary. These various sources of error (e.g., mislabelled cases) and uncertainty (e.g., ambiguous class membership) may degrade mapping and the effect may vary between mapping methods. As a result, it is important to know the sensitivity of mapping methods to error in the data used to generate them. This paper aims to explore the sensitivity of mapping methods to error and uncertainty in the reference datasets used in map derivation. It focuses on thematic mapping such as species distribution maps and land cover.
2. Reference Data Quality and Mapping
Reference data may sometimes be obtained from databases that bring together data from a variety of sources. While this is useful, there may also be a range of problems with such resources. One key issue is that the contributed data may have been acquired using very different methods. For example, different sample designs may have been used, and if this variation is not addressed in later analyses it could cause problems (e.g., imbalanced samples, etc.). The quality of the labelling of cases in a database may also vary. This is a major concern in common applications such as mapping land cover from remotely sensed data because the reference dataset is typically used as if it is perfect yet even a small deviation can be a problem. For example, in assessing the accuracy of maps or making estimates of class areal extent from them, small reference data errors can be a source of large error [
4]. Here, the focus is on the reference data used in map production (e.g., training a supervised image classification) as the quality of the training stage can have a substantial effect on the quality of the land cover map derived.
The accuracy of land cover maps obtained from remote sensing is often viewed as being inadequate (e.g., [
5]). A variety of reasons can be put forward to explain this situation [
6], which has driven considerable research to address potential sources of error ranging from the development of new sensors to the generation of new image analysis techniques. Despite these various advances, it is still sometimes a challenge for many users to map land cover with sufficient accuracy from remotely sensed data. One of the reasons for this situation lies beyond the issues connected with remote sensing and with the ground reference data that are central to supervised digital image classifications.
Ground reference data play a fundamental role in supervised image classification. The ground dataset used is typically assumed to be perfect (i.e., ground truth) but in reality is normally imperfect. Datasets such as the Global Biodiversity Information Facility (GBIF, [
7]) for example, hold valuable information on species observations that could be used to aid mapping species directly or from remotely sensed data. However, the data contained in the database are highly variable. The contents include data aggregated from many sources, ranging from authoritative, systematic plot censuses and field surveys to casual observations contributed by “citizen scientists.” Standardizing the data in terms of factors, such as sampling effort or labelling quality, is a challenge. Mislabelling is, for example, a common error in ground data, even that acquired by authoritative sources [
3]. This error may arise in a variety of ways, from simple typographical or transcription errors through to ambiguity in class membership, and the magnitude can be large. For example, expert aerial photograph interpreters may typically disagree on the class label for ~30% of cases [
8], yet such data are widely used as ground data to support supervised classifications of satellite remote sensor data. Similarly, the accuracy of species identification in the field can vary greatly depending on the skill and expertise of the surveyor [
3,
9]. This type of issue may be a particular concern in relation to the use of volunteers as a source of data. There is considerable potential for volunteered geographic information and citizen contributions [
10,
11] in the provision of ground reference data, notably in helping to acquire timely data over large areas, but also substantial concerns linked to the quality of the data, which can hinder its use [
12].
It is known that ground data errors can substantially degrade the assessment of classification or map accuracy [
13,
14], even if the amount of error is small [
4]. The effects of ground data error on training a supervised classifier are less well-defined although a growing literature highlights a range of issues and concerns (e.g., [
15]).
Mislabelled training cases may be expected to impact upon the training stage of a supervised classification in a variety of ways. The mislabelled cases could be viewed as a type of noise and it is known that noise can have both negative and positive impacts on a classification (e.g., [
16,
17]). The effect will also vary in relation to key aspects of the nature of the error. For example, the effects of mislabelling differ between instances in which mislabelling is spread relatively uniformly through the data and instances where mislabelling is perhaps focused on just a small sub-set of the classes involved [
16]. The importance of this type of issue will also vary between users and their planned use of the thematic map; for any specific use case, some errors will be more critical than others [
18]. As a general starting point, however, mislabelled cases in a ground dataset will be expected to degrade the training statistics and so ultimately the accuracy of a supervised digital image classification. The specific effects of mislabelled cases would, however, depend on the details of the approach to classification adopted. Classifiers, for example, can differ greatly in how they use a training set (e.g., some focus upon summary statistical features such as the class centroid while others rely directly upon subsets of the individual cases available) [
16,
19,
20,
21,
22] and so their sensitivity to mislabelling will be expected to vary. Additionally, there are a variety of methods that may be adopted to reduce the effects of mislabelling on a classification analysis.
It is hypothesized that the magnitude of the effect of mislabelled training cases will be a function of the magnitude of the error, the nature of the error, and the classifier used. Here, particular attention is paid to classification by the support vector machine (SVM), which has become a popular classifier for the generation of land cover maps from remotely sensed data. Numerous comparative studies have shown that the SVM is able to generate land cover maps more accurately than a suite of alternative methods used by the remote sensing community [
23,
24,
25]. While classification by SVM can be sensitive to imbalanced training sets, in which the classes are represented unequally, the means to address this issue are available and hence knowledge of relative class abundance and sampling concerns can be constructively used to facilitate accurate mapping [
26]. The SVM has also been claimed to have a range of attributes that make it particularly attractive for use in mapping land cover from remotely sensed data. In particular, it has been claimed that the SVM is insensitive to the Hughes effect [
27], that it only requires a small training set [
28,
29], and that it is insensitive to error in the training set [
30]. The first claim, about freedom from the Hughes effect, has been shown to be untrue [
31]. The second claim, about the potential for accurate classification from small training sets, has been demonstrated but the training cases have to be collected with care to fulfil this potential [
32]. The focus of this article is on the final attribute that is claimed: that is, the low sensitivity of the SVM to error in the training dataset. The literature does include studies that show that the accuracy of classification by SVM can be affected by error in the training set [
33,
34], and this issue is explored in this article from a remote sensing perspective.
Here, the impacts of training data with variable type and magnitude of mislabelling error on the accuracy of SVM classification are explored. For context, a comparative assessment is also made relative to a conventional statistical classifier, a discriminant analysis, the relevance vector machine (RVM), and sparse multinomial logistic regression (SMLR), which, like the SVM, offers the potential for accurate classification from small training sets [
35]. The key focus is on the impacts arising from the nature and magnitude of mislabelling. Here, two types of mislabelling error are considered. The first is random error, which has been explored in other studies, but the second is error involving similar classes. The latter is of particular importance as in many instances error will not be expected to be random but rather to involve confusion between relatively similar classes. For example, in many studies some of the land cover classes are defined in such a way that sites on the ground that are very similar belong to different classes. For example, the class forest is often defined using a variable such as the percentage canopy cover [
36]. Two sites on the ground made up of the same species and having similar environmental conditions could belong to completely different classes due to miniscule differences in their canopy cover if close to the threshold value used in the definition of the classes. As a result, error disproportionately affects cases that one would expect to be similar both on the ground and spectrally.
This paper will briefly highlight imbalances in databases, often linked to sampling, which may require attention prior to a classification before focusing, in more detail, on the effects of mislabelled training cases on map accuracy.
3. Variation in Sampling
In many mapping studies the available data are simply used without explicit accommodation for their detailed nature. For example, in land cover mapping from remotely sensed data it is common for a proportion of the available reference data to be used for training a classifier and the remainder used for validation. However, in some datasets there may be problems with such an approach. One problem with large international databases is that the data contributed may have been acquired following very different methods. Critically, for example, the sampling effort may vary greatly. This could lead to substantial problems with, for example, sampling being more intensive in some regions than others, leading to datasets that are artificially imbalanced in terms of class composition if the geographical distributions of the classes differ. This latter issue can be a major problem as popular mapping methods such as the SVM can sometimes be highly sensitive to imbalanced training sets [
26] and a failure to account for sampling variations may hinder the use of advanced machine learning classifiers. In this section the aim is to simply illustrate the magnitude of sampling problems, using a major database as an example.
An important and increasingly used source of species field observations is the GBIF [
7]. GBIF data comprises a large range of species occurrence observations collected with a wide variety of sampling approaches. In addition, there may be differences in the methodologies used to observe and record occurrences per taxon. Plots, and plots within transects, are common practice in vegetation censuses, while transects, point counts, and live traps are preferred in the case of animals. Moreover, factors such as national biodiversity monitoring schemes, funding schemes, focal ecosystems, and accessibility to remote areas act to add additional sources of variation, especially at multinational scales [
37]. Undoubtedly, all those sources of variation combined result in non-homogeneous sampling and that has important consequences not only for the development of accurate species distribution models but, more importantly, for the conservation and management decisions informed by the derived maps of species distribution.
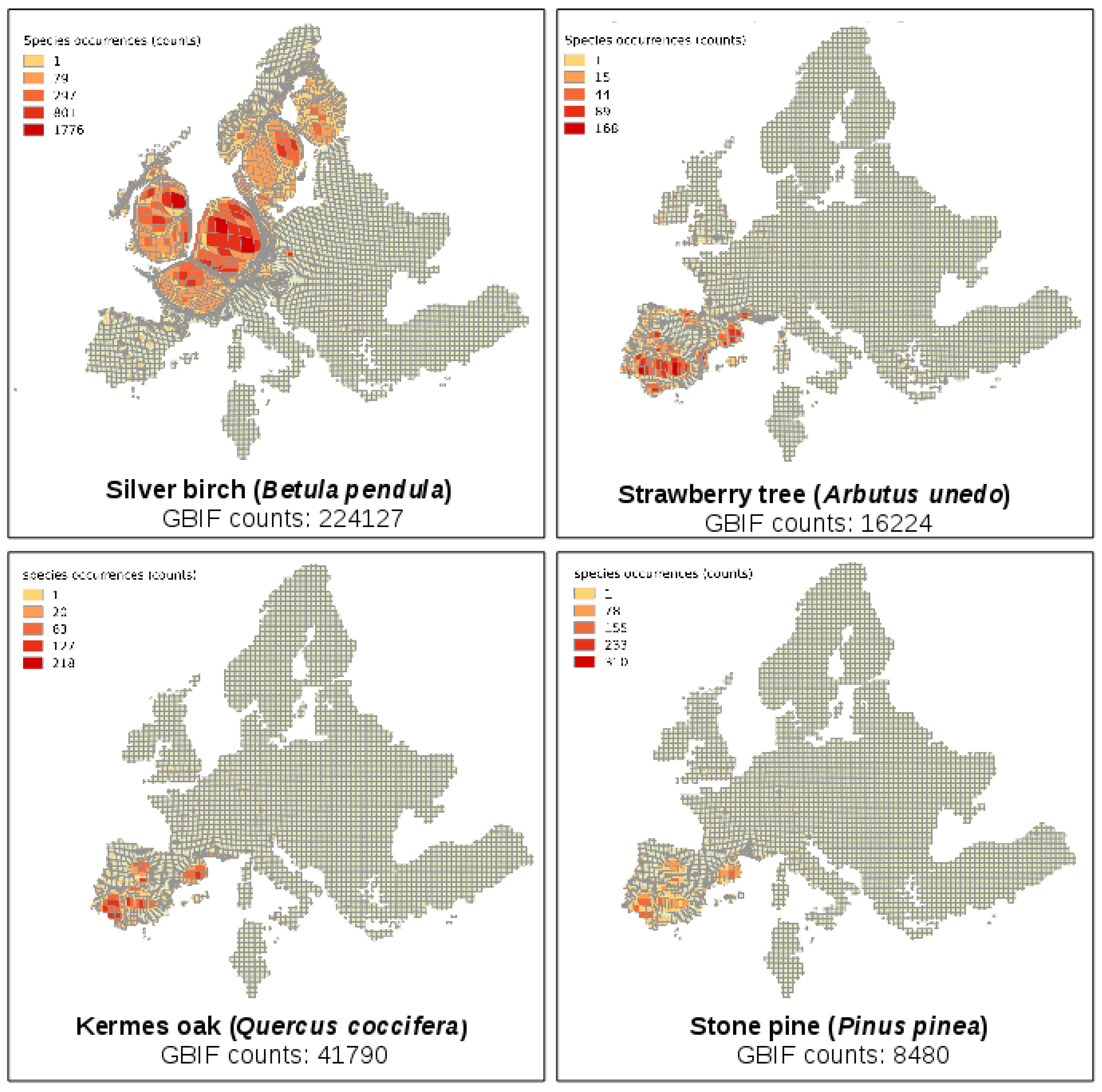
Here, cartograms are used to facilitate the visualization of spatial uncertainty in the results by changing the size of the polygons based on the density of information contained (e.g., number of observations, sampling effort, etc.), thus illustrating the variation in sampling effort and occurrences in field surveys. Using this approach, maps showing the differences in sampling effort (number of different survey dates in the database) and occurrences (observations counts) for a set of plant species over an equal sized grid of Europe were generated (
Figure 1). The cartograms were developed using the free and open source software ScapeToad (
http://scapetoad.choros.ch/).
The cartograms were generated based on two metrics, number of field surveys (proxy: dates) and number of observations per grid cell. The size of error is given by the size the grid cell should have in terms of the real spatial area it covers, over the actual proportion, as calculated by the number of observations/area. Uncertainty is shown at the per grid cell scale and corresponds to the deformation of the original cell size, that is, cells bigger than their original size required strategies to reduce the effect of oversampling on the products derived from the GBIF data, while cells displayed as smaller than their original size required more sampling efforts. Critically, methods to account for the differences in sampling effort and occurrences (e.g., [
26]) may be used to enhance a mapping activity.
5. Conclusions
Reference datasets used in map production are typically imperfect in some way. In this article it has been stressed that the reference data may have a heterogeneous nature in relation to issues such as sampling effort and may contain errors such as mislabelling. These imperfections can be expected to impact negatively on a mapping project. This is especially the case with the use of contemporary classifiers such as machine learning techniques like SVM. Imbalanced training samples can, for example, impact on SVM, but if the nature of the samples contributed to a reference dataset are known it may be possible to reduce the problem. Mislabelling has been proposed to be less of an issue (e.g., [
30]), but here was given particular focus. Here, it was shown that the quality of datasets, in terms of the accuracy of their class labelling, is important in the production of land cover maps from remotely sensed data. Training data are often used as if error-free yet are unlikely to be so. Error may arise from a variety of sources, not just simple, random errors. In many instances error may involve relatively similar classes and be concentrated in the border area between classes in feature space. It was shown that mislabelled training cases drawn from border locations can degrade the accuracy of widely used supervised image classifiers. In particular, it was evident that the magnitude of the effect was a function of the amount of mislabelled cases, the nature of the mislabelling, and the classifier used.
Critically, the results presented show that SVM is, contrary to some discussion in the literature, sensitive to mislabelled training cases, which highlights the need to consider the effect of training data quality on classification by SVM. The key conclusions arising from the results of the analyses performed were:
Mislabelled training data typically degraded the accuracy of image classification, and especially for SVM.
The effects of mislabelled training were greater when the mislabelling was to a similar class rather than a randomly selected class.
The effects of training data error varied between the classes involved.
The number of support vectors required for a classification increased with training data error.
The SVM changed from the most accurate to the least accurate of the four classifiers investigated as the training data error rose from 0% to 20%.
With knowledge of training data quality, it should be possible to adjust a classification analysis to reduce the negative impacts associated with mislabelled cases. For example, if there were concerns about relatively spectrally extreme training cases that lie in the border area between classes in feature space (e.g. there may be real similarity between the cases on the ground because they inter-grade with each other and hence are also spectrally similar), these could in some instances be ignored or we could use a classifier that was based on the general description of the classes and so less influenced by individual training cases.