Areal Delineation of Home Regions from Contribution and Editing Patterns in OpenStreetMap
Abstract
:1. Introduction
2. Contribution Patterns in OSM
3. Areal Delineation of OSM Contributor Information
3.1. Data Preparation and Contributor Selection
| OSM Member | Created Nodes | Modified Nodes | No. of Changesets | No. of Countries | Active Days (abs.) | Active Days (%) |
|---|---|---|---|---|---|---|
| 1 | 325,139 | 145,951 | 2369 | 12 | 1456 | 57% |
| 2 | 429,962 | 146,510 | 3811 | 15 | 1084 | 82% |
| 3 | 917,417 | 164,612 | 4486 | 13 | 833 | 77% |
| 4 | 402,783 | 119,269 | 6915 | 8 | 1280 | 87% |
| 5 | 333,075 | 101,109 | 7470 | 3 | 896 | 56% |
| 6 | 779,798 | 338,749 | 14,810 | 11 | 1586 | 86% |
| 7 | 573,133 | 79,008 | 4577 | 4 | 722 | 87% |
| 8 | 920,702 | 112,489 | 20,398 | 14 | 1827 | 84% |
| 9 | 774,395 | 299,257 | 16,340 | 7 | 1402 | 87% |
| 10 | 475,366 | 2,090,481 | 21,188 | 4 | 1979 | 88% |
| 11 | 949,472 | 330,927 | 5946 | 4 | 1298 | 81% |
| 12 | 471,268 | 60,759 | 1137 | 3 | 727 | 84% |
| 13 | 340,912 | 200,771 | 2260 | 11 | 625 | 85% |
| Operations | Node | Way | |
|---|---|---|---|
| Core edits | Remove/add/update tag | x | x |
| Remove/add/update primary tag | x | x | |
| Add geometry (new feature) | x | x | |
| Change geometry position | x | ||
| Remove node from way | x | ||
| Add node to way | x | ||
| Attribute changes | Name | x | x |
| Address | x | x | |
| Traffic signs | x | ||
| Crossing | x | ||
| Cycleway | x | ||
| Surface | x | ||
| Foot | x | ||
| Oneway | x | ||
| Restrictions motorized | x | ||
| General restrictions | x |
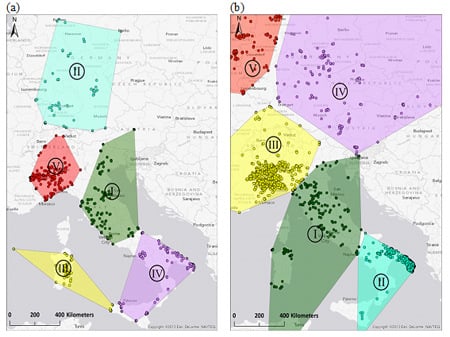
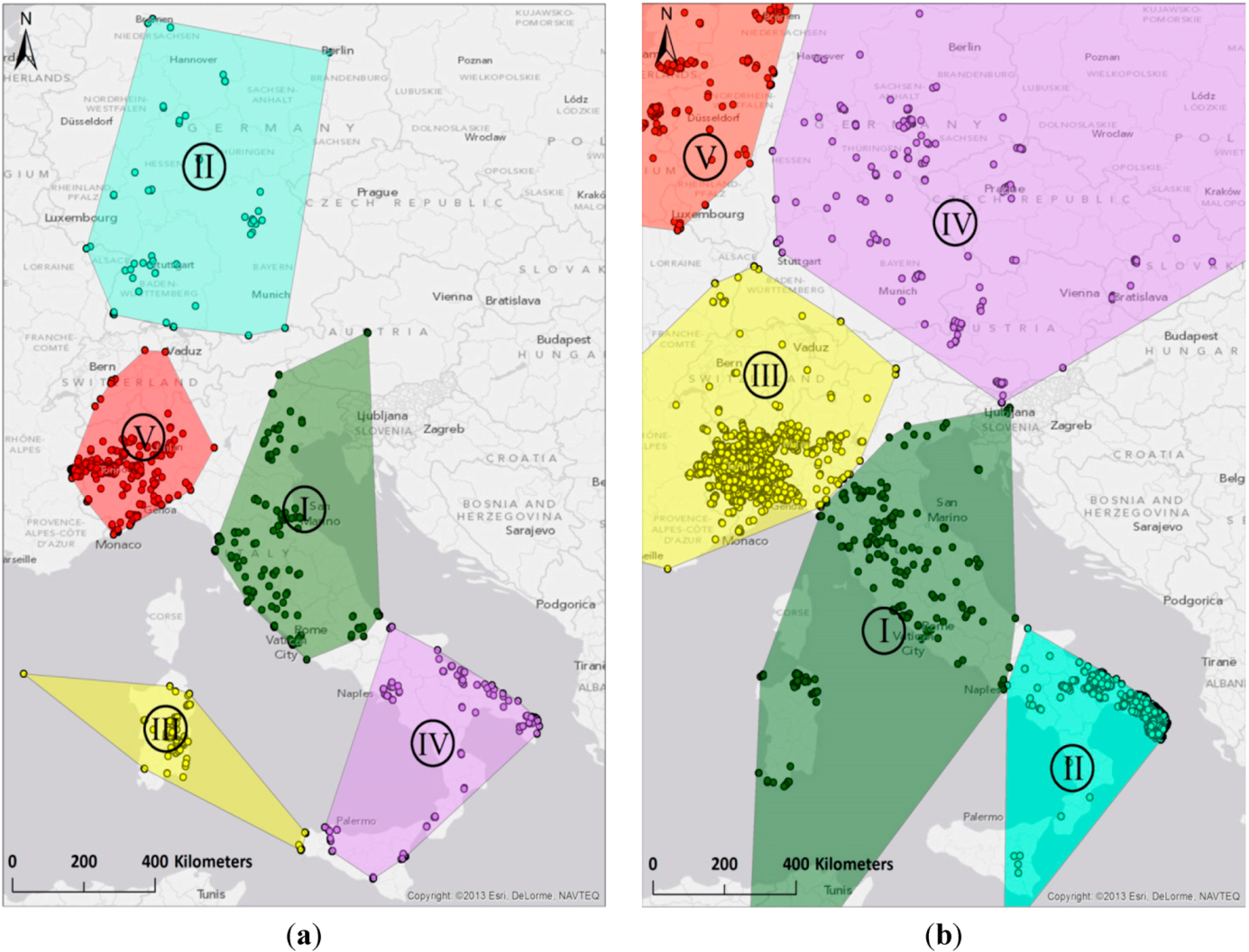
3.2. Clustering Step 1: Spatial Delineation of Activity Areas through k-Means Clustering
| K_grp | K_grp Size | Rem Tag | Add Tag | Upd Tag | … | Key Sum1 | Key Sum2 | … | KeyVal Sum1 | KeyVal Sum2 | … |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 245 | 0.000 | 0.012 | 0.000 | … | 0.000 | 0.992 | … | 0.000 | 0.976 | … |
| 2 | 97 | 0.000 | 0.010 | 0.010 | … | 0.000 | 0.763 | … | 0.000 | 0.763 | … |
| 3 | 91 | 0.000 | 0.000 | 0.000 | … | 0.000 | 0.989 | … | 0.000 | 0.989 | … |
| 4 | 231 | 0.000 | 0.013 | 0.000 | … | 0.000 | 0.961 | … | 0.000 | 0.887 | … |
| 5 | 1662 | 0.016 | 0.223 | 0.076 | … | 0.002 | 0.764 | … | 0.001 | 0.487 | … |
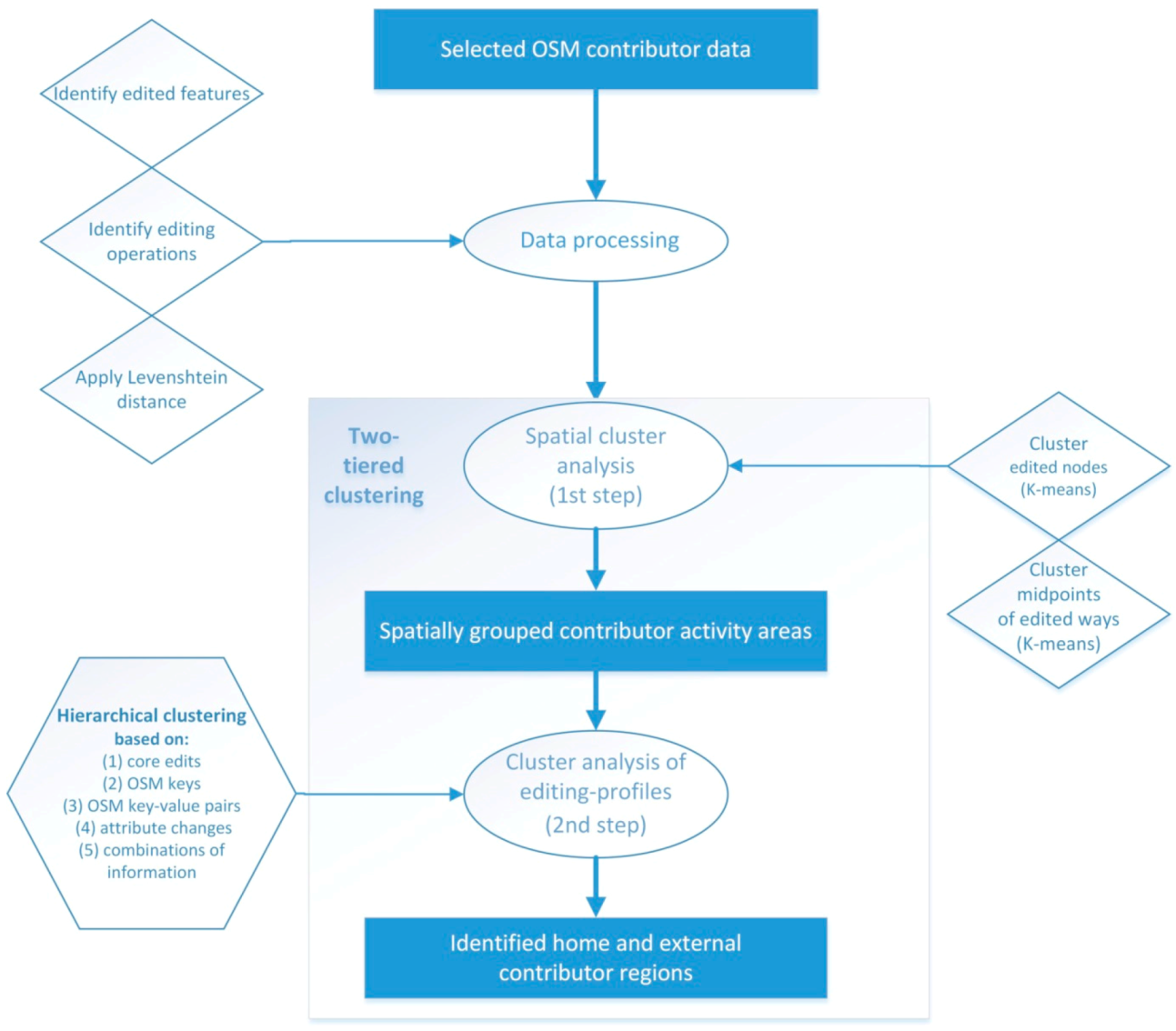
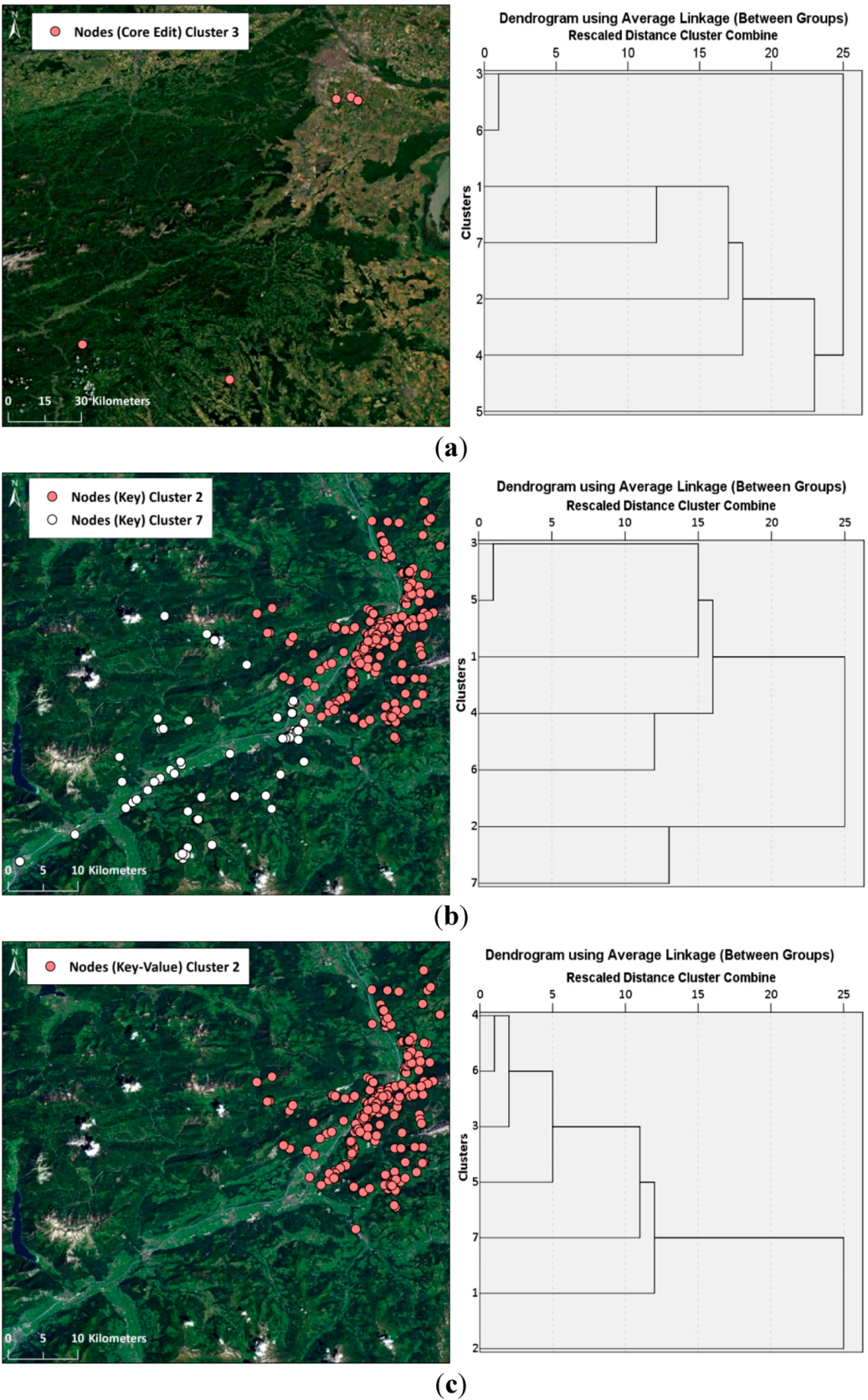
3.3. Clustering Step 2: Identification of Home and External Region through Hierarchical Clustering of Region-Based Editing Profiles
| OSM Member | Core Edits | Keys | Key-Values | |||
|---|---|---|---|---|---|---|
| Nodes | Ways | Nodes | Ways | Nodes | Ways | |
| 1 | - | - | 2 | 1 | 1 | 1 |
| 2 | 1 | - | 1 | 1 | 1 | 1 |
| 3 | 1 | - | 1 | 2 | 1 | 2 |
| 4 | - | - | - | - | 1 | 1 |
| 5 | - | - | - | 1 | 1 | 1 |
| 6 | 1 | - | 1 | 1 | 1 | 1 |
| 7 | - | - | 1 | 1 | 1 | 1 |
| 8 | - | - | - | - | 1 | 1 |
| 9 | - | 1 | 1 | - | 1 | 1 |
| 10 | 1 | - | - | - | 1 | 1 |
| 11 | - | - | 1 | - | - | - |
| 12 | - | - | - | - | 1 | 1 |
| 13 | - | - | - | 1 | 1 | 1 |
| TOTAL SUCCESS | 4 | 1 | 7 | 7 | 12 | 11 |
4. Evaluation
4.1. Comparison of Cluster Methods
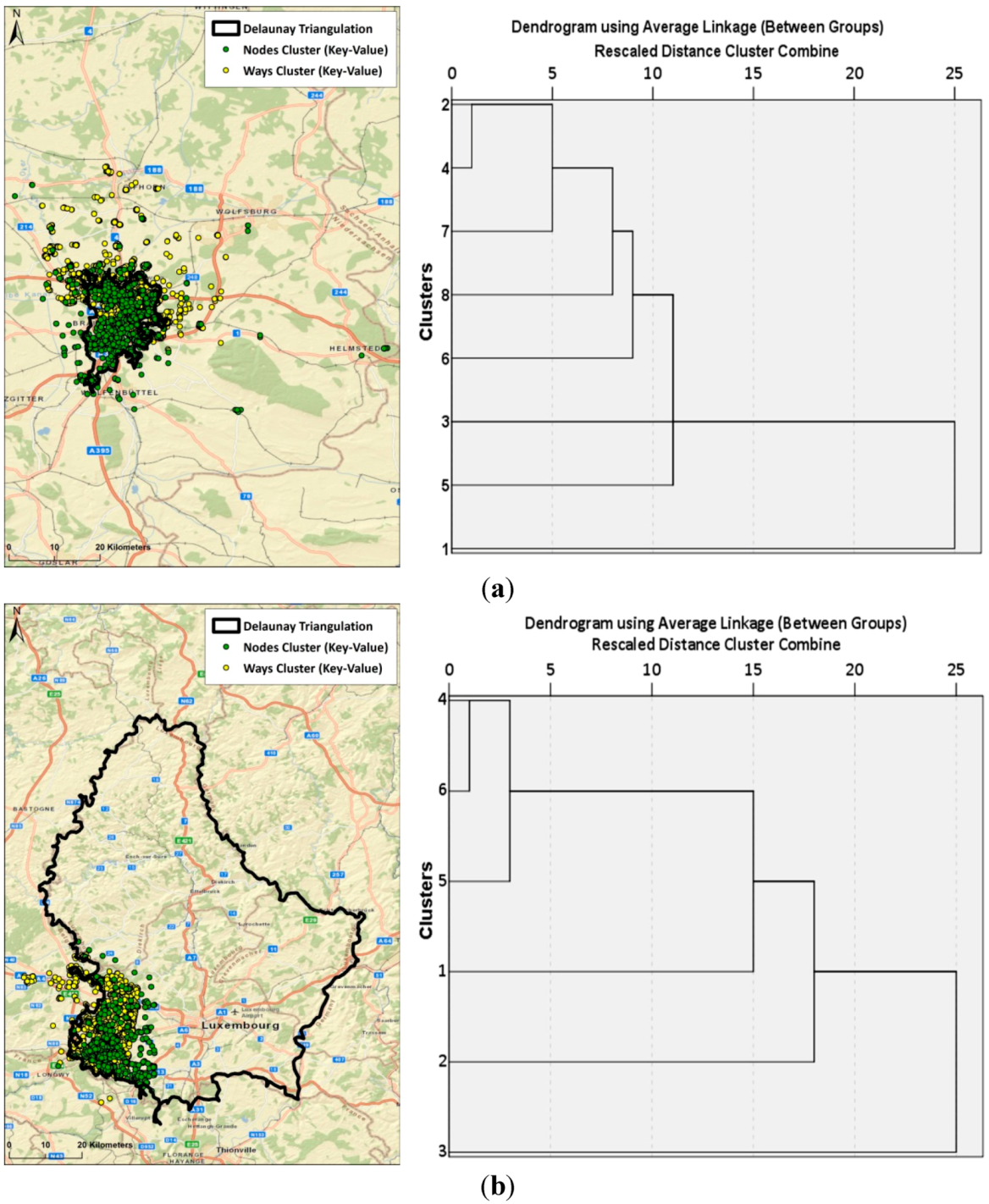
4.2. Classification Sensitivity
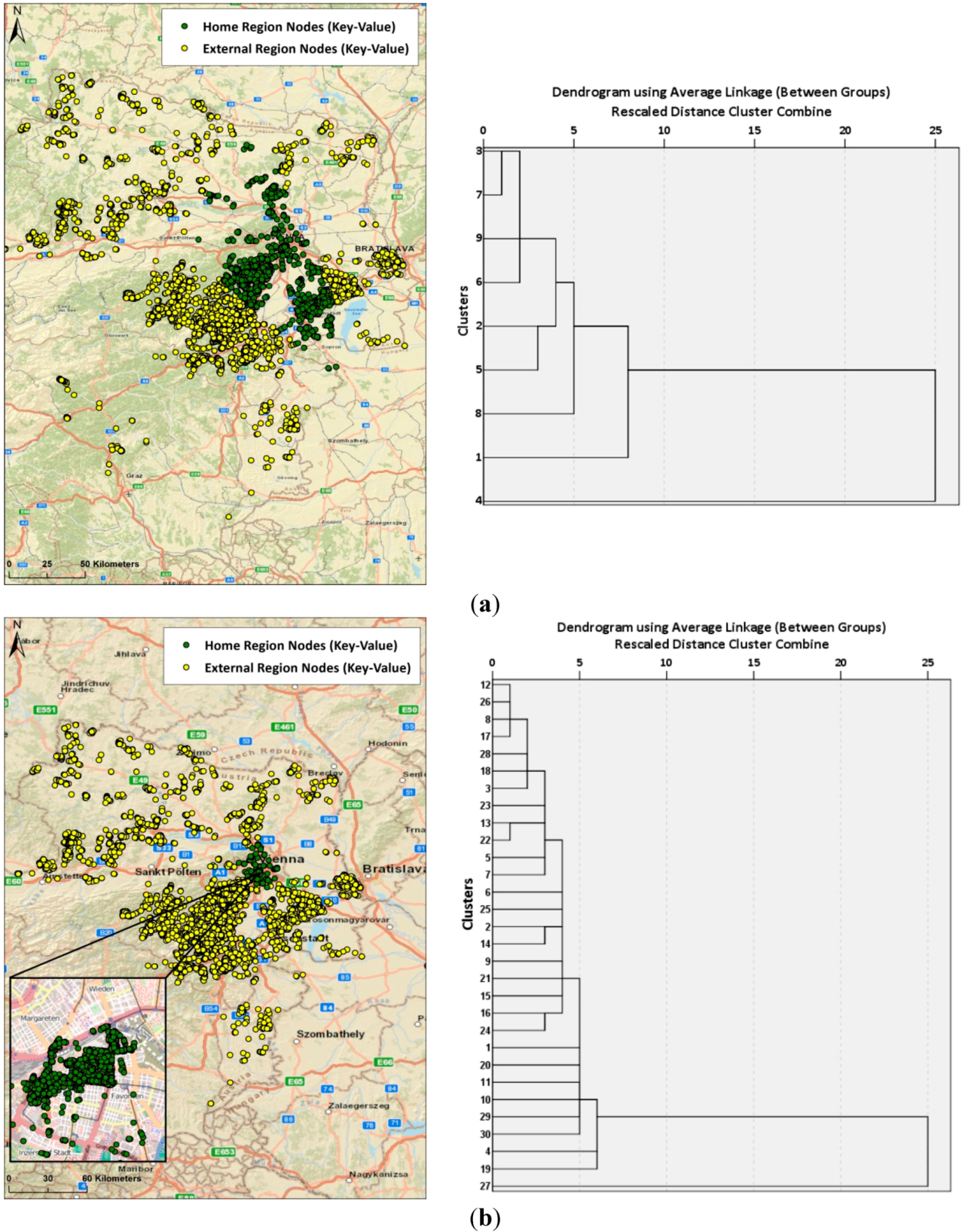
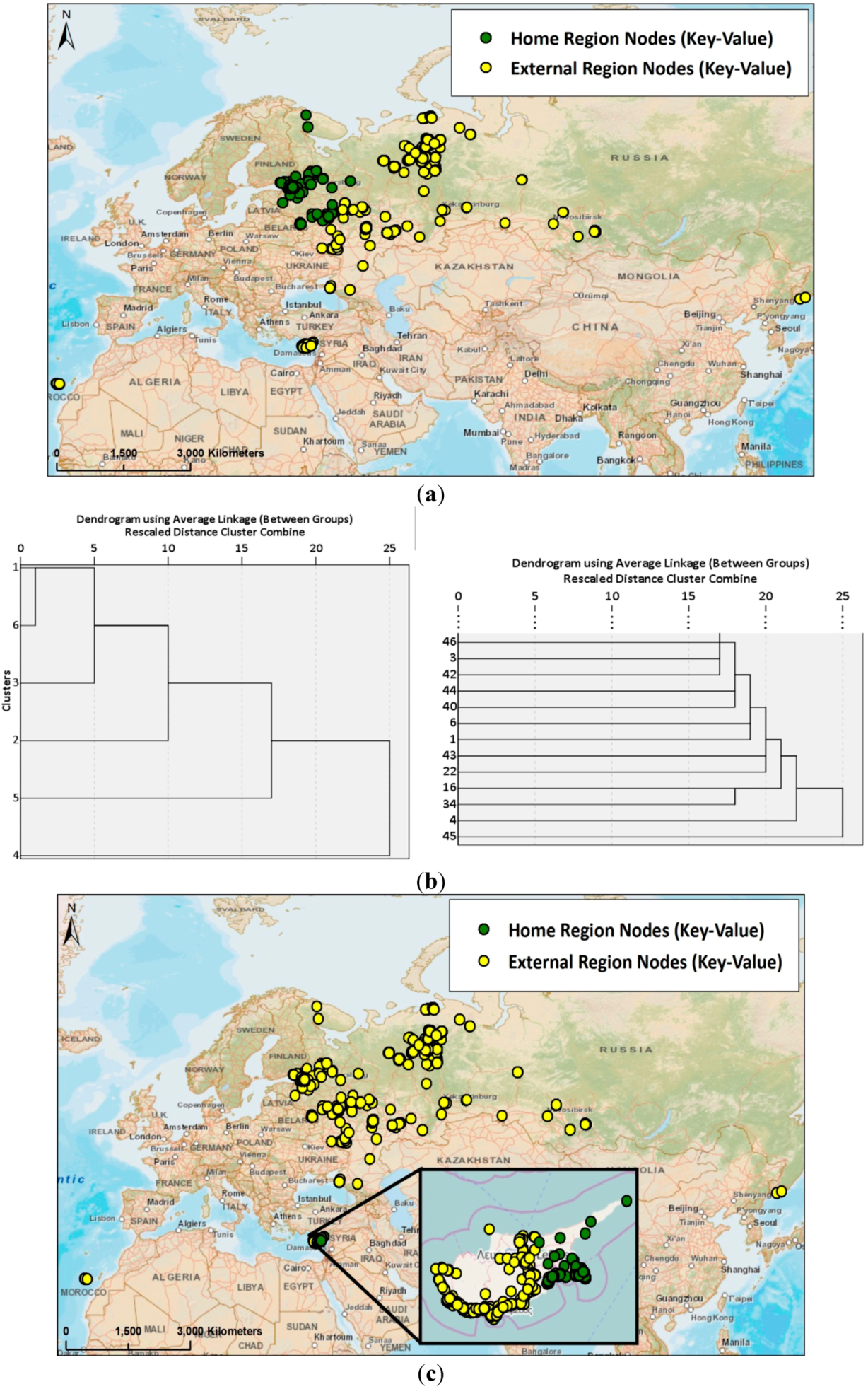
4.3. Diversity and Activity
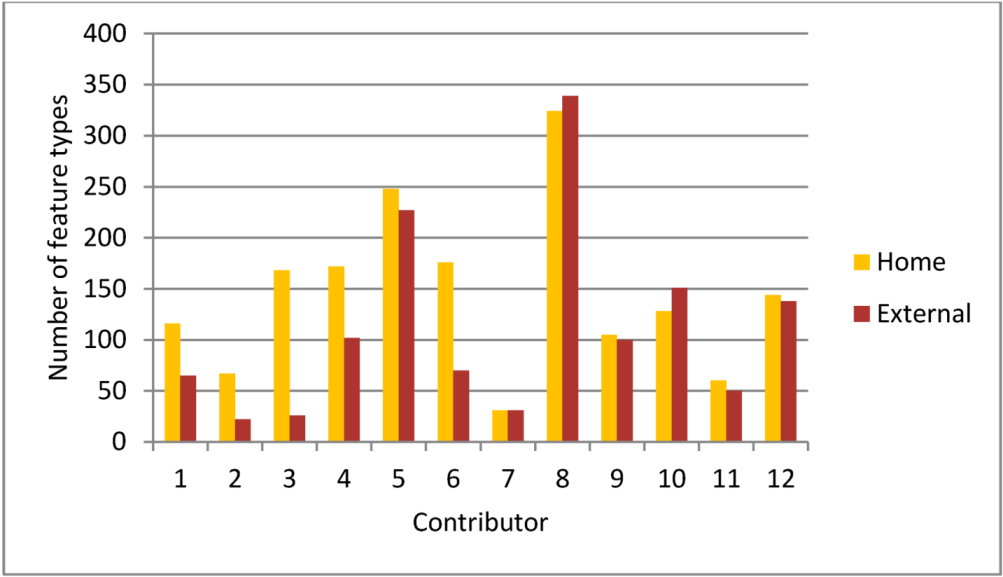
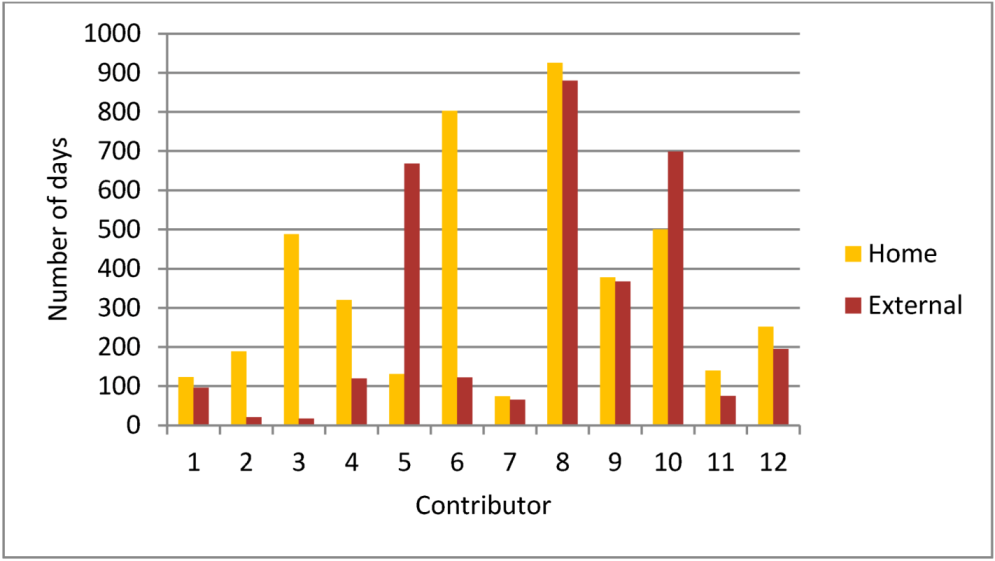
5. Summary and Conclusions
Author Contributions
Conflicts of Interest
References
- Goodchild, M.F. Citizens as voluntary sensors: Spatial data infrastructure in the World of Web 2.0. Int. J. Spat. Data Infrastruct. Res. (IJSDIR) 2007, 2, 24–32. [Google Scholar]
- Girardin, F.; Blat, J.; Calabrese, F.; Fiore, F.D.; Ratti, C. Digital footprinting: Uncovering tourists with user-generated content. Pervasive Comput. 2008, 7, 36–43. [Google Scholar] [CrossRef]
- Andrienko, G.; Andrienko, N.; Bak, P.; Kisilevich, S.; Keim, D. Analysis of community-contributed space- and time-referenced data (example of flickr and panoramio photos). In Proceedings of the IEEE Symposium on Visual Analytics Science and Technology, Atlantic City, NJ, USA, 12–13 October 2009; pp. 213–214.
- Chen, L.; Roy, A. Event detection from flickr data through wavelet-based spatial analysis. In Proceedings of the 18th ACM Conference on Information and Knowledge Management, Hong Kong, China, 2–6 November 2009; ACM: New York, NY, USA; pp. 523–532.
- Schlieder, C.; Matyas, C. Photographing a city: An analysis of place concepts based on spatial choices. Spat. Cogn. Comput. 2009, 9, 212–228. [Google Scholar]
- Hollenstein, L.; Purves, R.S. Exploring place through user-generated content: Using flickr to describe city cores. J. Spat. Inf. Sci. 2010, 1, 21–48. [Google Scholar]
- Andrienko, G.; Andrienko, N.; Bosch, H.; Ertl, T.; Fuchs, G.; Jankowski, P.; Thom, D. Thematics patterns in georeferenced tweets through space-time visual analytics. Comput. Sci. Eng. 2013, 15, 72–82. [Google Scholar] [CrossRef]
- Krumm, J.; Caruana, R.; Counts, S. Learning likely locations. In User Modeling, Adaption, and Personalization; Carberry, S., Weibelzahl, S., Micarelli, A., Semeraro, G., Eds.; Springer: Berlin, Germany; pp. 64–76.
- Li, Y.; Shan, J. Understanding the spatio-temporal pattern of tweets. Photogramm. Eng. Remote Sens. 2013, 79, 769–773. [Google Scholar] [CrossRef]
- Collins, C.; Hasan, S.; Ukkusuri, S.V. A novel transit rider satisfaction metric: Rider sentiments measured from online social media data. J. Public Transp. 2013, 16, 21–45. [Google Scholar]
- Mitchell, L.; Frank, M.R.; Harris, K.D.; Dodds, P.S.; Danforth, C.M. The geography of happiness: Connecting twitter sentiment and expression, demographics, and objective characteristics of place. PLoS One 2013, 8, e64417. [Google Scholar] [CrossRef] [PubMed]
- Noulas, A.; Scellato, S.; Mascolo, C.; Pontil, M. An empirical study of geographic user activity patterns in foursquare. In Proceedings of the 5th International AAAI Conference on Weblogs and Social Media, Menlo Park, CA, USA, 19–21 July 2011; Adamic, L., Baeza-Yates, R., Counts, S., Eds.; The AAAI Press: Palo Alto, CA, USA; pp. 570–573.
- Mooney, P.; Corcoran, P. Characteristics of heavily edited objects in OpenStreetMap. Future Internet 2012, 4, 285–305. [Google Scholar] [CrossRef]
- Arsanjani, J.J.; Barron, C.; Bakillah, M.; Helbich, M. Assessing the quality of OpenStreetMap contributors together with their contributions. In Proceedings of the AGILE 2013, Leuven, Belgium, 5–9 August 2013.
- Haklay, M.; Basiouka, S.; Antoniou, V.; Ather, A. How many volunteers does it take to map an area well? The validity of Linus’ law to volunteered geographic information. Cartogr. J. 2010, 47, 315–322. [Google Scholar] [CrossRef]
- Neis, P.; Zielstra, D.; Zipf, A. Comparison of volunteered geographic information data contributions and community development for selected world regions. Future Internet 2013, 5, 282–300. [Google Scholar] [CrossRef]
- Neis, P.; Zipf, A. Analyzing the contributor activity of a volunteered geographic information Project—The case of OpenStreetMap. ISPRS Int. J. Geo. Inf. 2012, 1, 146–165. [Google Scholar] [CrossRef]
- Heipke, C. Crowdsourcing geospatial data. ISPRS J. Photogramm. Remote Sens. 2010, 65, 550–557. [Google Scholar] [CrossRef]
- Mooney, P.; Corcoran, P. Analysis of interaction and co-editing patterns amongst OpenStreetMap contributors. Trans. GIS 2013, 18, 633–659. [Google Scholar] [CrossRef]
- Gröchenig, S.; Brunauer, R.; Rehrl, K. Estimating completeness of VGI datasets by analyzing community activity over time periods. In Connecting a Digital Europe through Location and Place; Huerta, J., Schade, S., Granell, C., Eds.; Springer: Berlin, Germany, 2014; pp. 3–18. [Google Scholar]
- Rehrl, K.; Gröchenig, S.; Hochmair, H.H.; Leitinger, S.; Steinmann, R.; Wagner, A. A conceptual model for analyzing contribution patterns in the context of VGI. In Progress in Location Based Services; Krisp, J.M., Ed.; Springer: Berlin, Germany, 2013; pp. 373–388. [Google Scholar]
- Gröchenig, S. Using Spatial and Temporal Editing Patterns for Evaluation of Open Street Map Data. MSc Thesis, Carinthia University of Applied Sciences, Villach, Carinthia, Austria, 2012. [Google Scholar]
- Steinmann, R.; Brunauer, R.; Gröchenig, S.; Rehrl, K. Wie aktiv sind freiwillige Mapper? Ein Vergleich der OpenStreetMap-Aktivitäten in den Jahren 2005–2012 am Beispiel der DACH-Region. In Angewandte Geoinformatik; Strobl, J., Blaschke, T., Griesebner, G., Zagel, B., Eds.; Wichmann: Berlin, Germany, 2013; pp. 173–182. [Google Scholar]
- Steinmann, R.; Gröchenig, S.; Rehrl, K.; Brunauer, R. Contribution profiles of voluntary mappers in OpenStreetMap. In Proceedings of Action and Interaction in Volunteered Geographic Information (ACTIVITY) Workshop at AGILE 2013, Leuven, Belgium, 14 May 2013.
- Haklay, M. How good is Volunteered Geographical Information? A comparative study of OpenStreetMap and Ordnance Survey datasets. Environ. Plan. B Plan. Des. 2010, 37, 682–703. [Google Scholar]
- Zielstra, D.; Zipf, A. OpenStreetMap data quality research in Germany. In Proceedings of the 6th International Conference on Geographic Information Science (GIScience), Zurich, Switzerland, 14–17 September 2010.
- Neis, P.; Zielstra, D.; Zipf, A. The street network evolution of crowdsourced maps: OpenStreetMap in Germany 2007–2011. Future Internet 2012, 4, 1–21. [Google Scholar]
- Zielstra, D.; Hochmair, H.H. Using free and proprietary data to compare shortest-path lengths for effective pedestrian routing in street networks. Transp. Res. Record 2012, 2299, 41–47. [Google Scholar] [CrossRef]
- Zielstra, D.; Hochmair, H.H. A comparative study of pedestrian accessibility to transit stations using free and proprietary network data. Transp. Res. Record 2011, 2217, 145–152. [Google Scholar] [CrossRef]
- Hochmair, H.H.; Zielstra, D.; Neis, P. Assessing the completeness of bicycle trail and designated lane features in OpenStreetMap for the United States. Trans. GIS 2014, in press. [Google Scholar]
- Zook, M.A.; Graham, M.; Shelton, T.; Gorman, S. Volunteered geographic information and crowdsourcing disaster relief: A case study of the Haitian earthquake. World Med. Health Policy 2010, 2, 7–33. [Google Scholar] [CrossRef]
- Parker, C.J.; May, A.J.; Mitchell, V. The role of VGI and PGI in supporting outdoor activities. Appl. Ergon. 2012, 44, 886–894. [Google Scholar] [CrossRef] [PubMed]
- Parker, C.J.; May, A.J.; Mitchell, V. User centred design of neogeography: The impact of volunteered geographic information on trust of online map “mashups”. Ergonomics 2014, 57, 987–997. [Google Scholar] [CrossRef] [PubMed]
- Parker, C.J.; May, A.J.; Mitchell, V. Understanding design with VGI using an information relevance framework. Trans. GIS 2012, 16, 545–560. [Google Scholar] [CrossRef]
- Girres, J.F.; Touya, G. Quality assessment of the French OpenStreetMap dataset. Trans. GIS 2010, 14, 435–459. [Google Scholar] [CrossRef]
- Mooney, P.; Corcoran, P. The annotation process in OpenStreetMap. Trans. GIS 2012, 16, 561–579. [Google Scholar] [CrossRef]
- Keßler, C.; de Groot, R. Trust as a Proxy Measure for the quality of volunteered geographic information in the case of OpenStreetMap. In Geographic Information Science at the Heart of Europe; Vandenbroucke, D., Bucher, B., Crompvoets, J., Eds.; Springer: Heidelberg, Germany, 2013; pp. 21–37. [Google Scholar]
- Keßler, C.; Trame, J.; Kauppinen, T. Provenance and trust in volunteered geographic information: The case of OpenStreetMap. In Proceedings of the Conference on Spatial Information Theory: COSIT’11, Belfast, ME, USA, 12–16 September 2011; pp. 1–3.
- Zielstra, D.; Hochmair, H.H.; Neis, P. Assessing the effect of data imports on the completeness of OpenStreetMap—A United States case study. Trans. GIS 2013, 17, 315–334. [Google Scholar] [CrossRef]
- Hochmair, H.H.; Zielstra, D. Development and completeness of points of interest in free and proprietary data sets: A Florida case study. In Proceedings of GI_Forum 2013, Creating the GISociety, Salzburg, Austria, 2–5 July 2013; Jekel, T., Car, A., Strobl, J., Griesebner, G., Eds.; Wichmann: Berlin, Germany; pp. 39–48.
- Perkins, C.; Dodge, M. The potential of user-generated cartography: A case study of the OpenStreetMap project and Mapchester mapping party. North West Geogr. 2008, 8, 19–32. [Google Scholar]
- Bacher, J.; Wenzig, K.; Vogler, M. Twostep Cluster: A First Evaluation. 2004. Available online: http://www.opus.ub.uni-erlangen.de/opus/volltexte/2004/81/pdf/a_04-02.pdf (accessed on 16 August 2014).
- Abubaker, M.; Ashour, W. Efficient data clustering algorithms: Improvements over Kmeans. Int. J. Intell. Syst. Appl. 2013, 5, 37–49. [Google Scholar]
- Humanitarian OpenStreetMap Team [HOT]. Available online: http://hot.openstreetmap.org/projects (accessed on 16 August 2014).
- OpenStreetMap Operation Cowboy. Available online: http://wiki.openstreetmap.org/wiki/Operation_Cowboy (accessed on 16 August 2014).
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zielstra, D.; Hochmair, H.H.; Neis, P.; Tonini, F. Areal Delineation of Home Regions from Contribution and Editing Patterns in OpenStreetMap. ISPRS Int. J. Geo-Inf. 2014, 3, 1211-1233. https://doi.org/10.3390/ijgi3041211
Zielstra D, Hochmair HH, Neis P, Tonini F. Areal Delineation of Home Regions from Contribution and Editing Patterns in OpenStreetMap. ISPRS International Journal of Geo-Information. 2014; 3(4):1211-1233. https://doi.org/10.3390/ijgi3041211
Chicago/Turabian StyleZielstra, Dennis, Hartwig H. Hochmair, Pascal Neis, and Francesco Tonini. 2014. "Areal Delineation of Home Regions from Contribution and Editing Patterns in OpenStreetMap" ISPRS International Journal of Geo-Information 3, no. 4: 1211-1233. https://doi.org/10.3390/ijgi3041211
APA StyleZielstra, D., Hochmair, H. H., Neis, P., & Tonini, F. (2014). Areal Delineation of Home Regions from Contribution and Editing Patterns in OpenStreetMap. ISPRS International Journal of Geo-Information, 3(4), 1211-1233. https://doi.org/10.3390/ijgi3041211