A Concept for Uncertainty-Aware Analysis of Land Cover Change Using Geovisual Analytics
Abstract
:1. Introduction
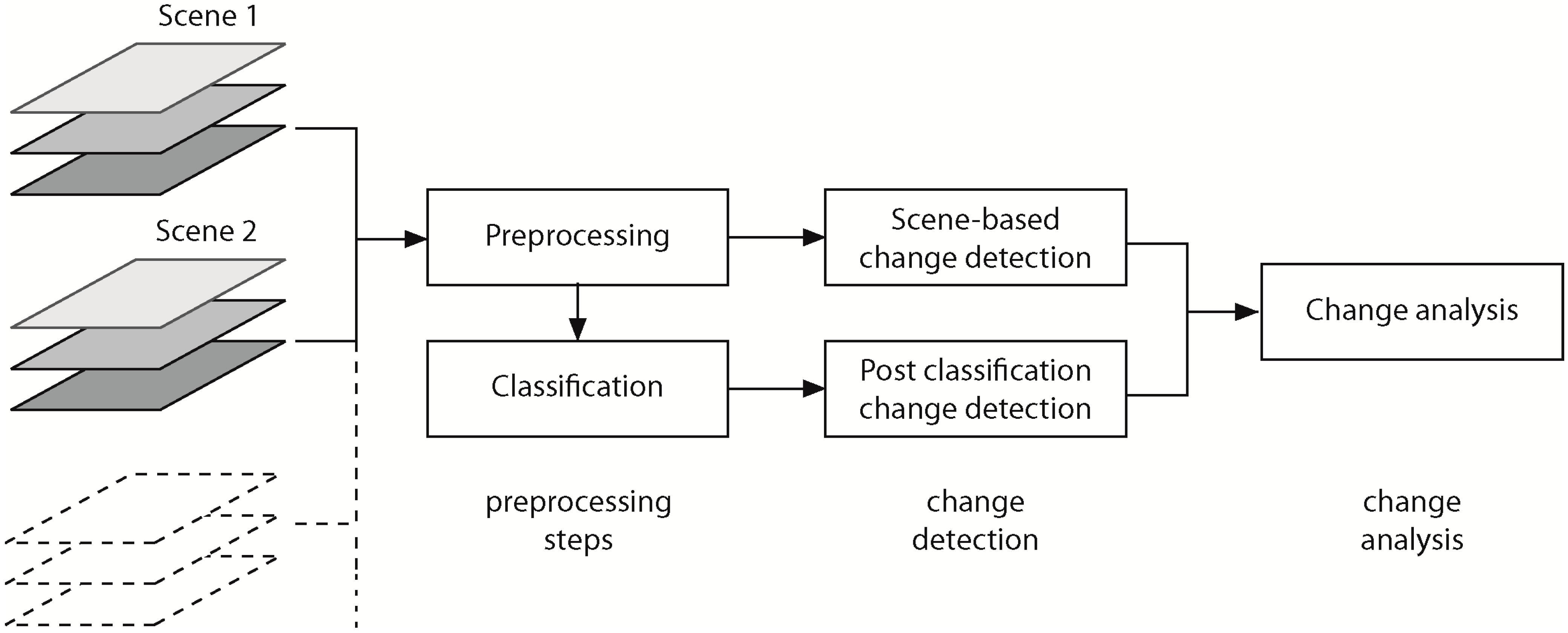
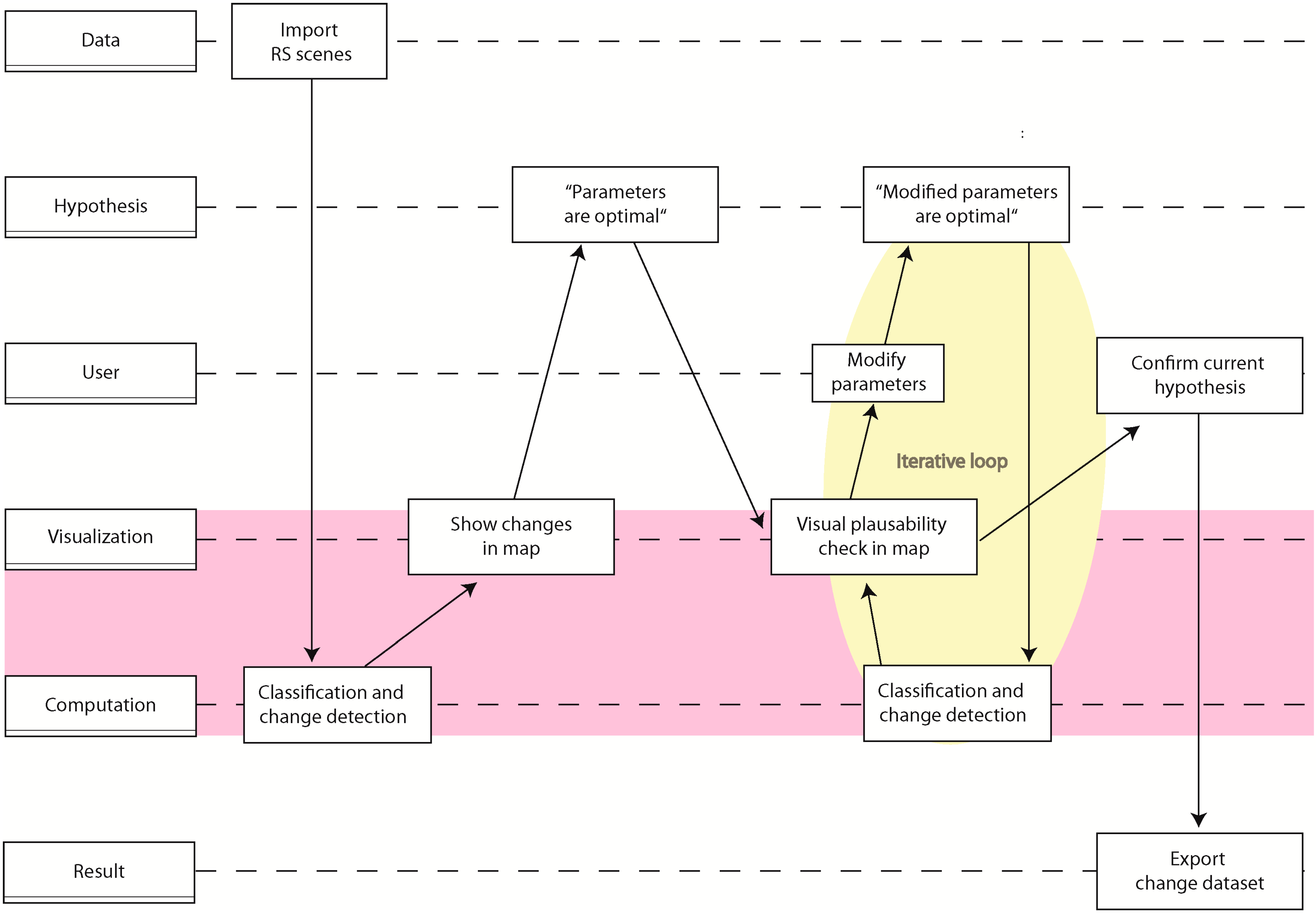
2. Concept
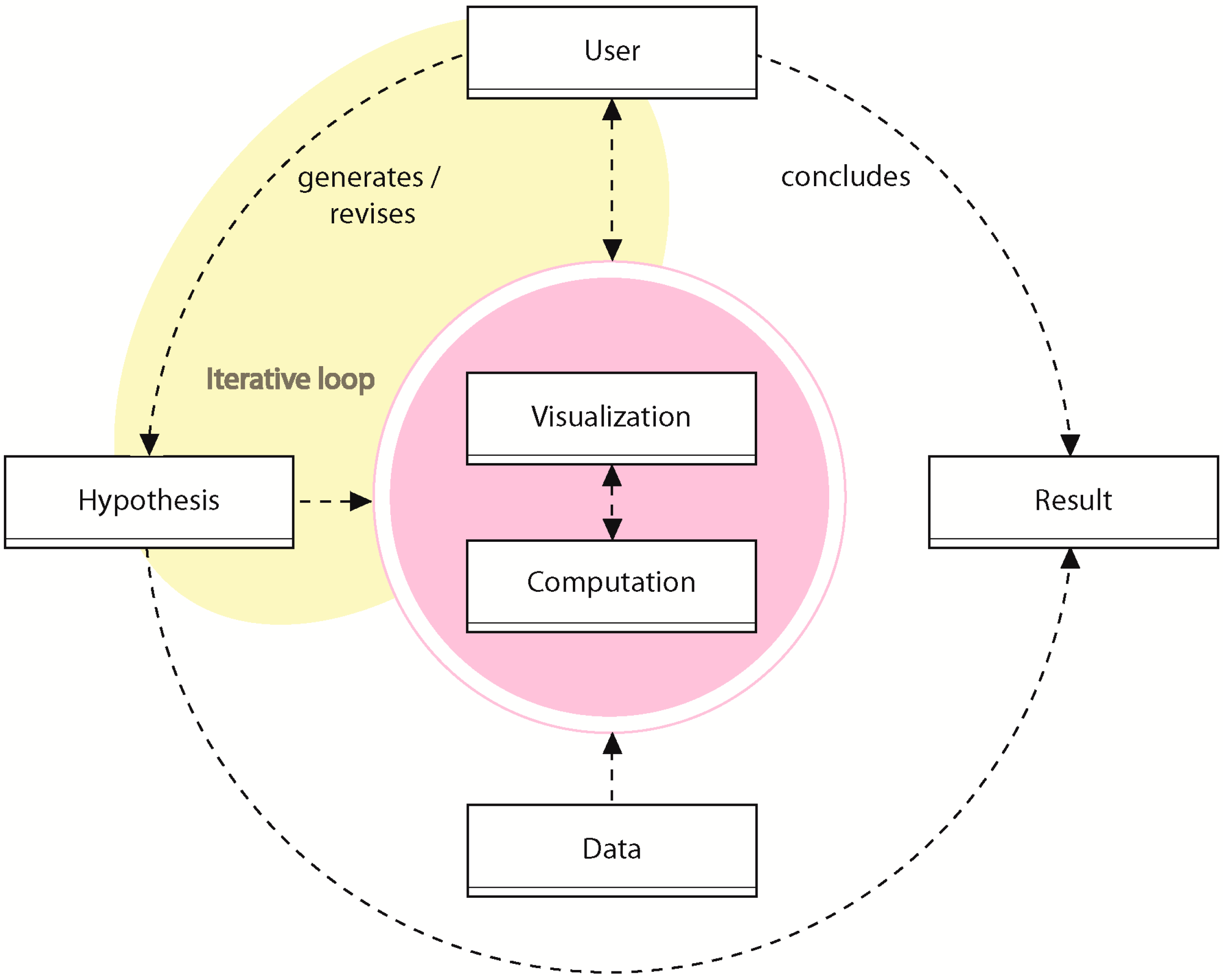
2.1. Geovisual Analytics
- Data: The data used during analysis (e.g., RS imagery, GIS layers, etc.)
- User: User interaction (e.g., choosing a threshold)
- Hypothesis: A hypothesis about change (e.g., “this area was falsely detected as change”)
- Computation: Computational steps in the workflow (e.g., classification of RS data)
- Visualization: Visual communication to the user (e.g., display of change uncertainty in a map)
- Result: The resulting change set
2.2. Change Uncertainty
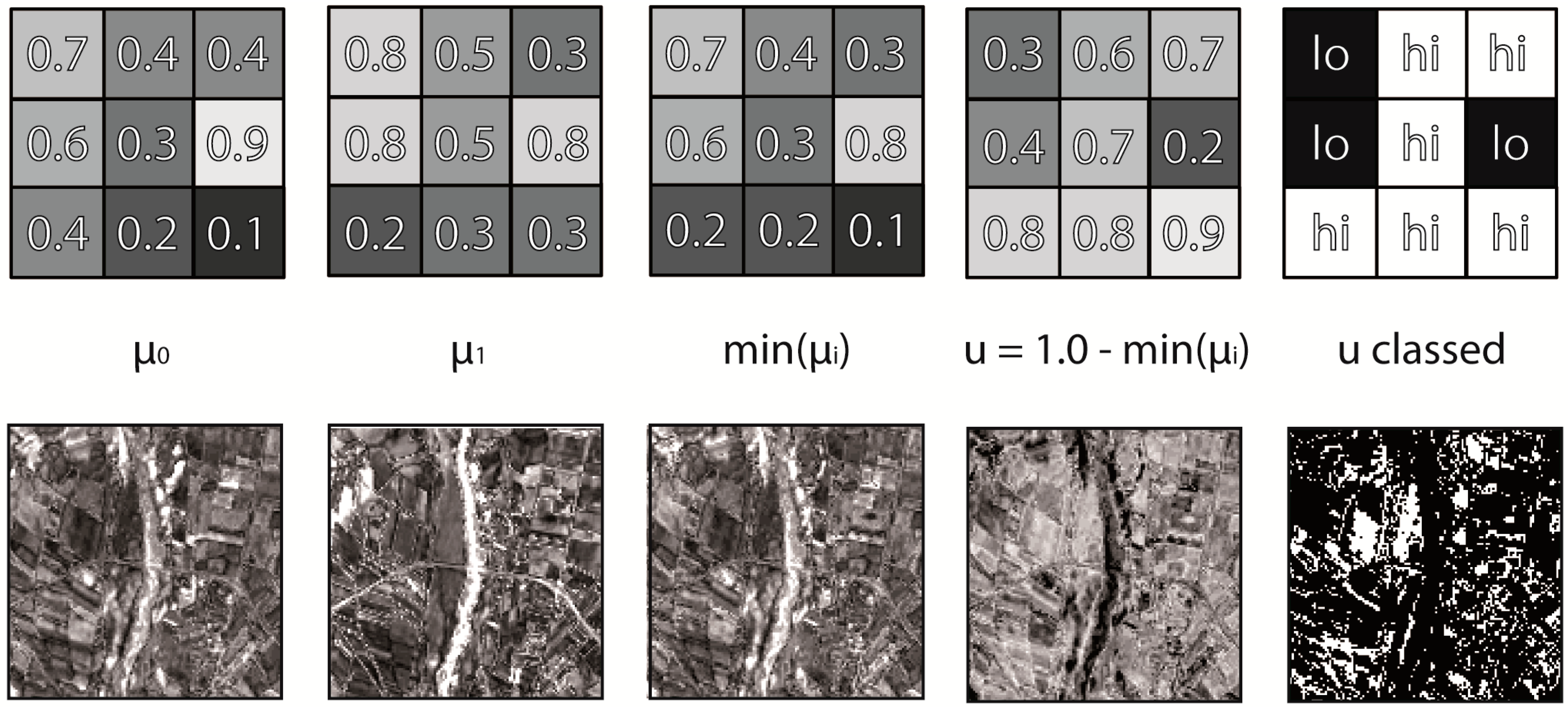
3. Applications
3.1. Enable Better Informed Analysis
3.2. Optimize Change Detection Parameters
3.3. Reduce False-Positive Change
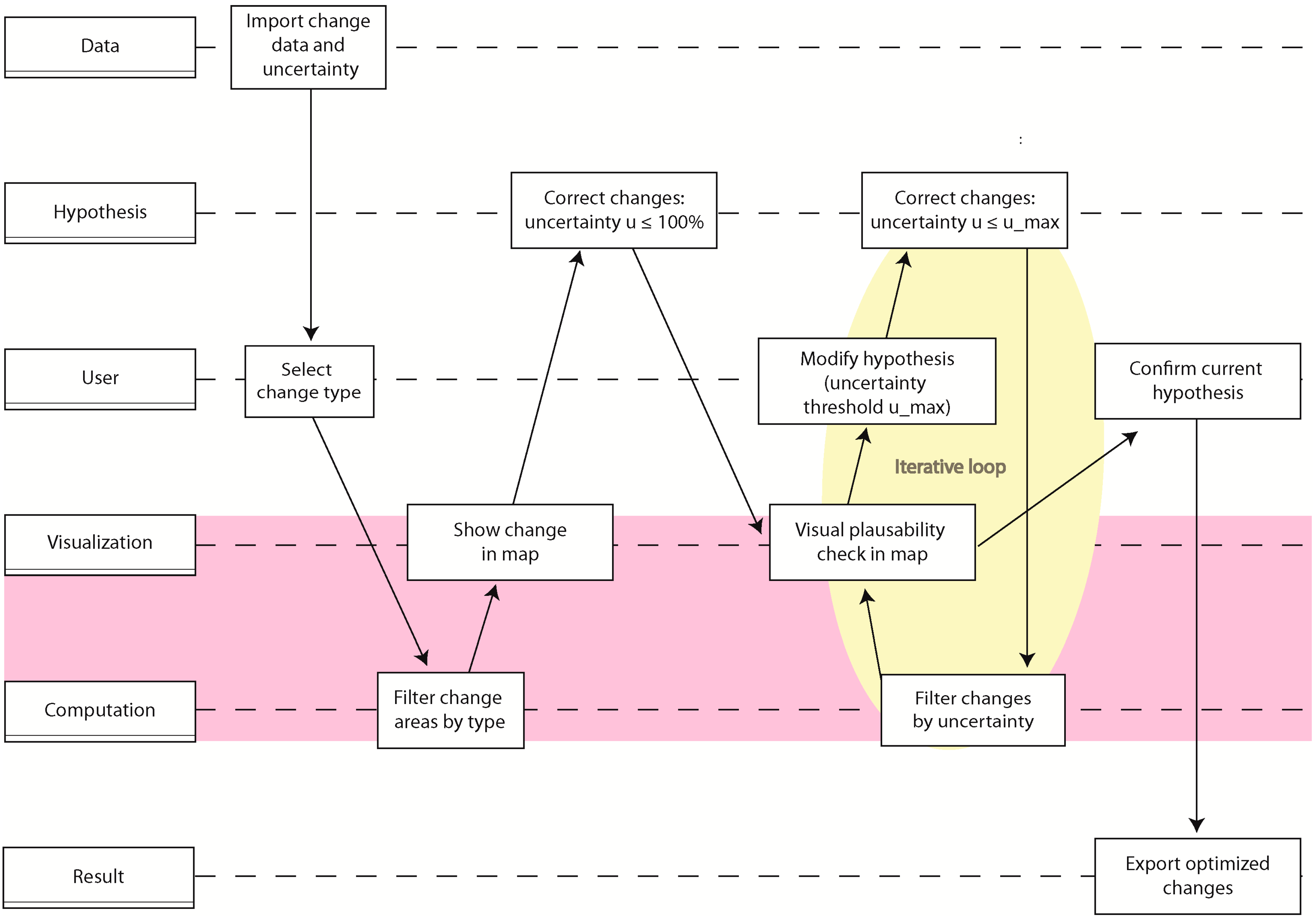
4. Case Study
4.1. Change Detection
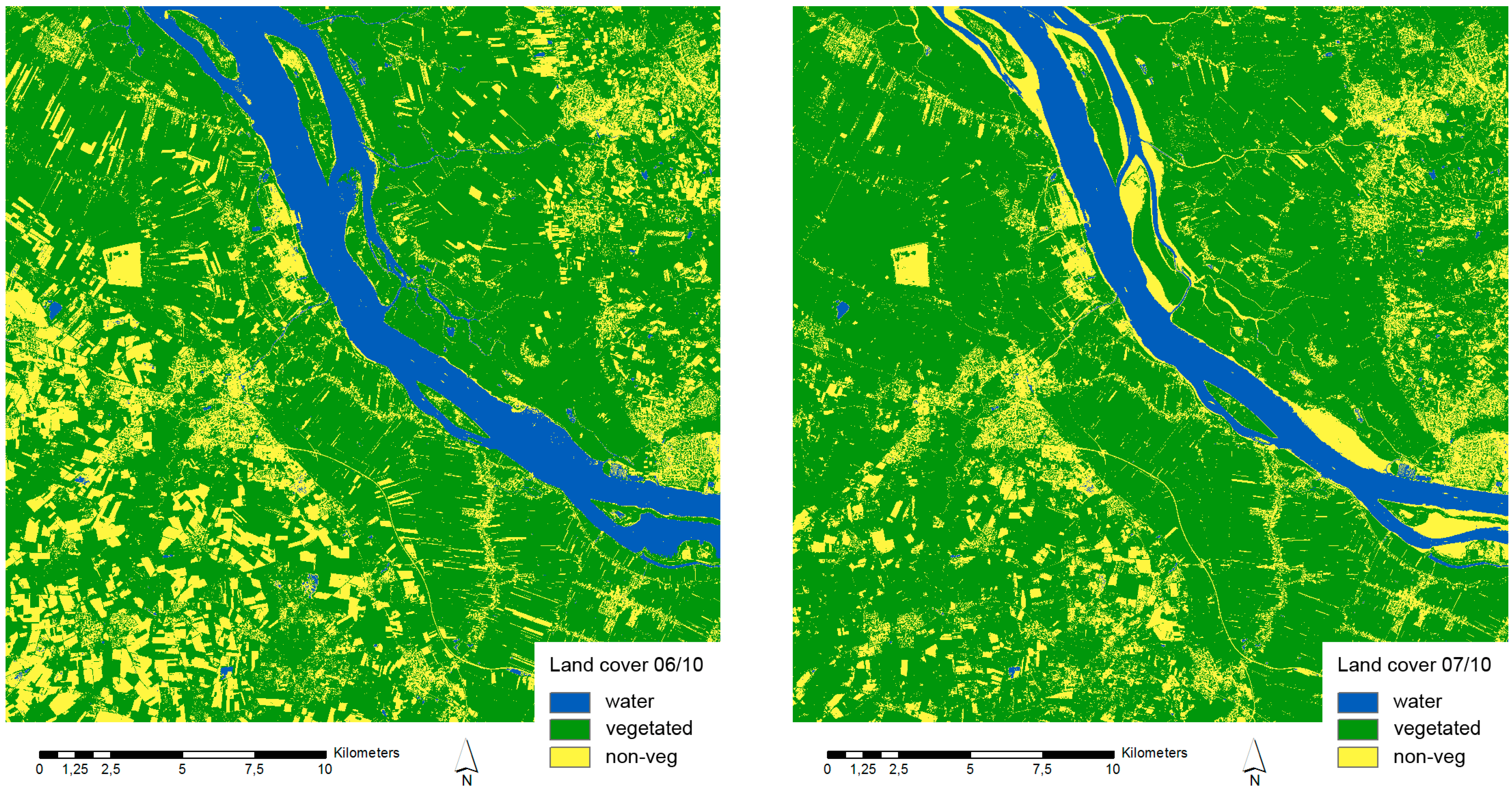
4.2. Change Analysis
| Change Type | Proportion of Overall Area | Number of Sample Points | CorrectChange | Erroneous Change |
|---|---|---|---|---|
| All | 100% | 323 | - | - |
| No change | 77.7% | 251 | - | - |
| Water to non-vegetated | 2.9% | 9 | 66.7% | 33.3% |
| Vegetated to non-vegetated | 6.3% | 21 | 80.9% | 19.1% |
| Non-vegetated to vegetated | 12.9% | 42 | 85.7% | 14.3% |
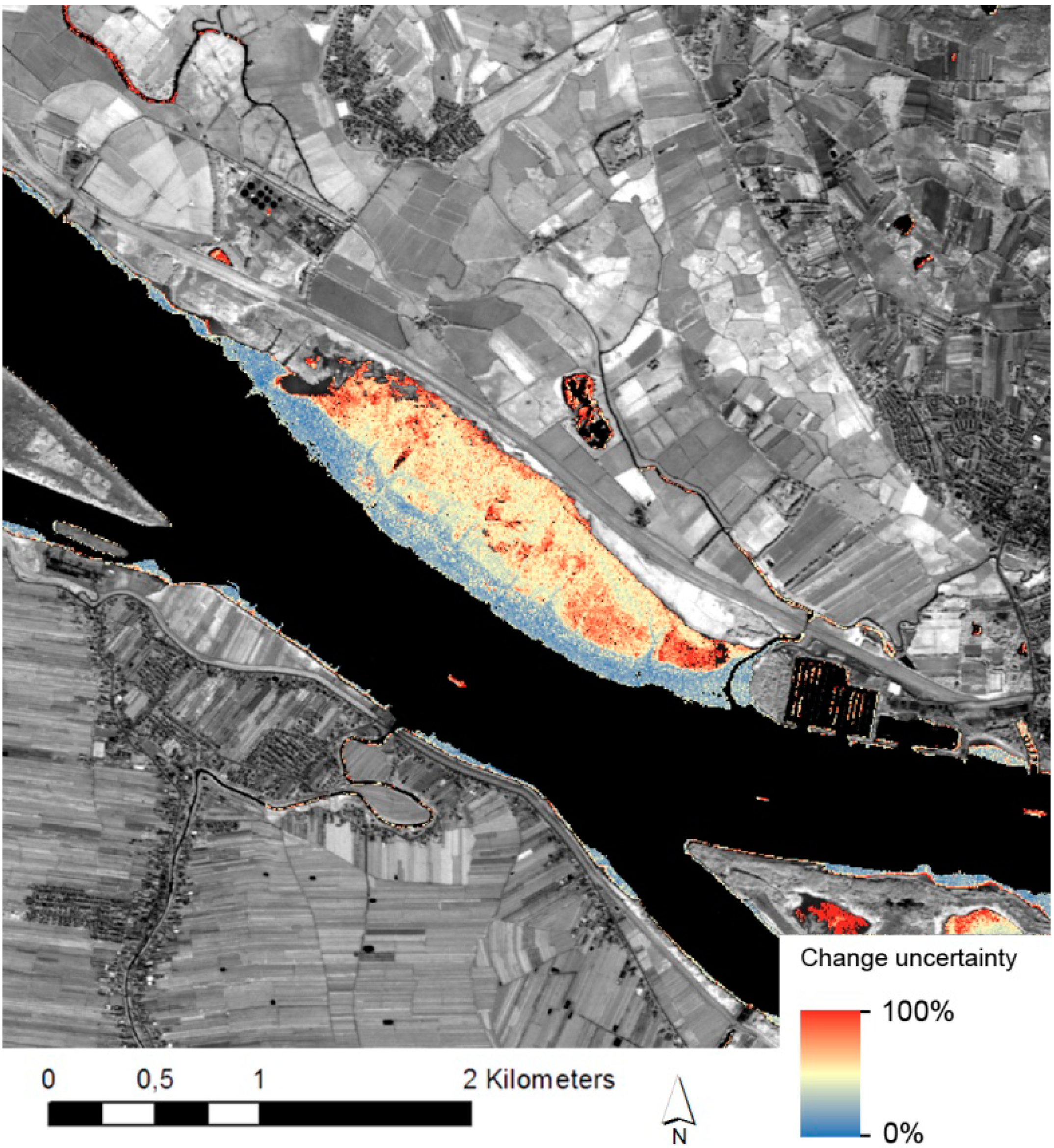
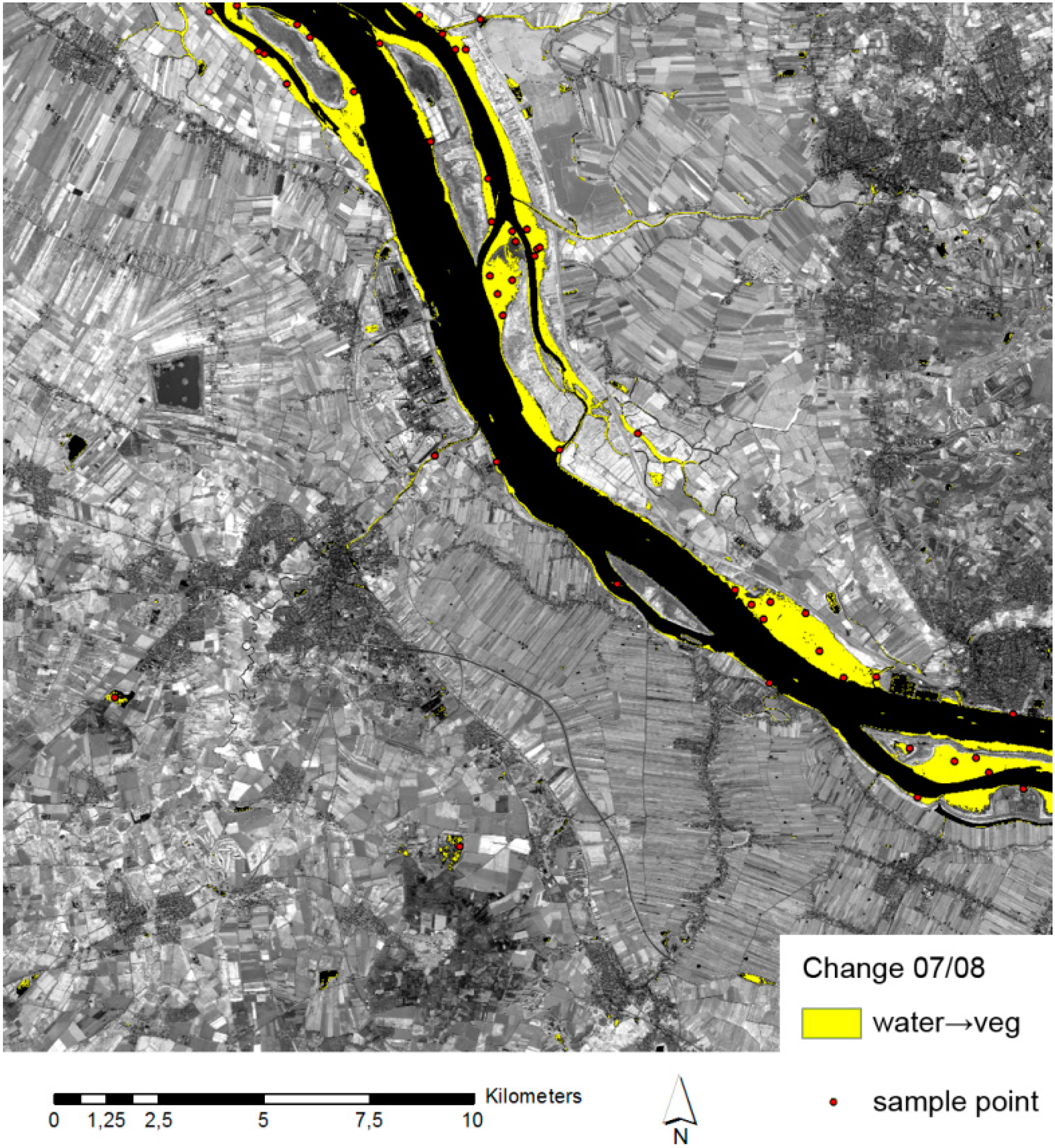
4.3. Reduce False-Positive Change
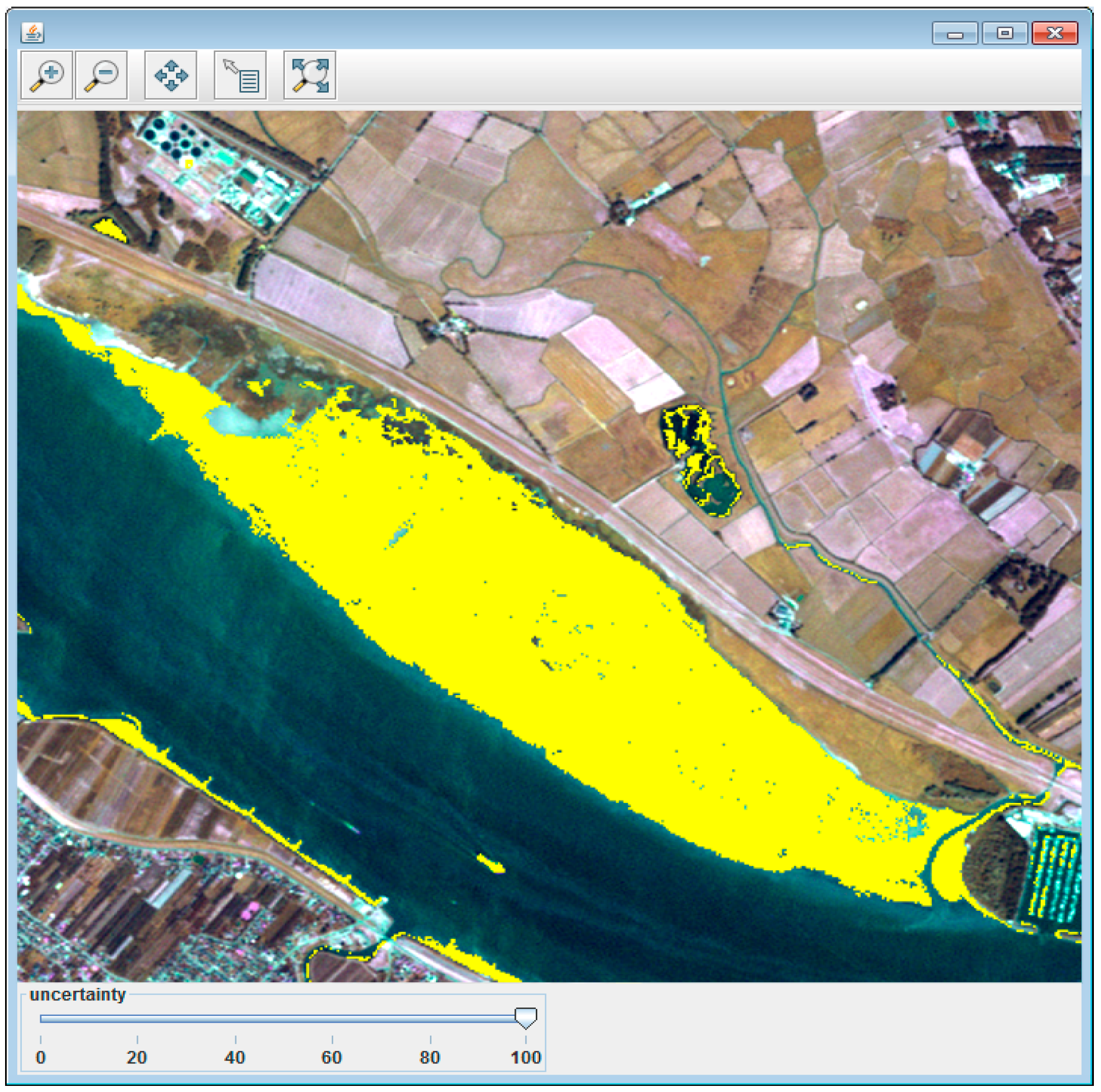
4.4. Discussion
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Zhang, J.; Goodchild, M.F. Uncertainty in Geographical Information; Taylor & Francis: London, UK, 2002. [Google Scholar]
- Pontius, R.G., Jr.; Lippitt, C.D. Can error explain map differences over time? Cartogr. Geogr. Inf. Sci. 2008, 33, 159–171. [Google Scholar] [CrossRef]
- Coppin, P.; Jonckheere, I.; Nackaerts, K.; Muys, B. Digital change detection methods in ecosystem monitoring: A review. Int. J. Remote Sens. 2004, 25, 1565–1596. [Google Scholar] [CrossRef]
- De Chiara, D. From GeoVisualization to Visual-Analytics: Methodologies and Techniques for Human-Information Discourse. Ph.D. Thesis, University of Salerno, Salerno, Italy, February 2012. [Google Scholar]
- Tomaszewski, B.M.; Robinson, A.C.; Weaver, C.; Stryker, M.; MacEachren, A.M. Geovisual analytics and crisis management. In Proceedings of the 4th International Information Systems for Crisis Response and Management (ISCRAM) Conference, Delft, The Netherlands, 13–16 May 2007.
- Schiewe, J. Geovisualisation and geovisual analytics: The interdisciplinary perspective on cartography. In Proceedings of 26th International Cartographic Conference ICC 2013, Dresden, Germany, 25–30 August 2013; pp. 122–126.
- Wang, T.D.; Wongsuphasawat, K.; Plaisant, C.; Shneiderman, B. Extracting insights from electronic health records: Case studies, a visual analytics process model, and design recommendations. J. Med. Syst. 2011, 35, 1135–1152. [Google Scholar] [CrossRef]
- Schreck, T.; Tekušová, T.; Kohlhammer, J.; Fellner, D. Trajectory-based visual analysis of large financial time series data. ACM SIGKDD Explor. Newsl. 2007, 9, 30–37. [Google Scholar] [CrossRef]
- Lucieer, A. Uncertainties in Segmentation and Their Visualization. Ph.D. Thesis, Utrecht University, Enschede, The Netherlands, 2004. [Google Scholar]
- Ahlqvist, O. Extending post-classification change detection using semantic similarity metrics to overcome class heterogeneity: A study of 1992 and 2001 U.S. National Land Cover Database changes. Remote Sens. Environ. 2008, 112, 1226–1241. [Google Scholar] [CrossRef]
- Bastin, L.; Fisher, P.; Wood, J. Visualizing uncertainty in multi-spectral remotely sensed imagery. Comput. Geosci. 2002, 28, 337–350. [Google Scholar] [CrossRef]
- Zurita-Milla, R.; Blok, C.; Retsios, V. Geovisual analytics of Satellite Image Time Series. In Proceedings of the 2012 International Congress on Environmental Modelling and Software, Leipzig, Germany, 1–5 July 2012; Seppelt, R., Voinov, A.A., Lange, S., Bankamp, D., Eds.; International Environmental Modelling and Software Society (iEMSs): Leipzig, Germany, 2012; pp. 1431–1438. [Google Scholar]
- Green, K. Change matters. Photogramm. Eng. Remote Sens. 2011, 77, 305–309. [Google Scholar] [CrossRef]
- Hoeber, O.; Wilson, G.; Harding, S.; Enguehard, R.; Devillers, R. Visually representing geo-temporal differences. In Proceedings of the IEEE Conference on Visual Analytics Science and Technology 2010, Salt Lake City, USA, 25–26 October 2010; MacEachren, A., Miksch, S., Eds.; IEEE Press: New York, NY, USA, 2010; pp. 229–230. [Google Scholar]
- Foody, G.M.; Atkinson, P.M. (Eds.) Uncertainty in Remote Sensing and GIS; Wiley: Hoboken, NJ, USA, 2002. [CrossRef]
- Shi, W.; Fisher, P.F.; Goodchild, M.F. (Eds.) Spatial Data Quality; Taylor & Francis: New York, NY, USA, 2002.
- Fisher, P.; Arnot, C.; Wadsworth, R.; Wellens, J. Detecting change in vague interpretations of landscapes. Ecol. Inform. 2006, 1, 163–178. [Google Scholar] [CrossRef]
- Brown, K.M.; Foody, G.M.; Atkinson, P.M. Deriving thematic uncertainty measures in remote sensing using classification outputs. In Proceedings of the 7th International Symposium on Spatial Accuracy Assessment in Natural Resources and Environmental Sciences, Lisbon, Portugal, 5–7 July 2006; Caetano, M., Painho, M., Eds.; Instituto Geográfico Português: Lisbon, Portugal, 2006. [Google Scholar]
- Lowry, J.H.; Ramsey, R.D.; Langs Stoner, L.; Kirby, J.; Schulz, K. An ecological framework for evaluating map errors using fuzzy sets. Photogramm. Eng. Remote Sens. 2008, 74, 1509–1519. [Google Scholar] [CrossRef]
- Burnicki, A.C. Modeling the probability of misclassification in a map of land cover change. Photogramm. Eng. Remote Sens. 2011, 77, 39–49. [Google Scholar]
- Schuster, C.; Förster, M.; Kleinschmit, B. Testing the red edge channel for improving land-use classifications based on high-resolution multi-spectral satellite data. Int. J. Remote Sens. 2012, 33, 5583–5599. [Google Scholar] [CrossRef]
- Khorram, S. Accuracy Assessment of Remote Sensing-Derived Change Detection; American Society for Photogrammetry and Remote Sensing: Bethesda, MD, USA, 1999. [Google Scholar]
- Congalton, R.G.; Green, K. Assessing the Accuracy of Remotely Sensed Data: Principles and Practices, 2nd ed.; CRC Press/Taylor & Francis: Boca Raton, FL, USA, 2009. [Google Scholar]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kinkeldey, C. A Concept for Uncertainty-Aware Analysis of Land Cover Change Using Geovisual Analytics. ISPRS Int. J. Geo-Inf. 2014, 3, 1122-1138. https://doi.org/10.3390/ijgi3031122
Kinkeldey C. A Concept for Uncertainty-Aware Analysis of Land Cover Change Using Geovisual Analytics. ISPRS International Journal of Geo-Information. 2014; 3(3):1122-1138. https://doi.org/10.3390/ijgi3031122
Chicago/Turabian StyleKinkeldey, Christoph. 2014. "A Concept for Uncertainty-Aware Analysis of Land Cover Change Using Geovisual Analytics" ISPRS International Journal of Geo-Information 3, no. 3: 1122-1138. https://doi.org/10.3390/ijgi3031122
APA StyleKinkeldey, C. (2014). A Concept for Uncertainty-Aware Analysis of Land Cover Change Using Geovisual Analytics. ISPRS International Journal of Geo-Information, 3(3), 1122-1138. https://doi.org/10.3390/ijgi3031122




