Geospatial Narratives and Their Spatio-Temporal Dynamics: Commonsense Reasoning for High-Level Analyses in Geographic Information Systems
Abstract
: The modeling, analysis and visualization of dynamic geospatial phenomena has been identified as a key developmental challenge for next-generation Geographic Information Systems (GIS). In this context, the envisaged paradigmatic extensions to contemporary foundational GIS technology raises fundamental questions concerning the ontological, formal representational and (analytical) computational methods that would underlie their spatial information theoretic underpinnings. We present the conceptual overview and architecture for the development of high-level semantic and qualitative analytical capabilities for dynamic geospatial domains. Building on formal methods in the areas of commonsense reasoning, qualitative reasoning, spatial and temporal representation and reasoning, reasoning about actions and change and computational models of narrative, we identify concrete theoretical and practical challenges that accrue in the context of formal reasoning about space, events, actions and change. With this as a basis and within the backdrop of an illustrated scenario involving the spatio-temporal dynamics of urban narratives, we address specific problems and solution techniques chiefly involving qualitative abstraction, data integration and spatial consistency and practical geospatial abduction.1. Introduction
Geographic Information Systems (GIS) are confronted with massive quantities of micro- and macro-level spatio-temporal data. In a conventional GIS systems, this data takes the form of spatio-temporal databases of precise measurements pertaining to environmental features, aerial imagery and, more recently, sensor network databases that store real-time information about natural and artificial processes and phenomena. Within next-generation GIS systems, the fundamental information theoretic modalities are envisioned to undergo radical transformations: high-level ontological entities, such as objects, events, actions and processes; and the capability to model and reason about these is expected to be a native feature of next-generation GIS. Indeed, one of the crucial developmental goals in GIS systems of the future is a fundamental paradigmatic shift in the underlying “spatial informatics” of these systems.
1.1. Time and GIS
Integrating time with GIS is necessary toward the development of GIS capable of monitoring and analyzing successive states of spatial entities [1–3]. Such capability, necessitating the representation of instances of geographic entities and their change over time rather than change to layers or scenes, is the future of GIS and has been emphasized in the National Imagery and Mapping Agency’s (NIMA; now the National Geospatial-Intelligence Agency (NGA)) vision for Integrated Information Libraries [4]. A temporal GIS (TGIS) should, in addition to accounting for spatial changes, also consider the events behind changes and the facts that enable observation of these changes [5]. In the words of Claramunt and Thériault [1]:
“To respond adequately to scientific needs, a TGIS should explicitly preserve known links between events and their consequences. Observed relationships should be noted (e.g., entities A and B generate entity C) to help scientists develop models that reproduce the dynamics of spatio-temporal processes. Researchers will thus be able to study complex relationships, draw conclusions and verify causal links that associate entities through influence and transformation processes”.
Clearly, this facility necessitates a formal approach encompassing events, actions and their effects toward representing and reasoning about dynamic spatial changes. Such an approach will be advantageous in GIS applications concerned with retrospective analysis or diagnosis of observed spatial changes involving either fine-scale object-level analysis or macro-level (aggregate) analysis of dynamic geospatial phenomena. For instance, within GIS, spatial changes could denote (environmental) changes in the geographic sphere at a certain temporal granularity and could bear a significant relationship to natural events and human actions, e.g., changes in land-usage, vegetation, cluster variations among aggregates of demographic features and wild-life migration patterns.
1.2. Geospatial Semantics
Conceptual models for representing geospatial events and processes in general have been the focus of extensive research efforts in the last decade. Research in the area of geospatial semantics, taxonomies of geospatial events and processes and basic ontological research into the nature of processes in a specific geospatial context has garnered specific interest from several quarters [6–9]. Fundamental epistemological aspects concerning, for instance, event and object identity have received special attention in the community [10,11]. This has mainly been spurred by the realization that purely snapshot-based temporal GIS does not provide for an adequate basis for analyzing spatial events and processes and performing spatio-temporal reasoning. Event-based and object-level reasoning at the spatial level could serve as a basis of explanatory analyses within a GIS [12–15]. For instance, a useful reasoning mechanism that applications may benefit from could be the task of causal explanation, which is the process of retrospective analysis by the extraction of an event-based explanatory model from available spatial data. Indeed, the explanation would essentially be an event-based history of the observed spatial phenomena defined in terms of both domain-independent and domain-dependent occurrences.
1.3. Narrative as a Model of Perceptual Sense Making
Researchers in computational logics of action and change have interpreted narratives in several ways (e.g., in the context of formalisms, such as the situation calculus and event calculus) [16–20]:
“a sequence of events about which we may have incomplete, conflicting or incorrect information”
“accounts of sets of events, not necessarily given as sequences; a narrative is an account of what happened”
The significance of narratives in everyday discourse, interpretation, interaction, belief formation and decision-making has been acknowledged and studied in a range of scientific, humanistic and artistic disciplines. Narrativization of everyday perceptions by humans, and the significance of narratives, e.g., in communication and interaction, has been investigated under several frameworks and through several interdisciplinary initiatives involving the arts, humanities and social sciences, e.g., the narrative paradigm [21], narrative analysis [22], narratology [23–25], discourse analysis and computational narratology [26–29].
We regard narratives and high-level processes of (computational) narrativization emanating therefrom as a general underlying structure serving the crucial function of perceptual sense-making, i.e., as a link between problem-specific perceptual sensing (i.e., data) and the (computational) formation of sensible impressions concerned with interpretation and analytical tasks. The particular form of the proposed narrative structure is that of a cognitively inspired computational model of narrativization involving high-level commonsense reasoning with space, events, actions, change and interaction [30]. We posit that computational narrativization pertaining to space, actions and change provides a useful model of visual and spatio-temporal thinking within a wide-range of problem-solving tasks and application areas, with geospatial dynamics being the focus of this paper.
Computational models of geospatial narratives, therefore, by definition, are aimed at making sense of massive quantities of micro- and macro-level spatio-temporal data pertaining to environmental, socio-economic and demographic processes operating in a geospatial context. Such narratives are constructed on the basis of spatio-temporal databases of precise measurements about environmental features, aerial imagery, sensor network databases with real-time information about natural and artificial processes and phenomena, etc. Geospatial narratives typically span a temporal horizon encompassing generational change, but these could also pertain to the scale of everyday “life in the city”, natural environmental processes, etc.
1.4. Narratives and High-Level Analytical Interpretation in GIS
The core development goal for constructing a narrative-centered representational and computational apparatus for next-generation GIS is indeed aimed at making sense of enormous quantities of geographic data. This has to be done in order to empower analysts and decision-makers at all levels of the socio-political and economic policy-making hierarchy in both public, as well as private spheres.
Advances in formal methods in the areas of commonsense reasoning, qualitative spatio-temporal representation and reasoning, reasoning about space, actions and change and spatio-temporal dynamics [30–32] provide interesting new perspectives for the development of the foundational spatial informatics underlying next-generation GIS systems. The basic requirements within these systems encompass:
Knowledge engineering, semantics and modeling: Introduction of the capability to include object-, event- and process-based abstractions of spatio-temporal phenomena as native, first-class entities, enshrined with rich semantic characterizations within the ontology and conceptual model of the GIS system in a manner that is interoperable across systems and implementations.
Analytical reasoning: From a computational viewpoint, generic high-level reasoning mechanisms that leverage upon the semantics of the formally modeled or axiomatized properties of domain-independent and -dependent aspects are necessary. These mechanisms could be used to ground and model environmental (natural and human) phenomena from domains, such as epidemiology, urban dynamics, vegetation monitoring, wild-life biology, transportation dynamics, cultural heritageand so forth (Section 2.1).
Indeed, it is expected that these knowledge representation and reasoning capabilities will provide a basis for high-level analytical and decision-making tasks, either individually or in conjunction with other forms of analytical techniques from the field of spatial statistics or quantitative analysis in GIS.
1.5. Contributions and Organization of the Paper
This paper aims to bring formal methods concerning Knowledge Representation and Reasoning (KR) into the domain of Geographic Information Systems. In this context, and with a particular focus on the use of KR-based formal commonsense reasoning methods, this paper:
demonstrates basic representation and computational challenges pertaining to space, actions and change
presents an overarching framework for high-level modeling and (explanatory) analysis for the geospatial domain and
addresses concrete representational and computational problems that accrue in this context and provides a unified view of a consolidated architecture in the backdrop of an illustrated application scenario from the domain of urban dynamics.
The paper is organized as follows:
Section 2 presents application-guided perspectives from several domains, where the notion of geospatial dynamics is recognized as being applicable; we also provide two concrete motivating scenarios concerning the spatio-temporal dynamics of urban narratives.
Section 3 presents a brief overview of formal methods in commonsense, qualitative spatial representation and reasoning and may be skipped by readers familiar with the topic.
Section 4 presents an intuitive overview of the core spatial informatics—representational and computational challenges—that accrue whilst modeling and reasoning with dynamic geospatial phenomena.
Section 5 contextualizes the dynamic geospatial spatial informatics by way of a consolidated framework: We describe the overall architecture and its components using a running example and illustrate how basic representational and computational challenges may be met within the formal theory of space, events, actions and change.
Section 6 concludes the paper with a discussion of our research perspective and a summary of contributions.
2. Geospatial Dynamics: Application Perspectives
In recent years, modeling and analysis of dynamic geospatial phenomena and the integration of time in GIS have emerged as major research topics within the GIS community. Although, at present, the representational and analytical apparatus to examine the dynamics of such phenomena is nascent at best, the issue has been considered a major research priority in GIS [33].
Here, we briefly indicate a select range of domains where the notion of geospatial dynamics is applicable and also provide motivating scenarios from the field of urban dynamics and environmental development.
2.1. Application Areas
A wide-range of priority areas where high-level analytical ability is crucial come to the fore:
► Epidemiology. This is a classic application domain, which from a spatial perspective, involves the study of diffusive processes (e.g., the spread of disease) with either point-based or aggregate entities in space and time.
► Moving data analysis. This domain involves the analysis of (typically people-centered) motion data for purposes of prediction and explanation. For instance, studies involving vehicles/people trajectories, transportation data, crime statistics have found significant attention in this area.
► Land-use analysis. This corresponds to the analysis of land-use patterns, e.g., in urban areas, on the basis of remote sensing and other ground data. For instance, one objective here could be to study the nature of land-use dynamics either together or in isolation with data involving socio-economic dimensions.
► Disaster management. This corresponds to assistive technologies that provide managerial and analytical capabilities both before/after and in times of natural and man-made calamities (e.g., fire, flooding, hurricanes, tornado, landslides, earthquakes).
► Environmental modeling, wildlife biology. These domains involve modeling and analysis of environmental phenomena at the ecological level, e.g., integrated systems and relationships involving flora and fauna. Typical studies involve vegetation monitoring (e.g., forestry/deforestation), climatic change (e.g., glaciers, sea level change) and monitoring of pollution, soil, air quality, water quality, etc.
► Archeology, cultural heritage. GIS technology is employed by archaeologists to reconstruct historical events and developments, as well as to predict sites of potential archeological interest. Resulting archeological records are made accessible to the public in the form of cultural heritage portals. To facilitate intuitive access to cultural heritage information, for instance, by tourists, a spatio-temporal ontology of changes in political and administrative regions is required.
2.2. Urban Dynamics: Models, Metrics and Tools
We single out the domain of urban dynamics here, as it will serve as the exemplary application domain that we have chosen in this paper to illustrate our approach and conceptual framework. Models for urban development and growth have been designed and investigated for decades, predominantly under the view of a city as a complex system. This research includes the simulation and modeling of urban dynamics using computational approaches, such as cellular automata (e.g., [34–36]) to simulate diffusion processes and multi-agent systems (e.g., [37]), in particular, to simulate movement, transportation and human behavior on the level of the individual and the collective level (see [37,38] for overviews). The role of the environment in multi-agent systems can be manifold, including being limited to supporting the movement of agents, a resource for agents used to facilitate actions, or of being a complex system with its own dynamics potentially formed by agents themselves [37]. Urban modeling approaches have been integrated into traditional GIS systems, and vice versa, GIS functionalities have been incorporated into urban modeling packages (see, for instance, [39]).
In spite of major progress in the development of models, metrics and software tools for geospatial urban and environmental modeling and simulation, the integration and application of advanced land-use and simulation models in the (urban) planning process has been problematic [40,41]. As Briassoulis [40] emphasize in the context of land-use theorizing and modeling, and policy making and planning:
“shifts that have taken place since the late 1980s…, away from ‘classical’ thinking (positivism, reductionism, and linear and static world-views) and towards complex systems (CS) thinking (alternative epistemologies, holism, and nonlinear and dynamic worldviews)”
The principal focus in the field of modeling of urban dynamics (e.g., for planning) has been on data-driven quantitative predictive simulation models with powerful computational tools. Stevens et al. [42] develop iCity, a tool for the predictive modeling of urban growth and land-use change in assisting spatial decision making for urban planning. Their underlying method extends a traditional cellular automata (CA) formalization with an irregular CA with the main emphasis on facilitating the implementation of model logic and to run the model to simulate urban growth. Vermeiren et al. [43] propose a spatially-explicit logistic regression model for predicting future urban scenarios, in particular, focusing on predicting predict patterns of urban growth based on existing indicators quantified from data, such as LANDSATimagery. Arsanjani et al. [44] extend the performance of the standard logistic regression model with a hybrid model consisting of logistic regression, Markov chain (MC) and cellular automata (CA). The model can be used to simulate and predict the spatiotemporal states of built-up land use. Ramachandra et al. [45] quantify the urban dynamics using temporal remote sensing data with the help of well-established landscape metrics. Shannon’s entropy measure, population densities signifying the level of urbanization at local levels, landscape metrics providing detailed knowledge about the sprawl and principal component analysis for prioritizing the metrics for detailed analyses have been applied. Kong et al. [46] develop and apply an urban growth potential model incorporating spatial metrics with the aim of providing decision support documents for urban planners and stakeholders with spatially explicit information for future planning and monitoring plans.
van Kouwen et al. [47] propose to link advanced simulation models with flexible and simple tools for policy-making; van Kouwen et al. [47] base their work on the hypothesis that advanced simulation models offer high-end analytical value (at the expense of understandability by policy-makers), whereas simple methods (in their case, a qualitative cognitive mapping tool) help retain comprehensibility. Weber [48] applies an interaction model for the understanding of the mutual relationships between social and spatial systems; this method involves observing, quantifying and modeling the effects of urban spatial forms on social systems and, in counterpart, the effects of social dynamics on a spatial urban environment. The interaction model may be integrated in a GIS system, which would allow co-relations and associations between information available in different layers (e.g., such a model could interact with an object and event-based view of dynamic geospatial phenomena in the manner that has been proposed in this paper).
Such paradigmatic shifts in environmental modeling and simulation thinking, and technologies notwithstanding, it is not yet possible to determine which approach is superior [40]. In so far as the broad underlying premises are concerned, the motivation of the core proposal of this research resonated with that of van Kouwen et al. [47], Weber [48]; our high-level narrative-based commonsense analysis framework is aimed at synergizing with other quantitatively-driven models and metrics for the people-centered understanding of urban geospatial dynamics. Our model is aimed at interpretation from large-scale geospatial data, and predictive analysis is not a part of our framework; however, we propose that semantic and qualitative analysis of data cannot only offer useful insights for quantitatively driven simulation models, but can also be an invaluable asset in the hands of human experts and analysts involved in planning and policy formation.
2.3. Urban Narratives and Their Spatio-Temporal Dynamics: An Example
Urbanization and high-level narratives of urban dynamics can be interpreted with respect to the sum total of a range of demographic, environmental (both natural and artificial), sociological and economic processes. Indeed, urban dynamics, and “the urban narrative” may not be trivialized as being strictly as such, but for the present discussion, this interpretation suffices.
Urbanization over 28 years
As an example, consider the phenomena of urbanization during 1984–2012 for the cities of Las Vegas (USA) and Dubai (UAE); the following expert analyses in (N1–N2) describes the high-level geospatial, demographic, economic, environmental and other related processes pertaining to urbanization. The strictly spatio-temporal determinants of urbanization in these cities are depicted in Figures 1 and 2, respectively. The data and analyses have been sourced via the publicly available TimeLapse initiative (Listing 1).
Listing 1. TimeLapse.
TimeLapse is a collaborative project involving Google, the US Geological Survey (USGS), NASA, TIMEand Carnegie Mellon University’s CREATELab. TimeLapse has recently released an interactive animation constructed from satellite images of the Earth; the satellite images, sourced from the Landsatprogram, represent images dating back to 1984 detailing a year-by-year progression of changes to the surface of the Earth.
The preliminary view of the generated data depicts phenomena, such as deforestation in the Amazon, the effects of coal mining in Wyoming, the urban expansion of Shanghai and Las Vegas and the drying of the largest lake in the Middle East, Lake Urmia. We use some of these publicly available examples from TimeLapse to establish a context for the overall context of this paper and introduce the idea of narrative-centered interpretation in the geospatial domain.
Google, NASA, Time. http://world.time.com/timelapse/
N1. Las Vegas
“Throughout the 1990s and much of the 2000s, the boundaries of metro Las Vegas kept expanding, asnew housing developments were thrown up to accommodate the throngs of Americans who wanted to take advantage of the region’s booming economy. From 2000 to 2010, the city’s population grew by nearly 50%—a rate that’s hard to find outside the developing world.
But if Las Vegas boomed along with the housing sector during the first several years of the 21st century, it went bust when the recession hit. The city was ground zero for the foreclosure crisis. As late as 2012, Las Vegas had one foreclosure filing for every 99 housing units, good for the fourth highest rate in the country. And as economically unsustainable as Las Vegas’ growth has proved to be over the past several years, it may be even more environmentally unsustainable. The city receives almost no rain, and most of its water comes from nearby Lake Mead. But as can be clearly seen in the TimeLapse images, Lake Mead is drying up, the victim of a prolonged drought—potentially abetted by climate change—and the increasing demand placed on it by Las Vegas’ growing population. Lake Meads water level has fallen from a little over 1,200 ft. (365 m) to 1,125 ft. (343 m) now. In recent years, officials in Las Vegas have taken admirable steps to reduce water waste, but if Lake Mead keeps shrinking, Sin City will stop growing”.
N2. Dubai
“In the mid-1980s, […], Dubai was a small desert city of about 300,000 people, overshadowed by nearby Abu Dhabi, the capital of the United Arab Emirates. What growth Dubai had experienced was mostly recent; in the 1950s it was little more than a village, with pearl diving its chief industry. Today, Dubai’s population exceeds 2.1 million, and the metropolis has asserted itself as the financial center of the Middle East.
Dubai is a city that seemed to grow almost overnight, like a desert oasis made real. It has the worlds tallest skyscraper—the Burj Khalifa, …,—as well as its largest mall, its biggest theme park and its longest indoor ski run…Not content with simply building in the desert, over the past couple of decades Dubai has built out into the sea. Sand dredged from the seafloor has been used to create artificial islands of recognizable shapes—including a pair of palm trees. In the lower-right corner of the Time-lapse images, areas of empty sand are filled up with new buildings, as the city grows further and further away from the sea, pushing into the desert. That breakneck pace of development has slowed somewhat in recent years, as Dubai was hit hard by the global recession of 2008”.
In general, high-level expert analysis encompassing commonsense, qualitative interpretation (e.g., the underlined parts in N1–N2 above) of urban/geospatial processes may be identified from measurable low-level spatial and temporal features, themselves obtainable from a range of data sources, such as satellite imagery and remote sensing, land-surveys, physical environmental sensing a la sensor networks, etc. In particular, the complex dynamics underlying the identification of urbanization processes may encompass several data sources, such as:
Satellite imagery
Remote sensing
Land use statistics and databases, Gazetteers
Demographic data (e.g., from census surveys)
Economic data (income, growth, economic activity, currency and stock market performance, etc.)
The focus of the narrative-centered model presented in this paper is strictly on the spatio-temporal aspects of the dynamic geospatial phenomena that underlie perceivable geospatial change at the object or feature level. The spatio-temporal aspects can be co-related with other kinds of quantitative and qualitative data (e.g., economic and demographic measures and census studies); however, a formal treatment of such correlations is beyond the scope of this paper. We emphasize that modeling and reasoning about such correlations would indeed be possible and also be within the scope of the overall narrative-based analytical framework for GIS that has been proposed in this paper.
3. Qualitative Spatial Representation and Reasoning
The field of qualitative spatio-temporal representation and reasoning (QSTR) seeks to define formal models of spatial and temporal relations dealing with different aspects of space, such as topology, direction, distance, size, etc. QSTR has evolved as a specialized discipline within Artificial Intelligence [31,32,49–51]. Formal methods in QSTR provide a commonsensical interface to abstract and reason about quantitative spatial information.
The common characteristic of the developed formal models, often termed qualitative calculi, is that, in contrast to quantitative approaches, just a small number of basic relations is distinguished. Qualitative spatial/temporal calculi are relational-algebraic systems pertaining to one or more aspects of space. They abstract from metrical details and focus on properties that make a difference in a particular application domain. This allows for an analysis of spatio-temporal data on a high-level of abstraction and directly with respect to human spatio-temporal concepts and commonsense reasoning. As such, they provide one means to represent and analyze data in an abstract way that is more natural to humans, a key challenge identified for future GIS (e.g., [52–54]). The basic tenets in QSTR consist of constraint-based reasoning algorithms over an infinite (spatial) domain to solve consistency problems in the context of spatial calculi. The key idea here is to partition an infinite quantity space into finite disjoint categories and utilize the special relational properties of such a partitioned space for reasoning purposes.
In general, qualitative spatial calculi can be classified into two groups: topological and positional calculi. With topological calculi, such as the Region Connection Calculus (RCC), the primitive entities are spatially extended regions of space and could possibly even be 4D spatio-temporal histories, e.g., for motion-pattern analyses. Alternatively, within a dynamic domain involving translational motion, point-based abstractions with orientation calculi suffice. Examples of orientation calculi include [32]: the Oriented-Point Relation Algebra , the Double-Cross Calculus and the line-segment-based Dipole Calculus.
Similar to these works, which are situated within an artificial intelligence/Knowledge Representation (KR) context, many crucial advances have accrued from other communities concerned with the development of formalisms and algorithms for modeling and reasoning about spatial information, a prime example here being the domain of spatial information theory for Geographic Information Systems (GIS) [55,56]. The most widely adopted and applied qualitative spatial (topological) calculi are the RCC-8 calculus [57] and 9-Intersection Model [58], which both essentially distinguish the same eight basic topological relations between two spatial regions as shown in Figure 3. (In this paper, we will use RCC-8 in all our examples.) The fundamental operation underlying most qualitative reasoning techniques is the composition of two relations: Given the relation holding between entities A and B and the relations between B and C, the composition operation tells us which relations can hold between A and C. For instance, in the case of RCC-8, A as the tangential proper part of B and B disconnected from C implies A as the non-tangential proper part of C For many qualitative calculi, composition-based reasoning allows for deciding consistency, as well as for deducing new information from a given set of relations (see [32] for details).
Relevant applications in GIS and urban planning
Qualitative spatial calculi have, for instance, been utilized in the GIS domain to describe spatial relationships in query and retrieval scenarios [59,60], to formalize (geo)spatial concepts and processes [61–64], and to specify background knowledge and integrity constraints in the context of spatial and spatio-temporal database applications [65–67]. The notion of conceptual neighborhood [68,69] has been introduced to describe spatial change on the level of qualitative spatial relations and forms the basis to perform temporal reasoning in the form of simulation, interpolation and planning.
Tools
Spatial reasoning techniques manifest themselves in several ways as practical tools aimed at providing general spatial abstraction, reasoning, consistency and constraint satisfaction tasks, prime examples here being the systems, CLP(QS) [70,71], SparQ [72], GQR [73] and the generic toolkit, QAT, for n-ary calculi [74].
4. The Spatial Informatics of Geospatial Dynamics
The spatial information theoretic challenges underlying the development of high-level analytical capability in dynamic GIS consist of fundamental representational and computational problems pertaining to: the semantics of spatial occurrences, practical abduction in GIS and to support these, problems of data abstraction, integration and spatial consistency.
4.1. Spatial Occurrences: Analyses with Events and Objects
Our objective is to develop the functionality that enables reasoning about spatio-temporal narratives consisting of events and processes at the geographic scale. We do not attempt an elaborate ontological characterization of events and processes, a topic of research that has been addressed in-depth in the state-of-the-art. For the purposes of this paper, we utilize a minimal, yet rich, conceptual model consisting of a range of events, such that it may be used to qualitatively ground metric geospatial datasets consisting of spatial and temporal footprints of human and natural phenomena at the geographic scale.
Spatial occurrences may be defined at two levels: (I) domain-independent; and (II) domain-dependent:
4.1.1. Domain-Independent Spatial Occurrences
These occurrences are those that may be semantically characterized within a general theory of space and spatial change. These may be grounded with respect to either a qualitative theory or an elaborate typology of geospatial events. These may be grounded with respect to either a qualitative theory or an elaborate typology of geospatial events (e.g., growth, shrinkage, cloning, death, transmission [14])).
Spatial Changes at a Qualitative Level
In so far as a general qualitative theory of spatial change is concerned, there is only one type of occurrence, viz., a transition from one qualitative state (relation) to another state (relation) as (possibly) governed by the continuity constraints of the relation space. At this level, the only identifiable notion of an occurrence is that of a qualitative spatial transition that the primitive objects in the theory undergo, e.g., the transition of an object (o1) from being disconnected to another object (o2) to being a tangential-proper-part (see again Figure 3). At the level of a spatial theory, it is meaningless to ascribe a certain spatial transition as being an event or action; such distinctions demand a slightly higher level of abstraction. For instance, the example of a transition from disconnected to tangential-proper-part could either coarsely represent the volitional movement of a person into a room or the motion of a ball. Whereas the former is an action performed by an agent, the latter is a deterministic event that will necessarily occur in normal circumstances. Our standpoint here is that such distinctions can only be made in a domain-specific manner; as such, the classification of occurrences into actions and events will only apply at the level of the domain with the general spatial theory dealing only with one type of occurrence, namely primitive spatial transitions that are definable in it.
Typology of Events and Patterns
At the domain-independent level, the explanation may encompass behaviors, such as emergence, growth and shrinkage, disappearance, spread, stability, etc., in addition to the sequential/parallel composition of the behavioral primitives aforementioned, e.g., emergence followed by growth, spread/movement, stability and disappearance during a time-interval. Certain kinds of typological elements, e.g., growth and shrinkage, may even be directly associated with spatial changes at the qualitative level. The appearance of new objects and the disappearance of existing ones, either abruptly or explicitly formulated in the domain theory, is also characteristic of non-trivial dynamic (geo)spatial systems. Within event-based GIS, appearance and disappearance events are regarded as being an important typological element for the modeling of dynamic geospatial processes [1,14]. For instance, Claramunt and Thériault [1] identify the basic processes used to define a set of low-order spatio-temporal event,s which, among other things, include appearance and disappearance events as fundamental. Similarly, toward event-based models of dynamic geographic phenomena, Worboys [14] suggests the use of the appearance and disappearance events at least in so far as single object behaviors are concerned (see Figure 4). Appearance, disappearance and re-appearances are also connected to the issue of object identity maintenance in GIS [10,11].
4.1.2. Domain-Specific Spatial Occurrences
At a domain-dependent level, behavior patterns may characterize high-level processes, environmental/natural and human activities, such as deforestation, urbanization, land-use transformations, etc. These are domain-specific occurrences that induce a transformation on the underlying spatial structures being modeled [15]. Basically, these are domain-specific events or actions that have (explicitly) identifiable occurrence criteria and effects that can be defined in terms of qualitative spatial changes and the fundamental typology of spatial changes. For instance, in the example in Figure 4, we can clearly see that region a has continued to shrink during 1950 to 1990, eventually disappearing altogether. The following general notion of a “spatial occurrence” is identifiable [75]:
“Spatial occurrences are events or actions with explicitly specifiable occurrence criteria and/or pre-conditions, respectively, and effects that may be identified in terms of a domain independent taxonomy of spatial change that is native to a general qualitative spatial theory”.
As an example, consider an event that will cause a region to split or make it grow/shrink. Likewise, an aggregate cluster of geospatial entities (e.g., in wildlife biology domain) may move and change its orientation with respect to other geospatial entities. Thinking in agent terms, a spatial action by the collective/aggregate entity, e.g., turn south-east, will have the effect of changing the orientation of the cluster in relation to other entities. In certain situations, there may not be a clearly identifiable set of domain-specific occurrences with explicitly known occurrence criteria or effects that are definable in terms of a typology of spatial change, e.g., a cluster of alcohol-related crime abruptly appearing and disappearing at a certain time. However, even in such situations, an analysis of the domain-independent events and inter-event relationships may lead to an understanding of spatio-temporal relationships and help with practical hypothesis generation [5].
4.2. Practical Abduction for GIS
Explanatory reasoning requires the ability to perform abduction with spatio-temporal information. In the context of formal spatio-temporal calculi, and logics of action and change, this translates to the ability to provide scenario and narrative completion abilities at a high-level of abstraction.
Consider the GIS domain depicted in Figure 4 and the basic conceptual understanding of spatial occurrences described in Section 4.1. At a domain-independent level, the scene may be described using topological and qualitative size relationships. Consequently, the only changes that are identifiable at the level of the spatial theory are shrinkage and, eventual, disappearance—this is because a domain-independent spatial theory may only include a generic typology (appearance, disappearance, growth, shrinkage, deformation, splitting, merging, etc.) of spatial change. However, at a domain-specific level, these changes could characterize a specific event (or process), such as deforestation. The hypotheses or explanations that are generated during a explanation process should necessarily consist of the domain-level occurrences in addition to the underlying (associated) spatial changes (as per the generic typology) that are identifiable. Intuitively, the derived explanations more or less take the form of existential statements, such as: “Between time-points ti and ti, the process of deforestation is abducible as one potential hypothesis”. Derived hypotheses/explanations that involve both domain-dependent and, as well, their corresponding domain-independent typological elements are referred to as being “adequate” from the viewpoint of explanatory analysis for a domain. At both the domain-independent, as well as dependent levels, abduction requires the fundamental capability to interpolate missing information and understand partially available narratives that describe the execution of high-level real or abstract processes. In the following, we present an intuitive overview of the scenario and narrative completion process.
Scenario and Narrative Completion
Explanation problems demand the inclusion of a narrative description, which, from the logic-based viewpoint of this paper, is essentially a distinguished course of actual events about which we may have incomplete information [16,17]. Narrative descriptions are typically available as observations from the real/imagined execution of a system or process. Since narratives inherently pertain to actual observations, i.e., they are temporalized, the objective is often to assimilate/explain them with respect to an underlying process model and an approach to derive explanations.
Given partial narratives that describe the evolution of a system (e.g., by way of temporally-ordered scene observations in event-based GIS datasets) in terms of high-level spatio-temporal data, scenario and narrative completion corresponds to the ability to derive completions that bridge the narrative by interpolating the missing spatial and action/event information in a manner that is consistent with domain-specific and domain-independent rules/dynamics.
Consider the illustration in Figure 5 for a branching/hypothetical situation space that characterizes the complete evolution of a system. In Figure 5, the situation-based history < s0, s1, …, sn > represents one path, corresponding to an actual time-line < t0, t1, …, tn >, within the overall branching-tree structured situation space. Given incomplete narrative descriptions, e.g., corresponding to only some ordered time-points in terms of high-level spatial (e.g., topological, orientation) and occurrence information, the objective of causal explanation [75] in a spatio-temporal context is to derive one or more paths from the branching situation space that could best-fit the available narrative information. Of course, the completions that bridge the narrative by interpolating the missing spatial and action/event information have to be consistent with domain-specific and domain-independent rules/dynamics.
Explanation, in general, is regarded as a converse operation to temporal projection, essentially involving reasoning from effects to causes, i.e., reasoning about the past [76]. Logical abduction is one inference pattern that can be used to realize explanation. In Section 5, we present a practical illustration of the concept of scenario and narrative completion (by abduction) for explanatory analysis in the GIS domain.
4.3. Temporal Partitioning, Qualitative Abstraction and Integration
An event-based GIS system based on a narrative-centered ontological and computational model of geospatial dynamics requires the capability to handle data from multiple sources, for instance, from different sensors, remote sensing data, map data, etc. Such data itself is often afflicted by measurement errors, uncertainty, etc. In this section, we elaborate on some of the technical challenges concerning handling dynamic spatio-temporal data; the challenges are of a general nature, but have a special significance from the viewpoint of the narrative-centered model (Section 5; the first figure in Section 5) of this paper.
4.3.1. Temporal Partitioning and Qualitative Abstraction
To perform explanatory analysis on a level of qualitative spatial relations, geo-referenced quantitative input data about spatial objects from different sources needs to be translated into relations from several qualitative spatial models or calculi dealing with different aspects of space, a process we refer to as qualitative abstraction. A prerequisite for applying the qualitative abstraction procedure is that the input data is temporally partitioned such that each part is associated with a particular time point in an ordered sequence of time points. For each time point, the qualitative abstraction procedure takes the associated quantitative data and derives the spatial relations from the given qualitative models holding between the involved objects. The result is a static qualitative spatial description for each time point. If the uncertainty of quantitative information is explicitly represented, this needs to be taken into account and may lead to disjunctions of relations on the qualitative level.
4.3.2. Integration and Spatial Consistency
Due to the mentioned measurement errors and uncertainty of the quantitative input data, the qualitative descriptions resulting from the qualitative abstraction for particular time points may contain contradictions or violate integrity constraints stemming from background knowledge about the domain. Figure 6 illustrates the case of a spatial inconsistency on the level of topological relations when combining the information from four different sources (all concerning the same time point): From combining the fact that objects C and D (e.g., two climate phenomena) are reported to overlap by one source (a) with the reported relations, C is completely contained in A (b) and D is completely contained in B (c), it follows that the two regions, A and B, would need to overlap, as well. This contradicts the information from the fourth source (d), which could, for instance, be a spatial databases containing boundaries of administrative regions, that says that A and B are externally connected. Instead of the fourth source, we could also have introduced a general integrity constraint stating that administrative regions on the same level never overlap. This would have resulted in the same contradiction rendering the given information inconsistent.
As a result of the possibility of inconsistent input information occurring in geographic applications, frameworks for explanation and spatio-temporal analysis need the ability to at least detect these inconsistencies in order to exclude the contradicting information or, as a more appropriate approach, resolve the contradictions in a suitable way. Removing logical inconsistencies is crucial in the context of a logic-based abductive reasoning approach, as we suggest in this paper, as otherwise, incorrect conclusions can be abduced from an inconsistency, which will ultimately lead to incorrect results. While the view that logical inconsistencies are undesirable has been challenged (see [77]), explanatory analysis with inconsistent information raises many challenges going beyond the scope of this paper. In certain applications, it may be possible to derive that certain information is irrelevant for the explanatory task at hand and filter out this information in advance, such that no removal of inconsistencies wrt this information is required.
Deciding the consistency of a set of qualitative spatial relations has been studied as one of the fundamental reasoning tasks in qualitative spatial representation and reasoning [32]. The complexity of deciding consistency varies significantly over the different existing qualitative calculi. For most common qualitative calculi, such as RCC-8, the consistency can be decided in cubic time when the input description is a scenario, which means it does not contain disjunction of relations. This is achieved by the path consistency or algebraic closure method [78], which is ultimately based on a set of composition axioms that state which relation can hold between objects A and C given the relations holding between object A and B and between B and C. For a general description, including disjunctions, a more costly backtracking search has to be performed.
Integrity constraints have been investigated in the (spatial) database literature [79,80]. As the example above shows, integrity rules in a geographic context often come in the form of qualitative spatial relations that have to be satisfied by certain types of spatial entities. These kinds of spatial integrity constraints can be dealt with by employing terminological reasoning to determine whether a certain integrity rule has to be applied to a given tuple of objects and feeding the resulting constraints into a standard qualitative consistency checker together with the qualitative relations coming from the input data.
4.3.3. Conflict Resolution
As indicated in the previous section, when conflicts arise during the integration of spatial data, it is often desirable to not only detect the inconsistencies, but also to resolve conflicts in a reasonable manner to still be able to exploit all provided information in the actual logical reasoning approach for explanation and analysis. Methods for data integration and conflict resolution have, for instance, been studied under the term, information fusion [81]. They are commonly classified into quantitative approaches and symbolic approaches. Quantitative approaches mainly employ statistical methods, such as least-square adjustment to deal with multiple observations, while symbolic information fusion is concerned with the revision of logical theories under the presence of new evidence. An important distinction here is that between revision and update. In the case of revision, additional information about a particular state of the world becomes available and needs to be combined with what was known before. In the case of update, one assumes that the state may have changed and that the new information is more up-to-date than the previous knowledge. These different information fusion settings have led to the formulation of different rationality criteria that corresponding computational approaches should satisfy, such as the so-called AGM postulates for belief change [82]. Such computational solutions often consist of merging operators that compute a consistent model that is most similar to the inconsistent input data. In distance-based merging approaches, this notion of similarity is described using a distance measure between models. This idea has been applied to qualitative spatial representations [83,84] using the notion of conceptual neighborhood [68,69] to measure distance in terms of the number of neighborhood changes that need to be performed to get from inconsistent qualitative descriptions to consistent ones.
To illustrate the operation of a qualitative merging approach for conflict resolution, let us consider the example in Figure 7 in which information from two sources providing information about the city of Dubai (see again Figure 2) at a given time needs to be merged: Let us say the first source, G, provides geometries for two districts, GDeira and GMirdif (shown as polygons with fully drawn borders in Figure 7a, while the second source, G′, provides geometries for another district, , and for the city of Dubai itself, (both shown as polygons with dashed boundaries in Figure 7a. Let us further assume that we also have two integrity constraints for the integration result in this scenario. The first one states that the geometries of districts cannot overlap and, thus, have to be disjoint or touching (disjunction {ec, dc} in terms of RCC-8 relations). The second constraint demands that each geometry of a city district has to be completely contained in the geometry of the city. This corresponds to a disjunction of {ntpp, tpp} in terms of RCC-8 relations and applies to the relation of each of the three districts to . As Figure 7a illustrates, superimposing the geometries of both sources results in violations of both integrity constraints: GDeira and overlap (RCC-8 relation po), and GMirdif and overlap, as well. A qualitative merging approach would now resolve these conflicts on the qualitative level by computing the consistent scenario that is closest to the qualitative interpretation of the input information. A possible result is shown in Figure 7b. The relation between GDeira and has been changed to {ec} and that of GMirdif and to {tpp}, which corresponds to the actual spatial configuration depicted in Figure 7c.
5. Geospatial Analytics: A Narrative-Based Formal Framework
The discussions in Section 3 encompassed a range of representation and computational challenges that accrue in the context of dynamic geospatial analysis. We now describe our formal framework, and its corresponding conceptual architecture, for high-level qualitative modeling and explanatory analysis for the domain of geospatial dynamics illustrated in Figure 8.
5.1. Overview of Architecture
Our proposed architecture comprises the entire range of steps required to perform explanatory analysis of geospatial dynamics on a qualitative level of abstraction, starting with the processing of the actual (typically quantitative) data to form a consistent qualitative description, to the usage of abductive reasoning for narrative completion and to the recognition of high-level processes leading to a knowledge base that can be queried and utilized by application systems and decision makers. The main aspects of the proposed architecture are the following:
Input datasets. The input consists of datasets from several sources, such as remote sensing data, spatial databases, sensor data, etc.
Preprocessing. These datasets are then processed to derive qualitative spatial observations associated with specific time points to hand over to the actual reasoning component. This preprocessing is done by the Temporalpartitioning and Integration module responsible for partitioning the input data into time points and integrating data associated with the same time point, including the resolution of spatial conflicts.
Qualitative abstraction. This module is itself supported by the Qualitative abstraction module for performing the abstraction from quantitative to qualitative information and the Consistency checking module for testing whether a qualitative spatial descriptions is consistent or contains logical contradictions.
Scenario and (Partial) Narrative Descriptions. The qualitative temporally-ordered observations generated by the Temporal partitioning and Integration module constitute the scenario and narrative descriptions and serve as the input to the Reasoning module, which embeds in itself one or more forms of (explanatory) reasoning capabilities.
Explanatory Reasoning. The reasoning component leads to the derivation of spatio-temporal knowledge that can be utilized by external services and application systems that directly interface with humans (e.g., experts, decision makers). Access can be provided by a Query Processing module that allows for identifying high-level abducibles in the derived knowledge base.
In the following, we further explain the architecture and provide practical examples of the problems and solutions that we previously elaborated on in Section 4 in the context of a case study.
5.2. The Urban Dynamics Domain
Consider the following significantly trivialized urban narrative (inspired from the dynamics of a real city); the textual description has also been illustrated as a time-line in Figure 9, and the object-level changes along with their temporal progression are illustrated in Figure 10.
- The story of Bombaj. The contemporary city of Mumbaj was once a collection of closely located, tiny islands, surrounded by mangroves and other thick forests, along the coast of a huge landmass in the Arabian sea. Guided by Bombaj’s proximity to the sea and the Western world, humans deforested massive parts of the mangrove forests and undertook reclamation of the islands to form one continuous entity connected to the huge landmass; this continuous entity came to be know as the city of Bombaj (subsequently Mumbaj).
- Migration. Initially, there exists a thick forest (subsequently becoming an endangered national park) in the north-east, the sea on the west and small pockets of human settlements by way of semi-urban/low-rise and rural settlements. The idea of Bombaj—its semantic characterization as a place—is centered on these human settlements.
- Basic infrastructure setup. Infrastructure gets established in an attempt to provide accessibility/coverage within the city: major transportation links get established in addition to other initiatives. New conceptual zones gets established, and place-names are formed based on the division created by the transportation link; primarily, two main zones that get created and persist even today have been come to be known as East-Bombaj and West-Bombaj.
- Residential development. New residential areas come up, and the West Zone, by virtue of its proximity to the sea, acquires a socio-economic privilege. Thereafter, powerful economic forces dictate that low income/low-rise areas, populated by recent immigrants (i.e., worker groups), come up in the lesser attractive East Zone. The city now starts to acquire its real character.
- Industrialization. The East Zone, which is socio-economically perceived as being less attractive, starts to attract isolated pockets of industrialization. New industrial zones get established in close proximity to the human settlements.
- Infrastructure development. Industrialization, reinforced with further migration into the city, necessitates further infrastructure development. New transportation networks get built up, and major points of intersection/junctions get established/created; these junctions acquire significance as points of economic agglomeration. New industrial zones get established around these hubs of economic activity.
- Rapid urban migration. Large-scale deforestation of the thick forests and mangrove areas is undertaken as a result of the high financial value of land in the West Zone and massive population influx and re-development in the East Zone. Economic prosperity means that people in a lower income bracket are lifted, and there is a market for semi-urban settlements in the East Zone, which previously primarily consisted of rural settlements.
Example 5.1 (Process Analysis in the Urban Dynamics Domain) The urban dynamics domain consists of basic high-level processes, such as industrialization, migration, deforestation and relocation. The domain consists of the following entities: RuralZones: rz1, rz2, rz3; ForestZones: Park (prk1); Mangroves: mg1, mg2, mg3; SemiUrbanZones: suz1, suz2; HighRiseZone: hrs1; MunicipalZones: district1 (ds1), EastZone (ez), WestZone (wz), sea1; TransportationLinks: tl1, tl2; IndustrialZones: iz1, iz2, iz3.
From the viewpoint of high-level narrative reasoning, the components of the theory that need to be formally modeled include: (1) domain constraints, spatial relationships (based on observational data) and other existential properties concerning the (appearance and disappearance) of objects; (2) process dynamics, or the laws of the domain, that determine occurrence criteria and effects for domain-specific events; (3) high-level abducibles that provide the causal rules that may be used as a basis of process extraction from a logically abduced model consisting only of domain-independent events.
The domain constraints and the high-level abducibles together constitute the overall specification, referred to as the domain theory, for the urban dynamics domain. The high-level abducibles do not play a direct role in the narrative completion process, but are only required during a post-processing stage (as a means to query abduced/derived knowledge).
Within an object and event-based GIS system, one may imagine high-level symbolic information to be available from a range of data sources. Performing explanatory analysis with this information first requires temporal partitioning, qualitative abstraction and integration capabilities, presented next.
5.3. Temporal Partitioning, Qualitative Abstraction and Integration
To illustrate the role of temporal partitioning and integration with qualitative abstraction, consistency checking and conflict resolution (discussed previously in Section 4.3) in our example, let us assume that the input data (a) stems from different sources and that (b) each piece of information is associated with a timestamp specifying when the underlying measurement or observation has been performed. More specifically, let us say that Source 1 provides information about different land use zones, including parks, residential zones and industrial zones, which are derived by analyzing aerial images, while Source 2 provides information about natural reservoirs, which is about the park and mangroves, stemming from a spatial database. All other information in our example comes from additional sources, but does not play a role in this here. Let us furthermore assume that the land use types are defined in a mutually exclusive way, such that two different zones cannot overlap.
Since all geometries we get from Sources 1 and 2 are timestamped, the first thing that has to happen is a partitioning of the total covered time period into time intervals and, by this, inducing groups of spatial facts that are associated with each interval based on their timestamps. Each interval is represented by a time point, ti, in an ordered sequence of time points.
Figure 11a illustrates part of the combined information from all sources that after temporal partitioning fall into time period t4 shown in Figure 10d of Example 5.1. Sources 1 and 2 both contain geo-referenced polygons for the park, but this information does not match. To derive a consistent qualitative description for time period t4, the integration procedure follows Algorithm 1, which takes the set of observed geometries, , with object identifiers and a set of integrity constraints, , as input. The first step is to use the Qualitative Abstraction module to translate the combined geometric data into qualitative spatial relations, which results in a qualitative constraint network, Q. (Alternatively, information for each dataset could be qualified separately, resulting in several constraint networks that have to be combined by a suitable merging operator.) Using the relations from the RCC-8 calculus (see again Figure 3), this network looks as shown in Figure 11b (p and p′ represent the different geometries for the same park object). Next, the Consistency Checking module is used to test whether network Q is consistent and compliant with the integrity constraints. If this is the case, the result can directly be handed over as a qualitative observation for t4 to the reasoning module. However, as also shown in Figure 11b, this is not the case, as integrity constraints are violated in three places. These violations are indicated by listing possible relations following from the integrity constraint in brackets below the original relation. The relation between p and p′ should be eq simply because it is known that both represent the same object. The relation between rz2 and p should be either ec or dc because of the integrity constraints, and the same holds true for the relation between p′ and iz2. Therefore, the qualitative conflict resolution component needs to be called to find a qualitative representation that is as close as possible to the network from Figure 11b, but is overall consistent.
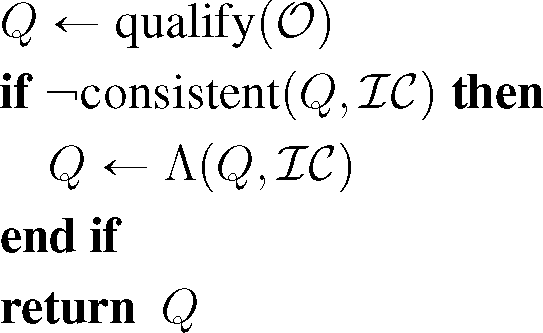 |
To achieve the conflict resolution, an operator, Λ, based on the idea of distance-based merging operators for qualitative spatial representations [83,84] is applied to Q. Our resolution operator, Λ, is based on a distance measure, d(s, s′), between two scenarios over the same set of objects. It is computed by simply summing up the distance of two base relations in the conceptual neighborhood graph of the involved calculus given by over all corresponding constraints, , in the input scenarios:
The resolved network, Λ(Q), is then constructed by taking the union of those scenarios that are consistent, compliant with the integrity constraints and have a minimal distance to Q according to d(s, s′) (Taking the union here means we build a new network by taking the union of all corresponding constraints.):
The result of applying the resolution operator to the network from Figure 11b is shown in Figure 11c: Both violations of integrity constraints have been resolved by assuming that instead of “overlap” the correct relation is “externally connected”. Interestingly, the resulting consistent qualitatively model contains two disjunctions, basically saying that the relation between the park and iz1 is either ec or dc. This is a consequence of the fact that both qualitative models are equally close to the input model, such that it is not possible to decide between the two hypotheses.
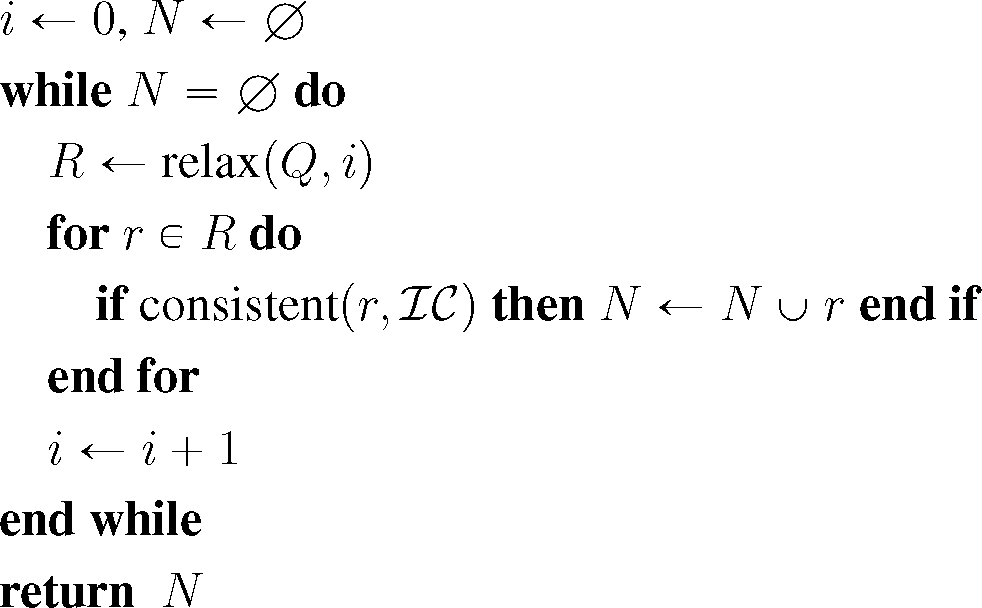 |
5.4. Observation Data: Urban Narrative Description
Given the qualitative abstraction, consistency detection and integration capabilities (as described so far), the objective now is to generate a temporally-ordered narrative of the processes that are reflected by the pre-processed datasets. Before exemplifying the narrative, some basic notation that we use from hereon follows:
Notation
We use a first-order many-sorted language with the following alphabet: {¬, ∧, ∨, ∀, ∃, ⊃, ≡}. There are sorts (and corresponding variables) for: events (Θ = {θ1, θ2, …, θn}), time-points, spatial objects, regions of space and a function symbol (extent: ) that determines the time-dependent spatial location of an entity. We only consider binary topological relationships of spatially extended regions in space. However, the theory encompasses point and line-segment based spatial calculi of arbitrary arity.
Let denote a reified n-ary qualitative spatial relationship space over an arbitrary qualitative spatial calculus. Φ = {ϕ1, ϕ2, …, ϕl} is the set of propositional and functional fluents, e.g., ϕsp(oi, oj) ϵ Φ is a functional fluent denoting the spatial relationship from between objects oi and oj. The special event-predicate, tran(ri, oi, oj) ϵ Θ, denotes a transition to a spatial relation, ri, between objects oi and oj. Finally, the ternary Holds(ϕ, r, t) ⊂ predicate is used for temporal property exemplification, and Happens(θ, t) denotes event occurrences. For notational convenience, we use the following syntactic sugar for fluent terms (ϕ): P (ϕ([xi, …, xn])) transforms to r P (ϕ(xi)) ∧ … ∧ P (ϕ)(xn))]. The use of [xi, …, xn] with event terms (Θ) represents a vector argument and is interpreted differently.
The temporally-ordered (five) observations in Equation (4) represent a formal description of the output of the Temporal Reasoning and Integration module for time points t1 to t6 corresponding to the snapshots depicted in the six images in Figure 10. They provide the grounding for a narrative description of the urban dynamics scenario under consideration: (To save space, the represented observations only show those facts that become true/false in a given observation. Furthermore, some implicit facts are omitted.)
Partial Description and Extension
When spatial relationships (Φspace) between some objects are omitted, a complete description (with disjunctive labels) can be derived on the basis of the composition theorems (cmp. Section 5.5.1) and other integrity constraints for the spatial domain under consideration. In the following, we elaborate on the treatment for a partial situation description using the notion of a monotonic extension. Let Ω denote a partial spatial state description consisting of facts expressed using the ternary Holds predicate. The following notion of a “monotonic extension” is necessary:
Definition 5.1 (Monotonic Extension) The monotonic extension of a partial spatial state description, Ω, is another description, Ω′, such that Ω ⊂ Ω′, and all semantic entailments with respect to the spatial information present in Ω are preserved in Ω′. For lack of space, we leave out the formal definition for the monotonicity condition.
The observation set (Ψ) constitutes the input to a high-level reasoning component. In the section to follow, we develop the formal domain-independent spatial theory that is used as the basis of reasoning or, in this specific case, for practical abductive reasoning in GIS.
5.5. A Domain-Independent Spatial Theory
From a dynamic spatial systems perspective, a domain-independent spatial theory (most crucially) consist of: (1) high-level axiomatic aspects that characterize a qualitative theory of spatial change; (2) phenomenal aspects inherent to dynamic (geo)spatial systems [75]. We adapt this general notion for the domain of geospatial dynamics.
5.5.1. Axiomatic Characterization of a Spatial Theory
Many spatial calculi exist, each corresponding to a different aspect of space. Here, it suffices to think of one spatial domain, e.g., topology, with a corresponding mereotopological axiomatization by way of the binary relationships of the RCC-8 calculus. From an axiomatic viewpoint, a spatial calculus defined with respect to an arbitrary relationship space, , has some general properties (described below in (P1–P5)). For any spatial calculus, it can be assumed that (P1–P5) are known a priori, i.e., these are the intentional properties that define the constitution of the calculus. To realize a domain-independent spatial theory that can be used for reasoning (e.g., spatio-temporal abduction) across different dynamic (geospatial) domains, it is necessary to preserve the high-level axiomatic semantics of these generic properties and, implicitly, the underlying algebraic properties, which collectively constitute a qualitative spatial calculus. A domain-independent spatial theory (Σspace) may be obtained by axiomatizing (P1–P5) as follows:The variables, r1, …, rn, correspond to the qualitative spatial relationships pertaining to spatial calculus being modeled; e.g., in the current case, these could be interpreted as the RCC-8 topological relations {dc, ec, po, eq, tpp, ntpp, tpp−1, ntpp−1}.
(P1–P2). Basic Calculus Properties (Σcp)
has the jointly exhaustive and pair-wise disjoint (JEPD) property, i.e., for any two entities in , one and only one spatial relationship from R holds in a given situation. The joint-exhaustiveness can be expressed using n ordinary state constraints of the form in Equation (6a).
Similarly, [n(n − 1)/2)] constraints of the form in Equation (6b) are sufficient to express the pair-wise disjointness of n relations. Other miscellaneous properties, such as symmetry Equation (7a) and asymmetry Equation (7b) of the base relations too can be expressed using ordinary constraints.
(P3). Conceptual Neighborhood (Σcn)
As we mentioned, the primitive relations of a qualitative calculus have a continuity structure, referred to as its conceptual neighborhood (CND) (see [68,69,85]), which determines the direct, continuous changes in the quality space (e.g., by deformation and/or translational motion). The binary (reflexive) predicate, neighbor(r, r′), denotes a continuity relation between relations r and r′.
Continuity constraints are only useful in scenarios involving spatio-temporal continuity (e.g., diffusive phenome, movement in (geo)space) and may serve a useful role in spatio-temporal interpolation and prediction, especially in scenarios where the available data is incomplete and/or error-prone.
(P4). Composition Theorems (Σct)
From an axiomatic viewpoint, a spatial calculus defined on is (primarily) based on the derivation of a set of composition theorems between the JEPD set, (Section 3). In general, for a (spatial, temporal or spatio-temporal) calculus consisting of n JEPD relationships (i.e., ), [n × n] compositions are precomputed. Each of these composition theorems is equivalent to ordinary state constraint Equation (9), which every spatial situation description should satisfy.
(P5). Axioms of Interaction (Σai)
These are applicable when more than one spatial calculus is modeled in a non-integrated manner (i.e., with independent composition theorems). These axioms explicitly characterize the relative entailments between interdependent aspects of space, e.g., topology and size (Tables 1 and 2). For instance, a spatial relationship of one type may directly entail or constrain a spatial relationship of another type Equation (10a). Such axioms could also possibly be compositional in nature, making it possible to compose spatial relations pertaining to two different aspects of space in order to yield a spatial relation of either or both spatial types used in composition Equation (10b).
5.5.2. Phenomenal Aspects: Geospatial Events (Σph)
Here, we define our exemplary interpretation for the geospatial events based on the semantic characterization in Section 4.1. The definitions also utilize additional (binary) Boolean function symbols—merge_cond and split_cond—that extralogically define (e.g., in a geometric sense) the conditions needed to check for events. (Outside of the logical theory, the merge and split conditions are basically geometric operations that may have an arbitrary characterization.)
Appearance and Disappearance
This is the simplest case, where the existential status of an object undergoes a change Equation (11). Here, we assume that identity is handled outside of the reasoning framework.
Split
A split involves an existing object that disintegrates into a set of n previously non-existing objects Equation (12):
Merge
A merge event Equation (13) is (formalized as) a dual of a split event:
Let Σspace ≡ def [Σcp ∪ Σcn ∪ Σct ∪ Σai ∪ Σph] denote a domain-independent spatial theory that is based on the axiomatizations encompassing (P1–P5) and the phenomenal aspects in Σph.
5.5.3. Physically Plausible Scenarios
Corresponding to each spatial situation (e.g., within a hypothetical situation space; Figure 5), there exists a situation description that characterizes the spatial state of the system. It is necessary that the spatial component of such a state be a “complete specification”, possibly with disjunctive information. For k (binary) spatial calculi being modeled, the initial situation description involving n domain objects requires a complete specification with [n(n − 1)/2] spatial relationships for each calculus (Precisely, under a unique names assumption for the fluents in Φ (i.e., [ϕsp(oi, oj) ≠ ϕsp(oj, oi)]), static spatial configurations actuality consist of [(k × [n(n − 1)/2]) × 2] unique functional fluents.)
Definition 5.2 (-Consistency) A scene description is-Consistent, i.e., compositionally consistent, if the state or spatial situation description corresponding to the situation satisfies all the composition constraints (P4 in Section 5.5.1; Section 5.5) of every spatial domain (e.g., topology, orientation, size) being modeled, as well as the relative entailments, as per the axioms of interaction (P5 in Section 5.5.1 and Tables 1 and 2; Section 5.5) among inter-dependent spatial calculi when more than one spatial calculus is modeled.
Recall that composition constraints and axioms of interaction have been formalized as part of the domain-independent spatial theory (P4–P5 in Section 5.5.1; Section 5.5). -Consistencyin Definition 5.2 ensures that those scene descriptions (i.e., their qualitative spatial configurations) that are not physically possible are disregarded during the reasoning process. From the viewpoint of model elimination of narrative descriptions during an (abductive) explanation process, -Consistency of scenario descriptions is a key (contributing) factor determining the commonsensical notion of the physically realizability of the (abduced) scenario completions. (Bhatt and Loke [75] show that a standard completion semantics with causal minimization in the presence of frame assumptions and ramification constraints, either using circumscription or predicate completion, preserves this notion of -Consistencyfor Σspace within a general class of action theories. Details are unessential here.)
5.6. Practical Abduction in GIS with Σspace
Let Σ be the background theory and Φ be an observation sentence, whose assimilation demands some explanation. According to the abductive approach to computing explanations, the task of assimilating Φ involves finding formulae Δ that when conjoined to Σ yield Φ as a logical consequence (i.e., Σ ∪ Δ ⊨ Φ).
Appendix A provides details of the precise abductive approach for computing explanations, as the details are not central for this paper. Instead, we focus on illustrating the nature of the high-level domain-independent abducibles that are generated as a result of the reasoning process in Sections 5.6.1–5.6.3.
5.6.1. Abducing Appearances and Disappearances
The following is with respect to the illustration in Figure 5: In Equations (14) and (15), Σchange corresponds to a general class of actions theories (e.g., in the manner described in [75]) capable of handling the frame and ramification problems: general laws determining what does and does not change within a dynamically changing system. Details are not necessary to understand the result of the abduction methods.
The derivation of Δ primarily involves non-monotonic reasoning in the form of minimizing change (“Caused” and “Happens” predicates), in addition to making the usual default assumptions about inertia and indirect effects; the details are beyond the scope of this paper and may be referred to in [75].
5.6.2. Abducing Splits and Merges
Below, Δ2 represents a subset of the minimal explanations that is derivable with respect to the observations in Ψe and Ψf:
In a manner methodologically similar to the case of geospatial events characterized so far, events, such as growth, shrinkage and basic transformation and cloning events may be subjected to particular concrete interpretations, as well.
As a next step in the reasoning process, we turn to the issue of extracting high-level, domain-specific knowledge from the result of the scenario and narrative completion task.
5.6.3. Inferring High-Level (Domain-Dependent) Urbanization Processes
The discussion so far focused on the domain-independent machinery needed to qualitatively represent and reason about certain aspects of dynamic (geo)spatial phenomena. Now, we turn to the urban dynamic domain, which is the focus of our running example. High-level urbanization processes (e.g., natural, human, economic) in this domain may be characterized via a combination of low-level domain-independent qualitative spatial changes and geospatial events identifiable as per a certain event taxonomy. In the domain of Example 5.1, these correspond to urbanization processes, such as: deforestation, migration, urban/rural re(construction) and relocation, industrialization and infrastructure development, etc. Given the primary/domain-independent scenario and narrative completions (obtained by abduction) in [Δi, Δj, …, Δn], high-level abducibles may be used in a domain-specific manner to infer the processes of interest (e.g., these abducibles may be constructed within standard query-based environment over a conventional GIS dataset). For instance, high-level abducibles Equation (16) (referring to high-level processes) may be inferred given the primary abductions in Equations (14) and (15):
The set of high-level (domain-dependent) abducibles may be either dynamically constructed within a query-based environment or may be pre-specified and invoked via some interfacing mechanism that connects the analytical capability with the real stake-holders in the analytical process. This would enable users and software services that utilize the narrative-based GIS architecture to independently define the semantics of the spatio-temporal phenomena in domain-specific ways.
For instance (building on the argument provided by one of the referees of this paper), a high-level domain-specific abducible could characterize the social and economic forces (e.g., gentrification, industrial agglomeration) that drove such spatial expressions of urban development to occur per se. Such linking of high-level complex and/or subjectively interpreted geographic processes, such as industrial agglomeration to spatial-temporal data that capture readily observable properties (e.g., via satellite imagery and land use), depends on problem-specific considerations:
An analyst may decide to completely correlate observable spatio-temporal processes (e.g., shrinkage, splits, disappearance) with complex socio-spatial phenomena, such as urbanization.
Spatio-temporal analysis (e.g., continual growth or shrinkage of a polygon) may be complemented with other data sources, and the influence of non-spatial datasets and quantitative analytical methods could be formally accounted for in the narrative framework, such that the abductive explanation framework consists of both spatio-temporal, as well as other kinds of abducibles (i.e., non-spatial evidences can be used to further enrich the interpretation of macro-geospatial processes).
As discussed already in the paper, the focus of the narrative-centered model of this paper has been on the spatio-temporal aspects of the dynamic geospatial phenomena. A formal treatment of incorporating non-spatial datasets as evidences in the explanation process, albeit possible, is beyond the scope of this paper. Our focus has been on employing formal methods from the field of commonsense reasoning about space, actions and change into the domain of dynamic GIS.
6. Discussion and Conclusions
The ability of semantic and qualitative analytical capability to complement and synergize with statistical and quantitatively-driven methods has been recognized as important within and beyond the range of GIS application domains (discussed in Section 2.1). Researchers in GIS and spatial information theory have investigated several fundamental ontological aspects concerning the modeling of events, processes, the practical development of taxonomies of events relevant to a geospatial context and the construction of formal methods in qualitative spatial information theory.
As we have emphasized, event- and object-based explanatory analysis is especially important (e.g., in the context of a query-based GIS system), where the available data needs to be analyzed for various purposes, such as managerial decision making, policy formation and so forth. Indeed, the development of high-level analytical capability within the emerging object, temporal and event-based geographic information systems has been identified to present a range of fundamental representational and computational challenges. It has been the objective of this paper to:
explicitly address some of these challenges from the viewpoint of the application of formal knowledge representation and reasoning methods concerning space, events, actions, and change.
The broad technical question that has been addressed in this paper is:
what is it that constitutes the core spatial informatics underlying (specific kinds) of analytical capability within a range of dynamic geospatial domains?
From a methodological viewpoint, the concrete goal of our research has been to:
investigate the theoretical foundations necessary to develop the computational capability for high-level commonsense, qualitative analysis of dynamic geospatial phenomena within next generation event and object-based GIS systems.
We have presented an overarching framework for narrative-centered high-level modeling and explanatory analyses in the geospatial domain and have provided a unified view of a consolidated architecture in the backdrop of an illustrated application scenario from the domain of urban dynamics. Building on existing foundations in the GIS community, and spatial information theory in particular, we have demonstrated fundamental challenges and presented solutions thereof encompassing aspects, such as qualitative abstraction and integration, spatial consistency and practical geospatial abduction within a logical setting.
Most importantly, we believe that we have developed inroads from classical Knowledge Representation and Reasoning (KR) sub-disciplines in artificial intelligence, specifically formal methods in spatial and temporal reasoning, reasoning about action and change and commonsense reasoning. We believe that these interdisciplinary inroads in GIS science open-up interesting possibilities toward the realization of next-generation analytical GIS software systems. From a topical viewpoint, we propose that this particularly demands a transdisciplinary scientific perspective that brings together geography, artificial intelligence and cognitive science.
Acknowledgments
We would like to thank the anonymous reviewers for their valuable comments and feedback.
Mehul Bhattt gratefully acknowledges the funding and support of the German Research Foundation (DFG, www.dfg.de), via the Spatial Cognition Research Center (SFB/TR8), and the SFB/TR 8 Project DesignSpace.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix
Computing Explanations: Logic-Based Abduction in GIS
Let Σ be a background theory and Φ be an observation sentence, whose assimilation demands some explanation. According to the abductive approach, the task of assimilating Φ involves finding formulae Δ that when conjoined to Σ yield Φ as a logical consequence (i.e., Σ ∪ Δ ⊨ Φ). Additionally, a set of predicates are distinguished as being abducible in order to avoid trivial explanations. It is essential that the explanation, Δ, must be in terms of predicates that have been designated as being abducible. Finally, an approach is needed to incorporate the non-effects and indirect effects of events and actions, thereby overcoming the frame and ramification problems. This is achieved by the use of a relevant minimization policy, which typically involves the use of circumscription (CIRC) [86]. Furthermore, it is also necessary that the explanation be minimal, i.e., the derived explanation should not be subsumed by other explanations. Definition (6.1) formalizes the commonly-understood notion of explanation by logical abduction [76].
Definition 6.1 (Explanation) A formula, Δ, essentially an existential statement, is an explanation of a ground observation sentence, Φobs, of language in terms of the abduction policy, η*, given a background theory [Σ ≡ Σchange ∪ Σspace] and a circumscription policy that minimizes ρ* and allows σ* to vary if:
CIRC[Σ ∧ Δ; ρ*; σ*] is consistent, and the models themselves are -Consistent(as per Definition 5.2),
Δ mentions only predicates in η* and
CIRC[Σ ^ Δ ; ρ* ; σ*] ⊨ Φobs
There is no explanation Δ′ of Φobs, such that Δ ⊨ Δ′ and Δ′ ⊭ Δ (i.e., the minimality criteria).
References
- Claramunt, C.; Thériault, M. Managing Time in GIS: An Event-Oriented Approach, Proceedings of the International Workshop on Temporal Databases, Zurich, Switzerland, 17–18 September 1995; pp. 23–42.
- Yuan, M.; Hornsby, K. Computation and Visualization for Understanding Dynamics in Geographic Domains—A Research Agenda; CRC Press: New York, NY, USA, 2007. [Google Scholar]
- Yuan, M. Representing complex geographic phenomena in GIS. Cartogr. Geogr. Inform. Sci. 2001, 28, 83–96. [Google Scholar]
- The Big Idea Framework; NIMA (National Imagery and Mapping Agency): Springfield, VA, USA, 2000.
- Beller, A. Spatio/Temporal Events in a GIS, Proceedings of the GIS/LIS, Atlanta, GA, USA, 28 October–1 November 1991; pp. 766–775.
- Grenon, P.; Smith, B. Snap and span: Towards dynamic spatial ontology. Spat. Cognit. Comput. 2004, 4, 69–104. [Google Scholar]
- Worboys, M.F.; Hornsby, K. From objects to events: Gem, the geospatial event model. Lect. Note. Comput. Sci. 2004, 3234, 327–344. [Google Scholar]
- Galton, A.; Mizoguchi, R. The water falls but the waterfall does not fall: New perspectives on objects, processes and events. Appl. Ontol. 2009, 4, 71–107. [Google Scholar]
- Hornsby, K.S.; Cole, S.J. Modeling moving geospatial objects from an event-based perspective. Trans. GIS 2007, 11, 555–573. [Google Scholar]
- Bennett, B. Physical Objects Identity and Vagueness, Proceedings of Eighth International Conference on Principles of Knowledge Representation and Reasoning (KR2002), Toulouse, France, 22–25 April 2002; pp. 395–408.
- Hornsby, K.; Egenhofer, M.J. Identity-based change: A foundation for spatio-temporal knowledge representation. Int. J. Geogr. Inf. Sci. 2000, 14, 207–224. [Google Scholar]
- Galton, A.; Hood, J. Qualitative Interpolation for Environmental Knowledge Representation, Proceedings of European Conference on Artificial Intelligence (ECAI), Valencia, Spain, 23–27 August 2013; pp. 1017–1018.
- Mondo, G.D.; Stell, J.G.; Claramunt, C.; Thibaud, R. A graph model for spatio-temporal evolution. J. UCS 2010, 16, 1452–1477. [Google Scholar]
- Worboys, M.F. Event-oriented approaches to geographic phenomena. Int. J. Geogr. Inf. Sci. 2005, 19, 1–28. [Google Scholar]
- Couclelis, H. The abduction of geographic information science: Transporting spatial reasoning to the realm of purpose and design. Lect. Note. Comput. Sci. 2009, 5756, 342–356. [Google Scholar]
- Miller, R.; Shanahan, M. Narratives in the situation calculus. J. Log. Comput. 1994, 4, 513–530. [Google Scholar]
- Pinto, J. Occurrences and narratives as constraints in the branching structure of the situation calculus. J. Log. Comput. 1998, 8, 777–808. [Google Scholar]
- Mueller, E.T. Modeling space and time in narratives about restaurants. LLC 2007, 22, 67–84. [Google Scholar]
- McCarthy, J.; Costello, T. Combining Narratives, Proceedings of the Sixth International Conference on Principles of Knowledge Representation and Reasoning, Trento, Italy, 2–5 June 1998; pp. 48–59.
- McCarthy, J. Chapter Concept of Logical AI. In Logic-Based Artificial Intelligence; Kluwer Academic Publishers: Norwell, MA, USA, 2000; pp. 37–56. [Google Scholar]
- Fisher, W.R. Human Communication as Narration: Toward a Philosophy of Reason, Value, and Action; University of South Carolina Press: Columbia, SC, USA, 1987. [Google Scholar]
- Riessman, C.K. Narrative Analysis; Sage Publications: Newbury Park, CA, USA, 1993. [Google Scholar]
- Prince, G. Narratology: The Form and Function of Narrative; Mouton De Gruyter: Berlin, Germany, 1982. [Google Scholar]
- Herman, D.; Jahn, M.; Ryan, M.-L. Routledge Encyclopedia of Narrative Theory; Routledge: London, UK, 2005. [Google Scholar]
- Meister, J.C. Narratology. In The Living Handbook of Narratology; Hühn, P., Meister, J.C., Pier, J., Schmid, W., Eds.; Hamburg University Press: Hamburg, Germany, 2011. [Google Scholar]
- Barthes, R.; Duisit, L. An introduction to the structural analysis of narrative. New Lit. Hist. 1975, 6, 237–272. [Google Scholar]
- Mani, I. Computational modeling of narrative. Synth. Lect. Hum. Lang. Technol. 2012, 5, 1–142. [Google Scholar]
- Mani, I. Computational Narratology. In The Living Handbook of Narratology; Hühn, P., Meister, J.C., Pier, J., Schmid, W., Eds.; Hamburg University Press: Hamburg, Germany, 2013. [Google Scholar]
- Goguen, J. CSE 87C Winter 2004 Freshman Seminar on Computational Narratology. New Lit. His. 2004. Available online: http://cseweb.ucsd.edu/goguen/courses/87w04/1.html accessed on 13 December 2013. [Google Scholar]
- Bhatt, M. Reasoning about Space, Actions and Change: A Paradigm for Applications of Spatial Reasoning. In Qualitative Spatial Representation and Reasoning: Trends and Future Directions; IGI Global: Hershey, PA, USA, 2012. [Google Scholar]
- Bhatt, M.; Guesgen, H.; Wölfl, S.; Hazarika, S. Qualitative spatial and temporal reasoning: Emerging applications, trends, and directions. Spat. Cognit. Comput. 2011, 11, 1–14. [Google Scholar]
- Cohn, A.G.; Renz, J. Qualitative Spatial Reasoning. In Handbook of Knowledge Representation; van Harmelen, F., Lifschitz, V., Porter, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Yuan, M.; Mark, D.M.; Egenhofer, M.J.; Peuquet, D.J. Chapter 5 Extensions to Geographic Representations. In A Research Agenda for Geographic Information Science; CRC Press: Boca Raton, FL, USA, 2004; pp. 129–156. [Google Scholar]
- Tobler, W. A computer movie simulating urban growth in the detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar]
- Tobler, W.R. Cellular Geography. In Philosophy in Geography; Gale, S., Olsson, G., Eds.; Reidel: Dordrecht, The Netherlands, 1979; pp. 379–386. [Google Scholar]
- Couclelis, H. Cellular worlds: A framework for modeling micro-macro dynamics. Environ. Plan. A 1985, 17, 585–596. [Google Scholar]
- Bretagnolle, A.; Daudet, E.; Pumain, D. From theory to modeling: Urban systems as complex systems. CyberGeo Eur. J. Geogr. 2006, 335, 1–17. [Google Scholar]
- Batty, M. Fifty Years of Urban Modeling: Macro-Statics to Micro-Dynamics. In The Dynamics of Complex Urban Systems; Albeverio, S., Andrey, D., Giordano, P., Vancheri, A., Eds.; Physica-Verlag HD: Heidelberg, Germany, 2008; pp. 1–20. [Google Scholar]
- Sui, D.Z. GIS-based urban modeling: Practices, problem, and prospects. Int. J. Geogr. Inf. Sci. 1998, 12, 651–671. [Google Scholar]
- Briassoulis, H. Land-use policy and planning, theorizing, and modeling: Lost in translation, found in complexity? Environ. Plan. B Plan. Des. 2008, 35, 16–33. [Google Scholar]
- Couclelis, H. Where has the future gone? Rethinking the role of integrated land-use models in spatial planning. Environ. Plan. A 2005, 37, 1353–1371. [Google Scholar]
- Stevens, D.; Dragicevic, S.; Rothley, K. iCity: A GIS-CA modeling tool for urban planning and decision making. Environ. Model. Softw. 2007, 22, 761–773. [Google Scholar]
- Vermeiren, K.; Rompaey, A.V.; Loopmans, M.; Serwajja, E.; Mukwaya, P. Urban growth of Kampala, Uganda: Pattern analysis and scenario development. Landsc. Urban Plan. 2012, 106, 199–206. [Google Scholar]
- Arsanjani, J.J.; Helbich, M.; Kainz, W.; Boloorani, A.D. Integration of logistic regression, markov chain and cellular automata models to simulate urban expansion. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 265–275. [Google Scholar]
- Ramachandra, T.; Aithal, B.H.; Sanna, D.D. Insights to urban dynamics through landscape spatial pattern analysis. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 329–343. [Google Scholar]
- Kong, F.; Yin, H.; Nakagoshi, N.; James, P. Simulating urban growth processes incorporating a potential model with spatial metrics. Ecol. Indic. 2012, 20, 82–91. [Google Scholar]
- Van Kouwen, F.; Schot, P.P.; Wassen, M.J. A framework for linking advanced simulation models with interactive cognitive maps. Environ. Model. Softw. 2008, 23, 1133–1144. [Google Scholar]
- Weber, C. Interaction model application for urban planning. Landsc. Urban Plan. 2003, 63, 49–60. [Google Scholar]
- Allen, J.F. Maintaining knowledge about temporal intervals. Commun. ACM 1983, 26, 832–843. [Google Scholar]
- Freksa, C. Qualitative Spatial Reasoning. In Cognitive and Linguistic Aspects of Geographic Space; Mark, D., Frank, A., Eds.; Kluwer: Dordrecht, The Netherlands, 1991; pp. 361–372. [Google Scholar]
- Renz, J.; Nebel, B. Qualitative Spatial Reasoning Using Constraint Calculi. In Handbook of Spatial Logics.; Springer Verlag: Berlin, Germany, 2007; pp. 161–215. [Google Scholar]
- Peuquet, D.J. Representations of geographic space: Toward a conceptual synthesis. Ann. Assoc. Am. Geogr. 1988, 78, 373–394. [Google Scholar]
- Mennis, J.; Peuquet, D.J.; Qian, L. A conceptual framework for incorporating cognitive principles into geographical database representation. Int. J. Geogr. Inf. Sci. 2000, 14, 501–520. [Google Scholar]
- Gahegan, M. Specifying the transformations within and between geographic data models. Trans. GIS 1996, 1, 137–152. [Google Scholar]
- Egenhofer, M.J.; Franzosa, R.D. Point set topological relations. Int. J. Geogr. Inf. Syst. 1991, 5, 161–174. [Google Scholar]
- Egenhofer, M.; Mark, D. Naive Geography. In Spatial Information Theory a Theoretical Basis for GIS; Springer: Berlin/Heidelberg, Germany, 1995; pp. 1–15. [Google Scholar]
- Randell, D.A.; Cui, Z.; Cohn, A. A Spatial Logic Based on Regions and Connection, Proceedings of the Third International Conference Principles of Knowledge Representation and Reasoning, Cambridge, MA, USA, 25–29 October 1992; pp. 165–176.
- Egenhofer, M.J. Reasoning about binary topological relations. Lect. Note. Comput. Sci. 1991, 525, 143–160. [Google Scholar]
- Clementini, E.; Sharma, J.; Egenhofer, M.J. Modeling topological spatial relations: Strategies for query processing. Comput. Graph. 1994, 18, 815–822. [Google Scholar]
- Abdelmoty, A.I.; Smart, P.; El-Geresy, B.; Jones, C. Supporting Frameworks for the Geospatial Semantic Web, Proceedings of the 11th International Symposium on Advances in Spatial and Temporal Databases, Aalborg, Denmark, 8–10 July 2009; pp. 355–372.
- Claramunt, C.; Thériault, M.; Parent, C. A Qualitative Representation of Evolving Spatial Entities in Two-Dimensional Spaces. In Innovations in GIS V; Carver, S., Ed.; Taylor and Francis: London, UK, 1997; pp. 119–129. [Google Scholar]
- Klippel, A.; Worboys, M.; Duckham, M. Identifying factors of geographic event conceptualisation. Int. J. Geogr. Inf. Sci. 2008, 22, 183–204. [Google Scholar]
- Jiang, J.; Worboys, M. Detecting Basic Topological Changes in Sensor Networks by Local Aggregation, Proceedings of the 16th ACM International Conference on Advances in Geographic Information Systems; pp. 1–10.
- Duckham, M.; Jeong, M.-H.; Li, S.; Renz, J. Decentralized Querying of Topological Relations between Regions without Using Localization, Proceedings of the 18th ACM SIGSPATIAL GIS, San Jose, CA, USA, 2–5 November 2010; pp. 414–417.
- Haarslev, V.; Möller, R. Spatioterminological Reasoning: Subsumption Based on Geometrical Inferences, Proceesings of International Workshop on Description Logics (DL’97), Gif sur Yvette, France, 27–29 September 1997; Levy, A.Y., Rousset, M.-C., Eds.; 410, pp. 74–78.
- Khan, A.; Schneider, M. Topological Reasoning between Complex Regions in Databases with Frequent Updates, Proceedings of the 18th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (ACM SIGSPATIAL GIS), San Jose, CA, USA, 2–5 November 2010; pp. 380–389.
- Rodríguez, M.A.; Brisaboa, N.; Meza, J.; Luaces, M.R. Measuring Consistency with Respect to Topological Dependency Constraints, Proceedings of the 18th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (ACM SIGSPATIAL GIS), San Jose, CA, USA, 2–5 November 2010; pp. 182–191.
- Freksa, C. Conceptual Neighborhood and Its Role in Temporal and Spatial Reasoning. In Decision Support Systems and Qualitative Reasoning; Singh, M., Travé-Massuyès, L., Eds.; North-Holland: Amsterdam, The Netherlands, 1991; pp. 181–187. [Google Scholar]
- Egenhofer, M.J.; Al-Taha, K.K. Reasoning about Gradual Changes of Topological Relationships, Proceedings of the International Conference GIS—From Space to Territory: Theories and Methods of Spatio-Temporal Reasoning on Theories and Methods of Spatio-Temporal Reasoning in Geographic Space, Pisa, Italy, 21–23 September 1992; pp. 196–219.
- Bhatt, M.; Lee, J.H.; Schultz, C. CLP(QS): A Declarative Spatial Reasoning Framework. Proceedings of Conference on Spatial Information Theory (COSIT), Belfast, ME, USA, 12–16 September 2011; pp. 210–230.
- Schultz, C.; Bhatt, M. Towards a Declarative Spatial Reasoning System, Proceedings of the ECAI 2012, Montpellier, France, 27–31 August 2012; pp. 925–926.
- Wallgrün, J.O.; Frommberger, L.; Wolter, D.; Dylla, F.; Freksa, C. Qualitative Spatial Representation and Reasoning in the Sparq-Toolbox. In Spatial Cognition V: Reasoning, Action, Interaction; Barkowsky, T., Knauff, M., Ligozat, G., Montello, D., Eds.; Springer-Verlag: Berlin/Heidelberg, Germany, 2007; Volume 4387, pp. 39–58. [Google Scholar]
- Westphal, M.; Woelfl, S.; Gantner, Z. GQR: A Fast Solver for Binary Qualitative Constraint Networks, Proceedings of the AAAI Spring Symposium on Benchmarking of Qualitative Spatial and Temporal Reasoning Systems, Stanford, CA, USA, 23–25 March 2009.
- Condotta, J.-F.; Saade, M.; Ligozat, G. A Generic Toolkit for n-ary Qualitative Temporal and Spatial Calculi, Proceedings of Thirteenth International Symposium on Temporal Representation and Reasoning, 2006 (TIME 2006), Budapest, Hungary, 15–17 June 2006; pp. 78–86.
- Bhatt, M.; Loke, S. Modeling dynamic spatial systems in the situation calculus. Spat. Cognit. Comput. 2008, 8, 86–130. [Google Scholar]
- Shanahan, M. Prediction is Deduction but Explanation is Abduction, Proceedings of 11th International Joint Conference on Artificial Intelligence (IJCAI), Detroit, MI, USA, 20–25 August 1989; pp. 1055–1060.
- Gabbay, D.M.; Hunter, A. Making inconsistency respectable: A logical framework for inconsistency in reasoning. Lect. Not. Comput. Sci. 1991, 535, 19–32. [Google Scholar]
- Mackworth, A. Consistency in networks of relations. Artif. Intell. 1977, 8, 99–118. [Google Scholar]
- Fagin, R.; Vardi, M.Y. The theory of data dependencies—An overview. Lect. Note. Comput. Sci. 1984, 172, 1–22. [Google Scholar]
- Cockcroft, S. A taxonomy of spatial data integrity constraints. GeoInformatica 1997, 1, 327–343. [Google Scholar]
- Grégoire, É.; Konieczny, S. Logic-based approaches to information fusion. Inf. Fusion. 2006, 7, 4–18. [Google Scholar]
- Alchourron, C.E.; Gärdenfors, P.; Makinson, D. On the logic of theory change: Partial meet contraction and revision functions. J. Symbol. Log. 1985, 50, 510–530. [Google Scholar]
- Condotta, J.-F.; Kaci, S.; Schwind, N. A Framework for Merging Qualitative Constraints Networks, Proceedings of the Twenty-First International Florida Artificial Intelligence Research Society Conference, Coconut Grove, FL, USA, 15–17 May 2008; pp. 586–591.
- Dylla, F.; Wallgrün, J.O. Qualitative spatial reasoning with conceptual neighborhoods for agent control. J. Intell. Robot. Syst. 2007, 48, 55–78. [Google Scholar]
- Galton, A. Qualitative Spatial Change, Spatial Information Systems; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- McCarthy, J. Circumscription—A form of non-monotonic reasoning. Artif. Intell. 1980, 13, 27–39. [Google Scholar]
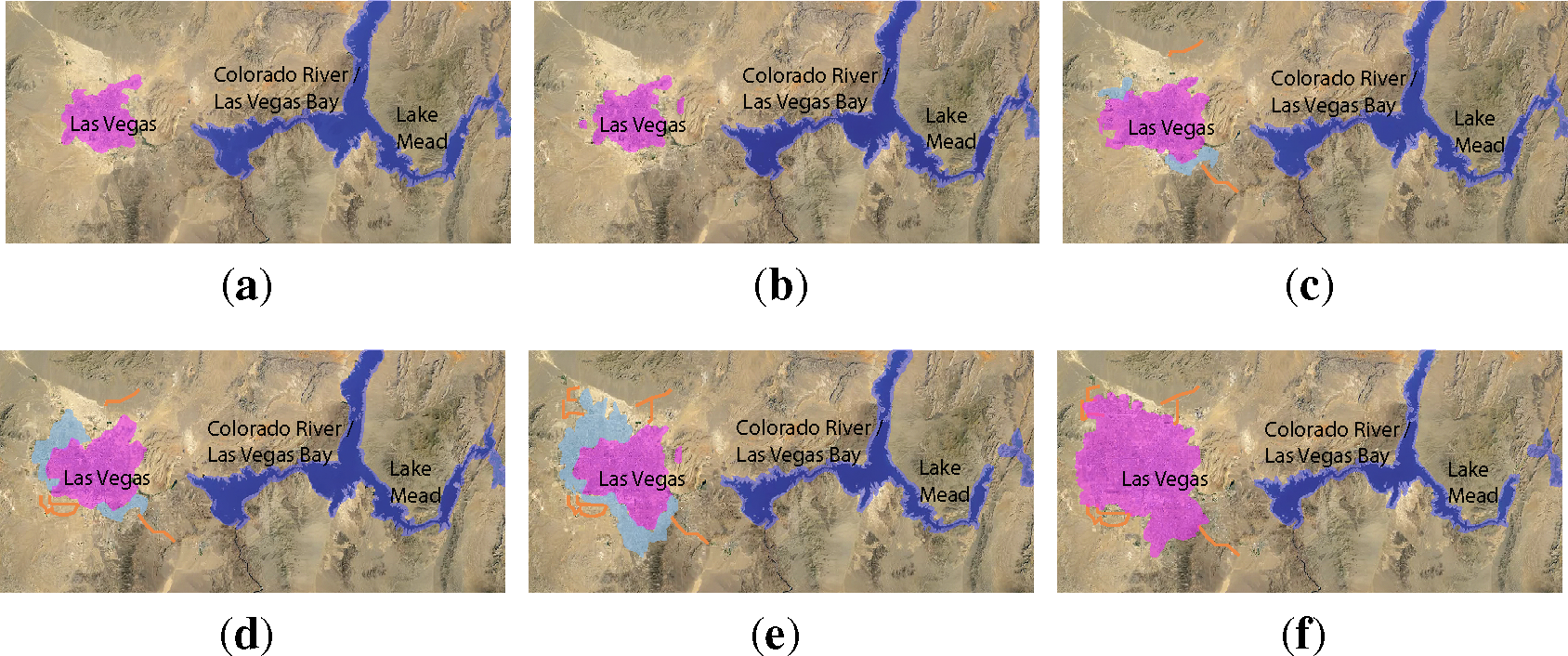
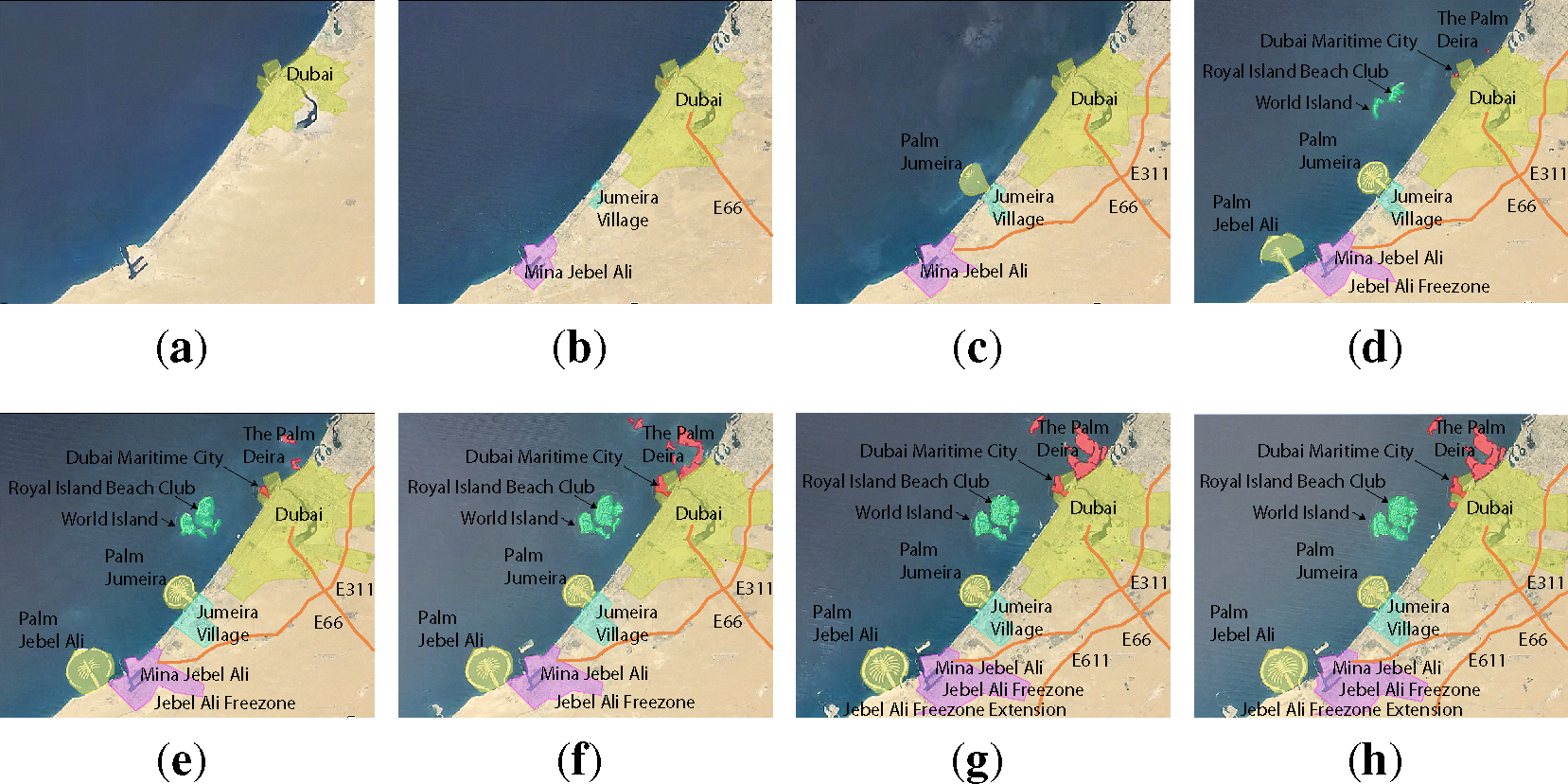


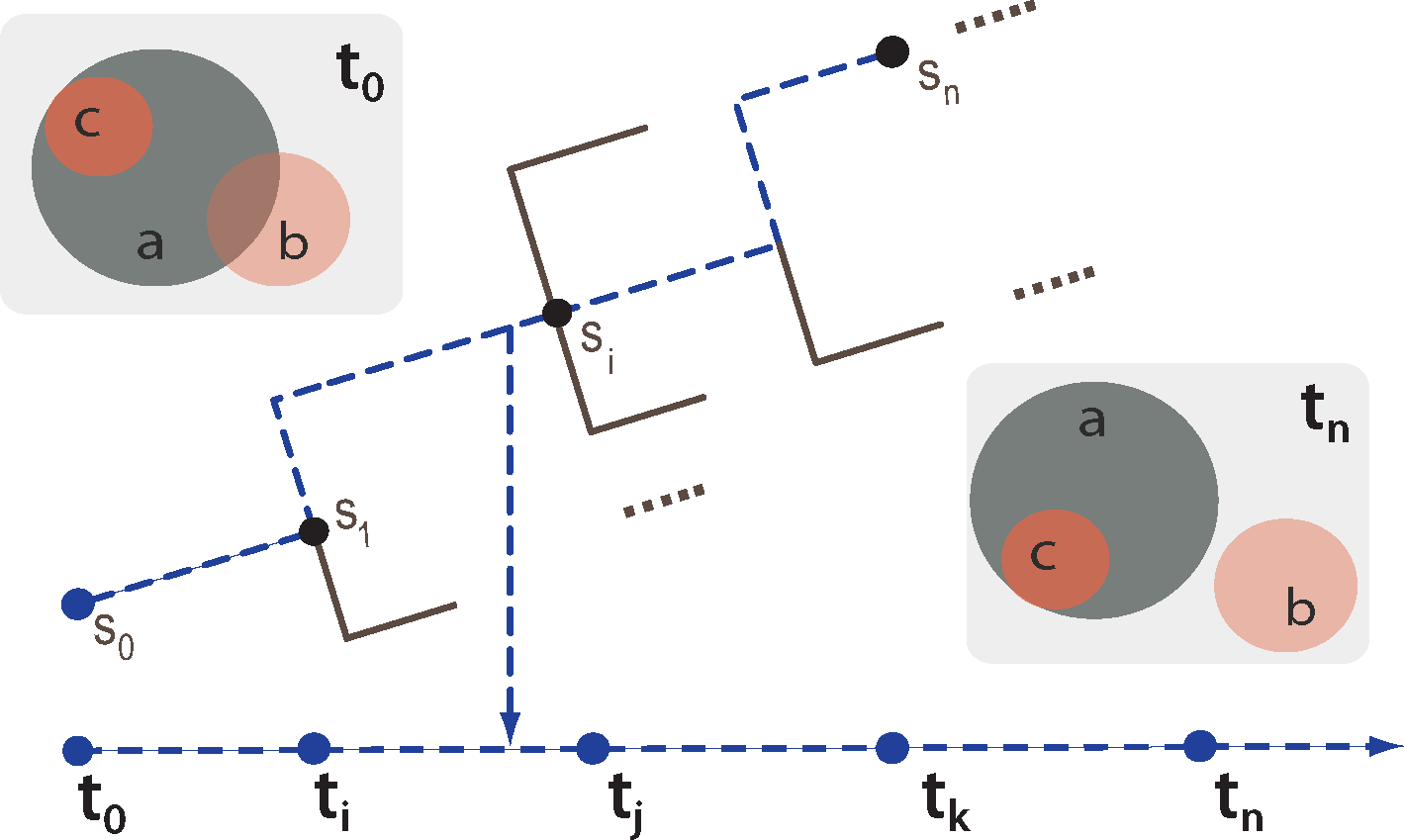
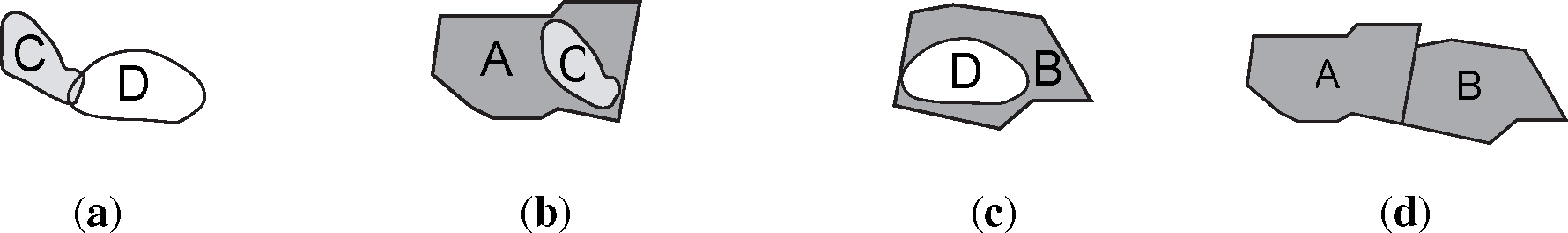
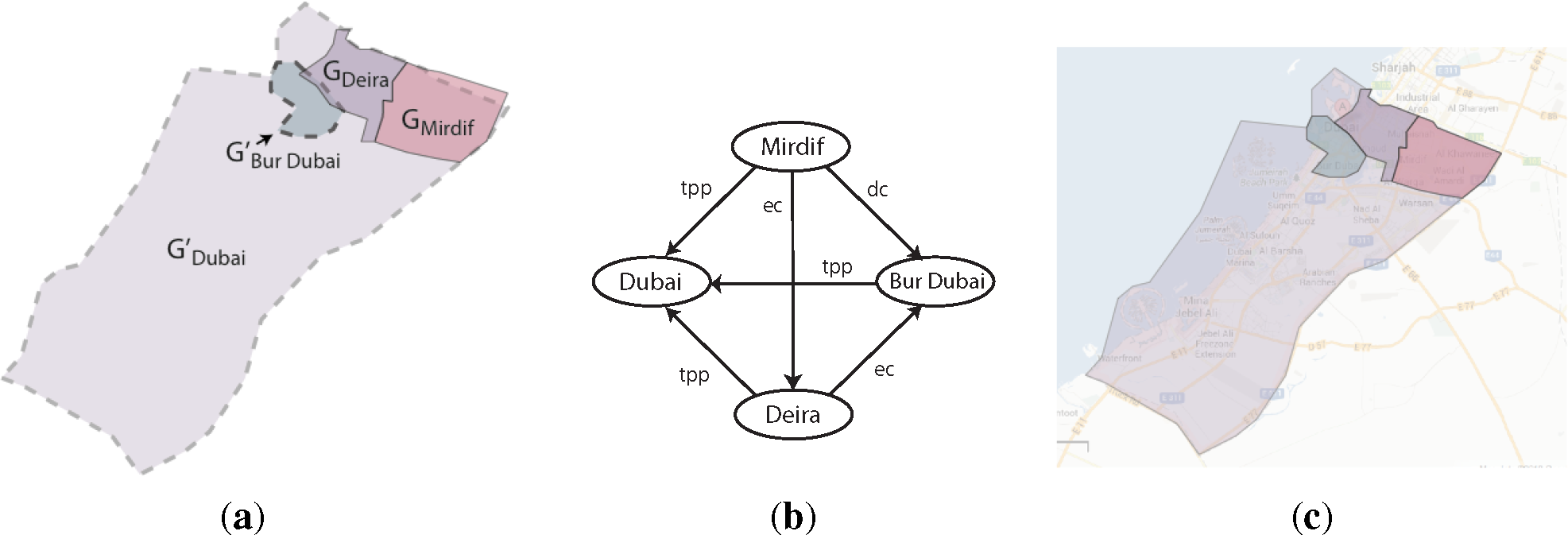
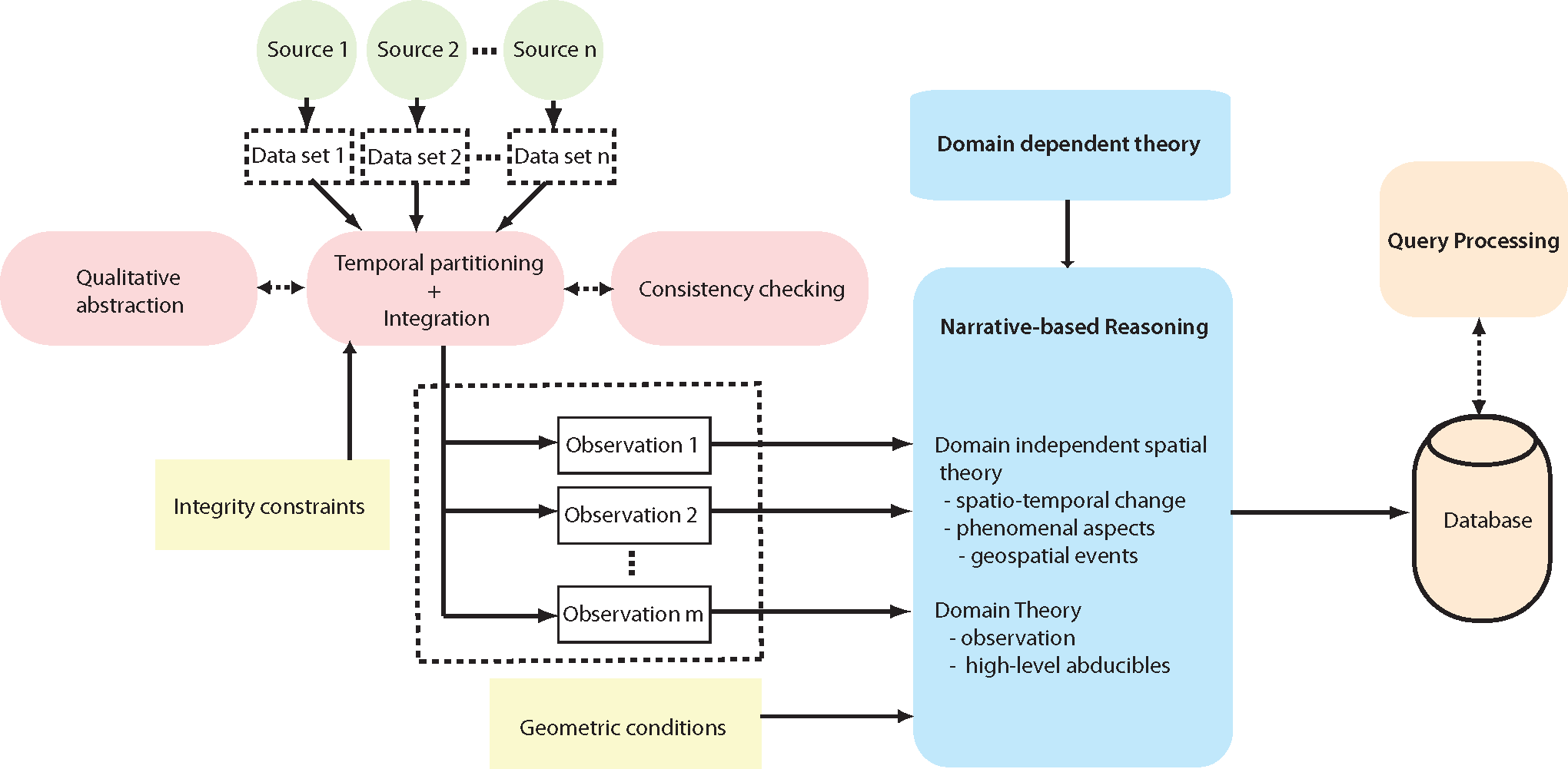
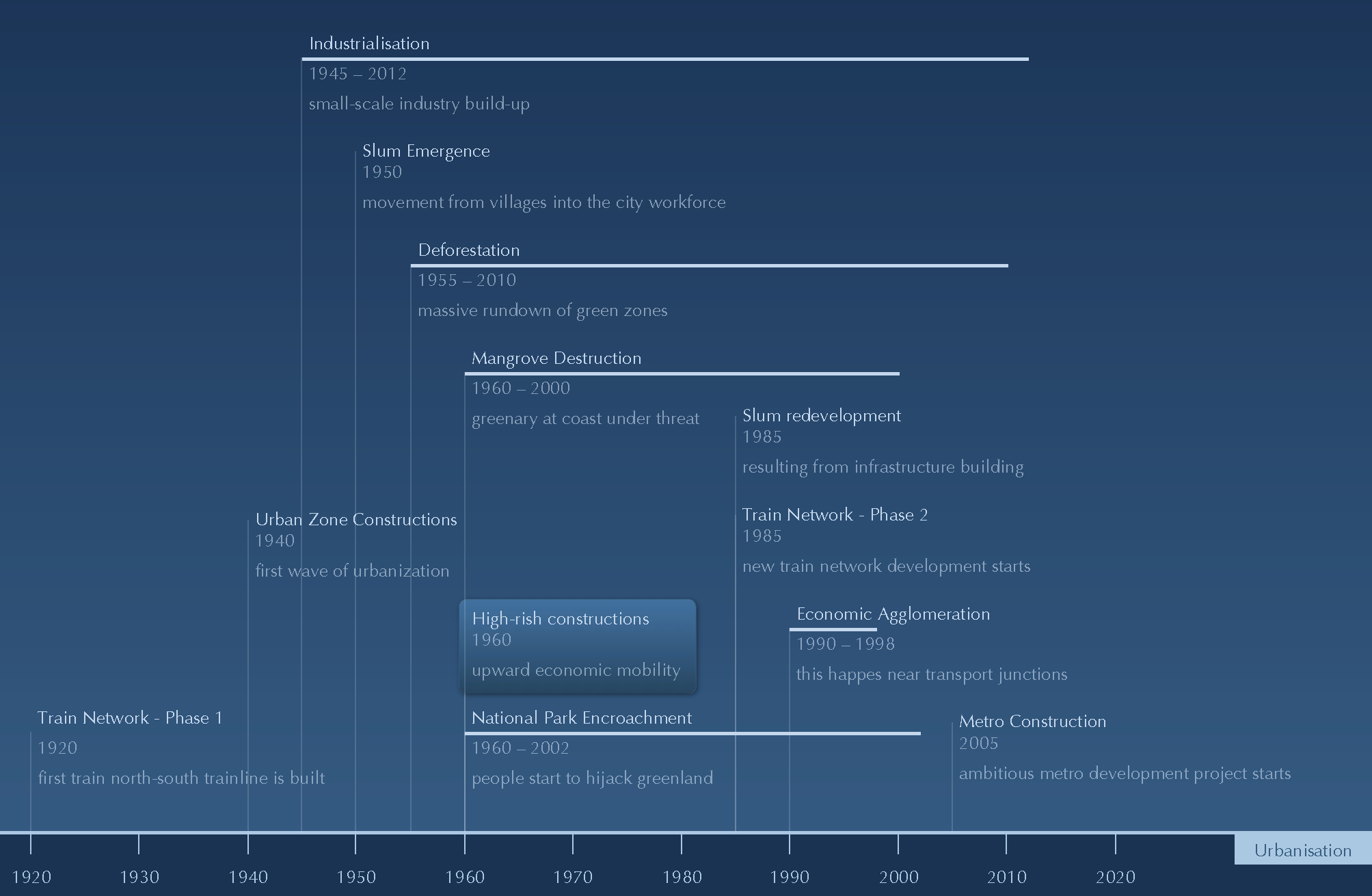
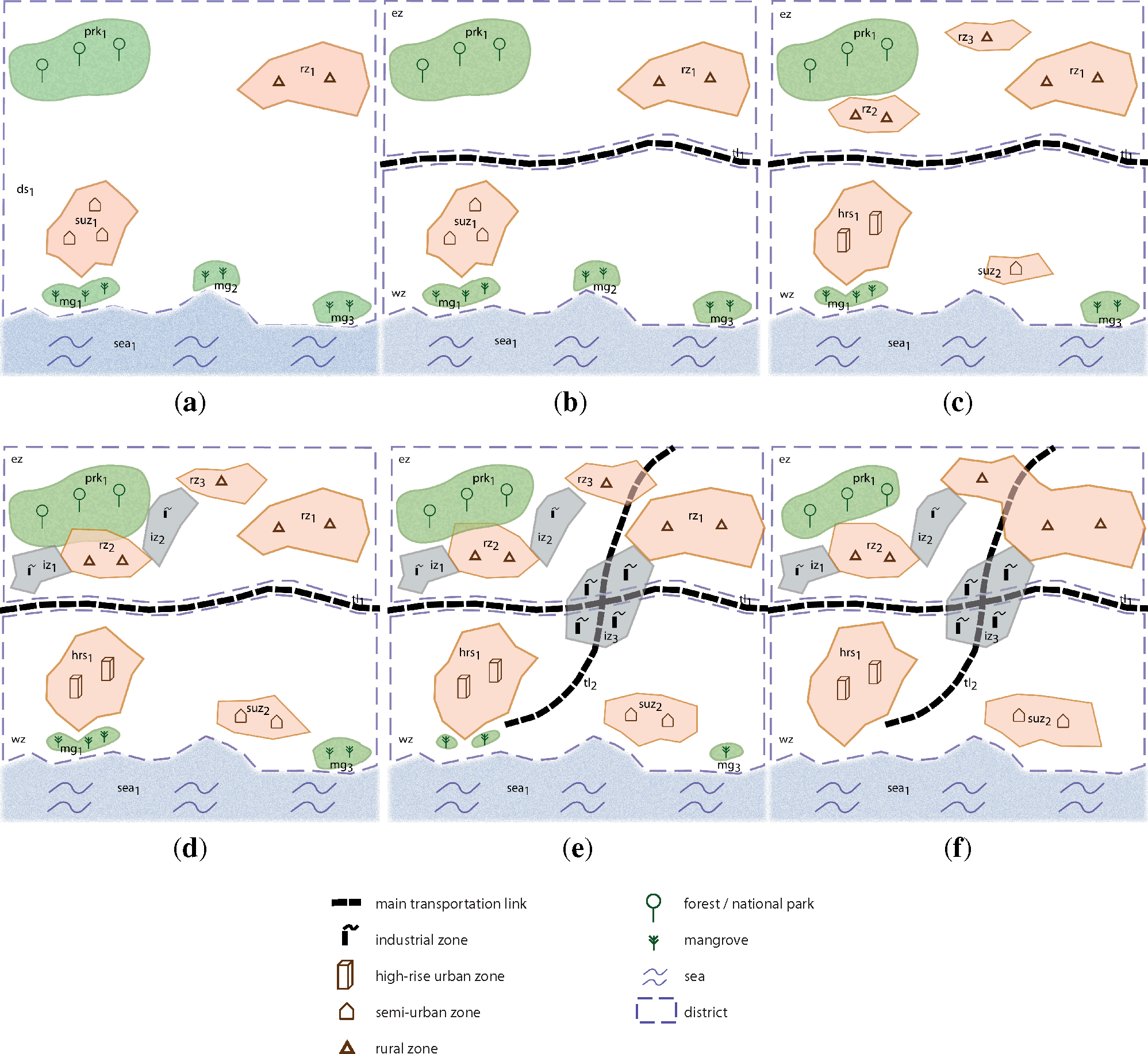
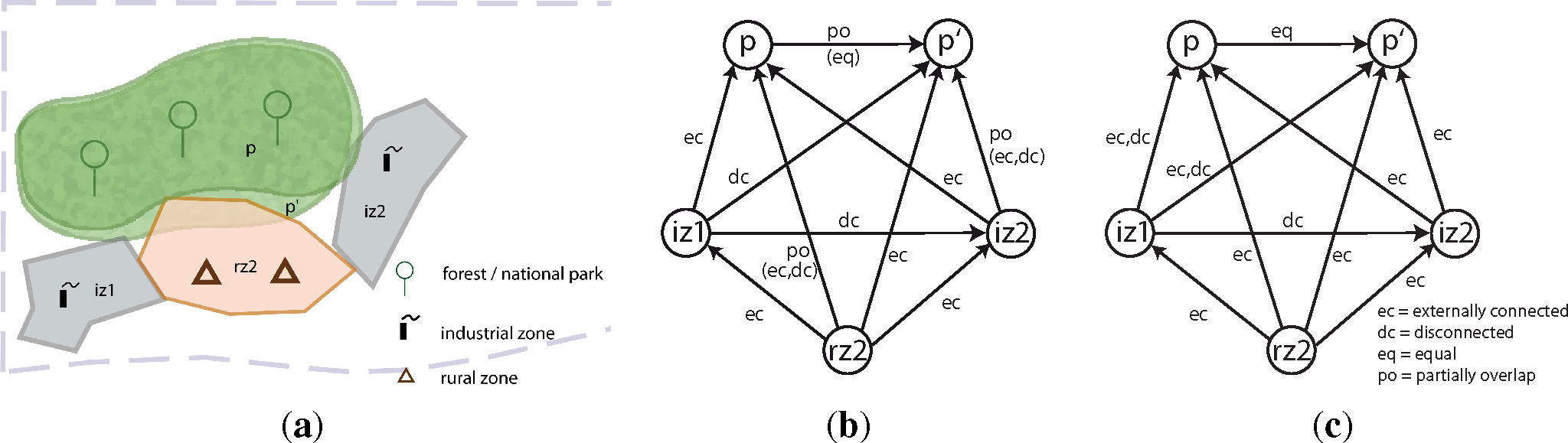
| ϕtop | ϕsize | ϕtop | ϕsize | ||
|---|---|---|---|---|---|
| tpp | ⊨ | < | dc | ⊨ | no-info |
| ntpp | ⊨ | < | ec | ⊨ | no-info |
| tpp−1 | ⊨ | > | po | ⊨ | no-info |
| ntpp−1 | ⊨ | > | eq | ⊨ | = |
| ϕsize | ϕtop | |
|---|---|---|
| = | ⊨ | dc ∨ ec ∨ po ∨ eq |
| > | ⊨ | dc ∨ ec ∨ po ∨ tpp−1 ∨ ntpp−1 |
| < | ⊨ | dc ∨ ec ∨ po ∨ tpp ∨ ntpp |
© 2014 by the authors; licensee MDPI, Basel, Switzerland This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Bhatt, M.; Wallgrün, J.O. Geospatial Narratives and Their Spatio-Temporal Dynamics: Commonsense Reasoning for High-Level Analyses in Geographic Information Systems. ISPRS Int. J. Geo-Inf. 2014, 3, 166-205. https://doi.org/10.3390/ijgi3010166
Bhatt M, Wallgrün JO. Geospatial Narratives and Their Spatio-Temporal Dynamics: Commonsense Reasoning for High-Level Analyses in Geographic Information Systems. ISPRS International Journal of Geo-Information. 2014; 3(1):166-205. https://doi.org/10.3390/ijgi3010166
Chicago/Turabian StyleBhatt, Mehul, and Jan Oliver Wallgrün. 2014. "Geospatial Narratives and Their Spatio-Temporal Dynamics: Commonsense Reasoning for High-Level Analyses in Geographic Information Systems" ISPRS International Journal of Geo-Information 3, no. 1: 166-205. https://doi.org/10.3390/ijgi3010166
APA StyleBhatt, M., & Wallgrün, J. O. (2014). Geospatial Narratives and Their Spatio-Temporal Dynamics: Commonsense Reasoning for High-Level Analyses in Geographic Information Systems. ISPRS International Journal of Geo-Information, 3(1), 166-205. https://doi.org/10.3390/ijgi3010166




