A Suite of Tools for ROC Analysis of Spatial Models
Abstract
:1. Introduction
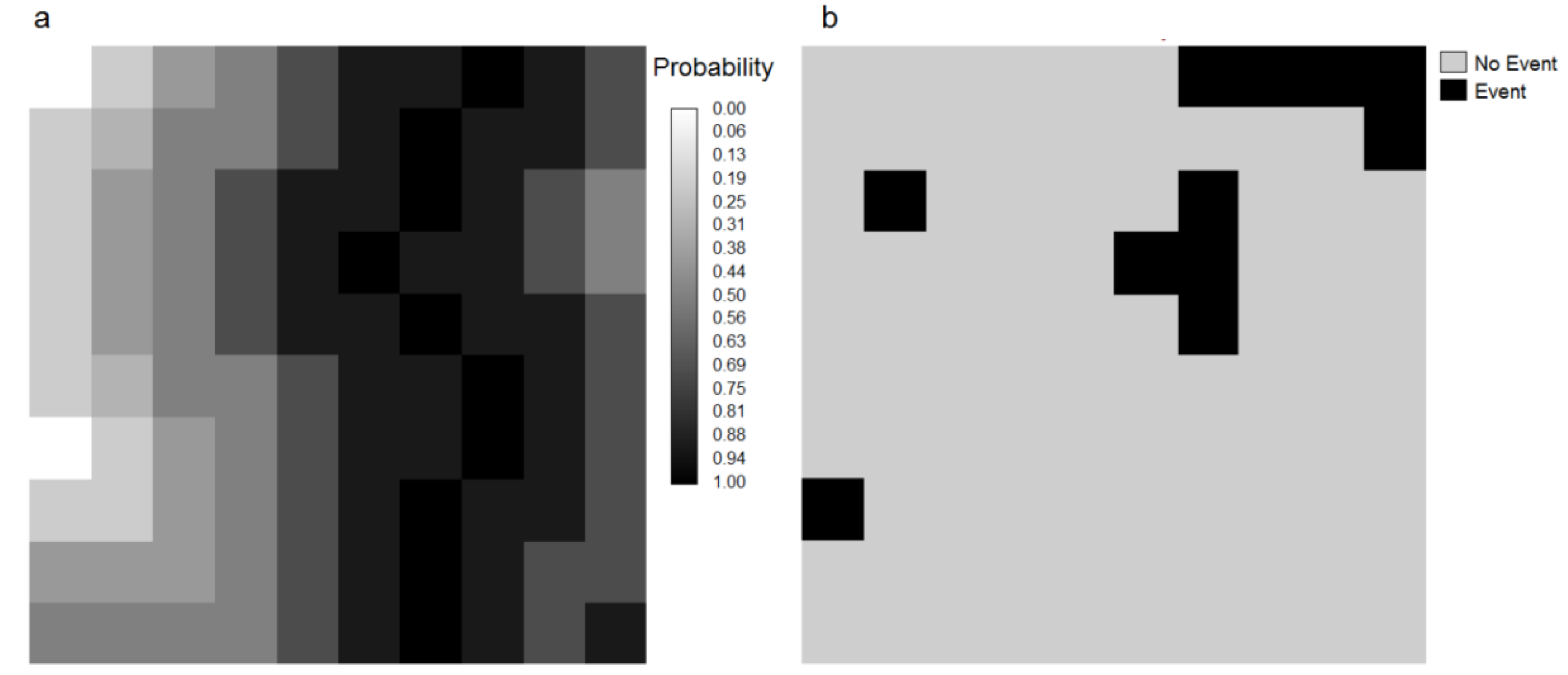
| Event Map | 1 (Event) | 0 (No event) | Threshold Total |
|---|---|---|---|
| Threshold Map | |||
| 1 (Modeled as event) | Ht | Ft | Ht + Ft |
| 0 (Modeled as No event) | Mt | Ct | Mt + Ct |
| Event total | Ht + Mt | Ft + Ct | 1 |
2. Dinamica EGO
3. Implementation of ROC Analysis for Raster Maps
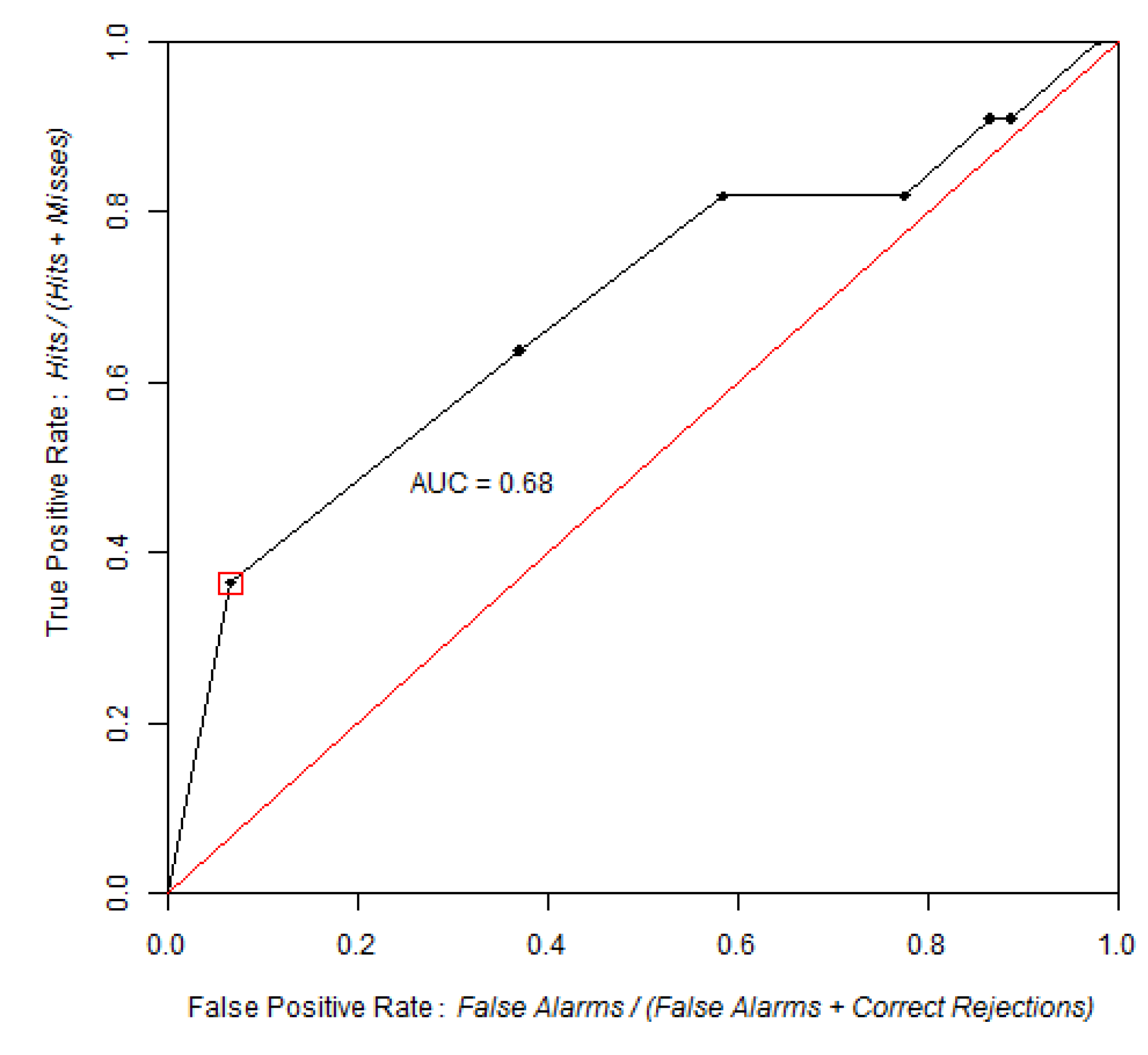
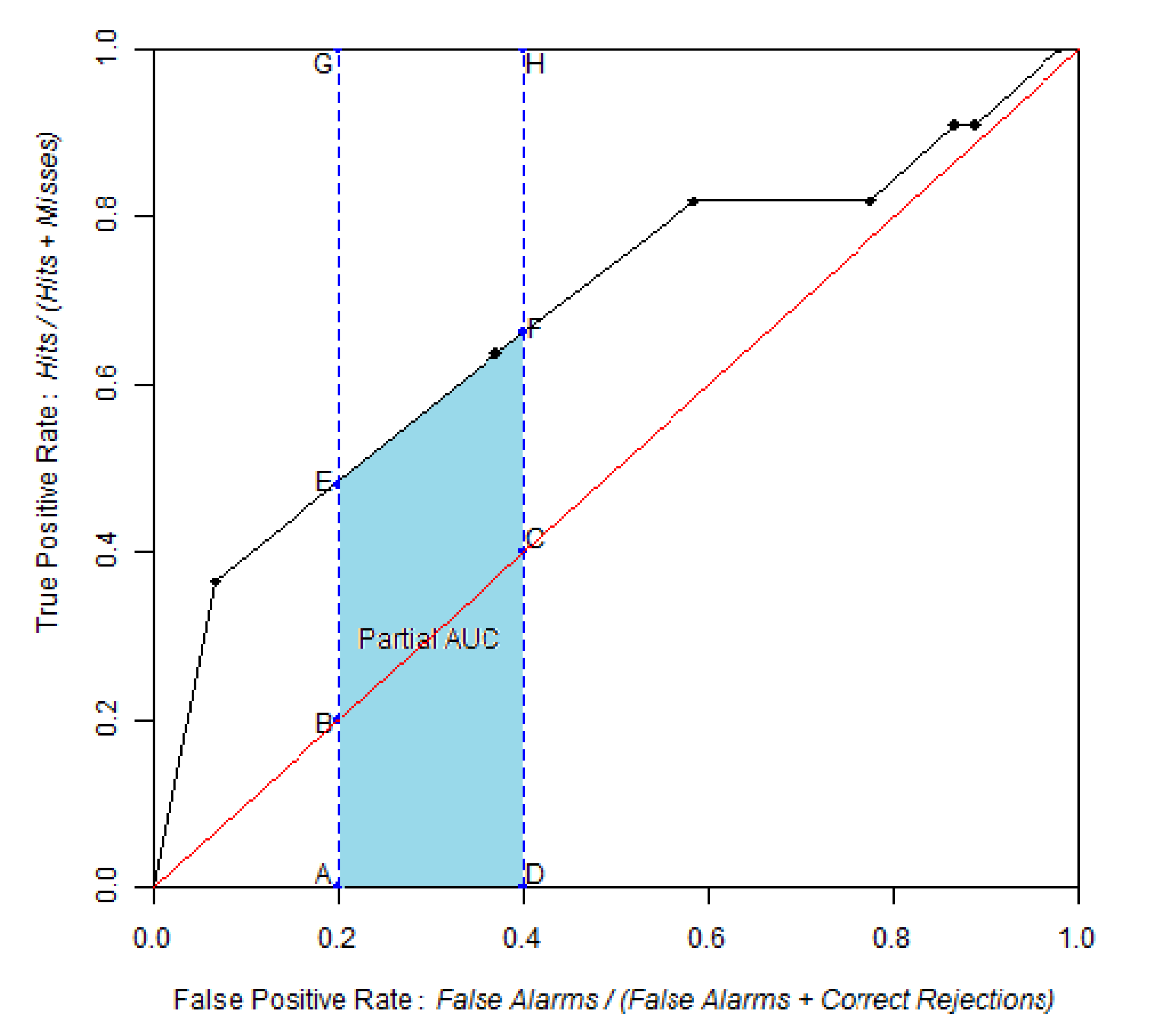
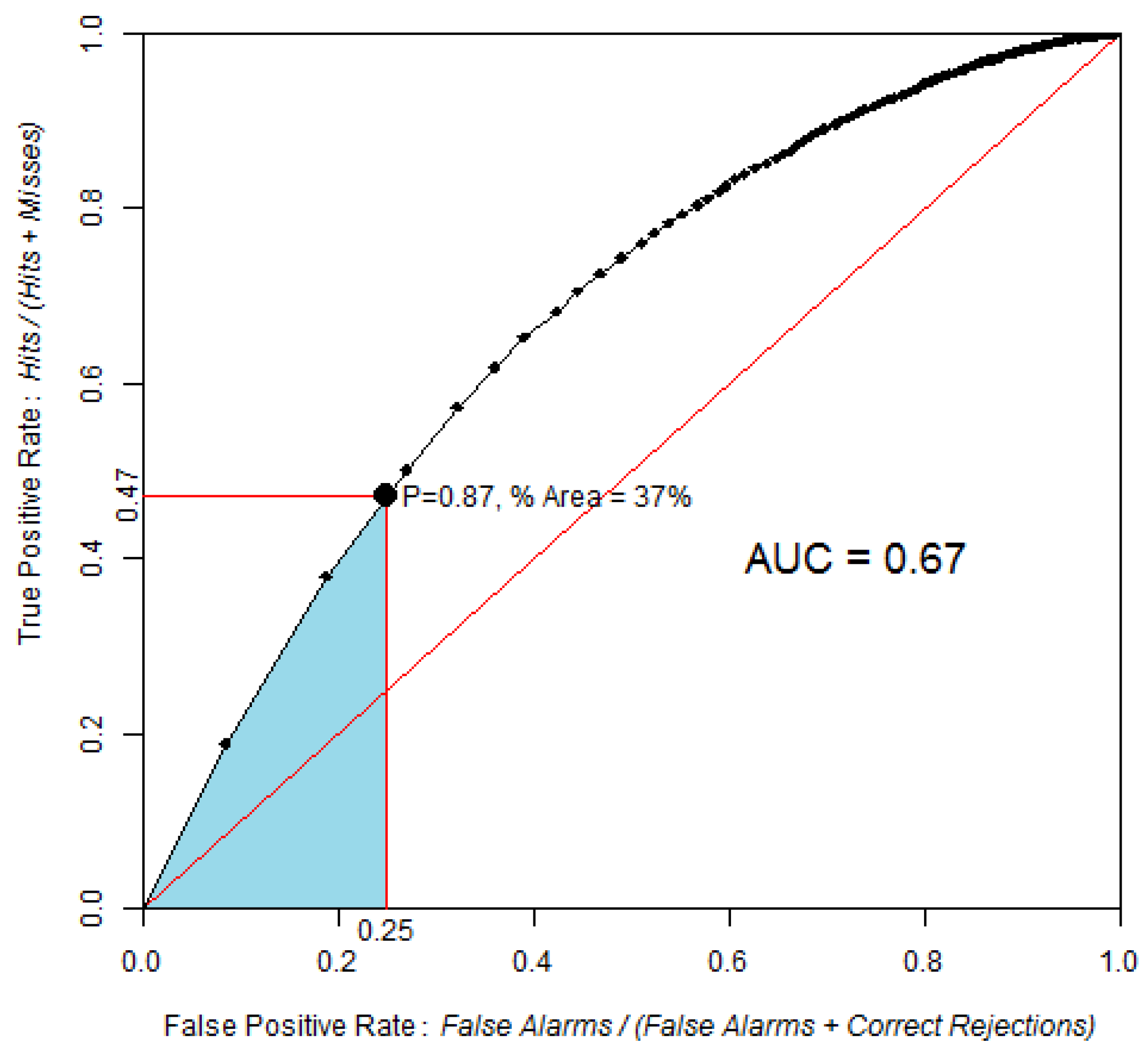
3.1. AUC and pAUC Estimation

3.2. Confidence Intervals



3.3. Comparison of Two ROC Curves

3.4. Improvements in the Use and Interpretation of ROC Curves

3.5. Decreasing Computing Time
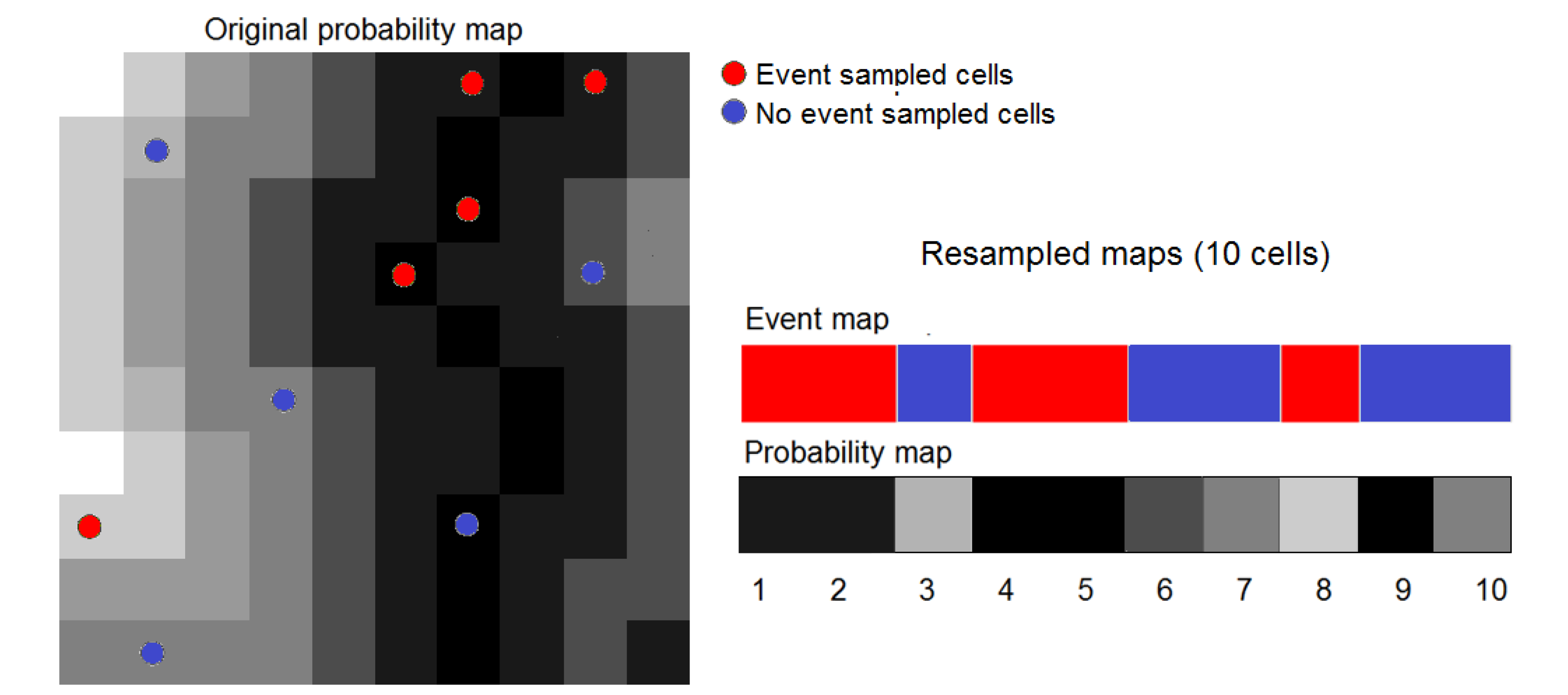
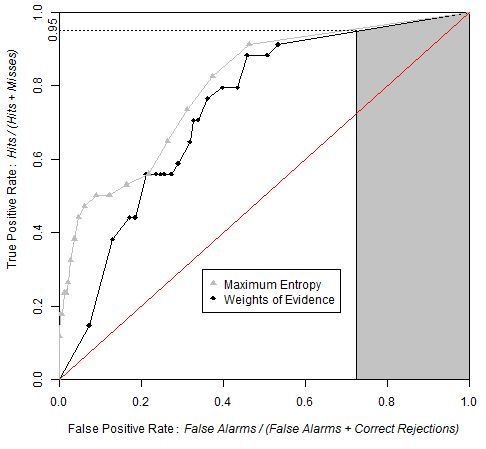
4. Applications
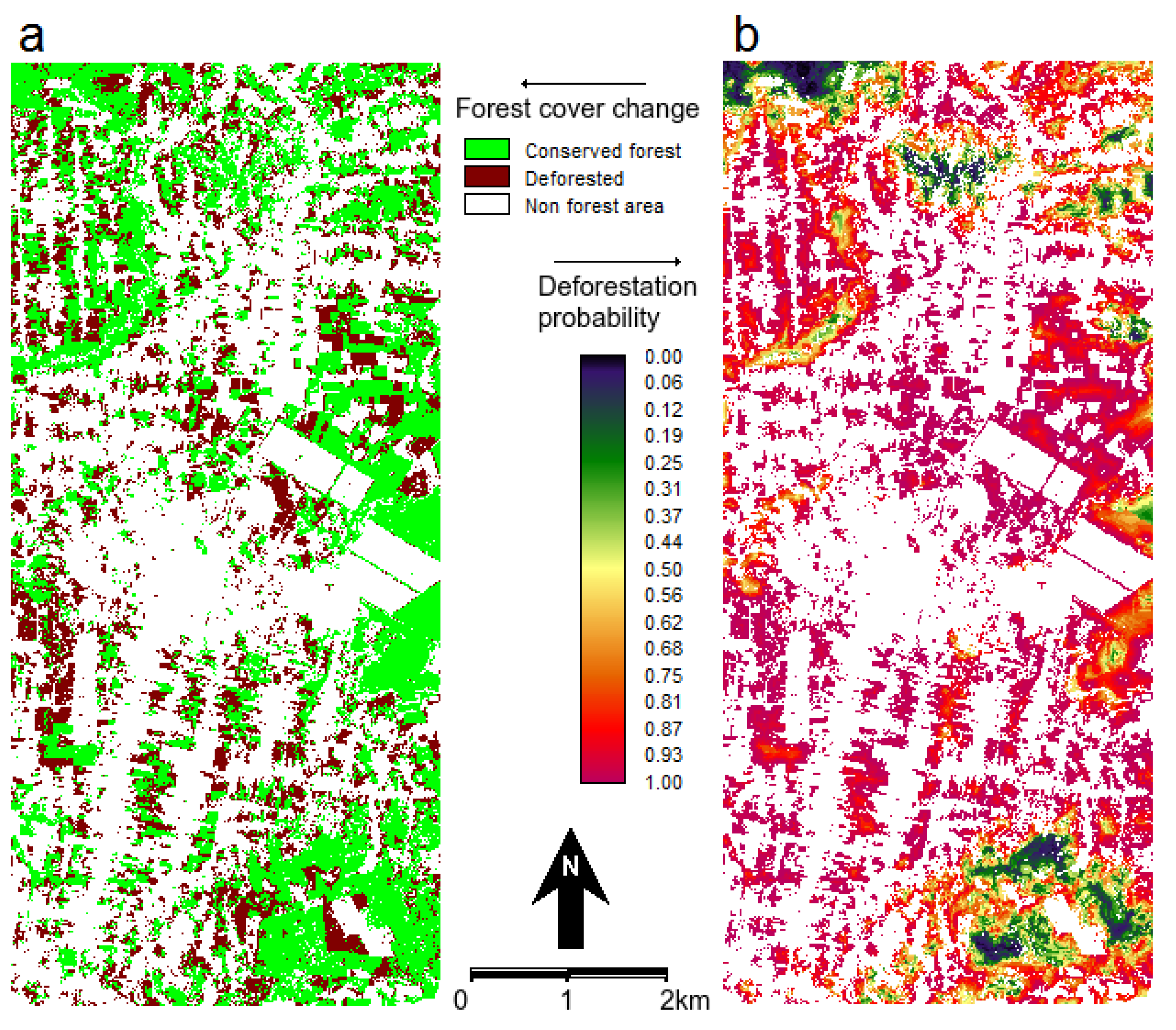
4.1. Land Use/Cover Change (LUCC) Model
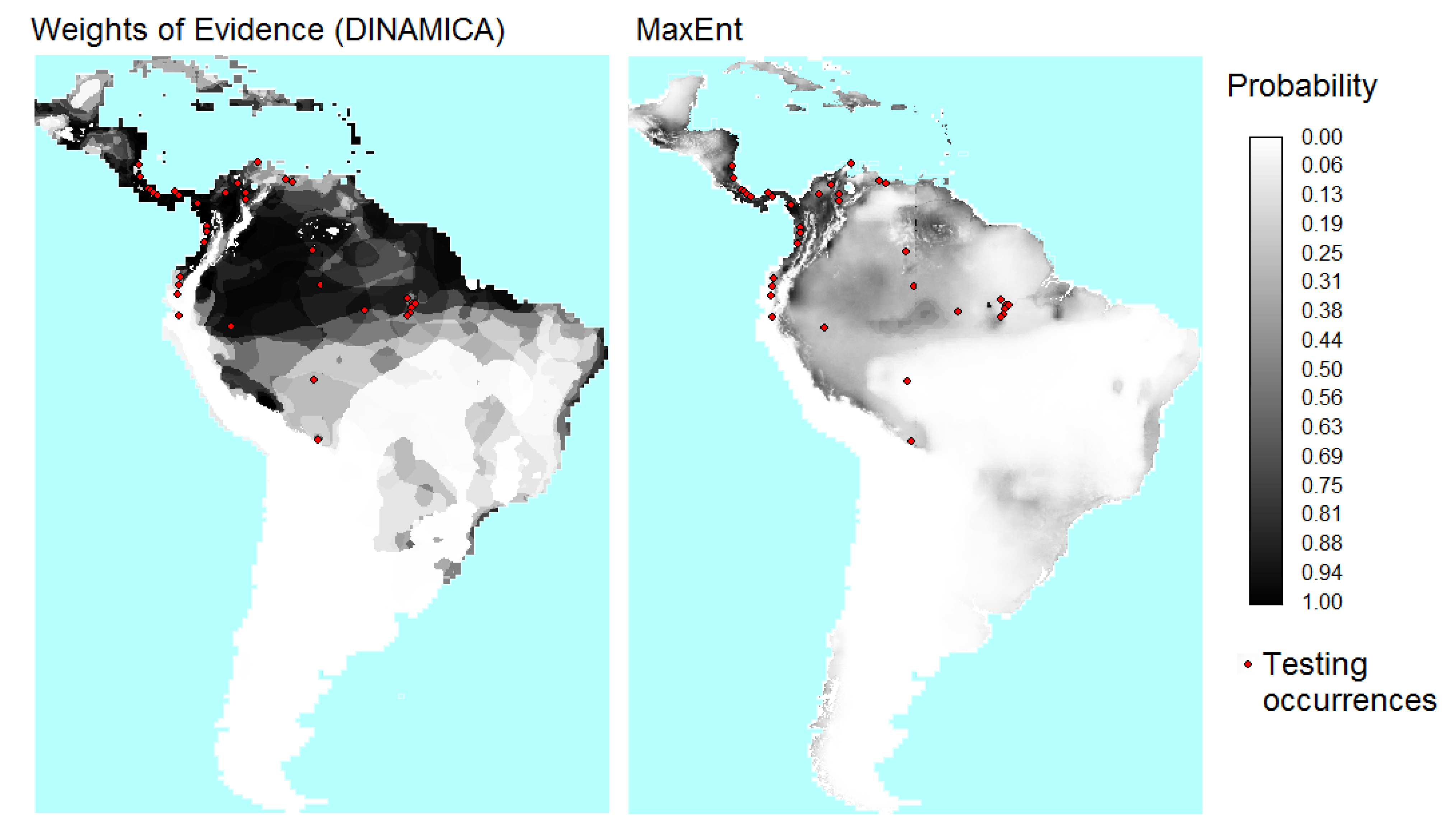
4.2. Models of Species Distribution

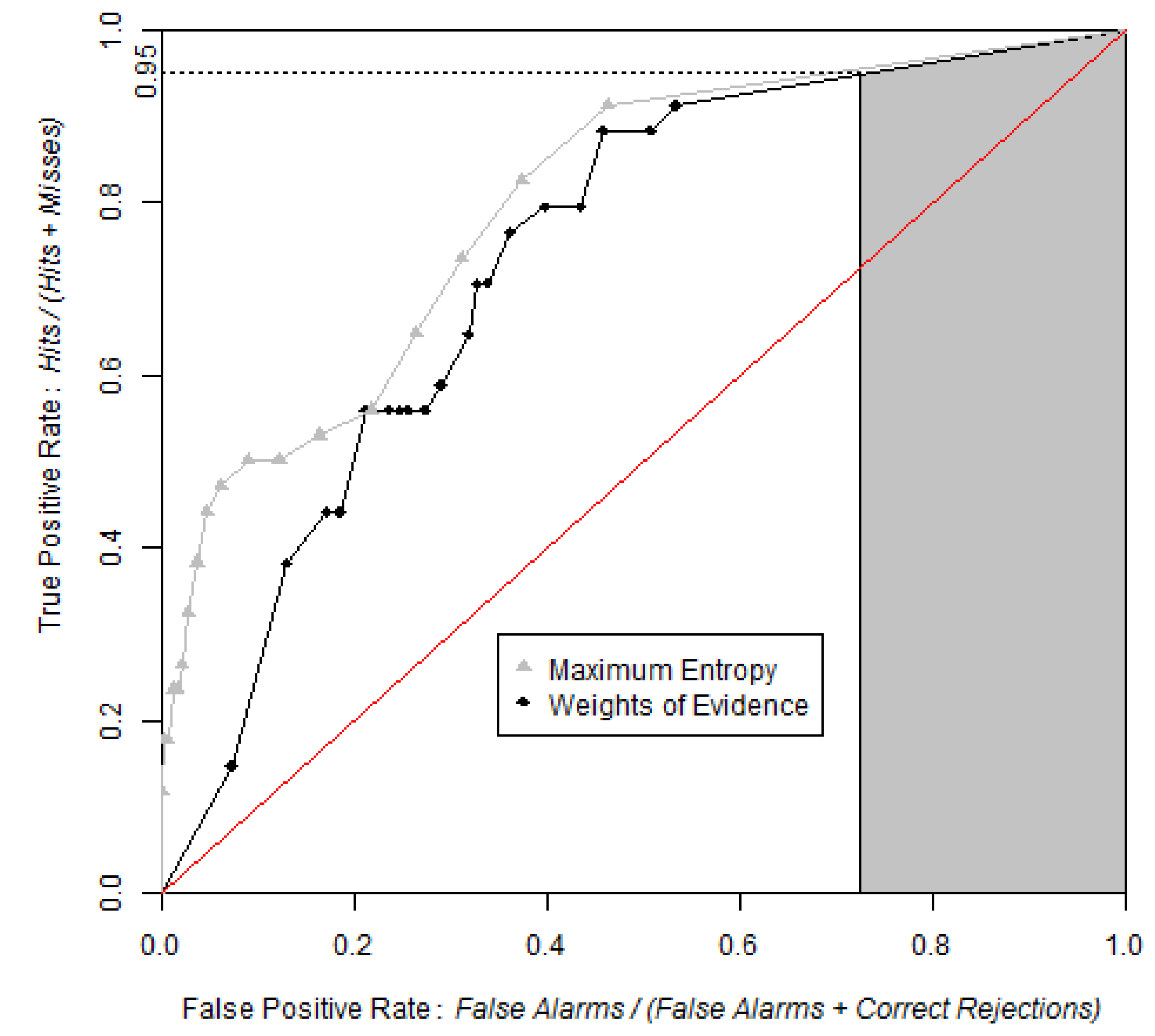
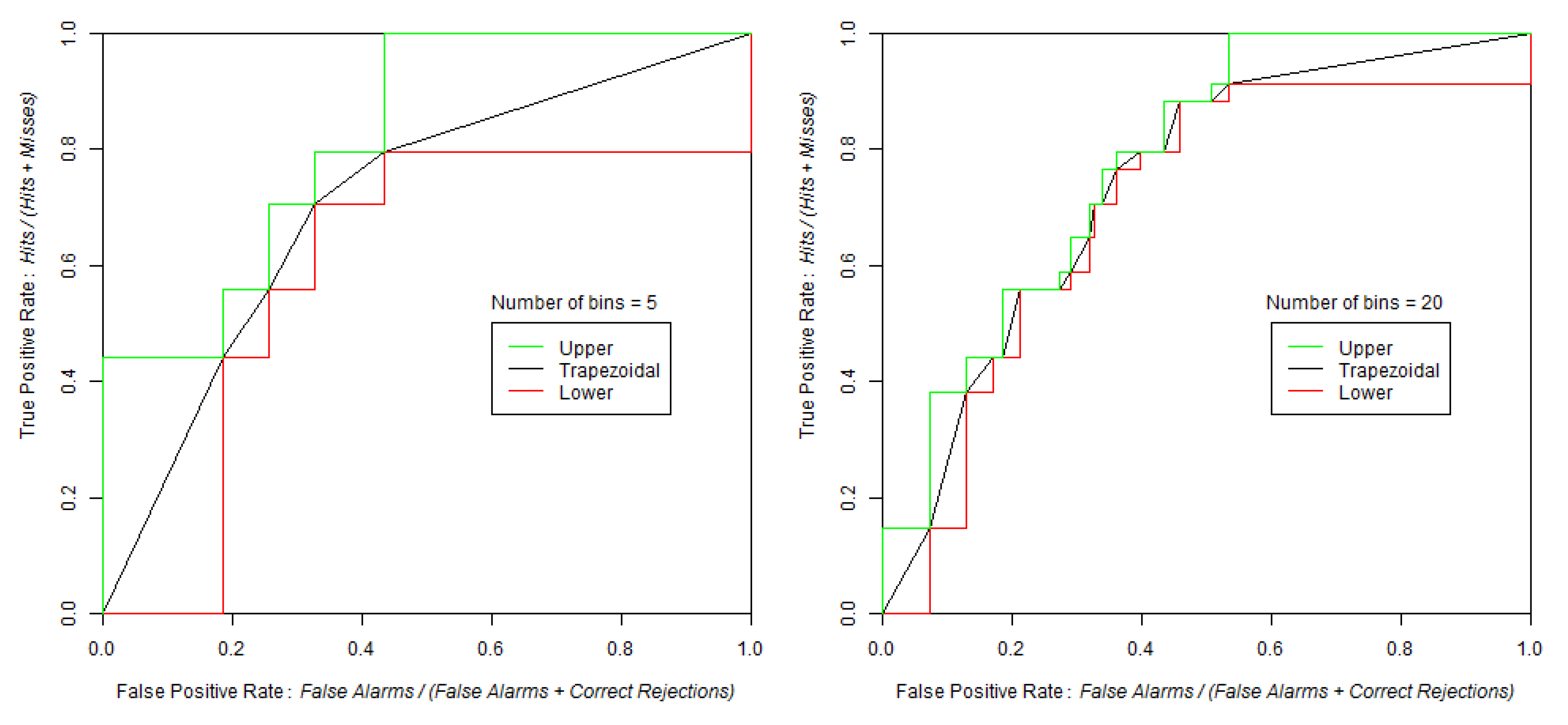
| AUC | Based on Entire Data | Based on Resampled Data | ||||||
|---|---|---|---|---|---|---|---|---|
| Number of bins | 100 | 20 | 10 | 5 | 100 | 20 | 10 | 5 |
| WofE | 0.746 (−0.3) | 0.739 (−1.2) | 0.734 (−1.8) | 0.709 (−5.3) | 0.746 (−0.3) | 0.738 (−1.3) | 0.734 (−1.9) | 0.709 (−5.2) |
| MaxEnt | 0.806 (−0.6) | 0.800 (−1.3) | 0.782 (−3.6) | 0.737 (−9.2) | 0.805 (−0.7) | 0.800 (−1.4) | 0.781 (−3.7) | 0.736 (−9.3) |
| AUC | Based on Entire Data | Based on Resampled Data | ||||||
|---|---|---|---|---|---|---|---|---|
| Number of bins | 100 | 20 | 10 | 5 | 100 | 20 | 10 | 5 |
| WofE | 0.704 (−5.9) | 0.687 (−8.1) | 0.665 (−11.1) | 0.656 (−12.3) | 0.703 (−6.0) | 0.687 (−8.1) | 0.665 (−11.1) | 0.657 (−12.2) |
| MaxEnt | 0.71 (−11.8) | 0.674 (−16.9) | 0.636 (−21.5) | 0.611 (−24.6) | 0.715 (−11.9) | 0.674 (-16.9) | 0.636 (−21.6) | 0.611 (−24.6) |
| Number of Bins | ||||
|---|---|---|---|---|
| 100 | 20 | 10 | 5 | |
| AUC upper | 0.7617 | 0.7780 | 0.8006 | 0.8218 |
| AUC | 0.7458 | 0.7385 | 0.7341 | 0.7085 |
| AUC lower | 0.7299 | 0.6990 | 0.6676 | 0.5952 |
| Software | Index | Inferior bound | Index Value | Superior bound |
|---|---|---|---|---|
| WofE | AUC | 0.6618 | 0.7382 | 0.8055 |
| MaxEnt | AUC | 0.7231 | 0.7996 | 0.8706 |
| WofE | pAUC | 0.7798 | 0.9051 | 0.9979 |
| MaxEnt | pAUC | 0.8352 | 0.9179 | 0.9990 |
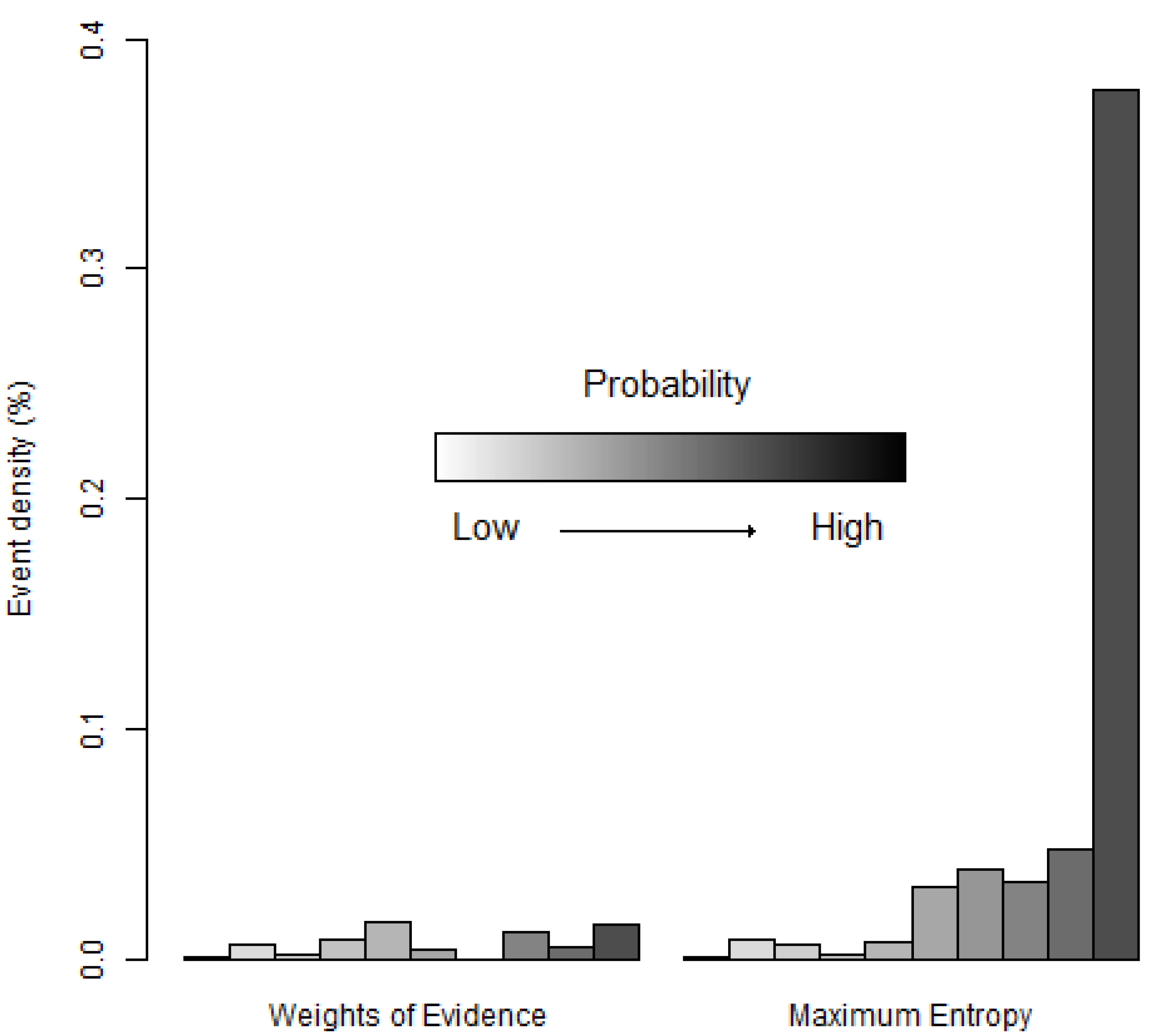
5. Discussion
6. Conclusion
Acknowledgments
Conflict of Interest
References
- Swets, J.A. Signal Detection Theory and ROC Analysis in Psychology and Diagnostics, 1st ed.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1996. [Google Scholar]
- Satchell, S.; Xia, W. Analytic Models of the ROC Curve: Applications to Credit Rating Model Validation. In The Analytics of Risk Model Validation, 1st ed.; Christodoulakis, G., Satchell, S., Eds.; Elsevier: London, UK, 2008. [Google Scholar]
- Sonego, P.; Kocsor, A.; Pongor, S. ROC analysis: Applications to the classification of biological sequences and 3D structures. Brief. Bioinform. 2008, 9, 198–209. [Google Scholar] [CrossRef]
- Li, R.; Guan, Q.; Merchant, J. A geospatial modeling framework for assessing biofuels-related land-use and land-cover change. Agr. Ecosyst. Environ. 2012, 161, 17–26. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr.; Batchu, K. Using the relative operating characteristic to quantify certainty in prediction of location of land cover change in India. Trans. GIS 2003, 7, 467–484. [Google Scholar]
- Pontius, R.G., Jr.; Parmentier, B. Recommendations for using the relative operating characteristic (ROC). Landsc. Ecol. 2013. submitted for publication. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern. Recogni. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Robin, X.; Turck, N.; Hainard, A.; Tiberti, N.; Lisacek, F.; Sanchez, J.C.; Müller, M. pROC: An open-source package for R and S+ to analyze and compare ROC curves. BMC Bioinforma. 2011, 12. [Google Scholar] [CrossRef]
- Soares-Filho, B.S.; Rodrigues, H.O.; Follador, M. A hybrid analytical-heuristic method for calibrating land-use change models. Environ. Model. Soft. 2013, 43, 80–87. [Google Scholar] [CrossRef]
- Peterson, A.T.; Papeş, M.; Soberón, J. Rethinking receiver operating characteristic analysis applications in ecological Niche modelling. Ecol. Model. 2008, 213, 63–72. [Google Scholar] [CrossRef]
- McClish, D.K. Analyzing a portion of the ROC curve. Med. Decis. Making 1989, 9, 190–195. [Google Scholar] [CrossRef]
- Santini, S. Computing the Binomial. Coefficients. 2007. Available online: http://arantxa.ii.uam.es/~ssantini/writing/notes/s667_binomial.pdf (accessed on 21 June 2013).
- Pontius, R.G., Jr.; Schneider, L.C. Land-cover change model validation by an ROC method for the Ipswich Watershed, Massachusetts, USA. Agr. Ecosyst. Environ. 2001, 85, 239–248. [Google Scholar] [CrossRef]
- Lobo, J.M.; Jiménez-Valverde, A.; Real, R. AUC: A Misleading measure of the performance of predictive distribution models. Glob. Ecol. Biogeogr. 2008, 17, 145–151. [Google Scholar] [CrossRef]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef]
- Mas, J.F.; Farfán, M.; Ghilen, C.; Lima, T.; Soares Filho, B. Una Comparación de dos Enfoques de Modelación de Nicho Ecológico. In Proceedings of Memorias de la XX Reunión SELPER, San Luis Potosí, México, 21–25 October 2013.
- Soares-Filho, B.S.; Alencar, A.; Nepstad, D.; Cerqueira, G.; Vera Diaz, M.; Rivero, S.; Solorzano, L.; Voll, E. Simulating the response of land-cover changes to road paving and governance along a major Amazon highway: The Santarém-Cuiabá Corridor. Glob. Change Biol. 2004, 10, 745–764. [Google Scholar] [CrossRef]
- Mas, J.F.; Pérez-Vega, A.; Clarke, K.C. Assessing simulated land use/cover maps using similarity and fragmentation indices. Ecol. Complex 2012, 11, 38–45. [Google Scholar] [CrossRef]
- Pontius, R.G., Jr.; Pacheco, P. Calibration and validation of a model of forest disturbance in the western Ghats, India 1920–1990. GeoJournal 2004, 61, 325–334. [Google Scholar] [CrossRef]
- R Development Core Team, R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2013.
© 2013 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Mas, J.-F.; Soares Filho, B.; Pontius, R.G.; Farfán Gutiérrez, M.; Rodrigues, H. A Suite of Tools for ROC Analysis of Spatial Models. ISPRS Int. J. Geo-Inf. 2013, 2, 869-887. https://doi.org/10.3390/ijgi2030869
Mas J-F, Soares Filho B, Pontius RG, Farfán Gutiérrez M, Rodrigues H. A Suite of Tools for ROC Analysis of Spatial Models. ISPRS International Journal of Geo-Information. 2013; 2(3):869-887. https://doi.org/10.3390/ijgi2030869
Chicago/Turabian StyleMas, Jean-François, Britaldo Soares Filho, Robert Gilmore Pontius, Michelle Farfán Gutiérrez, and Hermann Rodrigues. 2013. "A Suite of Tools for ROC Analysis of Spatial Models" ISPRS International Journal of Geo-Information 2, no. 3: 869-887. https://doi.org/10.3390/ijgi2030869
APA StyleMas, J.-F., Soares Filho, B., Pontius, R. G., Farfán Gutiérrez, M., & Rodrigues, H. (2013). A Suite of Tools for ROC Analysis of Spatial Models. ISPRS International Journal of Geo-Information, 2(3), 869-887. https://doi.org/10.3390/ijgi2030869