Economic Optimization of Bike-Sharing Systems via Nonlinear Threshold Effects: An Interpretable Machine Learning Approach in Xi’an, China
Abstract
1. Introduction
2. Literature Review
2.1. Economic Sustainability of Bike-Sharing Systems
2.2. Threshold Effects in Bike-Sharing Economic Optimization
2.3. Modeling Approaches for Threshold Effects in Bike-Sharing: From Econometrics to Explainable ML
3. Data and Methods
3.1. Study Area
3.2. Data Collection and Processing
3.2.1. Bike-Sharing Operational Data and Economic Metrics
3.2.2. Urban Built Environment Data
3.2.3. TAZ-Based Spatial Aggregation and Normalization
3.3. Research Methods
3.3.1. ESDA and Spatial Heterogeneity
3.3.2. Non-Linear Modeling with XGBoost
3.3.3. Interpretability Analysis and Threshold Identification with SHAP
4. Results
4.1. Variable Selection and Descriptive Statistics
4.2. Model Optimization and SHAP Factors
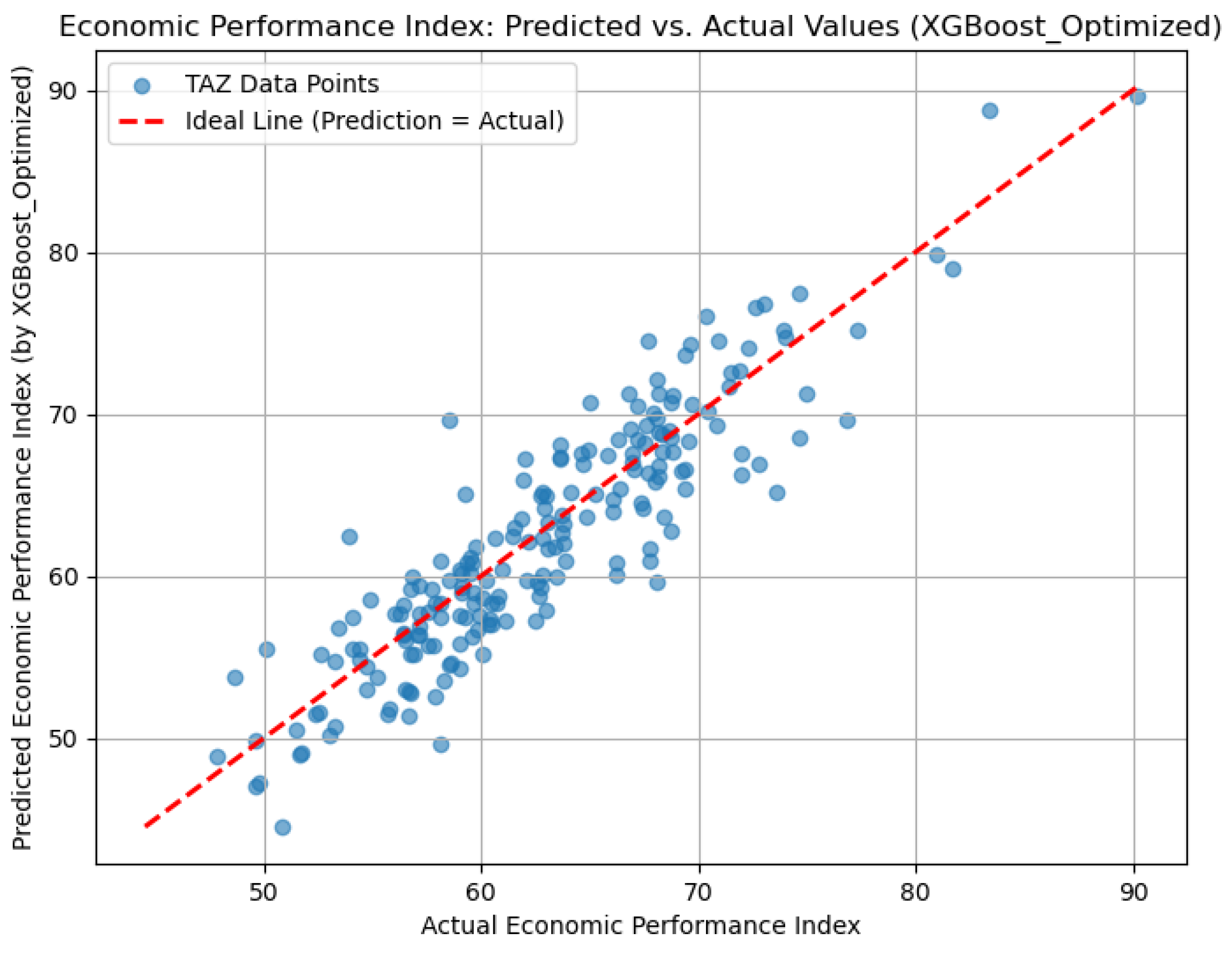
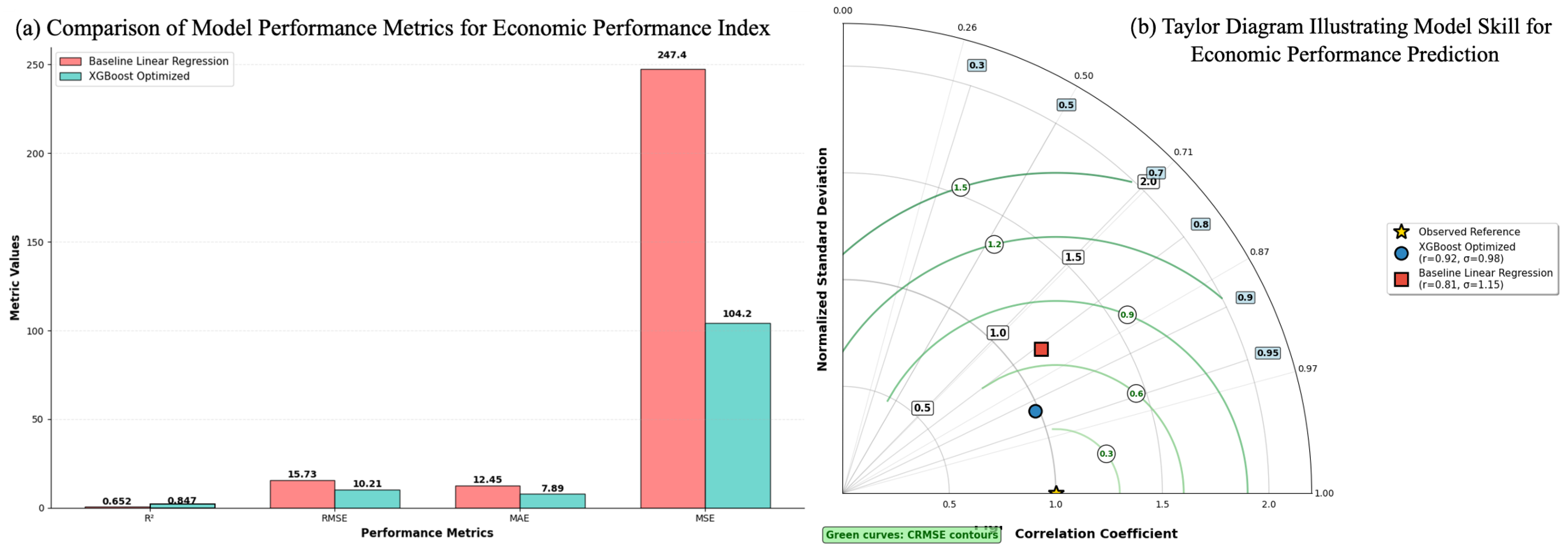
4.2.1. Model Training and Performance Evaluation
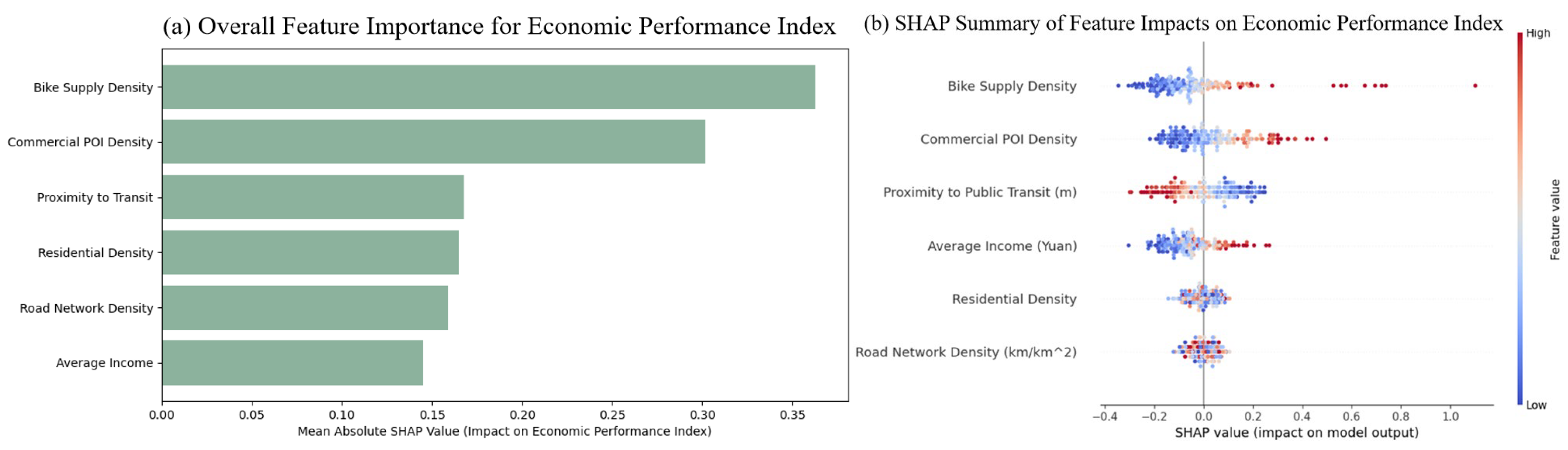
4.2.2. Identifying Factors of Bike-Sharing Economic Performance
4.3. Non-Linear Effects, Interactions, and Individual Explanations
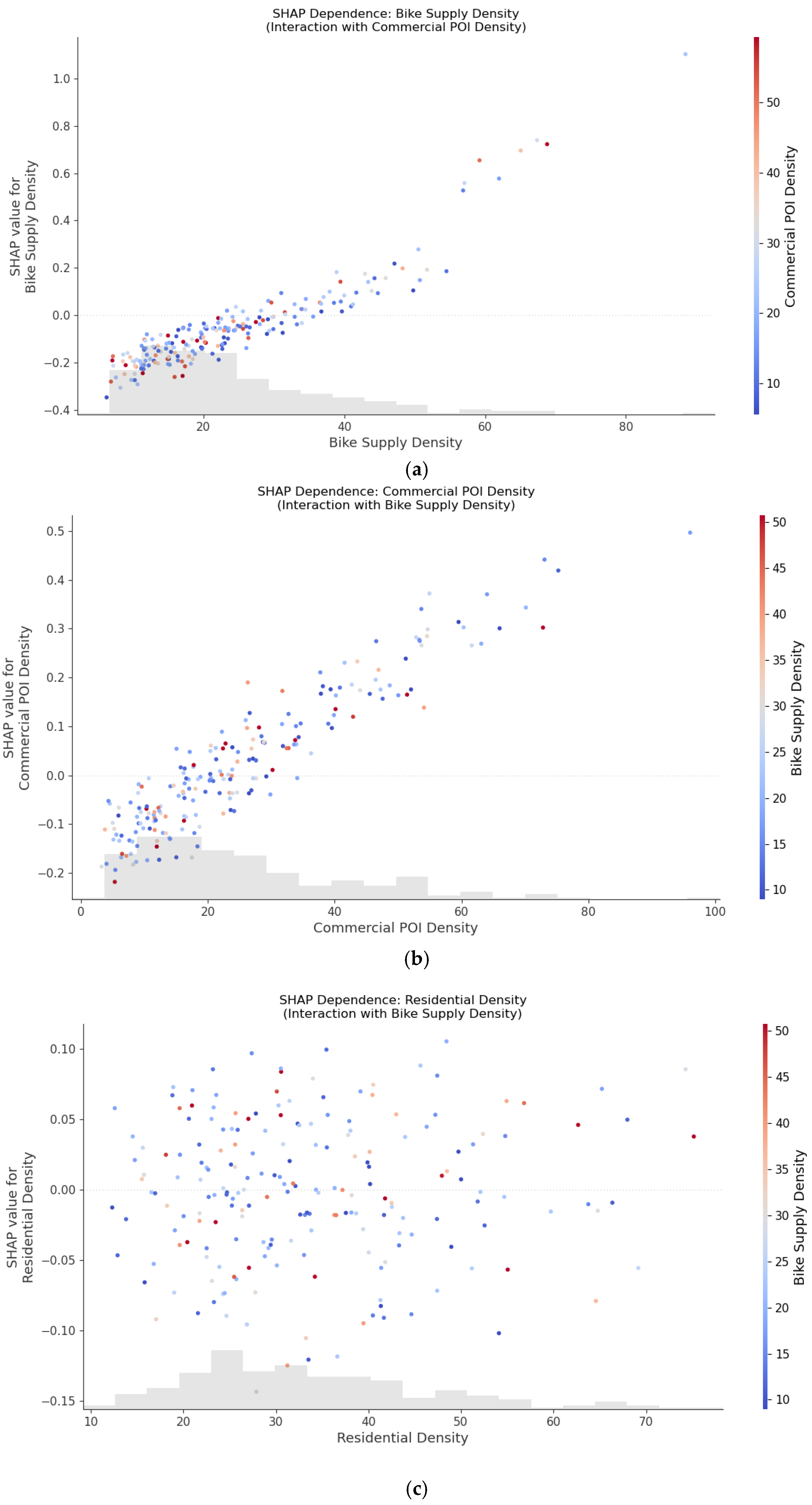
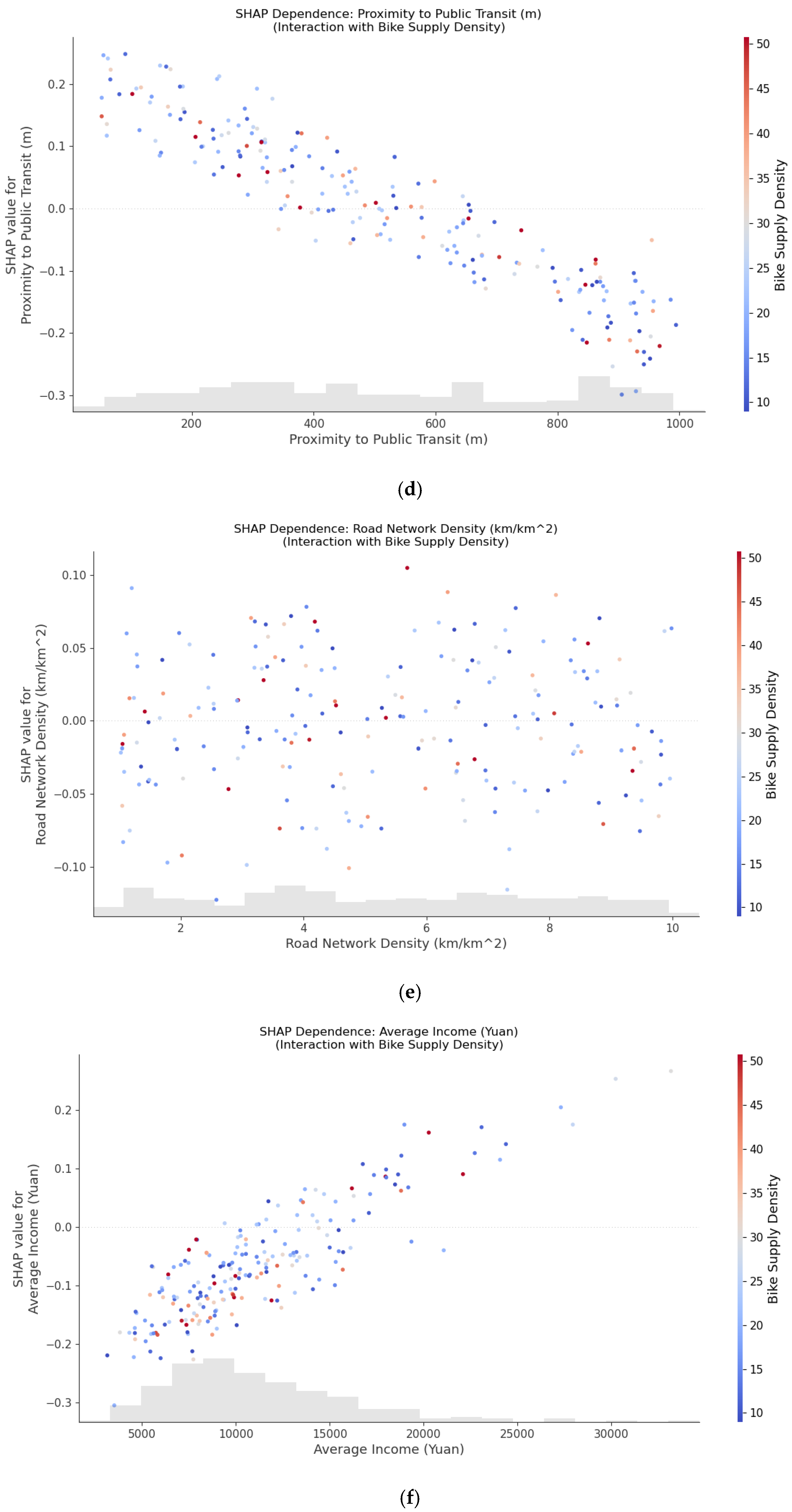
4.3.1. Non-Linear Effects and Primary Interactions
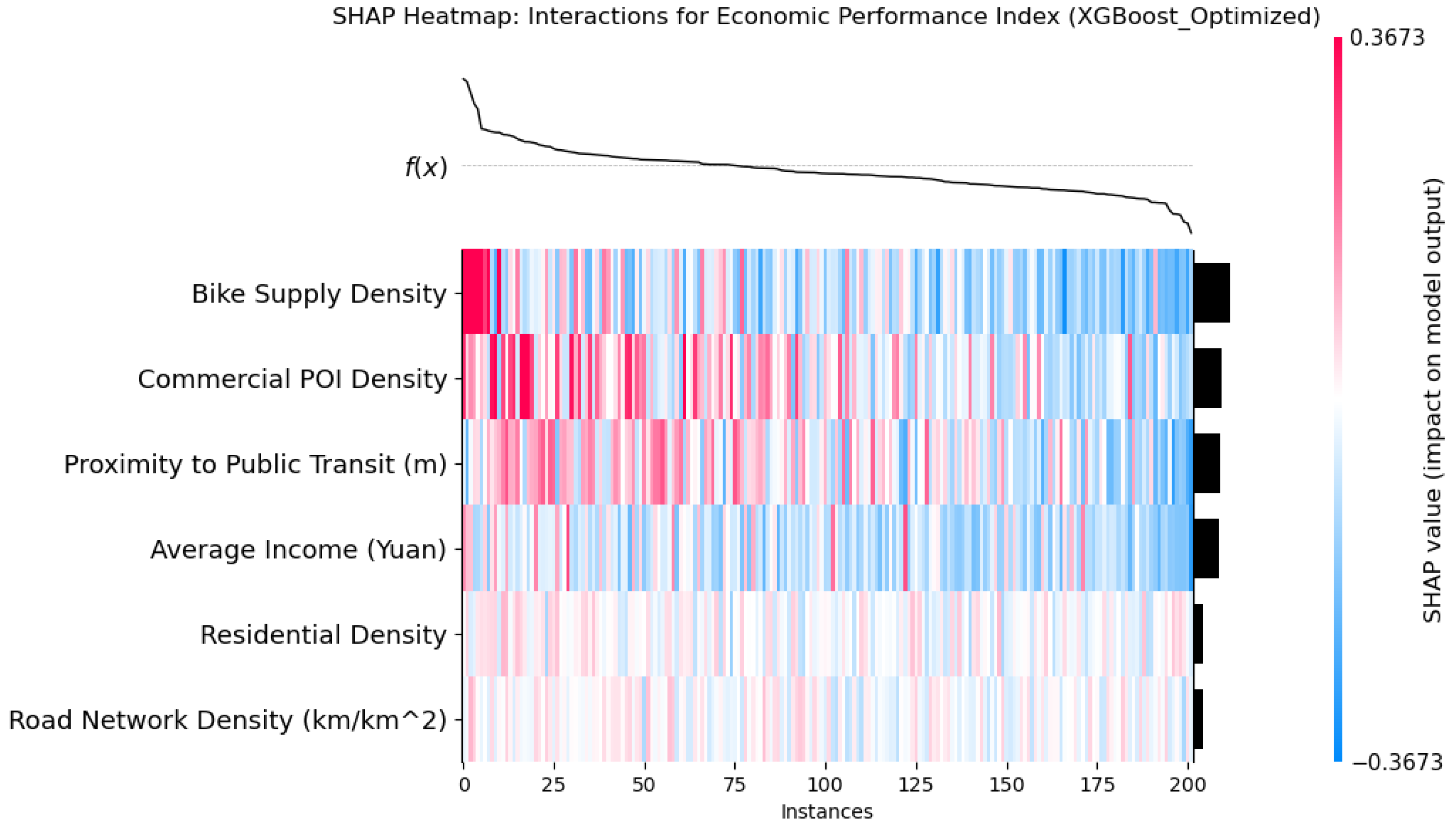
4.3.2. Interaction Effects Among Features
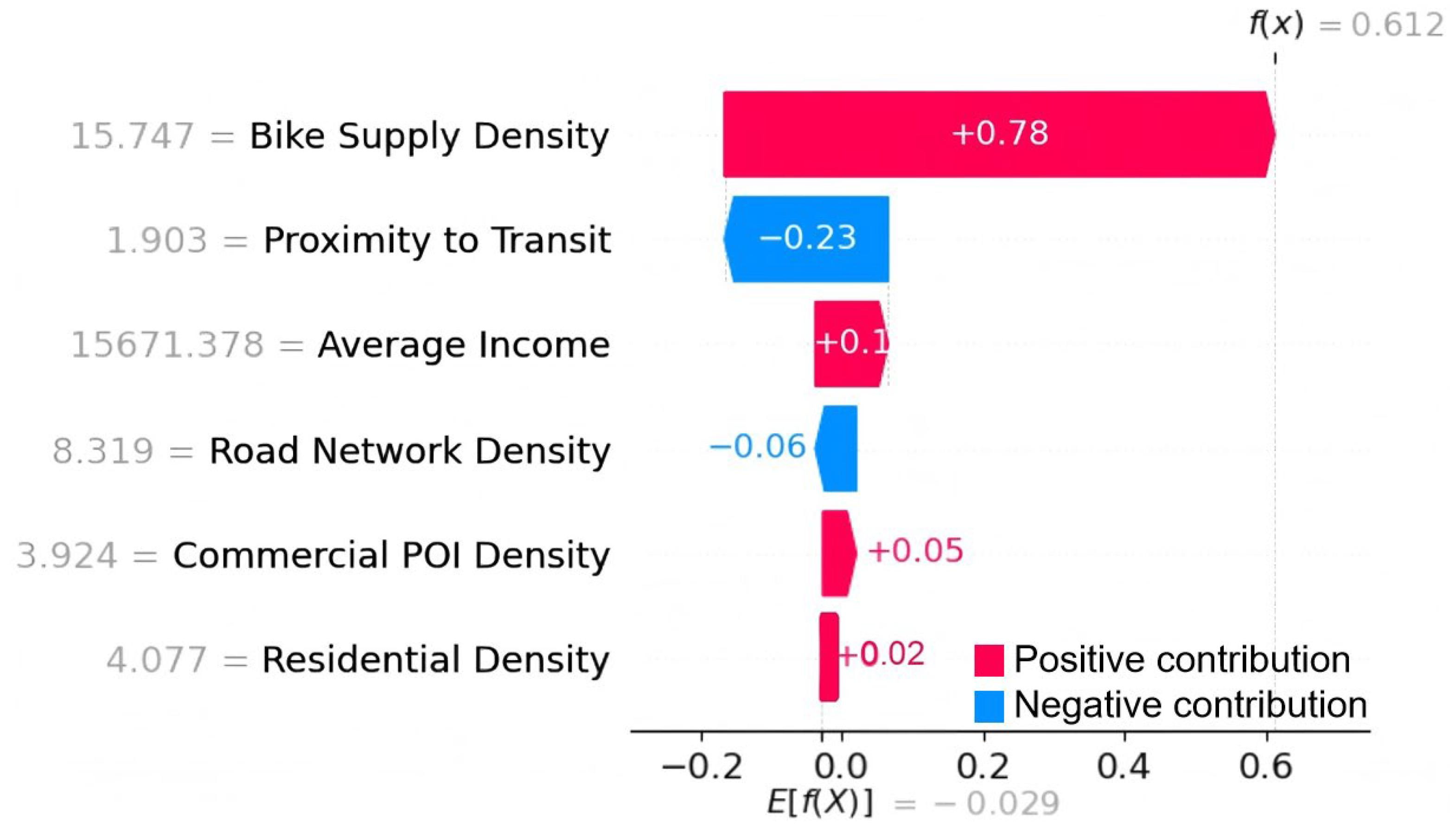
4.3.3. Attribution Analysis of Individual TAZ Predictions
5. Discussion
5.1. Spatial Heterogeneity and Threshold Effects in Bike-Sharing Economic Performance
5.2. Interaction Effects and Operational Complexity
5.3. Methodological Contributions and Policy Implications
5.4. Research Limitations and Future Directions
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Albuquerque, V.; Sales Dias, M.; Bacao, F. Machine Learning Approaches to Bike-Sharing Systems: A Systematic Literature Review. ISPRS Int. J. Geo-Inf. 2021, 10, 62. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, J.; Duan, Z.; Bryde, D. Sustainable Bike-Sharing Systems: Characteristics and Commonalities across Cases in Urban China. J. Clean. Prod. 2015, 97, 124–133. [Google Scholar] [CrossRef]
- Oostendorp, R.; Gebhardt, L. Combining Means of Transport as a Users’ Strategy to Optimize Traveling in an Urban Context: Empirical Results on Intermodal Travel Behavior from a Survey in Berlin. J. Transp. Geogr. 2018, 71, 72–83. [Google Scholar] [CrossRef]
- Cai, J.; Zheng, P.; Xie, Y.; Du, Z.; Li, X. Research on the Impact of Climate Change on Green and Low-Carbon Development in Agriculture. Ecol. Indic. 2025, 170, 113090. [Google Scholar] [CrossRef]
- Ma, Y.; Rong, K.; Mangalagiu, D.; Thornton, T.F.; Zhu, D. Co-Evolution between Urban Sustainability and Business Ecosystem Innovation: Evidence from the Sharing Mobility Sector in Shanghai. J. Clean. Prod. 2018, 188, 942–953. [Google Scholar] [CrossRef]
- Mooney, S.J.; Hosford, K.; Howe, B.; Yan, A.; Winters, M.; Bassok, A.; Hirsch, J.A. Freedom from the Station: Spatial Equity in Access to Dockless Bike Share. J. Transp. Geogr. 2019, 74, 91–96. [Google Scholar] [CrossRef]
- Qiu, L.-Y.; He, L.-Y. Bike Sharing and the Economy, the Environment, and Health-Related Externalities. Sustainability 2018, 10, 1145. [Google Scholar] [CrossRef]
- Nikitas, A. How to Save Bike-Sharing: An Evidence-Based Survival Toolkit for Policy-Makers and Mobility Providers. Sustainability 2019, 11, 3206. [Google Scholar] [CrossRef]
- Eren, E.; Uz, V.E. A Review on Bike-Sharing: The Factors Affecting Bike-Sharing Demand. Sustain. Cities Soc. 2020, 54, 101882. [Google Scholar] [CrossRef]
- Li, Z.; Wang, W.; Yang, C.; Ding, H. Bicycle Mode Share in China: A City-Level Analysis of Long Term Trends. Transportation 2017, 44, 773–788. [Google Scholar] [CrossRef]
- Hu, S.; Xiong, C.; Liu, Z.; Zhang, L. Examining Spatiotemporal Changing Patterns of Bike-Sharing Usage during COVID-19 Pandemic. J. Transp. Geogr. 2021, 91, 102997. [Google Scholar] [CrossRef]
- Chen, Q.; Fu, C.; Zhu, N.; Ma, S.; He, Q.-C. A Target-Based Optimization Model for Bike-Sharing Systems: From the Perspective of Service Efficiency and Equity. Transp. Res. Part B Methodol. 2023, 167, 235–260. [Google Scholar] [CrossRef]
- Saltykova, K.; Ma, X.; Yao, L.; Kong, H. Environmental Impact Assessment of Bike-Sharing Considering the Modal Shift from Public Transit. Transp. Res. Part Transp. Environ. 2022, 105, 103238. [Google Scholar] [CrossRef]
- Lin, L.; He, Z.; Peeta, S. Predicting Station-Level Hourly Demand in a Large-Scale Bike-Sharing Network: A Graph Convolutional Neural Network Approach. Transp. Res. Part C Emerg. Technol. 2018, 97, 258–276. [Google Scholar] [CrossRef]
- Jing, Y.; Sun, R.; Chen, L. A Method for Identifying Urban Functional Zones Based on Landscape Types and Human Activities. Sustainability 2022, 14, 4130. [Google Scholar] [CrossRef]
- Sugiarto, H.; Yanti, J.; Cahyani, D.; Junaidi, A.; Oktoriza, L.A. Exploration Financial Performance Optimization Strategies on Business Success: A Literature Review. SEIKO J. Manag. Bus. 2023, 6, 402–411. Available online: https://www.repository.unimas.ac.id/index.php?p=show_detail&id=335&keywords= (accessed on 25 August 2025).
- Siqueira-Gay, J.; Giannotti, M.; Sester, M. Learning about Spatial Inequalities: Capturing the Heterogeneity in the Urban Environment. J. Clean. Prod. 2019, 237, 117732. [Google Scholar] [CrossRef]
- Zhang, J.; Cheng, L. Threshold Effect of Tourism Development on Economic Growth Following a Disaster Shock: Evidence from the Wenchuan Earthquake, PR China. Sustainability 2019, 11, 371. [Google Scholar] [CrossRef]
- Chen, E.; Ye, Z. Identifying the Nonlinear Relationship between Free-Floating Bike Sharing Usage and Built Environment. J. Clean. Prod. 2021, 280, 124281. [Google Scholar] [CrossRef]
- Mavlutova, I.; Atstaja, D.; Grasis, J.; Kuzmina, J.; Uvarova, I.; Roga, D. Urban Transportation Concept and Sustainable Urban Mobility in Smart Cities: A Review. Energies 2023, 16, 3585. [Google Scholar] [CrossRef]
- Zhao, Q.; Jiang, M.; Zhao, Z.; Liu, F.; Zhou, L. The Impact of Green Innovation on Carbon Reduction Efficiency in China: Evidence from Machine Learning Validation. Energy Econ. 2024, 133, 107525. [Google Scholar] [CrossRef]
- Ustaoglu, F.; Islam, M.S. Potential Toxic Elements in Sediment of Some Rivers at Giresun, Northeast Turkey: A Preliminary Assessment for Ecotoxicological Status and Health Risk. Ecol. Indic. 2020, 113, 106237. [Google Scholar] [CrossRef]
- Gao, K.; Yang, Y.; Gil, J.; Qu, X. Data-Driven Interpretation on Interactive and Nonlinear Effects of the Correlated Built Environment on Shared Mobility. J. Transp. Geogr. 2023, 110, 103604. [Google Scholar] [CrossRef]
- Chikaraishi, M.; Garg, P.; Varghese, V.; Yoshizoe, K.; Urata, J.; Shiomi, Y.; Watanabe, R. On the Possibility of Short-Term Traffic Prediction during Disaster with Machine Learning Approaches: An Exploratory Analysis. Transp. Policy 2020, 98, 91–104. [Google Scholar] [CrossRef]
- Yang, C.; Chen, M.; Yuan, Q. The Application of XGBoost and SHAP to Examining the Factors in Freight Truck-Related Crashes: An Exploratory Analysis. Accid. Anal. Prev. 2021, 158, 106153. [Google Scholar] [CrossRef]
- Wang, L.; Zhao, C.; Liu, X.; Chen, X.; Li, C.; Wang, T.; Wu, J.; Zhang, Y. Non-Linear Effects of the Built Environment and Social Environment on Bus Use among Older Adults in China: An Application of the XGBoost Model. Int. J. Environ. Res. Public. Health 2021, 18, 9592. [Google Scholar] [CrossRef]
- Jiang, J.; Li, Y.; Li, Y.; Li, C.; Yu, L.; Li, L. Smart Transportation Systems Using Learning Method for Urban Mobility and Management in Modern Cities. Sustain. Cities Soc. 2024, 108, 105428. [Google Scholar] [CrossRef]
- Wu, P.; Zhang, Z.; Peng, X.; Wang, R. Deep Learning Solutions for Smart City Challenges in Urban Development. Sci. Rep. 2024, 14, 5176. [Google Scholar] [CrossRef]
- Shen, H.; Weng, J.; Lin, P. Exploring the Nuanced Correlation between Built Environment and the Integrated Travel of Dockless Bike-Sharing and Metro at Origin-Route-Destination Level. Sustain. Cities Soc. 2025, 119, 106090. [Google Scholar] [CrossRef]
- Lai, X.; Gao, C. Spatiotemporal Patterns Evolution of Residential Areas and Transportation Facilities Based on Multi-Source Data: A Case Study of Xi’an, China. ISPRS Int. J. Geo-Inf. 2023, 12, 233. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Long, X.; Li, W. Understanding the Intention to Use Bike-Sharing System: A Case Study in Xi’an, China. PLoS ONE 2021, 16, e0258790. [Google Scholar] [CrossRef]
- Gao, K.; Yang, Y.; Li, A.; Li, J.; Yu, B. Quantifying Economic Benefits from Free-Floating Bike-Sharing Systems: A Trip-Level Inference Approach and City-Scale Analysis. Transp. Res. Part Policy Pract. 2021, 144, 89–103. [Google Scholar] [CrossRef]
- Robinson, J. Cities in a World of Cities: The Comparative Gesture. Int. J. Urban Reg. Res. 2010, 35, 1–23. [Google Scholar] [CrossRef]
- Zhang, F.; Liu, W. An Economic Analysis of Integrating Bike Sharing Service with Metro Systems. Transp. Res. Part Transp. Environ. 2021, 99, 103008. [Google Scholar] [CrossRef]
- Storme, T.; Casier, C.; Azadi, H.; Witlox, F. Impact Assessments of New Mobility Services: A Critical Review. Sustainability 2021, 13, 3074. [Google Scholar] [CrossRef]
- Standing, C.; Standing, S.; Biermann, S. The Implications of the Sharing Economy for Transport. Transp. Rev. 2019, 39, 226–242. [Google Scholar] [CrossRef]
- Ricci, M. Bike Sharing: A Review of Evidence on Impacts and Processes of Implementation and Operation. Res. Transp. Bus. Manag. 2015, 15, 28–38. [Google Scholar] [CrossRef]
- Lan, J.; Ma, Y.; Zhu, D.; Mangalagiu, D.; Thornton, T.F. Enabling Value Co-Creation in the Sharing Economy: The Case of Mobike. Sustainability 2017, 9, 1504. [Google Scholar] [CrossRef]
- Gong, Y.; Palmer, S.; Gallacher, J.; Marsden, T.; Fone, D. A Systematic Review of the Relationship between Objective Measurements of the Urban Environment and Psychological Distress. Environ. Int. 2016, 96, 48–57. [Google Scholar] [CrossRef]
- Hua, M.; Chen, X.; Chen, J.; Huang, D.; Cheng, L. Large-Scale Dockless Bike Sharing Repositioning Considering Future Usage and Workload Balance. Phys.-Stat. Mech. ITS Appl. 2022, 605, 127991. [Google Scholar] [CrossRef]
- Zhu, B.; Hu, S.; Kaparias, I.; Zhou, W.; Ochieng, W.; Lee, D.-H. Revealing the Driving Factors and Mobility Patterns of Bike-Sharing Commuting Demands for Integrated Public Transport Systems. Sustain. Cities Soc. 2024, 104, 105323. [Google Scholar] [CrossRef]
- Jin, H.; Liu, S.; So, K.C.; Wang, K. Dynamic Incentive Schemes for Managing Dockless Bike-Sharing Systems. Transp. Res. Part C Emerg. Technol. 2022, 136, 103527. [Google Scholar] [CrossRef]
- Guo, Y.; Yang, L.; Chen, Y. Bike Share Usage and the Built Environment: A Review. Front. Public Health 2022, 10, 848169. [Google Scholar] [CrossRef]
- Li, R.; Li, L.; Wang, Q. The Impact of Energy Efficiency on Carbon Emissions: Evidence from the Transportation Sector in Chinese 30 Provinces. Sustain. Cities Soc. 2022, 82, 103880. [Google Scholar] [CrossRef]
- Ding, C.; Cao, X.; Yu, B.; Ju, Y. Non-Linear Associations between Zonal Built Environment Attributes and Transit Commuting Mode Choice Accounting for Spatial Heterogeneity. Transp. Res. Part-Policy Pract. 2021, 148, 22–35. [Google Scholar] [CrossRef]
- Simmie, J.; Sennett, J.; Wood, P.; Hart, D. Innovation in Europe: A Tale of Networks, Knowledge and Trade in Five Cities. Taylor Fr. 2002, 36, 47–64. [Google Scholar] [CrossRef]
- Liu, D.; Dong, H.; Li, T.; Corcoran, J.; Ji, S. Vehicle Scheduling Approach and Its Practice to Optimise Public Bicycle Redistribution in Hangzhou. IET Intell. Transp. Syst. 2018, 12, 976–985. [Google Scholar] [CrossRef]
- Hao, M.; Cai, M.; Fang, M.; Jin, S. Hierarchical Vehicle Scheduling Research on Tide Bicycle-Sharing Traffic of Autonomous Transportation Systems. J. Adv. Transp. 2023, 2023, 5725009. [Google Scholar] [CrossRef]
- Bloom, J.Z. Tourist Market Segmentation with Linear and Non-Linear Techniques. Tour. Manag. 2004, 25, 723–733. [Google Scholar] [CrossRef]
- Yang, J.; Su, P.; Cao, J. On the Importance of Shenzhen Metro Transit to Land Development and Threshold Effect. Transp. Policy 2020, 99, 1–11. [Google Scholar] [CrossRef]
- Batty, M. Cities as Complex Systems: Scaling, Interaction, Networks, Dynamics and Urban Morphologies. In Encyclopedia of Complexity and Systems Science; Springer: New York, NY, USA, 2009; pp. 1041–1071. ISBN 978-0-387-30440-3. [Google Scholar]
- Chen, Y.; Yin, C.; Sun, B. Nonlinear Associations of Built Environments around Residences and Workplaces with Commuting Satisfaction. Transp. Res. Part-Transp. Environ. 2024, 133, 104315. [Google Scholar] [CrossRef]
- Cao, J.; Tao, T. Using Machine-Learning Models to Understand Nonlinear Relationships between Land Use and Travel. Transp. Res. Part-Transp. Environ. 2023, 123, 103930. [Google Scholar] [CrossRef]
- Zhang, Y.; Hu, X. The Nonlinear Impact of Cycling Environment on Bicycle Distance: A Perspective Combining Objective and Perceptual Dimensions. J. Transp. Land Use 2024, 17, 241–267. [Google Scholar] [CrossRef]
- Behroozi, A.; Edrisi, A. Predicting Travel Demand of a Bike Sharing System Using Graph Convolutional Neural Networks. Public Transp. 2025, 17, 281–317. [Google Scholar] [CrossRef]
- Gu, W.; Zhang, Z.; Liu, O. Social Factors Influencing Healthcare Expenditures: A Machine Learning Perspective on Australia’s Fiscal Challenges. Smart Cities 2025, 8, 97. [Google Scholar] [CrossRef]
- Meng, M.; Toan, T.D.; Wong, Y.D.; Lam, S.H. Short-Term Travel-Time Prediction Using Support Vector Machine and Nearest Neighbor Method. Transp. Res. Rec. 2022, 2676, 353–365. [Google Scholar] [CrossRef]
- Deepika; Pandove, G. Prediction of Traffic Time Using XGBoost Model with Hyperparameter Optimization. Multimed. Tools Appl. 2025, 1, 1–46. [Google Scholar] [CrossRef]
- Lundberg, S.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Red Hook, NY, USA, 4 December 2017; pp. 4768–4777. [Google Scholar]
- Wen, X.; Xie, Y.; Jiang, L.; Li, Y.; Ge, T. On the Interpretability of Machine Learning Methods in Crash Frequency Modeling and Crash Modification Factor Development. Accid. Anal. Prev. 2022, 168, 106617. [Google Scholar] [CrossRef]
- Wang, Y.; Li, J.; Su, D.; Zhou, H. Spatial-Temporal Heterogeneity and Built Environment Nonlinearity in Inconsiderate Parking of Dockless Bike-Sharing. Transp. Res. Part Policy Pract. 2023, 175, 103789. [Google Scholar] [CrossRef]
- Wang, J.; Cui, M.; Wang, H.; Yang, H.; Guo, X.; Liu, X.; Fu, X. Trip Purpose Inference and Spatio-Temporal Characterization Based on Anonymized Trip Data: Empirical Study from Dockless Shared Bicycle Dataset in Xi’an, China. Transp. Res. Rec. J. Transp. Res. Board 2024, 2678, 251–266. [Google Scholar] [CrossRef]
- Shi, Y.; Zhang, Z.; Yan, Z. A Scientometric Review of Research on Built Environment Influence on Public Transportation Demand. J. Traffic Transp. Eng. Engl. Ed. 2025, 12, 652–665. [Google Scholar] [CrossRef]
- Mattson, J. Relationships between Density, Transit, and Household Expenditures in Small Urban Areas. Transp. Res. Interdiscip. Perspect. 2020, 8, 100260. [Google Scholar] [CrossRef]
- Gao, C.; Li, S.; Sun, M.; Zhao, X.; Liu, D. Exploring the Relationship between Urban Vibrancy and Built Environment Using Multi-Source Data: Case Study in Munich. Remote Sens. 2024, 16, 1107. [Google Scholar] [CrossRef]
- Guo, L.; Cheng, W.; Liu, C.; Zhang, Q.; Yang, S. Exploring the Spatial Heterogeneity and Influence Factors of Daily Travel Carbon Emissions in Metropolitan Areas: From the Perspective of the 15-Min City. Land 2023, 12, 299. [Google Scholar] [CrossRef]
- Niu, S.; Hu, A.; Shen, Z.; Huang, Y.; Mou, Y. Measuring the Built Environment of Green Transit-Oriented Development: A Factor-Cluster Analysis of Rail Station Areas in Singapore. Front. Archit. Res. 2021, 10, 652–668. [Google Scholar] [CrossRef]
- Chen, H.; Dong, Y.; Li, H.; Tian, S.; Wu, L.; Li, J.; Lin, C. Optimized Green Infrastructure Planning at the City Scale Based on an Interpretable Machine Learning Model and Multi-Objective Optimization Algorithm: A Case Study of Central Beijing, China. Landsc. Urban Plan. 2024, 252, 105191. [Google Scholar] [CrossRef]
- Jalali, H.; Yeganeh Khaksar, R.; Mohammadzadeh, S.D.; Karballaeezadeh, N.; Gandomi, A.H. Prediction of Vertical Displacement for a Buried Pipeline Subjected to Normal Fault Using a Hybrid FEM-ANN Approach. Front. Struct. Civ. Eng. 2024, 18, 428–443. [Google Scholar] [CrossRef]
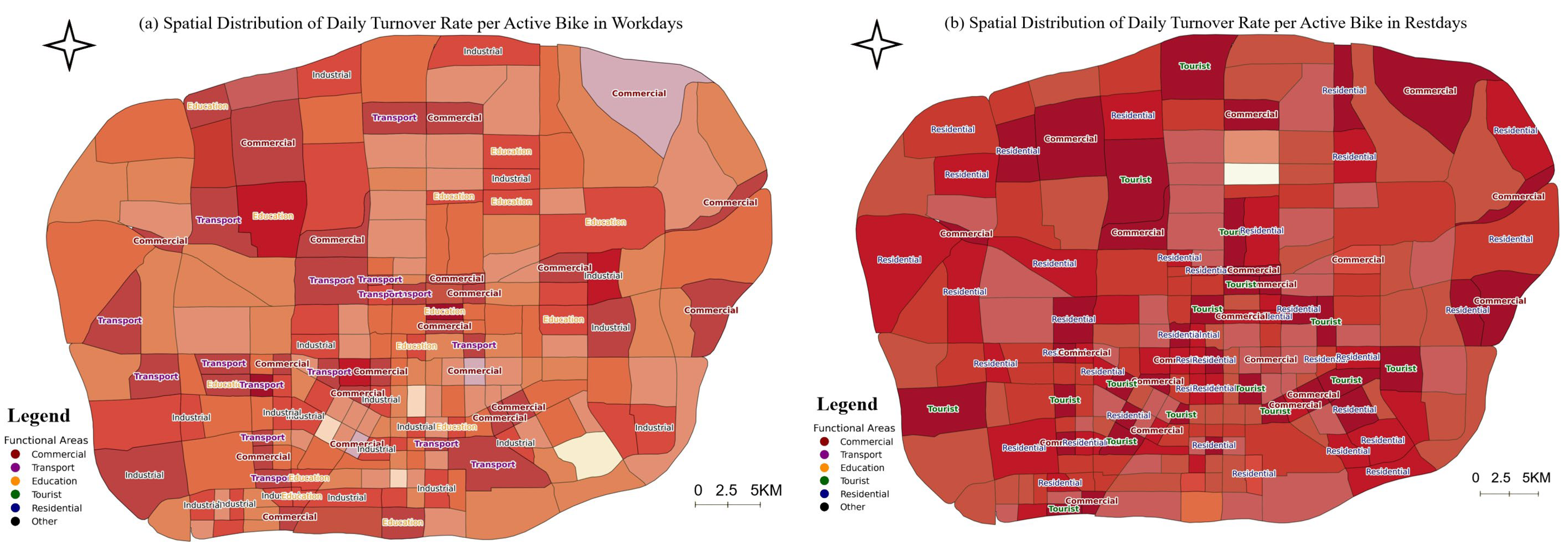
| Data Type | Key Attribute | Description | Unit/Format |
|---|---|---|---|
| Trip Detail Records (TDRs) | order_id | Anonymized unique identifier for each trip | Alphanumeric String |
| user_id | Anonymized unique identifier for each user | Alphanumeric String | |
| bike_id | Unique identifier for each bike | Alphanumeric String | |
| start_time | Timestamp of trip commencement | YYYY-MM-DD HH:MM:SS (UTC+8) | |
| end_time | Timestamp of trip conclusion | YYYY-MM-DD HH:MM:SS (UTC+8) | |
| start_lng | Longitude of the trip’s origin | Decimal Degrees (WGS84) | |
| start_lat | Latitude of the trip’s origin | Decimal Degrees (WGS84) | |
| end_lng | Longitude of the trip’s destination | Decimal Degrees (WGS84) | |
| end_lat | Latitude of the trip’s destination | Decimal Degrees (WGS84) | |
| distance_meter | Distance of trip as recorded by the system | Meters (Integer) | |
| duration_sec | Duration of the trip | Seconds (Integer) | |
| fee_yuan | Cost of the trip | Chinese Yuan (Decimal) | |
| Real-time Vehicle Status (RVS) Data | bike_id | Unique identifier for each bike | Alphanumeric String |
| timestamp | Timestamp of the RVS data point | YYYY-MM-DD HH:MM:SS (UTC+8) | |
| current_lng | Current longitude of the bike | Decimal Degrees (WGS84) | |
| current_lat | Current latitude of the bike | Decimal Degrees (WGS84) | |
| status | Code representing bike’s operational state | Integer (1: available, 2: in-use, etc.) |
| Category | Variables | Description | Potential Influence on Bike-Sharing EPMs | Data Source |
|---|---|---|---|---|
| POI Density | Commercial POI Density | Number of commercial establishments per km2 | Positive: Increases trip attractions/destinations, supports diverse needs. | OpenStreetMap (OSM), Baidu Maps API, Commercial vendors |
| Recreational POI Density | Number of parks, fitness centers, entertainment venues, etc., per km2 | Positive: Generates leisure-based trips, enhances area attractiveness. | OSM, Local Government GIS Departments | |
| Office/Employment POI Density | Number of office buildings and major employment sites per km2 | Positive: Drives commuter trips (first/last mile). | OSM, Business Databases, Planning Departments | |
| Land Use | Land Use Mix (Entropy Index) | Statistical measure of the diversity of land uses within a TAZ. | Positive: Facilitates shorter, multi-purpose trips; reduces reliance on cars. | Municipal Planning Dept. (Zoning Maps), Remote Sensing |
| Proportion of Residential Area | Percentage of TAZ area primarily classified or used for residential purposes. | Mixed: High origin potential (esp. AM peak), destination (PM peak). | Municipal Planning Dept. (Zoning Maps) | |
| Proportion of Commercial Area | Percentage of TAZ area primarily classified or used for commercial activities. | Positive: High destination potential, supports daytime/evening activity. | Municipal Planning Dept. (Zoning Maps) | |
| Demographics | Population Density | Number of inhabitants per km2. | Positive: Larger potential user base for bike-sharing services. | National Census Bureau, Local Statistical Yearbooks |
| Median Household Income (Proxy) | Estimated or aggregated median household income level within the TAZ. | Mixed: Higher income may mean more transport options, or higher willingness to pay. | Census Bureau | |
| Transport Infra. | Density of Metro Stations | Number of operational metro/subway stations per km2 or within a defined buffer. | Positive: Enhances first/last-mile connectivity to mass transit. | Public Transport Authority GIS Data, OSM |
| Bike Lane Density | Length of dedicated or protected bike lanes per km2 of TAZ area or road network length. | Positive: Improves cycling safety, comfort, and attractiveness. | Municipal Transportation Dept., OSM | |
| Road Intersection Density | Number of road intersections (3-way or more) per km2. | Positive: Generally, indicates better network permeability and accessibility. | OSM, Digital Road Network Databases |
| Technique | Formula | Output Range | Mean & Std Dev | Sensitivity to Outliers | Common Use Cases & Considerations |
|---|---|---|---|---|---|
| Min-Max Scaling | [0, 1] | Variable | High | Algorithms requiring feature inputs within a bounded range (e.g., some neural networks); image processing. | |
| Z-score Standardization | Unbounded | Mean = 0 StdDev = 1 | Moderate | Widely used for algorithms assuming normally distributed data or sensitive to feature scales (e.g., PCA, SVM, linear regression, gradient-based optimization in XGBoost). | |
| Robust Scaler | Unbounded | Variable | Low | Suitable for datasets containing significant outliers, as it uses percentiles (median and interquartile range) and is thus more robust to extreme values. | |
| Log Transformation | Variable | Variable | Reduces effect of outliers | Applied to positively skewed data to stabilize variance, reduce heteroscedasticity, and approximate a normal distribution; useful when relationships are multiplicative. |
| Variables | Count | Mean | Std | Min | 0.25 | 0.5 | 0.75 | Max | VIF |
|---|---|---|---|---|---|---|---|---|---|
| Bike Supply Density | 202 | 24.199 | 13.749 | 6.241 | 14.118 | 21.303 | 29.887 | 88.473 | 1.837 |
| Commercial POI Density | 202 | 25.595 | 17.171 | 3.244 | 12.237 | 21.889 | 33.95 | 96.016 | 2.154 |
| Residential Density | 202 | 33.709 | 13.012 | 12.317 | 24.288 | 31.259 | 41.107 | 75.156 | 1.676 |
| Proximity to Public Transit | 202 | 512.349 | 274.688 | 52.159 | 290.384 | 473.1 | 760.371 | 994.413 | 1.322 |
| Road Network Density | 202 | 5.292 | 2.652 | 1.029 | 3.203 | 5.085 | 7.475 | 9.984 | 1.984 |
| Average Income | 202 | 11,175.343 | 5034.454 | 3150.421 | 7771.434 | 10,059.569 | 13,444.793 | 33,172.167 | 2.453 |
| Hyperparameter | Value |
|---|---|
| n_estimators (Number of trees) | 250 |
| learning_rate (Learning rate) | 0.05 |
| max_depth (Max tree depth) | 6 |
| subsample (Subsample ratio) | 0.8 |
| colsample_bytree (Feature ratio) | 0.7 |
| gamma (Min split loss) | 0.1 |
| reg_alpha (L1 regularization) | 0.01 |
| reg_lambda (L2 regularization) | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, H.; Feng, C.; Gao, C. Economic Optimization of Bike-Sharing Systems via Nonlinear Threshold Effects: An Interpretable Machine Learning Approach in Xi’an, China. ISPRS Int. J. Geo-Inf. 2025, 14, 333. https://doi.org/10.3390/ijgi14090333
Yang H, Feng C, Gao C. Economic Optimization of Bike-Sharing Systems via Nonlinear Threshold Effects: An Interpretable Machine Learning Approach in Xi’an, China. ISPRS International Journal of Geo-Information. 2025; 14(9):333. https://doi.org/10.3390/ijgi14090333
Chicago/Turabian StyleYang, Haolong, Chen Feng, and Chao Gao. 2025. "Economic Optimization of Bike-Sharing Systems via Nonlinear Threshold Effects: An Interpretable Machine Learning Approach in Xi’an, China" ISPRS International Journal of Geo-Information 14, no. 9: 333. https://doi.org/10.3390/ijgi14090333
APA StyleYang, H., Feng, C., & Gao, C. (2025). Economic Optimization of Bike-Sharing Systems via Nonlinear Threshold Effects: An Interpretable Machine Learning Approach in Xi’an, China. ISPRS International Journal of Geo-Information, 14(9), 333. https://doi.org/10.3390/ijgi14090333









