1. Introduction
To reduce environmental pollution, it is necessary to use photovoltaic solar systems to produce electrical energy. However, estimating global solar radiation is beneficial not only for the photovoltaic industry. A number of environmental, agronomy, or forestry applications use information on solar energy distribution. Solar radiation affects microclimatic conditions, vegetation cover, and soil moisture. Terrain characteristics change the fraction of incoming solar radiation reflected from the land surface to remote sensing sensors. The use of solar geometry principles makes it possible to model the movement of heliotropic plants or increase the independence of monitoring devices. Solar radiation is an important phenomenon in architecture, affecting building heating and cooling as sunlight passes through exterior glazing. The aspect of the walls, together with the roof slope in the case of roof windows, determines the amount of natural light reaching the interior.
Direct radiation travelling in a straight line from the Sun to the Earth is a major component of global solar radiation. According to Meteonorm data processed by Gomes, Cabral, and Karlsson in [
1], the proportion of direct radiation in annual global radiation ranges from 43% in rainy equatorial regions to 77% in deserts. The share of direct radiation in the global radiation of a clear sky when the Sun is overhead may be slightly higher than 90%. Diffuse radiation accounts for the rest. Direct radiation is also called beam radiation.
The direct component of solar radiation’s distribution on the Earth’s surface depends on extraterrestrial radiation, the atmosphere’s geometric and physical conditions, and the angle of incidence or more concise and technical the incidence angle, which is also called the illumination angle. A direct irradiation incident on a horizontal or inclined surface on an Earth without an atmosphere is strictly defined according to the cosine of the changeable solar angle of incidence and a value of more stable magnitude of extraterrestrial radiation. The size of the incidence angle depends on the following five variables:
ω—solar hour angle;
δ—solar declination angle;
φ—geographical latitude;
S—slope angle of the impact surface;
A—aspect angle of the impact surface, often referred to as the azimuth angle of the impact surface.
Branches of mathematics, such as vector algebra and trigonometry, make it possible to express an incidence angle at the horizontal or inclined surface. It would appear that this does not require much discussion. However, the resulting function can be in the form of a composite function or contain both the sine and cosine of the time argument. This causes complications in defining derived temporal characteristics. A solution to this problem is applying a geographical approach utilizing an equivalent surface. An equivalent surface is a local horizon plane with the same angular relationship with the Sun as the observed inclined surface. For a horizontal plane, the fundamental equations of solar geometry are valid (Equations (4)–(7)). Therefore, applying the geographical approach makes it possible to understand the calculated values. The equation for the incidence angle is simple, and the derived sunrise and sunset solar hour angles are clearly interpretable. If we do not incorporate the shading provided by surrounding terrain shapes, the horizontal surface insolation is predictable based on experience. It is more complex in the case of an inclined surface. Determining the latitude of a location impacted by sunlight in the same way (effective latitude, i.e., the latitude of the equivalent surface) allows us to utilize experience for the inclined surface as well.
The main objective of this article is not to compare individual general equations of the incidence angle but to point out the advantages of the geographical approach, which allows us to derive equations for many temporal characteristics. The characteristics are calculated directly and approximate calculations are not necessary. It is possible to create a very simple solar radiation model.
2. Methods and Models
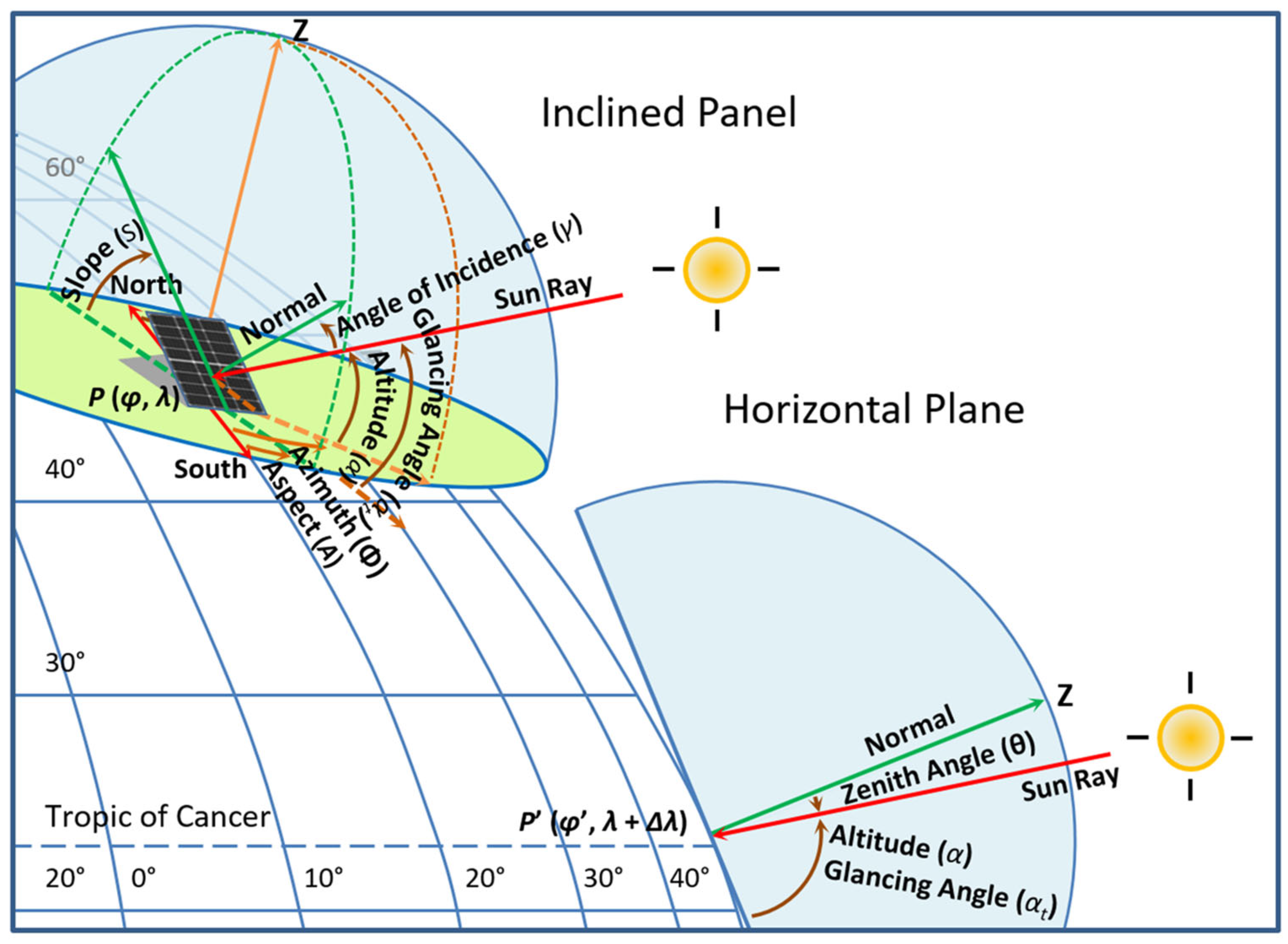
The solar radiation incidence angle (
γ) is measured between a plane orthogonal to the Sun’s rays and a tangential plane to the land surface (depicted in
Figure 1 as the angle between their normal vectors).
Expression of the angle
γ cosine in the following form is based on the application of the law of cosines to a spherical triangle:
θ is the solar zenith angle and
Φ is the solar azimuth angle. Equation (1) represents a composite function. The solar hour angle (
ω) is hidden in the formulas for the solar azimuth (
Φ) and solar zenith angle (
θ). That is why it is difficult to derive the formulas of some characteristics of solar time (sunrise and sunset time for an inclined surface, sunshine duration under clear sky, time of highest direct irradiance).
The dot product of a unit normal vector perpendicular to the impact surface and a unit sun vector that points to the centre of the Sun from the impact point defines the cosine of the angle
γ in the second explicit form:
Even this second form is not without problems. If
γ is equal to 90° (left side of Equation (2) is equal to zero),
S is non-zero, and
δ is the average daily declination, then we can rewrite
ω in Equation (2) as (
ωr,s)
t. Hour angles (
ωr)
t and (
ωs)
t determine the times when the inclined surface with which we replace the rotating Earth will be illuminated. (
ωr)
t is called the sunrise hour angle for an inclined surface and angle (
ωs)
t is called the sunset hour angle for an inclined surface [
2]. To solve the modified Equation (2), we must use a suitable trigonometric substitution. The result is a quadratic equation. The quadratic formula for solving a quadratic equation has two roots. Due to this ambiguity, it is necessary to test the results.
In addition, the land surface can be exposed to the Sun only after it rises above the horizon and can be shaded before the Sun sets below the horizon. The sunrise and sunset times are determined by the sunrise ((ωr)h) and sunset ((ωs)h) hour angles. Therefore, we need to decide which of the hour angles, (ωr)h or (ωr)t, is the hour angle (ωr) of the true onset of illumination by direct sunlight and which of the hour angles, (ωs)h or (ωs)t, is the hour angle (ωs) of the end of illumination. The hour angles ωr and ωs determine the potential sunshine duration. Let us keep in mind that if we use the integral to calculate the daily direct irradiation under clear sky conditions, ωr and ωs determine the interval of integration.
By convention, the hour angle is measured from noon, with the geographical aspect (compass) and solar azimuth from the north. This is counterproductive for the zone north of the Tropic of Cancer. In this case, it may be more appropriate to measure the aspect (
A) and solar azimuth (
Φ) from the south. Adapting the reference direction to measure these angles is not uncommon. Byram and Jenison [
3] achieved this as early as 1943, resulting in modification of Equation (1). Widen and Munkhammar [
4] and Iqbal [
2] measured the aspect and azimuth from the south and the hour angle from noon, clockwise in [
4] and counterclockwise in [
2]. In this study, the latter option was used.
In physic, the term of glancing incidence angle (
αt) is defined as the angle between the sunbeam incident on a surface and its projection on the tangent plane to the surface at the point of incidence. The incidence angle (
γ) and glancing angle (
αt) are complementary angles (
Figure 1). The following equation is valid:
The greater the complementary angle (αt), the more solar energy the active surface will absorb.
2.1. Daytime Duration
When the surface is horizontal
S = 0°, Equations (1) and (2) become
α is the solar elevation or solar altitude. The algorithm is less accurate and provides the height of the Sun with an accuracy of about 1.3° [
5].
In the local sunrise or sunset time, solar altitude is zero and Equation (4) transforms to the sunrise or sunset equation:
δ is the average daily declination or declination at noon. The function value in Equation (5) determines the cosine of angle (
ωr)
h, which is the sunrise hour angle or cosine of angle (
ωs)
h, which is the sunset hour angle. (
ωr,s)
h is within the range of 0° to 180°. Given the symmetry of the sunrise and sunset solar times, it follows that the sunrise hour angle value ((
ωr)
h) is opposite to the sunset hour angle value ((
ωs)
h). If the hour angle is measured counterclockwise, the Equation (5) defines cosine of angle (
ωr)
h and the sunrise ((
tr)
h) or sunset ((
ts)
h) solar time is given by following equations:
Otherwise, Equation (5) defines the cosine of angle (
ωs)
h, and the solar time (
tr)
h or (
ts)
h is given by following equations:
If hour angles (
ωr)
h and (
ωs)
h in Equations (6) and (7) are measured in radians, it is necessary to replace the value of 15 in denominators with π/12. Daytime duration at a given location is equal to the difference between (
ts)
h and (
tr)
h. The calculated daytime is accurate enough for geosciences applications, even though local sunrise and sunset do not occur exactly when the solar altitude is 0° due to atmospheric diffraction and the Earth’s curvature. If we accept the convention that sunrise occurs when the solar disc’s upper limb is just touching the ideal horizon of the observer, Equation (5) needs to be corrected. See, for example, [
6].
2.2. Equivalent Surface
The problem of ambiguity in determining the sunrise and sunset times for an inclined surface can be solved using the geographical coordinates of an equivalent surface. Slope (
S) and aspect (
A) at observation point P (
φ,
λ), where
φ is the latitude and
λ is the longitude, define an unknown geographical position of a tangent plane to the spherical Earth (equivalent surface) which is parallel to the reference inclined surface. The Sun’s path is then the same with respect to both surfaces. Geographical coordinates at the point of tangency P′ (
φ′,
λ + Δ
λ), are defined by effective latitude
φ′ and the sum of longitude
λ of the observation point and longitude shift Δ
λ. Effective latitude (
φ′) is determined by the following equation:
The following equation can be used when calculating the longitude shift:
Equations (8) and (9) are analogous to equations for transforming spherical coordinates on the unit sphere between two coordinate systems. The target coordinate system’s polar axis lies in the celestial axis. The source spherical coordinate system’s polar axis points to the zenith at observation point P (
φ,
λ), and the angular dimensions of the slope and aspect at the observation point determine the dimensions of the polar and azimuthal angle of the unknown point of tangency P′ (
φ′,
λ + Δ
λ). A more detailed explanation is found in
Appendix A. In this study, the aspect angle is measured counterclockwise from south and 0 ≤
A ≤ 2π or −π ≤
A ≤ π (
Figure 1). The range of values of the arctangent function is −π/2 ≤
y ≤ π/2. Only function atan2 return values in the desired range −π ≤ Δ
λ ≤ π.
Projecting interior lights in architecture often involves simulating sunlight penetration through the predominantly used vertical windows. The slope of a vertical wall or window is equal to 90°, and effective latitude (
φ′
wall) and longitude shift (Δ
λwall) can be defined as follows:
Including these variables in the following equations allows us to calculate the illumination of a vertical window even if the window is illuminated twice a day.
The complementary angle (
αt) to the incidence angle (
γ) at the point P (
φ,
λ) on the inclined surface is equal to the solar altitude angle (
α) at the point P′ (
φ′,
λ + Δ
λ). If, in Equation (4), we replace latitude (
φ) with effective latitude (
φ′) and subtract the longitude shift value (Δ
λ) from the hour angle value (
ω), we get the following equation:
where
ω is the hour angle, −π ≤
ω ≤ π, being zero at noon and negative in the afternoon. Because Equation (3) is valid, Equation (12) is the third form of the incidence angle equation. Using the third form makes it possible to avoid defining the temporal characteristics.
At the sunrise or sunset time for an inclined surface, Equation (12) is transformed into the following equation:
where (
ωr)
t is the sunrise hour angle for an inclined surface and (
ωr)
h′ is the local sunrise hour angle at the effective latitude (
φ′). If we replace the variable
φ with the variable
φ′ in Equation (5), the angle (
ωr)
h will be equal to the angle (
ωr)
h′. At sunset, the following equation is valid for an inclined surface:
The sunrise ((
tr)
t) and sunset ((
ts)
t) solar times for an inclined observed surface are given by the following equations:
2.3. Clear Sky Direct Solar Radiation Model
To calculate the total daily direct irradiance per unit area at the Earth without an atmosphere the following equation can be used:
where
E0 is the extra-terrestrial irradiance. If we consider the shield effect of the atmosphere, we need to adjust Equation (17). Cloud cover often varies, and it is therefore difficult to incorporate it into solar radiation models. A cloudless atmosphere is the nominal operating condition of a solar plant [
7]. The direct radiation model during clear sky cover may not be very complicated. This property is also present in the following equation:
The extra-terrestrial irradiance value (
E0) varies from 0% to ±3.35% as the Earth orbits the Sun (solar constant
I0 = 1.367 kW m
−2). The optical air mass value (
m) during the day ranges from 1 to 35.71; if
m = 1, then
α = 0° and if
m = 35.71, then
α = 90° [
8,
9]. The attenuation (extinction) coefficient (
Ar) is calculated according to Heindl and Koch [
10] as follows:
The Linke turbidity factor (
TL) was determined for rural areas of Slovakia located at low altitudes (100–200 m a. s. l.) by approximation from the average monthly values from [
11]. If the Sun’s rays are perpendicular to the surface at any time, then Equation (18) transforms into
where
DNI is the potential direct normal irradiation.
Equation (18) is very simple and highly idealized, but the author assumes that the accuracy of the results is sufficient for several generalizing statements.
3. Results
The interpretability of Equation (12) or Equation (13) is based on the use of geographical coordinates (
φ′,
λ + Δ
λ). To support this statement, we provide the following example: Solar azimuth (
Φ) in latitudes between the Tropic of Cancer and Arctic Circle can be northeast during the sunrise and northwest during the sunset. As a result, the Sun shines on the north-facing surface twice a day in the summer. Jenčo and Matečný in [
12] presented a simple interpretation. During the northern solstice day, points on the inclined surface with a slope angle greater than 64.43° located at 49th north parallel will be exposed to the Sun twice a day if the aspect angle (
A) ranges from 142.7° to 217.3°. In these cases, the geographical coordinates (
φ′,
λ + Δ
λ) determine points on the spherical Earth with the same sun movement but on the other side of the hemisphere. If (
tr)
t < (
ts)
h, (
ts)
t > (
tr)
h, and (
ts)
t < (
tr)
t at observation point P (
φ,
λ), then (
ts)
t determines the time of the first sunset, and the true sunrise is equal to (
tr)
h. The Sun’s path at tangential point P′ (
φ′,
λ + Δ
λ) of an equivalent surface between (
tr)
h and (
ts)
t time is in its afternoon decreasing phase until sunset. The time of the second sunrise is determined by (
tr)
t, and the true sunset is equal to (
ts)
h. The Sun’s path between (
tr)
t and (
ts)
h time is in its morning increasing phase after sunrise above the local horizon at the point P′ (
φ′,
λ + Δ
λ). The hour angle of the maximal glancing incidence angle to the north window is closet to either the hour angle of the first sunrise or the hour angle of the second sunset. The maximum daily incidence angle is obtained using Equation (12).
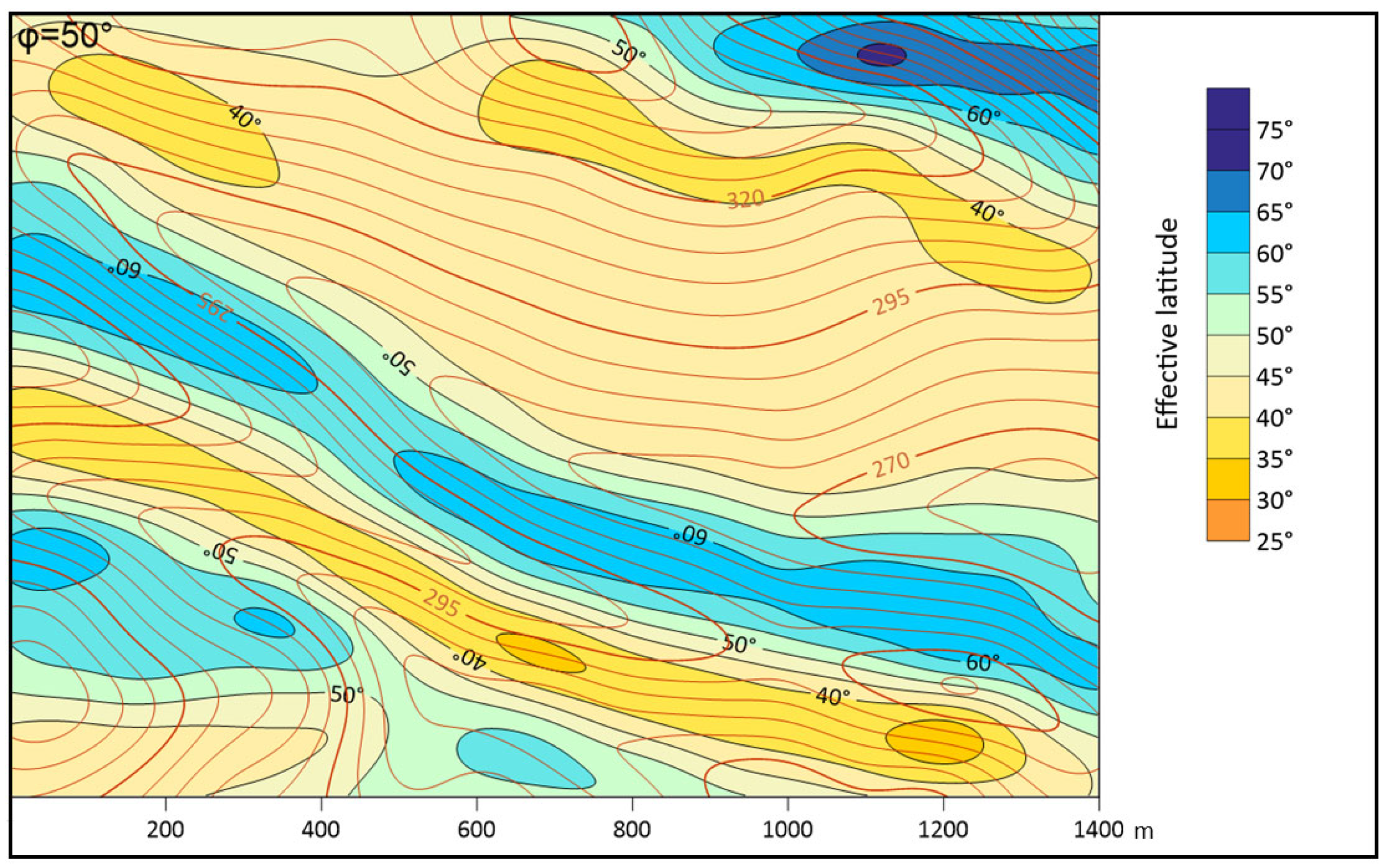
Information about the effective latitude can be very valuable in understanding habitat microclimatic conditions. The effective latitude (
Figure 2) provides basic information about the requirements of individual biocenosis for solar energy or, conversely, determines the potential biocenosis for a given site. The temperature differences between the southern and northern slopes are widely known. The corresponding effective latitudes indicate geographical zones with similar radiation conditions. Conditions can differ depending on cloud cover or due to longitude shift. Longitude shift can shorten sunshine duration on the southern and northern slopes, but only in the early morning or late evening during the phase where decreasing solar radiation influences microclimatic conditions minimally. This difference can be calculated by comparing true sunrise and sunset times for an inclined investigated location and sunrise and sunset times at the equivalent surface.
3.1. Extremes of Incidence Angle
If the magnitude of longitude shift (Δ
λ) ranges between
ωs and
ωr, then longitude shift is equal to the hour angle of the maximal complementary angle (
αt) to incidence angle (
γ) (
Figure 3). At the time of the maximum this angle, which is equal to half the sum of the sunrise time ((
tr)
t) and sunset time ((
ts)
t) for an inclined surface, Equation (12) transforms into the following form:
The maximal complementary angle (
αt) (
Figure 4) at a given day is equal to the maximal elevation angle at effective latitude (elevation of the Sun at solar noon). The temporal distribution of the maximal complementary angle (
αt) may have an impact on the temporal distribution of daily maximal surface temperature on the observed terrain.
3.2. Sun-Tracking Procedure
The properties of the equivalent surface make it possible to define an effective procedure for any natural or technical solar tracking system. Solar panels from the stationary solar energy conversion systems located at northern latitudes above the Tropic of Cancer are most often oriented to the south. Following Liu and Jordan [
13], a surface located at latitude (
φ) and tilted toward the equator at an angle
S is parallel to a horizontal surface at latitude
φ—
S. Angle
S is slope (
S) from this study, and the difference between latitude (
φ) and slope angle (
S) determines the value of effective latitude (
φ′). The tilt of a south-facing solar panel perpendicular to the Sun’s rays is equal to the difference between the latitude of a subsolar point at which the Sun is perceived to be directly overhead (
α = 90°) and latitude (
φ). Then the effective latitude (
φ′) is equal to solar declination (
δ) for noon. If
φ′ =
δ, Equation (21) is transformed into the following equation:
The surface perpendicular to the Sun’s rays must face the east side in the morning and the west side in the afternoon. Slope (
S⊥) of the surface, which at a given moment of the day will be perpendicular to the Sun’s rays, can be calculated after modifying Equation (12). If we modify Equation (8) to have a zero right-hand side and replace the variable
φ′ with
δ and
S with
S⊥, we get the following equation:
whereby
If we use the following substitution:
we get a quadratic equation. The quadratic formula is
whereby
is a formula that provides the solution to this equation. Equation (25) has two roots, namely cos
S1 and cos
S2. One of the roots determines the slope (
S⊥) of the surface perpendicular to the Sun. Hour angle
ω⊥ determines the time when the surface or solar panel with the set aspect (
A) will be perpendicular to the Sun’s rays. For north latitudes above the Tropic of Cancer, the following equation is valid:
Equation (26) is analogous to Equation (9).
Solar azimuth (
Φr) for the local sunrise time is measured similarly to aspect (
A) counterclockwise from south, and it is determined by the relation
Solar azimuth (Φr) for the local sunrise hour angle and solar azimuth (Φs) for the local sunset hour angle are the explementary angles that sum to 360°. Azimuth (Φr) and azimuth (Φs) determine the range of the aspect angles for a solar panel or any system perpendicular to the Sun’s rays on a given day.
Using the formulas above, each user can calculate the settings for a solar panel. If managing solar energy utilization is performed using simple tools, it can contribute to empowering local communities and increasing their ownership of climate change mitigation strategies. A key component of this effort is developing a simple photovoltaic generation model that users or small producers can easily adapt to local circumstances [
14].
3.3. Differences in Distribution of Beam Irradiation Between Surfaces with Different Slope and Geographical Position
During the peak of summer in the northern temperate zone, south-facing surfaces are not always subsidized by a larger quantity of direct irradiation than horizontal or slightly inclined surfaces. This is a consequence of daytime duration. Slope and southern aspect reduce the value of effective latitude (φ′). Incidence angles are smaller, but the range between hour angle (ωs)t and hour angle (ωr)t is less than the range between hour angle (ωs)h and hour angle (ωr)h. The horizontal surface is exposed to the Sun for longer time.
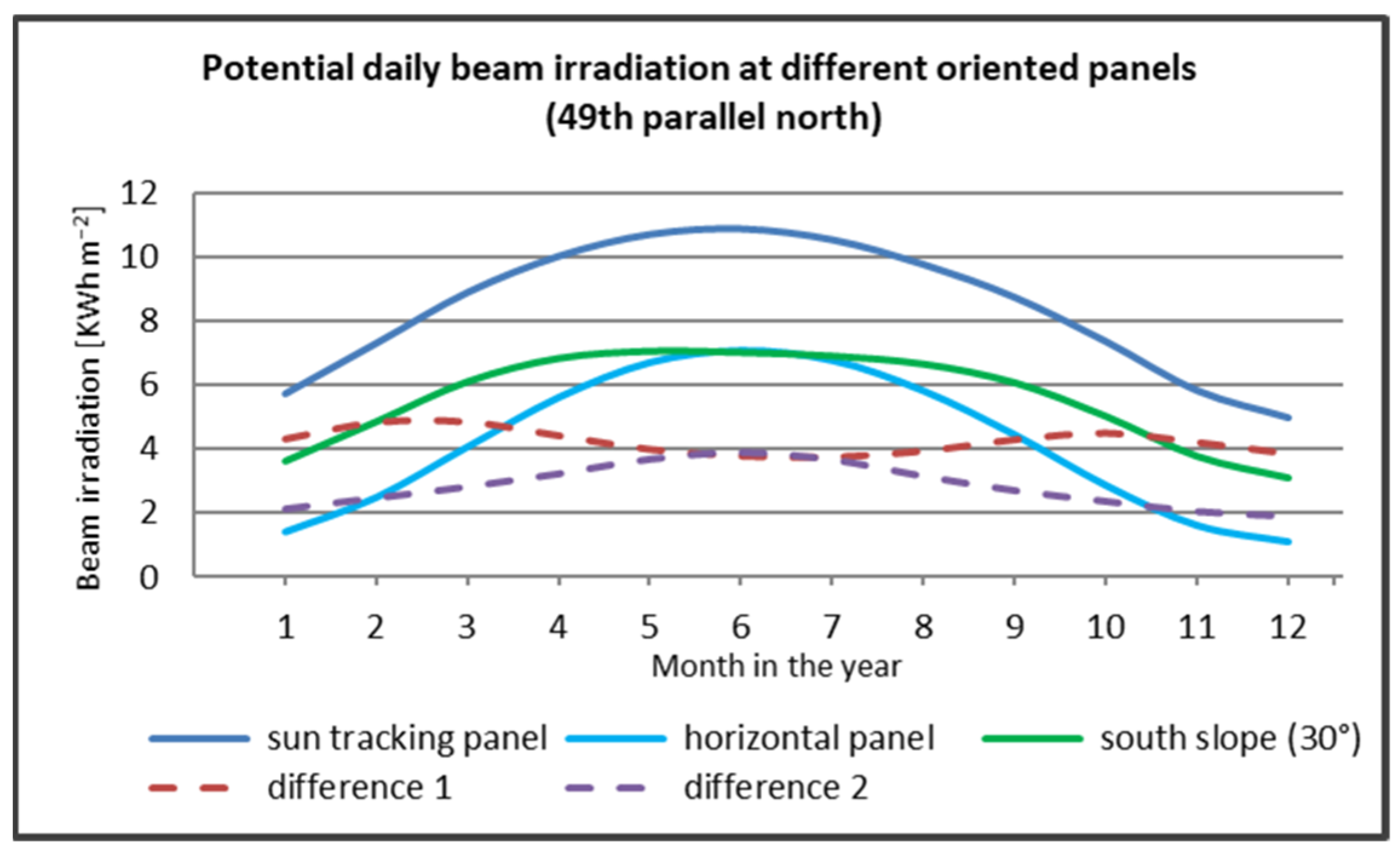
The dual-axis tracker from
Figure 5 compared to a horizontal installation has the potential to increase in power at the end of the year by three and a half times. The efficiency of a south-facing installation compared to a horizontal installation is higher, but in summer, its efficiency falls to the level of a horizontal installation. Of course, the true distribution of beam radiation in a particular location will depend on cloudiness.
The calculated differences in the amount of daily direct irradiation, always perpendicular to a rotating solar panel located at 49° north latitude and a fixed horizontal solar panel located next to it under a clear sky, range from 3.8 to 4.8 kWh m
−2 (
Figure 6). This is probably why young sunflowers follow the path of the Sun in the sky. Their flowers are approximately perpendicular to the Sun’s rays during the day. Sunflowers change their surface morphometric properties. The result is rapid temporal changes in the digital surface model and thus a change in the proportion of incoming solar radiation reflected from the land surface in the reflectance models.
Effective latitudes for different slopes indicate that the amount of beam solar radiation also changes with changes in geographic location. A sun-tracking solar panel located near the Arctic Circle under a cloudless sky receives more beam radiation during the peak of the warm season than a solar panel located near the equator. The reason for this is daytime duration. Therefore, in the warm half of the year, it is possible to find locations for solar photovoltaic installations with higher efficiency in non-equatorial zones. Even areas at high latitudes and subpolar zones have great potential for developing photovoltaic solutions.
Flattening of the Earth is not incorporated into Equation (18) and thus not Equation (20). Calculations were therefore only carried up to a latitude of 64°. Here, the values in the graph in
Figure 7 may already be distorted. The Linke turbidity factor (
LT) also changes significantly with the change in geographical position [
15]. This affects the comparability of the results calculated for individual geographical locations with different Linke turbidity factors. For this reason, a constant value of
LT = 3 was used for calculating the graphs in
Figure 7. These facts, together with the required cloudless sky conditions, are the main limitations. However, these limitations do not affect the main objective of this article, which is to highlight the advantages of the geographical approach when deriving the incidence angle and temporal solar characteristics.
4. Discussion
The solar hour angle (
ω) is hidden in the formulas for solar azimuth (
Φ) and solar zenith angle (
θ) in Equation (1). This is why it is difficult to derive the formulas of temporal solar characteristics. We can partially eliminate this problem by using Equation (2). If the left side of Equation (2) is equal to zero, then we get a quadratic equation to determine the sunrise hour angle for an inclined surface. The result will be, for example, Equation (33) from Krcho [
16] or Equations (1.6.13)–(1.6.15) from Iqbal [
2]. Alternatively, it could also be equations from the given explanatory notes for Equation (7) from Baba and Kanayama [
17] or Equation (13) from Allen et al. [
18]. These equations offer us twice solutions. It is necessary to decide which solution is right. If we continue to simplify the quadratic equation, we get separate equations for the east-facing surface and the west-facing surface (Equations (1.6.16)–(19) from Iqbal [
2]).
The ambiguity of the sunrise and sunset equations is the reason why most GIS-integrated solar radiation modules do not provide an exact calculated sunrise and sunset hour angle (
ωr and
ωs). A simple iteration is used. If the incidence angle is greater than zero, then the Sun does not set [
19,
20]. The accuracy depends on the unit of daily time integration. Increasing accuracy is always at the expense of calculation time.
An elegant solution involves calculating these temporal characteristics at effective latitude. The concept of an equivalent surface has appeared in older publications [
21,
22,
23,
24]. Formulas for the geographical coordinates of the tangent point P′ for an equivalent surface are not well known, as they are not often found in texts and papers published after 1965 [
24]. The formulas independently developed by Jenčo ([
8], in Slovak) are one of the exceptions. Equations (8) and (9) to determine effective latitude and longitude shift, as mentioned above, are the modified Equations (5) and (6) from this paper. These equations were used to calculate the incidence angle of solar irradiance and create an irradiation model r-sun using the free geographical information system GRASS GIS [
25]. Additionally, the equations were also used in a model for generating solar radiation maps with the use of triangle meshes [
26].
Dual-axis trackers that change the azimuth (aspect angle—
A) and slope (
S) of solar panels are more expensive than single-axis trackers. Single-axis trackers are more expensive than fixed mounts. If we use cheaper single-axis trackers that only change the solar panels’ azimuth or tilt, we cannot fully utilize the potential of the panels. Nevertheless, most solar photovoltaic system installations use fixed mounts if the maximum cost effectiveness is to be achieved. Although the horizontal solar panel efficiency is increased by diffuse radiation, the amount of global solar radiation is always higher in the case of optimally inclined solar panels [
27,
28] and even greater in the case of solar panels with adjustable tilt and horizontal angle mechanisms [
29,
30,
31,
32,
33].
Standard sun-tracking system software includes sun path diagrams or algorithms for solar altitude and solar azimuth calculations [
34]. The solar altitude and azimuth are calculated for a given time, and the panel position is changed in time steps. Two servo motors are necessary to change the solar panel’s position. For a regular change in the horizontal angle (aspect), it is necessary to determine it from the solar diagram or directly calculate the solar hour angle, in which the solar azimuth has a desired value. Equations (20)–(23) in [
8] make it possible to directly determine the time and inclination of a solar panel with a default aspect, but the solution presented here is both simple to execute and very effective for solar trackers. The constant rotation angle compared to the constant time step is advantageous in the morning and evening when the solar panel’s efficiency is less (more air mass) and the solar azimuth changes more slowly. In the case of using a discrete step which involves changing the solar panel’s horizontal setting, a simple stepper motor can be used for this action. This should be reflected in the reduction in the price of dual-axis solar trackers.
5. Conclusions
Determining the solar altitude angle at the geographical coordinates of an equivalent horizontal surface is an alternative to using equations for the incidence angle (Equations (1) and (2)). An indisputable advantage of algorithms based on this almost forgotten idea is the intelligibility of the results. The alternative offered is particularly advantageous in deriving and calculating temporal characteristics. The sunrise and sunset times for horizontal and inclined surfaces, the sunshine duration, the time of extreme angles of incidence, and their magnitude are meteorological and climatological characteristics that can be used in architecture, ecology, agriculture and forestry, and in many other fields of human activity. Calculating solar characteristics using effective latitude is simple and easily manageable. This opens opportunities for a broader community of professionals, users, and enthusiasts to create their own solar model with desired functionality, freeing themselves from the dependency on predefined characteristics offered by free available solar models.
Direct radiation is the most significant component of global radiation under clear sky conditions. Its importance increases in sun-tracking solar panels. The properties of the equivalent surface have made it possible to formulate equations for a new sun-tracking procedure. The algorithm determines the time and inclination for the sun-tracking solar panel with the default aspect. The orientation of the sun-tracking solar panel can then be set with respect to the regular change in rotation angle.
The modelled results contradict a still persistent myth in the photovoltaic commercial field, namely that the difference between the amount of beam irradiation received by fixed solar panels and sun-tracking solar panels is so small that, from an economic point of view, it is more beneficial to increase the active surface of fixed solar panels. Even a minimal percentage difference can reach double-digit values. Moreover, in the summer months, there is an increase in the efficiency of sun-tracking photovoltaic systems with an increase in latitude. The difference is so significant that it could lead to considering latitudinally migrating solar panels. This idea is also supported by climate change, which is accompanied by an increase in the number of summer cloudless days in some regions.