A Pyramid Convolution-Based Scene Coordinate Regression Network for AR-GIS
Abstract
1. Introduction
- (1)
- We introduce a novel pyramid convolution-driven scene coordinate regression network (PSN), engineered to bolster the resilience and versatility of camera tracking within the complexities of dynamic environments.
- (2)
- We present an advanced randomization method designed to disrupt the correlation between pixel blocks during training. This design is crafted to minimize gradient correlation, thereby effectively amplifying the efficiency of the model training process.
- (3)
- We conducted comprehensive experiments on multiple public and real-world datasets, which demonstrate that PSN achieves centimeter-level accuracy in small-scale scenes and decimeter-level accuracy in large-scale scenes within minutes of training. We also integrated PSN into real-time scenes to support AR-GIS visualization.
2. Related Work
2.1. AR Visualization
2.2. Camera Tracking
3. Methodology
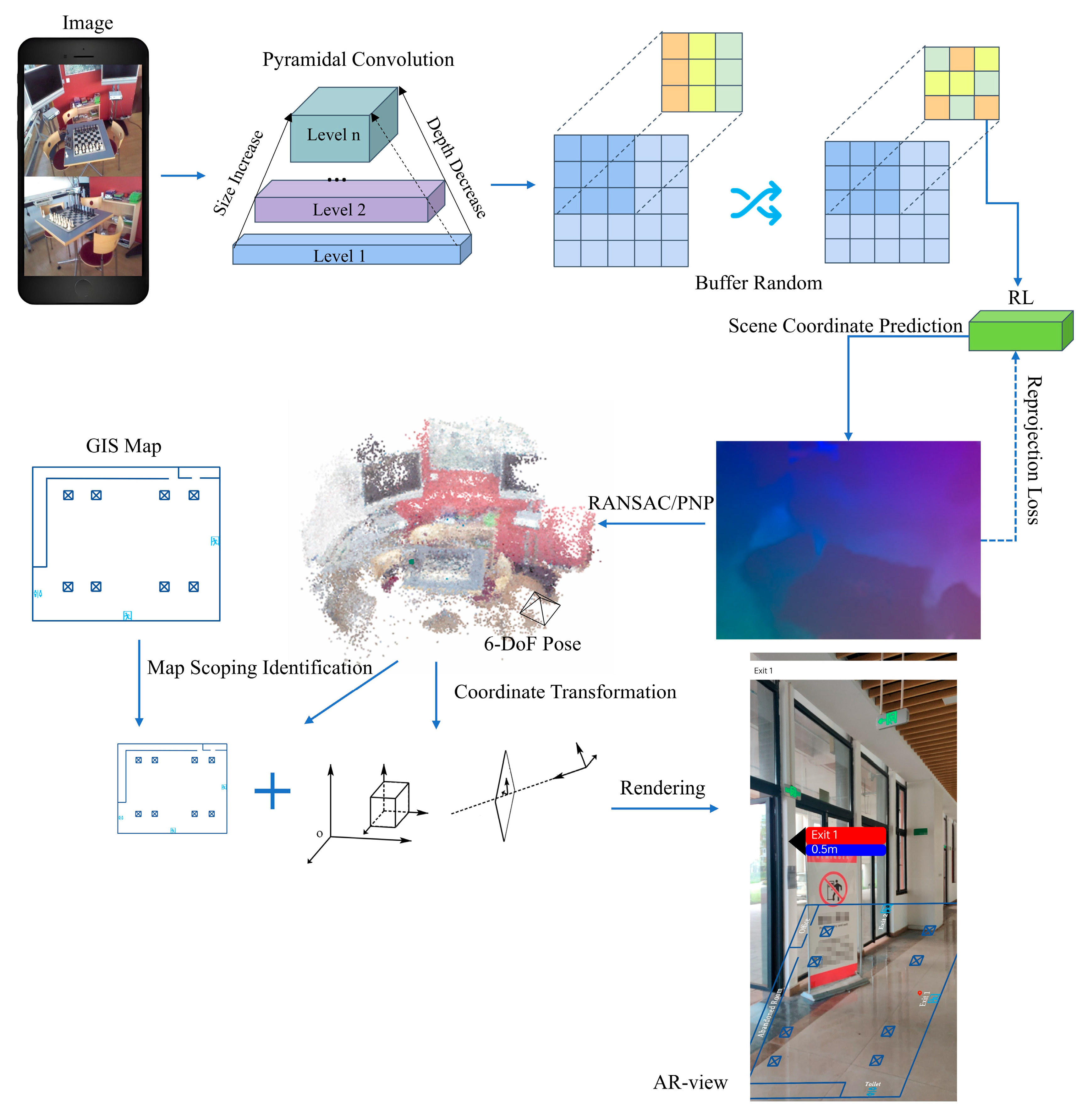
3.1. Overview
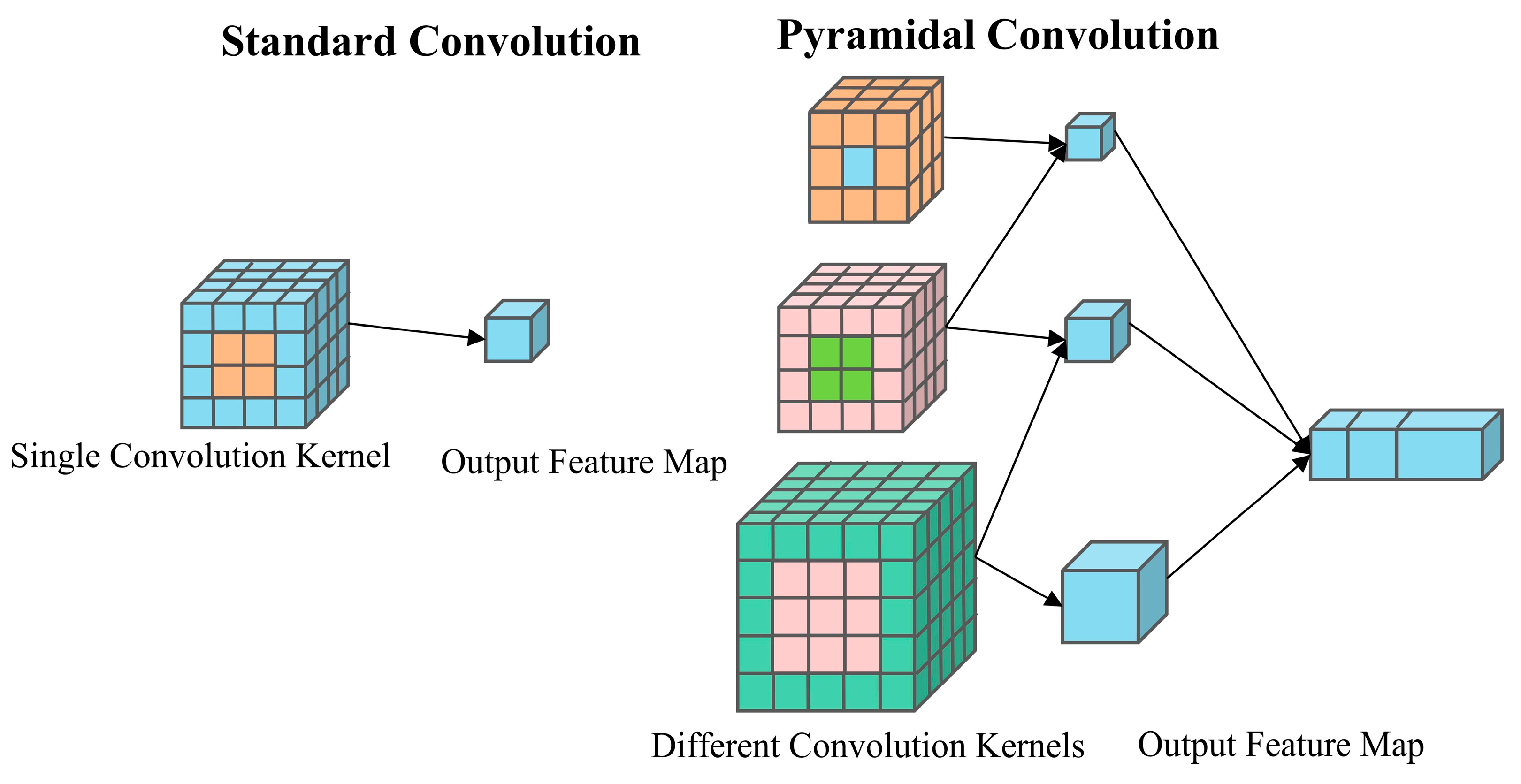
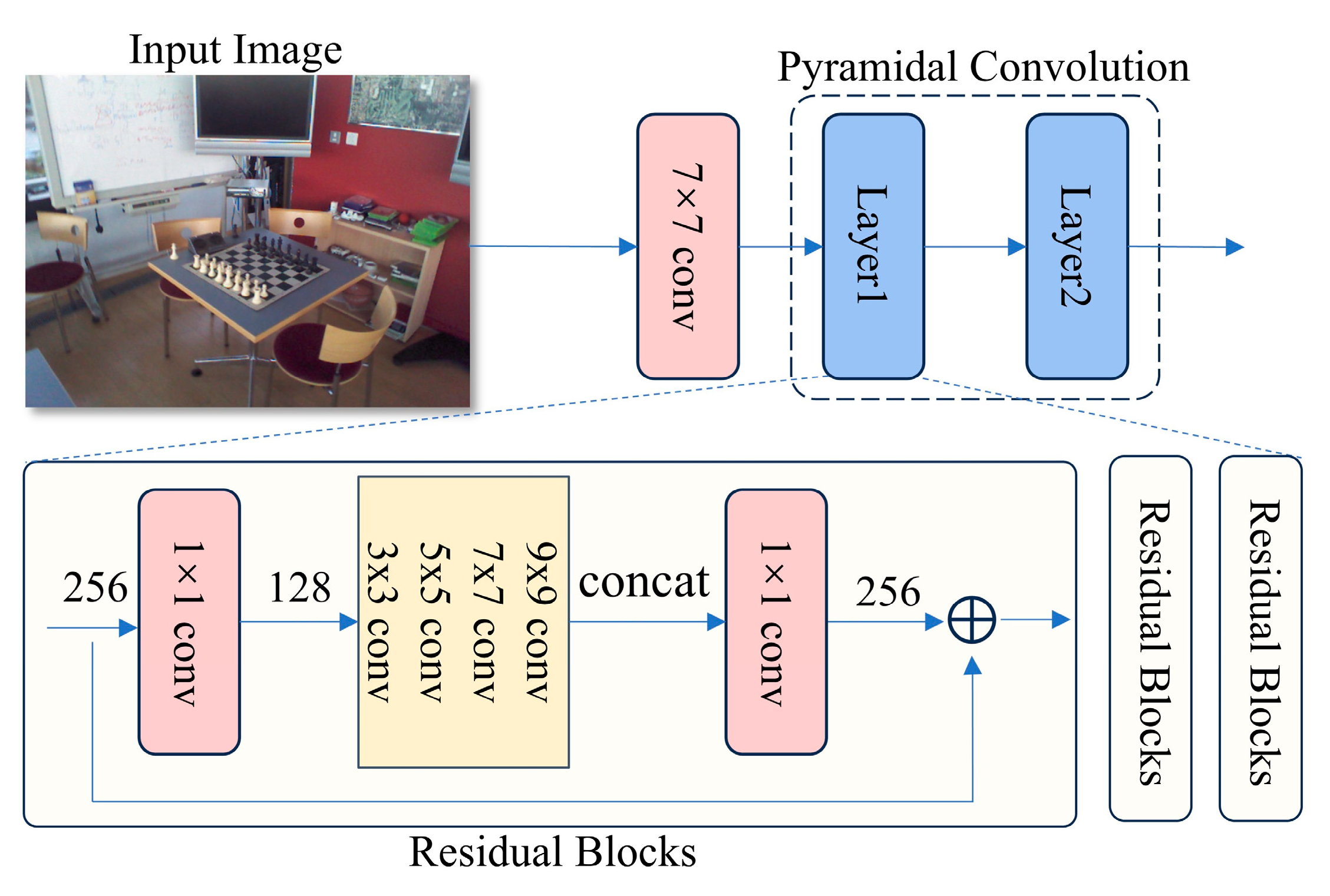
3.2. Pyramidal Convolution
3.3. Efficient Scene Coordinate Regression and Pose Estimation
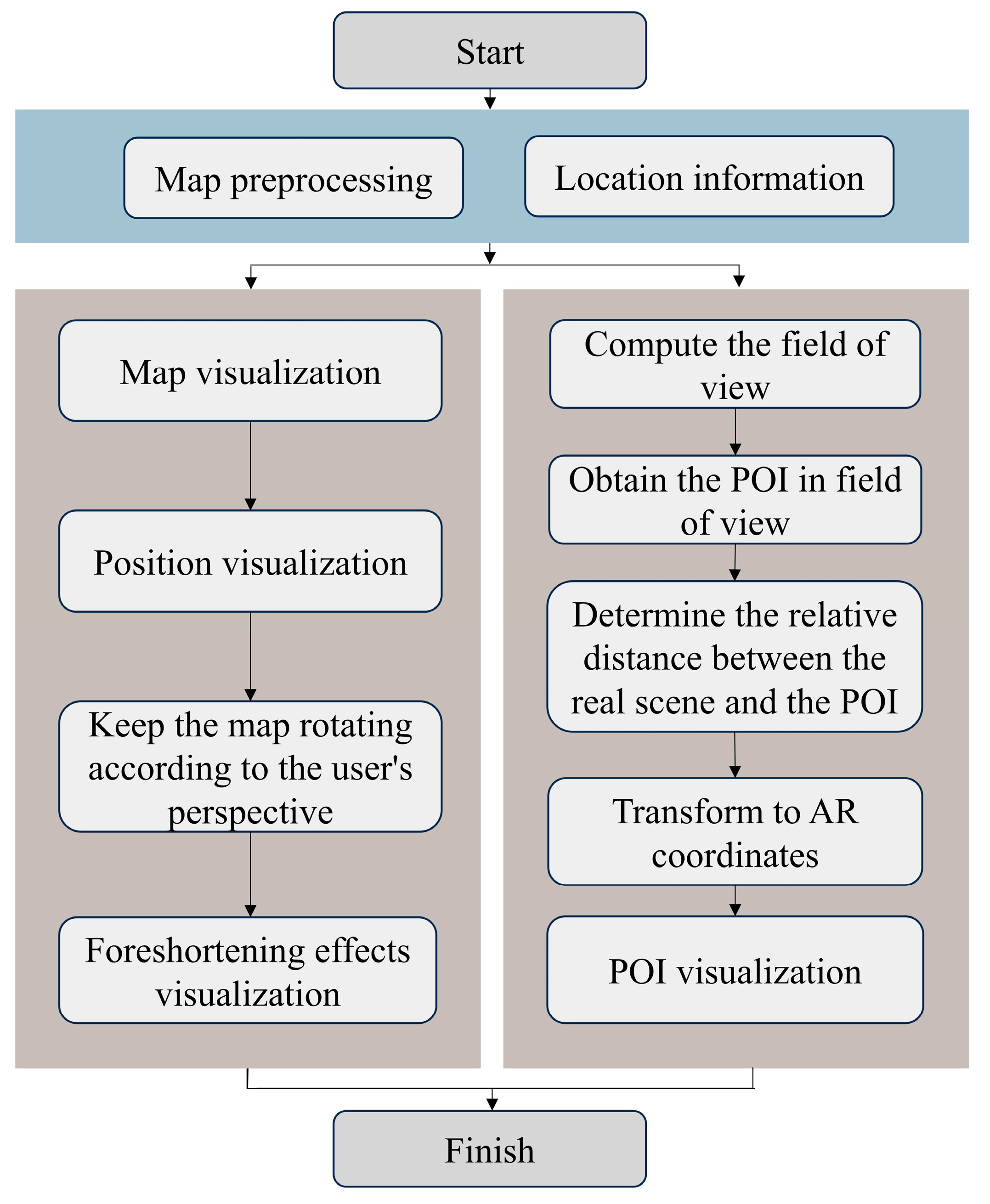
3.4. Augmented Reality and Map Visualization
4. Experimental
4.1. Camera Tracking Experiment
4.1.1. Experiment Settings
4.1.2. Results
4.2. AR-GIS Visualization
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Dargan, S.; Bansal, S.; Kumar, M.; Mittal, A.; Kumar, K. Augmented reality: A comprehensive review. Arch. Comput. Methods Eng. 2023, 30, 1057–1080. [Google Scholar] [CrossRef]
- Lameirão, T.; Melo, M.; Pinto, F. Augmented Reality for Event Promotion. Computers 2024, 13, 342. [Google Scholar] [CrossRef]
- Park, S.; Park, S.H.; Park, L.W.; Park, S.; Lee, S.; Lee, T.; Lee, S.H.; Jang, H.; Kim, S.M.; Chang, H.; et al. Design and Implementation of a Smart IoT Based Building and Town Disaster Management System in Smart City Infrastructure. Appl. Sci. 2018, 8, 2239. [Google Scholar] [CrossRef]
- Chen, A.; Jesus, R.; Vilarigues, M. Synergy of Art, Science, and Technology: A Case Study of Augmented Reality and Artificial Intelligence in Enhancing Cultural Heritage Engagement. J. Imaging 2025, 11, 89. [Google Scholar] [CrossRef]
- Joo-Nagata, J.; Rodríguez-Becerra, J. Mobile Pedestrian Navigation, Mobile Augmented Reality, and Heritage Territorial Representation: Case Study in Santiago de Chile. Appl. Sci. 2025, 15, 2909. [Google Scholar] [CrossRef]
- Liu, F.; Jonsson, T.; Seipel, S. Evaluation of Augmented Reality-Based Building Diagnostics Using Third Person Perspective. ISPRS Int. J. Geo-Inf. 2020, 9, 53. [Google Scholar] [CrossRef]
- Min, S.; Lei, L.; Wei, H.; Xiang, R. Interactive registration for augmented reality gis. In Proceedings of the International Conference on Computer Vision in Remote Sensing, Xiamen, China, 16–18 December 2012; pp. 246–251. [Google Scholar]
- Ma, W.; Zhang, S.; Huang, J. Mobile augmented reality based indoor map for improving geo-visualization. PeerJ Comput. Sci. 2021, 7, e704. [Google Scholar] [CrossRef]
- Sattler, T.; Leibe, B.; Kobbelt, L. Efficient & Effective Prioritized Matching for Large-Scale Image-Based Localization. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 1744–1756. [Google Scholar] [CrossRef]
- Sarlin, P.-E.; Cadena, C.; Siegwart, R.; Dymczyk, M. From coarse to fine: Robust hierarchical localization at large scale. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 12716–12725. [Google Scholar]
- Camposeco, F.; Cohen, A.; Pollefeys, M.; Sattler, T. Hybrid Scene Compression for Visual Localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 7645–7654. [Google Scholar]
- Zhou, Q.; Agostinho, S.; Ošep, A.; Leal-Taixé, L. Is Geometry Enough for Matching in Visual Localization? In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 407–425. [Google Scholar]
- Moreau, A.; Piasco, N.; Tsishkou, D.; Stanciulescu, B.; de La Fortelle, A. Coordinet: Uncertainty-aware pose regressor for reliable vehicle localization. In Proceedings of the IEEE Winter Conference on Applications of Computer Vision, Waikoloa, HI, USA, 1–6 January 2022; pp. 2229–2238. [Google Scholar]
- Chen, S.; Li, X.; Wang, Z.; Prisacariu, V.A. DFNet: Enhance Absolute Pose Regression with Direct Feature Matching. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 1–17. [Google Scholar]
- Chen, S.; Wang, Z.; Prisacariu, V. Direct-PoseNet: Absolute Pose Regression with Photometric Consistency. In Proceedings of the International Conference on 3D Vision, International Trave, Online, 1–3 December 2021; pp. 1175–1185. [Google Scholar]
- Bach, T.B.; Dinh, T.T.; Lee, J.-H. FeatLoc: Absolute pose regressor for indoor 2D sparse features with simplistic view synthesizing. ISPRS J. Photogramm. Remote Sens. 2022, 189, 50–62. [Google Scholar] [CrossRef]
- Brachmann, E.; Rother, C. Learning Less is More—6D Camera Localization via 3D Surface Regression. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 4654–4662. [Google Scholar]
- Cavallari, T.; Bertinetto, L.; Mukhoti, J.; Torr, P.; Golodetz, S. Let’s Take This Online: Adapting Scene Coordinate Regression Network Predictions for Online RGB-D Camera Relocalisation. In Proceedings of the International Conference on 3D Vision, Quebec City, QC, Canada, 16–19 September 2019; pp. 564–573. [Google Scholar]
- Cavallari, T.; Golodetz, S.; Lord, N.A.; Valentin, J.; Prisacariu, V.A.; Stefano, L.D.; Torr, P.H.S. Real-Time RGB-D Camera Pose Estimation in Novel Scenes Using a Relocalisation Cascade. IEEE Trans. Pattern Anal. Mach. Intell. 2020, 42, 2465–2477. [Google Scholar] [CrossRef] [PubMed]
- Brachmann, E.; Michel, F.; Krull, A.; Yang, M.Y.; Gumhold, S.; Rother, C. Uncertainty-Driven 6D Pose Estimation of Objects and Scenes from a Single RGB Image. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 3364–3372. [Google Scholar]
- Duta, I.C.; Liu, L.; Zhu, F.; Shao, L. Pyramidal convolution: Rethinking convolutional neural networks for visual recognition. arXiv 2020, arXiv:2006.11538. [Google Scholar] [CrossRef]
- Brachmann, E.; Cavallari, T.; Prisacariu, V.A. Accelerated Coordinate Encoding: Learning to Relocalize in Minutes Using RGB and Poses. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 5044–5053. [Google Scholar]
- Azuma, R.T. A survey of augmented reality. Presence Teleoperators Virtual Environ. 1997, 6, 355–385. [Google Scholar] [CrossRef]
- Herman, L.; Juřík, V.; Stachoň, Z.; Vrbík, D.; Russnák, J.; Řezník, T. Evaluation of user performance in interactive and static 3D maps. ISPRS Int. J. Geo-Inf. 2018, 7, 415. [Google Scholar] [CrossRef]
- Tonnis, M.; Klein, L.; Klinker, G. Perception thresholds for augmented reality navigation schemes in large distances. In Proceedings of the IEEE/ACM International Symposium on Mixed and Augmented Reality, Cambridge, UK, 15–18 September 2008; pp. 189–190. [Google Scholar]
- Zollmann, S.; Poglitsch, C.; Ventura, J. VISGIS: Dynamic situated visualization for geographic information systems. In Proceedings of the International Conference on Image and VisionComputing New Zealand (IVCNZ), Palmerston North, New Zealand, 21–22 November 2016; pp. 1–6. [Google Scholar]
- White, S.; Feiner, S. SiteLens: Situated visualization techniques for urban site visits. In Proceedings of the SIGCHI Conference on Human Factors in Computing Systems, Boston, MA, USA, 4–9 April 2009; pp. 1117–1120. [Google Scholar]
- Grasset, R.; Langlotz, T.; Kalkofen, D.; Tatzgern, M.; Schmalstieg, D. Image-driven view management for augmented reality browsers. In Proceedings of the IEEE International Symposium on Mixed and Augmented Reality (ISMAR), Atlanta, GA, USA, 5–8 November 2012; pp. 177–186. [Google Scholar]
- Keil, J.; Korte, A.; Ratmer, A.; Edler, D.; Dickmann, F. Augmented reality (AR) and spatial cognition: Effects of holographic grids on distance estimation and location memory in a 3D indoor scenario. PFG–J. Photogramm. Remote Sens. Geoinf. Sci. 2020, 88, 165–172. [Google Scholar] [CrossRef]
- Grübel, J.; Thrash, T.; Aguilar, L.; Gath-Morad, M.; Chatain, J.; Sumner, R.W.; Hölscher, C.; Schinazi, V.R. The Hitchhiker’s Guide to Fused Twins: A Review of Access to Digital Twins In Situ in Smart Cities. Remote Sens. 2022, 14, 3095. [Google Scholar] [CrossRef]
- Fenais, A.; Ariaratnam, S.T.; Ayer, S.K.; Smilovsky, N. Integrating geographic information systems and augmented reality for mapping underground utilities. Infrastructures 2019, 4, 60. [Google Scholar] [CrossRef]
- Huang, K.; Wang, C.; Wang, S.; Liu, R.; Chen, G.; Li, X. An Efficient, Platform-Independent Map Rendering Framework for Mobile Augmented Reality. ISPRS Int. J. Geo-Inf. 2021, 10, 593. [Google Scholar] [CrossRef]
- Galvão, M.L.; Paolo, F.; Ioannis, G.; Gerhard, N.; Markus, K.; Alinaghi, N. GeoAR: A calibration method for Geographic-Aware Augmented Reality. Int. J. Geogr. Inf. Sci. 2024, 38, 1800–1826. [Google Scholar] [CrossRef]
- Mo Adel, A.; Eleni, S. Augmented Reality Indoor-Outdoor Navigation Through a Campus Digital Twin. In Proceedings of the International Conference on Collaborative Advances in Software and COmputiNg (CASCON), Toronto, ON, Canada, 11–13 November 2024; pp. 1–6. [Google Scholar]
- Sundarramurthi, M.; Balasubramanyam, A.; Patil, A.K. NavPES: Augmented Reality Redefining Indoor Navigation in the Digital Era. In Proceedings of the International Conference on Digital Applications, Transformation & Economy (ICDATE), Miri, Malaysia, 14–16 July 2023; pp. 1–5. [Google Scholar]
- Liu, H.; Xue, H.; Zhao, L.; Chen, D.; Peng, Z.; Zhang, G. MagLoc-AR: Magnetic-Based Localization for Visual-Free Augmented Reality in Large-Scale Indoor Environments. IEEE Trans. Vis. Comput. Graph. 2023, 29, 4383–4393. [Google Scholar] [CrossRef]
- Ma, W.; Xiong, H.; Dai, X.; Zheng, X.; Zhou, Y. An Indoor Scene Recognition-Based 3D Registration Mechanism for Real-Time AR-GIS Visualization in Mobile Applications. ISPRS Int. J. Geo-Inf. 2018, 7, 112. [Google Scholar] [CrossRef]
- Pan, X.; Huang, G.; Zhang, Z.; Li, J.; Bao, H.; Zhang, G. Robust Collaborative Visual-Inertial SLAM for Mobile Augmented Reality. IEEE Trans. Vis. Comput. Graph. 2024, 30, 7354–7363. [Google Scholar] [CrossRef]
- Jiang, J.-R.; Subakti, H. An indoor location-based augmented reality framework. Sensors 2023, 23, 1370. [Google Scholar] [CrossRef] [PubMed]
- Gao, X.-S.; Hou, X.-R.; Tang, J.; Cheng, H.-F. Complete solution classification for the perspective-three-point problem. IEEE Trans. Pattern Anal. Mach. Intell. 2003, 25, 930–943. [Google Scholar]
- Schönberger, J.L.; Frahm, J.M. Structure-from-Motion Revisited. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 4104–4113. [Google Scholar]
- Pietrantoni, M.; Humenberger, M.; Sattler, T.; Csurka, G. SegLoc: Learning Segmentation-Based Representations for Privacy-Preserving Visual Localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Vancouver, BC, Canada, 17–24 June 2023; pp. 15380–15391. [Google Scholar]
- Sarlin, P.E.; Unagar, A.; Larsson, M.; Germain, H.; Toft, C.; Larsson, V.; Pollefeys, M.; Lepetit, V.; Hammarstrand, L.; Kahl, F.; et al. Back to the Feature: Learning Robust Camera Localization from Pixels to Pose. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Nashville, TN, USA, 20–25 June 2021; pp. 3246–3256. [Google Scholar]
- Sarlin, P.-E.; DeTone, D.; Malisiewicz, T.; Rabinovich, A. Superglue: Learning feature matching with graph neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 4938–4947. [Google Scholar]
- Panek, V.; Kukelova, Z.; Sattler, T. MeshLoc: Mesh-Based Visual Localization. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 589–609. [Google Scholar]
- Kendall, A.; Grimes, M.; Cipolla, R. Posenet: A convolutional network for real-time 6-dof camera relocalization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–15 June 2015; pp. 2938–2946. [Google Scholar]
- Kendall, A.; Cipolla, R. Modelling uncertainty in deep learning for camera relocalization. In Proceedings of the IEEE International Conference on Robotics and Automation, Stockholm Waterfront Congress Centre, Stockholm, Sweden, 16–21 May 2016; pp. 4762–4769. [Google Scholar]
- Shavit, Y.; Ferens, R.; Keller, Y. Learning Multi-Scene Absolute Pose Regression with Transformers. In Proceedings of the IEEE International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 2713–2722. [Google Scholar]
- Shotton, J.; Glocker, B.; Zach, C.; Izadi, S.; Criminisi, A.; Fitzgibbon, A. Scene Coordinate Regression Forests for Camera Relocalization in RGB-D Images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 2930–2937. [Google Scholar]
- Cavallari, T.; Golodetz, S.; Lord, N.A.; Valentin, J.; Stefano, L.D.; Torr, P.H.S. On-the-Fly Adaptation of Regression Forests for Online Camera Relocalisation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 218–227. [Google Scholar]
- Brachmann, E.; Krull, A.; Nowozin, S.; Shotton, J.; Michel, F.; Gumhold, S.; Rother, C. Dsac-differentiable ransac for camera localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6684–6692. [Google Scholar]
- Li, X.; Wang, S.; Zhao, Y.; Verbeek, J.; Kannala, J. Hierarchical Scene Coordinate Classification and Regression for Visual Localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Seattle, WA, USA, 13–19 June 2020; pp. 11980–11989. [Google Scholar]
- Brachmann, E.; Rother, C. Visual camera re-localization from RGB and RGB-D images using DSAC. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 44, 5847–5865. [Google Scholar] [CrossRef] [PubMed]
- Dong, Q.; Zhou, Z.; Qiu, X.; Zhang, L. A Survey on Self-Supervised Monocular Depth Estimation Based on Deep Neural Networks. IEEE Trans. Neural Netw. Learn. Syst. 2025, 1–21. [Google Scholar] [CrossRef]
- Bhat, S.F.; Birkl, R.; Wofk, D.; Wonka, P.; Müller, M. Zoedepth: Zero-shot transfer by combining relative and metric depth. arXiv 2023, arXiv:2006.11538. [Google Scholar]
- Lin, T.-Y.; Dollár, P.; Girshick, R.; He, K.; Hariharan, B.; Belongie, S. Feature pyramid networks for object detection. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2117–2125. [Google Scholar]
- Liu, X.; Hu, Y.; Chen, J. Hybrid CNN-Transformer model for medical image segmentation with pyramid convolution and multi-layer perceptron. Biomed. Signal Process. Control 2023, 86, 105331. [Google Scholar] [CrossRef]
- Zhang, J.; Zhao, L.; Jiang, H.; Shen, S.; Wang, J.; Zhang, P.; Zhang, W.; Wang, L. Hyperspectral Image Classification Based on Dense Pyramidal Convolution and Multi-Feature Fusion. Remote Sens. 2023, 15, 2990. [Google Scholar] [CrossRef]
- Kendall, A.; Cipolla, R. Geometric Loss Functions for Camera Pose Regression with Deep Learning. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6555–6564. [Google Scholar]
- Taira, H.; Okutomi, M.; Sattler, T.; Cimpoi, M.; Pollefeys, M.; Sivic, J.; Pajdla, T.; Torii, A. InLoc: Indoor Visual Localization with Dense Matching and View Synthesis. IEEE Trans. Pattern Anal. Mach. Intell. 2021, 43, 1293–1307. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Bai, Z.; Tang, C.; Li, H.; Furukawa, Y.; Tan, P. SANet: Scene Agnostic Network for Camera Localization. In Proceedings of the International Conference on Computer Vision, Seoul, Republic of Korea, 27 October–2 November 2019; pp. 42–51. [Google Scholar]
- Do, T.; Miksik, O.; DeGol, J.; Park, H.S.; Sinha, S.N. Learning to Detect Scene Landmarks for Camera Localization. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 11122–11132. [Google Scholar]
- Arnold, E.; Wynn, J.; Vicente, S.; Garcia-Hernando, G.; Monszpart, Á.; Prisacariu, V.; Turmukhambetov, D.; Brachmann, E. Map-Free Visual Relocalization: Metric Pose Relative to a Single Image. In Proceedings of the European Conference on Computer Vision, Tel Aviv, Israel, 23–27 October 2022; pp. 690–708. [Google Scholar]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Zhang, G.; Liu, X.; Wang, L.; Zhu, J.; Yu, J. Development and feasibility evaluation of an AR-assisted radiotherapy positioning system. Front. Oncol. 2022, 12, 921607. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.; Tan, Z.; Qiao, X.; Zhao, J.; Tian, F. Moving Visual-Inertial Ordometry into Cross-platform Web for Markerless Augmented Reality. In Proceedings of the IEEE Conference on Virtual Reality and 3D User Interfaces Abstracts and Workshops (VRW), Christchurch, New Zealand, 12–16 March 2022; pp. 624–625. [Google Scholar]
- Morgan, A.A. On the accuracy of BLE indoor localization systems: An assessment survey. Comput. Electr. Eng. 2024, 118, 109455. [Google Scholar] [CrossRef]
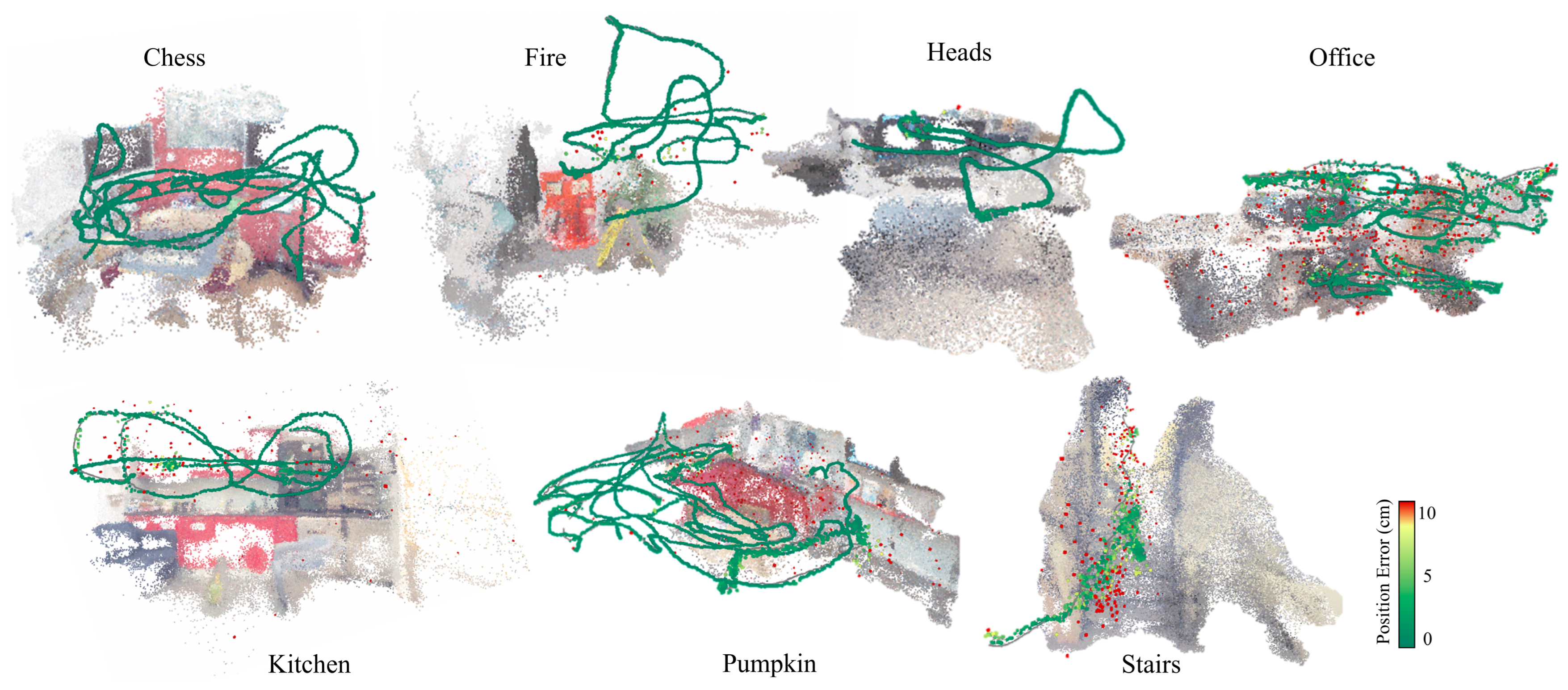
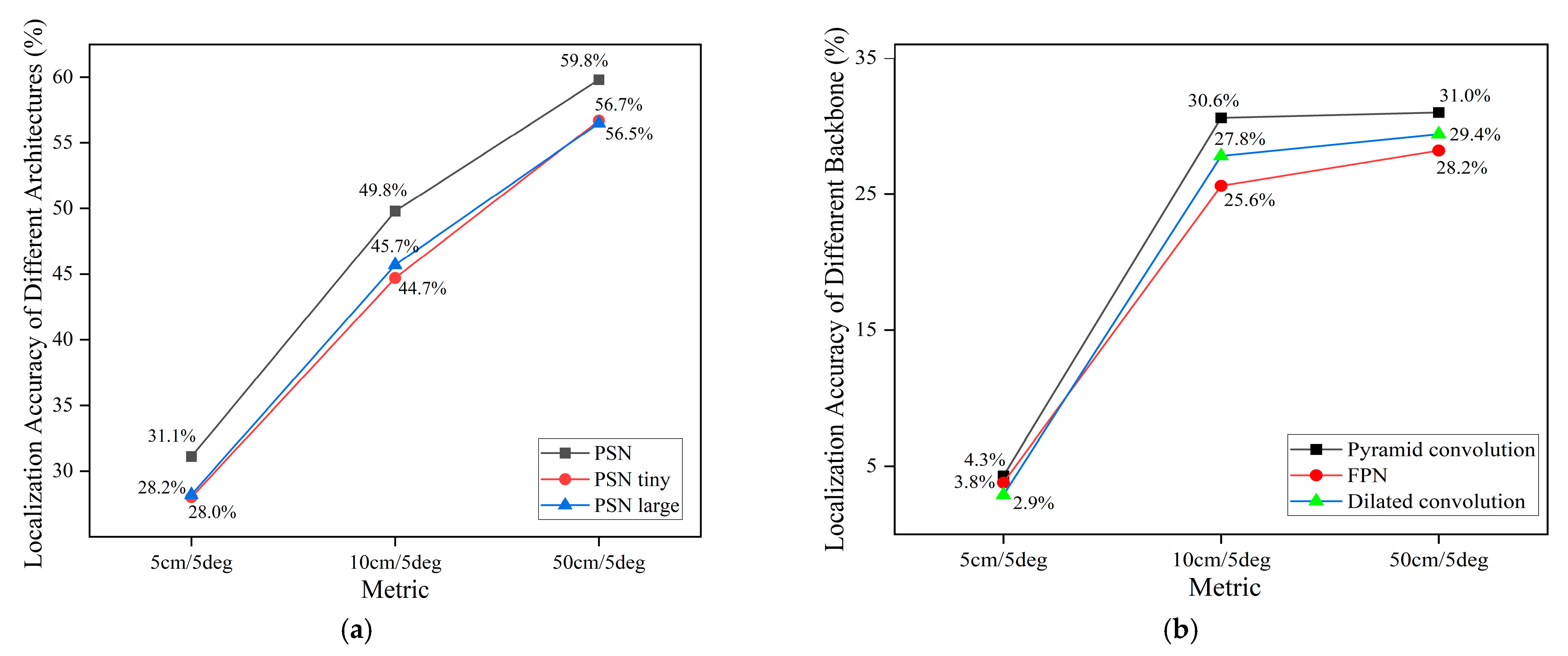



| Method | Chess | Fire | Heads | Office | Pumpkin | Kitchen | Stairs | Mapping Time | |
|---|---|---|---|---|---|---|---|---|---|
| APR | MST [48] | 11/4.7 | 24/9.6 | 14/12.2 | 17/5.6 | 18/4.4 | 17/6.0 | 26/8.4 | >60 min |
| Posenet17 [59] | 13/4.5 | 27/11.3 | 17/13 | 19/5.6 | 26/4.8 | 23/5.4 | 35/12.4 | >60 min | |
| FM | AS [9] | 2.6/0.9 | 2.3/1.0 | 1.1/0.8 | 4.0/1.2 | 6.5/1.7 | 5.3/1.7 | 3.8/1.1 | >90 min |
| Inloc [60] | 3.0/1.05 | 3.0/1.1 | 2.0/1.16 | 3.0/1.05 | 5.0/1.55 | 4.0/1.3 | 9.0/2.5 | >90 min | |
| Hloc [10] | 2.4/0.8 | 1.8/0.8 | 0.9/0.6 | 2.6/0.8 | 4.4/1.2 | 4.0/1.4 | 5.1/1.4 | >90 min | |
| SCR | SANet [61] | 3.0/2.9 | 3.0/1.1 | 2.0/1.5 | 3.0/1.0 | 5.0/1.3 | 4.0/1.4 | 16.0/4.6 | 3 min |
| NBE + SLD [62] | 2.2/0.8 | 1.8/0.7 | 0.9/0.7 | 3.2/0.9 | 5.6/1.6 | 5.3/1.5 | 5.5/1.4 | >60 min | |
| DSAC* (RGB) [53] | 1.9/1.1 | 1.9/1.2 | 1.1/1.8 | 2.6/1.2 | 4.2/1.4 | 3.0/1.7 | 4.1/1.4 | >100 min | |
| PSN (Ours) | 2.2/0.8 | 2.0/0.8 | 1.0/0.7 | 5.0/1.4 | 5.5/1.6 | 7.0/1.9 | 8.6/2.0 | 5 min | |
| Method | Great Court | K. College | Hospital | Shop | Church | Mapping Time | |
|---|---|---|---|---|---|---|---|
| APR | MST [48] | - | 0.83/1.5 | 1.81/2.4 | 0.86/3.1 | 1.62/4.0 | >100 min |
| Posenet17 [59] | 6.83/3.5 | 0.88/1.0 | 3.20/3.3 | 0.88/3.8 | 1.57/3.3 | >100 min | |
| DFNet [14] | - | 0.73/2.4 | 2.00/3.0 | 0.67/2.2 | 1.37/4.0 | >60 min | |
| FM | AS [9] | 0.24/0.1 | 0.13/0.2 | 0.20/0.4 | 0.04/0.2 | 0.08/0.3 | 35 min |
| Hloc [10] | 0.17/0.1 | 0.11/0.2 | 0.15/0.3 | 0.04/0.2 | 0.07/0.2 | 35 min | |
| PxLoc [43] | 0.30/0.1 | 0.14/0.2 | 0.16/0.3 | 0.05/0.2 | 0.10/0.3 | 35 min | |
| SCR | DSAC++ (RGB) [17] | 0.66/0.2 | 0.23/0.3 | 0.24/0.3 | 0.09/0.3 | 0.20/0.4 | >100 min |
| DSAC* (RGB) [53] | 0.34/0.2 | 0.18/0.3 | 0.21/0.4 | 0.05/0.3 | 0.15/0.6 | >100 min | |
| PSN (Ours) | 0.98/0.6 | 0.20/0.4 | 0.38/0.7 | 0.05/0.3 | 0.26/0.9 | 25 min | |
| Scene | APR | SCR | ||
|---|---|---|---|---|
| Posenet17 [59] | MST [48] | DSAC* [53] | PSN (Ours) | |
| Bears | 12.9%/35.7% | 0.5%/12.8% | 82.6%/91.6% | 76.9%/82.4% |
| Cubes | 0.0%/0.4% | 0.0%/9.9% | 83.8%/98.1% | 81.7%/96.3% |
| Inscription | 1.1%/6.3% | 1.3%/9.7% | 54.1%/69.7% | 53.9%/75.1% |
| Lawn | 0.0%/0.2% | 0.0%/0.0% | 34.7%/38.0% | 36.6%/37.7% |
| Map | 14.9%/49.1% | 5.6%/25.7% | 56.7%/87.1% | 53.9%/85.9% |
| Square Bench | 0.0%/3.0% | 0.0%/0.0% | 69.5%/97.9% | 63.8%/88.0% |
| Statue | 0.0%/0.0% | 0.0%/0.0% | 0.0%/0.0% | 0.0%/0.0% |
| Tendrils | 0.0%/0.0% | 0.9%/23.6% | 25.1%/26.5% | 30.6%/31.0% |
| The Rock | 21.2%/77.5% | 10.7%/52.6% | 100.0%/100.0% | 100.0%/100.0% |
| Winter Sign | 0.0%/0.0% | 0.0%/0.0% | 0.2%/5.7% | 0.2%/5.7% |
| Metric | Medium Room | Large Room |
|---|---|---|
| Median error | 0.16 m/0.3 deg | 0.36 m/0.4 deg |
| Position error | 79.6% | 59.8% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, H.; Zhu, C.; Wang, Y.; Zhu, H.; Ma, W. A Pyramid Convolution-Based Scene Coordinate Regression Network for AR-GIS. ISPRS Int. J. Geo-Inf. 2025, 14, 311. https://doi.org/10.3390/ijgi14080311
Xu H, Zhu C, Wang Y, Zhu H, Ma W. A Pyramid Convolution-Based Scene Coordinate Regression Network for AR-GIS. ISPRS International Journal of Geo-Information. 2025; 14(8):311. https://doi.org/10.3390/ijgi14080311
Chicago/Turabian StyleXu, Haobo, Chao Zhu, Yilong Wang, Huachen Zhu, and Wei Ma. 2025. "A Pyramid Convolution-Based Scene Coordinate Regression Network for AR-GIS" ISPRS International Journal of Geo-Information 14, no. 8: 311. https://doi.org/10.3390/ijgi14080311
APA StyleXu, H., Zhu, C., Wang, Y., Zhu, H., & Ma, W. (2025). A Pyramid Convolution-Based Scene Coordinate Regression Network for AR-GIS. ISPRS International Journal of Geo-Information, 14(8), 311. https://doi.org/10.3390/ijgi14080311







