Relationship Between Aggregation Index and Change in the Values of Some Landscape Metrics as a Function of Cell Neighborhood Choice

Abstract

Landscape metrics are one of the main tools for studying changes in the landscape and the ecological structure of the territory. However, the calculation of some metrics yields significantly different values depending on the configuration of the “Cell neighborhood” (CN) used. This makes the comparison of different analysis results often impossible. In fact, although the metrics are defined in the same way for all software, the choice of a CN with four cells, which includes only the elements on the same row or column, or eight cells, which also includes the cells on the diagonal, changes their value. QGIS’ LecoS plugin uses the value eight while GRASS’ r.li module uses the value four and these values are not modifiable by users. A previous study has shown how the value of the CN used for the calculation of landscape metrics is rarely explicit in scientific publications and its value cannot always be deduced from the indication of the software used. The difference in value for the same metric depends on the CN configuration and on the compactness of the patches, which can be expressed through the Aggregation Index (AI), of the investigated landscape. The scope of this paper is to explore the possibility of deriving an analytical relationship between the Aggregation Index and the variation in the values of some landscape metrics as the CN varies. The numerical experiments carried out in this research demonstrate that it is possible to estimate the differences in landscape metrics evaluated with a four and eight CN configuration using polynomials only for few metrics and only for some intervals of AI values. This analysis combines different Free and Open Source Software (FOSS) systems: GRASS GIS for the creation of test maps and R landscapemetrics package for the calculation of landscape metrics and the successive statistical analysis.

1. Introduction

Landscape metrics have had a great influence in the study of landscape change at different scales, from the local to the planetary. They have allowed for a different and more objective description, study and consideration of the landscape changes occurred through time in any given area of the world [1,2,3]. In the Anthropocene era we are living in, landscape change (e.g., due to deforestation or urbanization) is one of the major phenomenon that can be observed [4,5,6,7,8]. The concept of habitat loss and habitat fragmentation were certainly clear for the biologists, foresters and naturalists who worked in the field [9] but, due to a lack of clear quantification methods, they were less understandable for other scientists like engineers and mathematics because they were perceived as too qualitative. Landscape metrics combined with GIS techniques provide a tool to measure and quantify landscape, transforming this concept from qualitative to quantitative and helping to understand the concept of habitat fragmentation and to widen its adoption in ecology. This has created a new research field [10] and it is gaining popularity in education [11,12].

Landscape metrics are now a standard instrument for those who investigate landscape change dynamics in ecology [2,13,14,15,16,17,18,19] as well as in many other disciplines such as soil protection [20,21], water management [22,23,24,25], urban green spaces management [26,27,28,29] and disease spread [30]. For example in a recent review paper of the ecological restoration in Brazilian biomes, Guerra et al. [31] highlighted the need to expand research to assess landscape metrics to fill the gaps in research and helping prioritization, legislation and public policies. Some metrics like Patch Number (NP) or Mean Patch Size (MPS) are considered particularly robust and significant [32] and are extensively used in scientific literature [2,33] becoming a standard to compare different landscapes. New landscape metrics are currently proposed, such as the Ecological Land Evolution Index (ELEI) [34]. However, conceptual errors in the interpretation of landscape patterns, the intrinsic restrictions of landscape indices and inappropriate pattern index usage are well known limitations in the use of landscape metrics [35].

Although theoretically the calculation of these indices on the same data, given the same algorithm, should provide the same results, it has been proven that the lack of description of some parameters may affect the interpretation of the output in a dramatic way [32]. In fact, many scientific papers fail to describe in detail some important parameters, making it very difficult to correctly compare the results of different research even if they have been carried out in the same areas and/or using, at least apparently, exactly the same methods. In particular, the “Cell neighborhood” (CN) size is one of the most sensible parameters and Zatelli et al. [32] found that using a different software gives a different visibility to the setting of cell neighborhood size. Thus, when comparing different research works, it is extremely important to find a way to detect if the results are really comparable and in particular if landscape metrics have been evaluated using the same CN configuration.

Zatelli et al. [32] demonstrated that it is possible to use the values of the Aggregation Index (AI) to assess how the uncertainty on CN can affect some landscape metrics. This paper takes a step further, investigating the possibility of evaluating the influence of the choice of the CN value on the most frequently used landscape metrics. Moreover, a method to compute the differences between metrics evaluated with different CN is presented. These results can be used in two ways: (i) it is possible to estimate the difference in the metrics’ values with different CN configurations and, therefore, to assess the feasibility of using their values when the CN in use is unknown if the difference is small, and (ii) to evaluate the value of metrics with one CN configuration when the value for the other CN configuration is known but the map used to calculate them is not available.

The research question is, therefore, is it possible to estimate the differences in landscape metrics evaluated with a four and eight CN configuration using polynomials?

The paper is organized as follows: Section 2 introduces the Aggregation Index (AI) following the original formulation from He et al. [36], Section 3 describes the materials and methods used for the analysis, Section 4 illustrates the results that are discussed in Section 5 and finally the conclusions and future developments are presented in Section 6.

2. Aggregation Index

The Aggregation Index (AI) landscape metric has been introduced by He et al. in [36] as a way to quantify the presence of clusters in landscape patterns. Unlike its precursors contagion index (CI) and shape index (SI), AI is not affected by spatial patterning, landscape composition and patches’ shape. Moreover, AI is class specific, while CI evaluates the overall aggregation of the landscape combining all the classes. AI is defined as a ratio; therefore, it is independent from the scale or the map unit. This makes AI suitable not only for the comparison of the aggregation of different classes on the same map, but also for the examination of the same class on the same map at different resolutions.

The Aggregation Index (AI), formulated for raster data, is defined as the ratio between the total number of edges between pixels of the class and the maximum number of possible edges between pixels of the class [36]. Defining $e_{i,j}$ as the number of edges between cells of classes i and j, the number of total edges between cells of the same class is $e_{i,i}$. It is possible to define a level of aggregation of class i as the ratio between the total number of edges between cells of classes i and the total area $A_i$ of this class, $e_{i,i}/A_i$. For a given value of $A_i$, the maximum aggregation level, $max{e}_{i,i}/A_i$, corresponds to a configuration with a single clump of class A with the maximum value of $e_{i,i}$, $max{e}_{i,i}$.

For a four CN configuration, the value of $max{e}_{i,i}$ can be calculated with reference to the number n of pixels in the side of the largest square with area smaller than $A_i$. If the class consists of a single square patch, n is the number of pixels on each side. In general, it is possible to define $m=A_i-n^2$, the difference between the area $A_i$ of the patch and the area of the area of the largest square with area smaller than $A_i$, and to evaluate the maximum number of edges between cells of the class $A_i$, $max{e}_{i,i}$, as

$$\begin{array}{cccc}\hfill & max{e}_{i,i}=2n\left(n-1\right)\hfill & \hfill & \mathrm{when}m=0\mathrm{or}\hfill \\ \hfill & max{e}_{i,i}=2n\left(n-1\right)+2m-1\hfill & \hfill & \mathrm{when}m\le n\mathrm{or}\hfill \\ \hfill & max{e}_{i,i}=2n\left(n-1\right)+2m-2\hfill & \hfill & \mathrm{when}m>n\hfill \end{array}$$

(1)

The original definition in He et al. [36] has $m\ge 0$ as condition for the third line in Equation (1), but it is an obvious typo, and makes the case $m=n$ mistakenly correspond to the third instead of the second line in Equation (1). Implementations in popular software for AI evaluation, such as FRAGSTATS and R’s landscapemetrics use the correct formulation in Equation (1) [37,38].

Finally, the Aggregation Index (AI) for class i is defined as

$$AI={\displaystyle \frac{e_{i,i}}{max{e}_{i,i}}}$$

(2)

AI ranges from 0, $e_{i,i}=0$, i.e., there is no common edge between cells of class i and all cells of this class are isolated, to 1, when $e_{i,i}=max{e}_{i,i}$. In many implementations AI is expressed as a percentage by multiplying the ratio of Equation (2) by 100.

$$AI={\displaystyle \frac{e_{i,i}}{max{e}_{i,i}}}100$$

(3)

The range for AI values is, therefore, between 0 and 100. All AI values in this paper use the definition in Equation (3) and are expressed as percentages.

Using an eight CN configuration leads to different values of number of total edges between cells of the same class $e_{i,i}$ and $max{e}_{i,i}$, but their ratio, and therefore AI, remains the same.

AI is class specific, but an overall Landscape Aggregation Index ($A{I}_L$) can be defined as the sum of all the AIs for each class $A{I}_i$ weighted by their percentage area $A_i\%$ with respect to the total area of the map [36]:

$$A{I}_L=\sum _{i=1}^{n}A{I}_i{A}_i\%$$

(4)

The behavior of AI for different map configurations has been tested with respect to aggregation, number of patches and spatial resolutions. Following He et al. [36], the evaluation of the response of AI to different levels of aggregation is performed using a binary map with a resolution 1 ([pixel]) containing $7\times 7$ cells. The initial configuration contains nine isolated patches of 1 cell with a value of 1 and 40 background cells with a value of 0. The level of aggregation is then increased by incrementing the number of shared edges by one at a time, up to the final configuration where all the cells with a value of 1 are clumped in a single square (Figure 1).

A second set of maps is created with patches of the same size added at random locations. The map is $25\times 25$ cells with a resolution 1 ([pixel]) and the patches have size $4\times 4$ cells. Patches are added one by one without overlapping nor touching, up to 16 total patches (Figure 2). Since patch size remains constant and the number of pixels of class 1 increases, AI decreases, but the decrement is not linear with the number of patches. Note that the positions of the patches are not relevant, as long as the patches remain separate, because the number of edges between cells, and therefore AI, remains the same.

Maps in Figure 2 differ from those in He et al. [36] because the random sequence that places the patches is different. Since only the number of patches and not their locations influences the value of AI, its values should be the same as in He et al. [36].

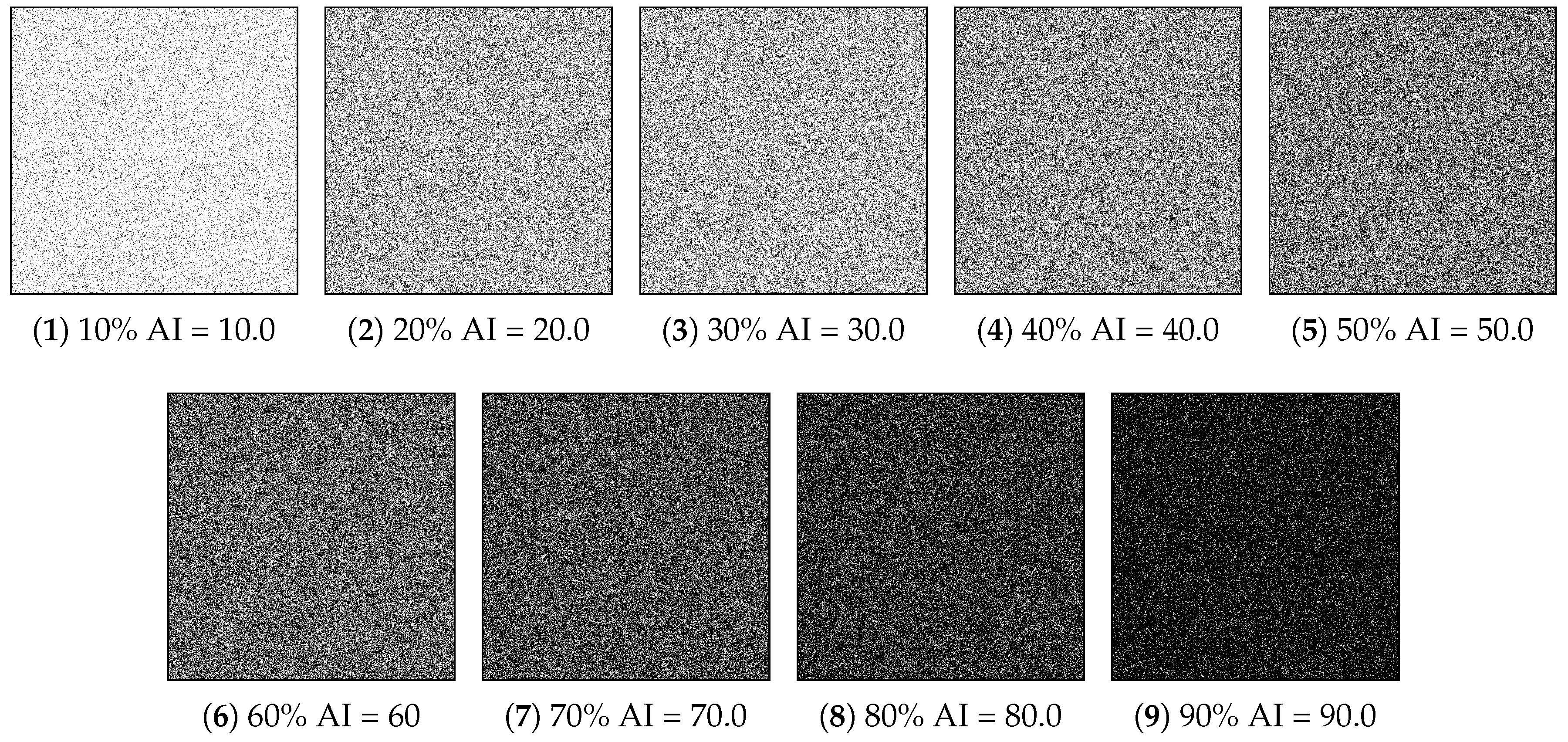
A third map set from He et al. [36] is composed of binary maps (Figure 3), $1024\times 1024$ cells, which have an increasing number of randomly placed cells of value 1, from 10% to 90% of the whole area with 10% increments. For each map, AI values correspond to the percentage of cells with a value of 1.

The approximation functions that express the relationship between the AI and the variation in the values of some metrics with different CN configurations will be checked using these maps.

3. Materials and Methods

The analysis of the variation in AI in landscape metrics has been investigated using R’s landscapemetrics package [38] (Section 3.2), while test map creation has been scripted in GRASS GIS (Section 3.1). A series of maps have been created to examine the relationship between AI and the variation in landscape metrics.

The first set of maps consists of ten artificial maps with an increasing number of randomly placed cells, from 10% to 90% of the whole area, with 10% increments (Figure 3). These maps have been used to estimate the coefficients of approximating functions expressing the relationship between the AI and the difference in the values of some metrics with different CN configurations.

A second set of artificial maps has been created to check the approximating functions. These maps (Figure 2), in part, correspond to the maps used in He et al. [36] to test AI response to the maps’ features such as level of aggregation, number of patches and spatial resolutions.

The third set of maps, represented in Section 3.3, is based on a real forest map, with the application of a high-pass filter and low-pass filter to create a series of maps with increasing levels of aggregation. These maps will be used to test the viability of using the approximating functions for real maps.

3.1. Test Software

The evaluation of all the landscape metrics, including AI, has been carried out using R’s landscapemetrics package [38]. R is a Free and Open Source Software (FOSS) environment for statistical computing and graphics [39]. The landscapemetrics package evaluates landscape metrics for raster maps (“objects” in R). It implements most of the original metrics from FRAGSTATS [37] plus some new metrics following recent developments in the field. It can also be used to build new custom metrics. It is possible to use this package to visualize the results of the analysis [38].

GRASS GIS [40] is a multi-purpose FOSS GIS for geospatial data production, analysis and mapping [41] available under the GNU Public License (GPL), and is used in research and education [11]. Ready-to-install packages are provided for the MS Windows, Apple Mac OSX and Linux operative systems. It is a project of the Open Source Geospatial Foundation (OSGeo). It has been used to script the creation of the artificial maps and maps derived from real maps.

The Landscapemetrics package performs all the operations about landscape metrics that are possible on Fragstat [38], with the option of using a 4 or 8 CN. It can be used to calculate an entire set of metrics (cell, class or whole landscape). It also accepts as input a user defined array of metrics to be calculated.

Landscapemetrics is based on Fragstat, so all the metrics that are used in the literature are available from this package [38]. The choice of other tools for landscape metrics evaluation would have been limiting, for example, in QGIS [42] the Lecos plugin [43] calculates only a limited array of metrics, while the r.le suite in GRASS GIS does not allow an 8 CN [32].

3.2. Landscape Metrics Calculation with R

A custom R script has been written to calculate the metrics for a set of maps, using both 4 CN and 8 CN configurations. The results of these calculations are stored in two different dataframes, which contain a row for each metric and a column for each map, with one containing the metrics values with a 4 CN and one containing the metrics values with an 8 CN. The second step performed by the R script is to subtract these two dataframes to quantify the differences in absolute value and in percentage for the two CN configurations. The differences can then be easily plotted and analyzed. The coefficients and the fitting statistics for 3-degree and 6-degree polynomials as a function of AI are evaluated for each metric difference. Finally, the differences for the area_mn metric for binary maps in Figure 3 between interpolated and evaluated values with an 8 CN are calculated to check the interpolated values.

The whole procedure is shown in the flowchart in Figure 4.

The script is available on a dedicated GitHub repository under the GNU license [44].

3.3. Maps

A set of maps have been built by applying filters to a real map of the forest coverage in the Val di Fassa, Italy, in 2006 (Figure 5(3)). This map has already been used to test the relevance of the cell neighborhood size in landscape metric evaluation in [32]. Val di Fassa is a valley in the north east of the Trentino region in the Alps in Northern Italy (Figure 5). A considerable expansion of the forested area has been registered in this area in the last century [2,38,45,46,47]. This trend is currently being analyzed in the Trentinoland project, investigating the forest coverage evolution of the whole Trentino region in Northern Italy [48].

The area covered by this map is 567.28 ${\mathrm{km}}^2$ (56,728 ha), of which 132.36 ${\mathrm{km}}^2$ (13,236 ha, 23.33%) were covered by forest in 2006. The region boundaries are 5157094 N, 5132029 S, 721983 E, 699351 W, in the ETRS89/UTM 32 N (EPSG 25832) datum. The raster map has a 10 m resolution, with 2509 rows and 2265 columns, for a total of 5,682,885 cells. The map is binary, with a value of 1 representing forest and a NULL value for other coverages.

To obtain maps with AI values covering the 0–100 range as much as possible, two sets of maps have been created from the original forest map. All the new maps cover the same area and have the same resolution of the original one.

The first set of maps has been created by applying a $5\times 5$ high-pass filter, with central value from 15 to 40 and with step 1 (

Table 1. High-pass filter used to generate maps with AI values from 2.7 to 72.9. The value of h varies from 15 to 39, with step 1, creating 24 different maps.

$-1$	$-1$	$-1$	$-1$	$-1$
$-1$	$-1$	$-1$	$-1$	$-1$
$-1$	$-1$	h	$-1$	$-1$
$-1$	$-1$	$-1$	$-1$	$-1$
$-1$	$-1$	$-1$	$-1$	$-1$

). All pixels with a value of 5 or above are set to 1, and the remaining pixels are set to 0. The resulting set contains 25 maps with AI values between 2.7 and 72.9. Images are shown in Figure A1 in Appendix A.

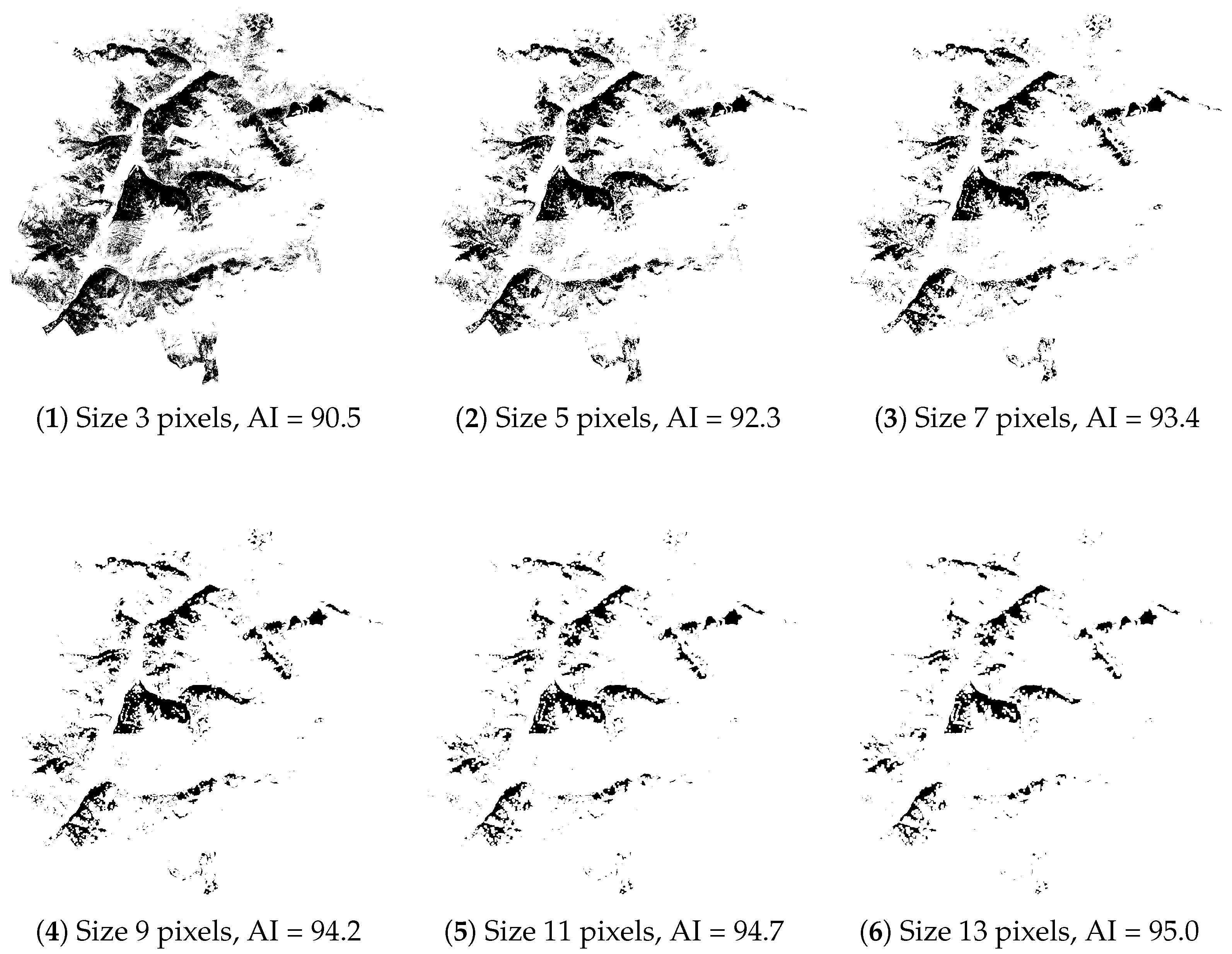
The second set contains thirteen maps, created by a moving window assigning the mode of the values to the central pixels. The size of the moving window varies from 3 to 25, using only odd numbers. For these maps AI ranges from 90.5 to 95.3. Images are shown in Figure A2 in Appendix A.

The union of these two map sets contains maps with AI values ranging from 2.7 to 95.3, providing a good sampling for the whole 0–100 variation interval for AI.

4. Results

Landscape metrics discussed in Section 3.2 have been evaluated for the test maps described in Section 2 and Section 3.3. All the maps are binary and all the landscape metrics have been evaluated for the class of a value of 1. This approach allows the isolation of the effects of different CN configurations on the metrics values from the influence of the presence of different classes with different metrics values.

All the metrics have been calculated using both four and eight CN configurations to assess the influence of this choice on the metrics values as a function of AI.

4.1. Metrics Selection

Landscape metrics whose values depend on the choice of CN have been selected by comparing their values when evaluated with a four or an eight CN configuration using R’s landscapemetrics package [32]. Metrics which are evaluated as ratios are independent from the choice of CN [32], because numerators and denominators change in the same way when the choice of CN changes.

The result is shown in

Table 2. Commonly used landscape metrics and their values dependence on the choice of a 4 or 8 CN configuration. Abbreviations correspond to R’s Landscapemetrics package names. The ✓ symbol indicates dependency of the metric from the choice of CN, ✗ implies independence.

Metric	Abbreviation	Difference?
Aggregation Index	AI	✗
Mean Class Area	area_mn	✓
Class Area	ca	✗
Cohesion	cohesion	✓
Core Class Area	cai_mn	✓
Clumpyness	clumpy	✗
Mean of Contiguity	contig_mn	✓
Mean of core area	core_mn	✗
Disjunct Core Area	dcore_mn	✓
Division	division	✓
Edge Density	ed	✗
Mean of euclidean nearest-neighbor distance	enn_mn	✓
Fractal index	frac_mn	✓
Gyrate radius	gyrate_mn	✓
Interspersion and Juxtaposition index	iji	✗
Landscape shape index	lsi	✗
Largest Patch Index	lpi	✓
Mesh size	mesh	✓
Number of Disjunct Core Area	ndca	✓
Normalized landscape shape index	nlsi	✗
Number of Patches	np	✓
Patch Density	pd	✓
Percentage of Like Adjacencies	pladj	✗
Percentage of landscape of class	pland	✗
Perimeter-Area Fractal Dimension	pafrac	✓
Perimeter area ratio	para_mn	✓
Shape index	shape_mn	✓
Splitting index	split	✓
Total Core Area	tca	✗
Total edge	te	✗

. The same table indicates the abbreviate names of the metrics used by R’s Landscapemetrics. These abbreviations will be used in the next sections.

The landscape metrics cohesion, frac_mn, pafrac, para_mn and shape_mn have not been used in the proceeding of this research because their evaluation is too memory intensive and would have required huge processing times.

Note that different software implementations use slightly different metric names.

4.2. Artificial Maps

Because the maps in He et al. [36] appear to be out of sequence and AI values seem dubious, AI values for maps in Section 2 have been re-evaluated using AI definition of Equation (3) and a four CN configuration.

Values of AI for the first set of maps (Figure 1) correspond to the values reported in He et al. [36].

The second set of maps has been created by adding randomly placed non overlapping $4\times 4$ patches on a map of $25\times 25$ cells with resolution 1 ([pixel]), from 1 to 16 patches (Figure 2). AI decreases when the number of patches increases, as shown in

Table 3. AI evaluation for artificial maps in Figure 2 with a 4 CN configuration. The “Map” column indicates the map in Figure 2. $e_{1,1}$ is the number of edges between cells with a value of 1 (in black on Figure 2), n is the number of pixels in the side of the largest square with area smaller than $A_i$ and $m=A_i-n^2$, as defined in Section 2. $max{e}_{1,1}$ is evaluated with Equation (1) and AI with Equation (3). The last column “Corr.” (Corresponds) indicates the correspondence with values reported in He et al. [36]. The value for the map in Figure 2(6) does not correspond; * denotes values that are swapped in He et al. [36].

Map	N. of Patches	${\mathit{e}}_{1,1}$	Area ${\mathit{A}}_1$	Sqrt. of ${\mathit{A}}_1$	n	m	$max{\mathit{e}}_{1,1}$	${\mathit{A}}_{\mathit{i}}$	Corr.
1	1	24	16	4.000	4	0	24	100	✓
2	2	48	32	5.657	5	7	52	92.3	✓
3	3	72	48	6.928	6	12	82	87.8	✓
4	4	96	64	8.000	8	0	112	85.7	✓
5	5	120	80	8.944	8	16	142	84.5	✓
6	6	144	96	9.798	9	15	172	83.7	✗
7	7	168	112	10.583	10	12	202	83.2	✓
8	8	192	128	11.313	11	7	233	82.4	✓
9	9	216	144	12.000	12	0	264	81.8	✓
10	10	240	160	12.649	12	16	294	81.6	✓
11	11	264	176	13.266	13	7	325	81.2	*
12	12	288	192	13.856	13	23	356	80.9	*
13	13	312	208	14.422	14	12	387	80.6	✓
14	14	336	224	14.967	14	28	418	80.4	✓
15	15	360	240	15.492	15	15	448	80.2	✓
16	16	384	256	16.000	16	0	480	80.0	✓

. In this table $e_{1,1}$ is the number of edges between cells with a value of 1 (in black on Figure 2), n is the number of pixels in the side of the largest square with area smaller than $A_i$ and $m=A_i-n^2$, as defined in Section 2. $max{e}_{1,1}$ is evaluated with Equation (1) and AI with Equation (3). The last column “Corresponds” indicates the correspondence with values reported in He et al. [36]. The AI value for the map in Figure 2(6) does not correspond, the value has probably been erroneously copied for the preceding one; * denotes values that are swapped in the original figure in He et al. [36].

AI values for the third map set from He et al. [36] (Figure 3), correspond to the percentage of cells with a value of 1, from 10% to 90% of the whole area with 10% increments. For these maps all the landscape metrics whose values depends on the CN choice have been evaluated and their values will be used to test polynomial functions to evaluate the differences in metrics values for different CN configurations. Landscape metric values are reported in

Table A1. Landscape metrics values for maps in Figure 3 for CN 4. N/A indicates that the value is not available.

Map	ai	area_mn	cai_mn	contig_mn	dcore_mn	division	enn_mn
1	10	$1.25{10}^{-4}$	$1.88{10}^{-3}$	$3.55{10}^{-2}$	$1.07{10}^{-4}$	$1.00$	$2.06$
2	20	$1.65{10}^{-4}$	$3.64{10}^{-2}$	$7.57{10}^{-2}$	$2.58{10}^{-3}$	$1.00$	$1.70$
3	30	$2.33{10}^{-4}$	$1.99{10}^{-1}$	$1.18{10}^{-1}$	$1.81{10}^{-2}$	$1.00$	$1.55$
4	40	$3.76{10}^{-4}$	$6.34{10}^{-1}$	$1.61{10}^{-1}$	$8.45{10}^{-2}$	$1.00$	$1.48$
5	50	$7.56{10}^{-4}$	$1.39$	$1.87{10}^{-1}$	$3.58{10}^{-1}$	$1.00$	$1.44$
6	60	$2.39{10}^{-3}$	$1.01$	$1.31{10}^{-1}$	$1.84$	$4.71{10}^{-1}$	$1.43$
7	70	$9.38{10}^{-3}$	$2.49{10}^{-1}$	$5.99{10}^{-2}$	$8.88$	$3.46{10}^{-2}$	$1.42$
8	80	$5.48{10}^{-2}$	$7.39{10}^{-2}$	$2.18{10}^{-2}$	$41.80$	$4.27{10}^{-3}$	$1.42$
9	90	$9.93{10}^{-1}$	$6.88{10}^{-1}$	$1.30{10}^{-2}$	$207.38$	$2.03{10}^{-4}$	N/A

and

Table A2. Landscape metrics values for maps in Figure 3 for CN 4.

Map	gyrate_mn	lpi	mesh	ndca	np	pd	split
1	$1.01{10}^{-1}$	$9.54{10}^{-3}$	$1.55{10}^{-4}$	9	$84,028$	$801,350.40$	$67,690.26$
2	$2.13{10}^{-1}$	$1.29{10}^{-2}$	$2.60{10}^{-4}$	329	$127,484$	$607,888.80$	$80,607.61$
3	$3.45{10}^{-1}$	$1.68{10}^{-2}$	$4.95{10}^{-4}$	2448	$134,877$	$428,762.20$	$63,593.53$
4	$5.22{10}^{-1}$	$2.74{10}^{-2}$	$1.24{10}^{-3}$	9419	$111,498$	$265,831.60$	$33,933.10$
5	$7.55{10}^{-1}$	$1.00{10}^{-1}$	$5.80{10}^{-3}$	$24,815$	$69,396$	$132,362.40$	$9044.64$
6	$0.49$	$72.67$	$33.26$	$48,560$	$26,364$	$41,904.42$	$1.89$
7	$0.21$	$98.25$	$70.86$	$69,496$	7822	$10,656.62$	$1.04$
8	$0.31$	$99.79$	$83.53$	$63,959$	1530	$1823.90$	$1.00$
9	$4.13$	$99.99$	$94.35$	$19,701$	95	$100.67$	$1.00$

for CN configurations equal to four and in

Table A3. Landscape metrics values for maps in Figure 3 for CN 8. N/A indicates that the value is not available.

Map	ai	area_mn	cai_mn	contig_mn	dcore_mn	division	enn_mn
1	10	$1.56{10}^{-4}$	$2.23{10}^{-3}$	$5.18{10}^{-2}$	$1.34{10}^{-4}$	$1.00$	$2.38$
2	20	$2.78{10}^{-4}$	$4.19{10}^{-2}$	$1.08{10}^{-1}$	$4.29{10}^{-3}$	$1.00$	$2.11$
3	30	$6.31{10}^{-4}$	$2.22{10}^{-1}$	$1.57{10}^{-1}$	$4.65{10}^{-2}$	$1.00$	$2.04$
4	40	$2.49{10}^{-3}$	$3.41{10}^{-1}$	$1.52{10}^{-1}$	$5.04{10}^{-1}$	$9.79{10}^{-1}$	$2.02$
5	50	$1.50{10}^{-2}$	$1.45{10}^{-1}$	$9.91{10}^{-2}$	$5.79$	$3.10{10}^{-2}$	$2.01$
6	60	$1.11{10}^{-1}$	$2.27{10}^{-2}$	$5.39{10}^{-2}$	$60.22$	$2.64{10}^{-3}$	$2.01$
7	70	$1.18$	$3.85{10}^{-1}$	$3.08{10}^{-2}$	$618.61$	$1.91{10}^{-4}$	$2.00$
8	80	$11.98$	$5.82$	$1.38{10}^{-1}$	$2898.86$	$1.67{10}^{-5}$	$2.00$
9	90	$94.37$	$65.32$	$8.99{10}^{-1}$	$1567.00$	0	N/A

and

Table A4. Landscape metrics values for maps in Figure 3 for CN 8.

Map	gyrate_mn	lpi	mesh	ndca	np	pd	split
1	$0.24$	$1.53{10}^{-2}$	$2.28{10}^{-4}$	9	$67,264$	$641,477.05$	$46,070.18$
2	$0.53$	$2.05{10}^{-2}$	$6.07{10}^{-4}$	323	$75,327$	$359,185.76$	$34,543.62$
3	$0.94$	$8.81{10}^{-2}$	$2.73{10}^{-3}$	2317	$49,879$	$158,560.97$	$11,508.93$
4	$1.05$	$7.54$	$8.97{10}^{-1}$	8485	$16,838$	$40,144.86$	$46.78$
5	$0.47$	$98.44$	$5.08{10}^1$	$20,310$	3505	$6685.26$	$1.03$
6	$0.86$	$99.87$	$62.75$	$34,085$	566	$899.63$	$1.00$
7	$6.37$	$99.99$	$73.39$	$38,354$	62	$84.47$	$1.00$
8	$56.05$	$100.00$	$83.88$	$20,292$	7	$8.34$	$1.00$
9	$391.75$	$100.00$	$94.37$	1567	1	$1.06$	$1.00$

for CN configurations equal to eight in Appendix B.1.

4.3. Real Maps

The fourth set of maps represent a modification of real forest maps, described in Section 3.3, with AI ranging from 2.70 to 95.3. The original forest map has an AI value of 86.7. Maps created using the low-pass filter described in Section 3.3 have AI values from 2.7 to 72.8, while maps resulting from the application of a low-pass filter range from 86.7 to 95.3 (

Table 4. AI values for maps derived from a real forest maps (Figure 5(3)) with high-pass and low-pass filter with different coefficients (high-pass) and sizes (low-pass).

Map	AI
Original map	86.7
High-pass filter 15	2.7
High-pass filter 16	9.9
High-pass filter 17	14.8
High-pass filter 18	21.7
High-pass filter 19	26.5
High-pass filter 20	33.7
High-pass filter 21	39.6
High-pass filter 22	50.2
High-pass filter 23	58.3
High-pass filter 24	72.9
High-pass filter 25	66.9
High-pass filter 26	62.1
High-pass filter 27	53.7
High-pass filter 28	49.7
High-pass filter 29	42.3
High-pass filter 30	39.0
High-pass filter 31	33.0
High-pass filter 32	30.4
High-pass filter 33	25.7
High-pass filter 34	23.5
High-pass filter 35	19.1
High-pass filter 36	16.8
High-pass filter 37	12.0
High-pass filter 38	9.3
High-pass filter 39	3.6
Low-pass filter mode 03	90.5
Low-pass filter mode 05	92.3
Low-pass filter mode 07	93.4
Low-pass filter mode 09	94.2
Low-pass filter mode 11	94.7
Low-pass filter mode 13	95.0
Low-pass filter mode 15	95.1
Low-pass filter mode 17	95.1
Low-pass filter mode 19	95.3
Low-pass filter mode 21	95.3
Low-pass filter mode 23	95.3
Low-pass filter mode 25	95.3

).

Metrics which have different values for four CN and eight CN configurations (see Section 4.1) have been evaluated for all the maps (Table A1, Table A2, Table A3, Table A4,

Table A5. Landscape metrics values for maps derived from a real forest maps with high-pass (Figure A1) and low-pass filters with different coefficients (high-pass) and sizes (low-pass) (Figure A2) for CN 4.

Map	ai	area_mn	cai_mn	contig_mn	dcore_mn	division	enn_mn
Original map	$86.66$	$3.74{10}^{-1}$	$1.04$	$1.18{10}^{-1}$	$6.29{10}^{-1}$	$8.45{10}^{-1}$	$19.93$
High-pass f. 15	$2.71$	$1.05{10}^{-2}$	0	$9.43{10}^{-3}$	$0.00$	$1.00$	$51.16$
High-pass f. 16	$9.91$	$1.24{10}^{-2}$	$1.31{10}^{-3}$	$3.59{10}^{-2}$	$6.53{10}^{-5}$	$1.00$	$29.52$
High-pass f. 17	$14.77$	$1.41{10}^{-2}$	$5.91{10}^{-3}$	$5.40{10}^{-2}$	$3.19{10}^{-4}$	$1.00$	$25.16$
High-pass f. 18	$21.73$	$1.72{10}^{-2}$	$4.31{10}^{-2}$	$8.00{10}^{-2}$	$2.97{10}^{-3}$	$1.00$	$21.72$
High-pass f. 19	$26.46$	$1.99{10}^{-2}$	$1.13{10}^{-1}$	$9.69{10}^{-2}$	$9.69{10}^{-3}$	$1.00$	$20.46$
High-pass f. 20	$33.70$	$2.60{10}^{-2}$	$3.21{10}^{-1}$	$1.22{10}^{-1}$	$3.67{10}^{-2}$	$1.00$	$18.81$
High-pass f. 21	$39.62$	$3.37{10}^{-2}$	$5.53{10}^{-1}$	$1.43{10}^{-1}$	$7.82{10}^{-2}$	$1.00$	$18.14$
High-pass f. 22	$50.21$	$5.98{10}^{-2}$	$1.01$	$1.50{10}^{-1}$	$2.60{10}^{-1}$	$1.00$	$18.53$
High-pass f. 23	$58.29$	$9.02{10}^{-2}$	$8.02{10}^{-1}$	$1.14{10}^{-1}$	$6.14{10}^{-1}$	$9.98{10}^{-1}$	$19.53$
High-pass f. 24	$72.86$	$2.22{10}^{-1}$	$1.39$	$1.31{10}^{-1}$	$1.76$	$9.13{10}^{-1}$	$20.23$
High-pass f. 25	$66.90$	$1.77{10}^{-1}$	$1.13$	$1.32{10}^{-1}$	$1.63$	$9.29{10}^{-1}$	$20.44$
High-pass f. 26	$62.08$	$1.43{10}^{-1}$	$1.24$	$1.43{10}^{-1}$	$1.13$	$9.95{10}^{-1}$	$20.16$
High-pass f. 27	$53.70$	$8.28{10}^{-2}$	$1.45$	$1.88{10}^{-1}$	$4.21{10}^{-1}$	$1.00$	$18.91$
High-pass f. 28	$49.73$	$6.30{10}^{-2}$	$1.24$	$1.95{10}^{-1}$	$2.53{10}^{-1}$	$1.00$	$18.49$
High-pass f. 29	$42.34$	$3.98{10}^{-2}$	$7.24{10}^{-1}$	$1.76{10}^{-1}$	$9.63{10}^{-2}$	$1.00$	$18.20$
High-pass f. 30	$38.97$	$3.33{10}^{-2}$	$5.18{10}^{-1}$	$1.60{10}^{-1}$	$6.07{10}^{-2}$	$1.00$	$18.48$
High-pass f. 31	$32.97$	$2.54{10}^{-2}$	$2.71{10}^{-1}$	$1.31{10}^{-1}$	$2.63{10}^{-2}$	$1.00$	$19.72$
High-pass f. 32	$30.41$	$2.29{10}^{-2}$	$1.94{10}^{-1}$	$1.19{10}^{-1}$	$1.73{10}^{-2}$	$1.00$	$20.67$
High-pass f. 33	$25.73$	$1.94{10}^{-2}$	$8.97{10}^{-2}$	$9.94{10}^{-2}$	$6.91{10}^{-3}$	$1.00$	$22.59$
High-pass f. 34	$23.48$	$1.81{10}^{-2}$	$5.32{10}^{-2}$	$8.97{10}^{-2}$	$3.83{10}^{-3}$	$1.00$	$23.74$
High-pass f. 35	$19.10$	$1.58{10}^{-2}$	$1.79{10}^{-2}$	$7.21{10}^{-2}$	$1.15{10}^{-3}$	$1.00$	$26.92$
High-pass f. 36	$16.79$	$1.48{10}^{-2}$	$7.49{10}^{-3}$	$6.31{10}^{-2}$	$4.50{10}^{-4}$	$1.00$	$28.97$
High-pass f. 37	$11.99$	$1.31{10}^{-2}$	0	$4.41{10}^{-2}$	0	$1.00$	$35.11$
High-pass f. 38	$9.32$	$1.22{10}^{-2}$	0	$3.40{10}^{-2}$	0	$1.00$	$40.63$
High-pass f. 39	$3.61$	$1.07{10}^{-2}$	0	$1.28{10}^{-2}$	0	$1.00$	$65.26$
Low-pass f. mode 03	$90.52$	$9.44{10}^{-1}$	$4.84$	$2.55{10}^{-1}$	$6.12{10}^{-1}$	$8.99{10}^{-1}$	$32.68$
Low-pass f. mode 05	$92.32$	$1.52$	$9.70$	$3.59{10}^{-1}$	$6.53{10}^{-1}$	$9.35{10}^{-1}$	$48.48$
Low-pass f. mode 07	$93.47$	$2.08$	$14.04$	$4.26{10}^{-1}$	$6.81{10}^{-1}$	$9.25{10}^{-1}$	$66.97$
Low-pass f. mode 09	$94.22$	$2.75$	$18.37$	$4.76{10}^{-1}$	$7.21{10}^{-1}$	$9.32{10}^{-1}$	$85.20$
Low-pass f. mode 11	$94.66$	$3.26$	$20.36$	$4.92{10}^{-1}$	$6.85{10}^{-1}$	$9.24{10}^{-1}$	$108.59$
Low-pass f. mode 13	$94.96$	$4.12$	$25.19$	$5.53{10}^{-1}$	$7.79{10}^{-1}$	$9.22{10}^{-1}$	$128.32$
Low-pass f. mode 15	$95.11$	$4.57$	$27.64$	$5.76{10}^{-1}$	$7.86{10}^{-1}$	$9.36{10}^{-1}$	$166.78$
Low-pass f. mode 17	$95.15$	$4.98$	$30.98$	$5.98{10}^{-1}$	$8.41{10}^{-1}$	$9.30{10}^{-1}$	$172.70$
Low-pass f. mode 19	$95.26$	$4.99$	$34.93$	$6.30{10}^{-1}$	$8.13{10}^{-1}$	$9.32{10}^{-1}$	$180.24$
Low-pass f. mode 21	$95.30$	$4.98$	$38.65$	$6.85{10}^{-1}$	$9.04{10}^{-1}$	$9.32{10}^{-1}$	$201.90$
Low-pass f. mode 23	$95.30$	$4.57$	$35.11$	$6.40{10}^{-1}$	$7.63{10}^{-1}$	$9.22{10}^{-1}$	$198.67$
Low-pass f. mode 25	$95.34$	$4.68$	$39.85$	$6.81{10}^{-1}$	$8.55{10}^{-1}$	$9.18{10}^{-1}$	$220.64$

,

Table A6. Landscape metrics values for maps derived from a real forest maps with high-pass (Figure A1) and low-pass filters with different coefficients (high-pass) and sizes (low-pass) (Figure A2) for CN 4.

Map	gyrate_mn	lpi	mesh	ndca	np	pd	split
Original map	$4.66$	$34.36$	$2.05{10}^3$	$22,296$	$35,432$	$267.68$	$6.47$
High-pass filter 15	$0.28$	$1.90{10}^{-2}$	$1.11{10}^{-2}$	0	9964	$9480.97$	$9509.16$
High-pass filter 16	$1.03$	$2.10{10}^{-2}$	$1.50{10}^{-2}$	2	$30,641$	$8050.94$	$25,323.02$
High-pass filter 17	$1.54$	$1.94{10}^{-2}$	$1.93{10}^{-2}$	14	$43,934$	$7108.37$	$32,059.10$
High-pass filter 18	$2.27$	$2.55{10}^{-2}$	$2.89{10}^{-2}$	183	$61,580$	$5825.83$	$36,538.23$
High-pass filter 19	$2.80$	$2.80{10}^{-2}$	$4.01{10}^{-2}$	692	$71,404$	$5015.17$	$35,471.53$
High-pass filter 20	$3.74$	$3.83{10}^{-2}$	$7.30{10}^{-2}$	3021	$82,325$	$3850.40$	$29,286.11$
High-pass filter 21	$4.71$	$7.09{10}^{-2}$	$1.31{10}^{-1}$	6346	$81,104$	$2969.05$	$20,919.34$
High-pass filter 22	$6.35$	$5.09{10}^{-1}$	$7.40{10}^{-1}$	$16,911$	$64,979$	$1673.63$	$5247.46$
High-pass filter 23	$5.46$	$1.83$	$1.11{10}^1$	$33,946$	$55,290$	$1108.45$	$448.08$
High-pass filter 24	$5.26$	$24.25$	$7.01{10}^2$	$63,668$	$36,203$	$451.42$	$11.45$
High-pass filter 25	$5.43$	$22.38$	$4.63{10}^2$	$60,130$	$36,883$	$563.87$	$14.14$
High-pass filter 26	$7.01$	$3.21$	$2.52{10}^1$	$43,903$	$38,736$	$701.35$	$219.31$
High-pass filter 27	$8.23$	$4.50{10}^{-1}$	$1.12$	$20,706$	$49,235$	$1207.09$	$3657.90$
High-pass filter 28	$7.56$	$1.92{10}^{-1}$	$3.92{10}^{-1}$	$14,159$	$55,876$	$1586.88$	$8979.24$
High-pass filter 29	$5.77$	$4.96{10}^{-2}$	$1.29{10}^{-1}$	6378	$66,232$	$2513.05$	$20,459.90$
High-pass filter 30	$5.01$	$4.80{10}^{-2}$	$9.29{10}^{-2}$	4127	$68,024$	$2999.21$	$24,412.98$
High-pass filter 31	$3.85$	$5.27{10}^{-2}$	$5.77{10}^{-2}$	1711	$65,000$	$3941.66$	$28,599.64$
High-pass filter 32	$3.43$	$6.15{10}^{-2}$	$4.86{10}^{-2}$	1052	$60,824$	$4358.49$	$28,738.75$
High-pass filter 33	$2.81$	$4.10{10}^{-2}$	$3.54{10}^{-2}$	346	$50,091$	$5146.12$	$27,481.61$
High-pass filter 34	$2.52$	$4.95{10}^{-2}$	$3.08{10}^{-2}$	171	$44,639$	$5538.89$	$26,170.53$
High-pass filter 35	$2.03$	$3.16{10}^{-2}$	$2.37{10}^{-2}$	39	$33,872$	$6312.76$	$22,597.95$
High-pass filter 36	$1.77$	$3.96{10}^{-2}$	$2.09{10}^{-2}$	13	$28,866$	$6738.34$	$20,487.39$
High-pass filter 37	$1.26$	$3.14{10}^{-2}$	$1.65{10}^{-2}$	0	$19,435$	$7648.20$	$15,436.85$
High-pass filter 38	$0.98$	$2.21{10}^{-2}$	$1.45{10}^{-2}$	0	$14,768$	$8173.95$	$12,482.33$
High-pass filter 39	$0.38$	$2.88{10}^{-2}$	$1.14{10}^{-2}$	0	6441	$9302.70$	$6069.66$
Low-pass f. mode 03	$13.06$	$27.32$	$7.74{10}^2$	4974	8124	$105.92$	$9.91$
Low-pass f. mode 05	$21.21$	$18.50$	$3.40{10}^2$	2238	3428	$65.71$	$15.33$
Low-pass f. mode 07	$28.58$	$21.15$	$2.88{10}^2$	1247	1830	$47.99$	$13.26$
Low-pass f. mode 09	$35.97$	$17.96$	$1.99{10}^2$	764	1060	$36.38$	$14.62$
Low-pass f. mode 11	$41.04$	$19.99$	$1.75{10}^2$	480	701	$30.64$	$13.10$
Low-pass f. mode 13	$50.96$	$21.60$	$1.43{10}^2$	345	443	$24.25$	$12.81$
Low-pass f. mode 15	$57.85$	$19.15$	$9.39{10}^1$	253	322	$21.88$	$15.67$
Low-pass f. mode 17	$66.15$	$20.70$	$8.39{10}^1$	201	239	$20.07$	$14.19$
Low-pass f. mode 19	$69.40$	$19.17$	$6.51{10}^1$	157	193	$20.03$	$14.81$
Low-pass f. mode 21	$72.94$	$20.94$	$5.28{10}^1$	142	157	$20.08$	$14.81$
Low-pass f. mode 23	$67.25$	$22.89$	$4.96{10}^1$	106	139	$21.89$	$12.81$
Low-pass f. mode 25	$69.61$	$23.19$	$4.22{10}^1$	94	110	$21.36$	$12.20$

,

Table A7. Landscape metrics values for maps derived from a real forest maps with high-pass (Figure A1) and low-pass filters with different coefficients (high-pass) and sizes (low-pass) (Figure A2) for CN 8.

Map	ai	area_mn	cai_mn	contig_mn	dcore_mn	division	enn_mn
Original map	$86.66$	$7.53{10}^{-1}$	$9.99{10}^{-1}$	$1.23{10}^{-1}$	$5.52{10}^{-1}$	$5.16{10}^{-1}$	$27.96$
High-pass f. 15	$2.71$	$1.08{10}^{-2}$	$0.00$	$1.15{10}^{-2}$	$0.00$	$1.00$	$52.85$
High-pass f. 16	$9.91$	$1.40{10}^{-2}$	$1.48{10}^{-3}$	$4.72{10}^{-2}$	$7.38{10}^{-5}$	$1.00$	$33.20$
High-pass f. 17	$14.77$	$1.71{10}^{-2}$	$6.93{10}^{-3}$	$7.04{10}^{-2}$	$3.88{10}^{-4}$	$1.00$	$29.47$
High-pass f. 18	$21.73$	$2.34{10}^{-2}$	$4.99{10}^{-2}$	$1.01{10}^{-1}$	$4.04{10}^{-3}$	$1.00$	$26.60$
High-pass f. 19	$26.46$	$2.93{10}^{-2}$	$1.24{10}^{-1}$	$1.19{10}^{-1}$	$1.39{10}^{-2}$	$1.00$	$25.68$
High-pass f. 20	$33.70$	$4.40{10}^{-2}$	$3.20{10}^{-1}$	$1.43{10}^{-1}$	$5.68{10}^{-2}$	$1.00$	$24.40$
High-pass f. 21	$39.62$	$6.60{10}^{-2}$	$5.12{10}^{-1}$	$1.56{10}^{-1}$	$1.33{10}^{-1}$	$1.00$	$24.33$
High-pass f. 22	$50.21$	$1.23{10}^{-1}$	$5.90{10}^{-1}$	$1.25{10}^{-1}$	$4.27{10}^{-1}$	$9.96{10}^{-1}$	$25.60$
High-pass f. 23	$58.29$	$1.68{10}^{-1}$	$5.75{10}^{-1}$	$1.15{10}^{-1}$	$7.93{10}^{-1}$	$8.79{10}^{-1}$	$26.23$
High-pass f. 24	$72.86$	$4.39{10}^{-1}$	$1.67$	$1.45{10}^{-1}$	$1.77$	$6.49{10}^{-1}$	$28.29$
High-pass f. 25	$66.90$	$3.46{10}^{-1}$	$1.24$	$1.48{10}^{-1}$	$1.88$	$6.94{10}^{-1}$	$28.46$
High-pass f. 26	$62.08$	$2.83{10}^{-1}$	$1.02$	$1.47{10}^{-1}$	$1.53$	$9.42{10}^{-1}$	$28.45$
High-pass f. 27	$53.70$	$1.89{10}^{-1}$	$9.51{10}^{-1}$	$1.61{10}^{-1}$	$7.61{10}^{-1}$	$9.91{10}^{-1}$	$27.64$
High-pass f. 28	$49.73$	$1.46{10}^{-1}$	$9.45{10}^{-1}$	$1.78{10}^{-1}$	$4.91{10}^{-1}$	$9.97{10}^{-1}$	$26.78$
High-pass f. 29	$42.34$	$8.37{10}^{-2}$	$7.39{10}^{-1}$	$1.95{10}^{-1}$	$1.79{10}^{-1}$	$1.00$	$25.43$
High-pass f. 30	$38.97$	$6.33{10}^{-2}$	$5.54{10}^{-1}$	$1.88{10}^{-1}$	$1.04{10}^{-1}$	$1.00$	$25.07$
High-pass f. 31	$32.97$	$4.06{10}^{-2}$	$2.94{10}^{-1}$	$1.58{10}^{-1}$	$3.95{10}^{-2}$	$1.00$	$25.65$
High-pass f. 32	$30.41$	$3.45{10}^{-2}$	$2.14{10}^{-1}$	$1.44{10}^{-1}$	$2.50{10}^{-2}$	$1.00$	$26.46$
High-pass f. 33	$25.73$	$2.67{10}^{-2}$	$1.01{10}^{-1}$	$1.22{10}^{-1}$	$9.22{10}^{-3}$	$1.00$	$28.21$
High-pass f. 34	$23.48$	$2.38{10}^{-2}$	$6.10{10}^{-2}$	$1.11{10}^{-1}$	$5.00{10}^{-3}$	$1.00$	$29.24$
High-pass f. 35	$19.10$	$1.95{10}^{-2}$	$2.09{10}^{-2}$	$8.93{10}^{-2}$	$1.42{10}^{-3}$	$1.00$	$32.24$
High-pass f. 36	$16.79$	$1.77{10}^{-2}$	$8.43{10}^{-3}$	$7.80{10}^{-2}$	$5.37{10}^{-4}$	$1.00$	$34.11$
High-pass f. 37	$11.99$	$1.47{10}^{-2}$	$0.00$	$5.47{10}^{-2}$	$0.00$	$1.00$	$39.84$
High-pass f. 38	$9.32$	$1.33{10}^{-2}$	$0.00$	$4.19{10}^{-2}$	$0.00$	$1.00$	$44.88$
High-pass f. 39	$3.61$	$1.11{10}^{-2}$	$0.00$	$1.55{10}^{-2}$	$0.00$	$1.00$	$68.08$
Low-pass f. mode 03	$90.52$	$1.18$	$5.17$	$2.65{10}^{-1}$	$5.24{10}^{-1}$	$8.93{10}^{-1}$	$40.29$
Low-pass f. mode 05	$92.32$	$1.71$	$1.02{10}^1$	$3.69{10}^{-1}$	$5.96{10}^{-1}$	$9.34{10}^{-1}$	$56.04$
Low-pass f. mode 07	$93.47$	$2.27$	$1.48{10}^1$	$4.39{10}^{-1}$	$6.12{10}^{-1}$	$9.24{10}^{-1}$	$75.78$
Low-pass f. mode 09	$94.22$	$2.93$	$1.91{10}^1$	$4.88{10}^{-1}$	$6.62{10}^{-1}$	$9.31{10}^{-1}$	$94.70$
Low-pass f. mode 11	$94.66$	$3.45$	$2.13{10}^1$	$5.08{10}^{-1}$	$6.49{10}^{-1}$	$9.24{10}^{-1}$	$116.51$
Low-pass f. mode 13	$94.96$	$4.29$	$2.57{10}^1$	$5.63{10}^{-1}$	$7.49{10}^{-1}$	$9.22{10}^{-1}$	$138.90$
Low-pass f. mode 15	$95.11$	$4.66$	$2.78{10}^1$	$5.77{10}^{-1}$	$7.53{10}^{-1}$	$9.36{10}^{-1}$	$171.19$
Low-pass f. mode 17	$95.15$	$5.11$	$3.16{10}^1$	$6.08{10}^{-1}$	$8.07{10}^{-1}$	$9.30{10}^{-1}$	$180.05$
Low-pass f. mode 19	$95.26$	$5.12$	$3.55{10}^1$	$6.36{10}^{-1}$	$8.09{10}^{-1}$	$9.32{10}^{-1}$	$188.74$
Low-pass f. mode 21	$95.30$	$5.04$	$3.91{10}^1$	$6.89{10}^{-1}$	$8.65{10}^{-1}$	$9.32{10}^{-1}$	$205.32$
Low-pass f. mode 23	$95.30$	$4.70$	$3.60{10}^1$	$6.50{10}^{-1}$	$7.78{10}^{-1}$	$9.22{10}^{-1}$	$206.18$
Low-pass f. mode 25	$95.34$	$4.81$	$3.98{10}^1$	$6.80{10}^{-1}$	$7.94{10}^{-1}$	$9.18{10}^{-1}$	$230.54$

and

Table A8. Landscape metrics values for maps derived from a real forest maps with high-pass (Figure A1) and low-pass filters with different coefficients (high-pass) and sizes (low-pass) (Figure A2) for CN 8.

Map	gyrate_mn	lpi	mesh	ndca	np	pd	split
Original map	$6.44$	$6.67{10}^1$	$6.41{10}^3$	9707	$17,578$	$132.80$	$2.07$
High-pass f. 15	$4.48{10}^{-1}$	$1.90{10}^{-2}$	$1.15{10}^{-2}$	0	9745	$9272.59$	$9164.77$
High-pass f. 16	$1.89$	$2.10{10}^{-2}$	$1.79{10}^{-2}$	2	$27,115$	$7124.48$	$21,272.49$
High-pass f. 17	$2.84$	$2.58{10}^{-2}$	$2.56{10}^{-2}$	14	$36,122$	$5844.41$	$24,143.11$
High-pass f. 18	$4.22$	$3.49{10}^{-2}$	$4.65{10}^{-2}$	183	$45,259$	$4281.77$	$22,741.19$
High-pass f. 19	$5.14$	$6.59{10}^{-2}$	$7.92{10}^{-2}$	676	$48,653$	$3417.22$	$17,975.28$
High-pass f. 20	$6.84$	$2.53{10}^{-1}$	$2.68{10}^{-1}$	2764	$48,643$	$2275.07$	$7975.39$
High-pass f. 21	$8.60$	$7.93{10}^{-1}$	$1.05$	5520	$41,380$	$1514.84$	$2612.28$
High-pass f. 22	$8.48$	$2.96$	$1.49{10}^1$	$13,413$	$31,443$	$809.86$	$260.17$
High-pass f. 23	$6.48$	$3.10{10}^1$	$6.04{10}^2$	$23,586$	$29,739$	$596.20$	$8.25$
High-pass f. 24	$7.41$	$5.63{10}^1$	$2.82{10}^3$	$32,362$	$18,280$	$227.94$	$2.85$
High-pass f. 25	$7.69$	$5.31{10}^1$	$2.00{10}^3$	$35,492$	$18,924$	$289.31$	$3.27$
High-pass f. 26	$8.54$	$1.85{10}^1$	$3.20{10}^2$	$29,843$	$19,484$	$352.78$	$17.26$
High-pass f. 27	$1.11{10}^1$	$7.25$	$3.49{10}^1$	$16,432$	$21,584$	$529.17$	$116.84$
High-pass f. 28	$1.18{10}^1$	$4.61$	$1.22{10}^1$	$11,806$	$24,041$	$682.76$	$287.89$
High-pass f. 29	$1.07{10}^1$	$7.84{10}^{-1}$	$1.07$	5633	$31,480$	$1194.45$	$2463.53$
High-pass f. 30	$9.28$	$2.50{10}^{-1}$	$4.23{10}^{-1}$	3736	$35,813$	$1579.01$	$5360.29$
High-pass f. 31	$6.89$	$1.38{10}^{-1}$	$1.38{10}^{-1}$	1601	$40,570$	$2460.20$	$11,920.11$
High-pass f. 32	$6.08$	$8.37{10}^{-2}$	$9.64{10}^{-2}$	1009	$40,393$	$2894.46$	$14,483.01$
High-pass f. 33	$4.89$	$4.82{10}^{-2}$	$5.69{10}^{-2}$	336	$36,440$	$3743.68$	$17,116.71$
High-pass f. 34	$4.36$	$5.20{10}^{-2}$	$4.60{10}^{-2}$	169	$33,807$	$4194.84$	$17,526.91$
High-pass f. 35	$3.42$	$4.28{10}^{-2}$	$3.19{10}^{-2}$	39	$27,514$	$5127.81$	$16,846.18$
High-pass f. 36	$2.96$	$5.36{10}^{-2}$	$2.71{10}^{-2}$	13	$24,196$	$5648.19$	$15,831.20$
High-pass f. 37	$2.07$	$5.11{10}^{-2}$	$1.95{10}^{-2}$	0	$17,295$	$6806.05$	$13,062.04$
High-pass f. 38	$1.57$	$2.21{10}^{-2}$	$1.63{10}^{-2}$	0	$13,589$	$7521.39$	$11,085.03$
High-pass f. 39	$5.96{10}^{-1}$	$2.88{10}^{-2}$	$1.19{10}^{-2}$	0	6263	$9045.62$	$5808.75$
Low-pass f. mode 03	$1.51{10}^1$	$2.81{10}^1$	$8.21{10}^2$	3406	6500	$84.75$	$9.35$
Low-pass f. mode 05	$2.33{10}^1$	$1.85{10}^1$	$3.44{10}^2$	1815	3043	$58.33$	$15.16$
Low-pass f. mode 07	$3.08{10}^1$	$2.12{10}^1$	$2.88{10}^2$	1029	1681	$44.08$	$13.24$
Low-pass f. mode 09	$3.81{10}^1$	$1.80{10}^1$	$2.00{10}^2$	657	993	$34.08$	$14.59$
Low-pass f. mode 11	$4.32{10}^1$	$2.00{10}^1$	$1.75{10}^2$	431	664	$29.02$	$13.10$
Low-pass f. mode 13	$5.30{10}^1$	$2.16{10}^1$	$1.43{10}^2$	319	426	$23.32$	$12.80$
Low-pass f. mode 15	$5.88{10}^1$	$1.92{10}^1$	$9.40{10}^1$	238	316	$21.47$	$15.67$
Low-pass f. mode 17	$6.78{10}^1$	$2.07{10}^1$	$8.39{10}^1$	188	233	$19.57$	$14.19$
Low-pass f. mode 19	$7.12{10}^1$	$1.92{10}^1$	$6.51{10}^1$	152	188	$19.51$	$14.80$
Low-pass f. mode 21	$7.38{10}^1$	$2.09{10}^1$	$5.28{10}^1$	134	155	$19.83$	$14.81$
Low-pass f. mode 23	$6.91{10}^1$	$2.29{10}^1$	$4.96{10}^1$	105	135	$21.26$	$12.81$
Low-pass f. mode 25	$7.19{10}^1$	$2.32{10}^1$	$4.23{10}^1$	85	107	$20.78$	$12.18$

in the Appendix B.1 and Appendix B.2). Then the difference for each map and each metric is evaluated as the value of the metric calculated with an eight CN configuration minus the value of the same metric using a four CN configuration (

Table A9. Landscape metrics differences (metrics for CN 8 minus metrics for CN 4) for maps in Figure 3. N/A indicates that the value is not available.

Map	ai	area_mn	cai_mn	contig_mn	dcore_mn	division	enn_mn
1	10	$3.11{10}^{-5}$	$3.47{10}^{-4}$	$1.63{10}^{-2}$	$2.67{10}^{-5}$	$-6.91-06$	$3.20{10}^{-1}$
2	20	$1.14{10}^{-4}$	$5.49{10}^{-3}$	$3.21{10}^{-2}$	$1.71{10}^{-3}$	$-1.65{10}^{-5}$	$4.14{10}^{-1}$
3	30	$3.97{10}^{-4}$	$2.33{10}^{-2}$	$3.91{10}^{-2}$	$2.83{10}^{-2}$	$-7.1{10}^{-5}$	$4.88{10}^{-1}$
4	40	$2.11{10}^{-3}$	$-2.93{10}^{-1}$	$-9.65{10}^{-3}$	$4.19{10}^{-1}$	$-2.13{10}^{-2}$	$5.44{10}^{-1}$
5	50	$1.42{10}^{-2}$	$-1.25$	$-8.84{10}^{-2}$	$5.44$	$-9.69{10}^{-1}$	$5.72{10}^{-1}$
6	60	$1.09{10}^{-1}$	$-9.86{10}^{-1}$	$-7.75{10}^{-2}$	$58.38$	$-4.69{10}^{-1}$	$5.79{10}^{-1}$
7	70	$1.17$	$1.36{10}^{-1}$	$-2.92{10}^{-2}$	$609.73$	$-3.44{10}^{-2}$	$5.81{10}^{-1}$
8	80	$1.19{10}^1$	$5.75$	$1.16{10}^{-1}$	$2857.05$	$-4.25{10}^{-3}$	$5.83{10}^{-1}$
9	90	$9.34{10}^1$	$6.46{10}^1$	$8.86{10}^{-1}$	$1359.62$	$-2.03{10}^{-4}$	N/A

,

Table A10. Landscape metrics differences (metrics for CN 8 minus metrics for CN 4) for maps in Figure 3.

Map	gyrate_mn	lpi	mesh	ndca	np	pd	split
1	$1.40{10}^{-1}$	$5.72{10}^{-3}$	$7.27{10}^{-5}$	0	$-16,764$	$-159,873.36$	$-21,620.09$
2	$3.18{10}^{-1}$	$7.63{10}^{-3}$	$3.47{10}^{-4}$	$-6$	$-52,157$	$-248,703.04$	$-46,063.99$
3	$5.93{10}^{-1}$	$7.12{10}^{-2}$	$2.24{10}^{-3}$	$-131$	$-84,998$	$-270,201.23$	$-52,084.60$
4	$5.31{10}^{-1}$	$7.52$	$8.95{10}^{-1}$	$-934$	$-94,660$	$-225,686.74$	$-33,886.31$
5	$-2.85{10}^{-1}$	$9.83{10}^1$	$5.08{10}^1$	$-4505$	$-65,891$	$-12,5677.14$	$-9043.61$
6	$3.73{10}^{-1}$	$2.72{10}^1$	$2.95{10}^1$	$-14,475$	$-25,798$	$-41,004.79$	$-8.89{10}^{-1}$
7	$6.16$	$1.74$	$2.53$	$-31,142$	$-7760$	$-10572.15$	$-3.57{10}^{-2}$
8	$5.57{10}^1$	$2.13{10}^{-1}$	$3.56{10}^{-1}$	$-43,667$	$-1523$	$-1815.56$	$-4.27{10}^{-3}$
9	$3.88{10}^2$	$1.02{10}^{-2}$	$1.92{10}^{-2}$	$-18134$	$-94$	$-99.61$	$-2.03{10}^{-4}$

,

Table A11. Landscape metrics differences (metrics for CN 8 minus metrics for CN 4) for maps derived from a real forest maps with high-pass (Figure A1 and low-pass filters with different coefficients (high-pass) and sizes (low-pass) (Figure A2).

Map	ai	area_mn	cai_mn	contig_mn	dcore_mn	division	enn_mn
Original map	$86.7$	$3.79{10}^{-1}$	$-3.94{10}^{-2}$	$4.35{10}^{-3}$	$-7.70{10}^{-2}$	$-3.29{10}^{-1}$	$8.03$
High-pass f. 15	$2.7$	$2.37{10}^{-4}$	$0.00$	$2.08{10}^{-3}$	$0.00$	$-3.95{10}^{-6}$	$1.69$
High-pass f. 16	$9.9$	$1.62{10}^{-3}$	$1.70{10}^{-4}$	$1.13{10}^{-2}$	$8.49{10}^{-6}$	$-7.52{10}^{-6}$	$3.68$
High-pass f. 17	$14.8$	$3.04{10}^{-3}$	$1.03{10}^{-3}$	$1.64{10}^{-2}$	$6.89{10}^{-5}$	$-1.02{10}^{-5}$	$4.31$
High-pass f. 18	$21.7$	$6.19{10}^{-3}$	$6.83{10}^{-3}$	$2.13{10}^{-2}$	$1.07{10}^{-3}$	$-1.66{10}^{-5}$	$4.87$
High-pass f. 19	$26.5$	$9.32{10}^{-3}$	$1.16{10}^{-2}$	$2.19{10}^{-2}$	$4.20{10}^{-3}$	$-2.74{10}^{-5}$	$5.22$
High-pass f. 20	$33.7$	$1.80{10}^{-2}$	$-1.73{10}^{-3}$	$2.08{10}^{-2}$	$2.01{10}^{-2}$	$-9.12{10}^{-5}$	$5.58$
High-pass f. 21	$39.6$	$3.23{10}^{-2}$	$-4.12{10}^{-2}$	$1.30{10}^{-2}$	$5.52{10}^{-2}$	$-3.35{10}^{-4}$	$6.19$
High-pass f. 22	$50.2$	$6.37{10}^{-2}$	$-4.25{10}^{-1}$	$-2.46{10}^{-2}$	$1.66{10}^{-1}$	$-3.65{10}^{-3}$	$7.07$
High-pass f. 23	$58.3$	$7.75{10}^{-2}$	$-2.27{10}^{-1}$	$7.00{10}^{-4}$	$1.79{10}^{-1}$	$-1.19{10}^{-1}$	$6.70$
High-pass f. 24	$72.9$	$2.17{10}^{-1}$	$2.80{10}^{-1}$	$1.43{10}^{-2}$	$1.17{10}^{-2}$	$-2.64{10}^{-1}$	$8.05$
High-pass f. 25	$66.9$	$1.68{10}^{-1}$	$1.12{10}^{-1}$	$1.59{10}^{-2}$	$2.45{10}^{-1}$	$-2.35{10}^{-1}$	$8.02$
High-pass f. 26	$62.1$	$1.41{10}^{-1}$	$-2.13{10}^{-1}$	$3.92{10}^{-3}$	$3.98{10}^{-1}$	$-5.34{10}^{-2}$	$8.29$
High-pass f. 27	$53.7$	$1.06{10}^{-1}$	$-4.96{10}^{-1}$	$-2.67{10}^{-2}$	$3.41{10}^{-1}$	$-8.29{10}^{-3}$	$8.74$
High-pass f. 28	$49.7$	$8.34{10}^{-2}$	$-2.92{10}^{-1}$	$-1.65{10}^{-2}$	$2.38{10}^{-1}$	$-3.36{10}^{-3}$	$8.30$
High-pass f. 29	$42.3$	$4.39{10}^{-2}$	$1.50{10}^{-2}$	$1.90{10}^{-2}$	$8.26{10}^{-2}$	$-3.57{10}^{-4}$	$7.22$
High-pass f. 30	$39.0$	$3.00{10}^{-2}$	$3.62{10}^{-2}$	$2.74{10}^{-2}$	$4.36{10}^{-2}$	$-1.46{10}^{-4}$	$6.59$
High-pass f. 31	$33.0$	$1.53{10}^{-2}$	$2.29{10}^{-2}$	$2.65{10}^{-2}$	$1.31{10}^{-2}$	$-4.89{10}^{-5}$	$5.93$
High-pass f. 32	$30.4$	$1.16{10}^{-2}$	$1.97{10}^{-2}$	$2.52{10}^{-2}$	$7.68{10}^{-3}$	$-3.43{10}^{-5}$	$5.79$
High-pass f. 33	$25.7$	$7.28{10}^{-3}$	$1.12{10}^{-2}$	$2.27{10}^{-2}$	$2.31{10}^{-3}$	$-2.20{10}^{-5}$	$5.62$
High-pass f. 34	$23.5$	$5.78{10}^{-3}$	$7.80{10}^{-3}$	$2.14{10}^{-2}$	$1.17{10}^{-3}$	$-1.88{10}^{-5}$	$5.50$
High-pass f. 35	$19.1$	$3.66{10}^{-3}$	$2.97{10}^{-3}$	$1.72{10}^{-2}$	$2.66{10}^{-4}$	$-1.51{10}^{-5}$	$5.32$
High-pass f. 36	$16.8$	$2.86{10}^{-3}$	$9.40{10}^{-4}$	$1.49{10}^{-2}$	$8.69{10}^{-5}$	$-1.44{10}^{-5}$	$5.14$
High-pass f. 37	$12.0$	$1.62{10}^{-3}$	$0.00$	$1.06{10}^{-2}$	$0.00$	$-1.18{10}^{-5}$	$4.74$
High-pass f. 38	$9.3$	$1.06{10}^{-3}$	$0.00$	$7.83{10}^{-3}$	$0.00$	$-1.01{10}^{-5}$	$4.25$
High-pass f. 39	$3.6$	$3.06{10}^{-4}$	$0.00$	$2.73{10}^{-3}$	$0.00$	$-7.40{10}^{-6}$	$2.81$
Low-pass f. mode 03	$90.5$	$2.36{10}^{-1}$	$3.31{10}^{-1}$	$9.35{10}^{-3}$	$-8.83{10}^{-2}$	$-6.10{10}^{-3}$	$7.61$
Low-pass f. mode 05	$92.3$	$1.93{10}^{-1}$	$5.03{10}^{-1}$	$9.87{10}^{-3}$	$-5.64{10}^{-2}$	$-7.34{10}^{-4}$	$7.56$
Low-pass f. mode 07	$93.5$	$1.85{10}^{-1}$	$7.47{10}^{-1}$	$1.32{10}^{-2}$	$-6.93{10}^{-2}$	$-1.31{10}^{-4}$	$8.81$
Low-pass f. mode 09	$94.2$	$1.85{10}^{-1}$	$7.55{10}^{-1}$	$1.18{10}^{-2}$	$-5.91{10}^{-2}$	$-1.19{10}^{-4}$	$9.50$
Low-pass f. mode 11	$94.7$	$1.82{10}^{-1}$	$9.48{10}^{-1}$	$1.58{10}^{-2}$	$-3.56{10}^{-2}$	$-5.17{10}^{-6}$	$7.92$
Low-pass f. mode 13	$95.0$	$1.65{10}^{-1}$	$4.76{10}^{-1}$	$9.45{10}^{-3}$	$-3.00{10}^{-2}$	$-6.74{10}^{-5}$	$1.06{10}^1$
Low-pass f. mode 15	$95.1$	$8.68{10}^{-2}$	$1.81{10}^{-1}$	$5.68{10}^{-4}$	$-3.25{10}^{-2}$	$-1.03{10}^{-5}$	$4.42$
Low-pass f. mode 17	$95.2$	$1.28{10}^{-1}$	$6.43{10}^{-1}$	$9.46{10}^{-3}$	$-3.41{10}^{-2}$	$-4.61{10}^{-7}$	$7.34$
Low-pass f. mode 19	$95.3$	$1.33{10}^{-1}$	$5.58{10}^{-1}$	$5.86{10}^{-3}$	$-4.96{10}^{-3}$	$-4.60{10}^{-6}$	$8.50$
Low-pass f. mode 21	$95.3$	$6.43{10}^{-2}$	$4.35{10}^{-1}$	$4.10{10}^{-3}$	$-3.99{10}^{-2}$	$-2.56{10}^{-6}$	$3.42$
Low-pass f. mode 23	$95.3$	$1.35{10}^{-1}$	$9.16{10}^{-1}$	$9.08{10}^{-3}$	$1.52{10}^{-2}$	$-9.10{10}^{-6}$	$7.51$
Low-pass f. mode 25	$95.3$	$1.31{10}^{-1}$	$-3.35{10}^{-2}$	$-1.83{10}^{-3}$	$-6.02{10}^{-2}$	$-1.04{10}^{-4}$	$9.90$

and

Table A12. Landscape metrics differences (metrics for CN 8 minus metrics for CN 4) for maps derived from a real forest maps with high-pass (Figure A1) and low-pass filters with different coefficients (high-pass) and sizes (low-pass) (Figure A2).

Map	gyrate_mn	lpi	mesh	ndca	np	pd	split
Original map	$1.78$	$3.23{10}^1$	$4.36{10}^3$	$-1.26{10}^4$	$-1.79{10}^4$	$-1.35{10}^2$	$-4.40$
High-pass f. 15	$1.65{10}^{-1}$	$0.00$	$4.15{10}^{-4}$	$0.00$	$-2.19{10}^2$	$-2.08{10}^2$	$-3.44{10}^2$
High-pass f. 16	$8.60{10}^{-1}$	$0.00$	$2.86{10}^{-3}$	$0.00$	$-3.53{10}^3$	$-9.26{10}^2$	$-4.05{10}^3$
High-pass f. 17	$1.30$	$6.46{10}^{-3}$	$6.32{10}^{-3}$	$0.00$	$-7.81{10}^3$	$-1.26{10}^3$	$-7.92{10}^3$
High-pass f. 18	$1.95$	$9.44{10}^{-3}$	$1.76{10}^{-2}$	$0.00$	$-1.63{10}^4$	$-1.54{10}^3$	$-1.38{10}^4$
High-pass f. 19	$2.35$	$3.79{10}^{-2}$	$3.91{10}^{-2}$	$-1.60{10}^1$	$-2.28{10}^4$	$-1.60{10}^3$	$-1.75{10}^4$
High-pass f. 20	$3.09$	$2.15{10}^{-1}$	$1.95{10}^{-1}$	$-2.57{10}^2$	$-3.37{10}^4$	$-1.58{10}^3$	$-2.13{10}^4$
High-pass f. 21	$3.89$	$7.22{10}^{-1}$	$9.15{10}^{-1}$	$-8.26{10}^2$	$-3.97{10}^4$	$-1.45{10}^3$	$-1.83{10}^4$
High-pass f. 22	$2.12$	$2.45$	$1.42{10}^1$	$-3.50{10}^3$	$-3.35{10}^4$	$-8.64{10}^2$	$-4.99{10}^3$
High-pass f. 23	$1.02$	$2.92{10}^1$	$5.93{10}^2$	$-1.04{10}^4$	$-2.56{10}^4$	$-5.12{10}^2$	$-4.40{10}^2$
High-pass f. 24	$2.14$	$3.20{10}^1$	$2.12{10}^3$	$-3.13{10}^4$	$-1.79{10}^4$	$-2.23{10}^2$	$-8.60$
High-pass f. 25	$2.26$	$3.07{10}^1$	$1.54{10}^3$	$-2.46{10}^4$	$-1.80{10}^4$	$-2.75{10}^2$	$-1.09{10}^1$
High-pass f. 26	$1.52$	$1.53{10}^1$	$2.95{10}^2$	$-1.41{10}^4$	$-1.93{10}^4$	$-3.49{10}^2$	$-2.02{10}^2$
High-pass f. 27	$2.91$	$6.80$	$3.38{10}^1$	$-4.27{10}^3$	$-2.77{10}^4$	$-6.78{10}^2$	$-3.54{10}^3$
High-pass f. 28	$4.26$	$4.41$	$1.18{10}^1$	$-2.35{10}^3$	$-3.18{10}^4$	$-9.04{10}^2$	$-8.69{10}^3$
High-pass f. 29	$4.96$	$7.34{10}^{-1}$	$9.41{10}^{-1}$	$-7.45{10}^2$	$-3.48{10}^4$	$-1.32{10}^3$	$-1.80{10}^4$
High-pass f. 30	$4.27$	$2.02{10}^{-1}$	$3.30{10}^{-1}$	$-3.91{10}^2$	$-3.22{10}^4$	$-1.42{10}^3$	$-1.91{10}^4$
High-pass f. 31	$3.05$	$8.54{10}^{-2}$	$8.07{10}^{-2}$	$-1.10{10}^2$	$-2.44{10}^4$	$-1.48{10}^3$	$-1.67{10}^4$
High-pass f. 32	$2.64$	$2.22{10}^{-2}$	$4.78{10}^{-2}$	$-4.30{10}^1$	$-2.04{10}^4$	$-1.46{10}^3$	$-1.43{10}^4$
High-pass f. 33	$2.08$	$7.18{10}^{-3}$	$2.14{10}^{-2}$	$-1.00{10}^1$	$-1.37{10}^4$	$-1.40{10}^3$	$-1.04{10}^4$
High-pass f. 34	$1.84$	$2.48{10}^{-3}$	$1.52{10}^{-2}$	$-2.00$	$-1.08{10}^4$	$-1.34{10}^3$	$-8.64{10}^3$
High-pass f. 35	$1.40$	$1.12{10}^{-2}$	$8.11{10}^{-3}$	$0.00$	$-6.36{10}^3$	$-1.18{10}^3$	$-5.75{10}^3$
High-pass f. 36	$1.19$	$1.40{10}^{-2}$	$6.15{10}^{-3}$	$0.00$	$-4.67{10}^3$	$-1.09{10}^3$	$-4.66{10}^3$
High-pass f. 37	$8.12{10}^{-1}$	$1.96{10}^{-2}$	$2.99{10}^{-3}$	$0.00$	$-2.14{10}^3$	$-8.42{10}^2$	$-2.37{10}^3$
High-pass f. 38	$5.93{10}^{-1}$	$0.00$	$1.82{10}^{-3}$	$0.00$	$-1.18{10}^3$	$-6.53{10}^2$	$-1.40{10}^3$
High-pass f. 39	$2.12{10}^{-1}$	$0.00$	$5.12{10}^{-4}$	$0.00$	$-1.78{10}^2$	$-2.57{10}^2$	$-2.61{10}^2$
Low-pass f. mode 03	$2.05$	$7.99{10}^{-1}$	$4.68{10}^1$	$-1.57{10}^3$	$-1.62{10}^3$	$-2.12{10}^1$	$-5.65{10}^{-1}$
Low-pass f. mode 05	$2.12$	$1.34{10}^{-2}$	$3.83$	$-4.23{10}^2$	$-3.85{10}^2$	$-7.38$	$-1.70{10}^{-1}$
Low-pass f. mode 07	$2.26$	$1.73{10}^{-2}$	$5.00{10}^{-1}$	$-2.18{10}^2$	$-1.49{10}^2$	$-3.91$	$-2.30{10}^{-2}$
Low-pass f. mode 09	$2.13$	$9.59{10}^{-3}$	$3.48{10}^{-1}$	$-1.07{10}^2$	$-6.70{10}^1$	$-2.30$	$-2.55{10}^{-2}$
Low-pass f. mode 11	$2.18$	$0.00$	$1.18{10}^{-2}$	$-4.90{10}^1$	$-3.70{10}^1$	$-1.62$	$-8.86{10}^{-4}$
Low-pass f. mode 13	$2.00$	$0.00$	$1.23{10}^{-1}$	$-2.60{10}^1$	$-1.70{10}^1$	$-9.31{10}^{-1}$	$-1.10{10}^{-2}$
Low-pass f. mode 15	$9.62{10}^{-1}$	$0.00$	$1.52{10}^{-2}$	$-1.50{10}^1$	$-6.00$	$-4.08{10}^{-1}$	$-2.54{10}^{-3}$
Low-pass f. mode 17	$1.65$	$0.00$	$5.49{10}^{-4}$	$-1.30{10}^1$	$-6.00$	$-5.04{10}^{-1}$	$-9.28{10}^{-5}$
Low-pass f. mode 19	$1.79$	$0.00$	$4.44{10}^{-3}$	$-5.00$	$-5.00$	$-5.19{10}^{-1}$	$-1.01{10}^{-3}$
Low-pass f. mode 21	$8.75{10}^{-1}$	$0.00$	$2.00{10}^{-3}$	$-8.00$	$-2.00$	$-2.56{10}^{-1}$	$-5.62{10}^{-4}$
Low-pass f. mode 23	$1.90$	$0.00$	$5.78{10}^{-3}$	$-1.00$	$-4.00$	$-6.30{10}^{-1}$	$-1.49{10}^{-3}$
Low-pass f. mode 25	$2.32$	$0.00$	$5.37{10}^{-2}$	$-9.00$	$-3.00$	$-5.83{10}^{-1}$	$-1.55{10}^{-2}$

in Appendix B.3).

The first result is that for 8 of the metrics out of 13, the differences are mostly positive (area_mn, cai_mn, contig_mn, dcore_mn, enm_mn, gyrate_mn, lpi and mesh), i.e., the value of the metric is mostly higher when calculated with an eight CN configuration, while for the other 4 metrics (division, np, pd, split), the differences are negative. This provides a hint on the expected behavior of the differences between metrics when AI varies. With increasing AI values the landscape becomes more aggregated; therefore, the difference between the two CN configurations should decrease. However, not all the metrics follow this trend. Furthermore, for most of the maps, regular behavior is not recognizable, nor can a general rule to forecast how the difference will behave be inferred. Most of the metrics are very unstable with respect to AI values.

This emphasizes once more how crucial it is to understand which CN configuration has been used when comparing findings from different research that employ landscape metrics.

4.4. Polynomial Approximation

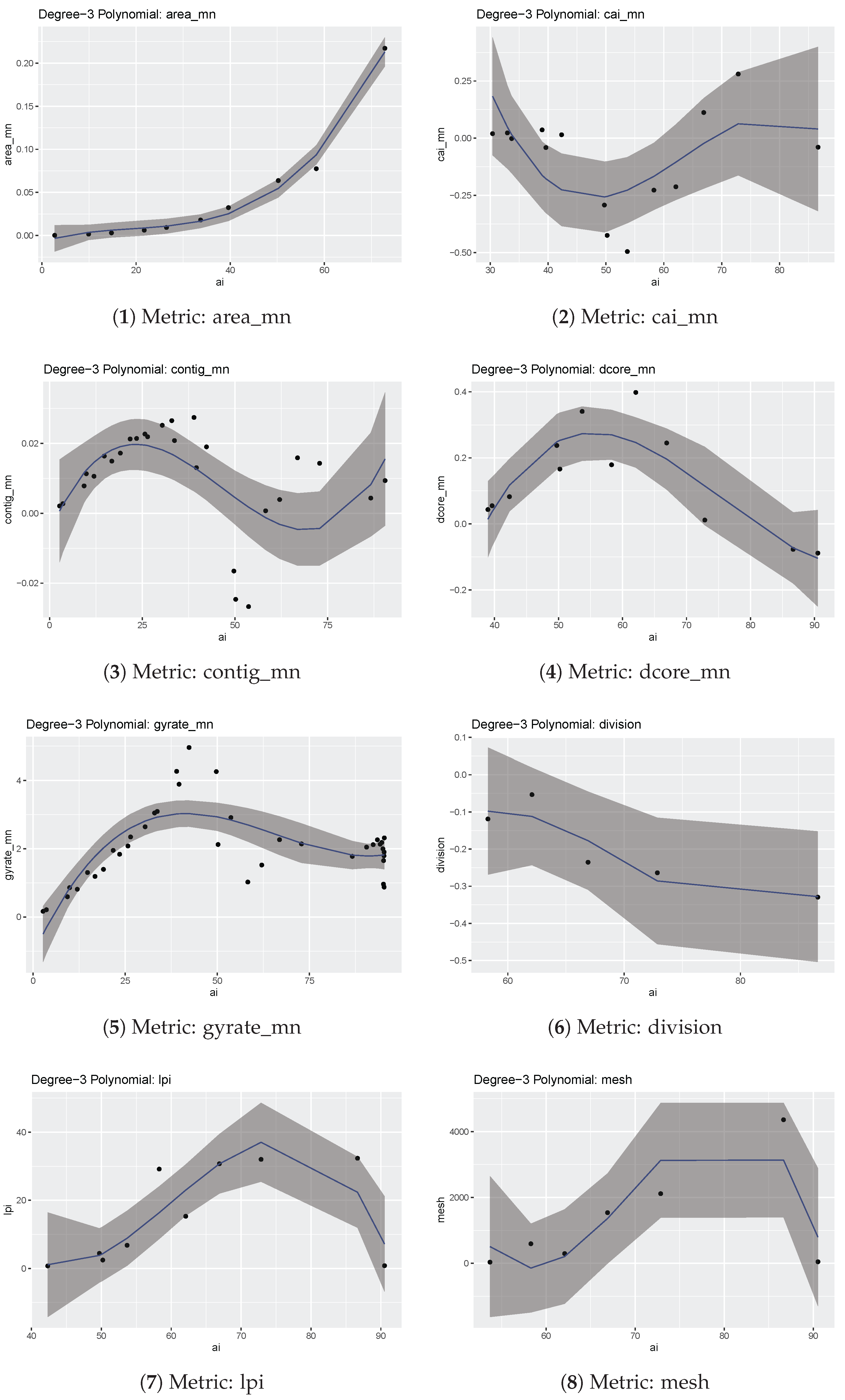
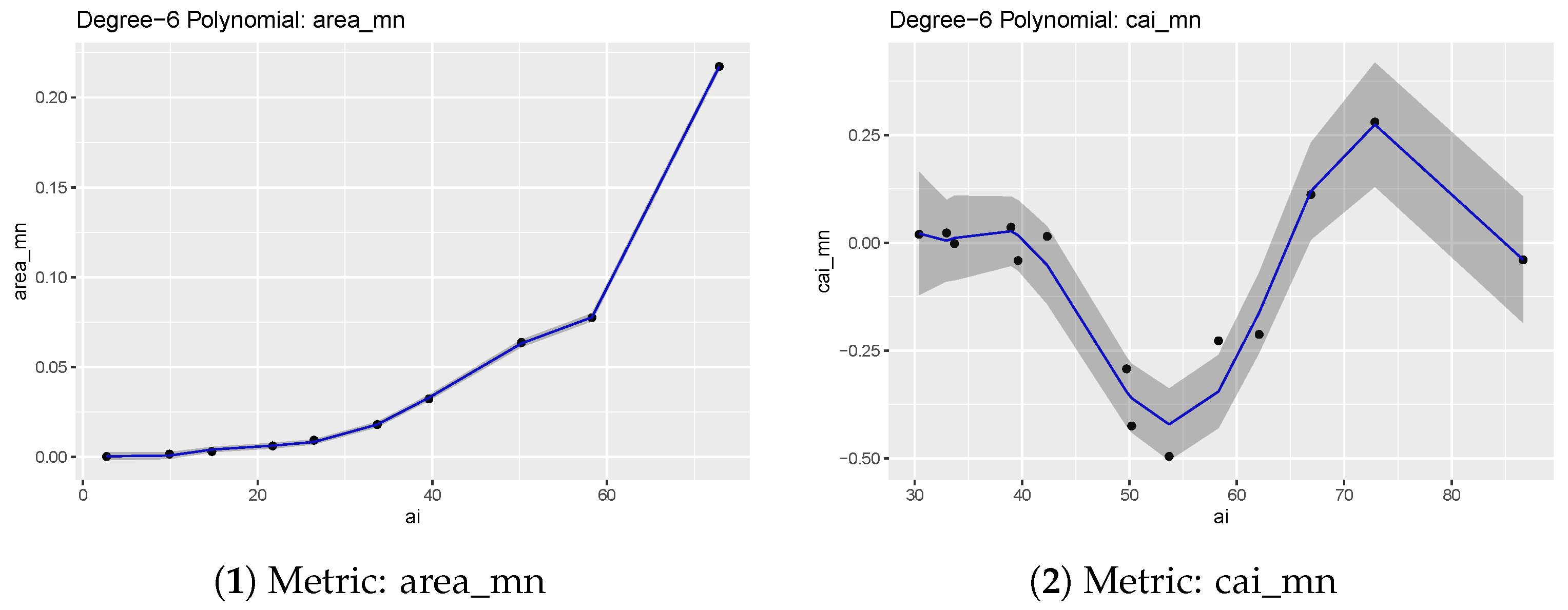
The coefficients and relevant statistics have been evaluated for 3 and 6-degree polynomials for the differences in each metric. The choice of the polynomial degrees depends on the following considerations: (i) a polynomial of 3 degrees is simple and fast to use, (ii) polynomials of 4 and 5 degrees do not provide tangible benefits with respect to 3-degree polynomial and (iii) the use of polynomials with an order above six is impossible for most of the metrics differences because the number of data points is limited. Since metric differences are non zero only on some intervals, which change for each metric, only the values where the differences are non-null have been used for the interpolation. Figure 6 illustrates this for metric cai_mn: when the whole 0–100 range is used for AI and also for values where the differences are null, with AI below 30, and where the difference behavior is very unstable, with AI above 90, they are used to estimate the interpolation coefficients. Therefore, to avoid the influence of the values in these intervals, only differences in the AI interval 30–90 are used. The interval boundaries for each metric are reported in

Table 5. Intervals and coefficients for polynomial interpolation of metrics differences (CN 8 minus CN 4) with order 3.

	Interval		Coefficients
Metric	Min.	Max.	Intercept	1	2	3
area_mn	0	$86.65$	$4.29{10}^{-2}$	$1.74{10}^{-1}$	$9.26{10}^{-2}$	$3.23{10}^{-2}$
cai_mn	30	90	$-8.92{10}^{-2}$	$2.29{10}^{-2}$	$3.83{10}^{-1}$	$-3.38{10}^{-1}$
contig_mn	0	90	$1.05{10}^{-2}$	$-1.84{10}^{-2}$	$-3.23{10}^{-3}$	$3.79{10}^{-2}$
dcore_mn	34	90	$1.33{10}^{-1}$	$-1.93{10}^{-1}$	$-3.89{10}^{-1}$	$1.30{10}^{-1}$
division	55	$86.65$	$-2.00{10}^{-1}$	$-1.95{10}^{-1}$	$4.59{10}^{-2}$	$4.57{10}^{-2}$
enn_mn	0	90	$5.97$	$7.96$	$-3.32$	$2.80{10}^{-3}$
gyrate_mn	0	90	$2.10$	$2.35$	$-4.16$	$1.56$
lpi	42	90	$1.55{10}^1$	$1.77{10}^1$	$-2.74{10}^1$	$-1.77{10}^1$
mesh	$53.69$	90	$1.28{10}^3$	$1.85{10}^3$	$-1.52{10}^3$	$-2.27{10}^3$
ndca	$21.73$	94	$-4.49{10}^3$	$-9.00{10}^3$	$2.34{10}^4$	$2.62{10}^4$
np	0	94	$-1.46{10}^4$	$5.45{10}^3$	$6.60{10}^4$	$3.33{10}^2$
pd	0	92	$-8.93{10}^2$	$1.47{10}^3$	$1.75{10}^3$	$-1.55{10}^3$
split	0	70	$-8.44{10}^3$	$-2.1{10}^3$	$2.94{10}^4$	$1.97{10}^3$

and

Table 6. Interval and coefficients for polynomial interpolation of metrics differences (CN 8 minus CN 4) with order 6.

	Interval		Coefficients
Metric	Min.	Max.	Intercept	1	2	3	4	5	6
area_mn	0	$86.65$	$4.29{10}^{-2}$	$1.74{10}^{-1}$	$9.26{10}^{-2}$	$3.23{10}^{-2}$	$1.47{10}^{-2}$	$1.25{10}^{-2}$	$8.22{10}^{-3}$
cai_mn	30	90	$-8.92{10}^{-2}$	$2.29{10}^{-2}$	$3.83{10}^{-1}$	$-3.38{10}^{-1}$	$-5.15{10}^{-1}$	$3.93{10}^{-2}$	$1.70{10}^{-1}$
contig_mn	0	90	$1.05{10}^{-2}$	$-1.84{10}^{-2}$	$-3.23{10}^{-3}$	$3.79{10}^{-2}$	$-1.90{10}^{-2}$	$-3.15{10}^{-2}$	$1.40{10}^{-2}$
dcore_mn	34	90	$1.33{10}^{-1}$	$-1.93{10}^{-1}$	$-3.89{10}^{-1}$	$1.30{10}^{-1}$	$1.12{10}^{-1}$	$-6.14{10}^{-2}$	$-7.60{10}^{-2}$
enn_mn	0	90	$5.97$	$7.96$	$-3.32$	$2.80{10}^{-3}$	$-8.14{10}^{-1}$	$1.08$	$-7.43{10}^{-1}$
gyrate_mn	0	90	$2.10$	$2.35$	$-4.16$	$1.56$	$2.14$	$-8.94{10}^{-1}$	$-1.31$
lpi	42	90	$1.55{10}^1$	$1.77{10}^1$	$-2.74{10}^1$	$-1.77{10}^1$	$-7.37$	$-1.19{10}^1$	$6.03{10}^{-1}$
mesh	$53.69$	90	$1.28{10}^3$	$1.85{10}^3$	$-1.52{10}^3$	$-2.27{10}^3$	$-1.82{10}^3$	$-4.78{10}^2$	$-6.09{10}^2$
ndca	$21.73$	94	$-4.49{10}^3$	$-9.00{10}^3$	$2.34{10}^4$	$2.62{10}^4$	$5.76{10}^3$	$-1.20{10}^4$	$-9.95{10}^3$
np	0	94	$-1.46{10}^4$	$5.45{10}^3$	$6.60{10}^4$	$3.33{10}^2$	$-1.53{10}^4$	$1.43{10}^4$	$8.22{10}^3$
pd	0	92	$-8.93{10}^2$	$1.47{10}^3$	$1.75{10}^3$	$-1.55{10}^3$	$-3.96$	$3.48{10}^2$	$8.54{10}^1$
split	0	70	$-8.44{10}^3$	$-2.01{10}^3$	$2.94{10}^4$	$1.97{10}^3$	$-1.33{10}^4$	$-4.15{10}^3$	$4.16{10}^3$

.

Both 3 and 6 degrees coefficients polynomials have been tested to assess whether low-degree polynomials can provide a sufficient approximation with a smaller number of coefficients. Results are reported in Table 5 and Table 6, while information to assess the goodness of fit is in

Table 7. Statistics for polynomial interpolation of metrics differences (CN 8 minus CN 4) with order 3.

Metric	Residual Std Err.	Multiple R-Squared	Adjusted R-Squared	F-Statistic	p-Value
area_mn	$8.61{10}^{-3}$	$0.9890$	$0.9835$	$179.40$	$2.92{10}^{-6}$
cai_mn	$1.83{10}^{-1}$	$0.4395$	$0.2714$	$2.61$	$1.09{10}^{-1}$
contig_mn	$1.23{10}^{-2}$	$0.3386$	$0.2523$	$3.93$	$2.13{10}^{-2}$
dcore_mn	$8.60{10}^{-2}$	$0.7764$	$0.6926$	$9.26$	$5.57{10}^{-3}$
division	$8.79{10}^{-2}$	$0.8458$	$0.3831$	$1.83$	$4.87{10}^{-1}$
enn_mn	$5.70{10}^{-1}$	$0.9088$	$0.8969$	$76.37$	$4.16{10}^{-12}$
gyrate_mn	$8.03{10}^{-1}$	$0.6302$	$0.5820$	$13.07$	$3.45{10}^{-5}$
lpi	$8.13$	$0.7769$	$0.6653$	$6.96$	$2.22{10}^{-2}$
mesh	$1.14{10}^3$	$0.7364$	$0.4727$	$2.79$	$2.11{10}^{-1}$
ndca	$3.82{10}^3$	$0.8182$	$0.7909$	$29.99$	$1.34{10}^{-7}$
np	$5.50{10}^3$	$0.8382$	$0.8209$	$48.35$	$3.37{10}^{-11}$
pd	$1.14{10}^2$	$0.9610$	$0.9561$	$197.00$	<$2.2{10}^{-16}$
split	$3.93{10}^3$	$0.7383$	$0.6991$	$18.81$	$4.86{10}^{-6}$

and

Table 8. Statistics for polynomial interpolation of metrics differences (CN 8 minus CN 4) with order 6. For metric mesh only 7 values are in the chosen interval; therefore, no statistics are available.

Metric	Residual Std Err.	Multiple R-Squared	Adjusted R-Squared	F-Statistic	p-Value
area_mn	$1.09{10}^{-3}$	$0.9999$	$0.9997$	$5656.00$	$3.64{10}^{-6}$
cai_mn	$7.32{10}^{-2}$	$0.9369$	$0.8828$	$17.33$	$7.06{10}^{-4}$
contig_mn	$9.82{10}^{-3}$	$0.6333$	$0.5232$	$5.76$	$1.29{10}^{-3}$
dcore_mn	$8.61{10}^{-2}$	$0.8600$	$0.6921$	$5.12$	$4.68{10}^{-2}$
enn_mn	$5.05{10}^{-1}$	$0.9378$	$0.9191$	$50.26$	$5.09{10}^{-11}$
gyrate_mn	$6.23{10}^{-1}$	$0.8068$	$0.7488$	$13.92$	$3.26{10}^{-6}$
lpi	$8.19$	$0.8869$	$0.6606$	$3.92$	$1.45{10}^{-1}$
mesh	−	−	−	−	−
ndca	$9.40{10}^2$	$0.9906$	$0.9873$	$299.80$	$2.80{10}^{-16}$
np	$3.69{10}^3$	$0.9348$	$0.9192$	$59.76$	$1.30{10}^{-13}$
pd	$9.28{10}^1$	$0.9772$	$0.9707$	$150.10$	$3.93{10}^{-16}$
split	$2.39{10}^3$	$0.9179$	$0.8890$	$31.69$	$2.52{10}^{-8}$

.

The interval for the metric division contains only five values (maps), thus the coefficients for a 6-degree polynomial cannot be evaluated: for this reason its coefficients and statistics are not reported in Table 6 and Table 8.

The interval chosen for the polynomial interpolation of the metric mesh contains only seven values, the same number of the unknowns for grade 6; therefore, no statistics is available.

5. Discussion

Results indicate that for values of AI above 90, the metric differences are either negligible or have an unpredictable behavior. Therefore, for very compact patches a small increment or decrement in the AI can lead to very different metric values regardless of the CN (four or eight) configuration choice. In this situation landscape metrics evaluated using the two configurations are simply impossible to compare.

In a similar way, for low AI values, metrics differences are usually null. However, the threshold below which this happens is different for every metric.

All the polynomial interpolations correspond to p-values for the F-test well below the chosen significance level of 5% (i.e., 0.05) (Table 7 and Table 8). Therefore both 3 and 6 degree polynomials provide a better fit to the metric differences than an intercept-only model. However, values of Multiple R-squared and Adjusted R-squared indicate that most of the 3-degree polynomials are not a good fit, while, as expected, using a 6-degree polynomial allows a better fit. Low Multiple R-squared values mean that most of the 3-degree polynomials do not provide a good model to predict the metrics differences. The same situation is indicated by low values of Adjusted R-squared, which incorporates the model’s degrees of freedom. The use of 6-degree polynomials provides more degrees of freedom, and therefore enhances the metric differences prediction, as indicated by higher values of Multiple R-squared and Adjusted R-squared.

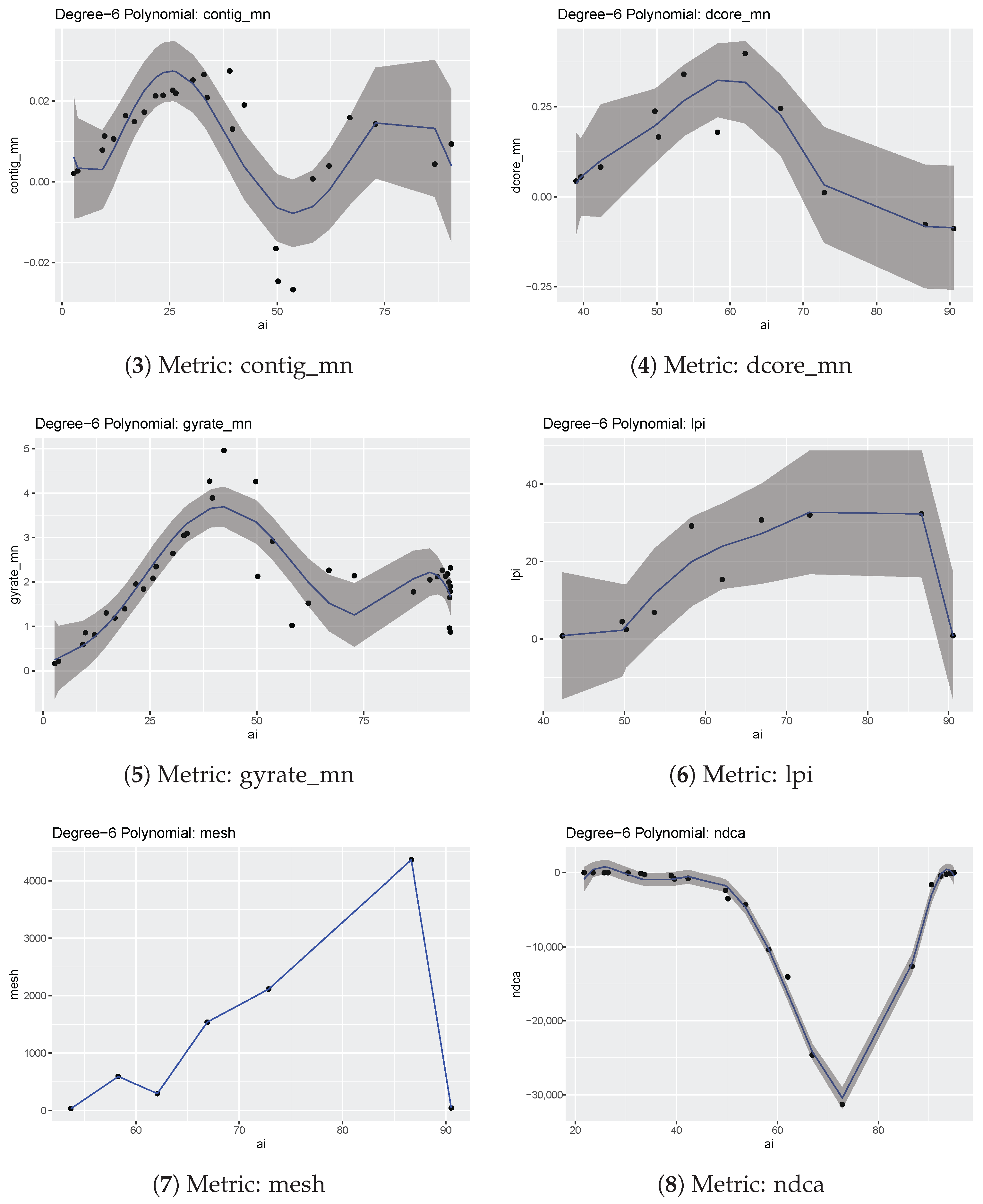
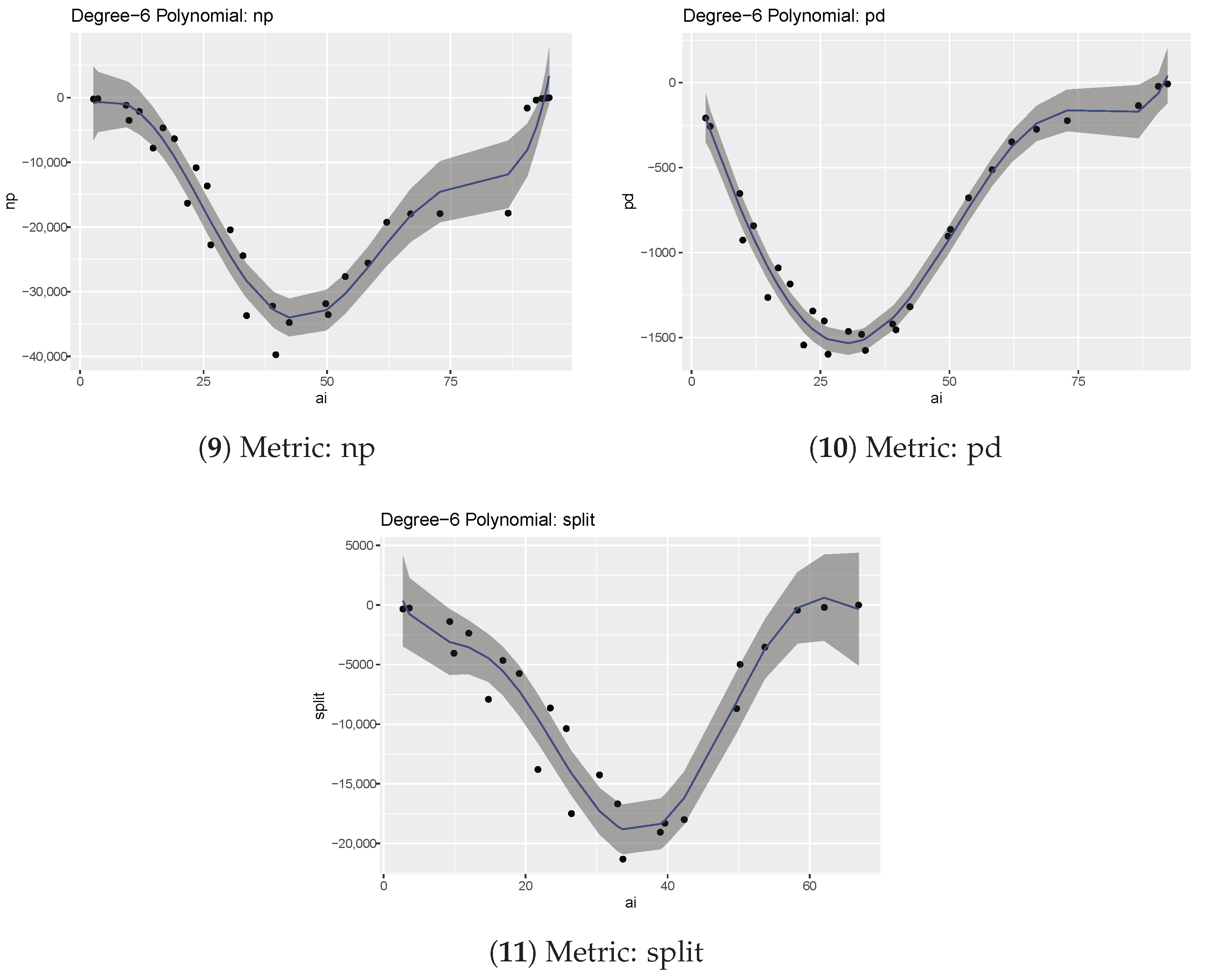
Choosing a threshold value of 0.9 for the Adjusted R-squared values, only the area_mn and pd metric differences can be properly fitted by a 3-degree polynomial. With the same threshold and a 6-degree polynomial, five metrics differences can be fitted (area_mn, ndca, pd, np, enn_mn).

A visual representation of this is given by Figure A3 in Appendix C for 3-degree polynomials and in Figure A4 in Appendix D for 6-degree polynomials.

Differences behave differently for each landscape metric:

area_mn

Shows a parabolic trend up to AI equal to 86.65, then it becomes unstable; in the AI interval 0–86.65 it can be fitted by a 3-degree polynomial, with an Adjusted R-squared of 0.9835;

cai_mn

Differences are negligible up to AI = 30 and are unstable above 90, with a parabolic trend in between; overall they have a larger variability than other metrics differences; fit for 3-degree polynomial is poor, with an Adjusted R-squared of 0.2714, while the 6-degree polynomial fares better with an Adjusted R-squared of 0.8828;

contig_mn

Shows a sinusoidal behavior for AI below 90, with unpredictable behavior above this value; fitting by both 3-degrees (Adjusted R-squared 0.2523) and 6-degrees (Adjusted R-squared 0.5232) is poor; fitting by a sinusoidal function could be tested;

dcore_mn

Differences are negligible for AI below 34, then their trend becomes sinusoidal up to AI equal to 90, then it is unstable; Adjusted R-squared values are similar for the 3-degrees (0.6926) and 6-degrees (0.6921) polynomial, indicating a rather poor fitting;

division

Differences are null up to AI = 55, then their trend is parabolic, becoming unstable above 90; fitting with a 3-degree polynomial is very poor (Adjusted R-squared 0.3831), while it is not possible to use a 6-degree polynomial, as only five data points are available in the chosen interval;

enn_mn

In the interval 0–90, the 3-degree polynomial provides a poor fit (Adjusted R-squared 0.4727), but the 6-degree polynomial is good (Adjusted R-squared 0.9191);

gyrate_mn

Unstable above AI = 33, both 3-degrees (Adjusted R-squared 0.6926) and 6-degrees (Adjusted R-squared 0.8890) polynomials provide an almost good fit;

lpi

Differences are basically null outside the 45–90 AI interval, while inside this interval they have an oscillatory behavior; polynomial approximation is poor, with Adjusted R-squared 0.6653 for grade 3 and Adjusted R-squared 0.6606 for grade 6;

mesh

Differences have a parabolic trend in the 55–100 AI interval, and they are null outside; a 3-degree polynomial fit is poor (Adjusted R-squared 0.4727), while there are not enough data points to estimate the coefficients of the 6-degree polynomial;

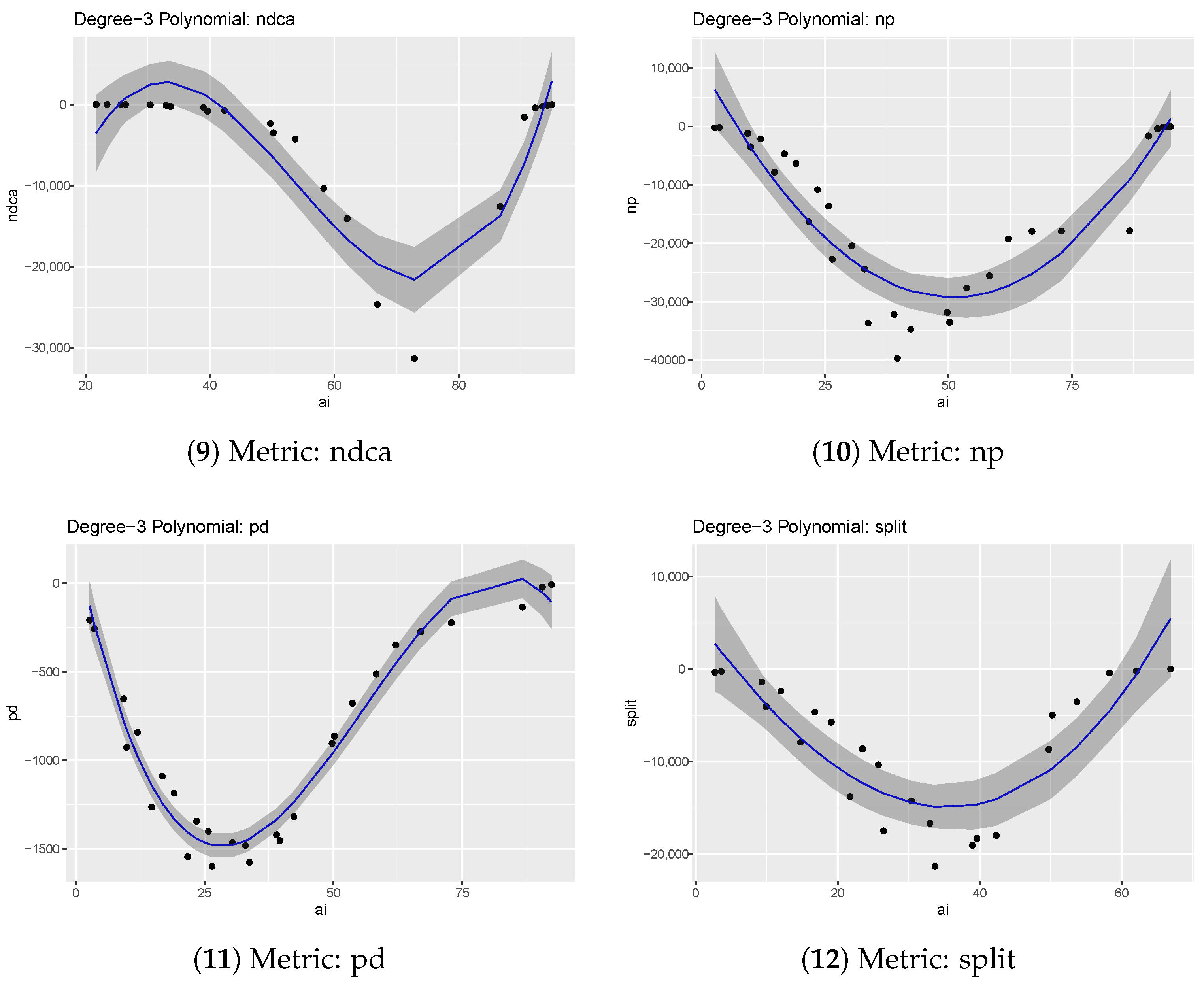
ndca

Differences are negligible outside the 22–94 AI range; the 3-degree polynomial is not a good fit (Adjusted R-squared 0.7909) but the 6-degree polynomial is (Adjusted R-squared 0.9873);

np

Differences have a parabolic trend with oscillations and they are basically null for AI values above 94; the 3-degree polynomial is quite a good fit (Adjusted R-squared 0.8209), while the 6-degree polynomial provides a good fit (Adjusted R-squared 0.9192);

pd

Differences have a trend similar to those for the metric np, parabolic trend with oscillations and up to AI = 92; both 3-degree (Adjusted R-squared 0.9561) and 6-degree (Adjusted R-squared 0.9707) polynomials provide a good fit;

split

Differences are negligible for AI above 70, then the 3-degree polynomial is not a good fit (Adjusted R-squared 0.6991), while the 6-degree polynomial fares better (Adjusted R-squared 0.8890).

An overall view of the goodness of fit for landscape metrics approximations with 3- and 6-degree polynomials is provided in

Table 9. Summary of goodness of fit for landscape metrics approximations with 3- and 6-degree polynomials. Threshold for Adjusted R-squared is set to 0.9; metric enn_mn has a value of 0.8969, so close to the threshold that it is considered acceptable. The ✓ symbol indicates a good fit, the ✗ symbol a poor fit.

	Adjusted R-Squared		Fit
Metric	3-Degree	6-Degree	3-Degree	6-Degree
area_mn	0.9835	0.9997	✓	✓
cai_mn	0.2714	0.8828	✗	✗
contig_mn	0.2523	0.5232	✗	✗
dcore_mn	0.6926	0.6921	✗	✗
division	0.3831	-	✗	✗
enn_mn	0.8969	0.9191	✓	✓
gyrate_mn	0.5820	0.7488	✗	✗
lpi	0.6653	0.6606	✗	✗
mesh	0.4727	-	✗	✗
ndca	0.7909	0.9873	✗	✓
np	0.8209	0.9192	✗	✓
pd	0.9561	0.9707	✓	✓
split	0.6991	0.8890	✗	✓

.

Table 9 shows that it is possible to fit the differences in three metrics, area_mn, enn_mn and pd, with both 3- and 6-degree polynomials. The differences in three more metrics, ndca, np and split, can be modeled using only 6-degree polynomials.

However, even for metrics with a good fit, metric difference evaluation using a polynomial does not provide reliable values. For example,

Table 10. Absolute and percent differences between interpolated and evaluated values of the area_mn metric for binary maps in Figure 3 with [CN] 8.

AI	Interpolated	Real	Differences	Differences %
10	$3.00{10}^{-3}$	$3.11{10}^{-5}$	$-2.97{10}^{-3}$	$-9.54{10}^3$
20	$2.65{10}^{-3}$	$1.14{10}^{-4}$	$-2.54{10}^{-3}$	$-2.23{10}^3$
30	$1.28{10}^{-2}$	$3.97{10}^{-4}$	$-1.24{10}^{-2}$	$-3.13{10}^3$
40	$3.59{10}^{-2}$	$2.11{10}^{-3}$	$-3.38{10}^{-2}$	$-1.60{10}^3$
50	$7.04{10}^{-2}$	$1.42{10}^{-2}$	$-5.62{10}^{-2}$	$-3.96{10}^2$
60	$1.19{10}^{-1}$	$1.09{10}^{-1}$	$-1.05{10}^{-2}$	$-9.61$
70	$1.91{10}^{-1}$	$1.17$	$9.84{10}^{-1}$	$8.37{10}^1$
80	$2.94{10}^{-1}$	$1.19{10}^1$	$1.16{10}^1$	$9.75{10}^1$
90	$4.25{10}^{-1}$	$9.34{10}^1$	$9.30{10}^1$	$9.95{10}^1$

shows the differences for the area_mn metric for binary maps in Figure 3, with differences between interpolated and evaluated values with CN eight of more than 1000% for low AI values.

6. Conclusions

The paper tries to assess whether it is possible to infer the value of landscape metrics evaluated with a CN value when the value of the same metric is known in the other CN configuration. The results in Section 4 demonstrate that this is possible only for some metrics and only for selected value intervals. Many landscape metrics are inherently very unstable with respect to variation in the AI and this makes it difficult to model their behavior with polynomials. Therefore, the answer to the initial research question is that it is possible to estimate the differences in landscape metrics evaluated with a four and eight CN configuration using polynomials only for few metrics and only for some intervals of AI values. Even in these favorable cases, however, the estimation of the differences between CN configuration is very approximate.

The results highlight the importance of the choice of the CN in the evaluation of the landscape metrics, whose values can change in various orders of magnitude for different CN choices. Moreover, one important conclusion is that landscape metric values can be very unstable with respect to the patch configurations they try to describe; therefore, their use should always be integrated by other information under expert judgment.

The difficulty of comparing results from different studies using landscape metric remains, unless the used CN is known. Results in Section 5 can help, at least in indicating for each metric the intervals of AI values for which differences between CN are negligible. However, the need to always indicate the CN in use or at least the software used to evaluate the landscape metrics, from which the CN can be usually deducted, must be strongly emphasized.

The possibility of comparing landscape metrics between different studies is becoming more important because long time-series of Land Use/Land Coverage maps are becoming available [49], as the digitalization of a large number of historic maps is underway [50,51,52,53], with the development of automatic or semi-automatic digitalization procedures [54,55,56,57].

The limitations of this study concern the difficulty of creating maps with a dense and regular distribution of AI values, which would provide a larger sample size. This could also allow a better selection of the intervals where the creation of interpolating functions for the metrics differences is relevant. Moreover, only 3- and 6-degree polynomial fitting has been tested: different interpolating functions could be chosen, even using a different function for each metric. Another limitation lies in the impossibility to test the interpolating functions in real applications from third parties, as no example of landscape metrics evaluated with both four and eight CN configurations could be found in the literature.

During the numeric experiments carried out for this research it has emerged that the use of an eight CN configuration leads to a significant increase in computing resource demand, in particular in terms of memory (RAM), which can be a limiting factor for some applications.

Future developments include the creation of a set of maps with a higher resolution variation in AI in the parts of the 1–100 interval where metric differences are not null nor unstable, so that the use of approximating functions can be better investigated. Fractal landscapes could provide an effective way to generate these maps. The use of other functions than polynomials could be tested; for example, the contig_mn and dcore_mn metrics show a sinusoidal behavior for some AI intervals. Finally, the application of the polynomials to real cases where metrics have been evaluated with both CN configurations could be interesting, but so far the literature review has not provided any data of this type.