Exploring the Spatial Association Between Spatial Categorical Data Using a Fuzzy Geographically Weighted Colocation Quotient Method

Abstract

Spatial association analysis is essential for understanding interdependencies, spatial proximity, and distribution patterns within spatial data. The spatial scale is a key factor that significantly affects the result of spatial association mining. Traditional methods often rely on a fixed distance threshold (bandwidth) to define the scale effect, which can lead to scale sensitivity and discontinuity results. To address these limitations, this study introduces the Fuzzy Geographically Weighted Colocation Quotient (FGWCLQ) method. By integrating fuzzy theory, FGWCLQ replaces binary distance cutoffs with continuous membership functions, providing a more flexible and stable approach to spatial association mining. Using Point of Interest (POI) data from the Beijing urban area, FGWCLQ was applied to explore both intra- and inter-category spatial association patterns among star hotels, transportation facilities, and tourist attractions at different fuzzy neighborhoods. The results indicate that FGWCLQ can reliably discover global prevalent spatial associations among diverse facility types and visualize the spatial heterogeneity at various spatial scales. Compared to the deterministic GWCLQ method, FGWCLQ delivers more stable and robust results across varying spatial scales and generates more continuous association surfaces, which enable clear visualization of hierarchical clustering. Empirical findings provide valuable insights for optimizing the location of star hotels and supporting decision-making in urban planning. The method is available as an open-source Matlab package, providing a practical tool for diverse spatial association investigations.

1. Introduction

With advancements in geographic information observation technology, there has been an explosion in the growth of spatial categorical data [1,2]. This type of data, which can be nominal, ordinal, or interval, often exhibits interrelationships and interdependencies in both spatial and temporal dimensions [3]. Spatial association, defined as the process of identifying the relationships between geographical locations and the features present at those locations [4], is a central focus in spatial data mining [5,6]. Understanding the spatial association between categories or features is crucial for identifying spatial patterns, trends, and relationships in specific locations. This analysis helps researchers explore how spatial factors influence various outcomes [7,8]. Unlike the analysis of numeric data, spatial association analysis in spatial categorical data must consider not only the characteristics of different categories, but also the inter-spatial relationship among the categories [9].

Traditional spatial association mining primarily focuses on spatial data comprising continuous variables, such as measurements, counts, or quantities associated with specific locations. These analyses aim to uncover how values change across space or how they correlate with other continuous attributes [10,11]. However, the spatial association rules in spatial categorical data, which consists of discrete categories or classes assigned to specific locations, often investigate the relationships between different categories and how they colocate or spatially influence each other. Mining spatial association rules in categorical data is a more complex task than mining in other spatial data. Two key factors contribute to this complexity: (1) the complex interaction between multiple categories and (2) the scale issues of the spatial objects. The former arises from the fact that different categories interact with each other with varying intensities and directions, at different places or times, presenting heterogeneity [12]. The latter refers to the fact that the association relationship may vary across different spatial scales [13]. Therefore, studying the spatial heterogeneity of relationships between categories and selecting an appropriate scale remain challenging tasks in analyzing spatial associations of categorical data.

Techniques for analyzing spatial association in spatial categorical data often involve colocation pattern analysis. A spatial colocation pattern represents a subset of spatial features whose instances are often located in close geographic proximity [14,15]. Existing approaches for discovering colocation rules can be primarily categorized into data mining methods and spatial statistical methods [15]. Data mining methods, such as the Apriori algorithm [16], FP-Growth algorithm [17], and decision tree methods [18], primarily focus on identifying frequent item sets and deriving association rules between different categories of spatial data. While these methods offer efficiency and flexibility, but can be algorithmically complex and may yield less interpretable results [16]. Spatial statistical methods, on the other hand, offer a robust theoretical foundation and intuitive results, and have been widely used in geographic analysis [19,20]. Several spatial statistical methods have been proposed to study the spatial association rules, including Nearest Neighbor Analysis [21], the cross-k-function [22], the Colocation Quotient [23,24]. These methods focus on finding statistically significant colocation patterns between two spatial categories using significance tests under the null hypothesis of independence [25]. The Colocation Quotient (CLQ) is a common method that measures the bivariate association between category pairs. It is defined as a ratio of probabilities, where the denominator calculates the expected proportion by chance, and the numerator is the observed number of category B points that are nearest neighbors of category A points [26]. The CLQ provides detailed spatial association analysis and visualizes the heterogeneity of relationships within the study area [27,28]. However, traditional spatial statistical methods often depend on the spatial scale and are sensitive to scale parameters.

In spatial colocation pattern mining, defining spatial scale or neighborhood is a critical step, where all points within that scale are considered close [21,29]. Different neighborhood definitions can lead to significant disparities in the analysis results [30,31,32]. A common approach to defining the neighbor relationship (K-neighbor) between instances is to set a distance threshold (referred to as bandwidth), which aligns with spatial data and provides realistic geographic context. Most spatial statistical methods use the kernel function to measure the decay of spatial effect. The scale parameter is a key parameter that influences the result. Traditional spatial statistical methods are highly sensitive to bandwidth selection, which poses challenges for determining an optimal bandwidth in practical applications [33]. Moreover, the optimal bandwidth always leads to a hard boundary (e.g., correlated within the bandwidth, uncorrelated beyond it) and overlooks the fuzziness of the concept of “adjacency” in geographical space, as the distance between objects is not a simple binary relationship but rather involves a gradual, fuzzy degree of proximity [34]. Therefore, using a single bandwidth not only leads to the loss of potential neighborhood associations but also undermines the objectivity of characterizing correlations among spatial features. As a result, the analysis becomes highly sensitive to bandwidth selection, introducing potential bias and instability [35].

To address the limitations of hard boundaries in spatial relationships, fuzzy theory has been introduced into spatial analysis [36]. It employs fuzzy concepts instead of rigid distance definitions [37,38], and has proved reliable and stable in spatial analysis, such as clustering [39,40], classification [41,42] and association rules [43,44]. Compared to traditional statistical methods, the fuzzy approach offers several advantages: (1) it is computationally more efficient [45]; (2) fuzzy neighborhoods more naturally and flexibly express the gradual nature of spatial proximity [34]; (3) fuzzy methods are less affected by parameters [46]. Due to these advantages, fuzzy methods have been incorporated into spatial statistical techniques, yielding reliable results. For example, Mason and Jacobson [47] proposed a fuzzy geographically weighted clustering method for geodemographic segmentation analysis. They incorporated space information into a clustering algorithm through spatial interaction, handling the geographical neighborhood effect, and improving the standard fuzzy c-means algorithm. Grekousis [48] improved the original FGWC and proposed a local fuzzy geographically weighted clustering method by applying a local spatial weight metric to handle spatial dependence and spatial heterogeneity, which is particularly important in spatial analysis. Although these methods demonstrated the flexibility and efficiency of fuzzy theory in spatial analysis, existing research still lacks a comprehensive framework that fully addresses the complex interactions among multiple categorical variables and the scale-related challenges inherent in spatial categorical data analysis.

Based on the above analysis, critical research gaps remain in spatial association analysis of categorical data. First, traditional spatial association mining primarily focuses on global associations but overlooks the spatial non-stationarity of these associations and fails to account for scale-dependent associations. Second, traditional statistical methods for categorical data, such as the Colocation Quotient (CLQ), are constrained by rigid single-bandwidth thresholds, which introduce distance bias and overlook the fuzzy nature of geographic adjacency. Lastly, few studies compare fuzzy versus deterministic methods (e.g., CLQ and GWCLQ) for capturing spatial heterogeneity, and most applications lack cross-domain generalizability. Collectively, these gaps highlight the need for a framework that integrates the flexibility of fuzzy methods with objective parameterization and multi-scale validation to effectively analyze complex urban data.

To fill the gap above, this study proposes an innovative Fuzzy Geographically Weighted Colocation Quotient (FGWCLQ) method to address the limitations of rigid single-bandwidth thresholds, significantly enhancing the precision and applicability of spatial association analysis from global and local perspectives. This method first defines a fuzzy neighborhood between spatial category objects and then proposes a new method to study both global and local associations in the category data. Finally, the method is validated through an empirical analysis of Point of Interest (POI) data in Beijing. The results indicate that FGWCLQ can explore complex associations between various categorical variables, yielding more robust and stable results. The innovations of this paper are threefold:

(1)

This study defines a fuzzy neighborhood between spatial categorical points and constructs a fuzzy geographically weighted matrix to measure spatial proximity.

(2)

This study proposes a new method, Fuzzy Geographically Weighted Colocation Quotient (FGWCLQ), to explore the association relationship between various categorical variables and visualize the spatial heterogeneity of these relationships.

(3)

This study proposes a multi-scale framework to explore the hidden spatial association rules among the different facility categories in Beijing using FGWCLQ.

This paper is structured as follows. The methodology is given in Section 2. Section 3 presents the study area and data sources. Section 4 presents the experimental results of the FGWCLQ method in analyzing the spatial relationships between star hotels, transportation facilities, and tourist attractions in Beijing, and compares the empirical results of the FGWCLQ with those of the GWCLQ. Section 5 discusses and summarizes the conclusions of this paper.

2. Methodology

In this section, the details of FGWCLQ were introduced. To formally describe the algorithmic part,

Table 1. Important notations used in this paper.

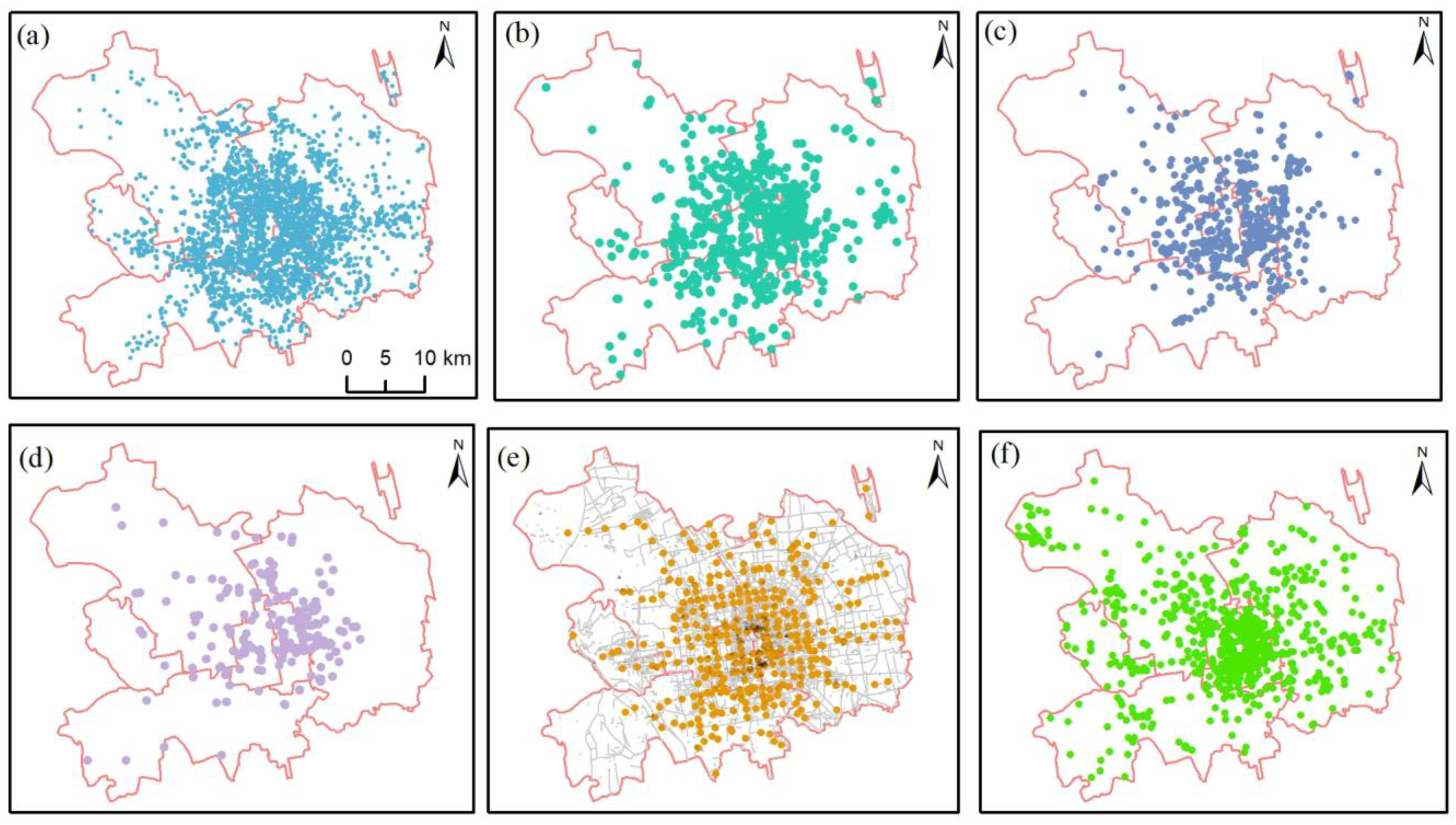
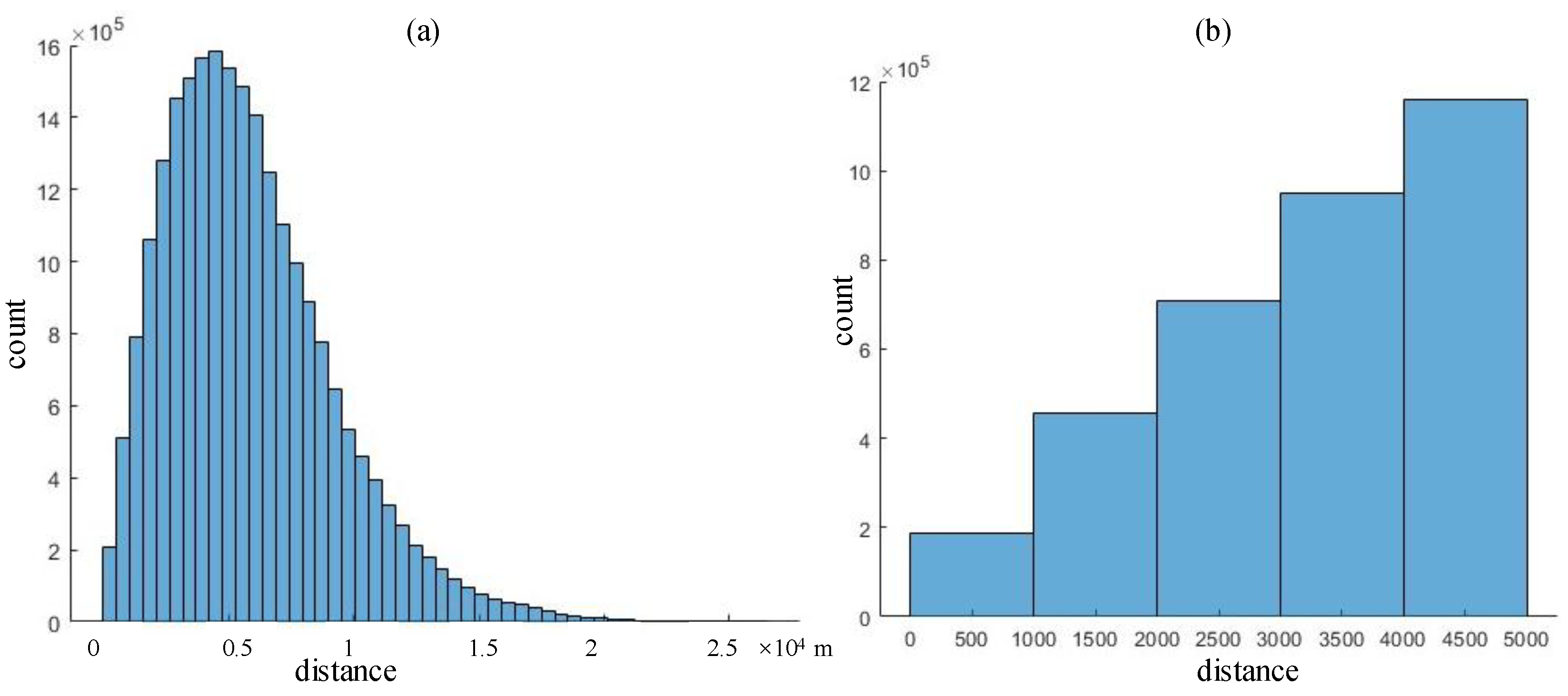
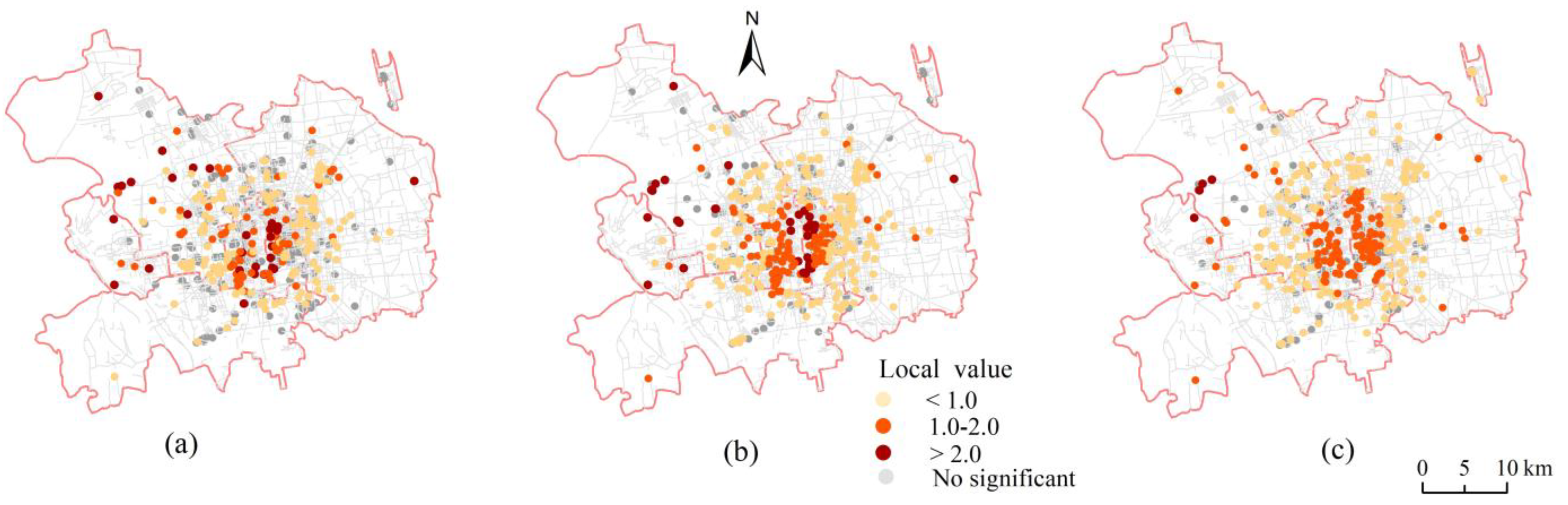
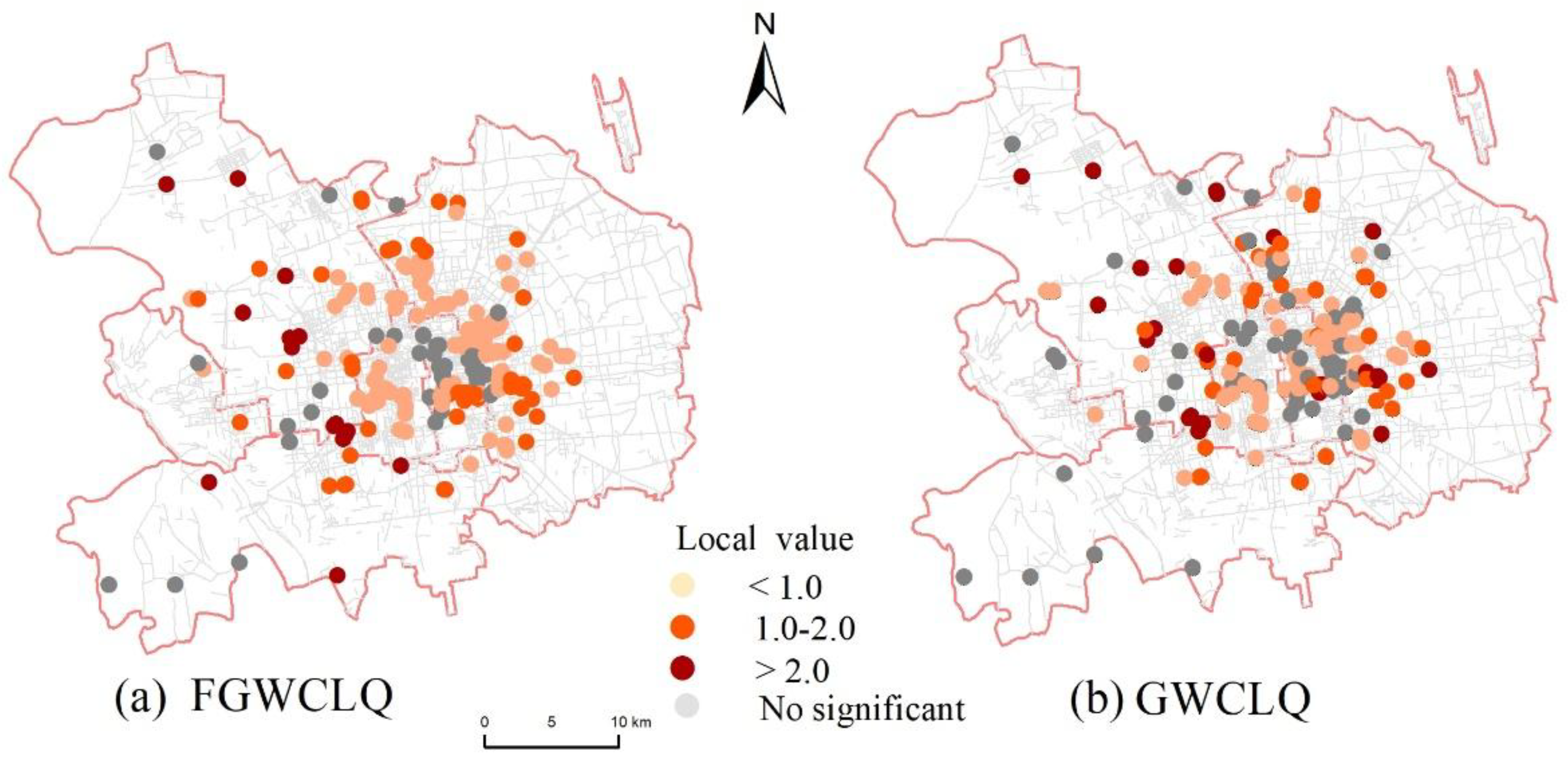
Notation	Definition
F	The categories of spatial objects
O	A set of spatial objects within the study area
fi, fj	Two different categories from the set F
oi, oj	Two different objects from dataset O
d(oi, oj)	Distance between two objects oi and oj
$O_{{\mathrm{f}}_{\mathrm{i}}}$	A set of category fi objects
$N_{{\mathrm{f}}_{\mathrm{i}}}$	The number of category fi
N	The total number of O

lists the main notations used in this paper.

2.1. Fuzzy Neighbor Relationship Between Spatial Categorical Data

Definition 1.

(Spatial categorical data) The spatial categorical data are represented as discrete spatial points with location and different categories/features, which are referred to as Equation (1):

$$\mathrm{O}=\{o_i\in \mathrm{O}|{ o}_i=(id,l\left(x_i,y_i\right),f_i),$$

(1)

where $l\left(x_i,y_i\right)$ is the location usually represented by the latitude and longitude, and $f_i\in F,(i=\mathrm{1,2},\dots ,K)$ is the category/feature of $o_i$.

Definition 2.

(Fuzzy relationship between spatial categorical points, FR) Suppose D is the distance between spatial points, D ∈ R⁺, then the fuzzy relationship FR between o_i and o_j in the spatial category points set O is defined as Equation (2):

$$\mathrm{F}\mathrm{R}\left(\mathrm{O}\right)=\left\{U\right(d(o_i,o_j)\left)\right|o_i,o_j\in \mathrm{O},d(o_i,o_j)\in \mathrm{D}$$

(2)

where $U\left(d\right(oi,oj\left)\right)$ is the fuzzy membership function of FR, indicating the probability that $d(o_i,o_j)$ belongs to FR [38]. The FR maps the distance between two points to a value within the interval [0, 1].

The fuzzy membership function $U\left(\right)$ is critical for the FR (O). There are various definitions for membership functions, including triangular and trapezoidal membership functions in the piecewise linear category, as well as other forms such as Gaussian and S-shaped membership functions [49,50]. Among them is the piecewise linear membership function, which is characterized by simplicity in calculation, ease of implementation, and understanding, making it suitable for different data analyses [51]. Considering the multi-scale analysis of the spatial pattern, this study uses a distance range [d₁, d₂] (d₂ > d₁) to define the fuzzy membership function, as follows in Equation (3) [33,52]:

$$U\left(d(o_i,o_j)\right)=\left\{\begin{array}{l}1,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}d(o_i,o_j)\le d_1\\ 1-{\displaystyle \frac{d(o_i,o_j)-d_1}{d_2-d_1}},d_1<d(o_i,o_j)\le \\ 0,\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}d(o_i,o_j)>d_2\end{array}\right.d_2$$

(3)

Definition 3.

(Fuzzy neighborhood set, FNS) Based on the definition of fuzzy relationship FR (O), the fuzzy neighborhood set FNS (O) is defined as in Equation (4):

$$FNS\left(O\right)=\left\{\right(o_i,o_j\left)\right|U\left(d\left(o_i,o_j\right)\right)>0\}$$

(4)

where U ( $d > 0)$ indicates that the fuzzy neighborhood membership degree is greater than 0 in the fuzzy neighbor relationship FR (O) [52].

Definition 4.

(The fuzzy geographically weighted, FGW) The fuzzy geographically weighted FGW ($o_i$, $o_j$) combines the traditional geographically weighted with the fuzzy membership degree $U\left(d(o_i,o_j)\right)$ and describes the strength and uncertainty of the spatial relationship between points o_i and o_j. The definition of FGW (o_i, o_j) is as in Equation (5):

$$\begin{array}{l}FGW(o_i,o_j)=U\left(d(o_i,o_j)\right)\times W(o_i,o_j)\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}=\left\{\begin{array}{l}exp(-0.5\times {\displaystyle \frac{d{(o_i,o_j)}^{\dot{2}}}{{d_1}^2}}),d(o_i,o_j)<d_1\\ (1-{\displaystyle \frac{d(o_i,o_j)-d_1}{d_2-d_1}})\times exp(-0.5\times {\displaystyle \frac{d{(o_i,o_j)}^{\dot{2}}}{{d_1}^2}}),d_1<d(o_i,o_j)<d_2\\ 0,otherwise\end{array}\right.\end{array}$$

(5)

$$W\left(o_i,o_j\right)=\exp \left(-{\displaystyle \frac{1}{2}}\left({\displaystyle \frac{{d(o_i,o_j)}^2}{d_1^2}}\right)\right)$$

(6)

where W (o_i, o_j) is a geographically weighted matrix which uses the Gaussian kernel function and  $d_1$ is the bandwidth. The fuzzy geographically weighted integrates traditional geographically weighted with fuzzy neighborhoods to redefine the decay pattern of spatial associations through a soft boundary interval of [d₁, d₂]. Specifically, in the core region ($d(o_i,o_j)\le d$₁), a Gaussian kernel function is employed to maintain the locality of the core area. Additionally, a transition zone is introduced ($d$₁$\le d(o_i,o_j)\le d$₂), which accelerates the decline of weights by incorporating an extra linear decay factor based on the original Gaussian kernel. This approach mitigates the influence of distant points while avoiding abrupt changes in weight. In the case of long distances ($d(o_i,o_j)>d$₂), weights are set to zero to eliminate interference from distant outliers.

2.2. The Fuzzy Neighborhood Boundary Setting Approach

The definition of fuzzy neighborhoods is fundamental to the fuzzy geographically weighted approach, which seeks to quantify graded spatial associations between target units and their surrounding entities. This is typically operationalized through two key parameters, d1 and d2. Establishing these parameters requires balancing theoretical rigor, data characteristics, and the specific study context. Two primary methodological approaches are commonly employed.

Knowledge-driven definition: This approach begins with a clear articulation of research objectives and contextual background, followed by a comprehensive review of relevant literature. It is further refined through consultations with domain experts and adjustments to neighborhood parameters based on specific characteristics of the study area, such as the spatial distribution and density of points.

Data-driven approaches: Two statistical methods are typically used to define fuzzy neighborhoods:

(1) Cumulative frequency analysis: This method utilizes distance histograms to identify structural breakpoints in distance distributions via cumulative frequency curves. Such breakpoints correspond to inflection points where the slope of the curve—that is, the rate of frequency change—shifts abruptly, indicating qualitative transitions in spatial interaction density across distance intervals. For histograms with approximately linear distribution characteristics, critical thresholds are determined using percentiles of cumulative frequencies (e.g., 10%, 20%, and 70%) of inter-entity distances, chosen to align with natural data divisions and reflect empirical spatial patterns [53].

(2) Rule-of-thumb: This method operationalizes parameter selection through statistically grounded heuristics, ensuring thresholds are anchored in quantifiable properties of the distance dataset. For example, Baride proposed a “Rule-of-thumb” for selecting these two parameters based on the mean and standard deviation of distances, defined as follows [54]:

$$d1=\max (0,m-\sigma )$$

(7)

$$d2=m+\sigma$$

(8)

where $m$ represents the mean distance between all data points, and $\sigma$ is the standard deviation of these distances.

In this study, we adopt both approaches to determine the bandwidth parameters and explore multi-scale spatial effects by testing different values.

2.3. The Fuzzy Geographically Weighted Colocation Quotient

Building on the fuzzy geographically weights introduced in the previous section, this study proposed the FGWCLQ, an extension of the Geographically Weighted Colocation Quotient (GWCLQ). Unlike the GWCLQ, FGWCLQ provides a more flexible representation of spatial proximity by recognizing gradual variations in the strength of spatial relationships, rather than adhering to a fixed distance threshold. Similar to the traditional colocation quotient (CLQ), the FGWCLQ also includes both global and local versions.

In general, the global FGWCLQ value between two categories, f_i and f_j, is defined as the ratio of the observed to expected proportion of category f_i within the neighborhood set of category f_j. The formulation of the global FGWCLQ is presented in Equation (7).

$$FGWCL{Q}_{f_i\to f_j}^{global}={\displaystyle \frac{{\displaystyle {\sum }_{o_i\in O_{f_i}}{\displaystyle {\sum }_{o_j\in O,o_i\ne o_j}FGW(o_i,o_j)\times x_{FN{S}_j}}}}{\frac{N_{f_j}}{N-1}{\displaystyle {\sum }_{o_i\in O_{f_i}}{\displaystyle {\sum }_{o_j\in O,o_i\ne o_j}FGW(o_i,o_j)}}}},N_{f_j}=N_{f_i}-1,if{f}_j=f_i$$

(9)

where $X_{{FNS}_j}$ is a binary variable that equals 1 if the j-th fuzzy neighborhood of the f_i-type point belongs to category $f_j$, and 0 otherwise. The global FGWCLQ provides a comprehensive overview of spatial association patterns.

The local Fuzzy Geographically Weighted Colocation Quotient, which assesses the spatial heterogeneity of association patterns across the study area, is defined as in Equation (8).

$$FGWCL{Q}_{f_i\to f_j}^{local}(i)={\displaystyle \frac{{\displaystyle {\sum }_{o_j\in O,o_i\ne o_j}FGW(o_i,o_j)\times x_{FN{S}_j}}}{\frac{N_{f_j}}{N-1}{\displaystyle {\sum }_{o_j\in O,o_i\ne o_j}FGW(o_i,o_j)}}}$$

(10)

The local FGWCLQ calculates the CLQ value at each individual point, rather than for a broader region. This index not only identifies whether a point pattern is clustered or dispersed but also facilitates mapping and visualization for interpretation, such as LISA.

The value of FGWCLQ is always positive. A higher FGWCLQ value indicates a stronger spatial attraction from category $f_i$ to $f_j$. Specifically, when the value of ${FGWCLQ}_{f_i\to f_j}$ is less than 1, it suggests that the points of category $f_i$ are not spatially associated with category $f_j$. Conversely, a value greater than 1 indicates an attraction from category $f_i$ to category $f_j$, while a value equal to 1 signifies a random spatial distribution between the two categories. Furthermore, FGWCLQ captures the directionality of spatial attraction. If both ${FGWCLQ}_{f_i\to f_j}$ and ${FGWCLQ}_{f_j\to f_i}$ exceed 1, the attraction between category $f_i$ and category $f_j$ is symmetrical. If only one of them exceeds 1, the spatial association is asymmetrical. Notably, ${FGWCLQ}_{f_i\to f_i}$ represents autocorrelation within category $f_i$.

To test the significance of FGWCLQ values, this study uses a Monte Carlo simulation method to calculate statistical test values. A p-value smaller than 0.05 indicates that the spatial association is statistically significant at the 95% confidence level [19].

3. Study Area and Data

3.1. Study Area

Beijing, as China’s political and economic center, boasts substantial economic and tourism resources that attract millions of visitors annually for both leisure and business purposes. The central urban area functions as the city’s heart, characterized by its dense population and clusters of infrastructure, making it a key focus of urban development and planning research. Due to well-developed transportation and a high concentration of tourist attractions, most hotels in Beijing are located in this area, offering tailored accommodation services. Thus, examining the hotel characteristics in this region is crucial for optimizing location selection and improving the tourist experience. This study covers the urban area of Beijing, which includes six districts: Dongcheng, Xicheng, Chaoyang, Fengtai, Shijingshan, and Haidian.

Hotels in urban areas are not randomly distributed. Instead, they tend to be highly clustered [55]. Several studies have focused on factors influencing the spatial and temporal distribution of hotels in Beijing, which show that traffic accessibility, commercial prosperity, and tourist attraction distribution are generally considered the key factors affecting hotel spatial layout [56]. However, these studies do not address the differences in patterns between different categories of star hotels and their surrounding infrastructures across various spatial scales. Accurately grasping the spatial correlation structure of distribution in star-rated hotels and its influencing factors is of great significance for promoting high-quality coordinated development of star-rated hotels and the regional tourism and transportation industry. This study will examine the spatial association between different types of star hotels and their surrounding infrastructures in the urban area of Beijing using the proposed FGWCLQ method.

3.2. Data Collection and Pre-Processing

The data used in this study were points of interest (POI) data, including star hotels, transportation facilities, and tourist attractions within Beijing, which were collected from Baidu Maps published in April 2022. We developed a data collection module using Baidu Maps API (http://api.map.baidu.com(accessed on 15 April 2022)), collecting attributes such as facility name, location, category, time, and district.

Since the raw data were unsuitable for analysis, several pre-processing steps were applied. First, missing features were filled in using the Baidu engine. Next, abnormal geo-location data were corrected by adjusting coordinates, interpolating with surrounding data, and excluding obviously erroneous entries. Consistency in naming conventions for fields such as category and district was also ensured. Finally, duplicate POIs were identified and removed by matching locations and other attributes. After pre-processing, a total of 6810 instances were achieved, including 5545 star hotels, 432 transportation facilities (TP), and 923 tourist attractions (TS). In this study, star hotels were classified into four quality levels: 2-star and below (2-STR), 3-star (3-STR), 4-star (4-STR), and 5-star (5-STR). The statistical characteristics and spatial distribution of these facilities are presented in

Table 2. Statistical characteristics of six categories of facilities in Beijing.

Categories	Explicate	Count	Portion
2-STR	Two Star Hotel and Economy Hotel	4051	59.49%
3-STR	Three Star Hotel	647	9.50%
4-STR	Four Star Hotel	525	7.71%
5-STR	Five Star Hotel	232	3.41%
Transportation (TP)	Subway Stations, Railway stations, Bus stations, and Airports	432	6.34%
Tourism (TS)	Urban squares, National scenic spots, and Famous scenic spots	923	13.55%
Total		6810	100.00%

and Figure 1.

4. Results

4.1. Experiment Setting

Urban facilities inherently exhibit distinct service ranges and influence radii. To quantify this for target facilities in Beijing, we first computed pairwise spatial distances between all data points and visualized their distribution via a histogram (Figure 2a). This histogram revealed a dominant peak at 5000 m, indicating this distance as the most prevalent among facility pairs. This study selected 5000 m as the service range for point facilities. This choice is justified because it corresponds both to the peak of the distance distribution and ensures that each point has at least one neighboring point within this radius. Furthermore, this distance aligns with previous research in the hotel research [55]. Therefore, drawing on both the character of the dataset and prior knowledge, this study adopts a 5 km service radius, beyond which the hotel’s influence is assumed to be negligible.

Within the influence range of the facilities, for single-scale analysis, the fuzzy neighborhood can be calculated through Equations (7) and (8), resulting in the range [2013 m, 4457 m]. However, as this study aims to explore the multi-scale distribution pattern of the facilities, three scales of fuzzy neighborhoods are selected for analysis to compare the distribution differences among these scales.

A histogram (Figure 2b) was constructed to characterize the distance distributions between diverse facilities within the 5 km influence radius. To operationalize the fuzzy neighborhoods, three critical thresholds (10%, 20%, and 70%) were identified based on the cumulative frequency of this histogram, corresponding to the intuitive cognitive distinctions of “nearby,” “medium,” and “faraway” in everyday distance perception. To enhance alignment with real-world behavioral contexts, these statistically derived points were further refined by integrating passenger travel behavior and decision-making processes, including typical commuting ranges and distance thresholds for facility utilization. The final definition of the three fuzzy neighborhoods, which synthesizes both spatial statistical distribution features and behavioral constraints, is presented in

Table 3. The division of spatial scale and the meaning of the fuzzy neighborhood.

Spatial Scale[d1, d2]	Fuzzy Neighborhood	Exploration
500–1000 m	nearby	5–10 min neighborhood: the walking distance at an average walking speed of around 1 m/s [57]
1000–2000 m	medium	15–20 min neighborhood: people’s daily needs can be satisfied within walkable or cyclable distances [58]
2000–5000 m	faraway	The service radius of the hotel that can be reached by car [55]

. This table details the classification of fuzzy neighborhoods alongside their geographical characteristics.

In addition to the fuzzy neighborhood setting, the Monte Carlo simulation for the significance test used a sample size of 1000 and was performed with 1000 random iterations, consistent with approaches employed in previous studies [59].

The experiments were conducted using MATLAB R2022b software on a 64-bit platform with 32 GB of RAM, an Intel Core i7 CPU, and a 2.00 GHz processor to validate the proposed method. The code and data are available at https://doi.org/10.6084/m9.figshare.26788822 (accessed on 21 August 2024).

4.2. The Results of Global FGWCLQ

After parameter setting, this study calculated the global values for six types of facilities in the urban area of Beijing using Equation (9). The results are shown in

Table 4. Global FGWCLQ values of four types of hotels and surrounding facilities at different fuzzy neighborhoods.

Fuzzy Neighborhood	Categories	2-STR	3-STR	4-STR	5-STR	TP	TS
500–1000 m	2-STR		0.943	0.938	0.935	0.946	0.907
	3-STR		1.084	1.130	1.247	1.010	0.926
	4-STR		1.070	1.411	1.555		0.996
	5-STR	0.858	1.111	1.463	2.611	0.881	0.934
	TP	0.859			0.872
	TS	0.798		0.898	0.895
1000–2000 m	2-STR	1.010	0.971	1.008	1.039	0.908
	3-STR	0.963	1.066	1.126	1.265	0.898	1.027
	4-STR	0.948	1.068	1.232		0.850	1.017
	5-STR	0.911	1.119		1.917	0.851	0.969
	TP	0.969		0.964	1.034	1.852	0.773
	TS	0.869	0.895	0.935	0.955	0.627	1.871
2000–5000 m	2-STR	0.992	1.020	1.049	1.100		1.036
	3-STR	0.965	1.061	1.089	1.238	0.882	1.056
	4-STR	0.958	1.051	1.130	1.264		1.072
	5-STR	0.936	1.112		1.517	0.792
	TP		1.024		1.024	1.132	0.933
	TS	0.906	0.976	1.027	1.099	0.743	1.513

Note: Blank values are not significant at 5% level.

.

First, the global FGWCLQ results reveal distinct spatial association relationships of star hotels across three fuzzy neighborhoods (shaded areas). Intra-category autocorrelation (main diagonal values) indicates that high-star hotels cluster significantly (autocorrelation >1), with clustering intensity diminishing as neighborhood scale increases. Specifically, 5-STR hotels exhibit the strongest clustering across all scales, peaking at the 1000-m radius (highest CLQ value). In contrast, 2-STR hotels display random distribution at all scales, likely due to their high numbers and dispersion, creating service gaps in suburban tourism zones. Beyond intra-category dynamics, inter-category associations strengthen with increasing neighborhood scale, peaking at 2000 m—indicating mixed star-rated clusters function as “hierarchical service systems” (e.g., 3-STR complementing 5-STR by catering to extended stays). A critical observation is that star hotels show stronger associations with tourist attractions (TS) than with transportation facilities (shown in the last two columns of Table 4), with this gap widening at larger scales, highlighting attraction proximity as a primary locational driver over mere transit access. These findings confirm that high-star hotels in Beijing’s core cluster are more intense than lower-star types, with diverse hotels aggregating around high-star establishments—disproportionately proximate to tourist attractions—underscoring their role as spatial anchors for star-rated hotel distribution [60]. Consequently, upgrade infrastructure within 1000 m of 5-STR clusters to reinforce agglomeration, incentivize 2-STR development near suburban transit/attractions to fill gaps, zone 2000 m mixed-star corridors for complementarity, and strengthen attraction-hotel connectivity via scale-appropriate infrastructure. These optimize tourism resource allocation using high-star hotels as anchors.

In addition to the intensity of spatial association, the symmetrical and asymmetrical dependences between the six categories, identified and classified based on the global results in Table 4, are visualized in Figure 3. As the spatial scale increases, spatial correlations between hotel categories become stronger, aligning with findings from previous studies [61]. Within the 500–1000 m range, spatial clustering is observed for 3-STR, 4-STR, and 5-STR hotels, each displaying significant autocorrelation (Figure 3a). Within 1000–2000 m, 3-STR and 4-STR hotels tend to cluster around the periphery of tourism attractions (TS), suggesting that the distribution of medium-star hotels is notably influenced by tourism facilities at this scale (Figure 3b). At the 2000–5000 m scale, relationships between star hotels and surrounding facilities become more complex and are characterized by mutual influence (Figure 3c). Notably, 5-STR hotels cluster near the periphery of other hotel categories and exhibit emerging associations with both transportation and scenic areas, indicating a marked increase in their spatial influence at broader scales.

The global results demonstrate the dependency and independence relationship among the six facilities, providing an overall association pattern in Beijing. However, the facilities display heterogeneous distribution, and the spatial association pattern will vary by location. To examine the differences in spatial association relationships across various districts, the local FGWCLQ results are analyzed in the following section.

4.3. The Results of Local FGWCLQ

The local FGWCLQ analysis allows for the examination of the spatial heterogeneity of associations among six types of facilities across Beijing. Using Equation (10), the local values for all the category points were calculated. According to the results of global analysis (Table 4), the spatial associations between 3-STR hotels and the above hotel and tourism attraction facilities are particularly strong. Therefore, this study presents only the local spatial association maps for these relationships in Figure 3.

As illustrated in Figure 3, the significant spatial associations between 3-STR hotels and other facilities exhibit distinct patterns across the 500–1000 m scale. First, high autocorrelation values (greater than 2) for 3-STR hotels are concentrated on the periphery of the city center periphery (Figure 4a), while their interrelationships with other facilities vary markedly by star rating: clustering with 4-STR hotels is centered on the urban core (e.g., near Tiananmen Square, Figure 4b), whereas clustering with 5-STR hotels is confined to the Dongcheng, Chaoyang district junction (Figure 4c). These divergences indicate that 3-STR hotels function as “complementary alternatives” to 4-STR hotels in core commercial zones (serving budget-conscious business travelers) but as “peripheral supplements” to 5-STR hotels in upscale mixed-use areas (supporting extended family or tour group stays). Beyond inter-hotel associations, 3-STR hotels show weakened spatial links to tourism attractions in the urban core, reflecting a critical “spatial mismatch” between mid-range accommodation demand and attraction accessibility, likely exacerbated by strict land-use regulations limiting new hotel development, with associations intensifying toward the periphery (Figure 4d). These findings inform targeted urban planning interventions: In the city core, incentivize 3-star hotels proximate to 4-star clusters to adopt family-friendly amenities (e.g., kitchenettes) to mitigate direct competition. For the Dongcheng-Chaoyang Corridor, integrate 3-star and 5-star hotels into cohesive “hospitality ecosystems,” with shared shuttles linking these establishments to convention centers. In peripheral areas, prioritize enhancing last-mile connectivity (e.g., metro feeders and bike-sharing) between 3-star clusters and emerging attractions, alongside targeted subsidies for 3-star development, to accelerate decentralized tourism and alleviate core-area congestion.

Given the strong spatial association between 4-STR hotels and TS, this study analyzed their relationship across fuzzy neighborhoods, as presented in Figure 5. Results indicate that peak association occurs at 1000–2000 m (Figure 5b), where clusters in historic districts and transit hubs define a “functional sweet spot”, balancing accessibility and mobility. Sparser clustering in <1000 m zones (Figure 5a) reflects niche proximity demand, while >2000 m associations (Figure 5c) align with business–tourism hybrids near offices/conventions. The result indicates that the optimal functional distance between 4-STR hotels and tourist attractions lies within a 1000–2000 m radius, balancing accessibility and land-use efficiency. Urban planners can capitalize on this spatial range to design integrated tourism zones by prioritizing 4-STR hotel development within 1000–2000 m of key tourist sites, thereby minimizing traveler transit distances and enhancing experiential quality. For zones < 1000 m, targeted incentives should be deployed to preserve niche functions while precluding overdevelopment. In zones >2000 m, 4-STR hotel density should be aligned with office and convention center capacity, supplemented by dedicated shuttle services connecting to attractions. These interventions leverage the distance-sensitive nature of 4-STR hotel-tourist attraction associations to optimize tourism system functionality across spatial scales.

4.4. Comparison with Deterministic Methods

To demonstrate the superior performance of FGWCLQ, this section compares it with deterministic methods in both global and local versions. Geographically Weighted Colocation Quotient (GWCLQ) is a typical deterministic method that uses a single threshold to define the spatial neighborhood [24]. For comparability, the GWCLQ employed a bandwidth of 1500 m, while the FGWCLQ method utilized a fuzzy neighborhood of 1000–2000 m. Both methods used the same parameters (sample size = 1000 and random iterations = 1000). The results are presented in

Table 5. Global value for six categories by two methods.

Method	Category	2-STR	3-STR	4-STR	5-STR	TP	TS
FGWCLQ (1000–2000 m)	2-STR	1.010	0.971	1.008	1.039	0.908
	3-STR	0.963	1.066	1.126	1.265	0.898	1.027
	4-STR	0.948	1.068	1.232		0.850	1.017
	5-STR	0.911	1.119		1.917	0.851	0.969
	TP	0.969		0.964	1.034	1.852	0.773
	TS	0.869	0.895	0.935	0.955	0.627	1.871
GWCLQ (1500 m)	2-STR	1.003	0.981	1.018	1.060	0.915	1.015
	3-STR	0.962	1.068	1.114	1.263		1.043
	4-STR		1.065	1.202		0.836	1.024
	5-STR	0.925	1.125	1.284	1.737	0.829
	TP		0.983	0.970	1.032	1.522	0.803
	TS	0.880		0.947	0.968		1.789

Note: Blank values are not significant at 5% level.

and Figure 6.

From Table 5, it can be seen that the global values for both methods are quite similar. However, there are some specific differences. First, the autocorrelation values for the six types of facilities in FGWCLQ are greater than those in GWCLQ. Additionally, the symmetric association relationships between 4-STR and 5-STR hotels are absent in the GWCLQ results. Lastly, the proportion of significant associations in the FGWCLQ is higher than that in GWCLQ.

To further investigate the differences between the two methods, this study selects five bandwidths for GWCLQ (ranging from 1000 m to 2000 m) and compares their corresponding global values. For clarity, five representative combinations have been selected for display, with the results presented in Figure 6. It is evident that the global values of GWCLQ show significant variation across the five bandwidths. Specifically, these variations include declines (e.g., 3-STR to 4-STR), increases (e.g., 4-STR to TS, and 2-STR to 3-STR), and patterns of initial decline followed by increase and stabilization (e.g., 3-STR autocorrelation). In contrast, the values of FGWCLQ remain constant across the entire bandwidth range, demonstrating its greater stability and robustness in identifying spatial association relationships. The GWCLQ method, relying on a single fixed distance, is proven to be sensitive to bandwidth changes.

Additionally, a comparison between the FGWCLQ and GWCLQ was conducted at the local scale. This study focuses on comparing the local values between 5-STR hotels and transportation facilities, with the results presented in Figure 7. Figure 7 shows that the FGWCLQ outperforms GWCLQ in visualizing fine-grained spatial heterogeneity. While GWCLQ produces fragmented hotspot maps, FGWCLQ generates continuous association surfaces, correlation intensity spreads from the city center to the suburbs (Figure 7a). Furthermore, there are fewer non-significant points in FGWCLQ. These findings prove that the FGWCLQ method, by incorporating fuzzy geographically weighted, is better equipped to capture local variations and complex spatial relationships. In contrast, the deterministic method GWCLQ, relying on a fixed bandwidth, tends to overlook potential neighborhood relationships and smooths out spatial heterogeneity.

Finally, the statistical results of local value are summarized in

Table 6. Comparison of statistical quantities between two methods.

Method	5-STR → TP		5-STR → TS		Bandwidth
	Number	Proportion	Number	Proportion
FGWCLQ	84	36.21%	73	31.46%	[1000 m, 2000 m]
GWCLQ	71	30.6%	62	26.72%	1500 m

, which illustrates the number of local values greater than 1 and exhibiting significance for “5-STR to TP” and “5-STR to TS” under the fuzzy bandwidth [1000 m, 2000 m] for FGWCLQ, as well as under a bandwidth of 1500 m for GWCLQ. Notably, FGWCLQ shows higher local clusters when fuzzy neighborhoods are considered.

The comparative analysis results above reveal that the FGWCLQ method is more accurate and robust than the deterministic method in exploring spatial association rules in categorical data. It can identify more association patterns overlooked by the traditional GWCLQ method, thereby providing a more comprehensive description of spatial association patterns.

4.5. Sensitivity Analysis

In this study, the configuration of fuzzy neighborhoods was identified as a critical parameter. To evaluate its impact on model results, a series of consecutive fuzzy distance thresholds, [d1, d2], were defined, ranging from 0 m to 5000 m in 500 m increments, resulting in ten distinct fuzzy neighborhoods (e.g., [0, 500 m], [500 m, 1000 m], etc.). The FGWCLQ algorithm was applied to each neighborhood to calculate the corresponding global values. For clarity, six representative combinations have been selected for display, with the results presented in Figure 8. The results indicate that as the fuzzy neighborhood distance increases, the growth in the global values gradually decelerates, becoming negligible beyond 2500 m. This suggests that the algorithm exhibits low sensitivity to large bandwidths, likely due to the influence range of various facilities being limited, beyond which their impact nearly stabilizes.

To comprehensively evaluate the sensitivity of the relationships among various facilities to the fuzzy neighborhood settings, this study utilized a widely accepted sensitivity index: Spatial Scale Sensitivity Index (SSSI) [62,63]. The formula for calculating this index is presented below:

$$SSSI={\displaystyle \frac{1}{n}}{\displaystyle {\sum }_{i=1}^{10}\frac{\left|R_i-R_{avg}\right|}{R_{avg}}}$$

(11)

Using this formula, the SSSI was calculated and compared at different fuzzy neighborhoods. The results are summarized in

Table 7. The SSSI between various facilities in different fuzzy neighborhoods.

Category	2-STR	3-STR	4-STR	5-STR	TP	TS
2-STR	0.025	0.031	0.042	0.066	0.024	0.063
3-STR	0.004	0.034	0.019	0.025	0.084	0.057
4-STR	0.023	0.012	0.110	0.097	0.043	0.040
5-STR	0.039	0.005	0.105	0.262	0.059	0.068
TP	0.064	0.050	0.076	0.067	0.564	0.157
TS	0.054	0.075	0.058	0.090	0.095	0.200

. The table indicates that most facilities exhibit low sensitivity to the fuzzy neighborhood settings, with sensitivity indices below 0.1. However, certain facilities show higher sensitivity, particularly the autocorrelation of transportation, followed by that of 5-STR hotels. Furthermore, the influence of transportation on tourism attractions is also notably affected by the fuzzy neighborhood settings, demonstrating strong sensitivity. These results suggest that the effect of fuzzy neighborhood settings on the algorithm is largely determined by the semantic attributes and spatial distribution of the geographic objects, rather than by the specific spatial scale.

5. Discussion

Traditional spatial statistical methods (such as geographically weighted approaches) typically use a fixed bandwidth (distance threshold or K-nearest neighbors) to define spatial relationships. Such a single bandwidth imposes an abrupt cutoff, thereby disrupting the continuous nature of geographic processes. Additionally, model performance demonstrates high sensitivity to bandwidth selection. This study proposes a Fuzzy Geographically Weighted Colocation Quotient (FGWCLQ) method, which employs fuzzy membership functions to model spatial continuity in a more flexible and natural manner. By defining fuzzy neighborhoods, this approach overcomes the constraints of traditional single-bandwidth methods. The results demonstrate that FGWCLQ can reliably and stably discover prevalent spatial associations, as well as visualize the spatial heterogeneity under different fuzzy neighborhood definitions. Sensitivity analyses confirm the robustness of FGWCLQ to changes in fuzzy neighborhood parameters.

Compared to other methods, the FGWCLQ approach fundamentally differs in its assumptions, performance metrics, and interpretability. In theoretical assumptions, unlike classical CLQ and GWCLQ, which rely on rigid distance thresholds to define spatial neighbors, FGWCLQ employs fuzzy membership functions to model the gradual decay of spatial relationships. This aligns with theoretical advancements in fuzzy spatial analysis, which recognize that geographic adjacency exists on a continuum rather than a binary boundary [33,36]. This assumption also differentiates FGWCLQ from fuzzy clustering techniques (e.g., FGWC or LFGWC), which define fuzzy neighborhoods based on feature similarity rather than spatial distances [48]. In terms of performance, FGWCLQ outperforms GWCLQ in capturing scale-varying associations and exhibits stable and robustness (Figure 5). For example, in analyzing Beijing’s 4-STR to TS attractions, GWCLQ exhibited unstable performance across bandwidths (e.g., 1000 m to 2000 m), with significant fluctuations in association (variance of the global value >0.25). In contrast, FGWCLQ’s fuzzy neighborhood framework maintained consistent performance, as the gradual membership decay mitigated sensitivity to arbitrary scale settings. This finding is consistent with prior studies showing that fuzzy methods reduce parameter-induced variance in spatial analyses [64]. Compared to FGWCLQ, fuzzy clustering methods emphasize attribute stability over spatial fidelity. Using static weight parameters disregards scale-related processes, producing overly smooth results that obscure subtle heterogeneous features. Regarding interpretability, the CLQ and GWCLQ methods exhibit pronounced boundary effects that disrupt the continuity of geographic processes. While fuzzy clustering methods offer interpretability within the attribute space, their membership values do not correspond to measurable geographic processes, resulting in a lack of interpretability at the spatial level. FGWCLQ addresses the limitation by grounding fuzzy memberships in distance decay, allowing local association values to be directly linked to real-world spatial phenomena. This enhances the method’s practical value for urban planners and policymakers. Collectively, these distinctions position FGWCLQ as a method that advances beyond the limitations of existing approaches by integrating theoretically grounded fuzzy spatial decay with robust performance and dual spatial-attribute interpretability [65].

The case study results demonstrate the effectiveness of FGWCLQ and enhance our understanding of spatial associations in urban facilities. By defining the linguistic predicates, such as “nearby,” “medium,” and “faraway,” using domain knowledge-based models for fuzzy neighborhoods and spatial effects, we identify the dependence and independence relationships among the six facilities and visualize the heterogeneity of spatial distribution patterns. For example, high-star hotels tend to show greater clustering over larger spatial ranges, whereas low-star hotels demonstrate stronger clustering within smaller spatial ranges. These findings are consistent with previous studies [66], which also reported significant spatial associations between hotels and surrounding facilities. However, notable distinctions also emerge. Traditional approaches by Yang et al. [53] identified discrete hotspot zones based on rigid bandwidths, while FGWCLQ reveals continuous association surfaces, highlighting hierarchical clustering patterns. This not only provides a more detailed visualization of spatial distributions but also better aligns with cognitive theories of human spatial perception.

However, this study has some limitations. While it demonstrates the effectiveness of the FGWCLQ method in analyzing the spatial correlations among three types of facilities in Beijing, there is currently insufficient evidence to confirm its universality and reproducibility across different contexts. In practice, factors such as urban environment, research objectives, and data structure can substantially influence the method’s performance. To address this limitation, a generalizable and adaptable application framework is essential to facilitate broader adoption of the FGWCLQ method. First, for spatial scale adaptation, fuzzy neighborhoods need to be calibrated to reflect spatial interaction patterns in different scenarios. In areas with dense point distributions, smaller-scale fuzzy neighborhoods are used to analyze fine-grained spatial dependencies; conversely, in sparse areas, larger-scale fuzzy neighborhoods are used to accommodate large-scale spatial patterns. Regarding the research objectives, parameter optimization aims to align with the interaction mechanisms specific to the domain. For example, in this study, we adopt a 5-km radius to represent the influence range of facilities. In contrast, in epidemiological applications such as disease transmission modeling, the fuzzy thresholds (d1,d2) are established based on epidemiological precedents; for instance, for locally transmitted airborne pathogens, the thresholds typically range from 500 m to 1.5 km [42]. Regarding data structure, parameterization strategies can be adapted to differences in spatial resolution and data sparsity. High-resolution datasets (e.g., POI points or crime incidents) employ refined, data-driven thresholds based on cumulative frequency breakpoints to preserve local spatial heterogeneity. In contrast, coarse-grained or sparse data (such as county-level disease incidence rates) utilize statistically robust thresholds (e.g., mean ± 1.5σ) or expert knowledge to mitigate the effects of random noise.

Second, this method relies on dual parameters (d1, d2) to define fuzzy neighborhood boundaries, introducing potential subjective bias that substantially affects analytical outcomes. The selection of fuzzy boundaries represents the “Achilles’ heel” of fuzzy mathematics, directly influencing model robustness, result interpretability, and cross-study reproducibility. As evidenced in our Beijing case study, such subjectivity manifests tangibly: a 50% variation in d2-d1 leads to 18–27% fluctuations in the association indices between 4-STR hotels and tourist attractions, with hotspot zones shifting spatially by up to 500 m (Table 4). This sensitivity may either overstate inter-category associations due to excessively broad neighborhood ranges or diminish the theoretical advantages of the fuzzy method when ranges are overly narrow. In this study, fuzzy boundaries were selected using a data-driven approach supplemented by prior knowledge, providing a scientific and reproducible framework for boundary determination; our findings further validate the feasibility of fuzzy neighborhoods. However, this research solely utilizes the spatial distribution and statistical characteristics of data for calculations. More precise and universally applicable methods could enhance the scientific rigor of fuzzy neighborhood determination. For example, cross-validation could be employed to select d1 and d2 parameters that maximize the model’s fit to observed spatial patterns [33], or machine learning-based techniques (e.g., Bayesian optimization) could enable automatic parameter tuning [36]. Additionally, integrating scale sensitivity indices (e.g., SSI) would quantify the impact of parameter variations, facilitating robust sensitivity analysis.

Furthermore, this study relies exclusively on spatial proximity to measure spatial associations, neglecting deeper functional couplings and semantic similarities between categorical data, an oversight that can readily create discrepancies between derived spatial association patterns and real-world scenarios. For instance, proximity-based metrics treat the 500-m distance between a 3-star hotel and a metro station as equivalent to the same distance between that hotel and a scenic spot, despite their fundamentally distinct roles in tourism functionality. Similarly, these metrics fail to account for semantic gradients. Two-star and three-star hotels, which share semantic and functional attributes aligned with budget travelers’ needs, should theoretically exhibit stronger spatial associations than either would with five-star hotels (catering to high-end tourists), yet proximity-only models conflate these relationships. Such limitations risk generating spatial association outcomes misaligned with real-world tourism dynamics. To address this, we propose integrating semantic similarity weights between categories via three approaches: expert knowledge (e.g., rating 4-star hotels’ relevance to scenic spots as 0.8 versus 0.5 for general transportation facilities), co-occurrence statistics (e.g., “5-star hotels” co-occur with “world heritage sites” 42 times per 1000 tourism reviews versus 11 times with “bus stations”), and ontological frameworks (e.g., “luxury hotels” share tourism service attributes with “scenic spot visitor centers” [semantic distance = 0.2] but not with “cargo terminals” [0.7]). Linear or non-linear integration of these semantic weights with geography weights will enable the model to distinguish meaningful tourism-related associations (e.g., hotels and scenic spots) from trivial spatial adjacencies (e.g., hotels and maintenance facilities), more accurately reflect functional and semantic affinities between tourism entities, and capture the multidimensional interactions among hotels, scenic spots, and transportation facilities that extend beyond mere spatial proximity.

In summary, the FGWCLQ not only addresses methodological limitations in spatial analysis but also advances theoretical frontiers in geographic information science. By integrating fuzzy theory with spatial statistics, FGWCLQ provides a formal framework to model the “geographic principle of distance decay” in its continuous form, resolving the long-standing contradiction between deterministic scale assumptions and real-world spatial complexity [34,36]. This theoretical innovation has profound implications for urban studies and offers policymakers a data-driven tool to design “fuzzy urban districts”. In practice application, this method is not only applicable to urban facilities to explore spatial association rules between different categories but can also be extended to other spatial categorical data, such as spatial associations between crime and disease, between house and work area, or industrial spatial pattern.

6. Conclusions

In this study, a novel fuzzy geographically weighted colocation quotient method was proposed for spatial association mining in spatial category data. Instead of selecting a single distance parameter, our approach uses a spatial range and introduces fuzzy theory to define geographic neighborhoods, constructing fuzzy geographic weights. This offers a new way to represent spatial proximity and closeness in spatial statistical models. Additionally, this study provides a framework for analyzing multi-scale patterns in spatial categorical data, which is valuable for spatial association mining. The proposed method has been validated through the analysis of the associations between hotels and their surrounding facilities in the Beijing urban area. The results demonstrate that the FGWCLQ method effectively maximizes the exploration of spatial associations between categorical data and exhibits greater robustness compared to GWCLQ, showing insensitivity to variations in bandwidth.

Several directions can be explored to further develop this research. First, this study considers only the statistical characteristics of data to define fuzzy neighborhoods. Incorporating both the spatial distribution patterns of data and prior knowledge would yield more refined results. Future work could leverage Moran’s I or sensitivity indices to optimize the selection of fuzzy neighborhoods. Second, future extensions could incorporate domain knowledge through semantic networks or knowledge graphs, assigning weighted memberships based on category-level functional similarity (e.g., using WordNet to measure semantic distances between “hotel” and “tourist attraction” concepts). Alternatively, integrating text mining of business descriptions (e.g., from POI metadata) could derive data-driven semantic weights, enhancing the model’s ecological validity. Finally, this study’s case analysis examines the spatial associations between hotels and facilities in Beijing. While the results clearly demonstrate the effectiveness of FGWCLQ in the Beijing urban area, spatial association patterns may vary significantly across different geographical contexts and application domains. Future research should investigate its application in various contexts to continuously improve the algorithm’s universality and efficacy.