R-MLGTI: A Grid- and R-Tree-Based Hybrid Index for Unevenly Distributed Spatial Data
Abstract
1. Introduction
2. Related Works
2.1. Spatial Indexing Based on Tree Structures
2.2. Spatial Indexing Based on Grids and Spatial Partitioning
2.3. Multi-Structure Hybrid Indexing Methods
3. Method
3.1. Data Applicable to Indexing
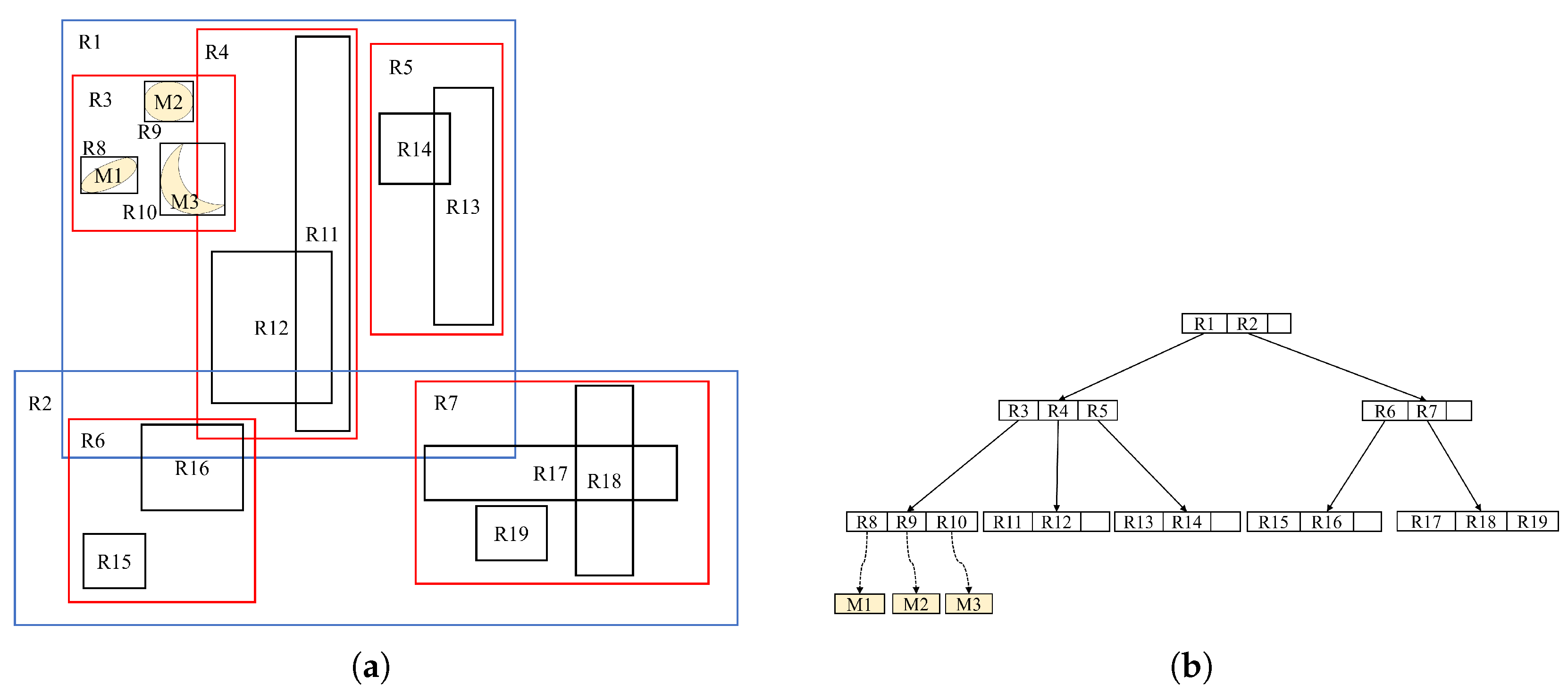
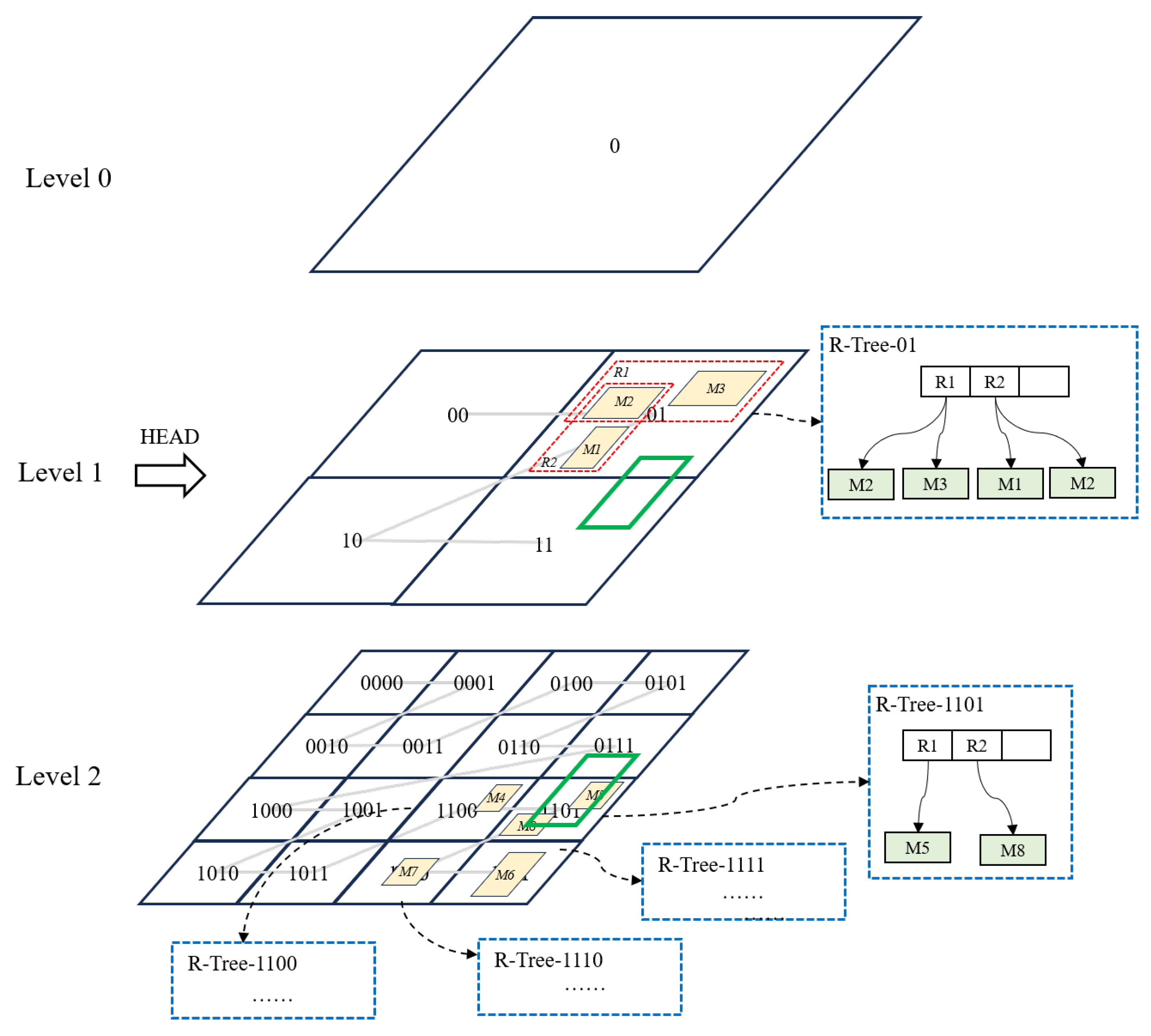
3.2. R-MLGTI Index Structure
3.2.1. Grid and R-Tree
3.2.2. Dynamic Grid Strategy
3.2.3. Phenomenon of Cross-Grid Overlap
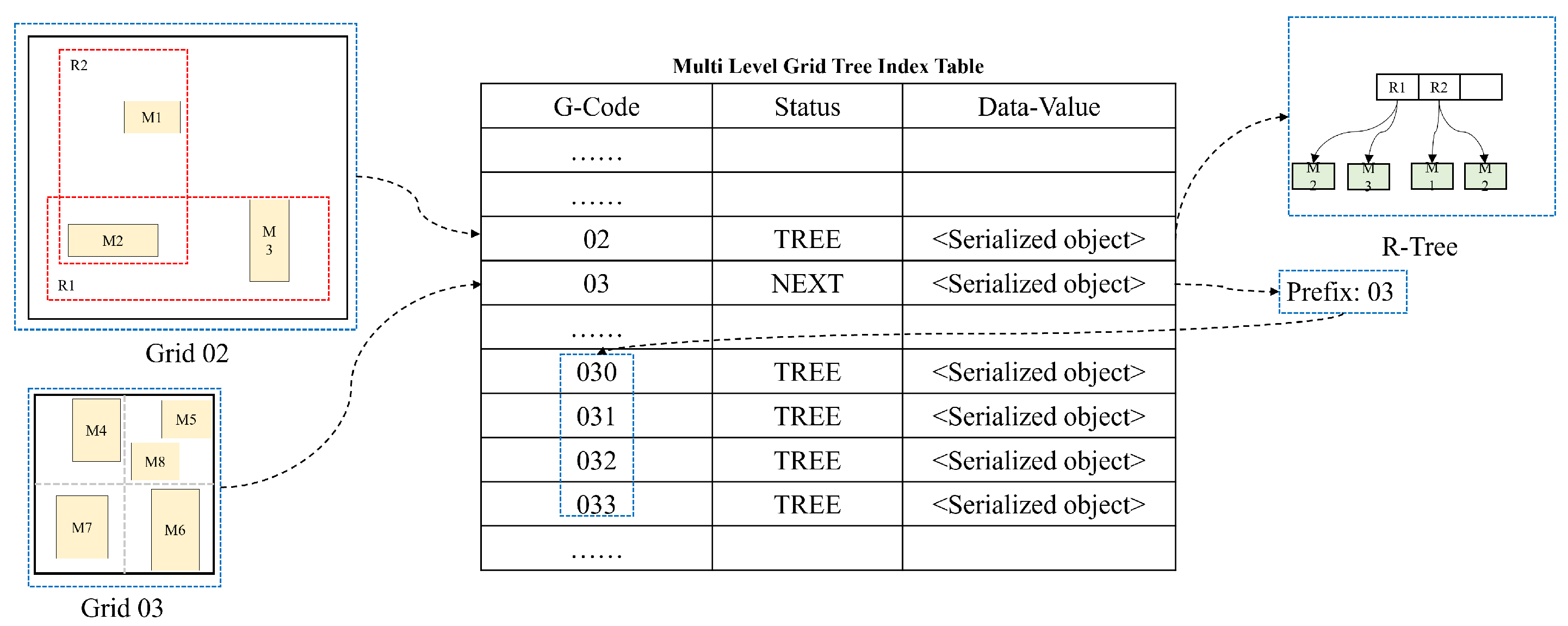
3.2.4. Storage Structure
3.3. Insertion Algorithm
3.4. Query Algorithm
| Algorithm 1: Inserting geospatial metadata into R-MLGTI |
 |
| Algorithm 2: Spatial data query |
 |
| Algorithm 3: Query in multi-level grid tree |
 |
4. Experiments and Results
4.1. Environment and Testing Methodology
4.1.1. Platform and Environment
4.1.2. Test Method
4.1.3. Code Warm-Up
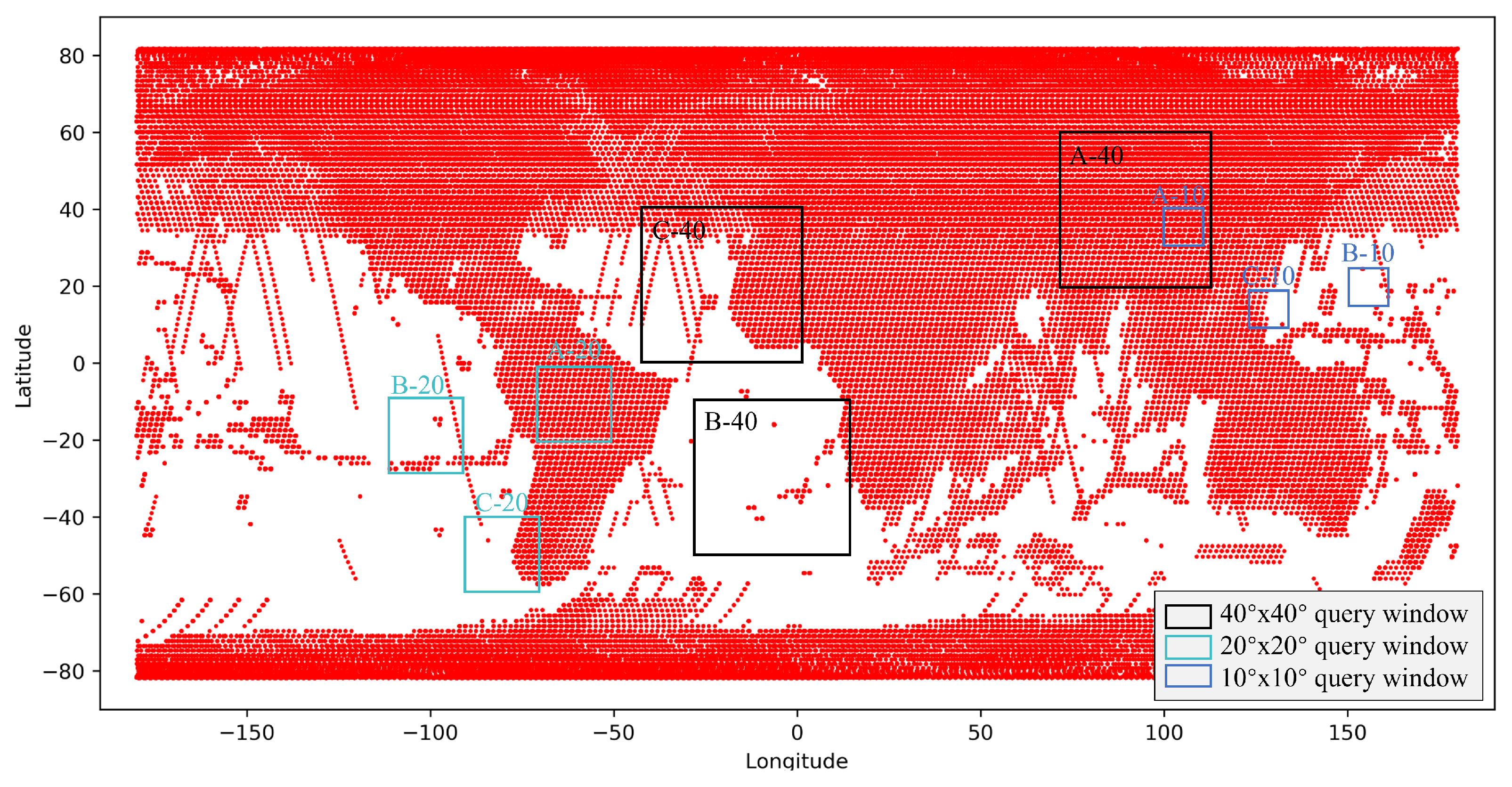
4.2. Experimental Data
4.3. Results and Analysis
4.3.1. Performance of Data Import
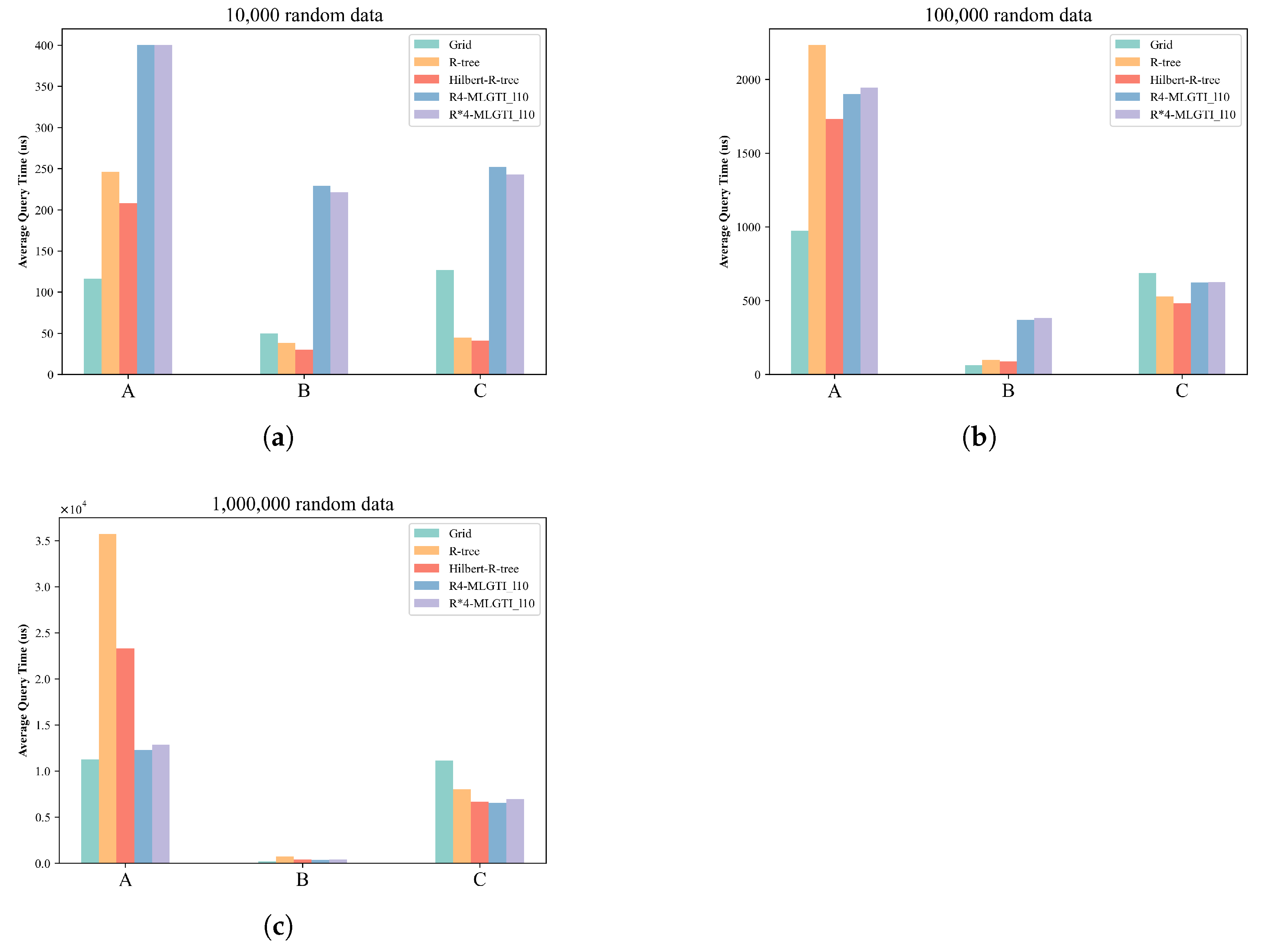
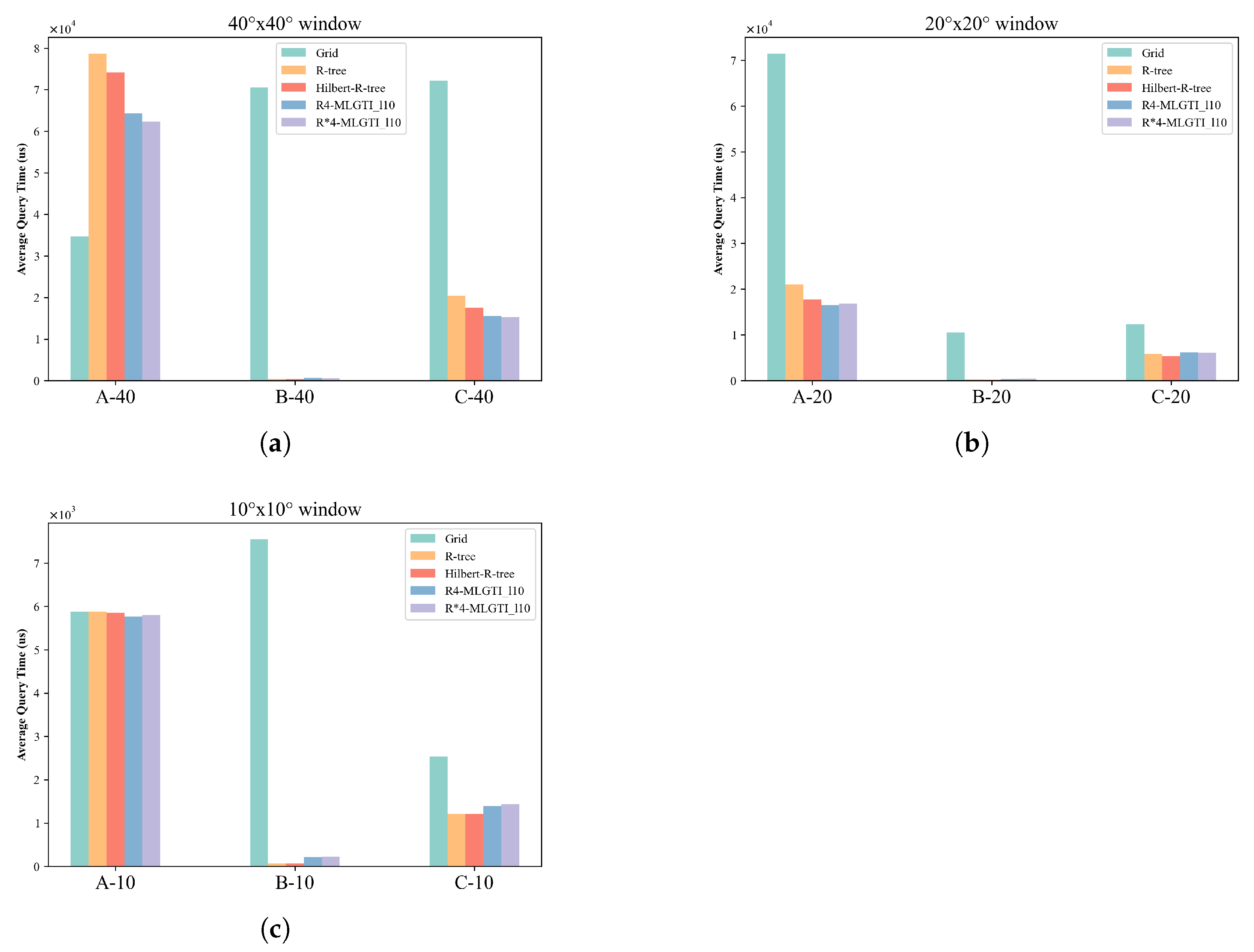
4.3.2. Performance of Spatial Query
- As the data scale increases, the retrieval time for all methods increases across the various query regions.
- The R-tree index is more advantageous for unevenly distributed data or smaller datasets. The experiment confirms the conclusion that excessive overlap of intermediate-node MBRs in the R-tree due to large data volumes negatively affects query efficiency. Therefore, it is best to avoid using a single R-tree index when the indexed objects are overly concentrated.
- The advantage of the grid index lies in its ability to maintain good performance when handling large amounts of uniformly distributed data. This is due to the fixed-partition structure of the grid, which divides the global latitude and longitude ranges and encodes the grid cells. Spatial information can then be queried using only the grid encoding field. However, the indexing performance deteriorates when the grid cells are of fixed size and the data is unevenly distributed.
- R-MLGTI, which combines the grid-partitioning concept and uses independent R-tree indexing for each partition, has a more complex structure. It actually incurs more query time when the data scale is small. As the data scale increases, the query performance gap between R-MLGTI and the other two methods gradually narrows, with a smaller increase in query time. It is more suitable for querying large-scale, unevenly distributed data.
- The grid-indexing method only had an advantage when the query window was sufficiently large and contained a large amount of data; otherwise, its performance was worse than that of the R-tree and R-MLGTI methods.
- The advantage of the R-tree method was similar on the simulated data. In datasets with uneven distribution and the same query window size, the R-tree method performed better when the data distribution was sparse (i.e., fewer data points per unit area).
- The R-MLGTI method performed better in large-scale data retrieval or regions with non-uniform distribution, and it outperformed the R-tree method on dense data retrieval over large areas.
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, J.; Wang, L.; Zhao, X.; Cheng, S. The relationship between urbanization and land use in Guiyang city. Earth Sci. 2019, 44, 2944–2954. [Google Scholar]
- Xiao, Y.; Wang, Q.; Zhang, H.K. Global Natural and Planted Forests Mapping at Fine Spatial Resolution of 30 m. J. Remote Sens. 2024, 4, 0204. [Google Scholar] [CrossRef]
- Sheng, M.; Lei, L.; Zeng, Z.C.; Rao, W.; Song, H.; Wu, C. Global land 1° mapping dataset of XCO2 from satellite observations of GOSAT and OCO-2 from 2009 to 2020. Big Earth Data 2023, 7, 170–190. [Google Scholar] [CrossRef]
- Li, M.; Peng, J.; Lu, Z.; Zhu, P. Research progress on carbon sources and sinks of farmland ecosystems. Resour. Environ. Sustain. 2023, 11, 100099. [Google Scholar] [CrossRef]
- Tian, J.; Zhang, Y.; Zhang, X. Impacts of heterogeneous CO2 on water and carbon fluxes across the global land surface. Int. J. Digit. Earth 2021, 14, 1175–1193. [Google Scholar] [CrossRef]
- Shekhar, S.; Evans, M.R.; Gunturi, V.; Yang, K.; Cugler, D.C. Benchmarking spatial big data. In Proceedings of the Specifying Big Data Benchmarks: First Workshop, WBDB 2012, San Jose, CA, USA, 8–9 May 2012, and Second Workshop, WBDB 2012, Pune, India, 17–18 December 2012; Revised Selected Papers. Springer: Berlin/Heidelberg, Germany, 2014; pp. 81–93. [Google Scholar]
- Tong, X.; Ben, J.; Liu, Y.; Zhang, Y. Modeling and expression of vector data in the hexagonal discrete global grid system. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 40, 15–25. [Google Scholar] [CrossRef]
- Li, S.; Pu, G.; Cheng, C.; Chen, B. Method for managing and querying geo-spatial data using a grid-code-array spatial index. Earth Sci. Inform. 2019, 12, 173–181. [Google Scholar] [CrossRef]
- Jagadish, H.V.; Ooi, B.C.; Tan, K.L.; Yu, C.; Zhang, R. iDistance: An adaptive B+-tree based indexing method for nearest neighbor search. ACM Trans. Database Syst. (TODS) 2005, 30, 364–397. [Google Scholar] [CrossRef]
- Guttman, A. R-trees: A dynamic index structure for spatial searching. In Proceedings of the 1984 ACM SIGMOD International Conference on Management of Data, Boston, MA, USA, 18–21 June 1984; pp. 47–57. [Google Scholar]
- Li, G.; Tang, J. A new R-tree spatial index based on space grid coordinate division. In Proceedings of the 2011, International Conference on Informatics, Cybernetics, and Computer Engineering (ICCE2011), Melbourne, Australia, 19–20 November 2011; Volume 2: Information Systems and Computer Engineering. Springer: Berlin/Heidelberg, Germany, 2012; pp. 133–140. [Google Scholar]
- Sellis, T.; Roussopoulos, N.; Faloutsos, C. The R+-tree: A dynamic index for multi-dimensional objects. In Proceedings of the 13th VLDB Conference, Brighton, UK, 1–4 September 1987. [Google Scholar]
- Kamel, I.; Faloutsos, C. Hilbert R-Tree: An Improved Rtree Using Fractals. In Proceedings of the VLDB, Citeseer, Santiago de Chile, Chile, 12–15 September 1994; Volume 94, pp. 500–509. [Google Scholar]
- Amiri, A.M.; Samavati, F.; Peterson, P. Categorization and conversions for indexing methods of discrete global grid systems. ISPRS Int. J. Geo-Inf. 2015, 4, 320–336. [Google Scholar] [CrossRef]
- Zhou, M.; Chen, J.; Gong, J. A pole-oriented discrete global grid system: Quaternary quadrangle mesh. Comput. Geosci. 2013, 61, 133–143. [Google Scholar] [CrossRef]
- Huang, M.; Hu, P.; Xia, L. A grid based trajectory indexing method for moving objects on fixed network. In Proceedings of the 2010 18th International Conference on Geoinformatics, Beijing, China, 18–20 June 2010; pp. 1–4. [Google Scholar]
- Nievergelt, J.; Hinterberger, H.; Sevcik, K.C. The grid file: An adaptable, symmetric multikey file structure. ACM Trans. Database Syst. (TODS) 1984, 9, 38–71. [Google Scholar] [CrossRef]
- Ficklin, D.L.; Letsinger, S.L.; Gholizadeh, H.; Maxwell, J.T. Incorporation of the Penman–Monteith potential evapotranspiration method into a Palmer Drought Severity Index tool. Comput. Geosci. 2015, 85, 136–141. [Google Scholar] [CrossRef]
- Guan, X.; Bo, C.; Li, Z.; Yu, Y. ST-hash: An efficient spatiotemporal index for massive trajectory data in a NoSQL database. In Proceedings of the 2017 25th International Conference on Geoinformatics, Buffalo, NY, USA, 2–4 August 2017; pp. 1–7. [Google Scholar]
- Huang, Z. Research on Hybrid Index Based on Multi-Level Grid and STR Tree. Master’s Thesis, Zhejiang University, Hangzhou, China, 2013. [Google Scholar]
- Tang, X.; Han, B.; Chen, H. A hybrid index for multi-dimensional query in HBase. In Proceedings of the 2016 4th International Conference on Cloud Computing and Intelligence Systems (CCIS), Beijing, China, 17–19 August 2016; pp. 332–336. [Google Scholar]
- Sieranoja, S. High Dimensional kNN-Graph Construction Using Space Filling Curves. Master’s Thesis, Itä-Suomen yliopisto, Joensuu, Finland, 2015. [Google Scholar]
- Laurini, R.; Thompson, D. Fundamentals of Spatial Information Systems; Academic Press: Cambridge, MA, USA, 1992; Volume 37. [Google Scholar]
- Zhai, W.; Qi, C.; Cheng, C.; Li, S. Spatial data management method with GeoSOT grid. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 5217–5220. [Google Scholar]
- Cheng, C.; Tong, X.; Chen, B.; Zhai, W. A subdivision method to unify the existing latitude and longitude grids. ISPRS Int. J. Geo-Inf. 2016, 5, 161. [Google Scholar] [CrossRef]
- Qi, K.; Cheng, C.; Hu, Y.; Fang, H.; Ji, Y.; Chen, B. An improved identification code for city components based on discrete global grid system. ISPRS Int. J. Geo-Inf. 2017, 6, 381. [Google Scholar] [CrossRef]
- Li, S.; Cheng, C.; Chen, B.; Meng, L. Integration and management of massive remote-sensing data based on GeoSOT subdivision model. J. Appl. Remote Sens. 2016, 10, 34003. [Google Scholar] [CrossRef]
- Zhai, W.; Yang, Z.; Wang, L.; Wu, F.; Cheng, C. The non-sql spatial data management model in big data time. In Proceedings of the 2015 IEEE international geoscience and remote sensing symposium (IGARSS), Milan, Italy, 26–31 July 2015; pp. 4506–4509. [Google Scholar]
- Tong, X.; Wang, R.; Wang, L.; Lai, G.; Ding, L. An efficient integer coding and computing method for multiscale time segment. Acta Geod. Cartogr. Sin. 2016, 45, 66. [Google Scholar]
- Qu, T.; Wang, L.; Yu, J.; Yan, J.; Xu, G.; Li, M.; Cheng, C.; Hou, K.; Chen, B. STGI: A spatio-temporal grid index model for marine big data. Big Earth Data 2020, 4, 435–450. [Google Scholar] [CrossRef]
- Liu, H.; Yan, J.; Huang, X. HBase-based spatial-temporal index model for trajectory data. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2022; Volume 1004, p. 12007. [Google Scholar]
- Guo, N.; Xiong, W.; Wu, Y.; Chen, L.; Jing, N. A geographic meshing and coding method based on adaptive Hilbert-Geohash. IEEE Access 2019, 7, 39815–39825. [Google Scholar] [CrossRef]
- Huang, X.; Deng, Z.; Yan, J.; Li, J.; Chen, Y.; Wang, L. A high-performance spatial range query-based data discovery method on massive remote sensing data via adaptive geographic meshing and coding. IEEE J. Miniaturization Air Space Syst. 2020, 2, 117–128. [Google Scholar] [CrossRef]
- Wu, Y.; Cao, X.; An, Z. A spatiotemporal trajectory data index based on the Hilbert curve code. In IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2020; Volume 502, p. 12005. [Google Scholar]
- Wang, X.; Sun, Y.; Sun, Q.; Lin, W.; Wang, J.Z.; Li, W. HCIndex: A Hilbert-Curve-based clustering index for efficient multi-dimensional queries for cloud storage systems. Clust. Comput. 2023, 26, 2011–2025. [Google Scholar] [CrossRef]
- Yang, J.; Huang, X. A hybrid spatial index for massive point cloud data management and visualization. Trans. GIS 2014, 18, 97–108. [Google Scholar] [CrossRef]
- Gong, J.; Zhu, Q.; Zhang, Y.; Li, X.; Zhou, D. A sub-three-dimensional R-tree index expansion method that takes into account multiple levels of detail. J. Surv. Mapping 2011, 40, 249–255. [Google Scholar]
- Sharifzadeh, M.; Shahabi, C. Vor-tree: R-trees with Voronoi diagrams for efficient processing of spatial nearest neighbor queries. Proc. VLDB Endow. 2010, 3, 1231–1242. [Google Scholar] [CrossRef]
- Gong, J.; Ke, S.; Zhu, Q.; Zhong, R. A LiDAR point cloud data management method integrating octree and 3D R-tree. J. Surv. Mapping 2012, 41, 597–604. [Google Scholar]
- Song, X.; Liu, X.; Zhang, Z.; Wang, D.; Li, C. Research on the spatial index structure of hybrid tree in 3D GIS. J. Shenyang Jianzhu Univ. 2006, 22, 377–381. [Google Scholar]
- Liu, Y.; Hao, T.; Gong, X.; Kong, D.; Wang, J. Research on hybrid index based on 3D multi-level adaptive grid and R+ Tree. IEEE Access 2021, 9, 146010–146022. [Google Scholar] [CrossRef]
- Liu, Z.; Chen, L.; Yang, A.; Ma, M.; Cao, J. Hiindex: An efficient spatial index for rapid visualization of large-scale geographic vector data. ISPRS Int. J. Geo-Inf. 2021, 10, 647. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, A.; Gao, M.; Liang, Y. Research on Three-Dimensional Electronic Navigation Chart Hybrid Spatial Index Structure Based on Quadtree and R-Tree. ISPRS Int. J. Geo-Inf. 2022, 11, 319. [Google Scholar] [CrossRef]
- Gao, J.; Cao, X.; Yao, X.; Zhang, G.; Wang, W. LMSFC: A Novel Multidimensional Index Based on Learned Monotonic Space Filling Curves. Proc. VLDB Endow. 2023, 16, 2605–2617. [Google Scholar] [CrossRef]
- R-Tree Implementation in Java. Available online: https://github.com/davidmoten/rtree (accessed on 12 January 2025).
- TheDeathFar. An Implementation of HilbertTree by Java. 2022. Available online: https://github.com/TheDeathFar/HilbertTree (accessed on 12 January 2025).
- Java Microbenchmark Harness (JMH). Available online: https://openjdk.org/projects/code-tools/jmh/ (accessed on 12 January 2025).
- Landsat 7 Enhanced Thematic Mapper Plus Level-1, Collection 1 [Dataset]. 2017. Available online: https://www.usgs.gov/centers/eros/science/usgs-eros-archive-landsat-archives-landsat-7-enhanced-thematic-mapper-plus-etm?qt-science_center_objects=0#qt-science_center_objects (accessed on 12 January 2025).





| No. | R-MLGTI Variant | Max. Grid Level | Max. Level Grid Resolution 1 | Child Num. of Trees | Tree Type |
|---|---|---|---|---|---|
| 1 | 8 | 4 | R | ||
| 2 | 10 | 4 | R | ||
| 3 | 15 | 4 | R | ||
| 4 | 10 | 4 | R* | ||
| 5 | 10 | 6 | R |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Yan, J.; Huang, X.; He, X.; Deng, Z.; Chen, Y. R-MLGTI: A Grid- and R-Tree-Based Hybrid Index for Unevenly Distributed Spatial Data. ISPRS Int. J. Geo-Inf. 2025, 14, 231. https://doi.org/10.3390/ijgi14060231
Li Y, Yan J, Huang X, He X, Deng Z, Chen Y. R-MLGTI: A Grid- and R-Tree-Based Hybrid Index for Unevenly Distributed Spatial Data. ISPRS International Journal of Geo-Information. 2025; 14(6):231. https://doi.org/10.3390/ijgi14060231
Chicago/Turabian StyleLi, Yuqin, Jining Yan, Xiaohui Huang, Xiangyou He, Ze Deng, and Yunliang Chen. 2025. "R-MLGTI: A Grid- and R-Tree-Based Hybrid Index for Unevenly Distributed Spatial Data" ISPRS International Journal of Geo-Information 14, no. 6: 231. https://doi.org/10.3390/ijgi14060231
APA StyleLi, Y., Yan, J., Huang, X., He, X., Deng, Z., & Chen, Y. (2025). R-MLGTI: A Grid- and R-Tree-Based Hybrid Index for Unevenly Distributed Spatial Data. ISPRS International Journal of Geo-Information, 14(6), 231. https://doi.org/10.3390/ijgi14060231









