Leveraging Principal Component Analysis for Data-Driven and Objective Weight Assignment in Spatial Decision-Making Framework for Qanat-Induced Subsidence Susceptibility Assessment in Railway Networks

Abstract

Railway networks are highly susceptible to land subsidence, which can undermine their functional stability and safety, resulting in recurring failures and vulnerabilities. This paper aims to evaluate the susceptibility of the railway network due to Qanat underground channels in the city of Bafq, Iran. The criteria considered for assessing the susceptibility of Qanats subsidence on the railway network in this study are Qanat channel density, Qanat well density, discharge rate of the Qanat, depth of the Qanat, railway traffic, and the railway passing load. The subjective determination of criteria weights in Multi-Criteria Decision-Making (MCDM) for susceptibility analysis is typically a complex, time-consuming, and biased task. Furthermore, there is no comprehensive study on the impact and relative significance of Qanat-related factors on railway subsidence in Iran. To address this gap, this study developed a novel spatial objective weighting approach based on Principal Component Analysis (PCA)—as an unsupervised Machine Learning (ML) technique—within a spatial decision-making framework specifically designed for railway susceptibility assessment. In the proposed framework, the final Qanat-induced subsidence susceptibility zoning was conducted using the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) method. This study identified 7.7 km² of the total area as a high-susceptibility zone, which encompasses 15 km of railway network requiring urgent attention. The developed framework demonstrated promising performance without deploying subjective information, providing a robust data-driven approach for susceptibility assessment in the study area.

1. Introduction

The subsidence of the railway substructure that causes deformation and deterioration of railway tracks is a critical safety concern in railway systems. The changes in the integrity of the rail tracks due to the land subsidence may lead to increased maintenance needs, operational delays, or even significant rail incidents such as derailments and collisions [1]. In this sense, the identification of key factors and sub-factors in the subsidence of tracks, and, consequently, the production of a track subsidence susceptibility map, is crucial.

In recent years, a significant challenge to the structural integrity of Iran’s railway infrastructure has emerged from an unexpected source: the traditional underground water supply system known as a Qanat. The Qanat (also called Kariz), a masterpiece of water engineering invented by the ancient Persians, is a water supply system that features an underground tunnel linked to the surface through a series of shafts [2,3,4,5,6]. This system utilizes gravity to channel groundwater from aquifers in higher-elevation areas to the surface of lower-elevation lands [7] (Figure 1).

The presence of these subterranean channels, some dating back hundreds of years, has begun to pose significant risks to the stability and safety of railway infrastructure constructed over or in proximity to them [9,10]. Several elements contribute to this hazard, including the gradual drying out of Qanats over the years, lack of proper and periodic maintenance, unprincipled blocking during construction operations, and the proximity of infrastructure [11,12,13]. These conditions can lead to soil loosening and subsidence, potentially causing severe damage to railway superstructures and other nearby infrastructure [14]. The situation is further complicated by the dynamic loading that occurs along railway tracks, which can exacerbate any existing deterioration and transform potential weak points into actual failure points. The impact of this dynamic loading is directly influenced by the traffic volume and weight of loads passing through the railway [15].

Multi-Criteria Decision-Making (MCDM) techniques have become an essential qualitative tool for addressing complex decision-making scenarios [16]. These methods are utilized across various geospatial fields such as susceptibility assessment and site selection [17,18,19]. The Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) approach is one of the robust MCDM methods that has been used reliably to address susceptibility assessment problems that involve selecting alternatives based on various criteria (e.g., see [19,20,21,22]). Several studies have focused on leveraging TOPSIS in susceptibility or risk assessment in railway applications. Norouzi and Namin [23] utilized TOPSIS with a fuzzy Best-Worst Method to evaluate and rank the risks associated with large-scale railway construction projects. Meanwhile, Majumdar et al. [24] employed the TOPSIS technique to identify and prioritize the primary factors influencing metro rail infrastructure from the perspective of commuters. Additionally, Zhang and Sun [25] developed a combined Delphi-DEMATEL-ANP-TOPSIS framework to analyze the risk response strategies for derailments during shunting operations at railway stations.

One of the most challenging aspects of many MCDM methods, including the TOPSIS approach, is the assignment of appropriate weights to criteria [26]. Since the weights assigned to criteria significantly impact the MCDM outcomes, it is crucial to emphasize the importance of effective weighting methods in establishing criteria preferences [27]. There are two major weighting methods in the domain of MCDM: subjective methods and objective methods.

In the subjective methods, the criterion weight is computed directly based on the assessments of the domain experts or the decision-makers. One of the limitations of subjective methods is that these methods depend on knowledge and human judgment about criteria, which may not always be readily available or comprehensive. Moreover, subjective weighting methods are influenced by personal preferences, and human intervention may sometimes distort the results from reality. Furthermore, as the number of criteria increases, the comparison process becomes more complex, making it difficult to weight the criteria properly [28,29,30]. In comparison with subjective methods of weight assignment, objective methods have been developed in recent years by leveraging mathematical models, statistical analyses, or machine learning algorithms to achieve data-driven weighting [31,32].

Automating [33,34] the weight-finding process using data-driven techniques aims to effectively address decision-making challenges, enhance efficiency, minimize human intervention and its consequent potential biases, and promote a clear, straightforward approach with strong interpretability [35]. However, most of these techniques may require substantial data and can be more complex to implement, potentially leading to challenges in interpretation and user acceptance [36].

Principal Component Analysis (PCA) is a statistical technique (and, in a broader definition, an unsupervised Machine Learning (ML) technique) used for multivariate analysis that aims to condense numerous variables into a new set of data referred to as components [31,37]. PCA creates linear vectors to capture the variability in data across multiple dimensions in multivariate problems [38]. This method has been widely utilized across various fields, including, but not limited to, classification [39], feature extraction [40], noise reduction [41], and decision-making processes [42]. In the context of decision-making applications, PCA has been primarily employed to condense multiple variables into a smaller set of Principal Components (PC) criteria (which reduce the dimensionality) (e.g., see [43,44]). Some previous MCDM studies outside of the geospatial domain have focused on developing PCA-based data-driven weighting, showing promising performance (e.g., see [45,46]). Compared with some other objective weighting methods, the PCA weighting method is not data-intensive and is relatively simple to implement, making it interesting for fast and automated weight assignment. Despite the aforementioned advantages of PCA-based weighting, to the best of our knowledge, this approach has not been used in the domain of spatial MCDM problems yet.

To date, no comprehensive study has been conducted to evaluate the impact of various Qanat-related factors on railway subsidence in Iran or to determine the relative significance of these factors in terms of their importance. Furthermore, to our knowledge, no previous study has been conducted to assess railway susceptibility associated with Qanats in Iran. Therefore, to fill the aforementioned research gaps, this study primarily aims to weigh the factors contributing to Qanat-induced subsidence using a novel, objective approach. To this end, a spatial PCA-based data-driven weighting approach was extended, to the best of our knowledge, for the first time, and then integrated into the TOPSIS spatial MCDM method for Qanat-induced subsidence susceptibility assessment in railway networks.

The remainder of this paper is structured as follows: Section 2 provides details on the background, case study, data, and methods used in this research, respectively. Section 3 and Section 4 illustrate the outcomes of the proposed decision-making framework and explores additional dimensions related to the research, respectively. Lastly, Section 5 offers concluding remarks and suggestions for future research.

2. Materials and Methods

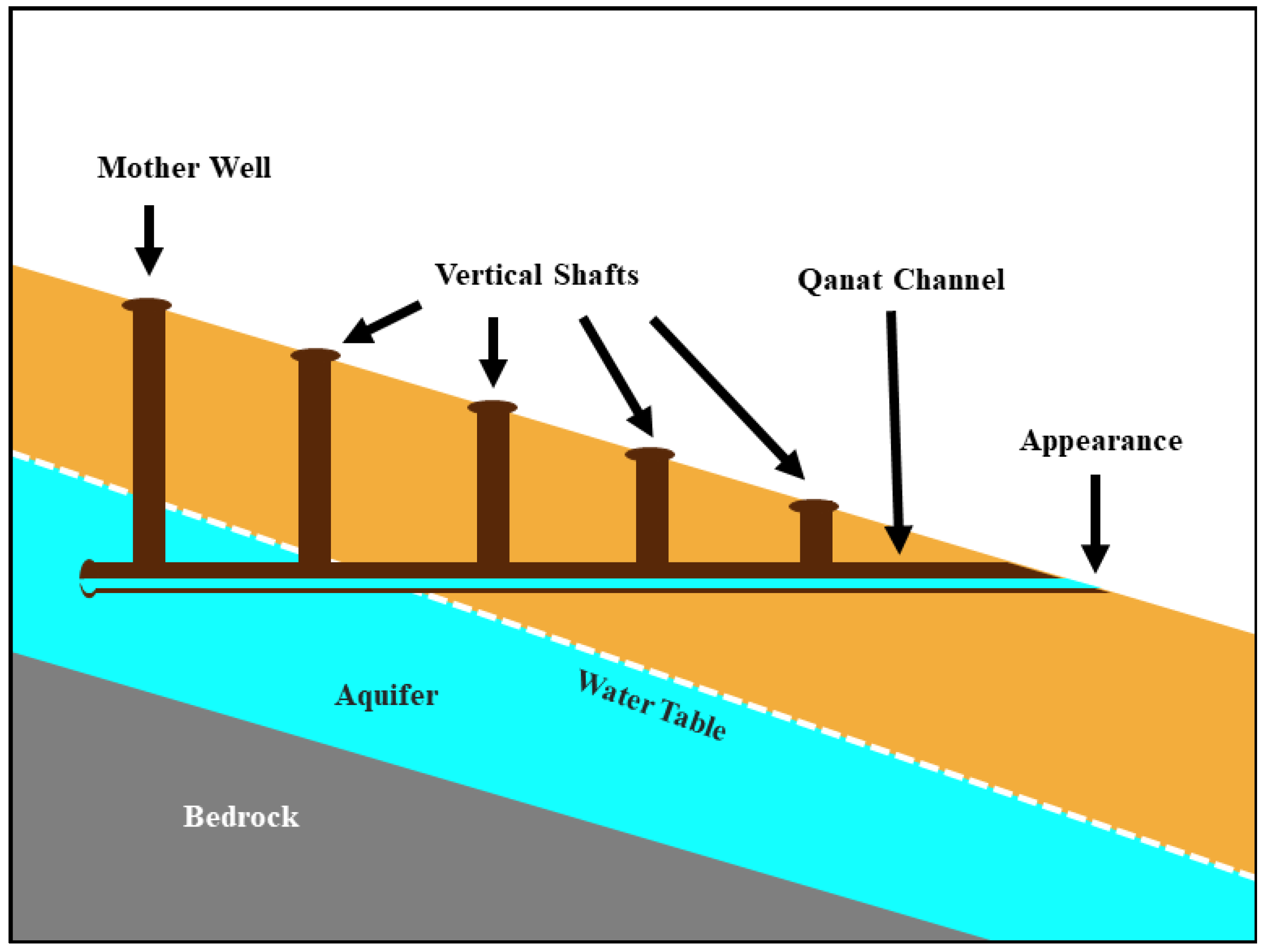
2.1. Background and Case Study

Qanats have been present on Iran’s mile-high plateau for at least two millennia, particularly in the arid central region. There are approximately 22,000 Qanats across Iran, featuring a total of 273,600 km of underground channels, all constructed by hand [47]. Some Qanat wells reach depths of up to 350 m. These remarkable structures have been recognized as a UNESCO World Heritage site [4].

The study area is situated between longitudes 55°37′ E and 55°57′ E and latitudes 31°44′ N and 31°67′ N, encompassing the city of Bafq in Yazd Province, central Iran (Figure 2). Covering a total area of about 441 km², it is located at an elevation of 927 m above sea level. The study area comprises 14 distinct Qanats, collectively extending 153.5 km of underground channels and includes 28 Qanat wells with an average depth of 45 m. This dense and interconnected underground infrastructure is located near and beneath the railway network, which has a total length of 60.8 km, creating a critical vulnerability to subsidence.

2.2. Data Source and Processing

The initial spatial dataset for this study consists of vector files representing three key layers: the point layer of Qanat wells and the line layer of Qanat channels (as shown in Figure 2), which include essential structural and hydrological Qanat-related attributes, as well as the line layer of railways containing relevant traffic information. These data were obtained from the Railways of the Islamic Republic of Iran and were projected into the Universal Transverse Mercator (UTM) (zone 40) map projection system. As the analysis and proposed workflow require pixel-based data, we converted all vector layers into raster files with a cell size of 10 m as a preparatory step in ArcGIS 10.8.2. The spatial database was created based on these products to facilitate the subsequent phases of this research.

2.3. Research Methodology

The main workflow of the proposed MCDM framework for evaluating susceptibility in the study area is shown in Figure 3. The process starts with the determination of criteria in Qanat-induced railway subsidence. Criteria layer creation and preparation is the next main step in the proposed framework. In this main step, the criteria maps are first produced using the Kernel Density Estimation (KDE) method, a statistical technique that determines feature concentrations by calculating smooth density values based on the distance to surrounding features [48]. Following this, the maps undergo a normalization process for data consistency. In the next main step, PCA is applied to the data presented in the normalized criteria maps (hereafter referred to as criteria maps). PCA serves two crucial roles in this main step: “Weight Calculation” and “Dimension Reduction”, which simplify the data and prioritize the criteria based on importance. Finally, a Qanat-induced subsidence susceptibility map is created using TOPSIS. The details of the proposed methodology, including some of its most important elements, are presented and discussed in the following sections.

2.4. Criteria Determination, Criteria Map Creation, and Criteria Map Preparation

Recognizing and defining the effective criteria in the occurrence of Qanat-origin land subsidence in our study area is a crucial step. To this end, we reviewed the existing literature and consulted with experts to determine the criteria. Ultimately, our investigation led to the identification of the following six distinct criteria:

• Qanat channel density: The susceptibility level of rail structures due to subsidence is directly related to the density of Qanat channels in the area—the higher the concentration of Qanat channels in an area, the greater the potential for increased subsidence vulnerability [49]. This criterion is represented as a Qanat channel density map, generated using KDE, which assigns density values based on the proximity to each channel.
• Qanat well density: Ground instability and subsidence due to excessive deep wells have been common challenges in many areas [50], and our study area is no exception. Qanat wells in the study area vary in depth from 28 to 68 m, deep enough to impact the surrounding environment. Regarding the depth of 28 Qanat wells in the region, a well density map was created using the KDE technique. The higher the concentration of deeper Qanat wells in an area, the greater the potential for increased subsidence vulnerability.
• Discharge rate of the Qanat: Many Qanats have lost their functionality due to various reasons and have dried up over time. Decreasing the discharge rate of Qanats can lead to soil moisture loss in the surrounding area and consequently weaken the underlying support structure [51]. Thus, the reduced soil stability may result in significant ground subsidence, especially when heavy surface structures are constructed above the deteriorated Qanat systems [14]. In this context, to quantify this criterion, a density map based on the average discharge rate of Qanat channels was produced using the KDE technique.
• Depth of the Qanat: The presence of Qanats beneath the surface can cause movements in the surrounding soil mass and disrupt the original stress conditions of the ground. However, by increasing the depth of Qanat channels from the ground surface level, the vulnerability to subsidence is reduced [9]. To quantify this criterion, a density map based on the channel depth of Qanats was produced using the KDE technique.
• Railway traffic: The railway traffic volume (i.e., the total number of wagons passing in both directions on the tracks) increases ground vibrations, which, in turn, intensify soil displacement [52,53]. This increased vibration and soil movement can heighten the susceptibility of subsidence in areas with underlying Qanat systems. In our study area, there are nine rail blocks that handle traffic ranging from 28,532 year-round wagons for the lowest traffic block to a maximum of 137,250 passing wagons. Thus, a traffic density map was created similar to other criteria, indicating that the heavier the traffic, the greater the impact on railway subsidence.
• Railway passing load: The dynamic load exerted by trains during operations generates significant forces on railway tracks. These forces, which are temporary and of considerable magnitude, are known as impact loading [54]. The post-construction settling of the tracks is generally attributed to the combined weight of the railway infrastructure and the moving train loads [55]. The weight of the passing load for each rail block is taken into account, varying from a minimum of 1,733,467 tons to a maximum of 7,674,007 tons. Considering this information, a railway passing load density map was generated, similar to other criteria, indicating that heavier loads have more detrimental effects on railway subsidence.

Figure 4 displays the criteria layers generated by KDE (with a search radius of 2 km) for use in the subsequent steps of the proposed MCDM framework. To prepare the produced criteria maps in the previous step for PCA analysis in the next step, they are normalized using a Min-Max scaling technique [56], adjusting the values to a range between 0 and 1. This normalization step is crucial as it ensures that each criterion contributes equally to the PCA.

This study employs an integrated approach that combines a spatially extended, objective data-driven PCA-based weighting approach with the TOPSIS, a well-established MCDM model, for Qanat-induced subsidence susceptibility assessment in railway networks.

2.5. PCA

PCA transforms a set of correlated variables into a smaller set of uncorrelated variables called principal components, derived as linear combinations of the original variables [32]. These components are ordered by the amount of variance they capture, from highest to lowest. PCA’s core purpose is to project the original data into a lower-dimensional space using an orthogonal basis [57]. This approach addresses the challenges of high dimensionality while retaining significant information from the original dataset [58]. The principal components (PCs) encapsulate the relationships among the original variables based on their correlation. By employing PCA in selection processes, one can identify critical factors that contribute most to the variability in the data. PCA offers significant advantages for decision-makers by reducing the dimensionality of the dataset and eliminating the need for subjective assignment of criteria weights, thereby enhancing the objectivity of the analysis [59].

In this research, PCA is not only used to reduce data dimensionality but also to determine the weights of the criteria based on the principal components. In the proposed workflow, all following processes are applied to each individual cell within the study area. The ArcGIS 10.8.2 software is used in this study to transform the criteria maps into its principal components. Each principal component, denoted as pc_j, is represented as a linear combination of the original n criteria.

The contribution of each criterion to the determination of each PC can be found in the eigenvector coefficients associated with that component [46]. These coefficients are essential for assessing the influence of each criterion on the transformed data, which subsequently influences the determination of the weight of each criterion in this study. Therefore, v_i,j will represent the eigenvector loading coefficient for the j-th PC corresponding to the i-th criterion. Thus, the j-th PC can be represented by [57]:

$$p{c}_j={\displaystyle \sum _{i=1}^n{v}_{i,j}}{\upsilon }_i,$$

(1)

where v_i corresponds to the unit vector of the metric i.

To express the relationship explicitly involving both the eigenvalues and eigenvectors, we can highlight that the eigenvalue λ_j associated with the j-th PC is determined by [60]:

$${\lambda }_j=v_j^{T}C{v}_j,$$

(2)

where C is the covariance matrix and v_j is the eigenvector corresponding to the j-th principal component. This relationship indicates how much variance is captured by each PC in relation to its corresponding eigenvector.

The proportion for the j-th eigenvalue e_j is expressed by [57]:

$$e_j={\displaystyle \frac{{\lambda }_j}{{\displaystyle \sum _{i=1}^m{\lambda }_i}}},$$

(3)

where λ_j represents the eigenvalue of the j-th principal component.

In this step, considering the dimensionality reduction process, the number of effective PCs for calculating weights is determined. Effective PCs refer to those components that explain a significant portion of the data variability, as indicated by their eigenvalues. Weights are subsequently calculated using the eigenvalue and eigenvectors of effective components as follows [45]:

$$w_i=\left|{\displaystyle \sum _{j=1}^H{v}_{i,j}{e}_j}\right|,$$

(4)

where H is the number of effective PCs, providing insight into the relative importance of each criterion in the analysis.

To ensure the weights are comparable and sum to 1, we can normalize the weights as follows [46]:

$$w_i^{norm}={\displaystyle \frac{w_i}{{\displaystyle \sum _{i=1}^n{w}_i}}},$$

(5)

where w_i^norm is the normalized weight for the i-th criterion and n is the total number of criteria. This normalization allows for consistent comparisons across the criteria by scaling the weights. The final calculated weights are applied in the TOPSIS method.

2.6. TOPSIS

TOPSIS was developed by Hwang and Yoon in 1981 [61] and was later presented by Chen and Hwang in 1992 [62]. This decision-making method is extended to evaluate multiple criteria to identify a balanced solution [63]. This technique asserts that the preferred alternative should be closest to the ideal solution while being the farthest from the least desirable option [64,65]. It is particularly useful in situations where criteria may conflict with one another [66]. This method evaluates the Euclidean distance from each alternative to both the positive and negative ideal solutions, allowing for a clear ranking and a more comprehensive evaluation of options based on multiple conflicting criteria. Within this methodology, the ideal solution aims to minimize cost criteria and maximize benefit criteria, whereas the negative ideal solution does the opposite [19].

Each decision problem can be viewed as a geometric framework comprising m points representing alternatives in a n-dimensional space. The goal is to select alternatives that are at the shortest possible distance from the positive ideal solution (Ai⁺) and at the greatest distance from the negative ideal solution (Ai⁻). The implementation of TOPSIS consists of several key steps [19]:

Step 1: A decision matrix (x_ij)_m×n with dimensions m × n, representing m alternatives and n criteria, is constructed.

Step 2: The next step involves normalizing the decision matrix to produce a normalized decision matrix (r_ij)_m×n with the same dimensions m × n:

$$r_{ij}={\displaystyle \frac{x_{ij}-x_{i,\min }}{x_{i,\max }-x_{i,\min }}},$$

(6)

Step 3: The weighted normalized decision matrix (c_ij)_m×n is calculated by multiplying the normalized decision matrix by the weights derived from the PCA method:

$$c_{ij}=w_j^{norm}{r}_{ij},$$

(7)

where w_i^norm, obtained from Equation (5), represents the original weight assigned to the criterion c_j, i = 1, 2, …, m and j = 1, 2, …, n.

Step 4: The positive ideal solution (A⁺) and the negative ideal solution (A⁻) are established:

$$\begin{array}{l}{A}^{+}=\left\{c_1^{+},c_2^{+},\dots ,c_j^{+},\dots ..,c_n^{+}\right\}where\\ c_j^{+}=\left\{\left.(\left.\max c_{ij}\right|j\in J^{+}).(\left.\min c_{ij}\right|j\in J^{-})\right|i=1,2,\dots ,m\right\}\end{array},$$

(8)

$$\begin{array}{l}{A}^{-}=\left\{c_1^{-},c_2^{-},\dots ,c_j^{-},\dots ..,c_n^{-}\right\}where\\ c_j^{-}=\left\{\left.(\left.\max c_{ij}\right|j\in J^{-}).(\left.\min c_{ij}\right|j\in J^{+})\right|i=1,2,\dots ,m\right\}\end{array},$$

(9)

where J⁺ corresponds to the benefit criteria, while J⁻ pertains to the cost criteria.

Step 5: In this step, the Euclidean distances are calculated:

$$d_i^{+}={\left\{{\left({\displaystyle \sum _{j=1}^n{c}_{ij}-c_j^{+}}\right)}^2\right\}}^{1/2},$$

(10)

$$d_i^{-}={\left\{{\left({\displaystyle \sum _{j=1}^n{c}_{ij}-c_j^{-}}\right)}^2\right\}}^{1/2},$$

(11)

representing the distance (d⁺_j) between the target alternative j and the positive ideal solution and the distance (d⁻_j) between the target alternative j and the negative ideal solution, respectively.

Step 6: The performance score P_j for each alternative, which indicates its relative closeness to the ideal solution, is then calculated by:

$$P_j={\displaystyle \frac{d_i^{-}}{d_i^{-}+d_i^{+}}},$$

(12)

The alternatives—individual pixels in this Spatial MCDM—are subsequently scored based on P_j; as the value approaches 1, the significance of the option increases [67].

The criteria maps (i.e., the normalized criteria maps) are introduced as the normalized decision matrix in the TOPSIS model. Next, the weights obtained from the PCA method are multiplied by these maps to create the weighted normalized decision matrix. Following the subsequent steps in the TOPSIS process, the final analysis is conducted, resulting in the Final Qanat-induced Subsidence Susceptibility Map. In this map, each alternative (or pixel) receives a performance score (P_j), with higher values indicating greater susceptibility.

The compensatory nature of this method allows for poor performance in one criterion to be offset by stronger performance in another, which aligns with real-world decision-making. Normalizing criteria ensures fair comparisons across different units and scales, while assigning weights based on the criteria’s significance reflects their inherent importance. Ultimately, TOPSIS delivers clear rankings of alternatives, enabling straightforward interpretation of results.

3. Results

This section presents the key findings of this research, highlighting the significance and exploring important dimensions of the proposed methodology. Through a detailed discussion, the results are contextualized within the broader scope of the susceptibility assessment field, providing insights into both its strengths and areas for potential improvement in the context of spatial MCDM.

Calculated Weights

The percentages of eigenvalues from the original data (variance), explained by the PCs, are displayed in Figure 5, and the comprehensive results of the PCA applied to criteria maps data are presented in

Table 1. Detailed results of PCA on the criteria maps.

	PC1	PC2	PC3	PC4	PC5	PC6
Eigenvalue	0.127	0.029	0.013	0.001	4.6 × 10−4	3 × 10−5
Proportion of Variance	0.747	0.172	0.074	0.005	0.003	1.8 × 10−4
Cumulative Percentage of Variance (%)	74.659	91.833	99.194	99.712	99.982	100
Criteria	Eigenvector
Qanat channel density	0.529	−0.196	0.012	0.801	0.196	−0.036
Qanat well density	0.230	0.316	0.916	−0.076	−0.047	0.008
Discharge rate of the Qanat	0.517	−0.206	−0.116	−0.193	−0.799	0.026
Depth of the Qanat	0.551	−0.242	−0.072	−0.559	0.565	0.011
Railway traffic	0.217	0.605	−0.259	−0.024	0.005	−0.721
Railway passing load	0.222	0.628	−0.274	0.033	0.036	0.692

.

Table 1 displays the detailed outcomes derived from the PCA algorithm applied to all criteria maps. The eigenvalues indicate the amount of variance captured by each principal component, along with the corresponding relative eigenvalues (proportion of variance) and cumulative eigenvalues (cumulative variance) for each component. Considering the cumulative percentage of variance, the first three PCs collectively account for approximately 99% of the original information (i.e., data of the criteria maps), as illustrated by the blue line in Figure 5. Specifically, the first PC explains 74.6% of the original data, while the second PC accounts for 17%. Each of the remaining four PCs explains less than 10% of the variance.

After identifying the effective PCs (based on the cumulative variance), and in line with the dimension reduction process, the first three PCs are selected as the determining components, which explain over 99% of the data, serving as the basis for calculating weights in subsequent analyses. It is important to note that the dimensionality reduction process occurs only during the weight determination stage, whereas, in the TOPSIS method, the entire dataset is utilized.

The proportion of variance obtained for each PC determines its weight in the calculations. Therefore, PC1, which captures the majority of the dataset’s variation, has a weight of 0.747, while PC2 is assigned a weight of 0.172. The bottom section of the table shows the eigenvectors, detailing how different variables (criteria) contribute to each PC (PC1 to PC6) and illuminating the relationship between the original variables and the new PCs formed through PCA. Based on our PCA analysis, the eigenvectors of the variables (criteria) in the PCs were plotted in Figure 6 to gain a deeper understanding of the research problem.

Each bar represents the value of each eigenvector, which explains the contribution of different variables to each PC, helping to identify the most influential variables in the dataset. This identification is essential for dimensionality reduction and uncovering patterns in complex data. For example, PC1 shows relatively high contributions from Qanat channel density, depth of the Qanat, and discharge rate of the Qanat, indicating that these variables are significant within this principal component. In contrast, it shows relatively low contributions from railway traffic and railway passing load. Similarly, PC2 exhibits significant contributions from railway traffic and railway passing load, while Qanat-related variables show relatively low contributions. PC3 highlights a relatively high contribution from Qanat well density, with relatively low contributions from other variables, suggesting that it captures a different aspect of the data. Each PC highlights different key variables, aiding in the understanding of the underlying structure of the dataset and focusing on the most relevant features for analysis. The final weights for each criterion were calculated using the absolute values obtained from the cross-multiplication of the first three principal components’ proportion value (eigenvalue) and the individual criteria values related to that component (eigenvector), as described in Equation (4). For instance, the absolute weight for the criterion “Qanat channel density” is calculated (using the first three PCs) as follows: |0.747 × 0.529 + 0.172 × −0.196 + 0.074 × −0.012| = 0.362. Finally, the weights obtained from Equation (4) were normalized using Equation (5), as shown in

Table 2. Final calculated weights.

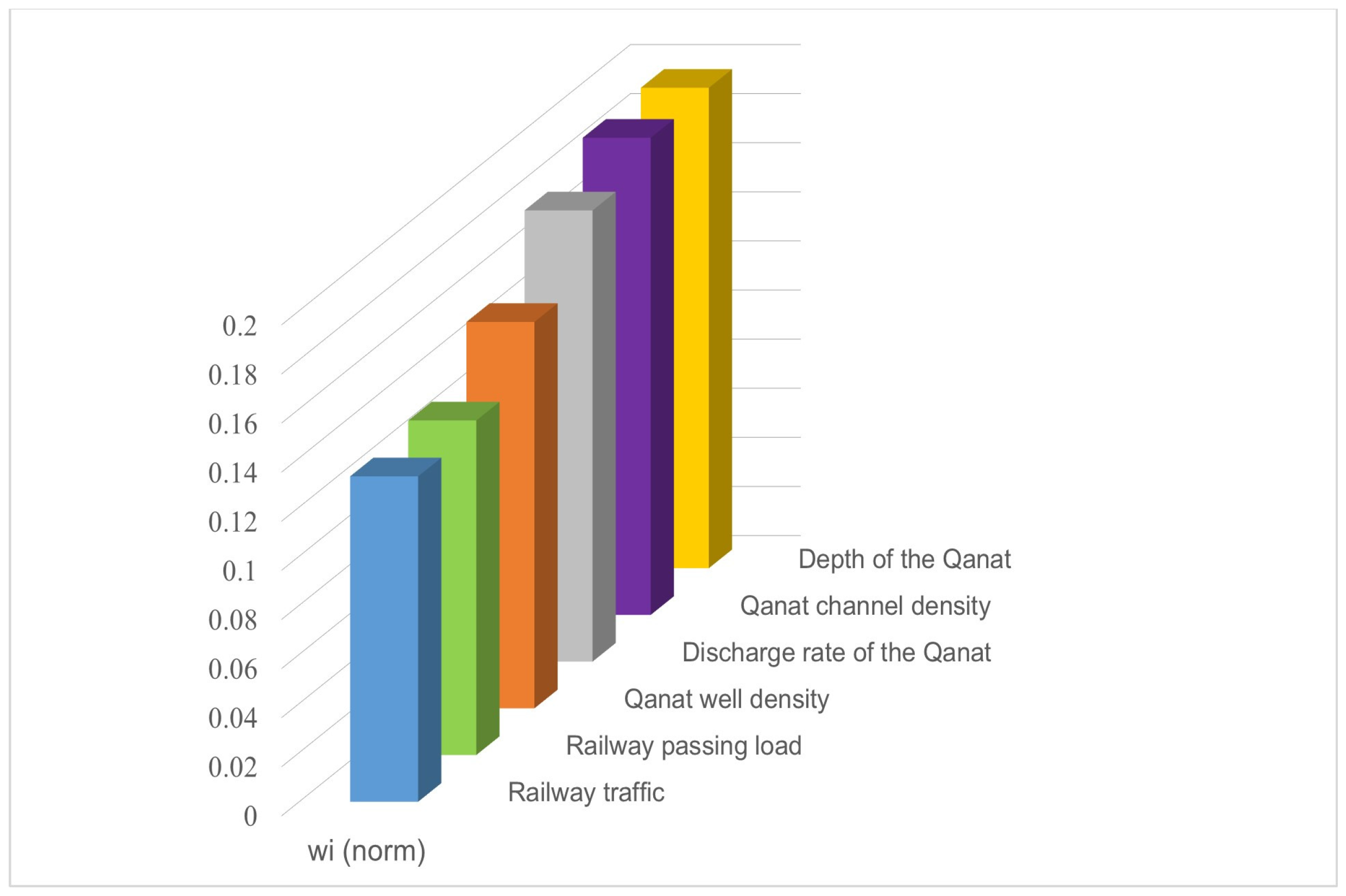
Criteria	wi (Calculated Weight)	winorm (Proportion of wi)
Qanat channel density	0.362	0.194
Qanat well density	0.293	0.157
Discharge rate of the Qanat	0.342	0.184
Depth of the Qanat	0.364	0.196
Railway traffic	0.247	0.133
Railway passing load	0.254	0.136

.

Table 2 presents the final calculated weights (w_i) and normalized weights (w_i^norm) assigned to various criteria related to the characteristics of Qanats and railways, reflecting their relative importance in the analysis. Qanat depth has the highest normalized weight at 19.6%, followed closely by 19.4% for Qanat channel density and 18.4% for the discharge rate of the Qanat. Qanat well density contributes 15.7%, indicating its significance as well. Among the railway-related criteria, railway passing load contributes 13.6%, while railway traffic accounts for 13.3%. This analysis emphasizes the substantial role of Qanat-related factors, particularly depth, channel density, and discharge rate, while also acknowledging the importance of railway traffic and passing load in the overall assessment.

Figure 7 presents a bar chart that ranks the criteria based on their calculated normalized weights (based on a data-driven approach), revealing their relative importance in influencing the study area. This comparison offers a comprehensive assessment of each criterion’s importance, aiding in understanding their impact on the study area and guiding informed decision-making.

To create the final zoning susceptibility map, the normalized weights assigned to each criterion from Table 2 were multiplied by their respective normalized criteria maps. These layers were then processed following the TOPSIS method. The resulting map illustrates areas ranging from low to high susceptibility (between 0 and 1), with higher performance scores (P_j) indicating greater susceptibility for the railway system.

Figure 8a provides a visual representation of the susceptibility levels (ranging from 0 to 1) across the railway system based on the calculated performance scores (P_j), depicting the Qanat-induced subsidence susceptibility map. The values of P_j range from around 0.314 for the lowest susceptibility areas to approximately 0.648 for the highest susceptibility areas. The final map is classified into 20 classes using equal intervals, offering a detailed and consistent distribution of susceptibility levels throughout the study area.

The color gradient effectively illustrates the variation in susceptibility, with warmer colors (yellow to brown) signifying areas of higher susceptibility, while cooler colors (like pink and blue) indicate zones of lower susceptibility. The map’s design facilitates visual identification of safe zones, which is essential for planning and susceptibility mitigation strategies. This gradient transition signifies a decrease in susceptibility factors, indicating areas where infrastructures, such as railways and Qanat channels, appear to be better managed.

Figure 8b indicates zones of heightened susceptibility, represented by warmer colors (reds and oranges) that are correlated with critical factors, such as increased Qanat density, proximity of deep wells to railway infrastructure, and higher railway traffic volumes, identified in earlier analyses. For example, within this area of only 8 km², there are seven Qanat wells, four of which exceed the average depth of 45 m. Additionally, this section alone accounts for approximately 51% of the total traffic and 50% of the total passing load in the entire region. This suggests a direct relationship between feature proximity and potential susceptibility exposure. The dense clustering of features in this region underscores the importance of monitoring and managing susceptibility effectively.

The green light areas in Figure 8a signify moderate susceptibility influenced by certain Qanat and railway features. Additionally, the areas located near the outer margins of the map, marked in blue, indicate lower susceptibility levels, suggesting these regions are less affected by the susceptibility factors related to railway operations and Qanat characteristics. Furthermore, the central region, represented by light pink hues, suggests a low-susceptibility zone, as well as decreased traffic and load, potentially influenced by greater channel depth and higher discharge rate flow, which can mitigate vulnerabilities associated with Qanats. For instance, while the average depth of the Qanat channels in the area is 45 m, the channels in the central region (considered low-susceptibility) have depths exceeding 60 m, which is more than 15 m above the average. Additionally, the overall average discharge rate of all channels in the studied region is 38 L per second, whereas the central channels experience discharge rates exceeding 50 L per second. Furthermore, the rail block that passes through this region accounts for only 5% of the total traffic and load volume in the area. All these factors contribute to reducing the susceptibility in the central region. Additionally, the central area’s distance from the Qanat wells further reduces its susceptibility profile.

Figure 8c,d highlights other high-susceptibility points, illustrating areas that require urgent attention. They provide a closer look at critical intersections where railway lines meet Qanat systems, indicating potential vulnerabilities. Identifying these intersections is crucial, as they may pose a dual susceptibility related to both transportation and water management considerations.

Table 3. Detailed analysis of spatial susceptibility assessment.

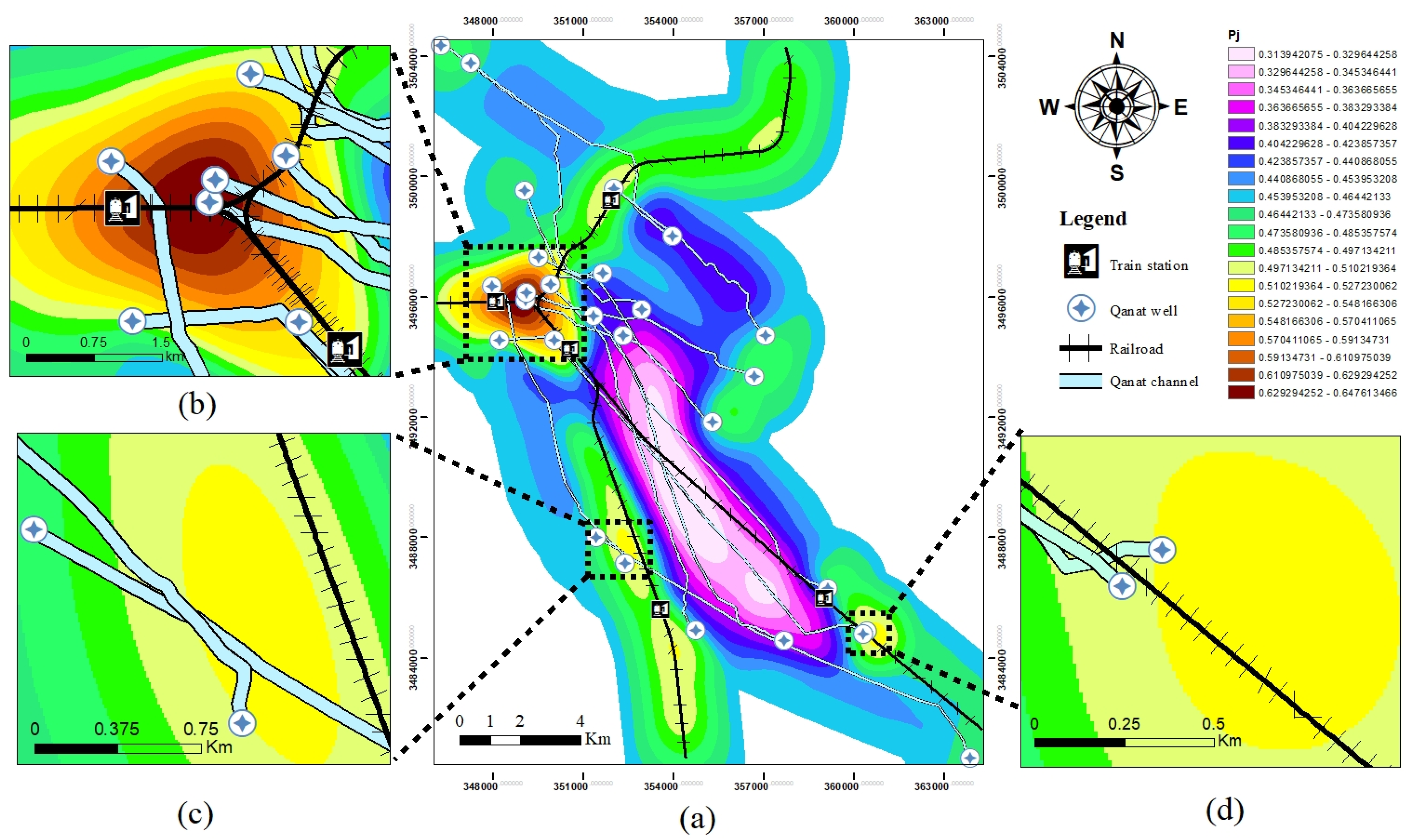
Category	Pj (Performance Score)	Area (km2)	Length of Railway (km)	Number of Railway Stations
Low susceptibility	0.314 < Pj < 0.430	53.4	11.8	1
Moderate susceptibility	0.430 < Pj < 0.530	206.4	34	3
High susceptibility	0.530 < Pj < 0.648	7.7	15	1

illustrates the susceptibility assessment of railway segments associated with each level in the case study, categorized by performance score (Pj) based on three classes using equal intervals. In this susceptibility-prone region, which has a total area of 267.5 km², the “Low susceptibility” category includes an area of 53.4 km², with a railway length of 11.8 km and one station, indicating relatively stable infrastructure with performance scores ranging from 0.314 to 0.430. In contrast, the “Moderate susceptibility” category covers a larger area of 206.4 km², extending the railway length to 34 km and including three stations, where performance scores range from 0.430 to 0.530. Finally, the “High susceptibility” category, although limited to 7.7 km², features a significant railway length of 15 km and one station, reflecting localized vulnerabilities with scores between 0.530 and 0.648. Overall, the analysis reveals that most railway infrastructure falls into the moderate susceptibility category, necessitating targeted interventions to enhance safety and reliability, particularly in the high-susceptibility areas that present the greatest potential for disruptions.

These findings offer valuable insights for prioritizing resource allocation in the monitoring and maintenance of railway infrastructure. Stakeholders can leverage the zoning susceptibility map to make informed decisions regarding infrastructure development, safety protocols, and susceptibility management strategies within the railway system. The comprehensive assessment presented in Figure 8 not only identifies various susceptibility levels but also emphasizes the complex interconnections between rail infrastructure and Qanat systems. This understanding is crucial for shaping local policy decisions, such as implementing enhanced safety measures and establishing low-speed zones in high-susceptibility areas. The results provide actionable recommendations for both policymakers and infrastructure managers, aimed at bolstering the operational efficiency of railway services.

4. Discussion

This study provides a comprehensive assessment of the susceptibility posed by Qanats to the railway network, highlighting critical vulnerabilities that land subsidence can create. A spatial objective weighting approach was developed, leveraging PCA to generate robust, data-driven weightings without relying on subjective information. Finally, using the TOPSIS method, the MCDM problem was effectively addressed, leading to the identification of high-susceptibility zones.

While PCA is a reliable method for uncovering underlying patterns in data and data-driven criteria weighting, objective methods still require further investigation to enhance their effectiveness and applicability. The main goal of this study was to develop a spatial PCA-based objective weighting method for the first time, while comparing our results with other existing spatial data-driven weighting methods, such as the Entropy-based weighting method [68], was beyond the scope of this research. While each weighting method has its pros and cons, previous studies outside the geospatial domain suggested combining the advantages of different methods to improve the efficiency and accuracy of weight determination [28,69,70]. This approach aims to reduce the potential bias of relying on a single method by hybridizing various objective weighting techniques [28]. Thus, to enhance the reliability of our spatial objective weighting approach, it is recommended that the PCA-driven weights be integrated with weights derived from other spatial objective weighting methods using a robust ensemble approach. Furthermore, while objective weighting methods aim to uncover hidden dimensions within the data, combining PCA-driven weights with expert knowledge and preferences (subjective-driven weights) within a well-structured integration framework can provide a more nuanced understanding of the spatial problem. This approach is particularly valuable in more uncertain and complex applications, such as susceptibility assessment and emergency management.

The findings from this study have several potential applications. Engineers and railway operators can prioritize and guide monitoring and maintenance in identified high-susceptibility zones vulnerable to Qanat-induced subsidence. In this context, more detailed fieldwork can be directed into areas initially recognized as highly susceptible, potentially accelerating the process and optimizing human resource allocation. By integrating susceptibility maps with sensor-based early warning systems, real-time deformation monitoring in vulnerable zones could be achieved. The developed framework enables targeted prioritization of high-susceptibility railway segments for immediate reinforcement measures, such as ground stabilization or track-bed modifications. Maintenance resources can be optimally allocated by directing budgets proportionally to areas with higher susceptibility scores. The developed framework can also facilitate subsidence susceptibility assessments for new railway projects prior to construction, enabling proactive interventions and consideration. From a broader perspective, this study provides a foundation for future research into the socio-economic impact assessment of Qanat subsidence on infrastructure, assets, and residents. Additionally, the developed framework can be extended to assess susceptibility in other similar fields.

Although this study presents a robust framework for assessing susceptibility associated with Qanat-induced subsidence, several limitations must be acknowledged. First, in the absence of comprehensive studies on Qanat-related subsidence, particularly in railway contexts—and given that no severe Qanat-induced damage has been reported to date—the criteria for this study were selected based on existing technical documents and consultations with a group of railway industry experts, whose engineering justifications supplemented limited data. While additional potential factors, such as geological and hydrological characteristics (e.g., soil and rock mass properties, groundwater table fluctuations), may influence subsidence, high-resolution spatial datasets for these drivers are unavailable in the study area. However, analysis of coarse-resolution geological maps indicates relative uniformity across the region, with no significant variations that would alter our MCDM framework. This conclusion should be validated with fine-scale field datasets, which are currently lacking in the study area. Additionally, further studies should be conducted to model the impact of hydrological factors on Qanat-induced subsidence. The lack of hydrological monitoring infrastructure and detailed datasets in this arid region made quantifying potential hydrological-related subsidence drivers impractical for the current study. Second, while the dataset used in this study was obtained from an authoritative source ensuring baseline data quality, uncertainty remains inherent in all measurements, including those from authoritative sources. Consequently, the lack of field validation for the adopted dataset represents a limitation of this study that may impact its overall assessment. Third, this study employs MCDM primarily to establish preventive guidelines, addressing the urgent need for proactive measures amid persistent drought conditions. The resulting susceptibility map produced in this study enables officials to prioritize investigations and guide preemptive decision-making, serving as a critical early warning tool for Qanat-induced railway subsidence damages. However, the absence of reported Qanat-related railway damage to date inherently limits validation opportunities against historical incidents, representing a constraint of this study. Fourth, the absence of previous studies related to Qanat-induced railway subsidence susceptibility assessment, particularly those based on data-driven weight assignment approaches, restricts opportunities for further comparisons and evaluations of our results against them. Addressing these limitations in future research could enhance the framework’s robustness and applicability.

5. Conclusions

This study developed an unsupervised learning method using a PCA-based technique to objectively determine the weights of factors contributing to Qanat-induced railway network subsidence, leveraging its ability to reduce dimensionality while preserving critical information. This extended spatial data-driven criteria weighting method was then integrated into the TOPSIS spatial MCDM method for assessing Qanat-induced subsidence susceptibility in railway networks. The developed framework demonstrated promising performance without relying on subjective information, offering a robust, data-driven approach for Qanat-induced subsidence susceptibility assessment in the study area. This methodology not only enhances the efficiency and objectivity of susceptibility evaluation but can also provide a replicable framework applicable to similar geohazard assessments in diverse regions and infrastructure systems, as well as other spatial MCDM problems where objective weighting is challenging or infeasible. Future research could focus on a thorough comparison of the developed PCA-based weighting method with other objective weighting techniques to evaluate its relative performance and applicability in different contexts. Additionally, combining the results of the extended PCA-based weighting method with various objective and/or subjective weighting methods through a robust ensemble framework could be explored to enhance the accuracy and reliability of the estimated weights for the criteria. While this study employed TOPSIS as a well-established MCDM approach, future research could investigate the integration of other spatial MCDM methods to enhance the framework’s performance and versatility. While this study identified six distinct criteria for assessing Qanat-induced railway subsidence, additional factors may influence subsidence dynamics, particularly in broader and more complex environmental contexts. These factors could include diverse geological, topographical, and hydrological conditions, as well as direct influencing factors related to the age and maintenance of railway infrastructure and the Qanat system. While we excluded these potential factors from our analysis due to the study area’s specific environmental context and inherent study limitations, future research should incorporate them—once further studies are conducted and sufficient data becomes available—to enable a more comprehensive assessment of Qanat-induced railway subsidence susceptibility, particularly in larger, more complex settings.