Analysis of Regional Spatial Characteristics and Optimization of Tourism Routes Based on Point Cloud Data from Unmanned Aerial Vehicles
Abstract
1. Introduction
1.1. Background Description
1.2. Related Works
1.2.1. Tourism Area Coverage Issues
1.2.2. Tourism Trajectory Planning Issues
1.2.3. Identified Gaps in the Literature and Contribution of This Paper
2. Problem Formulation
3. Main Results
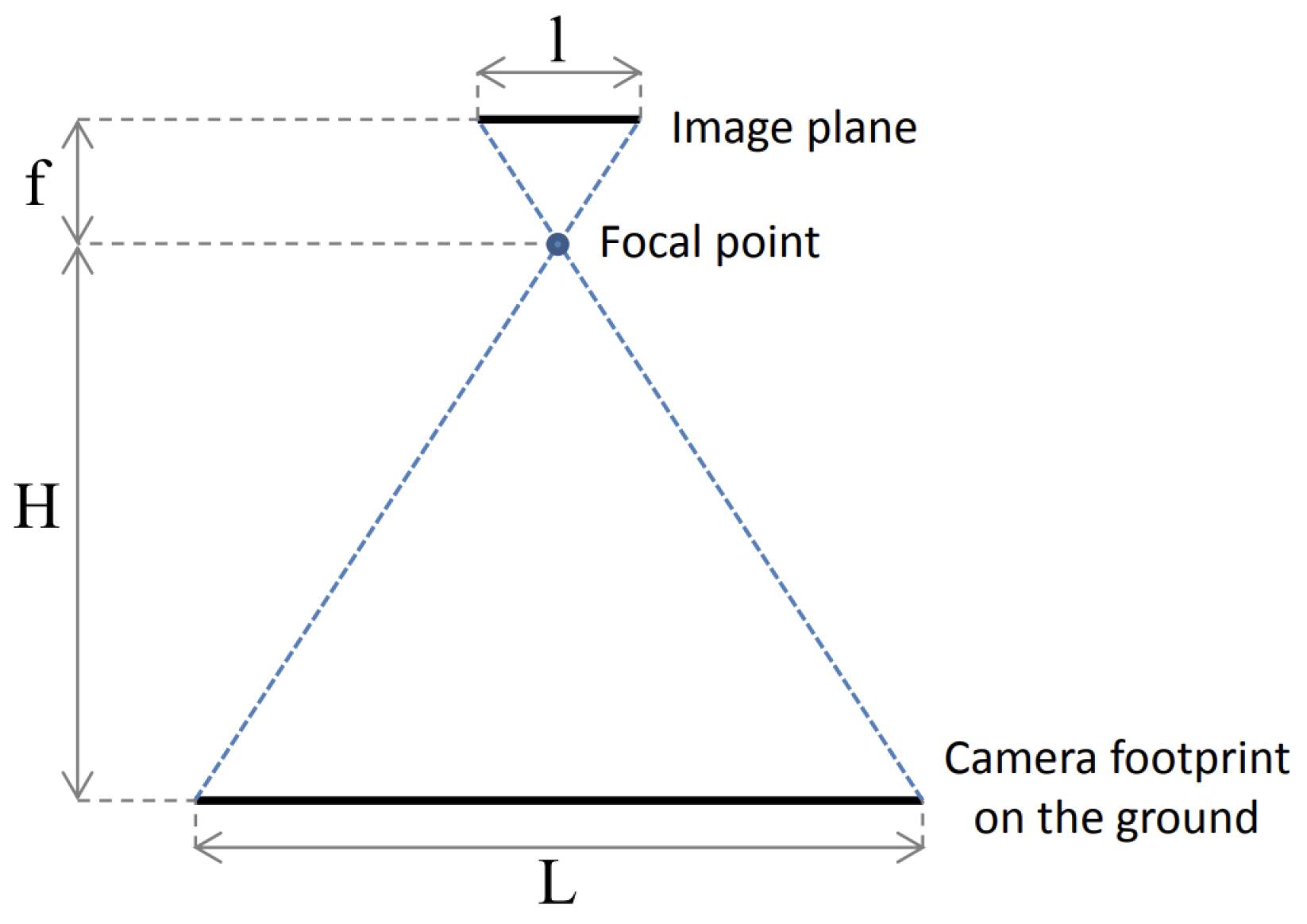
3.1. Point Cloud Collection
3.2. The Coverage Path Planning of Ground Areas Using UAVs
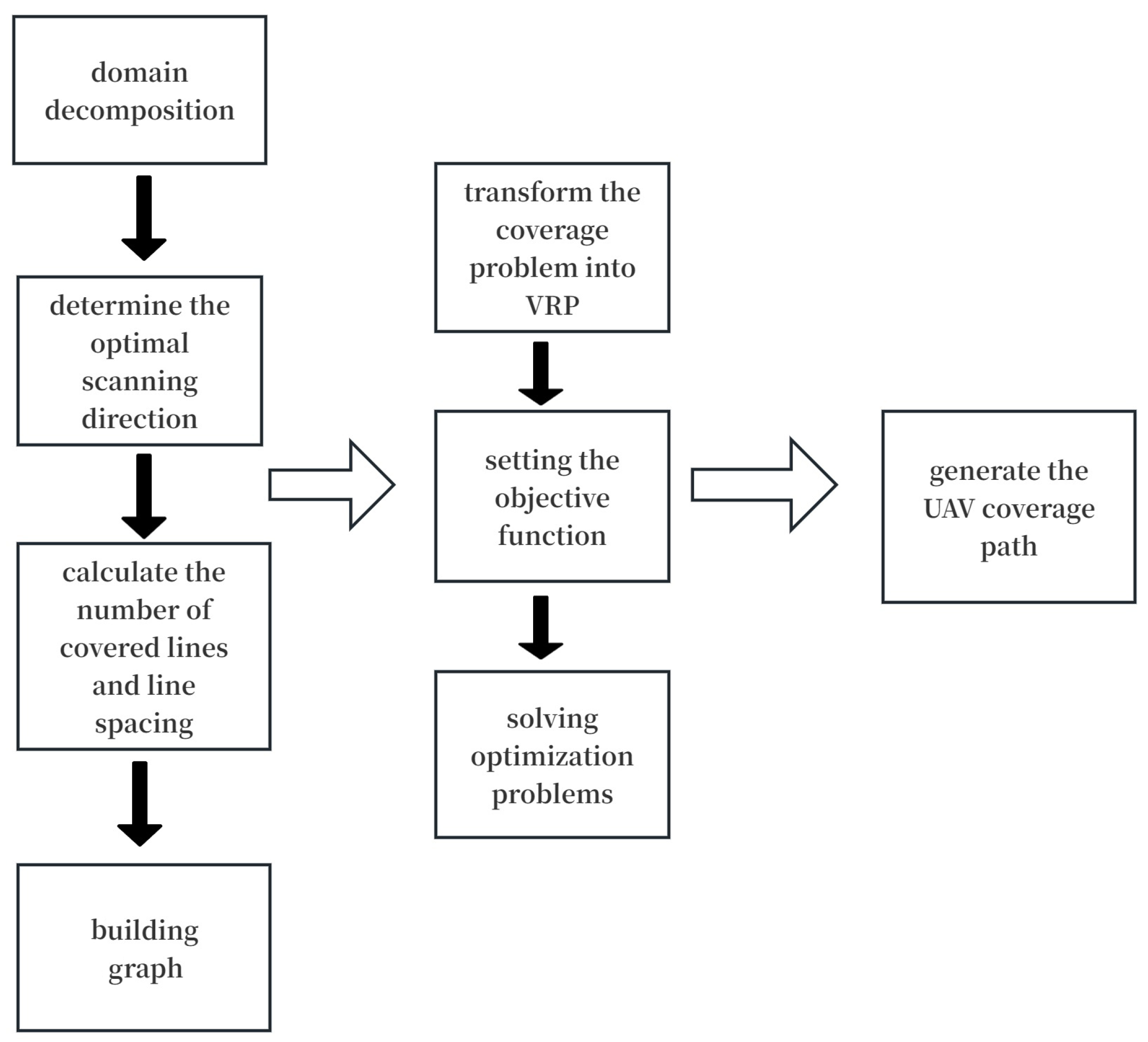
3.2.1. Regional Decomposition
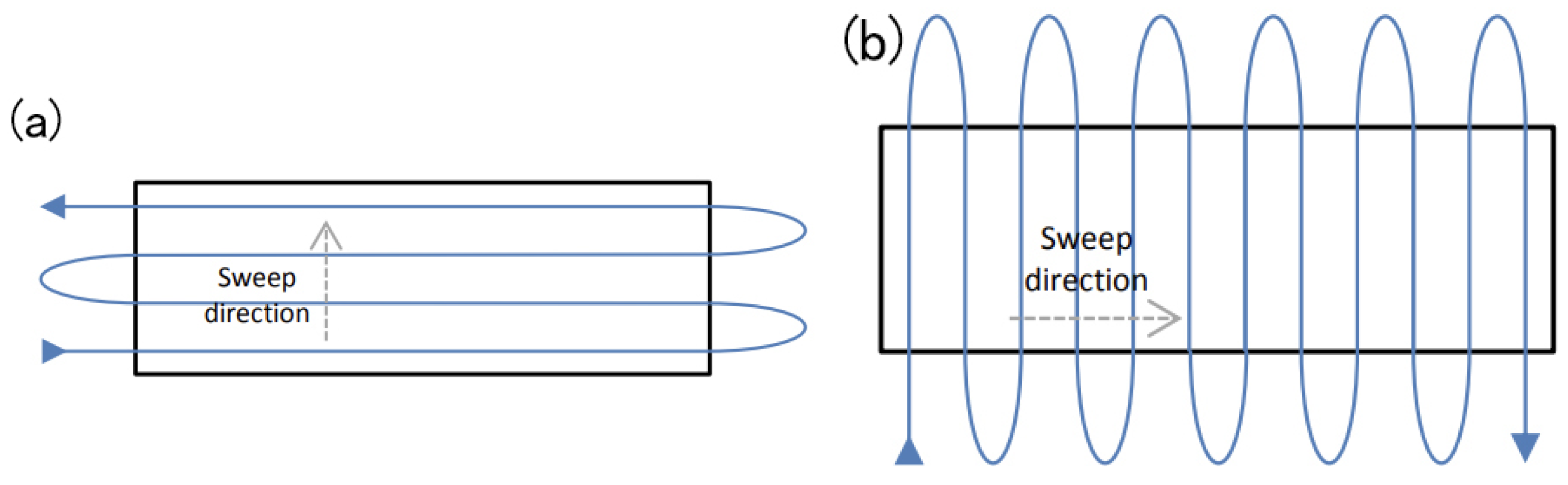
3.2.2. Coverage Path-Planning Strategy
3.3. The Three-Dimensional Tourism Trajectory Planning
3.3.1. Problem Definition
3.3.2. Three-Dimensional Trajectory-Planning Methods
- 1)
- Cost function of path length
- 2)
- Cost function of security
- 3)
- Climb altitude constraint
- 4)
- Smoothness cost function
- 5)
- Total cost function
- 1)
- Particle update equations
- 2)
- Position mapping
4. Experiment and Discussions
4.1. Search Coverage Flight Experiment and Discussions
4.1.1. Coverage Path-Planning Experiment 1
4.1.2. Coverage Path-Planning Experiment 2
4.2. Tourist Trajectory-Planning Simulation Experiment and Discussions
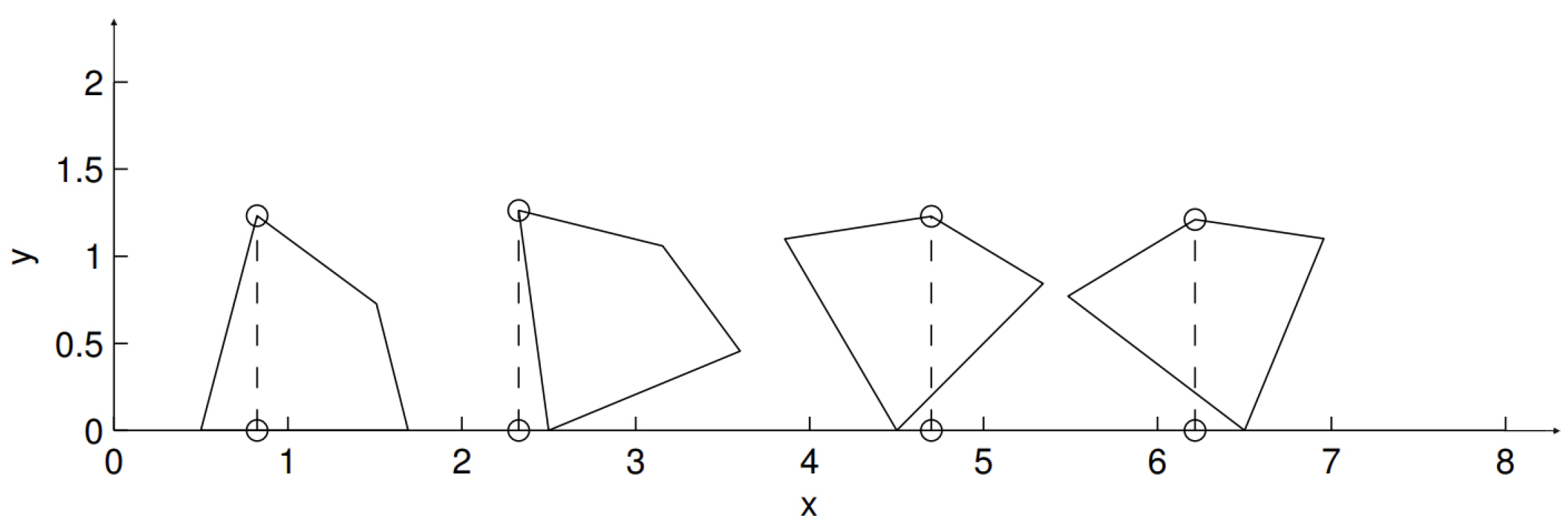
4.2.1. Selection of Trajectory Points
4.2.2. Selection of Obstacle Points
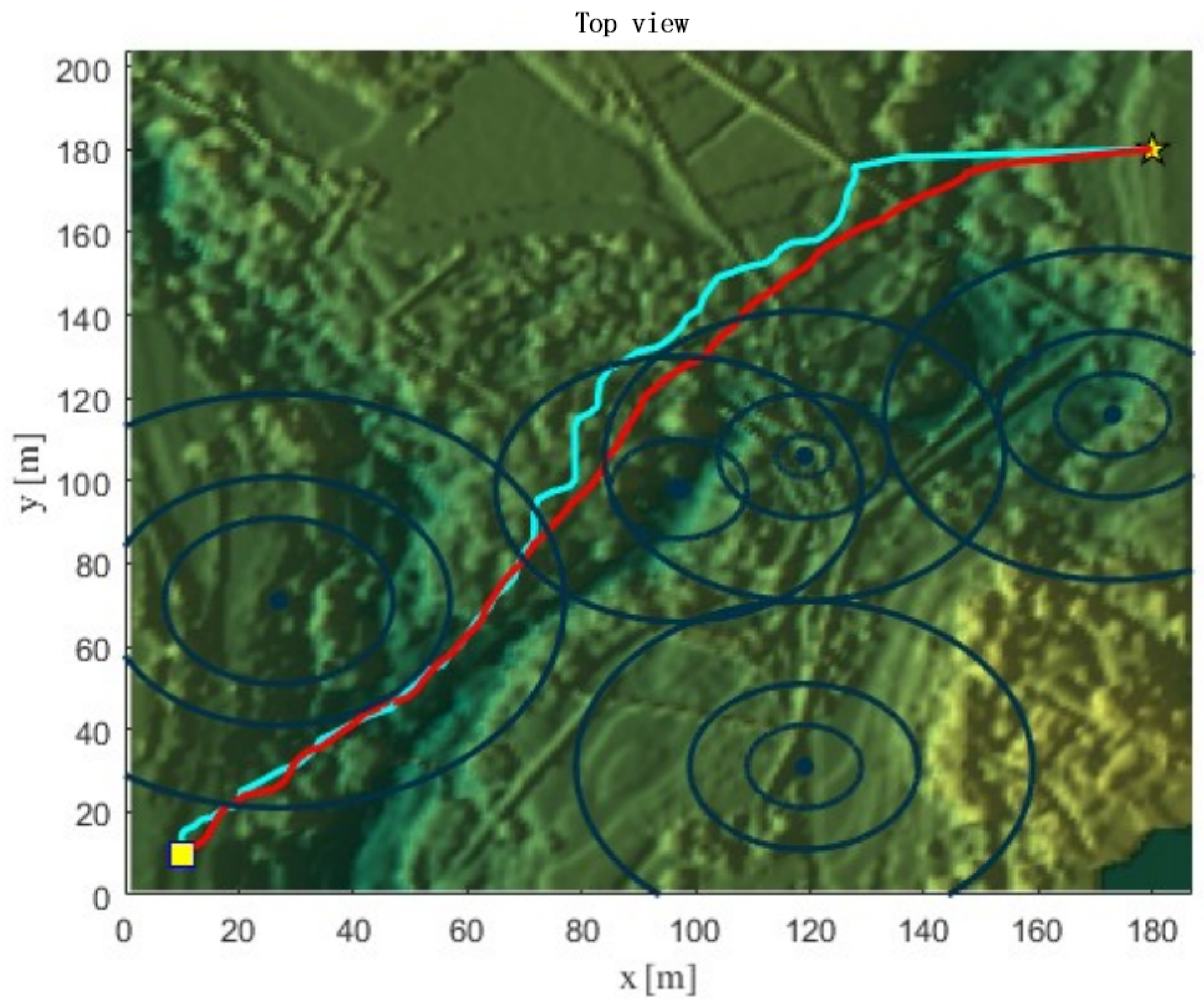
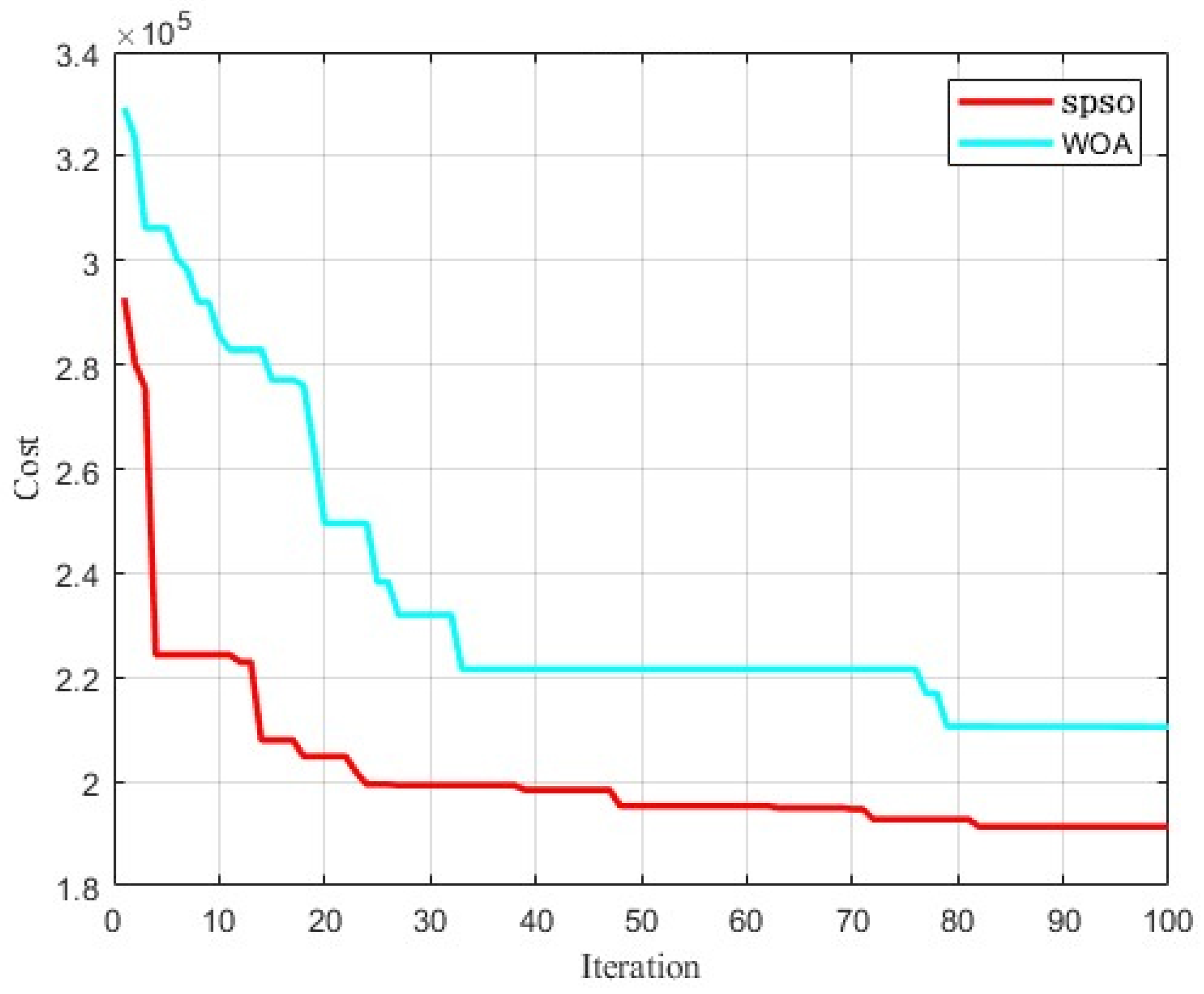
4.2.3. Simulation of Trajectory Planning
4.2.4. Refinement of Trajectory Planning
4.3. Limitations of the Study
5. Conclusions and Future Work
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAVs | Unmanned aerial vehicles |
| GA | Genetic algorithm |
| ACO | Ant colony algorithm |
| PSO | Particle swarm optimization algorithm |
| SPSO | Spherical vector-based PSO algorithm |
| RNNs | Recurrent neural networks |
| SAC | Soft actor–critic |
| VRP | Vehicle routing problem |
References
- Jiang, S.; Jiang, W.; Wang, L. Unmanned Aerial Vehicle-Based Photogrammetric 3D Mapping: A survey of techniques, applications, and challenges. IEEE Geosci. Remote. Sens. Mag. 2021, 10, 135–171. [Google Scholar] [CrossRef]
- Yao, H.; Qin, R.; Chen, X. Unmanned aerial vehicle for remote sensing applications—A review. Remote. Sens. 2019, 11, 1443. [Google Scholar] [CrossRef]
- Wen, H.; Zhou, S.; Wang, X.; Zhang, H. Research on emergency search and rescue strategy of UAV group in complex mountain environment. Comput. Technol. Autom. 2024, 43, 127–134. [Google Scholar] [CrossRef]
- Çoğay, S.; Seçinti, G. Phoenix: Aerial monitoring for fighting wildfires. Drones 2023, 7, 19. [Google Scholar] [CrossRef]
- Huang, R.; Zhou, H.; Liu, T.; Hanlin, S. Multi-UAV collaboration to survey Tibetan antelopes in Hoh Xil. Drones 2022, 6, 196. [Google Scholar] [CrossRef]
- Fan, X.; Li, H.; You, C.; Danna, D. UAV swarm search path planning method based on probability of containment. Drones 2022, 8, 132. [Google Scholar] [CrossRef]
- Du, L.; Fan, Y.; Gui, M.; Zhao, D. A multi-regional path-planning method for rescue UAVs with priority constraints. Drones 2023, 7, 692. [Google Scholar] [CrossRef]
- Ma, Y.; Zhao, Y.; Li, Z.; Yan, X.; Bi, H.; Królczyk, G. A new coverage path planning algorithm for unmanned surface mapping vehicle based on A-star based searching. Appl. Ocean Res. 2022, 123, 103163. [Google Scholar] [CrossRef]
- Jing, X.; Hou, M.; Li, W.; Chen, C.; Feng, Z.; Wang, M. Task parameter planning algorithm for UAV area complete coverage in EO sector scanning mode. Aerospace 2023, 10, 612. [Google Scholar] [CrossRef]
- Wang, X.; Wang, P.; Ding, M.; Lin, Z.; Lin, F.; Vucetic, B.; Hanzo, L. Performance analysis of terahertz unmanned aerial vehicular networks. IEEE Trans. Veh. Technol. 2020, 69, 16330–16335. [Google Scholar] [CrossRef]
- Cabreira, T.; Brisolara, L.; Ferreira, P.R., Jr. Survey on coverage path planning with unmanned aerial vehicles. Drones 2019, 3, 4. [Google Scholar] [CrossRef]
- Kumar, K.; Kumar, N. Region coverage-aware path planning for unmanned aerial vehicles: A systematic review. Phys. Commun. 2023, 59, 102073. [Google Scholar] [CrossRef]
- Jia, Y.; Zhou, S.; Zeng, Q.; Li, C.; Chen, D.; Zhang, K.; Liu, L.; Chen, Z. The UAV path coverage algorithm based on the greedy strategy and ant colony optimization. Electronics 2023, 11, 2667. [Google Scholar] [CrossRef]
- Xiao, P.; Li, N.; Xie, F.; Ni, H.; Zhang, M.; Wang, B. Clustering-based multi-region coverage-path planning of heterogeneous UAVs. Drones 2023, 7, 664. [Google Scholar] [CrossRef]
- Tong, Y.; Sheng, M.; Liu, J.; Zhao, N. Energy-efficient UAV-NOMA aided wireless coverage with massive connections. Sci. China Inf. Sci. 2023, 66, 222303. [Google Scholar] [CrossRef]
- Xiao, J.; Yuan, G.; Xue, Y.; He, J.; Wang, Y.; Zou, Y.; Wang, Z. A deep reinforcement learning based distributed multi-UAV dynamic area coverage algorithm for complex environment. Neurocomputing 2024, 595, 127904. [Google Scholar] [CrossRef]
- Yang, Y.; Feng, Y.; Liang, Y. UAV cluster dense obstacle area coverage route planning based on Dubins-RRT algorithm. Tact. Miss. Technol. 2024, 45, 83–98. [Google Scholar] [CrossRef]
- Yan, X.; Chen, R.; Jiang, Z. UAV cluster mission planning strategy for area coverage tasks. Sensors 2023, 23, 9122. [Google Scholar] [CrossRef]
- Lahmeri, M.A.; Kishk, M.A.; Alouini, M.S. Stochastic geometry-based analysis of airborne base stations with laser-powered UAVs. IEEE Commun. Lett. 2020, 24, 173–177. [Google Scholar] [CrossRef]
- Xing, S.; Chen, X.; Wang, W.; Xue, P. Multi-UAV coverage optimization method based on information map and improved ant colony algorithm. IEEE Commun. Lett. 2024, 43, 84–91+96. [Google Scholar] [CrossRef]
- Cao, X.; Xuqiong, L.; Jing, L.; Enfeng, H. Improved multi-UAV formation path planning method under artificial potential field method. J. Comput. Appl. 2024, 1–7. [Google Scholar]
- Zhu, J.; Changjian, Z.; Xiaoping, L.; Weimin, B. Multi-target assignment and intelligent decision based on reinforcement learning. Acta Armamentarii 2021, 42, 2040–2048. [Google Scholar] [CrossRef]
- Hart, P.E.; Nilsson, N.J.; Raphael, B. A formal basis for the heuristic determination of minimum cost paths. IEEE Trans. Syst. Sci. Man Cybern. 1968, 4, 100–107. [Google Scholar] [CrossRef]
- Li, Z.; Xu, X. Improved genetic algorithm applied to UAV path planning in earthquake scenarios. J. Saf. Environ. 2024, 25, 1–16. [Google Scholar] [CrossRef]
- Shao, S.; Peng, Y.; He, C.; Du, Y. Efficient path planning for UAV formation via comprehensively improved particle swarm optimization. ISA Trans. 2020, 97, 415–430. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, W. An efficient UAV localization technique based on particle swarm optimization. IEEE Trans. Veh. Technol. 2022, 71, 9544–9577. [Google Scholar] [CrossRef]
- Ye, Z.; Li, H.; Wei, W. Improved particle swarm optimization based on multi-strategy fusion for UAV path planning. Int. J. Intell. Comput. Cybern. 2024, 17, 213–235. [Google Scholar] [CrossRef]
- Hedjar, R.; Bounkhel, M. Real-time obstacle avoidance for a swarm of autonomous mobile robots. Int. J. Adv. Rob. Syst. 2014, 11, 36–47. [Google Scholar] [CrossRef]
- Rafai, A.N.A.; Adzhar, N.; Jaini, N.I. A review on path planning and obstacle avoidance algorithms for autonomous mobile robots. J. Rob. 2022, 2022, 1–14. [Google Scholar] [CrossRef]
- Chen, Y.; Dong, Q.; Shang, X.; Wu, Z.; Wang, J. Multi-UAV autonomous path planning in reconnaissance missions considering incomplete information: A reinforcement learning method. Drones 2022, 7, 10. [Google Scholar] [CrossRef]
- Tang, J.; Liang, Y.; Li, K. Dynamic scene path planning of UAVs based on deep reinforcement learning. Drones 2024, 8, 60. [Google Scholar] [CrossRef]
- Zhao, X.; Yang, R.; Zhong, L.; Hou, Z. Multi-UAV path planning and following based on multi-agent reinforcement learning. Drones 2024, 8, 18. [Google Scholar] [CrossRef]
- Li, G.; Chou, W. Path planning for mobile robot using self-adaptive learning particle swarm optimization. Sci. China Inf. Sci. 2018, 61, 052204. [Google Scholar]
- Han, Q.; Yang, X.; Song, H.; Du, W. Multi-objective ship path planning using non-dominant relationship-based WOA in marine meteorological environment. Ocean. Eng. 2022, 266, 112862. [Google Scholar]



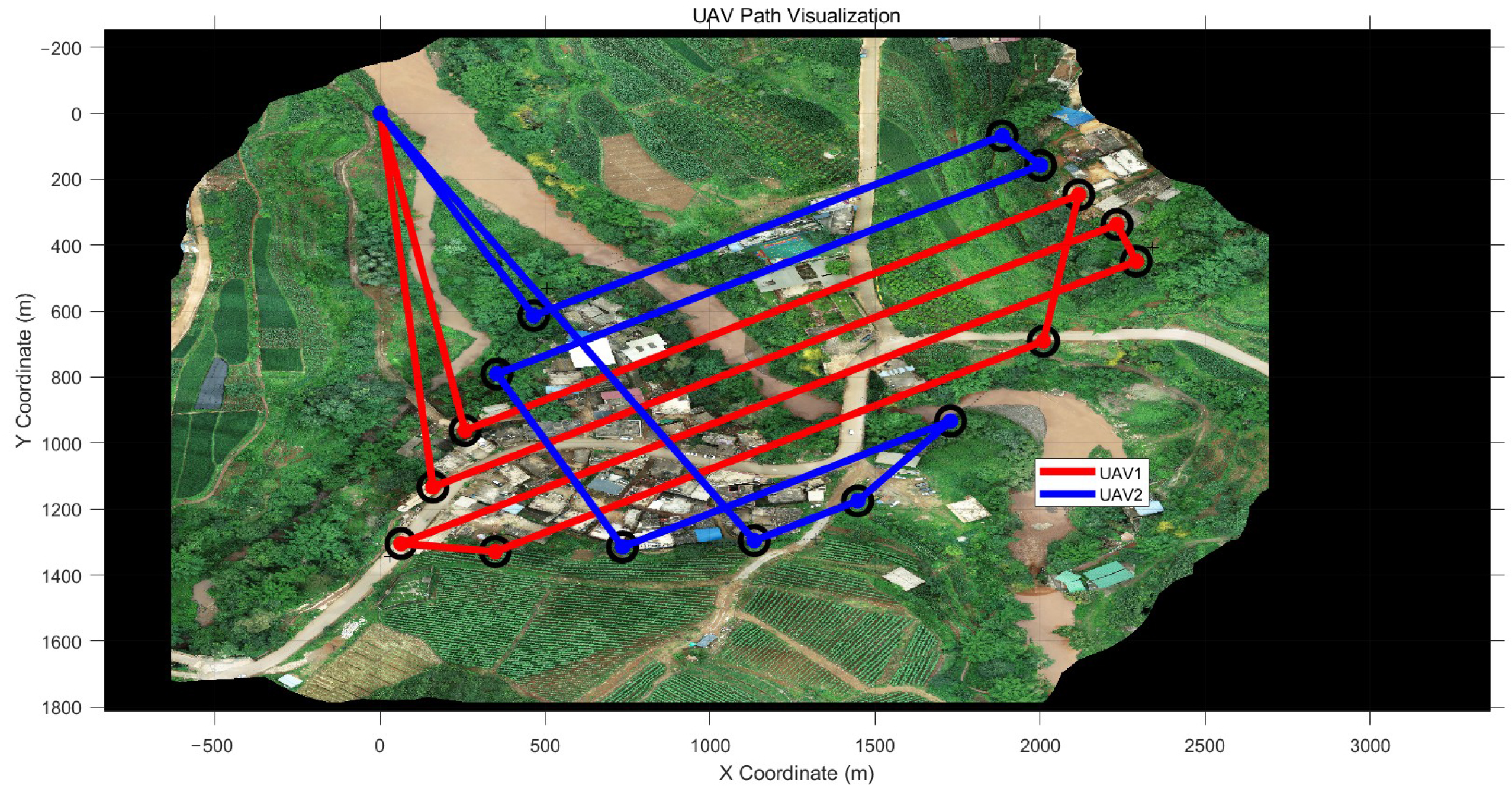
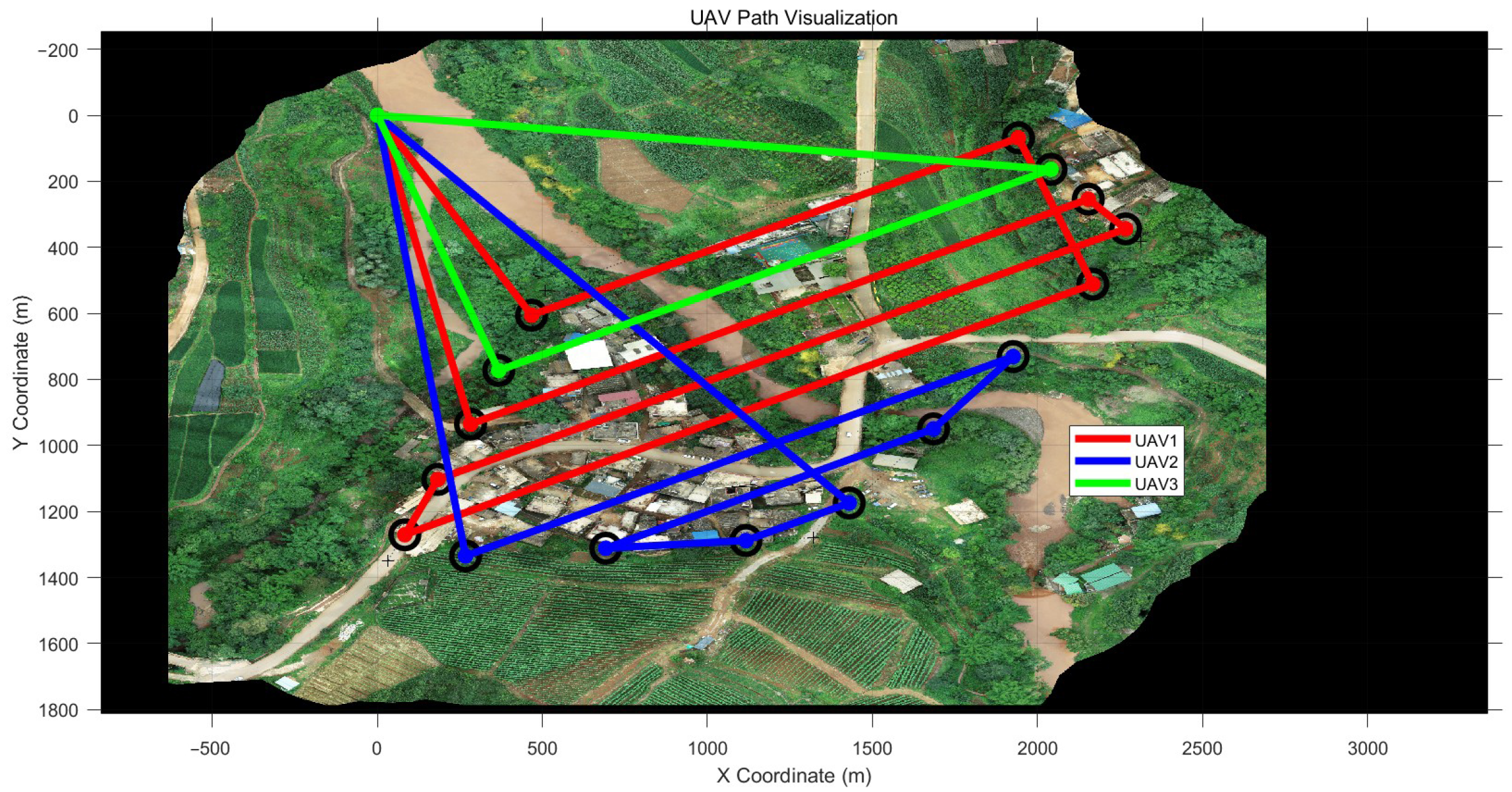



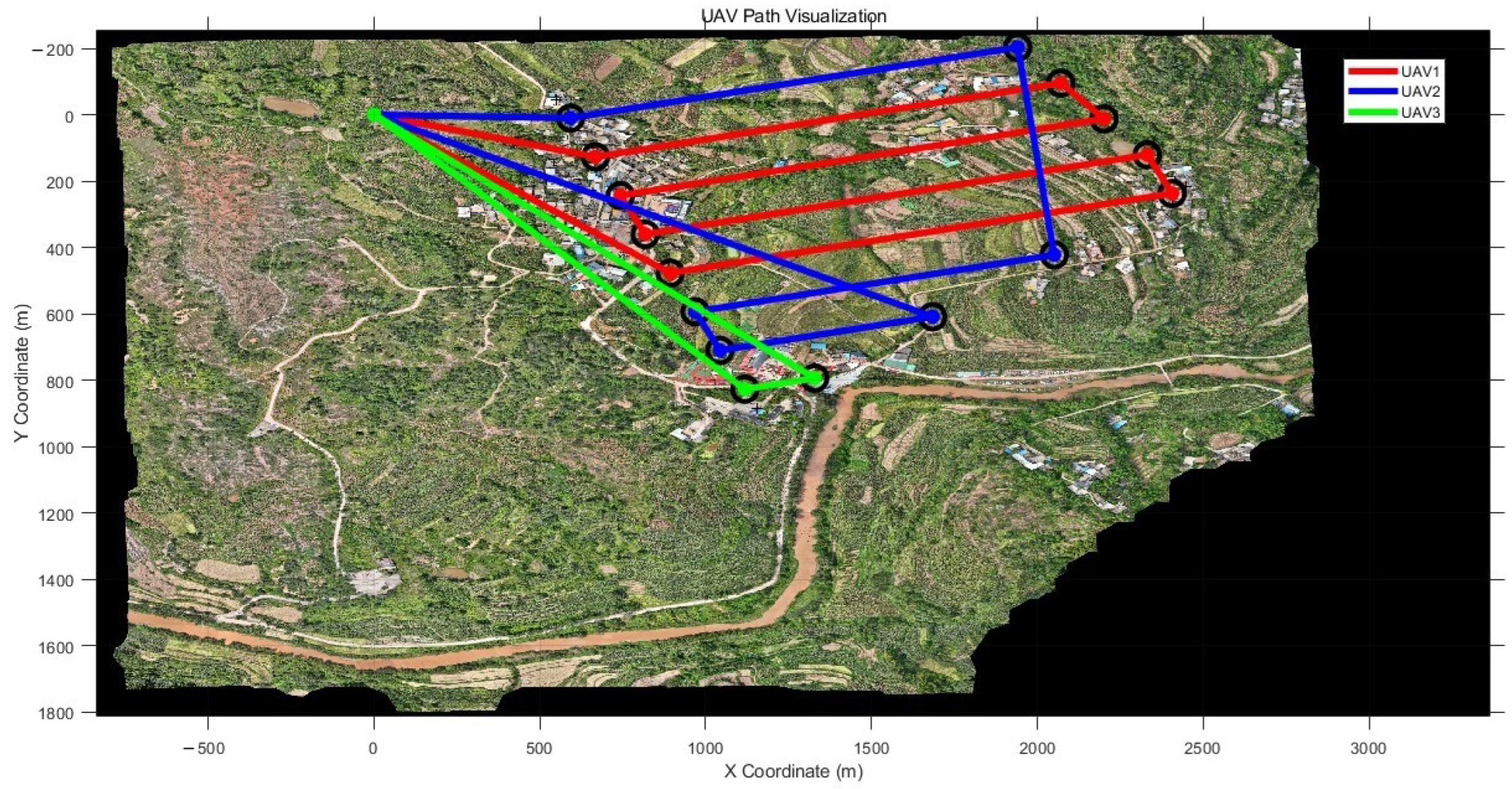






| Test Number | UAV Count | Task Completion Time (min) | Path Value (km) | Setup Time for Each UAV (min) | Notes |
|---|---|---|---|---|---|
| 1 | 1 | 27.87 | 129 | 4 | Task completion time for one UAV |
| 2 | 2 | 20.06 | 118.74 | 4 | Task completion time for two UAVs |
| 3 | 3 | 18.27 | 125.55 | 4 | Task completion time for three UAVs |
| Test Number | UAV Count | Task Completion Time (min) | Path Value (km) | Setup Time for Each UAV (min) | Notes |
|---|---|---|---|---|---|
| 1 | 1 Plane | 28.3567 | 185.4892 | 4 | Task completion time for one UAV |
| 2 | 2 Plane | 18.2345 | 175.7634 | 4 | Task completion time for one UAV |
| 3 | 3 Plane | 13.4567 | 172.08 | 4 | Task completion time for one UAV |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Zhong, H.; Yu, J. Analysis of Regional Spatial Characteristics and Optimization of Tourism Routes Based on Point Cloud Data from Unmanned Aerial Vehicles. ISPRS Int. J. Geo-Inf. 2025, 14, 145. https://doi.org/10.3390/ijgi14040145
Chen Y, Zhong H, Yu J. Analysis of Regional Spatial Characteristics and Optimization of Tourism Routes Based on Point Cloud Data from Unmanned Aerial Vehicles. ISPRS International Journal of Geo-Information. 2025; 14(4):145. https://doi.org/10.3390/ijgi14040145
Chicago/Turabian StyleChen, Yu, Hui Zhong, and Jianglong Yu. 2025. "Analysis of Regional Spatial Characteristics and Optimization of Tourism Routes Based on Point Cloud Data from Unmanned Aerial Vehicles" ISPRS International Journal of Geo-Information 14, no. 4: 145. https://doi.org/10.3390/ijgi14040145
APA StyleChen, Y., Zhong, H., & Yu, J. (2025). Analysis of Regional Spatial Characteristics and Optimization of Tourism Routes Based on Point Cloud Data from Unmanned Aerial Vehicles. ISPRS International Journal of Geo-Information, 14(4), 145. https://doi.org/10.3390/ijgi14040145






