Abstract
To address the variability and complexity of attack types, this paper proposes a multi-instance zero-watermarking algorithm that goes beyond the conventional one-to-one watermarking approach. Inspired by the class-instance paradigm in object-oriented programming, this algorithm constructs multiple zero watermarks from a single vector geographic dataset to enhance resilience against diverse attacks. Normalization is applied to eliminate dimensional and deformation inconsistencies, ensuring robustness against non-uniform scaling attacks. Feature triangle construction and angle selection are further utilized to provide resistance to interpolation and compression attacks. Moreover, angular features confer robustness against translation, uniform scaling, and rotation attacks. Experimental results demonstrate the superior robustness of the proposed algorithm, with normalized correlation values consistently maintaining 1.00 across various attack scenarios. Compared with existing methods, the algorithm exhibits superior comprehensive robustness, effectively safeguarding the copyright of vector geographic data.
1. Introduction
Vector geographic data are an essential resource in GIS-related industries and have found widespread applications in fields such as land surveying, military simulations, and urban planning. However, the conflict between data sharing and protection has become increasingly difficult to reconcile. Frequent copyright infringement incidents highlight the urgent need for effective protection measures [1,2,3]. Digital watermarking is a key technology for copyright protection. It establishes a strong relationship between digital data and watermark information, safeguarding the copyright of vector geographic data [4,5,6]. At the same time, attackers employ various methods to attack watermarks, making the improvement of watermark robustness a major research focus.
Current watermarking algorithms for vector geographic data can be broadly classified into embedded watermarking and constructive watermarking [7]. Embedded watermarking modifies the coordinates (including features derived from coordinates), the attribute, or the storage order to embed watermark information directly into the vector geographic data. For example, Peng et al. [8] used the Douglas–Peucker compression algorithm [9] to construct the feature vertex distance ratio (FVDR), embedding the watermark by adjusting the FVDR. Other approaches include embedding invisible characters into the attribute values of road data [10] or changing the storage order of vertices within polylines to embed the watermark information [11]. While embedded watermarking increases the relationship between the data and the watermark, it inevitably alters the data. Methods that embed watermarks into coordinates affect data precision, making them unsuitable for high data accuracy scenarios. Methods embedding watermarks into attributes increase file size and storage demands, potentially exposing the watermark to attackers. Furthermore, embedding watermarks into storage order may disrupt the semantic or functional meaning of the data, such as river flow directions or pipeline pathways. Therefore, the robustness of embedded watermarking is achieved at the cost of data integrity, limiting its application.
The second type is constructive watermarking, often referred to as zero watermarking [12,13,14]. Zero watermarking is distinguished by its non-intrusive nature, as it extracts features from the original data without introducing any modifications. The constructed watermark based on the features is then registered with third-party intellectual property rights (IPR) agencies for copyright protection. This type of method typically partitions data into sub-blocks using regular or irregular segmentation techniques, such as grids [15], rings [16], quadtrees [17], Delaunay triangulation [18], or object-based divisions [19,20,21,22,23]. Features such as geometric properties, vertex counts, or storage orders are quantified into watermark bits or indices, which are then combined to construct the zero watermark. For instance, Zhang et al. [15] employed a grid-based approach, partitioning the data into 64 × 64 blocks and subsequently quantifying the vertex count within each block to construct the watermark. Peng et al. [19] adopted an alternative strategy, treating individual polylines as the fundamental operational units. This approach, analogous to the embedded watermarking method described in the literature [8], utilized the FVDR as the basis for quantification, converting these features into watermark indices and bits. The constructed watermark was then refined through the majority voting mechanism. Similarly, Wang et al. [23] leveraged both the vertex count and the storage order features. Specifically, the vertex counts of arbitrary polyline or polygon pairs were quantified into watermark indices, while the storage order was used to generate watermark bits. Notably, such methods preserve the integrity of the original data by avoiding any modifications, thereby addressing the inherent limitations associated with embedded watermarking.
However, existing zero-watermarking methods, while advantageous in preserving data integrity, are constrained by their reliance on constructing a single watermark derived from the overall characteristics of the data. This scheme inherently limits their adaptability in resisting diverse and complex attack types. For instance, FVDR-based methods demonstrate robust performance against simplification attacks but remain vulnerable to non-uniform scaling. In contrast, vertex count-based methods excel in resisting non-uniform scaling and other geometric transformations but struggle under simplification and attacks that significantly modify vertex statistics. Consequently, these methods exhibit robustness in isolated scenarios but fail to achieve comprehensive resistance across multiple attack types.
In summary, embedded watermarking methods enhance robustness by embedding watermarks directly into the data, tightly coupling the watermark with the data. However, this approach inevitably compromises the original data’s usability and precision, limiting its applicability in scenarios demanding high data accuracy. Constructive watermarking, on the other hand, constructs watermarks from the data without modifying the data, effectively addressing the precision degradation issue of embedded methods. Nonetheless, existing constructive watermarking approaches still face challenges in achieving comprehensive robustness against diverse attack types. Therefore, developing algorithms capable of simultaneously resisting multiple attack types remains a critical research problem in the field of digital watermarking for vector geographic data.
To address these issues, this paper proposes a multi-instance zero-watermarking method for vector geographic data, inspired by the class-instance paradigm in object-oriented programming. By applying different preprocessing techniques, the proposed method constructs multiple zero watermarks from a single dataset, enabling it to adapt to the variability and complexity of attack types. Unlike existing approaches that segment the dataset to construct separate watermarks, the proposed algorithm constructs each zero watermark using the full set of data features, differentiated only by the preprocessing applied. The remainder of this paper is structured as follows: Section 2 introduces the methodology and its details, Section 3 describes the experimental setup, Section 4 presents the experimental results and analysis, Section 5 discusses the broader implications of the findings, and Section 6 concludes the study.
2. Proposed Approach
The proposed multi-instance zero-watermarking algorithm targets vector geographic data, specifically line data, as the watermarking carrier. Inspired by the class-instance paradigm in object-oriented programming, the algorithm treats the data as a “class” from which multiple “instances” (zero watermarks) are derived. By employing preprocessing techniques such as normalization, feature triangle construction, and angle selection, the algorithm generates multiple zero watermarks to resist various attack types. Normalization eliminates geometric deformations, enhancing robustness against non-uniform scaling attacks. Feature triangle construction and angle selection, inspired by the Douglas-Peucker algorithm, provide resilience against interpolation and simplification attacks. Furthermore, angle-based features are derived by quantizing the selected angles in the feature triangle. Previous studies [24,25,26] have demonstrated that these features exhibit robustness against translation, uniform scaling, and rotation. Their incorporation into the proposed method enhances its resistance to these geometric attacks. To address non-uniform scaling, interpolation, and simplification attacks, two zero watermarks are constructed. The main framework of the proposed algorithm is shown in Figure 1.
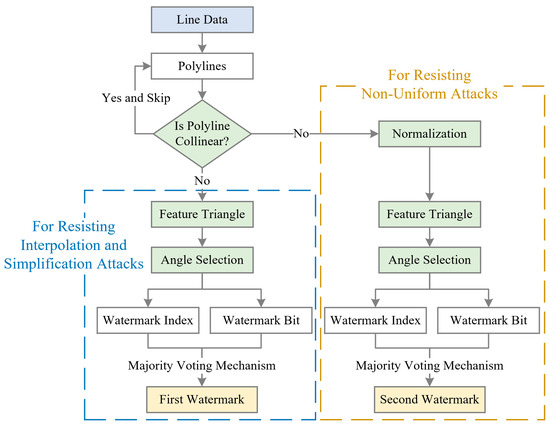
Figure 1.
Main framework of the proposed method.
As illustrated in Figure 1, the algorithm begins by extracting polylines from the line data. The overall process can be divided into three main parts: collinearity checks, the construction of the first zero watermark (for resisting interpolation and simplification attacks), and the construction of the second zero watermark (for resisting non-uniform scaling attacks). In the first part, for each polyline, collinearity checks are performed on its vertices. If all vertices of a polyline are collinear, it is skipped, and the next polyline is processed. Only non-collinear polylines are further proceeded to subsequent stages.
The second and third parts involve the generation of two zero watermarks. The primary difference between these two processes lies in the application of normalization. Specifically, normalization is applied in the construction of the second zero watermark to enhance robustness against non-uniform scaling attacks. However, normalization is avoided during the construction of the first zero watermark for robustness against interpolation and simplification attacks. This is because simplification may alter the bounding coordinates and lead to unintended deformations during normalization. Beyond normalization, the subsequent steps for generating both zero watermarks are identical, as summarized below: (1) Feature triangle construction: The polyline is reduced to its most essential form by retaining only three vertices, which form the feature triangle; (2) Angle selection: Two angles are selected from the three angles in the constructed feature triangle; (3) Watermark construction: The selected angles are quantified into watermark indices and bits, which are aggregated using the majority voting mechanism to construct two zero watermarks.
During copyright verification, the generated zero watermarks are evaluated for consistency. The steps of collinearity check, normalization, feature triangle construction, angle selection, zero-watermark construction, and watermark evaluation are detailed in the following subsections.
2.1. Collinearity Check
To ensure meaningful geometric features for watermark construction, the algorithm excludes polylines with collinear vertices. This process involves determining whether three vertices in a polyline are collinear based on their geometric properties. The collinearity check is divided into two cases: (1) For polylines with only two vertices, collinearity is inherent, and such polylines are skipped. (2) For polylines with more than two vertices, three vertices are iteratively selected from the vertex set to evaluate collinearity. This process is repeated times, where n is the total number of vertices in a polyline.
The collinearity of three vertices , , and is determined using the area method, defined as follows:
If the calculated area is less than a predefined threshold (), the vertices are considered collinear. The threshold is introduced to address the limitations of floating-point arithmetic, where numerical precision makes exact equality comparisons infeasible. Theoretically, collinearity requires the area formed by three vertices to be zero, but in practice, floating-point calculations may produce small non-zero values for collinear points. Thus, the threshold serves as a tolerance value to ensure robust and accurate detection of collinearity. Any polyline that does not contain at least one set of non-collinear vertices is excluded from subsequent steps. This ensures that all polylines used in watermark construction contribute to meaningful geometric features, improving the reliability of the resulting zero watermarks.
2.2. Normalization
Normalization is employed as a preprocessing step to eliminate deformation caused by non-uniform scaling. This ensures that the geometric features extracted from the data remain consistent, regardless of the scaling factors applied to the original coordinates. The process involves normalizing the x and y coordinates of the vertices using min–max normalization, as defined by the following equations:
Here, and represent the normalized coordinates, while , , , and denote the minimum and maximum values of the x and y coordinates within the polyline, respectively.
The stability of the normalized coordinates under non-uniform scaling has been validated theoretically. Zhang et al. [27,28] demonstrated that the normalized x and y coordinates remain invariant when the original coordinates are scaled by factors Sx and Sy. Specifically, after applying scaling, the normalized coordinates are recalculated as follows:
This invariance ensures that the geometric features extracted from the normalized coordinates remain robust against non-uniform scaling, a critical requirement for practical watermark construction.
Normalization is applied selectively. It is used to stabilize the geometry shape when addressing non-uniform scaling attacks. However, it is omitted when addressing interpolation and simplification attacks, as these attacks may alter the bounding coordinates, potentially introducing unintended deformations during normalization. This selective normalization provides the potential overall robustness to different attack scenarios.
2.3. Feature Triangle Construction
Feature triangle construction is a core step in the proposed algorithm, designed to extract robust geometric features from polylines. The method begins by connecting the first vertex A and the last vertex B of the polyline to form a line segment AB. Then, the algorithm iteratively examines the remaining vertices to identify point C, which is farthest from AB. The distance is calculated as the perpendicular distance from each vertex to the line segment. The three vertices, A, B, and C, form the feature triangle, encapsulating critical geometric properties of the polyline. Figure 2 provides a demonstration of feature triangle construction.
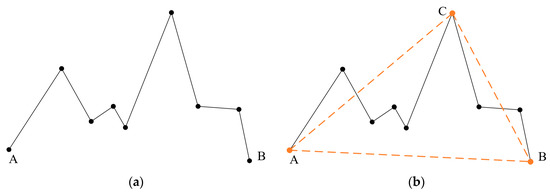
Figure 2.
Demonstration of feature triangle construction: (a) a polyline with nine vertices and (b) the feature triangle ABC.
As illustrated in Figure 2, a polyline consisting of nine vertices is shown in Figure 2a, where A and B represent the first and last points, respectively. The vertex C, identified as the farthest point from AB, completes the feature triangle, as depicted in Figure 2b. This construction method corresponds to the initial step of the Douglas–Peucker compression algorithm. However, unlike the Douglas–Peucker algorithm, which recursively divides the polyline to find additional feature points, the proposed method selects only the farthest point. This is not a simplification of the process but a deliberate choice to improve robustness against compression attacks. As noted in the literature [13], when fewer feature points are retained, the watermarking scheme exhibits greater resistance to compression, as excessive simplification would be required to disrupt the constructed triangle.
2.4. Angle Selection and Zero-Watermark Construction
From the feature triangle, two angles, and , are selected and denoted as α and β, respectively. These angles are calculated using the cosine rule as follows:
where AB, BC, and AC are the side lengths of the feature triangle, calculated from the coordinates of the vertices A, B, and C. The angles α and β are measured in radians, ensuring their range lies within (0, π). As ensured by the collinearity check in Section 2.1, the feature triangle is always valid with non-collinear vertices.
Next, α is used for quantifying the watermark index. The quantization process involves retaining all digits from the start of α up to and including the q-th digit after the decimal point:
where the round( ) function rounds the value to the nearest integer. The resulting is then passed as a seed to a uniformly distributed pseudorandom integer generator, denoted as . The watermark index, denoted as WI, is computed as follows:
where N is the watermark length. The last two arguments of the function represent the minimum and maximum values of the discrete uniform distribution, defining the range of the watermark index as [1, N]. Similarly, the angle β is processed to generate the watermark bit. After extracting the integer in the same manner as , the watermark bit, denoted as WB, is calculated as follows:
Here, the watermark bit takes a value of either 0 or 1.
Since a line dataset typically contains multiple polylines, multiple watermark indices and bits are generated. These are aggregated using a majority voting mechanism, as described in the literature [8,21]. Specifically, an array Stat, equal in length to the watermark, is initialized with all elements set to 0. For each watermark index and its corresponding watermark bit, the following update rules are applied:
where refers to the specific index in the watermark corresponding to i-th polyline, and represents the corresponding bit. After processing all indices and bits, the binary watermark W is finalized based on the values in Stat:
The resulting W is a binary sequence composed of 0 s and 1 s, completing the construction of the zero watermark.
2.5. Watermark Evaluation
The proposed algorithm constructs two zero watermarks from the original dataset, which are registered with an authoritative third-party IPR agency. In the event of a copyright dispute, two zero watermarks are also constructed from the suspicious dataset for comparison. The normalized correlation (NC) is introduced as a quantitative metric to evaluate the similarity between the watermarks, calculated using the following formula:
where W and W′ represent the binary sequences of the registered and reconstructed watermarks, respectively. The NC value lies within the range of (0, 1], where a value closer to 1 indicates greater similarity.
To determine whether the watermarks match, a predefined NC threshold is introduced. The two watermarks are considered identical if the NC value exceeds the threshold. The suspicious dataset’s two zero watermarks are compared against the two registered zero watermarks, resulting in four NC values theoretically. In practice, a fixed one-to-one mapping is enforced, whereby the first constructed watermark is aligned with the first registered watermark, and the second constructed watermark is aligned with the second registered watermark. This mapping reduces the comparison to two NC values, denoted as NC1 and NC2, which quantify the similarity between each pair of corresponding watermarks. The final detection result is determined by selecting the maximum value between NC1 and NC2. This approach ensures that even if one instance of the watermark is affected by an attack, the other instance can still provide a reliable match. The redundancy introduced by the multi-instance scheme enhances the robustness of the algorithm, allowing it to handle diverse attack scenarios. Therefore, this evaluation process ensures that the algorithm effectively quantifies the similarity between watermarks, providing a robust copyright validation and infringement detection mechanism.
3. Experiments
3.1. Datasets
The experiments utilize a vector geographic dataset representing waterways, as shown in Figure 3. This dataset comprises line data from regions located at the intersection of Hunan, Jiangxi, and Guangdong provinces in China. The coordinate reference system is CGCS2000, with a 3-degree Gauss–Kruger projection and a central meridian at 114° E. The dataset contains 1540 polylines, with an average of 56 vertices per polyline. The maximum number of vertices in a single polyline is 550, while the minimum is 2, and the median is 45, making it suitable for evaluating the proposed algorithm’s robustness and efficiency.
Figure 3.
Waterways dataset used in the experiments.
3.2. Parameter Settings and Comparison Algorithms
The proposed algorithm is configured with key parameters to balance robustness and computational efficiency. The angle quantization precision q is set to 4, meaning the quantization process retains all digits from the start of the number up to and including the fourth digit after the decimal point. The watermark length N is chosen as 64, providing a suitable trade-off between performance and computational cost. An NC threshold of 0.75 is adopted, referencing values commonly used in prior literature [7,21,29,30]. These settings are empirically determined to provide reliable performance under various attack scenarios.
For comparison algorithms, two zero-watermarking methods are selected and denoted as the method Peng [19] and the method Wang [23]. As mentioned in Section 1, partitioning data into sub-blocks is a common strategy in zero-watermarking algorithms. Among these sub-blocking methods, the object-based division is particularly stable because data modifications are typically performed at the object level. Peng and Wang adopted the object-based division method, consistent with the approach in the proposed algorithm. The method Peng extracts the FVDR from polylines, while the method Wang uses vertex count and storage order features. Both of them are configured with the same watermark length as the proposed method to ensure consistency. Additionally, the method Peng employs the Douglas–Peucker algorithm for feature point extraction, with a relative threshold of 0.3. All algorithms are evaluated using the NC metric to provide a fair basis for comparison.
3.3. Attack Design
To comprehensively evaluate the robustness of the proposed algorithm, six types of attacks commonly encountered in vector geographic data processing are applied: rotation, uniform scaling, non-uniform scaling, translation, interpolation, and simplification. Each attack is configured with parameters referenced from the literature [21] to simulate real-world data distortions. Table 1 summarizes the configurations of these attacks.

Table 1.
Attack configurations.
In Table 1, most attacks, such as rotation, scaling, and translation, are standard transformations applied to the entire dataset without altering the density of vertices. However, interpolation and simplification deserve special attention, as they directly impact the dataset’s vertex density. New vertices are inserted into segments exceeding the specified tolerance for interpolation, increasing the data’s density. In contrast, simplification reduces vertex count by removing coordinates while preserving the overall shape, with larger tolerances resulting in more aggressive vertex removal. These complementary attack types can provide valuable insights into the robustness of watermarking algorithms.
Figure 4 provides a visual demonstration of the attack effects on the dataset. As shown in Figure 4a–c,f, rotation, uniform scaling, and translation attacks do not alter the shape of the data. Conversely, non-uniform scaling attacks lead to visible distortions in the data shape, as illustrated in Figure 4d,e. For instance, when Sx = 0.4, the data appear significantly narrower in the horizontal direction than when Sx = 0.8. To facilitate the visualization of the attack effects, Figure 4g,h overlay the attacked data onto the original data. Interpolation attacks increase the number of vertices in the data, as shown in Figure 4g, where the interpolation tolerance of 10 m adds new points to segments shorter than the specified distance. In contrast, simplification attacks reduce the number of vertices by removing coordinates, resulting in sharper geometries, as depicted in Figure 4h.
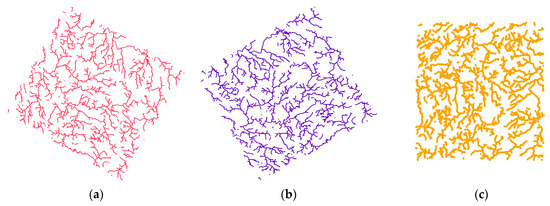
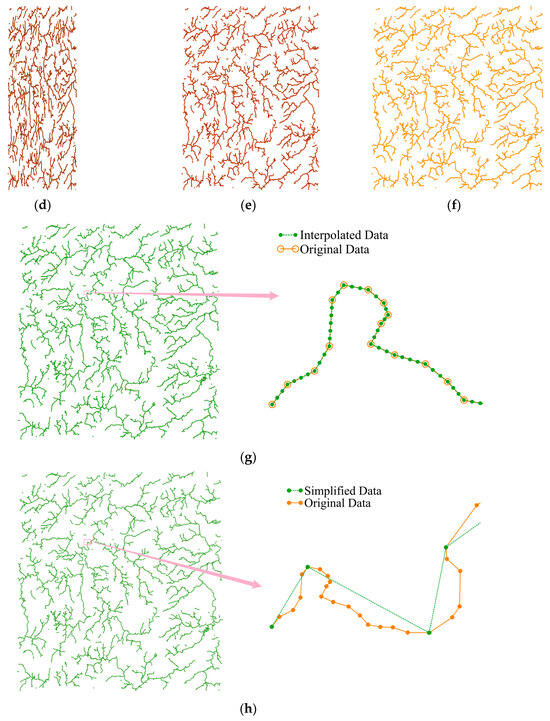
Figure 4.
Visualization of attack effects: (a) rotation (60°); (b) rotation (120°); (c) uniform scaling (Sx = Sy = 0.4); (d) non-uniform scaling (Sx = 0.4, Sy = 1); (e) non-uniform scaling (Sx = 0.8, Sy = 1); (f) translation (60 m); (g) interpolation (tolerance = 10 m); and (h) simplification (tolerance = 60 m).
4. Results and Analysis
The robustness of the proposed algorithm and the comparison algorithms is evaluated across six types of attacks, as described in Section 3. The experimental results are divided into two categories for detailed analysis.
4.1. RST Attacks
Figure 5, Figure 6, Figure 7 and Figure 8 illustrate the robustness of the proposed algorithm and the comparison methods under RST (rotation, scaling, and translation) attacks. Overall, the three algorithms demonstrate consistent resistance to rotation, uniform scaling, and translation attacks. However, their performance varies under non-uniform scaling attacks.
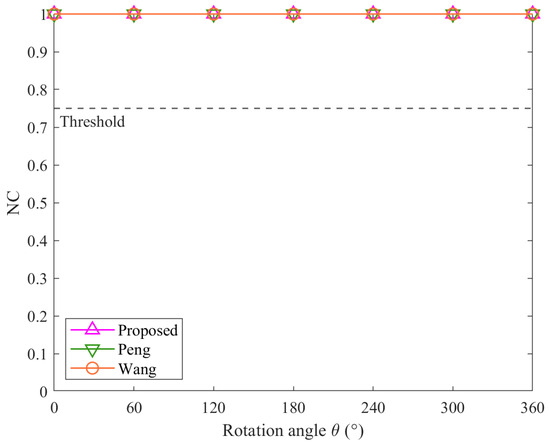
Figure 5.
Results of rotation attacks.
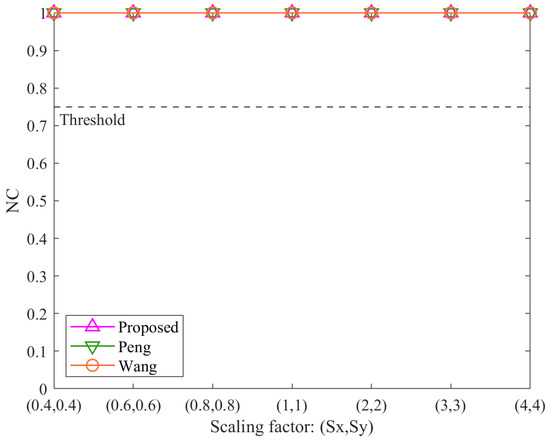
Figure 6.
Results of uniform scaling attacks.
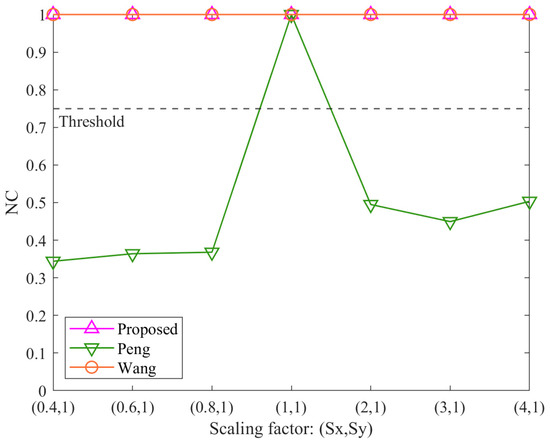
Figure 7.
Results of non-uniform scaling attacks.
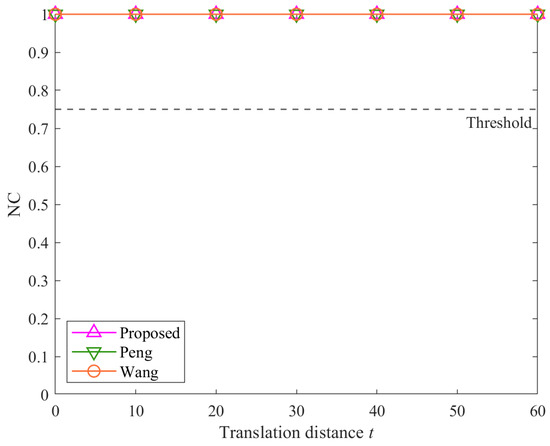
Figure 8.
Results of translation attacks.
From Figure 5, Figure 6, and Figure 8, it is evident that regardless of attack intensity, all three algorithms achieve NC values of 1.00, significantly above the threshold of 0.75. This indicates that the proposed algorithm, like the method Peng and the method Wang, is robust against rotation, uniform scaling, and translation attacks. These results affirm that the angular features used in the proposed method are invariant to these geometric transformations.
In contrast, the results for non-uniform scaling attacks in Figure 7 highlight distinct differences. The proposed algorithm and the method Wang maintain NC values of 1.00 across all tested scaling factors (Sx ≠ Sy), demonstrating their stability. The method Peng, however, shows a significant decline, with NC values falling below the threshold except when Sx = Sy = 1 (no scaling). This indicates that the method Peng is unable to resist non-uniform scaling attacks. The superior performance of the proposed method confirms the effectiveness of its normalization step, which eliminates distortions caused by non-uniform scaling. The method Wang also performs well under non-uniform scaling due to its reliance on vertex count and storage order features, which remain stable during such transformations.
4.2. Interpolation and Simplification Attacks
Figure 9 and Figure 10 present the NC values of the proposed method, the method Peng, and the method Wang under interpolation and simplification attacks. Overall, the NC values of all three algorithms remain above the threshold, but their robustness varies significantly depending on the attack type and intensity.
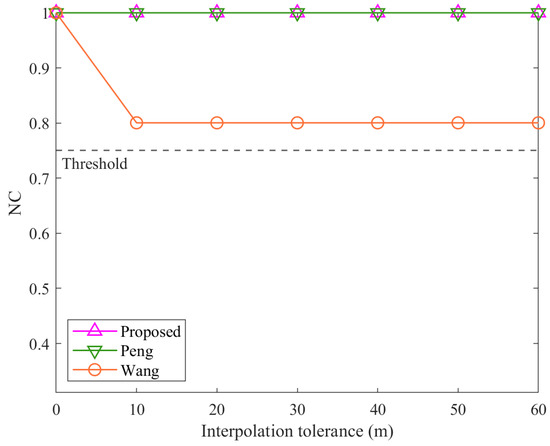
Figure 9.
Results of interpolation attacks.
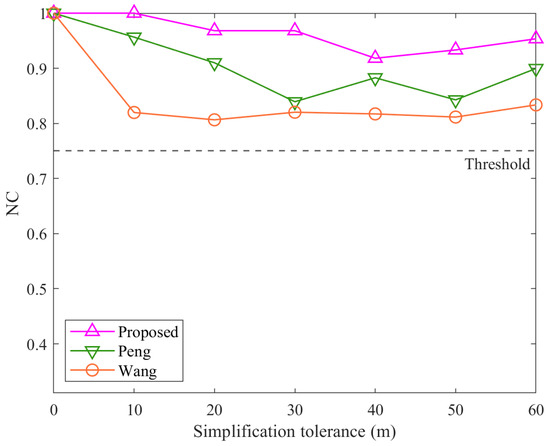
Figure 10.
Results of simplification attacks.
As shown in Figure 9, under interpolation attacks, the proposed algorithm and the method Peng consistently achieve NC values of 1.00 across all interpolation tolerances. In contrast, the NC values of the method Wang decrease immediately after the interpolation tolerance increases from 0 and stabilize around 0.8. This disparity is due to the feature extraction mechanisms of each algorithm. The method Peng leverages the Douglas–Peucker algorithm to construct FVDR features, effectively ignoring additional vertices introduced by interpolation. Similarly, the proposed algorithm relies on feature triangle construction, which also employs the Douglas–Peucker algorithm, rendering it immune to the effects of interpolation. However, the method Wang, which constructs its watermark based on vertex count, is directly influenced by the increased number of vertices, leading to reduced robustness. Despite this, the NC values of the method Wang remain above the threshold due to its use of relative values across all polyline combinations.
In simplification attacks, as shown in Figure 10, the overall trend is that the proposed algorithm outperforms the method Peng, which in turn outperforms the method Wang. As the simplification tolerance increases, the number of vertices in the polylines decreases, causing a gradual decline in NC values across all algorithms. The superior performance of the proposed algorithm can be explained by its reliance on only three critical points within each polyline: the start point, the endpoint, and the farthest point from the line segment connecting them. This design ensures that the watermark remains intact unless a polyline is reduced to just two points. In comparison, the method Peng, which uses a relative threshold of 0.3 in its FVDR construction, performs well but cannot match the proposed algorithm’s resilience. Notably, if the method Peng had used a properly selected threshold, it would have achieved comparable robustness to the proposed algorithm under simplification attacks. However, the original publication of the method Peng does not specify such a value explicitly, and 0.3 was chosen for this experiment as a reasonable compromise to reflect typical scenarios. The method Wang, as with interpolation attacks, is heavily impacted by changes in vertex count, resulting in the lowest robustness among the three algorithms.
4.3. Analysis of Individual Zero Watermarks
Figure 11, Figure 12 and Figure 13 present the NC results for the two zero watermarks under rotation, non-uniform scaling, and simplification attacks, respectively. For other types of attacks, including uniform scaling, translation, and interpolation, the NC values for both watermarks are identical and consistently equal to 1.00. Thus, these results are not presented to avoid redundancy. Overall, the NC values indicate that at least one of the two zero watermarks consistently remains above the threshold, highlighting their complementary characteristics.
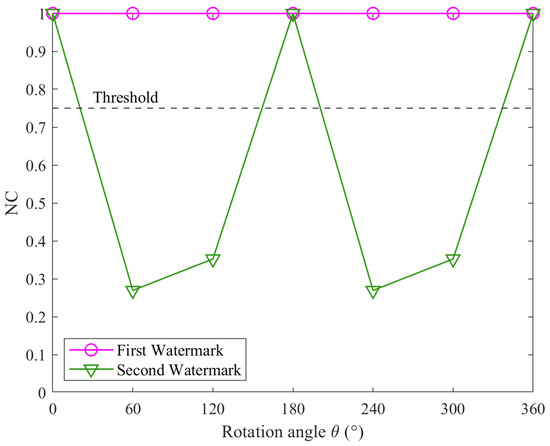
Figure 11.
Results for individual watermarks under rotation attacks.
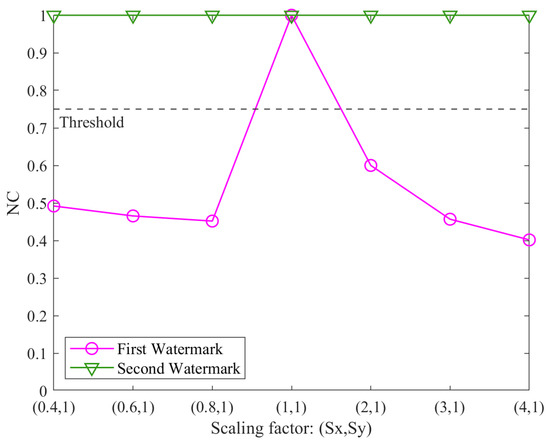
Figure 12.
Results for individual watermarks under non-uniform scaling attacks.
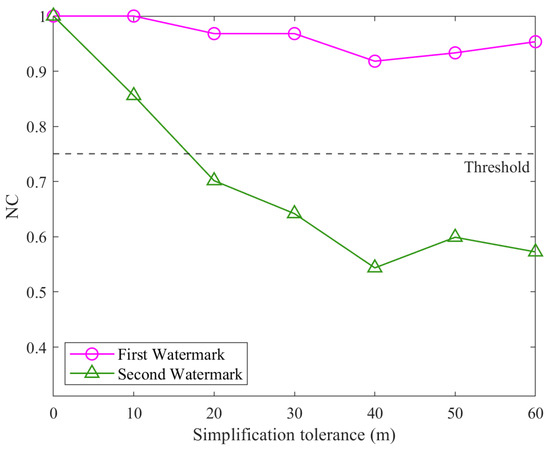
Figure 13.
Results for individual watermarks under simplification attacks.
In Figure 11, under rotation attacks, the first watermark maintains an NC value of 1.00 across all rotation angles. In contrast, the second watermark’s NC falls below the threshold at 60°, 120°, 240°, and 300°. This is due to changes in the data’s extrema, which affect the min–max normalization used by the second watermark, making it sensitive to variations in the data range and causing distortion. In Figure 12, the NC values of the second watermark remain consistently at 1.00, while the NC values of the first watermark fall below the threshold except when the scaling factor is (1, 1), where its NC value equals 1.00. This behavior can be attributed to the second watermark’s incorporation of normalization, which effectively mitigates distortions caused by non-uniform scaling attacks. In Figure 13, as the simplification tolerance increases, the NC values for both watermarks show a declining trend. Notably, the NC values of the second watermark drop below the threshold when the simplification tolerance exceeds 20 m and remain below the threshold thereafter. This observation corroborates the theoretical analysis in Section 2, which highlighted that normalization could diminish the watermark’s resistance to simplification attacks. The analysis validates the complementary nature of the two watermarks. By determining the final NC value as the maximum of the two watermarks’ NCs, the proposed algorithm ensures reliable detection even if one watermark is adversely affected by an attack. This result underscores the effectiveness of the multi-instance scheme in enhancing the robustness of the algorithm.
Overall, the proposed algorithm demonstrates superior robustness compared to the method Peng under non-uniform scaling attacks and outperforms the method Wang under interpolation and simplification attacks. The experimental results confirm that the proposed algorithm achieves the highest overall robustness among the three methods, validating the effectiveness of the multi-instance scheme.
5. Discussion
5.1. Adaptation for Two-Vertex Polylines
As highlighted in Section 2.3, feature triangle construction serves as the core of the proposed algorithm, requiring at least three vertices. Consequently, the algorithm is not applicable to polylines containing only two vertices. To address this limitation, an adaptation can be introduced for such datasets.
The algorithm can be modified for polylines with only two vertices by normalizing all points in the dataset instead of normalizing each polyline individually. For a given two-vertex polyline, the nearest vertex from other polylines is identified to construct a feature triangle. The remaining steps of the algorithm remain unchanged. This adaptation effectively transforms the process of finding the farthest point within a polyline into finding the nearest point between polylines. By selecting the nearest vertex, the algorithm can retain a certain resistance to cropping attacks while extending its applicability to two-vertex polylines. This modification enhances the versatility of the proposed algorithm, making it suitable for a broader range of vector geographic datasets.
5.2. Performance Under Composite Attacks
To further assess the robustness of the proposed algorithm, its performance under composite attacks was analyzed. Composite attacks involve combining multiple types of distortions, which may create challenging scenarios for watermark detection. The two zero watermarks in the proposed algorithm, one incorporating normalization and the other not, serve a pivotal role in mitigating these challenges. However, the complementary design introduces variations in robustness when specific types of attacks are combined.
Attacks are classified into conflicting combinations and non-conflicting combinations. Conflicting combinations involve attacks that require normalization (e.g., non-uniform scaling) paired with attacks that must avoid normalization (e.g., simplification or rotation). Non-conflicting combinations, on the other hand, do not involve such conflicts. Table 2 illustrates the experimental results for eight composite attack scenarios. The results demonstrate that the algorithm maintains strong robustness under non-conflicting combinations (IDs 1–6), with NC values consistently above the threshold of 0.75. In contrast, conflicting combinations (IDs 7 and 8) result in a significant decline in NC values. Specifically, ID 8, which combines rotation and non-uniform scaling, reduces the NC to 0.50, falling below the threshold.

Table 2.
Results of composite attacks.
These findings highlight the algorithm’s limitations under conflicting combinations while reaffirming its strong robustness under non-conflicting scenarios. The results validate the complementary nature of the multi-instance scheme in most scenarios but underscore the need for further enhancements to address conflicts. Future work could focus on developing techniques to resist non-uniform scaling without relying on normalization or mitigating simplification attacks independently of feature triangle-based methods.
5.3. Integration into Real-World Applications
The proposed algorithm is designed to enhance the security of vector geographic data, making it highly relevant for integration into GIS workflows and other real-world applications. In modern GIS platforms, vector geographic data are frequently processed for tasks such as mapping, analysis, and sharing across multiple stakeholders. The algorithm can be integrated as either a preprocessing or validation step to ensure that copyrighted datasets are protected during these processes.
Specifically, the collinearity checks and feature triangle construction steps can be seamlessly incorporated into existing data preparation pipelines, while the watermark generation and verification stages can be integrated as additional modules in GIS software (e.g., QGIS 3.28). For example, during data sharing, zero watermarks generated using the proposed method can be registered with intellectual property agencies, enabling robust copyright protection. When disputes arise, the registered watermarks can be compared with reconstructed watermarks to verify data authenticity and ownership.
Moreover, the multi-instance design enhances resilience against geometric transformations commonly encountered in real-world workflows. For instance, routine updates to geographic datasets often involve geometric transformations such as RST attacks. Data modifications tailored to meet specific application requirements may lead to interpolation and simplification attacks. Two case studies illustrating these applications include the following:
- (1)
- Transportation Planning and Road Network Simplification
In large-scale transportation planning, road networks are often represented as polylines in GIS systems. These datasets may undergo simplification to reduce computational complexity for routing or network analysis. For instance, a GIS database of a city’s road network may involve removing minor routes or reducing segment density for visualization purposes. Such modifications can distort the geometry of the original data, complicating copyright enforcement. By applying the proposed algorithm before simplification, zero watermarks embedded into the dataset remain detectable after these modifications, ensuring copyright verification even under significant simplification attacks.
- (2)
- Hydrological Modeling and River Network Interpolation
In hydrological modeling, river networks represented as vector polylines often require interpolation to fill missing segments or connect disjointed features for flow analysis. For example, in flood modeling, missing tributary connections may be interpolated to provide a complete representation of the network. Such modifications can alter the geometry of the dataset, making copyright protection challenging. Embedding zero watermarks into the river network before interpolation ensures that the dataset retains its copyright markers, allowing robust verification of ownership after modifications.
To facilitate efficient implementation in large-scale systems, computational optimizations such as parallel processing and database indexing can accelerate steps like angle selection and watermark evaluation. Future research could explore integrating the algorithm into distributed GIS platforms and cloud-based services to ensure scalability and real-time copyright enforcement.
6. Conclusions
How to address the diversity and complexity of attacks in the copyright protection of vector geographic data remains a critical scientific challenge. This study proposes a multi-instance zero-watermarking algorithm for vector geographic data to solve this issue. The method constructs two robust zero watermarks by employing key techniques such as normalization, feature triangle construction, angle selection, and quantization. The following capabilities are demonstrated as follows: (1) leveraging angle-based features ensures resistance to common geometric transformations, including rotation, uniform scaling, and translation; (2) incorporating normalization effectively eliminates distortions caused by non-uniform scaling; and (3) adopting principles from the Douglas–Peucker algorithm enables resilience against interpolation and simplification attacks. Experimental results validate the theoretical advantages of the proposed method, highlighting its superior overall robustness compared to existing algorithms.
Moreover, introducing the multi-instance scheme broadens the theoretical and technical scope of robustness in zero watermarking. This study also discusses an adaptation to extend the algorithm’s applicability to two-vertex polylines, further demonstrating its flexibility and practicality for diverse vector geographic data. Future research could explore ways to improve scalability and integrate the algorithm into distributed GIS platforms and cloud-based services to support large-scale applications.
Author Contributions
Conceptualization, Qifei Zhou, Lin Yan and Na Ren; methodology, Qifei Zhou and Na Ren; software, Lin Yan and Zihao Wang; validation, Qifei Zhou and Changqing Zhu; formal analysis, Lin Yan and Qifei Zhou; resources, Qifei Zhou; writing—original draft preparation, Qifei Zhou and Na Ren; writing—review and editing, Na Ren and Changqing Zhu; visualization, Zihao Wang; supervision, Changqing Zhu and Na Ren; funding acquisition, Qifei Zhou and Na Ren. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China under Grant 2023YFB3907100, the National Natural Science Foundation of China under Grant 42301482, Hunan Provincial Natural Science Foundation of China under Grant 2024JJ8365, and the Open Topic of Hunan Engineering Research Center of Geographic Information Security and Application under Grant HNGISA2023002.
Data Availability Statement
The data presented in this study are openly available in the GitHub repository at https://github.com/zhouqf01/Multi-Instance-Zero-Watermarking.git (accessed on 4 December 2024).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Dai, Q.; Wu, B.; Liu, F.; Bu, Z.; Zhang, H. Commutative Encryption and Reversible Watermarking Algorithm for Vector Maps Based on Virtual Coordinates. ISPRS Int. J. Geo-Inf. 2024, 13, 338. [Google Scholar] [CrossRef]
- AL-ardhi, S.; Thayananthan, V.; Basuhail, A. A New Vector Map Watermarking Technique in Frequency Domain Based on LCA-Transform. Multimed. Tools Appl. 2020, 79, 32361–32387. [Google Scholar] [CrossRef]
- Abubahia, A.; Cocea, M. Advancements in GIS Map Copyright Protection Schemes—A Critical Review. Multimed. Tools Appl. 2017, 76, 12205–12231. [Google Scholar] [CrossRef]
- Tantriawan, H.; Munir, R. Watermarking Study on The Vector Map. Indones. J. Artif. Intell. Data Min. 2023, 6, 84. [Google Scholar] [CrossRef]
- Qiu, Y.; Zheng, J.; Xiao, Q.; Luo, J.; Duan, H. Construct Self-Correcting Digital Watermarking Model for Vector Map Based on Error-Control Coding. Geomat. Inf. Sci. Wuhan Univ. 2025, 50, 164–173. [Google Scholar] [CrossRef]
- Tareef, A.; Al-Tarawneh, K.; Sleit, A. Block-Based Watermarking for Robust Authentication and Integration of GIS Data. Eng. Technol. Appl. Sci. Res. 2024, 14, 16340–16345. [Google Scholar] [CrossRef]
- Zhou, Q. Lossless Watermarking Algorithms for Vector Geographic Data Based on Characteristics of Features; Nanjing Normal University: Nanjing, China, 2022. [Google Scholar]
- Peng, Z.; Yue, M.; Wu, X.; Peng, Y. Blind Watermarking Scheme for Polylines in Vector Geo-Spatial Data. Multimed. Tools Appl. 2015, 74, 11721–11739. [Google Scholar] [CrossRef]
- Douglas, D.H.; Peucker, T.K. Algorithms for the Reduction of the Number of Points Required to Represent a Digitized Line or Its Caricature. Cartogr. Int. J. Geogr. Inf. Geovisualization 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Lyu, X.; Ren, N.; Zhou, Q.; Zhu, C. A Digital Watermark Algorithm Suitable for OpenDrive Format High Precision Maps under Invisible Characters. J. Geo-Inf. Sci. 2024, 26, 1–12. [Google Scholar] [CrossRef]
- Zhou, Q.; Ren, N.; Zhu, C.; Zhu, A.-X. Blind Digital Watermarking Algorithm against Projection Transformation for Vector Geographic Data. ISPRS Int. J. Geo-Inf. 2020, 9, 692. [Google Scholar] [CrossRef]
- Wen, Q.; Sun, T.F.; Wang, S.X. Concept and Application of Zero-Watermark. Acta Electron. Sin. 2003, 31, 214–216. [Google Scholar]
- Xi, X.; Hua, Y.; Chen, Y.; Zhu, Q. Zero-Watermarking for Vector Maps Combining Spatial and Frequency Domain Based on Constrained Delaunay Triangulation Network and Discrete Fourier Transform. Entropy 2023, 25, 682. [Google Scholar] [CrossRef]
- Shaik, A.; Masilamani, V. Zero-Watermarking in Transform Domain and Quadtree Decomposition for Under Water Images Captured by Robot. Procedia Comput. Sci. 2018, 133, 385–392. [Google Scholar] [CrossRef]
- Zhang, Z.; Sun, S.; Wang, Y.; Zheng, K. Zero-Watermarking Algorithm for 2D Vector Map. Comput. Eng. Des. 2009, 30, 1473–1476. [Google Scholar] [CrossRef]
- Wang, X.; Huang, D.; Zhang, Z. A Robust Zero-Watermarking Algorithm for Vector Digital Maps Based on Statistical Characteristics. J. Softw. 2012, 7, 2349–2356. [Google Scholar] [CrossRef]
- Fan, Y.; Chai, J.; Han, Z.; Tian, C. A Zero-Watermarking Algorithm Based on Minimum Quad-Tree Division and Feature Angle. Geomat. Spat. Inf. Technol. 2018, 41, 1–4. [Google Scholar]
- Li, A.; Zhu, A.-X. Copyright Authentication of Digital Vector Maps Based on Spatial Autocorrelation Indices. Earth Sci. Inform. 2019, 12, 629–639. [Google Scholar] [CrossRef]
- Peng, Y.; Yue, M. A Zero-Watermarking Scheme for Vector Map Based on Feature Vertex Distance Ratio. J. Electr. Comput. Eng. 2015, 2015, 1–6. [Google Scholar] [CrossRef]
- Tan, T.; Zhang, L.; Zhang, M.; Wang, S.; Wang, L.; Zhang, Z.; Liu, S.; Wang, P. Commutative Encryption and Watermarking Algorithm Based on Compound Chaotic Systems and Zero-Watermarking for Vector Map. Comput. Geosci. 2024, 184, 105530. [Google Scholar] [CrossRef]
- Zhou, Q.; Zhu, C.; Ren, N.; Chen, W.; Gong, W. Zero Watermarking Algorithm for Vector Geographic Data Based on the Number of Neighboring Features. Symmetry 2021, 13, 208. [Google Scholar] [CrossRef]
- Xi, X.; Zhang, X.; Liang, W.; Xin, Q.; Zhang, P. Dual Zero-Watermarking Scheme for Two-Dimensional Vector Map Based on Delaunay Triangle Mesh and Singular Value Decomposition. Appl. Sci. 2019, 9, 642. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, L.; Zhang, Q.; Li, Y. A Zero-Watermarking Algorithm for Vector Geographic Data Based on Feature Invariants. Earth Sci. Inform. 2023, 16, 1073–1089. [Google Scholar] [CrossRef]
- Kim, J. Robust Vector Digital Watermarking Using Angles and a Random Table. Int. J. Adv. Inf. Sci. Serv. Sci. 2010, 2, 79–90. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, F.; Gao, K.; Dong, W.; Song, J. A Zero-Watermarking Scheme with Embedding Timestamp in Vector Maps for Big Data Computing. Clust. Comput. 2017, 20, 3667–3675. [Google Scholar] [CrossRef]
- Peng, F.; Jiang, W.-Y.; Qi, Y.; Lin, Z.-X.; Long, M. Separable Robust Reversible Watermarking in Encrypted 2D Vector Graphics. IEEE Trans. Circuits Syst. Video Technol. 2020, 30, 2391–2405. [Google Scholar] [CrossRef]
- Zhang, L. On Digital Watermarking Algorithms for Vector Geospatial Data; Lanzhou Jiaotong University: Lanzhou, China, 2016. [Google Scholar]
- Yan, H.; Zhang, L.; Yang, W. A Normalization-Based Watermarking Scheme for 2D Vector Map Data. Earth Sci. Inform. 2017, 10, 471–481. [Google Scholar] [CrossRef]
- Xiong, Y.; Wang, R. An Audio Zero-Watermark Algorithm Combined DCT with Zernike Moments. In Proceedings of the 2008 International Conference on Cyberworlds, Hangzhou, China, 22–24 September 2008; pp. 11–15. [Google Scholar]
- Dong, S.; Li, J.; Liu, S. Frequency Domain Digital Watermark Algorithm Implemented in Spatial Domain Based on Correlation Coefficient and Quadratic DCT Transform. In Proceedings of the 2016 International Conference on Progress in Informatics and Computing (PIC), Shanghai, China, 23–25 December 2016; pp. 596–600. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).