PGTFT: A Lightweight Graph-Attention Temporal Fusion Transformer for Predicting Pedestrian Congestion in Shadow Areas

Abstract

Forecasting pedestrian congestion in urban back streets is challenging due to “shadow areas” where CCTV coverage is absent and trajectory data cannot be directly collected. To address these gaps, we propose the Peak-aware Graph-attention Temporal Fusion Transformer (PGTFT), a lightweight hybrid model that extends the Temporal Fusion Transformer by integrating a non-parametric attention-based Graph Convolutional Network, a peak-aware Gated Residual Network, and a Peak-weighted Quantile Loss. The model leverages both physical connectivity and functional similarity between roads through a fused adjacency matrix, while enhancing sensitivity to high-congestion events. Using real-world trajectory data from 38 CCTVs in Anyang, South Korea, experiments show that PGTFT outperforms LSTM, TFT, and GCN-TFT across different sparsity settings. Under sparse 5 m neighbor conditions, the model achieved the lowest MAE (0.059) and RMSE (0.102), while under denser 30 m settings it maintained superior accuracy with standard quantile loss. Importantly, PGTFT requires only 1.54 million parameters—about half the size of conventional Transformer–GCN hybrids—while delivering equal or better predictive performance. These results demonstrate that PGTFT is both parameter-efficient and robust, offering strong potential for deployment in smart city monitoring, emergency response, and transportation planning, as well as a practical approach to addressing data sparsity in urban sensing systems.

1. Introduction

In densely populated cities, road networks consist not only of major arterial roads but also of narrow and intricately connected back streets within residential areas. As these back streets serve as vital components of everyday urban life, the deployment of CCTV for crime prevention, public safety, and integrated monitoring has increased markedly in recent years. Trajectory data collected from these systems are now widely used for applications such as pedestrian congestion estimation, anomaly detection, and illegal parking analysis [1,2,3,4,5,6].

For effective monitoring, CCTV cameras should ideally be installed at intervals of about 30 m, corresponding to their typical range. In practice, however, comprehensive coverage is infeasible due to installation and maintenance costs. As a result, CCTV is often concentrated along major roads, leaving many alleys and narrow streets unmonitored. These “shadow areas” create gaps in observational data and limit the ability to capture congestion patterns.

Addressing this challenge requires predictive models capable of inferring pedestrian congestion in shadow areas based on sparse and partially observed data. Accurate estimation in such contexts would contribute to the early prevention of accidents and other risks, while also supporting broader smart city initiatives. Recent advances in graph-based deep learning and Transformer architectures have demonstrated strong performance for road network modeling by exploiting connectivity, correlation, and spatial dependency [7,8,9,10,11,12,13,14]. Yet most existing approaches assume relatively dense and uniformly distributed data, focusing on arterial roads with near-complete coverage. Research on congestion forecasting under sparse conditions remains limited, and studies specifically targeting shadow areas are particularly scarce [15,16,17].

To fill this gap, we propose the Peak-aware Graph-attention Temporal Fusion Transformer (PGTFT), a lightweight hybrid model that integrates a non-parametric attention-based Graph Convolutional Network (GCN) with the Temporal Fusion Transformer (TFT). The model leverages both physical and semantic relationships among road segments and incorporates a peak-weighted loss function to improve accuracy during high-risk congestion periods. By focusing on environments where continuous monitoring is infeasible, PGTFT addresses the overlooked but socially significant issue of sparse surveillance coverage in urban back streets, offering a practical step toward safer and more cost-efficient smart city monitoring.

The main contributions of this study are as follows. First, we present a hybrid deep learning model—PGTFT—that integrates a non-parametric attention-based GCN with a modified TFT. Unlike conventional graph–temporal models, our approach introduces a soft-attention mechanism that dynamically assigns edge weights based on input statistics rather than parameterized attention, thereby capturing both structural connectivity and functional similarity between road segments. Second, we propose a hybrid adjacency matrix that combines topological proximity (hop distance) with semantic similarity (cosine similarity of congestion distributions), allowing the model to account for non-local but behaviorally similar road segments. Third, we introduce a peak-aware learning strategy, including a novel Peak-weighted Quantile Loss (PWQL), which enhances sensitivity to high-congestion periods that are critical for real-time monitoring and public safety management. To the best of our knowledge, this is the first study to dynamically weight the loss function based on observed congestion magnitudes rather than static attributes.

The remainder of this paper is organized as follows. Section 2 reviews related work on graph- and Transformer-based models in traffic and spatial analytics. Section 3 details the architecture of PGTFT. Section 4 presents experimental results using a pedestrian congestion dataset collected from urban back streets, including comparisons with baseline models such as TFT [15], GCN-TFT [16], and LSTM [17], as well as an ablation study. Section 5 concludes with implications and directions for future research.

2. Related Works

Recent studies have increasingly explored the use of Transformer and GCN models—two core components of the proposed framework—for traffic flow prediction and sparse-data inference. Attention-based Transformer architectures, which have demonstrated strong performance across multiple domains, have been widely adopted for traffic forecasting [15,18,19,20,21]. In parallel, GCN-based approaches that model road networks as graphs have been applied to traffic prediction, congestion estimation, and sparse-data analysis [11,22,23,24].

GCNs are widely used for capturing spatial dependencies in structured data such as those of road networks. Yu et al. [22] formulated traffic prediction as a time-series problem over a graph and proposed ST-GCN, a purely convolutional model without recurrent structures, which alternates temporal and spatial graph convolutions to capture spatiotemporal patterns. Zhao et al. [11] combined GCN and GRU to jointly model spatial and temporal features, while Ding et al. [24] introduced IDG-PSAtt, which employs a dynamically learned spatiotemporal graph structure with a probabilistic sparse self-attention mechanism. These approaches highlight the flexibility of GCNs in representing road connectivity and spatiotemporal interactions.

Transformer architectures and their variants are particularly effective for long-term time-series forecasting and have been widely applied to traffic prediction. Wang et al. [20] proposed the Spatiotemporal Fusion Transformer (STFT), which incorporates seasonality encoding, tubelet embedding for efficiency, and a diffusion-based token permutator for regional traffic forecasting. Xu et al. [19] developed Spatial-Temporal Transformer Networks (STTN), alternating between spatial and temporal Transformers to capture directional dependencies and long-range dynamics. Zhang et al. [25] designed a Sparse Attention-based Transformer to improve prediction in congestion-prone segments, while He et al. [18] introduced TEA-GCN, which combines Transformer layers with an adaptive GCN module and local-global temporal attention for dynamic spatiotemporal learning. Among these, the TFT proposed by Lim et al. [15] has become a widely adopted framework for complex time-series forecasting, integrating static covariate encoders, variable selection networks, and multi-head attention. Li et al. [16] further extended TFT by incorporating GCN to model graph structures in spatiotemporal data.

In urban environments, traffic data from back streets are often sparse or incomplete due to limited sensor deployment and high infrastructure costs, which has prompted increasing interest in methods to address these gaps. Tan et al. [26] used matrix completion with day-mode similarity to impute missing data, while Sun et al. [27] improved prediction in low-data regions by transferring models trained on data-rich areas. Kong et al. [28] proposed GraphSparceNet (GSNet), a scalable GNN with linear time and space complexity, designed to balance efficiency with predictive accuracy in large-scale traffic datasets.

Despite these advances, high-precision predictions still require dense, fine-grained data at the node and edge level. For back streets, however, physical limitations and sparse sensor coverage make it difficult to collect such structured data. Consequently, congestion forecasting in shadow areas remains severely constrained. Moreover, models trained on datasets from arterial roads often fail to capture the unique spatial and contextual dynamics of back streets. To address these challenges, it is essential to develop models tailored to sparse conditions and trained with data that reflect the specific characteristics of such environments. This study responds to this need by proposing a sparse-data-based predictive model designed to operate effectively in shadow areas with limited information.

3. Proposed Method

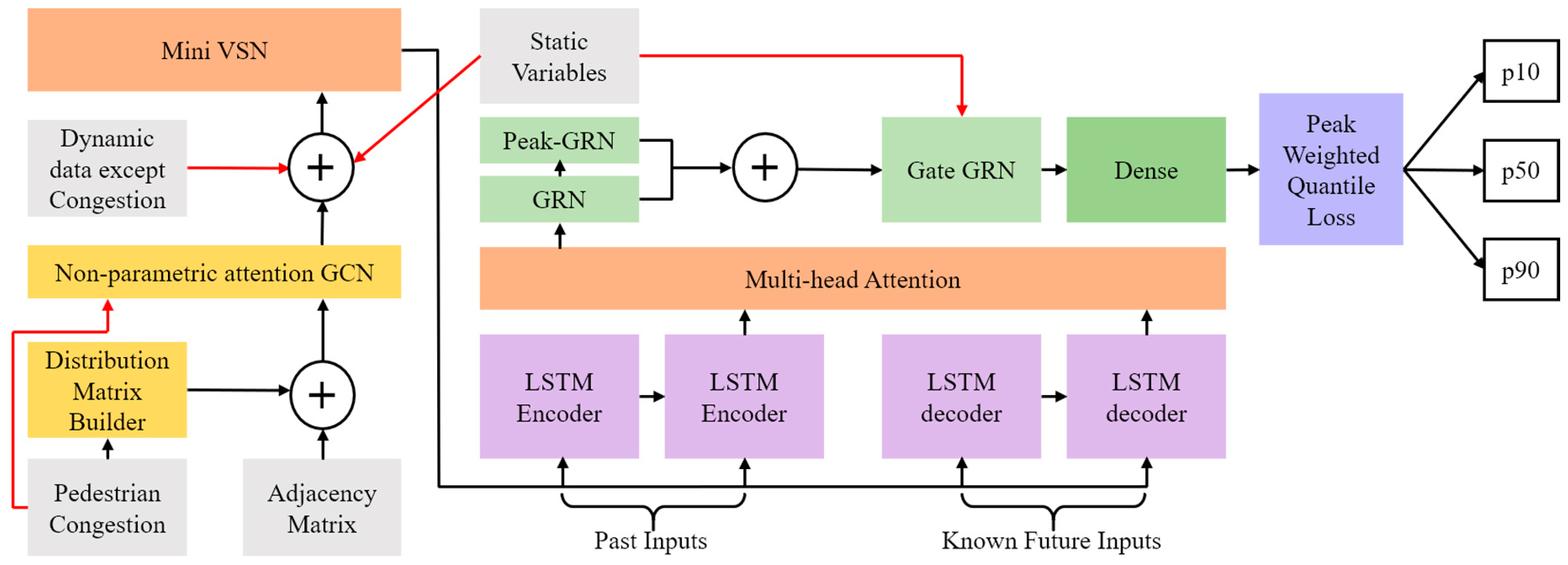
This study proposes the PGTFT, a fusion deep learning model designed to jointly learn the structural connectivity of road networks and the irregular volatility of sparse data (Figure 1). PGTFT builds upon the TFT introduced by Lim et al. [15], extending it to integrate time-series forecasting with road network structures.

TFT consists of key components such as the Variable Selection Network (VSN), GRN, and interpretable multi-head attention, which together provide strong capabilities for modeling both dynamic temporal patterns and static contextual features. While retaining these strengths, PGTFT introduces several modifications and simplifications to better address the unique characteristics of pedestrian and vehicle data collected from sparsely monitored and highly variable back streets.

The major architectural innovations of PGTFT are as follows:

• Non-parametric attention GCN: A non-parametric attention mechanism is incorporated into the GCN to dynamically estimate the relative influence of road segments based on structural connectivity.
• Hybrid adjacency matrix: To capture both topological proximity and functional similarity, PGTFT combines hop-based adjacency with cosine similarity of congestion distributions, enabling more precise modeling of inter-road interactions.
• Simplified variable selection: Recognizing the limited informativeness of static features in back street environments, the original VSN is simplified to avoid unnecessary re-learning and reduce computational overhead.
• Lightweight attention mechanism: The static enrichment step in TFT’s interpretable attention module is removed, retaining only the attention weight outputs to balance accuracy with computational efficiency.
• Peak-aware GRN: An additional GRN module is used to re-encode high and low attention values from the multi-head attention block, enhancing sensitivity to congestion peaks in time-series data.
• PWQL: Replacing the standard quantile loss, the proposed loss function emphasizes peak values, improving prediction performance for high-congestion segments that are critical for real-time urban monitoring.

3.1. PGTFT

3.1.1. Non-Parametric Attention GCN

In this study, we introduce a lightweight attention mechanism into the GCN by applying GELU activation and softmax normalization to the output of the fused adjacency matrix and input features prior to linear transformation. This design simplifies the attention mechanism of the Graph Attention Network (GAT) [29] while retaining its essential functionality. Equation (1) illustrates how GAT computes the attention coefficient between a target node i and its neighboring nodes $N_i$. GAT uses masked attention to avoid full pairwise computation, but the cost still increases with the number of neighbors. Let ${\overrightarrow{h}}_i$ and ${\overrightarrow{h}}_j$ denote the input features of nodes i and j respectively, $\mathit{W}$ a shared linear transformation, and $\overrightarrow{a}$ a learnable vector:

$$\begin{array}{c}{\alpha }_{ij}={\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}}_j\left(e_{ij}\right)={\displaystyle \frac{\exp \left(e_{ij}\right)}{{\sum }_{k\in N_i}\exp \left(e_{ik}\right)}}\\ e_{ij}=\mathrm{LeakyReLU}({\overrightarrow{a}}^{\top }[\mathit{W}{\overrightarrow{h}}_i||\mathit{W}{\overrightarrow{h}}_j])\end{array}$$

(1)

To better handle real-time, congestion-sensitive data, our model replaces the pairwise operations with matrix multiplication and introduces the GELU activation [30], which probabilistically suppresses less relevant signals while enhancing informative ones. In the subsequent GCN layer, the attention coefficients are used for message passing. Following Kipf and Welling [31], who noted that activation functions in GCNs can be flexibly chosen, we adopt the Swish (SiLU) activation [32] for its self-gating and gradient-friendly properties:

$$\begin{array}{c}\mathit{W}=\mathrm{Softmax}\left(\mathrm{GELU}\left(\mathit{A}·\mathit{X}\right)\right)\\ {\mathit{H}}_{out}=\mathrm{SiLU}\left(\mathit{W}·{\mathit{W}}_{lin}+\mathit{b}\right)\end{array}$$

(2)

where $\mathit{A}$ is the fused adjacency matrix, $\mathit{X}$ is the input feature matrix, and $\mathit{W}$ and $\mathit{b}$ the attention-like weights and bias. GELU is defined as $\mathrm{G}\mathrm{E}\mathrm{L}\mathrm{U}\left(x\right)=x\cdot \mathsf{\Phi }\left(x\right)$, where $\mathsf{\Phi }\left(x\right)$ is the Gaussian cumulative distribution function, and SiLU as $\mathrm{S}\mathrm{i}\mathrm{L}\mathrm{U}\left(x\right)=x\cdot \sigma \left(x\right)$, where $\sigma \left(x\right)$ is the sigmoid function.

This non-parametric attention design offers several advantages. Unlike conventional GCNs, which aggregate neighbor features using fixed adjacency weights, our model dynamically generates softmax-based importance scores directly from the inputs. In contrast to GAT, where attention coefficients are learned as parameters, our approach derives them non-parametrically, reducing computational cost while preserving flexibility. The combination of GELU and SiLU further improves gradient flow, resulting in more stable and effective training.

3.1.2. Hybrid Adjacency Matrix

In a GCN, the input consists of two main components: the node feature matrix X and the adjacency matrix A, which defines the connectivity between nodes. In this study, node features are defined as the congestion levels of the six nearest neighboring roads surrounding each target shadow road. The adjacency matrix is initially constructed with weights determined by hop distance (Algorithm 1). The selection of six neighbors reflects a one-hop configuration—three adjacent nodes on each side when a shadow node lies between two intersections. If fewer than six one-hop neighbors exist, we progressively include the nearest nodes from higher-order neighborhoods (up to five hops). Any remaining vacancies are zero-padded to preserve a fixed input size, and padded nodes are excluded from adjacency computations.

Algorithm 1 Compute Adjacency Matrix based on Hop Distance Similarity.

Require: neighbors data: list of neighbor nodes with id and hop attributes

Require: top n: number of neighbors (including padding)

Ensure: adj: adjacency matrix of size top n × top n

1: Initialize adj ← zero matrix of size top n × top n

2: for i = 1 to top n do

3:  if neighbors data[i].id = ‘PAD’ then

4:     continue

5:  end if

6:  hop i ← neighbors data[i].hop

7:  for j = 1 to top n do

8:     if neighbors data[j].id = ‘PAD’ then

9:     continue

10:   end if

11:   hop j ← neighbors data[j].hop

12:   hop difference ← |hop i − hop j|

13:   node-to-node similarity ← 1/(1 + hop difference)

14:   adj[i][j] ← node-to-node similarity

15:   end for

16:   adj[i][i] ← 1.0

17: end for

18: return adj

The hop-based adjacency matrix ${\mathit{A}}^{\left(hop\right)}$ measures similarity between nodes according to the difference in hop distance from the target node. Specifically, the weight between nodes i and j is defined as:

$${\mathit{A}}_b^{\left(\mathit{hop}\right)}={\mathit{A}}_{ij}={\displaystyle \frac{1}{1+\left|{\mathrm{h}\mathrm{o}\mathrm{p}}_i-{\mathrm{h}\mathrm{o}\mathrm{p}}_j\right|}}$$

(3)

In graph-based deep learning, adjacency matrices typically assign weights in the range [0, 1] to capture spatial proximity. However, hop distance alone may not fully represent the complexity of real-world interactions. To incorporate functional similarity, we compute a distribution feature vector for each neighboring road segment based on statistical descriptors of congestion: mean ${\mu }_{b,n}$, standard deviation ${\sigma }_{b,n}$, skewness ${\mathit{Skew}}_{b,n}$, and kurtosis ${\mathit{Kurt}}_{b,n}$:

$$\begin{array}{c}\mathbf{X}\in {\mathbb{R}}^{B\times T\times N}\\ {\mu }_{b,n}={\displaystyle \frac{1}{T}}{\displaystyle \sum _{t=1}^T}{\mathbf{X}}_{b,t,n},\hspace{1em}\hspace{1em}{\sigma }_{b,n}=\sqrt{{\displaystyle \frac{1}{T}}{\displaystyle \sum _{t=1}^T}{\left({\mathbf{X}}_{b,t,n}-{\mu }_{b,n}\right)}^2+ϵ}\\ {Skew}_{b,n}={\displaystyle \frac{1}{T}}{\displaystyle \sum _{t=1}^T}{\left({\displaystyle \frac{{\mathbf{X}}_{b,t,n}-{\mu }_{b,n}}{{\sigma }_{b,n}}}\right)}^3,\hspace{1em}\hspace{1em}{Kurt}_{b,n}={\displaystyle \frac{1}{T}}{\displaystyle \sum _{t=1}^T}{\left({\displaystyle \frac{{\mathbf{X}}_{b,t,n}-{\mu }_{b,n}}{{\sigma }_{b,n}}}\right)}^4\\ {\mathbf{f}}_{\mathrm{b},\mathrm{n}}=\left[{\mu }_{b,n},{\sigma }_{b,n},{Skew}_{b,n},{Kurt}_{b,n}\right]\in {\mathbb{R}}^4,\hspace{1em}\hspace{1em}{\mathbf{F}}_b={\left[{\mathbf{f}}_{b,1},\cdots ,{\mathbf{f}}_{b,N}\right]}^{\mathrm{\top }}\end{array}$$

(4)

Using these descriptors, we construct a distribution-based adjacency matrix ${\mathit{A}}^{\left(\mathit{dist}\right)}$ by computing cosine similarity between normalized feature vectors:

$${\mathit{A}}_b^{\left(\mathit{dist}\right)}=\cos \left({\mathbf{F}}_b,{\mathbf{F}}_b\right)={\widehat{\mathbf{F}}}_b·{\widehat{\mathbf{F}}}_b^{\top }\in {\mathbb{R}}^{N\times N}, {\widehat{\mathbf{f}}}_{b,n}={\displaystyle \frac{{\mathbf{f}}_{b,n}}{ \parallel {\mathbf{f}}_{b,n}{\parallel }_2}}$$

The final fused adjacency matrix is defined as a weighted average of the hop-based and distribution-based matrices:

$${\mathit{A}}_b=\alpha ·{\mathit{A}}_b^{\left(\mathit{hop}\right)}+\left(1-\alpha \right)·{\mathit{A}}_b^{\left(\mathit{dist}\right)}, \alpha \in [\mathrm{0,1}]$$

(5)

This design allows the model to capture both physical and functional relationships between roads. For example, (1) physically adjacent roads may exert varying influence depending on the similarity of their congestion patterns, and (2) physically distant roads may still strongly influence a target road if their congestion profiles are functionally similar.

3.1.3. MiniVSN

In the standard TFT architecture, the VSN and the Static Covariate Encoder employ a GRN to extract salient features from the input variables. As defined in Equation (6), the GRN alleviates the vanishing gradient problem through a Gated Linear Unit (GLU [33]) and dynamically adjusts the contribution of each variable. Specifically, $\mathit{a}$ denotes the input data, $\mathit{c}$ the contextual vector, ${\mathit{W}}_{\left(.\right)}$ and ${\mathit{b}}_{\left(.\right)}$ the trainable weights and biases, and ⨀ the element-wise Hadamard product.

$$\begin{array}{c}{\mathrm{G}\mathrm{R}\mathrm{N}}_{\omega }\left(\mathit{a},\mathit{c}\right)=\mathrm{L}\mathrm{a}\mathrm{y}\mathrm{e}\mathrm{r}\mathrm{N}\mathrm{o}\mathrm{r}\mathrm{m}\left(\mathit{a}+{\mathrm{G}\mathrm{L}\mathrm{U}}_{\omega }\left({\mathit{\eta }}_1\right)\right),\\ {\mathit{\eta }}_1={\mathit{W}}_{1,\omega } {\mathit{\eta }}_2+{\mathit{b}}_{1,\omega }, \\ {\mathit{\eta }}_2=\mathrm{E}\mathrm{L}\mathrm{U}\left({\mathit{W}}_{2,\omega } \mathit{a}+{\mathit{W}}_{3,\omega } \mathit{c}+{\mathit{b}}_{2,\omega }\right),\\ {\mathrm{G}\mathrm{L}\mathrm{U}}_{\omega }\left(\mathit{\gamma }\right)=\sigma \left({\mathit{W}}_{4,\omega } \mathit{\gamma }+{\mathit{b}}_{4,w}\right)\odot \left({\mathit{W}}_{5,\omega } \mathit{\gamma }+{\mathit{b}}_{5,\omega }\right)\end{array}$$

(6)

While this architecture is highly effective for large-scale time-series tasks, uniformly applying such complexity to sparse datasets may reduce efficiency and robustness. To address this, we propose a simplified VSN (miniVSN) tailored for sparse pedestrian data.

Given $\mathbf{X}\in {\mathbb{R}}^{B\times T\times N\times D}$, where B is batch size, T the sequence length, N the number of variables, and $D$ the feature dimension, miniVSN computes variable importance scores and weighted representations through lightweight operations. Specifically, a dot product between each variable representation ${\mathbf{h}}_{b,t,i}$ and a learnable vector $\mathit{w}$ yields a scalar importance score, which is normalized across variables using softmax. A corresponding weighted representation $s_2$ is then derived, and both outputs are aggregated via a weighted sum:

$$\begin{array}{c}{s}_1={\mathbf{h}}_{b,t,i}^{\top }·\mathit{w}+b,\hspace{1em}\hspace{1em}{s}_2={\mathbf{x}}_{b,t,i}^{\top }·{\mathit{w}}_i+b_i\\ {\mathrm{m}\mathrm{i}\mathrm{n}\mathrm{i}\mathrm{V}\mathrm{S}\mathrm{N}}_{b,t}={\displaystyle \sum _{i=1}^N}{\mathrm{s}\mathrm{o}\mathrm{f}\mathrm{t}\mathrm{m}\mathrm{a}\mathrm{x}}_i\left(s_1\right)·s_2\end{array}$$

(7)

Through this process, miniVSN assigns higher weights to informative features while suppressing less relevant ones, thereby producing a refined representation with substantially lower computational cost. This design allows PGTFT to selectively emphasize the most critical variables for prediction while avoiding the overhead of full GRN-based selection.

3.1.4. Peak Aware GRN

In the original TFT, contextual information is not only processed in the VSN but also further refined in the GRN together with outputs from the multi-head attention mechanism, thereby enriching temporal features. This design is effective for large and diverse datasets; however, in road networks with sparse coverage and limited variability across segments, static data often provides little additional information. In such settings, emphasizing peak patterns in the time series becomes more valuable than repeatedly propagating static features.

To this end, we introduce a Peak-aware GRN, an additional operation that strengthens peak-related signals by reusing the output of the multi-head attention layer and its gating mechanism. Specifically, the attention output ${\mathit{A}}_{attn}$ is first processed through a GRN to reinforce baseline temporal context. The same output is then reused as both input and context in a secondary GRN, denoted as ${\mathrm{GRN}}_{peak}$, to further amplify peak patterns. This process is defined as:

$$\begin{array}{c}\mathrm{P}\mathrm{e}\mathrm{a}\mathrm{k} \mathrm{A}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{e}={\mathrm{G}\mathrm{R}\mathrm{N}}_{peak}\left({\mathit{A}}_{attn},{\mathit{A}}_{attn}\right)\\ {\mathit{A}}_{enhanced}={\mathit{A}}_{attn}+\mathrm{P}\mathrm{e}\mathrm{a}\mathrm{k} \mathrm{A}\mathrm{w}\mathrm{a}\mathrm{r}\mathrm{e}\end{array}$$

(8)

By explicitly reinforcing peaks, the model captures sharp variations in congestion more effectively, which is particularly important for real-time monitoring in narrow urban back streets where sudden fluctuations pose safety and management challenges.

3.2. Loss Function: Peak Weighted Quantile Loss

The original TFT adopts the quantile loss function proposed by Zhou [34], shown in Equation (9). Quantile loss evaluates errors at multiple quantile levels (e.g., 10th, 50th, 90th percentiles), making it robust to non-Gaussian distributions and more resilient to over- and under-estimation compared to conventional losses such as Mean Squared Error. Let $\Omega$ denote the training dataset with M samples, W the model parameters, and Q the set of target quantiles:

$$\begin{array}{c}L\left(\Omega ,W\right)={\displaystyle \sum _{y_t\in \Omega }}{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{\tau =1}^{{\tau }_{max}}}{\displaystyle \frac{\mathrm{Q}\mathrm{L}\left(y_t,\widehat{y}\left(q,t-\tau ,\tau \right),q\right)}{M{\tau }_{max}}}\\ \mathrm{Q}\mathrm{L}\left(y,\widehat{y},q\right)={q\left(y-\widehat{y}\right)}_{+}+{\left(1-q\right)\left(\widehat{y}-y\right)}_{+},\hspace{1em}\hspace{1em}q\in Q\\ {\left(.\right)}_{+}=max\left(0,.\right)\end{array}$$

(9)

Building on this framework, PGTFT introduces the PWQL to improve prediction accuracy in high-congestion scenarios. PWQL amplifies the penalty for larger target values, making the model more sensitive to peak regions. As defined in Equation (10), the quantile loss is scaled by a weighting function $w\left(y_t\right),$ where the coefficient $\alpha \in \left[\mathrm{0,1}\right]$ controls the degree of emphasis. In this study, $\mathsf{\alpha }=0.7$.

$$\begin{array}{c}L\left(\Omega ,W\right)={\displaystyle \sum _{y_t\in \Omega }}{\displaystyle \sum _{q\in Q}}{\displaystyle \sum _{\tau =1}^{{\tau }_{max}}}{\displaystyle \frac{\mathrm{P}\mathrm{W}\mathrm{Q}\mathrm{L}}{M{\tau }_{max}}}\\ \mathrm{P}\mathrm{W}\mathrm{Q}\mathrm{L}=w\left(y_t\right)·\mathrm{Q}\mathrm{L}\left(y,\widehat{y},q\right)\\ {\left(.\right)}_{+}=max\left(0,.\right)\\ w\left(y_t\right)=1+\alpha ·y_t\end{array}$$

(10)

Unlike conventional weighted quantile loss functions that adjust weights based on sample reliability or predefined importance, PWQL directly uses the target value to determine the weight. To the best of our knowledge, this is the first study to adopt such a strategy, representing a key methodological contribution. Notably, when $q=0.5$, quantile loss reduces to the Mean Absolute Error (MAE). Consistent with the original TFT, experiments in this study were conducted using $Q=\{0.1,0.5,0.9\}$.

4. Performance Evaluation

4.1. Datasets

The dataset used in this study was derived from pedestrian and vehicle trajectories collected at one-second intervals from 38 CCTVs installed in the Indeokwon area of Anyang, Republic of Korea, between 20 and 27 May 2024. Congestion values were computed at one-minute intervals.

Congestion was quantified by estimating the minimum spatial area required for each moving entity based on instantaneous speed, direction, and acceleration. At each time step, the Time to Collision (TTC) was calculated between the current and predicted positions one second ahead. From this, a minimum safety buffer was derived for each entity, representing the region in which it could move without risk of collision. The union of all safety buffers was then computed, and its ratio to the total road area defined the congestion level. In total, the dataset includes 387,427 pedestrian trajectories and 317,990 vehicle trajectories, yielding 62,223,691 spatio-temporal points. Details of the calculation process are available in [1].

As shown in Figure 2, the presence of numerous shadow nodes results in substantial data sparsity across the study area. Figure 3 presents a one-hour aggregated heatmap, illustrating distinct spatial and temporal variations in congestion across back streets. Because ground-truth values are unavailable for shadow nodes, a masking strategy was employed for model evaluation: nodes with observed values were temporarily treated as unobserved, their congestion inferred from neighboring nodes, and predictions compared against actual observations.

For each target road segment, the six nearest adjacent roads were used as reference inputs. The prediction task was designed to forecast congestion over the next two hours using the preceding six hours of historical data. Dynamic variables included: (1) pedestrian congestion on adjacent roads, (2) a binary peak-hour indicator, (3) the rate of change in congestion relative to the previous minute, and (4) average congestion across 1-hop neighbors. Static variables included: (1) hop distance from the target road, (2) road length, and (3) road width.

Connectivity within the network was represented by hop counts between road segments. Each CCTV corresponded to a specific road segment (Figure 2). For instance, segment V0002 has four 1-hop neighbors (V0000, V0001, V0003, V9032) and seven 2-hop neighbors (V0005, V0007, V0016, V9028, V9030, V9034, V9051). The six adjacent roads were selected from within a 1–5 hop range, with zero-padded virtual roads added when fewer than six neighbors were available; these padded nodes were excluded from adjacency computations using a padding mask. Peak hours were defined as 07:00–10:00 (morning commute), 12:00–14:00 (lunch), and 17:00–20:00 (evening commute).

4.2. Model Training and Hyperparameters Tuning

All experiments were performed in Python 3.10 using the PyTorch 2.2.2 deep learning framework with CUDA 11.8 for GPU acceleration. Training was performed for up to 20 epochs with a batch size of 12 and a learning rate of 0.001. The hidden dimension was set to 128, with 8 self-attention heads and 2 layers across all experiments. Optimization was carried out using AdamW with an L2 regularization (weight decay) coefficient of 0.001 to improve generalization and stabilize learning by preventing excessively large weight updates.

Model performance was evaluated using both average quantile loss and the proposed PWQL. Quantiles were set to p10, p50, and p90, with losses computed individually and then aggregated. For PWQL, the weighting coefficient α was fixed at 0.7, as comparative experiments with alternative values indicated this setting yielded the best balance of accuracy and stability. Additional experiments analyzed loss behavior with respect to the proportion of padding nodes among the six adjacent road inputs.

To evaluate model robustness under varying levels of data sparsity, we generated two modified datasets by applying distance thresholds of 5 m and 30 m when defining neighboring roads. The 5 m threshold represents a stricter criterion in which only very close neighbors are considered. In dense metropolitan networks, this often results in fewer than six valid neighbors, requiring the use of padding nodes (PAD) to maintain a consistent input size. In contrast, the 30 m threshold relaxes this criterion, allowing more distant neighbors to be included. This setting typically provides sufficient valid neighbors, thereby reducing the proportion of padding nodes and yielding more complete inputs. Comparing model performance under these two scenarios—PAD-dominated inputs at 5 m versus densely observed inputs at 30 m—provides clear insight into how different degrees of input sparsity influence predictive accuracy.

Computational complexity was assessed by comparing the total number of trainable parameters across models, peak GPU memory consumption, and inference time across models, providing a measure of efficiency relative to baseline architectures. All experiments were conducted on a system equipped with an NVIDIA GeForce RTX 3080 Ti GPU (12 GB), a 12-core Intel64 Family 6 Model 151 Stepping 2 CPU, 16 GB of system memory, and Windows 10.

4.3. Benchmarks

To verify the effectiveness of the proposed PGTFT, we conducted comparative experiments with existing time-series and graph-based models, as well as ablation studies to assess the contribution of each component. All experiments were performed on the same dataset with identical input settings and evaluation metrics to ensure fair comparison.

4.3.1. Baseline

Three baseline models were selected:

• LSTM: A recurrent neural network commonly used for time-series forecasting. Performance was evaluated using quantile loss.
• TFT: A Transformer-based model designed for complex time-series tasks. Two versions were tested: one with quantile loss and another with PWQL.
• GCN-TFT: An extension of TFT that incorporates a GCN layer to represent road connectivity through adjacency matrices. This model was also evaluated with both quantile loss and PWQL.

4.3.2. Ablation

To evaluate the impact of each core component, ablation experiments were conducted with the following variants:

• PGTFT-GCN (Q loss): Replaces the non-parametric attention with standard GCN-based spatiotemporal learning, trained with quantile loss.
• PGTFT-GCN (Peak Q loss): Same as above but trained with PWQL.
• PGTFT with non-parametric attention (Q loss): Uses the proposed non-parametric attention module but without peak-weighted loss.
• PGTFT with non-parametric attention (Peak Q loss): The full proposed model, integrating non-parametric attention with peak-weighted loss.

4.4. Evaluation Metrics

Model performance was comprehensively evaluated using 5-fold cross-validation, and the best-performing fold for each model was reported. Prediction accuracy was assessed through MAE, Root Mean Squared Error (RMSE), and Mean Quantile Loss, with quantile-specific errors at the 10th, 50th, and 90th percentiles calculated to reflect the distributional nature of time-series forecasting. These accuracy metrics capture both central tendency and variability, enabling a more detailed evaluation of model robustness in sparse-data settings.

To assess computational efficiency and validate the lightweight design of PGTFT, additional complexity-related metrics were reported. Alongside the total number of trainable parameters, which represents structural compactness, we measured peak GPU memory usage and average inference time. These indicators provide practical evidence of model efficiency, complementing traditional accuracy metrics by highlighting trade-offs between predictive performance and resource consumption. FLOPs were not used, as precise estimation is challenging for attention-based architectures; instead, the selected indicators more directly reflect the computational cost of training and real-time deployment.

By jointly considering accuracy, quantile-based uncertainty, and efficiency measures, the evaluation framework enables a balanced comparison of predictive capability and computational burden across all models.

4.5. Experimental Results

The experimental results are presented in four parts to provide a comprehensive evaluation of the proposed PGTFT model. First, we compare predictive accuracy under different neighbor thresholds and examine how loss functions affect performance (Section 4.5.1). Second, we analyze model compactness and computational efficiency using parameters, GPU memory, and inference time (Section 4.5.2). Third, we present visual comparisons between predicted and observed congestion values as well as quantile-based uncertainty analyses (Section 4.5.3). Finally, we investigate the effect of the fused adjacency matrix by contrasting it with the hop-only design and discussing its implications for different urban contexts (Section 4.5.4).

4.5.1. Performance Under Different Neighbor Thresholds

When the neighbor threshold was set to 5 m, the results (

Table 1. Test performance of benchmark models and PGTFT under the 5 m neighbor threshold.

Model	GCN Type	Loss Type	MAE	RMSE	Mean Loss	50%	90%
LSTM		Q	0.080	0.135	0.025	0.040	0.023
TFT		Q	0.066	0.124	0.023	0.033	0.023
		Peak Q	0.094	0.155	0.035	0.055	0.034
GCN-TFT	GCN	Q	0.069	0.129	0.024	0.035	0.023
		Peak Q	0.075	0.132	0.028	0.044	0.024
PGTFT (Ours)	GCN	Q	0.082	0.170	0.026	0.041	0.022
		Peak Q	0.079	0.139	0.031	0.046	0.034
	Non-parametric attention GCN	Q	0.071	0.130	0.024	0.035	0.021
		Peak Q	0.059	0.102	0.023	0.033	0.018

) show that the proposed PGTFT combined with PWQL achieved the highest overall performance. Incorporating peak values into the loss function proved particularly effective in sparse data environments, as evidenced by the lowest MAE (0.059), lowest RMSE (0.102), and the best 90% quantile loss (0.018), outperforming all baseline models. Under the 30 m threshold, where most neighboring nodes contained valid observations, the best performance across all metrics (MAE, RMSE, and quantile losses) was achieved by PGTFT integrating the non-parametric attention GCN with the standard Quantile Loss (

Table 2. Test performance of benchmark models and PGTFT under the 30 m neighbor threshold.

Model	GCN Type	Loss Type	MAE	RMSE	Mean Loss	50%	90%
LSTM		Q	0.074	0.130	0.024	0.037	0.024
TFT		Q	0.073	0.131	0.025	0.037	0.022
		Peak Q	0.074	0.132	0.032	0.045	0.036
GCN-TFT	GCN	Q	0.081	0.145	0.024	0.041	0.021
		Peak Q	0.073	0.121	0.028	0.043	0.025
PGTFT (Ours)	GCN	Q	0.080	0.154	0.026	0.040	0.024
		Peak Q	0.091	0.165	0.036	0.059	0.032
	Non-parametric attention GCN	Q	0.062	0.115	0.019	0.031	0.016
		Peak Q	0.071	0.123	0.026	0.041	0.022

).

For GCN-TFT, applying PWQL improved MAE and RMSE relative to the standard Quantile Loss, but the latter performed better for mean quantile loss and for the 50% and 90% quantiles. A similar trend was observed for PGTFT, where the standard Quantile Loss produced more stable results when sufficient data were available. These findings suggest that peak-sensitive loss functions are beneficial under sparse conditions, but conventional quantile loss remains more effective in well-observed settings. Notably, PGTFT demonstrated reliable performance even without peak weighting, indicating its robustness across different data densities.

Across both experimental settings, PGTFT consistently outperformed baselines. Under the 5 m threshold, results were comparable to TFT in terms of mean and 50% quantile loss, but the non-parametric attention GCN provided additional advantages by assigning softmax-based importance scores within the graph. This improved performance relative to models with standard GCNs, highlighting the role of non-parametric attention in enhancing accuracy. The Swish activation function, with its self-gating properties, also contributed to superior training stability compared to ReLU.

These results further indicate that, under the 5 m threshold, models trained with PWQL achieved consistently lower errors than those trained with the standard Quantile Loss, confirming the advantage of PWQL for peak detection in sparse settings. In contrast, under the 30 m threshold, the standard Quantile Loss yielded superior performance, suggesting that conventional loss functions remain more effective when sufficient observational data are available.

4.5.2. Model Compactness and Efficiency

Model compactness in this study was evaluated using the total number of trainable parameters, peak GPU memory usage, and average inference time, which together provide practical evidence of computational efficiency beyond predictive accuracy.

Table 3. Five-fold average performance and efficiency of models under the 5 m neighbor threshold.

Model	GCN Type	Loss Type	Mean MAE	Mean RMSE	Mean Peak GRU Memory (MB)	Mean Inference Time (ms)	Total Params
LSTM		Q	0.112 ± 0.028	0.193 ± 0.051	23.45 ± 0.64	0.28 ± 0.02	208,131
TFT		Q	0.107 ± 0.030	0.196 ± 0.057	90.24 ± 9.67	8.88 ± 0.25	3,019,773
		Peak Q	0.113 ± 0.025	0.204 ± 0.045	90.24 ± 9.67	8.69 ± 0.07	3,019,773
GCN-TFT	GCN	Q	0.094 ± 0.023	0.168 ± 0.040	118.37 ± 12.64	9.86 ± 0.78	4,030,189
		Peak Q	0.097 ± 0.022	0.172 ± 0.039	118.37 ± 12.64	9.40 ± 0.07	4,030,189
PGTFT (Ours)	GCN	Q	0.100 ± 0.020	0.179 ± 0.033	65.19 ± 4.98	5.48 ± 0.11	1,540,356
		Peak Q	0.105 ± 0.025	0.186 ± 0.045	65.19 ± 4.98	5.60 ± 0.09	1,540,356
	Non-parametric attention GCN	Q	0.094 ± 0.023	0.167 ± 0.041	65.78 ± 5.10	5.55 ± 0.13	1,540,356
		Peak Q	0.091 ± 0.031	0.162 ± 0.053	65.78 ± 5.10	5.57 ± 0.15	1,540,356

and

Table 4. Five-fold average performance and efficiency of models under the 30 m neighbor threshold.

Model	GCN Type	Loss Type	Mean MAE	Mean RMSE	Mean Peak GRU Memory (MB)	Mean Inference Time (ms)	Total Params
LSTM		Q	0.104 ± 0.023	0.191 ± 0.043	23.45 ± 0.64	0.29 ± 0.05	208,131
TFT		Q	0.098 ± 0.018	0.183 ± 0.036	90.24 ± 9.67	8.47 ± 0.04	3,019,773
		Peak Q	0.107 ± 0.021	0.203 ± 0.041	90.24 ± 9.67	8.42 ± 0.13	3,019,773
GCN-TFT	GCN	Q	0.099 ± 0.014	0.180 ± 0.032	118.37 ± 12.64	9.06 ± 0.10	4,030,189
		Peak Q	0.095 ± 0.019	0.169 ± 0.034	118.37 ± 12.64	9.28 ± 0.17	4,030,189
PGTFT (Ours)	GCN	Q	0.100 ± 0.020	0.177 ± 0.038	65.52 ± 5.15	5.41 ± 0.19	1,540,356
		Peak Q	0.114 ± 0.015	0.205 ± 0.025	65.52 ± 5.15	5.23 ± 0.07	1,540,356
	Non-parametric attention GCN	Q	0.116 ± 0.046	0.206 ± 0.088	65.79 ± 5.10	5.45 ± 0.20	1,540,356
		Peak Q	0.104 ± 0.026	0.177 ± 0.049	65.79 ± 5.10	5.31 ± 0.10	1,540,356

present the averaged five-fold results, including standard deviations, under the 5 m and 30 m neighbor threshold settings, respectively.

As shown in Table 3, under the 5 m threshold, PGTFT with non-parametric attention and PWQL achieved the best overall predictive performance, with an average MAE of 0.091 and RMSE of 0.162. In terms of efficiency, PGTFT with a GCN-based design demonstrated the most favorable balance, requiring only 65.52 MB of GPU memory and 5.23 ms of inference time. The non-parametric variant showed comparable efficiency, with only marginal differences. Importantly, PGTFT maintained a lightweight structure with approximately 1.54 million parameters—roughly half the size of TFT and GCN-TFT (3–4 million)—while still delivering equal or superior accuracy. Although LSTM required the fewest parameters (about 200,000) and was the most computationally efficient, its predictive accuracy lagged significantly. These findings confirm that PGTFT achieves an effective trade-off between efficiency and accuracy by simplifying variable selection while reinforcing peak-sensitive learning.

In contrast, Table 4 summarizes results under the 30 m threshold. Here, GCN-TFT with PWQL achieved the lowest MAE and RMSE values. However, these improvements came at a substantial computational cost, requiring 118.37 MB of GPU memory, approximately 9 ms of inference time, and over 4 million parameters. Given the marginal performance gains relative to this added complexity, PGTFT remains the more practical and efficient alternative for real-world applications.

4.5.3. Visualization of Prediction Performance

To provide an intuitive understanding of model performance, we visualized the prediction results under the 5 m threshold and examined both median predictions and quantile-based forecasts. These visualizations complement the quantitative metrics by showing how closely the proposed model aligns with observed values and how effectively it captures peak events and predictive uncertainty.

Figure 4 compares the ground truth with PGTFT predictions under the 5 m threshold. The black line represents observed congestion, the red line denotes PGTFT trained with PWQL, and the gray dashed line corresponds to PGTFT with the standard Quantile Loss. Across all cases, PGTFT predictions most closely follow the ground truth. In Figure 4a,b,d, the model accurately captures both the timing and magnitude of peaks, while in Figure 4c, where peak activity is minimal, the predictions are slightly smoothed yet still closer to the ground truth than those of competing models.

Figure 5 illustrates the quantile-based predictions generated by PGTFT. By producing forecasts at the 10th, 50th, and 90th percentiles, the model provides a distributional view of congestion dynamics. The median prediction (Q50) tracks the overall trend but underrepresents extreme peaks, whereas the Q10–Q90 range reflects predictive uncertainty. Most observed peaks fall within the Q90 band, indicating the model’s ability to probabilistically anticipate extreme events. This demonstrates that PGTFT not only captures central tendencies but also provides uncertainty-aware forecasts for high-risk congestion scenarios.

4.5.4. Analysis of the Fused Adjacency Matrix

This experiment was designed to evaluate the practical effect of the hybrid fused adjacency matrix, which combines hop-based and distribution-based similarities, on prediction performance. While the conceptual details of this design were introduced earlier in Section 3.1.2, here we focus on visualizing and interpreting its impact through the experimental results shown in Figure 6.

Figure 6 presents the fused adjacency matrix for a target road segment. Compared to the hop-only matrix, the fused matrix shows visibly richer structure, as even when hop-based weights are low, blending them with cosine similarity in a 1:1 ratio (α = 0.5) elevates the overall inter-node similarity values. This integration highlights both local structural consistency and functional similarities across distant but behaviorally similar roads. The choice of α = 0.5 was made based on empirical comparisons, which confirmed it provided the most balanced and effective representation for this dataset.

Although the fused matrix exhibits clear numerical differences from the hop-only version, the predictive performance remained largely unchanged. This outcome can be explained by the proportional increase in all neighbor weights, which preserved relative importance among nodes after softmax normalization in the non-parametric attention GCN. The result underscores both the robustness of the proposed architecture and the adequacy of hop-based structural information for the current dataset.

Nonetheless, the fused design has broader implications. In dense urban networks, where neighboring roads are highly connected and congestion patterns vary significantly, relying solely on hop-based proximity may fail to capture functional similarities across distant segments. In such cases, the fused matrix can reduce predictive uncertainty and improve generalization. Conversely, in suburban or highway settings with linear road structures and limited external influences, hop-based adjacency may be more reliable. These findings suggest that while hop-only adjacency was sufficient in the present case, the fused design provides a flexible and adaptive strategy that may yield stronger benefits in more complex or heterogeneous traffic environments.

5. Conclusions

In many urban back streets, pedestrian and traffic conditions can be partially monitored using CCTV-derived trajectory data; however, cost and infrastructure constraints prevent full coverage, creating “shadow areas” where no observations are available. These gaps limit the accuracy and continuity of congestion forecasting across the road network. To address this challenge, this study proposes PGTFT, a lightweight extension of the TFT designed to infer congestion in unmonitored segments by leveraging partially observed data from surrounding roads. The model integrates a non-parametric attention-based GCN, a peak-aware GRN, and a PWQL, enabling it to capture irregular congestion patterns while maintaining computational efficiency.

The contributions of this work are fourfold. First, PGTFT demonstrates robustness under sparse conditions, maintaining stable performance even when neighboring data are limited. Second, the incorporation of peak-aware components improves sensitivity to high-congestion periods. Third, the model achieves accuracy comparable to or exceeding more complex baselines while requiring only 1.54 million parameters, highlighting its efficiency. Fourth, the use of a hybrid adjacency matrix allows the simultaneous representation of both physical connectivity and functional similarity between road segments.

Experimental results across different sparsity levels confirmed that PGTFT consistently outperformed conventional baselines while preserving lightweight complexity. Although the fused adjacency matrix provided only marginal improvements for the dataset used, it is expected to yield greater benefits in settings with more heterogeneous congestion patterns.

This study also has limitations. The dataset was restricted to a single region in Korea, which constrains generalizability, though a neighbor-threshold strategy was applied to diversify connectivity scenarios. In addition, performance varied between the 5 m and 30 m threshold settings, reflecting the influence of data sparsity. Future research should address these limitations by incorporating larger and more diverse datasets and by exploring reinforcement learning strategies for dynamically modeling road connectivity.

The practical implications of this study are significant. By filling observation gaps in areas with limited CCTV coverage, PGTFT offers municipalities a cost-effective tool for enhancing urban safety and monitoring. Its applicability extends beyond congestion forecasting to support intelligent transportation systems, including optimal routing, emergency response planning, and urban design in environments with uneven sensing infrastructure. In addition, the adaptability of the proposed framework suggests broader utility in domains such as vehicular traffic management and urban logistics, where uneven sensing infrastructure similarly limits data availability. Furthermore, the lightweight design makes PGTFT suitable for real-time applications on resource-constrained platforms, enabling integration with edge devices or mobile sensing units.

In conclusion, PGTFT provides a parameter-efficient and adaptable solution that balances predictive accuracy with computational cost. Building on its demonstrated capability to infer congestion in shadow areas, the model holds strong promise for real-world deployment in smart city applications, while future work should further validate its scalability and extend its functionality across diverse urban contexts.