Abstract
Aiming at the problem that the current double direction buffering algorithm is easy to use to seal the “bottleneck” area when simplifying coastlines, an adaptive simplification method for coastlines using a skeleton line “bridge” double direction buffering algorithm is proposed. Firstly, from the perspective of visual constraints, the relationship between the buffer distance and the coastline line width and the minimum recognition distance of the human eye is theoretically derived and determined. Then, based on the construction of the coastline skeleton binary tree, the “bridge” skeleton line is extracted using the “source tracing” algorithm. Finally, the shoreline adaptive simplification is realized by constructing a visual buffer of “bridge” skeleton lines to bridge the original resulting coastline and the local details. The experimental results show that the proposed method can effectively solve the problem that the current double direction buffering algorithm has, which can significantly improve the quality of simplification.
1. Introduction
The coastline, as an important line element on nautical charts, has always been the focus of attention in the field of automatic synthesis [1]. Unlike general line element simplification, coastline simplification needs to consider specific principles, such as “expanding land and shrinking sea”, so ordinary line element simplification algorithms are not suitable for coastline simplification [1,2].
Based on the currently available literature, many scholars have focused their research on this topic in the following two aspects.
One is that methods for identifying and simplifying shoreline bends are constantly being proposed [3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23]. This simplification method mainly uses bending identification methods (the monotonic segment identification method or the Delaunay triangulation method) to identify bends and select them based on their attributes (area, width, depth, etc.) to achieve the purpose of coastline simplification. However, in the process of coastline simplification, directly selecting bends as a whole does not conform to their gradual change process with scale changes [16]. To address this issue, for complex estuary coastlines, one study [17] constructs a binary tree model of estuary skeleton lines supported by constrained Delaunay triangulation and then implements progressive coastline simplification through certain steps, such as small bend deletion, deletion of small parts of bends, and local enlargement, thus improving the quality of simplification. On this basis, for coastlines and island shorelines nearby, another study [18] proposes a hierarchical triangular mesh partitioning method for collaborative coastline simplification, effectively solving the problem of collaborative coastline simplification. At the same time, with the rapid development of artificial intelligence technology, Fang Wu, Jiawei Du, Zikang Song, and others have attempted to use machine-learning-related methods to automatically simplify coastlines [19,20,21,22,23].
The second is that the bidirectional buffer method is constantly being improved [24,25,26,27,28,29]. The bidirectional buffer zone method first establishes an outer buffer zone on one side of the coastline to be simplified towards the sea with a fixed radius r and then establishes an inner buffer zone on the other side of the outer buffer zone towards the land with the same fixed radius r. The final inner buffer zone boundary is used as the simplified coastline. This method can achieve progressive coastline simplification with scale changes, and it has relatively simple processes. It has also been applied maturely in bathymetric line simplification [30]. However, there are also some drawbacks when using this method for coastline simplification. For example, when simplifying “bottleneck” areas, it is easy for a “sealing” phenomenon to appear, resulting in a large area of sea turning into land and causing an excessive simplification scale, thus restricting the application of this method in coastline simplification.
To address these issues, this paper proposes a coastline simplification method that bridges bidirectional buffer zones with skeleton lines. Firstly, the basic principle and existing defects of the existing bidirectional buffer zone method are analyzed. Then, based on the above defects, the proposed method realizes adaptive coastline simplification through certain steps, such as visually constrained buffer distance determination, construction of a coastline skeleton line binary tree, extraction of “bridging” skeleton lines using the “source tracing” algorithm, and bridging between the original result and local details.
2. Bidirectional Buffer Zone Method
2.1. Basic Principles
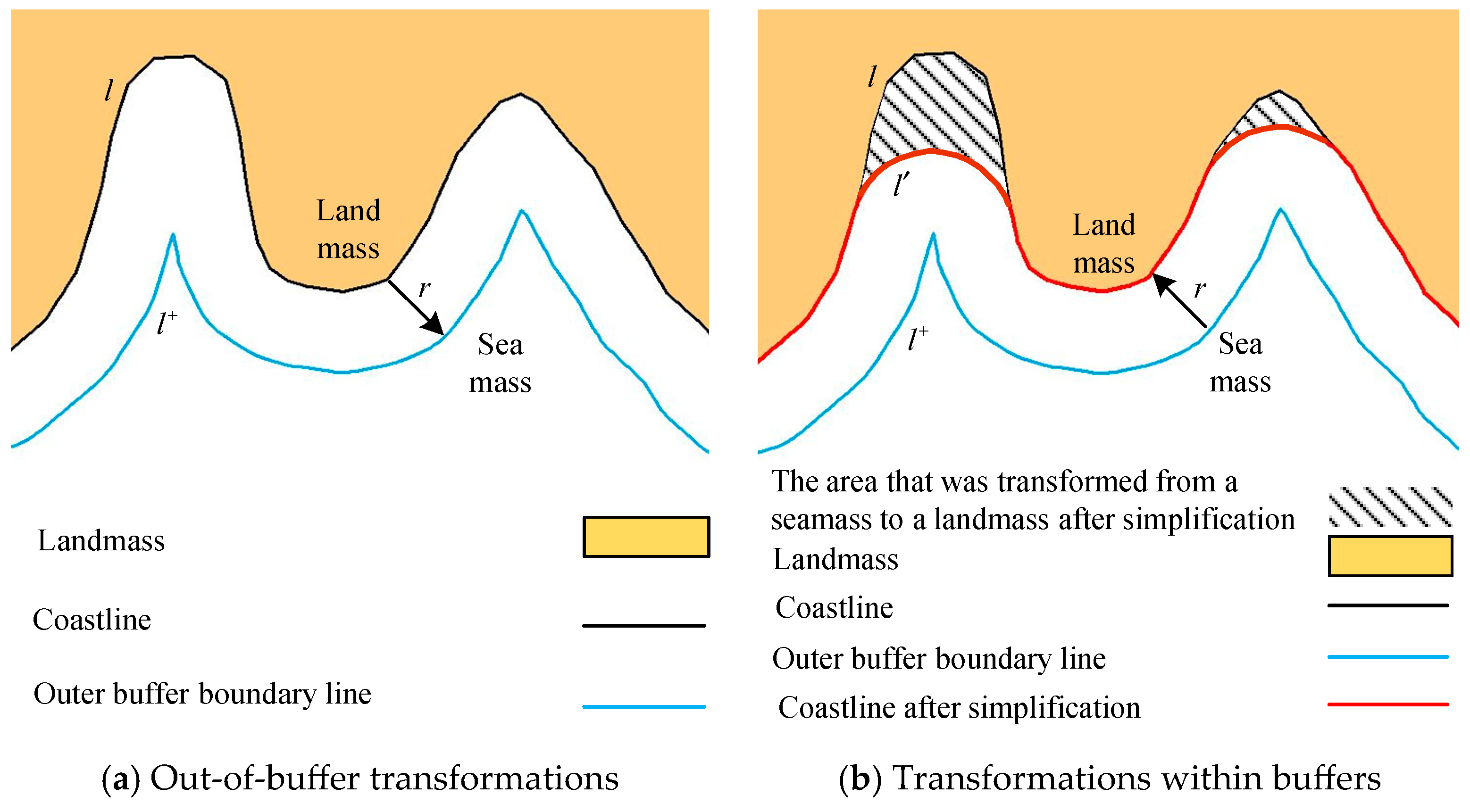
The basic process of coastline simplification using the bidirectional buffer zone method is as follows. As shown in Figure 1a, for the original coastline to be simplified, an outer buffer zone is first created on the seaward side with a fixed distance r as its radius (referred to as the buffer zone external transformation). Then, an inner buffer zone is created on the landward side of the outer buffer zone boundary with a fixed distance r as its radius (referred to as the buffer zone internal transformation). The boundary of the inner buffer zone is then taken as the simplified coastline (as shown in Figure 1b).
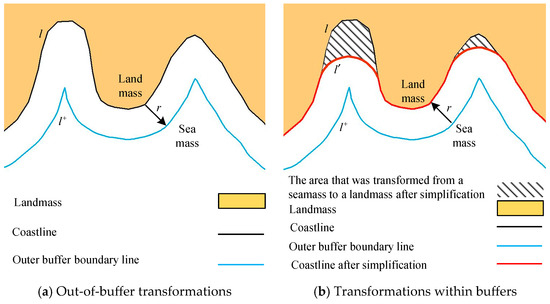
Figure 1.
The schematic diagram of the double direction buffering algorithm.
As it can be seen from Figure 1b, this method performs simplification on the curved concave parts while maintaining the convex parts. The scale of simplification is related to the transformation radius r (referred to as the buffer distance [26,27,28,29]). The larger the transformation radius r, the greater the scale of simplification [26].
2.2. Existing Flaws
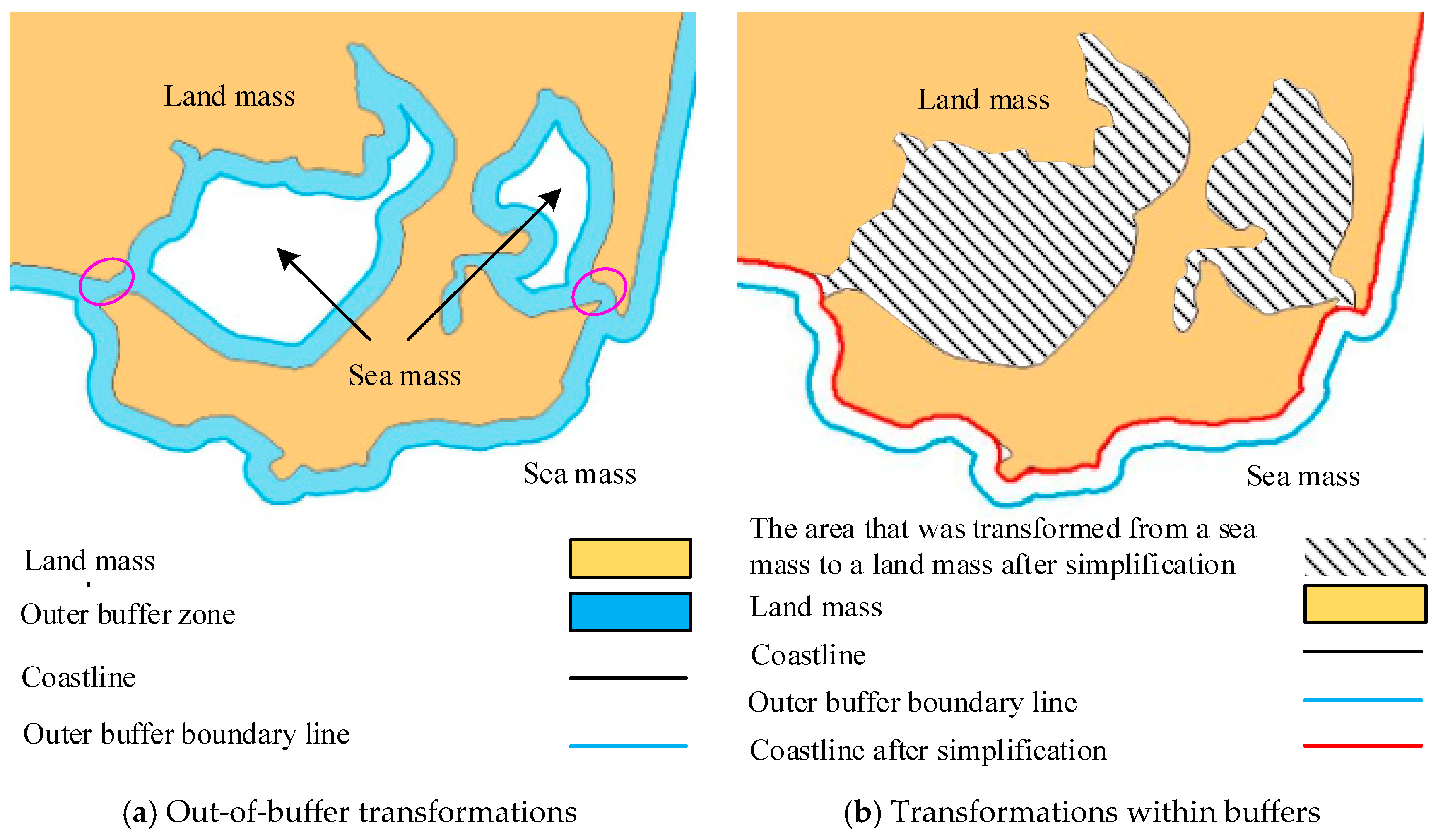
According to the relevant description in Section 2.1, it can be observed that for general-type coastlines, the bidirectional buffer zone method can obtain a smoother and satisfactory simplification result that meets the requirements of specification [2]. However, in some “bottleneck” areas, this method may lead to a “sealing” phenomenon. As shown in Figure 2a, an outer buffer zone is created on the seaward side of the original coastline in this area. From the figure, the buffer zone overlaps in the “bottleneck” area (the red-circle-marked area), resulting in the formation of two inner rings within the buffer zone. According to the existing bidirectional buffer zone method, these inner rings will be ignored. Then, an inner buffer zone is created on the landward side of the outer buffer zone boundary line (as shown in Figure 2b), and a simplified coastline is obtained. As shown in Figure 2b, under the radius of this buffer zone, the simplified coastline “seals off” the lagoon spit, causing a large area of sea to become land, resulting in an excessively large simplification scale, altering the original geographical features, and making the simplification result unable to meet the relevant requirements of specification [2].
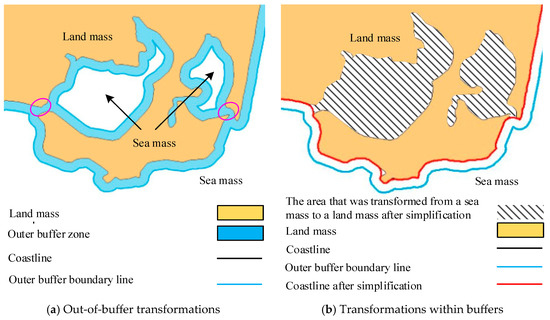
Figure 2.
The disadvantage of the double direction buffering algorithm.
3. Skeleton Line “Bridging” Bidirectional Buffer Zone
3.1. Basic Philosophy
Through the analysis in Section 2.2, it can be understood that the main reason for errors in the bidirectional buffer zone method is that this method ignores the inner rings within the outer buffer zone during the internal transformation process of the buffer zone, thus failing to effectively consider its local details, which leads to the “bottleneck” being sealed off and resulting in a simplification result that cannot meet the relevant requirements of the specification. To address this issue, this paper attempts to retain these inner rings and perform appropriate processing to improve the quality of simplification.
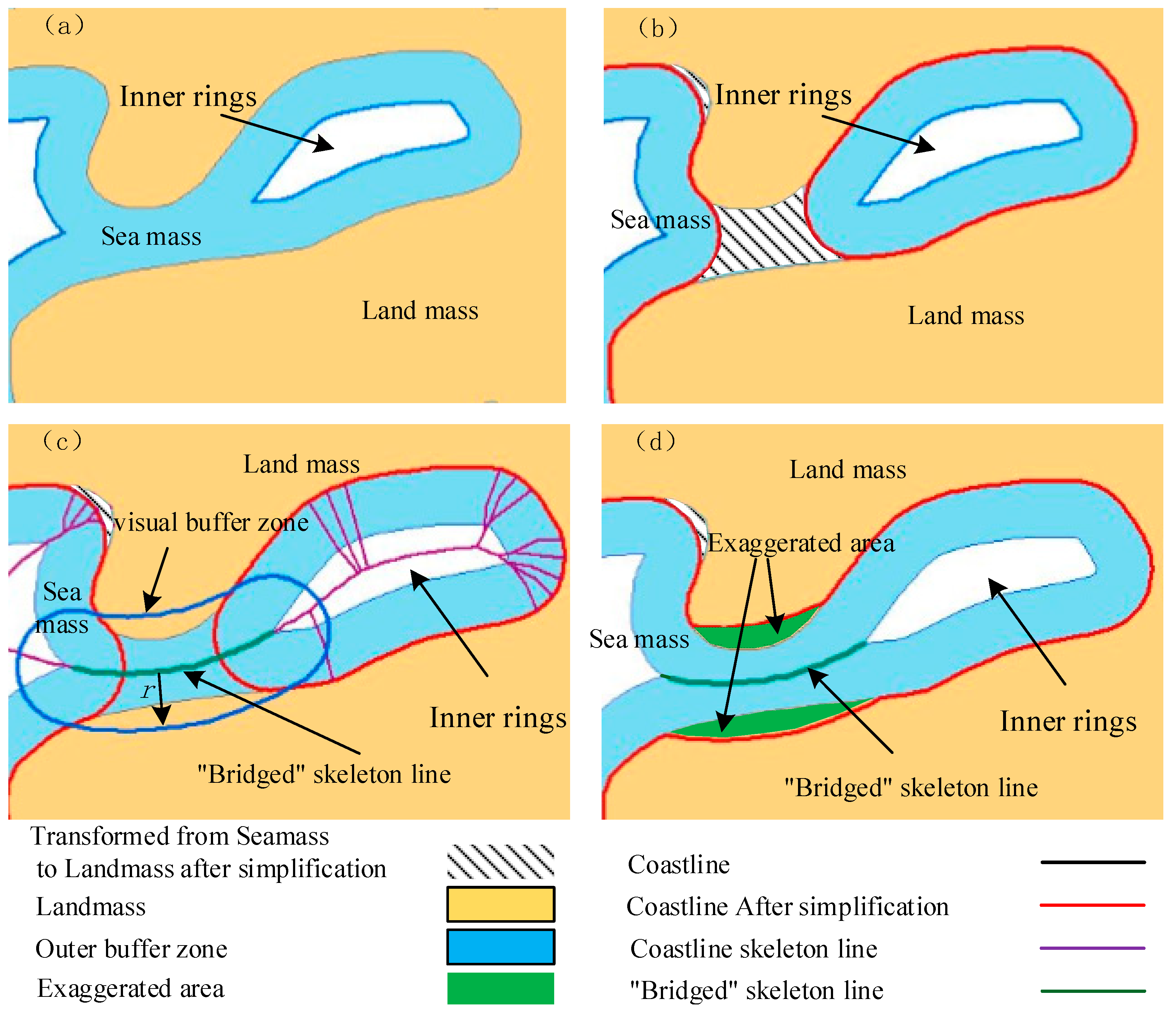
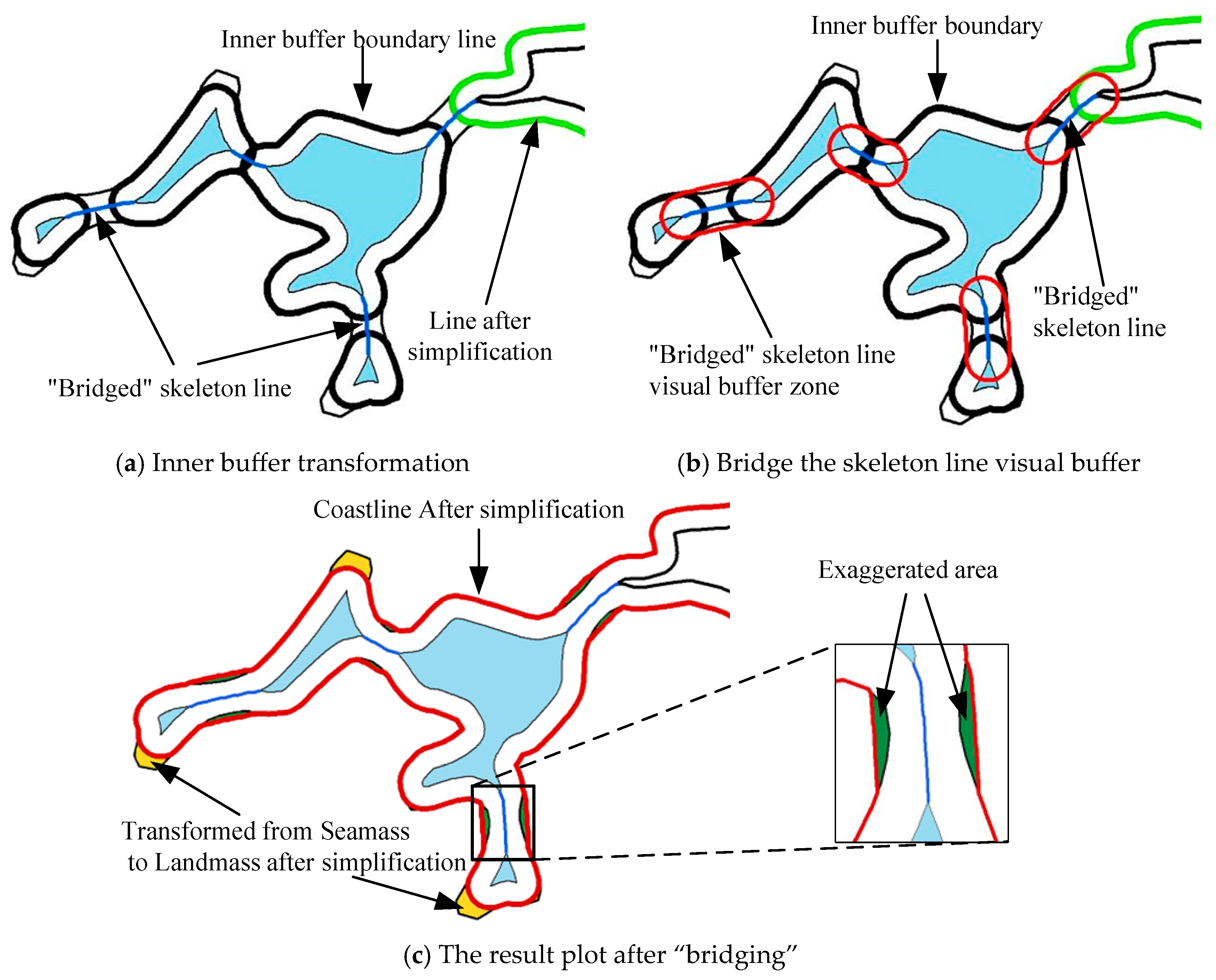
As shown in Figure 3, performing buffer zone external transformation on the coastline in the area shown in the figure results in the formation of inner rings within the outer buffer zone due to the presence of partial bottleneck areas (as shown in Figure 3a). Firstly, an attempt is made to directly perform bidirectional buffer zone internal transformation on the outer buffer zone containing inner rings, resulting in the simplified coastline shown in Figure 3b. From the figure, it can be observed that even when retaining the inner rings within the outer buffer zone, the simplification result still exhibits the phenomenon of “blocking” the bottleneck areas. To address this, this paper extracts the coastline skeleton line (as shown in Figure 3c). The skeleton line can better connect the inner rings within the outer buffer zone and the boundary line of the buffer zone. Additionally, the skeleton line itself reflects the morphological characteristics of the coastline in this area. Therefore, a portion of the skeleton line that connects the inner rings within the outer buffer zone and the boundary line is extracted (referred to as the “bridging” skeleton line), and a buffer zone is constructed with a radius equal to the buffer distance (in this paper, the buffer distance mainly adopts half of the minimum perceptible distance of human eyesight; hence, the buffer zone with a radius equal to this distance is referred to as the visual buffer zone, as shown in Figure 3c). Then, the “bottleneck” areas that are “blocked” in Figure 3b are replaced using the visual buffer zone, achieving a “bridging” between the local detail portion and the original simplified result line. The “bottleneck” areas are also appropriately adaptively exaggerated (as shown in Figure 3d), thereby improving the quality of simplification using the original bidirectional buffer zone method.
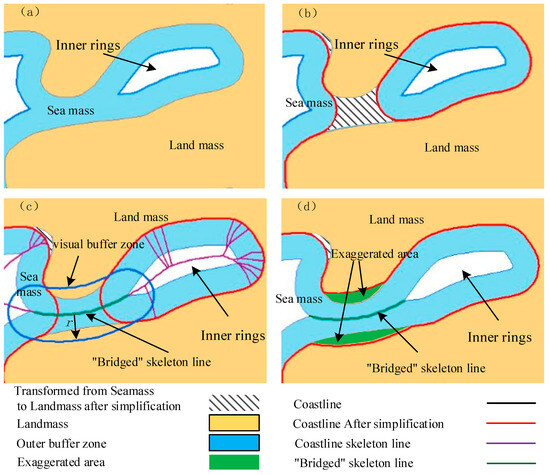
Figure 3.
The schematic diagram of the proposed method. (a) Out-of-buffer transformations; (b) Transformations within buffers; (c) Extracts the “Bridged” skeleton line and its visual buffer zone; (d) “Bottleneck” areas Exaggerated.
It should be noted that the basic principle for cases with multiple inner rings in the same bend is like the case with one inner ring mentioned above; therefore, it will not be further elaborated in this paper. The main flow of the method proposed in this paper is shown in Figure 4.

Figure 4.
The flow chart of the proposed method.
3.2. Critical Steps
3.2.1. Determination of Buffer Distance under Visual Constraints
The size of the buffer distance (the radius of buffer transformation) directly controls the scale of coastline simplification and has a direct impact on the quality of the simplification. Therefore, it is of great significance to scientifically determine the buffer distance to improve the quality of coastline simplification. This paper mainly explores the relationship between the buffer distance and the scale of simplification based on visual constraints to obtain it.
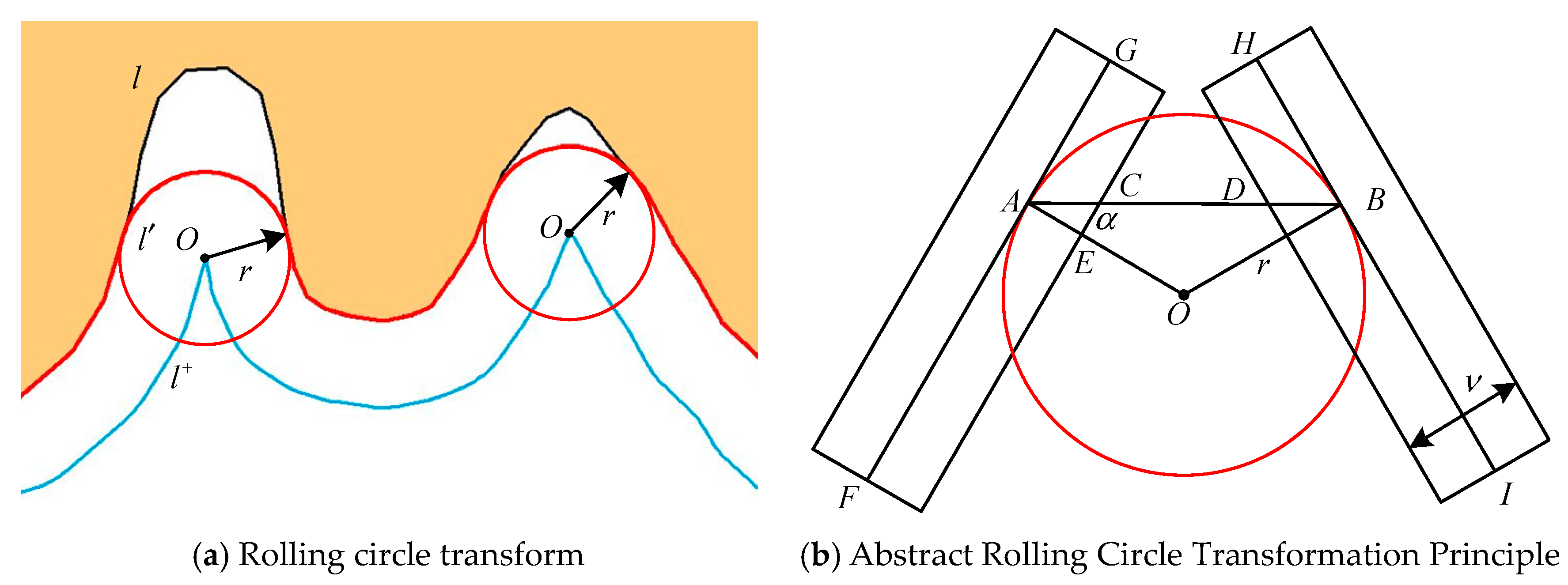
According to the relevant description in reference [27], the bidirectional buffer zone is essentially an approximation of a rolling circle transformation. The simplification process can be viewed as the rolling motion of a rolling circle (as shown in Figure 5a). The outer boundary of the buffer zone is the trajectory of the rolling circle’s center, while the inner boundary (i.e., the final simplified result line) is the movement path of the tangent points between the rolling circle and the coastline to be simplified. Any part that cannot be in contact with the rolling circle is replaced by the boundary of the rolling circle, which is the simplified region. This process can be abstracted, as shown in Figure 5b, where and are local segments of the coastline with a width of . Line segments and are the central lines of the coastline, and circle is a rolling circle with a radius of . Points and are the tangent points between the rolling circle and the central line of the coastline. By connecting these two tangent points and intersecting them with the coastline boundary at points and , we obtain segment , which intersects the coastline boundary at point . According to the principle of rolling circle transformation, the coastline segment to will be simplified.
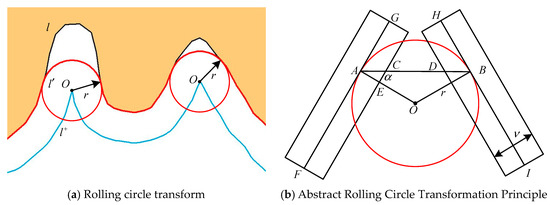
Figure 5.
The calculation process of the buffer distance.
According to visual constraints [17] (that is, there is no invisible part of the simplified coastline), then there must be (where represents the minimum distance that can be recognized by human eyes). Letting , we can derive
then
When , the extremum can be obtained ( is the coastline stroke width and is the minimum distance perceivable by the human eye). Therefore, the relationship between the buffer distance considering visual constraints, the coastline stroke width, and the minimum distance perceivable by the human eye can be derived.
3.2.2. Shoreline Skeleton Line Binary Tree Construction
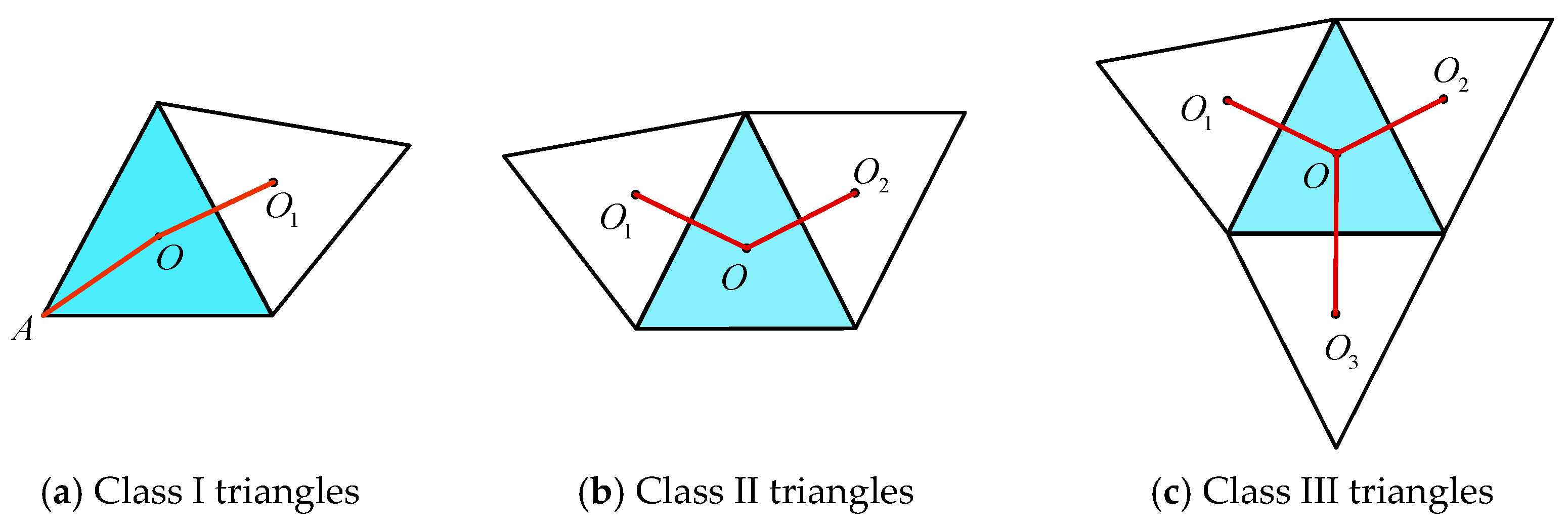
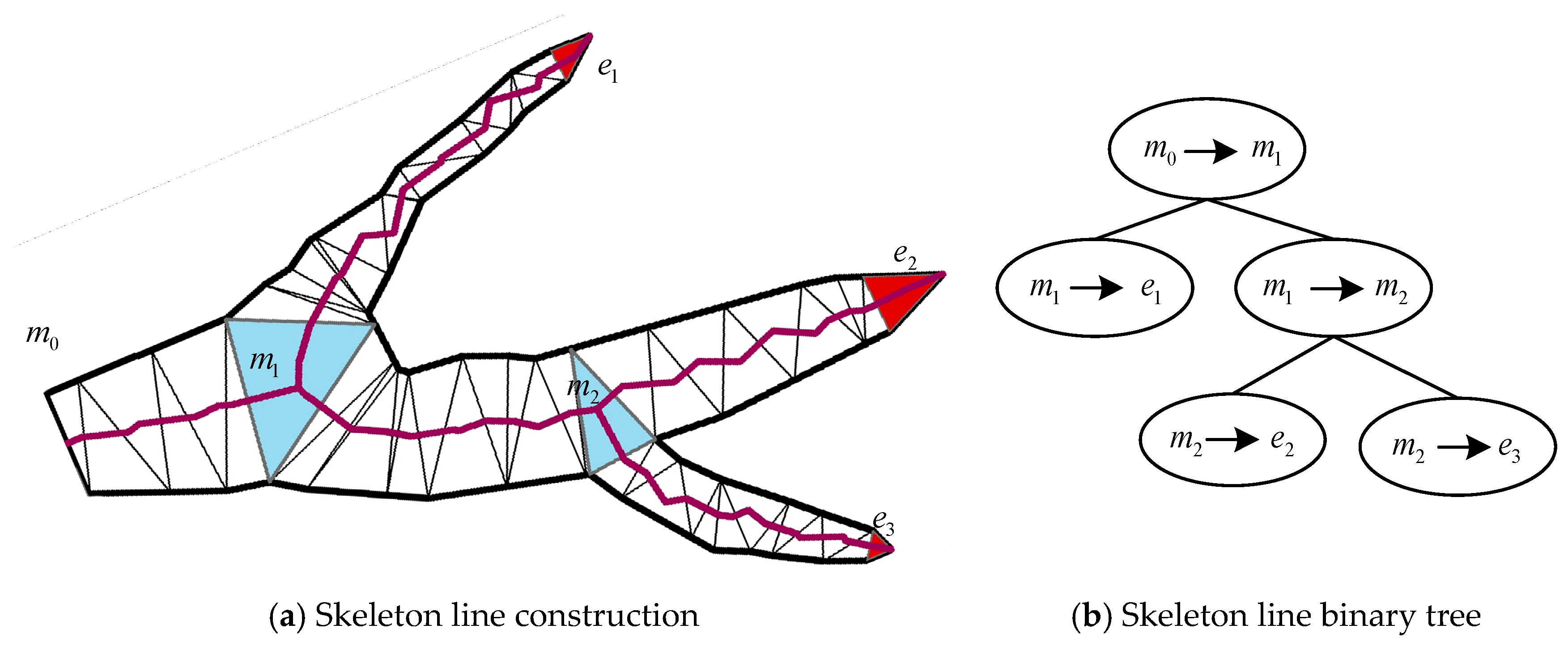
According to the basic idea described in Section 3.1, after performing the outer buffer zone transformation on the coastline, the next step is to extract the “bridging” skeleton line. The extraction of bridging skeleton lines is based on the extraction of coastline skeleton lines, and there are many methods for extracting line element skeleton lines [5,6,7,8,9,10,11,12,13,14,15,16,17,18,31,32,33,34,35]. In this paper, we first construct a constrained Delaunay triangulation network based on the data points on the coastline and extract the triangles located in the sea area. Then, we classify the triangles into three categories (I, II, and III) based on the number of neighboring triangles, as proposed in reference [31], and we connect the skeleton lines between triangles according to their neighboring relationship (the common edge between two neighboring triangles is called a neighbor edge). For I-type triangles, we connect the opposite vertices of the neighbor edges with the circumcenter of the triangle and the circumcenter of the neighboring triangle; for II-type and III-type triangles, we connect the circumcenter of each triangle with the circumcenter of its neighboring triangle. The resulting skeleton lines are shown in Figure 6. Finally, we construct a binary tree of skeleton lines, as described in reference [17] (shown in Figure 7).
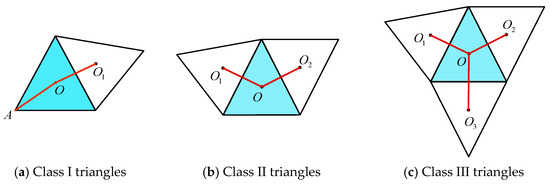
Figure 6.
Skeleton line connection ways for three categories of triangles, respectively.
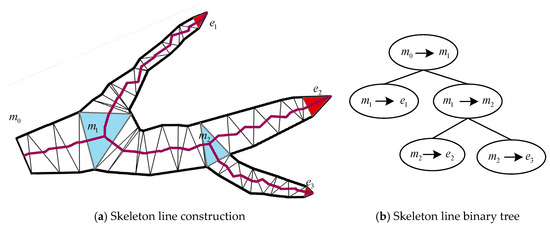
Figure 7.
The binary tree structure of skeletons.
3.2.3. “Source Tracing” Algorithm Extracts “Bridging” Skeleton Lines
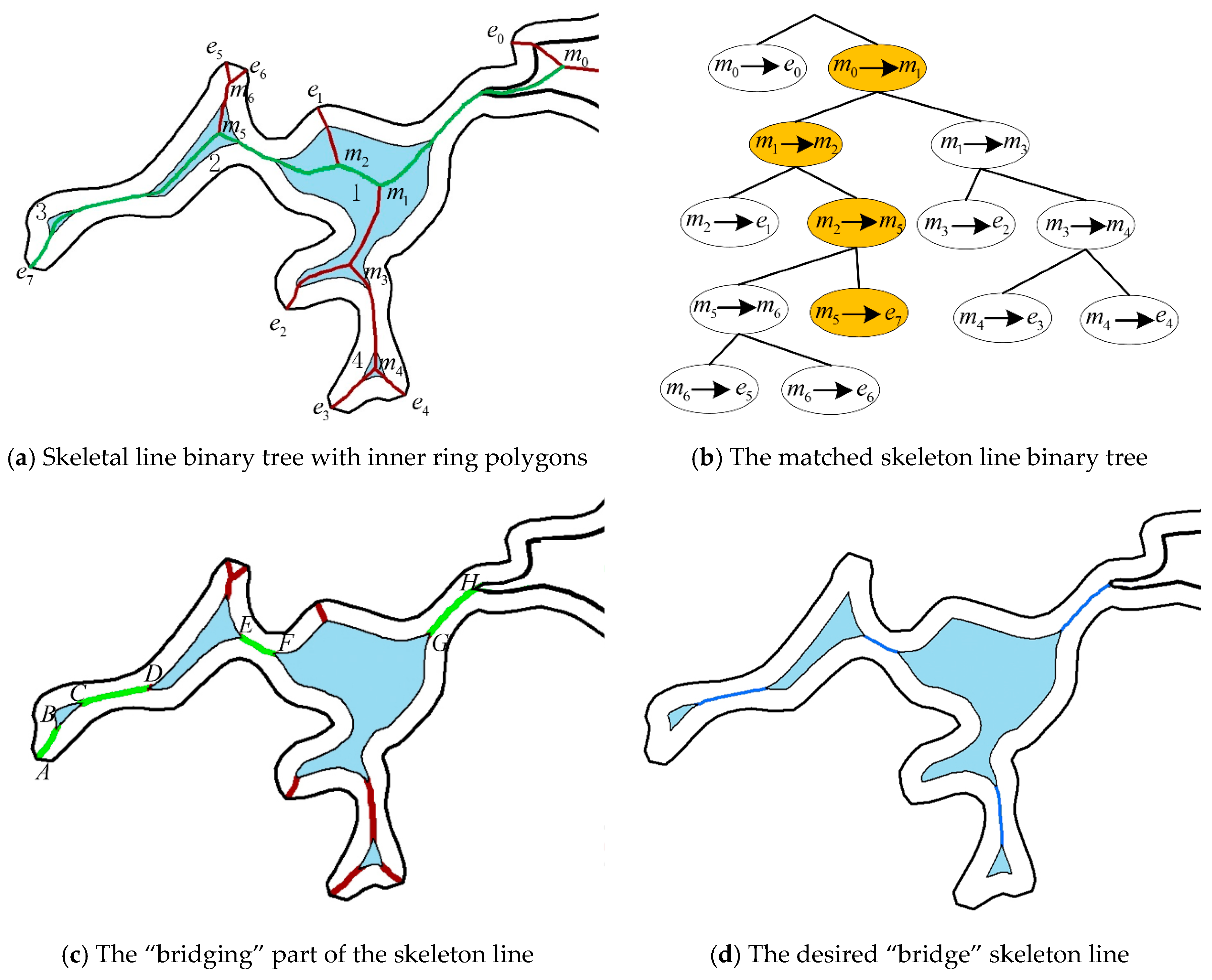
After the construction of the skeleton line binary tree, the next step is to match the skeleton lines with the inner and outer rings and extract the “bridging” skeleton lines. To analyze this process in depth, we selected a local coastline and used the relevant methods mentioned above to obtain the skeleton line, the inner ring, and the outer ring, as shown in Figure 8a, and the constructed binary tree is shown in Figure 8b. It is not difficult to see from the figure that the skeleton lines have different shapes, a large number, and overlap with the inner ring. The desired “bridging” skeleton lines are mainly located between different inner or outer rings. In order to obtain the skeleton line of this area, combined with Figure 8, the specific steps are described as follows.
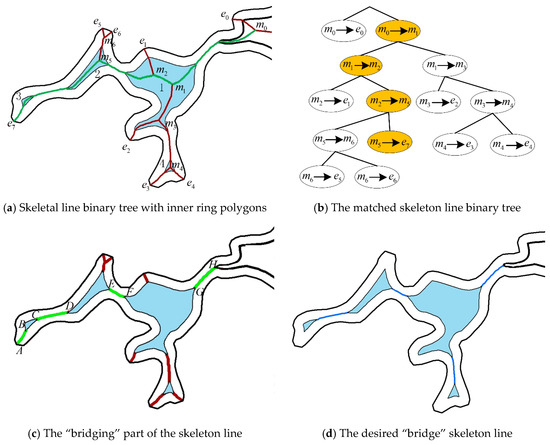
Figure 8.
The schematic diagram of “bridging” skeleton line extraction.
Step 1: Select any end node , and continuously “backtrack” the previous parent node according to the skeleton line binary tree until it reaches the root node (as shown by the yellow node in Figure 8b).
Step 2: Connect the skeleton line segments stored in the above nodes to form a complete skeleton line (as shown by the green skeleton line in Figure 8a), and remove the overlapping parts with the original inner and outer rings to obtain , , , and skeleton line segments, as shown in Figure 8c.
Step 3: Select the skeleton line segments (, , and ) adjacent to the inner and outer rings at both ends, which are the desired “bridging” skeleton lines.
Step 4: Traverse other end nodes in the region, calculate the “bridging” skeleton line according to the above steps, remove duplicate “bridging” skeleton line fragments, and output the result (as shown in the blue line skeleton line in Figure 8d).
3.2.4. “Bridging” of the Original Result Line and Local Details
In Section 3.2.3, a detailed description of the extraction of “bridging” skeleton lines is provided. After extracting the “bridging” skeleton lines, the next step is to use them to bridge the simplified coastline results and local details. Combining Figure 9, the specific steps are described as follows.
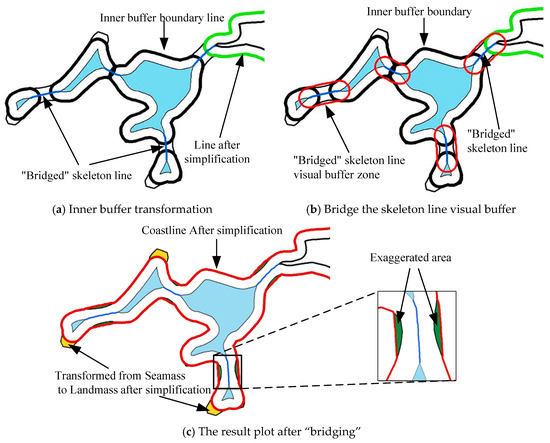
Figure 9.
The diagram of the bridging process.
Step 1: Perform an inner buffer zone transformation on the outer buffer zone boundary and each inner ring to obtain the original simplified result line and local details (as shown in Figure 9a); then, proceed to Step 2.
Step 2: According to the “bridging” skeleton lines extracted in Section 3.2.3, create a “bridging” skeleton line visual buffer zone with a radius equal to the buffer distance obtained in Section 3.2.1 (as shown in Figure 9b); then, proceed to Step 3.
Step 3: Perform a “difference” operation between the original simplified result line polygon and the “bridging” skeleton line visual buffer zone, as well as the local detail inner ring polygon, to obtain the simplified coastline after “bridging,” and output the simplification result (as shown in Figure 9c).
It should be noted that the above steps rely on the visual buffer zone of the “bridging” skeleton line to exaggerate the bottleneck area. However, for some areas with very narrow land widths, such as sandbars and waterways, when the scale is very small, it may lead to the phenomenon of large area land loss. Therefore, readers must ensure that the sum of the widths of the land and ocean parts of the area is greater than twice the visual buffer radius at the target scale during use.
4. Experiments and Analysis
4.1. Evaluation of the Effectiveness of the Methodology
To validate the effectiveness and applicability of this method, this paper selects three typical estuary coastlines, a lagoon coastline, and a complicated coastline for experimentation. The width of the coastline is set to 0.01 cm, the minimum recognition distance of human eyes is set to 0.02 cm, and, according to the buffer zone formula, the transformed widths of the buffer zone and the visual buffer zone of the “bridging” skeleton line are set to 0.015 cm. Based on the GDAL/OGR library’s buffer function, and using C++ programming, the following experiments are implemented. In order to better display the simplified results, the original and simplified coastlines will be plotted in the same graph simultaneously. The blue lines ( ) represent the simplified coastline, while the black lines (
) represent the simplified coastline, while the black lines ( ) represent the original coastline.
) represent the original coastline.
 ) represent the simplified coastline, while the black lines (
) represent the simplified coastline, while the black lines ( ) represent the original coastline.
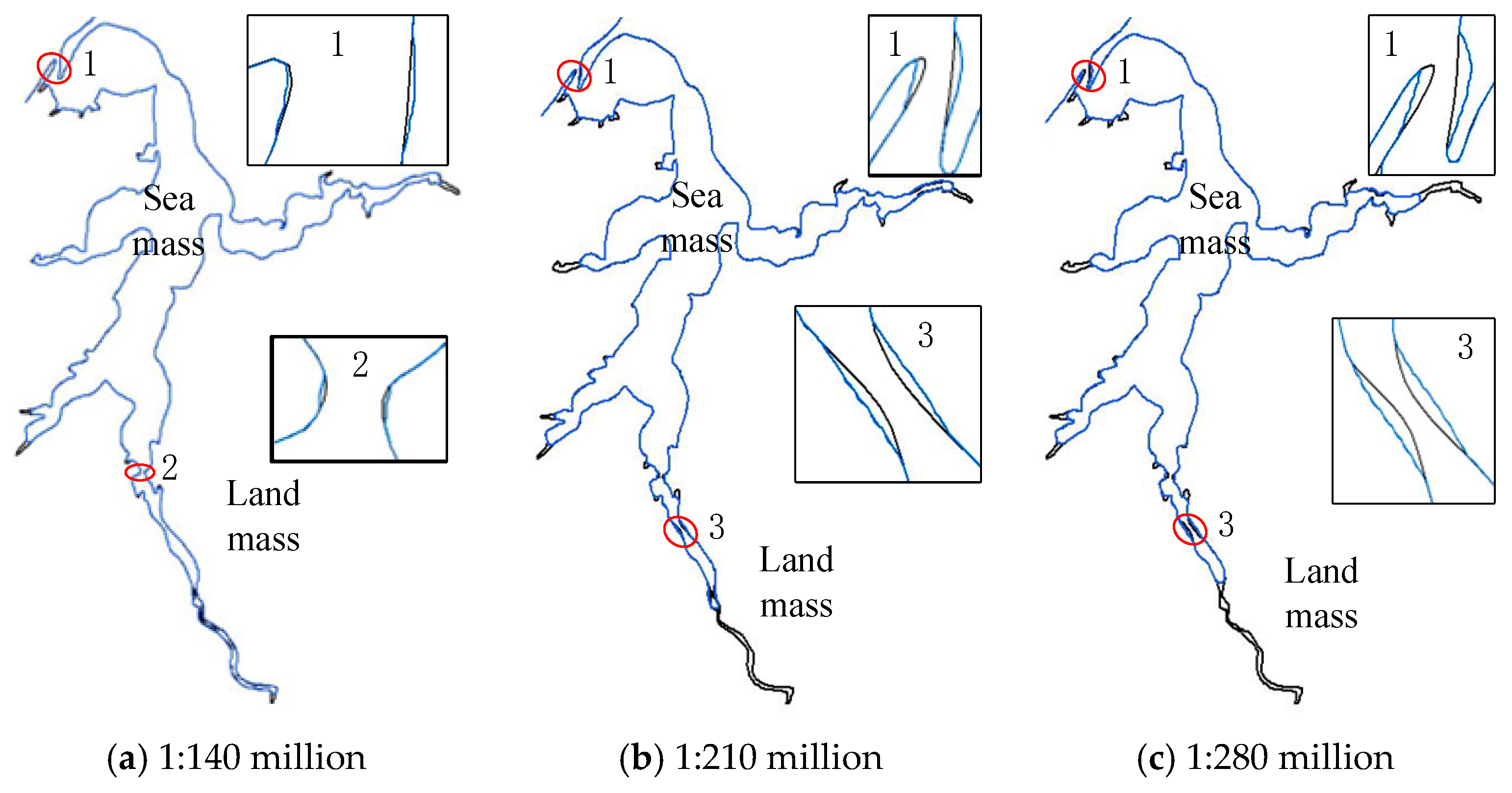
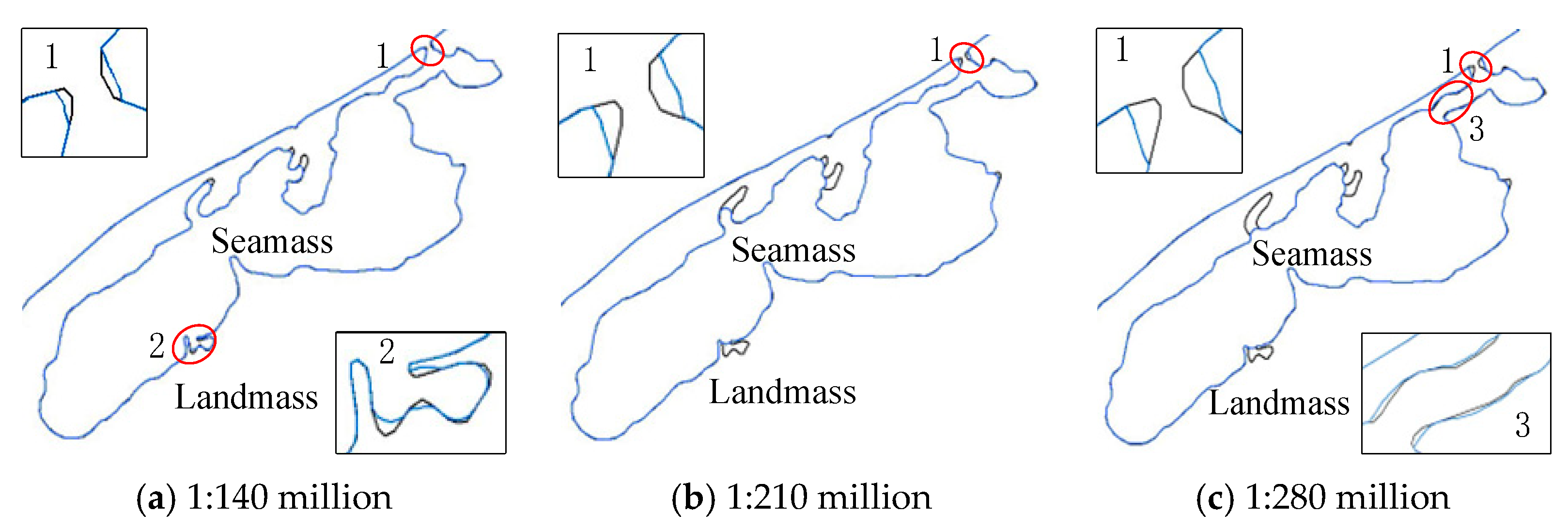
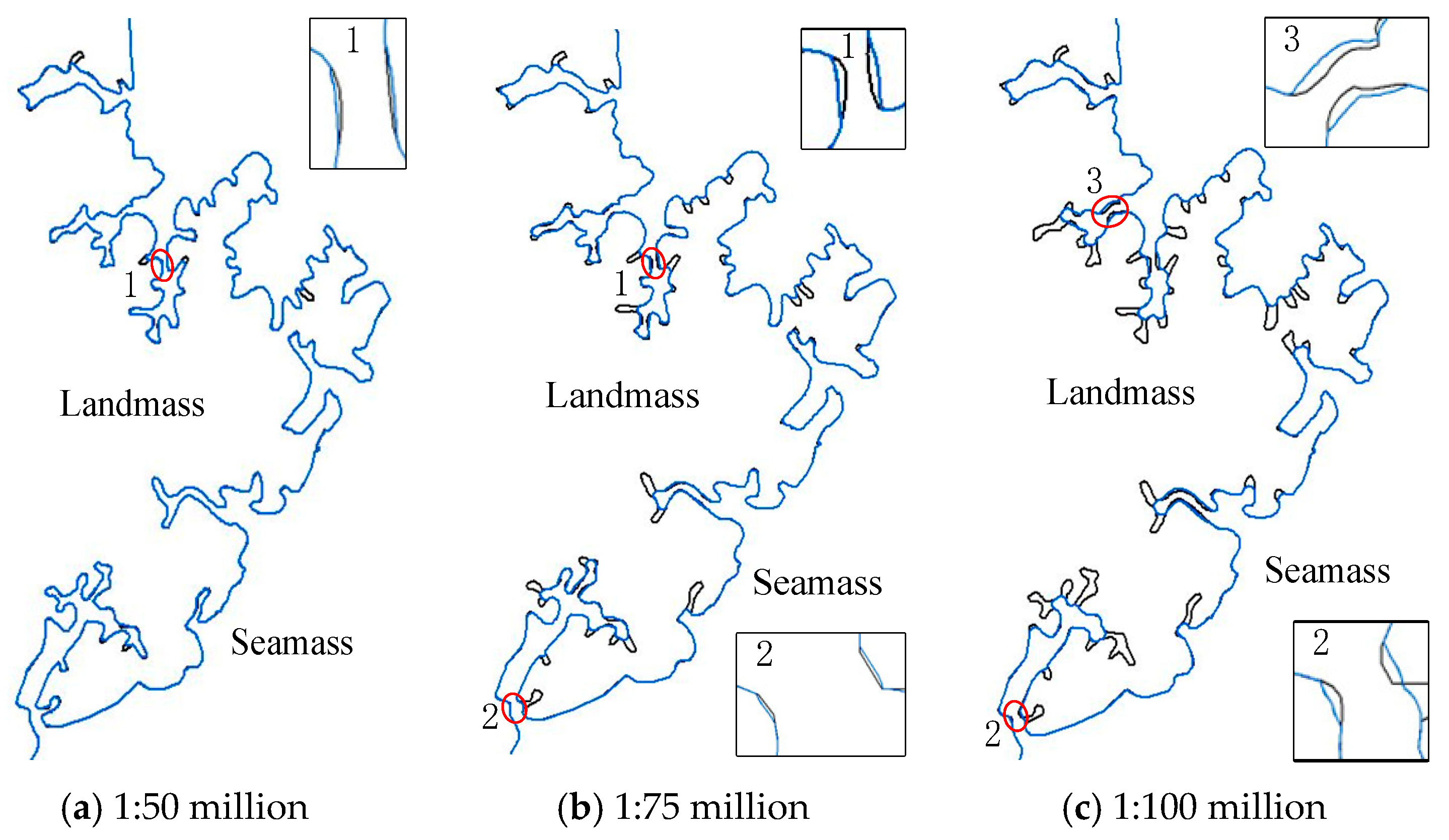
) represent the original coastline.From the above simplification results, it can be observed that the scale of coastline simplification also gradually increases with the reduction in scale, which is consistent with the progressive simplification principle [17]. The simplified results are relatively smooth and of good quality. As shown in Figure 10, the method proposed in this paper basically maintains the basic shape of the coastline in this area and always retains the estuary (circle 1 in the figure) while appropriately adaptively amplifying the estuary and local narrow areas (circles 2 and 3 in the figure) after reducing the scale. For the lagoon coastline in Figure 11, its most prominent feature lies in whether the lagoon spit (circle 1 in the figure) should be retained. From the figure, it can be observed that the lagoon spit in this area is always retained, and adaptive amplification is applied to both the spit and local narrow areas (circles 2 and 3 in the figure). As for the sea area shown in Figure 12, its coastline distribution is relatively complex, including numerous bottleneck narrow areas and long and narrow curves, providing a good assessment of the effectiveness and applicability of the method. According to the simplification results of the method, this paper takes into account the safety principle of “expanding land and shrinking sea” by performing unilateral simplification on the coastline. After reducing the scale, adaptive amplification is applied to local narrow areas as appropriate.
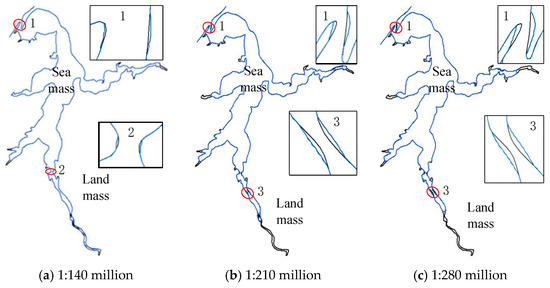
Figure 10.
Estuary coastline simplified results obtained through the proposed method.
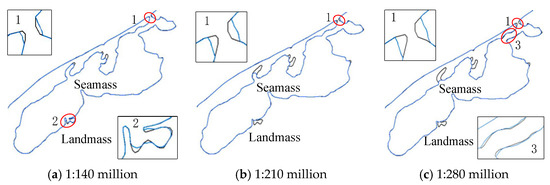
Figure 11.
Lagoon coastline simplified results obtained through the proposed method.
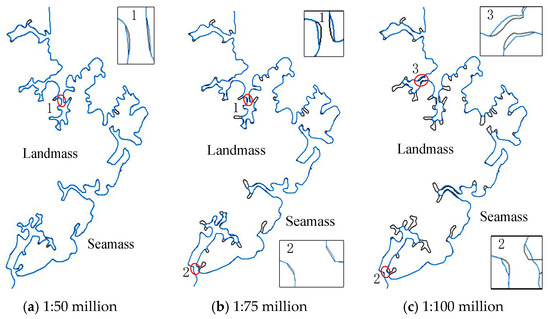
Figure 12.
Complicated coastline simplified results obtained through the proposed method.
Therefore, it can be concluded that for estuary coastlines, lagoon coastlines, and complex region coastlines, this method can achieve good simplification results and meet various simplification principles.
4.2. Methods Comparative Analysis and Evaluation
4.2.1. Qualitative Assessment
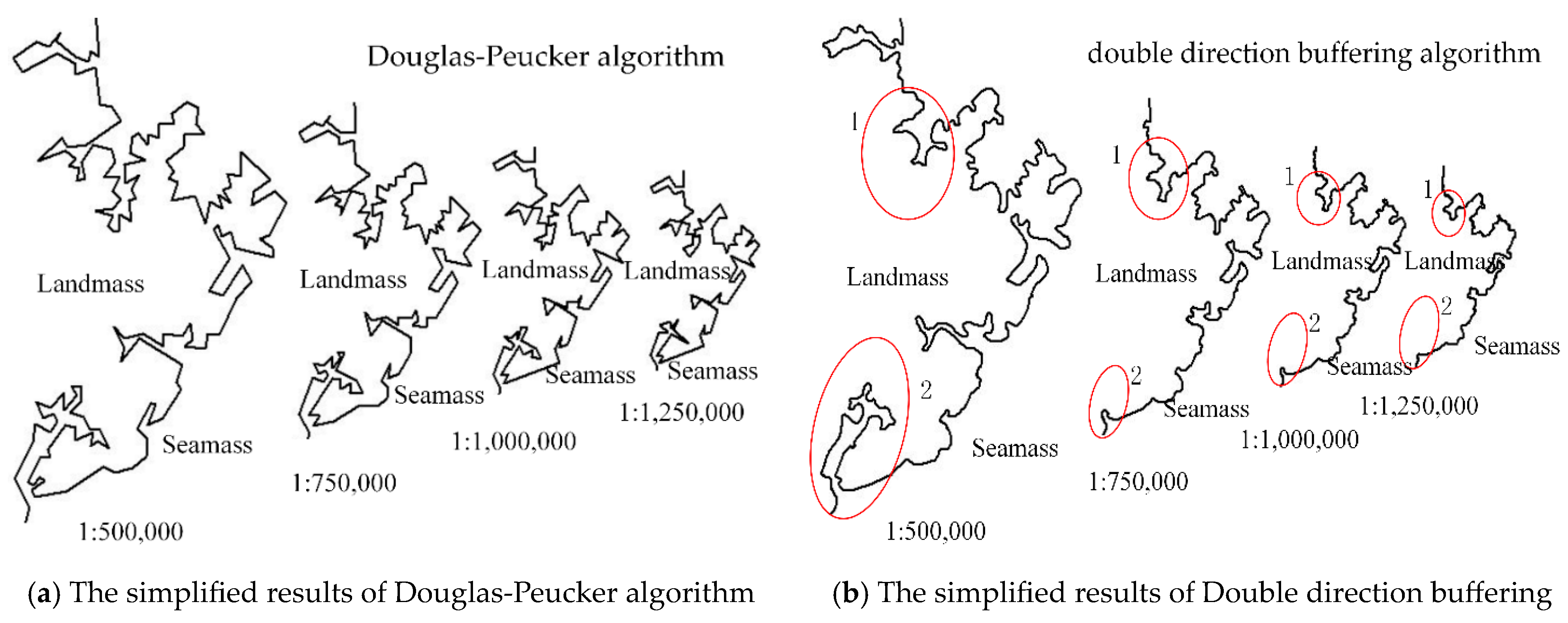
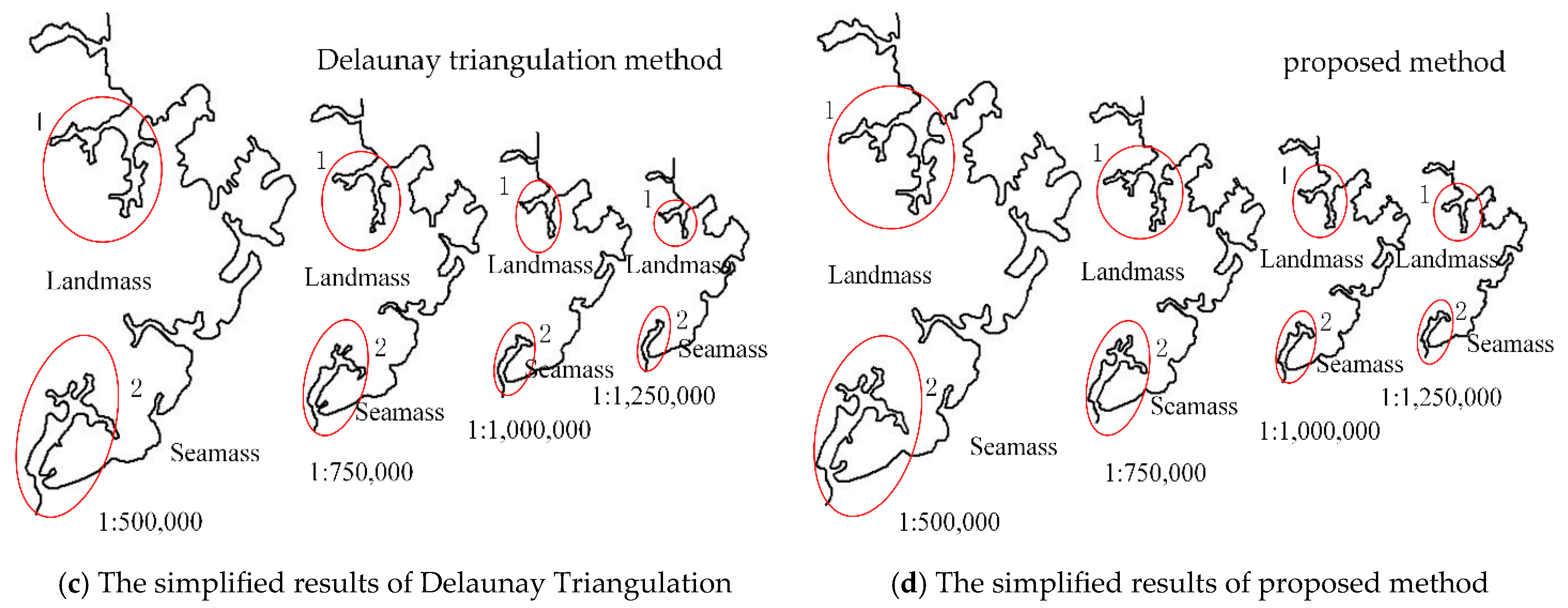
To further evaluate the superiority of the proposed method, the Douglas–Peucker method, the original bidirectional buffer zone method, and the constrained Delaunay triangulation method are selected as comparison methods. The threshold of the Douglas–Peucker method is set to 0.016 cm, the buffer distance of the original bidirectional buffer zone method is the same as that in this paper, and the threshold of the constrained Delaunay triangulation method is set according to reference [17]. The simplification results of the various methods are shown in Figure 13.
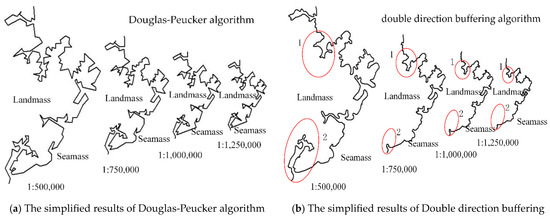
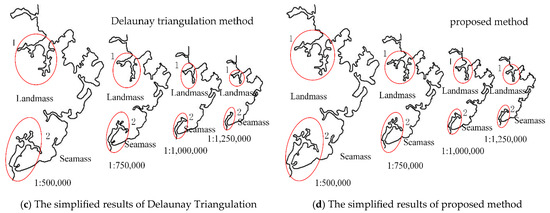
Figure 13.
The simplified results obtained through the different methods.
From the above simplification results, it can be observed that the simplification result of the Douglas–Peucker algorithm has a sharper shape and undergoes significant changes compared to the original coastline. It also suffers from self-intersection issues, making it unsuitable for simplifying complex regional coastlines. The bidirectional buffer zone method produces smoother simplification results. However, as mentioned in Section 2.2 of this paper, this method tends to block off “bottleneck” areas during the simplification process, resulting in the deletion of large fjords (as shown in circles 1 and 2 in the figure) and causing the loss of important geographical elements and poor simplification quality. In contrast, both the constrained Delaunay triangulation method and the proposed method in this paper produce better simplification results, without self-intersection or significant loss of important geographical elements. However, as seen from the figures, the simplification scale of the constrained Delaunay triangulation method is slightly larger than that of the proposed method in this paper. The proposed method retains some details and curves, providing a more comprehensive representation overall. Therefore, the simplification quality of the proposed method is generally comparable to that of the constrained Delaunay triangulation method.
4.2.2. Quantitative Assessment
To further evaluate and compare the above methods, this paper conducts a comparative analysis based on positional accuracy. The evaluation of positional accuracy mainly utilizes the average displacement [36] as a representation, including positive and negative offsets. The positive offset indicates the average distance at which the simplified coastline shifts towards the sea, while the negative offset primarily represents the average distance at which the simplified coastline shifts towards the land. The experimental data are selected from chart number 16,700, which depicts the coastline near the west side of Qinzhou Port (shown in Figure 12). The positional accuracy of each method’s simplification results is presented in Table 1.

Table 1.
Each method’s effect position accuracy statistics table.
As it can be seen from the above table, both the positive and negative offsets of the Douglas–Peucker algorithm are relatively large. Compared to other methods, the bidirectional buffer zone method has a larger positive positional offset and zero negative offset. This is mainly because this method blocks off a large number of existing “bottleneck” areas (as shown in circles 1 and 2 in Figure 13), resulting in a large area of sea becoming land. In addition, because this method does not have a mechanism to handle “bottleneck” areas, the negative offset is zero. Compared to the Douglas–Peucker algorithm and the bidirectional buffer zone method, the constrained Delaunay triangulation method has a smaller positive offset and higher positional accuracy. The proposed method has a negative offset that is basically the same as the constrained Delaunay triangulation method, and it has the smallest positive offset, closely following the original coastline and achieving high positional accuracy compared to the other three methods.
5. Conclusions
Through theoretical derivation and experimental comparison and analysis, the following conclusions are drawn:
- (1)
- The original bidirectional buffer zone method tends to have an excessive simplification scale when dealing with bottleneck areas, as it lacks a mechanism to handle these regions. In this paper, the coastline is adaptively simplified by extracting “bridging” skeleton lines, constructing a visual buffer zone based on the “bridging” skeleton lines, and “bridging” the simplified result line of the original bidirectional buffer zone with local details. Additionally, it can adaptively exaggerate and represent local narrow areas. The simplification quality of this method is generally comparable to that of the constrained Delaunay triangulation method.
- (2)
- Compared to existing methods, the proposed method in this paper has higher simplification accuracy, closely follows the original coastline, and does not contain any non-visible detail parts after simplification, meeting the relevant requirements of the “Standard for Nautical Chart Production”.
Of course, different coastal types have different evolutionary forms [37], and different methods also have different application ranges. At the target scale, this method is mainly applicable to sea areas where the shoreline changes are relatively gentle, such as lagoons and river valleys, and the sum of the width of land and sea areas is greater than twice the visual buffer zone radius. For other types of coastlines that require the expression of coastline cutting, rupture, and multi-angular features (such as island and reef coasts, fjord coasts, etc.), as well as for the multi-scale simplification of coastlines in artificial coasts and other areas, this needs to be gradually addressed in later research.
Author Contributions
Conceptualization, Lulu Tang and Lihua Zhang; methodology, Lulu Tang; software, Lulu Tang; validation, Lulu Tang, Lihua Zhang and Jian Dong; formal analysis, Lulu Tang; investigation, Hongcheng Wei; resources, Shuai Wei; data curation, Shuai Wei; writing—original draft preparation, Lulu Tang; writing—review and editing, Lihua Zhang; visualization, Lulu Tang; supervision, Jian Dong; project administration, Lulu Tang; funding acquisition, Jian Dong All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by National Natural Science Foundation of China grant number [42071439, 41871369].
Data Availability Statement
The raw data supporting the conclusions of this article will be made available by the authors on request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wang, H.; Li, J. Generalization of Nautical Charts; Surveying and Mapping Press: Beijing, China, 1999. [Google Scholar]
- GB12320-1998; Specifications for Chinese Nautical Charts. The State Bureau of Quality and Technical Supervasion: Beijing, China, 1998.
- Liu, H.; Xie, S.; Wang, F. Study on the Method of Automatic Cartographic Generalization of Coastline. J. Geomat. Sci. Technol. 2010, 27, 225–228. [Google Scholar]
- Liu, Y.; Zhai, J. The Research on Pattern Presentation and Automatic Generalization of Coastlines. Geomat. Spatial Inf. Technol. 2005, 28, 78–81. [Google Scholar]
- Chen, H.; Peng, R.; Zheng, Y.; Li, S. Coastline Generalization Basedon Skeleton Line of Curve Bends. Geomat. Inf. Sci. Wuhan Univ. 2011, 36, 1418–1422. [Google Scholar]
- Chen, H.; Zheng, Y.; Guan, H. Improvement of Douglas-Peucker Algorithm Based on Skeleton Line. Hydrogr. Surv. Charting 2011, 31, 18–20. [Google Scholar]
- Visvalingam, M.; Whelan, J.C. Implications of Weighting Metrics for Line Generalization with Visvalingam’s Algorithm. Cartogr. J. 2016, 53, 253–267. [Google Scholar] [CrossRef]
- Ai, T.; Zhou, Q.; Zhang, X.; Huang, Y.; Zhou, M. A Simplification of Ria Coastline with Geomorphologic Characteristics Preserved. Mar. Geod. 2014, 37, 167–186. [Google Scholar] [CrossRef]
- Ai, T.; Ke, S.; Yang, M.; Li, J. Envelope generation and simplification of polylines using Delaunay triangulation. Int. J. Geogr. Inf. Sci. 2017, 31, 297–319. [Google Scholar] [CrossRef]
- Huang, Y.; Yi, T.; Liu, Y.; Zhang, H. Geographic-Feature Oriented Ria Coastline Simplification. Acta Geod. Cartogr. Sin. 2013, 42, 595–601. [Google Scholar]
- Ai, T.H.; Guo, R.Z.; Chen, X.D. Simplification and Aggregation of Polygon Object Supported by Delaunay Triangulation Structure. J. Image Graph. 2001, 6, 703–709. [Google Scholar]
- Ai, T.; Guo, R.; Liu, Y. A Binary Tree Representation of Curve Hierarchical Structure in Depth. Acta Geod. Et Cartogr. Sin. 2001, 30, 343–348. [Google Scholar]
- Poorten, P.V.D.; Jones, C.B. Characterisation and Generalisation of Cartographic Lines Using Delaunay Triangulation. Int. J. Geogr. Inf. Sci. 2002, 16, 773–794. [Google Scholar] [CrossRef]
- Zheng, X.; Xiong, H.; Gong, J.; Yue, L. A Robust Channel Network Extraction Method Combining Discrete Curve Evolution and the Skeleton Construction Technique. Adv. Water Resour. 2015, 83, 17–27. [Google Scholar] [CrossRef]
- Zhai, R.; Fang, W.; Li, Z. Structured Representation of Curve Shape. Geomat. Inf. Sci. Wuhan Univ. 2009, 34, 1021–1024. [Google Scholar]
- Zhao, G. Geographic-Feature Oriented Map Generalization of Complex Lake. Master’s Thesis, Nanjing Normal University, Nanjing, China, 2016. [Google Scholar]
- Du, J.; Wu, F.; Li, J.; Xing, R.; Gong, X. A Progressive Simplification Method for the Estuary Coastline. Acta Geod. Cartogr. Sin. 2018, 47, 547–556. [Google Scholar] [CrossRef]
- Zhang, L.; Tang, L.; Jia, S.; Dai, Z. A Collaborative Simplification Method for Multiple Coastlines Based on the Hierarchical Triangulation Network Partition. Acta Geod. Cartogr. Sin. 2018, 47, 547–556. [Google Scholar] [CrossRef]
- Du, J.; Wu, F.; Zhu, L.; Liu, C.; Wang, A. An Ensemble Learning Simplification Approach Based on Multiple Machine-learning Algorithms with the Fusionusing of Raster and Vector Data and a Use Case of Coastline Simplification. Acta Geod. Cartogr. Sin. 2022, 51, 373–387. [Google Scholar] [CrossRef]
- He, H.; Qian, H.; Duan, P.; Xie, L.; Luo, D. Automatic Line Simplification Algorithm Selecting and Parameter Setting Based on Case-Based Reasoning. Geomat. Inf. Sci. Wuhan Univ. 2020, 45, 344–352. [Google Scholar] [CrossRef]
- Wu, F.; Du, J.; Qian, H.; Zhai, R. Overview of Research Progress and Reflections in Intelligent Map Generalization. Geomat. Inf. Sci. Wuhan Univ. 2022, 47, 1675–1687. [Google Scholar]
- Duan, P.; Qian, H.; He, H.; Xie, L.; Luo, D. A Line Simplification Method Based on Support Vector Machine. Geomat. Inf. Sci. Wuhan Univ. 2020, 45, 744–753. [Google Scholar]
- Ai, T. Some Thoughts on Deep Learning Enabling Cartography. Acta Geod. Cartogr. Sin. 2021, 50, 1170–1182. [Google Scholar]
- Wang, L.; Wu, Y.; Tang, J. A Coastline Generalization Method for Marine Delimitation. Sci. Surv. Mapp. 2015, 40, 18–21. [Google Scholar] [CrossRef]
- Christensen, A.H.J. Cartographic Line Generalization with Waterlines and Medial-Axes. Cartogr. Geogr. Inf. Sci. 1999, 26, 19–32. [Google Scholar] [CrossRef]
- Gao, W.J.; Peng, R.C.; Chen, Y.; Guo, L.X.; Liu, G.H. The research of the double direction buffering algorithm and its application on the generalizing of chart linear feature. Sci. Surv. Mapp. 2009, 34, 187–190. [Google Scholar]
- Dong, J.; Peng, R.; Zhang, L.; Liu, G.; Zhu, Q. Multi-scale Representation of Digital Depth Model Based on Double Direction Rolling Ball Transform according to the Reality Principle. Acta Geod. Cartogr. Sin. 2017, 46, 789–801. [Google Scholar] [CrossRef]
- Dong, J.; Peng, R.; Zhang, L.; Wang, Z. An Algorithm of Filtering Noises in Multi-beam Data Based on Rolling Circle Transform. Geomat. Inf. Sci. Wuhan Univ. 2016, 41, 86–92. [Google Scholar]
- Dong, J.; Peng, R.; Zhang, L.; Liu, G.; Zhu, Q. Multi-scale Representation of Digital Depth Model Based on Rolling Ball Transform. J. Geo-Inf. Sci. 2012, 14, 704–711. [Google Scholar] [CrossRef]
- Wen, L. Evaluate, Regulate and Control Quantificationally the Quality of Simplification of a Depth-Contour in Nautical Chart. Master’s Thesis, Dalian Naval Academy, Dalian, China, 2016. [Google Scholar]
- Ai, T.; Guo, R. Extracting Center-lines and Building Street Network Based on Constrained Delaunay Triangulation. Acta Geod. Et Cartogr. Sin. 2000, 29, 348–354. [Google Scholar]
- Dong, J.; Peng, R.; Chen, Y.; Li, N. An Algorithm for Centre Line Generation Based on Model of Approaching Intersection of Buffering Borderline from Reciprocal Direction. Geomat. Inf. Sci. Wuhan Univ. 2011, 36, 1120–1123. [Google Scholar]
- Liu, X.; Wu, Y.; Hu, H. A Method of Extracting Multiscale Skeletons for Polygonal Shapes. Acta Geod. Cartogr. Sin. 2013, 42, 588–594. [Google Scholar]
- Shen, L.; Wu, B.; Yang, N. Areal Feature Main Skeleton Extraction Algorithm. Geomat. Inf. Sci. Wuhan Univ. 2014, 39, 767–771. [Google Scholar]
- Wang, T.; Wu, H. Extraction of Hierarchical Skeleton of Areal Object Based on Multivariate Analysis. Geomat. Inf. Sci. Wuhan Univ. 2004, 29, 533–536. [Google Scholar]
- Wu, F.; Zhu, K. Geometric Accuracy Assessment of Linear Features’ Simplification Algorithms. Geomat. Inf. Sci. Wuhan Univ. 2008, 33, 600–603. [Google Scholar]
- Leucci, G.; Persico, R.; De Giorgi, L.; Lazzari, M.; Colica, E.; Martino, S.; D’Amico, S. Stability Assessment and Geomorphological Evolution of Sea Natural Arches by Geophysical Measurement: The Case Study of Wied Il-Mielah Window (Gozo, Malta). Sustainability 2021, 13, 12538. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).