Abstract
Spatial epidemiology investigates the patterns and determinants of health outcomes over both space and time. Within this field, Bayesian spatiotemporal models have gained popularity due to their capacity to incorporate spatial and temporal dependencies, uncertainties, and intricate interactions. However, the complexity of modelling and computations associated with Bayesian spatiotemporal models vary across different diseases. Presently, there is a limited comprehensive overview of Bayesian spatiotemporal models and their applications in epidemiology. This article aims to address this gap through a thorough review. The review commences by delving into the historical development of Bayesian spatiotemporal models concerning disease mapping, prediction, and regression analysis. Subsequently, the article compares these models in terms of spatiotemporal data distribution, general spatiotemporal data models, environmental covariates, parameter estimation methods, and model fitting standards. Following this, essential preparatory processes are outlined, encompassing data acquisition, data preprocessing, and available statistical software. The article further categorizes and summarizes the application of Bayesian spatiotemporal models in spatial epidemiology. Lastly, a critical examination of the advantages and disadvantages of these models, along with considerations for their application, is provided. This comprehensive review aims to enhance comprehension of the dynamic spatiotemporal distribution and prediction of epidemics. By facilitating effective disease scrutiny, especially in the context of the global COVID-19 pandemic, the review holds significant academic merit and practical value. It also aims to contribute to the development of improved ecological and epidemiological prevention and control strategies.
1. Introduction
Epidemics pose significant threats to public health, characterized by rapid spread, extensive environmental impact, and challenges in their prevention and control. The recent COVID-19 pandemic has underscored the importance of establishing robust public health surveillance and implementing the best practices [1,2]. The twenty-first century has witnessed the emergence of numerous new health challenges for humanity. This era has seen a heightened focus on public health, driven by rapid advancements in computer technology and an increased awareness of the pivotal role of spatial epidemiology [3]. Spatial epidemiology, leveraging spatial statistics and map visualization techniques, plays a crucial role in characterizing and analysing the spatial distribution of human diseases, health conditions, and the associated environmental factors. By harnessing spatial information, this discipline conducts in-depth investigations into epidemic data [4]. Through its application, spatial epidemiology contributes to a comprehensive understanding of the geographic distribution and incidence trends of diseases, providing valuable theoretical insights for disease surveillance and the development of preventive interventions [4].
In recent years, Bayesian spatiotemporal models have emerged as potent tools for unravelling the intricacies of disease spread, seamlessly integrating both spatial and temporal dimensions [5]. The challenge of tackling high-dimensional integral operations in Bayesian statistics, particularly when estimating numerous parameters, has been effectively addressed through rapid advancements in computer technology and the refinement of the Markov Chain Monte Carlo (MCMC) approach. This progress has propelled Bayesian statistics into the spotlight, garnering substantial attention [6]. Parameter estimates, a key aspect of Bayesian spatiotemporal modelling, are acquired through a conventional statistical technique known as frequency inference, grounded in the likelihood function. Guided by the Bayesian statistical ideological framework, the spatiotemporal model discerns patterns of change inherent in spatiotemporal data [7]. Through the specification of prior distributions and the incorporation of geographical and temporal dependencies, the Bayesian approach quantifies uncertainty in predictions or inferential estimates using probabilities. The primary distinctions between classical statistics and Bayesian statistics are twofold. Firstly, in classical statistics, all unknown parameters are treated as constants, while in Bayesian statistics, these parameters are regarded as random variables and characterized by probability distributions in the pursuit of statistical inference. Secondly, classical statistics relies on overall information and sample information for statistical inference, whereas Bayesian statistics incorporates prior information alongside overall and sample information. Bayesian statistics places a particular emphasis on the extraction, processing, and utilization of prior information [8]. In the Bayesian framework, the foundation for parameter estimates, inference, and prediction lies in the posterior distribution [9]. The posterior distribution is produced by integrating (i) the current sample using the likelihood function, and (ii) the previous distribution of the parameters based on historical or other types of external information [10]. Through the incorporation of prior knowledge modelling, the Bayesian spatiotemporal model delineates the impacts, time effects, and interaction effects in the spatiotemporal domain, offering a comprehensive understanding of the dynamics of disease spread [10].
While spatiotemporal analysis effectively captures features through a series of maps, Bayesian approaches prove instrumental in addressing prevalent modelling challenges in spatial epidemiology, such as non-normality, limited sample sizes, missing data, and clustered data structures. By identifying regions or times of heightened risk, Bayesian methods can uncover disease patterns that persist or evolve predictably over time and across diverse spatial units [11]. The development of a Bayesian spatiotemporal model aims to accomplish key tasks, including the following:
- To assess the anticipated value and uncertainty of a specific outcome variable at a defined spatial point throughout the observation period.
- To forecast the expected value of an outcome variable at a specific location.
- To identify evolving patterns of diseases that persist or undergo predictable changes over time and across various spatial units.
- To analyse the influence of environmental factors on the spatiotemporal dynamics of disease.
In recent years, there have been several reviews on Bayesian spatiotemporal models, most of which followed the Preferred Reporting Items for Systematic Reviews and Meta-analysis (PRISMA) framework [12,13]. These reviews have covered various applications, including spatial and spatiotemporal methods for mapping malaria risk [14], modelling dengue fever [15], analysing COVID-19 epidemiology [16], and exploring joint spatial and spatiotemporal methods in health research [17]. However, it is noted that only a limited number of these reviews have delved specifically into spatiotemporal models or Bayesian inference methods. This suggests that while there is a growing body of research in the broader field of Bayesian spatiotemporal modelling, the detailed exploration of spatiotemporal models and Bayesian inference techniques remains a niche within these systematic reviews.
This review systematically focuses on key aspects of Bayesian spatiotemporal models, including their theoretical foundations, modelling techniques, and computational methods. It provides a detailed examination of the spatiotemporal distribution of data, Bayesian deduction principles, spatiotemporal evolution rules, and calculation methods employed in these models. This comprehensive review not only serves to elucidate the intricacies of Bayesian spatiotemporal models but also underscores their pivotal role in advancing the understanding and control of disease transmission. The integration of advanced statistical methods and computational tools is expected to further propel progress in spatial epidemiology, offering valuable insights into the spatial and temporal dimensions of health events.
2. Literature Review
Epidemiological data frequently exhibit discernible structures in both space and time. Analysing the evolution of diseases enables the identification of patterns and areas of heightened risk. Over the past three decades, significant research efforts have been dedicated to exploring this aspect through the application of spatiotemporal modelling techniques.
Bernardinelli et al. [18] and Bernardinelli et al. [11] employed a Poisson log-linear model by modelling the logarithm of rates as a linear function of time, incorporating spatiotemporal effects. Waller et al. [19] utilized a spatiotemporal conditional autoregressive (CAR)-based model to explore how heterogeneity and spatial patterns evolve over time, considering both temporal effects and spatiotemporal interactions. Waller et al. [20] introduced a random effect for each year, assuming temporal effects are independent of geographical effects. Sun et al. [21] and Kim et al. [22] assumed a linear shape for the temporal trend. Moreover, Kim and Oleson [23] presented a modified technique incorporating an autoregressive process of order one to capture nonlinearity in the temporal trend.
Spatial epidemiology has also made use of the Bayesian nonparametric spatial modelling technique. A unique dynamic mixture model was developed by Böhning et al. [24] to simultaneously discover space–time clusters. By adding spatial dependency and permitting a random number of mixture components in a spatiotemporal environment through the Dirichlet process prior, Kottas et al. [25] expanded the mixture model. In contrast, Yan and Clayton [26] expanded upon Gangnon and Clayton [27]’s spatial cluster model to allow for the space–time clustering of disease counts data.
To concurrently investigate the spatiotemporal variations in disease risks, Richardson et al. [28] undertook a combined modelling approach for two interconnected diseases. Disease risk is decomposed into two components: a common part and a unique part capturing the distinctions between the diseases. Building upon Richardson et al. [28]’s strategy, Musio et al. [29] extended the approach by integrating a model for zero-inflated data with semi-parametrically structured additive predictors. Given that time was treated as a categorical variable in the dataset, the interaction effects were modelled using a changing coefficient approach [30,31].
To account for variations in underlying rates across different seasons within a given year, Torabi and Rosychuk [32] proposed a model incorporating both seasonal and spatiotemporal effects. This modelling technique finds applications in diverse fields, such as the study of malaria diseases [33] and influenza [34,35]. Addressing the challenge of fitting Bayesian spatiotemporal models to large datasets, Chen et al. [36] advocated for a two-stage spatiotemporal technique. In the initial stage, each year’s data were fitted using various geographic models. Subsequently, in the second stage, temporal trends in parameter estimates from each year were analysed, aiming to reduce the computational burden.
Abellan et al. [37] assessed underlying spatial patterns using a two-component joint mixture model for space–time interactions. The first component addresses residual noise, while the second captures deviations from space and time’s main effects. Schrödle et al. [38] compared parameter-driven and observation-driven models, applying Bayesian inference with integrated nested Laplace approximations for parameter-driven models and maximum likelihood for observation-driven models. Cameletti et al. [39] introduced a spatiotemporal modelling approach for particulate matter concentration using the stochastic partial differential equation technique. Bukhari et al. [40] employed correlation methods, seasonal and trend decomposition, hotspot analysis, and conditional autoregressive Bayesian models to assess spatiotemporal clustering and the impact of climatic and socio-economic covariates on disease occurrence in Mexico. In the spread of the COVID-19 pandemic, numerous studies have employed Bayesian spatiotemporal models to discern spatial and spatiotemporal variations [16]. Ref. [41] have devised a Bayesian spatiotemporal model featuring a non-separable, stationary Matern covariance function, which adeptly handles spatial and temporal dependencies by capturing the intricate space–time interactions among geographical locations. Sun et al. [42] considered six spatiotemporal Bayesian hierarchical models based on two spatial conditional autoregressive priors.
Over the past three decades, significant advancements have been made in Bayesian spatiotemporal models in addressing spatial distribution, temporal trends, and the intricate interaction between space and time. These models have evolved to consider various factors, including seasonal changes, the challenges posed by large datasets, and the exploration of multiple model variations. Today, aided by robust computer technology, Bayesian spatiotemporal modelling methods have found widespread and impactful applications.
3. Bayesian Spatiotemporal Models
3.1. Probability Distribution in Spatial Epidemiology
There are two primary types in spatial epidemiology: (1) case event data, encompassing georeferenced instances of cases along with their respective times of diagnosis, registration, or onset, and (2) count data, representing the tally of disease cases within defined tracts over successive time intervals. The seamless extension of spatial data analysis into the temporal domain is readily achievable, as highlighted by Lawson [9]. Figure 1 visually illustrates the progression of space–time dynamics in geographical epidemiology.
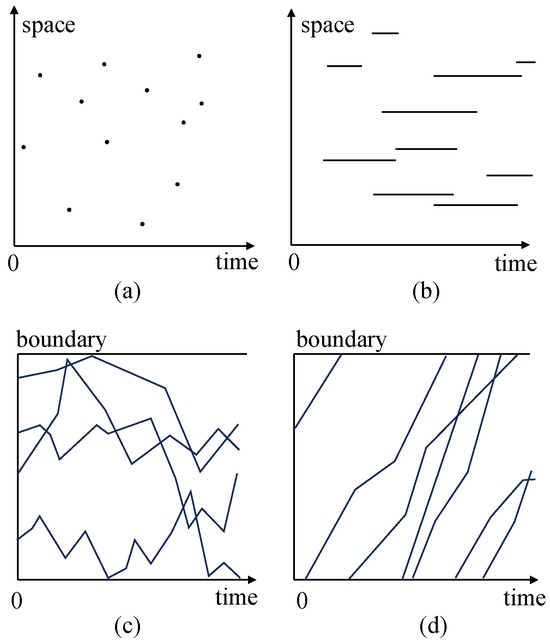
Figure 1.
Evolution of space–time in geographical epidemiology. (a) Representation of space–time points. (b) Dynamic points with temporal changes while maintaining a constant spatial location. (c) Points constrained by static barriers that evolve over time. (d) Temporal influence on the entry at point 0 and exit at point B (adapted from Cox and Isham (1980)).
Several parametric statistical probability distributions common in epidemiology, such as Poisson, binomial, and negative binomial, can be used for the case event data and count data. A brief summary of these distributions is shown in Table 1 (https://mkram01.github.io/EPI563-SpatialEPI/disease-mapping-i-aspatial-empirical-bayes.html, accessed on 22 February 2024).

Table 1.
Probability distributions common to disease mapping.
The Poisson likelihood has been a cornerstone in the toolkit of Bayesian spatiotemporal models for modelling diverse diseases [43]. Typically, a Poisson distribution is favoured when low observed values are expected for each location and period, making it well-suited for situations where disease cases are relatively rare.
Conversely, binomial distribution becomes a valuable choice when describing the occurrence of non-rare or common disease processes, particularly in areas where the incidence of disease (or mortality) is high. This distribution provides an effective framework for situations where events are not rare and their outcomes involve binary states.
For scenarios characterized by rapidly rising disease cases and over-dispersed infectious outbreaks, such as the initial wave of COVID-19 in New England regions in 2020, the negative binomial likelihood, incorporating an additional dispersion parameter, proves more adaptable. Several studies show the efficacy of this model in capturing the heightened variability observed during such outbreaks [1,44,45,46]. In spatial epidemiology, over-dispersion is common due to the presence of often undisclosed factors influencing disease prevalence in each location.
In summary, the choice of likelihood in Bayesian spatiotemporal models is contingent upon the specific characteristics of the disease data, with the Poisson, binomial, and negative binomial distributions offering versatile tools tailored to different scenarios and levels of disease prevalence.
3.2. Models
3.2.1. General Effect Model
In a general form, a spatiotemporal model assumes a logarithmic connection between rates and time within a given area, with variations in the time trend across different regions [11]. Under the framework of general spatiotemporal models, the connection between time and rates within an area is presumed to be log-linear, and time trends are considered to differ across regions [11].
The linear predictor, a rescaled version of the risk designed to enhance the reliability of predictions, is essentially the logarithm or log-odds of the risk (or, less frequently, another link function of the risk), depending on the chosen model for observation [47]. Typically, the additive expression of the linear predictor is the summation of several elements or effects, each representing distinct and independent contributions to risk for a specific area and time period. Generalized linear mixed models (GLMM) over space and time are mostly used in the related research. This concept is exemplified in the following examples:
where the regression models include the following:
- Intercept overall rate ;
- Spatial group ;
- Temporal group ;
- Space-time interaction group .
The pioneering example of modelling space–time relative risk was introduced by Bernardinelli et al. [11]. In their methodology, they embraced a model for the log relative risk, formulated as
where is an area (tract) random effect, is a linear trend term, and is an interaction random effect. Here, , , .
Following this, Waller et al. [20] presented a model incorporating both uncorrelated and correlated heterogeneity terms. Subsequently, Xia and Carlin [48] further advanced and streamlined this model to be
where is a linear time trend, and is a variable measured within the tract unit. In this formulation, , , .
Knorr-Held and Besag [49] devised a model employing binomial likelihood for the number at risk with a probability for the counts. They utilized a logit link to the linear predictor, and the formulation is as follows:
where
is a time-based random intercept, is a th age group effect at time , is a gender × race effect for combination at time , is a fixed covariate effect term with an urbanization index , and encompass both correlated and uncorrelated heterogeneity terms, and notably, these terms are not contingent on time variations. In this formulation, , , .
Recent advancements in spatiotemporal modelling encompassed extensions of mixture models, as demonstrated by Böhning et al. [24]. These models investigated temporal periods independently, without mutual interaction, and for the spatial random effects, they employed a variation of a full multivariate normal spatial prior distribution [21]. Another notable extension involved the modification of the Knorr-Held and Besag model to incorporate diverse forms of random interaction terms, as proposed by Knorr-Held [50].
In exploring the spatiotemporal distribution of disease, the loglinear relative risk can be considered and modelled as a GLMM accounting for spatiotemporal dependence and heterogeneity as follows:
Here, , , , are the spatially structured (spatial autocorrelation), spatially unstructured (spatial heterogeneity), temporally structured (serial autocorrelation), and temporally unstructured (temporal heterogeneity) random effects, respectively, and is the interaction of a pair of the four random effects above. The random effects implicitly capture the determinants of the relative risk [51].
3.2.2. Infectious Disease Model
In the context of the infectious disease mechanism, a susceptible–infected–removed (SIR) model was presumed, as proposed by Wormser and Pourbohloul [52]. The specific variant of the SIR model being evaluated was introduced by Morton and Finkenstädt [53], and was initially applied to analyse measles epidemic time series and later was expanded into the spatiotemporal domain by Lawson and Song [54] for an investigation into influenza outbreaks. The size of the susceptible population at risk in region and period is denoted as . The accounting formula for the SIR model is as follows:
The susceptible population for the current period is obtained by subtracting the previous disease counts, denoted as , and the removed population, denoted as , from the susceptible population of the previous period. This equation takes into account the removals from the population , which could be attributed to factors such as death, relocation, and other reasons.
The two-component endemic–epidemic model proposed by Held et al. [55] can be applied to Bayesian spatiotemporal models. In this model, the authors separated the endemic and epidemic components of the log-linear mean model. Two dissemination patterns for infectious diseases were identified: the local epidemic effect and the lagged epidemic impact. The lagged epidemic effect posited that the pattern of disease counts from the prior period influences the current disease count. Consequently, in areas where disease counts were higher in the prior period, disease dissemination may be more intense.
3.2.3. Environmental Covariates
Bayesian spatiotemporal models offer the capability to integrate diverse data types, including demographic, environmental, and healthcare data. This integration of various data sources can significantly enhance the comprehension of the fundamental processes influencing the spread of diseases [56,57]. The types and quantity of covariates generally exhibit a wide range of variations. Six distinct categories of covariates were identified, as reported in the review by Aswi et al. [15], including climatic, demographic, socioeconomic, entomological, geographic, and temporal covariates. This comprehensive classification was based on the insights derived from the aforementioned review, providing a framework for a more holistic understanding of the spatiotemporal dynamics of disease.
In certain scenarios where factors can influence the linear predictor, an additional component is introduced as follows:
Covariates can be either time-varying or time-invariant accounting for uncertainty arising from measured confounders, where is the environmental covariates’ matrix for county and time and is a vector of regression parameters [9,58,59].
3.2.4. Prior Distribution
Bayesian inference takes all the parameters as random variables with prior probability distributions. In Bayesian disease mapping, a spatially structured random effect is commonly addressed in a hierarchical model’s second level using random effects with CAR prior distributions, falling under the category of Markov random fields. Besag et al. [60] introduced intrinsic and convolution CAR priors, but these lack clear differentiation between structured and unstructured random effects, causing identification issues [61]. Leroux et al. [62] proposed the Leroux prior to explicitly distinguish between structured and unstructured spatial variation, offering greater flexibility in representing various spatial correlation scenarios [63]. Krisztin et al. [64] suggested using spatial econometrics, applying the Spatial Autoregressive (SAR) model to quantify spatial spillover, also known as the spatial error model in spatial econometrics.
In the unstructured heterogeneity model, the spatial effects are assumed to be sampled from a normal distribution with mean 0 and precision ,
In the clustering model, the Gaussian CAR distribution was employed, enabling the mean of the structured effect to depend on its neighbouring values [65]. The CAR prior model postulates that the risk of disease occurrence in a given spatial area is influenced by its nearby geographical neighbours, thereby exhibiting spatial autocorrelation. In essence, it assumes that spatial areas in close proximity share more similar disease occurrence risks. Formally, the joint distribution of is denoted:
where indicates that areas and are neighbors, is the number of areas that share boundaries with the th area, and is the variance component. Spatial dependence in is modelled with a CAR prior that extends the well-known Besag model [66] with a Gaussian distribution. This implies that each is conditional on its neighbour with variance being dependent on the number of neighbouring counties of county .
Based on the existing knowledge of the primary risk variables, the choice between heterogeneity and clustering models can be made. A clustering model emerges when risk factors extend beyond the boundaries of one or more areas, leading to comparable risk values in neighbouring regions. On the other hand, a heterogeneity model arises when the scope of risk determinants is smaller than the size of a region.
Among the various suggestions proposed in the literature for implementing risk smoothing, the approach presented by Besag et al. [60] has exerted the most significant influence. Referred to as the BYM specification, this method formed the basis for spatial modelling in the majority of the models examined in this evaluation [67]. The integration of clustering effects and heterogeneity plays a pivotal role in determining the risk associated with a specific area.
The temporal components also include two random effects: the term is the unstructured time effect, which is specified using an independent mean–zero normal prior to the unknown variance :
The term represents the organized temporal impact and is dynamically modelled using a neighbouring structure. In this instance, the structured temporal impact precedes the random walk dynamic model [10], with its prior density expressed as follows:
Similar to CAR, the random walk prior model posits that nearby time points (temporal correlation), represented as a smoothly fluctuating nonlinear curve, exert an influence on the temporal fluctuation of the risk of disease occurrence [68].
For a temporal trend, a random walk prior of order one (RW1):
or order two (RW2):
is appropriate for the temporal trend , with as the variance hyperparameter of .
For the unstructured temporal effects , the exchangeable prior could be:
where is the variance hyperparameter of .
The spatially structured, spatially unstructured, temporally structured, and spatially unstructured effect with the distribution are schematically shown in Figure 2.
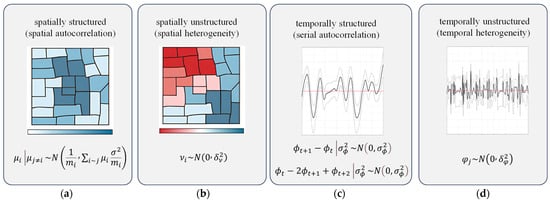
Figure 2.
Schematic diagram of spatially structured (a), spatially unstructured (b), temporally structured (c), and spatially unstructured (d) effect and their distribution.
For the four interaction components, the priors are the products of the priors of the corresponding components. The crucial element in spatiotemporal models is the spatiotemporal interaction, which can be particularly challenging given the array of options and the absence of a universally recognized benchmark that consistently performs well. Knorr-Held [50] introduced a classification system comprising four potential types of interaction between spatial and temporal random effects [47,69], shown in Table 2 and Figure 3.

Table 2.
Four types of space–time interaction (proposed by Knorr-Held [50] and adopted from [69]). (✓ means it has correlation; - means it doesn’t have correlation.)
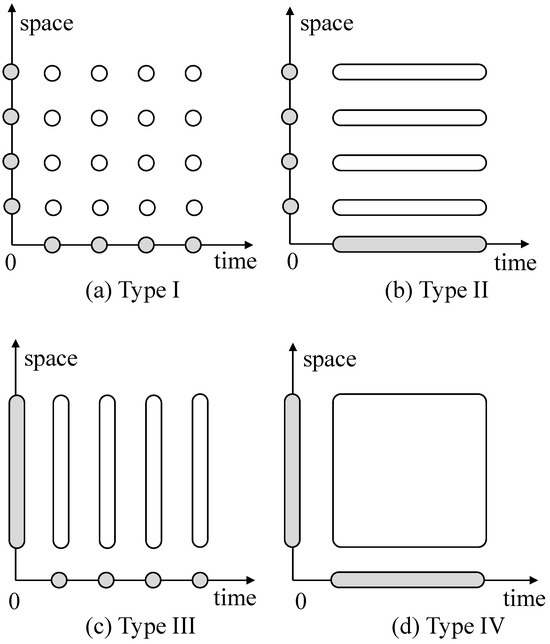
Figure 3.
Symbolic representation of the four possible types of interactions. Circles represent prior independence and ovals represent prior dependence (adopted from Knorr-Held [50]).
A Type I space–time interaction can be conceptualized as distinct, with unstructured unobserved factors for every possible combination of location and period. In this case, the assumption is that risk is independent in space but similar throughout time. A Type II interaction consists of temporally organized but geographically unstructured effects. Here, the assumption is that risk shows a temporal correlation but is independent across different locations. A Type III interaction assumes that risk exhibits geographic autocorrelation for each time period but is independent over time. This type comprises spatially structured but temporally unstructured effects. A Type IV space–time interaction assumes that global trends are both spatially and temporally connected, capturing both spatial and temporal structures’ risks.
In the Bayesian framework, a notable challenge arises when selecting appropriate prior distributions and determining the corresponding parameter values. The intricacies of hierarchical modelling are further compounded by the imperative to define prior distributions for both model parameters and variance parameters, commonly known as hyperparameters. Widely employed distributions in this context encompass logGamma for log-inverse variance, Half-Cauchy, Penalized Complexity, and Uniform distribution for hyperparameter standard deviation [70].
3.3. Bayesian Inference
The Bayesian approach, named after Thomas Bayes, an English clergyman (1702–1761), revolved around a method of data analysis that emphasizes conditional probabilities linking observed and unknown quantities. This paradigm enables the assessment of the likelihood of a specific hypothesis based on the observed data.
Bayesian methods offer the advantage of incorporating prior information with observed data to estimate parameters and make predictions. Although frequentist statistical analysis still underpins the majority of practical statistical applications, Bayesian methods have emerged as the standard in numerous fields, particularly in the modelling of spatiotemporal epidemiology. Their utility is particularly evident in public health policy and clinical settings, where study results can directly influence decision making.
Bayes’ theorem, as articulated by Gelman [71], is fundamental to Bayesian statistics and states that
which means Posterior likelihood × prior, where is the observed data and is the unobservable vector quantities or population parameters of interest. As elucidated by Austin et al. [72], the probability distribution of a parameter was derived by multiplying its prior probability distribution by the likelihood function and then dividing the result by the probability of the data, conditioned on the observed data. The resulting distribution is referred to as the posterior distribution.
This theorem provides a framework for updating beliefs (posterior probability) based on new evidence (likelihood) and prior knowledge (prior probability). The versatility of Bayesian methods makes them valuable tools in exploring complex relationships and uncertainties, offering a comprehensive approach to statistical modelling in various disciplines.
A tutorial on the Bayesian workflow for disease transmission modelling in Stan has been provided (https://mc-stan.org/users/documentation/case-studies/boarding_school_case_study.html, accessed on 28 December 2023). The tutorial illustrates the processes of constructing, fitting, and assessing disease transmission models utilizing a fundamental susceptible–infected–recovered (SIR) model. Figure 4 provides an overview of the Bayesian model’s functionality through a simplified process (adapted from Martin et al. [73]).
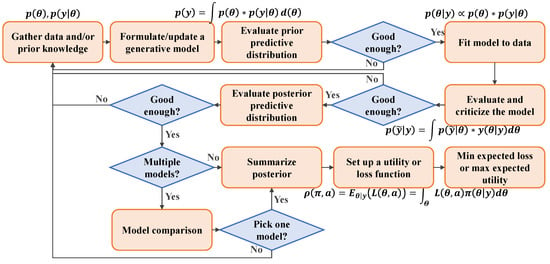
Figure 4.
Bayesian workflow (modified from Martin et al. [73]).
3.4. Computational Algorithms
3.4.1. Markov Chain Monte Carlo
Markov chain Monte Carlo (MCMC) methods, which simulate direct draws from complex distributions of interest, are widely employed in Bayesian computation. MCMC algorithms generate a Markov chain by utilizing past sample values to randomly generate the next sample value. Typically, the Markov chain begins at any random point and gradually converges to the desired distribution. The Gibbs sampler [74] and the Metropolis algorithm [75,76] are commonly used in a variety of Bayesian applications. For further details and variations on MCMC approaches, refer to Gilks et al. [77].
3.4.2. Integrated Nested Laplace Approximation
Rue et al. [78] have introduced the integrated nested Laplace approximation (INLA) as an alternative to sampling-based methods, addressing the slow convergence and high computational cost associated with MCMC methods. INLA is particularly useful for latent Gaussian field structured additive regression models, providing an approximation for Bayesian inference.
In each equation, the symbol can be employed to represent the vector of all Gaussian variables and the vector of hyperparameters, which are not necessarily Gaussian. Another approach to express the marginal posterior density of an image is as follows:
To approximate the first component , three different approaches are possible: a Gaussian approximation, a full Laplace approximation, and a simplified Laplace approximation. Rue et al. [78] introduced the simplified Laplace approximation, which was based on a series expansion of the full Laplace approximation. This method is less time consuming and proves to be highly competitive in many applications. Finally, an approximation of the posterior marginal density is given using
As computation with INLA has gained popularity, several comparisons between INLA methods and MCMC algorithms have been conducted. These investigations have consistently demonstrated that the two strategies perform similarly. According to Schrödle and Held [69], the outcomes of MCMC simulations and the full Laplace approximation of INLA are nearly identical. Other studies, including posterior predictive checking by Held et al. [79], and survival models by Martino et al. [80], have reported very similar outcomes between INLA and MCMC. The INLA software package, recently developed in R (Integrated Nested Laplace Approximation), has become a commonly used approach for implementing Bayesian models [16].
3.5. Model Fit Criteria
In disease mapping studies, the Deviance Information Criterion (DIC), introduced by Spiegelhalter et al. [81], was widely employed as one of the goodness-of-fit statistics. DIC relies on comparing the average deviance and the deviance of the posterior parameter estimates. It is defined as
where D[.] is the deviance of the model, and θ is the parameter set of the model. In model comparison, a smaller DIC indicates a better goodness-of-fit.
Another goodness-of-fit statistic could be Watanabe–Akaike information criterion (WAIC) [82].
The Mean Squared Error (MSE) for comparing data points and posterior mean estimates is given by Kim et al. [1]:
where is the number of MCMC samples, is the total number of the area, and is the total number of time periods. The MSE is computed as the sum of the squared differences between the actual data and posterior estimates at each sampling period and then averaged over the entire time, space, and sampling periods.
For short-term prediction evaluation, the one-step-ahead prediction from the posterior estimates of the last time period can be compared with real data, as suggested by Kim et al. [1].
For each sampling period , is sampled from the estimated, while is calculated using the values from the previous time period .
In addition to the measures mentioned above, the predictive performance of models can be further evaluated by assigning numerical scores based on their predictive distributions. In accordance with this approach, given a set of spatiotemporal observations , the logarithmic score (LS) [83], and probability integral transform (PIT) [84] are defined as follows:
and
where represents the conditional predictive ordinate [85]. It signifies the cross-validated predictive probability mass at the observed count .
A smaller LS indicates a better prediction. The PIT histogram provides an indication of the model fit across all observations. The closer the PIT histogram aligns with the uniform distribution histogram, the better the overall fit of the model [86].
Various model selection criteria used in studies include Bayesian cross-validation criterion (BCV), mean absolute percentage error (MAPE), Root Mean Squared Error (RMSE), Continuous Ranked Probability Score (CRPS), highest probability (HPM), mean absolute error (MAE), Pearson correlation coefficient (r) [87], which are appropriate statistics for prediction of performance evaluation, and for the best prediction (BPM) [16]. Each criterion provides a different perspective on model performance, and the choice often depends on the specific goals and characteristics of the analysis.
4. Early-Stage Modelling Work
4.1. Data Collection
4.1.1. Epidemic Data
Several websites provide epidemic data and updates on infectious diseases. Here are some reputable sources for epidemic data in Table 3.

Table 3.
Reputable sources for epidemic data.
4.1.2. Geographical and Socioeconomic Data
There are several reputable sources that provide a wide range of geological and Earth science information. Here are some key websites for geosciences data in Table 4.

Table 4.
Key websites for geosciences data.
There are some websites that provide meteorological data and information, where you can access weather-related data. Here are some key websites for meteorological data in Table 5.

Table 5.
Key websites for meteorological data.
There are several reputable sources that provide socioeconomic data, where you can access a wide range of information related to social and economic indicators. Here are some key websites for socioeconomic data in Table 6.

Table 6.
Key websites for socioeconomic data.
Other products such as daily land surface temperature (LST) measurements, North American Land Data Assimilation System (NLDAS) data, normalized difference vegetation index (NDVI) raster data, are also accessible in Google Earth Engine™ [88].
Socioeconomic data can also come from the Statistical Yearbook Sharing Platform in China, including the land area of the administrative region, the total population at the end of the year, the gross domestic product (GDP), the total power of agricultural machinery, and the number of beds in medical and health institutions.
4.2. Data Preprocessing
4.2.1. Preprocessing for Data Integrity
To ensure data integrity, preprocessing steps encompass interpolation [89], classification, normalization, and standardization. Addressing missing values is crucial; we must adopt appropriate handling methods, incorporating imputation if necessary. When examining environmental and social risk factors for infectious diseases using a Bayesian spatiotemporal framework, the population is interpolated linearly across the study period and extrapolated for the other period from the trend [89]. Equally important is the identification and appropriate handling of outliers, as they can significantly impact the model’s results.
Normalization or standardization of variables is vital to ensure that they are on similar scales, particularly when merging variables with different units. Additionally, it is crucial to verify that spatial data are accurately georeferenced and align with the coordinate system used in the analysis. To avoid biases in model estimation, thorough exploration and addressing of spatial autocorrelation is necessary.
4.2.2. Preprocessing for Data Statistics
Preprocessing for data statistics involves assessing the normality and multicollinearity of the data. The normality test utilizes the Kolmogorov–Smirnov (K–S) method. To address spatial autocorrelation and prevent biases in model estimation, a comprehensive exploration should be conducted.
Multicollinearity is assessed by calculating the variance inflation factor (VIF). Variables with VIF ≥ 10 indicate multicollinearity, prompting the removal of one variable at a time until multicollinearity is resolved.
In the presence of a correlation between influencing factors, principal component analysis (PCA) can be employed to reduce dimensions and avoid collinearities. The cumulative contribution rate reaching over 80% guides the determination of the number of principal components, aligning with the actual meaning of each component.
For credible intervals, computation involves fitting the full model. These intervals, serving as the Bayesian counterpart to frequentist confidence intervals, allow for the identification of parameters that are not significant predictors if their credible intervals contain 0 [90].
4.3. Statistical Software
A statistical analysis can be conducted using various tools including ArcGIS Desktop/ArcGIS Pro, GeoDa, SaTScan, QGIS, and R. Additionally, specialized software like GWR4, BayesX, and WinBUGS can be employed for specific spatial analyses [16].
For the development of Poisson regression models within a region-level Bayesian framework, WinBUGS proves useful, offering a platform for Bayesian model iteration [91]. OpenBUGS software facilitates the assessment of the spatial sociological impact of diseases through Gibbs sampling, generating a Markov chain from the complete conditional probability distribution. GeoBUGS, an OpenBUGS add-on, fits spatial models and produces diverse maps as outputs, allowing for the mapping of relative risk for different regions [92].
An interface with R, called R-INLA, provides an alternative for model specification and fitting within the R environment. Downloadable from http://www.r-inla.org/ (accessed on 9 March 2024), it offers documentation, numerous worked examples, and a discussion forum. R-INLA is versatile, handling fixed effects, non-linear terms, and random effects in a formula argument, providing flexibility for the specification of different models and priors options [10].
5. Applications
The Bayesian spatiotemporal model serves the crucial purpose of estimating disease transmission risk, pinpointing areas with elevated spatial incidence, and aptly considering the susceptibility–infection–recovery model within the population. Simultaneously, this model is adept at assessing the influence of physical geographical and socioeconomic factors on disease incidence. Natural factors encompass elements like temperature, rainfall, and air pollution, while socioeconomic factors include aspects such as economic indicators, healthcare accessibility, and population demographics.
The applications of Bayesian spatiotemporal models are diverse. Here are the four key areas:
Disease surveillance: offering real-time risk estimates and assisting dynamic disease surveillance.
Epidemic forecasting: by modelling the spatiotemporal dynamics of diseases, these models enable the forecasting of future outbreaks, facilitating timely intervention and resource planning.
Identifying hotspots: effectively pinpointing spatial and temporal hotspots, these models highlight areas with consistently high disease risk or where risk is escalating over time.
Public health planning: the insights derived from Bayesian spatiotemporal models play a pivotal role in guiding public health planning and resource allocation, identifying priority areas and populations at high risk.
Bayesian spatiotemporal models serve as powerful tools for comprehensively analysing the distribution and trends of both non-communicable and infectious diseases across diverse regions and over varying time periods.
In the realm of non-communicable diseases (e.g., cardiovascular diseases, cancers, chronic respiratory diseases, and diabetes), these models play a pivotal role. For instance, in cardiovascular disease research, Bayesian spatiotemporal models can effectively map cardiovascular mortality, pinpoint regions with elevated prevalence [93,94], identify associated risk factors [95], and evaluate the nuanced impacts of these factors. Likewise, in cancer epidemiology, these models facilitate the meticulous analysis of cancer incidence and mortality. They empower researchers to identify clusters of cancer cases, delve into potential environmental risk factors [96], and gauge the effectiveness of interventions [97]. Moreover, in the study of diseases like asthma or chronic obstructive pulmonary disease, Bayesian spatiotemporal models prove invaluable by helping identify areas with high prevalence and investigating potential environmental triggers [98]. In the context of diabetes, these models are instrumental in the analysis of spatial and temporal patterns of diabetes prevalence. They contribute to predicting trends and assessing influential factors contributing to the global prevalence of diabetes in recent years [99].
In the realm of infectious diseases, the significance of Bayesian spatiotemporal models is heightened, as they provide a nuanced understanding of disease dynamics and interactions. The detailed importance of these models is elucidated below.
5.1. Viral Infection
The virus typically spreads through respiratory droplets, direct contact, or vectors like mosquitoes. Consequently, in densely populated areas, viral infections often experience swift and extensive dissemination. Geographically, viral infections can have a global distribution, but prevalence rates vary based on factors such as the environment, population density, and socioeconomic conditions. Temporally, viral infections may display seasonal patterns distinct from other infection patterns. For instance, COVID-19 and influenza are more prevalent during colder months.
5.1.1. COVID-19
Bayesian spatiotemporal models have been widely utilized for COVID-19 analysis and forecasting globally, including in the United States [100,101,102], England [103,104], Spain, Italy, Germany, Sweden [87,105,106,107], Africa [108], and in some regional areas such as the West Java Province, Indonesia [109], and the Greater Seoul Area, Korea [110]. As an illustration, Nazia et al. [111] applied a Bayesian hierarchical spatiotemporal model to assess the COVID-19 risk. Their model incorporated satellite-derived remote sensing data on land surface temperature and various socioeconomic covariates from January 2020 to October 2021 for 140 neighbourhoods in Toronto. The resulting spatial relative risk and spatiotemporal trends were visually represented, revealing heterogeneous risk patterns, particularly in western and southern Toronto (Figure 5).
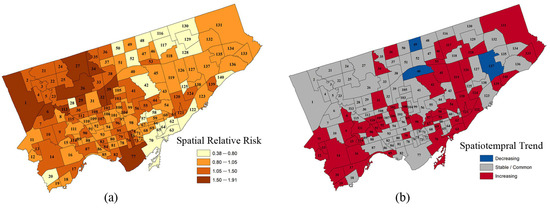
Figure 5.
(a) The estimated overall spatial pattern derived from the posterior means of the spatial relative risks for COVID-19 within neighbourhoods of Toronto from January 2020 to October 2021. (b) The spatiotemporal trend of the relative risks in Toronto from January 2020 to October 2021. (Adopted from Nazia et al. [111]).
5.1.2. Influenza
A Bayesian spatial CAR model assessed the spatiotemporal distribution of H7N9 infection risk in Shanghai from February 19 to 14 April 2013, revealing high variations in the east and centre of the city [112]. Another study focused on China, using a Bayesian hierarchical conditional autoregressive model with five covariates to predict seasonal relative risk for human H7N9 infection [113]. Lemey et al. [114] applied Bayesian inference to H1N1pdm genetic data for global epidemic spread considering meteorological and socioeconomic variables and accounting for spatial autocorrelation. [115] used Bayesian phylogeography on H5N1 and H7N9 haemagglutinin sequences to identify migration patterns and investigate associated risk factors [2].
5.1.3. Haemorrhagic Fever
Two Bayesian spatiotemporal CAR models were employed, one allowing for discontinuities in risk between neighbouring areas. Utilizing these models facilitates the identification of distinct groups of areas and assesses the impact of climatic covariates, offering valuable insights for informing policy decisions [116]. Another study focused on HFRS incidence in mainland China from 2015 to 2018, employing a Bayesian hierarchical spatiotemporal distribution model. The analysis revealed significant positive associations between HFRS development and woodland and grassland areas, economic factors, and traffic levels, with traffic having the most substantial promoting effect [117].
5.1.4. Ebola
Bayesian model inference was employed to assess the Ebola outbreak in Western Africa (2014–2015), integrating individual-level spatial information with epidemiological data. Superspreaders were identified as crucial for sustaining epidemic transmission [118]. A Bayesian hierarchical Poisson model estimated Ebola virus disease risk, linking it to factors like households lacking radios, increasing rainfall, and urban land in districts [119]. Utilizing fully Bayesian geostatistical analysis through stochastic partial differential equations revealed a positive association between violent events in affected areas and reported Ebola virus disease cases and deaths [120].
5.1.5. Dengue
The Bayesian method suggests a spatial and temporal positive correlation between the spreading pattern of Aedes aegypti, as indicated by Dengue haemorrhagic fever incidence in East Java [121]. The relationship between egg numbers and climatic/environmental variables was examined through Bayesian zero-inflated spatiotemporal models [122]. Martínez-Bello et al. [123] employed alternative models to assess dengue transmission risk. A systematic review by Aswi et al. [15] summarized Bayesian spatial and spatiotemporal approaches for modelling dengue fever. To better understand the effects of niche variables in the epidemiological process, Poisson-lognormal and binomial models were explored using various Bayesian spatiotemporal methods [124]. Different structure models, including autoregressive and random walk, were developed for dengue counts in Kendari, Indonesia [125].
5.1.6. Rabies
The absence of human-to-human transmission means that the spread of rabies is not substantially influenced by human distribution or migration [126]. Bayesian hierarchical frameworks were employed to assess spatial and spatiotemporal patterns of rabies infection among striped skunk cases in the North Central Plains of the US [127]. In eastern Germany, a hierarchical Bayesian state–space model was applied to analyse three decades of fox rabies cases and oral rabies vaccination campaigns [128]. Spatiotemporal Bayesian regression models were used to evaluate the impact of accessibility to rabies on post-exposure prophylaxis patients, generating a risk map for optimal new centre locations in Cambodia [129]. In a One Health approach focusing on Thailand, a Bayesian spatial regression model, specifically a CAR Bayesian zero-inflated Poisson regression, quantified the location-based risk of dog-mediated rabies for both human and animal populations [130]. The study further modelled ecological and socio-economic variables associated with dog rabies using univariate analyses with zero-inflated negative binomial regression and multivariable spatial analyses. In China, annual rabies incidence data at the province level from 2004 to 2019 were analysed using a Bayesian hierarchical spatiotemporal model to determine the impacts of environmental, economic, and demographic factors [131]. Kanankege et al. [130] also fitted a conditional autoregressive Bayesian model for human and animal rabies, emphasizing factors such as dog bites and ownership.
5.2. Bacterial Infection
Bacterial infections can spread through various avenues, such as person-to-person contact, contaminated food or water, and vectors. From a spatial standpoint, these infections often manifest in localized patterns, influenced by environmental factors and population dynamics. The prevalence can vary based on factors like sanitation and living conditions. Temporally, bacterial infections typically exhibit a slower spread compared to viruses. Predicting their temporal distribution is more challenging than that of viral infections. Some bacterial diseases endure year-round, while others experience intermittent outbreaks, adding complexity to their overall temporal dynamics.
5.2.1. Salmonellosis
A Bayesian hierarchical spatiotemporal model identified significant spatial and temporal influences on Salmonella spp. isolation from litter, along with notable effects from broiler house size, total housing area per farm, broiler house type, and the number of litter recycles [132]. Subsequently, Bayesian spatial regression, using a reparametrized Besag-York-Mollié Poisson model, was employed to quantify structured and unstructured spatial effects while considering potential risk factors for Salmonella infection at the province level [133].
5.2.2. Tuberculosis
Bayesian spatiotemporal models have been applied to study tuberculosis in various countries, including India [134], China [135,136,137], Kenya [138], Indonesia [139], Ethiopia [140]. Srinivasan and Venkatesan [134] examined disease rates among Indian states, assessing neighbourhood tuberculosis infections and their causes using Bayesian models with a CAR approach for spatial and temporal pattern changes in two survey periods. Cao et al. [137] identified influencing factors for tuberculosis in certain cases. Li et al. [135] employed a Bayesian spatiotemporal model to analyse the correlation of socioeconomic, healthcare, demographic, and meteorological factors with the population-level number of tuberculosis cases. Amsalu et al. [141] used a Bayesian CAR model to explore the spatial–temporal pattern of tuberculosis in the geriatric population and its association with meteorological and sociodemographic factors. Liu et al. [142] constructed Bayesian spatiotemporal models to analyse the association between ambient air pollutants and pulmonary tuberculosis incidence, adjusting for socioeconomic covariates. Wahyuni and Syam [143] employed a Bayesian approach for spatiotemporal modelling of tuberculosis cases in Makassar City, comparing seven Bayesian Spatiotemporal CAR models using measures like DIC and WAIC. Madden et al. [144] explored different spatiotemporal random-effects models, including the negative binomial Besag-York-Mollié model, using comprehensive data to examine the association between covariates and the number of bovine tuberculosis cases.
5.2.3. Brucellosis
Ahasan et al. [145] used spatial analysis to estimate the true prevalence of brucellosis and assess test performances. In South Korea, Lim et al. [146] conducted spatial analysis to examine the relationship between human and bovine brucellosis. Rahmanian et al. [147] analysed temporal trends of human brucellosis in Yazd Province, Iran, between 2013 and 2018, predicting future incidence trends. Liang et al. [148] estimated the spatiotemporal distribution of human brucellosis in Inner Mongolia, China, and identified influencing factors using Bayesian spatiotemporal models.
5.2.4. Anthrax
Bayesian spatiotemporal models for anthrax were applied in Vietnam [149,150] and Kenya [151]. In Kenya, a Bayesian approach was employed to analyse a long-term dataset of livestock anthrax cases from 2006 to 2020. Spatial and spatiotemporal models were developed to investigate the distribution and socio-economic drivers of anthrax occurrence and incidence at both national and sub-county levels [151].
5.3. Parasitic Infection
Parasitic infections typically propagate through vectors, such as mosquitoes transmitting malaria, or through the consumption of contaminated water and food. The life cycle of a parasite often spans multiple hosts, impacting both its spatial and temporal distribution. Geographically, the prevalence of parasitic infections is shaped by the habitat and behaviour of vectors or intermediate hosts participating in the transmission cycle. Temporally, parasitic infections can manifest with intricate life cycles; certain parasitic diseases may experience seasonal variations, while others may be characterized by more extended periods aligned with the parasite’s life cycle.
5.3.1. Malaria
Bayesian spatiotemporal models for malaria have been employed in various regions, including Burkina Faso [152], Pará [153], Nigeria [154], Rwanda [155], and Thailand [156]. Alegana et al. [157] utilized a Bayesian conditional–autoregressive model to assess spatial and temporal variations in malaria incidence, considering test positivity rates and health facility utilization. Haddawy et al. [158] applied Bayesian networks to model malaria, creating village-level models with weekly temporal resolution in the Tha Song Yang district, Thailand, using cases and environmental covariates, including NDVI, LST, rainfall, slope, distance to nearest stream, stream density, and distance to border. Semakula et al. [159] used spatiotemporal models to estimate excess probability for decision making for malaria incidence reduction, employing SIR and BYM models with routine health facility data from 2012 to 2018 in Rwanda. A systematic review on spatial and spatiotemporal methods for mapping malaria risk was conducted by Odhiambo et al. [14]. In their review, approximately half (44%) of the studies employed variable selection techniques prior to mapping with rainfall and temperature selected in over 50% of the studies. Malaria incidence (47%) and prevalence (35%) were the most commonly mapped outcomes, with Bayesian geostatistical models often (31%) being the preferred approach to risk mapping.
5.3.2. Toxoplasmosis
Bayesian spatiotemporal models for toxoplasmosis have been utilized in various regions, including China [160], Brazil [161], and Africa [162]. In Jiangsu province, China, Yang et al. [163] employed Bayesian spatiotemporal models to analyse Schistosoma japonicum infection risk, determining relationships between key climatic factors and infection prevalence at the county level. Welton and Ades [164] presented a Bayesian evidence synthesis model combining data on toxoplasmosis seroprevalence, seroconversion, and tests of recent infection to estimate its current incidence in the UK, incorporating a hierarchical structure over geographic regions, a random-walk model for temporal effects, and a fixed-age effect. Hu et al. [160] identified high-risk counties for schistosomiasis in Anhui province, China, and described trends using a Bayesian hierarchical spatiotemporal model with annual parasitological and environmental data. Melo et al. [165] assessed the temporal trend, spatial analysis, and spatiotemporal clusters of infant mortality associated with congenital toxoplasmosis in Brazil, with spatial analysis (including Global Moran Index, Global Geary’s Contiguity, and Getis-Ord General statistics) and spatiotemporal scan methods.
5.4. Other Infections
The assessment of Mediterranean spotted fever, rickettsiosis in Italy, involved the analysis of spatiotemporal distribution using hospitalization records, as explored in the records of Gomez-Barroso et al. [166]. In Brazil, Baquero and Machado [167] investigated the spatiotemporal dynamics and risk factors associated with Leptospirosis. Similarly, in Mahasarakham province, Thailand, Viroj et al. [168] delved into the spatiotemporal aspects of Leptospirosis. Meanwhile, Dhewantara et al. [169] studied Leptospirosis in China, contributing insights into the disease’s dynamics and associated risk factors. These studies collectively provide a comprehensive view of the spatiotemporal dynamics and risk factors associated with Leptospirosis across diverse geographic regions, emphasizing the importance of understanding the spatial and temporal dimensions of infectious diseases for their effective management and prevention strategies. Consequently, the predominant application of Bayesian spatiotemporal models in the context of infectious diseases is visually depicted in Figure 6.
Figure 6.
Application of Bayesian spatiotemporal models for infectious diseases.
6. Discussion
6.1. Difficulties
The Bayesian spatiotemporal modelling approach is effective for handling uncertainty in the scientific inference, offering a robust foundation, greater power, flexibility, and delivering results in a natural and intuitive form. Yet, challenges exist in applying Bayesian methodology to statistical analysis.
- (1)
- Computational complexity: Bayesian spatiotemporal models, particularly for large datasets, can be computationally demanding due to integrations over uncertain parameters, often requiring intensive numerical methods like MCMC algorithms. Despite this, the Bayesian hierarchical framework is widely used for its flexibility, allowing the construction of complex models through a hierarchical structure that combines data and prior information using prior distributions for each parameter.
- (2)
- Model interpretability: Complex Bayesian spatiotemporal models can pose challenges for result interpretation, as their structures demand a prior distribution on the parameters of interest. The use of different priors can yield varied results, introducing subjectivity and controversy. Striking a balance between complexity and interpretability is crucial in model development to enhance decision making.
- (3)
- Incorporating dynamic factors: enhancements in modelling dynamic factors influencing disease spread, such as human mobility or climate changes, are areas for future research.
- (4)
- Validation and comparison: while there have been reviews on Bayesian models, there is a continued need for standardized validation procedures and comparisons among various Bayesian spatiotemporal models to evaluate their performance and generalizability.
6.2. Advantages
- (1)
- Bayesian spatiotemporal models yield more reasonable results than traditional methods. Unlike traditional approaches that rely on p values, Bayesian methods extract the mean, mode, confidence intervals, and other indicators from the posterior distribution of unknown parameters, providing a more comprehensive and interpretable representation of uncertainty. Bayesian methods can naturally handle missing data through their probabilistic framework, providing a more robust analysis in situations where traditional methods may struggle. Bayesian spatiotemporal models often involve hierarchical structures that allow for borrowing strength across space and time. This helps in improving parameter estimation, especially in regions or time periods with limited data. In situations where new data become available, Bayesian models can be easily updated to incorporate this information, allowing for dynamic and adaptive modelling. Traditional methods may require more extensive modifications to accommodate new data.
- (2)
- The Bayesian spatiotemporal model integrates prior information, treating unknown parameters as random variables influenced by both sample and prior information. By incorporating information about spatial and temporal structures as initial assumptions in the model, it becomes more realistic and gains valuable insights from past experiences, leading to a more accurate representation of the data.
- (3)
- Bayesian spatiotemporal models benefit from computational advantages, enabled using the MCMC algorithm and improved calculation speed. MCMC iteratively generates parameter samples, simplifying the estimation of posterior distributions. This approach facilitates the Bayesian analysis of complex datasets, addressing challenges such as missing observations and multidimensional outcomes.
- (4)
- The Bayesian spatiotemporal model adeptly handles statistical challenges in disease research, including small areas, low case counts, and significant regional differences. By incorporating prior information and adjacent spatiotemporal data, these models improve the realism of model estimation in spatial analyses, offering dependable solutions for addressing statistical issues in disease research.
6.3. Considerations
- (1)
- Spatial and temporal scale: Using Bayesian spatiotemporal models presents a challenge known as the scale effect, where varying spatial or time scales may produce inconsistent or contradictory results. Spatial scales generally refer to provinces, cities, counties, and time scales refers to years, quarters, months, weeks. Careful consideration of both spatial scales and time scales is essential when comparing conclusions from spatiotemporal analyses of the same disease. The stable correlation observed with certain factors in one space–time dimension may not hold in another.
- (2)
- Selection of prior information: Bayesian statistical methods benefit from the use of prior information, but its effectiveness depends on careful selection. Defining a Bayesian prior requires a thorough understanding of the relevant scientific literature. Extracting useful information from the literature and combining it with expert knowledge helps in choosing an appropriate prior distribution and setting parameters. In cases without support from the literature, opting for an uninformative prior ensures that results remain unbiased using uncertain prior information, preventing misleading conclusions.
- (3)
- Reasonable model selection: Conventional spatiotemporal model analysis methods may overlook mean regression bias and unobserved heterogeneity, leading to unstable and biased parameter estimates. Additionally, methods like spatial autoregression face challenges with multi-level data and population-level random effects. In contrast, the full Bayesian framework is more flexible, easily extending to models with random effects that serve as surrogates for unobserved or missing covariates with spatial or temporal structures.
7. Conclusions
This study is designed to address the specific requirements of spatiotemporal modelling in spatial epidemiology. It takes into account the diverse and intricate nature of Bayesian spatiotemporal models, identifying those most suited to the task. The review encompasses a detailed examination of research on Bayesian spatiotemporal models within spatial epidemiology. The methodological intricacies, ranging from the spatiotemporal distribution of data to Bayesian deduction, spatiotemporal evolution rules, and calculation methods, are thoroughly discussed. Furthermore, the application fields, advantages, and necessary precautions associated with this method are critically reviewed. Bayesian spatiotemporal models naturally accommodate uncertainty in parameter estimates and facilitate the incorporation of both spatial and temporal dependencies, which are pivotal in advancing our understanding of the dynamics of diseases. The integration of diverse data sources, such as environmental variables and demographic information, into a unified framework, enhances the analysis of the complex interplay of factors influencing disease dynamics. Despite facing challenges, ongoing research endeavours are anticipated to refine these models, enhancing their accessibility, interpretability, and applicability to a broader spectrum of spatial epidemiological inquiries. The fusion of advanced statistical methodologies and computational tools is poised to continue propelling advancements in this field. This study serves to elucidate the Bayesian model and its practical utilization in spatial epidemiology including both non-communicable and infectious diseases, and the understanding of control factors of these diseases. Such advancements are of profound significance in fostering better comprehension and control of epidemic transmission.
Author Contributions
Writing—original draft preparation, Yufeng Wang and Xue Chen; visualization, Yufeng Wang and Xue Chen; data curation, Yufeng Wang; writing—review and editing, Xue Chen and Feng Xue.; funding acquisition, Feng Xue. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key Research and Development Program of China (2021YFA0910200, 2021YFD1800500, 2023YFF0611500), Hainan Province Science and Technology Special Fund (ZDYF2022XDNY248), Jiangsu Agricultural Science and Technology Independent Innovation Fund Project (CX(21)2038), Sanya Nanjing Agricultural University Research Institute Guiding Fund Project (NAUSY-ZD08).
Conflicts of Interest
The authors declare no conflict of interest.
Correction Statement
Due to an error in article production, incorrect references were previously listed in the main text. This information has been updated and this change does not affect the scientific content of the article.
References
- Kim, J.; Lawson, A.B.; Neelon, B.; Korte, J.E.; Eberth, J.M.; Chowell, G. Evaluation of Bayesian spatiotemporal infectious disease models for prospective surveillance analysis. BMC Med. Res. Methodol. 2023, 23, 171. [Google Scholar] [CrossRef]
- Zhang, P.; Wang, J.; Atkinson, P.M. Identifying the spatio-temporal risk variability of avian influenza A H7N9 in China. Ecol. Model. 2019, 414, 108807. [Google Scholar] [CrossRef]
- Tatem, A.J. Innovation to impact in spatial epidemiology. BMC Med. 2018, 16, 209. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, S.; Bauer, C.X.; Hendricks, B.; Stopka, T.J. Spatial epidemiology: An empirical framework for syndemics research. Soc. Sci. Med. 2022, 295, 113352. [Google Scholar] [CrossRef] [PubMed]
- Lawson, A.B. Evaluation of Predictive capability of Bayesian Spatio-temporal models for Covid-19 spread. BMC Med. Res. Methodol. 2023, 23, 182. [Google Scholar] [CrossRef]
- Brooks, S. Markov chain Monte Carlo method and its application. J. R. Stat. Soc. Ser. D 1998, 47, 69–100. [Google Scholar] [CrossRef]
- van de Schoot, R.; Depaoli, S.; King, R.; Kramer, B.; Märtens, K.; Tadesse, M.G.; Vannucci, M.; Gelman, A.; Veen, D.; Willemsen, J. Bayesian statistics and modelling. Nat. Rev. Methods Primers 2021, 1, 1. [Google Scholar] [CrossRef]
- Bolstad, W.M.; Curran, J.M. Introduction to Bayesian statistics; John Wiley, Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Lawson, A.B. Bayesian Disease Mapping: Hierarchical Modeling in Spatial Epidemiology; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Blangiardo, M.; Cameletti, M.; Baio, G.; Rue, H. Spatial and spatio-temporal models with R-INLA. Spat. Spatio-Temporal Epidemiol. 2013, 7, 39–55. [Google Scholar] [CrossRef] [PubMed]
- Bernardinelli, L.; Clayton, D.; Pascutto, C.; Montomoli, C.; Ghislandi, M.; Songini, M. Bayesian analysis of space-time variation in disease risk. Stat. Med. 1995, 14, 2433–2443. [Google Scholar] [CrossRef]
- Liberati, A.; Altman, D.G.; Tetzlaff, J.; Mulrow, C.; Gøtzsche, P.C.; Ioannidis, J.P.; Clarke, M.; Devereaux, P.J.; Kleijnen, J.; Moher, D. The PRISMA statement for reporting systematic reviews and meta-analyses of studies that evaluate health care interventions: Explanation and elaboration. Ann. Intern. Med. 2009, 339, b2700. [Google Scholar]
- Moher, D.; Liberati, A.; Tetzlaff, J.; Altman, D.G.; Group, P. Preferred reporting items for systematic reviews and meta-analyses: The PRISMA statement. Int. J. Surg. 2010, 8, 336–341. [Google Scholar] [CrossRef] [PubMed]
- Odhiambo, J.N.; Kalinda, C.; Macharia, P.M.; Snow, R.W.; Sartorius, B. Spatial and spatio-temporal methods for mapping malaria risk: A systematic review. BMJ Glob. Health 2020, 5, e002919. [Google Scholar] [CrossRef]
- Aswi, A.; Cramb, S.; Moraga, P.; Mengersen, K. Bayesian spatial and spatio-temporal approaches to modelling dengue fever: A systematic review. Epidemiol. Infect. 2019, 147, e33. [Google Scholar] [CrossRef]
- Nazia, N.; Butt, Z.A.; Bedard, M.L.; Tang, W.-C.; Sehar, H.; Law, J. Methods used in the spatial and spatiotemporal analysis of COVID-19 epidemiology: A systematic review. Int. J. Environ. Res. Public Health 2022, 19, 8267. [Google Scholar] [CrossRef] [PubMed]
- Tesema, G.A.; Tessema, Z.T.; Heritier, S.; Stirling, R.G.; Earnest, A. A systematic review of joint spatial and spatiotemporal models in Health Research. International Journal of Environmental Research and Public Health 2023, 20, 5295. [Google Scholar] [CrossRef] [PubMed]
- Bernardinelli, L.; Clayton, D.; Montomoli, C. Bayesian estimates of disease maps: How important are priors? Stat. Med. 1995, 14, 2411–2431. [Google Scholar] [CrossRef] [PubMed]
- Waller, L.A.; Carlin, B.P.; Xia, H.; Gelfand, A.E. Hierarchical spatio-temporal mapping of disease rates. J. Am. Stat. Assoc. 1997, 92, 607–617. [Google Scholar] [CrossRef]
- Waller, L.A.; Carlin, B.P.; Xia, H. Structuring correlation within hierarchical spatio-temporal models for disease rates. In Modelling Longitudinal and Spatially Correlated Data; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Sun, D.; Tsutakawa, R.K.; Kim, H.; He, Z. Spatio-temporal interaction with disease mapping. Stat. Med. 2000, 19, 2015–2035. [Google Scholar] [CrossRef]
- Kim, H.; Sun, D.; Tsutakawa, R.K. A bivariate Bayes method for improving the estimates of mortality rates with a twofold conditional autoregressive model. J. Am. Stat. Assoc. 2001, 96, 1506–1521. [Google Scholar] [CrossRef]
- Kim, H.; Oleson, J.J. A Bayesian Dynamic Spatio-Temporal Interaction Model: An Application to Prostate Cancer Incidence. Geogr. Anal. 2008, 40, 77–96. [Google Scholar] [CrossRef]
- Böhning, D.; Dietz, E.; Schlattmann, P. Space-time mixture modelling of public health data. Stat. Med. 2000, 19, 2333–2344. [Google Scholar] [CrossRef] [PubMed]
- Kottas, A.; Duan, J.A.; Gelfand, A.E. Modeling disease incidence data with spatial and spatio temporal Dirichlet process mixtures. Biom. J. J. Math. Methods Biosci. 2008, 50, 29–42. [Google Scholar] [CrossRef] [PubMed]
- Yan, P.; Clayton, M.K. A cluster model for space–time disease counts. Stat. Med. 2006, 25, 867–881. [Google Scholar] [CrossRef] [PubMed]
- Gangnon, R.E.; Clayton, M.K. Bayesian detection and modeling of spatial disease clustering. Biometrics 2000, 56, 922–935. [Google Scholar] [CrossRef] [PubMed]
- Richardson, S.; Abellan, J.J.; Best, N. Bayesian spatio-temporal analysis of joint patterns of male and female lung cancer risks in Yorkshire (UK). Stat. Methods Med. Res. 2006, 15, 385–407. [Google Scholar] [CrossRef]
- Musio, M.; Sauleau, E.A.; Buemi, A. Bayesian semi-parametric ZIP models with space–time interactions: An application to cancer registry data. Math. Med. Biol. A J. IMA 2010, 27, 181–194. [Google Scholar] [CrossRef] [PubMed]
- Hastie, T.; Tibshirani, R. Varying-coefficient models. J. R. Stat. Soc. Ser. B Stat. Methodol. 1993, 55, 757–779. [Google Scholar] [CrossRef]
- Gamerman, D.; Moreira, A.R.; Rue, H. Space-varying regression models: Specifications and simulation. Comput. Stat. Data Anal. 2003, 42, 513–533. [Google Scholar] [CrossRef]
- Torabi, M.; Rosychuk, R.J. Spatio-temporal modelling of disease mapping of rates. Can. J. Stat. 2010, 38, 698–715. [Google Scholar] [CrossRef]
- Mabaso, M.; Craig, M.; Vounatsou, P.; Smith, T. Towards empirical description of malaria seasonality in southern Africa: The example of Zimbabwe. Trop. Med. Int. Health 2005, 10, 909–918. [Google Scholar] [CrossRef]
- Greene, S.K.; Ionides, E.L.; Wilson, M.L. Patterns of influenza-associated mortality among US elderly by geographic region and virus subtype, 1968–1998. Am. J. Epidemiol. 2006, 163, 316–326. [Google Scholar] [CrossRef] [PubMed]
- Zhang, R.; Lai, K.Y.; Liu, W.; Liu, Y.; Lu, J.; Tian, L.; Webster, C.; Luo, L.; Sarkar, C. Community-level ambient fine particulate matter and seasonal influenza among children in Guangzhou, China: A Bayesian spatiotemporal analysis. Sci. Total Environ. 2022, 826, 154135. [Google Scholar] [CrossRef] [PubMed]
- Chen, J.T.; Coull, B.A.; Waterman, P.D.; Schwartz, J.; Krieger, N. Methodologic implications of social inequalities for analyzing health disparities in large spatiotemporal data sets: An example using breast cancer incidence data (Northern and Southern California, 1988–2002). Stat. Med. 2008, 27, 3957–3983. [Google Scholar] [CrossRef] [PubMed]
- Abellan, J.J.; Richardson, S.; Best, N. Use of space–time models to investigate the stability of patterns of disease. Environ. Health Perspect. 2008, 116, 1111–1119. [Google Scholar] [CrossRef] [PubMed]
- Schrödle, B.; Held, L.; Rue, H. Assessing the impact of a movement network on the spatiotemporal spread of infectious diseases. Biometrics 2012, 68, 736–744. [Google Scholar] [CrossRef] [PubMed]
- Cameletti, M.; Lindgren, F.; Simpson, D.; Rue, H. Spatio-temporal modeling of particulate matter concentration through the SPDE approach. AStA Adv. Stat. Anal. 2013, 97, 109–131. [Google Scholar] [CrossRef]
- Bukhari, M.H.; Shad, M.Y.; Nguyen, U.-S.D.T.; Treviño, C.J.A.; Jung, W.; Bajwa, W.U.; Gallego-Hernández, A.L.; Robinson, R.; Corral-Frías, N.S.; Hamer, G.L.; et al. A Bayesian spatiotemporal approach to modelling arboviral diseases in Mexico. Trans. R. Soc. Trop. Med. Hyg. 2023, 117, 867–874. [Google Scholar] [CrossRef] [PubMed]
- Otieno, F.A.; Tamba, C.L.; Okenye, J.O.; Orawo, L.A. Dynamic Spatio-Temporal Modeling in Disease Mapping. Open J. Stat. 2023, 13, 893–916. [Google Scholar] [CrossRef]
- Sun, N.; Bursac, Z.; Dryden, I.; Lucchini, R.; Dabo-Niang, S.; Ibrahimou, B. Bayesian spatiotemporal modelling for disease mapping: An application to preeclampsia and gestational diabetes in Florida, United States. Environ. Sci. Pollut. Res. 2023, 30, 109283–109298. [Google Scholar] [CrossRef]
- Zhou, H.; Lawson, A.B. EWMA smoothing and Bayesian spatial modeling for health surveillance. Stat. Med. 2008, 27, 5907–5928. [Google Scholar] [CrossRef]
- McGough, S.F.; Johansson, M.A.; Lipsitch, M.; Menzies, N.A. Nowcasting by Bayesian Smoothing: A flexible, generalizable model for real-time epidemic tracking. PLoS Comput. Biol. 2020, 16, e1007735. [Google Scholar] [CrossRef] [PubMed]
- Neelon, B.; Mutiso, F.; Mueller, N.T.; Pearce, J.L.; Benjamin-Neelon, S.E. Spatial and temporal trends in social vulnerability and COVID-19 incidence and death rates in the United States. PLoS ONE 2021, 16, e0248702. [Google Scholar] [CrossRef]
- Mutiso, F.; Pearce, J.L.; Benjamin-Neelon, S.E.; Mueller, N.T.; Li, H.; Neelon, B.J. Bayesian negative binomial regression with spatially varying dispersion: Modeling COVID-19 incidence in Georgia. Spat. Stat. 2022, 52, 100703. [Google Scholar] [CrossRef] [PubMed]
- López-Quılez, A.; Munoz, F. Review of Spatio-Temporal Models for Disease Mapping. In Final Report for the EUROHEIS; 2009; p. 2. Available online: https://www.researchgate.net/publication/237063293_Review_of_spatio-temporal_models_for_disease_mapping (accessed on 1 March 2024).
- Xia, H.; Carlin, B.P. Spatio-temporal models with errors in covariates: Mapping Ohio lung cancer mortality. Stat. Med. 1998, 17, 2025–2043. [Google Scholar] [CrossRef]
- Knorr-Held, L.; Besag, J. Modelling risk from a disease in time and space. Stat. Med. 1998, 17, 2045–2060. [Google Scholar] [CrossRef]
- Knorr-Held, L. Bayesian modelling of inseparable space-time variation in disease risk. Stat. Med. 2000, 19, 2555–2567. [Google Scholar] [CrossRef] [PubMed]
- Kazembe, L.N. Spatial modelling and risk factors of malaria incidence in northern Malawi. Acta Trop. 2007, 102, 126–137. [Google Scholar] [CrossRef] [PubMed]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2008; p. 408. [Google Scholar]
- Morton, A.; Finkenstädt, B.F. Discrete time modelling of disease incidence time series by using Markov chain Monte Carlo methods. J. R. Stat. Soc. Ser. C Appl. Stat. 2005, 54, 575–594. [Google Scholar] [CrossRef]
- Lawson, A.B.; Song, H.-R. Bayesian hierarchical modeling of the dynamics of spatio-temporal influenza season outbreaks. Spat. Spatio-Temporal Epidemiol. 2010, 1, 187–195. [Google Scholar] [CrossRef]
- Held, L.; Hofmann, M.; Höhle, M.; Schmid, V. A two-component model for counts of infectious diseases. Biostatistics 2006, 7, 422–437. [Google Scholar] [CrossRef]
- Myer, M.H.; Johnston, J.M. Spatiotemporal Bayesian modeling of West Nile virus: Identifying risk of infection in mosquitoes with local-scale predictors. Sci. Total Environ. 2019, 650, 2818–2829. [Google Scholar] [CrossRef] [PubMed]
- Cheng, J.; Bambrick, H.; Tong, S.; Su, H.; Xu, Z.; Hu, W. Winter temperature and myocardial infarction in Brisbane, Australia: Spatial and temporal analyses. Sci. Total. Environ. 2020, 715. [Google Scholar] [CrossRef] [PubMed]
- Khana, D.; Rossen, L.M.; Hedegaard, H.; Warner, M. A Bayesian spatial and temporal modeling approach to mapping geographic variation in mortality rates for subnational areas with R-INLA. J. Data Sci. JDS 2018, 16, 147. [Google Scholar] [PubMed]
- MacNab, Y.C. Adaptive Gaussian Markov random field spatiotemporal models for infectious disease mapping and forecasting. Spat. Stat. 2023, 53, 100726. [Google Scholar] [CrossRef] [PubMed]
- Besag, J.; York, J.; Mollié, A. Bayesian image restoration, with two applications in spatial statistics. Ann. Inst. Stat. Math. 1991, 43, 1–20. [Google Scholar] [CrossRef]
- MacNab, Y.C. On Gaussian Markov random fields and Bayesian disease mapping. Stat. Methods Med. Res. 2011, 20, 49–68. [Google Scholar] [CrossRef] [PubMed]
- Leroux, B.G.; Lei, X.; Breslow, N. Estimation of disease rates in small areas: A new mixed model for spatial dependence. In Statistical Models in Epidemiology, the Environment, and Clinical Trials; Springer: Berlin/Heidelberg, Germany, 2000; pp. 179–191. [Google Scholar]
- Lee, D. A comparison of conditional autoregressive models used in Bayesian disease mapping. Spat. Spatio-Temporal Epidemiol. 2011, 2, 79–89. [Google Scholar] [CrossRef] [PubMed]
- Krisztin, T.; Piribauer, P.; Wögerer, M. The spatial econometrics of the coronavirus pandemic. Lett. Spat. Resour. Sci. 2020, 13, 209–218. [Google Scholar] [CrossRef]
- Besag, J.; Kooperberg, C. On conditional and intrinsic autoregressions. Biometrika 1995, 82, 733–746. [Google Scholar]
- Besag, J. Spatial interaction and the statistical analysis of lattice systems. J. R. Stat. Soc. Ser. B 1974, 36, 192–225. [Google Scholar] [CrossRef]
- Morris, M.; Wheeler-Martin, K.; Simpson, D.; Mooney, S.J.; Gelman, A.; DiMaggio, C. Bayesian hierarchical spatial models: Implementing the Besag York Mollié model in stan. Spat. Spatio-Temporal Epidemiol. 2019, 31, 100301. [Google Scholar] [CrossRef]
- Song, C.; Shi, X.; Bo, Y.; Wang, J.; Wang, Y.; Huang, D. Exploring spatiotemporal nonstationary effects of climate factors on hand, foot, and mouth disease using Bayesian Spatiotemporally Varying Coefficients (STVC) model in Sichuan, China. Sci. Total Environ. 2019, 648, 550–560. [Google Scholar] [CrossRef] [PubMed]
- Schrödle, B.; Held, L. Spatio-temporal disease mapping using INLA. Environmetrics Off. J. Int. Environmetrics Soc. 2011, 22, 725–734. [Google Scholar] [CrossRef]
- Jaya, I.G.N.M.; Kristiani, F.; Andriyana, Y.; Chadidjah, A. Sensitivity Analysis on Hyperprior Distribution of the Variance Components of Hierarchical Bayesian Spatiotemporal Disease Mapping. Mathematics 2024, 12, 451. [Google Scholar] [CrossRef]
- Gelman, A. Parameterization and Bayesian modeling. J. Am. Stat. Assoc. 2004, 99, 537–545. [Google Scholar] [CrossRef]
- Austin, P.C.; Brunner, L.J.; Sm, J.E.H.M. Bayeswatch: An overview of Bayesian statistics. J. Eval. Clin. Pract. 2002, 8, 277–286. [Google Scholar] [CrossRef] [PubMed]
- Martin, O.A.; Kumar, R.; Lao, J. Bayesian Modeling and Computation in Python; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Geman, S.; Geman, D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Trans. Pattern Anal. Mach. Intell. -6.
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of state calculations by fast computing machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Metropolis, N.; Ulam, S. The monte carlo method. J. Am. Stat. Assoc. 1949, 44, 335–341. [Google Scholar] [CrossRef] [PubMed]
- Gilks, W.R.; Richardson, S.; Spiegelhalter, D. Markov Chain Monte Carlo in Practice; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Rue, H.; Martino, S.; Chopin, N. Approximate Bayesian inference for latent Gaussian models by using integrated nested Laplace approximations. J. R. Stat. Soc. Ser. B Stat. Methodol. 2009, 71, 319–392. [Google Scholar] [CrossRef]
- Held, L.; Schrödle, B.; Rue, H. Posterior and cross-validatory predictive checks: A comparison of MCMC and INLA. In Statistical Modelling Regression Structures: Festschrift in Honour of Ludwig Fahrmeir; Springer: Berlin/Heidelberg, Germany, 2010; pp. 91–110. [Google Scholar]
- Martino, S.; Akerkar, R.; Rue, H. Approximate Bayesian inference for survival models. Scand. J. Stat. 2011, 38, 514–528. [Google Scholar] [CrossRef]
- Spiegelhalter, D.J.; Best, N.G.; Carlin, B.P.; Van Der Linde, A. Bayesian measures of model complexity and fit. J. R. Stat. Soc. Ser. B Stat. Methodol. 2002, 64, 583–639. [Google Scholar] [CrossRef]
- Watanabe, S.; Opper, M.J. Asymptotic equivalence of Bayes cross validation and widely applicable information criterion in singular learning theory. J. Mach. Learn. Res. 2010, 11, 3571–3594. [Google Scholar]
- Gneiting, T.; Raftery, A.E. Strictly proper scoring rules, prediction, and estimation. J. Am. Stat. Assoc. 2007, 102, 359–378. [Google Scholar] [CrossRef]
- Dawid, A.P. Present position and potential developments: Some personal views statistical theory the prequential approach. J. R. Stat. Soc. Ser. A 1984, 147, 278–290. [Google Scholar] [CrossRef]
- Pettit, L. The conditional predictive ordinate for the normal distribution. J. R. Stat. Soc. Ser. B 1990, 52, 175–184. [Google Scholar] [CrossRef]
- Jaya, I.G.N.M.; Folmer, H. Bayesian spatiotemporal mapping of relative dengue disease risk in Bandung, Indonesia. J. Geogr. Syst. 2020, 22, 105–142. [Google Scholar] [CrossRef]
- Saavedra, P.; Santana, A.; Bello, L.; Pacheco, J.-M.; Sanjuán, E. A Bayesian spatio-temporal analysis of mortality rates in Spain: Application to the COVID-19 2020 outbreak. Popul. Health Metr. 2021, 19, 27. [Google Scholar] [CrossRef] [PubMed]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Lal, A.; Marshall, J.; Benschop, J.; Brock, A.; Hales, S.; Baker, M.G.; French, N.P. A Bayesian spatio-temporal framework to identify outbreaks and examine environmental and social risk factors for infectious diseases monitored by routine surveillance. Spat. Spatio-Temporal Epidemiol. 2018, 25, 39–48. [Google Scholar] [CrossRef]
- Watson, S.C.; Liu, Y.; Lund, R.B.; Gettings, J.R.; Nordone, S.K.; McMahan, C.S.; Yabsley, M.J. A Bayesian spatio-temporal model for forecasting the prevalence of antibodies to Borrelia burgdorferi, causative agent of Lyme disease, in domestic dogs within the contiguous United States. PLOS ONE 2017, 12, e0174428. [Google Scholar] [CrossRef]
- Raubenheimer, L.; Southey, R.; Radlof, S.E. Bayesian disease mapping: A literature review with an application, using WinBugs software. Stat. Optim. Inf. Comput. 2022, 10, 829–857. [Google Scholar] [CrossRef]
- He, X.; Dong, S.; Li, L.; Liu, X.; Wu, Y.; Zhang, Z.; Mei, S. Using a Bayesian spatiotemporal model to identify the influencing factors and high-risk areas of hand, foot and mouth disease (HFMD) in Shenzhen. PLOS Neglected Trop. Dis. 2020, 14, e0008085. [Google Scholar] [CrossRef] [PubMed]
- Baptista, E.A. Cardiovascular Diseases Mortality in Mexican Municipalities: A Spatio-Temporal Approach. Appl. Spat. Anal. Policy 2024, 1–14. [Google Scholar] [CrossRef]
- Wang, W.; Li, J.; Liu, Y.; Ye, P.; Xu, C.; Yin, P.; Liu, J.; Qi, J.; You, J.; Lin, L.; et al. Spatiotemporal trends and ecological determinants of cardiovascular mortality among 2844 counties in mainland China, 2006–2020: A Bayesian modeling study of national mortality registries. BMC Med. 2022, 20, 467. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Sun, J.; Gou, Y.; Sun, X.; Zhang, D.; Xue, F. Analysis of short-term effects of air pollution on cardiovascular disease using Bayesian spatio-temporal models. Int. J. Environ. Res. Public Health 2020, 17, 879. [Google Scholar] [CrossRef]
- Liu, B.; Lee, F.F.; Boscoe, F. Residential mobility among adult cancer survivors in the United States. BMC Public Health 2020, 20, 1601. [Google Scholar] [CrossRef]
- Wah, W.; Ahern, S.; Earnest, A. A systematic review of Bayesian spatial–temporal models on cancer incidence and mortality. Int. J. Public Health 2020, 65, 673–682. [Google Scholar] [CrossRef] [PubMed]
- Nandram, B.; Sedransk, J.; Pickle, L.W. Bayesian analysis and mapping of mortality rates for chronic obstructive pulmonary disease. J. Am. Stat. Assoc. 2000, 95, 1110–1118. [Google Scholar] [CrossRef]
- Li, J.; Wang, S.; Han, X.; Zhang, G.; Zhao, M.; Ma, L. Spatiotemporal trends and influence factors of global diabetes prevalence in recent years. Soc. Sci. Med. 2020, 256, 113062. [Google Scholar] [CrossRef]
- Dayaratna, K.D.; Gonshorowski, D.; Kolesar, M. Hierarchical Bayesian spatio-temporal modeling of COVID-19 in the United States. J. Appl. Stat. 2023, 50, 2663–2680. [Google Scholar] [CrossRef]
- Ma, S.; Zhang, X.; Wang, K.; Zhang, L.; Wang, L.; Zeng, T.; Tang, M.L.; Tian, M. Exploring the risk factors of COVID-19 Delta variant in the United States based on Bayesian spatio-temporal analysis. Transbound. Emerg. Dis. 2022, 69, e2731–e2744. [Google Scholar] [CrossRef] [PubMed]
- Rawat, S.; Deb, S. A spatio-temporal statistical model to analyze COVID-19 spread in the USA. J. Appl. Stat. 2023, 50, 2310–2329. [Google Scholar] [CrossRef] [PubMed]
- Sahu, S.; Böhning, D. BayesIan spatio-temporal joint disease mapping of Covid-19 cases and deaths in local authorities of England. Spat. Stat. 2021, 49, 100519. [Google Scholar] [CrossRef] [PubMed]
- Sartorius, B.; Lawson, A.; Pullan, R. Modelling and predicting the spatio-temporal spread of COVID-19, associated deaths and impact of key risk factors in England. Sci. Rep. 2021, 11, 5378. [Google Scholar] [CrossRef] [PubMed]
- Jalilian, A.; Mateu, J. A hierarchical spatio-temporal model to analyze relative risk variations of COVID-19: A focus on Spain, Italy and Germany. Stoch. Environ. Res. Risk Assess. 2021, 35, 797–812. [Google Scholar] [CrossRef]
- Rohleder, S.; Bozorgmehr, K. Monitoring the spatiotemporal epidemiology of Covid-19 incidence and mortality: A small-area analysis in Germany. Spat. Spatio-Temporal Epidemiol. 2021, 38, 100433. [Google Scholar] [CrossRef]
- Jaya, I.G.N.M.; Folmer, H.; Lundberg, J. A joint Bayesian spatiotemporal risk prediction model of COVID-19 incidence, IC admission, and death with application to Sweden. Ann. Reg. Sci. 2022, 72, 107–140. [Google Scholar] [CrossRef]
- Gayawan, E.; Awe, O.O.; Oseni, B.M.; Uzochukwu, I.C.; Adekunle, A.; Samuel, G.; Eisen, D.P.; Adegboye, O.A. The spatio-temporal epidemic dynamics of COVID-19 outbreak in Africa. Epidemiol. Infect. 2020, 148, e212. [Google Scholar] [CrossRef] [PubMed]
- Jaya, I.G.N.M.; Folmer, H. Bayesian spatiotemporal forecasting and mapping of COVID-19 risk with application to West Java Province, Indonesia. J. Reg. Sci. 2021, 61, 849–881. [Google Scholar] [CrossRef]
- Lym, Y.; Lym, H.; Kim, K.-J. Local-level spatiotemporal dynamics of COVID-19 transmission in the Greater Seoul Area, Korea: A view from a Bayesian perspective. Epidemiol. Health 2022, 44, e2022016. [Google Scholar] [CrossRef]
- Nazia, N.; Law, J.; Butt, Z.A. Identifying spatiotemporal patterns of COVID-19 transmissions and the drivers of the patterns in Toronto: A Bayesian hierarchical spatiotemporal modelling. Sci. Rep. 2022, 12, 9369. [Google Scholar] [CrossRef] [PubMed]
- Hu, W.; Zhang, W.; Huang, X.; Clements, A.; Mengersen, K.; Tong, S.J. Weather variability and influenza A (H7N9) transmission in Shanghai, China: A Bayesian spatial analysis. Environ. Res. Lett. 2015, 136, 405–412. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, X.; Li, Y.; Ma, J. Spatiotemporal analysis of influenza in China, 2005–2018. Sci. Rep. 2019, 9, 19650. [Google Scholar] [CrossRef]
- Lemey, P.; Suchard, M.; Rambaut, A. Reconstructing the initial global spread of a human influenza pandemic: A Bayesian spatial-temporal model for the global spread of H1N1pdm. PLoS Curr. 2009, 1, RRN1031. [Google Scholar] [CrossRef] [PubMed]
- Bui, C.M.; Adam, D.C.; Njoto, E.; Scotch, M.; MacIntyre, C.R. Characterising routes of H5N1 and H7N9 spread in China using Bayesian phylogeographical analysis. Emerg. Microbes Infect. 2018, 7, 184. [Google Scholar] [CrossRef] [PubMed]
- Aswi, A.; Cramb, S.; Duncan, E.; Hu, W.; White, G.; Mengersen, K. Climate variability and dengue fever in Makassar, Indonesia: Bayesian spatio-temporal modelling. Spat. Spatio-Temporal Epidemiol. 2020, 33, 100335. [Google Scholar] [CrossRef]
- Teng, J.; Ding, S.; Zhang, H.; Wang, K.; Hu, X. Bayesian spatiotemporal modelling analysis of hemorrhagic fever with renal syndrome outbreaks in China using R-INLA. Zoonoses Public Health 2023, 70, 46–57. [Google Scholar] [CrossRef] [PubMed]
- Lau, M.S.; Dalziel, B.D.; Funk, S.; McClelland, A.; Tiffany, A.; Riley, S.; Metcalf, C.J.E.; Grenfell, B.T. Spatial and temporal dynamics of superspreading events in the 2014–2015 West Africa Ebola epidemic. Proc. Natl. Acad. Sci. USA 2017, 114, 2337–2342. [Google Scholar] [CrossRef] [PubMed]
- Zinszer, K.; Morrison, K.; Verma, A.; Brownstein, J.S. Spatial determinants of Ebola virus disease risk for the West African epidemic. PLoS Curr. 2017, 9. [Google Scholar] [CrossRef][Green Version]
- Adegboye, O.; Gayawan, E.; James, A.; Adegboye, A.; Elfaki, F. Bayesian spatial modelling of Ebola outbreaks in Democratic Republic of Congo through the INLA-SPDE approach. Zoonoses Public Health 2021, 68, 443–451. [Google Scholar] [CrossRef]
- Astutik, S.; Rahayudi, B.; Iskandar, A.; Fitriani, R. Bayesian spatial-temporal autologistic regression model on dengue hemorrhagic fever in East Java, Indonesia. Appl. Math. Sci. 2013, 7, 435–443. [Google Scholar] [CrossRef]
- Costa, A.C.C.; Codeço, C.T.; Honório, N.A.; Pereira, G.R.; Pinheiro, C.F.N.; Nobre, A.A. Surveillance of dengue vectors using spatio-temporal Bayesian modeling. BMC Med. Inform. Decis. Mak. 2015, 15, 93. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Bello, D.; López-Quílez, A.; Prieto, A.T. Spatiotemporal modeling of relative risk of dengue disease in Colombia. Stoch. Environ. Res. Risk Assess. 2018, 32, 1587–1601. [Google Scholar] [CrossRef]
- Ye, J.; Moreno-Madriñán, M.J. Comparing different spatio-temporal modeling methods in dengue fever data analysis in Colombia during 2012–2015. Spat. Spatio-Temporal Epidemiol. 2020, 34, 100360. [Google Scholar] [CrossRef] [PubMed]
- Sani, A.; Abapihi, B.; Mukhsar; Tosepu, R.; Usman, I.; Rahman, G.A. Bayesian temporal, spatial and spatio-temporal models of dengue in a small area with INLA. Int. J. Model. Simul. 2023, 43, 939–951. [Google Scholar] [CrossRef]
- Chen, S. Spatial and temporal dynamic analysis of rabies: A review of current methodologies. Geospatial Health 2022, 17. [Google Scholar] [CrossRef] [PubMed]
- Raghavan, R.K.; Hanlon, C.A.; Goodin, D.G.; Davis, R.; Moore, M.; Moore, S.; Anderson, G.A. Bayesian spatiotemporal pattern and eco-climatological drivers of striped skunk rabies in the North Central Plains. PLoS Neglected Trop. Dis. 2016, 10, e0004632. [Google Scholar] [CrossRef] [PubMed]
- Baker, L.; Matthiopoulos, J.; Müller, T.; Freuling, C.; Hampson, K. Local rabies transmission and regional spatial coupling in European foxes. PLoS ONE 2020, 15, e0220592. [Google Scholar] [CrossRef] [PubMed]
- Baron, J.N.; Chevalier, V.; Ly, S.; Duong, V.; Dussart, P.; Fontenille, D.; Peng, Y.S.; Martínez-López, B. Accessibility to rabies centers and human rabies post-exposure prophylaxis rates in Cambodia: A Bayesian spatio-temporal analysis to identify optimal locations for future centers. PLoS Neglected Trop. Dis. 2022, 16, e0010494. [Google Scholar] [CrossRef]
- Kanankege, K.S.; Errecaborde, K.M.; Wiratsudakul, A.; Wongnak, P.; Yoopatthanawong, C.; Thanapongtharm, W.; Alvarez, J.; Perez, A. Identifying high-risk areas for dog-mediated rabies using Bayesian spatial regression. One Health 2022, 15, 100411. [Google Scholar] [CrossRef]
- Li, H.; Li, Y.; Chen, Y.; Chen, B.; Su, Q.; Hu, Y.; Xiong, C. Mapping rabies distribution in China: A geospatial analysis of national surveillance data. Int. J. Infect. Dis. 2023, 131, 140–146. [Google Scholar] [CrossRef] [PubMed]
- Machado Junior, P.C.; Chung, C.; Hagerman, A. Modeling Salmonella spread in broiler production: Identifying determinants and control strategies. Front. Vet. Sci. 2020, 7, 564. [Google Scholar] [CrossRef] [PubMed]
- Teng, K.T.-Y.; Martinez Aviles, M.; Ugarte-Ruiz, M.; Barcena, C.; De la Torre, A.; Lopez, G.; Moreno, M.A.; Dominguez, L.; Alvarez, J. Spatial trends in Salmonella infection in pigs in Spain. Front. Vet. Sci. 2020, 7, 345. [Google Scholar] [CrossRef] [PubMed]
- Srinivasan, R.; Venkatesan, P. Bayesian spatio-temporal model for tuberculosis in India. Indian J. Med. Res. 2015, 141, 478. [Google Scholar]
- Li, Q.; Liu, M.; Zhang, Y.; Wu, S.; Yang, Y.; Liu, Y.; Amsalu, E.; Tao, L.; Liu, X.; Zhang, F. The spatio-temporal analysis of the incidence of tuberculosis and the associated factors in mainland China, 2009–2015. Infect. Genet. Evol. 2019, 75, 103949. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.-Y.; Deng, X.-Y.; Zou, Y.; He, Y.; Chen, S.-J.; Wang, Q.-T.; Xing, D.-G.; Zhang, Y. A Spatio-temporal Bayesian model to estimate risk and influencing factors related to tuberculosis in Chongqing, China, 2014–2020. Arch. Public Health 2023, 81, 42. [Google Scholar] [CrossRef]
- Cao, K.; Yang, K.; Wang, C.; Guo, J.; Tao, L.; Liu, Q.; Gehendra, M.; Zhang, Y.; Guo, X. Spatial-temporal epidemiology of tuberculosis in mainland China: An analysis based on Bayesian theory. Int. J. Environ. Res. Public Health 2016, 13, 469. [Google Scholar] [CrossRef] [PubMed]
- Otiende, V.A.; Achia, T.N.; Mwambi, H.G. Bayesian hierarchical modeling of joint spatiotemporal risk patterns for Human Immunodeficiency Virus (HIV) and Tuberculosis (TB) in Kenya. PLoS ONE 2020, 15, e0234456. [Google Scholar] [CrossRef] [PubMed]
- Sunengsih, N.; Jaya, I. A Bayesian spatiotemporal autoregressive model with constant and temporally varying coefficients: An application to hotspot detection of childhood tuberculosis in Bandung City, Indonesia. Commun. Math. Biol. Neurosci. 2021, 2021, 58. [Google Scholar]
- Gemechu, L.L.; Debusho, L.K. Bayesian spatial modelling of tuberculosis-HIV co-infection in Ethiopia. PLoS ONE 2023, 18, e0283334. [Google Scholar] [CrossRef]
- Amsalu, E.; Liu, M.; Li, Q.; Wang, X.; Tao, L.; Liu, X.; Luo, Y.; Yang, X.; Zhang, Y.; Li, W. Spatial-temporal analysis of tuberculosis in the geriatric population of China: An analysis based on the Bayesian conditional autoregressive model. Arch. Gerontol. Geriatr. 2019, 83, 328–337. [Google Scholar] [CrossRef] [PubMed]
- Liu, F.; Zhang, Z.; Chen, H.; Nie, S. Associations of ambient air pollutants with regional pulmonary tuberculosis incidence in the central Chinese province of Hubei: A Bayesian spatial-temporal analysis. Environ. Health Perspect. 2020, 19, 51. [Google Scholar] [CrossRef] [PubMed]
- Wahyuni, M.S.; Syam, R. Comparison of Bayesian Spatio-temporal Models of Tuberculosis in Makassar, Indonesia. J. Phys. Conf. Ser. 2021, 2123, 012048. [Google Scholar]
- Madden, J.M.; McGrath, G.; Sweeney, J.; Murray, G.; Tratalos, J.A.; More, S.J. Spatio-temporal models of bovine tuberculosis in the Irish cattle population, 2012–2019. Spat. Spatio-Temporal Epidemiol. 2021, 39, 100441. [Google Scholar] [CrossRef]
- Ahasan, M.S.; Rahman, M.S.; Rahman, A.A.; Berkvens, D. Bovine and Caprine Brucellosis in Bangladesh: Bayesian evaluation of four serological tests, true prevalence, and associated risk factors in household animals. Trop. Anim. Health Prod. 2017, 49, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Lim, J.-S.; Min, K.-D.; Ryu, S.; Hwang, S.-S.; Cho, S.-I. Spatial analysis to assess the relationship between human and bovine brucellosis in South Korea, 2005–2010. Sci. Rep. 2019, 9, 6657. [Google Scholar] [CrossRef] [PubMed]
- Rahmanian, V.; Bokaie, S.; Rahmanian, K.; Hosseini, S.; Firouzeh, A.T. Analysis of temporal trends of human brucellosis between 2013 and 2018 in Yazd Province, Iran to predict future trends in incidence: A time-series study using ARIMA model. Asian Pac. J. Trop. Med. 2020, 13, 272–277. [Google Scholar]
- Liang, D.; Liu, D.; Yang, M.; Wang, X.; Li, Y.; Guo, W.; Du, M.; Wang, W.; Xue, M.; Wu, J. Spatiotemporal distribution of human brucellosis in Inner Mongolia, China, in 2010–2015, and influencing factors. Sci. Rep. 2021, 11, 24213. [Google Scholar] [CrossRef] [PubMed]
- Walker, M.A.; Tan, L.M.; Van Khang, P.; Ha, H.T.T.; Hung, T.T.M.; Dung, H.H.; Anh, D.D.; Duong, T.N.; Hadfield, T.; Thai, P.Q. Spatiotemporal Patterns of Anthrax, Vietnam, 1990–2015. Emerg. Infect. Dis. 2022, 28, 2206. [Google Scholar] [CrossRef]
- Luong, T.; Pham, A.H.; Hoang, T.T.-H.; Pham, Q.T.; Tran, T.M.H.; Luong, M.H.; Pham, T.L.; Blackburn, J.K. Spatial analysis of human and livestock anthrax in Lai Chau province, Vietnam (2004–2021). Acta Trop. 2024, 249, 107044. [Google Scholar] [CrossRef]
- Ndolo, V.A.; Redding, D.W.; Lekolool, I.; Mwangangi, D.M.; Odhiambo, D.O.; Deka, M.A.; Conlan, A.J.; Wood, J.L. Drivers and potential distribution of anthrax occurrence and incidence at national and sub-county levels across Kenya from 2006 to 2020 using INLA. Sci. Rep. 2022, 12, 20083. [Google Scholar] [CrossRef] [PubMed]
- Rouamba, T.; Samadoulougou, S.; Tinto, H.; Alegana, V.A.; Kirakoya-Samadoulougou, F. Bayesian spatiotemporal modeling of routinely collected data to assess the effect of health programs in malaria incidence during pregnancy in Burkina Faso. Sci. Rep. 2020, 10, 2618. [Google Scholar] [CrossRef] [PubMed]
- Nobre, A.A.; Schmidt, A.M.; Lopes, H.F. Spatio-temporal models for mapping the incidence of malaria in Pará. Environmetrics: Off. J. Int. Environmetrics Soc. 2005, 16, 291–304. [Google Scholar] [CrossRef]
- Ibeji, J.U.; Mwambi, H.; Iddrisu, A.-K. Bayesian spatio-temporal modelling and mapping of malaria and anaemia among children between 0 and 59 months in Nigeria. Malar. J. 2022, 21, 311. [Google Scholar] [CrossRef] [PubMed]
- Semakula, M.; Niragire, F.; Faes, C. Spatio-Temporal Bayesian Models for Malaria Risk Using Survey and Health Facility Routine Data in Rwanda. Int. J. Environ. Res. Public Health 2023, 20, 4283. [Google Scholar] [CrossRef]
- Rotejanaprasert, C.; Lawpoolsri, S.; Sa-Angchai, P.; Khamsiriwatchara, A.; Padungtod, C.; Tipmontree, R.; Menezes, L.; Sattabongkot, J.; Cui, L.; Kaewkungwal, J. Projecting malaria elimination in Thailand using Bayesian hierarchical spatiotemporal models. Sci. Rep. 2023, 13, 7799. [Google Scholar] [CrossRef] [PubMed]
- Alegana, V.A.; Atkinson, P.M.; Wright, J.A.; Kamwi, R.; Uusiku, P.; Katokele, S.; Snow, R.W.; Noor, A.M. Estimation of malaria incidence in northern Namibia in 2009 using Bayesian conditional-autoregressive spatial–temporal models. Spat. Spatio-Temporal Epidemiol. 2013, 7, 25–36. [Google Scholar] [CrossRef] [PubMed]
- Haddawy, P.; Hasan, A.I.; Kasantikul, R.; Lawpoolsri, S.; Sa-Angchai, P.; Kaewkungwal, J.; Singhasivanon, P. Spatiotemporal Bayesian networks for malaria prediction. Artif. Intell. Med. 2018, 84, 127–138. [Google Scholar] [CrossRef] [PubMed]
- Semakula, M.; Niragire, F.; Faes, C. Bayesian spatio-temporal modeling of malaria risk in Rwanda. PLoS ONE 2020, 15, e0238504. [Google Scholar] [CrossRef]
- Hu, Y.; Ward, M.P.; Xia, C.; Li, R.; Sun, L.; Lynn, H.; Gao, F.; Wang, Q.; Zhang, S.; Xiong, C. Monitoring schistosomiasis risk in East China over space and time using a Bayesian hierarchical modeling approach. Sci. Rep. 2016, 6, 24173. [Google Scholar] [CrossRef]
- da Paz, W.S.; Duthie, M.S.; de Jesus, A.R.; de Araújo, K.C.G.M.; Dos Santos, A.D.; Bezerra-Santos, M. Population-based, spatiotemporal modeling of social risk factors and mortality from schistosomiasis in Brazil between 1999 and 2018. Acta Trop. 2021, 218, 105897. [Google Scholar] [CrossRef] [PubMed]
- Brooker, S. Spatial epidemiology of human schistosomiasis in Africa: Risk models, transmission dynamics and control. Trans. R. Soc. Trop. Med. Hyg. 2007, 101, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.-J.; Vounatsou, P.; Zhou, X.-N.; Tanner, M.; Utzinger, J. A Bayesian-based approach for spatio-temporal modeling of county level prevalence of Schistosoma japonicum infection in Jiangsu province, China. Int. J. Parasitol. 2005, 35, 155–162. [Google Scholar] [CrossRef] [PubMed]
- Welton, N.; Ades, A. A model of toxoplasmosis incidence in the UK: Evidence synthesis and consistency of evidence. J. R. Stat. Soc. Ser. C Appl. Stat. 2005, 54, 385–404. [Google Scholar] [CrossRef]
- Melo, M.S.; Cabrera, L.A.A.; Lima, S.V.M.A.; Dos Santos, A.D.; Oliveira, L.M.G.B.; de Oliveira, R.C.; de Sousa Menezes, J.; de Figueiredo, J.A.; de Moura Lane, V.F.; de Lima Júnior, F.E.F. Temporal trend, spatial analysis and spatiotemporal clusters of infant mortality associated with congenital toxoplasmosis in Brazil: Time series from 2000 to 2020. Trop. Med. Int. Health 2023, 28, 476–485. [Google Scholar] [CrossRef] [PubMed]
- Gomez-Barroso, D.; Vescio, M.F.; Bella, A.; Ciervo, A.; Busani, L.; Rizzo, C.; Rezza, G.; Pezzotti, P. Mediterranean spotted fever rickettsiosis in Italy, 2001–2015: Spatio-temporal distribution based on hospitalization records. Ticks Tick-Borne Dis. 2019, 10, 43–50. [Google Scholar] [CrossRef] [PubMed]
- Baquero, O.S.; Machado, G. Spatiotemporal dynamics and risk factors for human Leptospirosis in Brazil. Sci. Rep. 2018, 8, 15170. [Google Scholar] [CrossRef] [PubMed]
- Viroj, J.; Claude, J.; Lajaunie, C.; Cappelle, J.; Kritiyakan, A.; Thuainan, P.; Chewnarupai, W.; Morand, S. Agro-environmental determinants of leptospirosis: A retrospective spatiotemporal analysis (2004–2014) in Mahasarakham province (Thailand). Trop. Med. Infect. Dis. 2021, 6, 115. [Google Scholar] [CrossRef]
- Dhewantara, P.W.; Zhang, W.; Al Mamun, A.; Yin, W.-W.; Ding, F.; Guo, D.; Hu, W.; Magalhães, R.J.S. Spatial distribution of leptospirosis incidence in the Upper Yangtze and Pearl River Basin, China: Tools to support intervention and elimination. Sci. Total Environ. 2020, 725, 138251. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).