Abstract
Visualization and interpretation of user-generated spatial content such as Volunteered Geographic Information (VGI) is challenging because it combines enormous data volume and heterogeneity with a spatial bias. When dealing with point data on a map, these characteristics can lead to point clutter, reducing the readability of the map product and misleading users to false interpretations of patterns in the data, e.g., regarding specific clusters or extreme values. With this work, we provide a framework that is able to generalize point data, preserving spatial clusters and extreme values simultaneously. The framework consists of an agent-based generalization model using predefined constraints and measures. We present the architecture of the model and compare the results with methods focusing on extreme value preservation as well as clutter reduction. As a result, we can state that our agent-based model is able to preserve elementary characteristics of point datasets, such as the point density of clusters, while also retaining the existing extreme values in the data.
1. Introduction
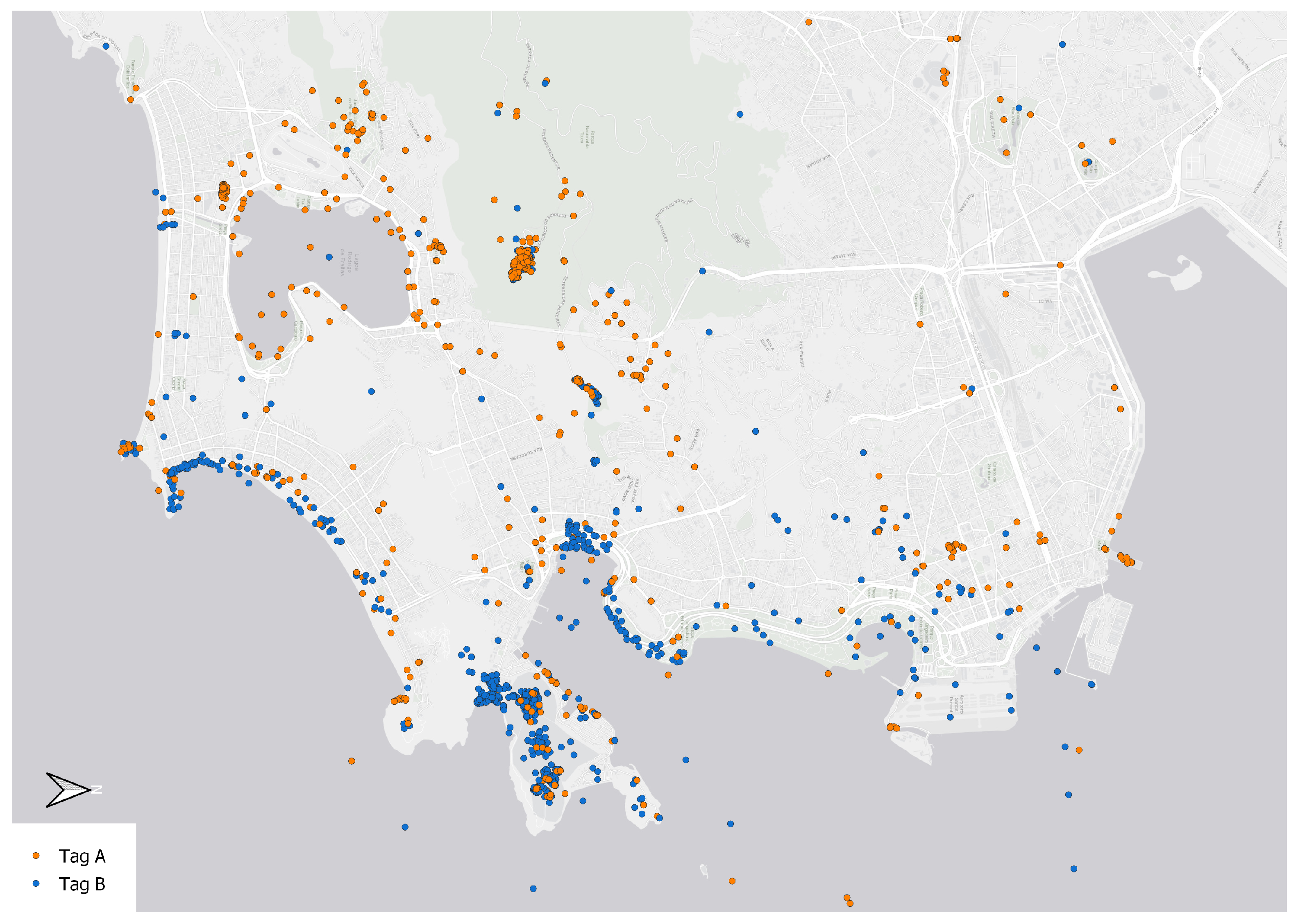
User-generated geographic content (UGGC) has emerged as one of the main data sources for researchers in recent years, often referred to as Volunteered Geographic Information (VGI) [1]. The visualization and interpretation of VGI data are challenging because of its enormous volume and heterogeneity, and when compared to traditional spatial sampling techniques, VGI point data samples such as points of interest or locations of social media posts often have a spatial bias [2] (see Figure 1, where the number of Flickr posts does not reflect the quality of the view towards the landmark but mainly the popularity of the place). If VGI point data are presented on a map, these data characteristics could reduce the readability due to overlapping point symbols, which could possibly hide specific spatial patterns in the data—such as extreme values, clusters or hot spots. Accordingly, a reduction in the overall number of points is needed to improve the readability of the map, while at the same time, the spatial patterns within the data have to be preserved.
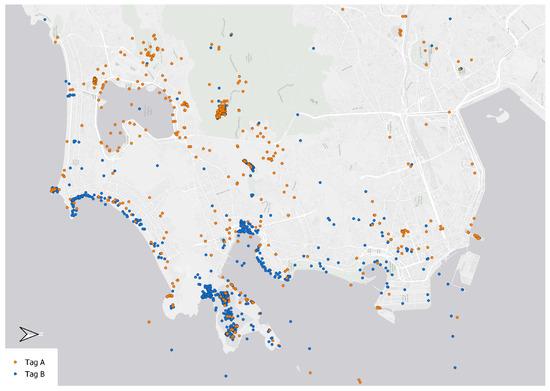
Figure 1.
Location of Flickr posts tagged with variations in the names of either Cristo Redentor (“Tag A”) or the Sugarloaf Mountain (“Tag B”) in Rio de Janeiro. The spatial distribution of points in this dataset mainly originates from the popularity of the places and not only in the quality of their line of sight toward the two landmarks. Therefore, it is not possible to derive the best photo spots just from the number of posts at the respective locations.
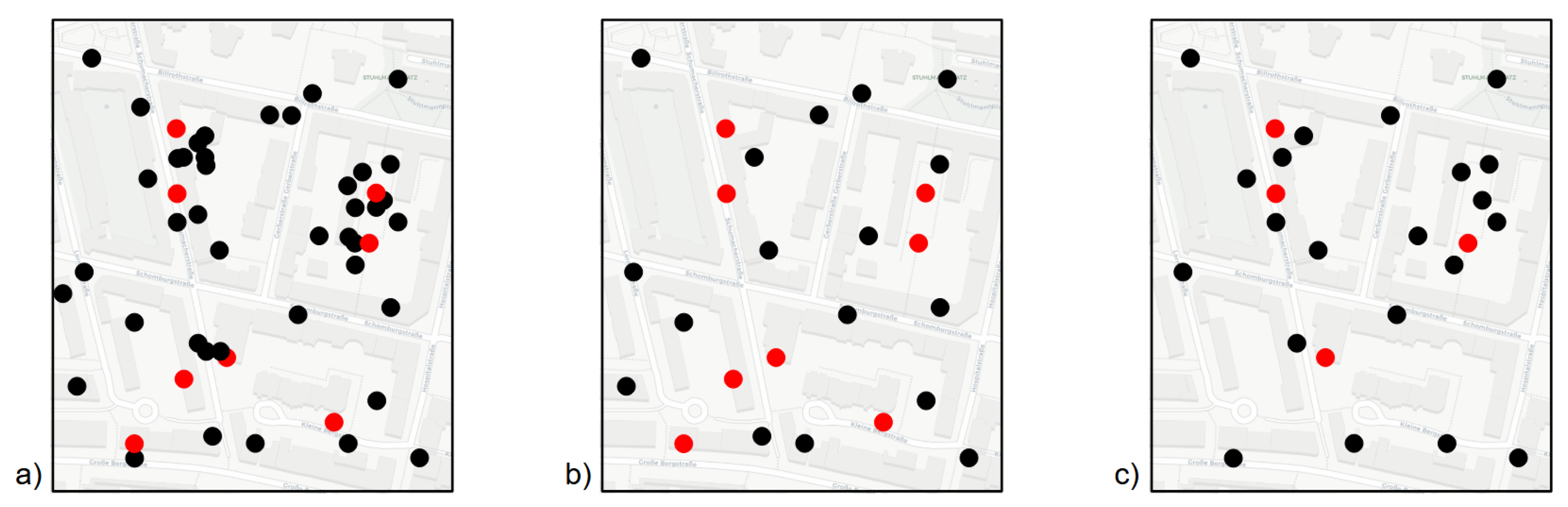
The cartographic solution to the problem of overlapping point symbols—i.e., the display of clutter [3,4]—is point generalization, using operations such as selection, aggregation, simplification, or displacement. However, if these generalizations are applied incautiously, specific characteristics of the data, such as extreme values, may disappear, misleading users to false interpretations of the underlying spatial phenomena (see Figure 2). Therefore, it is key to preserve spatial patterns during the generalization process. More generally, preserving spatial patterns contributes to the principle task of map generalization, which is to provide the best representation of the map content without neglecting readability.
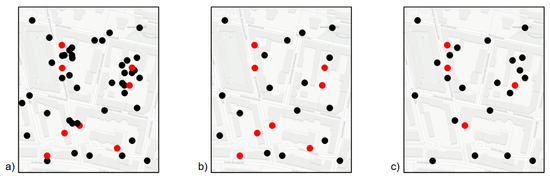
Figure 2.
Example of point generalization. (a) Original data of 50 points with two main clusters and eight extreme values (in red). (b) Generalized data of 25 points using point selection based on value. All eight extreme values are preserved during generalization, while the two-point clusters disappeared in the resulting map. (c) Generalized data of 25 points using point simplification based on location. Both clusters are preserved, while only four of the eight extreme values are preserved. If both the spatial distribution of events and the occurrence of extreme values are of interest, both generalization results can mislead users to false interpretations of the underlying spatial phenomena.
In recent decades, different approaches evolved to mimic the work of human cartographers with the aim of automating the map generalization process. The rule-based approaches were built on stepwise, local transformations of map objects, following unambiguous pre-defined rules [5]. While rule-based generalization was—and still is—a very promising tool for a variety of applications, a major shortcoming in the past was the problem that these automated systems do not have the ability to respond to data variation or specific, task-related requirements in a way that human cartographers could do by modifying these rules. This led to the introduction of the constraint-based approach, where constraints operate as requirements that shall be fulfilled in the final—i.e., generalized—map but without any predefined actions bound to them. Map generalization using a constraint-based approach is, therefore, an optimization problem, where the task is to find a map state that best fulfils all predefined—and sometimes contradicting—constraints, while a set of generalization operations is used to reach this optimal map state by manipulating the map objects.
For the optimization process, Harrie and Weibel [6] argued that agent-based modelling (ABM) is the most powerful modelling method in terms of applicability. In this case, the agents are autonomous map objects attempting to minimize a given cost function, which consists of constraint measures. Duchêne et al. [7] described this technique in detail. In this paper, we want to follow this research, implementing an agent-based model using predefined constraints, which are deduced by Knura and Schiewe [8] based on a study analyzing user behavior when solving interpretation tasks on point data [9].
The remainder of this paper is structured as follows: In the second chapter, we summarize approaches from the literature for point generalization (Section 2.1), pattern preservation (Section 2.2) and agent-based modeling in cartography (Section 2.3). In the third section, we describe the constraints we used during the optimization process (Section 3.1 and introduce our model (Section 3.2). We then conduct experiments (Section 4) and discuss the results (Section 5) before concluding our work (Section 6).
2. Related Work
2.1. Point Generalization
Focusing on the problem of point generalization, operations such as aggregation, simplification, selection, and displacement are of major interest. When using aggregation (i.e., point clustering), point clusters are replaced with aggregator markers. Different cluster initialization methods can thereby trigger quite different results for the same data (e.g., see [10]). Furthermore, Meier [11] evaluates and compares marker cluster techniques and similar approaches, including heatmaps and tiled heatmaps. Point simplification describes a point reduction based on geometric criteria, such as minimum distances between points [12]. When semantic criteria are used to reduce the overall number of points, a point selection takes place, e.g., based on scale [13]. In contrast, point displacement relocates points to reduce point clutter, using an iterative workflow of overlap detection, relocation, and re-evaluation [14].
While these operations all represent the traditional method of point generalization based on cartographic scene judgement, there are also data-driven methods such as deep learning [15], which can be utilized for the application of point generalization, as performed by Xiao et al. [16]. Based on training data created through manual labeling, their model predicts the probability for each point in the dataset to be retained after generalization. Depending on the number of points requested for the final map, the respective points with the highest retaining prediction are then selected.
2.2. Preserving Spatial Patterns
The aforementioned operations focus on the first task of map generalization—increasing map legibility—mainly by removing a certain amount of points. By contrast, preserving the present information of the point data as much as possible is the second task of map generalization—and possibly contradicting the first. Thereby, the question arises as to which spatial point patterns are of interest. A study conducted by Knura and Schiewe [9] analyzed user behavior when interpreting spatial point patterns and thereby revealed two main aspects. First, the proportion of points between different patterns, as well as between dense and sparse areas, was crucial for the task-solving process of the participants. Second, the proportion between different classes within an area—or their respective absence—was frequently described during decision-making. As a result of this study, point pattern preservation can be described as a multi-criteria decision, a technique that has already been proposed in cartography for specific tasks within the workflow of automated map generalization [17] and for class interval selection [18]. Based on the latter work on choropleth maps, Chang and Schiewe [19] were able to preserve spatial patterns such as local extreme values and hot or cold spots. As an example of preserving a spatial point pattern for visualization purposes, Qiang et al. [20] used a pyramid modeling framework and point density metrics in their work. For some applications, it could also be useful to visualize point patterns with respect to other geometry objects, such as street networks [21]. To the best of our knowledge, approaches for point pattern preservation with respect to point density and local extreme values are still missing.
2.3. Agent-Based Modeling in Map Generalization
In addition to the numerous advances in the optimization of individual generalization operations, there is also considerable work regarding the orchestration of these operations. Even before Harrie and Weibel [6] identified agent-based modeling as the most powerful applicable modelling method, there were multiple research studies for automated generalization systems that relied on this approach. For a detailed overview, we refer to the work of Duchêne et al. [7], who explain the basic principles of this approach, describe different implementations of agent-based models at the French National Mapping Agency (IGN), and discuss the advantages and drawbacks of multi-agent systems for cartographic generalization. Accordingly, the implementations introduced in the following sections of this paper are based on this work.
These multi-agent systems rely on the definition of a set of constraints and their respective measures, which define the level of satisfaction for each constraint. Thereby, Mackaness and Ruas [22] distinguish between three levels of measures: micro-measures focus on individual features of map objects, meso-measures describe properties of groups of objects, and macro measures deal with characteristics of the whole map data. Furthermore, the authors distinguish between internal measures that describe single datasets, and external measures that describe relations between different datasets or map states, for example between the original and the generalized map. With regard to content, Beard [5] classified constraints into six thematic categories: position, topology, shape, structure, function, and legibility. Consequently, our work also relies on a subset of these constraints.
3. Method
3.1. Definition of Constraints
We define three different types of constraints and respective measures that can guide the generalization process within our agent-based model. The first type is constraints that correspond with the specific kind of tasks we aim for, such as the identification of extreme values or dense clusters, and therefore ensure that spatial patterns are maintained. The second type of constraints supports the task-solving process of the users and result from the aforementioned user study [9]. The last type of constraint reflects the fundamental requirements of successful point generalization, such as a reduction in clutter or the preservation of Gestalt Law rules within the map.
Table 1 lists these constraints. For more details on the definition of these measures, we refer to the work of Knura and Schiewe [8], in which the authors identified a set of constraints by translating the outcomes of their study [9] into measurable values.

Table 1.
Relevant constraints and measures based on [8]. Constraints are derived from either task requirements (type 1), results of a user study [9] (type 2) or fundamentals of point generalization (type 3).
3.2. Architecture of the Agent-Based Model
3.2.1. General Architecture
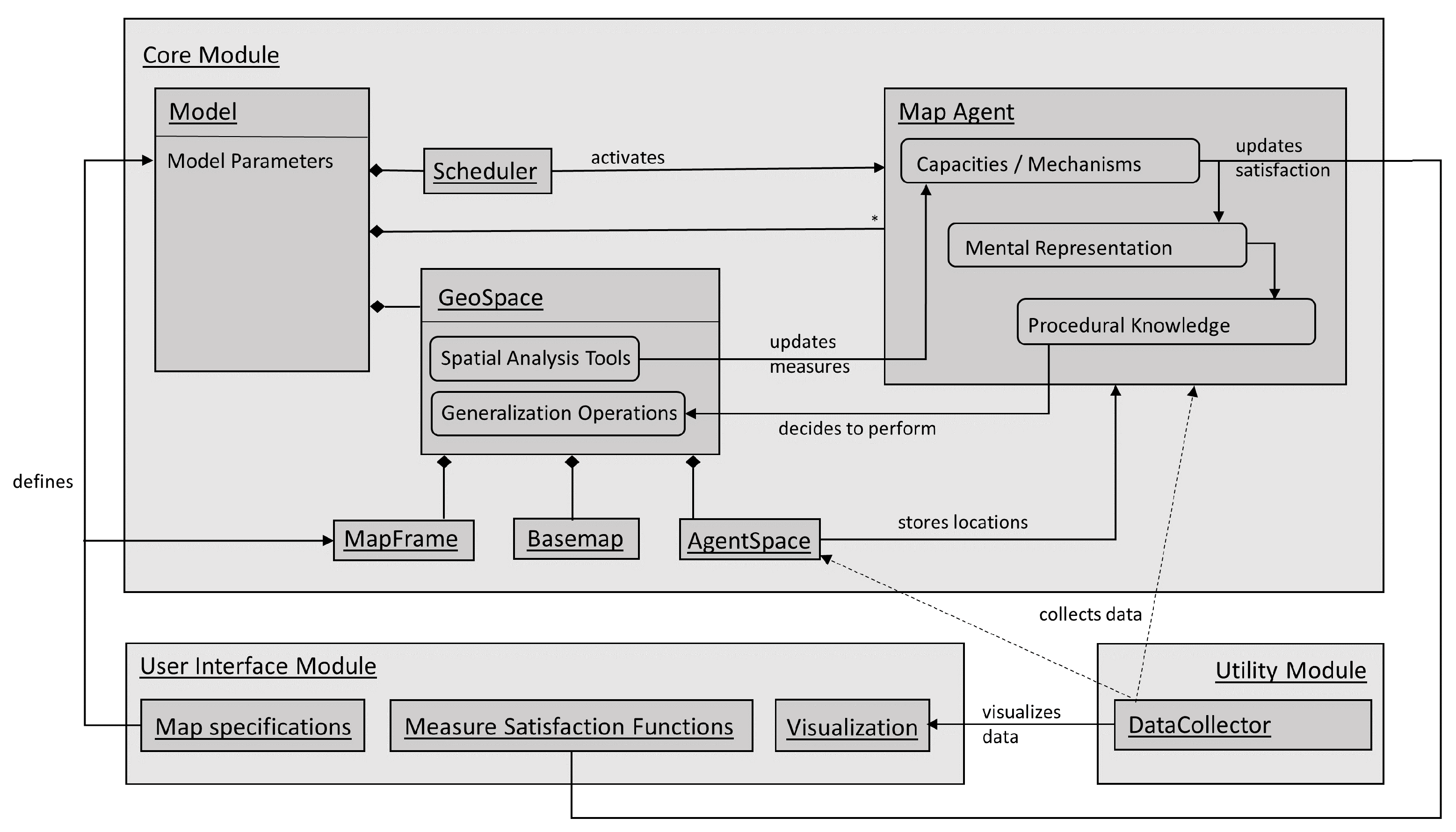
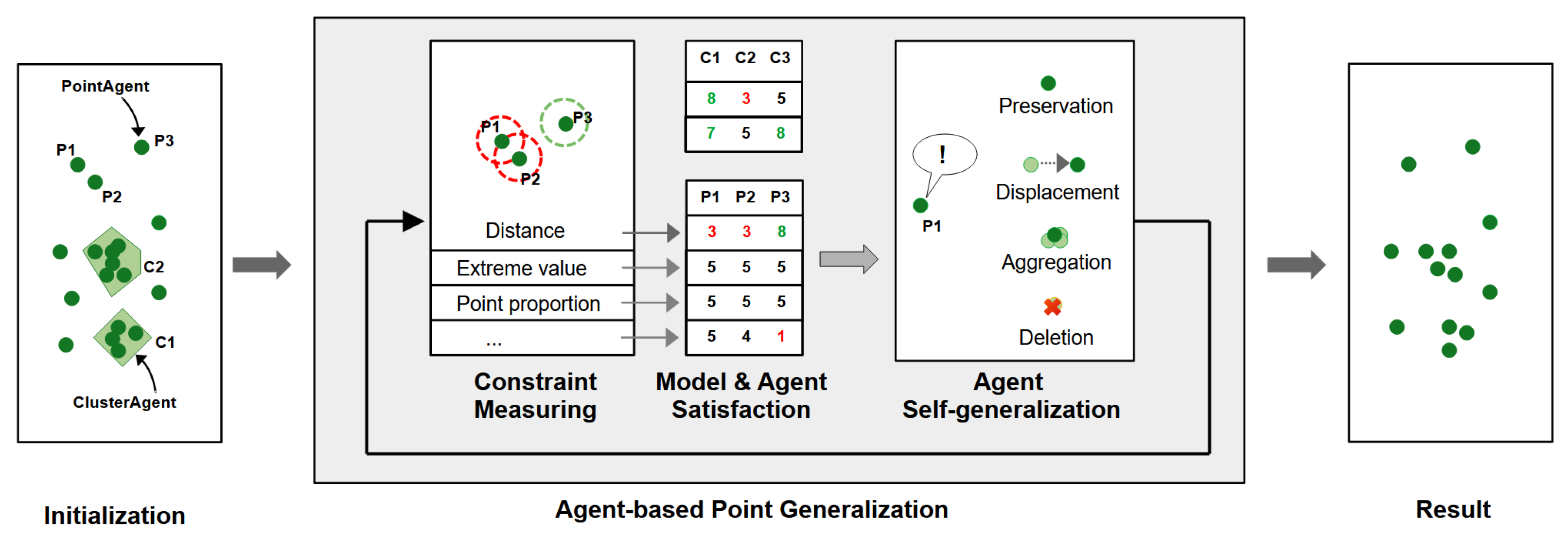
The agent-based model is implemented using the open-source framework Mesa [26] and its spatial extension Mesa-Geo [27]. Mesa is written in Python and offers the basic ABM functionalities by providing four core components (Model, Agent, Schedule and Space) alongside two additional components for analysis and visualization. The Model class is the main class of the framework and controls the major components of the system. In this class, the initial state of the model is defined, as well as the actions that happen while the model is running. The Model class also creates the agents that implement the Agent class and the Scheduler class, which controls the time and the activations during runtime. Mesa offers four different schedule activations, namely the BaseScheduler, which activates agents one at a time in the starting order, RandomActivation, which activates the agents in random order, SimultaneousActivation, which activates all agents at the same time, and StagedActivation, where the action within one model step is divided into several stages, and all agents execute one stage before moving to the next stage. For models that require the concept of space, the respective Space class in Mesa has five general definitions of space: ContinuousSpace where agents have (x,y) positions, NetworkGrid, which implements graphs with nodes and edges, and three types of grids (SingleGrid, MultiGrid and HexaGrid). However, Mesa does not directly support the integration of geographical data into the model, and so the spatial extension Mesa-Geo was developed by Wang et al. [27], allowing users to import, manipulate, visualize and export geographical data. Therefore, the new class GeoSpace was added, which can consist of multiple layers of vector and raster data. Furthermore, Mesa-Geo distinguishes between AgentLayers, which contain GeoAgents that carry out activities during the simulation, and VectorLayers, which remain static (e.g., road networks).
Figure 3 shows the architecture of our ABM application for point generalization, which consists of three modules. The Core Module contains the main Model class, a class for different types of MapAgents, the Scheduler class and several instances of the GeoSpace class. The DataCollector class of the Utility Module collects and provides the information during runtime for the Visualization class of the User Interface Module, which also contains two classes for the specification of the map and the parametrization of the constraints and measures of the model. In the following, the modules and their interconnections are explained in detail.
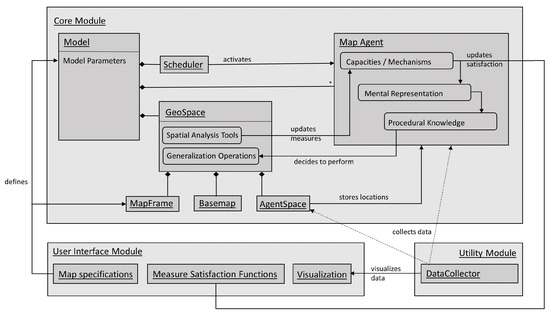
Figure 3.
Architecture of the agent-based point generalization model.
3.2.2. User Interface Module
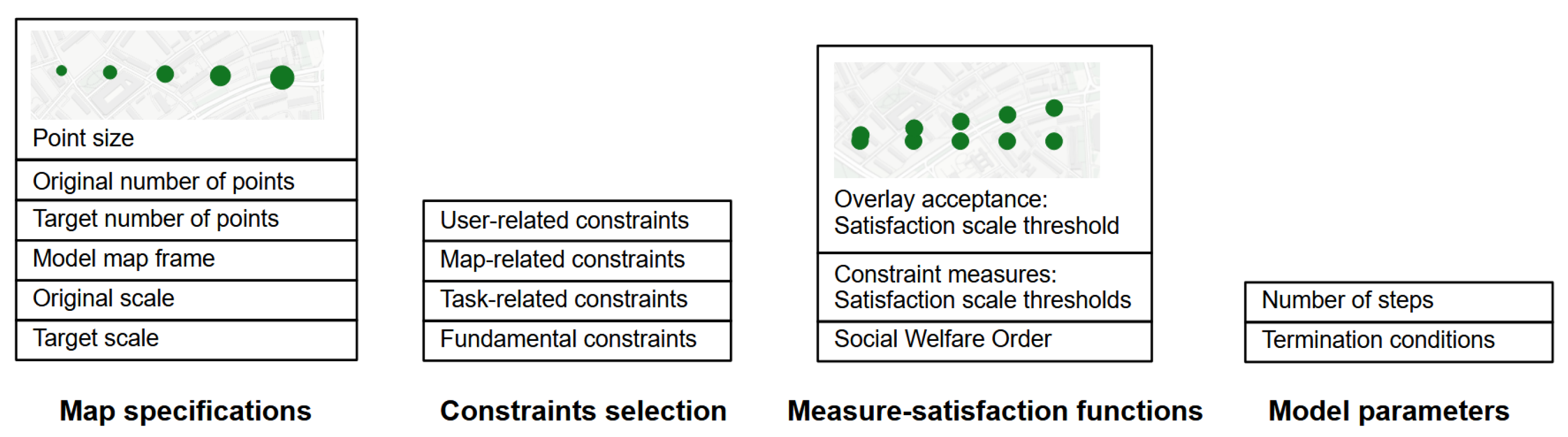
The first step to run the model is to define global map specifications, such as the scale of the original and the target map, the borders of the map frame, and whether the original data set is already fulfilling legibility constraints. If this is the case, the target number of points after generalization can be calculated, e.g., using the Radical Law [24]. Furthermore, the desired behavior of the map agents regarding their fulfillment of the selected constraints has to be predefined. The common workflow in agent-based map generalization to translate a list of constraints into a satisfaction value representing the status of a map agent consists of two steps [28]: First, the respective measures for the constraints are translated into a Likert-like satisfaction scale according to predefined threshold values, ranging from 1 (“unacceptable”) to 8 (“perfect”). Second, global satisfaction is calculated based on the individual satisfaction values, for example by calculating the mean value or by utilizing principles from Social Welfare Orderings (SWO) [28].
Figure 4 lists the different types of parameters that have to be defined before running the agent-based model. In addition to the aforementioned global map specifications, the basic model parameters, and a list of constraints, as presented in Table 1, the definition of, reasonable threshold values are essential for the success of an agent-based map generalization model, but it is also a complex task. To help with this process of model parametrization, we adapted an approach of Taillandier and Gaffuri [29] using a human–machine dialogue. Therefore, we offer a guided user interface to adjust the thresholds for each measure satisfaction function and visualize the impact of selected thresholds via samples on a map to obtain a better understanding of the impacts of the thresholds on the constraint satisfaction and on the expected results of the generalization process in general. For example, decreasing the threshold values for the minimum distance between agents ensures that the agents are more likely to decide to perform generalization operations that improve their satisfaction regarding this measure, such as increasing the distance to their neighbors using displacement, or deleting themselves as a result of a selection operation. As a result, the distance between individual agents will likely increase on the final map, while the number of points will decrease.
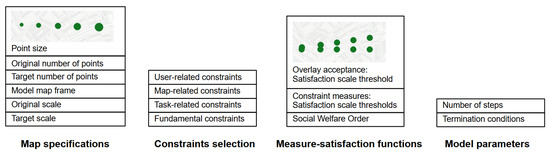
Figure 4.
List of parameters and examples for manual parameter definitions using a human–machine dialogue as suggested by Taillandier and Gaffuri [29]. As an example, adjusting the overlay acceptance thresholds for the respective measure-satisfaction function by allowing a smaller distance between PointAgents will probably result in several overlapping points still existing in the final map.
3.2.3. Core Module
A simplified model flow is shown in Figure 5. When initializing the model, a MapAgent is created for every point within the data set, which should be generalized. Furthermore, MapAgents are created for every cluster within the original point data set. MapAgents are the central part of our model and their decision-making process follows the work of Duchêne et al. [7], which decomposes the “brain” of agents in map generalization systems into three main components: capacities, mental representation and procedural knowledge. The capacities of MapAgents include the ability to perceive their surrounding space—i.e., points in their neighborhood—to evaluate their own state, to communicate with other agents, and to perform generalization operations on themselves. Spatial operations for self-evaluation and self-generalization are thereby provided and controlled by the GeoSpace class. The part of the brain that represents the mental state of the agents compares its current status with the goals the agents are aiming for—i.e., the mental representation of MapAgents describes their fulfillment towards the predefined map constraints, using the measure satisfaction functions retrieved as described above. Furthermore, this part of the MapAgents’ brain memorizes all previous decisions and their respective outcomes. The actual decision-making is undertaken in the procedural knowledge part of the MapAgents. Using the information about its current state of constraint satisfaction and its former decisions and their outcomes, each MapAgent decides which generalization operation it wants to perform next.
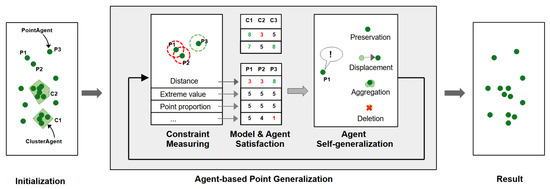
Figure 5.
Simplified model flow chart without details of the decomposed “brain” of the MapAgents. After initializing the MapAgents for points and clusters, each model step begins by calculating the measures to analyze the actual state of constraint fulfillment. Using the measure-satisfaction functions for each constraint, all MapAgents receive a list of satisfaction values ranging from 1 (worst) to 8 (best) representing their own state. Based on this, MapAgents can calculate their own overall satisfaction, and a general model state can be determined. If the overall model state does not reach an equilibrium model state—or match the model termination conditions—MapAgents can perform generalization operations on themselves, and the next step is initialized.
4. Experiments
We want to test our model by generalizing a test data set from a scale of 1:15,000 to a scale of 1:30,000. The aim is to support the preservation of spatial patterns during point generalization. In addition to specific patterns such as local extreme values, it is also of interest to maintain point densities within clusters as well as in sparse areas.
Because approaches for point pattern preservation considering both point density and local extreme values are still missing, we want to compare the results of our model with different methods focusing on spatial distribution and extreme value preservation. For the generalization of spatial distribution characteristics, we utilized a quad tree structure. We fill this quad tree structure (capacity = 1) sequentially with a point data set and then delete all points that are assigned to leaves with an area below the point signature size threshold for the target scale. In other words, we only retain points that are assigned to leaves of the quad tree of a predefined threshold level or higher. For the preservation of local extreme values, we used the discrete isolation algorithm of Gröbe and Burghardt [13], which calculates a point’s distance to the closest point with a higher value, which in the next step can be used as a selection parameter for point generalization.
4.1. Data
We utilized a data set that shows the locations of social media images from the platform Flickr that contain at least one bicycle [30]. Our test data set contains 800 of these data points, which are all located in the area of Dresden, Germany. We chose this dataset because it fulfils two requirements we want to test our model with: First, the point distribution is clearly biased in a way that is characteristic of VGI data, as the majority of points are located in a relatively small area around the city center, while there are only few outliers spread over the suburbs. Second, the data set provides the number of bicycles per social media image, which can be used to determine local extreme values, i.e., photos that show a high number of bicycles.
4.2. Performance Metrics
To evaluate the performance of our model in comparison to the quad tree generalization and the discrete isolation algorithm, we define metrics to evaluate point density preservation, as well as local extreme value preservation. For point density preservation, we first define clusters within the original dataset using the DBScan algorithm. Based on these eight clusters, we measure the point density before and after generalization for each cluster, and calculate the mean preserved density (MPD) and its standard deviation (SDPD) over all clusters. Furthermore, we want to take a closer look at two specific clusters that are characteristic of VGI data. The first cluster has 44 points and is located around the Theaterplatz in Dresden, where several historic sites such as Semperoper, Hofkirche, Zwinger and Grünes Gewölbe are in proximity, but without a specified center. The second cluster has 68 points and is located at the Frauenkirche, where a high amount of photos is located in a small area of interest. We expect that our proposed model and the quad tree generalization perform better than the discrete isolation algorithm with these clusters, as the objective of the latter is point selection based on high values, but we also want to analyze if these clusters are generalized differently.
For the preservation of local extreme values, we identify all extreme values and count the number of preserved points in the generalized datasets. For this test, we expect that the discrete isolation algorithm and our model perform better than the quad tree generalization, as the latter takes only the point location into account during generalization, but not its attributes.
4.3. Results
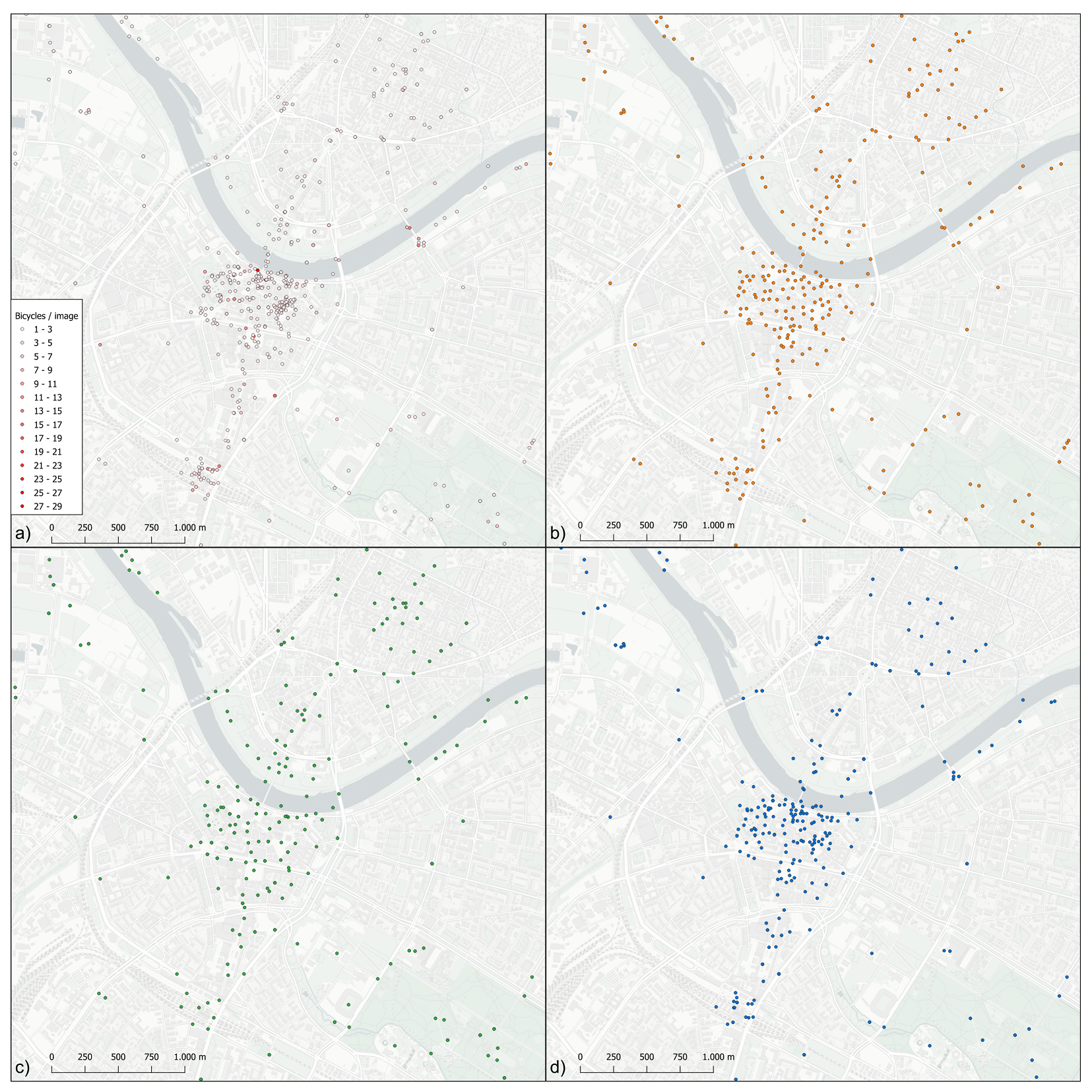
Figure 6 shows the generalization results for the three methods. It can be seen that the result of the discrete isolation algorithm is more spread out compared to the other methods, which preserve the overall shape of the central clusters better. In the quad tree generalization result (Figure 6b), all clutters are resolved, but due to the applied method, some of these clutters are completely removed. The same can be stated for the discrete isolation algorithm (Figure 6c), which is even more spread out in the former cluster areas. Looking at the less dense areas of the map, both the quad tree and the discrete isolation method preserved the majority of points, which is in fact the intended behavior of both algorithms. In the resulting map of our agent-based model (Figure 6d), the original shape of the point distribution, as well as spots with points in close proximity within the clusters, are preserved, but with the downside that there are still a few overlapping points existing after the generalization.
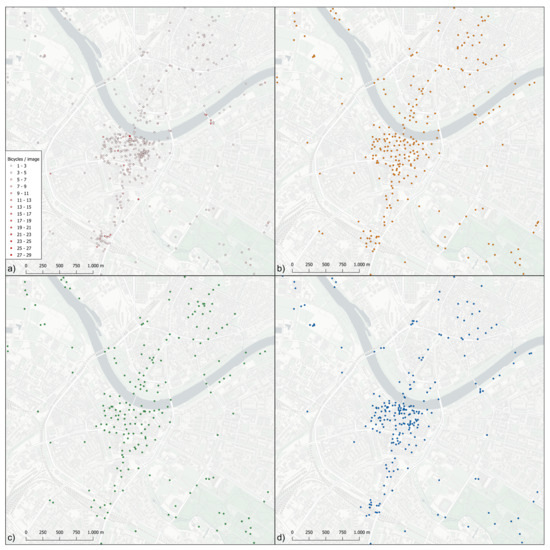
Figure 6.
Results of the point generalization. (a) Original data (800 points), (b) quad tree generalization (394 points), (c) discrete isolation algorithm (404 points), (d) our agent-based model (398 points). While the discrete isolation algorithm focuses on preserving extreme values and therefore disperses the tight cluster structure in the city center, both the quad tree generalization and the agent-based approach preserve the specific cluster shape. Note that quantities are only visualized in the original map for a better understanding of the dataset.
Table 2 presents the results of our experiments using the performance metrics, which confirm the findings stated above. While the point density within the eight clusters is reduced to 26% for the quad tree and 35% for our model compared to the original dataset, the discrete isolation algorithm maintains only 12% of the original density. In return, most of the extreme values (25/27) are preserved with this method, while the quad tree (20/27) and our model (23/27) preserve less extreme values. With respect to the number of points retained in the two focus clusters, all generalization methods retained more or the same number of points in the cluster around the Theaterplatz, although it has fewer total points than the one at the Frauenkirche.

Table 2.
Results of the experiments evaluating our model compared to the quad tree generalization and the discrete isolation algorithm. MPD = mean preserved density, SDPD = std.dev preserved density, EXT = preserved extreme values, Ptp = preserved points at the Theaterplatz, Pfk = preserved points at the Frauenkirche.
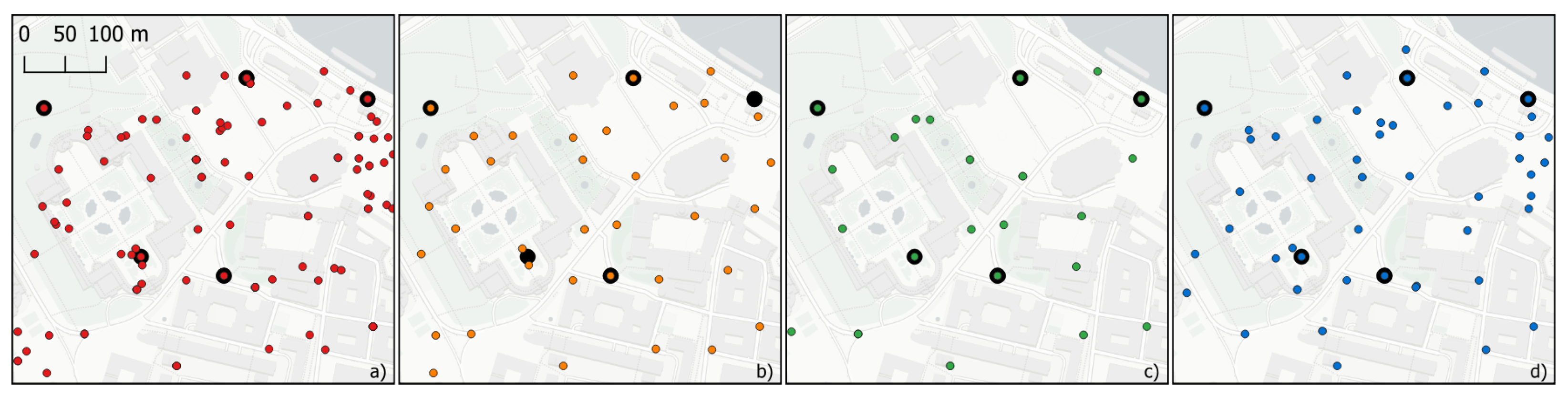
A detailed view of the generalization results around the Theaterplatz area can be seen in Figure 7. As stated in Table 2, our agent-based model retained more points in this area than the other two methods, followed by the quad tree generalization and the discrete isolation algorithm. It also maintains significant parts of the dense cluster in the northeastern corner of the map, while the other approaches both delete all but one or two points in this area. Furthermore, our approach—as with the discrete isolation algorithm—preserves all extreme values in the map, while the quad tree approach only preserves three of the five points.
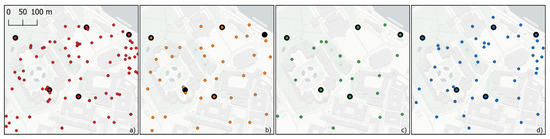
Figure 7.
Detailed view of the generalization results around the Theaterplatz. (a) Original data, (b) quad tree generalization, (c) discrete isolation algorithm, (d) our agent-based model. Original positions of extreme values are highlighted with a big black dot.
5. Discussion
The findings of our experiments show that our model is able to preserve both the point density of clusters and extreme values, which was the main goal of this paper. Using the performance metrics of point density preservation and extreme value preservation, the results of the agent-based model are comparable to the better performance of the two benchmark models, respectively. Elementary characteristics of the point dataset, such as clusters with a specific point density, and the existence of local and global extreme values are better preserved during generalization. To what extent the resulting maps of our approach are able to improve the actual decision-making of users has to be tested in an appropriate user study and is a major part of our future work.
In addition, we were able to implement an agent-based model for map generalization in the programming language Python, using the spatial extension of the open-source framework Mesa. To the best of our knowledge, this is the first time a Python-based framework is used for agent-based map generalization, and we can show that Mesa-Geo satisfies all the requirements we had for the implementation of our model. Furthermore, the implementation in Python allows us to provide a plugin for QGIS in the near future, which could considerably improve the usability of our model.
Nevertheless, there are some shortcomings of our approach. In Section 3.1, we present the constraints and measures we implemented in our model. Before the model is able to run, six of these measures require manual parameter adjustment to translate them into satisfaction values. Although we think this is still a feasible number while adapting an intuitive approach for setting suitable parameters, this process has been identified as one of the major drawbacks of the agent-based approach in map generalization in general [7]. Although the manual parameter adjustment makes it difficult to transfer our approach of point generalization to other applications, our first experiments with different datasets also showed that most of the parameters can be transferred to obtain at least reasonable results, especially when the same target scale and point size are used. A main part of our future work will therefore be a user study with experienced cartographers to further evaluate the outcome of our model while using different combinations of input parameters. At best, the results can also be used to automate the parameter adjustment for the measure satisfaction functions, reducing the number of parameters to fundamental inputs such as target map scale and point size. The method itself, together with our set of constraints and measures, can be transferred to—or implemented in—existing agent-based models for map generalization, as we utilize the best practices from this research field.
Compared to the discrete isolation algorithm, a second drawback of our approach is the computational performance. Because of the time-consuming calculation of measures that rely on geospatial operations with logarithmic time complexity such as Voronoi diagrams, the computing time depends mainly on the number of points to generalize. Using an AMD Ryzen 7 with 3.2 GHz and 32 GB RAM, generalizing the whole dataset used in the study takes nearly ten minutes of runtime, compared to a few seconds for discrete isolation and less than a minute for the quad tree generalization. Additionally, the complexity of a point distribution—in terms of how often the original dataset violates the intended map constraints—has an influence on the number of calculation steps that are needed to reach an equilibrium model state, i.e., a state of the model where the majority of map agents have reached a satisfying state for themselves, and variables such as the total number of (visible) points and the distribution of points between the clusters are mostly stable. Therefore, on-the-fly point generalization [31] is not yet possible with our approach, but the framework of our model can already be deployed for map generalization on a regular basis. However, there is still room for improvement on the computational side of our model. As an example, we do not implement multi-thread computation yet, which could reduce the computational time considerably. Especially when dealing with large datasets, it can be useful to split them into smaller subsets, which can then be generalized seperately and simultaneously, while using the same parameters and measuring satisfaction functions.
As a result, we can state that our approach is the best if a combination of preserving local and global extreme values, while also maintaining spatial patterns such as clusters is of interest, with the downside of a higher complexity and therefore longer computation time. If the focus is mainly on the preservation and visualization of extreme values, the discrete isolation algorithm is the best choice, as it is faster in computation and easy to use as a QGIS plugin. If just a rough and general view of the distribution of clusters is needed, the quad tree generalization can be used, as it is slightly faster in computation compared to our approach, although there is no easy-to-use implementation available yet.
A different way to deal with the problem of point generalization while preserving specific spatial patterns could be the integration of novel learning techniques. In this case, our model and its output can be used to create training data for the learning model—similar to the work of [16], or in return, parametrization can be learned and automated based on manually created results.
6. Conclusions
The visualization and interpretation of VGI data are challenging because of its enormous volume and heterogeneity, and datasets actively or passively retrieved from volunteers often have a spatial bias. If the data are presented on maps, these specific characteristics of VGI often reduce the map readability due to overlapping point symbols. Even worse, these point clusters can hide specific spatial patterns in the data, misleading users to the wrong conclusion. In this paper, we develop an agent-based model that generalizes point data by reducing the overall number of points, while specific spatial patterns such as extreme values and clusters are preserved. We present the framework of the model and test the performance in comparison to solutions focusing on pattern analysis and point selection. With the results, we can show that our agent-based model is able to preserve spatial patterns such as clusters, as well as local and global extreme values.
Author Contributions
Conceptualization, Martin Knura and Jochen Schiewe; Methodology, Martin Knura and Jochen Schiewe; Software, Martin Knura; Validation, Martin Knura; Formal analysis, Martin Knura and Jochen Schiewe; Investigation, Martin Knura; Resources, Jochen Schiewe; Data curation, Martin Knura; Writing—original draft, Martin Knura; Writing—review and editing, Martin Knura and Jochen Schiewe; Visualization, Martin Knura; Supervision, Jochen Schiewe; Project administration, Jochen Schiewe; Funding acquisition, Jochen Schiewe. All authors have read and agreed to the published version of the manuscript.
Funding
This research is part of the project Improvement of task-oriented visual interpretation of VGI point data (TOVIP), founded by the German Research Foundation (DFG) (Grant No. SCHI 1008/11-1) within the priority program SPP 1894—Volunteered Geographic Information: Interpretation, Visualisierung und Social Computing.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Goodchild, M.F. Citizens as Voluntary Sensors: Spatial Data Infrastructure in the World of Web 2.0. Int. J. Spat. Data Infrastruct. Res. 2007, 2, 24–32. [Google Scholar]
- Zhang, G.; Zhu, A.X. The representativeness and spatial bias of volunteered geographic information: A review. Ann. GIS 2018, 24, 151–162. [Google Scholar] [CrossRef]
- Rosenholtz, R.; Li, Y.; Nakano, L. Measuring visual clutter. J. Vis. 2007, 7, 17. [Google Scholar] [CrossRef] [PubMed]
- Touya, G.; Hoarau, C.; Christophe, S. Clutter and Map Legibility in Automated Cartography: A Research Agenda. Cartogr. Int. J. Geogr. Inf. Geovisual. 2016, 51, 198–207. [Google Scholar] [CrossRef]
- Beard, K. Constraints on rule formation. Map Generalization: Making Rules for Knowledge Representation; Addison-Wesley Longman Ltd.: Toronto, ON, Canada, 1991; pp. 121–135. [Google Scholar]
- Harrie, L.; Weibel, R. Modelling the Overall Process of Generalisation. In Generalisation of Geographic Information; Mackaness, W.A., Ruas, A., Sarjakoski, L.T., Eds.; International Cartographic Association, Elsevier Science B.V.: Amsterdam, The Netherland, 2007; pp. 67–87. [Google Scholar] [CrossRef]
- Duchêne, C.; Touya, G.; Taillandier, P.; Gaffuri, J.; Ruas, A.; Renard, J. Multi-Agents Systems for Cartographic Generalization: Feedback from Past and On-going Research; Research report; IGN (Institut National de l’Information Géographique et Forestière); LaSTIG, équipe COGIT: Saint-Mandé, France, 2018. [Google Scholar]
- Knura, M.; Schiewe, J. Improvement of Task-Oriented Visual Interpretation of VGI Point Data. In Volunteered Geographic Information; Burghardt, D., Demidova, E., Keim, D.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2023; pp. 89–111. [Google Scholar] [CrossRef]
- Knura, M.; Schiewe, J. Analysis of User Behaviour While Interpreting Spatial Patterns in Point Data Sets. KN J. Cartogr. Geogr. Inf. 2022, 72, 229–242. [Google Scholar] [CrossRef]
- Yan, H.; Weibel, R. An algorithm for point cluster generalization based on the Voronoi diagram. Comput. Geosci. 2008, 34, 939–954. [Google Scholar] [CrossRef]
- Meier, S. The Marker Cluster: A Critical Analysis and a New Approach to a Common Web-based Cartographic Interface Pattern. Int. J. Agric. Environ. Inf. Syst. 2016, 7, 28–43. [Google Scholar] [CrossRef]
- Slocum, T.; McMaster, R.; Kessler, F.; Howard, H. Thematic Cartography and Geovisualization; Prentice Hall Series in Geographic Information Science; Pearson Prentice Hall: Upper Saddle River, NJ, USA, 2009. [Google Scholar]
- Gröbe, M.; Burghardt, D. Scale-Dependent Point Selection Methods for Web Maps. KN J. Cartogr. Geogr. Inf. 2021, 71, 143–154. [Google Scholar] [CrossRef]
- Mackaness, W.A.; Purves, R.S. Automated Displacement for Large Numbers of Discrete Map Objects. Algorithmica 2001, 30, 302–311. [Google Scholar] [CrossRef]
- Touya, G.; Zhang, X.; Lokhat, I. Is deep learning the new agent for map generalization? Int. J. Cartogr. 2019, 5, 142–157. [Google Scholar] [CrossRef]
- Xiao, T.; Ai, T.; Yu, H.; Yang, M.; Liu, P. A point selection method in map generalization using graph convolutional network model. Cartogr. Geogr. Inf. Sci. 2024, 51, 20–40. [Google Scholar] [CrossRef]
- Touya, G. Multi-Criteria Geographic Analysis for Automated Cartographic Generalization. Cartogr. J. 2022, 59, 18–34. [Google Scholar] [CrossRef]
- Armstrong, M.P.; Xiao, N.; Bennett, D.A. Using Genetic Algorithms to Create Multicriteria Class Intervals for Choropleth Maps. Ann. Assoc. Am. Geogr. 2003, 93, 595–623. [Google Scholar] [CrossRef]
- Chang, J.; Schiewe, J. An open source tool for preserving local extreme values and hot/cold spots in choropleth maps. KN J. Cartogr. Geogr. Inf. 2018, 68, 307–309. [Google Scholar] [CrossRef]
- Qiang, Y.; Buttenfield, B.; Xu, J. Analyzing multi-scale spatial point patterns in a pyramid modeling framework. Cartogr. Geogr. Inf. Sci. 2022, 49, 370–383. [Google Scholar] [CrossRef]
- Zahtila, M.; Knura, M. Visualizing Point Density on Geometry Objects: Application in an Urban Area Using Social Media VGI. KN J. Cartogr. Geogr. Inf. 2022, 72, 187–200. [Google Scholar] [CrossRef]
- Mackaness, W.A.; Ruas, A. Evaluation in the Map Generalisation Process. In Generalisation of Geographic Information; Mackaness, W.A., Ruas, A., Sarjakoski, L.T., Eds.; International Cartographic Association, Elsevier Science B.V.: Amsterdam, The Netherlands, 2007; pp. 89–111. [Google Scholar] [CrossRef]
- Harrie, L.; Stigmar, H. An evaluation of measures for quantifying map information. ISPRS J. Photogramm. Remote Sens. 2010, 65, 266–274. [Google Scholar] [CrossRef]
- Töpfer, F.; Pillewizer, W. The Principles of Selection. Cartogr. J. 1966, 3, 10–16. [Google Scholar] [CrossRef]
- Edelsbrunner, H.; Kirkpatrick, D.; Seidel, R. On the shape of a set of points in the plane. IEEE Trans. Inf. Theory 1983, 29, 551–559. [Google Scholar] [CrossRef]
- Kazil, J.; Masad, D.; Crooks, A. Utilizing Python for Agent-Based Modeling: The Mesa Framework. In Proceedings of the Social, Cultural, and Behavioral Modeling; Thomson, R., Bisgin, H., Dancy, C., Hyder, A., Hussain, M., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 308–317. [Google Scholar]
- Wang, B.; Hess, V.; Crooks, A. Mesa-Geo: A GIS Extension for the Mesa Agent-Based Modeling Framework in Python. In Proceedings of the 5th ACM SIGSPATIAL International Workshop on GeoSpatial Simulation, Seattle, WA, USA, 1 November 2022; Association for Computing Machinery: New York, NY, USA, 2022. GeoSim ’22. pp. 1–10. [Google Scholar] [CrossRef]
- Touya, G. Social Welfare to Assess the Global Legibility of a Generalized Map. In Geographic Information Science; Springer: Berlin/Heidelberg, Germany, 2012; pp. 198–211. [Google Scholar] [CrossRef]
- Taillandier, P.; Gaffuri, J. Designing generalisation evaluation function through human-machine dialogue. arXiv 2012, arXiv:1204.4332. [Google Scholar]
- Knura, M.; Kluger, F.; Zahtila, M.; Schiewe, J.; Rosenhahn, B.; Burghardt, D. Using Object Detection on Social Media Images for Urban Bicycle Infrastructure Planning: A Case Study of Dresden. ISPRS Int. J. Geo-Inf. 2021, 10, 733. [Google Scholar] [CrossRef]
- Jabeur, N.; Boulekrouche, B.; Moulin, B. Using Multiagent Systems to Improve Real-Time Map Generation. In Proceedings of the Advances in Artificial Intelligence; Lamontagne, L., Marchand, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 37–48. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).