Urban Spatiotemporal Event Prediction Using Convolutional Neural Network and Road Feature Fusion Network
Abstract
1. Introduction
- In this paper, an urban spatiotemporal event prediction method based on CNN and FFN is proposed. It is useful in urban safety management due to its ability to predict the occurrence of events in advance and thus reduce disaster losses.
- The prediction is initially performed by constructing feature map construction using a CNN and an optimization search operation is conducted on the size of the feature map and the structure of the CNN. Then, an innovative FFN is used to extract urban road network information using multiscale convolution and incorporate the extracted road network feature information into the CNN.
- Experiments are conducted using the urban patrol dataset of Zhengzhou City in China and the proposed method is compared with other advanced methods. The experimental results demonstrate the effectiveness of this method in urban spatiotemporal event prediction.
2. Related Work
3. Methodology
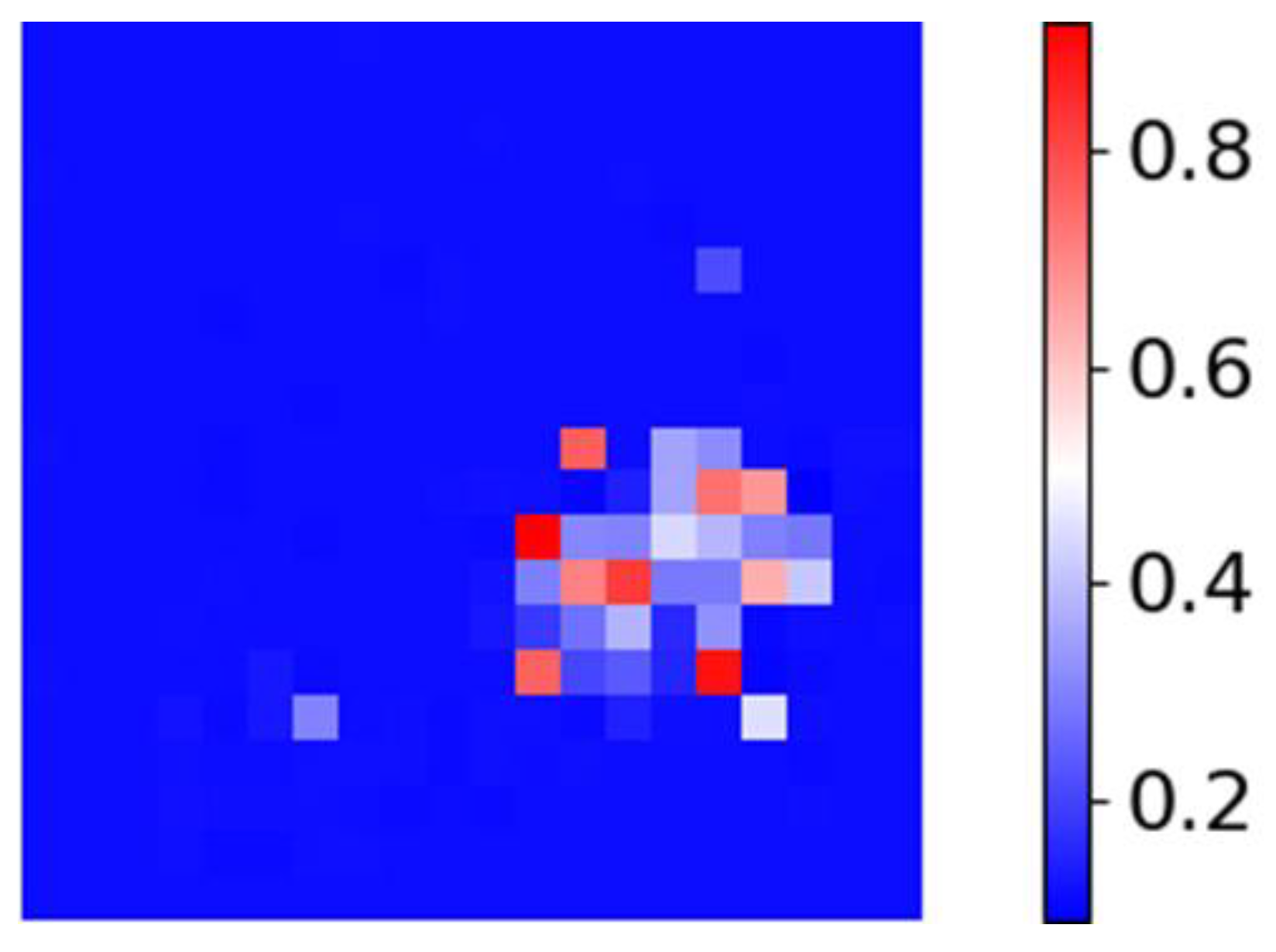
3.1. Feature Map Construction
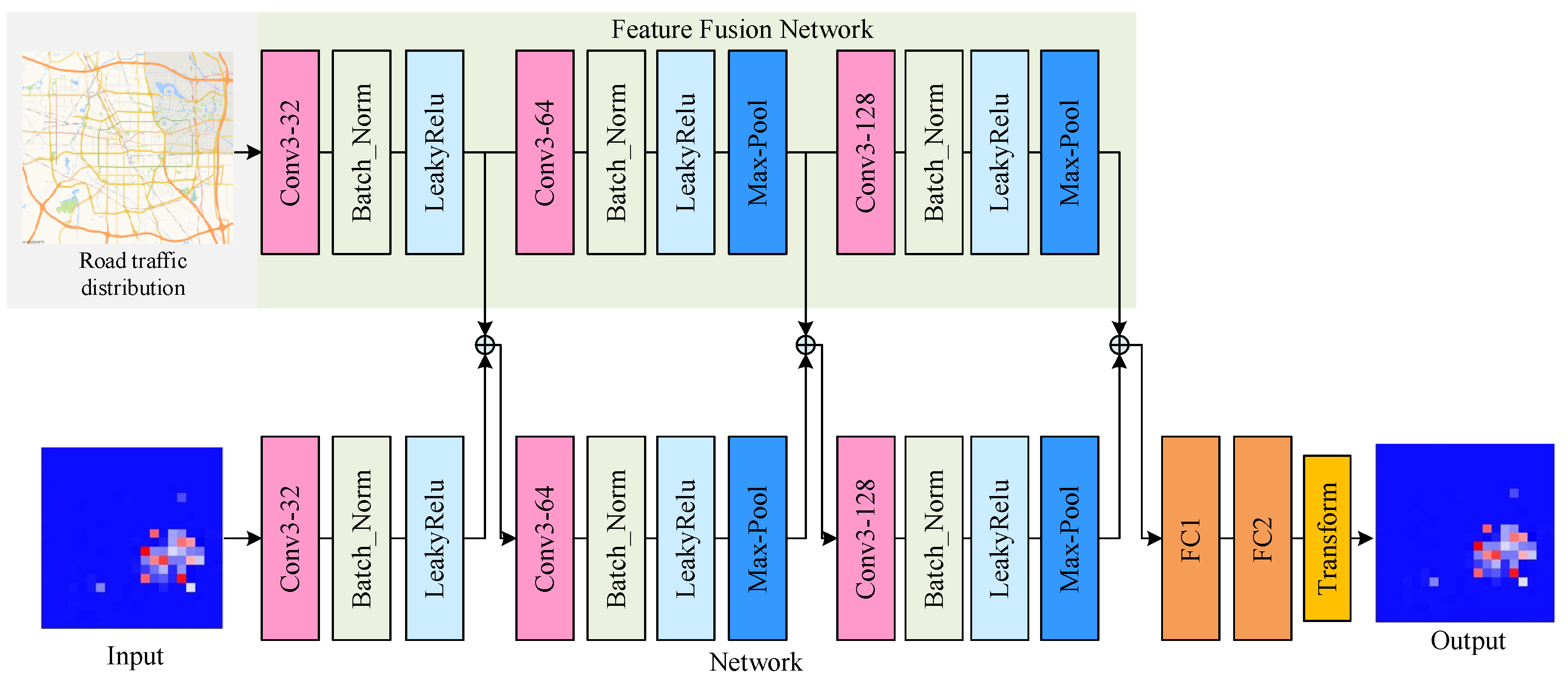
3.2. Architecture of the Neural Network
3.3. CNN
3.4. FFN
4. Case Study
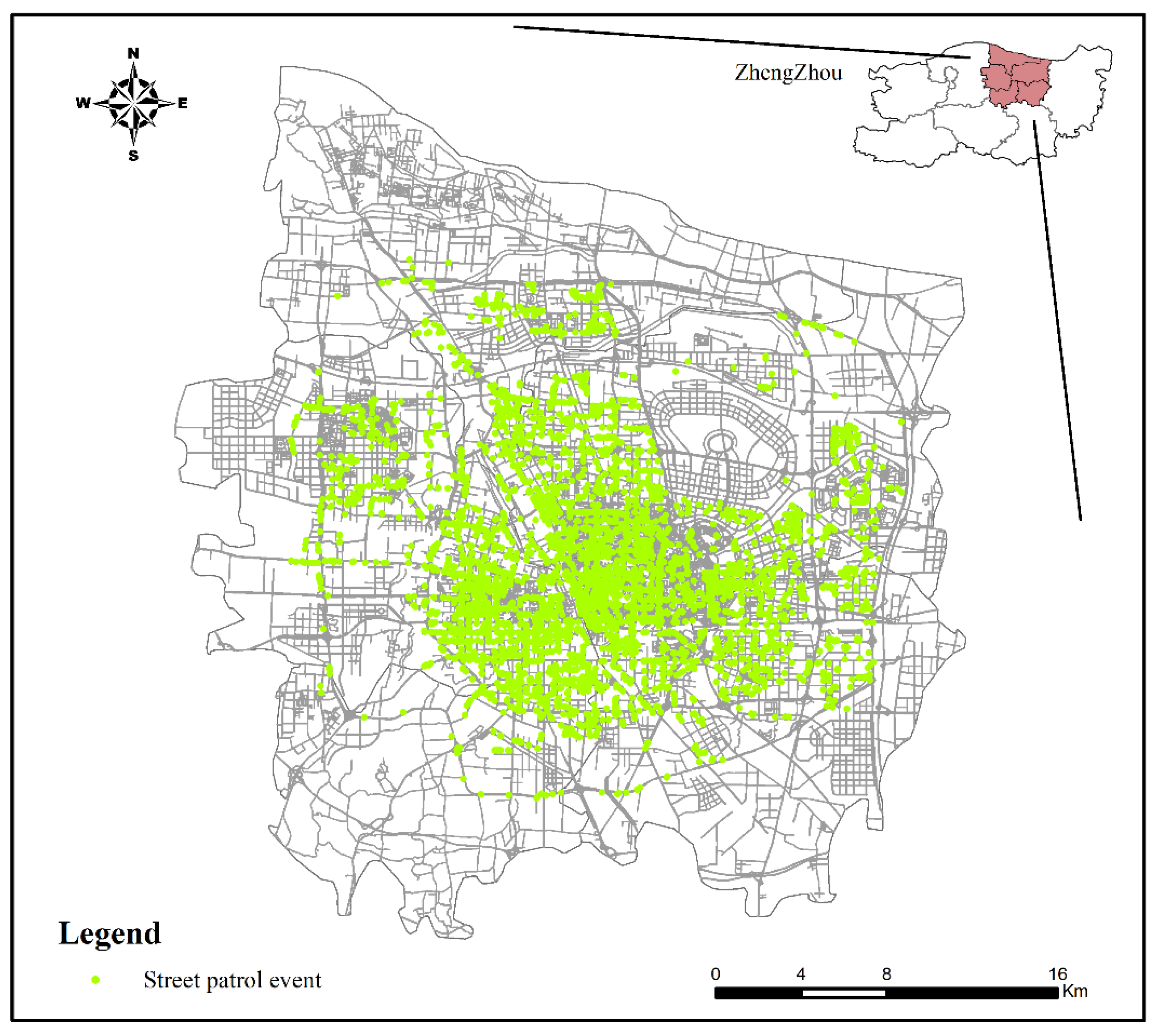
4.1. Source of the Experimental Data
4.2. Experimental Details
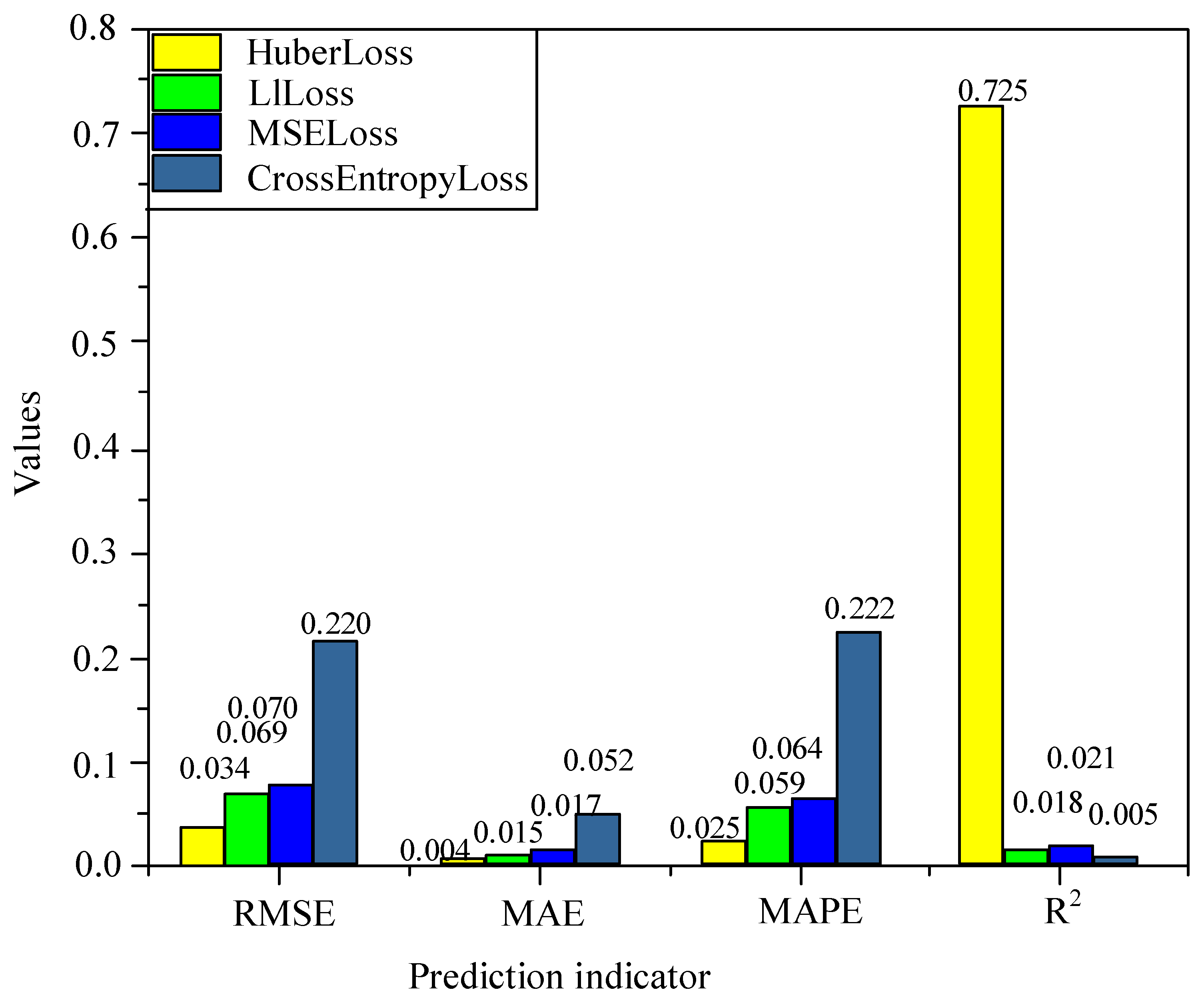
4.3. Result Analysis
4.4. Finding the Optimal Number of CNN Layers
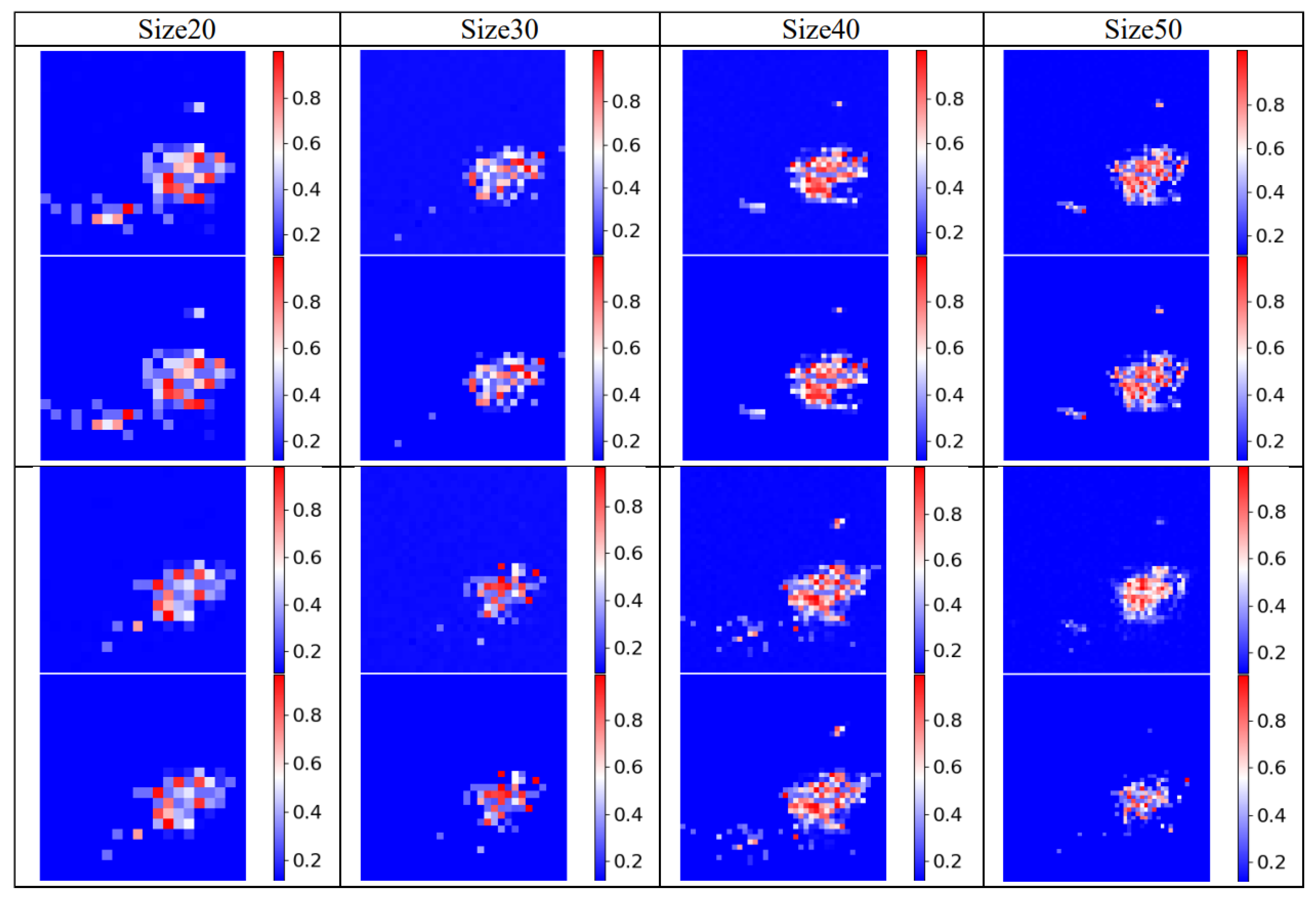
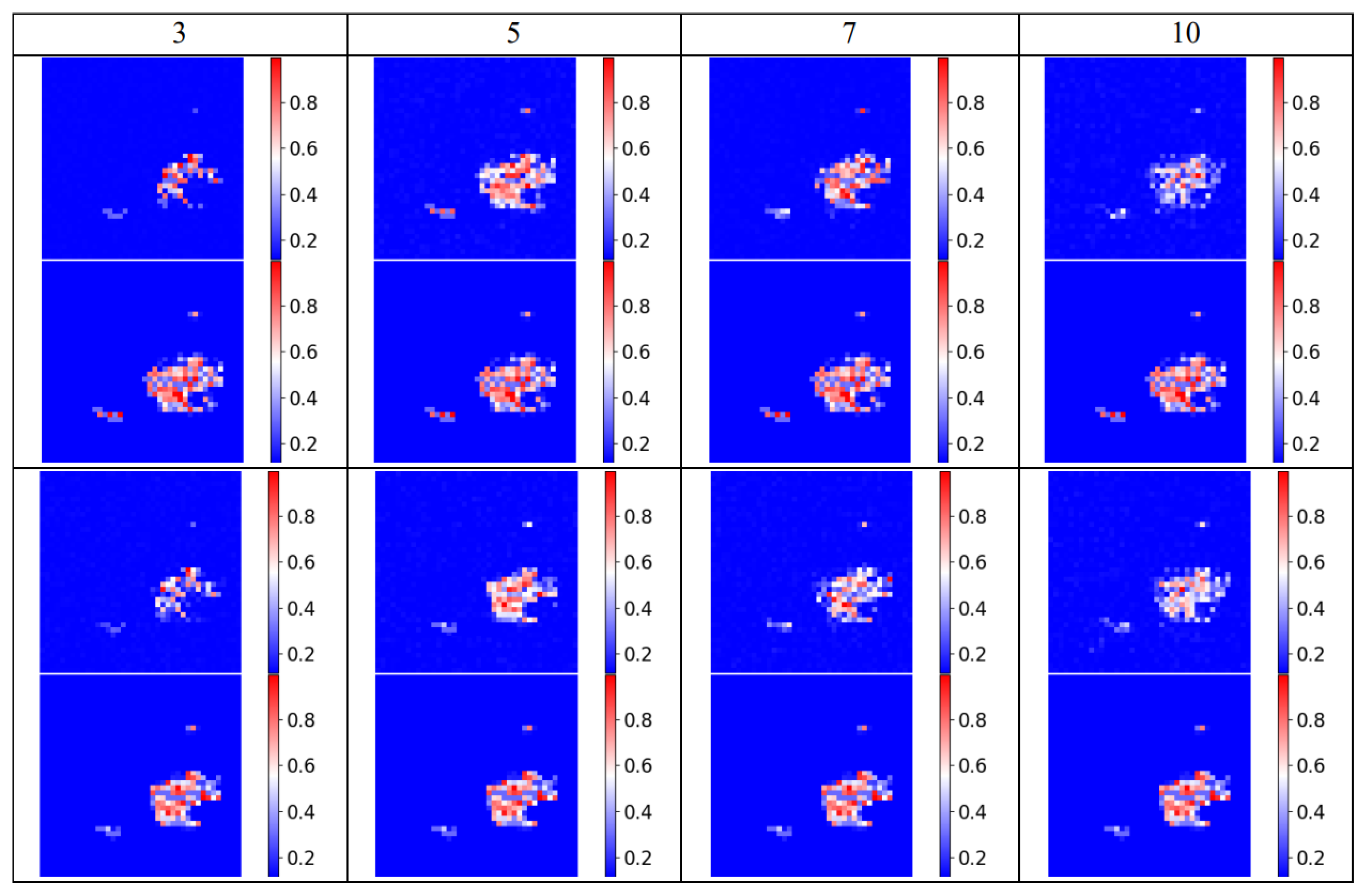
4.5. Finding the Optimal Number of Size of Feature Map
5. Discussions
5.1. Impact of the Time Factor
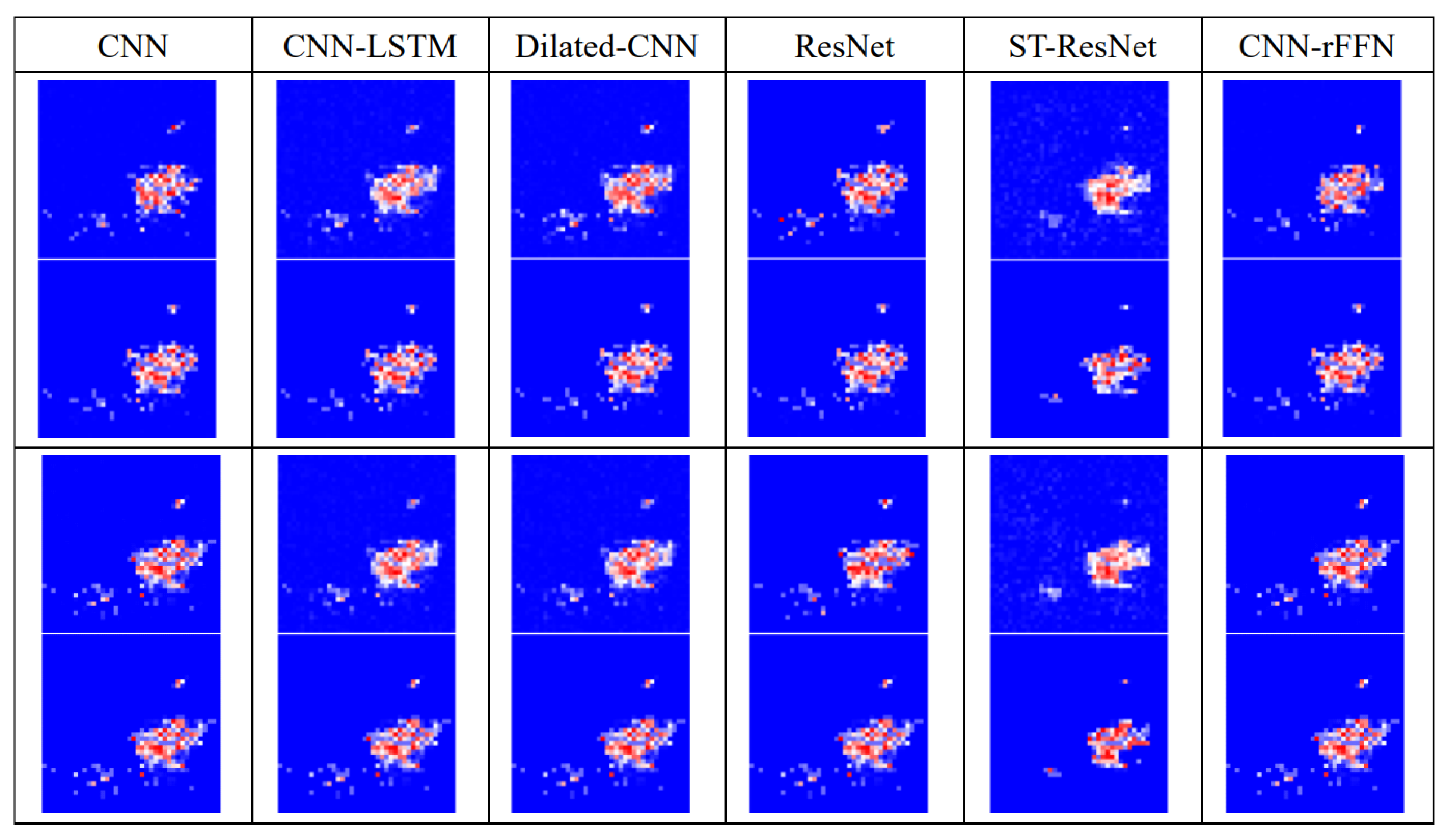
5.2. Comparison with Other Algorithms
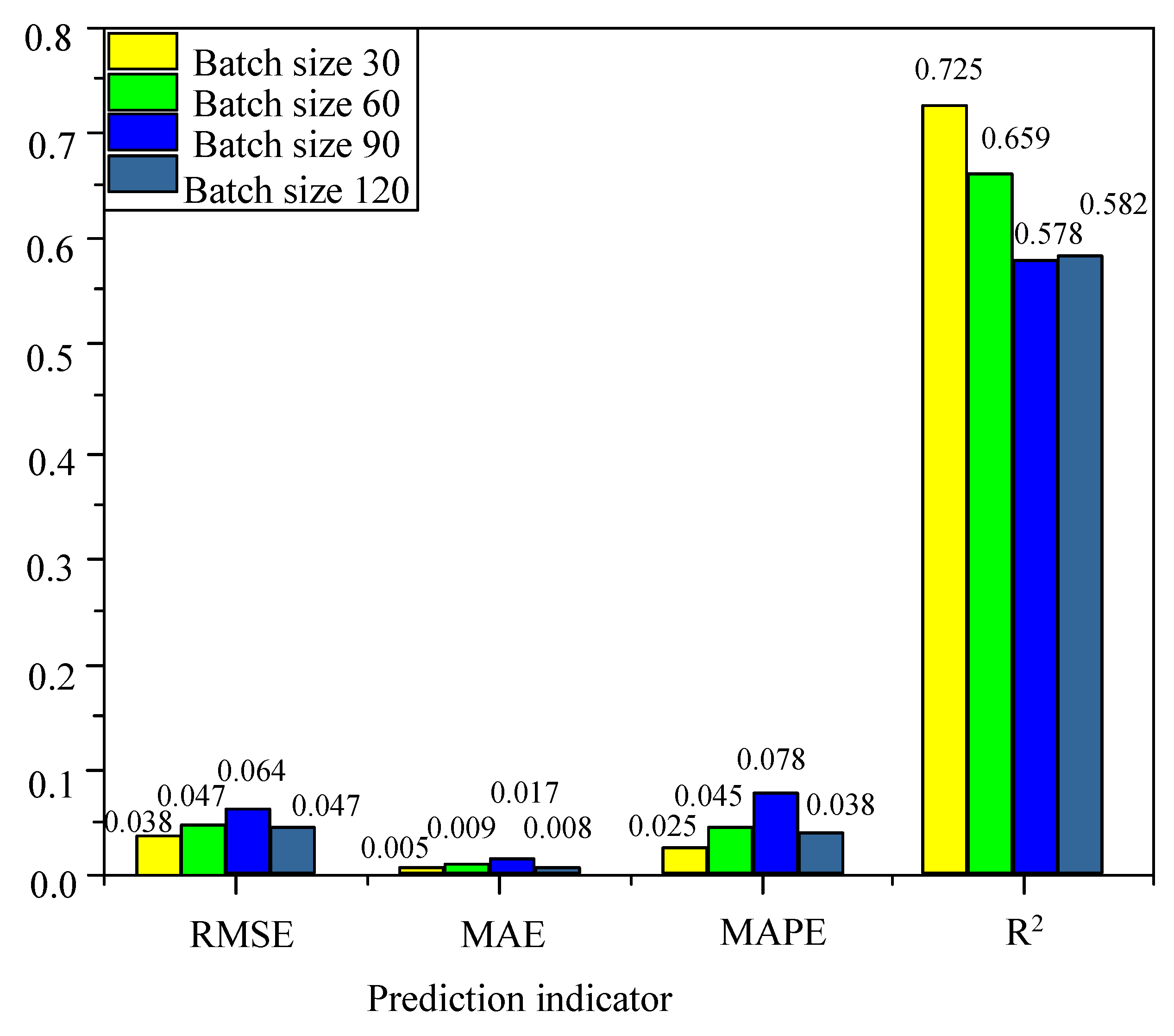
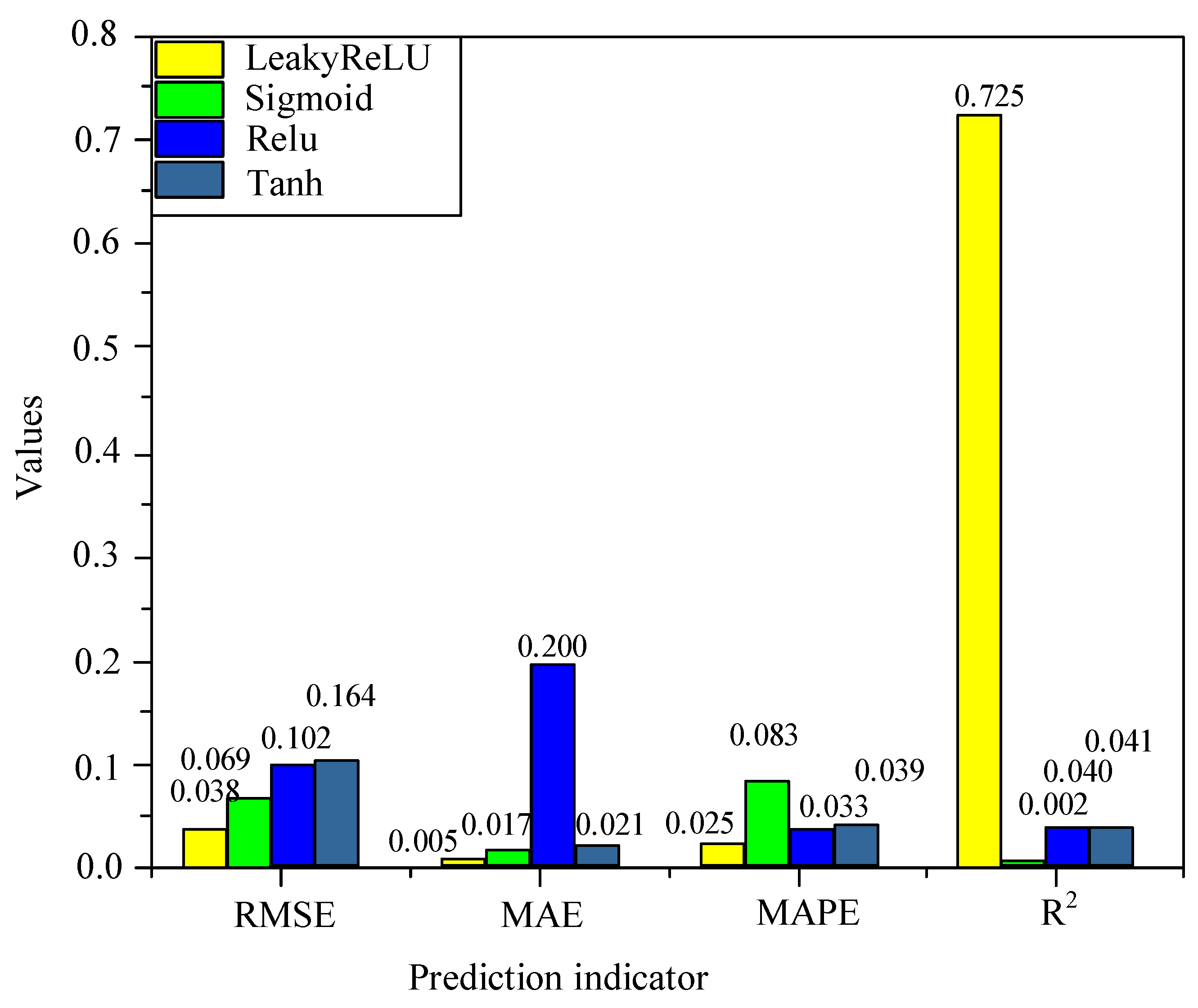
5.3. Parameter Sensitivity Analysis
5.4. Ablation Experiment
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zheng, Y.; Capra, L.; Wolfson, O.; Yang, H. Urban computing: Concepts, methodologies, and applications. ACM Trans. Intell. Syst. Technol. TIST 2014, 5, 1–55. [Google Scholar] [CrossRef]
- Kim, D.; Kim, S. Role and challenge of technology toward a smart sustainable city: Topic modeling, classification, and time series analysis using information and communication technology patent data. Sustain. Cities Soc. 2022, 82, 103888. [Google Scholar] [CrossRef]
- Catlett, C.; Cesario, E.; Talia, D.; Vinci, A. Spatiotemporal crime predictions in smart cities: A data-driven approach and experiments. Pervasive Mob. Comput. 2019, 53, 62–74. [Google Scholar] [CrossRef]
- Okawa, M.; Iwata, T.; Kurashima, T.; Tanaka, Y.; Toda, H.; Ueda, N. Deep mixture point processes: Spatiotemporal event prediction with rich contextual information. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Anchorage, AK, USA, 4–8 August 2019; pp. 373–383. [Google Scholar] [CrossRef]
- Butt, U.M.; Letchmunan, S.; Hassan, F.H.; Ali, M.; Baqir, A.; Sherazi, H.H.R. Spatiotemporal crime hotspot detection and prediction: A systematic literature review. IEEE Access 2020, 8, 166553–166574. [Google Scholar] [CrossRef]
- Jin, G.; Liu, C.; Xi, Z.; Sha, H.; Liu, Y.; Huang, J. Adaptive Dual-View WaveNet for urban spatio–temporal event prediction. Inf. Sci. 2022, 588, 315–330. [Google Scholar] [CrossRef]
- Zhang, Y.; Cheng, T. Graph deep learning model for network-based predictive hotspot mapping of sparse spatiotemporal events. Comput. Environ. Urban Syst. 2020, 79, 101403. [Google Scholar] [CrossRef]
- Shen, B.; Liang, X.; Ouyang, Y.; Liu, M.; Zheng, W.; Carley, K.M. Stepdeep: A novel spatiotemporal mobility event prediction framework based on deep neural network. In Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, London, UK, 19–23 August 2018; pp. 724–733. [Google Scholar] [CrossRef]
- Yu, M.; Bambacus, M.; Cervone, G.; Clarke, K.; Duffy, D.; Huang, Q.; Li, J.; Li, W.; Li, Z.; Liu, Q.; et al. Spatiotemporal event detection: A review. Int. J. Digit. Earth 2020, 13, 1339–1365. [Google Scholar] [CrossRef]
- Fox, J.; Brown, D.E. Using temporal indicator functions with generalized linear models for spatiotemporal event prediction. Procedia Comput. Sci. 2012, 8, 106–111. [Google Scholar] [CrossRef][Green Version]
- Chen, L.; Zhang, D.; Wang, L.; Yang, D.; Ma, X.; Li, S.; Wu, Z.; Pan, G.; Nguyen, T.M.T.; Jakubowicz, J. Dynamic cluster-based over-demand prediction in bike sharing systems. In Proceedings of the 18th Ubicomp, ACM, Singapore, 8–12 October 2016; pp. 841–852. [Google Scholar] [CrossRef]
- Hoang, M.X.; Zheng, Y.; Singh, A.K. FCCF: Forecasting citywide crowd flows based on big data. In Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Francisco, CA, USA, 31 October 2016. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Y.; Qi, D.; Li, R.; Yi, X.; Li, T. Predicting citywide crowd flows using deep spatiotemporal residual networks. Artif. Intell. 2018, 259, 147–166. [Google Scholar] [CrossRef]
- Wendland, H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995, 4, 389–396. [Google Scholar] [CrossRef]
- Tian, C.; Chan, W.K. Spatio-temporal attention wavenet: A deep learning framework for traffic prediction considering spatio-temporal dependencies. IET Intell. Transp. Syst. 2021, 15, 549–561. [Google Scholar] [CrossRef]
- Zhang, J.; Zheng, Y.; Sun, J.; Qi, D. Flow prediction in spatiotemporal networks based on multitask deep learning. IEEE Trans. Knowl. Data Eng. 2019, 32, 468–478. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, Y.; Qi, Y.; Shu, F.; Wang, Y. Short-term traffic flow prediction based on spatiotemporal analysis and CNN deep learning. Transp. A Transp. Sci. 2019, 15, 1688–1711. [Google Scholar] [CrossRef]
- Cao, P.; Dai, F.; Liu, G.; Yang, J.; Huang, B. A survey of traffic prediction based on deep neural network: Data, methods and challenges. In Proceedings of the Cloud Computing: 11th EAI International Conference, CloudComp 2021, Virtual Event, 9–10 December 2021; Springer International Publishing: Cham, Switzerland, 2022; pp. 17–29. [Google Scholar] [CrossRef]
- Yao, H.; Liu, Y.; Wei, Y.; Tang, X.; Li, Z. Learning from multiple cities: A meta-learning approach for spatiotemporal prediction. In Proceedings of the World Wide Web Conference, San Francisco, CA, USA, 13–17 May 2019; pp. 2181–2191. [Google Scholar] [CrossRef]
- Kumar, S.V. Traffic flow prediction using Kalman filtering technique. Procedia Eng. 2017, 187, 582–587. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Chen, Z.; Zhang, C.; Yu, H. Spatiotemporal forecasting in earth system science: Methods, uncertainties, predictability and future directions. Earth-Sci. Rev. 2021, 222, 103828. [Google Scholar] [CrossRef]
- Guo, J.; Huang, W.; Williams, B.M. Adaptive Kalman filter approach for stochastic short-term traffic flow rate prediction and uncertainty quantification. Transp. Res. Part C Emerg. Technol. 2014, 43, 50–64. [Google Scholar] [CrossRef]
- Kumar, S.V.; Vanajakshi, L. Short-term traffic flow prediction using seasonal ARIMA model with limited input data. Eur. Transp. Res. Rev. 2015, 7, 21. [Google Scholar] [CrossRef]
- Chen, P.; Yuan, H.; Shu, X. Forecasting crime using the arima model. In Proceedings of the 2008 Fifth International Conference on Fuzzy Systems and Knowledge Discovery, Jinen, China, 18–20 October 2008; Volume 5, pp. 627–630. [Google Scholar] [CrossRef]
- Chamlin, M.B. Crime and arrests: An autoregressive integrated moving average (ARIMA) approach. J. Quant. Criminol. 1988, 4, 247–258. [Google Scholar] [CrossRef]
- Alghamdi, T.; Elgazzar, K.; Bayoumi, M.; Sharaf, T.; Shah, S. Forecasting traffic congestion using ARIMA modeling. In Proceedings of the 15th International Wireless Communications & Mobile Computing Conference (IWCMC), Tangier, Morocco, 24–28 June 2019; pp. 1227–1232. [Google Scholar] [CrossRef]
- Okutani, I.; Stephanedes, Y.J. Dynamic prediction of traffic volume through Kalman filtering theory. Transp. Res. Part B Methodol. 1984, 18, 1–11. [Google Scholar] [CrossRef]
- Lu, B.; Martin, C.; Fotheringhama, A.S. Geographically weighted regression using a non-Euclidean distance metric with a study on London house price data. Procedia Environ. Sci. 2011, 7, 92–97. [Google Scholar] [CrossRef]
- Yao, S.; Wei, M.; Yan, L.; Wang, C.; Dong, X.; Liu, F.; Xiong, Y. Prediction of crime hotspots based on spatio factors of random forest. In Proceedings of the 15th International Conference on Computer Science & Education (ICCSE), Piscataway, NJ, USA, 18–22 August 2020; pp. 811–815. [Google Scholar] [CrossRef]
- Cheng, R.; Zhang, M.; Yu, X. Prediction model for road traffic accident based on random forest. In Proceedings of the Education Science and Development of the International Conference (ICESD), Jakarta, Indonesia, 19–20 January 2019; pp. 12–13. [Google Scholar]
- Nasridinov, A.; Ihm, S.Y.; Park, Y.H. A decision tree-based classification model for crime prediction. In Information Technology Convergence; Springer: Dordrecht, The Netherlands, 2013; pp. 531–538. [Google Scholar] [CrossRef]
- Hassani, H.; Huang, X.; Silva, E.S.; Ghodsi, M. A review of data mining applications in crime. Stat. Anal. Data Min. ASA Data Sci. J. 2016, 9, 139–154. [Google Scholar] [CrossRef]
- Kim, S.; Joshi, P.; Kalsi, P.S.; Taheri, P. Crime analysis through machine learning. In Proceedings of the 2 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON), Vancouver, BC, Canada, 1–3 November 2018; pp. 415–420. [Google Scholar] [CrossRef]
- Khan, M.; Ali, A.; Alharbi, Y. Predicting and Preventing Crime: A Crime Prediction Model Using San Francisco Crime Data by Classification Techniques. Complexity 2022, 2022, 4830411. [Google Scholar] [CrossRef]
- Jiang, W.; Luo, J.; He, M.; Gu, W. Graph neural network for traffic forecasting: The research progress. ISPRS Int. J. Geo-Inf. 2023, 12, 100. [Google Scholar] [CrossRef]
- Geng, Z.; Xu, J.; Wu, R.; Zhao, C.; Wang, J.; Li, Y.; Zhang, C. STGAFormer: Spatial–temporal Gated Attention Transformer based Graph Neural Network for traffic flow forecasting. Inf. Fusion 2024, 105, 102228. [Google Scholar] [CrossRef]
- Chen, J.; Zheng, L.; Hu, Y.; Wang, W.; Zhang, H.; Hu, X. Traffic flow matrix-based graph neural network with attention mechanism for traffic flow prediction. Inf. Fusion 2024, 104, 102146. [Google Scholar] [CrossRef]
- Ilhan, F.; Tekin, S.F.; Aksoy, B. Spatiotemporal Crime Prediction with Temporally Hierarchical Convolutional Neural Networks. In Proceedings of the 28th Signal Processing and Communications Applications Conference (SIU), Gaziantep, Turkey, 5–7 October 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Xiao, Y.; Wang, X.; Feng, W.; Tian, H.; Wu, S.; Li, L. Predicting crime locations based on long short term memory and convolutional neural networks. Data Anal. Knowl. Discov. 2018, 2, 15–20. [Google Scholar]
- Haque, M.R.; Hafiz, R.; Al Azad, A.; Adnan, Y.; Mishu, S.A.; Khatun, A.; Uddin, M.S. Crime detection and criminal recognition to intervene in interpersonal violence using deep convolutional neural network with transfer learning. Int. J. Ambient Comput. Intell. IJACI 2021, 12, 1–14. [Google Scholar] [CrossRef]
- Andersson, V.O.; Birck MA, F.; Araujo, R.M. Investigating crime rate prediction using street-level images and siamese convolutional neural networks. In Proceedings of the Latin American Workshop on Computational Neuroscience, Porto Alegre, Brazil, 22–24 November 2017; Springer: Cham, Switzerland, 2017; pp. 81–93. [Google Scholar] [CrossRef]
- Andersson, V.O.; Birck, M.A.; Araújo, R.M.; Cechinel, C. Towards crime rate prediction through street-level images and siamese convolutional neural networks. ENIAC-Encontro Nac. Inteligência Artif. E Comput. 2017, 14, 448–458. Available online: https://www.researchgate.net/publication/321779586_Towards_Crime_Rate_Prediction_through_Street-level_Images_and_Siamese_Convolutional_Neural_Networks (accessed on 19 September 2024).
- Miao, J.; Yang, T.; Sun, L.; Fei, X.; Niu, L.; Shi, Y. Graph regularized locally linear embedding for unsupervised feature selection. Pattern Recognit. 2022, 122, 108299. [Google Scholar] [CrossRef]
- Li, Y.; Hao, Z.; Lei, H. Survey of convolutional neural network. J. Comput. Appl. 2016, 36, 2508. [Google Scholar]
- Li, Z.; Liu, F.; Yang, W.; Peng, S.; Zhou, J. A survey of convolutional neural networks: Analysis, applications, and prospects. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 6999–7019. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Sohail, A.; Zahoora, U.; Qureshi, A.S. A survey of the recent architectures of deep convolutional neural networks. Artif. Intell. Rev. 2020, 53, 5455–5516. [Google Scholar] [CrossRef]
- Sakib, S.; Ahmed, N.; Kabir, A.J.; Ahmed, H. An overview of convolutional neural network: Its architecture and applications. Preprints 2019. [Google Scholar] [CrossRef]
- Ghosh, A.; Sufian, A.; Sultana, F.; Chakrabarti, A.; De, D. Fundamental concepts of convolutional neural network. In Recent Trends and Advances in Artificial Intelligence and Internet of Things; Springer: Cham, Switzerland, 2020; pp. 519–567. [Google Scholar] [CrossRef]
- Aloysius, N.; Geetha, M. A review on deep convolutional neural networks. In Proceedings of the International Conference on Communication and Signal Processing (ICCSP), Melmaruvathur, India, 6–8 April 2017; pp. 588–592. [Google Scholar] [CrossRef]
- Liu, M.; Shi, J.; Li, Z.; Li, C.; Zhu, J.; Liu, S. Towards better analysis of deep convolutional neural networks. IEEE Trans. Vis. Comput. Graph. 2016, 23, 91–100. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Zhang, M.; Chen, T.; Sun, Z.; Ma, Y.; Yu, B. Recent advances in convolutional neural network acceleration. Neurocomputing 2019, 323, 37–51. [Google Scholar] [CrossRef]
- Dhillon, A.; Verma, G.K. Convolutional neural network: A review of models, methodologies and applications to object detection. Prog. Artif. Intell. 2020, 9, 85–112. [Google Scholar] [CrossRef]
- Porzi, L.; Rota Bulò, S.; Lepri, B.; Ricci, E. Predicting and understanding urban perception with convolutional neural networks. In Proceedings of the 23rd ACM International Conference on Multimedia, Brisbane, Australia, 13 October 2015; pp. 139–148. [Google Scholar] [CrossRef]
- Bouvrie, J. Notes on Convolutional Neural Network. 2006. Available online: http://web.mit.edu/jvb/www/papers/cnn_tutorial.pdf (accessed on 19 September 2024).
- Zhang, Q. Convolutional neural networks. In Proceedings of the 3rd International Conference on Electromechanical Control Technology and Transportation, Chongqing, China, 19–21 January 2018; pp. 434–439. [Google Scholar]
- Varshini, A.G.P.; Kumari, K.A.; Janani, D.; Soundariya, S. Comparative analysis of Machine learning and Deep learning algorithms for Software Effort Estimation. J. Phys. Conf. Series 2021, 1767, 012019. [Google Scholar] [CrossRef]
- Aptula, A.O.; Jeliazkova, N.G.; Schultz, T.W.; Cronin, M.T.D. The better predictive model: High q2 for the training set or low root mean square error of prediction for the test set. QSAR Comb. Sci. 2005, 24, 385–396. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.J.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaria, J.; Fadhel, M.A.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, CNN architectures, challenges, applications, future directions. J. Big Data 2021, 8, 1–74. [Google Scholar] [CrossRef]
- Rostamian, A.; O’Hara, J.G. Event prediction within directional change framework using a CNN-LSTM model. Neural Comput. Appl. 2022, 34, 17193–17205. [Google Scholar] [CrossRef]
- Borovykh, A.; Bohte, S.; Oosterlee, C.W. Dilated convolutional neural networks for time series forecasting. J. Comput. Financ. Forthcom. 2018. [Google Scholar] [CrossRef]
- Wu, Z.; Shen, C.; Van Den Hengel, A. Wider or deeper: Revisiting the resnet model for visual recognition. Pattern Recognit. 2019, 90, 119–133. [Google Scholar] [CrossRef]
- Radiuk, P.M. Impact of training set batch size on the performance of convolutional neural networks for diverse datasets. Inf. Technol. Manag. Sci. 2017, 20, 20–24. Available online: https://itms-journals.rtu.lv/article/view/itms-2017-0003 (accessed on 19 September 2024). [CrossRef]
- Konar, J.; Khandelwal, P.; Tripathi, R. Comparison of various learning rate scheduling techniques on convolutional neural network. In Proceedings of the IEEE International Students’ Conference on Electrical, Electronics and Computer Science (SCEECS), Bhopal, India, 22–23 February 2020; pp. 1–5. [Google Scholar] [CrossRef]
- Menon, A.; Mehrotra, K.; Mohan, C.K.; Ranka, S. Characterization of a class of sigmoid functions with applications to neural networks. Neural Netw. 1996, 9, 819–835. [Google Scholar] [CrossRef]
- Li, H.; Xu, Z.; Taylor, G.; Studer, C.; Goldstein, T. Visualizing the loss landscape of neural nets. Adv. Neural Inf. Process. Syst. 2018, 31, 6391–6401. Available online: https://dl.acm.org/doi/abs/10.5555/3327345.3327535 (accessed on 19 September 2024).




| Study | Methodology | Pros | Cons |
|---|---|---|---|
| Alghamdi et al. [26] | ARIMA | Simple modelling | Many parameters |
| Okutani et al. [27] | Kalman filtering | Simple modelling | Computational complexity |
| Yao et al. [31] | Decision tree | Simple modelling | High stochasticity |
| Khan et al. [34] | Random forest | High accuracy and robustness | Observations not intuitive |
| Geng et al. [36] | Graph neural network | Long-term forecasting | Overfitting risk |
| Haque et al. [40] | Convolutional neural network | Multiscale feature extraction | Overfitting risk |
| Object-ID | Time | Coordinate_x | Coordinate_y |
|---|---|---|---|
| 1 | 17 December 2018 | 482,484.9 | 3,801,871 |
| 2 | 28 December 2018 | 482,564.4 | 3,803,236 |
| 3 | 17 November 2018 | 482,561.8 | 3,803,244 |
| 4 | 6 November 2018 | 482,562.4 | 3,803,248 |
| 5 | 6 December 2018 | 482,565.2 | 3,803,429 |
| 6 | 14 November 2018 | 482,562.6 | 3,803,430 |
| 7 | 12 November 2018 | 482,579.4 | 3,803,439 |
| 8 | 10 December 2018 | 482,575.2 | 3,803,517 |
| 9 | 1 November 2018 | 482,608.4 | 3,803,613 |
| 10 | 21 December 2018 | 482,613.3 | 3,803,657 |
| Name | Detail |
|---|---|
| CNN layer 1 | input_size = 3, hidden_size = 32, kernel_size = 3, stride = 1, padding = 1, dropout = 0.5. |
| CNN layer 2 | input_size = 32, hidden_size = 64, kernel_size = 3, stride = 1, padding = 1, dropout = 0.5, maxpool. |
| CNN layer 3 | input_size = 64, hidden_size = 128, kernel_size = 5, stride = 1, padding = 1, dropout = 0.5, maxpool. |
| Feature fusion CNN layer 1 | input_size = 3, hidden_size = 32, kernel_size = 3, stride = 1, padding = 1, dropout = 0.5. |
| Feature fusion CNN layer 2 | input_size = 32, hidden_size = 64, kernel_size = 3, stride = 1, padding = 1, dropout = 0.5, maxpool. |
| Feature fusion CNN layer 3 | input_size = 64, hidden_size = 128, kernel_size = 5, stride = 1, padding = 1, dropout = 0.5, maxpool. |
| Full connected layer (FC3) | in_features = 9 × 9 × 128, out_features = 64 × 64 |
| Full connected layer (FC3) | in_features = 64 × 64, out_features = 40 × 40 |
| Output layer(out) | out_features = 40 × 40 |
| Batch_size | 30 |
| Optimiser | AdamW |
| Loss function | Huberloss |
| Activation function | LeakyRelu |
| Epochs | 1000 |
| Learning rate | 0.001 |
| Layer | MAPE | MAE | RMSE | R2 |
|---|---|---|---|---|
| 1 | 0.0557 | 0.0099 | 0.0407 | 0.7910 |
| 2 | 0.0642 | 0.0111 | 0.0396 | 0.6610 |
| 3 | 0.0274 | 0.0061 | 0.0376 | 0.9131 |
| 4 | 0.0320 | 0.0068 | 0.0380 | 0.8437 |
| Size | MAPE | MAE | RMSE | R2 |
|---|---|---|---|---|
| 20 | 0.0303 | 0.0069 | 0.0385 | 0.8848 |
| 30 | 0.0436 | 0.0092 | 0.0388 | 0.7772 |
| 40 | 0.0379 | 0.0072 | 0.0348 | 0.9036 |
| 50 | 0.0434 | 0.0079 | 0.0374 | 0.8279 |
| Size | MAPE | MAE | RMSE | R2 |
|---|---|---|---|---|
| 3 | 0.0679 | 0.0231 | 0.0582 | 0.000237 |
| 5 | 0.0557 | 0.0181 | 0.0348 | 0.000319 |
| 7 | 0.0780 | 0.0276 | 0.1145 | 0.000276 |
| 10 | 0.0912 | 0.0219 | 0.0799 | 0.000102 |
| Model | MAPE | MAE | RMSE | R2 |
|---|---|---|---|---|
| CNN | 0.0440 | 0.0083 | 0.0383 | 0.9105 |
| CNN-LSTM | 0.0672 | 0.0159 | 0.0598 | 0.8689 |
| Dilated-CNN | 0.0291 | 0.0059 | 0.0376 | 0.9174 |
| ResNet | 0.0273 | 00061 | 0.0375 | 0.9120 |
| ST-ResNet | 0.0270 | 0.0237 | 0.0380 | 0.7710 |
| CNN-rFFN | 0.0265 | 0.0058 | 0.0375 | 0.9430 |
| Model | MAPE | MAE | RMSE |
|---|---|---|---|
| Fusion 1 | 0.0732 | 0.0192 | 0.0939 |
| Fusion 2 | 0.0680 | 0.0185 | 0.0592 |
| Fusion 3 | 0.0807 | 0.0187 | 0.0739 |
| Fusion 4 | 0.0500 | 0.0107 | 0.0528 |
| CNN-rFFN | 0.0416 | 0.0091 | 0.0447 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Published by MDPI on behalf of the International Society for Photogrammetry and Remote Sensing. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Zhao, S.; Li, H.; Wu, H.; Zhu, W. Urban Spatiotemporal Event Prediction Using Convolutional Neural Network and Road Feature Fusion Network. ISPRS Int. J. Geo-Inf. 2024, 13, 341. https://doi.org/10.3390/ijgi13100341
Jiang Y, Zhao S, Li H, Wu H, Zhu W. Urban Spatiotemporal Event Prediction Using Convolutional Neural Network and Road Feature Fusion Network. ISPRS International Journal of Geo-Information. 2024; 13(10):341. https://doi.org/10.3390/ijgi13100341
Chicago/Turabian StyleJiang, Yirui, Shan Zhao, Hongwei Li, Huijing Wu, and Wenjie Zhu. 2024. "Urban Spatiotemporal Event Prediction Using Convolutional Neural Network and Road Feature Fusion Network" ISPRS International Journal of Geo-Information 13, no. 10: 341. https://doi.org/10.3390/ijgi13100341
APA StyleJiang, Y., Zhao, S., Li, H., Wu, H., & Zhu, W. (2024). Urban Spatiotemporal Event Prediction Using Convolutional Neural Network and Road Feature Fusion Network. ISPRS International Journal of Geo-Information, 13(10), 341. https://doi.org/10.3390/ijgi13100341






