Modelling Global Deforestation Using Spherical Geographic Automata Approach
Abstract
1. Introduction
2. Materials and Methods
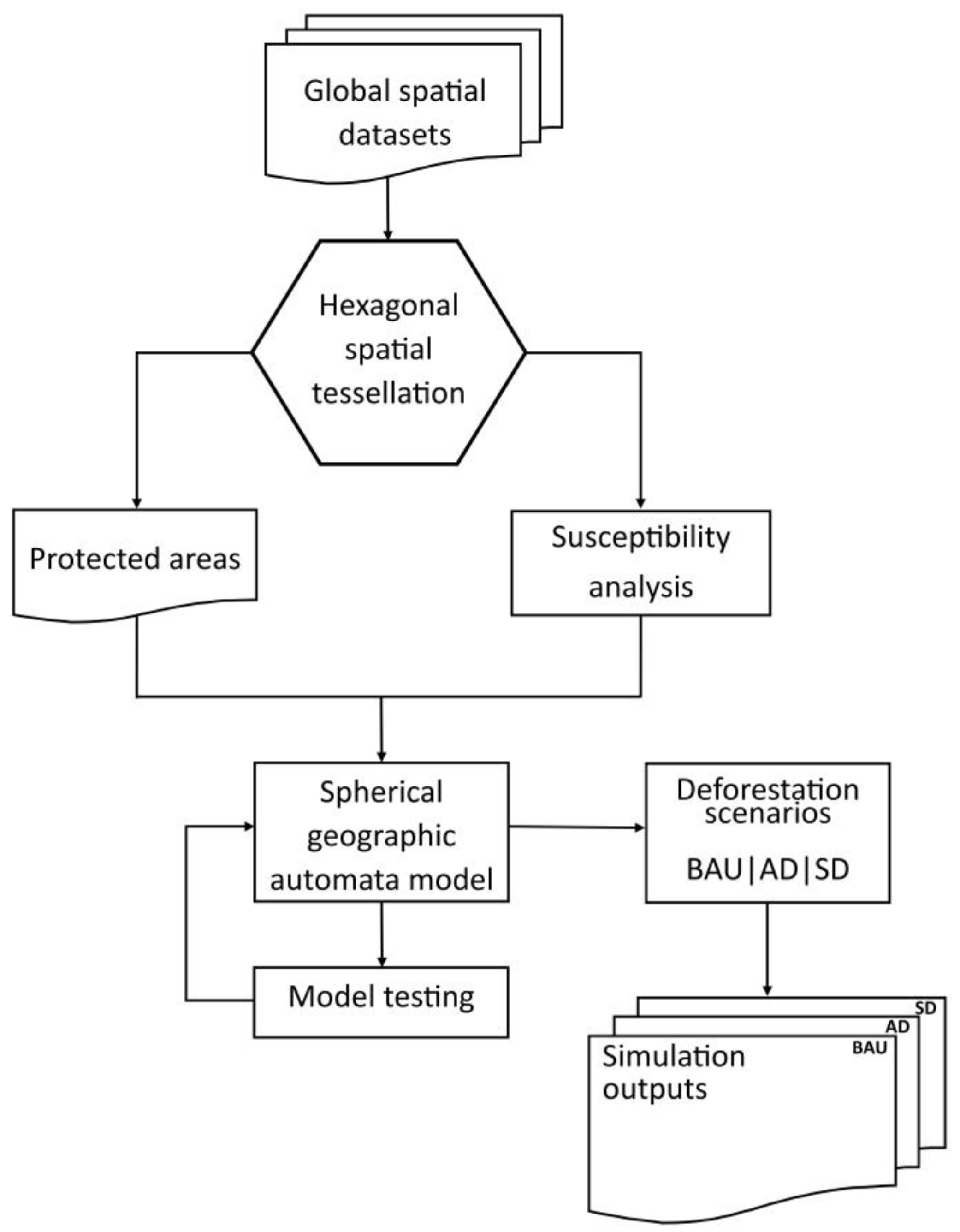
2.1. Spherical Deforestation Model Overview
2.2. Global Deforestation Spherical Geographic Automata
2.3. Datasets
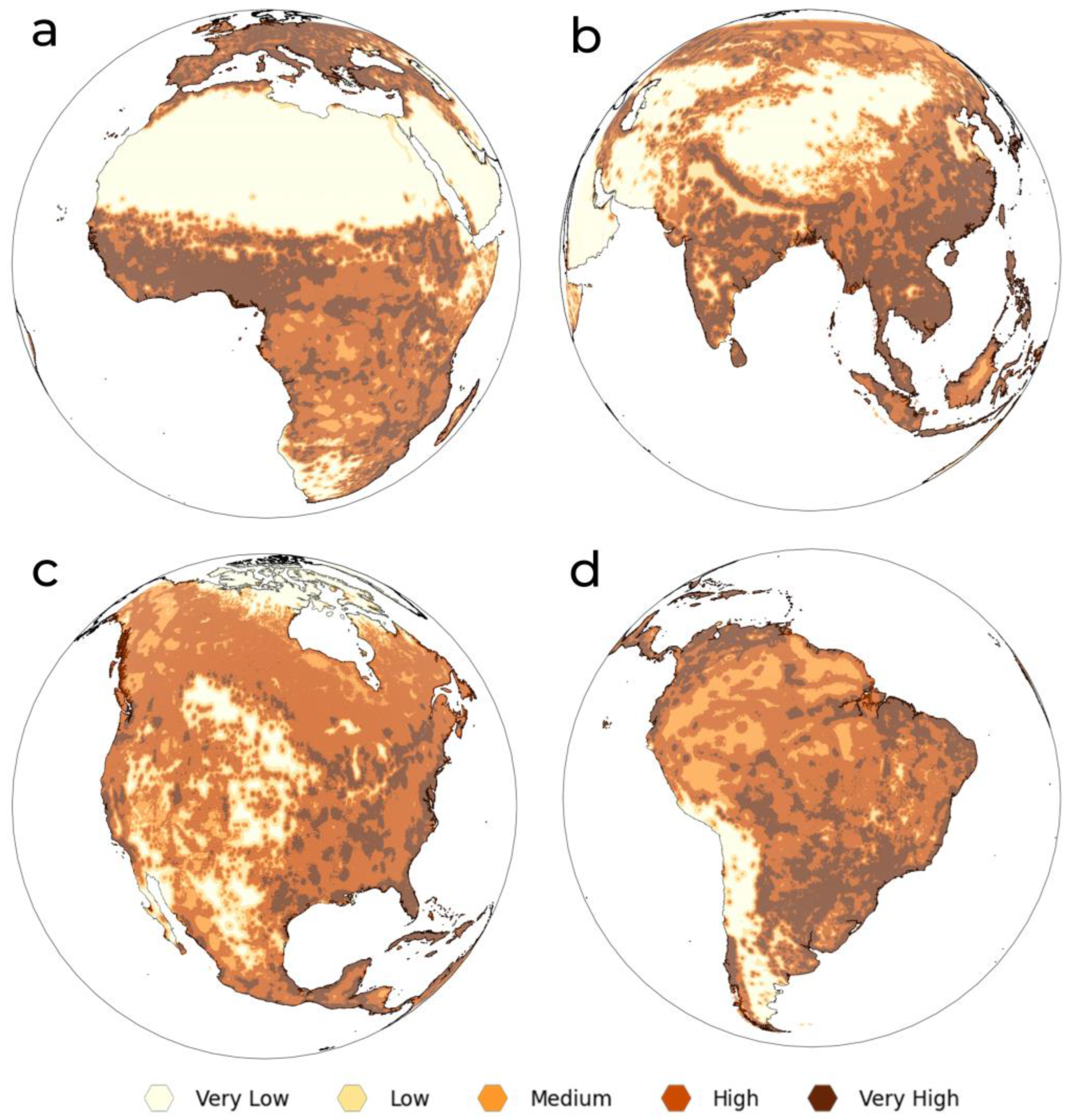
2.4. Susceptibility Analysis
2.5. Criterion Weight Generation and Global Susceptibility Maps
2.6. Deforestation Scenarios
2.7. Model Implementation and Evaluation
3. Results
3.1. Global and Regional Variations in Forest-Cover Change
3.2. Forest Change in Protected Areas
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Van Asselen, S.; Verburg, P.H. Land cover change or land-use intensification: Simulating land system change with a global-scale land change model. Glob. Chang. Biol. 2013, 19, 3648–3667. [Google Scholar] [CrossRef] [PubMed]
- Foley, J.A.; DeFries, R.; Asner, G.P.; Barford, C.; Bonan, G.; Carpenter, S.R.; Chapin, F.S.; Coe, M.T.; Daily, G.C.; Gibbs, H.K.; et al. Global consequences of land use. Science 2005, 309, 570–574. [Google Scholar] [CrossRef] [PubMed]
- Lambin, E.F.; Geist, H.J. Regional differences in tropical deforestation. Environ. Sci. Policy Sustain. Dev. 2003, 45, 22–36. [Google Scholar] [CrossRef]
- Hoang, N.T.; Kanemoto, K. Mapping the deforestation footprint of nations reveals growing threat to tropical forests. Nat. Ecol. Evol. 2021, 5, 845–853. [Google Scholar] [CrossRef]
- Curtis, P.G.; Slay, C.M.; Harris, N.L.; Tyukavina, A.; Hansen, M.C. Classifying drivers of global forest loss. Science 2018, 361, 1108–1111. [Google Scholar] [CrossRef]
- Brockerhoff, E.G.; Barbaro, L.; Castagneyrol, B.; Forrester, D.I.; Gardiner, B.; González-Olabarria, J.R.; Lyver, P.O.B.; Meurisse, N.; Oxbrough, A.; Taki, H.; et al. Forest biodiversity, ecosystem functioning and the provision of ecosystem services. Biodivers. Conserv. 2017, 26, 3005–3035. [Google Scholar] [CrossRef]
- Felipe-Lucia, M.R.; Soliveres, S.; Penone, C.; Manning, P.; van der Plas, F.; Boch, S.; Prati, D.; Ammer, C.; Schall, P.; Gossner, M.M.; et al. Multiple forest attributes underpin the supply of multiple ecosystem services. Nat. Commun. 2018, 9, 4839. [Google Scholar] [CrossRef] [PubMed]
- Food and Agriculture Organization of the United Nations. Global Gorest Resources Assessment 2020: Main Report; FAO: Rome, Iatly, 2020. [Google Scholar]
- Keenan, T.F.; Williams, C.A. The terrestrial carbon sink. Annu. Rev. Environ. Resour. 2018, 43, 219–243. [Google Scholar] [CrossRef]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef]
- Ren, Y.; Lü, Y.; Comber, A.; Fu, B.; Harris, P.; Wu, L. Spatially explicit simulation of land use/land cover changes: Current coverage and future prospects. Earth-Sci. Rev. 2019, 190, 398–415. [Google Scholar]
- Vannier, C.; Cochrane, T.A.; Zawar Reza, P.; Bellamy, L. An analysis of agricultural systems modelling approaches and examples to support future policy development under disruptive changes in New Zealand. Appl. Sci. 2022, 12, 2746. [Google Scholar]
- Sun, J.; Zhang, Y.; Qin, W.; Chai, G. Estimation and simulation of forest carbon stock in Northeast China forestry based on future climate change and LUCC. Remote Sens. 2022, 14, 3653. [Google Scholar] [CrossRef]
- Yu, Z.; Ciais, P.; Piao, S.; Houghton, R.A.; Lu, C.; Tian, H.; Agathokleous, E.; Kattel, G.R.; Sitch, S.; Goll, D.; et al. Forest expansion dominates China’s land carbon sink since 1980. Nat. Commun. 2022, 13, 5374. [Google Scholar] [CrossRef] [PubMed]
- Bos, A.B.; De Sy, V.; Duchelle, A.E.; Herold, M.; Martius, C.; Tsendbazar, N.-E. Global data and tools for local forest cover loss and REDD+ performance assessment: Accuracy, uncertainty, complementarity and impact. Int. J. Appl. Earth Obs. Geoinf. 2019, 80, 295–311. [Google Scholar]
- Messier, C.; Puettmann, K.; Filotas, E.; Coates, D. Dealing with non-linearity and uncertainty in forest management. Curr. For. Rep. 2016, 2, 150–161. [Google Scholar] [CrossRef]
- Kura, A.L.; Beyene, D.L. Cellular automata Markov chain model based deforestation modelling in the pastoral and agro-pastoral areas of southern Ethiopia. Remote Sens. Appl. Soc. Environ. 2020, 18, 100321. [Google Scholar] [CrossRef]
- Moreno, N.; Quintero, R.; Ablan, M.; Barros, R.; Dávila, J.; Ramírez, H.; Tonella, G.; Acevedo, M.F. Biocomplexity of deforestation in the Caparo tropical forest reserve in Venezuela: An integrated multi-agent and cellular automata model. Environ. Model. Softw. 2007, 22, 664–673. [Google Scholar] [CrossRef]
- Vázquez-Quintero, G.; Solís-Moreno, R.; Pompa-García, M.; Villarreal-Guerrero, F.; Pinedo-Alvarez, C.; Pinedo-Alvarez, A. Detection and projection of forest changes by using the Markov chain model and cellular automata. Sustainability 2016, 8, 236. [Google Scholar] [CrossRef]
- Adhikari, S.; Southworth, J. Simulating forest cover changes of Bannerghatta National Park based on a CA-Markov model: A remote sensing approach. Remote Sens. 2012, 4, 3215–3243. [Google Scholar]
- Kucsicsa, G.; Dumitrică, C. Spatial modelling of deforestation in Romanian Carpathian Mountains using GIS and Logistic Regression. J. Mt. Sci. 2019, 16, 1005–1022. [Google Scholar] [CrossRef]
- Miranda-Aragón, L.; Treviño-Garza, E.J.; Jiménez-Pérez, J.; Aguirre-Calderón, O.A.; González-Tagle, M.A.; Pompa-García, M.; Aguirre-Salado, C.A. Modeling susceptibility to deforestation of remaining ecosystems in North Central Mexico with logistic regression. J. For. Res. 2012, 23, 345–354. [Google Scholar] [CrossRef]
- Monjardin-Armenta, S.A.; Plata-Rocha, W.; Pacheco-Angulo, C.E.; Franco-Ochoa, C.; Rangel-Peraza, J.G. Geospatial simulation model of deforestation and reforestation using multicriteria evaluation. Sustainability 2020, 12, 10387. [Google Scholar] [CrossRef]
- Takam Tiamgne, X.; Kanungwe Kalaba, F.; Raphael Nyirenda, V.; Phiri, D. Modelling areas for sustainable forest management in a mining and human dominated landscape: A geographical information system (GIS)-multi-criteria decision analysis (MCDA) approach. Ann. GIS 2022, 28, 343–357. [Google Scholar] [CrossRef]
- Mas, J.F.; Puig, H.; Palacio, J.L.; Sosa-López, A. Modelling deforestation using GIS and artificial neural networks. Environ. Model. Softw. 2004, 19, 461–471. [Google Scholar] [CrossRef]
- Ball, J.G.C.; Petrova, K.; Coomes, D.A.; Flaxman, S. Using deep convolutional neural networks to forecast spatial patterns of Amazonian deforestation. Methods Ecol. Evol. 2022, 13, 2622–2634. [Google Scholar] [CrossRef]
- Deadman, P.; Robinson, D.; Moran, E.; Brondizio, E. Colonist household decisionmaking and land-use change in the Amazon Rainforest: An agent-based simulation. Environ. Plan. B: Plan. Des. 2004, 31, 693–709. [Google Scholar]
- Manson, S.M.; Evans, T. Agent-based modeling of deforestation in southern Yucatán, Mexico, and reforestation in the Midwest United States. Proc. Natl. Acad. Sci. USA 2007, 104, 20678–20683. [Google Scholar] [CrossRef]
- Ellis, E.C.; Gauthier, N.; Klein Goldewijk, K.; Bliege Bird, R.; Boivin, N.; Díaz, S.; Fuller, D.Q.; Gill, J.L.; Kaplan, J.O.; Kingston, N.; et al. People have shaped most of terrestrial nature for at least 12,000 years. Proc. Natl. Acad. Sci. USA 2021, 118, e2023483118. [Google Scholar] [CrossRef]
- Cao, M.; Zhu, Y.; Quan, J.; Zhou, S.; Lü, G.; Chen, M.; Huang, M. Spatial sequential modeling and predication of global land use and land cover changes by integrating a global change assessment model and cellular automata. Earth’s Future 2019, 7, 1102–1116. [Google Scholar] [CrossRef]
- Li, X.; Chen, G.; Liu, X.; Liang, X.; Wang, S.; Chen, Y.; Pei, F.; Xu, X. A new global Land-use and land-cover change product at a 1-km resolution for 2010 to 2100 based on human–environment interactions. Ann. Am. Assoc. Geogr. 2017, 107, 1040–1059. [Google Scholar]
- Hu, X.; Næss, J.S.; Iordan, C.M.; Huang, B.; Zhao, W.; Cherubini, F. Recent global land cover dynamics and implications for soil erosion and carbon losses from deforestation. Anthropocene 2021, 34, 100291. [Google Scholar] [CrossRef]
- Chen, G.; Li, X.; Liu, X.; Chen, Y.; Liang, X.; Leng, J.; Xu, X.; Liao, W.; Qiu, Y.A.; Wu, Q.; et al. Global projections of future urban land expansion under shared socioeconomic pathways. Nat. Commun. 2020, 11, 537. [Google Scholar] [CrossRef] [PubMed]
- Gao, J.; O’Neill, B.C. Mapping global urban land for the 21st century with data-driven simulations and Shared Socioeconomic Pathways. Nat. Commun. 2020, 11, 2302. [Google Scholar] [CrossRef] [PubMed]
- Meiyappan, P.; Dalton, M.; O’Neill, B.C.; Jain, A.K. Spatial modeling of agricultural land use change at global scale. Ecol. Model. 2014, 291, 152–174. [Google Scholar] [CrossRef]
- Malczewski, J. A GIS-based approach to multiple criteria group decision-making. Int. J. Geogr. Inf. Syst. 1996, 10, 955–971. [Google Scholar] [CrossRef]
- Feng, H.; Lim, C.W.; Chen, L.; Zhou, X.; Zhou, C.; Lin, Y. Sustainable deforestation evaluation model and system dynamics analysis. Sci. World J. 2014, 2014, 106209. [Google Scholar] [CrossRef]
- Deribew, K.T.; Dalacho, D.W. Land use and forest cover dynamics in the North-eastern Addis Ababa, central highlands of Ethiopia. Environ. Syst. Res. 2019, 8, 8. [Google Scholar] [CrossRef]
- Gharaibeh, A.A.; Shaamala, A.H.; Ali, M.H. Multi-criteria evaluation for sustainable urban growth in An-Nuayyimah, Jordan; post war study. Procedia Manuf. 2020, 44, 156–163. [Google Scholar] [CrossRef]
- Addae, B.; Dragićević, S. Enabling geosimulations for global scale: Spherical geographic automata. Trans. GIS 2023, 27, 821–840. [Google Scholar] [CrossRef]
- Sahr, K.; White, D.; Kimerling, A.J. Geodesic discrete global grid systems. Cartogr. Geogr. Inf. Sci. 2003, 30, 121–134. [Google Scholar] [CrossRef]
- Addae, B.; Dragićević, S. Integrating multi-criteria analysis and spherical cellular automata approach for modelling global urban land-use change. Geocarto Int. 2022, 2152498. [Google Scholar] [CrossRef]
- European Space Agency. ESA CCI Land Cover Map Series 1992–2020; European Space Agency: Paris, France, 2022. [Google Scholar]
- Meijer, J.R.; Huijbegts, M.A.J.; Schotten, C.G.J.; Schipper, A.M. Global patterns of current and future road infrastructure. Environ. Res. Lett. 2018, 15, 064006. [Google Scholar] [CrossRef]
- United Nations Environment Programme World Conservation Monitoring Centre (UNEP-WCMC) and the International Union for Conservation of Nature (IUCN). The World Databse on Protected Areas (WDPA); UNEP-WCMC and IUCN: Cambridge, UK, 2023. [Google Scholar]
- Artés, T.; Oom, D.; de Rigo, D.; Durrant, T.H.; Maianti, P.; Libertà, G.; San-Miguel-Ayanz, J. A global wildfire dataset for the analysis of fire regimes and fire behaviour. Sci. Data 2019, 6, 296. [Google Scholar] [CrossRef] [PubMed]
- Rose, A.N.; McKee, J.J.; Sims, K.M.; Bright, E.A.; Reith, A.E.; Urban, M.L. LandScan 2019, 2019 ed.; Oak Ridge National Laboratory: Oak Ridge, TN, USA, 2020. [Google Scholar]
- United State Geological Survey. Digital Elevation—Shuttle Radar Topography Mission (SRTM) 1 Arc-Second Global; Earth Resources Observation and Science (EROS) Center: Sioux Falls, SD, USA, 2022. [Google Scholar]
- Sahr, K. Hexagonal discrete global GRID systems for geospatial computing. Arch. Photogramm. Cartogr. Remote Sens. 2011, 22, 363–376. [Google Scholar]
- Williams, B.A.; Venter, O.; Allan, J.R.; Atkinson, S.C.; Rehbein, J.A.; Ward, M.; Di Marco, M.; Grantham, H.S.; Ervin, J.; Goetz, S.J.; et al. Change in terrestrial human footprint drives continued loss of intact ecosystems. One Earth 2020, 3, 371–382. [Google Scholar] [CrossRef]
- Dinerstein, E.; Joshi, A.R.; Vynne, C.; Lee, A.T.L.; Pharand-Deschênes, F.; França, M.; Fernando, S.; Birch, T.; Burkart, K.; Asner, G.P.; et al. A “Global Safety Net” to reverse biodiversity loss and stabilize Earth’s climate. Sci. Adv. 2020, 6, eabb2824. [Google Scholar] [CrossRef]
- Gleeson, T.; Befus, K.M.; Jasechko, S.; Luijendijk, E.; Cardenas, M.B. The global volume and distribution of modern groundwater. Nat. Geosci. 2016, 9, 161–167. [Google Scholar] [CrossRef]
- Robertson, C.; Chaudhuri, C.; Hojati, M.; Roberts, S.A. An integrated environmental analytics system (IDEAS) based on a DGGS. ISPRS J. Photogramm. Remote Sens. 2020, 162, 214–228. [Google Scholar] [CrossRef]
- Sharma, P.; Thapa, R.B.; Matin, M.A. Examining forest cover change and deforestation drivers in Taunggyi District, Shan State, Myanmar. Environ. Dev. Sustain. 2020, 22, 5521–5538. [Google Scholar] [CrossRef]
- Hyandye, C.; Martz, L.W. A Markovian and cellular automata land-use change predictive model of the Usangu Catchment. Int. J. Remote Sens. 2017, 38, 64–81. [Google Scholar] [CrossRef]
- Jana, A.; Jat, M.K.; Saxena, A.; Choudhary, M. Prediction of land use land cover changes of a river basin using the CA-Markov model. Geocarto Int. 2022, 37, 14127–14147. [Google Scholar] [CrossRef]
- Grinand, C.; Vieilledent, G.; Razafimbelo, T.; Rakotoarijaona, J.-R.; Nourtier, M.; Bernoux, M. Landscape-scale spatial modelling of deforestation, land degradation, and regeneration using machine learning tools. Land Degrad. Dev. 2020, 31, 1699–1712. [Google Scholar] [CrossRef]
- Uusivuori, J.; Lehto, E.; Palo, M. Population, income and ecological conditions as determinants of forest area variation in the tropics. Glob. Environ. Chang. 2002, 12, 313–323. [Google Scholar] [CrossRef]
- Vieilledent, G.; Grinand, C.; Vaudry, R. Forecasting deforestation and carbon emissions in tropical developing countries facing demographic expansion: A case study in Madagascar. Ecol. Evol. 2013, 3, 1702–1716. [Google Scholar] [CrossRef] [PubMed]
- Adhikari, S.; Fik, T.; Dwivedi, P. Proximate causes of land-use and land-cover change in Bannerghatta National Park: A spatial statistical model. Forests 2017, 8, 342. [Google Scholar]
- Liang, E.; Wang, Y.; Piao, S.; Lu, X.; Camarero, J.J.; Zhu, H.; Zhu, L.; Ellison, A.M.; Ciais, P.; Peñuelas, J. Species interactions slow warming-induced upward shifts of treelines on the Tibetan Plateau. Proc. Natl. Acad. Sci. USA 2016, 113, 4380–4385. [Google Scholar] [CrossRef] [PubMed]
- Georg, M.; Sabine, M.; Jonas, V.; Sonam, C.; Duo, L. Highest treeline in the northern hemisphere found in Southern Tibet. Mt. Res. Dev. 2007, 27, 169–173. [Google Scholar]
- Barber, C.P.; Cochrane, M.A.; Souza, C.M.; Laurance, W.F. Roads, deforestation, and the mitigating effect of protected areas in the Amazon. Biol. Conserv. 2014, 177, 203–209. [Google Scholar] [CrossRef]
- Southworth, J.; Marsik, M.; Qiu, Y.; Perz, S.; Cumming, G.; Stevens, F.; Rocha, K.; Duchelle, A.; Barnes, G. Roads as drivers of change: Trajectories across the Tri-National frontier in MAP, the Southwestern Amazon. Remote Sens. 2011, 3, 1047–1066. [Google Scholar] [CrossRef]
- Bax, V.; Francesconi, W.; Quintero, M. Spatial modeling of deforestation processes in the Central Peruvian Amazon. J. Nat. Conserv. 2016, 29, 79–88. [Google Scholar] [CrossRef]
- González-González, A.; Villegas, J.C.; Clerici, N.; Salazar, J.F. Spatial-temporal dynamics of deforestation and its drivers indicate need for locally-adapted environmental governance in Colombia. Ecol. Indic. 2021, 126, 107695. [Google Scholar] [CrossRef]
- Doggart, N.; Morgan-Brown, T.; Lyimo, E.; Mbilinyi, B.; Meshack, C.K.; Sallu, S.M.; Spracklen, D.V. Agriculture is the main driver of deforestation in Tanzania. Environ. Res. Lett. 2020, 15, 034028. [Google Scholar] [CrossRef]
- Pendrill, F.; Gardner, T.A.; Meyfroidt, P.; Persson, U.M.; Adams, J.; Azevedo, T.; Bastos Lima, M.G.; Baumann, M.; Curtis, P.G.; De Sy, V.; et al. Disentangling the numbers behind agriculture-driven tropical deforestation. Science 2022, 377, eabm9267. [Google Scholar] [CrossRef] [PubMed]
- Gibbs, H.K.; Ruesch, A.S.; Achard, F.; Clayton, M.K.; Holmgren, P.; Ramankutty, N.; Foley, J.A. Tropical forests were the primary sources of new agricultural land in the 1980s and 1990s. Proc. Natl. Acad. Sci. USA 2010, 107, 16732–16737. [Google Scholar] [CrossRef]
- Broadbent, E.N.; Asner, G.P.; Keller, M.; Knapp, D.E.; Oliveira, P.J.C.; Silva, J.N. Forest fragmentation and edge effects from deforestation and selective logging in the Brazilian Amazon. Biol. Conserv. 2008, 141, 1745–1757. [Google Scholar] [CrossRef]
- Precinoto, R.S.; Prieto, P.V.; Figueiredo, M.d.S.L.; Lorini, M.L. Edges as hotspots and drivers of forest cover change in a tropical landscape. Perspect. Ecol. Conserv. 2022, 20, 314–321. [Google Scholar] [CrossRef]
- Brown, S.; Hall, M.; Andrasko, K.; Ruiz, F.; Marzoli, W.; Guerrero, G.; Masera, O.; Dushku, A.; DeJong, B.; Cornell, J. Baselines for land-use change in the tropics: Application to avoided deforestation projects. Mitig. Adapt. Strateg. Glob. Chang. 2007, 12, 1001–1026. [Google Scholar] [CrossRef]
- Hamunyela, E.; Brandt, P.; Shirima, D.; Do, H.T.T.; Herold, M.; Roman-Cuesta, R.M. Space-time detection of deforestation, forest degradation and regeneration in montane forests of Eastern Tanzania. Int. J. Appl. Earth Obs. Geoinf. 2020, 88, 102063. [Google Scholar] [CrossRef]
- Lima, A.; Silva, T.S.F.; Aragão, L.E.O.e.C.d.; Feitas, R.M.d.; Adami, M.; Formaggio, A.R.; Shimabukuro, Y.E. Land use and land cover changes determine the spatial relationship between fire and deforestation in the Brazilian Amazon. Appl. Geogr. 2012, 34, 239–246. [Google Scholar] [CrossRef]
- Veronesi, F.; Schito, J.; Grassi, S.; Raubal, M. Automatic selection of weights for GIS-based multicriteria decision analysis: Site selection of transmission towers as a case study. Appl. Geogr. 2017, 83, 78–85. [Google Scholar]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1977. [Google Scholar]
- Malczewski, J. On the use of weighted linear combination method in GIS: Common and best practice approaches. Trans. GIS 2000, 4, 5–22. [Google Scholar] [CrossRef]
- Galford, G.L.; Melillo, J.M.; Kicklighter, D.W.; Cronin, T.W.; Cerri, C.E.P.; Mustard, J.F.; Cerri, C.C. Greenhouse gas emissions from alternative futures of deforestation and agricultural management in the southern Amazon. Proc. Natl. Acad. Sci. USA 2010, 107, 19649–19654. [Google Scholar] [CrossRef] [PubMed]
- Prevedello, J.A.; Winck, G.R.; Weber, M.M.; Nichols, E.; Sinervo, B. Impacts of forestation and deforestation on local temperature across the globe. PLoS ONE 2019, 14, e0213368. [Google Scholar] [CrossRef] [PubMed]
- Ceccherini, G.; Duveiller, G.; Grassi, G.; Lemoine, G.; Avitabile, V.; Pilli, R.; Cescatti, A. Abrupt increase in harvested forest area over Europe after 2015. Nature 2020, 583, 72–77. [Google Scholar] [CrossRef]
- Kindermann, G.E.; Obersteiner, M.; Rametsteiner, E.; McCallum, I. Predicting the deforestation-trend under different carbon-prices. Carbon Balance Manag. 2006, 1, 15. [Google Scholar] [CrossRef] [PubMed]
- Mollicone, D.; Freibauer, A.; Schulze, E.D.; Braatz, S.; Grassi, G.; Federici, S. Elements for the expected mechanisms on ‘reduced emissions from deforestation and degradation, REDD’ under UNFCCC. Environ. Res. Lett. 2007, 2, 045024. [Google Scholar] [CrossRef]
- Van Rossum, G.; Drake, F. Python 3 Reference Manual; CreateSpace: Scotts Valley, CA, USA, 2009. [Google Scholar]
- Sahr, K. DGGRID Version 7.5. Available online: https://github.com/sahrk/DGGRID (accessed on 13 March 2023).
- Swets, J.A. Measuring the accuracy of diagnostic systems. Science 1988, 240, 1285–1293. [Google Scholar] [CrossRef]
- Pontius, R.G.; Boersma, W.; Castella, J.-C.; Clarke, K.; de Nijs, T.; Dietzel, C.; Duan, Z.; Fotsing, E.; Goldstein, N.; Kok, K.; et al. Comparing the input, output, and validation maps for several models of land change. Ann. Reg. Sci. 2008, 42, 11–37. [Google Scholar] [CrossRef]
- Mas, J.-F.; Soares Filho, B.; Pontius, R.G.; Farfán Gutiérrez, M.; Rodrigues, H. A suite of tools for ROC analysis of spatial models. ISPRS Int. J. Geo-Inf. 2013, 2, 869–887. [Google Scholar] [CrossRef]
- Gilmore Pontius, R.; Pacheco, P. Calibration and validation of a model of forest disturbancein the Western Ghats, India 1920–1990. GeoJournal 2004, 61, 325–334. [Google Scholar] [CrossRef]
- Camacho Olmedo, M.T.; Mas, J.-F.; Paegelow, M. Validation of Soft Maps Produced by a Land Use Cover Change Model. In Land Use Cover Datasets and Validation Tools: Validation Practices with QGIS; García-Álvarez, D., Camacho Olmedo, M.T., Paegelow, M., Mas, J.F., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 189–203. [Google Scholar]
- Pontius, R.G.; Parmentier, B. Recommendations for using the relative operating characteristic (ROC). Landsc. Ecol. 2014, 29, 367–382. [Google Scholar] [CrossRef]
- Paegelow, M. LUCC Based Validation Indices: Figure of Merit, Producer’s Accuracy and User’s Accuracy. In Geomatic Approaches for Modeling Land Change Scenarios; Camacho Olmedo, M.T., Paegelow, M., Mas, J.-F., Escobar, F., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 433–436. [Google Scholar]
- Čengić, M.; Steinmann, Z.J.N.; Defourny, P.; Doelman, J.C.; Lamarche, C.; Stehfest, E.; Schipper, A.M.; Huijbregts, M.A.J. Global maps of agricultural expansion potential at a 300 m resolution. Land 2023, 12, 579. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Hejazi, M.; Wise, M.; Vernon, C.; Iyer, G.; Chen, W. Global urban growth between 1870 and 2100 from integrated high resolution mapped data and urban dynamic modeling. Commun. Earth Environ. 2021, 2, 201. [Google Scholar] [CrossRef]
- Li, X.; Yu, L.; Sohl, T.; Clinton, N.; Li, W.; Zhu, Z.; Liu, X.; Gong, P. A cellular automata downscaling based 1 km global land use datasets (2010–2100). Sci. Bull. 2016, 61, 1651–1661. [Google Scholar] [CrossRef]
- Chen, M.; Vernon, C.R.; Graham, N.T.; Hejazi, M.; Huang, M.; Cheng, Y.; Calvin, K. Global land use for 2015–2100 at 0.05° resolution under diverse socioeconomic and climate scenarios. Sci. Data 2020, 7, 320. [Google Scholar] [CrossRef]
- d’Annunzio, R.; Sandker, M.; Finegold, Y.; Min, Z. Projecting global forest area towards 2030. For. Ecol. Manag. 2015, 352, 124–133. [Google Scholar] [CrossRef]
- Qin, Y.; Xiao, X.; Liu, F.; de Sa e Silva, F.; Shimabukuro, Y.; Arai, E.; Fearnside, P.M. Forest conservation in Indigenous territories and protected areas in the Brazilian Amazon. Nat. Sustain. 2023, 6, 295–305. [Google Scholar] [CrossRef]
- Food and Agriculture Organization and The United Nations Environment Programme. The State of the World’s Forests 2020; FAO: Rome, Italy, 2020. [Google Scholar]
- Saaty, T.L. The Analytical Hierarchy Process; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Yager, R.R. On ordered weighted averaging aggregation operators in multicriteria decisionmaking. IEEE Trans. Syst. Man Cybern. 1988, 18, 183–190. [Google Scholar] [CrossRef]
- Dujmovic, J.J.; Tré, G.D.; Weghe, N.V. LSP suitability maps. Soft Comput. 2010, 14, 421–434. [Google Scholar] [CrossRef]
- Angelsen, A. Policy Options to Reduce Deforestation. In REDD+: National Strategy and Policy Options; Angelsen, A., Brockhaus, M., Kanninen, M., Sills, E., Sunderlin, W.D., Wertz-Kanounnikoff, S., Eds.; Center for International Forestry Research (CIFOR): Bogor, Indonesia, 2009; pp. 125–138. [Google Scholar]
- Organisation for Economic Co-operation and Development (OECD). Rethinking Urban Sprawl: Moving Towards Sustainable Cities; OECD Publishing: Paris, France, 2018. [Google Scholar]


| Category | Deforestation Criteria | Susceptibility Functions | Rationale | Criteria Weights |
|---|---|---|---|---|
| Socioeconomic | Population density | 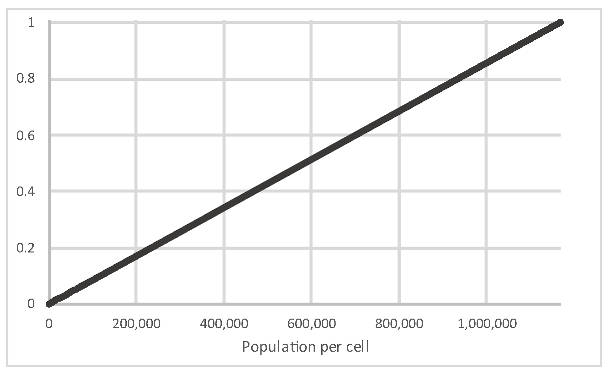 | Population density is an indicator for the concentration of human activities and thus closeness of possible deforestation processes. | 0.03418 |
| Terrain | Slope | 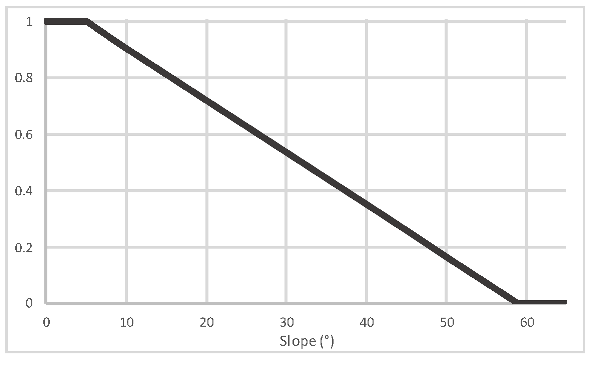 | Areas with gentle slopes are more suitable for land-use/land-cover change | 0.04323 |
| Elevation | 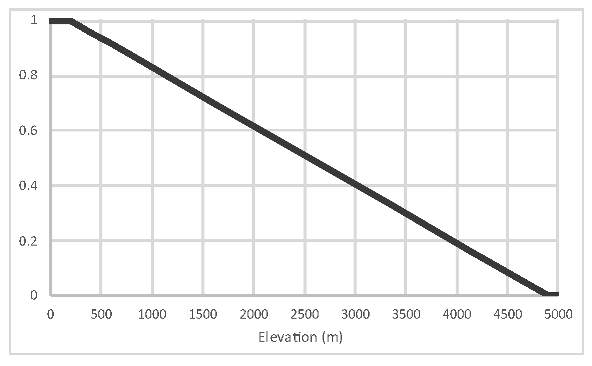 | Areas at lower elevation are more prone to deforestation as they are more accessible. | 0.17615 | |
| Proximity | Proximity to urban areas | 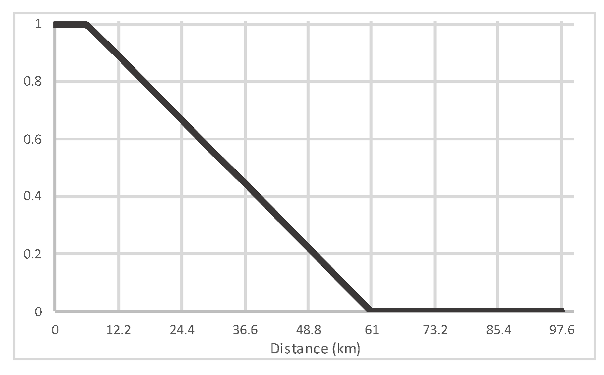 | Urbanization creates demand for land to support urban activities and infrastructure, thus entailing deforestation of adjacent forests. | 0.00824 |
| Proximity to major roads |  | Connection to transportation networks enhances deforestation by providing easy access to forest areas. | 0.04777 | |
| Proximity to water bodies | 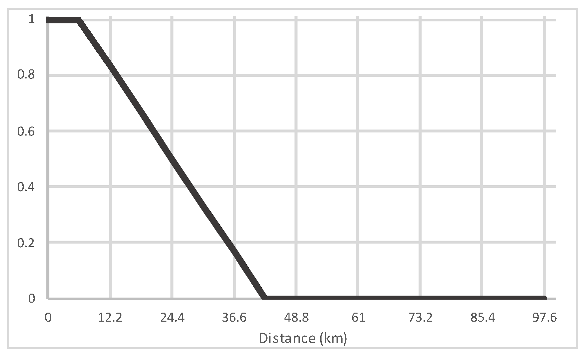 | Water bodies provide access ways to forest regions and remote areas, thus increasing the possibility of deforestation. | 0.00645 | |
| Proximity to agriculture |  | Forest areas closer to agricultural land are more prone to deforestation due to expansion of farmlands and agroforestry. | 0.12282 | |
| Proximity to forest edges | 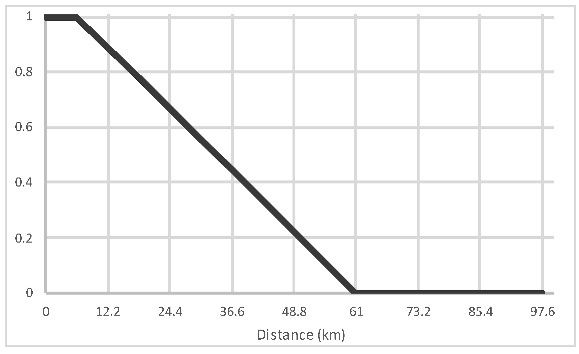 | Deforestation typically starts from the edges of existing forest regions as they are much easier to clear. | 0.38784 | |
| Proximity to past forest disturbances | 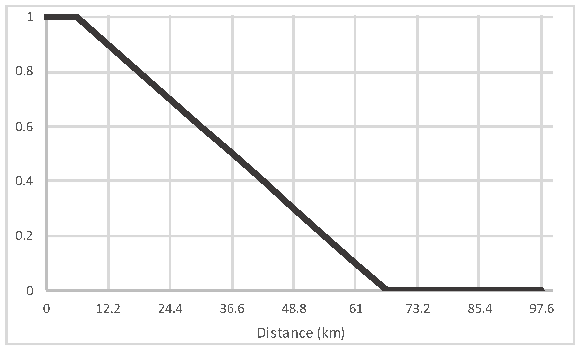 | Past forest disturbance areas are often precursors to future forest degradation or agricultural use. | 0.17331 |
| Continent | 2020 (106 km2) | Scenario | 2030 | 2040 | 2050 | 2060 | 2070 | 2080 | 2090 | 2100 | Lost (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Africa | 8.42 | BAU | 8.34 | 8.27 | 8.20 | 8.12 | 8.05 | 7.98 | 7.91 | 7.84 | 6.85 |
| AD | 8.31 | 8.20 | 8.09 | 7.98 | 7.88 | 7.77 | 7.67 | 7.57 | 10.08 | ||
| SD | 8.38 | 8.34 | 8.31 | 8.29 | 8.27 | 8.25 | 8.23 | 8.22 | 2.40 | ||
| Asia | 7.28 | BAU | 7.19 | 7.11 | 7.03 | 6.94 | 6.86 | 6.78 | 6.70 | 6.62 | 9.03 |
| AD | 7.15 | 7.02 | 6.90 | 6.78 | 6.66 | 6.55 | 6.43 | 6.32 | 13.18 | ||
| SD | 7.24 | 7.20 | 7.15 | 7.13 | 7.11 | 7.09 | 7.07 | 7.05 | 3.21 | ||
| Australia | 1.10 | BAU | 1.08 | 1.07 | 1.05 | 1.04 | 1.03 | 1.01 | 1.00 | 0.98 | 10.20 |
| AD | 1.07 | 1.05 | 1.03 | 1.01 | 0.99 | 0.97 | 0.95 | 0.93 | 14.97 | ||
| SD | 1.09 | 1.08 | 1.07 | 1.07 | 1.07 | 1.06 | 1.06 | 1.06 | 3.61 | ||
| Europe | 12.12 | BAU | 11.88 | 11.64 | 11.39 | 11.15 | 10.92 | 10.68 | 10.46 | 10.24 | 15.48 |
| AD | 11.75 | 11.39 | 11.03 | 10.68 | 10.34 | 10.02 | 9.70 | 9.40 | 22.45 | ||
| SD | 12.00 | 11.88 | 11.77 | 11.71 | 11.65 | 11.58 | 11.52 | 11.46 | 5.41 | ||
| North America | 7.97 | BAU | 7.83 | 7.70 | 7.57 | 7.45 | 7.33 | 7.20 | 7.08 | 6.96 | 12.74 |
| AD | 7.77 | 7.57 | 7.38 | 7.19 | 7.01 | 6.84 | 6.66 | 6.49 | 18.61 | ||
| SD | 7.90 | 7.84 | 7.77 | 7.74 | 7.71 | 7.67 | 7.64 | 7.61 | 4.51 | ||
| Oceania | 0.51 | BAU | 0.50 | 0.50 | 0.49 | 0.49 | 0.48 | 0.48 | 0.48 | 0.47 | 6.58 |
| AD | 0.50 | 0.49 | 0.49 | 0.48 | 0.47 | 0.47 | 0.46 | 0.46 | 9.67 | ||
| AD | 0.50 | 0.49 | 0.49 | 0.48 | 0.47 | 0.47 | 0.46 | 0.46 | 9.67 | ||
| South America | 10.40 | BAU | 10.30 | 10.20 | 10.10 | 10.00 | 9.91 | 9.82 | 9.73 | 9.64 | 7.33 |
| AD | 10.25 | 10.10 | 9.95 | 9.81 | 9.68 | 9.55 | 9.42 | 9.30 | 10.58 | ||
| SD | 10.35 | 10.30 | 10.25 | 10.22 | 10.20 | 10.18 | 10.15 | 10.13 | 2.65 |
| Scenario (%) | Africa | Asia | Australia | Europe | North America | Oceania | South America |
|---|---|---|---|---|---|---|---|
| Base year 2020 | 20.92 | 11.22 | 32.53 | 14.55 | 10.70 | 3.91 | 35.90 |
| BAU 2100 | 22.44 | 12.34 | 36.23 | 17.21 | 12.26 | 4.18 | 38.73 |
| AD 2100 | 23.25 | 12.85 | 38.26 | 18.76 | 13.15 | 4.33 | 40.14 |
| SD 2100 | 21.43 | 11.60 | 33.75 | 15.38 | 11.21 | 4.00 | 36.88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Addae, B.; Dragićević, S. Modelling Global Deforestation Using Spherical Geographic Automata Approach. ISPRS Int. J. Geo-Inf. 2023, 12, 306. https://doi.org/10.3390/ijgi12080306
Addae B, Dragićević S. Modelling Global Deforestation Using Spherical Geographic Automata Approach. ISPRS International Journal of Geo-Information. 2023; 12(8):306. https://doi.org/10.3390/ijgi12080306
Chicago/Turabian StyleAddae, Bright, and Suzana Dragićević. 2023. "Modelling Global Deforestation Using Spherical Geographic Automata Approach" ISPRS International Journal of Geo-Information 12, no. 8: 306. https://doi.org/10.3390/ijgi12080306
APA StyleAddae, B., & Dragićević, S. (2023). Modelling Global Deforestation Using Spherical Geographic Automata Approach. ISPRS International Journal of Geo-Information, 12(8), 306. https://doi.org/10.3390/ijgi12080306







