Machine-Learning-Based Forest Classification and Regression (FCR) for Spatial Prediction of Liver Fluke Opisthorchis viverrini (OV) Infection in Small Sub-Watersheds

Abstract

Infection of liver flukes (Opisthorchis viverrini) is partly due to their suitability for habitats in sub-basin areas, which causes the intermediate host to remain in the watershed system in all seasons. The spatial monitoring of fluke at the small basin scale is important because this can enable analysis at the level of the factors involved that influence infections. A spatial mathematical model was weighted by the nine spatial factors X₁ (index of land-use types), X₂ (index of soil drainage properties), X₃ (distance index from the road network, X₄ (distance index from surface water resources), X₅ (distance index from the flow accumulation lines), X₆ (index of average surface temperature), X₇ (average surface moisture index), X₈ (average normalized difference vegetation index), and X₉ (average soil-adjusted vegetation index) by dividing the analysis into two steps: (1) the sub-basin boundary level was analyzed with an ordinary least square (OLS) model used to select the spatial criteria of liver flukes aimed at analyzing the factors related to human liver fluke infection according to sub-watersheds, and (2) we used the infection risk positional analysis level through machine-learning-based forest classification and regression (FCR) to display the predictive results of infection risk locations along stream lines. The analysis results show four prototype models that import different independent variable factors. The results show that Model 1 and Model 2 gave the most AUC (0.964), and the variables that influenced infection risk the most were the distance to stream lines and the distance to water bodies; the NDMI and NDVI factors rarely affected the accuracy. This FCR machine-learning application approach can be applied to the analysis of infection risk areas at the sub-basin level, but independent variables must be screened with a preliminary mathematical model weighted to the spatial units in order to obtain the most accurate predictions.

1. Introduction

Severe liver fluke infections have been detected in Ponna Kaeo district, Sakon Nakhon Province, Thailand [1]. The liver fluke, scientifically named Opisthorchis viverrini (OV), causes cholangiocarcinoma (CCA) [2,3,4]. CCA is a cancer of the bile ducts of the liver, a disease that has no symptoms. The patient may have signs and symptoms in the early stages of cholangiocarcinoma. The prevalence of liver flukes and cholangiocarcinoma has been reported to be the highest in the eastern provinces of Thailand. The cause of cholangiocarcinoma comes from the liver fluke [5]. It is caused by eating raw fish contaminated with contagious larvae, as well as the popular consumption of raw or semi-cooked and semi-raw fish. Fluke infections from fish products, such as fermented fish, have also been reported [6]. Every year, more than 1000 new cases of CCA are identified in Sakon Nakhon Hospital. This incidence has not decreased over the past decade although the major risk factors for OV infection are known [7,8]. Another study reported the incidence of CCA in four major regions of Thailand (Sakon Nakhon, Phrae, Roi Et, and Nong Bua Lamphu) [8,9,10,11]. Those with a high severity of OV infection (>6000 eggs/g. feces) were 14.1 times more likely (odds) to develop CCA than people who were not infected [12]. The proportion of humans who have been infected with OV that has developed into CCA is about 10%, causing serious health emergencies throughout the region [13,14]. The OV infection can produce bile duct, liver, and connective tissue inflammation, resulting in the development of CCA [4,15]. The five-year survival rate of intrahepatic, distal extrahepatic, and hilar CCA patients undergoing surgery was 22–44%, 27–37%, and 11–41%, respectively [15]. People were infected with liver fluke by their habitat near water bodies; large bodies of water contribute to the continued existence of liver fluke intermediate hosts because fish can come to live during the dry season. Therefore, the study of the potential for infection needs to focus on the boundaries between large bodies of water flowing into the small river basin.

Due to the geographical features of the area, there is a subdistrict boundary with the largest natural water contact zone in the northeast, namely Nong Han. The physical nature of the swamp is a large natural water source, full of water throughout the year, as it is a waterfront source from several streams, making it an important food source for the community. The livelihood of people living in the watershed derives from finding fish, which is an important source of protein, and there is a consumption culture that is familiar with the taste of raw fish [1,4]. According to preliminary screening results from 2019 to 2021 [2], a small number of people contracted liver flukes. In addition, studies conducted on the prevalence of liver fluke infection in fish (contagious larvae) showed that Sakon Nakhon Province had an infection area of 33.33% [13], and a 2016–2017 study of the density of contact larvae in fish showed a density of 10–20 metacercaria per kilogram of fish [12]. As a result, liver fluke outbreaks are still present in Sakon Nakhon Province, where the liver fluke’s eggs are transfused with feces, potentially contaminating soil and water bodies and causing recurrent infections and an endless cycle of infection.

The application of a geographic information system (GIS) as an analysis tool is especially useful for predicting liver fluke infection when analyzed in conjunction with remote-sensing (RS) data. Satellite imagery, which is the collection of RS data, can be used to acquire spatially meaningful moisture indicators. This allows for a thorough investigation of the distribution and likelihood of liver flukes [14], such as with the standardized vegetation index, soil moisture index, soil cover index [16], and other indices that may be associated with the habitation of liver fluke intermediates. The study approach focuses on spatial modeling in small areas with the connection of water flow lines covered in the area, unlike other studies that focus on regional modeling. The datasets were homogenized to have the same extents and pixel size, this study creates independent variables to correlate the number of infected individuals. Various studies have used spatial statistics to analyze correlation factors with liver fluke infection [17], such as [18,19], which analyzed a large area, resulting in discrepancies and incoherence in the raster data. Based on the findings of [20,21,22], the limitations of data acquisition at the area level are sometimes inconsistent with the image point size from satellite imagery, which results in model discrepancies as these limitations accumulate. As a result, models studied at the regional scale area cannot be used as representations at the small watershed level. The GWR (geographically weighted regression) model is typically thought of as the ideal model that can be used to study and model at a large spatial level, but the model has the limitation of having continuous, evenly distributed data in spatial units, which is occasionally unsuitable for small watersheds. However, in this study, the OLS (ordinary least square) model was applied, which is a global operation model that is sufficient for analyzing areas with a small number of spatial units. Because GWR models require large enough units of space to be weighted by coefficients, OLS models are a satisfying alternative for small-space solutions.

However, since many indices are to be constructed as independent variables to accurately analyze them, the principles of geo-statistics [23], the OLS modeling method of local operations in particular, require the creation of sub-spatial units [20], such as sub-basins, defined from the flow boundary of the sub-basin to the modeling control boundary. This makes OLS models effective in predicting and analyzing spatial relationships as well [24]. To build spatial models for analyzing relationships in small areas such as sub-basin levels [25], there is a need to use appropriate models and design sub-area units to suit the distribution of data and dependent and independent variables. The application of only OLS models in independent multivariate analysis often provides satisfactory accuracy since many independent factors create a lot of variability for the model. However, in this study, OLS modeling was used to analyze the relationship between a set of independent variables and the percentage of infections before OV. Past research on spatial modeling has not used the application of OLS models and sub-spatial unit boundaries in small watershed systems to track liver fluke infections. This was carried out to screen for the independent variables associated with infection, and then alternative OLS models were used to select the set of independent variables that gave the best statistical values to predict the likelihood of infection in the streamline, and for this, it is necessary to develop models with the accuracy of predictive prototypes. When using forecasts from spatial statistical models, risk analysis can only be carried out at the sub-basin level, which requires sufficient independent variable data to create appropriate trendlines. Machine learning (ML) is, therefore, necessary and is used to predict the risk of water source location with potential infection by learning from spatial factors.

Modern research has applied ML to spatial risk assessment tasks, such as in [26]. In recent years, advances in ML algorithms, computing power, and geospatial innovations, including software, have made it easier to create spatial maps [27]. The precision of spatial maps can be improved using machine-learning algorithms, such as knowledge-based methods [28], multivariate logistic regression methods [29,30,31], and multivariate binary logistic regression [32], which have all been presented in recent papers. General linear model [33,34], quadratic discriminant analysis [33,35], boosted regression tree [34,36], random forest classification (RFC) [37,38,39,40], multivariate adaptive regression splines [41,42], classification and regression tree [34,43], support vector machine [44,45,46], naïve Bayes [47,48], generalized additive model [33,43], neuro-fuzzy and adaptive neuro-fuzzy inference [49,50,51], fuzzy logic [52], artificial neural networks [53,54,55,56,57,58], maximum entropy [59,60], and decision tree [31,61,62] methods have also been presented. ML applications were also widely used to create landslide maps (LSM). Merghadi et al. [63] assessed the performance and competency of various ML techniques in the literature and discovered that tree-based ensemble optimization algorithms outcompete other ML algorithms. In a comparison analysis, Sahin [64] found that Catboost had the best precision (85%) followed by XGBoost (83.36%), since the proportion of samples determined by Catboost was more precisely anticipated than other models. The primary advantages of ML and probabilistic processes are their objective statistical foundation, repeatability, capacity to quantitatively analyze the effect of variables on spatial prediction, and the capacity to update them regularly.

Several studies in ML applications have shown that the random forest classification method always has a higher receiver operating characteristic (ROC) and area under the ROC curve (AUC) effect than other models, but it also depends on the factors that bring the machine to learning, including the number of learning and testing points. Machine-learning models can be built using a variety of spatial conditioning factors (land use, slope, aspect, elevation, road network, water body, factors from proximity, etc.). Several studies on flood-prone landslide susceptibility and land-use change evaluation have been undertaken using remote sensing and GIS techniques [65,66,67].

Because there is currently no direct model that can predict the likelihood of locating water bodies infected with liver flukes, studies on spatial fluke infection in small river basins are lacking. To fill this gap, this study used a forest-based classification and regression (FCR) modeling approach to hypothesize that spatial factors could be an indicator of infection. The study’s focus was on identifying the characteristics that are most important to infection within the small river basin and using these factors to predict using FCR as a model for model creation. Compared to earlier research, no work has utilized FCR for this type of prediction.

In this research, the FCR approaches were applied to predict the percentage of infection risk with spatial factors at both the watershed level and the location of learning points which are the locations of water bodies with infected fish. Therefore, if it can be demonstrated that the spatial characteristics in the distribution of each parasite are important to any subspace unit at the sub-basin level, then the sub-basin level can be properly managed for protection [68]. For example, breaking the cycle of intermediary hosts, such as mollusks, can prevent future illnesses and result in healthy communities. The community is strengthened, and the burden of medical care can be reduced.

1.1. The Study Area

Phon Na Kaeo is a district in Sakon Nakhon Province; in the north, it borders the Kusumal district; in the east, it borders the Pla Pak district (Nakhon Phanom Province); in the south, it borders the Wangyang district (Nakhon Phanom Province), Khok Si Suphan district, and Mueang Sakon Nakhon district; and in the west, it borders the Mueang Sakon Nakhon district. Its geographical co-ordinates are 17°13′18″ N, 104°17′24″ E, as shown in Figure 1.

There are five subdistricts: Ban Phon, Na Kaeo, Nadong Wattana, Ban Khae, and Chiang Shi. The Phon Na Kaeo district’s area of Sakon Nakhon Province is located in the east of the Songkram watershed, adjacent to Nakhon Phanom Province and adjacent to the Nong Harn marsh, which is a large natural water source. There is an exchange of Mekong fish and fish habitat in the area at a distance of about 40 km from the Mekong River, resulting in the travel of many Mekong/tributary fish in the Phon Na Kaeo district and the potential for fish to increase the number of liver fluke infections.

1.2. Datasets and Analyses

Liver flukes and cholangiocarcinoma have long been a public health problem in Thailand, and at present, at least 20,000 people in the northeast die from cholangiocarcinoma each year [69,70]. Currently, 6–8 million people have been infected with liver flukes, so screening people for liver fluke infection to eliminate parasites is very important in reducing the risk of cholangiocarcinoma [71].

The data on people infected with liver fluke in this research were obtained from the Sakon Nakhon Provincial Public Health Office (SKKO) [72] https://skko.moph.go.th/dward/web/index.php?module=skko (accessed on 20 July 2021). Stool examination is a standard screening method that has been in practice for a long time. For example, the intensive examination of parasite eggs in feces using the modified Kato–Katz technique has been an effective method in the past when there were prevalent parasite outbreaks. Stool specimens were examined for O. viverrini eggs within hours of collection using the modified Kato–Katz technique [73]. The results of infection showed that most people were infected in the Phon Na Kaeo district, Sakon Nakhon Province [72]. For people during the age of between 40 and 60 years, the prevalence of infection tends to increase. Other testing methods include the FECT (formalin–ethyl acetate concentration technique) and the enzyme-linked immunosorbent assay (ELISA) [74], which are more effective than stool testing. It also provides quantitative results that correlate with the density of the parasite and can be used for post-drug assessment to determine the rate of reinfection or new infection [74,75,76]. However, in this study, such methods were not used since they require a high budget. However, the secondary data obtained from SKKO of the number of people infected with liver flukes (measured using the modified Kato–Katz method) are reliable because it is an appropriate method for measuring many people. The prevalence of liver fluke infection in Sakon Nakhon Province tends to increase in patients aged 20–30 years, as shown in

Table 1. Comparison of number of people with cholangiocarcinoma in 2019/2020 [77].

Provinces	Number of People with Cholangiocarcinoma in 2019	Number of People with Cholangiocarcinoma in 2020
Nongkhai	22	37
Buengkarn	8	7
Loei	54	84
Nakhon Phanom	7	10
Udon Thani	50	88
Nongbualumphu	19	12
Sakon Nakhon	161	130

.

From 2019 to 2021, 12,063 cases were detected in national stool tests according to data from the 8th Health District Office (Region, (R8)) [78] https://r8way.moph.go.th/r8way/index (accessed on 17 June 2021). Of the 2832 stool tests, 599 cases were found in Sakon Nakhon Province, with the highest number of liver fluke infections in neighboring provinces in the watershed systems connecting Nakhon Phanom and Bueng Kan [79]. The summary of reported cases detected as a percentage is shown in Figure 2. Sakon Nakhon Province has the largest freshwater supply in the northeast and is a water source that breeds animals during the rainy season [2]. Phon Na Kaeo has the highest average infection rate in Sakon Nakhon Province. Provincial health authorities monitored the situation in this study on the likelihood of infection within the sub-basin that could increase the number of people infected with liver flukes in Phon Na Kaeo district. The distribution of the percentage of infected persons to the population density is shown in Figure 3a and shows the percentage of infected persons according to the sub-basin boundary, where the percentage index of infections from 2019 to 2021 was 0.840–7.840%, which is developed as a dependent variable in the OLS model and is linked to other independent data layers using the geographic information system, namely the spatial join method, as shown in Figure 3b.

The guidelines for the analysis of free compound factors associated with the spread of gastric influenza are selected from a total of nine groups of factors prioritized by provincial health authorities and can be defined as the following categories: land-use types, soil drainage properties, road network, water resources, flow accumulation lines, surface temperature, normalized difference moisture index (NDMI), normalized difference vegetation index (NDVI), and soil-adjusted vegetation index (SAVI). All factors are adjusted to a comparable score range with the approach of scale normalization. All factors were used to verify positional and temporal accuracy with Sentinel-2 satellite imagery based on land-use data via the Google Earth Engine (GEE) (See Supplementary Materials). The green wavelength, NIR, and SWIR are the surface reflectance of the Sentinel-2 satellite in Band 3, with the green visible spectrum (wavelength: 0.53–0.59 μm), Band 5 wavelength NIR (wavelength: 0.85–0.88 μm), and Band 6 wavelength SWIR (wavelength: 1.57–1.65 μm), respectively. In general, a positive NDMI value (NDMI > 0) is interpreted as referring to the threshold surface area used to measure the water surface index. Maximum and minimum values are used as a measurement to distinguish the water surface from the forest and the ground.

2. Materials and Methods

2.1. Ordinary Least Square (OLS) Approach for Spatial Modeling (Analysis at the Level of Infected in Sub-Basins)

The surface moisture factors and surface cover indicators analyzed using satellite images are represented by calculations of the independent variables from X₆ to X₉. An OLS modeling study was used to analyze spatial correlations in terms of liver fluke infection (OV) from the remote-sensing data of sub-basin-level prototype areas. The research algorithm is divided into three stages: (1) data collection and manipulation to collect and manage data for use in analyzing the relationship of liver flukes to watershed areas in sub-basins (See Supplementary Materials). Starting with the preparation of the Sentinel-2 satellite imagery data used in the study (January–April 2019, 2020, and 2021), the dry season of each year is when mollusks are embedded in moist soils, waiting for rain to come during the rainy season. A total of 12 satellite imagery data (4 images per year for 3 years) were taken to average the image points and were used to calculate the indices X₆, X₇, X₈, and X₉ for use as independent variables in the OLS model; (2) independent variable screening; and (3) alternative modeling. A detailed display of the steps can be shown as follows.

The two steps to perform the modeling process are as follows:

(1)

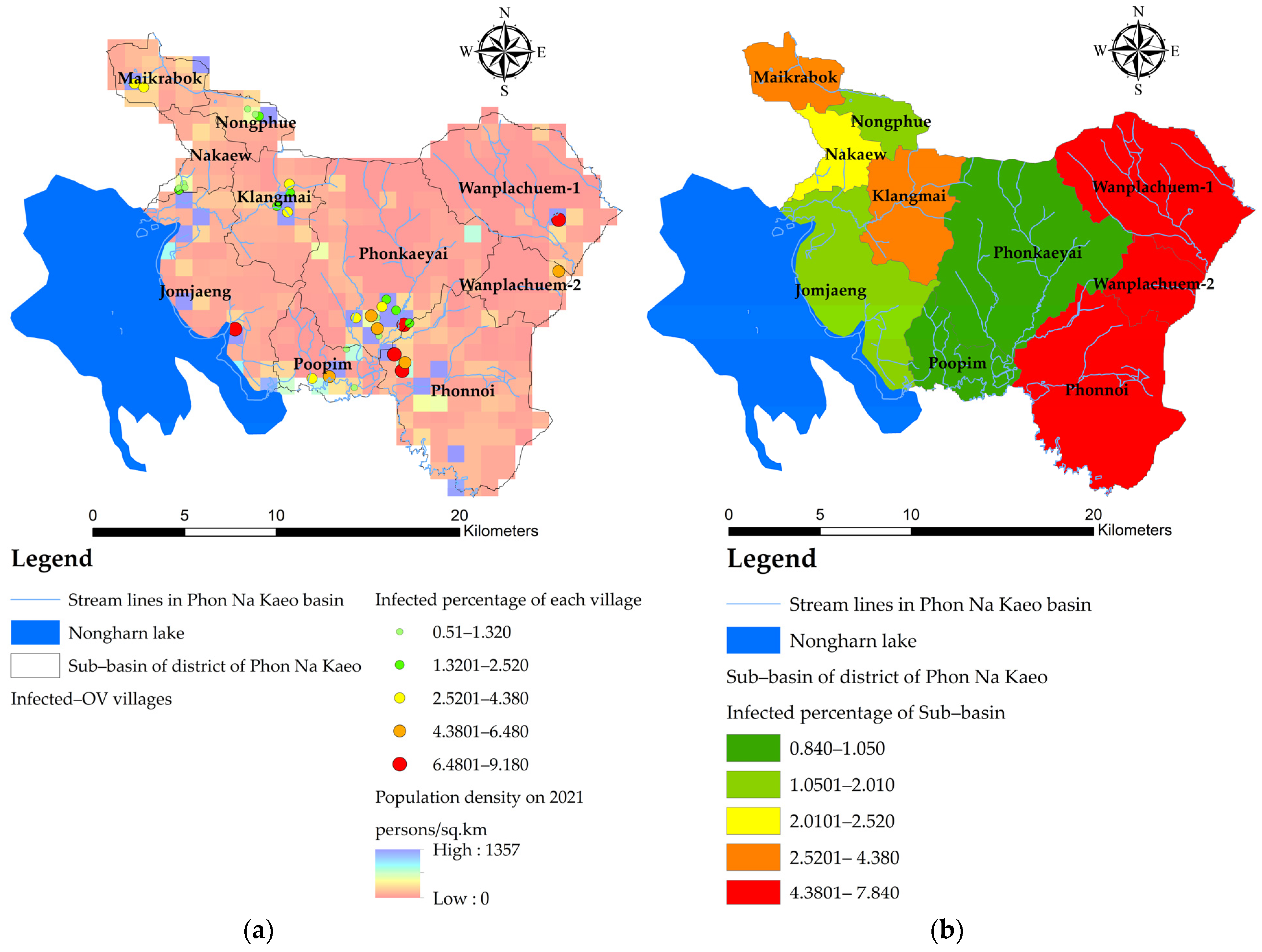
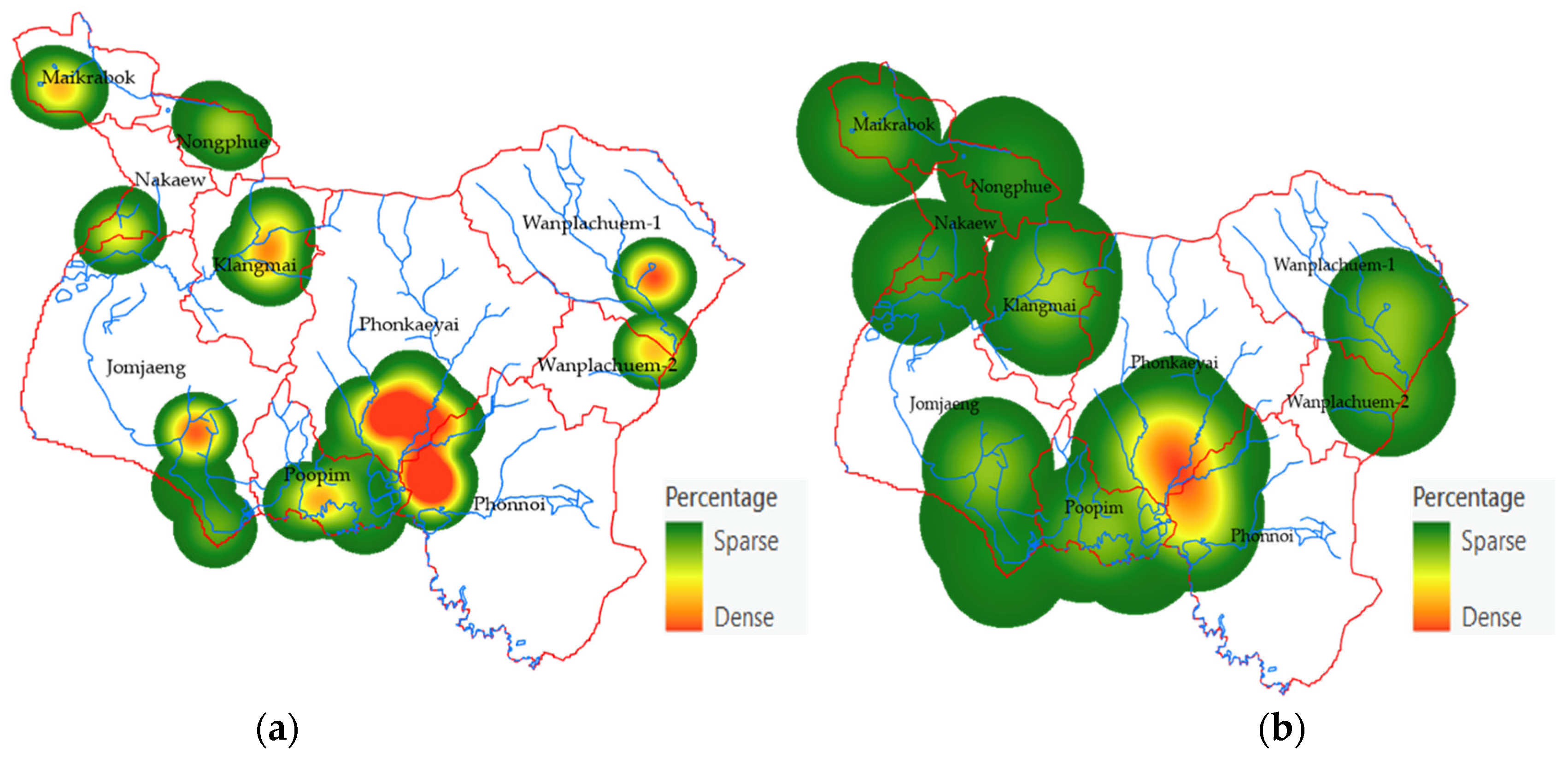
The OLS model uses the principle of estimating the coefficients of the equation with the same squared method as the conventional linear model, but the creation of a variable dataset is a geostatistical statistic that can generate a dataset from a smaller sample but retain a Z value that is similar to the original Z value. The area that seems to be the ideal area for shellfish implantation is the buffer area away from the accumulated flow line of water [20]. The variable data are generated as points of location in the village where the OV data were surveyed. The dependent variable (Y,OV%) is the point data of the location that each village regularly used to find fish for the period 2019–2021, where fish samples were collected and tested for liver fluke infection. Points that represent the percentage of infected people are converted into raster data to reflect the continuous distribution of dependent variables and use the average of infected people to represent that sub-basin. The location data of infected villages are used to create density maps to ensure the continuity of infection. In this study, a heat map was created with a kernel density approach. The density is calculated using the kernel density method, the same algorithm used by the kernel density geoprocessing tool in ArcGIS pro.

The Independent variable Group 1 (spatial variables) was represented as the variable X₅ (distance index from the flow accumulation lines); the mean of the line length, the Level 3 to 3 water flow level, is a variable that shows the likelihood of embedding the host’s intermediary of liver flukes along two sides of the stream by 500–2000 m. OLS creates a local regression equation for each feature in the dataset. When the correlation test was obtained, a set of variables was used as representations; problems with local multicollinearity are more likely. The conditional number (Cond) field in the output feature class indicates when the result is unstable due to local multicollinearity.

(2)

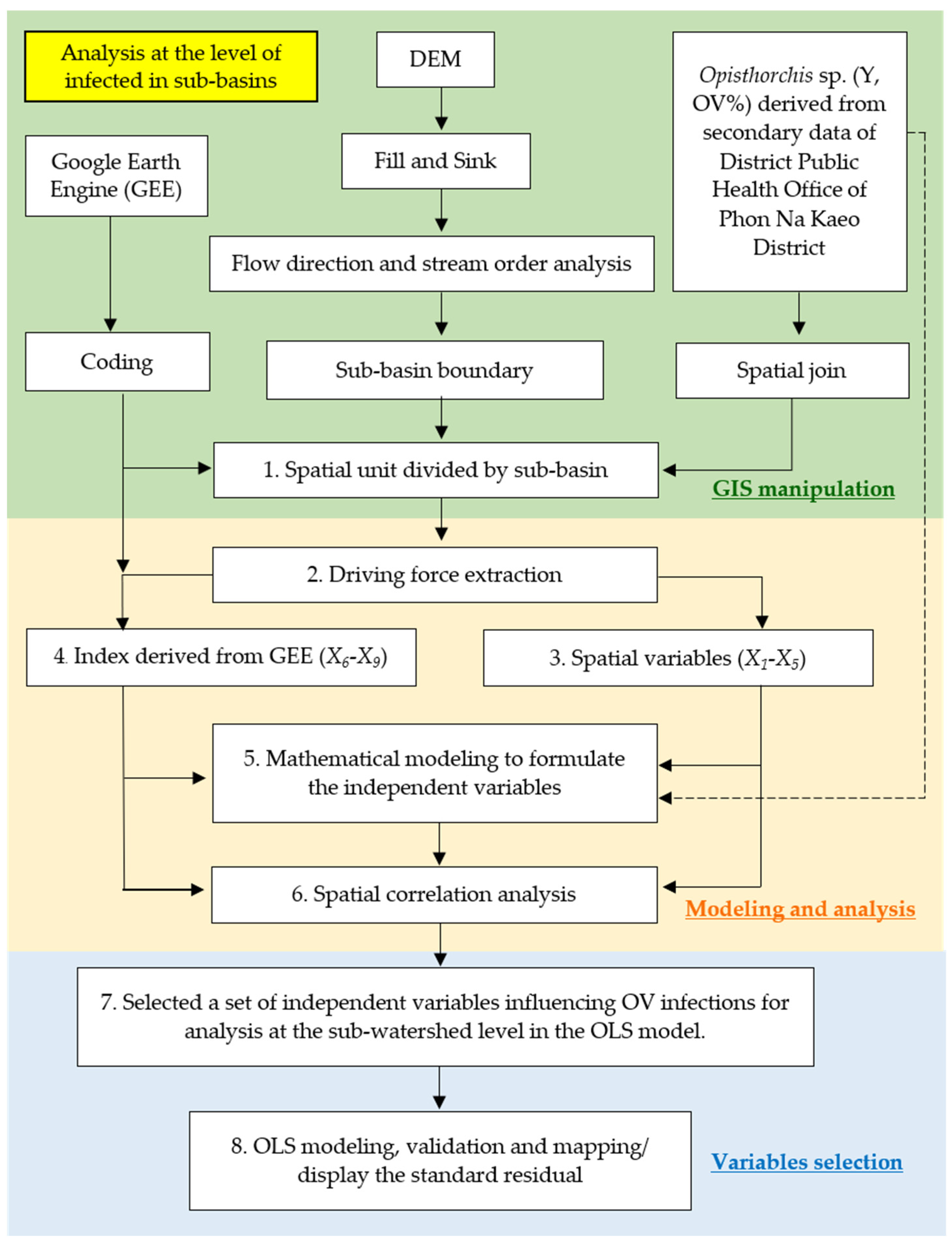
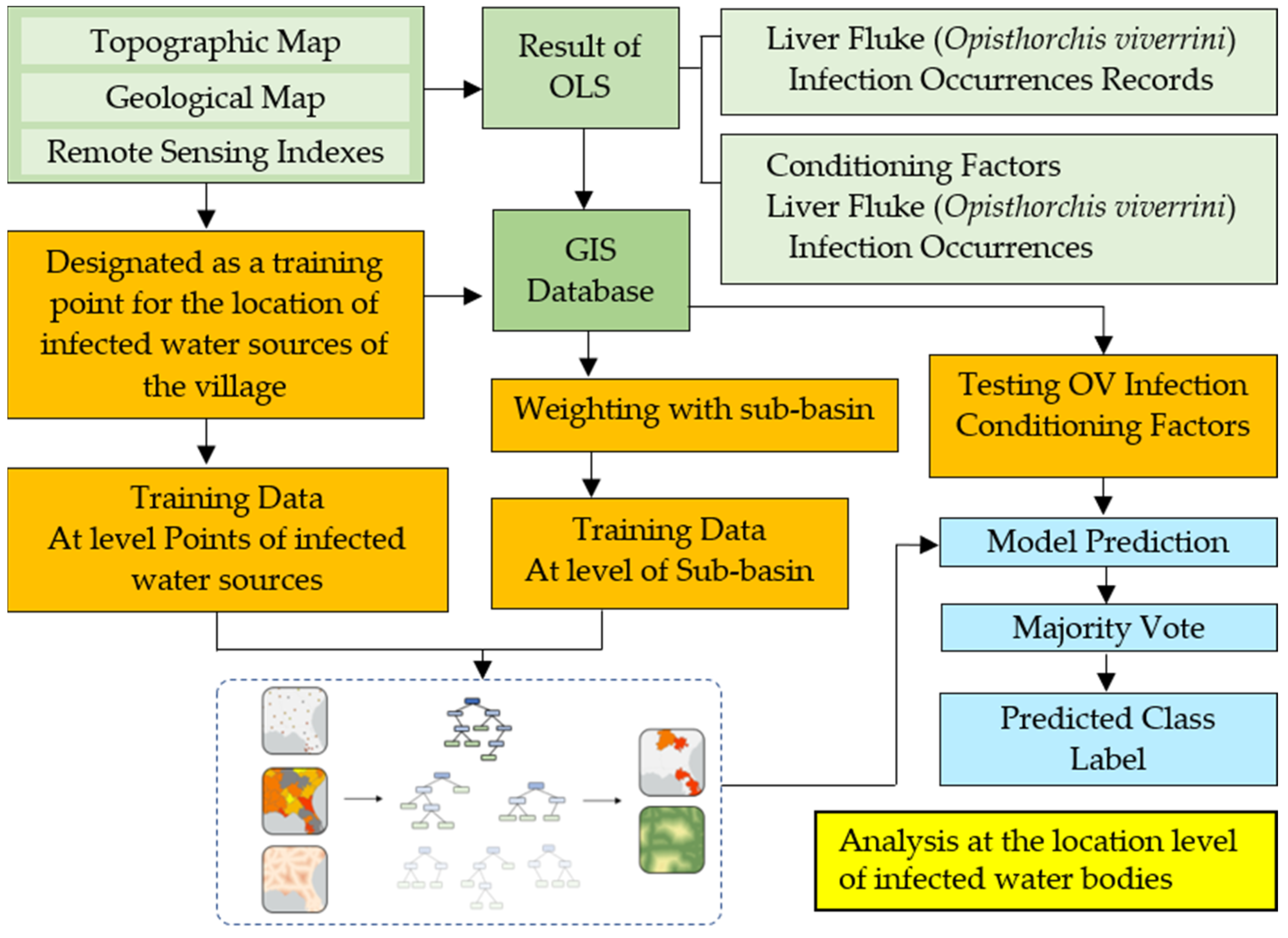
When modeling the relationship between liver flukes, other types of parasites, and spatial factors, OLS uses a global model of spatial statistics, i.e., a model created specifically for each sub-basin, which allows for predicting liver flukes and other types of parasites and analyzing the relationships. The model serves to determine the coefficient of the relationship between the independent and dependent variables using the distance reciprocal weighting method, where OLS obtains a model to predict every unit area with a difference in coefficients [9,21,22]. OLS modeling must create a data layer based on this research, namely the percentage of liver fluke infection of the sub-basin region to be analyzed from 5 m DEM data, the import of independent variables, consisting of the index variables generated from the wavelength correlation of satellite images in mathematical functions, and other spatial factors, such as the distance from water bodies and roads; the detailed procedure is shown in Figure 4, and OLS is shown in Equation (1) [25].

$$\begin{gathered} y_i={\beta }_0+{\beta }_1\left(land use\right)+{\beta }_2\left(soil\right)+{\beta }_3\left(road\right)+{\beta }_4\left(water body\right)+{\beta }_5\left(stream lines\right) \\ +{\beta }_6\left(surface temp\right)+{\beta }_7\left(ndmi\right)+{\beta }_8\left(ndvi\right)+{\beta }_9\left(savi\right)+\left[\epsilon \right] \end{gathered}$$

(1)

where $y_i=$ the value observed for the dependent variable at point i;

• ${\beta }_0=$ the interception point y (constant value);
• ${\beta }_n=$ the regression coefficient or slope of the explanatory variable n at point i;
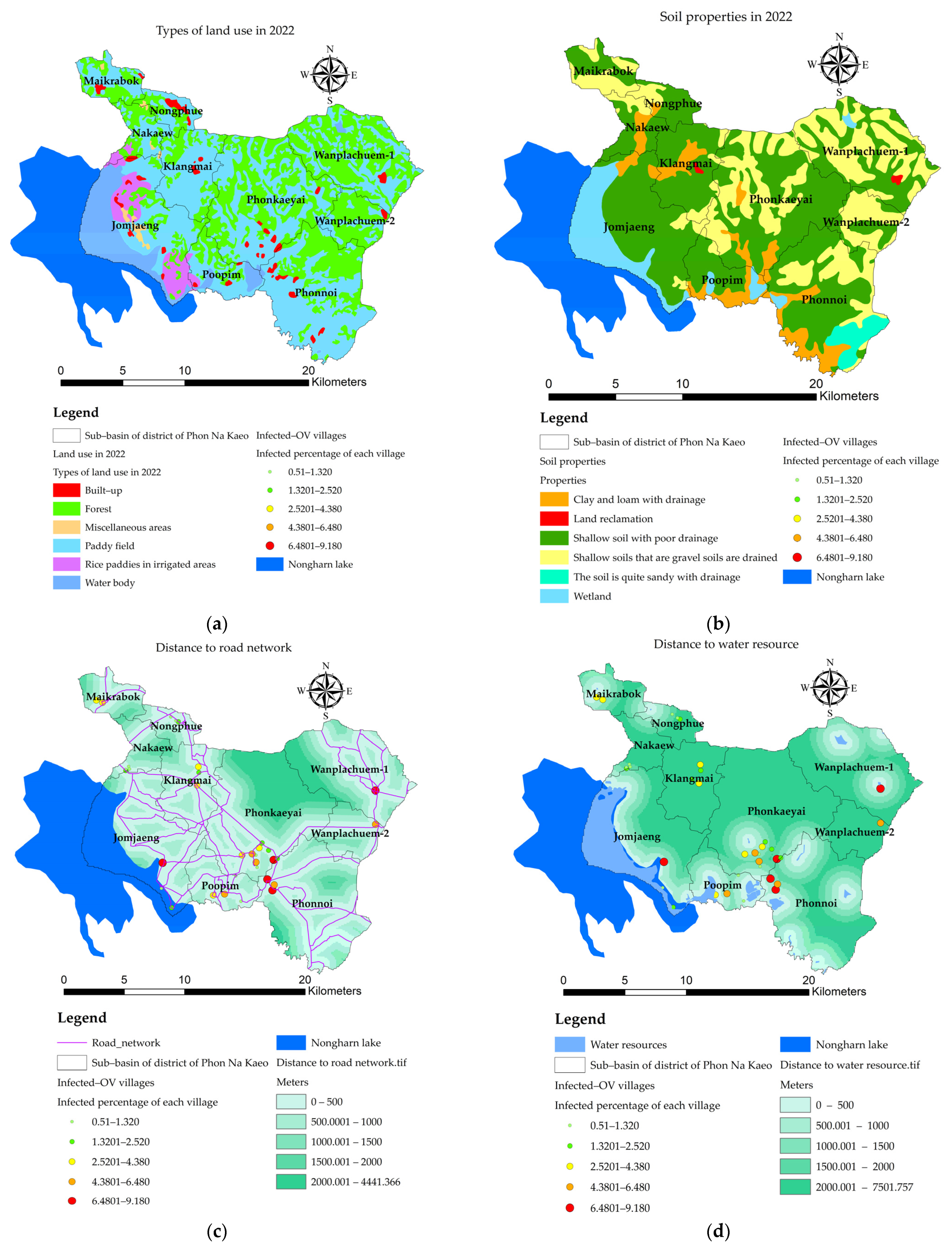
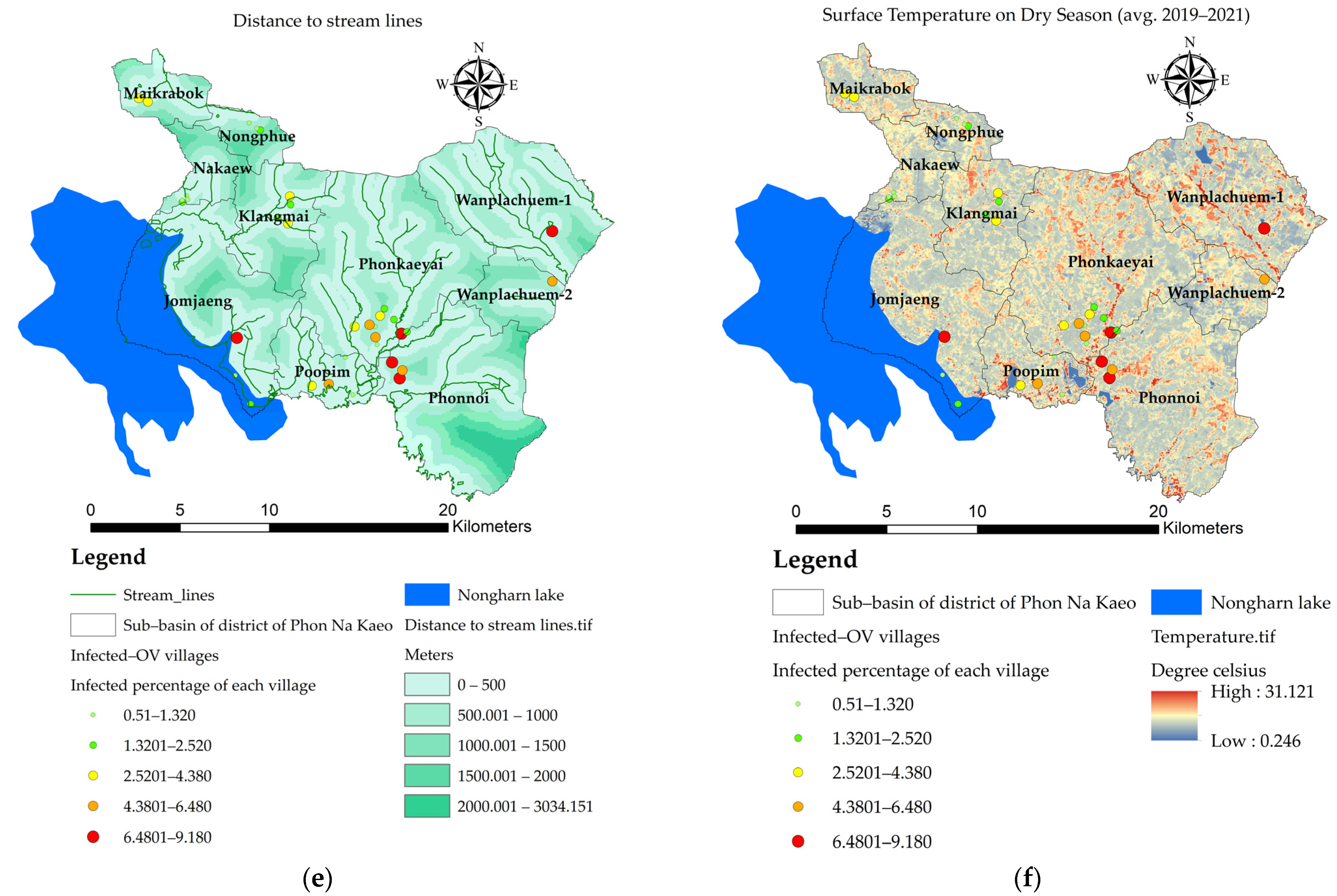
• $x_n=$ the value of the variable n at point i. The X variable can be described as X₁ (index of land-use types), X₂ (index of soil drainage properties), X₃ (distance index from the road network, X₄ (distance index from surface water sources), X₅ (distance index from the stream lines or flow accumulation lines), X₆ (index of average surface temperature), X₇ (average surface moisture index), X₈ (average normalized difference vegetation index), and X₉ (average soil-adjusted vegetation index);
• $\left[\epsilon \right]=$ the error of the regression equation.

The expected outcome is a set of independent variables that illustrates the relationship between the independent variables and dependent variables obtained using geographically weighted analysis and least square regression equations, with the difference in the independent variables affecting the dependent variables in each sub-region (spatial nit). Therefore, if it is possible to analyze the spatial characteristics of the distribution of each type of parasite, the agency or organization can know the areas where the analysis results are used to correctly manage the parasite infection prevention system [81]. Preventing future illnesses can help communities to stay healthy and reduce the burden of medical expenses.

2.2. Independent Variable Modeling

The independent variable set consists of nine factors, namely X₁ (index of land-use types), X₂ (index of soil drainage properties), X₃ (the distance index from the road network, X₄ (distance index from surface water resources), X₅ (distance index from the flow accumulation lines), X₆ (index of average surface temperature), X₇ (average surface moisture index), X₈ (average normalized difference vegetation index), and X₉ (average soil-adjusted vegetation index). Socio-economic or demographic data were not used in this analysis because the populations living in the majority of sub-basins had similar incomes and similar habits of living and fishing from water bodies, and when these variables were introduced into the model, they did not create a trend, but this study showed a map of population density so that we could determine the order of surveillance areas for infected people from this population. The reasons for selecting these nine factors from the above (from the inspection of the area) was that we found that the spread of liver flukes in every season showed that those areas with good retention of surface moisture in the dry season were positively consistent with the number of infected people, but the surface moisture factors were also related to other factors from different types of land use. The indexing of each independent variable is based on a 10 m spatial resolution, allowing for a sufficient number of independent variables to be able to represent OLS models to find trends by calculating them on a raster basis with ArcGIS pro v.2.9.0 under the map algebra function.

Each factor is calculated to determine the average division per sub-basin area, and in addition, Factors 6 to 9 calculated from the remote-sensing index using the raster calculator function are the average of the Sentinel-2 image range from January to April of 2019–2021, which is a picture of the dry season, allowing for the analysis of the area where the host medium survives while waiting for the rainy season to arrive. Mathematical models have evolved from the fundamental factors based on a variety of research related to variables influencing liver fluke infection in watershed-level areas. This is shown in the mathematical model for calculating each factor in Equations (2)–(13) as follows:

$$X_1=\frac{{\mathrm{W}\mathrm{L}}_j{\mathrm{L}}_j}{A_k}$$

(2)

where $X_1$ is the index of land-use types suitable for intermediary host housing. ${\mathrm{W}\mathrm{L}}_j$ = any type i land-use weight value where i = (1 = built-up), (2 = forest), (3 = miscellaneous), (4 = paddy field), or (5 = rice paddies in irrigated areas and water body). ${\mathrm{L}}_j$ = area of land-use category j unit (sq·m). $A_K$ = size of sub-basin area at any k unit (sq·m) (adapted from the research of [12]).

$$X_2=\frac{{\mathrm{W}}_j{\mathrm{S}}_j}{A_k}$$

(3)

where $X_2$ is the index of soil drainage properties suitable for the habitation of the intermediate host. ${\mathrm{S}}_j$ = area size of drainage properties of any type j soil. ${\mathrm{W}}_j$ = weight value of drainage of any type j soil (adapted from the research of [7]).

$$X_3=\frac{{\sum }_{i=1}^n{\sum }_{j=1}^m{DR}_i{B}_j}{A_k}$$

(4)

where $X_3$ is the distance index from the road network used to analyze the suitability of the intermediary host from water trapped by the road network. ${DR}_i$ is the distance from the road line out to any distance, k (meters), where k starts from 500 m, 1000 m, 1500 m, 2000 m, and more. $B_j$ is the buffer distance at any k distance where k starts from 500 m, 1000 m, 1500 m, 2000 m, and above (adapted from the research of [16]).

$$X_4=\frac{{\sum }_{i=1}^n{\sum }_{j=1}^m{DW}_i{B}_j}{A_k}$$

(5)

where $X_4$ is the distance index from the surface water sources used to analyze the suitability of the medium host (from embedding to the soil surface) when moisture still accumulates in the dry season. ${DW}_i$ is the distance from any surface water source, i, that goes out at any distance, k, where k starts from 500 m, 1000 m, 1500 m, 2000 m, and over (adapted from the research of [6]).

$$X_5=\frac{{\sum }_{i=1}^n{\sum }_{j=1}^m{DS}_i{B}_j}{A_k}$$

(6)

where $X_5$ is the distance index from the stream lines or accumulated flow lines of water used to analyze the suitability of the medium host regarding waterlogging and moisture accumulation in the dry season. ${DS}_i$ is the distance from any of the accumulated flow lines of water at any distance, k, where k starts from 500 m, 1000 m, 1500 m, 2000 m, and over [20].

$$X_6=\frac{{\sum }_{i=1}^n{T}_i{A}_{ik}}{A_k}$$

(7)

where $X_6$ is the index of average surface temperature in any sub-basin used to analyze the suitability of the medium host from subsurface embedding to the sub-basin. $T_i$ is any grid temperature value in degrees Celsius. $A_{ik}$ is the total area of temperature at i degrees Celsius within the sub-basin boundary at k (adapted from the research of [9]).

$$X_7=\frac{{\sum }_{i=1}^n{NDMI}_i{A}_{ik}}{A_k}$$

(8)

where $X_7$ is the average surface moisture index in any sub-basin used to analyze the suitability of host media from subsurface embedding in the sub-basin. ${NDMI}_i$ is any grid surface moisture value. $A_{ik}$ is the total area of surface moisture at i, that is, within the sub-basin boundary at k (adapted from the research of [18]). Waterbody distribution: Water availability boosts the variety of species and natural resources, which helps extract the location of areas where surface moisture can be maintained, which are clearly separated from the dry soil surface, using the NDMI to emphasize this chosen satellite picture. NDMI ranges from −1 to 1, with water bodies usually having NDMI values greater than 0.4. In the distribution classification of water bodies, NDMI values were divided into five groups, with the higher values indicating the high likelihood of intermediary host habitat. The following equation was used to determine the NDMI of the study area using

$$NDMI=\frac{GREEN-SWIR}{NGREEN-SWIR}$$

(9)

$$X_8=\frac{{\sum }_{i=1}^n{NDVI}_i{A}_{ik}}{A_k}$$

(10)

where $X_8$ is the average vegetation index in any sub-basin used to analyze the suitability of the medium host from subsurface embedding to sub-basin. ${NDVI}_i$ is any grid-normalized difference vegetation index. $A_{ik}$ is the total area of the vegetation index at i within the sub-basin boundary at k (adapted from the research of [18]).

A total of 12 sets of satellite images were downloaded from Sentinel-2. The following equation was used to determine the NDVI:

$$NDVI=\frac{NIR-RED}{NIR+RED}$$

(11)

For Sentinel-2, NIR represents the near-infrared Band 8 (0.842–0.865 µm) and RED the corresponding Band 4 (0.665–0.704 µm). NDVI values are straightforward visual indicators that may be used to examine remotely-sensed data and determine whether there is living, green vegetation present [12]. The NDVI ranges from −1.0 to +1.0, a positive value indicating dense and healthy vegetation. The research identified five unique vegetation distribution groups based on NDVI values, with greater values indicating a region with a suitable potential of host intermediaries.

$$X_9=\frac{{\sum }_{i=1}^n{SAVI}_i{A}_{ik}}{A_k}$$

(12)

where $X_9$ is the vegetation index for adjusting the average soil in any sub-basin to analyze the suitability of the medium host from subsurface embedding in the sub-basin. ${SAVI}_i$ is the i-th grid soil adjusted vegetation index value. $A_{ik}$ is the total area of the soil-adjusted vegetation index at i within the sub-basin boundary at k (adapted from the research of [19]). The soil-adjusted vegetation index (SAVI) is the vegetation index created for the calculation of vegetation in the study area with relatively low vegetation content and has a similar calculation formula to NDVI, but a constant value (0.5) was provided for the Sentinel-2 image to reduce the influence of reflection from the lower ground soil of vegetation.

$$SAVI=\frac{NIR-RED}{NIR+RED+0.5}\times (1+0.5)$$

(13)

2.3. Data Preparation for OLS and FCR Models

Starting with the process of data modification indicated in Figure 4 and

Table 2. The percentage of liver fluke infections, and the mean of independent variables used to model spatial correlation analysis with OLS models.

Sub-Basin	Y (% of OV)	X1 (lu)	X2 (soil)	X3 (road)	X4 (water)	X5 (stream)	X6 (temp)	X7 (ndmi)	X8 (ndvi)	X9 (savi)
Jomjaeng	2.01	14.773	9.144	14.755	7.361	14.293	5.966	−0.064	0.075	0.143
Poopim	1.05	49.947	33.838	47.748	29.494	43.984	7.954	−0.060	0.115	0.218
Phonnoi	7.84	17.688	6.252	15.376	6.922	13.931	7.925	−0.083	0.118	0.225
Phonkaeyai	0.84	14.279	11.576	14.489	6.149	15.661	8.210	−0.081	0.124	0.237
Wanplachuem-1	9.18	20.042	8.565	19.993	5.129	7.122	8.241	0.152	0.119	0.224
Wanplachuem-2	6.48	60.884	24.128	64.132	14.349	61.311	7.593	−0.037	0.104	0.199
Klangmai	4.38	37.048	24.577	37.011	5.862	32.838	7.677	0.042	0.117	0.227
Nakaew	2.52	60.758	29.858	74.811	40.229	59.603	7.740	−0.035	0.116	0.224
Nongphue	1.95	80.795	34.581	90.847	18.963	79.482	7.909	−0.049	0.119	0.227
Maikrabok	3.66	5.235	19.740	4.753	15.510	7.539	7.920	−0.050	0.121	0.232

, the result of this procedure is to import satellite image data and standardize the data into a format that can be compared with a mathematical model. The DEM data are then fine-tuned to different heights to build a water flow line, and the final data are case statistics, which are point data of infected villages utilized to create a raster data layer using the heatmap technique.

Table 2 shows the index of the nine stationary independent variable subbasins, which is computed from Figure 4 Substep 2. The findings of utilizing OLS models for independent variable analysis to determine the consistency of each aspect associated with infection were chosen and incorporated to the FCR model. Each fishing port’s point data, representing each sub-basin, are displayed, along with the average value of each factor.

In addition to using correlation analysis to choose variables, the Pareto plot method is also used. The correlation results demonstrated from the Pareto plot can show different correlation values and can observe preliminary correlation trends. The variable factor based on the average of infection percentages showed that the area with the average infection rate Y (% of OV) differed from the other basin areas for as many as five basins by observing the curve intersecting the y-axis at 80%, namely Maikrabok, Klangmai, Wanplachuem-1 and 2, and Phonnoi, respectively, for the mean difference, as shown in Figure 5a. The Pareto graphs showing correlation screening over a similar number of river basins include the X₁, X₂, X₃, X₄, and X₅ variable analysis graphs that have similar trend curves, and we culled the river basins that found significant correlations in the range of five to six river basins, as shown in Figure 5b–h.

The Pareto graph of the correlation analysis of the factors calculated from most remote-sensing indices can screen areas on a scale of two to three watersheds, and this still has a significant correlation for the index mean, with the highest screenable factors being X₅, X₆, X₈, and X₇, respectively, as shown in Figure 5g–j. However, this correlation analysis shows that in many sub-basins, each factor has shown a significant correlation, which makes it possible to formulate a hypothesis that each factor can be modeled in the analysis of those coefficients related to infection. This analysis is based on the average of factors divided by the watershed, resulting in large-scale analysis, but the infection-prediction targets focus on predicting the location of risk areas, so the number of independent variables and the maximum associations associated with infection must be considered for further introduction into machine learning using FCR.

2.4. Forest-Based Classification and Regression (Analysis at the Location Level of Infected Water Bodies)

• Definition of the FCR for liver fluke (Opisthorchis viverrini) infection prediction

The principle of the random forest is to create several models from a decision tree (from 10 models to more than 1000 models), with each model receiving a different dataset, which is a subset of all datasets. When making a prediction, let each decision tree make a prediction of the dataset and calculate the prediction result by voting an output that is most selected by the decision tree (in the case of classification) or finding the mean value from the output of each decision tree (in the case of regression). The forest-based classification and regression (FCR) tool trains a model based on known values (infected OV points) provided as part of a training dataset. This prediction model can then be used to predict unknown values in a prediction dataset that has the same associated independent variables. The tool creates models and generates predictions using an adaptation of Leo Breiman’s random forest algorithm [82], which is a supervised machine-learning method.

• Description of the pre-processing

Each decision tree model in the random forest is considered a weak learner, meaning it is estimated that it is not a very good model, but when each decision tree is used to make predictions together, the user will obtain a total model that is more competent and accurate than the decision tree that makes a single prediction. The process of connecting OLS and machine learning is shown in Figure 6.

• Dimension of the dataset

The location of the water bodies where the fish infected with liver flukes were found was used as a set of points for machine learning, which is the boundary location of the banks of the water bodies. This section presents the experimental results of the FCR model used to predict spatial fluke infection. Sensitivity mapping, as previously stated, was used to train and test the ability to predict the original model. The datasets were randomly divided into training (60%) and testing (40%) sets.

• Processor for feature selection

In all datasets, training and testing were carried out. The number of survey points where parasites were detected was 35–21 modeling points and 14 testing points, respectively—as shown in Figure 7. In addition, to reduce the bias caused by sampling in the data-sampling process, repeated sampling was performed over 100 runs, which is the standard value of the FCR model of ArcGIS pro, including the learning setting: number of trees = 100, leaf size = 5, and tree depth range = 1–5.

• Description of the different modeling tested and rationale behind the model construction

The experimental results of the explanatory variable range diagnostics FCR model are reported in

Table 3. The explanatory variable range diagnostics.

Explanatory Variable Range Diagnostics	Training		Testing		Share
	Minimum	Maximum	Minimum	Maximum	Training a	Testing b
Model 1 distance to stream lines	0.48	1055.51	133.04	610.29	1	0.45 *
Model 2 distance to stream lines	0.48	1055.51	594.64	610.29	1	0.01 *
distance to water resource	108.65	6054.45	970.21	1604.04	1	0.11 *
Model 3 distance to stream lines	0.48	1055.51	195.81	527.24	1	0.31 *
distance to water resource	108.65	6054.45	1319.44	1756.75	1	0.07 *
NDMI	−0.13	0.14	0.04	0.1	1	0.20 *
Model 4 distance to stream lines	0.48	928.08	610.29	1055.51	0.88 *	0.34 *
distance to water resource	108.65	6054.45	1243.77	1604.04	1	0.06 *
NDMI	−0.13	0.1	0.07	0.14	0.85 *	0.10 *
NDVI	0.05	0.16	0.17	0.18	0.82 *	0.00 *

(a) % of overlap between the ranges of the training data and the input explanatory variable. (b) % of overlap between the ranges of the testing data and the training data. * Data ranges do not coincide. Training or testing is occurring with incomplete data. Ranges of the training data and prediction data do not coincide, and the tool is attempting to extrapolate.

. Forecasting model integration uses a boosting method, with the principle that multiple data classification models are created. Each model uses the same set of training data to build it, each of which has an additional weighted value. Weighted voting methods were used, and new data groups were assigned with the highest number of votes (majority voting), which, in this study, used two methods: average and weighted.

• Validation protocol to analyze FCR models’ performance

Machine-learning-based FCR simulation was integrated into four models, which describe the synthesis of the ranges of independent variables. We found that the degree of overlap between the range of training data and the input explanatory variables of Model 1 has a share value of 1 and a test value of 0.45. The percentage of overlap between the range of monitoring data and training data ranges from 0.00 to 0.45. These data show that the location of the learning point can be the test point for the accuracy of the FCR model. Model 1 uses independent variables as the distance to the stream lines, Model 2 uses independent variables as the distance to the stream lines and the distance to the water bodies, Model 3 uses independent variables as the distance to the stream lines and the distance to water bodies, as well as NDMI, and Model 4 uses independent variables as the distance to the stream lines and the distance to the water bodies, as well as NDMI and NDVI, respectively, which are used to simulate the spatial distribution of the infection. The training range of Model 1 ranges from 0.48 m to 1055.51 m, and the testing ranges from 133.04 m to 610.29 m. The training share value can be used in all the same ways as in the examples of Model 2 and Model 3, whereas Model 4 has only a secondary factor that can use overlapping learning points.

3. Results

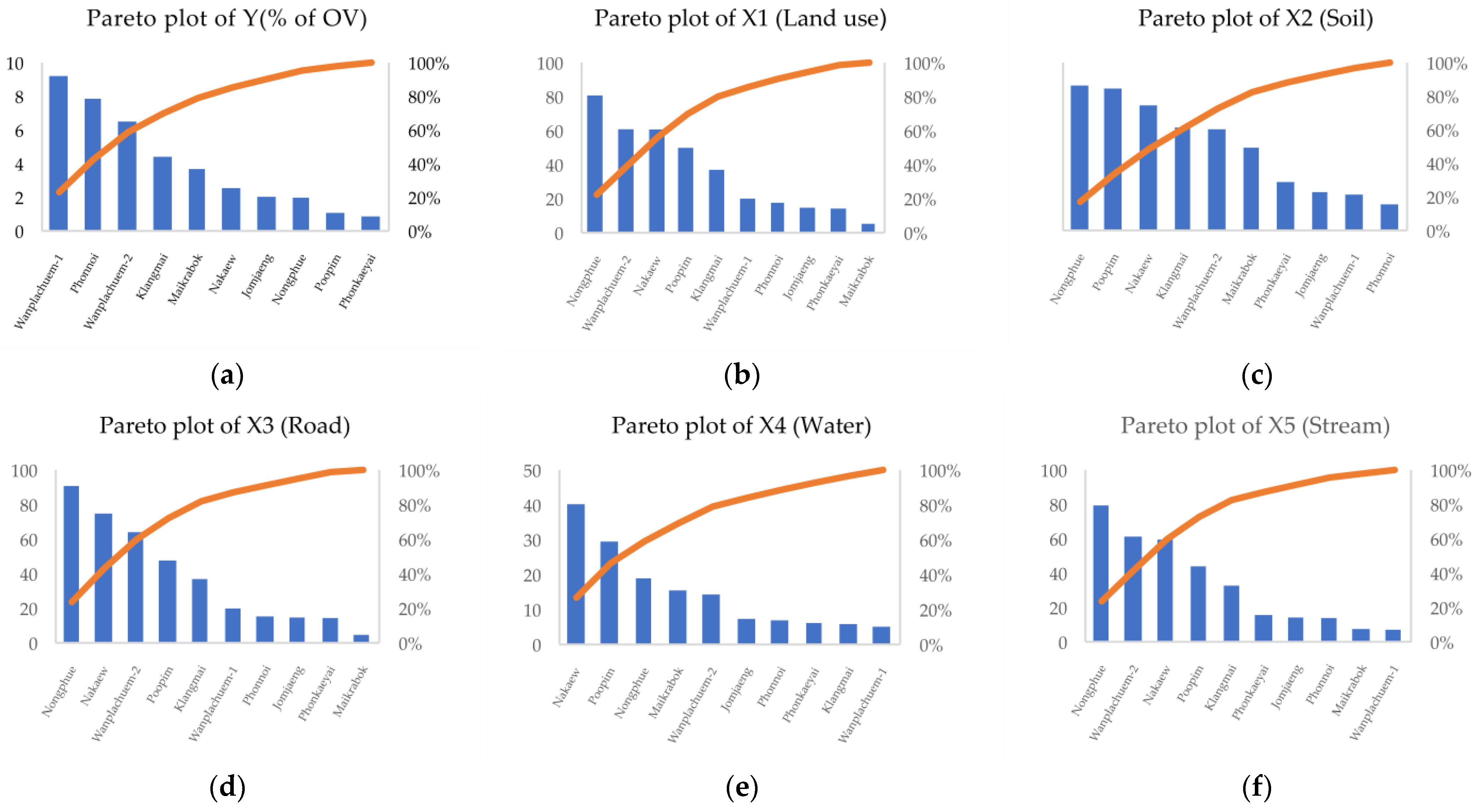
3.1. Factor Selected for OLS with Liver Fluke Infection (Watershed Level)

Comparing multiple alternative models increases the chance of selecting the most suitable model for predictions [83,84]. Spatial factor correlation simulation involves the use of an independent group of variables as an alternative to OLS modeling to visualize the trends of tolerances at the small area unit level. The set of independent variables imported into the models was selected using correlation analysis, and the variables X₅ to X₉ were selected, simulated, and displayed, as shown in

Table 4. The OLS alternative modeling results.

Alternative OLS Models for OV-Predicted at the Watershed Level	Independent Variables	Coefficients	t-Stat	p-Value a	R2
Y (%OV1)	Intercept	0.465	4.373 ***	0.000 ***	0.524
	X8 (ndvi)	−1.534	−0.878 n/s	0.226 n/s
	X9 (savi)	−6.032	−2.212 n/s	0.125 n/s
Y (%OV2)	Intercept	4.528	1.975 ***	0.000 ***	0.672
	X7 (ndmi)	1.125	0.769 ***	0.044 ***
	X8 (ndvi)	−3.116	−0.890 ***	0.023 ***
	X9 (savi)	−9.852	−2.326 n/s	3.024 n/s
Y (%OV3)	Intercept	62.042	3.031 ***	0.000 ***	0.713
	X5 (stream)	−5.047	−2.068 ***	0.048 ***
	X7 (ndmi)	4.246	1.875 ***	0.034 ***
	X8 (ndvi)	−9.874	−2.661 ***	0.021 ***
Y (%OV4)	Intercept	57.410	0.979 ***	0.000 ***	0.681
	X5 (stream)	−0.0350	−3.462 ***	0.031 ***
	X6 (temp)	20.210	0.734 n/s	1.263 n/s
	X7 (ndmi)	7.220	0.540 ***	0.044 ***
	X8 (ndvi)	−1524.360	−0.548 ***	0.026 ***
	X9 (savi)	−2732.160	−2.356 n/s	0.895 n/s

*** = significant at 5% level. n/s = not significant.

. An appropriate OLS model to predict the percentage of infected people can be observed from the analysis results; R² is high. The variable is significant at a high level (i.e., the t statistics are very high or the p value is very low) [84,85]. The results of the models in the table show a comparison of the precision between the four models to visualize the difference in their accuracies [86].

An alternative model is proposed based on the observations of high values of R² and the acceptance or rejection of independent variables, as can be observed from the t statistics and p value. The alternative model proposes four alternative models: Y (%OV1), Y (%OV2), Y (%OV3), and Y (%OV4), as shown in Table 4. The OLS Model 1 Y (%OV1) imported two independent variables, X_8ndvi and X_9savi, to test whether they were expected to be negative per percentage of infected people. The results of spatial nonstationarity [18,20] and the R² values were compared to the OLS models. The model shows negative coefficients at the scales of −1.534 and −6.032, respectively, t statistic values of −0.878 and −2.212, and p values of 0.226 and 0.125, indicating that both factors have not yet correlated significantly with the percentage of infected people. Additionally, the model displays an R² value for the OLS model that is higher than 0.524. Both factors show an acceptable level of relationship with R² and, therefore, need to be tested in the second alternative model.

The second OLS model, Y (%OV2), shows the correlation coefficient of the factor X₇ (ndmi) positively, but the X₈ (ndvi) and X₉ (savi) factors begin to show negative results, indicating that the more areas of separation between vegetation cover, the lower the percentage of infected people. The X₉ (savi) factor showed statistical significance with a t statistic (−2.326) that was greater than the other two factors and a p value (0.038) of less than 0.05, which made it possible to find a tendency for the mid-range and less-than-peak soil correction index factors to increase the chance of a percentage of people infected with liver fluke. Alternative Models 3 and 4 incorporated the X₅ (stream) factor, resulting in an increase in R² accuracy to 0.713 and 0.681. The coefficients of X₅ (stream), X₇ (ndmi), and X₈ (ndvi) reveal a t statistic and p value that are more significant than other variables and show a negative trend together. An optimal OLS model for predicting the case percentage was Model 3 Y (%OV3) because it could provide a confidence level greater than 71.3%, and there were still not too many independent variables that could cause the prediction results to be inaccurate. Even if Model 4 Y (%OV4) has a higher R² value than Model 1 Y (%OV1) and Model 2 Y (%OV2), it may cause duplication of the independent variable set and coincidence, resulting in a higher R² trade.

The standard residual index (SR) was used to determine the prediction accuracy of a model [87] (as an index used to verify the accuracy of a model) by displaying the standard value in intervals of 0.5 [20,25], as shown in Figure 8. Sub-basin units with SR values ranging from −0.5 to 0.5 are sub-basin areas where the OLS models can predict accurately and have lower tolerances than other areas. The sub-basins Maikrabok, Nongphue, Nakaew, and Klangmai, which show a range of −0.5 to 0.5, are shown in yellow in OLS Model 3 and have a tolerance of three units lower than the OLS models. This is also confirmed by the SR results obtained from OLS Model 3 Y (%OV3). Regarding the testing of alternative models to exclude highly correlated independent variables to reduce model collinearity in practice, the use of surface temperature factors to analyze trends in liver fluke increases in small river basins may be difficult due to frequent changes in the floodplain areas, which may be unstable compared to other factors over a 3-year data period. Therefore, the best model created is an independent, selective factor agent that is further applied to predict the likelihood of liver fluke infection, where representatives of those factors that are highly correlated to surface temperature are X₇ (ndmi) and X₈ (ndvi) and a group of X₅ (stream) factors and surface water bodies are used in the FCR model to predict infection areas along the waterways that connect to the sub-basin.

3.2. Mapping the Spatial OV Infection (Y, Dependent Variable)

Spatial subspace unit boundaries need to be created to define the amount of data. In this study, by using digital elevation model (DEM) data with a cell size of 12.5 m to generate the sub-basin layer data, the results of the analysis were obtained from 10 sub-basin boundaries (sub-basins distributed according to the flow sequence level (3 to 6) from upstream to downstream at the marshes, as shown in Figure 9) and other descriptive information of the sub-basin, such as its size. The DEM dataset was readjusted for spatial height using the fill and sink function, which is a hydrological analysis method that uses GIS processes to process the altitude data as realistically as possible and enable continuous water flow analysis.

The highest spatial height mean was 180 m at the river basin named Wanplachuem-1, followed by the Wanplachuem-2 and Phonkaeyai basins. They have values of 174 and 172 m, respectively, with the upper basin of the Phon Na Kaeo district considered to have this height. However, even though it is in the upper basin, there is a high percentage of people infected with OV in these areas. Due to the multiple seasons, flooding causes surface water to flood up to the upper basin, making it possible for intermediate host mollusks and carp groups to move and feed in these areas.

The Jomjaeng, Poopim, and Phonnoi basins have a risk of infection that is greater than 6.48% due to the low altitude of the area, allowing water to flood large areas of these basins during the rainy season and increase the chances of central host habitat. The case percentage data shown as points are converted into raster data with a heat map command to use these raster data to find the average of the percentage infected and link it with other independent variable data using raster images, as shown in Figure 10. The display of the case percentage data shows the continuity of the number of infected people so that the average calculation is equal for all sub-basins, but it will vary depending on the large and small values of the points used to calculate the raster. In this case, the Z value is the percentage of infected people in the village position. The radius used to create a raster map using a heatmap covers from 2 km to 4 km so that the raster data can be connected to all subtleties. The green areas show sparse percentages of infected people, and the red areas show higher density and a high chance of encountering infected people. The OLS model requires a continuity value of raster data, where the creation of the heatmaps of infected people enables consistent analysis in terms of positional data and the other rasters of the independent variables, which can generate trend graphs.

3.3. Mapping of the Independent Variables

The values of the indexes of the nine independent variables used to create mathematical models from Equations (1)–(9) are shown as descriptive data values, as shown in the results of the analysis in Figure 11a–i. An important step in the GIS process is used in the creation of multi-rasters and vectors, and all methods of spatial data interpolation were used in the preparation of independent variable sets. The percentage of cases was very high in the Wanplachuem-1, Phonnoi, and Wanplachuem-2 sub-basins, with values of 9.18, 7.84, and 6.489, respectively. The areas of the three watersheds are adjacent to each other and are connected by an outlet. When observing almost all the values of the index, it was found that the value of the Wanplachuem-2 basin was more valuable than other basins due to the size of the denominator, which is a smaller area than in the other basins. The spatial units of the sub-basin with similar index values for the X₁ index for Jomjaeng, Phonnoi, and Phonkaeyai are 14.7, 17.6, and 14.2, respectively. The island values of X₂ for Wanplachuem-2, Klangmai, and Nakaew are 24.1, 24.5, and 29.8, respectively. The island groups of X₃, X₄, and X₅ are in the same basins: Jomjaeng, Phonnoi, Phonkaeyai, and Wanplachuem-1. The groups of remote-sensing indices are not much different, but they need to be analyzed together with other factors in OLS modeling and screened for the duplication of factors again using correlation analysis. Different groups of factor index values require data standardization using mathematical models. Standardizing data to a comparable range allows OLS models to increase the accuracy (of build-and-fit models) better than using raw data directly to import models.

The results of the raster map data of the X₁ variant were distributed within a buffer distance of up to 500 m, distributed over most of the areas of all sub-basins, and the results were similar to the X₃ index values, but there was a difference in the upper basin areas with low index values due to the lack of road networks. The X₄ and X₅ index map values showed high scores scattered mainly in the lower basin and low values scattered in the upper areas because the lower ones are close to large freshwater marshes. The X₆ index mainly shows the distribution of the intermediate index on the map; Figure 11f shows, in yellow, a flat surface temperature in the range of 26–28 degrees Celsius, whereas the high-temperature areas are shown in red and are mostly structures such as road and village structures. The X₇ index shows the distribution of high-level indices that are suitable habitat substrate host areas, which are mainly areas near water bodies with index values greater than 0.6 or more. The X₈ and X₉ indices are similarly distributed because they are made up of the vegetation index, but the X₉ index adds a constant value to make the vegetation value more reflective, both of which can be used interchangeably. To ensure accurate modeling, consistent results can be observed from the correlation, and the red area of both indices indicates that they are suitable areas that are similar to the X₇ index.

3.4. Spatial Prediction of OV-Infection Using Forest-Based Classification and Regression (FCR) (Location Level)

The FCR model in this study provides a method that makes decisions for each model independent of each other by using the same algorithm but allows each instance to learn from different payloads using random selection. This mechanism was called bagging and pasting; the difference is that bagging can randomly select the same item, but pasting does not allow duplicates to be randomized at all. This results in more stable models and is often more accurate than pasting.

The model for out-of-bag errors is shown in

Table 5. The model out-of-bag errors.

Model Out-of-Bag Errors	Model 1		Model 2		Model 3		Model 4
Number of Trees	50	100	50	100	50	100	50	100
MSE	7.167	6.985	7.298	7.074	9.075	8.93	10.203	8.98
% of variation explained	−3.432	−1.358	−5.511	−2.267	−33.117	−31.003	−46.689	−29.111

. The set of independent variables that were introduced to FCR’s machine learning was used in all four factors based on the selection results of the OLS model, with the highest R² value being 0.713: distance to streams, distance to water bodies, NDMI, and NDVI. The distance factor from the water resource was also included in the simulation because the importance of similar factors of the water source was known. The results showed that the number of cycles increased from 50 to 100, and the number of trees in all MSE tests showed a decrease in every set of independent variables for the distance to streams factor from 10.203 to 8.98, which equates to the addition of a set of four independent variables, with the percentage of variation explaining between −46.689 and −29.111. When considering the importance of each variable, it was found that the order of weight values for distance to water, distance to stream lines, NDVI, and NDMI showed an importance of 23.18, 39.7, 20.32, and 22.79%, or 37, 22, 22, and 19%, respectively, as shown in

Table 6. The top variable in terms of importance.

Top Variable Importance	Model 1		Model 2		Model 3		Model 4
Variables	Importance	%	Importance	%	Importance	%	Importance	%
Distance to stream lines	105.09	100	52.72	47	34.91	37	23.18	22
Distance to water resource			58.75	53	32.32	34	39.7	37
NDMI					27.89	29	20.32	19
NDVI							22.79	22

. The four predictive simulations were created to confirm that the distance to the water resource variable affects the percentage of infection in every test. When analyzed individually, it was found that the distance to water resource factor, when analyzed with NDMI, yielded a slightly higher R² value of 0.859 and a decrease of 0.849 when used in combination with both NDMI and NDVI. Therefore, for the alternative models, when imported, only the distance to water resources and distance to stream lines, which are slightly less important, can make the FCR model predict that being closer to a water source will have a greater impact on the chance of finding fish infected with liver flukes than fish found at distances beyond the edge of the bank.

3.5. Spatial Prediction of OV-Infected

When only one independent factor with a high priority weight for the distance to stream lines was imported, the results of the machine-learning dataset and regression synthesis had an R² value of 0.775, and when the other three factors were imported, the R² values were 0.853, 0.859, and 0.849, respectively, as shown in

Table 7. The training data: regression diagnostics.

Training Data: Regression Diagnostics	Model 1	Model 2	Model 3	Model 4
R-Squared	0.775	0.853	0.859	0.849
p value	0	0	0	0
Standard Error	0.053	0.06	0.043	0.051

Predictions for the data used to train the model compared to the observed categories for those features.

. The standard error of Model 3 is the lowest at 0.043, and the highest is for Model 2, but these are not considered to be significantly far apart. When observing the preliminary statistics, it is evident that there is no difference between Model 2 and Model 4, but from the observation of Model 1, only one variable of learning is imported, but this also provides a satisfactory level of accuracy, indicating that the distance to stream lines affects machine learning.

Therefore, it was necessary to show all four models to see the trends of the changes in the percentage of liver fluke infection. This was used to provide spatial confirmation of how the location of infection risk in all four models can confirm location and severity. The location used to predict infection is a point simulation based on the location of the fishing area of the villagers who regularly use it, which was obtained from the inquiry. These locations are linked to the spatial resolution data of the 10 m point Sentinel-2 satellite imagery.

The receiver operating characteristic (ROC) curve is a popular method that is used to measure the accuracy of forecasts. The ROC curve is a graph with a correlation between the y-axis (instead of sensitivity (true positive rate)) and the x-axis (instead of 1-specificity (false positive rate)), as shown in Figure 12. As shown in Figure 12a–e or in the area under the ROC curve, the ROC curve indicates the validity or reliability of the prediction model; the prediction model that has the most space below the AUC (ROC curve) is considered the most effective.

The results of Model 1 and Model 2 for FCR using resampling techniques could accurately predict the percentage of infected fish in an accuracy range of 0.775 to 0.859, as shown in Table 6. Figure 12a,b display the ROC, which is a popular method used to measure the accuracy performance of forecasts. For FCR, Model 1 and Model 2 could predict the severity of the percentage of infected fish, with an area value under the ROC curve of 0.964; both models had the highest area value under the ROC curve of all the prediction models. A false positive rate below 10% and a true positive rate above 90% also use a smaller number of model coaching data. This makes the training time shorter for the models to predict the severity of the percentage of infected fish but does not affect the space under the graph. The ROC curve of Model 3 and Model 4 is also very high, and these models could be used for prediction as well.

The FCR simulation results of each model are shown in Figure 12, with Figure 12a showing the simulation of the chance of infection of Model 1, which ranges from 2.027 to 6.222. The range with the highest percentage of infections ranges from more than 5%, with 10 points showing the distribution in the sub-basins of Phonnoi, Nakaew, Maikrabok, Nongphue, Phonkaeyai, Wanplachuem-1, and Wanplachuem-2, which are found to have one point each. The Model 2 estimates show that the highest-risk locations have been reduced to a high-risk level of infection, with 10 points reduced to 3 points, and 3 points with high-risk levels are shown as orange dots, with the top 2 sub-basins still experiencing the highest risk of infection: Phonnoi and Maikrabok, respectively, as shown in Figure 12b. The predictions by Model 3 and Model 4 were similar in terms of the order of the same three highest-infection-risk locations and the same sub-basins, Phonnoi and Maikrabok, as shown in Figure 12c and Figure 12d, respectively. However, the results of both models are noteworthy in that the number of high-risk positions is second to the highest level, which is 8 and 11 points. The predictive results of both models make it necessary to watch for orange dots that have a chance of developing into red dots, although both models require more than one independent variable, but infection development opportunities can be seen from such simulations. Based on the predictions of the four models, it is evident that the location showing a moderate risk level in the range of 3.001 to 4.000 was the location with the largest number of distribution points, indicating that all sub-basins are at risk of infection. The length of the stream line connecting the large marsh can flow for more than 60 km. This shows the locations along the sub-river as the points used to simulate the model’s risk level of 2% or more, and the model also shows the highest risk locations displayed at the adjacent and shared boundaries of the sub-basin.

The final forecast was a positional simulation of villagers’ fishing sites along the tributary streams that flow into the sub-basin within the boundaries of the district. The total number of positions used to simulate the forecast was 103 points, as shown in Figure 13a–d. It was a location used by locals and fishermen in the area to go fishing for consumption. These positions, obtained through field inquiries and inspections, were located within 30 m of the stream line layers and water bodies.

4. Discussion

4.1. Redundancy of Independent Variable Sets Associated with Spatial Liver Infection

The groups of vector-type independent variables from X₃ (road), X₄ (water), and X₅ (stream) were duplicated from the analysis (buffer distance) and were subsequently converted into raster data. The data sources may be different, both vector and raster, but once the data layer has undergone manipulation, it is converted into a raster format so that all can be compared. This approach to analyzing this group of data measures the distance away from the vector data, and this was then generated using the Euclidean distance function to determine the score range according to the distance of infection risk, making this set of variables redundant. Before applying the three independent variables to the model, only the representative factor X₅ (stream) must be selected, but this is different from the X₁ (land use) and X₂ (soil) sets, which were different types of datasets that determined the scoring values of each type differently according to the relationship to infection. The raster variable set created from satellite imagery indices is also redundant in some indices, such as the X₆ (temp), X₈ (ndvi), and X₉ (savi) variables. When the model is imported, it does not increase accuracy, and when observed using correlation, it is automatically correlated, whereas the X₇ (ndmi) factor can also create a trend for the model. The best modeling result is, therefore, the use of independent variables consisting of X₅ (stream), X₇ (ndmi), and X₉ (savi). Although the results were lower than the bulk inputs in Model 4, the results of the R², t statistic, and p value statistics were sufficient to confirm the selection of the models and an appropriate set of independent variables to predict liver fluke cases in small basin systems. Mathematical modeling to adapt independent variable data into measurable standards is very important in creating OLS models, which are models that provide precision results based on the division of unit areas to suit the distribution of dependent variables.

Independent variable redundancy needs to be reduced in the number of variables so that OLS models can still create models that maintain R² values at acceptable levels [88]. Spatial correlation analysis was the method used to screen for independent variables [89] in this study. The group of independent variables are classified into two groups: those variables generated from vector data, solving factors X₁ to X₅, which are characterized by points, polylines, and polygons. Importing this type of data, which are analyzed together with other variables, does not require first generating raster data and assigning score values to different data ranges to measurable standards. Factors X₆ to X₉ are already raster data, but they were calculated in the form of mathematical models to standardize the data so that they could be correlated with the previous set of variables.

Table 8. The correlation between the independent variables (X₁ to X₉) and dependent variables (OV-infection percentages) for the analysis of OLS-modelled variable groups.

	Y (% of OV)	X1 (Lu)	X2 (Soil)	X3 (Road)	X4 (Water)	X5 (Stream)	X6 (Temp)	X7 (Ndmi)	X8 (Ndvi)	X9 (Savi)
Y (% of OV)	1.000	-	-	-	-	-	-	-	-	-
X1	−0.167	1.000		-	-	-	-	-	-	-
X2	−0.437	0.826	1.000	-	-	-	-	-	-	-
X3	−0.189	0.992	0.813	1.000	-	-	-	-	-	-
X4	−0.402	0.599	0.739	0.635	1.000	-	-	-	-	-
X5	−0.226	0.985	0.838	0.984	0.612	1.000	-	-	-	-
X6	0.173	0.116	0.184	0.106	0.109	0.067	1.000	-	-	-
X7	0.395	0.060	−0.143	−0.061	−0.258	−0.193	0.243	1.000	-	-
X8	0.082	0.092	0.227	0.095	0.134	0.062	0.969	0.171	1.000	-
X9	0.079	0.097	0.242	0.103	0.144	0.074	0.950	0.150	0.997	1.000

shows that factors X₃ to X₅ are negatively correlated with the percentage of people infected with OV, which suggests that the further the distance away from that set of factors, the lower the likelihood of catching fish infected with flukes; however, on the contrary, the closer the distance, the greater the risk of infection if the fish are consumed in a radius near water bodies. Factors X₁ and X₂ show that the poorer the drainage, the greater the risk of infection, because the soil can retain moisture better than well-drained soil, and the more agricultural land used near irrigation canals, the more moisture the soil surface has to use when compared to other types of land. When analyzing the correlation of vector factors, the factor X₅ can represent the factors X₁ to X₄ because it correlates with the percentage of infected people −0.226. Factors X₁ to X₄ were 0.985, 0.838, 0.984, and 0.612, respectively.

In addition to screening the variables that were used to create the OLS model, namely the set of independent variables X₅ to X₉, this set of variables was used to create correlation graphs to analyze the regression of the model. To determine the properties of the regression patterns, two methods of residual plot graph analysis were used. The first is residual plots, which are plots of the values. Residuals are estimates of Y (% of OV)-fitted values and should be randomly distributed when observations occur. The second method is to plot the normal probability plots of the error coupled with the expected value. If the plot is shaped close to a straight line, the discrepancy has a normal distribution. The X₅ variable set demonstrates the normal distribution of data compared to the variables according to the section. Variables X₆ to X₉ have a vertical distribution in the dataset, which translates into a narrow range of index values that can predict the percentage of infections over a wide range, as shown in Figure 14.

4.2. Limitations of Spatial OLS Model

The OLS model uses the Gaussian model, which uses the method of determining the boundary distance from the location where an infected person is found. This generates raster data and can be used to analyze trends in data changes, which provides a way to increase the number of cells in the data and can be used to graph the trend of independent variables more efficiently than other models [82,83]. Ensuring the continuity of the surface of the data is an advantage of the OLS model’s optimization approach. In addition, the model screens independent variables that significantly correlate fluke infection with the t statistic and p value indices to make the model compact. This can control the number of factors and reduce redundancy. A major limitation of OLS is that it exaggerates positive and negative predictions, making predictions impossible to implement. A large number of units of space contributes to the accuracy of the model, with the general specification of 12 units, and the more detailed the quality of the raster data, the greater the number of samples, but also the more time it takes to process results. Data quality enhancement must begin with the resolution of DEM data so that the number and boundaries of sub-basins can be simulated corresponding to the actual flow. A limitation of OLS models is that independent variable datasets must be created within the boundaries of appropriate spatial unit areas for independent variables to create trends that can predict dependent variables. When applying the OLS model to predicting the percentage of fluke infections in a small area, it is necessary to create spatial units from the actual correlation formed by an independent set of variables. In this study, the independent input of variables was recommended by the Sakon Nakhon Provincial Public Health Office, a local agency that has been studying liver fluke infection for a long time.

4.3. FCR Improvement Approach for Spatial Prediction

The FCR model used supervised learning in terms of the classification algorithm to model liver fluke infection risk prediction. However, practicing straightforward predictive models tends to bias predictive models due to the unbalanced nature of the data in the sense that the number of locations where infected fish were found and where infected fish were not found varied widely. For the number of infection locations, if unbalanced data are not properly managed, the model predicts most of the sample data and does not recognize the sample of minority data; that is, the model will likely choose to predict that the infection is not severe. The FCR model in this study was able to import the model (predicted as a non-binary data range) and used the capabilities of regression analysis to weigh the independent variables. Improving the capabilities of the FCR model can take a variety of practical approaches. The forest model should be trained using at least several hundred features for the best results, and it is not an appropriate tool for very small datasets. The tool may perform poorly when trying to predict using explanatory variables that are out of range of the explanatory variables used to train the model. Forest-based models do not extrapolate; they can only classify or predict according to the value range on which the model was trained. When predicting a value based on explanatory variables much higher or lower than the range of the original training dataset, the model will estimate the value to be around the highest or lowest value in the original dataset.

4.4. The Importance of the Single Variables to the Models

Subarea division can classify independent variable factors to reduce redundancy and increase heterogeneity by dividing them into sub-basins. It affects the division of the size and number of the boundaries, units, and areas. The origin of this analysis affects the overall accuracy of the OLS modeling sequence, which can help to reduce the number of independent variables, but the model is not suitable for predicting infected water sources due to the limitations that the results can be negative and exaggerated. The creation of factor data as raster data makes it possible to increase the number of samples by measuring the distance from the location infected with liver flukes, which is where fishermen often fish. However, the creation of independent variables based on narrative data converted from the experiences of residents and the knowledge of officials from public health authorities has made this a model study that can predict liver fluke infection in similar watersheds. The FCR model can predict the chance of liver fluke infection by using factors that are related to the chance of infection in the sub-basin. The FCR test approach, which shows variable importance, screens and selects distance variables from water sources as the most important factor in forecasting. Testing all four alternative models confirms that the factors involved are both NDMI and NDVI. Therefore, the FCR forecasting approach can predict the likelihood of infection by importing the relevant variables without using a large number of independent variables to provide accurate prediction results. Determining high AUC values is likely to indicate suitability to the training data. But considering the number of checkpoint leads, as well as the grid size of raster data, this also contributes to the accuracy of the model. In this study, a 10 m grid size was determined with 14 test points and 21 learning points when comparing the locations with a total of 35 case data. The smaller this grid size is, the greater the chance of a lower performance in the actual predictive scenario. The level of these AUCs is acceptable if the scope of the number of independent variables is not too large and the impact of each variable can be assessed. The risk of liver fluke infection in a small basin can be determined by using NDMI, NDVI, and the distance to water resources to develop models; however, for that hypothesis to hold true, the tiny basin needs to have a watershed outlet connected to a major body of water. Reducing the amount of soil cover that collects surface moisture around the borders of water bodies is necessary for practical control and a decrease in the risk of liver fluke infection, as it provides habitat for the host.

5. Conclusions

The conclusions of the research can be summarized as three approaches to proper spatial linear regression modeling to obtain independent variable factors related to infection. We considered spatial forecasting at the position level by using machine-learning-based FCR. Finally, the guidelines for local authorities for applying the results of the model can be summarized as follows:

• An OLS model was developed in this study to track liver fluke infection. This spatial statistical model is suitable for analysis at the local process level, and the results were compared to confirm that Model 3 was more accurate and more appropriate than Model 1, Model 2, and Model 4. However, to make full use of the model, the spatial unit data layer should first be designed to separate the variables accordingly and independently [90,91,92]. Often, OLS models provide low coefficients of decision because sub-area unit assignments are not suitable. In this study, OLS could be used as a prototype for a method for analyzing spatial relationships with liver fluke infections by creating sub-basin units with continuous, adjacent boundaries. Local fluke case data should be continuously collected so that a curve can be created between the percentage of infected people and an independent set of variables. The factors used in this study are only prototypes of OLS model testing; in more advanced studies, spatial survey factors such as soil moisture in the field where mollusks are found should be used. Mathematical modeling is used to adjust database measures so that they can be measured together as an alternative approach to optimizing the prediction of the model [22]. Finally, the results of this study can guide the creation of spatial models at the scale of small watersheds to track spatial infections of liver flukes in other areas with similar watershed characteristics.
• Improving prediction at the position level by using machine learning and the FCR method: in order to improve performance when extracting values from explanatory training rasters and calculate the distances by using explanatory training distance features, consider training the model on 100% of the data without excluding data for testing, and choose to create output trained features [27,44]. Although the default number of trees parameter value is 100, this number is not data-driven. The number of trees needed increases with the complexity of the relationships between the explanatory variables, the size of the dataset, and the variable used to predict, in addition to variations in these variables. Increase the number of trees in the forest value and keep track of the out-of-bags (OOBs) or classification errors [93]. It is recommended to increase the number of trees by least three times up to at least 500 trees to best evaluate model performance. Tool execution time is highly sensitive to the number of variables used per tree. Using a small number of variables per tree decreases the chances of overfitting [27]; however, be sure to use many trees if the model is using a small number of variables per tree to improve model performance. In order to create a model that does not change in every run, a seed can be set in the random number generator environment setting. There will still be randomness in the model, but that randomness will be consistent between runs.