A Motion-Based Conceptual Space Model to Support 3D Evacuation Simulation in Indoor Environments
Abstract
:1. Introduction
2. Related Works
2.1. Three-Dimensional Pedestrian Motions
2.2. Pedestrian Shapes in 3D Motions
2.3. Indoor Space Classification
3. Assumptions, Definitions and Specifications
3.1. Fundamental Assumptions
- We assume the standard shape and average size of a pedestrian. This study only considers an individual rather than a group of pedestrians. Also, we assume that a pedestrian carries no bag or luggage. Moreover, we exclude wheeled motions (e.g., wheelchairs, scooters, trolleys). The walking mode is most widely used in indoor spaces as a consensus in the evacuation domain to simulate pedestrian evacuation.
- Referential expressions from a first-person perspective are utilised to describe the placement of a pedestrian and a physical component, providing a nuanced understanding of placements in the context of 3D evacuation simulation. The vertical relations of above and below are primarily considered in the context of the simulation, with examples such as a pedestrian crawling below a computer desk and bent-over walking above a bed.
3.2. Three-Dimensional Pedestrian Motions
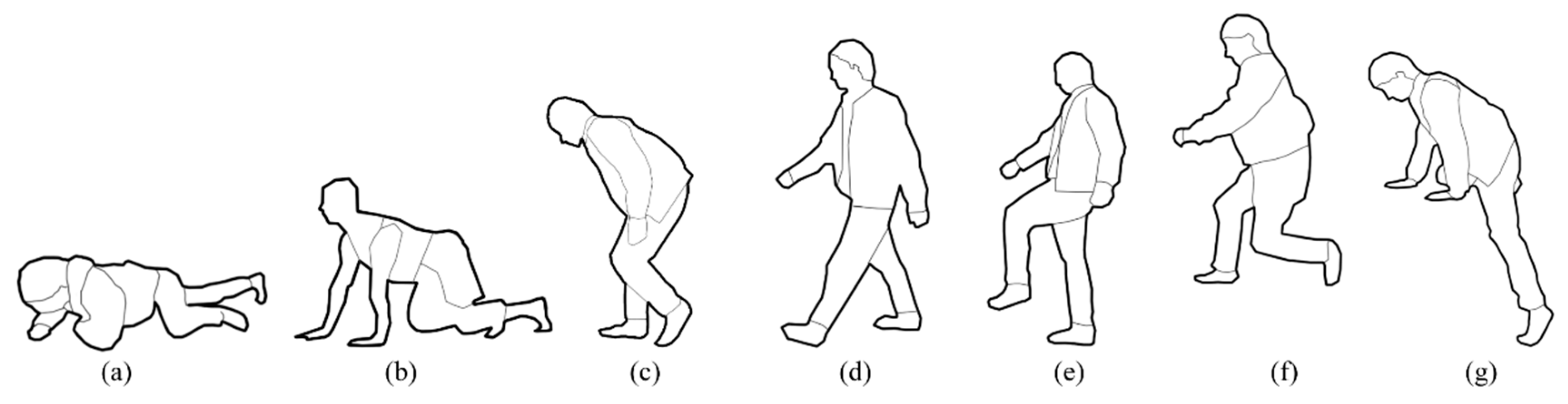
3.2.1. Definitions of 3D Pedestrian Motions
- Low crawling corresponds to dragging the body close to some physical components’ surfaces (e.g., floor slabs, desks, ramps) (see Figure 1a).
- Knee and hand crawling refers to moving forward using hands and knees (see Figure 1b).
- Bent-over walking is bending the body forward and downward, sometimes simultaneously bending the knees (see Figure 1c).
- Walking upright means moving in full size by lifting and setting down each foot in turn, without a need to have both feet off the ground at once (see Figure 1d).
- Stepping up/down refers to lifting and setting down one’s foot or one foot after the other to move up/down a higher or lower position, never having both feet off the ground at once (see Figure 1e).
- Jumping up/down is pushing oneself off a surface and having both feet into the air (see Figure 1f).
- Climbing up/down is moving to a higher or lower position with effort, typically using both hands and feet (see Figure 1g).
3.2.2. Parameterisation of 3D Pedestrian Motions
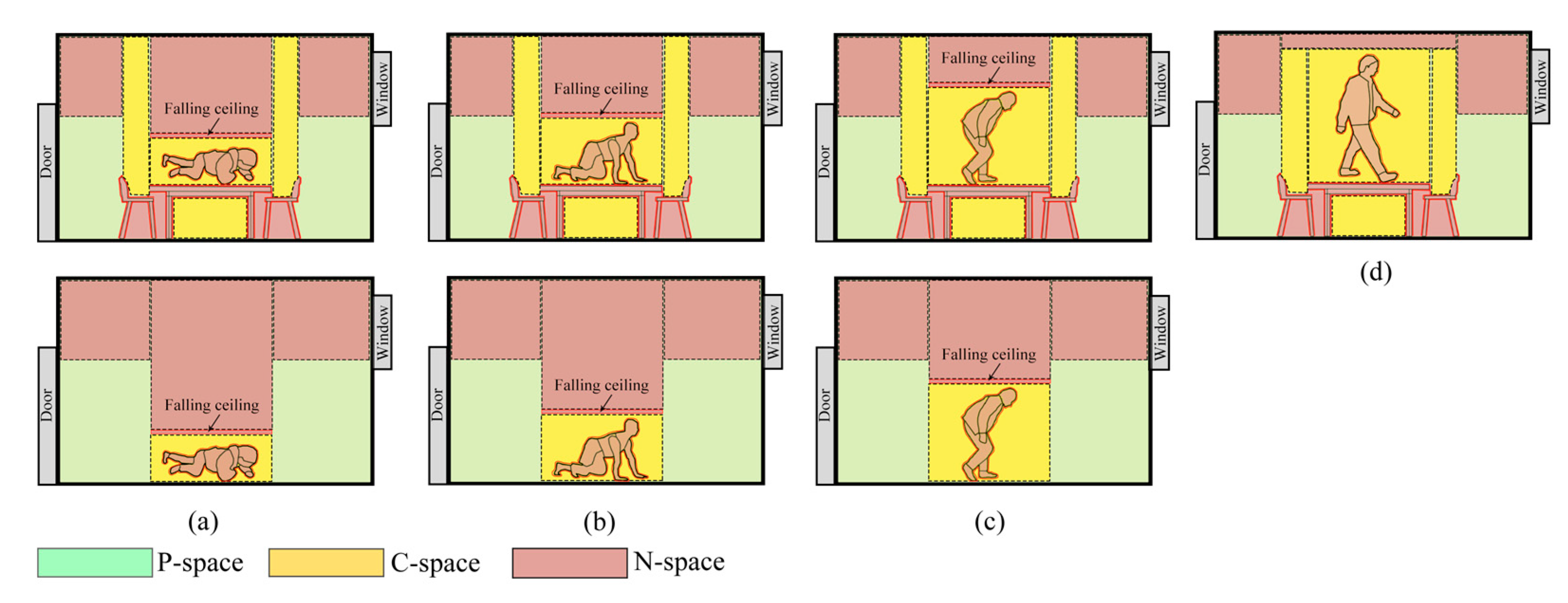
3.3. Space Components
3.3.1. Definition of Space Components
- 1.
- P-spaces refer to unoccupied spaces available for pedestrians to walk upright on the following static objects: floor slabs, stairs and ramps.
- 2.
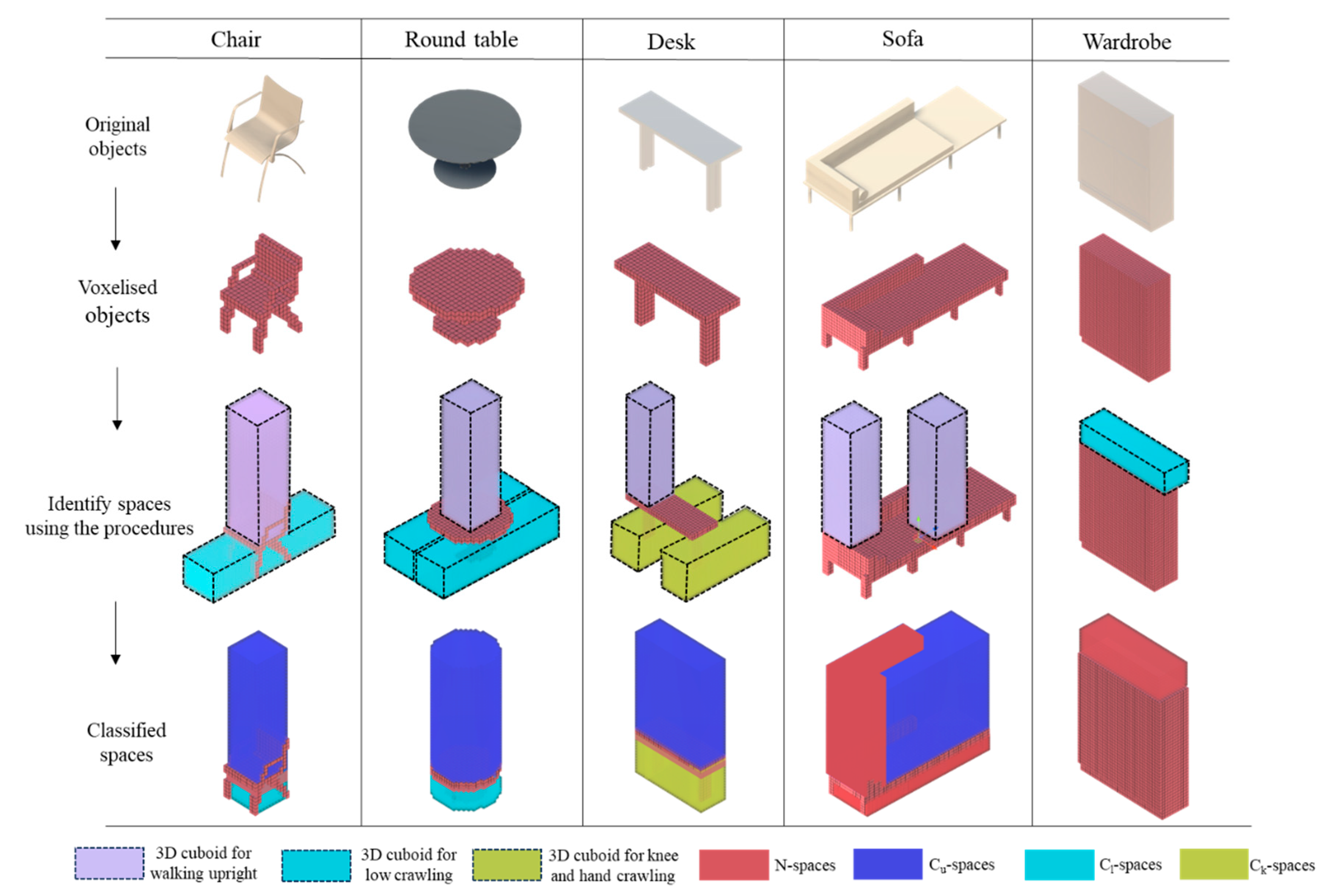
- C-spaces refer to spaces above/below physical components, where pedestrians can move through using 3D movements in abnormal circumstances. C-spaces are located above the top surface of movable objects (e.g., chairs, sofas) or stationary dynamic objects (e.g., cleaning robots) that require 3D actions, or below the bottom surface of static objects (e.g., low roofs/ceilings, stairs) or movable objects (e.g., tables). According to the four types of 3D movements, the C-spaces are further classified into:
- Cl-spaces, where pedestrians can only move through the spaces using low crawling.
- Ck-spaces, where pedestrians can move through the spaces using knee and hand crawling.
- Cb-spaces, where pedestrians can move through the spaces using bent-over walking.
- Cu-spaces, where pedestrians walk upright on movable or dynamic objects to move through the spaces.
- 3.
- N-spaces refer to spaces that
- Are occupied by static, movable and dynamic objects;
- Any of the 3D movements cannot move through;
- Are unreachable through any of the 3D actions;
- Are not used for evacuation simulation.
3.3.2. Specifications of Space Components
- P-spaces
- 2.
- C-spaces
- Semantics of physical component: If the semantics of physical components indicate movable or dynamic objects, C-spaces are above them. If the semantics refers to the floor slabs, stairs and ramps of static objects, but the surface where pedestrians move on remains the same, C-spaces are below static or movable objects. A typical example is a movable object “table”. C-spaces can be identified both above and below the table.
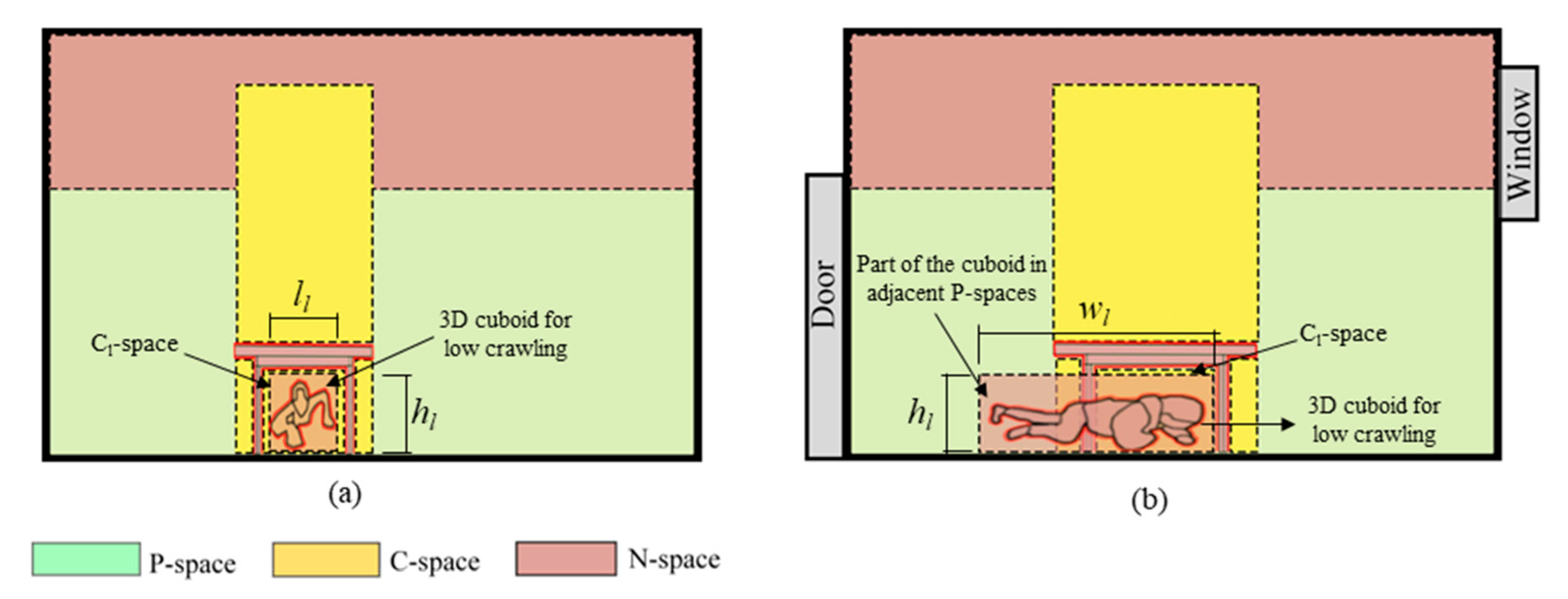
- Dimension of 3D cuboids: A space is identified as a C-space only when it accommodates an entire cuboid, i.e., considering height, length and width. This rule has one exception: spaces below static or movable objects can be classified into C-spaces if (1) the height and length of the cuboids for bend walking, knee crawling and low crawling can be fit within the space and (2) adjacent spaces (P-spaces or C-spaces) can accommodate a portion of their width. A table is a good illustration of this exception (see Figure 6). Additionally, the height of a C-space corresponds to that of the cuboid it accommodates. The horizontal size and shape of a C-space above a movable or dynamic object align with the dimensions of the object’s top surface. The horizontal size and shape of a C-space positioned below a static or movable object, on the other hand, match the dimensions of the object’s bottom surface. For each subtype of C-spaces apart from Cl-spaces, some spaces in one subtype may be used for another movement, given that the length and width of that movement can be ensured. For example, Cu-spaces can be used for bent-over walking, knee and hand crawling and low crawling if the Cu-space is large enough to allow for the lengths lb, lk and ll and the widths wb, wk and wl of the three movements.
- Maximum height threshold of climbing up/down: To identify if a C-space above movable or dynamic objects is reachable, a parameter defines the clearance from the current to the targeted surface of movement, denoted as hn (see Figure 7). The clearance hn must be greater than 20 cm and less than the maximum height threshold of climbing up/down, i.e., 20 cm < hn ≤ hcl. The threshold of 20 cm is strictly specified to indicate that regular stair treads do not involve a 3D action. The maximum height threshold depends on a person’s physical characteristics.
- 3.
- N-spaces
4. Demonstration of the Conceptual Space Model
4.1. Procedures of Space Identification and Classification
- Voxelisation: An IFC indoor model is voxelised. We enclose the IFC indoor model within a bounding box that aligns with the coordinate axes (X, Y, Z). Each voxel carries the IFC semantics about the physical components and spaces it represents.
- Label voxels: The voxel labels are organised based on the original IFC semantics. All voxels with the IFC semantics related to physical components (e.g., IfcSlab, IfcStair, IfcRamp and IFCWalls) are labelled as occupied voxels, while the rest of the voxels are marked as unoccupied voxels. Furthermore, some occupied voxels are marked as static object, movable object or dynamic object types. The static object only incorporates the semantic information of floor slabs, stairs and ramps.
- Locate an occupied voxel: We traverse the voxels to locate an occupied voxel. The voxel space is traversed once, voxel by voxel, from the bottom to top, left to right and front to back of the bounding box.
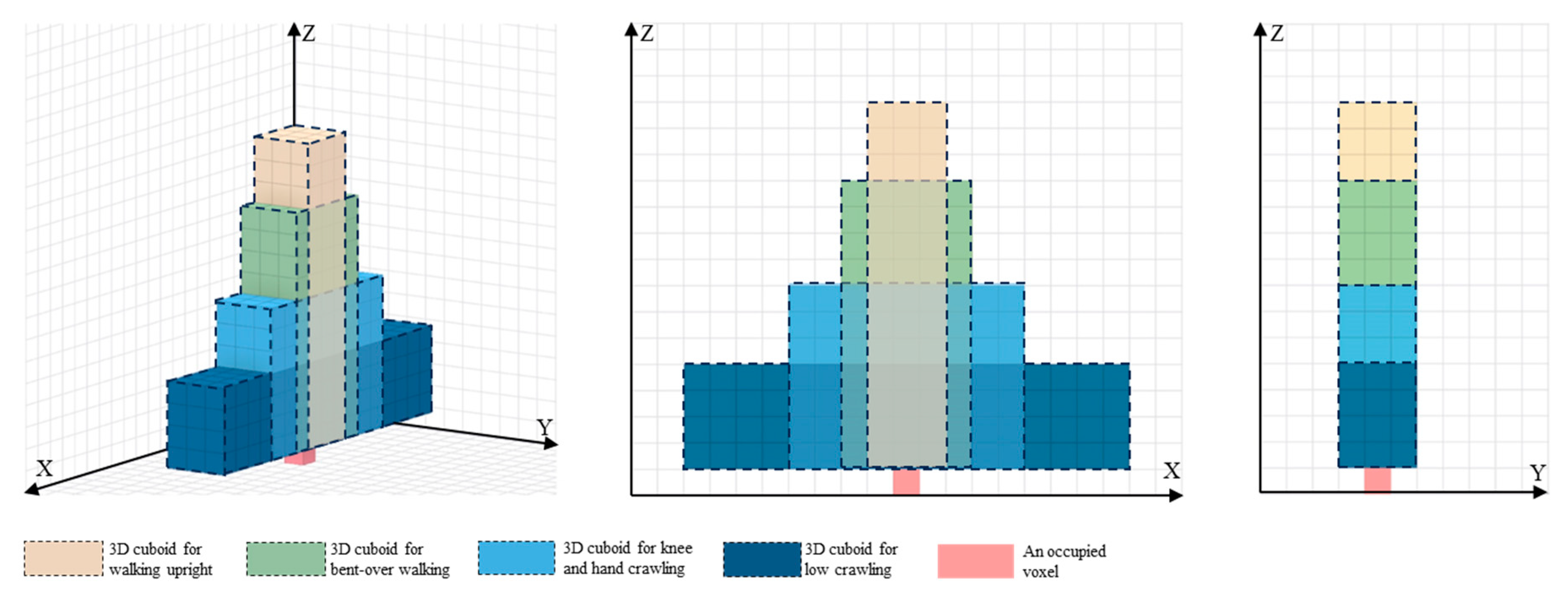
- Define 3D cuboids: Four types of 3D cuboids are simultaneously defined above the traversed occupied voxel. The voxel number of each 3D cuboid depends on the voxel resolution and corresponds to the lengths lu, lb, lk, ll, widths wu, wb, wk, wl and heights hu, hb, hk, hl. The occupied voxel is suggested to be right below the bottom centre of the 3D cuboids and towards the main direction of movements (see Figure 9).
- Detect overlap: We detect if any of the 3D cuboids overlap with physical components. If no overlap is detected, i.e., the space/voxels overlapping with the 3D cuboids are all unoccupied, they are classified into a potential P-space or C-space (to be checked in the next steps). In contrast, if the examined voxel space has occupied voxels that overlap with the 3D cuboid, the corresponding space cannot accommodate the 3D cuboids. Thus, if one or more 3D cuboids without an overlap exist, the procedures progress to the subsequent set of rules. If all the 3D cuboids overlap with physical components, the procedures go back to traverse the next occupied voxel.
- Check for static objects: The semantics associated with the traversed occupied voxel are checked. If the voxel has the semantics of a static object, the examined voxel space could potentially be P-spaces or C-spaces below static or movable objects. We proceed to recognise the used 3D cuboid in step (7). Otherwise, the space may be C-spaces above movable or dynamic objects. We proceed directly to step (8).
- Distinguish the used 3D cuboid: We distinguish the 3D cuboid without an overlap that is used for recognising and classifying space components. A classification sequence prioritises the 3D cuboid for walking upright, followed by the cuboid for bent-over walking, subsequently the one for knee and hand crawling, and lastly the cuboid for low crawling. For example, if the cuboid for walking upright does not overlap with any physical components, the unoccupied voxels within the cuboid will be assigned in the next step. Other 3D cuboids will not be used for classification. If the cuboid for walking upright experiences an overlap, the following bent-over walking cuboid is checked. The procedure continues until a 3D cuboid that does not overlap with any occupied voxel is found. The unoccupied voxels are potential P- and C-spaces and are classified in step (13).
- Check for movable/dynamic objects: When the semantics of the traversed occupied voxel are not a static object, we further check if the semantics correspond to a movable object or dynamic object. If the semantics align with either of these, we proceed to the subsequent steps. Otherwise, we begin to locate a new occupied voxel.
- Check the hn: The clearance hn is checked if it falls in the range of 20 cm < hn ≤ hcl. To this end, we search unoccupied voxels within X and Y dimensions that surround and adjoin horizontally to the movable or dynamic object that the traversed occupied voxel belongs to. Afterwards, we detect whether any occupied voxels with the semantics of static object, movable object or dynamic object are situated directly below these searched unoccupied voxels within the distance range. If the occupied voxel exists, the procedures start with the next rules. If no occupied voxel is within the range, the procedures return to traverse the next occupied voxel.
- Distinguish the used 3D cuboid: This step remains consistent with step (7), which prioritises different 3D cuboids for recognising and classifying space components.
- Detect surface area: The top surface of the movable or dynamic object is checked for whether the used 3D cuboid can be placed on it. We perform a voxel search in the horizontal plane, neighbouring the currently traversed occupied voxel, within the X and Y dimensions. Then, we check if these voxels are all occupied. If yes, the cuboid can be placed on the surface, and we continue with the classification process. If not, we revert to traverse the next occupied voxel.
- Obtain unoccupied voxels above the surface: We obtain unoccupied voxels above the entire top surface of the movable or dynamic object. A horizontal search is performed to find all adjacent occupied voxels that surround the traversed occupied voxel and possess the semantics of a movable object or dynamic object. For each occupied voxel of the whole surface, a neighbouring search in the Z dimension is conducted to find unoccupied voxels. The search commences from the entire surface and terminates at a height equivalent to that of the 3D cuboid.
- Classify P- and C-spaces: According to the type of used 3D cuboid, the unoccupied voxels within the 3D cuboid or above the whole surface are added to different predefined 3D arrays for P-spaces, Cu-spaces, Cb-spaces, Ck-spaces or Cl-spaces. For instance, if the traversed occupied voxel’s semantics is a movable object or dynamic object and the cuboid for walking upright is used, unoccupied voxels above the surfaces are assigned into 3D arrays for Cu-spaces. Each unoccupied voxel can only be added to a 3D array. We exclude the duplicates from within the array. After classifying the unoccupied voxels, this classification associated with the traversed occupied voxel finishes.
- Classify N-spaces: We check if all the occupied voxels are traversed. If all the occupied voxels have been traversed, all occupied voxels and the rest of the unoccupied voxels that are not classified as P-spaces and C-spaces are categorised into N-spaces. The whole procedure is then finished. If not, the procedures revert to locate another occupied voxel.
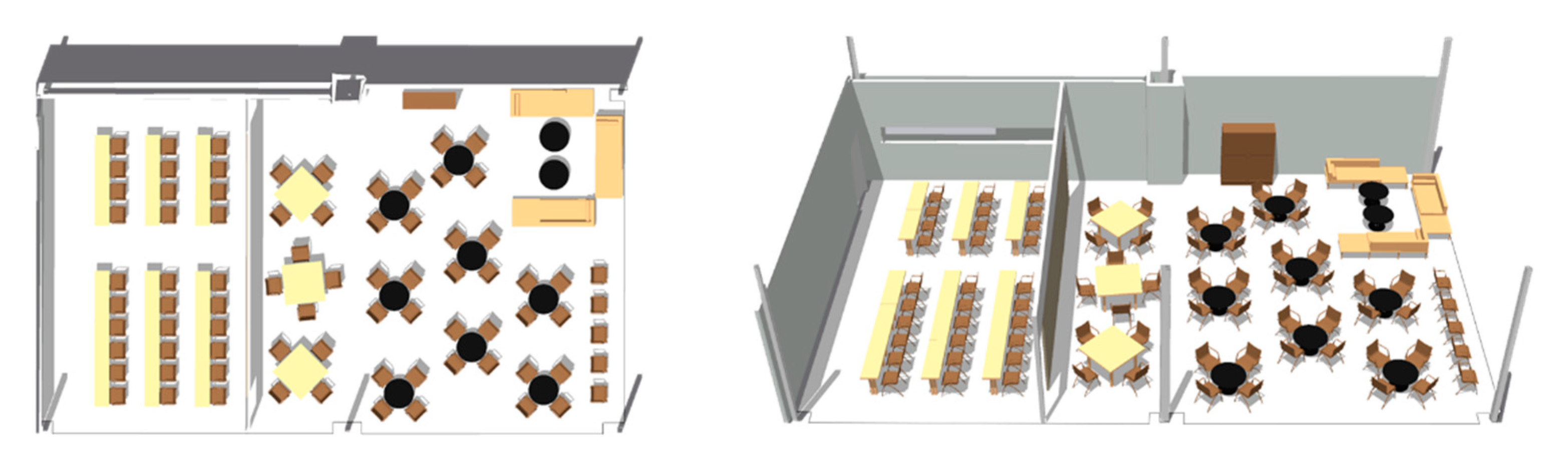
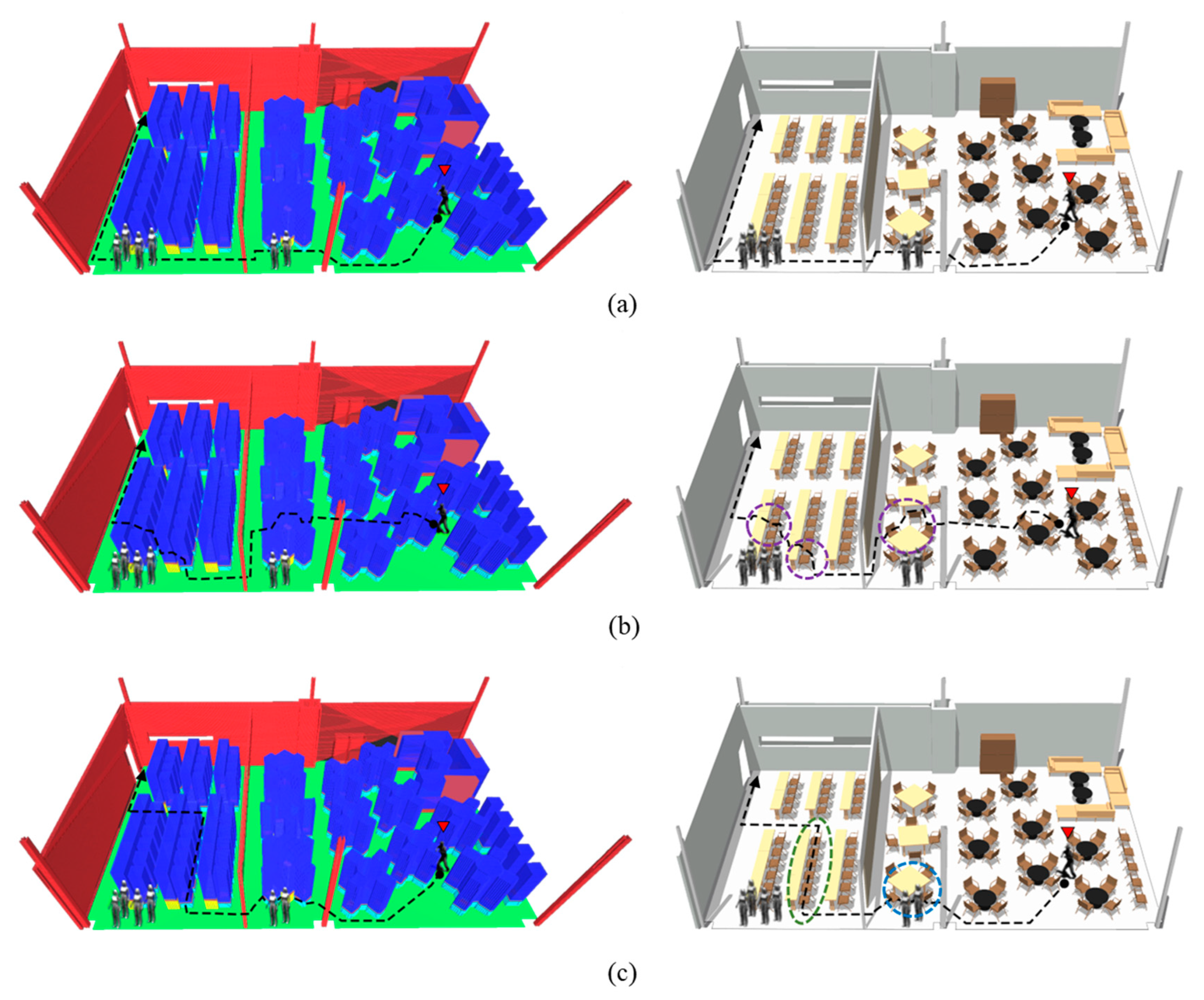
4.2. Demonstrating the Model for a Room of a Building
5. Conclusions and Future Work
- Identifying how spaces may vary in size and distribution if different 3D cuboids are tailored to different pedestrian groups (e.g., kids, the aged).
- Determining how various height-related 3D actions effectively connect space components and the different thresholds of various height-related 3D actions.
- Investigating more details in methods/algorithms to classify indoor spaces automatically, especially different types of C-spaces.
- Investigating how the classified spaces are used for 3D evacuation simulations. Whether evacuation paths derived from space components and their connections are based on graphs or voxels warrants thorough analysis and comparison.
- Identifying key factors useful to simulate 3D pedestrian motions and establishing a 3D evacuation simulation model to simulate the motions, for example, simulating how different pedestrians decide to choose different motions and utilise different motions to adjust evacuation routes, etc.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Xie, R.; Zlatanova, S.; Lee, J. 3D indoor environments in pedestrian evacuation simulations. Automat. Constr. 2022, 144, 104593. [Google Scholar] [CrossRef]
- Haghani, M.; Sarvi, M. Simulating dynamics of adaptive exit-choice changing in crowd evacuations: Model implementation and behavioural interpretations. Transp. Res. Part C Emerg. Technol. 2019, 103, 56–82. [Google Scholar] [CrossRef]
- Wang, X.; Mohcine, C.; Chen, J.; Li, R.; Ma, J. Modeling boundedly rational route choice in crowd evacuation processes. Saf. Sci. 2022, 147, 105590. [Google Scholar] [CrossRef]
- Feliciani, C.; Murakami, H.; Shimura, K.; Nishinari, K. Efficiently informing crowds—Experiments and simulations on route choice and decision making in pedestrian crowds with wheelchair users. Transp. Res. Part C Emerg. Technol. 2020, 114, 484–503. [Google Scholar] [CrossRef]
- Fu, Z.; Jia, Q.; Chen, J.; Ma, J.; Han, K.; Luo, L. A fine discrete field cellular automaton for pedestrian dynamics integrating pedestrian heterogeneity, anisotropy, and time-dependent characteristics. Transp. Res. Part C Emerg. Technol. 2018, 91, 37–61. [Google Scholar] [CrossRef]
- Chooramun, N.; Lawrence, P.J.; Galea, E.R. An agent-based evacuation model utilising hybrid space discretisation. Saf. Sci. 2012, 50, 1685–1694. [Google Scholar] [CrossRef]
- Liu, Q.; Lu, L.; Zhang, Y.; Hu, M. Modeling the dynamics of pedestrian evacuation in a complex environment. Phys. A Stat. Mech. Its Appl. 2022, 585, 126426. [Google Scholar] [CrossRef]
- Guo, N.; Ding, J.; Ding, Z.; Zhu, K.; Wu, C. Crawling evacuation from a room: Experiment and modeling. J. Stat. Mech. Theory Exp. 2021, 2021, 33415. [Google Scholar] [CrossRef]
- Song, Y.; Liu, J.; Liu, Q. Dynamic decision-making process of evacuees during post-earthquake evacuation near an automatic flap barrier gate system: A broken windows perspective. Sustainability 2021, 13, 8771. [Google Scholar] [CrossRef]
- Delcea, C.; Cotfas, L.; Craciun, L.; Molanescu, A.G. An agent-based modeling approach to collaborative classrooms evacuation process. Saf. Sci. 2020, 121, 414–429. [Google Scholar] [CrossRef]
- Xie, R.; Zlatanova, S.; Lee, J.B. 3D indoor-pedestrian interaction in emergencies: A review of actual evacuations and simulation models. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2022, XLVIII-4/W4-2022, 183–190. [Google Scholar] [CrossRef]
- Gorte, B.; Aleksandrov, M.; Zlatanova, S. Towards egress modelling in voxel building models. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, IV-4/W9, 43–47. [Google Scholar] [CrossRef]
- Aleksandrov, M.; Heslop, D.J.; Zlatanova, S. 3D indoor environment abstraction for crowd simulations in complex buildings. Buildings 2021, 11, 445. [Google Scholar] [CrossRef]
- You, L.; Zhang, C.; Hu, J.; Zhang, Z. A three-dimensional cellular automata evacuation model with dynamic variation of the exit width. J. Appl. Phys. 2014, 115, 224905. [Google Scholar] [CrossRef]
- Wei, J.; Zhang, H.; Guo, Y.; Gu, M. Experiment of bi-direction pedestrian flow with three-dimensional cellular automata. Phys. Lett. A 2015, 379, 1081–1086. [Google Scholar] [CrossRef]
- Jun, H.; Huijun, S.; Juan, W.; Xiaodan, C.; Lei, Y.; Musong, G. Experiment and modeling of paired effect on evacuation from a three-dimensional space. Phys. Lett. A 2014, 378, 3419–3425. [Google Scholar] [CrossRef]
- Bandi, S.; Thalmann, D. Space discretization for efficient human navigation. Comput. Graph. Forum 1998, 17, 195–206. [Google Scholar] [CrossRef]
- Li, F.; Zlatanova, S.; Koopman, M.; Bai, X.; Diakité, A. Universal path planning for an indoor drone. Automat. Constr. 2018, 95, 275–283. [Google Scholar] [CrossRef]
- Han, B.; Qu, T.; Tong, X.; Jiang, J.; Zlatanova, S.; Wang, H.; Cheng, C. Grid-optimized UAV indoor path planning algorithms in a complex environment. Int. J. Appl. Earth Obs. 2022, 111, 102857. [Google Scholar] [CrossRef]
- Beno, P.; Pavelka, V.; Duchon, F.; Dekan, M. Using octree maps and RGBD cameras to perform mapping and a navigation. In Proceedings of the 2016 International Conference on Intelligent Networking and Collaborative Systems (INCoS), Ostrava, Czech Republic, 7–9 September 2016; pp. 66–72. [Google Scholar] [CrossRef]
- Zhao, J.; Xu, Q.; Zlatanova, S.; Liu, L.; Ye, C.; Feng, T. Weighted octree-based 3D indoor pathfinding for multiple locomotion types. Int. J. Appl. Earth Obs. 2022, 112, 102900. [Google Scholar] [CrossRef]
- Rodenberg, O.; Verbree, E.; Zlatanova, S. Indoor A* pathfinding through an octree representation of a point cloud. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 4, 249–255. [Google Scholar] [CrossRef]
- Fichtner, F.W.; Diakité, A.A.; Zlatanova, S.; Voûte, R. Semantic enrichment of octree structured point clouds for multi-story 3D pathfinding. Trans. GIS 2018, 22, 233–248. [Google Scholar] [CrossRef]
- Zlatanova, S.; Liu, L.; Sithole, G.; Zhao, J.; Mortari, F. Space subdivision for indoor applications. GISt Rep. No. 66 2014. Available online: http://resolver.tudelft.nl/uuid:c3ef4c87-9c35-4d05-8877-a074c3f7fdbf (accessed on 19 November 2021).
- Wang, Q.; Song, W.; Zhang, J.; Ye, R.; Ma, J. Experimental study on knee and hand crawling evacuation for different age group students. Int. J. Disaster Risk Reduct. 2020, 48, 101613. [Google Scholar] [CrossRef]
- Jia, X.; Feliciani, C.; Yanagisawa, D.; Nishinari, K. Experimental study on the evading behavior of individual pedestrians when confronting with an obstacle in a corridor. Phys. A Stat. Mech. Its Appl. 2019, 531, 121735. [Google Scholar] [CrossRef]
- Nagai, R.; Fukamachi, M.; Nagatani, T. Evacuation of crawlers and walkers from corridor through an exit. Phys. A Stat. Mech. Its Appl. 2006, 367, 449–460. [Google Scholar] [CrossRef]
- Kady, R.A.; Davis, J. The effect of occupant characteristics on crawling speed in evacuation. Fire Saf. J. 2009, 44, 451–457. [Google Scholar] [CrossRef]
- Kady, R.A.; Davis, J. The impact of exit route designs on evacuation time for crawling occupants. J. Fire Sci. 2009, 27, 481–493. [Google Scholar] [CrossRef]
- Gallagher, S.; Pollard, J.; Porter, W.L. Locomotion in restricted space: Kinematic and electromyographic analysis of stoopwalking and crawling. Gait Posture 2011, 33, 71–76. [Google Scholar] [CrossRef]
- Davis, J.; Gallagher, S. Physiological demand on firefighters crawling during a search exercise. Int. J. Ind. Ergonom. 2014, 44, 821–826. [Google Scholar] [CrossRef]
- Cao, L.; Davis, G.A.; Gallagher, S.; Schall, M.C.; Sesek, R.F. Characterizing posture and associated physiological demand during evacuation. Saf. Sci. 2018, 104, 1–9. [Google Scholar] [CrossRef]
- Ma, J.; Shi, D.; Li, T.; Li, X.; Xu, T.; Lin, P. Experimental study of single-file pedestrian movement with height constraints. J. Stat. Mech. Theory Exp. 2020, 2020, 73409. [Google Scholar] [CrossRef]
- Ding, Z.; Shen, Z.; Guo, N.; Zhu, K.; Long, J. Evacuation through area with obstacle that can be stepped over: Experimental study. J. Stat. Mech. 2020, 2020, 23404. [Google Scholar] [CrossRef]
- Thompson, P.A. Developing New Techniques for Modelling Crowd Movement. KB Thesis Scanning Project 2015. Ph.D. Thesis, University of Edinburgh, Edinburgh, UK, 1994. [Google Scholar]
- Wąs, J.; Gudowski, B.; Matuszyk, P.J. Social distances model of pedestrian dynamics. In Proceedings of the Cellular Automata: 7th International Conference on Cellular Automata, for Research and Industry, ACRI 2006, Perpignan, France, 20–23 September 2006; Proceedings 7. pp. 492–501. [Google Scholar] [CrossRef]
- Waş, J.; Lubaś, R. Adapting Social Distances Model for Mass Evacuation Simulation. J. Cell. Autom. 2013, 8, 395–405. [Google Scholar]
- Chraibi, M.; Seyfried, A.; Schadschneider, A. Generalized centrifugal-force model for pedestrian dynamics. Phys. Rev. E. 2010, 82, 46111. [Google Scholar] [CrossRef]
- Li, M.; Zhao, Y.; He, L.; Chen, W.; Xu, X. The parameter calibration and optimization of social force model for the real-life 2013 Ya’an earthquake evacuation in China. Saf. Sci. 2015, 79, 243–253. [Google Scholar] [CrossRef]
- Alonso-Marroquín, F.; Busch, J.; Ramírez-Gómez, Á.; Lozano, C. A discrete spheropolygon model for calculation of stress in crowd dynamics. In Traffic and Granular Flow’13; Springer: Cham, Switzerland, 2015; pp. 179–186. [Google Scholar] [CrossRef]
- Alonso-Marroquín, F.; Busch, J.; Chiew, C.; Lozano, C.; Ramírez-Gómez, Á. Simulation of counterflow pedestrian dynamics using spheropolygons. Phys. Rev. E 2014, 90, 63305. [Google Scholar] [CrossRef]
- Chraibi, M.; Kemloh, U.; Schadschneider, A.; Seyfried, A. Force-based models of pedestrian dynamics. Netw. Heterog. Media 2011, 6, 425. [Google Scholar] [CrossRef]
- Hidalgo, R.C.; Parisi, D.R.; Zuriguel, I. Simulating competitive egress of noncircular pedestrians. Phys. Rev. E 2017, 95, 42319. [Google Scholar] [CrossRef]
- Wang, K.; Fu, Z.; Li, Y.; Qian, S. Influence of human-obstacle interaction on evacuation from classrooms. Automat. Constr. 2020, 116, 103234. [Google Scholar] [CrossRef]
- Maniccam, S. Traffic jamming on hexagonal lattice. Phys. A Stat. Mech. Its Appl. 2003, 321, 653–664. [Google Scholar] [CrossRef]
- Zheng, Y.; Jia, B.; Li, X.; Jiang, R. Evacuation dynamics considering pedestrians’ movement behavior change with fire and smoke spreading. Saf. Sci. 2017, 92, 180–189. [Google Scholar] [CrossRef]
- Yakhou, N.; Thompson, P.; Siddiqui, A.; Abualdenien, J.; Ronchi, E. The integration of building information modelling and fire evacuation models. J. Build. Eng. 2023, 63, 105557. [Google Scholar] [CrossRef]
- Król, A.; Król, M. Numerical investigation on fire accident and evacuation in a urban tunnel for different traffic conditions. Tunn. Undergr. Sp. Tech. 2021, 109, 103751. [Google Scholar] [CrossRef]
- Huang, Y.; Guo, Z.; Chu, H.; Sengupta, R. Evacuation Simulation Implemented by ABM-BIM of Unity in Students’ Dormitory Based on Delay Time. ISPRS Int. J. Geo-Inf. 2023, 12, 160. [Google Scholar] [CrossRef]
- Unity Technologies. Unity User Manual 2020.3 (LTS). Available online: https://docs.unity3d.com/Manual/index.html (accessed on 21 December 2021).
- Thunderhead Engineering. Pathfinder Technical Reference Manual. Available online: https://support.thunderheadeng.com/docs/pathfinder/2021-4/technical-reference-manual/ (accessed on 21 December 2021).
- Chen, J.; Shi, T.; Li, N. Pedestrian evacuation simulation in indoor emergency situations: Approaches, models and tools. Saf. Sci. 2021, 142, 105378. [Google Scholar] [CrossRef]
- Lee, J.; Li, K.-J.; Zlatanova, S.; Kolbe, T.H.; Nagel, C.; Becker, T. Open Geospatial Consortium IndoorGML v. 1.0, OGC. Available online: https://docs.ogc.org/is/14-005r3/14-005r3.html (accessed on 2 June 2014).
- Kolbe, T.H.; Kutzner, T.; Smyth, C.S.; Nagel, C.; Roensdorf, C.; Heazel, C. Open Geospatial Consortium CityGML. Available online: https://docs.ogc.org/guides/20-066.html (accessed on 19 May 2022).
- Boguslawski, P.; Gold, C.M.; Ledoux, H. Modelling and analysing 3D buildings with a primal/dual data structure. ISPRS J. Photogramm. 2011, 66, 188–197. [Google Scholar] [CrossRef]
- Zlatanova, S.; Liu, L.; Sithole, G. A conceptual framework of space subdivision for indoor navigation. In Proceedings of the fifth ACM SIGSPATIAL International Workshop on Indoor Spatial Awareness, Orlando, FL, USA, 5 November 2013; pp. 37–41. [Google Scholar] [CrossRef]
- Mortari, F.; Clementini, E.; Zlatanova, S.; Liu, L. An indoor navigation model and its network extraction. Appl. Geomat. 2019, 11, 413–427. [Google Scholar] [CrossRef]
- Kr, U.; Minaitundefined, M.; Zlatanova, S. Indoor space subdivision for indoor navigation. In ISA ’14; ACM: New York, NY, USA, 2014; pp. 25–31. [Google Scholar] [CrossRef]
- Zlatanova, S.; Yan, J.; Wang, Y.; Diakité, A.; Isikdag, U.; Sithole, G.; Barton, J. Spaces in spatial science and urban applications—State of the Art Review. ISPRS Int. J. Geo-Inf. 2020, 9, 58. [Google Scholar] [CrossRef]
- Richter, K.; Winter, S.; Rüetschi, U. Constructing hierarchical representations of indoor spaces. In Proceedings of the 2009 Tenth International Conference on Mobile Data Management: Systems, Services and Middleware, Taipei, Taiwan, 18–20 May 2009; pp. 686–691. [Google Scholar] [CrossRef]
- Yan, J.; Diakité, A.A.; Zlatanova, S. A generic space definition framework to support seamless indoor/outdoor navigation systems. Trans. GIS 2019, 23, 1273–1295. [Google Scholar] [CrossRef]
- Diakité, A.A.; Zlatanova, S. Spatial subdivision of complex indoor environments for 3D indoor navigation. Int. J. Geogr. Inf. Sci. 2018, 32, 213–235. [Google Scholar] [CrossRef]
- Nikoohemat, S.; Diakité, A.A.; Zlatanova, S.; Vosselman, G. Indoor 3D reconstruction from point clouds for optimal routing in complex buildings to support disaster management. Automat. Constr. 2020, 113, 103109. [Google Scholar] [CrossRef]
- Claridades, A.R.C.; Choi, H.; Lee, J. An indoor space subspacing framework for implementing a 3d hierarchical network-based topological data model. ISPRS Int. J. Geo-Inf. 2022, 11, 76. [Google Scholar] [CrossRef]
- Sithole, G.; Zlatanova, S. Position, location, place and area: An indoor perspective. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci 2016, 3, 89–96. [Google Scholar] [CrossRef]
- Gorte, B. Analysis of very large voxel datasets. Int. J. Appl. Earth Obs. 2023, 119, 103316. [Google Scholar] [CrossRef]
- Liu, L.; Li, B.; Zlatanova, S.; van Oosterom, P. Indoor navigation supported by the Industry Foundation Classes (IFC): A survey. Automat. Constr. 2021, 121, 103436. [Google Scholar] [CrossRef]
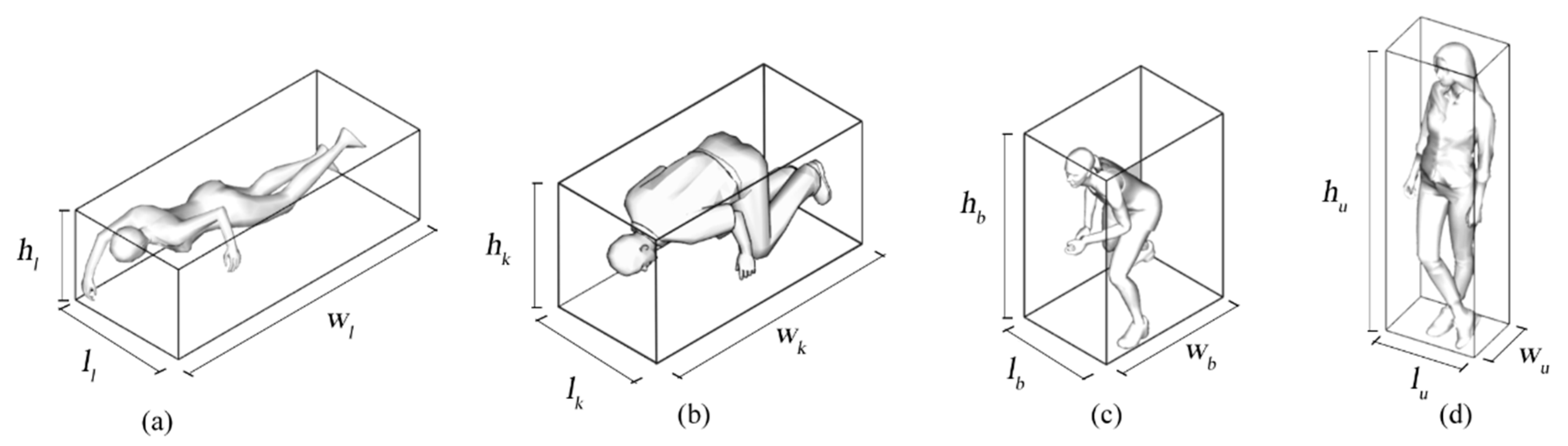





| Size of 3D Cuboids (cm) | Height | Length | Width |
|---|---|---|---|
| Walking upright | 170 (hu) | 30 (lu) | 30 (wu) |
| Bent-over walking | 140(hb) | 30 (lb) | 70 (wb) |
| Knee and hand crawling | 90 (hk) | 30 (lk) | 110 (wk) |
| Low crawling | 40 (hl) | 30 (hl) | 170 (wl) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, R.; Zlatanova, S.; Lee, J.; Aleksandrov, M. A Motion-Based Conceptual Space Model to Support 3D Evacuation Simulation in Indoor Environments. ISPRS Int. J. Geo-Inf. 2023, 12, 494. https://doi.org/10.3390/ijgi12120494
Xie R, Zlatanova S, Lee J, Aleksandrov M. A Motion-Based Conceptual Space Model to Support 3D Evacuation Simulation in Indoor Environments. ISPRS International Journal of Geo-Information. 2023; 12(12):494. https://doi.org/10.3390/ijgi12120494
Chicago/Turabian StyleXie, Ruihang, Sisi Zlatanova, Jinwoo (Brian) Lee, and Mitko Aleksandrov. 2023. "A Motion-Based Conceptual Space Model to Support 3D Evacuation Simulation in Indoor Environments" ISPRS International Journal of Geo-Information 12, no. 12: 494. https://doi.org/10.3390/ijgi12120494
APA StyleXie, R., Zlatanova, S., Lee, J., & Aleksandrov, M. (2023). A Motion-Based Conceptual Space Model to Support 3D Evacuation Simulation in Indoor Environments. ISPRS International Journal of Geo-Information, 12(12), 494. https://doi.org/10.3390/ijgi12120494






_Lee.png)

