Flow-Data-Based Global Spatial Autocorrelation Measurements for Evaluating Spatial Interactions
Abstract
:1. Introduction
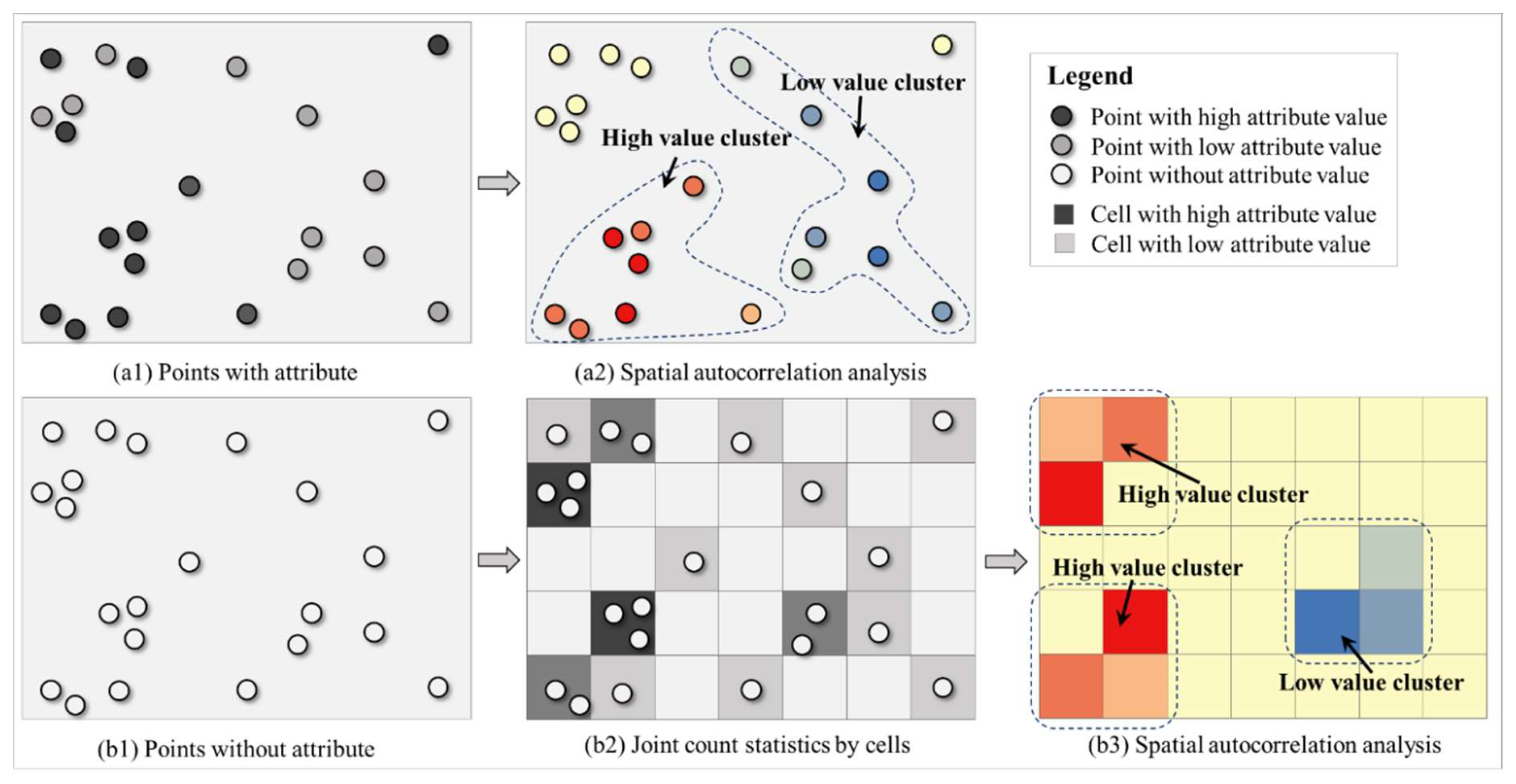
2. Literature Review
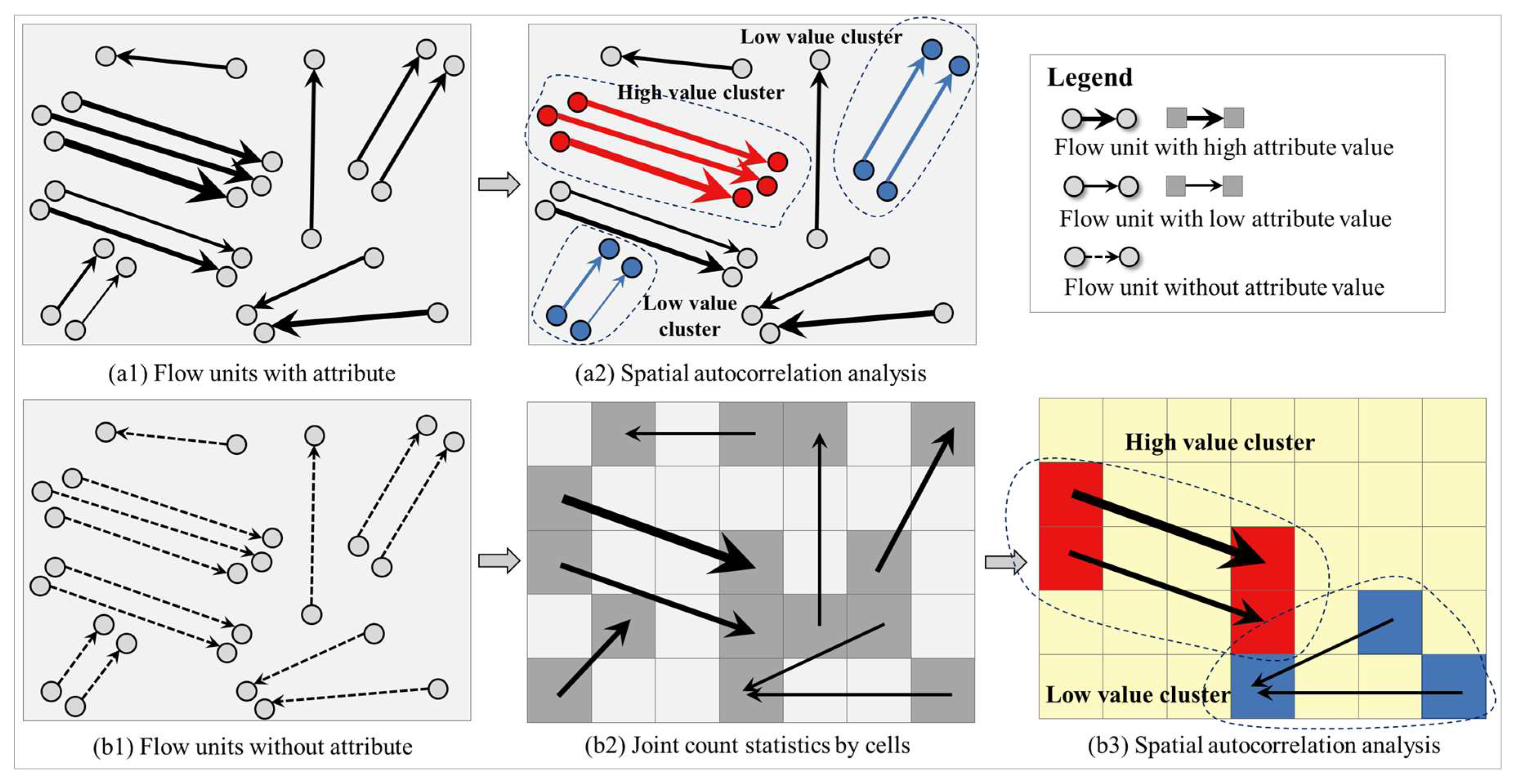
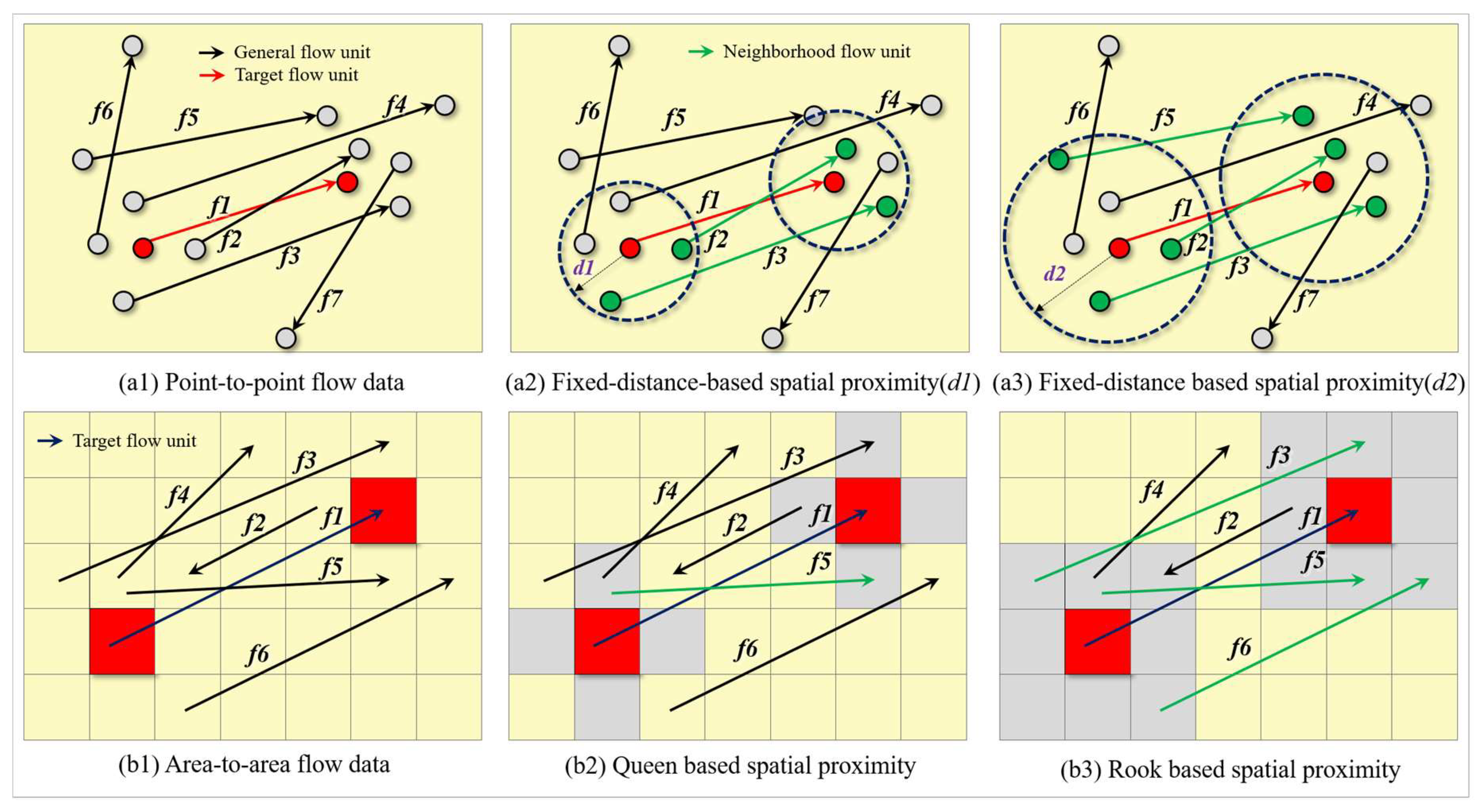
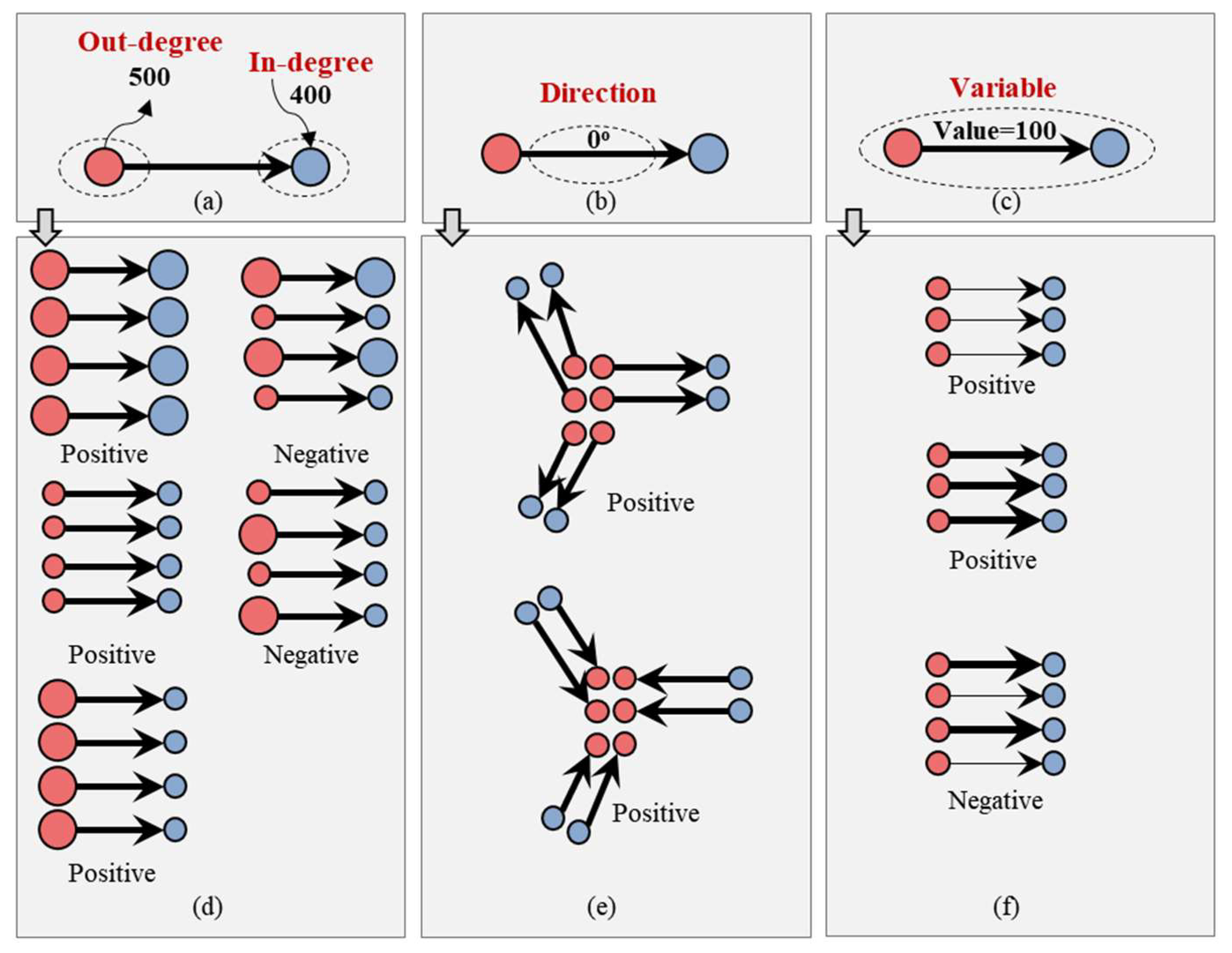
3. Definition of Flow Unit and Its Spatial Proximity
3.1. Types of Flow Unit
3.2. Spatial Proximity of the Flow Unit
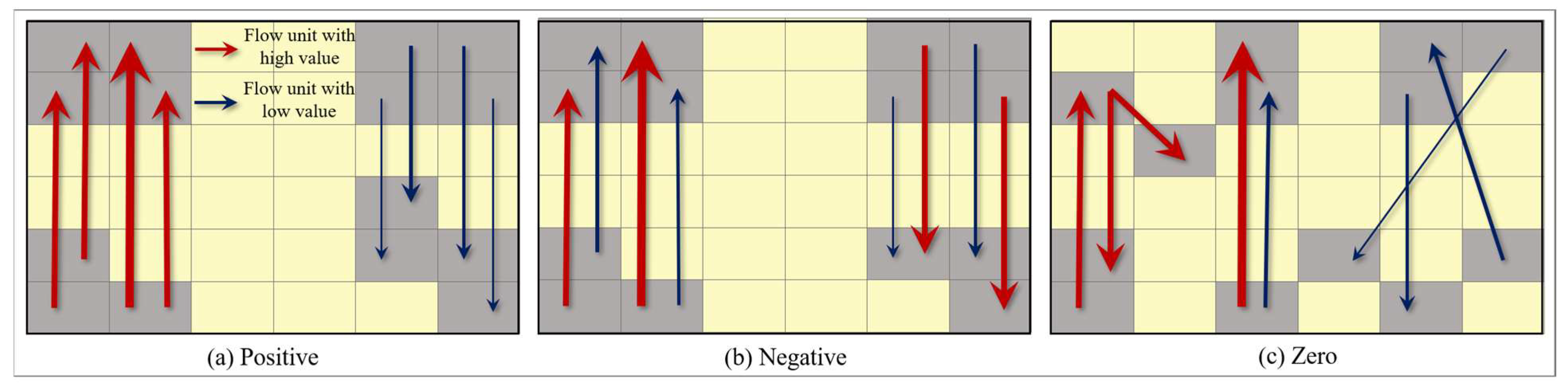
4. Modeling Global Spatial Autocorrelation of Flow
4.1. Measuring Global Moran’s Index of OD Flow
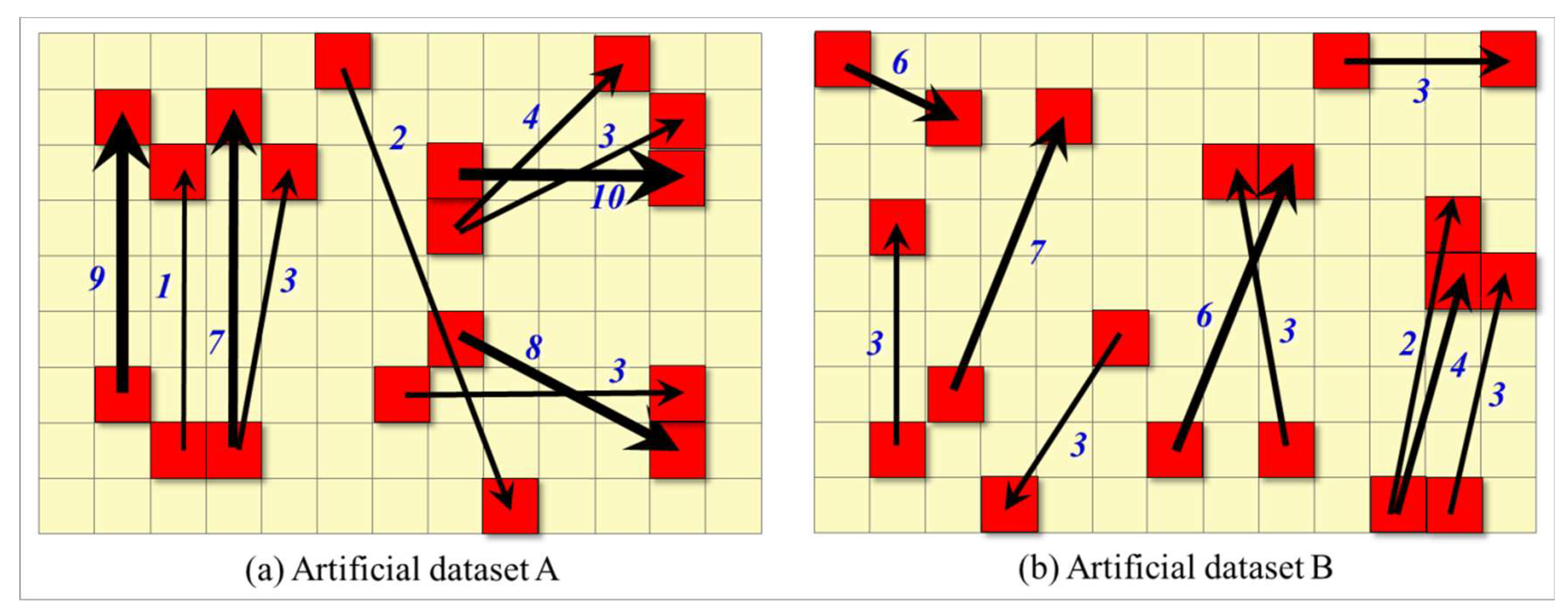
4.2. Evaluation Efficiency of Model by Artificial Data Set
5. Application
5.1. Study Area and Data Description
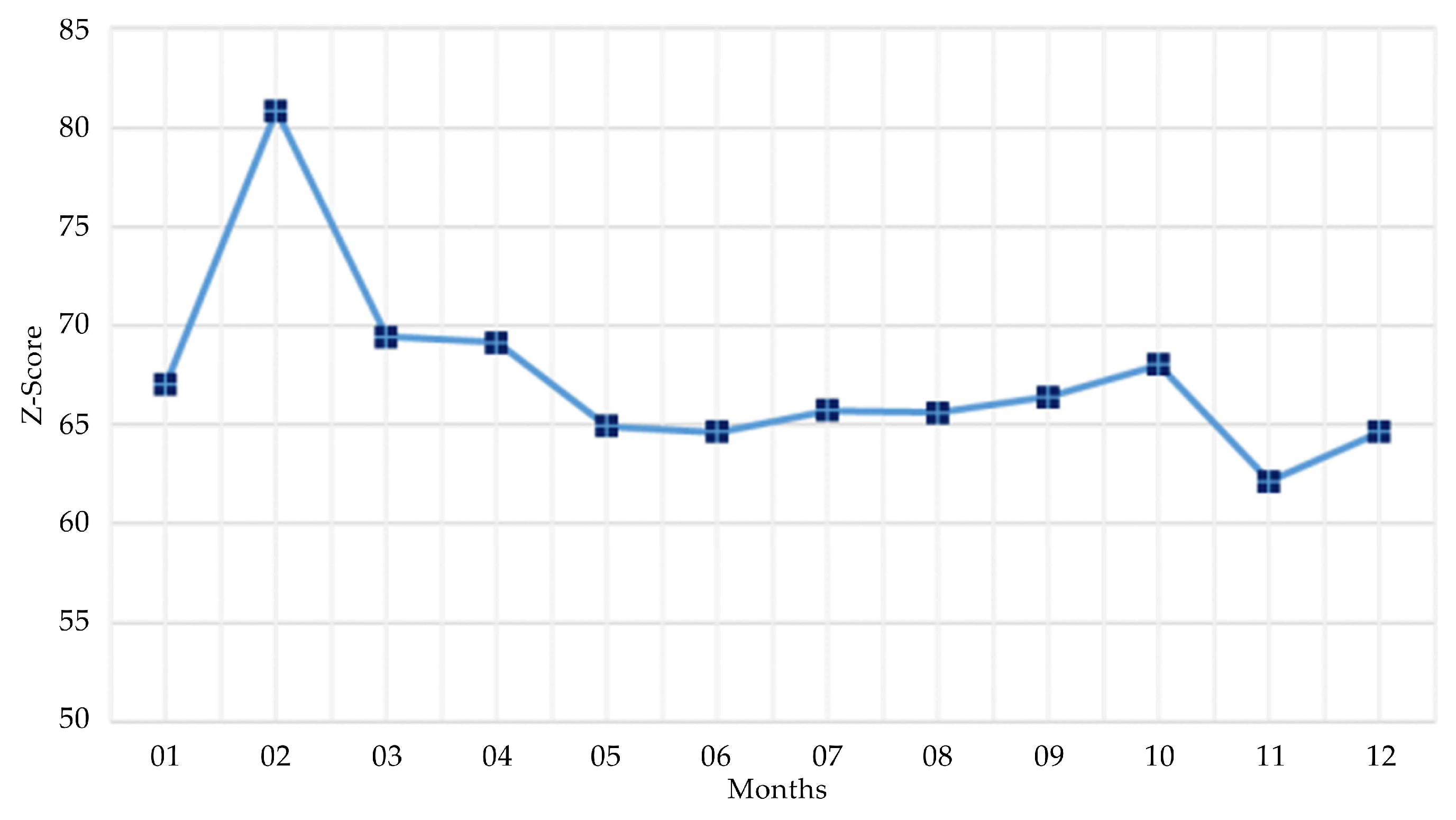
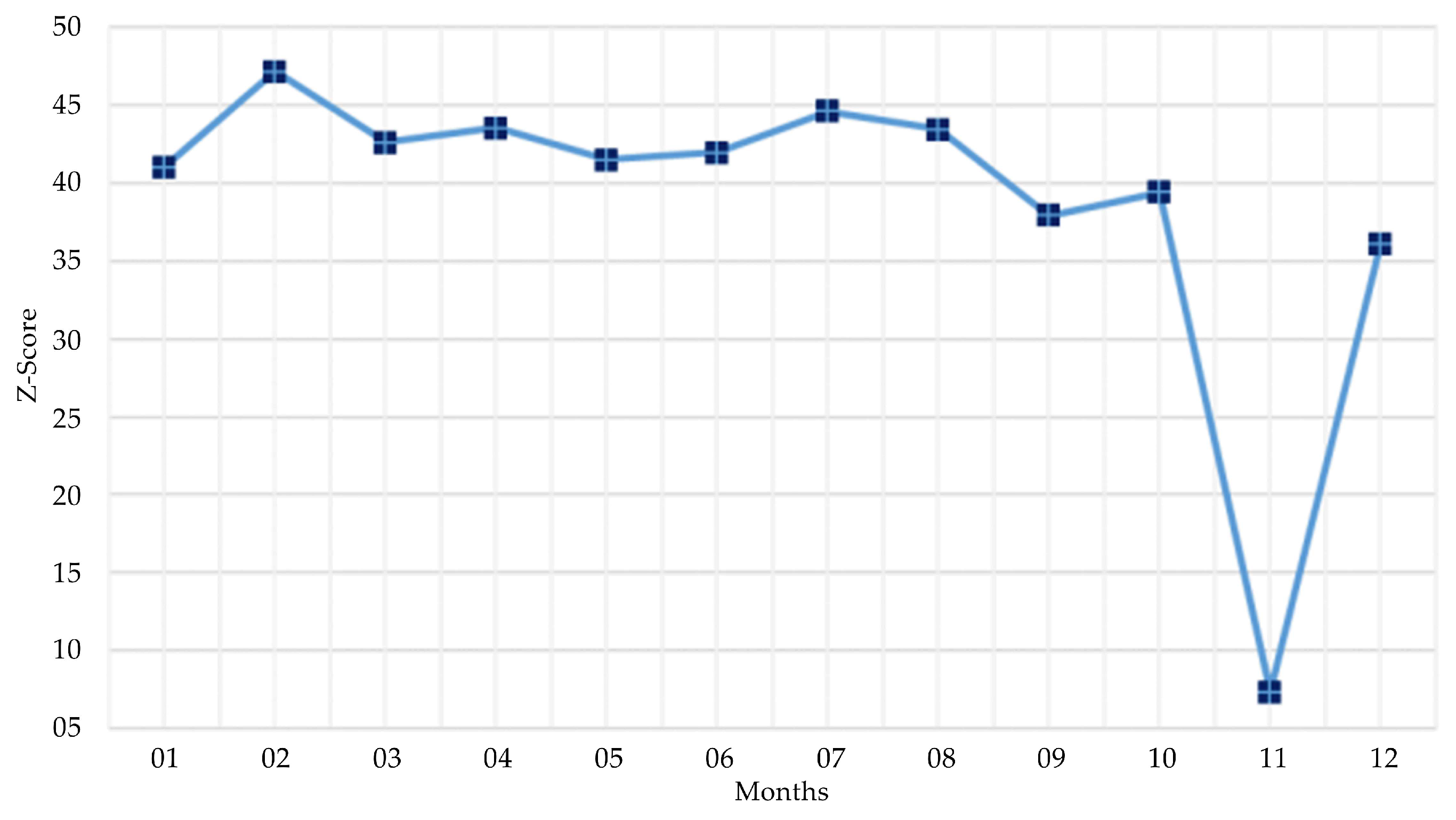
5.2. Result
6. Discussion and Conclusions
6.1. Discussion
6.2. Conclusion and Future Directions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Anselin, L. Local indicators of spatial association—LISA. Geogr. Anal. 1995, 27, 93–115. [Google Scholar] [CrossRef]
- Griffith, D.A.; Paelinck, J.H.; Griffith, D.A.; Paelinck, J.H. Spatial Autocorrelation and the p-Median Problem. Morphisms Quant. Spat. Anal. 2018, 51, 9–24. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Andris, C.; Liu, X.; Ferreira, J. Challenges for social flows. Comput. Environ. Urban Syst. 2018, 70, 197–207. [Google Scholar] [CrossRef]
- Griffith, D.A.; Chun, Y. Spatial autocorrelation in spatial interactions models: Geographic scale and resolution implications for network resilience and vulnerability. Netw. Spat. Econ. 2015, 15, 337–365. [Google Scholar] [CrossRef]
- Liu, Y.; Tong, D.; Liu, X. Measuring spatial autocorrelation of vectors. Geogr. Anal. 2015, 47, 300–319. [Google Scholar] [CrossRef]
- Tao, R.; Thill, J.-C. BiFlowLISA: Measuring spatial association for bivariate flow data. Comput. Environ. Urban Syst. 2020, 83, 101519. [Google Scholar] [CrossRef]
- Getis, A. Spatial interaction and spatial autocorrelation: A cross-product approach. Perspect. Spat. Data Anal. 2010, 23, 23–33. [Google Scholar]
- Bolduc, D.; Laferriere, R.; Santarossa, G. Spatial autoregressive error components in travel flow models. Reg. Sci. Urban Econ. 1992, 22, 371–385. [Google Scholar] [CrossRef]
- Cliff, A.; Martin, R.L.; Ord, J. Evaluating the friction of distance parameter in gravity models. Reg. Stud. 1974, 8, 281–286. [Google Scholar] [CrossRef]
- Haynes, K.E.; Fotheringham, A.S. Gravity and Spatial Interaction Models; WVU Research Repository: Morgantown, WV, USA, 2020. [Google Scholar]
- Cliff, A.; Martin, R.; Ord, J. A Reply to the Final Comment; Taylor & Francis: Abingdon, UK, 1976. [Google Scholar]
- LeSage, J.P.; Llano, C. A spatial interaction model with spatially structured origin and destination effects. Spat. Econom. Interact. Model. 2016, 171–197. [Google Scholar] [CrossRef]
- Ord, K. Estimation methods for models of spatial interaction. J. Am. Stat. Assoc. 1975, 70, 120–126. [Google Scholar] [CrossRef]
- Haining, R.P. Estimating spatial-interaction models. Environ. Plan. A 1978, 10, 305–320. [Google Scholar] [CrossRef]
- Fotheringham, A.S. A new set of spatial-interaction models: The theory of competing destinations. Environ. Plan. A Econ. Space 1983, 15, 15–36. [Google Scholar] [CrossRef]
- Mátyás, L. Proper econometric specification of the gravity model. World Econ. 1997, 20, 363–368. [Google Scholar] [CrossRef]
- Van Bergeijk, P.A.; Brakman, S. The Gravity Model in International Trade: Advances and Applications; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Fotheringham, A.S.; O’Kelly, M.E. Spatial Interaction Models: Formulations and Applications; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1989; Volume 1. [Google Scholar]
- Bogataj, D.; Bogataj, M.; Drobne, S. Interactions between flows of human resources in functional regions and flows of inventories in dynamic processes of global supply chains. Int. J. Prod. Econ. 2019, 209, 215–225. [Google Scholar] [CrossRef]
- Anselin, L. Spatial econometrics. In Handbook of Spatial Analysis in the Social Sciences; Edward Elgar Publishing: Cheltenham, UK, 2022; pp. 101–122. [Google Scholar]
- Anselin, L. Thirty years of spatial econometrics. Pap. Reg. Sci. 2010, 89, 3–25. [Google Scholar] [CrossRef]
- Black, W.R. Network autocorrelation in transport network and flow systems. Geogr. Anal. 1992, 24, 207–222. [Google Scholar] [CrossRef]
- Chun, Y.; Griffith, D.A. Modeling network autocorrelation in space–time migration flow data: An eigenvector spatial filtering approach. Ann. Assoc. Am. Geogr. 2011, 101, 523–536. [Google Scholar] [CrossRef]
- Griffith, D.A. The Moran coefficient for non-normal data. J. Stat. Plan. Inference 2010, 140, 2980–2990. [Google Scholar] [CrossRef]
- LeSage, J.P.; Pace, R.K. Spatial econometric modeling of origin-destination flows. J. Reg. Sci. 2008, 48, 941–967. [Google Scholar] [CrossRef]
- Beenstock, M.; Felsenstein, D. Double Spatial Dependence in Gravity Models: Migration from the European Neighborhood to the European Union. Spat. Econom. Interact. Model. 2016, 225–251. [Google Scholar] [CrossRef]
- Loglisci, C.; Appice, A.; Malerba, D. Collective regression for handling autocorrelation of network data in a transductive setting. J. Intell. Inf. Syst. 2016, 46, 447–472. [Google Scholar] [CrossRef]
- Storm, H.; Heckelei, T. Using Multiple Neighboring Interaction Effects in Spatial Regression Specifications to Reduce Omitted Variable Bias. In Proceedings of the 56th Annual Conference, Bonn, Germany, 28–30 September 2016. [Google Scholar]
- Peeters, D.; Thomas, I. Network autocorrelation. Geogr. Anal. 2009, 41, 436–443. [Google Scholar] [CrossRef]
- Bavaud, F. Testing spatial autocorrelation in weighted networks: The modes permutation test. Spat. Econom. Interact. Model. 2016, 15, 67–83. [Google Scholar]
- Zhou, J.; Tu, Y.; Chen, Y.; Wang, H. Estimating spatial autocorrelation with sampled network data. J. Bus. Econ. Stat. 2017, 35, 130–138. [Google Scholar] [CrossRef]
- Delgado, M.S.; Florax, R.J. Difference-in-differences techniques for spatial data: Local autocorrelation and spatial interaction. Econ. Lett. 2015, 137, 123–126. [Google Scholar] [CrossRef]
- Bavaud, F.; Kordi, M.; Kaiser, C. Flow autocorrelation: A dyadic approach. Ann. Reg. Sci. 2018, 61, 95–111. [Google Scholar] [CrossRef]
- Hird, M.D.; Pfotenhauer, S.M. How complex international partnerships shape domestic research clusters: Difference-in-difference network formation and research re-orientation in the MIT Portugal Program. Res. Policy 2017, 46, 557–572. [Google Scholar] [CrossRef]
- LeSage, J.P.; Thomas-Agnan, C. Interpreting spatial econometric origin-destination flow models. J. Reg. Sci. 2015, 55, 188–208. [Google Scholar] [CrossRef]
- Griffith, D.A. A linear regression solution to the spatial autocorrelation problem. J. Geogr. Syst. 2000, 2, 141–156. [Google Scholar] [CrossRef]
- Griffith, D.A.; Fischer, M.M.; LeSage, J. The spatial autocorrelation problem in spatial interaction modelling: A comparison of two common solutions. Lett. Spat. Resour. Sci. 2017, 10, 75–86. [Google Scholar] [CrossRef]
- Chun, Y.; Griffith, D.A.; Lee, M.; Sinha, P. Eigenvector selection with stepwise regression techniques to construct eigenvector spatial filters. J. Geogr. Syst. 2016, 18, 67–85. [Google Scholar] [CrossRef]
- Krisztin, T.; Fischer, M.M. The gravity model for international trade: Specification and estimation issues. Spat. Econ. Anal. 2015, 10, 451–470. [Google Scholar] [CrossRef]
- Chun, Y. Modeling network autocorrelation within migration flows by eigenvector spatial filtering. J. Geogr. Syst. 2008, 10, 317–344. [Google Scholar] [CrossRef]
- Patuelli, R. Spatial autocorrelation and spatial interaction. Encycl. GIS 2016, 1–7. [Google Scholar] [CrossRef]
- Zhang, H.; Zhou, X.; Tang, G.; Zhang, X.; Qin, J.; Xiong, L. Detecting colocation flow patterns in the geographical interaction data. Geogr. Anal. 2022, 54, 84–103. [Google Scholar] [CrossRef]
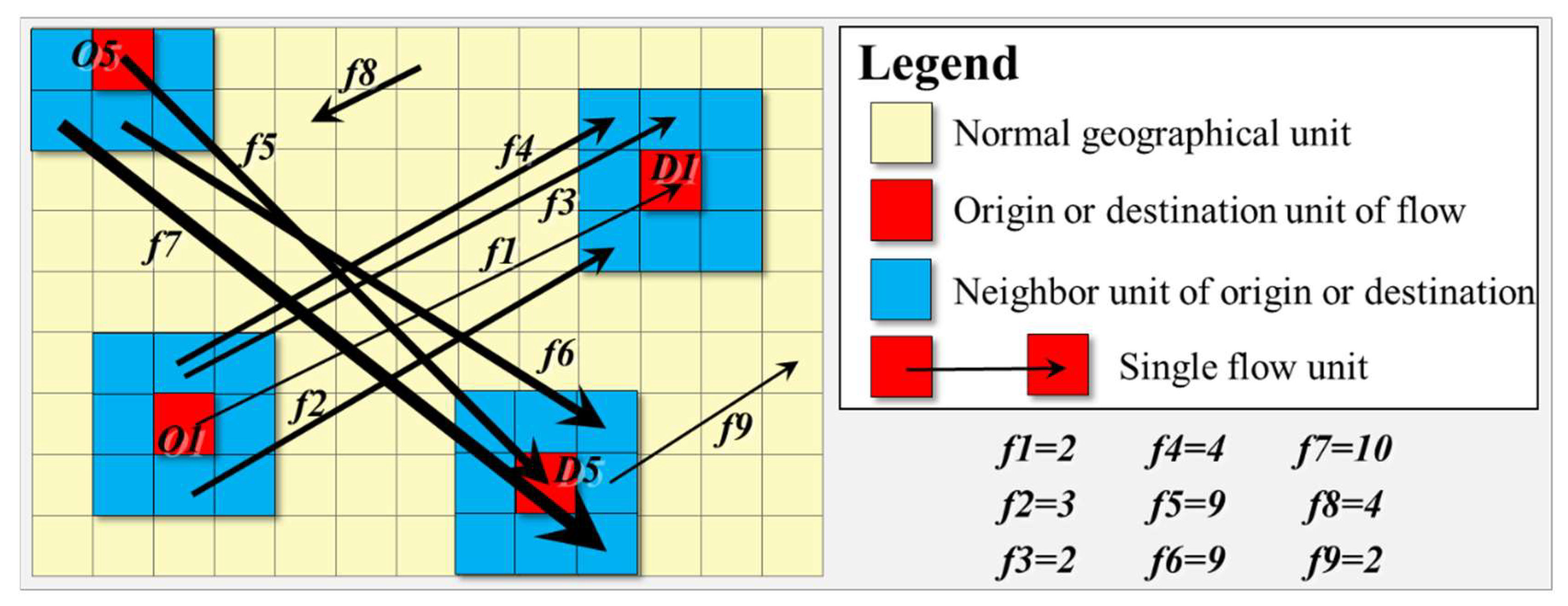

| i | j | |||
|---|---|---|---|---|
| 1 | 2 | 1 | (2 − 5) (3 − 5) | 6 |
| 1 | 3 | 1 | (2 − 5) (2 − 5) | 9 |
| 1 | 4 | 1 | (2 − 5) (4 − 5) | 3 |
| 2 | 1 | 1 | (3 − 5) (2 − 5) | 6 |
| 3 | 1 | 1 | (2 − 5) (2 − 5) | 9 |
| 3 | 4 | 1 | (2 − 5) (4 − 5) | 3 |
| 4 | 1 | 1 | (4 − 5) (2 − 5) | 3 |
| 4 | 3 | 1 | (4 − 5) (2 − 5) | 3 |
| 5 | 6 | 1 | (9 − 5) (9 − 5) | 16 |
| 5 | 7 | 1 | (9 − 5) (10 − 5) | 20 |
| 6 | 5 | 1 | (9 − 5) (9 − 5) | 16 |
| 7 | 5 | 1 | (10 − 5) (9 − 5) | 20 |
| Flow Data Set Name | Moran’s I | Expected Index | Standard Deviation | Z-Score |
|---|---|---|---|---|
| Artificial data set A | −0.761 | −0.111 | 0.347 | −1.874 |
| Artificial data set B | 0.256 | −0.111 | 0.422 | 0.870 |
| Month | Moran’s I | Expected Index | Standard Deviation | Z-Score |
|---|---|---|---|---|
| January | 0.349 | −0.0004 | 0.0052 | 67.064 |
| February | 0.378 | −0.0003 | 0.0047 | 80.863 |
| March | 0.349 | −0.0004 | 0.0050 | 69.454 |
| April | 0.350 | −0.0004 | 0.0051 | 69.154 |
| May | 0.344 | −0.0004 | 0.0053 | 64.946 |
| June | 0.346 | −0.0004 | 0.0054 | 64.639 |
| July | 0.359 | −0.0005 | 0.0055 | 65.742 |
| August | 0.363 | −0.0005 | 0.0055 | 65.628 |
| September | 0.347 | −0.0004 | 0.0052 | 66.412 |
| October | 0.352 | −0.0004 | 0.0052 | 68.041 |
| November | 0.333 | −0.0004 | 0.0054 | 62.161 |
| December | 0.354 | −0.0004 | 0.0055 | 64.656 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, S.; Zhang, H. Flow-Data-Based Global Spatial Autocorrelation Measurements for Evaluating Spatial Interactions. ISPRS Int. J. Geo-Inf. 2023, 12, 396. https://doi.org/10.3390/ijgi12100396
Sun S, Zhang H. Flow-Data-Based Global Spatial Autocorrelation Measurements for Evaluating Spatial Interactions. ISPRS International Journal of Geo-Information. 2023; 12(10):396. https://doi.org/10.3390/ijgi12100396
Chicago/Turabian StyleSun, Shuai, and Haiping Zhang. 2023. "Flow-Data-Based Global Spatial Autocorrelation Measurements for Evaluating Spatial Interactions" ISPRS International Journal of Geo-Information 12, no. 10: 396. https://doi.org/10.3390/ijgi12100396
APA StyleSun, S., & Zhang, H. (2023). Flow-Data-Based Global Spatial Autocorrelation Measurements for Evaluating Spatial Interactions. ISPRS International Journal of Geo-Information, 12(10), 396. https://doi.org/10.3390/ijgi12100396





