Abstract
Interest in studying the urban real estate market, especially in investigating the relationship between house prices and related housing characteristics, is rapidly growing. However, this increasing attention is handicapped by a limited consideration of the multi-scale spatial heterogeneity in these relationships. This study uses the rental price data of 72,466 apartments in the Tokyo metropolitan area to examine spatial heterogeneity in the real estate market at multiple spatial scales. Within the framework of spatially varying coefficient (SVC) modeling, we utilized a random effect eigenvector spatial filtering-based SVC (RE-ESF-SVC) model, an approach not previously employed in real estate studies, and compared it with the traditional ESF-SVC model, which has no random effects. Our results show that: (1) except for one housing characteristic that impacts prices consistently throughout the Tokyo metropolitan area, relationships between other characteristics and prices vary from local to global spatial scales; (2) because of the utilization of random effects, RE-ESF-SVC has the unique advantage of making estimations flexibly while maintaining a high performance.
1. Introduction
Due to the close interaction between housing prices and socioeconomic activities, the urban housing market is seen as an important indicator of a city’s development status [1,2,3]. The changes in housing prices and the relationships with price-determining effects have caught the attention of those in the fields of real estate and urban planning [4,5,6,7].
Based on Lancaster’s consumer behavior theory [8], Rosen [9] proposed the famous hedonic price model, a prominent approach widely applied in real estate studies to quantify the influence of associated determinants on housing prices. The basic idea of the hedonic price model is that the price of a house is determined by a bundle of values of related housing attributes (e.g., building age, overall size, floor, the distance to the nearest station, and so on). Prices and attributes are treated as the dependent variable and explanatory variables in the context of linear regression, respectively. Hence, the traditional hedonic model allows the analyst to distinguish the impact of changing a particular attribute on price fluctuations by observing the coefficient of each explanatory variable.
The traditional hedonic model assumes that the influence of housing prices’ related factors are consistent throughout the whole region. For example, no matter where the house is located, the marginal price increase associated with each additional square meter is constant. Additionally, the traditional hedonic model is estimated under the assumption that the residual of the model is uncorrelated. However, these assumptions are less reasonable for the real estate market because location plays a major role in housing price formation, leading to two special properties of housing price data: spatial autocorrelation and spatial heterogeneity [10]. Spatial autocorrelation can be explained by Tobler’s first law of geography, which states that “nearby things are more related than distant things” [11]. Hence, for the real estate market, houses in the same neighborhood capitalize on shared locational amenities and have similar prices, which leads to correlated model residuals and inefficient estimates. Furthermore, spatial heterogeneity describes the inconsistent relationship between associated determinants and prices over space. Differences in regional characteristics such as living environment, economic conditions, and consumer types affect the property valuation in different areas, making the impacts of associated determinants on housing prices different throughout the region [12,13].
Meanwhile, it is essential to note that spatial heterogeneity could operate at multiple spatial scales. In the urban housing market, the impacts of some housing attributes tend to gradually change throughout the whole region, resulting in a global-scale spatial pattern. In contrast, other attributes may change at a smaller scale and show a localized spatial pattern. Scale is a fundamental concept in spatial analysis, and its variation significantly affects the model performance [14]. Jang and Kang [15] suggested that analyzing the relationship between specific factors and housing prices at different scales may lead to contrary estimation results. In addition, Murakami et al. [16] suggested that capturing scale effects could make the modeling of spatial heterogeneity more stable and flexible. Therefore, it is essential to consider spatial heterogeneity at multiple spatial scales meticulously to avoid any possible misspecification.
The development of spatial analysis motivates the proposal of analyzing multi-scale spatial heterogeneity by spatially varying coefficient (SVC) models. The multi-scale geographically weighted regression (MGWR) model, proposed by Fotheringham et al. [17], has been widely used in many fields [18,19,20]. In addition, based on the assumption of a certain prior distribution of coefficients, the Bayesian SVC (B-SVC) model [21] computes their posterior distribution on which the estimation and inference are performed. Nevertheless, previous studies claimed that the computational costs of both MGWR and B-SVC increase significantly when the sample size increases [22]. Hence, neither MGWR nor B-SVC can analyze the urban real estate market where massive transaction data is easily collected and provided by governments or companies currently.
The eigenvector spatial filtering-based SVC (ESF-SVC) model [23] considers spatial scales for each heterogeneous relationship by introducing eigenvectors of a pre-defined spatial weight matrix into a linear regression model. Coefficients could be estimated through a computationally efficient OLS method, making ESF-SVC easily used in actual application [24,25,26]. Nevertheless, if all eigenvectors are used in ESF-SVC, the increasing number of variables may result in an overfitting problem. Instead, when selecting and applying only a set of eigenvectors, ESF-SVC cannot fully identify spatial scales of the data because some eigenvectors that contain important information are excluded. Currently, Murakami et al. [27] extended the traditional ESF-SVC into a random effect version, namely the random effects ESF-SVC (RE-ESF-SVC) model. The most crucial advantage of the RE-ESF-SVC is that it assumes the coefficients of the eigenvectors as random variables with unique probability distributions, which makes RE-ESF-SVC quantify a distinct spatial scale for each coefficient without selecting eigenvectors. Additionally, Murakami and Griffith [28] proposed a fast estimation algorithm to reduce the computational burdens of calculating eigenvectors and estimating parameters, making the RE-ESF-SVC capable of handling over 10,000 data points. The application of the RE-ESF-SVC may be seen in references [29,30].
Although many studies have demonstrated the spatial heterogeneity of the urban real estate market so far [31,32,33,34,35], the promising RE-ESF-SVC model has not been used in any previous analysis and the discussion of measuring potential multi-scale spatial heterogeneity in the price formation process remains lacking, especially for highly developed metropolitan areas, such as Tokyo. Therefore, the main objective of this study is to utilize RE-ESF-SVC to efficiently explore and characterize the multi-scale spatial heterogeneity of urban housing prices, taking the Tokyo metropolitan area real estate market as a case. This study is an extension of reference [36], which did not sufficiently explain the formation of the spatial distribution of each housing factor. Our research is aimed at making a further and more detailed exploration.
Based on the above, the following contributions to the literature are established. First, the application of RE-ESF-SVC confirms the existence of spatially varying relationships between housing attributes and rental prices at different spatial scales. For example, the time to the nearest station affects prices locally, whereas the impact of other spatially varying housing attributes changes globally in the Tokyo metropolitan area. Second, by analyzing how to characterize, and what to characterize in, the multi-scale spatial heterogeneity, we can better understand the process that shapes the current real estate market and further promote policies related to real estate and urban planning. Finally, the advantages of RE-EFS-SVC are examined by comparing it with the traditional ESF-SVC model, which provides new insight into utilizing this novel approach in more expansive fields related to spatial analysis.
The rest of this paper is structured as follows: First, Section 2 introduces the traditional ESF-SVC model as well as the RE-ESF-SVC model. Section 3 shows the study area and the housing price data. Section 4 discusses the estimation results of the RE-ESF-SVC. Section 5 summarizes the model comparison, and Section 6 concludes this study.
2. Methods
2.1. The ESF-SVC Model
ESF-SVC is a spatial regression approach proposed by Griffith [23]. ESF-SVC is built based on a spatial autocorrelation diagnostic statistic called the Moran coefficient (MC). For the vector that records observations at N locations, its is formulated as follows:
where is an symmetric spatial weight matrix representing the adjacent relationship among observations. is an projection matrix for centering, where is an identity matrix and is an vector of ones. MC quantifies the extent of spatial autocorrelation by comparing covariation among N sample values in . Therefore, positive MC indicates the presence of positive spatial autocorrelation in , and negative MC in case of negative spatial autocorrelation.
Eigenvectors are decomposed from the centralized spatial weight matrix , which is also a part of the numerator of . Generally, only eigenvectors with corresponding positive eigenvalues are utilized in analyses [37]. Griffith [38] further concluded that each eigenvector portrays a distinct map pattern of spatial autocorrelation and the scale depends on the corresponding eigenvalue. To elaborate, an eigenvector with a larger positive eigenvalue explains stronger positive spatial autocorrelation with a larger positive MC value and shows a more global map pattern. As the eigenvalue decreases, the spatial pattern of the corresponding eigenvector will also become local.
Based on this property, ESF-SVC extracts spatial heterogeneity of data by introducing interaction terms between eigenvectors and explanatory variables as shown in the following specification:
where is an vector of response variable and is an matrix that includes a constant variable and all explanatory variables, the matrix consists of L eigenvectors corresponding to positive eigenvalues, “∘” is the element-wise product operator, is the spatially varying coefficient of the kth () explanatory variable , in which is the average value, and is the spatially varying component representing local modifications of the average value. Since each element in determines the weight attributed to each eigenvector in , with different being estimated, the resulting will describe a different scale of spatial pattern for each , by which ESF-SVC addresses the multi-scale spatial heterogeneity.
Note that utilizing many eigenvectors will significantly increase the number of interaction terms between eigenvectors and explanatory variables, leading to severe overfitting. To select a smaller set of eigenvectors, Griffith and Chun [39] first retain only eigenvectors whose corresponding eigenvalues satisfy the criterion , and further conduct a stepwise variable selection. However, the selection will exclude eigenvectors representing necessary local-scale spatial heterogeneity. Thus, the reduction in the number of eigenvectors will lead to a lower estimation accuracy, and ESF-SVC cannot identify the critical local characteristics of the housing market.
2.2. The RE-ESF-SVC Model
To address the above limitation, Murakami et al. [27] improved the conventional ESF-SVC model by introducing random effects into spatially varying terms, yielding the random effects ESF-SVC (RE-ESF-SVC) model whose specification is shown as follows:
where is an vector of spatially varying coefficients regarding the kth explanatory variable and is composed of L eigenvectors with corresponding positive eigenvalues. In addition, the coefficient is a random variable with zero mean and is an diagonal matrix with the lth entry being , where is the eigenvalue corresponding to the lth eigenvector . and are parameters that determine the variance and scale of , respectively.
The RE-ESF-SVC model is a linear mixed model with the fixed effect coefficient and the random effect coefficient estimated by the restricted maximum likelihood method [27,40]. The computational cost of eigen-decomposition and the restricted likelihood maximization depend on the sample size, which will increase quickly as more data are included. According to reference [28], an eigenfunction approximation based on the Nystrom extension is expected to accelerate the eigen-decomposition process, and a fast parameter estimation algorithm that reduces the matrix operations is applied to further shorten the computation time.
Compared to ESF-SVC, which is a fixed effect model, RE-ESF-SVC treats as a random effect coefficient, which makes RE-ESF-SVC more flexible. The scale parameter controls the spatial scale of spatial variations in the kth regression coefficient . To elaborate, a large will shrink coefficients of eigenvectors with small eigenvalues (local-scale spatial pattern) strongly toward 0 and intensify the impact of eigenvectors with large eigenvalues (global-scale spatial pattern) at the same time. Thus, the resulting describes a global map pattern for . On the contrary, presents a local map pattern with a small . By estimating different for each , RE-ESF-SVC could automatically adjust the effect of eigenvectors to quantify different scales of spatial heterogeneity without additional variable selection. Therefore, RE-ESF-SVC is a flexible model that could overcome the limitations of ESF-SVC. We will compare ESF-SVC and RE-ESF-SVC in the following application to further illustrate this issue.
3. Study Area and Data
3.1. Study Area and Rental Housing Data
This study focuses on the Tokyo metropolitan area, which is known as Japan’s political and economic center and one of the world’s most highly developed urban areas. The Tokyo metropolitan area consists of 23 municipalities (wards, “” in Japanese) with a total area of about 619 km. The considerable total population of about 9.572 million assures a substantial demand for the real estate market and the distinct regional characteristics of each ward give rise to possible spatial heterogeneity in housing prices.
We use the Tokyo metropolitan area rental apartment prices data for the year of 2017, which is collected by At Home Co., Ltd. (Tokyo, Japan). Rental apartments are suitable for this study because the large sample size and wide spatial distribution of the transaction data are helpful to reflect the overall features of the market and reduce the estimation error. We removed apartments above 14 floors because the pricing strategy of high-rise condominiums differs from that of low-rise apartments. We also removed apartments built before 1981 because the old seismic design standards of buildings are not applicable after 1981. Consequently, the data set consists of 72,466 observations with geographic coordinates and detailed dwelling characteristics. Figure 1 shows the study area and spatial distribution of the apartment rent data.
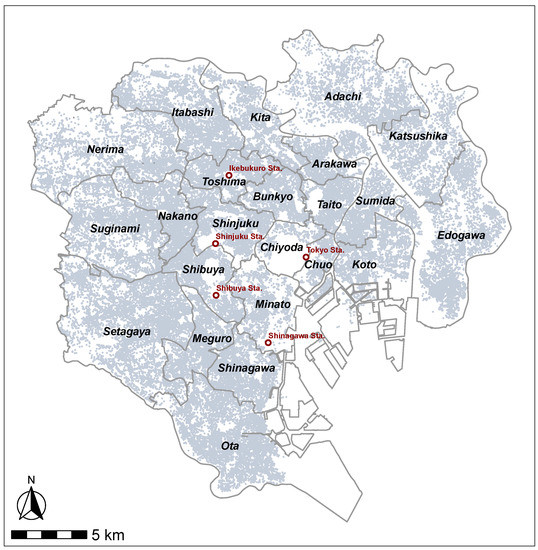
Figure 1.
The study area and distribution of the apartment rent data.
3.2. Variables
Table 1 shows the summary statistics of the variables. Following the specification used in the traditional hedonic model, the dependent variable in this study is the natural logarithm of rent per square meter, and the explanatory variables consist of structural and locational characteristics.

Table 1.
Summary of variables.
In particular, structural characteristics are apartment age, apartment size, and floor number. Apartment age generally has a negative impact on rent per square meter because of the property depreciation over time, while the floor number is commonly expected to have a positive impact because higher floors are considered quieter and have a better view. In addition, locational characteristics include the time to the nearest station and the accessibility to major stations. Specifically, the accessibility to major stations is defined as the average commute time from the nearest station of each house to five major stations, including Tokyo, Shinagawa, Shibuya, Shinjuku, and Ikebukuro Station, which are located in the central part of the Tokyo metropolitan area. Because commute time increases as traffic conditions worsen, both these locational attributes should negatively affect rental housing prices. All of the above explanatory variables are logarithmically transformed to reduce the influence of a skewed distribution on estimation.
4. Results of RE-ESF-SVC
This study first examined the estimation results derived from the RE-ESF-SVC model. The estimates and distributions of the coefficients revealed the fact that some housing attributes impact prices on different spatial scales, which highlighted the importance of considering the multi-scale spatial heterogeneity of the Tokyo metropolitan area real estate market.
We extracted eigenvectors from the centralized spatial weight matrix . The th element of the matrix is calculated based on the following exponential distance decay function:
where is the Euclidean distance between observation sites i and j. Following references [27,41], we fixed the range parameter r as the longest distance in the minimum spanning tree that connects all sample points. Using the fast eigen-decomposition method [28], 200 eigenvectors corresponding to positive eigenvalues were extracted and applied in RE-ESF-SVC. The ”spmoran” package in R [42] was used to estimate RE-ESF-SVC parameters.
4.1. Summary of Estimates
Table 2 summarizes the estimated coefficients and diagnostic information of RE-ESF-SVC. The Adjusted suggests that explanatory variables can explain 81.6% of the variation in logged rental prices in the context of RE-ESF-SVC. No significant residual correlation is detected by the Moran coefficient (0.005).

Table 2.
Results of the RE-ESF-SVC model.
As shown in Table 2, coefficients of the floor number were estimated to be constant, indicating no significant spatial variations in this attribute in the study area. The zero estimate of confirms that the impact of floor number on rental prices is consistent. On the contrary, coefficients of all other attributes are varying on different spatial scales, with each having a distinct positive value. This result verifies that the average estimation by the traditional hedonic price model may be flawed. Among attributes with spatially varying coefficients, the apartment age is negatively associated with rental prices across the study area. Regarding two variables having locational characteristics, although their estimates reveal both negative and positive effects on rent per square meter, those positive values are not significant at the confidence level. It is interesting that the apartment size shows both significant negative and positive effects on prices. The above results provide strong evidence that the multi-scale spatial heterogeneity model is not negligible in the Tokyo metropolitan area real estate market.
4.2. Distributions of Coefficients
Figure 2 visualizes four spatially varying coefficients. We note that only samples whose coefficient estimates are statistically significant at the confidence level are colored.
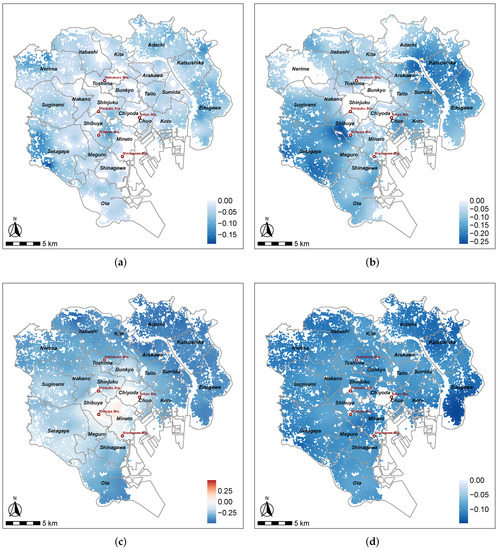
Figure 2.
The distribution of spatially varying coefficients estimated by RE-ESF-SVC. (a) Time to the nearest station. (b) Accessibility to major stations. (c) Apartment size. (d) Apartment age.
In Figure 2a, we see that as the time from the property to the nearest station increases, rent per square meter declines, which is applicable across the whole region. This negative influence presents a relatively localized spatial pattern because of the small value (0.424). From Figure 2b, compared to the time to the nearest station, coefficients regarding the accessibility to major stations change at a global scale because of the large value (1.542). The estimates are intuitively reasonable because these two properties are commonly used local and global measures to reflect the traffic accessibility. Although the accessibility to major stations encourages rental housing price growth across the Tokyo metropolitan area, significant negative values are mainly located in the northeastern and southwestern suburbs, where land use is mainly for residential and industrial purposes. In contrast, the impact is less pronounced in central Tokyo, which has a high concentration of public, political, and commercial facilities within a short distance. Thus, the high convenience of living and the diversity of demand diminish the impact of commute time on rental housing prices.
Figure 2c shows a global-scale spatial variation of the coefficients regarding the apartment size. Negative impacts are observed in the surroundings of the study area, especially in the three northeastern wards. Conversely, positive impacts can be found in Minato ward, where the increase in the apartment size contributed to higher rent per square meter. This result seems to be against our expectations, but it is reasonable when regional characteristics are taken into consideration. As one of the most luxurious areas of Tokyo, Minato ward is where the majority of business and diplomatic activities are concentrated. Many extra-large premium residences, whose price valuations are different from other apartments, are located there, leading to higher rents with increased property sizes.
Finally, the apartment age is statistically significant across the entire study area. Although the large value (1.309) suggests a global-scale spatial heterogeneity of the apartment age, the small value (0.001) indicates that its negative impacts do not vary as drastically as other variables, consequently yielding a relatively smooth map pattern shown in Figure 2d.
5. Model Comparison
As mentioned in Section 2, compared to ESF-SVC, RE-ESF-SVC could analyze multi-scale spatial heterogeneity more flexibly while maintaining a high accuracy at the same time. This section verifies the advantages of RE-ESF-SVC by comparing these two models. Two ESF-SVC models are compared with RE-ESF-SVC. The first one uses the same 200 eigenvectors (hereinafter referred to as the full ESF-SVC) as RE-ESF-SVC. The other one uses only 14 eigenvectors, whose corresponding eigenvalues are beyond the threshold of (hereinafter referred to as the selected ESF-SVC).
As shown in Table 3, which summarizes the estimates of the two ESF-SVC models, all housing characteristics were estimated to have spatially varying effects on prices. In contrast, RE-ESF-SVC could identify the consistent effect of the floor number and quantify the distinct scale of spatial variation for other spatially varying coefficients through parameter (see Table 2). The Adjusted value of the full ESF-SVC is the same as RE-ESF-SVC, but the lower BIC of RE-ESF-SVC suggests a lower information redundancy and better generalization performance, which is critical for applications to other data. Additionally, among the three models, the selected ESF-SVC has the lowest adjusted value and the highest residual standard error, indicating that the selection of eigenvectors in the ESF-SVC model leads to the decrease in explanatory power and estimation accuracy.

Table 3.
Results of ESF-SVC models.
For illustrative purposes, taking the coefficient of the apartment age as an example, Figure 3 visualizes the estimates given by the RE-ESF-SVC and ESF-SVC models. When all eigenvectors were input into the full ESF-SVC, unnecessary local spatial variations represented by some eigenvectors with small eigenvalues are redundant, leading to an overly localized spatial pattern that is hard to interpret. Instead, directly excluding all eigenvectors with small eigenvalues through selection will lose necessary local information, so the result of the selected ESF-SVC displays an overly smooth map pattern where almost no spatial variation can be observed. On the contrary, RE-ESF-SVC could find a good balance between the global and local spatial variations. Although all eigenvectors were used, RE-ESF-SVC adjusted appropriate eigenvectors for the variable to represent its distinct spatial heterogeneity, resulting in an understandable map pattern where the global-scale negative impacts are more evident in the surrounding area than the central area. The above comparison confirms the flexibility and higher accuracy of RE-ESF-SVC.
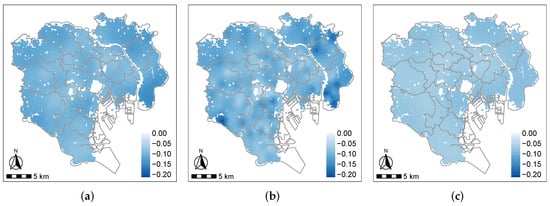
Figure 3.
Distributions of the coefficient for the apartment age estimated by RE-ESF-SVC and ESF-SVC. (a) RE-ESF-SVC. (b) The full ESF-SVC. (c) The selected ESF-SVC.
6. Conclusions
There is growing interest in real estate and urban planning studies to investigate the relationship between housing prices and related housing characteristics. However, this increasing attention is handicapped by the limited consideration of multiple scales of spatial heterogeneity in the data. In this study, we collected data on 72,466 rental apartments in the Tokyo metropolitan area and utilized the RE-ESF-SVC model to analyze how different housing characteristics are related to prices on different spatial scales. The analysis results lead us to the following findings.
First, it is necessary to consider multiple scales of the spatial heterogeneity in the Tokyo metropolitan area real estate market. The different customer preferences and distinct regional characteristics of each ward lead to varying relationships between prices and associated attributes. RE-ESF-SVC could extract these inconsistent relationships by allowing coefficients to vary according to location. According to the estimates and distributions of the coefficients of the RE-ESF-SVC, the time to the nearest station negatively affects prices locally, whereas accessibility to major stations, apartment age, and apartment size have global-scale impacts. The various spatial scales are quantified by different estimated values of .
Second, the comparison with the traditional ESF-SVC model, which has no random effects, suggests that RE-ESF-SVC is more flexible and effective. We compared the RE-ESF-SVC model with two ESF-SVC models, one using the same number of eigenvectors as RE-ESF-SVC and the other one using only a selected set of eigenvectors. The highest adjusted and the lowest BIC value of RE-ESF-SVC suggest that RE-ESF-SVC statistically outperforms ESF-SVC. In addition, RE-ESF-SVC treats the coefficients of eigenvectors as random variables, with each having its own possibility distribution. This allows RE-ESF-SVC to automatically adjust eigenvectors to determine a distinct spatial scale for each spatially varying coefficient without a previous variable selection, which is necessary for ESF-SVC, resulting in interpretable spatial patterns and a more accurate estimation.
Third, we attempted to provide an application of RE-ESF-SVC in a spatial analysis. RE-ESF-SVC is a novel method whose application is still limited, especially in urban real estate analysis. RE-ESF-SVC has its benefits by efficiently handling large amounts of data and flexibly identifying the spatial heterogeneity of data, which give rise to the possibility of applying RE-ESF-SVC in more expansive fields, such as ecology and transportation. We believe our findings could serve as inspiration for further studies.
There are, however, some limitations to this research. The explanatory variables of the models only consist of five structural and locational factors due to the limitations of the data collection. It is suggested to investigate how neighborhood factors, such as the diversity of land use, the distribution of public services, and the concentration of people, impact rental prices at the same time. These determinants are becoming increasingly influential in the context of livable and attractive cities. Therefore, we hope to incorporate complementary indicators for a more general explanation of the spatial variability in the urban real estate market in the future. In addition, we note that spatial heterogeneity in the real estate market could operate on a discrete spatial scale. For example, significant price changes may occur in specific local regions with well-defined boundaries, such as the brand-name area, a reputable school district, and the surroundings of major stations. Future work will focus on investigating discrete spatial heterogeneity at the same time.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/ijgi11050283/s1, A part of the dataset is openly available in Mendeley Data at 10.17632/fjtbpb628j.1, reference number [43].
Author Contributions
Conceptualization, Zhan Peng; methodology, Zhan Peng; software, Zhan Peng; validation, Zhan Peng; formal analysis, Zhan Peng; investigation, Zhan Peng; resources, Ryo Inoue; data curation, Zhan Peng; writing—original draft preparation, Zhan Peng; writing—review and editing, Ryo Inoue and Zhan Peng; visualization, Zhan Peng; supervision, Ryo Inoue; project administration, Ryo Inoue; funding acquisition, Ryo Inoue. All authors have read and agreed to the published version of the manuscript.
Funding
This research was founded by the Japan Society for the Promotion of Science KAKENHI, Grant Numbers JP18H01552 and JP21H01447.
Data Availability Statement
The original real estate rent data provided by At Home Co., Ltd. cannot be made publicly available due to the data disclosing policy of the data owner. Therefore, we disclose a part of the dataset recorded on 8000 properties that is openly in Supplementary Materials. The dependent variable, rent per square meter of properties, was transformed logarithmically and the explanatory variables, the attributes of properties, were also transformed logarithmically and then normalized to mean 0 and variance 1. Noises were added to the geographic coordinates of the data.
Acknowledgments
This research was the result of joint research with the Center of Spatial Information Science, The University of Tokyo (No. 815). We thank At Home Co, Ltd. for providing the apartment rental data used in this study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Campbell, J.Y.; Cocco, J.F. How do house prices affect consumption? Evidence from micro data. J. Monet. Econ. 2007, 54, 591–621. [Google Scholar] [CrossRef] [Green Version]
- Kishor, N.K.; Marfatia, H.A. The dynamic relationship between housing prices and the macroeconomy: Evidence from OECD countries. J. Real Estate Financ. Econ. 2017, 54, 237–268. [Google Scholar] [CrossRef]
- Agnello, L.; Castro, V.; Sousa, R.M. Economic activity, credit market conditions, and the housing market. Macroecon. Dyn. 2018, 22, 1769–1789. [Google Scholar] [CrossRef] [Green Version]
- Kuethe, T.H.; Pede, V.O. Regional housing price cycles: A spatio-temporal analysis using US state-level data. Reg. Stud. 2011, 45, 563–574. [Google Scholar] [CrossRef] [Green Version]
- Czembrowski, P.; Kronenberg, J. Hedonic pricing and different urban green space types and sizes: Insights into the discussion on valuing ecosystem services. Landsc. Urban Plan. 2016, 146, 11–19. [Google Scholar] [CrossRef]
- Belke, A.; Keil, J. Fundamental determinants of real estate prices: A panel study of German regions. Int. Adv. Econ. Res. 2018, 24, 25–45. [Google Scholar] [CrossRef] [Green Version]
- Yuan, F.; Wei, Y.D.; Wu, J. Amenity effects of urban facilities on housing prices in China: Accessibility, scarcity, and urban spaces. Cities 2020, 96, 102433. [Google Scholar] [CrossRef]
- Lancaster, K.J. A new approach to consumer theory. J. Political Econ. 1966, 74, 132–157. [Google Scholar] [CrossRef]
- Rosen, S. Hedonic prices and implicit markets: Product differentiation in pure competition. J. Political Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Anselin, L. What Is Special about Spatial Data? Alternative Perspectives on Spatial Data Analysis; Technical Report 89-4; UC Santa Barbara: National Center for Geographic Information and Analysis: Santa Barbara, CA, USA, 1989. [Google Scholar]
- Tobler, W.R. A computer movie simulating urban growth in the Detroit region. Econ. Geogr. 1970, 46, 234–240. [Google Scholar] [CrossRef]
- Sheppard, S. Hedonic analysis of housing markets. In Handbook of Regional and Urban Economics, 1st ed.; Cheshire, P.C., Mills, E.S., Eds.; Elsevier: Amsterdam, The Netherlands, 1999; Volume 3, Chapter 41; pp. 1595–1635. [Google Scholar] [CrossRef]
- McMillen, D.P.; Redfearn, C.L. Estimation and hypothesis testing for nonparametric hedonic house price functions. J. Reg. Sci. 2010, 50, 712–733. [Google Scholar] [CrossRef]
- Pan, Y.; Roth, A.; Yu, Z.; Doluschitz, R. The impact of variation in scale on the behavior of a cellular automata used for land use change modeling. Comput. Environ. Urban Syst. 2010, 34, 400–408. [Google Scholar] [CrossRef]
- Jang, M.; Kang, C.D. Retail accessibility and proximity effects on housing prices in Seoul, Korea: A retail type and housing submarket approach. Habitat Int. 2015, 49, 516–528. [Google Scholar] [CrossRef]
- Murakami, D.; Lu, B.; Harris, P.; Brunsdon, C.; Charlton, M.; Nakaya, T.; Griffith, D.A. The importance of scale in spatially varying coefficient modeling. Ann. Am. Assoc. Geogr. 2019, 109, 50–70. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Yang, W.; Kang, W. Multiscale geographically weighted regression (MGWR). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Wu, C.; Ren, F.; Hu, W.; Du, Q. Multiscale geographically and temporally weighted regression: Exploring the spatiotemporal determinants of housing prices. Int. J. Geogr. Inf. Sci. 2019, 33, 489–511. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Yue, H.; Li, Z. Examining the influences of air quality in China’s cities using multi-scale geographically weighted regression. Trans. GIS 2019, 23, 1444–1464. [Google Scholar] [CrossRef]
- Mollalo, A.; Vahedi, B.; Rivera, K.M. GIS-based spatial modeling of COVID-19 incidence rate in the continental United States. Sci. Total Environ. 2020, 728, 138884. [Google Scholar] [CrossRef]
- Gelfand, A.E.; Kim, H.J.; Sirmans, C.; Banerjee, S. Spatial modeling with spatially varying coefficient processes. J. Am. Stat. Assoc. 2003, 98, 387–396. [Google Scholar] [CrossRef]
- Finley, A.O. Comparing spatially-varying coefficients models for analysis of ecological data with non-stationary and anisotropic residual dependence. Methods Ecol. Evol. 2011, 2, 143–154. [Google Scholar] [CrossRef]
- Griffith, D.A. Spatial-filtering-based contributions to a critique of geographically weighted regression (GWR). Environ. Plan. A 2008, 40, 2751–2769. [Google Scholar] [CrossRef]
- Patuelli, R.; Schanne, N.; Griffith, D.A.; Nijkamp, P. Persistence of regional unemployment: Application of a spatial filtering approach to local labor markets in Germany. J. Reg. Sci. 2012, 52, 300–323. [Google Scholar] [CrossRef]
- Helbich, M.; Griffith, D.A. Spatially varying coefficient models in real estate: Eigenvector spatial filtering and alternative approaches. Comput. Environ. Urban Syst. 2016, 57, 1–11. [Google Scholar] [CrossRef]
- McCord, M.J.; McCord, J.; Davis, P.T.; Haran, M.; Bidanset, P. House price estimation using an eigenvector spatial filtering approach. Int. J. Hous. Mark. Anal. 2019, 13, 845–867. [Google Scholar] [CrossRef]
- Murakami, D.; Yoshida, T.; Seya, H.; Griffith, D.A.; Yamagata, Y. A Moran coefficient-based mixed effects approach to investigate spatially varying relationships. Spat. Stat. 2017, 19, 68–89. [Google Scholar] [CrossRef] [Green Version]
- Murakami, D.; Griffith, D.A. Spatially varying coefficient modeling for large datasets: Eliminating N from spatial regressions. Spat. Stat. 2019, 30, 39–64. [Google Scholar] [CrossRef] [Green Version]
- Yu, D.; Murakami, D.; Zhang, Y.; Wu, X.; Li, D.; Wang, X.; Li, G. Investigating high-speed rail construction’s support to county level regional development in China: An eigenvector based spatial filtering panel data analysis. Transp. Res. Part B Methodol. 2020, 133, 21–37. [Google Scholar] [CrossRef]
- Yang, F.; Li, K.; Jin, M.; Shi, W. Does financial deepening drive spatial heterogeneity of PM2. 5 concentrations in China? New evidence from an eigenvector spatial filtering approach. J. Clean. Prod. 2021, 291, 125945. [Google Scholar] [CrossRef]
- Helbich, M.; Brunauer, W.; Vaz, E.; Nijkamp, P. Spatial heterogeneity in hedonic house price models: The case of Austria. Urban Stud. 2014, 51, 390–411. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Wei, Y.D.; Yu, Z.; Tian, G. Amenity, accessibility and housing values in metropolitan USA: A study of Salt Lake County, Utah. Cities 2016, 59, 113–125. [Google Scholar] [CrossRef]
- Wen, H.; Jin, Y.; Zhang, L. Spatial heterogeneity in implicit housing prices: Evidence from Hangzhou, China. Int. J. Strateg. Prop. Manag. 2017, 21, 15–28. [Google Scholar] [CrossRef]
- Inoue, R.; Ishiyama, R.; Sugiura, A. Identifying local differences with fused-MCP: An apartment rental market case study on geographical segmentation detection. Jpn. J. Stat. Data Sci. 2020, 3, 183–214. [Google Scholar] [CrossRef] [Green Version]
- Inoue, R.; Ishiyama, R.; Sugiura, A. Identification of Geographical Segmentation of the Rental Housing Market in the Tokyo Metropolitan Area by Generalized Fused Lasso. J. Jpn. Soc. Civ. Eng. Ser. D3 (Infrastruct. Plan. Manag.) 2020, 76, 251–263. [Google Scholar] [CrossRef]
- Peng, Z.; Inoue, R. Specifying multi-scale spatial heterogeneity in the rental housing market: The case of the Tokyo metropolitan area. In Proceedings of the GIScience 2021 Short Paper Proceedings, Poznań, Poland, 27–30 September 2021. [Google Scholar]
- Griffith, D.A. Spatial autocorrelation and eigenfunctions of the geographic weights matrix accompanying geo-referenced data. Can. Geogr./Le Géogr. Can. 1996, 40, 351–367. [Google Scholar] [CrossRef]
- Griffith, D.A. Spatial Autocorrelation and Spatial Filtering. Gaining Understanding through Theory and Visualization; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar] [CrossRef]
- Griffith, D.A.; Chun, Y. Spatial autocorrelation and eigenvector spatial filtering. In Handbook of Regional Science; Springer: Berlin/Heidelberg, Germany, 2014; pp. 1477–1507. [Google Scholar] [CrossRef]
- Bates, D.; Mächler, M.; Bolker, B.; Walker, S. Fitting Linear Mixed-Effects Models Using lme4. J. Stat. Softw. 2015, 67, 1–48. [Google Scholar] [CrossRef]
- Dray, S.; Legendre, P.; Peres-Neto, P.R. Spatial modelling: A comprehensive framework for principal coordinate analysis of neighbour matrices (PCNM). Ecol. Model. 2006, 196, 483–493. [Google Scholar] [CrossRef]
- Murakami, D. Spmoran: Moran’s Eigenvector-Based Spatial Regression Models; R Package Version 0.2.2.2. 2022. Available online: https://CRAN.R-project.org/package=spmoran (accessed on 18 March 2022).
- Peng, Z.; Inoue, R. Tokyo Metropolitan Area Rent Data. Mendeley Data; V1. 2022. Available online: https://data.mendeley.com/datasets/fjtbpb628j/1 (accessed on 18 March 2022).
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).