Quantitative Relations between Topological Similarity Degree and Map Scale Change of Contour Clusters in Multi-Scale Map Spaces
Abstract
1. Introduction
2. Datasets and Their Pre-Processing
2.1. Experimental Datasets
2.2. Pre-Processing of the Datasets
3. Methodology
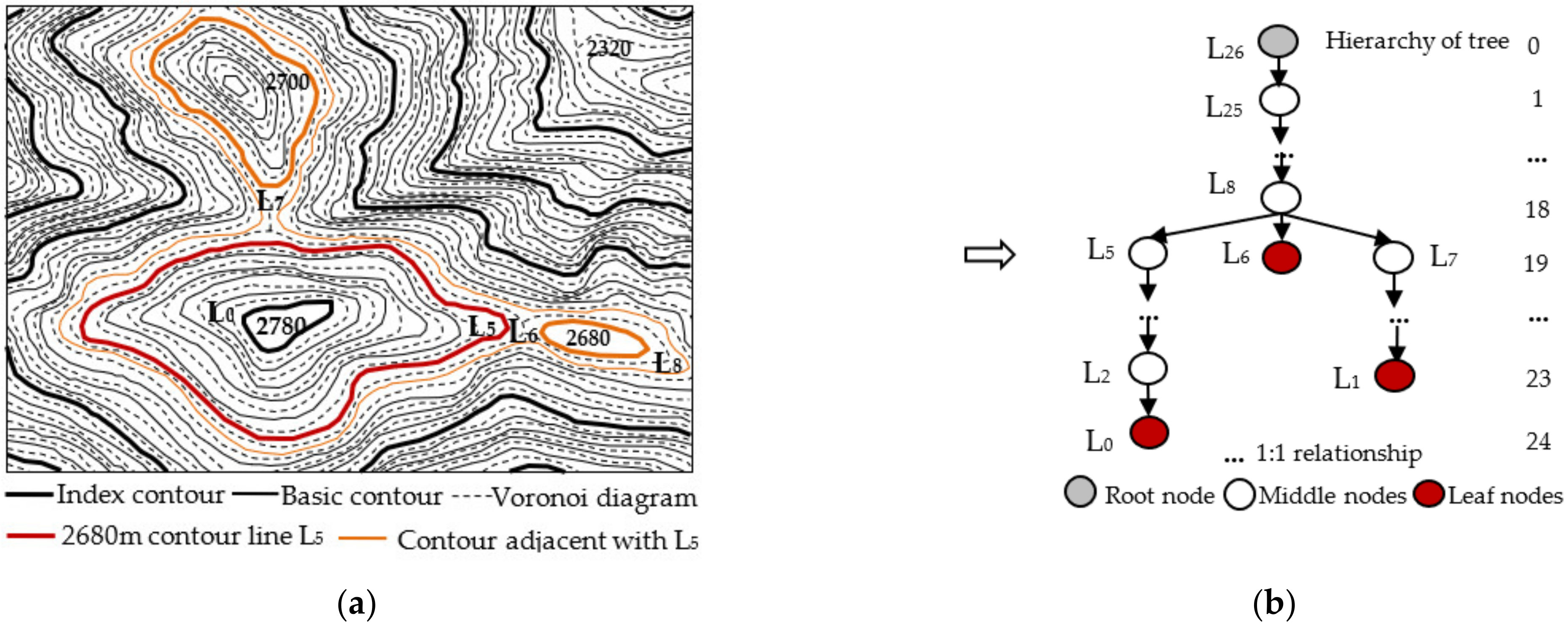
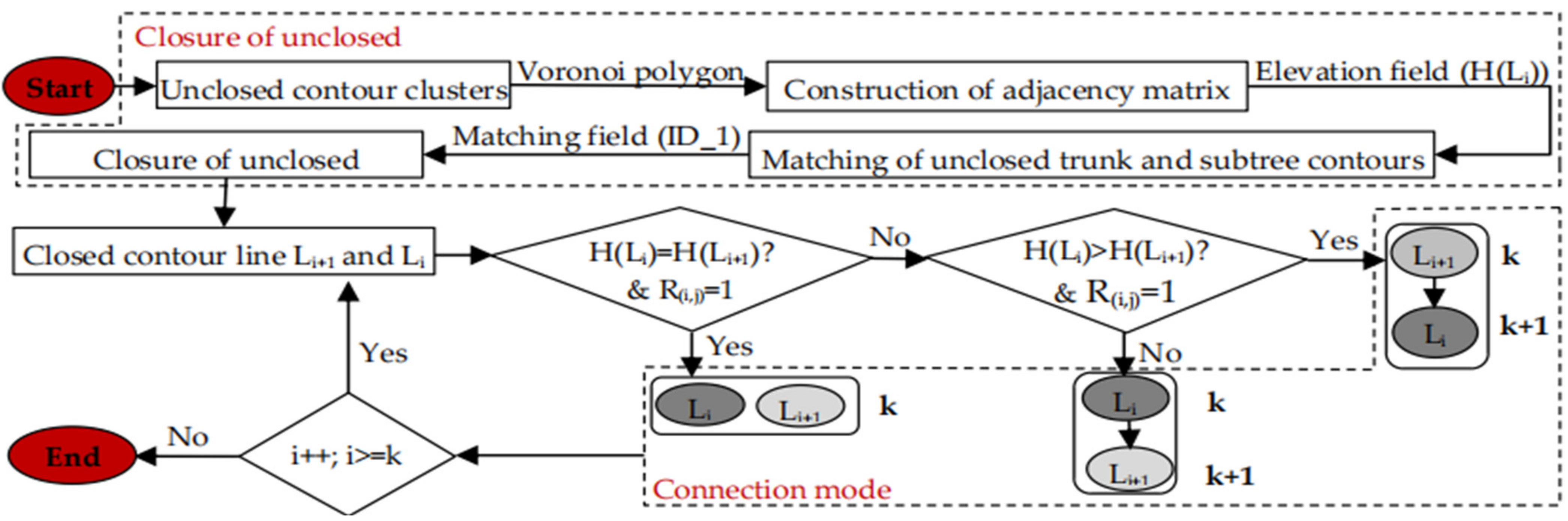
3.1. Construction of Directed Contour Tree
3.2. Quantitative Expression Method of Topological Relations
3.2.1. Topologically Contained Relation
3.2.2. Topologically Neighboring Relation
3.2.3. Topologically Disjoint Relation
3.3. A Formula for Calculating Multi-Scale Topological Indexes
3.3.1. Definition of Contour Interval Change
3.3.2. Adjacent Scale Topological Index Ratio
3.3.3. Multi-Scale Topological Indexes
4. Experiments and Results
4.1. Validation of Directed Contour Trees
4.2. Analysis of the Influencing Factors of Topological Indexes
- (1)
- Different from topologically disjoint and topologically neighboring relation, the average of the total number of topologically contained relation of mountain topography is consistently higher than that of fluvial landform and loess geomorphy, whatever the map scale is.
- (2)
- From different macro-geomorphological types at the same map scale perspective, the standard deviation of directed contour tree depth and the total number of topologically contained relations corresponding to mountains topography and fluvial landform is significantly greater than that of loess geomorphy. However, the variation coefficient of the total number of closed contours is just the other way around.
- (3)
- From the viewpoint of different map scales of the same geomorphological types, with the decrease of map scale, except for variation coefficients of the total number of closed contours corresponding to mountains topography and fluvial landform remain unchanged, the standard deviation of the other topological indexes decreases gradually. In contrast, the variation coefficient of the total number of topologically disjoint relations of mountain topography gradually increases.
4.3. Quantitative Trends of Multi-Scale Topological Indexes
4.3.1. Adjacent Scale Topological Indices
- (1)
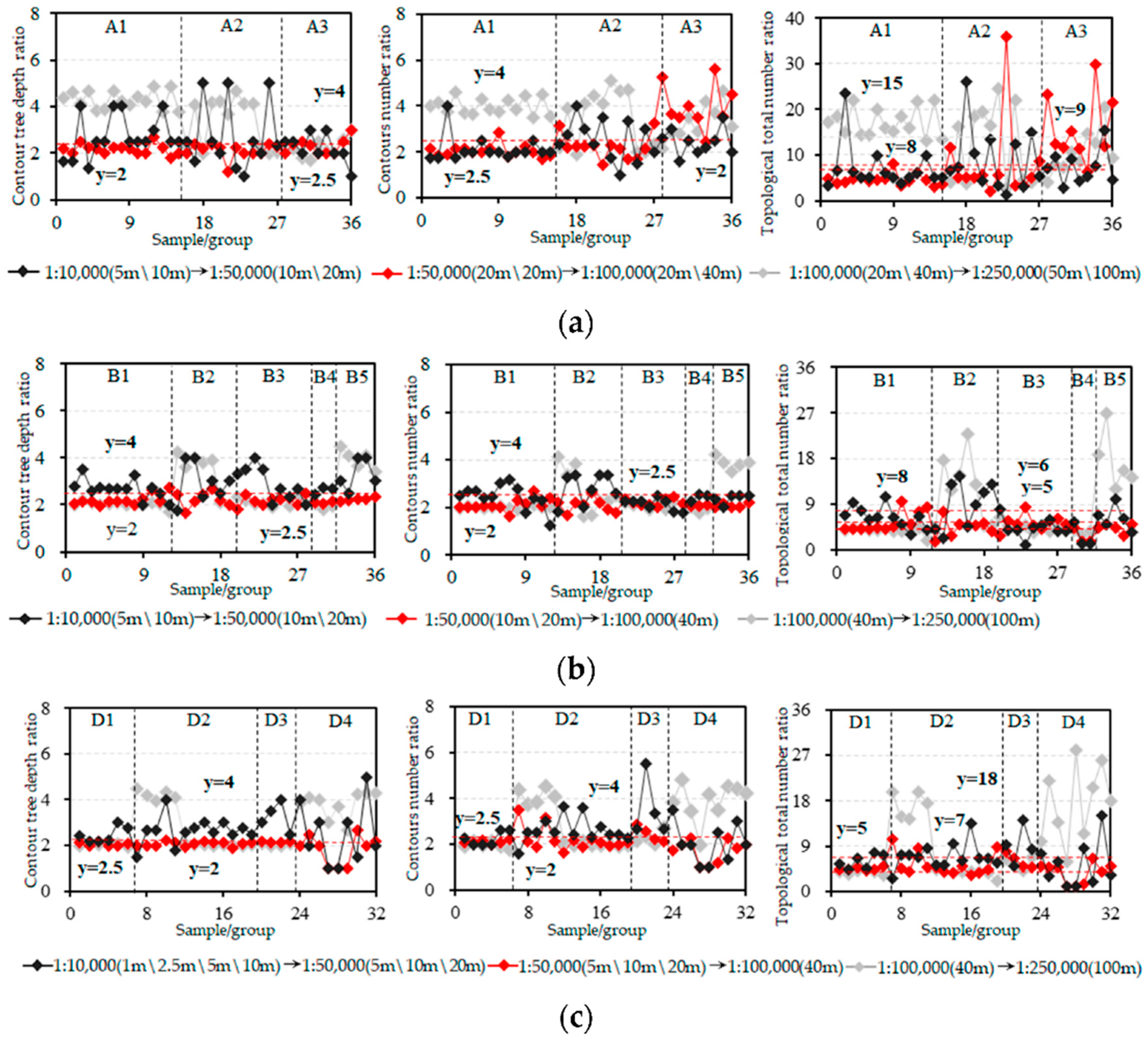
- Although different samples, which belong to the same map scale and micro-geomorphological types, have different contour intervals, the average of contours number ratio or the average of contour trees depth ratio is equal to the contour interval ratio of the adjacent scale contour cluster. However, due to the difference of surface relief, steep slope and surface fragmentation degree, the adjacent scale contours number ratio or the adjacent scale contour trees depth ratio is not a constant but fluctuates around the adjacent scale contour interval ratio. When the map scale change is 2.5, i.e., when contour cluster is generalized from 1:100,000 to 1:250,000, the adjacent scale topology indexes tend to be more volatile.
- (2)
- Different from the former, the average of adjacent scale topological total number ratio is positively correlated with the corresponding contour interval ratio, but there is no proportional relation between them. For example, when the contour interval ratio of mountainous topography is {2, 2.5, 4}, the corresponding average of topological total number ratio is {5, 6, 8}. Even though the adjacent scale contour interval ratios are the same, there are significant differences in topological total number ratio for the adjacent scale contour clusters of different macro-geomorphological types, e.g., when both the former are 2.5, the latter are 15 and 8 for loess geomorphy and mountainous topography, respectively. Therefore, the following sections further explore the trends of topological similarity (i.e., the topological total number of contour cluster) with the change of map scale.
4.3.2. Multi-Scale Topological Indices
- (1)
- With the increase of map scale change, multi-scale topological index ratio decreases gradually compared within any group of samples (red line > black > gray). Nevertheless, it is not all true between different groups of samples. For example, in Figure 4b, the map scale change, contour interval change and topological similarity degrees of the 15th and 30th groups contour clusters are {10, 4, 0.0772} and {5, 4, 0.0622}, respectively. The contour interval change of the two samples is 4, and the map scale change of the former is greater than that of the latter, but topological similarity degree of the former is also larger than that of the latter.
- (2)
- Although map scale change and macro-geomorphological type are the same, multi-scale topological index ratios of different micro-geomorphological types are remarkably different. For example, as shown by the red curve in Figure 4b, the map scale change and macro-geomorphological type of the 13th–17th groups and 1th–12th groups are the same, all belonging to mountainous topography, but micro-geomorphological type of the former is medium and high altitude and moderate relief mountains and the latter is medium altitude and moderate relief mountains, and corresponding multi-scale topological similarity degrees fluctuate around 0.06 and 0.24, respectively. It can be known from Table 1 that the contour interval changes of the 13th–17th groups and 1st–12th groups are 4 and 2, respectively.
- (3)
- If the contour interval changes of two groups of samples are the same, their corresponding topological indexes ratios also are very close, which all fluctuate around its average. For example, it can be known from Figure 4b and Table 1 that the contour interval change and macro-geomorphological type of the 1st–12th groups and 13th–17th groups are the same, and micro-geomorphological type of the former is medium altitude and moderate relief mountains, the latter is medium and high altitude and moderate relief mountains, micro-geomorphological type is different, but multi-scale topological similarity degrees of them are very close, which all fluctuates around 0.24.
4.4. Quantitative Relations between Multi-Scale Topological Similarity Degree and Map Scale Change
4.4.1. Quantitative Trends
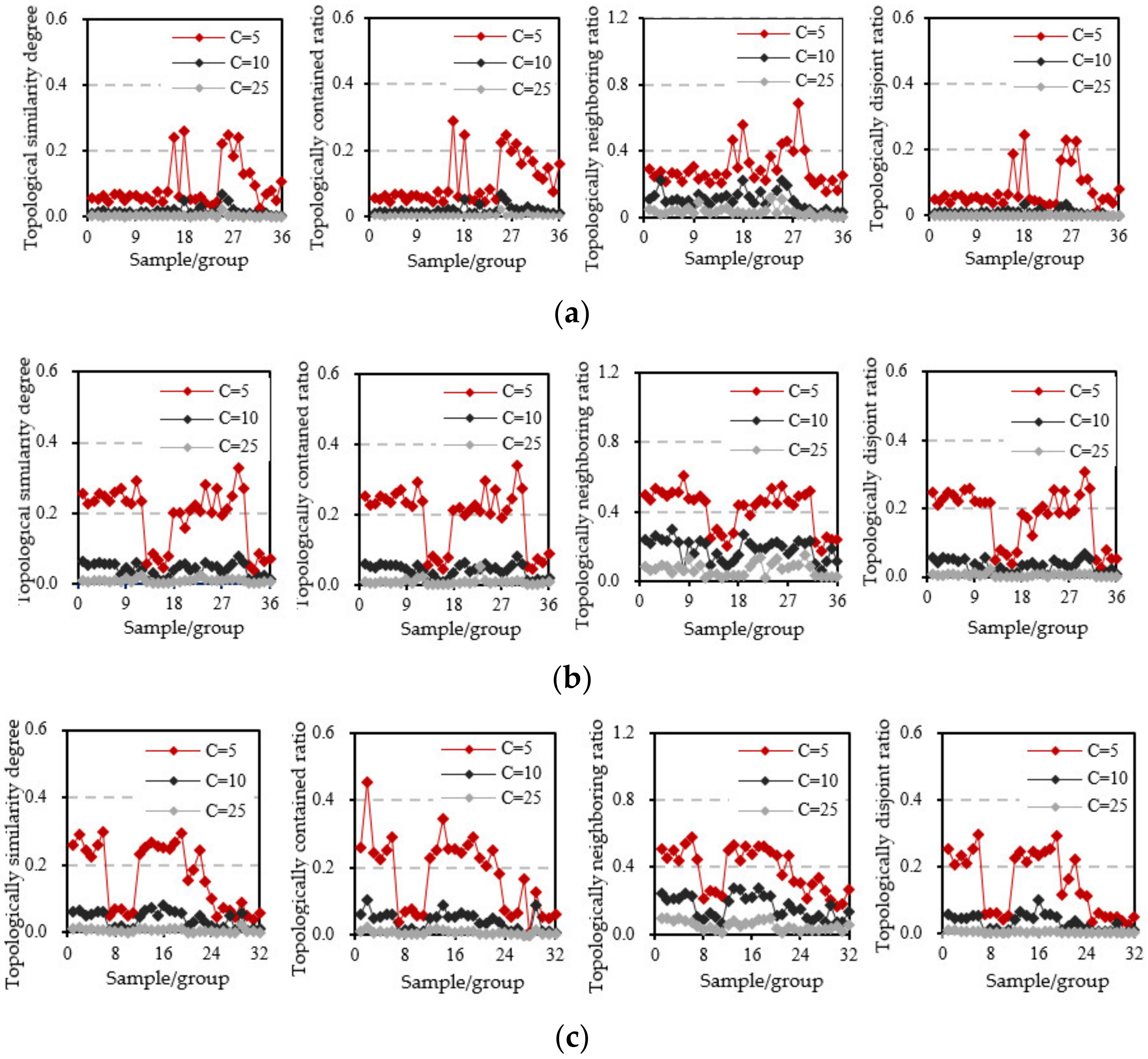
- (1)
- With the increase of map scale change, multi-scale topological similarity degree and its standard deviation decrease gradually, but variation coefficient increases gradually. For example, with the map scale change increases from 5 to 25, corresponding standard deviations of multi-scale topological similarity degree of mountainous topography decrease from 0.0849 to 0.0054, but the variation coefficients increase from 0.4501 to 0.6993, which indicated that with the increase of map scale change, the dispersion degree of multi-scale topological similarity degree decreases gradually, but the relative fluctuation between topological similarity degrees increase gradually. This trend is consistent with the results in Figure 4.
- (2)
- If the contour interval remains unchanged before and after generalization, the multi-scale topological index ratio tends to be 1. In the experiment, four groups of multi-scale contour clusters of different micro-geomorphological types were selected and were generalized from 1:5000 to 1:10,000, and the contour interval before and after generalization is 5 m, and corresponding closed contour line number ratio, contour tree depth ratio and topological similarity degree are {0.9294, 0.9853, 0.8728}, {1, 1, 1}, {0.9881, 0.9863, 1}, and {1, 1, 0.9669}, respectively.
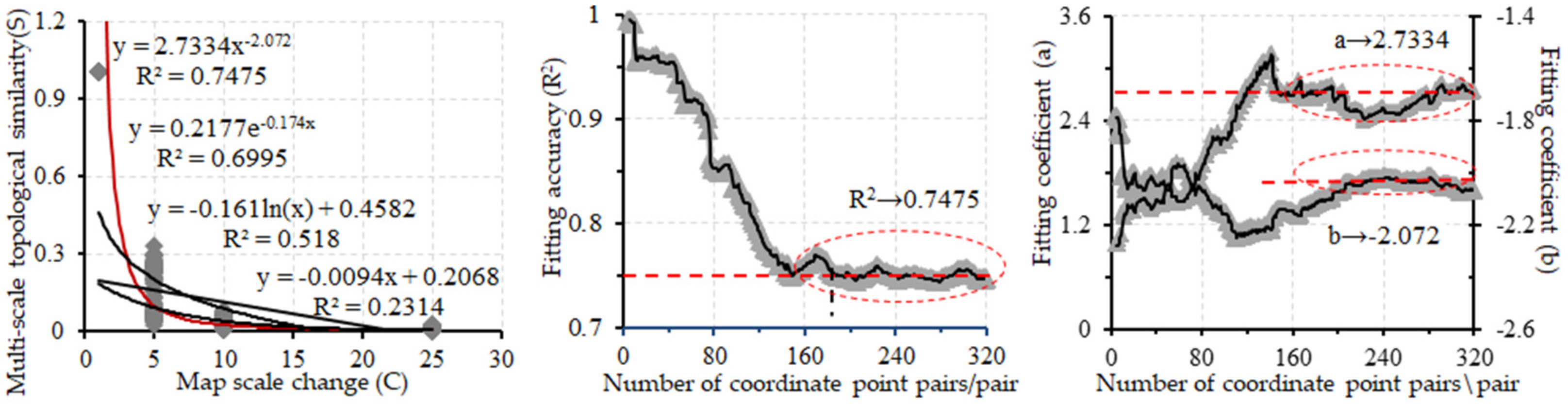
4.4.2. Influence of Sample Size on the Types and Precisions of Fitting Function
5. Discussion
6. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yan, H.W.; Li, J. Spatial Similarity Relations in Multi-Scale Map Spaces; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Chehreghan, A.; Abbaspour, R.A. An assessment of spatial similarity degree between polylines on multi-scale, multi-source maps. Geocarto Int. 2017, 32, 471–487. [Google Scholar] [CrossRef]
- Wei, Z.W.; Guo, Q.S.; Chen, L.; Liu, Y.; Tong, Y. Shape similarity measurement based on DNA alignment for buildings with multiple orthogonal features. Acta Geod. Cartogr. Sin. 2021, 50, 1683–1693. [Google Scholar]
- Li, W.W.; Raskin, R.; Goodchil, M.F. Semantic similarity measurement based on knowledge mining: An artificial neural net approach. Int. J. Geogr. Inf. Sci. 2012, 26, 1415–1435. [Google Scholar] [CrossRef]
- Gao, X.R.; Yan, H.W.; Lu, X.M. Semantic similarity measurement for building polygon aggregation in multi-scale map space. Acta Geod. Cartogr. Sin. 2022, 51, 95–103. [Google Scholar]
- Li, B.; Fonseca, F. TDD: A comprehensive model for qualitative spatial similarity assessment. Spat. Cogn. Comput. 2006, 6, 31–62. [Google Scholar] [CrossRef]
- Zhang, L.; Guilbert, E. Evaluation of river network generalization methods for preserving the drainage pattern. Int. J. Geo-Inf. 2016, 5, 230. [Google Scholar] [CrossRef]
- Yan, X.F.; Ai, T.H.; Yang, M.; Yin, H. A graph convolution neural network for classification of building patterns using spatial vector data. ISPRS J. Photogramm. Remote Sens. 2019, 150, 259–273. [Google Scholar] [CrossRef]
- Yan, X.F.; Ai, T.H.; Yang, M. A simplification of residential feature by the shape cognition and template matching method. Acta Geod. Cartogr. Sin. 2016, 45, 874–882. [Google Scholar]
- Fan, H.C.; Zipf, A.; Fu, Q.; Neis, P. Quality assessment for building footprints data on OpenStreetMap. Int. J. Geogr. Inf. Sci. 2014, 28, 700–719. [Google Scholar] [CrossRef]
- Zhao, Y.P.; Sun, Q.; Liu, X.G.; Cheng, M.; Yu, T.; Li, Y.F. Geographical entity-oriented semantic similarity measurement method and its application in road matching. Geomat. Inf. Sci. Wuhan Univ. 2020, 45, 728–735. [Google Scholar]
- Fan, H.C.; Yang, B.S.; Zipf, A.; Rousell, A. A polygon-based approach for matching openstreetmap road network with regional transit authority data. Int. J. Geogr. Inf. Sci. 2016, 30, 748–764. [Google Scholar] [CrossRef]
- Chehreghan, A.; Abbaspour, R.A. A geometric-based approach for road matching on multi-scale datasets using a genetic algorithm. Cartogr. Geogr. Inf. Sci. 2018, 45, 255–269. [Google Scholar] [CrossRef]
- Ruas, A. Automating the generalization of geographical data. In Proceedings of the 20th International Cartographic Conference, Beijing, China, 18 May 2010; pp. 1943–1953. [Google Scholar]
- Yang, W.F.; Yan, H.W.; Li, J. Formula for calculating spatial similarity degrees between point clouds on multi-scale maps taking map scale change as the only independent variable. Geod. Geodyn. 2015, 6, 113–125. [Google Scholar] [CrossRef][Green Version]
- Wang, J.Y.; He, Z.Y.; Pu, Y.X. Cartography; Surveying and Mapping Press: Beijing, China, 2016. [Google Scholar]
- Li, Z.L.; Sui, H.G. An integrated technique for automated generalization of contour maps. Cartogr. J. 2000, 37, 29–37. [Google Scholar] [CrossRef]
- Guo, R.Z. Spatial Analysis; Higher Education Press: Beijing, China, 2001. [Google Scholar]
- Yan, H.W.; Wang, J.Y. Description Approaches and Automates Generalization Algorithms for Groups of Map Objects; The Science Press: Beijing, China, 2009. [Google Scholar]
- Qiao, C.F.; Zhao, R.L.; Chen, J.; Chen, Y.H. A voronoi interior adjacency-based approach for generating a contour tree. Geomat. Inf. Sci. Wuhan Univ. 2005, 30, 801–804. [Google Scholar]
- Zhang, Y.; Fan, H.; Huang, W. The method of generating contour tree based on contour Delaunay triangulation. Acta Geod. Cartogr. Sin. 2012, 41, 461–474. [Google Scholar]
- Chen, J.; Li, C.M.; Li, Z.L.; Gold, C. A Voronoi-based 9-intersection Model for Spatial Relations. ISPRS J. Geogr. Inf. Sci. 2001, 15, 201–220. [Google Scholar] [CrossRef]
- Chen, J.; Zhao, R.L.; Li, Z.L. Voronoi-based k-order Neighbor Relations for Spatial Analysis. ISPRS J. Photogramm. Remote Sens. 2004, 59, 60–72. [Google Scholar] [CrossRef]
- Li, Z.L.; Huang, P.Z. Quantitative Measures for Spatial Information of Maps. Int. J. Geogr. Inf. Sci. 2002, 16, 699–709. [Google Scholar] [CrossRef]
- Qiao, C.F.; Zhao, R.L.; Chen, J.; Chen, Y.H. A method for generating contour tree based on voronoi interior adjacency. Geo-Spat. Inf. Sci. 2005, 8, 287–290. [Google Scholar]
- Chen, J.; Qiao, C.F.; Zhao, R.L. A Voronoi Interior Adjacency based Approach for Generating a Contour Tree. Comput. Geosci. 2004, 30, 355–367. [Google Scholar] [CrossRef]
- Guo, W.Y.; Liu, H.Y.; Sun, Q.; Yu, A.Z.; Chen, H.X. A Contour Group Mixed Similarity Measurement Model for Region Incremental Updating. J. Geo-Inf. Sci. 2019, 21, 147–156. [Google Scholar]
- Guo, W.Y.; Liu, H.Y.; Sun, Q.; Yu, A.Z.; Ding, Z.Y. A multisource contour matching method considering the similarity of geometric features. Acta Geod. Cartogr. Sin. 2019, 48, 643–653. [Google Scholar]
- Ai, T.H. The drainage network extraction from contour lines for contour line generalization. ISPRS J. Photogramm. Remote Sens. 2007, 62, 93–103. [Google Scholar] [CrossRef]
- Zhou, X.; Li, W.; Arundel, S.T. A spatio-contextual probabilistic model for extracting linear feature in hilly terrain from high-resolution DEM data. Int. J. Geogr. Inf. Sci. 2019, 33, 666–686. [Google Scholar] [CrossRef]
- Bjorke, J.T.; Nilsen, S. Wavelets applied to simplification of digital terrain models. Int. J. Geogr. Inf. Sci. 2003, 17, 601–621. [Google Scholar] [CrossRef]
- Ai, T.H.; Li, J.Z. A DEM generalization by minor valley branch detection and grid filling. ISPRS J. Photogramm. Remote Sens. 2010, 65, 198–207. [Google Scholar] [CrossRef]
- Zhou, Q.M.; Chen, Y.M. Generalization of DEM for terrain analysis using a compound method. ISPRS J. Photogramm. Remote Sens. 2011, 66, 38–45. [Google Scholar] [CrossRef]
- Chen, C.F.; Li, Y. An orthogonal least-square-based method for DEM generalization. Int. J. Geogr. Inf. Sci. 2013, 27, 154–167. [Google Scholar] [CrossRef]
- Wang, J.Y. Geomorphology and Its Generalization; Surveying & Mapping Publishing House: Beijing, China, 2019. [Google Scholar]
- Chen, W.M.; Zhou, C.H.; Li, B.Y.; Chai, H.X.; Zhao, S.M. Quantitative extraction and analysis of basic morphological types of land geomorphology in china. J. Geogr. Sci. 2011, 21, 771–790. [Google Scholar]
- Hao, X.Y. Map Information Recognition and Extraction Technology; Surveying & Mapping Publishing House: Beijing, China, 2001. [Google Scholar]
- Wu, H.H. GIS and Basic Model and Algorithm of Map Information Generalization; Wuhan University Press: Wuhan, China, 2012. [Google Scholar]
- Guo, Q.S.; Wu, H.H.; Li, P.C. Spatial relation rules and progressive graphic simplification of contours. Geomat. Inf. Sci. Wuhan Univ. 2000, 25, 31–34. [Google Scholar]
- Nigel, W. Geographical Data Analysis; Wiley & Sons Ltd.: New York, NY, USA, 1995. [Google Scholar]

| Macro-Geomorphological Types (C) | Micro-Geomorphology Types (Type Encoding) | Samples | di\m | CI | |||
|---|---|---|---|---|---|---|---|
| S1 | S2 | S3 | S4 | ||||
| A. Loess geomorphy (5, 10, 25) 36 groups | IMiddle altitude loess tableland (A1) | Sample1–Sample15 | 5 | 20 | 40 | 100 | (4, 8, 20) |
| Middle and high altitude loess ridge (A2) | Sample17, Sample19–24 | 5 | 20 | 40 | 100 | (4, 8, 20) | |
| Middle altitude loess ridge (A3) | Sample36 | 5 | 20 | 40 | 100 | (4, 8, 20) | |
| Middle and high altitude loess ridge (A2) | Sample16, Sample18 | 10 | 20 | 40 | 100 | (2, 4, 10) | |
| Sample25–Sample27 | 5 | 10 | 20 | 50 | (2, 4, 10) | ||
| Middle altitude loess ridge (A3) | Sample28–Sample35 | 5 | 10 | 20 | 50 | (2, 4, 10) | |
| B. Mountainous topography (5, 10, 25) 36 groups | Middle altitude and moderate relief mountain (B1) | Sample1–Sample12 | 10 | 20 | 40 | 100 | (2, 4, 10) |
| Middle and high altitude and moderate relief mountain (B2) | Sample18, Sample19 | 10 | 20 | 40 | 100 | (2, 4, 10) | |
| High altitude and high relief mountain (B3) | Sample20–Sample28 | 10 | 20 | 40 | 100 | (2, 4, 10) | |
| Middle and high altitude and high relief mountain (B4) | Sample29–Sample31 | 10 | 20 | 40 | 100 | (2, 4, 10) | |
| Middle and high altitude and moderate relief mountain (B2) | Sample13–Sample17 | 5 | 20 | 40 | 100 | (4, 8, 20) | |
| High altitude and moderate relief mountain (B5) | Sample32–Sample36 | 5 | 20 | 40 | 100 | (4, 8, 20) | |
| C. Fluvial landform (5, 10, 25) 32 groups | Middle altitude alluvial diluvial tableland (D1) | Sample1–Sample6 | 5 | 10 | 20 | 50 | (2, 4, 10) |
| Middle altitude alluvial diluvial plain (D2) | Sample12–Sample19 | 10 | 20 | 40 | 100 | (2, 4, 10) | |
| Middle altitude diluvial plain (D3) | Sample20–Sample23 | 5 | 10 | 20 | 50 | (2, 4, 10) | |
| Middle altitude alluvial diluvial plain (D1) | Sample7–Sample11 | 5 | 20 | 40 | 100 | (4, 8, 20) | |
| Middle and high altitude alluvial plain (D4) | Sample24–Sample28 | 5 | 20 | 40 | 100 | (4, 8, 20) | |
| Middle and high altitude alluvial plain (D4) | Sample29–Sample32 | 2.5 | 10 | 20 | 50 | (4, 8, 20) | |
| FID | ID_1 | Elev | FID | ID_1 | Elev | FID | ID_1 | Elev |
|---|---|---|---|---|---|---|---|---|
| 7 | 0 | 2780 | 25 | 11 | 2580 | 51 | 16 | 2480 |
| 6 | 1 | 2760 | 64 | 12 | 2560 | 52 | 16 | 2480 |
| 11 | 2 | 2760 | 65 | 12 | 2560 | 53 | 17 | 2460 |
| 5 | 3 | 2740 | 66 | 12 | 2560 | 54 | 17 | 2460 |
| 4 | 4 | 2720 | 67 | 12 | 2560 | 55 | 17 | 2460 |
| 1 | 5 | 2700 | 68 | 12 | 2560 | 56 | 17 | 2460 |
| 3 | 6 | 2680 | 39 | 13 | 2540 | 57 | 17 | 2460 |
| 12 | 7 | 2660 | 40 | 13 | 2540 | 13 | 18 | 2440 |
| 26 | 8 | 2640 | 41 | 13 | 2540 | 14 | 19 | 2420 |
| 27 | 8 | 2640 | 42 | 13 | 2540 | 37 | 20 | 2400 |
| 28 | 8 | 2640 | 43 | 13 | 2540 | 38 | 20 | 2400 |
| 18 | 9 | 2620 | 44 | 14 | 2520 | 62 | 21 | 2380 |
| 19 | 9 | 2620 | 45 | 14 | 2520 | 63 | 21 | 2380 |
| 20 | 9 | 2620 | 46 | 14 | 2520 | 58 | 22 | 2360 |
| 29 | 10 | 2600 | 47 | 14 | 2520 | 59 | 22 | 2360 |
| 30 | 10 | 2600 | 48 | 14 | 2520 | 60 | 23 | 2340 |
| 32 | 10 | 2600 | 34 | 15 | 2500 | 15 | 24 | 2320 |
| 21 | 11 | 2580 | 35 | 15 | 2500 | 16 | 25 | 2300 |
| 22 | 11 | 2580 | 36 | 15 | 2500 | 17 | 26 | 2280 |
| 23 | 11 | 2580 | 49 | 16 | 2480 | |||
| 24 | 11 | 2580 | 50 | 16 | 2480 |
| FID | ID_1 | Elev |
|---|---|---|
| 8 | 30 | 2680 |
| 2 | 29 | 2700 |
| 9 | 28 | 2720 |
| 10 | 27 | 2740 |
| 11 | 2 | 2760 |
| FID | ID_1 | Elev |
|---|---|---|
| 3 | 6 | 2680 |
| Si | Ti | Loess Geomorphy | Mountainous Topography | Fluvial Landform | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| 1:10,000 | Depth | 31.7500 | 13.4725 | 0.4243 | 50.2778 | 19.9078 | 0.3960 | 42.4848 | 17.4053 | 0.4097 |
| M | 66.8889 | 31.6831 | 0.4737 | 58.2778 | 18.7214 | 0.3212 | 55.7273 | 23.1129 | 0.4147 | |
| 3836.0556 | 2819.0186 | 0.7349 | 3434.6944 | 2278.3595 | 0.6633 | 2544.9512 | 2370.9353 | 0.9316 | ||
| 1168.2778 | 687.0929 | 0.5881 | 1646.3889 | 1123.9848 | 0.6827 | 1403.5758 | 1026.1380 | 0.7311 | ||
| 2541.7222 | 2418.7397 | 0.9516 | 1729.6944 | 1144.6050 | 0.3254 | 1697.4848 | 1227.7492 | 0.7233 | ||
| 126.0556 | 130.8458 | 1.0380 | 58.6111 | 19.9007 | 0.6617 | 60.8485 | 25.4486 | 0.4182 | ||
| 1:50,000 | Depth | 9.1111 | 2.7545 | 0.3023 | 21.3056 | 10.5338 | 0.4944 | 14.6585 | 8.6793 | 0.5921 |
| M | 18.6667 | 11.2122 | 0.6007 | 25.9167 | 11.7215 | 0.4523 | 26.0000 | 17.9109 | 0.6889 | |
| 363.4444 | 493.4889 | 1.3578 | 774.8056 | 884.0768 | 1.1410 | 719.8537 | 976.8114 | 1.3570 | ||
| 137.1944 | 215.6154 | 1.5716 | 380.5278 | 441.1854 | 1.1594 | 224.5122 | 203.8794 | 0.9081 | ||
| 189.5278 | 345.6884 | 1.8239 | 368.1111 | 431.0448 | 1.1710 | 424.5366 | 733.8932 | 1.7287 | ||
| 36.7222 | 47.2269 | 1.2861 | 26.1667 | 12.9692 | 0.4956 | 70.8049 | 173.2333 | 2.4466 | ||
| 1:100,000 | Depth | 4.2222 | 1.3117 | 0.3107 | 9.8889 | 5.1922 | 0.5251 | 7.3846 | 3.9909 | 0.5404 |
| M | 7.0833 | 2.2216 | 0.3136 | 11.6667 | 5.1713 | 0.4433 | 10.0513 | 4.5128 | 0.4490 | |
| 41.8056 | 25.9128 | 0.6198 | 192.5833 | 330.3559 | 1.7154 | 93.8049 | 81.3432 | 0.8672 | ||
| 17.6389 | 9.3202 | 0.5284 | 69.4444 | 67.4496 | 0.9713 | 44.0769 | 38.7430 | 0.8790 | ||
| 15.7778 | 13.0693 | 0.8283 | 112.0000 | 267.8495 | 2.3915 | 43.4615 | 40.0025 | 0.9204 | ||
| 8.3889 | 4.6431 | 0.5535 | 11.1389 | 5.1556 | 0.4628 | 11.0769 | 7.9650 | 0.7191 | ||
| 1:250,000 | Depth | 1.8056 | 0.8218 | 0.4552 | 3.6389 | 2.0508 | 0.5657 | 2.7692 | 1.7839 | 0.6442 |
| M | 3.1111 | 1.3044 | 0.4193 | 4.8333 | 2.0213 | 0.4182 | 3.7692 | 1.7390 | 0.4614 | |
| 7.2222 | 5.8900 | 0.8155 | 88.1944 | 283.1588 | 3.2106 | 13.4878 | 14.1512 | 1.0492 | ||
| 3.1944 | 2.0677 | 0.6473 | 12.6667 | 12.1232 | 0.9571 | 7.6154 | 7.9161 | 1.0395 | ||
| 1.3611 | 2.2316 | 1.6396 | 71.3611 | 274.7458 | 3.8501 | 3.7949 | 4.9746 | 1.3109 | ||
| 2.6667 | 2.2168 | 0.8313 | 4.1667 | 2.2104 | 0.5305 | 2.7692 | 1.7085 | 0.6170 | ||
| Types | C | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| A. Loess geomorphology | 5 | 0.0584 | 0.0540 | 0.0664 | 0.0453 | 0.0692 | 0.0696 | 0.0498 | 0.0631 | 0.0663 | 0.0538 |
| 10 | 0.0120 | 0.0144 | 0.0166 | 0.0092 | 0.0135 | 0.0162 | 0.0111 | 0.0129 | 0.0081 | 0.0158 | |
| 25 | 0.0035 | 0.0022 | 0.0007 | 0.0015 | 0.0027 | 0.0032 | 0.0011 | 0.0021 | 0.0016 | 0.0041 | |
| C | |||||||||||
| 5 | 0.0626 | 0.0462 | 0.0756 | 0.0455 | 0.0742 | 0.0615 | 0.0545 | 0.0512 | 0.0605 | 0.0406 | |
| 10 | 0.0144 | 0.0077 | 0.0168 | 0.0152 | 0.0202 | 0.0122 | 0.0107 | 0.0090 | 0.0303 | 0.0073 | |
| 25 | 0.0029 | 0.0013 | 0.0017 | 0.0030 | 0.0040 | 0.0016 | 0.0010 | 0.0021 | 0.0023 | 0.0022 | |
| C | |||||||||||
| 5 | 0.0327 | 0.0455 | 0.1076 | 0.2394 | 0.2603 | 0.2222 | 0.2480 | 0.1847 | 0.2406 | 0.1290 | |
| 10 | 0.0098 | 0.0139 | 0.0050 | 0.0207 | 0.0509 | 0.0667 | 0.0477 | 0.0213 | 0.0103 | 0.0104 | |
| 25 | 0.0073 | 0.0011 | 0.0011 | 0.0031 | 0.0020 | 0.0222 | 0.0032 | 0.0040 | 0.0014 | 0.0011 | |
| C | |||||||||||
| 5 | 0.1339 | 0.0938 | 0.0244 | 0.0678 | 0.0783 | 0.0485 | 0.0924 | 0.0682 | 0.7384 | ||
| 10 | 0.0115 | 0.0062 | 0.0021 | 0.0108 | 0.0026 | 0.0041 | 0.0158 | 0.0135 | 0.8540 | ||
| 25 | 0.0041 | 0.0007 | 0.0005 | 0.0020 | 0.0003 | 0.0003 | 0.0028 | 0.0036 | 1.311 | ||
| B. Mountains geomorphy | C | ||||||||||
| 5 | 0.2542 | 0.2273 | 0.2344 | 0.2533 | 0.2464 | 0.2339 | 0.2599 | 0.2700 | 0.2323 | 0.2246 | |
| 10 | 0.0614 | 0.0530 | 0.0563 | 0.0595 | 0.0563 | 0.0565 | 0.0565 | 0.0280 | 0.0452 | 0.0301 | |
| 25 | 0.0088 | 0.0057 | 0.0072 | 0.0097 | 0.0087 | 0.0054 | 0.0087 | 0.0055 | 0.0148 | 0.0046 | |
| C | |||||||||||
| 5 | 0.2923 | 0.2020 | 0.2018 | 0.1578 | 0.2073 | 0.2230 | 0.2025 | 0.2819 | 0.2019 | 0.2699 | |
| 10 | 0.0583 | 0.0376 | 0.0530 | 0.0551 | 0.0358 | 0.0441 | 0.0239 | 0.0582 | 0.0470 | 0.0474 | |
| 25 | 0.0149 | 0.0033 | 0.0041 | 0.0068 | 0.0091 | 0.0110 | 0.0233 | 0.0131 | 0.0097 | 0.0080 | |
| C | |||||||||||
| 5 | 0.1944 | 0.2128 | 0.2318 | 0.2466 | 0.3290 | 0.2683 | 0.0561 | 0.0840 | 0.0662 | 0.0437 | |
| 10 | 0.0317 | 0.0426 | 0.0374 | 0.0566 | 0.0772 | 0.0589 | 0.0075 | 0.0290 | 0.0133 | 0.0091 | |
| 25 | 0.0084 | 0.0111 | 0.0224 | 0.0104 | 0.0110 | 0.0088 | 0.0030 | 0.0022 | 0.0009 | 0.0020 | |
| C | |||||||||||
| 5 | 0.0776 | 0.0532 | 0.0371 | 0.0827 | 0.0640 | 0.0696 | 0.1887 | 0.0849 | 0.4501 | ||
| 10 | 0.0157 | 0.0123 | 0.0074 | 0.0184 | 0.0220 | 0.0136 | 0.0393 | 0.0190 | 0.4834 | ||
| 25 | 0.0018 | 0.0018 | 0.0015 | 0.0018 | 0.0036 | 0.0038 | 0.0077 | 0.0054 | 0.6993 | ||
| D. Fluvial landform | C | ||||||||||
| 5 | 0.0509 | 0.0674 | 0.0698 | 0.0507 | 0.0571 | 0.1011 | 0.0455 | 0.0722 | 0.0667 | 0.0465 | |
| 10 | 0.0049 | 0.0150 | 0.0181 | 0.0058 | 0.0118 | 0.0199 | 0.0094 | 0.0147 | 0.0505 | 0.0065 | |
| 25 | 0.0019 | 0.0020 | 0.0025 | 0.0009 | 0.0014 | 0.0027 | 0.0007 | 0.0024 | 0.0003 | 0.0003 | |
| C | |||||||||||
| 5 | 0.0868 | 0.0485 | 0.0383 | 0.0559 | 0.2985 | 0.2606 | 0.2906 | 0.2449 | 0.2228 | 0.2591 | |
| 10 | 0.0590 | 0.0074 | 0.0096 | 0.0110 | 0.0601 | 0.0599 | 0.0656 | 0.0499 | 0.0529 | 0.0603 | |
| 25 | 0.0208 | 0.0013 | 0.0019 | 0.0010 | 0.0082 | 0.0110 | 0.0151 | 0.0076 | 0.0118 | 0.0077 | |
| C | |||||||||||
| 5 | 0.2313 | 0.2523 | 0.2661 | 0.2539 | 0.2496 | 0.2491 | 0.2660 | 0.2923 | 0.1838 | 0.1548 | |
| 10 | 0.0472 | 0.0634 | 0.0710 | 0.0511 | 0.0789 | 0.0661 | 0.0611 | 0.0559 | 0.0283 | 0.0197 | |
| 25 | 0.0091 | 0.0121 | 0.0074 | 0.0084 | 0.0058 | 0.0102 | 0.0093 | 0.0098 | 0.0006 | 0.0007 | |
| C | |||||||||||
| 5 | 0.2417 | 0.1489 | 0.1632 | 0.0973 | 0.5958 | ||||||
| 10 | 0.0477 | 0.0308 | 0.0379 | 0.0241 | 0.6347 | ||||||
| 25 | 0.0011 | 0.0012 | 0.0055 | 0.0052 | 0.9391 |
| Contour Interval Change | Sample Size (N)/Pair | Optimal Fitting Function |
| {1, 2, 4, 10} | N∈[4, 5], N∈N+ | Exponential function |
| N = 6 | Power function | |
| N∈[7, 23], N∈N+ | Exponential function | |
| N∈[24, 228], N∈N+ | Power function | |
| {1, 4, 8, 20} | N∈[4, 188], N∈N+ | Power function |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Yan, H.; Lu, X. Quantitative Relations between Topological Similarity Degree and Map Scale Change of Contour Clusters in Multi-Scale Map Spaces. ISPRS Int. J. Geo-Inf. 2022, 11, 268. https://doi.org/10.3390/ijgi11040268
Wang R, Yan H, Lu X. Quantitative Relations between Topological Similarity Degree and Map Scale Change of Contour Clusters in Multi-Scale Map Spaces. ISPRS International Journal of Geo-Information. 2022; 11(4):268. https://doi.org/10.3390/ijgi11040268
Chicago/Turabian StyleWang, Rong, Haowen Yan, and Xiaomin Lu. 2022. "Quantitative Relations between Topological Similarity Degree and Map Scale Change of Contour Clusters in Multi-Scale Map Spaces" ISPRS International Journal of Geo-Information 11, no. 4: 268. https://doi.org/10.3390/ijgi11040268
APA StyleWang, R., Yan, H., & Lu, X. (2022). Quantitative Relations between Topological Similarity Degree and Map Scale Change of Contour Clusters in Multi-Scale Map Spaces. ISPRS International Journal of Geo-Information, 11(4), 268. https://doi.org/10.3390/ijgi11040268






