Abstract
Thoughtful consideration of the enumeration unit size in choropleth map design is important to ensure the correct communication of spatial information. However, the enumeration unit size and its influence on pattern conveying in choropleth maps have not yet been the subject of in-depth empirical studies. This research aims to address this gap. We focused on the issue concerning whether the ability to recognize spatial patterns on an Equal Area Unit Map is related to the hexagonal enumeration unit size, defined by the number of pixels. The aim is to indicate the range of the enumeration unit sizes, namely, at what point the upper and lower borders of the range where the spatial patterns start, and where the end is visible and recognizable by users. To address this problem, we conducted an empirical study with 488 users. The results show that the enumeration unit size has an impact on the users’ spatial pattern recognition abilities. Choropleth maps with enumeration unit sizes of 26, 52, and 104 pixels were, in the majority, indicated by participants as those most suitable for indicating spatial patterns. This was in contrast to choropleth maps with enumeration unit sizes of 1664 and 3328 pixels, which users indicated as not being useful. However, there were some exceptions to this general finding. Thus, determining the optimal enumeration unit size is a challenging task, and requires further insightful investigations.
1. Introduction
The preservation, which also allows for recognition, of the characteristic elements of the mapped phenomena are important in map design, especially in map generalization. The importance of preserving and even highlighting spatial patterns constitutes one of the significant challenges in cartographic generalization [1,2]. Cartographic generalization, which assumes tailoring the map to its purpose, detail level, and intended audience requirements, is a difficult but necessary task for the map designer. Without careful and meaningful generalization, maps will not convey the essential spatial patterns of the mapped phenomena [3,4,5,6]. It should also be noted that the application’s context, namely a visualization purpose and characteristics of the presented phenomena, plays an essential role. This is a very important factor, and it influences the decision about what level of resolution or degree of generalization is sufficient and how detailed the patterns are that should be identified.
Knowledge about how humans recognize spatial patterns is also essential for the automation of map generalization. Since the 1960s, when research on automated generalization began, the issues connected with pattern recognition and preservation have also been tackled from many aspects. Early research connected with automated generalization resulted in a proposal for generalization models, by which the researchers wanted to simplify and control the generalization process [7,8,9,10]. In all proposed models, structure recognition and preservation have been treated as important issues.
In thematic mapping, including choropleth maps, cartographic generalization and pattern recognition play an essential role. In this case, generalization takes place when either the number of classes decreases or the enumeration unit size (EUS) increases. Choropleth maps can be designed with too small detail level, so increasing their size provides no additional information. Thus, especially in the case of choropleth maps, a change of scale is not necessarily connected to a change in generalization level [11]. While aspects related to optimal data classification methods and the number of classes have been extensively examined [11,12,13,14], the EUS, as well as its influence on pattern conveying and recognition, has not been the subject of in-depth empirical studies so far. Consequently, in the case of the EUS in choropleth maps, the challenge is to find the optimal generalization level at which the spatial patterns present in the data are adequately apparent to the user. This research aims to contribute to the existing body of knowledge concerning the specification of the optimal hexagonal EUS range, that is, to indicate the upper and lower borders of the range of spatial pattern visibility. In this research, we consider hexagonal shaped EUSs, however, we are aware of the fact that in choropleth maps administrative units (e.g., countries, NUTS at different levels, states, and counties, etc.) are most commonly used. Therefore, this choropleth map design should also be explored and studied with regard to administrative EUSs. However, due to the fact that one of the most often indicated limitations of this kind of choropleth map is their uneven unit sizes (and even the huge differences in their areas), it may considerably distort the perception of the presented patterns [15]. We decided to start the investigations using an Equal Area Unit Map (EAUM) solution, which is free from this limitation. Among geometrical EUSs, there are various shapes, namely squares, triangles or hexagonal and more. We have selected hexagonal EUSs as in geometry, the hexagonal tiling or hexagonal tessellation is a regular tiling of the Euclidean plane, in which three hexagons meet at each vertex. Hexagonal tiling is the densest way to arrange circles in two dimensions. This is assumed the best way to divide a surface into regions of equal area with the least total perimeter [16]. Moreover, EAUMs have recently gained popularity in online atlases, books and news media (News media: https://archive.nytimes.com/www.nytimes.com/interactive/2013/06/26/us/scotus-gay-marriage.html (The New York Times, accessed: 16 August 2021). https://www.bloomberg.com/graphics/2015-pace-of-social-change/ (Bloomberg, accessed: 16 August 2021). https://www.theguardian.com/us-news/ng-interactive/2014/oct/22/-sp-voting-rights-identification-how-friendly-is-your-state (The Guardian, accessed: 16 August 2021). https://www.visualcapitalist.com/us-states-top-tech-salaries-2021/?fbclid=IwAR1bJHOsD96mAHwuJ7QkDQunOYZGeM1VJ0xfNIqgEMrEIvqLEa3JBqhWN8k (visual capitalist, accessed: 16 August 2021). Online atlases and books: http://atlas2022.uw.edu.pl/mapa-miesiaca-pogranicze-prawoslawno-katolickie/ (Atlas of Poland’s Political Geography, awarded by ICA in 2019, accessed: 16 August 2021. https://gistbok.ucgis.org/bok-topics/common-thematic-map-types (GIS&T Body of Knowledge, accessed: 16 August 2021)). We treat this as the first step in the investigation, which should be further developed and modified to test the conditions with regard to administrative units. This research attempts to tackle three research questions.
RQ1. Is the estimated similarity to the raw data presentation proportional to the EUS applied in a choropleth map?
RQ2. Does the user’s preference for specific EUSs coincide with the ability to recognize spatial patterns?
RQ3. Is the ability to recognize spatial patterns related to the EUS?
2. Related Works
The effectiveness with which thematic maps communicate spatial information is connected to map design [17]. It is also often linked to map complexity [18], which is influenced by many factors, including the number of classes, the degree of autocorrelation present in the data, the choice of class intervals, and the shape and size of the enumeration areas [19]. Map complexity is regarded as being the “visual intricacy of the spatial patterns formed by the map symbols” [19] (p. 15). It is important to preserve these specific patterns during the thematic map generalization process.
Every choropleth map is the result of generalization, as it requires data classification and decisions about the number of classes. In order to further generalize the data for effective pattern presentation, one can select different enumeration unit sizes and thus change the generalization level of a choropleth map.
2.1. The Enumeration Unit’s Role in Choropleth Map Generalization
Optimal enumeration unit size plays an essential role in choropleth map generalization. When considering the advantages of generalizing choropleth maps, the following might be indicated: faster reading by map users due to there being less data to be understood and fewer details to be noticed compared to a more detailed choropleth map. However, we believe that the most important purpose of searching for an appropriately generalized choropleth map is to enable map users to notice the important patterns within the geographical distribution of the mapped phenomenon. In thematic maps, an EUS that is too small (i.e., too small a generalization level) results in a dispersed image and a difficulty with perceiving characteristic elements in the data: the image is fragmented and diffused. A user loses the picture of the whole and the characteristic elements of the structure (spatial patterns); she/he is no longer able to see the relevant regularities [20]. On the other hand, a generalization level that is too large, expressed in a choropleth map by an EUS that is too large, also causes those characteristic elements in the data to be lost. The resulting image is too general. An oversimplification of the map pattern might result in the loss of valuable information for the map reader [21]. In [22] it is also stated that the enumeration unit areas of a region, form a pattern that acts as a spatial generalization filter. Once an EUS gets too large, the spatial variation existing in the data tends to be reduced or averaged out. Thus, the authors are in favor of rather smaller enumeration units [11,21,22]. Moreover, they suggest using units of equal size and similar shape [23]. This recommendation is met in a choropleth map consisting of geometric units, for example, squares, triangles, and hexagons.
The role of pattern preservation in thematic maps is highlighted and illustrated in [7] using a group of lakes as an example. However, it can also refer to other types of objects, including enumeration units in choropleth maps. The elements of the process are (1) recognizing the shape of a group of lakes, (2) identifying the individual shapes of the individual lakes included in the group (they may have a specific direction and a specific orientation), (3) identifying the characteristic structure and patterns within the group of lakes, and (4) the phenomenon of the visual grouping of larger lakes [7]. In our research, stages 3 and 4 are crucial. In [7] the phenomenon of the formation of so-called “similarity groups” is emphasized. These groups are the result of perceiving the similarity of the shapes and sizes of the objects included in their composition [23,24,25]. An example of a generalization that takes into account the similarity of groups of objects can be found in Figure 1.
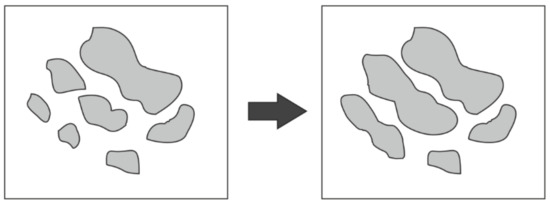
Figure 1.
An example of a generalization solution where the similarity of the objects is taken into account.
Similarly, the EUS in thematic maps should be designed in a way that preserves the characteristic patterns. Thus, the challenge is to find the optimal generalization level at which the spatial patterns present in the data are successfully conveyed to the user.
The role of choosing an appropriate geographic unit to design a choropleth map is highlighted in [26]. The authors claim that the main characteristics of choropleth mapping units are a high degree of resolution, the homogeneity of the mapped phenomenon, a uniformity of land area, the observation of minimum phenomenon attribute values, temporal stability and currency, compactness of shape, audience familiarity, data availability, and the functional relevance of the unit to the phenomena being mapped. They also present guidelines for choosing geographic unit sizes that take into account the above criteria by considering 12 geographic units ranging from census blocks to states. Even allowing for differences in scale and purpose, some units confer clear advantages over others. On the one hand, in [26] authors are in favor of smaller geographic units, arguing that the higher the spatial resolution the greater the information content. They assume that if the map contains a larger number of smaller units it offers more insights into local pattern identification. However, they also note that global spatial patterns are sometimes more evident at a coarser scale than at a finer scale [26,27,28].
The decision about which areal unit of aggregation to use is also very much related to a classic and well-studied issue called the Modifiable Areal Unit Problem–MAUP [29,30,31,32,33]. The MAUP is an effect of the geographical units’ artificial demarcation. As a result, the boundaries of the geographical units may be modified. Moreover, acquiring data according to different boundary definitions results in gathering different data sets. Thus, analyzing these data sets leads to different and inconsistent results. In the MAUP, two spatial aspects are of importance, namely, zoning and scale effects. The zoning effect takes place when the number of units stays constant within a given region, but new boundaries can be used to create a new zoning system. The data assigned according to these different zoning systems will then produce inconsistent analytical results. The scale effect is the result of the aggregation or disaggregation of spatial units resulting in the modification of the spatial resolution of the data. Smaller spatial units can be aggregated into larger ones that will, however, be fewer in number. This results in a lower spatial resolution of the data. On the other hand, they can be disaggregated into smaller spatial units. This also leads to inconsistent analytical results [31]. In this research the scale effect can be especially relevant, because when the EUS generalization level is changed, the EUS increases and, thus, the spatial resolution of the data decreases. Thus, even while considering the EUSs of the same size, MAUP should be thoughtfully noted and one should be aware of its consequences.
2.2. Empirical Evaluation of Pattern Preservation on Thematic Maps
An effective thematic map design, understood, among other factors, as the successful conveying of underlying patterns to the map user, has already been the subject of empirical studies. Psychologists distinguish two types of memory response, namely, recognition and recall [34]. In relation to map patterns, recognition is understood to be the ability to recognize a pattern among a broader set of patterns, while recall involves the reconstruction of the pattern from the memory.
In a study [34] the research questions concerned, among others, the factors that influence the map reader’s ability to recognize patterns. In the recognition experiment, the respondents were given eight similar, graduated circle maps (with different black circle arrangements) and were asked to rank these maps from most similar to least similar in relation to a map they had seen earlier. The respondents remembered larger circles and groups of circles better than smaller and isolated circles. However, different respondents identified different pattern shapes. The users noticed patterns of various shapes, including the shape of a “C,” an obtuse triangle, and a hook. The visual perception of spatial patterns on choropleth maps has also been considered in [15]. Three biases were examined. First the “dark-is-more bias,” which is the intuitive ranking of color lightness; second the “area-size bias,” which is the neglect of small areas, since these are less dominant in the perception than larger ones; and the “data-classification bias,” which is the attention to data classification when interpreting spatial patterns. The users were asked to detect extreme values, central tendencies, or homogeneities of values as well as comment on their task solving certainty. From the point of view of the reported study, the second bias is most relevant. It concerned the following question: to what degree is the effect of neglecting small areas caused by the fact that these areas are visually less dominant compared to larger areas and thus are commonly overseen? In the study in [15], administrative enumeration units were used, and the research hypotheses were concentrated on the question of the legend’s role in area-size-bias limitation. The results showed that the detection of small areas with globally extreme values was worse than those of large areas. In cases where a legend was provided, the results were improved, however, an unacceptable error rate of about 20% remained. The author points to, among others, Equal Area Unit Maps (EAUMs) as a possible solution to these problems and partially confirms this in the follow up research [35]. In the next study concerning the effectiveness of the use of EAUMs versus geographical EUSs [35], it is empirically confirmed that EAUMs are more effective in tasks concerning local patterns, namely local extrema identification, especially in cases of small EUSs, while global patterns and hot spots are more effectively noticed in the case of geographical EUSs. However, in [15,35], only a comparison between geographical units and EAUMs has been conducted. The influence of EUSs’ size on spatial pattern recognition abilities has not been taken into account.
In another study, [18] the authors examined the relative effectiveness of choropleth and isopleth maps, and how effectiveness was influenced by visual complexity. A general distribution of population was presented using choropleth and isopleth maps. The visual complexity was regarded as the degree to which the combination of map elements (understood as a number, size, and distribution of delineated areas on the map) resulted in a specific pattern. Two hypotheses were tested. The first was that isopleth maps are more effective at communicating spatial distribution than choropleth maps. The second hypothesis concerned the assumption that the effectiveness of map communication remains constant with increasing complexity up to some critical level. However, beyond this level effectiveness decreases while complexity increases. The author tested map pairs: one in which the number of classes was held constant while the distribution was varied, and the other in which the number of classes for a single distribution was varied. As a result, it appeared that an increase in both the complexity of distribution and the number of classes results in a decrease in map effectiveness in terms of pattern identification. What is more, the changes in the complexity of distribution seemed to have more impact on the effectiveness of pattern identification than the number of classes. It also seemed that general map patterns were remembered better with isopleth than with choropleth maps, and so the first hypothesis was accepted. The second hypothesis was only partially confirmed. It was proved that with increasing map complexity the effectiveness decreases. However, the hypothesized “critical” level of complexity, up to which the effectiveness would be constant and beyond which the effectiveness would decrease, was not found. The reason for this could be that none of the maps used in the experiment had a level of visual complexity low enough for the “critical level” to be manifested.
Spatial pattern recognition also plays an essential role in communicating geographic statistics concerning health in a more effective manner. For the design of the Atlas of United States Mortality at the National Center for Health Statistics (NCHS), a series of user studies was conducted to determine how effectively readers extract statistical information from choropleth maps [36,37,38]. The questions asked for statistical maps considered issues of mortality rate in certain places, general pattern recognition concerning geographic trends in the data or clusters of high- or low-rate areas, and the existence of mortality patterns among males and females, or blacks and whites. The users were also asked about which enumeration units were the most helpful in solving the tasks. As a result of the research, it appeared that maps using familiar geographical units (US states) supported the recall of information better than less familiar and smaller geographical units.
The similarity between choropleth maps has been empirically verified with regard to map complexity [39,40]. In [39] the relative importance of three map attributes (correlation, blackness, and complexity) for judging the similarity of choropleth maps was determined. As a result of several analyses on variance procedures, it was concluded that blackness was the most critical attribute for judging similarity, followed by correlation and complexity, which were cited as being least important for judging choropleth map similarity. Based on the presented empirical studies, it can be concluded that, to date, the influence of the EUS has not gained enough attention and that there is a lack of comprehensive empirical research considering various EUSs. Thus, after comprehensive research concerning the optimal number of classes for choropleth maps [19], research concerning the influence of the EUS on users’ ability to recognize spatial patterns, and aimed at defining an optimal EUS range, seems to complement the previous works.
3. Materials and Methods
We conducted an empirical study to verify if choropleth maps with particular EUSs, result in a more effective perception of characteristic patterns in data. We therefore addressed the research questions listed in Section 1 to approximating where the limit of the EUS lies, after exceeding which, users lose the possibility of effectively perceiving the spatial patterns presented on thematic maps.
3.1. Materials
Choropleth maps with eight EUSs were compared to a symbol map. The symbol map assumes that every symbol (every dot) represents one geographical object. Some authors name this kind of map a dot map arguing that a dot map is the result of a nominal map of points [41]. A dot map may also be confused with a dot density map. Thus, we call this kind of map a symbol map. For the purpose of this study, nine maps were designed. The maps presented a fictional area and a fictional phenomenon. All maps presented the same phenomenon but with different levels of generalization, which was expressed by the EUS. The symbol map presented the distribution of the phenomenon in a discreet way and was considered to be a presentation of the raw data. Based on the symbol map, eight choropleth maps using hexagonal shaped units and a range of EUSs were prepared. Eight EUSs were assessed, namely hexagonal units with an area of 2, 4, 8, 16, 32, 64, 128, and 256 km2. The maps were carefully selected in a way that represented different sizes of EUS, from smaller to larger. Every EUS is twice as big as the previous one; thus, they follow a geometrical order. The smallest EUS (2 km2) is intentionally very close to the raw data (symbol map), while the largest (256 km2) is quite distant from the raw data. The EUSs’ sizes were selected in such a way as to represent various levels of generalization for choropleth maps. The maps were generated in ArcMap 10.6.1 using the “generate tessellation” tool. The maps were designed at 1:1,400,000 scale. Thus, 1 pixel equaled about 0.2 mm × 0.2 mm, and 1 mm2 equaled 25 pixels. The hexagonal unit sizes were recalculated into pixels. They correspond to 26, 52, 104, 208, 416, 832, 1664, and 3328 pixels (Figure 2). The maps were assigned the letters from A to F in an unordered way, neither increasing nor decreasing in the EUS order.
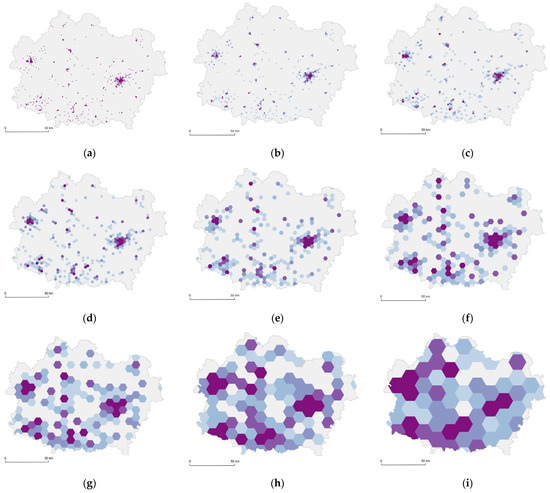
Figure 2.
The maps used in the study with their corresponding applied EUSs. The maps used in this table are also presented in Supplementary Materials in a larger scale (Figure S1). (a) Symbol map, (b) A. 26 pixels, (c) C. 52 pixels, (d) E. 104 pixels, (e) H. 208 pixels, (f) B. 416 pixels, (g) G. 832 pixels, (h) F. 1664 pixels, (i) D. 3328 pixels.
3.2. Study Design and Tasks
One independent and three dependent variables were defined. The EUS was considered an independent variable. The dependent variables were: (1) answer time, (2) users’ preference for particular EUS for solving the given task, and (3) the expected response. The expected response was applied due to the exploratory character of the tasks in this study. The majority of the tasks applied in this research were tasks where there was no specific correct answer (except T7: correct or incorrect spatial pattern). Instead, the most common answer was explored. Thus, in the case of the majority of tasks, the expected response metric was applied during data analysis. We provide further details and comments about time recording in Section 3.2 “Study design and tasks.” We decided to include answer time as one of usability performance metrics. This metric is often applied in cartographic user studies. The time recording was conducted using a tailored web application. The web application was used to design the test, to display each task, and to record and save the received answers and answer times. In order to omit answer time distortions that may result from not focusing on the test during the whole time of test’s execution, we decided that there would always be one participant from the project team present in the room where the participants worked during the test.
Each participant solved seven tasks. Four tasks were open and three tasks were closed (Table 1). Within the open questions, the users were asked to rank all choropleth map variants according to their similarity or dissimilarity (exclusion) to the reference symbol map (task 1 [T1] and task 2 [T2]). In T1 and T2, the symbol map and choropleth maps along with all tested EUSs, were presented to the participants. In task 5 (T5) they were asked to compare the symbol map with a choropleth map having a particular EUS in order to find and draw, on both maps, the corresponding areas in which the presented phenomenon was of similar shape and density. Further, they were asked to draw three lines that corresponded with the phenomenon’s concentration on each map variant (task 6 [T6]). In T6, one choropleth map was presented to the users.

Table 1.
Tasks that were tested in the study. The maps used in this table are presented in Supplementary Materials (Figure S1).
Within the closed tasks, the users were to use a 5 steps Likert scale to show which choropleth map (among all eight tested) they would prefer to use to describe the main characteristics of the phenomenon presented on the symbol map (task 3 [T3]). In task 4, again using a 5 step Likert scale, they answered the question asking how well the choropleth maps with their different unit sizes reflect the main characteristics (spatial patterns) of the phenomenon presented on the symbol map. For T3 and T4 again, map pairs consisting of the symbol map and a choropleth map were presented to participants. Finally, in task 7 they were presented with a symbol map with four patterns marked (two of them were correct and two incorrect) and a choropleth map. The participants had to choose which of the four patterns presented on the symbol map could be found on the presented choropleth map.
3.3. Procedure
The study was conducted in 22 high schools in 12 cities across Poland. The tasks were presented through an application available in a web browser. In each task, one or more maps were located at the left side of the screen, and the task description was located on the right side (Figure 3).
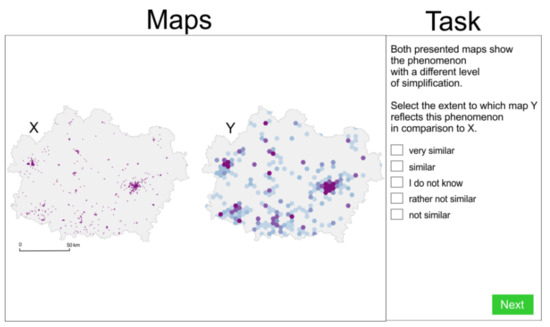
Figure 3.
The layout of one particular task in the study.
Before the study, the participants were informed that they were anonymously taking part in a study concerning thematic maps and they were asked to work independently. They were briefly told how to mark their answers. However, the participants were not disturbed during task solution once the test started.
After the main study, the participants were asked to fill in a personal questionnaire with questions about the participants’ gender, age, and frequency of map use.
3.4. Participants
The participants constituted 488 high school students. The group consisted of 268 women and 220 men, 55% and 45%, respectively. The average age was 17, and ages ranged between 15 and 20. Asked about using maps, 11% participants declared that they used them every day, 32% once a week, 21% once a month, 19% once every few months, 6% once a year, and 11% used maps less than once a year. Out of the total, 28% of the participants reported that they came from a city with a population above 200,000 inhabitants, 62% came from a city with a population under 200,000 inhabitants, and 10% came from villages. The participants were students from the two last years of high school education. Empirical data was collected at the end of the school year; therefore, most participants had already completed the majority of their courses, including those connected with map reading and interpretation. We believe that they had received training to build their knowledge and abilities similarly to most citizens who have completed this obligatory stage of education.
3.5. Data Analysis
Chi-square and Cramér’s V tests were used for the statistical inference to determine which EUS was most often selected for the tasks and perceived as presenting similar patterns to the raw, symbol map. Response times were analyzed using the Kolmogorov–Smirnov test and the Kruskal–Wallis test with Bonferroni’s correction. Additionally, a pairwise analysis was performed, which concerned the statistical differences between the EUSs. These were conducted between consecutively tested EUSs, since we wanted to indicate the range sizes resulting from better scores, therefore the upper and lower border of the range aimed to check when the effect began to be visible and when it ended. The analyses were carried out using SPSS software.
4. Results
In this section we report the results by considering two metrics: the expected answers and the answer time. Within the collected answers, we report the results of particular tasks, organizing the tasks into three groups that are related to the research questions specified in the Introduction. The first task group concerns Map ranking and map exclusion (T1 and T2), and is related to RQ1. The second considers User preferences: usefulness and degree of similarity (T3 and T4), and is thus related to RQ2. The third task group deals with Spatial pattern recognition (T5, T6, T7), and addresses RQ3.
4.1. Expected Answers
4.1.1. Map Ordering and Map Exclusion
Task 1 (T1) concerned ordering the maps: beginning with the map that best shows the main feature of the distribution of phenomenon. The data collected within this task was filtered and analyzed. The sequences indicated by only one user were excluded from further analysis; there were 136 sequences of this kind out of 488, which constitutes 28% of all sequences. The repeating sequences of EUSs were summarized. Among these, there were 23 different sequences. The most frequent sequences are presented in Figure 4.
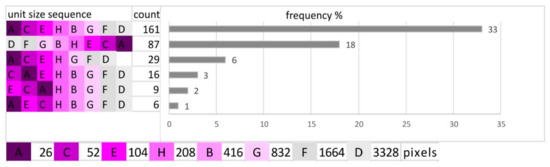
Figure 4.
The most frequent EUS sequences made by participants.
The most frequent EUS sequence was the sequence in which the EUS was in perfectly increasing order (33% answers). The second most frequent sequence was a reverse of the previous one: EUSs were in a decreasing order (18%). It is possible that in the cases where sequences are in reverse order, the users might not have understood the question properly. Therefore, the most frequent sequence, together with its reversed version, constitutes 51%.
Moreover, as we can see in Figure 4, in two out of six cases (or in 3 out of 6 if we take the reversed order sequence into account), the smallest EUS (marked with the letter “A” with the darkest background) is not ranked by the users as most similar to the symbol map. We can note this in the case of the fourth (CAEHBGFD) and fifth (ECAHBGFD) most frequent EUS sequences. They constitute, in sum, only 5% of the users’ answers. This means that every 20th user does not directly apply the EUS that is too small or too close to the symbol map. Based on this, we cannot clearly define the lower limit for the preferred EUS. On the other hand, the upper limit of the EUS range is more clearly visible based on the answers for task 1. In four out of six sequences in this task the users indicated the five largest EUSs (labelled with H, B, G, F, D on Figure 2) as being least similar to the symbol map. This means that the larger the EUS gets, the less similar it becomes to the symbol map.
In task 2 we wanted to examine which EUS did not show (according to users) the main characteristics of the phenomenon presented on the symbol map.
Based on the results of task 2, we can see the upper limit of the EUS range as the three largest EUSs, and are most often indicated as being those that do not show the main characteristics (Figure 5). This results in 17% of indications being for 832 pixels, 23% of indications being for 1664 pixels, and 24% of users’ indications being for 3328 pixels. This constitutes 64% of all users’ choices. At the same time, similar to the task 1 results, it is not clear from the task 2 results where the lower enumeration size limit lies. This limit is not as clearly indicated by the users as the upper limit.
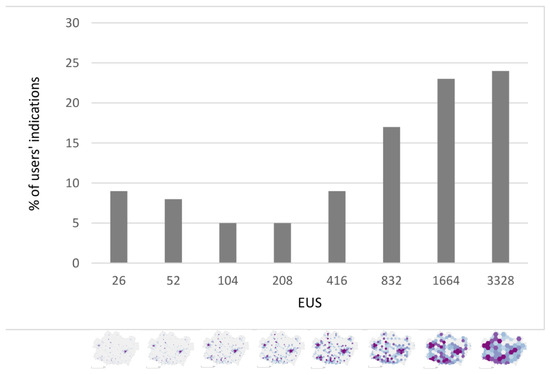
Figure 5.
Enumeration unit sizes that, according to the users, do not show the main characteristics of the phenomenon presented on the symbol map.
4.1.2. Perceived Usefulness and Degree of Similarity between EUS and Raw Data
In task 3, we wanted to obtain feedback on users’ preferences, namely the perceived usefulness and suitability of a particular EUS for indicating the main characteristics of the phenomenon presented on the symbol map (raw data). Participants were asked to rate the usefulness on a 5-point Likert scale, from very unuseful to very useful. The results are presented in Figure 6 and Table 2.
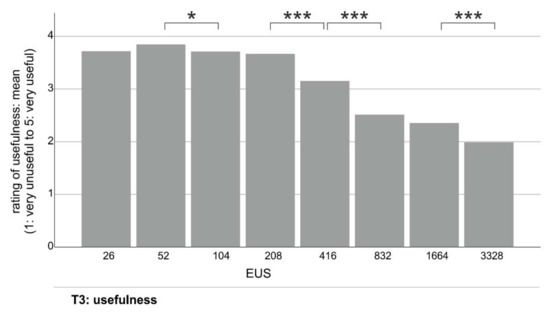
Figure 6.
Participants’ ratings concerning the usefulness of particular EUSs for indicating the main characteristics of the phenomenon presented on the symbol map, * p < 0.05, *** p ≤ 0.001.

Table 2.
The pairwise comparison of the collected answers for task 3. * p < 0.05, *** p ≤ 0.001.
The statistically significant differences were between four pairs of EUSs: 52 and 104 pixels, 208 and 416 pixels, 416 and 832 pixels, and 1664 and 3328 pixels.
In task 4, participants were asked to rate the degree of similarity between a map with a particular EUS and the symbol map. Participants were asked to rate the similarity on a 5-point Likert scale, from not similar to very similar. The results of this task are presented in Figure 7 and Table 3.
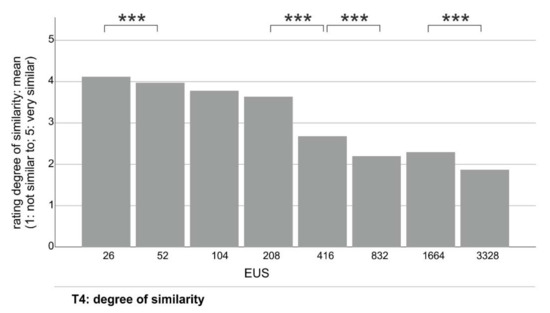
Figure 7.
Participants’ ratings concerning the degree of similarity between a particular EUS and the symbol map, *** p ≤ 0.001.

Table 3.
The pairwise comparison of collected answers for task 4. *** p ≤ 0.001.
Similarly to task 3, the users point to the choropleth map with smaller EUSs as being more similar to the symbol map. However, there is one exception to this rule: the choropleth map with a EUS of 1664 pixels was selected by some users as the one that reflects spatial patterns better than the choropleth map, which had a smaller EUS of 832 pixels.
Based on the pairwise comparison in Table 3, we can see that the difference between 26 and 52 pixels was statistically significant (V = 0.297, p < 0.001). The differences between the following pairs were also statistically significant: 208 and 416 pixels (V = 0.455, p < 0.001), 416 and 832 pixels (V = 0.339, p < 0.001), and 1664 and 3328 pixels (V = 0.286, p < 0.001).
4.1.3. Spatial Pattern Recognition
In task 5, the users were presented with pairs of maps—the symbol map together with a particular EUS—and were asked to identify and draw areas of similar shape and density on both maps. In T6, the users were presented with one map, namely a choropleth map with a particular EUS. They were asked to identify and draw at least three lines along which the phenomenon was concentrated. For the purpose of map vectorization analysis, the following methodology was adopted.
The collected answers, in the form of drawings, were analyzed using ArcMap 10.6.1 in the local coordinate system. To calculate an average for the most commonly vectorized polygon, a net of rectangular squares was overlaid on the drawn polygons. The cell size of the net was the same for all tested enumeration units and equaled two square units in the local ArcMap coordinate system. Then, the net was intersected with the polygons that had been vectorized by the users, for each enumeration unit. The resulting table of the intersection was joined to the net layer and based on the sum of the area in each cell (Figure 8). The resulting maps were unified in terms of the data classification. Manual classification was adopted with the same break values for each enumeration unit to enable a comparison of the results between all tested EUSs. For T6 the adopted methodology was designed in the same way, with the exception that in the resulting map the sum of the length of the lines drawn by the users were used for the design of the thematic map (Figure 9).

Figure 8.
Results of T5 vectorization task analysis.
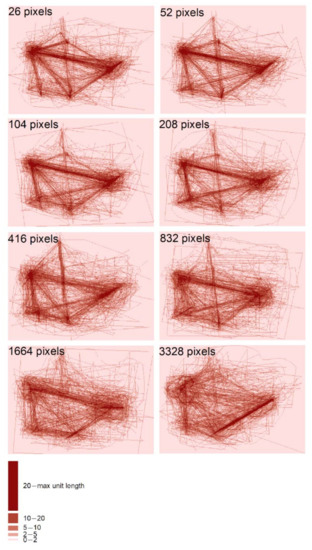
Figure 9.
Results of T6 vectorization task analysis.
The users were consistent in finding spatial patterns in task 5. In all resulting images, we can see they drew across three main areas of the phenomenon’s concentration. For both the two smallest EUSs (26 and 52 pixels), as well as for the larger EUSs (416, 832 and 3328 pixels), the picture is more blurred, and the polygons are larger and less specific. However, for 1664 pixels the images of the spatial patterns are well preserved, although this EUS is larger. The most consistent view of the spatial pattern seems to be presented on the choropleth map with an EUS of 104 pixels.
The users’ answers for task 6 differ between the various EUSs. In the case of the two largest EUSs, namely 1664 and 3328 pixels, the lines along which the phenomenon was concentrated are less visible and more blurred, especially in the case of the 3328 pixels enumeration unit.
In task 7 the users were given two maps: the symbol map and a map with a particular EUS. Based on the spatial distribution of the presented phenomenon on the symbol map, four spatial patterns were marked. Two of these were correct and two were incorrect. The users were asked which of the areas of similar density presented on the symbol map they could also identify on the choropleth map variant. Users could choose more than one answer. The results, presented in Figure 10, show the correct answers of participants using different EUSs. Table 4 presents the pairwise comparison of the collected answers for task 7.
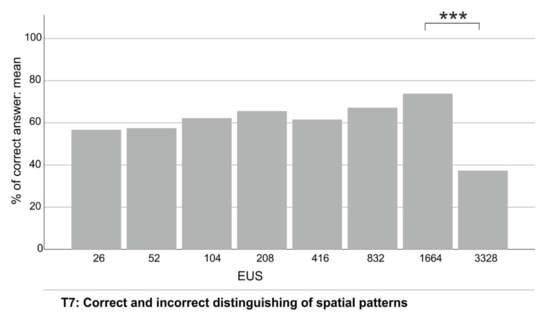
Figure 10.
Participants’ answers concerning being able to distinguish correct and incorrect spatial patterns according to particular enumeration unit sizes, *** p ≤ 0.001.

Table 4.
The pairwise comparison of collected answers for task 7, *** p ≤ 0.001, ** p < 0.01.
4.2. Answer Times
Based on the answer time analysis, we can note that out of the analyzed tasks, T1 was the most time consuming (M = 93.04 s, SD = 38.83). Task T2 was also quite challenging for the users (M = 41.06 s, SD = 18.29). While the tasks concerning user preferences (T3 and T4) were less time consuming than T1 and T2. The average answer time for T3 was M = 16.74 s, SD = 12.52 and for T4 was M = 11.06 s, SD = 7.83. The average answer time for T7 was M = 14.97 s and SD = 12.13. Therefore, the least time consuming and the less complicated task for the users was T4.
For further pairwise analysis, the tasks concerning usefulness, degree of similarity, and spatial pattern recognition (T3, T4, and T7) were taken into account. The tasks that concerned map ranking and exclusion (T1 and T2) were excluded from the detailed pairwise analysis as they do not concern the independent variable: the EUS. Tasks T5 and T6 were excluded from the answer time analysis as they concerned pattern vectorization and therefore participants’ drawing skills may have affected their answer times, not the perceived patterns.
4.2.1. Usefulness and Degree of Similarity—Answer Time Comparison
For T3 and T4, pairwise time comparison analysis was conducted to compare the answer times between pairs of EUSs (Figure 11 and Figure 12).

Figure 11.
Participants’ answer times concerning T3: Usefulness of the particular enumeration unit sizes, *** p ≤ 0.001.
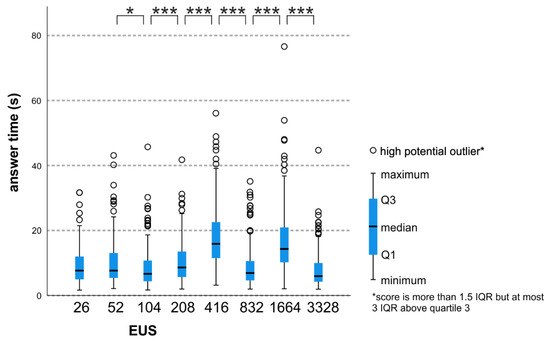
Figure 12.
Participants’ answer times pairwise comparison concerning T4: Degree of similarity of the particular enumeration unit sizes, * p < 0.05, *** p ≤ 0.001.
Based on Table 5, we can see that statistically significant differences were noted between all pairs of EUSs.

Table 5.
The pairwise comparison of the answer times for task 3, *** p ≤ 0.001.
The results of the pairwise comparison for T4 are presented in Figure 12 and the details of the pairwise comparison for T4 are presented in Table 6.

Table 6.
Task 4 and the pairwise comparison of the answer times, * p < 0.05, *** p ≤ 0.001.
Based on Table 6, we can see that statistically significant differences were noted between all pairs of successive EUSs, with the exception of 26 and 56 pixels.
4.2.2. Spatial Pattern Recognition—Answer Time Analysis
For T7, pairwise time comparison analysis was conducted to compare the answer time between pairs of EUSs (Figure 13).
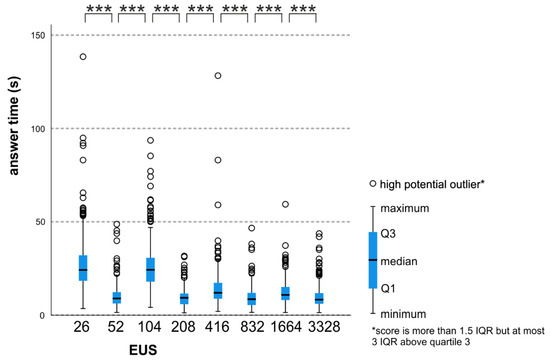
Figure 13.
Participants’ answer times pairwise comparison concerning T7: Correct and incorrect spatial patterns of the particular enumeration unit sizes, *** p ≤ 0.001.
Based on the pairwise comparison presented in Table 7, we can see that statistically significant differences were noted between all EUS pairs.

Table 7.
Task 7 and the pairwise comparison of the answer times, *** p ≤ 0.001.
5. Discussion
To find the optimal generalization level for choropleth maps, as expressed by the EUS, where the spatial patterns present in the data are adequately transformed and recognized by the user, we conducted an empirical study among 488 high school students. We used a symbol map as a raw data presentation and choropleth maps with eight EUSs, ranging from 2, 4, 8, 16, 32, 64, 128, and 256 km2, and corresponding respectively to 26, 52, 104, 208, 416, 832, 1664, and 3328 pixels. We formulated three research questions: RQ1 concerning choropleth map ordering and map exclusion, RQ2 concerning user preferences, and RQ3 concerning users’ ability to recognize spatial patterns. The presented research aimed to approximate the answer as to where the limit lies, expressed by the EUS, which, after exceeding the limit, the user loses the possibility of correct and effective perception of the spatial patterns presented on choropleth maps, as suggested in [11,21,22]. The discussion section is organized according to the stated research questions.
RQ1. Is the estimated similarity to the raw data presentation proportional to the EUS applied in a choropleth map?
For map ordering and map exclusion tasks (T1 and T2) the observations are quite consistent. In T1, concerning ranking the choropleth map variants from the most to the least similar against the symbol map, the users chose most often the sequence in which the EUSs were organized in an increasing unit size order. When we take into account the six most indicated sequences (Figure 4), we realize that in all cases, the smaller EUSs were pointed to as being most similar, while the larger EUSs, also quite consistently, were indicated as being least similar. These results clearly show that the users considered maps with larger EUS to be those that did not show the main characteristics of the distribution of the phenomenon presented on the symbol map. This confirms earlier suggestions found in the literature, that in case of too large an enumeration unit, spatial patterns are less clearly visible [11,21,22]. The results of T2 are mostly in line with T1: the users’ task was to indicate which of the choropleth maps, with their particular EUSs, do not show the main characteristics of the phenomenon presented on the symbol map. As a result, the users pointed most often to the maps with larger EUSs (1664 and 3328 pixels). On the other hand, the smallest tested enumeration units (26 and 52 pixels) were also often excluded (in sum, by 17% of users). Therefore, we can conclude that as well as the too large EUSs, the too small units were also not convenient for showing the distribution properly. Yet, the smallest sizes did not give such clear and uniform answers as did the largest. In both tasks, the preference for smaller EUSs is visible. At the same time, it is difficult, based on these two tasks, to indicate a sharp limit or range for EUSs, the application of which makes it possible to effectively convey spatial patterns. Nevertheless, we can answer RQ1 positively, as the results confirm that the estimated similarity to the raw data presentation is indeed proportional to an EUS applied in choropleth maps.
RQ2. Does the user’s preference for specific EUSs coincide with the ability to recognize spatial patterns?
The users’ preferences according to the usefulness (T3) and similarity (T4) of particular choropleth map variants follow the same tendency. In both T3 and T4, smaller EUSs were, in the majority, evaluated as being those that were most suitable for indicating the main characteristics of the phenomenon presented on the symbol map, in contrast to choropleth maps with larger EUSs, which were indicated as being less useful for this task. This is also confirmed in earlier research, where the authors conclude that the larger units are less useful [36,37,38]. However, there are some interesting findings and exceptions. In T3, the choropleth map variant with the smallest EUS (26 pixels) was indicated as being more useful than the neighboring tested unit size of 52 pixels. There were, however, statistically significant differences between 208 and 416 pixels, and 416 and 832 pixels, as well as between 1664 and 3328 pixels. Within these EUS pairs, the smaller EUSs were perceived by users as being better in each case. The difference between 416 and 832 pixels is quite evident in the case of T3. In T4, a statistically significant difference between 208 and 416 pixels as well as 416 and 832 pixels can also be noted, similar to T3. This shows that, in general, for T3 and T4, the users evaluated smaller EUSs (52, 104, and 208 pixels) as being better and more helpful for pattern recognition tasks. On the other hand, we can make quite an interesting observation in the case of T4, where the choropleth map variant with a larger EUS (1664 pixels) was indicated as being both similar and useful compared to the symbol map. This may indicate that it is not always the larger EUSs that are evaluated as not useful. This is also confirmed in earlier research [26,27,28,35]. The authors note that a map at fine scale offers more insights into local pattern identification. However, they also note that global spatial patterns are sometimes more evident at a coarser scale than at a finer one.
The results of the pairwise answer time comparison analysis conducted for T3 and T4 are also interesting. For T3, the most time-consuming tasks were for 26 and 104 pixels, while the least time consuming were for 3328 and 1664 pixels. In the case of T4, the most time consuming were 416 and 1664 pixels, while the least time consuming were the 3328- and 832-pixel EUSs. On the other hand, in the case of T4, in general the users needed more time to solve the task for larger than for smaller EUSs. Based on the answer time analysis we can see that answer time is not proportional to EUS increase, it varies for different EUSs. Thus, we can see that the short answer times could result for various reasons, either the spatial patterns were evident and the users were fast in answering, or the spatial patterns were so blurred that the users neglected them while solving the tasks. Based on these findings we can answer RQ2 only partially in the positive, as the findings confirm that, as a general rule, the users prefer and indicate smaller EUSs as being more helpful in recognizing spatial patterns, however, this has not been reflected in the answer time analysis. Thus, this question needs further investigations.
RQ3. Is the ability to recognize spatial patterns related to the EUS?
Out of all the tasks, T5 and T6 were the most challenging and took more time to solve. In the case of T5, the users were asked to draw polygons for phenomenon that had similar shape and density. The users noticed and drew patterns of various shapes, including triangle, square, and circle shapes, similarly to the research conducted in [34]. For T5, the most visible and distinct patterns were identified for enumeration units not at the extreme (max and min) sizes: 104 and 1664 pixels. The most blurred patterns were identified for the smallest (26, 208) and the largest (3328 pixels). These results show that both the smallest and the largest tested EUSs seemed not to be an optimal solution for spatial pattern recognition. This proves that there exists an optimal EUS range, however, it is difficult to indicate the upper and lower border of this range. This observation is in-line with earlier research [18]. Surprisingly, for one of the largest unit sizes (1664 pixels) the patterns were clearly marked. This result is consistent with T4. In the case of T6 the most blurred patterns are also identified in the case of largest enumeration units. The most visible and distinct patterns are indicated for smaller and middle EUSs. However, the users were also able to identify the main characteristics of the presented phenomenon. A spatial pattern recognition task was also expected from the users in T7. In T7, the indications closest to the correct answer were achieved for middle EUSs. Out of the larger enumeration units, in the case of 1664 pixels EUS, the biggest percentage of correct answers was achieved. The least performing enumeration unit was 3328 pixels. The pairwise comparison between 1664 and 3328 pixels shows a statistically significant difference. This shows that the EUS with 1664 is better evaluated than the 3328 pixels EUS. The results of T5, T6, and T7 confirm the general trends visible in other tasks’ results.
In terms of answer time analysis for T7, the most time consuming were the 26- and 104-pixel EUSs, while the least time consuming were the 832-, 208-, and 26-pixel EUSs. This result is consistent with the answer time analysis for T3, the users needed more time to solve the tasks for smaller enumeration units than for larger EUSs, but a decrease in answer time is not directly connected with a decrease in the EUS. Thus, in the case of RQ3 we can answer that the ability to recognize spatial patterns is definitely related to the EUS. The users performed better in middle EUSs, namely from 104 to 1664 pixels, than in the smaller (26 and 52 pixels) or the largest (3328 pixels).
6. Conclusions
In this paper, we aimed to contribute to finding the optimal generalization level in choropleth maps. The generalization level was expressed as the EUS. Eight EUSs of hexagonal shape were considered. We evaluated selected EUSs by conducting a user study with 488 high school students. We wanted to specify the enumeration unit range at which the spatial patterns of the presented phenomenon are retained and at which it is possible for the patterns to be noticed by users. The findings of this research show that specifying the optimal EUS is a challenging and not straightforward task. The conducted study confirms previous opinions [11,21,22] that, in general, the smaller EUSs are perceived by users as being more optimal than the larger. However, it was also noted that spatial patterns are sometimes more evident at a coarser scale than at a finer one, thus we can conclude that not all large EUSs are unuseful. This also confirms earlier conclusions [26,27,28,35]. Based on the conducted study we conclude that the largest EUS (3328 pixels) is the least useful for pattern recognition—in all tasks it performed the worst. The smallest EUSs (26 and 52 pixels) seem also not to be optimal, as they performed well in less than half of the tasks (2 out of 7 tasks). Thus, based on the results of all the analyses, we can conclude that the optimal EUS range is between 104 and 1664 pixels, however, similar to earlier research [18], at this stage we are not able to specify the sharp borders of the optimal EUS range.
As shown in the Related works section there are not many studies investigating this issue, and there are many problems to be analyzed within this topic, for example, comparing between the different types of distribution of the studied phenomenon, and of different levels of clustering. As in the case of every study, the collected results should be transferred carefully, with all the limitations considered. To omit, at least partially, this challenge we decided to define the tested EUSs in pixels in order to be able to refer to other enumeration units of different areas and presented in different map scales to those applied in this study. We are aware that because equal sized enumeration units have been applied, it is difficult to directly transfer the result to every other type of choropleth map, including the most commonly used choropleth maps with administrative units. However, we believe that the collected results can be considered a starting point for further investigations, also in regard to more common map types. As a first step, we believe it is worthwhile relating the results to shapes other than the hexagon shape applied to the Equal Area Unit Map (EAUM), for example, triangles. As a further consideration, the typical choropleth map with administrative units could be considered. In conducting research on EUSs, especially concerning geographical units and EAUM aggregation, one has to be aware and carefully consider the MAUP problem, especially its scale effect aspect [29,30,31,32,33].
Moreover, this research is important not only from the point of view of thematic mapping, especially choropleth maps, but also because it has the potential to be used in topographic mapping for the purpose of spatial pattern recognition and the evaluation of cartographic generalization results. Therefore, the collected findings require further analysis and investigation in order to determine the optimal EUS and formulate a general rule of thumb.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/ijgi10090576/s1, Figure S1: Maps used in the empirical study.
Author Contributions
Conceptualization, methodology, software, validation, formal analysis, Izabela Karsznia, Izabela Małgorzata Gołębiowska, Jolanta Korycka-Skorupa and Tomasz Nowacki; investigation, resources, data curation, Izabela Karsznia.; writing—original draft preparation, Izabela Karsznia writing—review and editing, Izabela Karsznia, Izabela Małgorzata Gołębiowska, Jolanta Korycka-Skorupa, Tomasz Nowacki; visualization, Izabela Karsznia.; supervision, project administration, funding acquisition, Izabela Małgorzata Gołębiowska, Jolanta Korycka-Skorupa and Izabela Karsznia. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Centre, Poland, grant number UMO-2016/23/B/HS6/03846, “Evaluation of cartographic presentation methods in the context of map perception and effectiveness of visual transmission”.
Institutional Review Board Statement
The study was conducted according to the guidelines of the Declaration of Helsinki and approved by the Ethics Committee of Faculty of Geography and Regional Studies, University of Warsaw.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Acknowledgments
We would like to thank all the students who participated in this study for their time and efforts. Moreover, we express our thanks to EMPREK Team colleagues Katarzyna Słomska, Tomasz Panecki, and Wojciech Pokojski for their help at the data collection stage.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Mackaness, W.A.; Ruas, A.; Sarjakoski, L.T. Generalization of Geographic Information: Cartographic Modelling and Applications; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Burghardt, D.; Duchêne, C.; Mackaness, W.A. Abstracting Geographic Information in a Data Rich World: Methodologies and Applications of Map Generalization; Springer International: Cham, Switzerland, 2014. [Google Scholar]
- Maceachren, A.M.; Ganter, J.H. A pattern identification approach to cartographic visualization. Cartogr. Int. J. Geogr. Inf. Geovis. 1990, 27, 64–81. [Google Scholar] [CrossRef]
- Mackaness, W.A.; Edwards, G. The importance of modelling pattern and structure in automated map generalization. In Proceedings of the Joint ISPRS/ICA Workshop on Multi-Scale Representations of Spatial Data, Ottawa, ON, Canada, 7–8 July 2002. [Google Scholar]
- Zhang, L.; Guilbert, E. Evaluation of River Network Generalization Methods for Preserving the Drainage Pattern. ISPRS Int. J. Geo. Inf. 2016, 5, 230. [Google Scholar] [CrossRef]
- Yu, W. Quality assessment in point feature generalization with pattern preserved. Trans. GIS 2018, 22, 872–888. [Google Scholar] [CrossRef]
- Bertin, J. Semiology of Graphics: Diagrams, Networks, Maps; University of Wisconsin Press: Madison, WI, USA, 1967. [Google Scholar]
- McMaster, R.B.; Shea, K.S. Cartographic Generalization in a Digital Environment: A Framework for Implementation in a Geographic Information System. Unkn. J. 1988, 1, 240–249. [Google Scholar]
- Brassel, K.E.; Weibel, R. A review and conceptual framework of automated map generalization. Int. J. Geogr. Inf. Syst. 1988, 2, 229–244. [Google Scholar] [CrossRef]
- Grünreich, D. Development of Computer-Assisted Generalization. In GIS and Generalization: Methodology and Practice; Müller, J.-C., Lagrange, J.-P., Weibel, R., Eds.; Taylor & Francis: London, UK, 1995; pp. 47–55. [Google Scholar]
- Dent, B.D.; Torguson, J.S.; Hodler, T.W. Cartography Thematic Map Design, 6th ed.; McGraw Hill: New York, NY, USA, 2009. [Google Scholar]
- Chang, K.-T. Data differentiation and cartographic symbolization. Cartogr. Int. J. Geogr. Inf. Geovis. 1976, 13, 60–68. [Google Scholar] [CrossRef]
- Slocum, T.A.; McMaster, R.B.; Kessler, F.C.; Howard, H.H. Thematic Cartography and Geovisualization, 3rd ed.; Pearson: Hoboken, NJ, USA, 2008. [Google Scholar]
- Cabello, S.; Haverkort, H.; Van Kreveld, M.; Speckmann, B. Algorithmic Aspects of Proportional Symbol Maps. Algorithmica 2009, 58, 543–565. [Google Scholar] [CrossRef]
- Schiewe, J. Empirical Studies on the Visual Perception of Spatial Patterns in Choropleth Maps. KN J. Cartogr. Geogr. Inf. 2019, 69, 217–228. [Google Scholar] [CrossRef]
- Hales, T.C. The Honeycomb Conjecture. Discret. Comput. Geom. 2001, 25, 1–22. [Google Scholar] [CrossRef]
- Montello, D.R. Cognitive Map-Design Research in the Twentieth Century: Theoretical and Empirical Approaches. Cartogr. Geogr. Inf. Sci. 2002, 29, 283–304. [Google Scholar] [CrossRef]
- MacEachren, A.M. The Role of Complexity and Symbolization Method in Thematic Map Effectiveness. Ann. Assoc. Am. Geogr. 1982, 72, 495–513. [Google Scholar] [CrossRef]
- Mersy, J.E. Trends in colour and map use research. Cartogr. Int. J. Geogr. Inf. Geovis. 1990, 27, 5–19. [Google Scholar] [CrossRef]
- Wright, J.; Robinson, A.; Sale, R.; Morrison, J. Elements of Cartography. Geogr. J. 1979, 145, 355. [Google Scholar] [CrossRef]
- Bregt, A.K.; Wopereis, M.C.S. Comparison of complexity measures for choropleth maps. Cartogr. J. 1990, 27, 85–91. [Google Scholar] [CrossRef]
- Robinson, A.H.; Morrison, J.L.; Muehrcke, P.C.; Kimerling, A.J.; Guptill, S.C. Elements of Cartography, 6th ed.; Wiley: New York, NY, USA, 1995. [Google Scholar]
- Steiniger, S.; Burghardt, D.; Weibel, R. Recognition of island structures for map generalization. In Proceedings of the 14th annual ACM international symposium on Advances in geographic information systems, Virginia, VA, USA, 10–11 November 2006; pp. 67–74. [Google Scholar]
- Touya, G.; Bucher, B.; Falquet, G.; Jaara, K.; Steiniger, S. Modelling Geographic Relationships in Automated Environments. In Lecture Notes in Geoinformation and Cartography; Cartwright, W., Gartner, G., Meng, L., Peterson, M.P., Eds.; Springer Science and Business Media LLC: Berlin, Germany, 2014; pp. 53–82. [Google Scholar]
- Sayidov, A.; Weibel, R. Constraint-based approach in geological map generalization. In Proceedings of the 19th ICA Workshop on Generalization and Multiple Representation, Helsinki, Finland, 14 July 2016. [Google Scholar]
- Boscoe, F.P.; Pickle, L.W. Choosing Geographic Units for Choropleth Rate Maps, with an Emphasis on Public Health Applications. Cartogr. Geogr. Inf. Sci. 2003, 30, 237–248. [Google Scholar] [CrossRef]
- Edsall, R.M.; Harrower, M.; Mennis, J.L. Tools for visualizing properties of spatial and temporal periodicity in geographic data. Comput. Geosci. 2000, 26, 109–118. [Google Scholar] [CrossRef][Green Version]
- Talbot, T.O.; Kulldorff, M.; Forand, S.P.; Haley, V.B. Evaluation of spatial filters to create smoothed maps of health data. Stat. Med. 2000, 19, 2399–2408. [Google Scholar] [CrossRef]
- Openshaw, S. (Ed.) The modifiable areal unit problem. In Concepts and Techniques in Modern Geography 38; Geo Books: Norwich, UK, 1984; p. 41. [Google Scholar]
- Wong, D.W.S. The Modifiable Areal Unit Problem (MAUP). In WorldMinds: Geographical Perspectives on 100 Problems; Janelle, D.G., Warf, B., Hansen, K., Eds.; Springer Science and Business Media LLC: Berlin, Germany, 2004; pp. 571–575. [Google Scholar]
- Fotheringham, A.S.; Wong, D.W.S. The Modifiable Areal Unit Problem in Multivariate Statistical Analysis. Environ. Plan. A Econ. Space 1991, 23, 1025–1044. [Google Scholar] [CrossRef]
- Dark, S.J.; Bram, D. The modifiable areal unit problem (MAUP) in physical geography. Prog. Phys. Geogr. Earth Environ. 2007, 31, 471–479. [Google Scholar] [CrossRef]
- De Andrade, S.C.; Restrepo-Estrada, C.; Nunes, L.H.; Rodriguez, C.A.M.; Estrella, J.C.; Delbem, A.C.B.; de Albuquerque, J.P. A multicriteria optimization framework for the definition of the spatial granularity of urban social media analytics. Int. J. Geogr. Inf. Sci. 2021, 35, 43–62. [Google Scholar] [CrossRef]
- Cole, D.G. Recall vs. Recognition and Task Specificity in Cartographic Psychophysical Testing. Am. Cartogr. 1981, 8, 55–66. [Google Scholar] [CrossRef]
- Schiewe, J. Distortion Effects in Equal Area Unit Maps. KN J. Cartogr. Geogr. Inf. 2021, 71, 71–82. [Google Scholar] [CrossRef]
- Brewer, C.A.; MacEachren, A.M.; Pickle, L.W.; Herrmann, D. Mapping Mortality: Evaluating Color Schemes for Choropleth Maps. Ann. Assoc. Am. Geogr. 1997, 87, 411–438. [Google Scholar] [CrossRef]
- Brewer, C.A.; Pickle, L. Evaluation of Methods for Classifying Epidemiological Data on Choropleth Maps in Series. Ann. Assoc. Am. Geogr. 2002, 92, 662–681. [Google Scholar] [CrossRef]
- Lewis, D.R.; Pickle, L.W.; Zhu, L. Recent Spatiotemporal Patterns of US Lung Cancer by Histologic Type. Front. Public Health 2017, 5, 82. [Google Scholar] [CrossRef] [PubMed]
- Steinke, T.R.; Lloyd, R.E. Cognitive Integration of Objective Choropleth Map Attribute Information. Cartogr. Int. J. Geogr. Inf. Geovis. 1981, 18, 13–23. [Google Scholar] [CrossRef]
- Steinke, T.; Steinke, R. Judging the Similarity of Choropleth Map Images. Cartogr. Int. J. Geogr. Inf. Geovis. 1983, 20, 35–42. [Google Scholar] [CrossRef]
- Kraak, M.J.; Roth, R.E.; Ricker, B.; Kagawa, A.; Le Sourd, G. Mapping for a Sustainable World; The United Nations: New York, NY, USA, 2020. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).