Mining Topological Dependencies of Recurrent Congestion in Road Networks
Abstract
1. Introduction
2. Related Work
2.1. Congestion Analysis
2.2. Spatio-Temporal Data Mining
2.3. Data Sources
3. Problem Statement and Formalisation
- the subgraphs are located in spatial proximity,
- the subgraphs are typically simultaneously affected by Recurrent Congestion or
- the road network topology causes the correlation of the congestion on these subgraphs.
4. Proposed Solution
4.1. Identification of Affected Units
4.2. Identification of Affected Subgraphs
4.3. Spatial Merging of Affected Subgraphs
| Algorithm 1 Merge Subgraphs |
| Input: C: Set of subgraphs |
| Output: SG: Set of merged subgraphs |
| 1: |
| 2: |
| 3: for all do |
| 4: for all do |
| 5: |
| 6: changed← True |
| 7: while changed do |
| 8: changed ← False
{Generate candidates} |
| 9: candidates |
| 10: for all do |
| 11: candidates ← candidates {Compute similarities} |
| 12: |
| 13: for all candidates do |
| 14: similarity {Merge subgraphs} |
| 15: visited |
| 16: for all ordered do |
| 17: if visited visited then |
| 18: continue |
| 19: if then |
| 20: |
| 21: |
| 22: visited ← visited |
| 23: update(commonUnits) |
| 24: changed ← True |
| 25: return |
4.4. Identification of Spatio-Temporal Dependencies
| Algorithm 2 Determine Spatio-Temporal Subgraph Dependencies |
| Input: : Set of subgraphs : Set of time points |
| Output: Set of pairs of subgraphs, ordered by dependency score |
| 1: |
| 2: for all do |
| 3: for all do |
| 4: if then |
| 5: |
| 6: else |
| 7: {Determine candidate pairs} |
| 8: candidates |
| 9: for all do |
| 10: if candidates then |
| 11: continue |
| 12: for all |
| 13: if then |
| 14: candidates ← candidates |
| 15: break {Compute dependency} |
| 16: |
| 17: for all do |
| 18: score ←dependency |
| 19: |
| 20: return ordered |
5. Datasets
5.1. OpenStreetMap
5.2. Traffic Dataset
6. Experiments and Discussion
6.1. Structural Dependencies
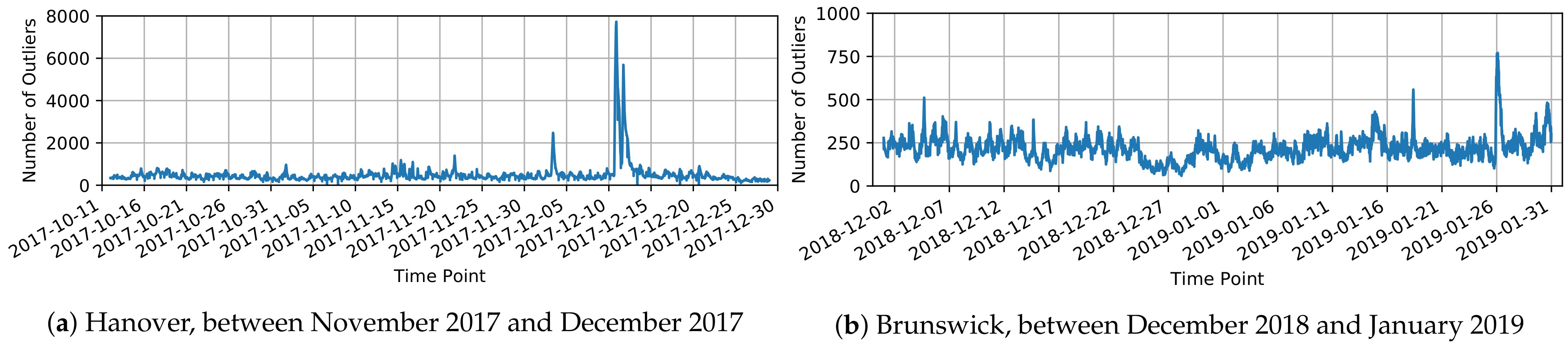
6.2. Analysis of Affected Units and Subgraphs
6.2.1. Distribution of Affected Units
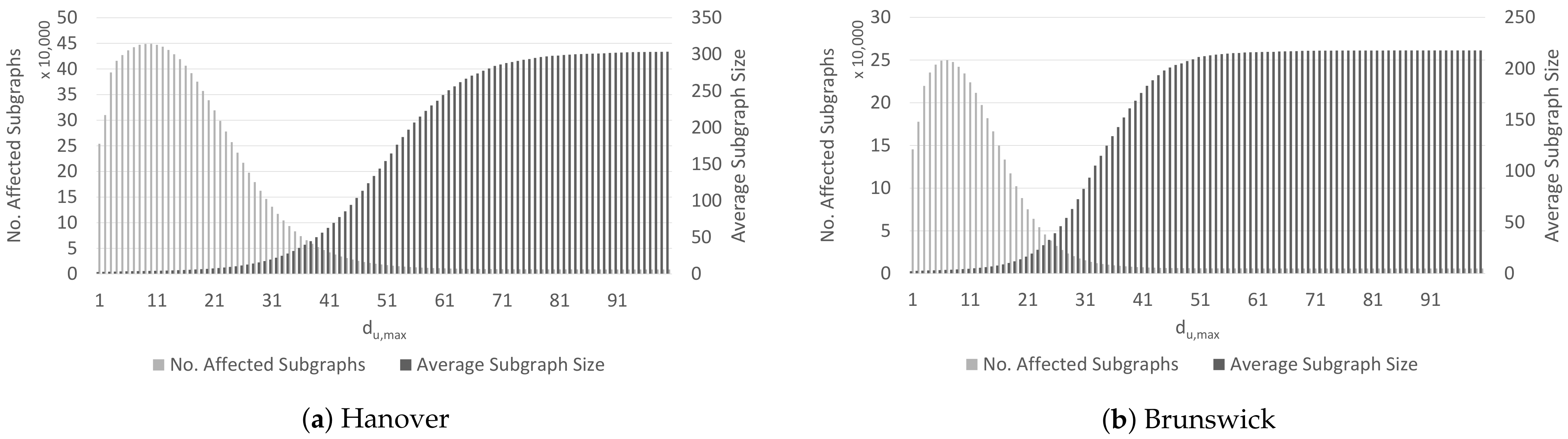
6.2.2. Distribution of Affected Subgraphs
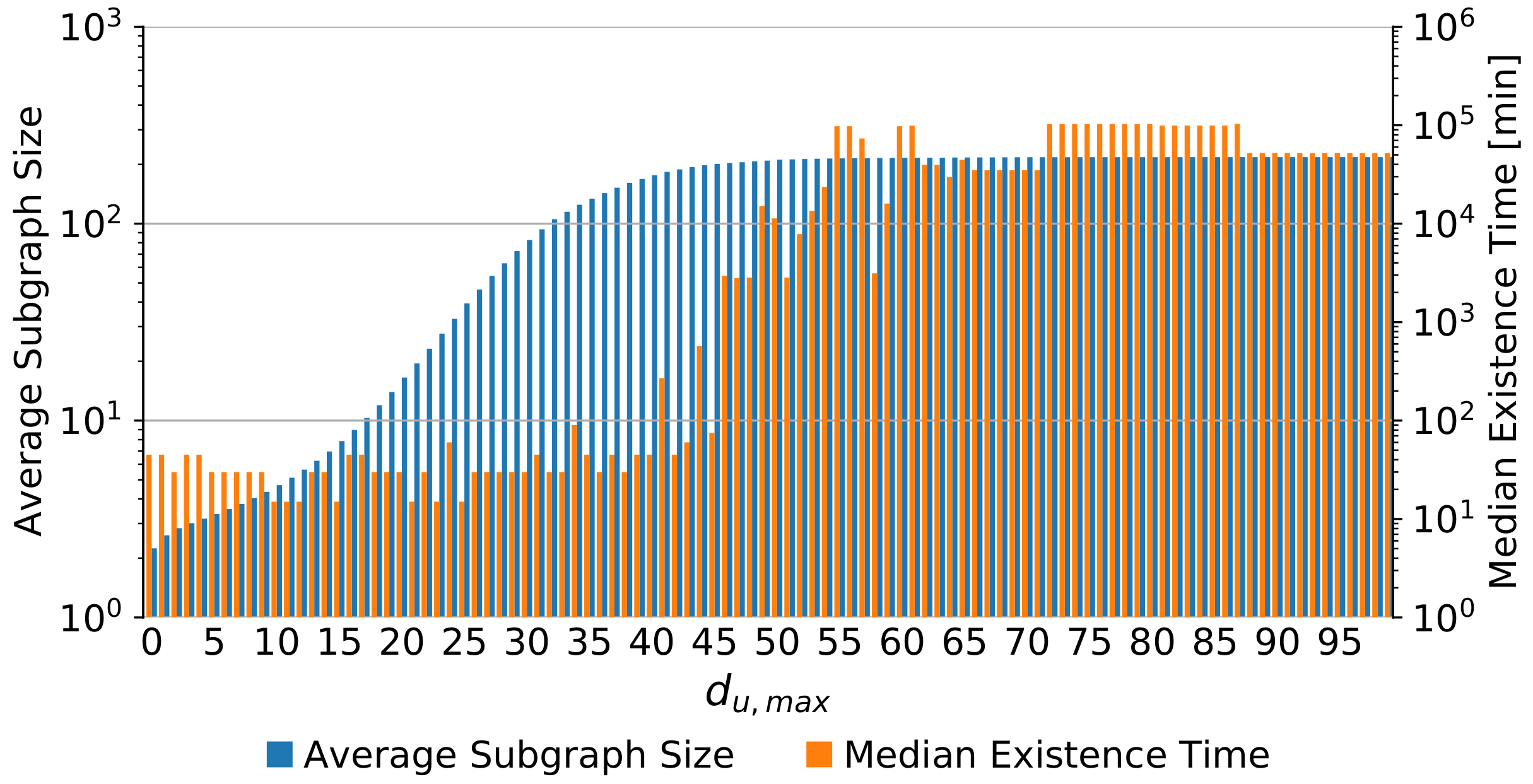
6.2.3. Temporal Persistence of Affected Subgraphs
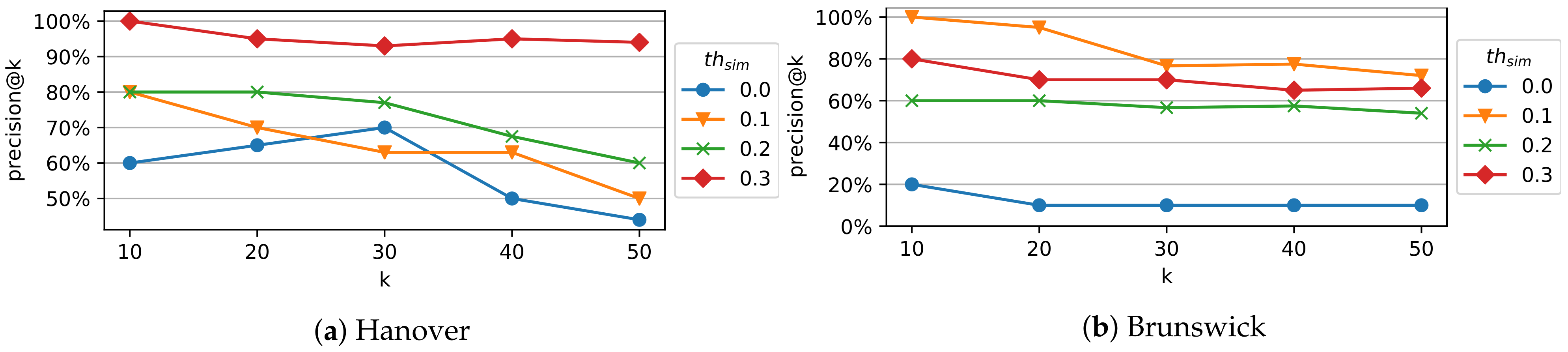
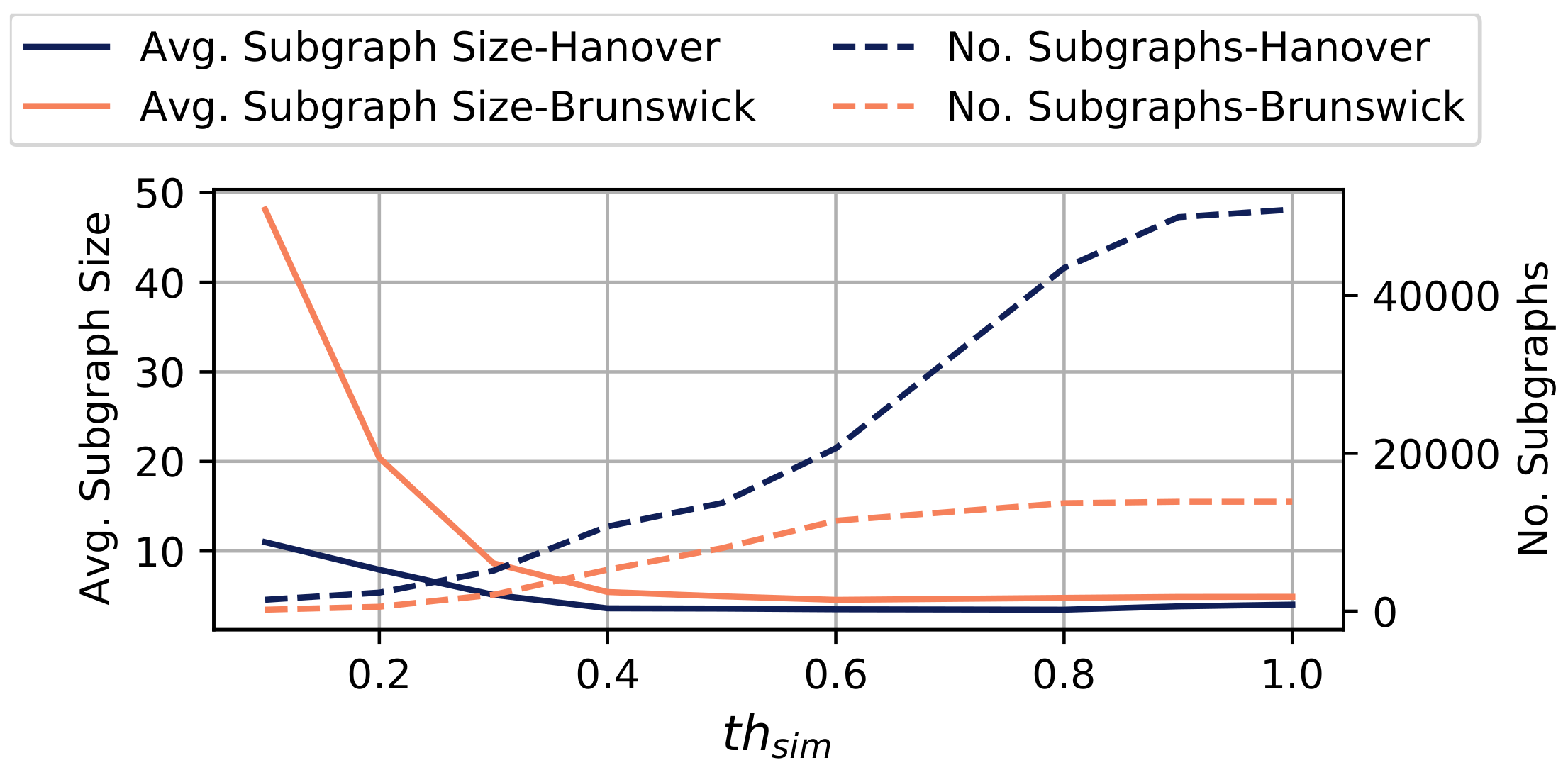
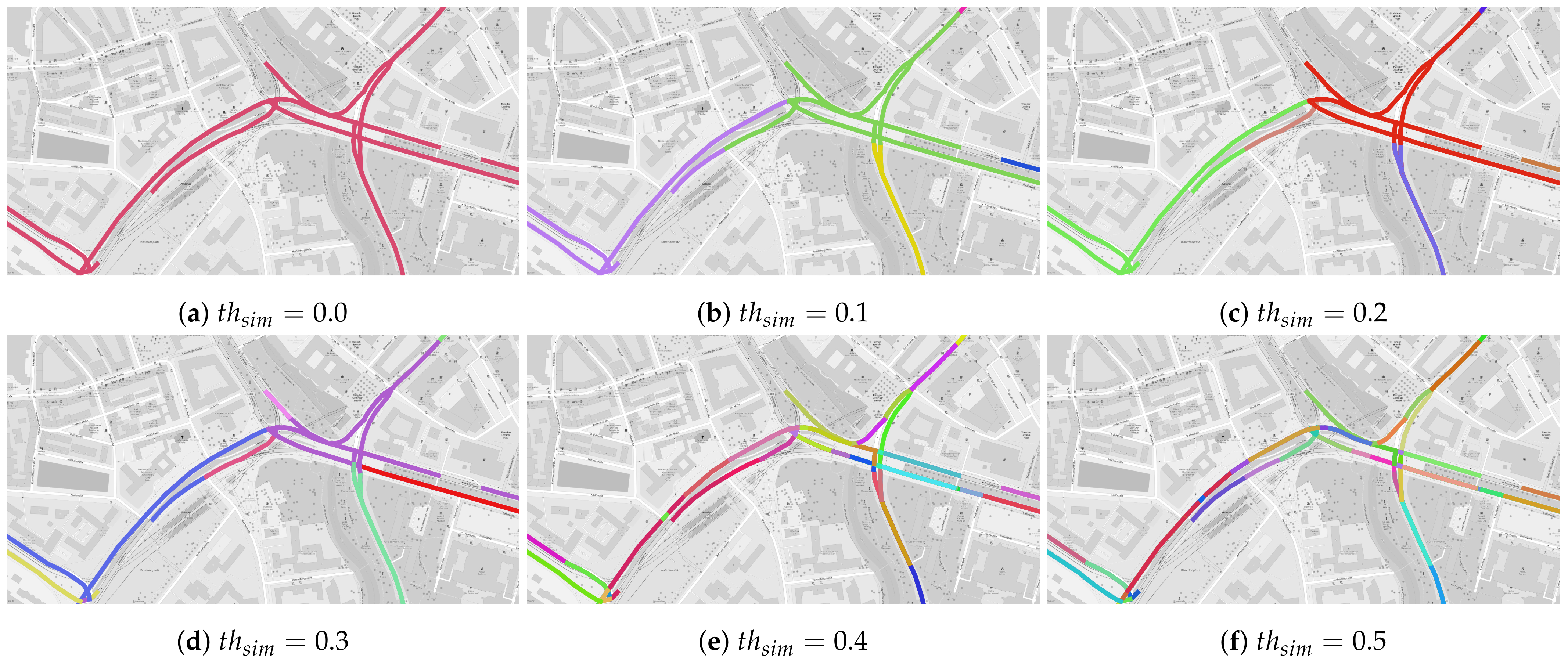
6.3. Evaluation of Subgraph Merging
7. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Guo, S.; Zhou, D.; Fan, J.; Tong, Q.; Zhu, T.; Lv, W.; Li, D.; Havlin, S. Identifying the most influential roads based on traffic correlation networks. EPJ Data Sci. 2019, 8, 1–17. [Google Scholar] [CrossRef]
- Dowling, R.; Skabardonis, A.; Carroll, M.; Wang, Z. Methodology for Measuring Recurrent and Nonrecurrent Traffic Congestion. Transp. Res. Rec. 2004, 1867, 60–68. [Google Scholar] [CrossRef]
- An, S.; Yang, H.; Wang, J. Revealing Recurrent Urban Congestion Evolution Patterns with Taxi Trajectories. ISPRS Int. J. Geo-Inf. 2018, 7, 128. [Google Scholar]
- An, S.; Yang, H.; Wang, J.; Cui, N.; Cui, J. Mining urban recurrent congestion evolution patterns from GPS-equipped vehicle mobility data. Inf. Sci. 2016, 373, 515–526. [Google Scholar] [CrossRef]
- Tempelmeier, N.; Feuerhake, U.; Wage, O.; Demidova, E. ST-Discovery: Data-Driven Discovery of Structural Dependencies in Urban Road Networks. In Proceedings of the 27th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Chicago, IL, USA, 5–8 November 2019. [Google Scholar]
- Tempelmeier, N.; Sander, A.; Feuerhake, U.; Löhdefink, M.; Demidova, E. TA-Dash: An Interactive Dashboard for Spatial-Temporal Traffic Analytics. In Proceedings of the 28th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, Seattle, WA, USA, 3–6 November 2020. [Google Scholar]
- Wu, F.; Wang, H.; Li, Z. Interpreting traffic dynamics using ubiquitous urban data. In Proceedings of the 24th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems, San Francisco, CA, USA, 31 October–3 November 2016. [Google Scholar]
- Pan, B.; Demiryurek, U.; Gupta, C.; Shahabi, C. Forecasting Spatiotemporal Impact of Traffic Incidents for Next-generation Navigation Systems. Knowl. Inf. Syst. 2015, 81–88. [Google Scholar] [CrossRef]
- Rettore, P.H.L.; Santos, B.P.; Rigolin, F.; Lopes, R.; Maia, G.; Villas, L.A.; Loureiro, A.A.F. Road Data Enrichment Framework Based on Heterogeneous Data Fusion for ITS. IEEE Trans. Intell. Transp. Syst. 2020, 21, 1751–1766. [Google Scholar] [CrossRef]
- Lee, J.; Hong, B.; Lee, K.; Jang, Y. A Prediction Model of Traffic Congestion Using Weather Data. In Proceedings of the IEEE International Conference on Data Science and Data Intensive Systems, Sydney, Australia, 11–13 December 2015. [Google Scholar]
- Chung, Y. Assessment of non-recurrent congestion caused by precipitation using archived weather and traffic flow data. Transp. Policy 2012, 19, 167–173. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, H. Prediction of Road Traffic Congestion Based on Random Forest. In Proceedings of the 10th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 9–10 December 2017. [Google Scholar]
- Tempelmeier, N.; Dietze, S.; Demidova, E. Crosstown traffic—supervised prediction of impact of planned special events on urban traffic. GeoInformatica 2020, 24, 339–370. [Google Scholar] [CrossRef]
- Kwoczek, S.; Martino, S.D.; Nejdl, W. Stuck Around the Stadium? An Approach to Identify Road Segments Affected by Planned Special Events. In Proceedings of the IEEE 18th International Conference on Intelligent Transportation Systems, Las Palmas de Gran Canaria, Spain, 15–18 September 2015. [Google Scholar]
- Anbaroglu, B.; Heydecker, B.; Cheng, T. Spatio-temporal clustering for non-recurrent traffic congestion detection on urban road networks. Transp. Res. Part C Emerg. Technol. 2014, 48, 47–65. [Google Scholar] [CrossRef]
- Laflamme, E.M.; Ossenbruggen, P.J. Effect of time-of-day and day-of-the-week on congestion duration and breakdown: A case study at a bottleneck in Salem, NH. J. Traffic Transp. Eng. (Engl. Ed.) 2017, 4, 31–40. [Google Scholar] [CrossRef]
- Fouladgar, M.; Parchami, M.; Elmasri, R.; Ghaderi, A. Scalable deep traffic flow neural networks for urban traffic congestion prediction. In Proceedings of the 2017 International Joint Conference on Neural Networks (IJCNN), Anchorage, AK, USA, 14–19 May 2017. [Google Scholar]
- Gu, Y.; Wang, Y.; Dong, S. Public Traffic Congestion Estimation Using an Artificial Neural Network. ISPRS Int. J. Geo Inf. 2020, 9, 152. [Google Scholar] [CrossRef]
- Zhu, L.; Krishnan, R.; Guo, F.; Polak, J.W.; Sivakumar, A. Early Identification of Recurrent Congestion in Heterogeneous Urban Traffic. In Proceedings of the IEEE Intelligent Transportation Systems Conference (ITSC), Auckland, NZ, USA, 27–30 October 2019. [Google Scholar]
- Tseng, F.; Hsueh, J.; Tseng, C.; Yang, Y.; Chao, H.; Chou, L. Congestion Prediction With Big Data for Real-Time Highway Traffic. IEEE Access 2018, 6, 57311–57323. [Google Scholar] [CrossRef]
- Vlahogianni, E.I.; Karlaftis, M.G.; Golias, J.C. Short-term traffic forecasting: Where we are and where we are going. Transp. Res. Part C Emerg. Technol. 2014, 43, 3–19. [Google Scholar] [CrossRef]
- Xie, D.; Wang, M.; Zhao, X. A Spatiotemporal Apriori Approach to Capture Dynamic Associations of Regional Traffic Congestion. IEEE Access 2019, 8, 3695–3709. [Google Scholar] [CrossRef]
- Xiong, H.; Vahedian, A.; Zhou, X.; Li, Y.; Luo, J. Predicting Traffic Congestion Propagation Patterns: A Propagation Graph Approach. In Proceedings of the 11th ACM SIGSPATIAL International Workshop on Computational Transportation Science, Seattle, WA, USA, 6 November 2018. [Google Scholar]
- Chen, Z.; Yang, Y.; Huang, L.; Wang, E.; Li, D. Discovering Urban Traffic Congestion Propagation Patterns with Taxi Trajectory Data. IEEE Access 2018, 6, 69481–69491. [Google Scholar] [CrossRef]
- Saeedmanesh, M.; Geroliminis, N. Dynamic clustering and propagation of congestion in heterogeneously congested urban traffic networks. Transp. Res. Procedia 2017, 23, 962–979. [Google Scholar] [CrossRef]
- Atluri, G.; Karpatne, A.; Kumar, V. Spatio-Temporal Data Mining: A Survey of Problems and Methods. ACM Comput. Surv. 2018, 51, 1–41. [Google Scholar] [CrossRef]
- Xu, M.; Wu, J.; Liu, M.; Xiao, Y.; Wang, H.; Hu, D. Discovery of Critical Nodes in Road Networks Through Mining From Vehicle Trajectories. IEEE Trans. Intell. Transp. Syst. 2019, 20, 583–593. [Google Scholar] [CrossRef]
- Brunauer, R.; Schmitzberger, N.; Rehrl, K. Recognizing Spatio-Temporal Traffic Patterns at Intersections Using Self-Organizing Maps. In Proceedings of the 11th ACM SIGSPATIAL Int. Workshop on Computational Transportation Science, Seattle, WA, USA, 6 November 2018. [Google Scholar]
- Li, X.; Li, Z.; Han, J.; Lee, J. Temporal Outlier Detection in Vehicle Traffic Data. In Proceedings of the 2009 IEEE 25th International Conference on Data Engineering, Shanghai, China, 29 March–2 April 2009. [Google Scholar]
- Asakura, Y.; Kusakabe, T.; Nguyen, L.X.; Ushiki, T. Incident detection methods using probe vehicles with on-board GPS equipment. Transp. Res. Part Emerg. Technol. 2017, 81, 330–341. [Google Scholar] [CrossRef]
- Taylor, M.A. Critical transport infrastructure in Urban areas: Impacts of traffic incidents assessed using accessibility-based network vulnerability analysis. Growth Chang. 2008, 39, 593–616. [Google Scholar] [CrossRef]
- Scott, D.M.; Novak, D.C.; Aultman-Hall, L.; Guo, F. Network robustness index: A new method for identifying critical links and evaluating the performance of transportation networks. J. Transp. Geogr. 2006, 14, 215–227. [Google Scholar] [CrossRef]
- Kokoska, S.; Zwillinger, D. CRC Standard Probability and Statistics Tables and Formulae; CRC Press: Boca Raton, FL, USA, 2000. [Google Scholar]
- Fonseca, L.M.G.; Ii, F.M. Satellite imagery segmentation: A region growing approach. SimpóSio Bras. Sensoriamento Remoto 1996, 8, 677–680. [Google Scholar]
- Kuhn, H. The Hungarian Method for the Assignment Problem. Nav. Res. Logist. Q. 1955, 2, 83–97. [Google Scholar] [CrossRef]
Short Biography of Authors

| Hanover | Brunsiwck | |
|---|---|---|
| No. Units | 23,125 | 7678 |
| No. Records | ||
| Avg. No. Records/Unit | 8422.79 | 5674.91 |
| Time Span | October 2017–January 2018 | December 2018–January 2019 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tempelmeier, N.; Feuerhake, U.; Wage, O.; Demidova, E. Mining Topological Dependencies of Recurrent Congestion in Road Networks. ISPRS Int. J. Geo-Inf. 2021, 10, 248. https://doi.org/10.3390/ijgi10040248
Tempelmeier N, Feuerhake U, Wage O, Demidova E. Mining Topological Dependencies of Recurrent Congestion in Road Networks. ISPRS International Journal of Geo-Information. 2021; 10(4):248. https://doi.org/10.3390/ijgi10040248
Chicago/Turabian StyleTempelmeier, Nicolas, Udo Feuerhake, Oskar Wage, and Elena Demidova. 2021. "Mining Topological Dependencies of Recurrent Congestion in Road Networks" ISPRS International Journal of Geo-Information 10, no. 4: 248. https://doi.org/10.3390/ijgi10040248
APA StyleTempelmeier, N., Feuerhake, U., Wage, O., & Demidova, E. (2021). Mining Topological Dependencies of Recurrent Congestion in Road Networks. ISPRS International Journal of Geo-Information, 10(4), 248. https://doi.org/10.3390/ijgi10040248






