Nationwide Determination of Required Total Lengths of Multiple Borehole Heat Exchangers under Variable Climate and Geology in Japan
Abstract
:1. Introduction
2. Materials and Methods
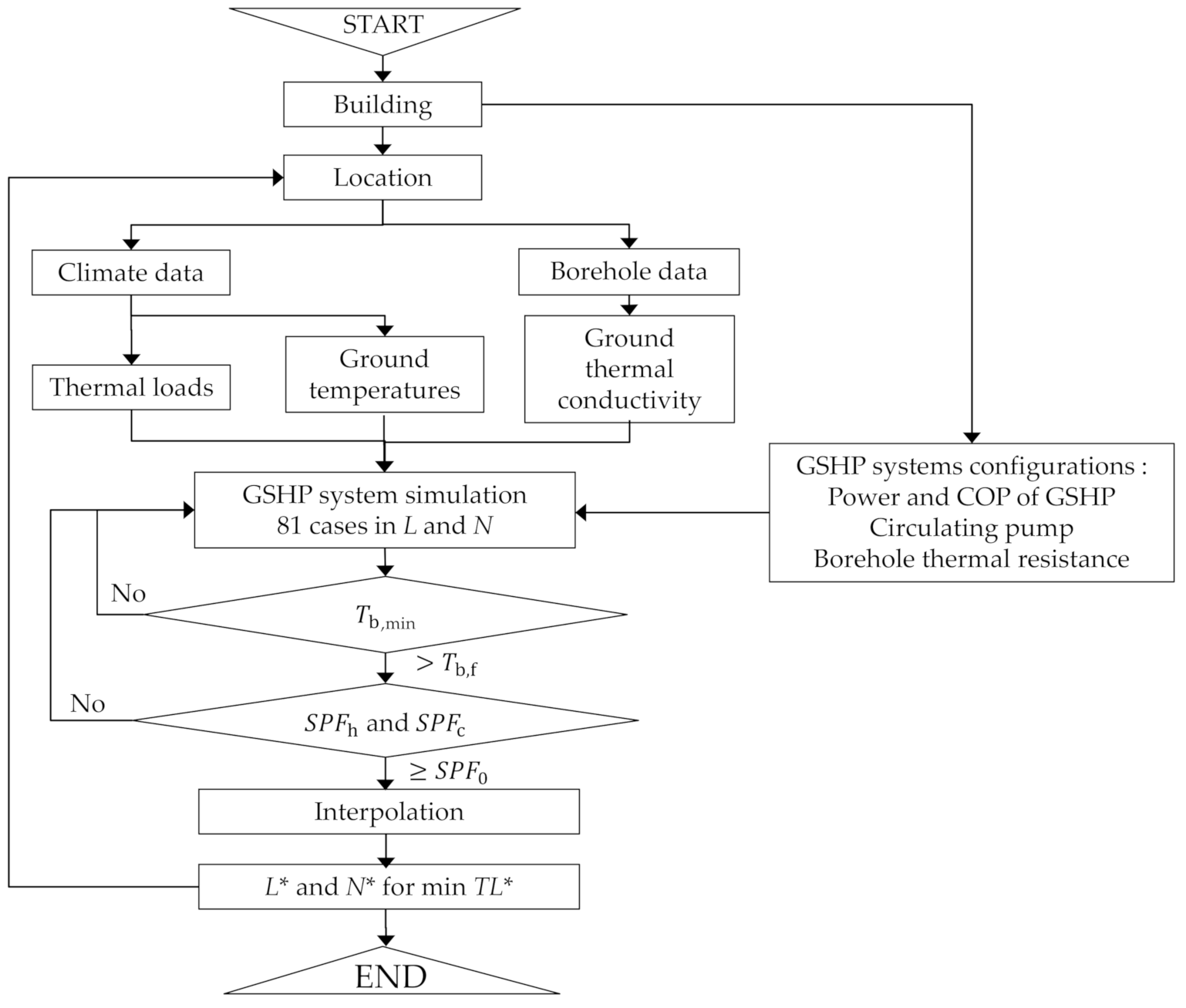
2.1. Simulation Approach for Determination of Total Lengths of Multiple Borehole Heat Exchangers (BHEs)
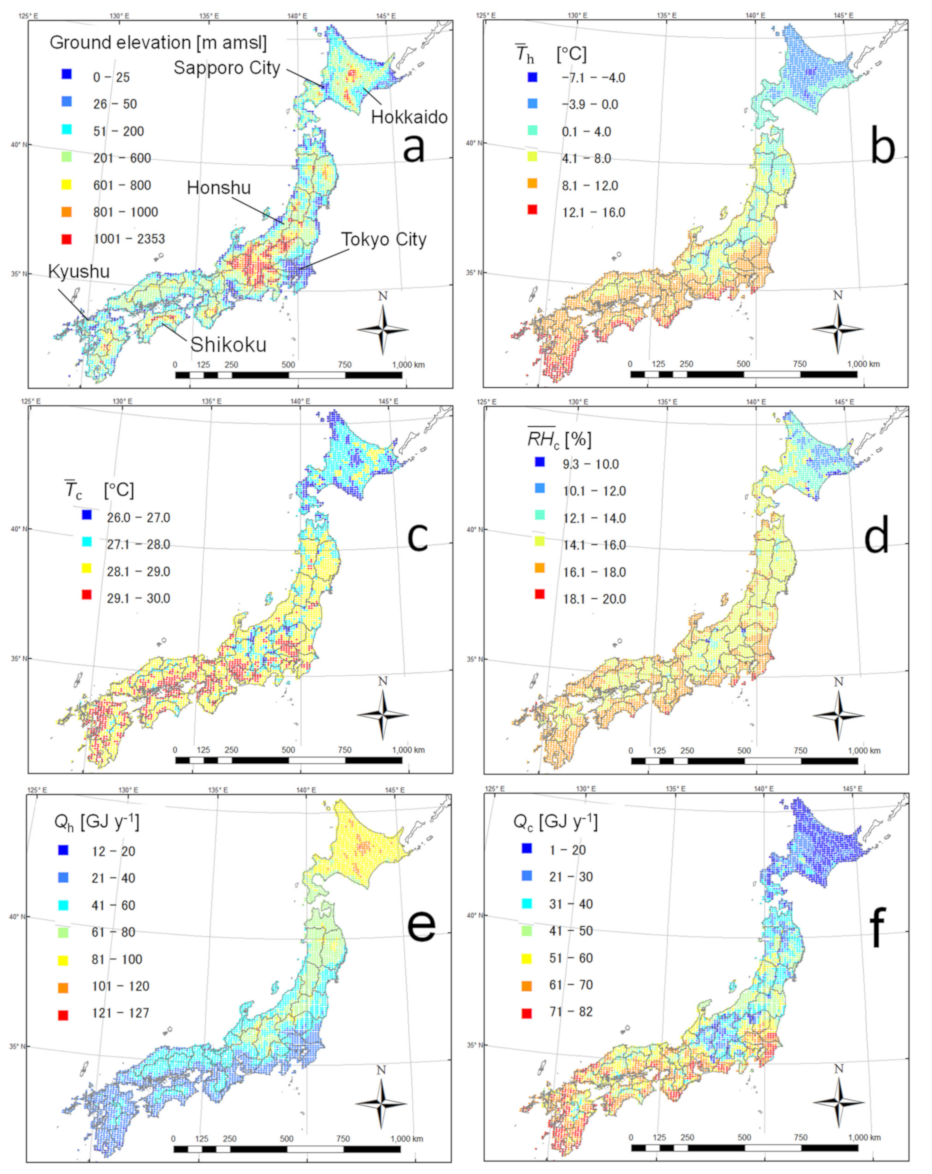
2.2. Geo-Information for Analysis
2.2.1. Climate and Thermal Loads
2.2.2. Thermal Properties Underground
2.3. System Configurations and Performance Target
2.4. Comparison between Simulated and Conventional Methods
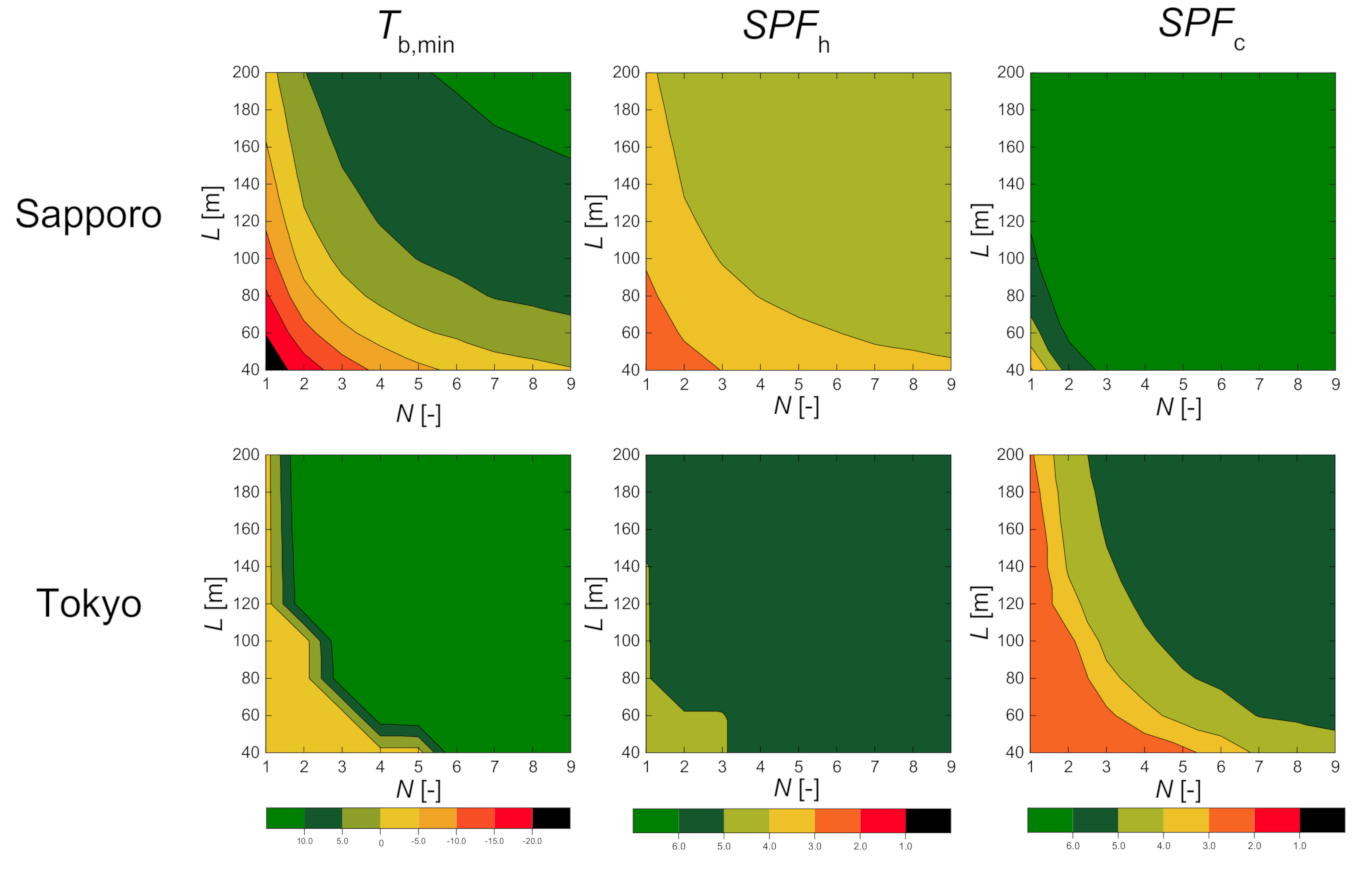
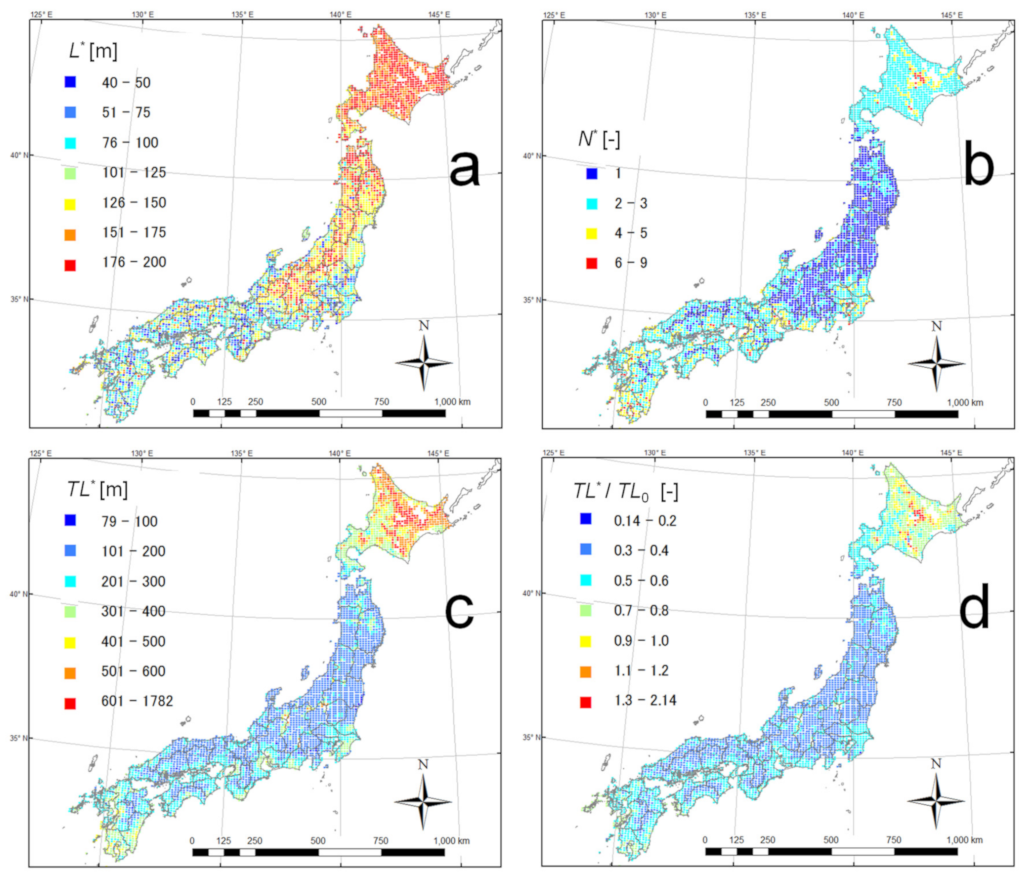
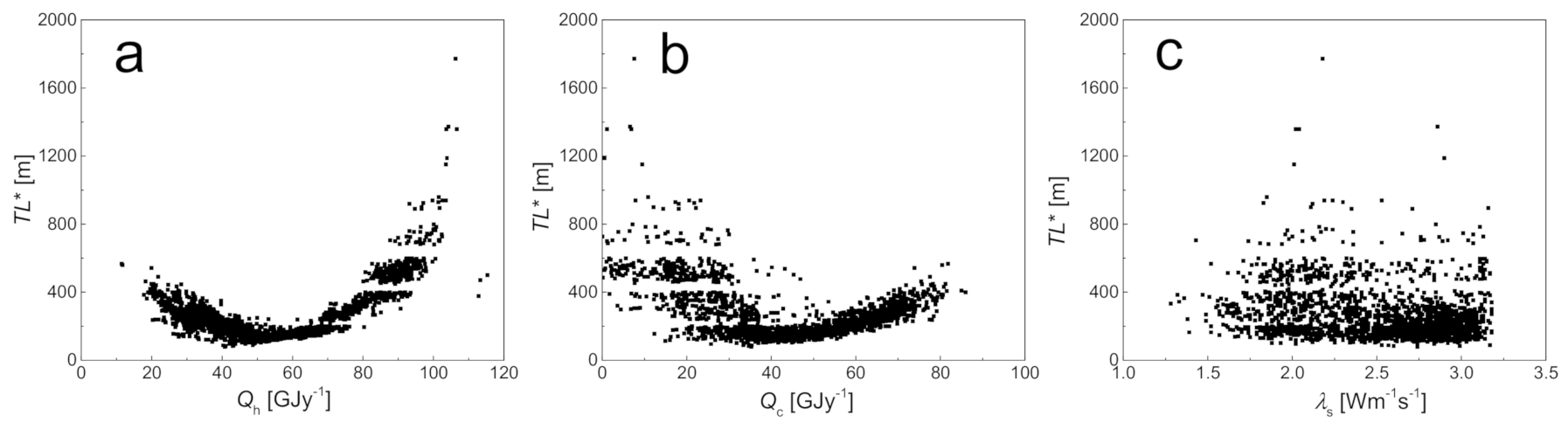
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- IEA Tracking Buildings 2020 Heating and Cooling. 2020. Available online: https://www.iea.org/reports/tracking-buildings-2020/ (accessed on 10 October 2019).
- Kavanaugh, S.; Rafferty, K. Geothermal Heating and Cooling; ASHRAE: Atlanta, GA, USA, 2014; pp. 1–15. [Google Scholar]
- Self, S.J.; Reddy, B.V.; Rosen, M.A. Geothermal heat pump systems: Status review and comparison with other heating options. Appl. Energy 2013, 101, 341–348. [Google Scholar] [CrossRef]
- Sarubu, I.; Sebarchievici, C. General review of ground-source heat pump systems for heating and cooling of buildings. Energy Build. 2014, 70, 441–454. [Google Scholar] [CrossRef]
- De Swardt, C.A.; Meyer, J.P. A performance comparison between an air-source and a ground-source reversible heat pump. Int. J. Energy Res. 2001, 25, 899–910. [Google Scholar] [CrossRef]
- Schiel, K.; Baume, O.; Caruso, G.; Leopold, U. GIS-based modelling of shallow geothermal energy potential for CO2 emission mitigation in urban areas. Renew. Energy 2016, 86, 1023–1036. [Google Scholar] [CrossRef]
- Lund, J.W.; Boyd, T.L. Direct utilization of geothermal energy 2015 worldwide review. Geothermics 2016, 60, 66–93. [Google Scholar] [CrossRef]
- FY2018 Report of Shallow Geothermal Energy Utilization in Japan. Available online: https://www.env.go.jp/press/files/jp/111221.pdf (accessed on 10 March 2020).
- Sanner, B.; Karytsas, C.; Mendrinos, D.; Rybachc, L. Current status of ground source heat pumps and underground thermal energy storage in Europe. Geothermics 2003, 32, 579–588. [Google Scholar] [CrossRef]
- ASHRAE. Chapter 35 Geothermal energy. In 2019 ASHRAE Handbook; ASHRAE: Atlanta, GA, USA, 2019; pp. 35.1–35.51. [Google Scholar]
- Closed-Loop Vertical Borehole Design, Installation & Materials Standards. Available online: https://www.gshp.org.uk/ (accessed on 20 September 2019).
- VDI Part 2 Thermal use of the ground. Ground source heat pump systems. In VDI Richtlinien 4640; VDI: Berlin, Germany, 2000; pp. 15–28. [Google Scholar]
- Takasugi, S.; Takeshima, J.; Uchida, Y.; Nakagawa, S. Planning and design of ground source heat pump systems In Construction Guide of Ground Source Heat Pump Systems; Ohm-sha: Tokyo, Japan, 2014; pp. 16–37. [Google Scholar]
- Spitler, J.; Bernier, M. Vertical borehole ground heat exchanger design methods In Advances in Ground Source Heat Pump Systems; Elsevier: Duxford, UK, 2016; pp. 29–61. [Google Scholar]
- Luo, J.; Rohn, J.; Bayer, M.; Priess, A. Thermal performance and economic evaluation of double U-tube borehole heat exchanger with three different borehole diameters. Energy Build. 2013, 42, 69–75. [Google Scholar] [CrossRef]
- GLHEPro 5.0. 2016. Available online: https://igshpa.org/software/ (accessed on 10 March 2020).
- Earth Energy Designer (EED) v3.2. 2015. Available online: https://www.buildingphysics.com/manuals/EED3.pdf (accessed on 10 March 2020).
- Diersch, H.J.G.; Bauer, D.; Heidemann, W.; Rühaak, W.; Schätzl, P. Finite element modeling of borehole heat exchanger systems. Part 1. Fundamentals. Comput. Geosci. 2010, 37, 1122–1135. [Google Scholar] [CrossRef]
- Śliwa, T.; Gołaś, A.; Wołoszyn, J.; Gonet, A. Numerical model of borehole heat exchanger in Ansys CFX software. Arch. Min. Sci. 2012, 57, 375–390. [Google Scholar]
- Retkowski, W.; Ziefle, G.; Thöming, J. Evaluation of different heat extraction strategies for shallow vertical ground-source heat pump systems. Appl. Energy 2015, 149, 259–271. [Google Scholar] [CrossRef]
- Montagud, C.; Corberán, J.M.; Montero, Á. In situ optimization methodology for the water circulation pumps frequency of ground source heat pump systems. Energy Build. 2014, 68, 42–53. [Google Scholar] [CrossRef]
- Wu, W.; You, T.; Wang, B.; Shi, W.; Li, W. Simulation of a combined heating, cooling and domestic hot water system based on ground source absorption heat pump. Appl. Energy 2014, 126, 113–122. [Google Scholar] [CrossRef]
- Retkowski, W.; Thöming, J. Thermoeconomic optimization of vertical ground-source heat pump systems through nonlinear integer programming. Appl. Energy 2014, 114, 492–503. [Google Scholar] [CrossRef]
- Casasso, A.; Sethi, R. Assessment and mapping of the shallow geothermal potential in the province of Cuneo (Piedmont, NW Italy). Renew. Energy 2017, 102, 306–315. [Google Scholar] [CrossRef]
- Ondreka, J.; Rüsgen, M.I.; Stober, I.; Czurda, K. GIS-supported mapping of shallow geothermal potential of representative areas in south-western Germany. Renew. Energy 2007, 32, 2186–2200. [Google Scholar] [CrossRef]
- Nam, Y.; Ooka, R. Numerical simulation of ground heat and water transfer for groundwater heat pump system based on real-scale experiment. Energy Build. 2010, 42, 69–75. [Google Scholar] [CrossRef]
- Iorio, M.; Carotenuto, A.; Corniello, A.; Di Fraia, S.; Massarotti, N.; Mauro, A.; Somma, R.; Vanoli, L. Low Enthalpy Geothermal Systems in Structural Controlled Areas: A Sustainability Analysis of Geothermal Resource for Heating Plant (The Mondragone Case in Southern Appennines, Italy). Energies 2020, 13, 1237. [Google Scholar] [CrossRef] [Green Version]
- Walcha, A.; Mohajerib, N.; Gudmundsson, A.; Scartezzini, J.L. Quantifying the technical geothermal potential from shallow borehole heat exchangers at regional scale. Renew. Energy 2021, 67, 217–224. [Google Scholar] [CrossRef]
- Spitler, J.; Bernier, M. Editorial ground source heat pump systems: The first century and beyond. J. HVAC Res. 2011, 17, 891–894. [Google Scholar]
- Nagano, K.; Katsura, T.; Takeda, S. Development of a design and performance prediction for the ground source heat pump system. Appl. Therm. Eng. 2006, 26, 1578–1592. [Google Scholar] [CrossRef]
- Katsura, T.; Nagano, K.; Takeda, S. Method of calculation of the ground temperature for multiple ground heat exchangers. Appl. Therm. Eng. 2008, 28, 1995–2004. [Google Scholar] [CrossRef]
- Sakata, Y.; Katsura, T.; Nagano, K. Estimation of ground thermal conductivity through Indicator kriging: Nation-scale application and vertical Profile analysis in Japan. Geothermics 2020, 88, 101881. [Google Scholar] [CrossRef]
- Lamarche, L.; Kajl, S.; Beauchamp, B. A review of methods to evaluate borehole thermal resistances in geothermal heat-pump systems. Geothermics 2010, 39, 187–200. [Google Scholar] [CrossRef]
- Zanchini, E.; Jahanbin, A. Effects of the temperature distribution on the thermal resistance of double U-tube borehole heat exchangers. Geothermics 2018, 71, 46–54. [Google Scholar] [CrossRef]
- Javed, S.; Spitler, J. Accuracy of borehole thermal resistance calculation methods for grouted single U-tube ground heat exchangers. Appl. Energy 2017, 187, 790–806. [Google Scholar] [CrossRef]
- Digital Elevation Mesh. 2008. Available online: https://fgd.gsi.go.jp/download/mapGis.php?tab=dem (accessed on 10 June 2019).
- Expanded AMeDAS Weather Data: Standard Year File 2001–2010. 2019. Available online: https://www.metds.co.jp/product/ea/ (accessed on 8 April 2020).
- SHASE. Simplified Calculation Methods of Cooling and Heating Loads; SHASE: Tokyo, Japan, 2010; pp. 1–26. [Google Scholar]
- TES-FS. 2015. Available online: https://www.hptcj.or.jp/Portals/0/data0/technology/manual/ (accessed on 12 June 2015).
- Ito, M.; Kameo, Y.; Satoguchi, F.; Masuda, F.; Hiroki, Y.; Takano, O.; Nakajima, T.; Suzuki, N. Neogene-Quaternary sedimentary successions. In The Geology of Japan; Geological Society of London: London, UK, 2016; pp. 309–338. [Google Scholar]
- Chiasson, A.D. Geothermal Heat Pump and Heat Engine Systems; John & Wiley Sons: West Sussex, UK, 2016; pp. 185–186. [Google Scholar]
- Domenico, P.A.; Schwartz, F.W. Physical and Chemical Hydrogeology, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1998; pp. 191–214. [Google Scholar]
- Chiasson, A.D.; Ree, S.; Spitler, J.D. A preliminary assessment of the effects of ground-water flow on closed-loop ground-source heat pump systems. ASHRAE Trans. 2000, 106, 380–393. [Google Scholar]
- Sakata, Y.; Katsura, T.; Nagano, K.; Marui, A. Nation-Scale Evaluation of Required Borehole Heat Exchangers Considering Advection Effects of Groundwater Flow in Japan; IAH Congress: Malaga, Spain, 2019. [Google Scholar]
- Sakata, Y.; Katsura, T.; Nagano, K. Importance of groundwater flow on life cycle costs of a household ground heat pump system in Japan. Jour JSRAE 2018, 35, 313–324. [Google Scholar]
- Arai, T. Hydrology for Regional Analysis; Kokon-shoin: Tokyo, Japan, 2004; pp. 140–161. [Google Scholar]
- Fujii, H.; Ishikami, T.; Ohshima, K. Improvement of thermal properties in grouting materials of heat exchange wells in ground-coupled heat pump systems. Shigen-to-Sozai 2003, 119, 403–409. [Google Scholar] [CrossRef] [Green Version]
- Lam, Y.; Law, E.; Dworkin, S.B. Characterization of the effects of borehole configuration and interference with long term ground temperature modelling of ground source heat pumps. Appl. Energy 2016, 179, 1032–1047. [Google Scholar]
- Sakata, Y.; Katsura, T.; Nagano, K. 500 m-gridded estimation of required lengths for a closed-type borehole heat exchangers in a ground-source heat pump systems. Jour JSCE 2019, 75, I_177–I_183. [Google Scholar]
- Katsura, T.; Shoji, Y.; Sakata, Y.; Nagano, K. Method for calculation of ground temperature in scenario involving multiple ground heat exchangers considering groundwater advection. Energy Build. 2020, 220, 110000. [Google Scholar] [CrossRef]


| City | Simulation Conditions | Simulation Results | ||||||
|---|---|---|---|---|---|---|---|---|
| Qh [Gjy−1] | Qc [Gjy−1] | λs [Wm−1K−1] | L* [m] | N* [-] | TL* [m] | TL0 [m] | TL*/TL0 [-] | |
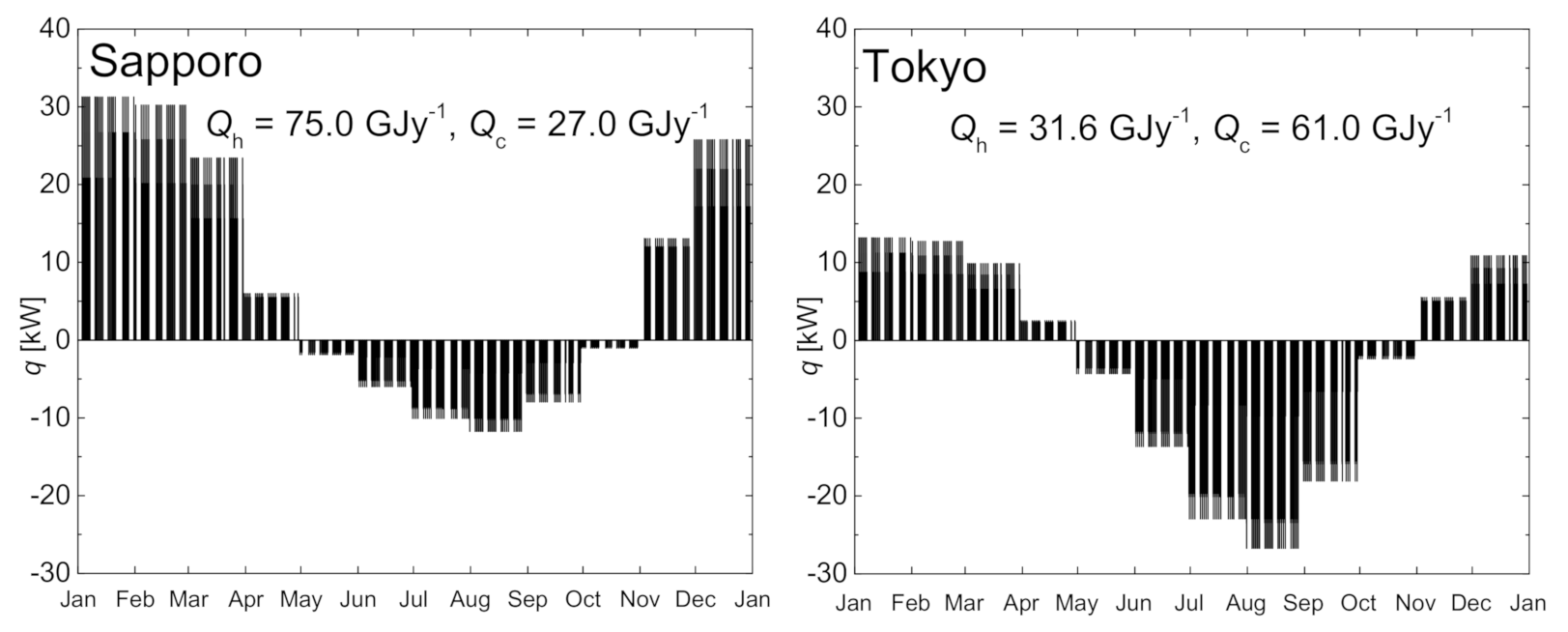
| Sapporo | 75.0 | 27.0 | 1.79 | 134 | 2 | 268 | 634 | 0.42 |
| Tokyo | 31.6 | 61.0 | 1.70 | 90 | 3 | 270 | 559 | 0.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sakata, Y.; Katsura, T.; Nagano, K. Nationwide Determination of Required Total Lengths of Multiple Borehole Heat Exchangers under Variable Climate and Geology in Japan. ISPRS Int. J. Geo-Inf. 2021, 10, 205. https://doi.org/10.3390/ijgi10040205
Sakata Y, Katsura T, Nagano K. Nationwide Determination of Required Total Lengths of Multiple Borehole Heat Exchangers under Variable Climate and Geology in Japan. ISPRS International Journal of Geo-Information. 2021; 10(4):205. https://doi.org/10.3390/ijgi10040205
Chicago/Turabian StyleSakata, Yoshitaka, Takao Katsura, and Katsunori Nagano. 2021. "Nationwide Determination of Required Total Lengths of Multiple Borehole Heat Exchangers under Variable Climate and Geology in Japan" ISPRS International Journal of Geo-Information 10, no. 4: 205. https://doi.org/10.3390/ijgi10040205
APA StyleSakata, Y., Katsura, T., & Nagano, K. (2021). Nationwide Determination of Required Total Lengths of Multiple Borehole Heat Exchangers under Variable Climate and Geology in Japan. ISPRS International Journal of Geo-Information, 10(4), 205. https://doi.org/10.3390/ijgi10040205








