Modeling of the German Wind Power Production with High Spatiotemporal Resolution
Abstract
1. Introduction
2. Data
2.1. Plant Dataset
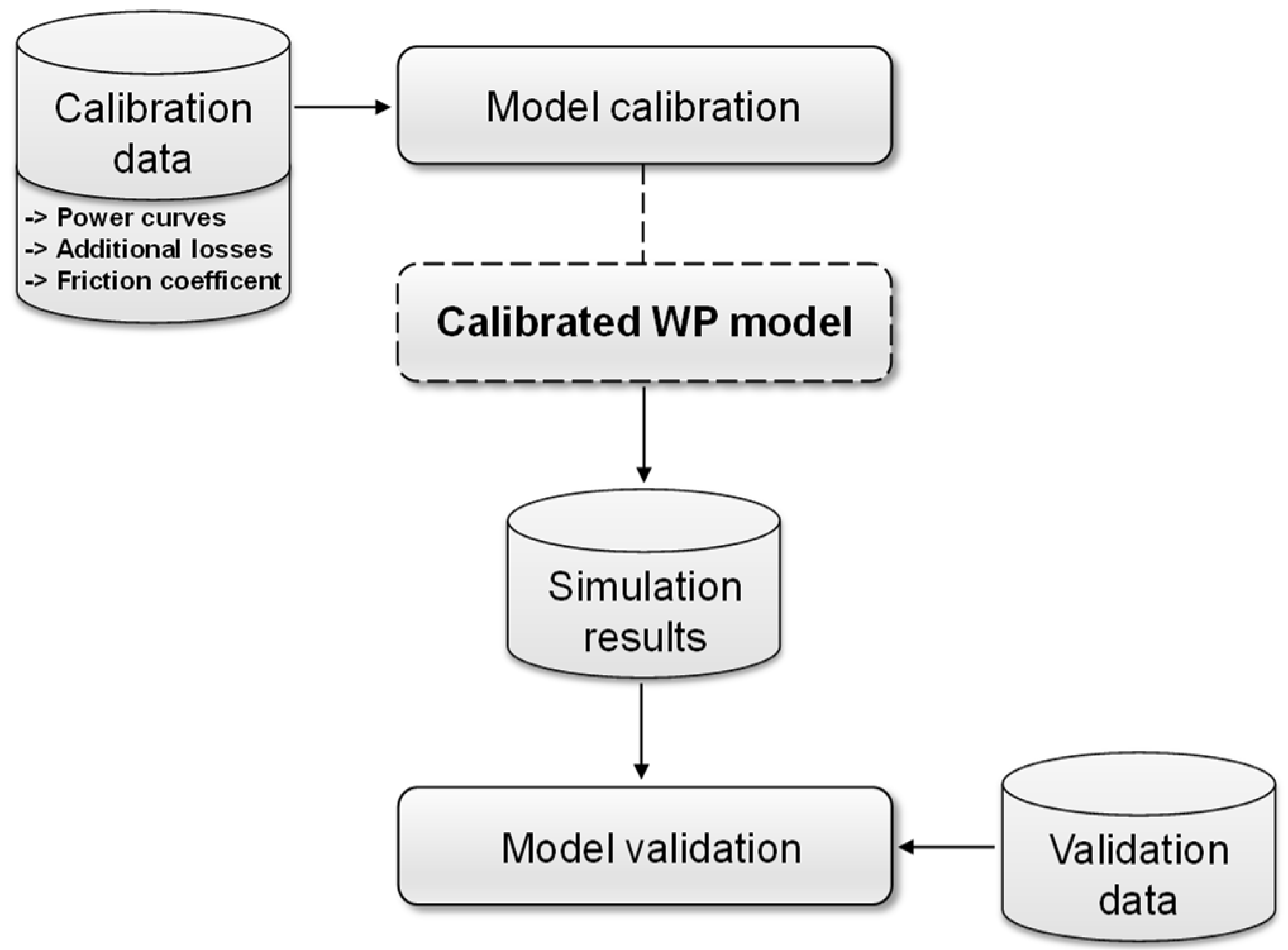
2.2. Calibration Data
- Power losses due to mutual shading of adjacent turbines (wake effect).
- Switch-offs due to wind turbine revisions or bird and bat protection.
- Feed-in interruptions due to energy surpluses in the power grids.
2.3. Weather Database
2.4. Validation Data
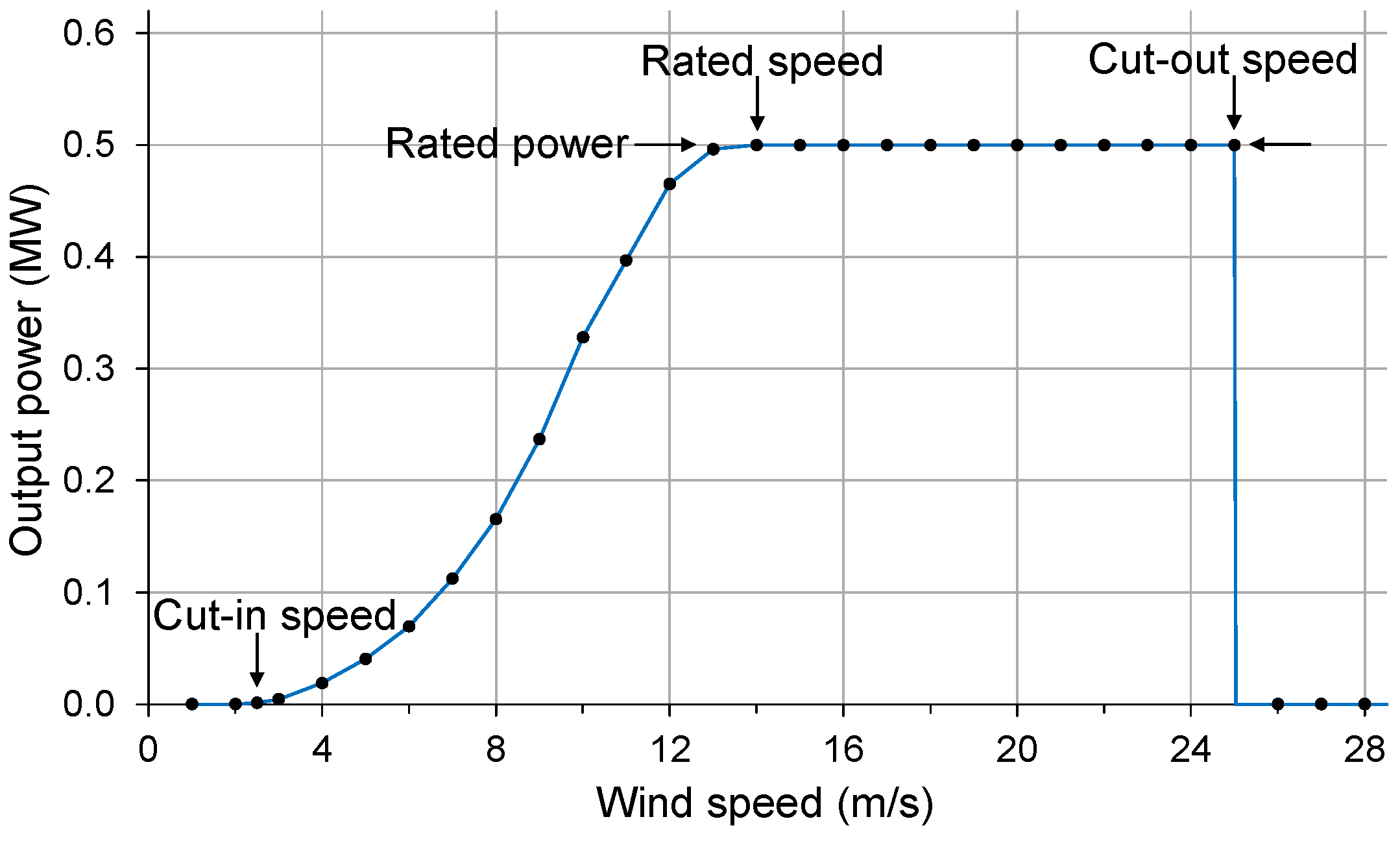
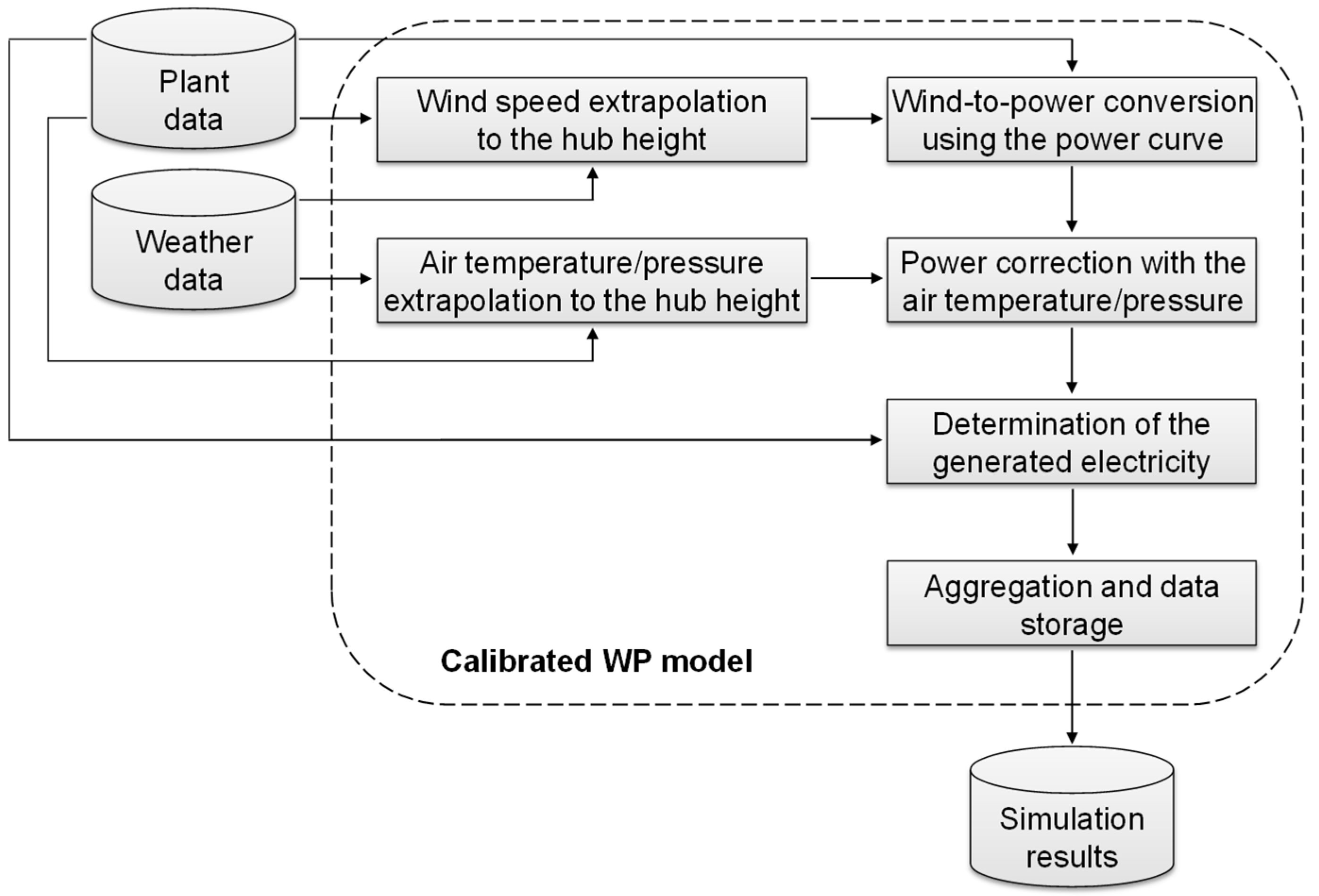
3. Model
- Extrapolation of the weather data provided for the specified plant location to the hub height.
- Wind-to-power conversion with the help of the specific power curve of the wind turbine.
- Correction of the output power using the air temperature and pressure at hub height.
- Calculation of the produced electricity considering additional losses and the date of (de-)commissioning.
- Temporal aggregation of the simulated time series and data storage.
4. Results
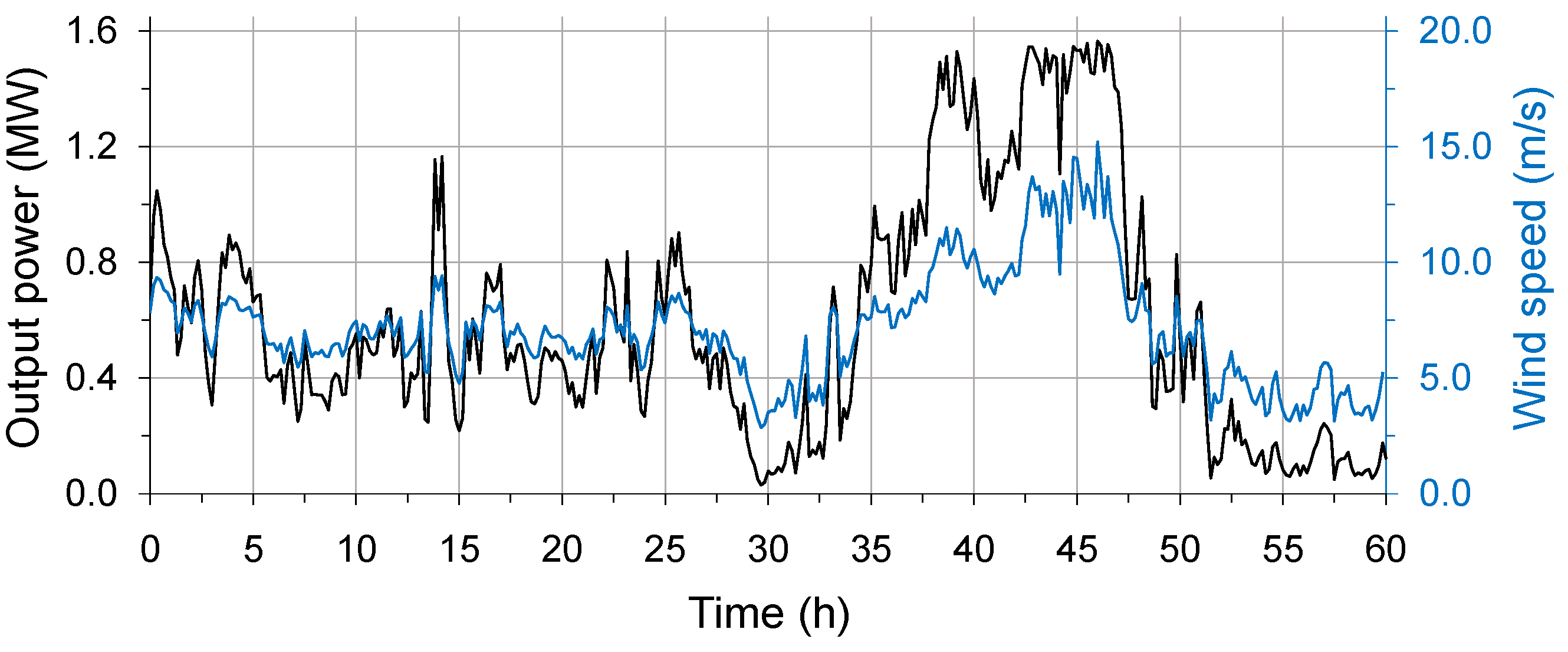
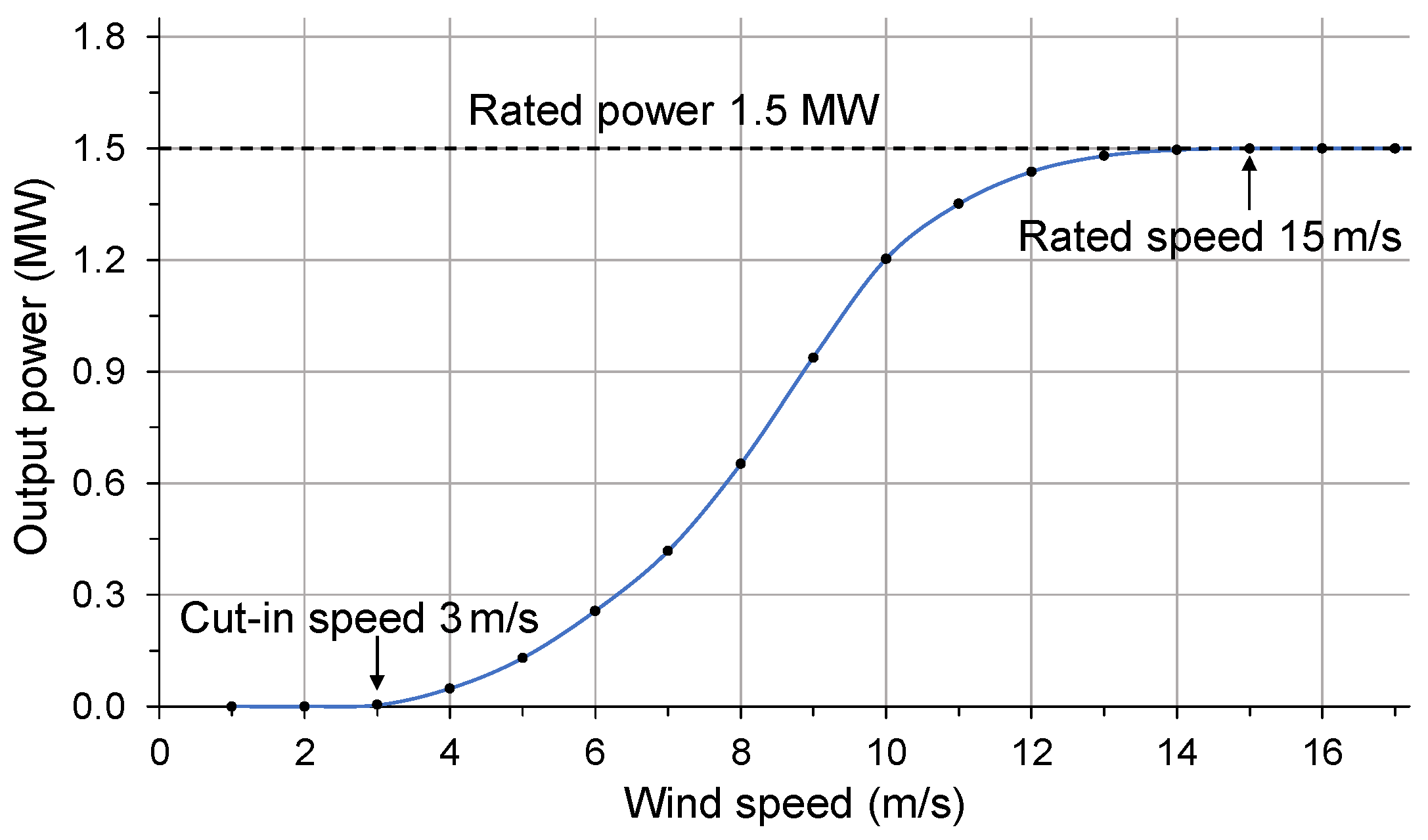
4.1. Simulation of a Single Wind Turbine
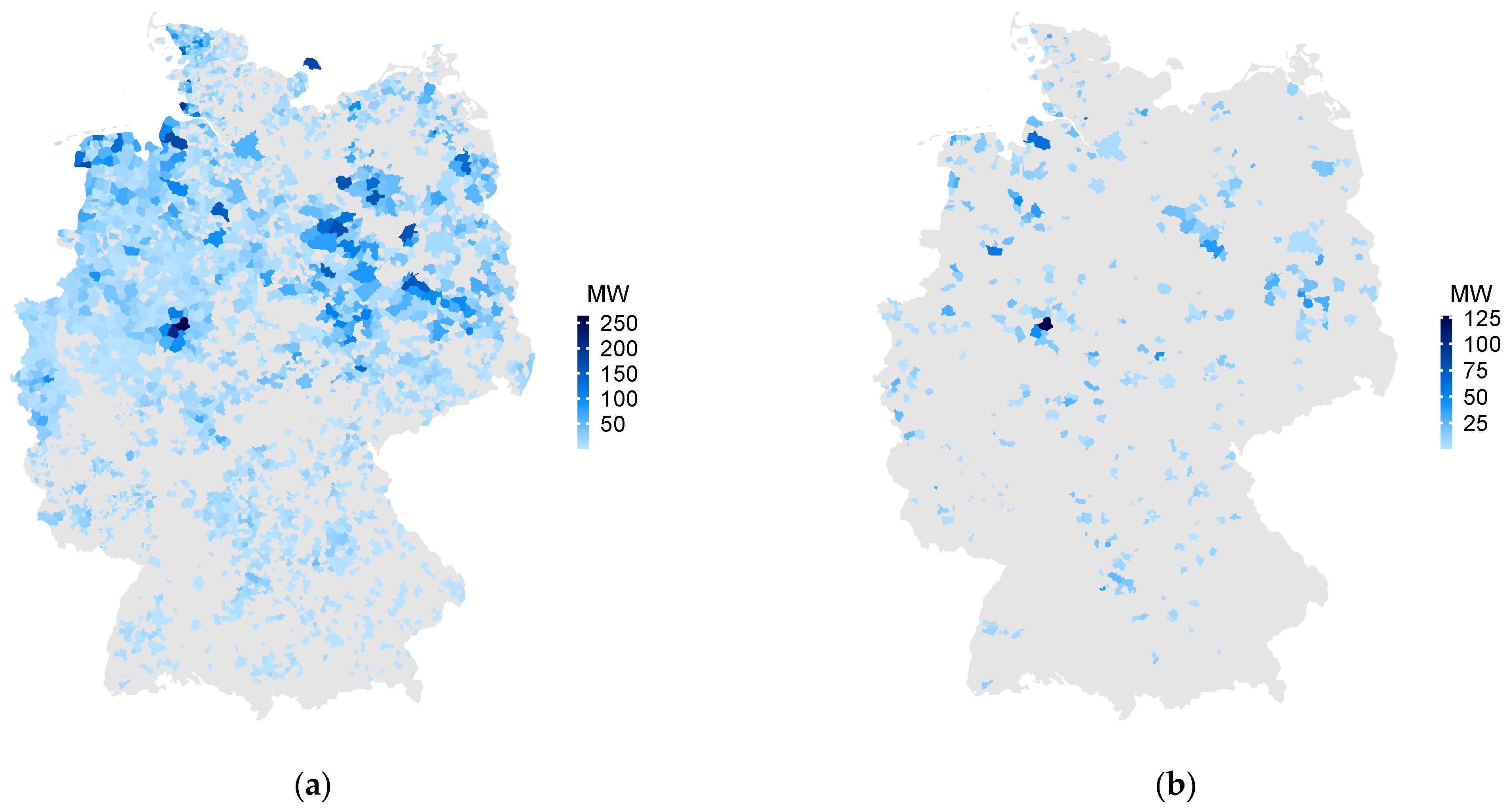
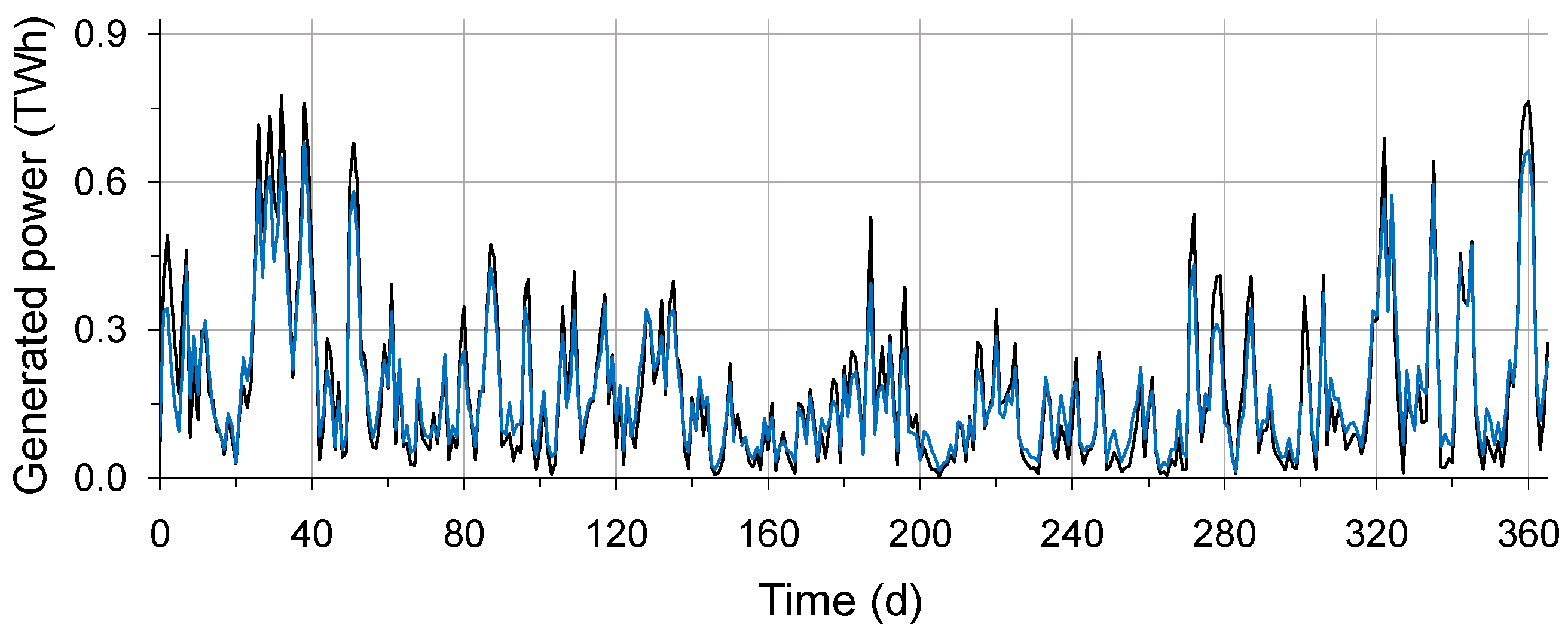
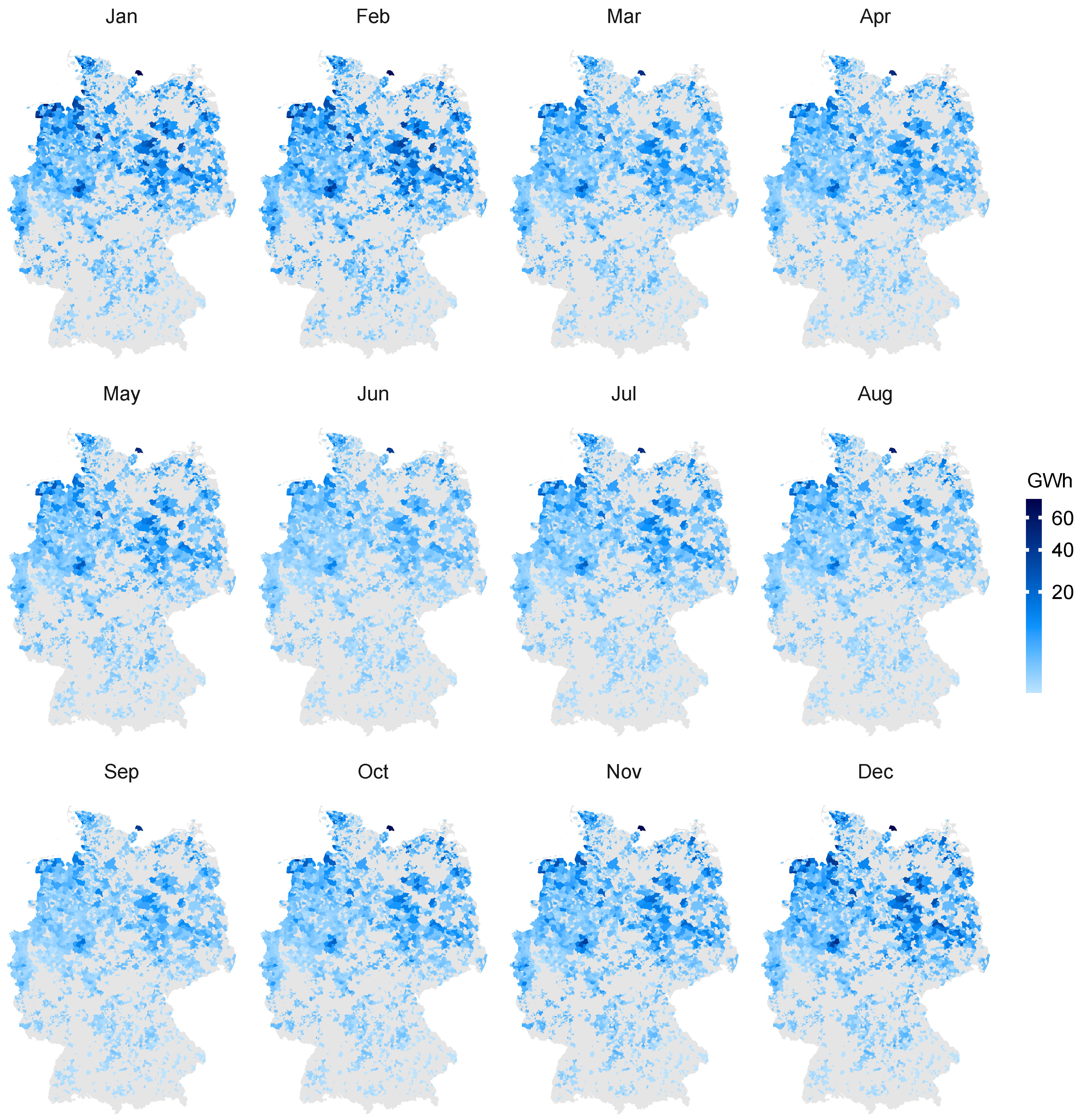
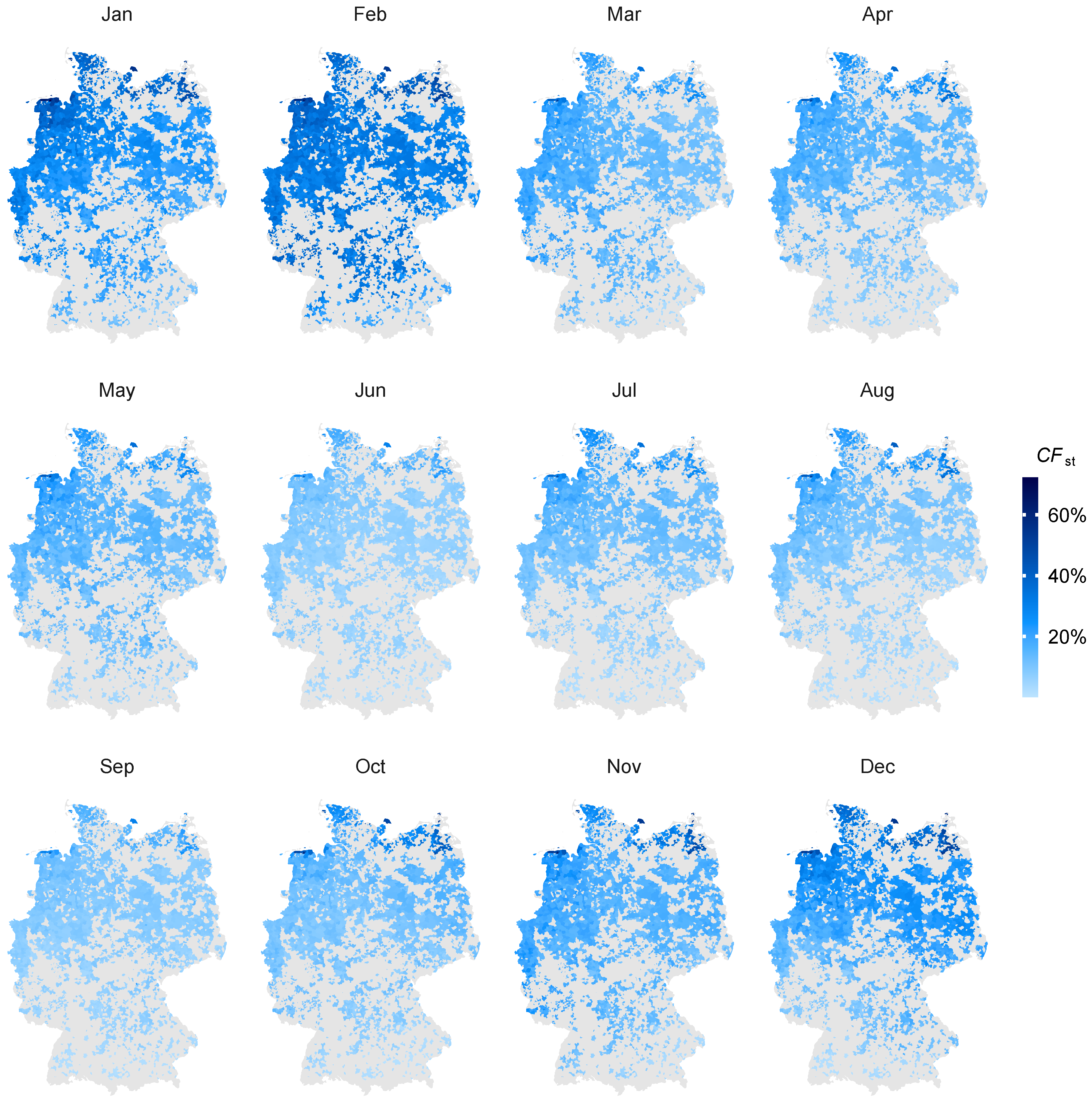
4.2. Simulation of the Plant Ensemble
- Deviations through the Hellmann’s exponential law with wind speeds at 10 m.
- The uncertainties of the weather data and the fact of hourly averaged values.
- Weather-related changes in air pressure are not considered in the model.
- The assignment of wind turbines to the corresponding power classes.
5. Discussion
6. Conclusions
Author Contributions
Funding
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- GWEC. Global Wind Report 2019; Global Wind Energy Council: Brussels, Belgium, 2020. [Google Scholar]
- BMWi Zeitreihen zur Entwicklung der erneuerbaren Energien in Deutschland unter Verwendung von Daten der Arbeitsgruppe Erneuerbare Energien-Statistik (AGEE-Stat). Available online: https://www.erneuerbare-energien.de (accessed on 30 July 2020).
- IRENA. Renewable Power Generation Costs in 2019; International Renewable Energy Agency (IRENA): Abu Dhabi, UAE, 2020. [Google Scholar]
- Rauner, S.; Eichhorn, M.; Thrän, D. The Spatial Dimension of the Power System: Investigating Hot Spots of Smart Renewable Power Provision. Appl. Energy 2016, 184, 1038–1050. [Google Scholar] [CrossRef]
- Ramirez Camargo, L.; Gruber, K.; Nitsch, F.; Dorner, W. Hybrid Renewable Energy Systems to Supply Electricity Self-Sufficient Residential Buildings in Central Europe. Energy Procedia 2019, 158, 321–326. [Google Scholar] [CrossRef]
- Ramirez Camargo, L.; Nitsch, F.; Gruber, K.; Valdes, J.; Wuth, J.; Dorner, W. Potential Analysis of Hybrid Renewable Energy Systems for Self-Sufficient Residential Use in Germany and the Czech Republic. Energies 2019, 12, 4185. [Google Scholar] [CrossRef]
- Ottenburger, S.S.; Çakmak, H.K.; Jakob, W.; Blattmann, A.; Trybushnyi, D.; Raskob, W.; Kühnapfel, U.; Hagenmeyer, V. A Novel Optimization Method for Urban Resilient and Fair Power Distribution Preventing Critical Network States. Int. J. Crit. Infrastruct. Prot. 2020, 29, 100354. [Google Scholar] [CrossRef]
- Lehneis, R.; Manske, D.; Schinkel, B.; Thrän, D. Modeling of the Power Generation from Wind Turbines with High Spatial and Temporal Resolution. EGU Gen. Assem. Conf. Abstr. 2020. [Google Scholar] [CrossRef]
- Thrän, D.; Bunzel, K.; Klenke, R.; Koblenz, B.; Lorenz, C.; Majer, S.; Manske, D.; Massmann, E.; Oehmichen, G.; Peters, W.; et al. Naturschutzfachliches Monitoring des Ausbaus der Erneuerbaren Energien im Strombereich und Entwicklung von Instrumenten zur Verminderung der Beeinträchtigung von Natur und Landschaft; Bundesamt für Naturschutz: Bonn, Germany, 2020. [Google Scholar]
- Eichhorn, M.; Scheftelowitz, M.; Reichmuth, M.; Lorenz, C.; Louca, K.; Schiffler, A.; Keuneke, R.; Bauschmann, M.; Ponitka, J.; Manske, D.; et al. Spatial Distribution of Wind Turbines, Photovoltaic Field Systems, Bioenergy, and River Hydro Power Plants in Germany. Data 2019, 4, 29. [Google Scholar] [CrossRef]
- Olauson, J.; Bergkvist, M. Modelling the Swedish Wind Power Production Using MERRA Reanalysis Data. Renew. Energy 2015, 76, 717–725. [Google Scholar] [CrossRef]
- Engelhorn, T.; Müsgens, F. How to Estimate Wind-Turbine Infeed with Incomplete Stock Data: A General Framework with an Application to Turbine-Specific Market Values in Germany. Energy Econ. 2018, 72, 542–557. [Google Scholar] [CrossRef]
- Becker, R.; Thrän, D. Completion of Wind Turbine Data Sets for Wind Integration Studies Applying Random Forests and K-Nearest Neighbors. Appl. Energy 2017, 208, 252–262. [Google Scholar] [CrossRef]
- Federal Network Agency Core Energy Market Data Register. Available online: https://www.bundesnetzagentur.de/EN (accessed on 30 July 2020).
- Pierrot, M. The Wind Power. Available online: https://www.thewindpower.net/ (accessed on 25 June 2020).
- Datasheet ENERCON E-40/5.40. ENERCON GmbH, Dreekamp 5, 26605 Aurich (Germany). 2003. Available online: https://www.enercon.de (accessed on 19 May 2020).
- Staffell, I.; Pfenninger, S. Using Bias-Corrected Reanalysis to Simulate Current and Future Wind Power Output. Energy 2016, 114, 1224–1239. [Google Scholar] [CrossRef]
- Olauson, J. ERA5: The New Champion of Wind Power Modelling? Renew. Energy 2018, 126, 322–331. [Google Scholar] [CrossRef]
- González-Aparicio, I.; Monforti, F.; Volker, P.; Zucker, A.; Careri, F.; Huld, T.; Badger, J. Simulating European Wind Power Generation Applying Statistical Downscaling to Reanalysis Data. Appl. Energy 2017, 199, 155–168. [Google Scholar] [CrossRef]
- Bosch, J.; Staffell, I.; Hawkes, A.D. Temporally-Explicit and Spatially-Resolved Global Onshore Wind Energy Potentials. Energy 2017, 131, 207–217. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Bollmeyer, C.; Keller, J.D.; Ohlwein, C.; Wahl, S.; Crewell, S.; Friederichs, P.; Hense, A.; Keune, J.; Kneifel, S.; Pscheidt, I.; et al. Towards a High-Resolution Regional Reanalysis for the European CORDEX Domain. Q. J. R. Meteorol. Soc. 2015, 141, 1–15. [Google Scholar] [CrossRef]
- Satellite Application Facility on Climate Monitoring (CM SAF). Available online: https://www.cmsaf.eu/EN/Home/home_node.html (accessed on 18 March 2020).
- EU Science Hub—Photovoltaic Geographical Information System (PVGIS). Available online: https://ec.europa.eu/jrc/en/pvgis (accessed on 25 June 2020).
- Lehneis, R.; Manske, D.; Thrän, D. Generation of Spatiotemporally Resolved Power Production Data of PV Systems in Germany. ISPRS Int. J. Geo Inform. 2020, 9, 621. [Google Scholar] [CrossRef]
- SMARD—Strommarktdaten, Stromhandel und Stromerzeugung in Deutschland. Available online: https://www.smard.de/home/ (accessed on 18 March 2020).
- Ekström, J.; Koivisto, M.; Mellin, I.; Millar, R.J.; Lehtonen, M. A Statistical Modeling Methodology for Long-Term Wind Generation and Power Ramp Simulations in New Generation Locations. Energies 2018, 11, 2442. [Google Scholar] [CrossRef]
- Bañuelos-Ruedas, F.; Angeles-Camacho, C.; Rios-Marcuello, S. Methodologies Used in the Extrapolation of Wind Speed Data at Different Heights and Its Impact in the Wind Energy Resource Assessment in a Region. In Wind Farm—Technical Regulations, Potential Estimation and Siting Assessment; BoD–Books on Demand: Norderstedt, Germany, 2011. [Google Scholar] [CrossRef]
- Petersen, E.L.; Mortensen, N.G.; Landberg, L.; Højstrup, J.; Frank, H.P. Wind Power Meteorology. Part I: Climate and Turbulence. Wind Energy 1998, 1, 2–22. [Google Scholar] [CrossRef]
- Witterung und Klima: Eine Einführung in die Meteorologie und Klimatologie, 11th ed.; Hupfer, P., Kuttler, W., Eds.; Vieweg+Teubner Verlag: Wiesbaden, Germany, 2005; ISBN 978-3-322-96749-7. [Google Scholar]
- DIN EN 61400-12-1 VDE 0127-12-1:2017-12 Windenergieanlagen. Available online: https://www.beuth.de/de/norm/din-en-61400-12-1/279191705 (accessed on 5 March 2020).
- Krebs, H.; Kuntzsch, J. Betriebserfahrungen mit Windkraftanlagen auf komplexen Binnenlandstandorten. Erneuerbare Energ. 2000, 12, 2000. [Google Scholar]
- Pfenninger, S.; Staffell, I. Renewables.Ninja. Available online: https://www.renewables.ninja/ (accessed on 29 September 2020).
- Becker, R.; Thrän, D. Optimal Siting of Wind Farms in Wind Energy Dominated Power Systems. Energies 2018, 11, 978. [Google Scholar] [CrossRef]
- Estrella, H.F.; Korn, M.; Alberts, K. Analysis of the Influence of Wind Turbine Noise on Seismic Recordings at Two Wind Parks in Germany. J. Geosci. Environ. Prot. 2017, 5, 76–91. [Google Scholar] [CrossRef]


| Parameter | Usage |
|---|---|
| Latitude | required |
| Longitude | required |
| LAU-Id 1 | optional |
| Rated power | required |
| Hub height | required |
| Turbine type | optional |
| Commission date | required |
| Decommission date | optional |
| Power Class (MW) | Power Range (MW) | Turbine Type |
|---|---|---|
| 0.1 | PR ≤ 0.15 | Fuhrländer FL100 |
| 0.2 | 0.15 < PR ≤ 0.25 | Enercon E-30 |
| 0.5 | 0.25 < PR ≤ 0.75 | Enercon E-40 |
| 1 | 0.75 < PR ≤ 1.50 | Vestas V52 |
| 2 | 1.50 < PR ≤ 2.50 | Enercon E-82 |
| 3 | 2.50 < PR ≤ 3.50 | Vestas V112 |
| 5 | PR > 3.50 | Enercon E-126 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lehneis, R.; Manske, D.; Thrän, D. Modeling of the German Wind Power Production with High Spatiotemporal Resolution. ISPRS Int. J. Geo-Inf. 2021, 10, 104. https://doi.org/10.3390/ijgi10020104
Lehneis R, Manske D, Thrän D. Modeling of the German Wind Power Production with High Spatiotemporal Resolution. ISPRS International Journal of Geo-Information. 2021; 10(2):104. https://doi.org/10.3390/ijgi10020104
Chicago/Turabian StyleLehneis, Reinhold, David Manske, and Daniela Thrän. 2021. "Modeling of the German Wind Power Production with High Spatiotemporal Resolution" ISPRS International Journal of Geo-Information 10, no. 2: 104. https://doi.org/10.3390/ijgi10020104
APA StyleLehneis, R., Manske, D., & Thrän, D. (2021). Modeling of the German Wind Power Production with High Spatiotemporal Resolution. ISPRS International Journal of Geo-Information, 10(2), 104. https://doi.org/10.3390/ijgi10020104







