A Decentralized Semantic Reasoning Approach for the Detection and Representation of Continuous Spatial Dynamic Phenomena in Wireless Sensor Networks
Abstract
1. Introduction
2. Related Works and Concepts
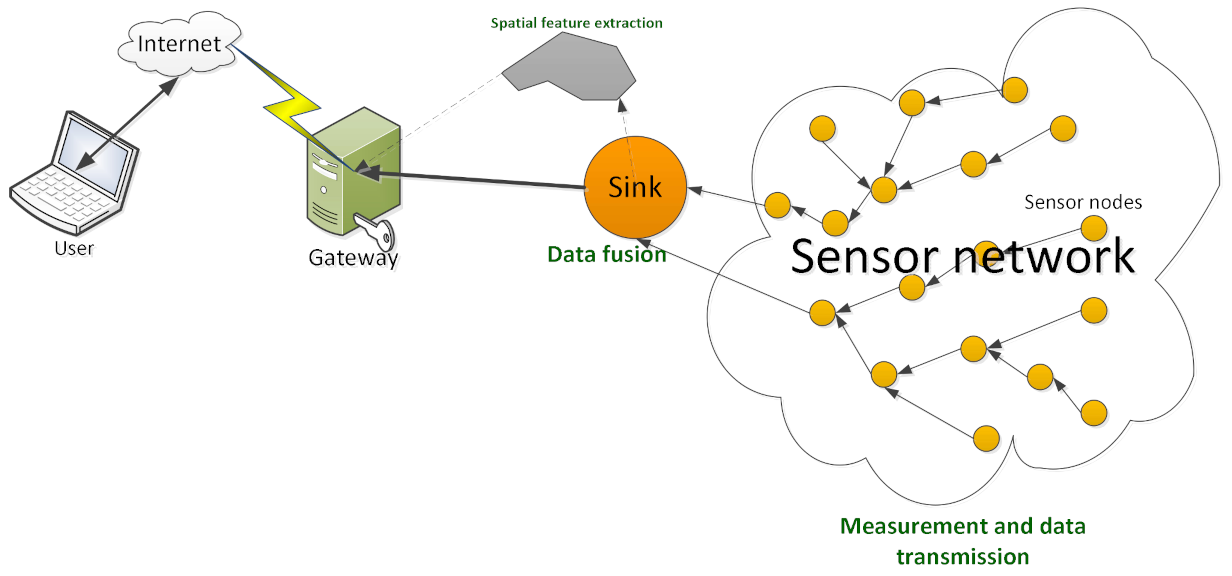
2.1. Spatial Computing in Sensor Networks
2.2. Sensor Data Geosemantics
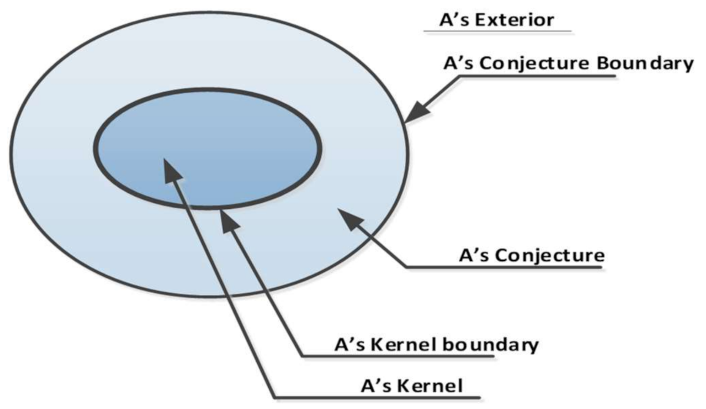
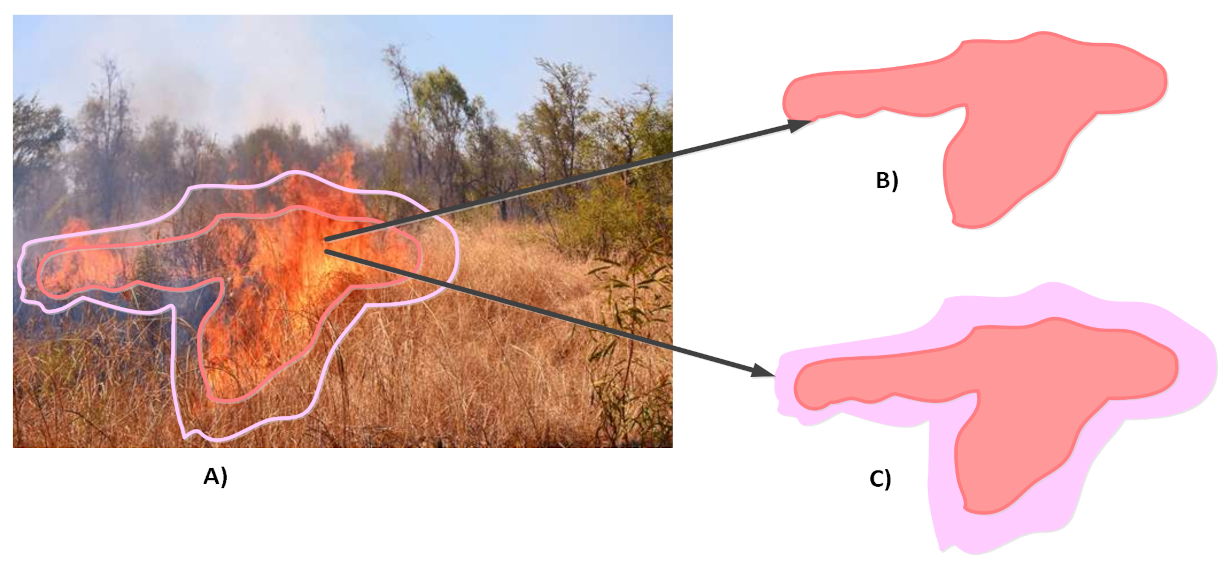
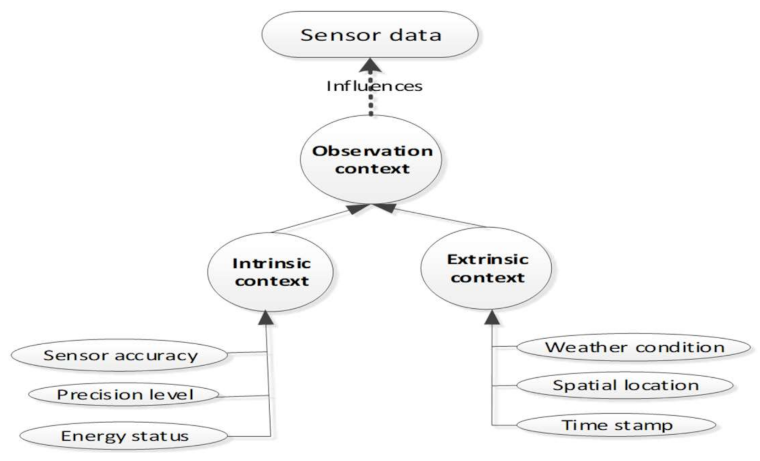
2.3. Inherent Uncertainties Related to the Observation and Representation of a Dynamic Phenomenon from Rsd
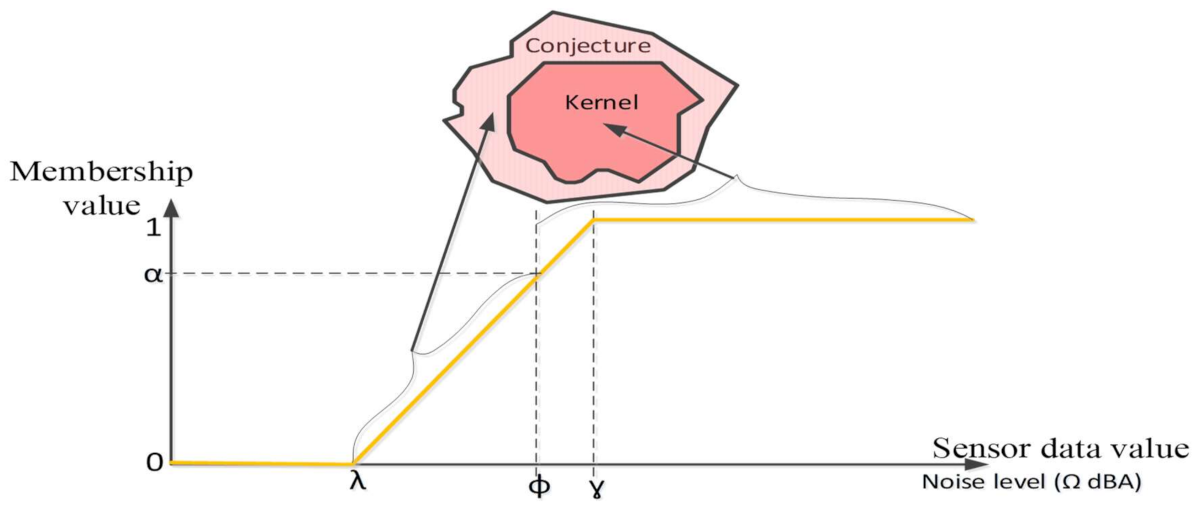
- The existential uncertainty expressing how sure we are that a given phenomenon really exists at a particular position in space and time from recorded sensor data,
- The extensional uncertainty expressing how the area covered by the monitored phenomenon can only be determined,
- The geometric uncertainty refers to the precision with which the boundary of the object representing the monitored phenomenon can be detected.
3. Building Vague Spatial Objects in Sensor Networks Using A Decentralized Semantic Reasoning Approach
- 1.
- Fuzzy rule-based detection of a monitored phenomenon: here, sensor nodes use a built-in reasoning engine to evaluate the membership of their location to different parts of the spatial extent of a monitored phenomenon using a MF and the observed data at a given time. The MF shape and definition need to cope with the semantics of sensor network data, the phenomenon and its spatial model. Defuzzification rules based on three valued logic are also set accordingly.
- 2.
- Decentralized fuzzy inference of spatial boundaries of a monitored phenomenon: each node collaborates with one-hop neighbors based on their phenomenon detections and the semantic of adopted spatial model to infer their relative position to phenomenon boundaries.
- 3.
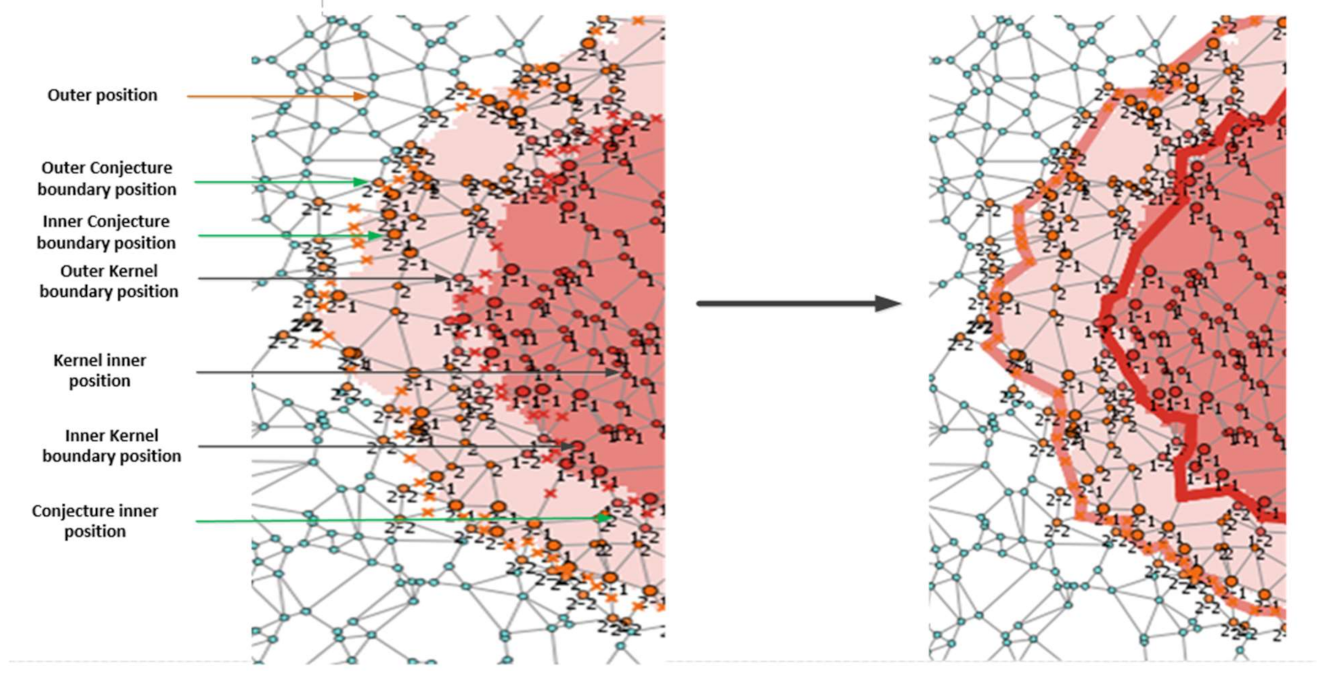
- Spatial computation of vertices, edges and geometry of monitored phenomenon snapshots: using the relative positions of linked nodes to detect boundaries, vertices, location, and categories (kernel or conjecture) are determined. Fuzzy boundary edges are built based on vertices position and categories, forming the geometry of spatial objects representing phenomenon snapshots at a given time.
3.1. Fuzzy Rule-Based Detection of a Sensed Phenomenon from RSD
3.2. Stage 1: Preparing the Sensors Reasoning Engine
- Knowledge base and rule base preparation
- ○
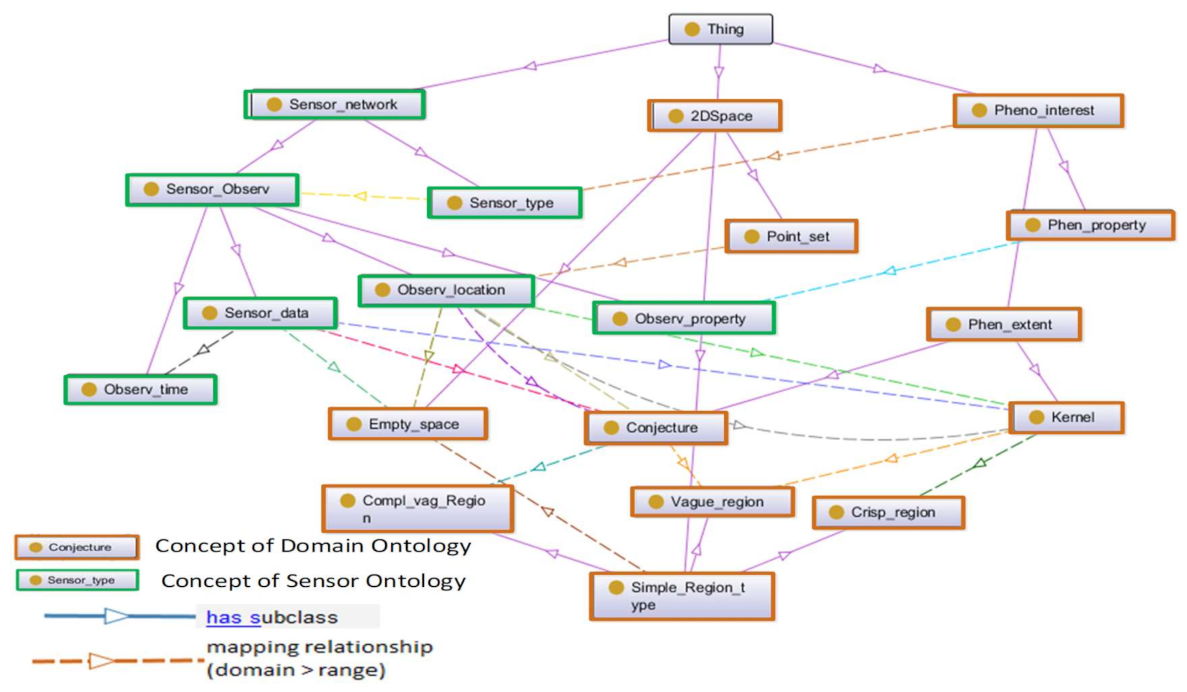
- A sensor ontology such as the semantic sensor network ontology (SSN) [43], from which the meaning of sensor network data can be explicitly specified. This is the case of the observation procedure, which defines the way sensors execute its measurements.
- ○
- A domain ontology designed for describing particular domain entities or a certain activity [44], from which the monitored phenomenon can be explicitly interpreted or represented from sensor observations.
- sensor_type (Sensor_ID, Sensor_model, Measured_Propert, Unit),
- sensor_range_value (Type_model, Minvalue,Maxvalue),
- phenom_sensor (Type_phenomenon, Sensor_model,Pehnom_prop),
- Value ≥ Minvalue, Value ≤ Maxvalue.
- Setting the fuzzifier unit
- Setting the defuzzifier unit
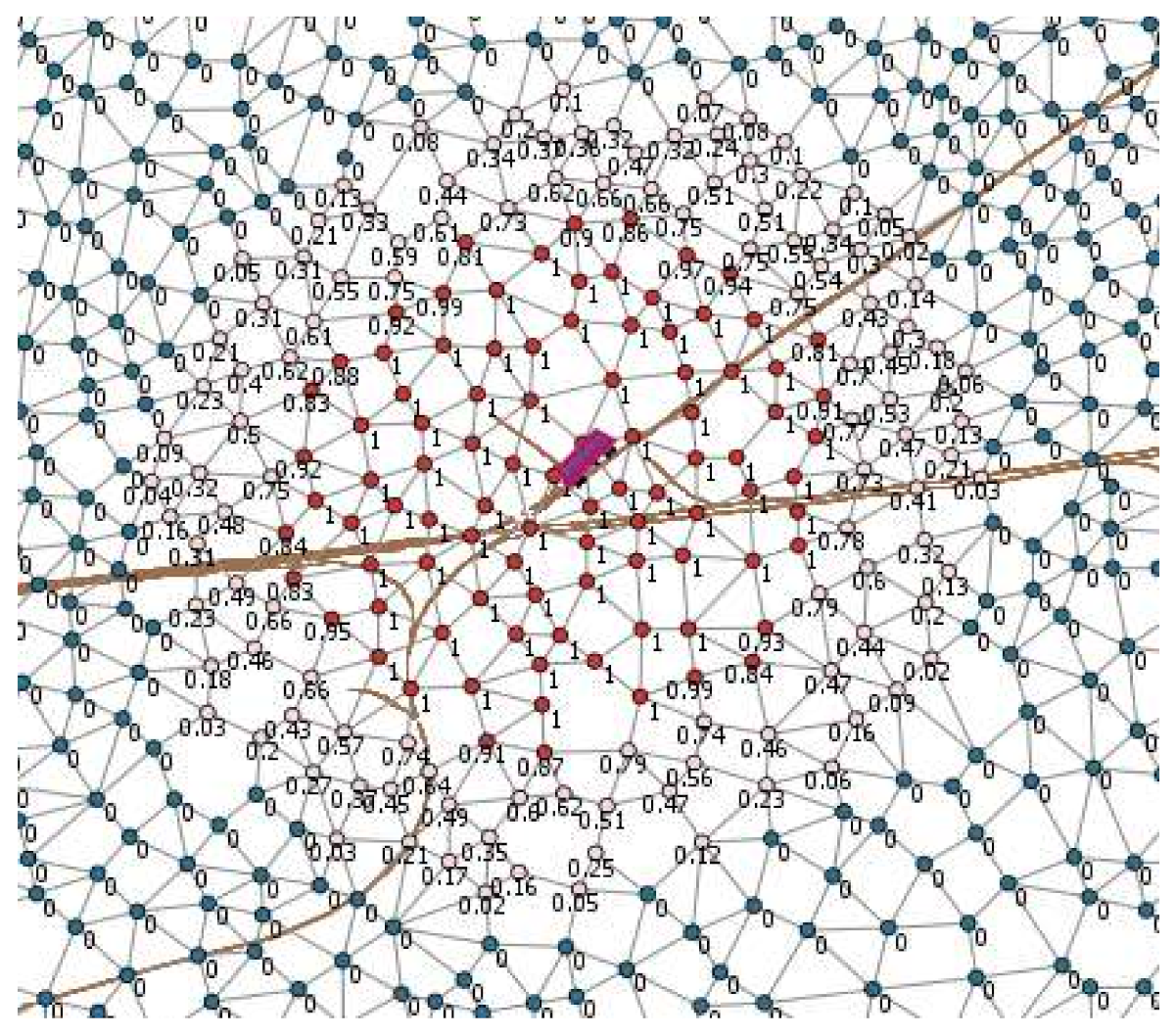
3.3. Stage 2: Fuzzy Spatial Reasoning from Rsd: Fuzzification and Defuzzification Processes
3.4. Local Collaborative Spatial Reasoning for Boundaries Detection Using a Geosensor Network
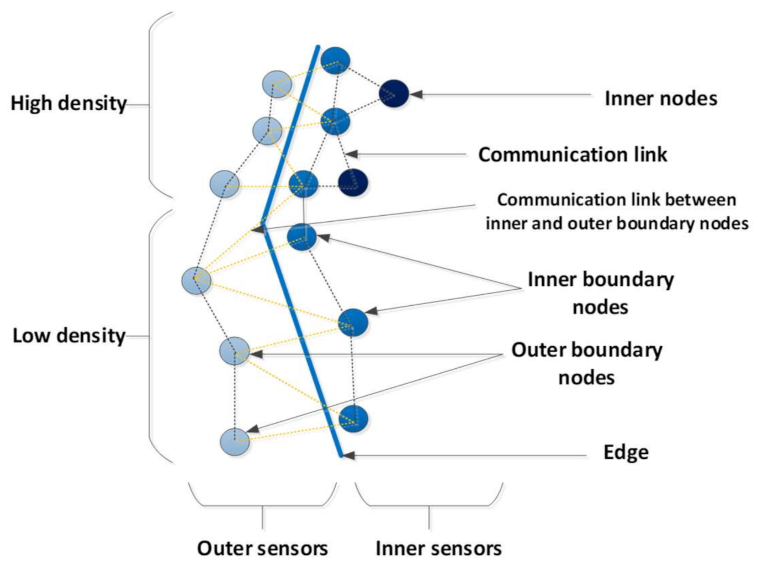
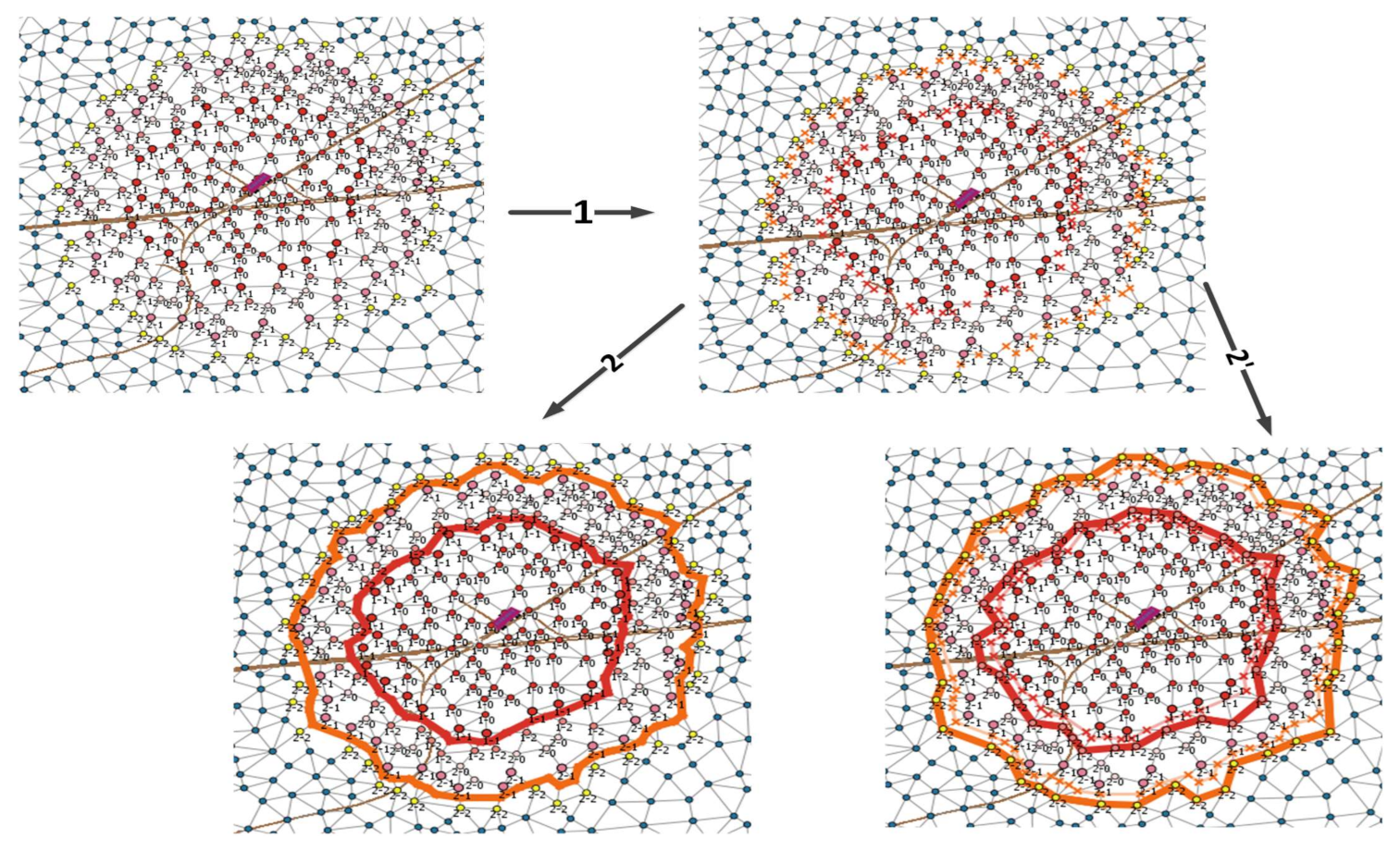
3.5. Spatial Representation of Sensed Phenomena in SN: Vague Object Geometry
- Inner kernel boundary nodes, noted:
- Outer kernel boundary nodes, noted:
- Inner conjecture boundary nodes, noted:
- Outer conjecture boundary nodes, noted:
- its membership value with ;
- the set of one-hop neighbors with different position type (inner - outer) along the same boundary ;
- the distance to these one-hop neighbors of other type with dx and dy the x and y components of the distance.
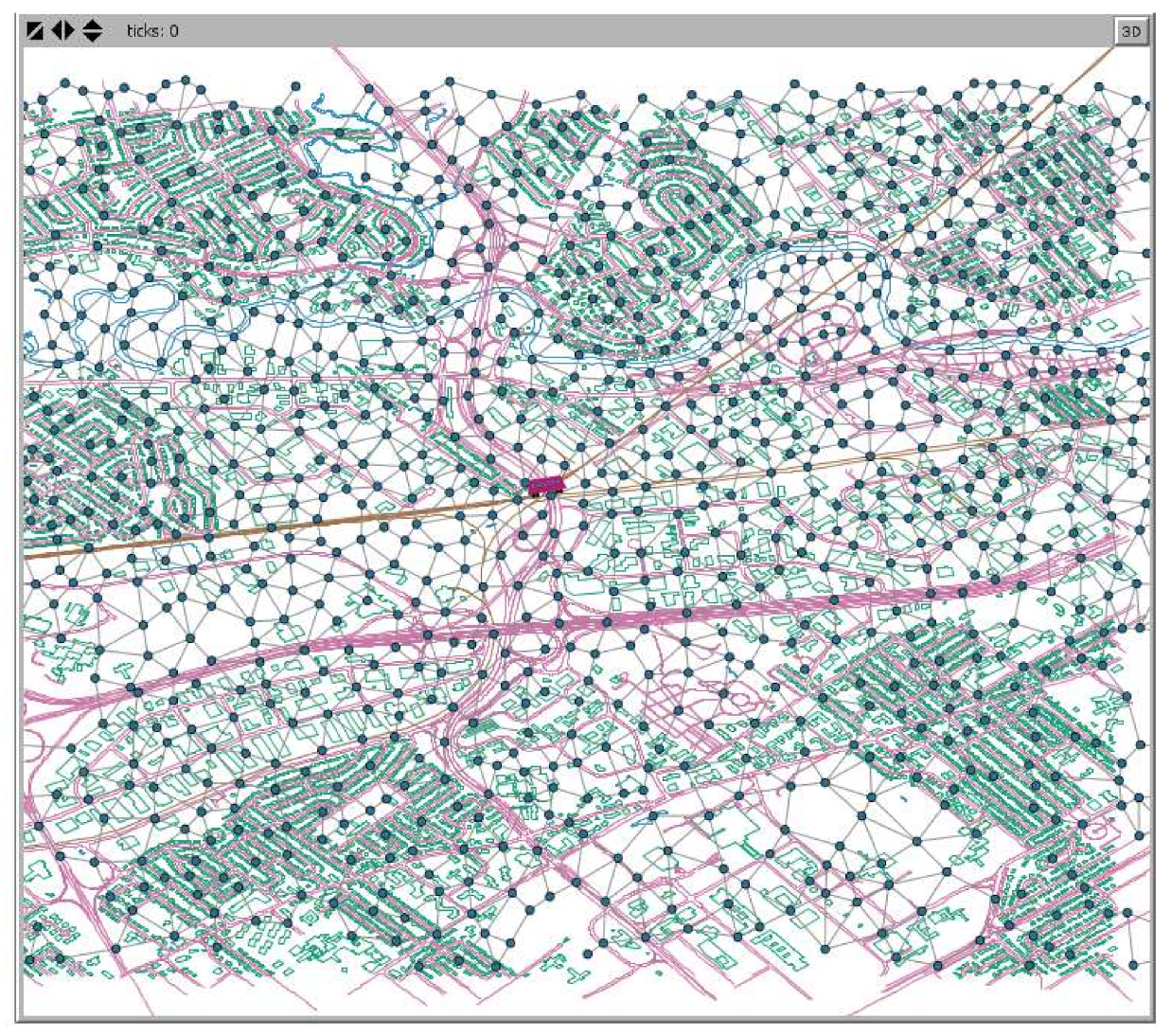
4. Case Study: Monitoring Noise Pollution Caused by Railway Activities in Quebec City
- Setting a model in Netlogo for the detection of noise polluted areas due to railway activities
5. Conclusions and Future Works
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Whittier, J.C.J.; Nittel, S.; Subasinghe, I. Real-time Earthquake Monitoring with Spatio- Temporal Fields. In Proceedings of the International Symposium on Spatiotemporal Computing, Cambridge, MA, USA, 6–7 August 2017; pp. 215–222. [Google Scholar]
- Nittel, S. A survey of geosensor networks: Advances in dynamic environmental monitoring. Sensors 2009, 9, 5664–5678. [Google Scholar] [CrossRef] [PubMed]
- Navarro, G.; Huertas, I.E.; Costas, E.; Flecha, S.; Díez-Minguito, M.; Caballero, I.; López-Rodas, V.; Prieto, L.; Ruiz, J. Use of a real-time remote monitoring network (RTRM) to characterize the Guadalquivir estuary (Spain). Sensors 2012, 12, 1398–1421. [Google Scholar] [CrossRef] [PubMed]
- Wang, Q.; Balasingham, I. Wireless sensor networks-an introduction. Wirel. Sens. Netw. Appl. Des. 2010, 13225, 13. [Google Scholar]
- Estrin, D.; Culler, D.; Pister, K.; Sukhatme, G. Connecting the physical world with pervasive networks. Pervasive Comput. IEEE 2002, 1, 59–69. [Google Scholar] [CrossRef]
- Chong, C.-Y.; Kumar, S.P. Sensor networks: Evolution, opportunities, and challenges. Proc. IEEE 2003, 91, 1247–1256. [Google Scholar] [CrossRef]
- Argany, M.; Mostafavi, M.; Karimipour, F.; Gagné, C. A GIS based wireless sensor network coverage estimation and optimization: A Voronoi approach. In Transactions on Computational Science XIV SE-6; Gavrilova, M., Tan, C.J.K., Mostafavi, M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6970, pp. 151–172. ISBN 978-3-642-25248-8. [Google Scholar]
- Duckham, M. Decentralized Spatial Computing: Foundations of Geosensor Networks; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 3642308538. [Google Scholar]
- Kulik, L. A Geometric Theory of Vague Boundaries Based on Supervaluation. In Spatial Information Theory SE-4; Montello, D., Ed.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2001; Volume 2205, pp. 44–59. ISBN 978-3-540-42613-4. [Google Scholar]
- Molenaar, M. Three conceptual uncertainty levels for spatial objects. Int. Arch. Photogramm. Remote Sens. 2000, 33, 670–677. [Google Scholar]
- Janowicz, K.; Compton, M. The Stimulus-Sensor-Observation Ontology Design Pattern and its Integration into the Semantic Sensor Network Ontology. In Proceedings of the 3rd International workshop on Semantic Sensor Networks 2010 (SSN10) in conjunction with the 9th International Semantic Web Conference (ISWC 2010), Shanghai, China, 7–11 November 2010. [Google Scholar]
- Hall, D.L.; Llinas, J. An introduction to multisensor data fusion. In Proceedings of the IEEE International Symposium on Circuits and Systems (Cat. No.98CH36187), Monterey, CA, USA, 31 May–3 June 1998; Volume 85, pp. 6–23. [Google Scholar] [CrossRef]
- Malewski, C.; Bröring, A.; Maué, P.; Janowicz, K. Semantic Matchmaking & Mediation for Sensors on the Sensor Web. IEEE JSTARS 2012, 7, 929–934. [Google Scholar]
- Bleisch, S.; Duckham, M.; Kealy, A.; Richter, K.-F.; Winter, S.; Kininmonth, S.; Klippel, A.; Laube, P.; Lyon, J.; Medyckyj-Scott, D. Challenges in supporting extraction of knowledge about environmental objects and events from geosensor data. In Proceedings of the AutoCarto, Columbus, OH, USA, 16–18 September 2012; p. 12. [Google Scholar]
- Nakayama, Y.; Akama, S.; Murai, T. Deduction System for Decision Logic based on Partial Semantics. In Proceedings of the SEMAPRO, Barcelona, Spain, 12–16 November 2017; pp. 8–11. [Google Scholar]
- Bendadouche, R.; Roussey, C.; De Sousa, G.; Chanet, J.-P.; Hou, K.M. Etat de l’art sur les ontologies de capteurs pour une intégration intelligente des données. INFORSID 2012, 2012, 89–104. [Google Scholar]
- Stasch, C.; Janowicz, K.; Bröring, A.; Reis, I.; Kuhn, W. A Stimulus-Centric Algebraic Approach to Sensors and Observations. In GeoSensor Networks SE-17; Trigoni, N., Markham, A., Nawaz, S., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5659, pp. 169–179. ISBN 978-3-642-02902-8. [Google Scholar]
- Sadeq, M.J.; Duckham, M.; Worboys, M.F. Decentralized detection of topological events in evolving spatial regions. Comput. J. 2013, 56, 1417–1431. [Google Scholar] [CrossRef]
- Nowak, R.; Mitra, U. Boundary Estimation in Sensor Networks: Theory and Methods. In Information Processing in Sensor Networks SE-6; Zhao, F., Guibas, L., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2003; Volume 2634, pp. 80–95. ISBN 978-3-540-02111-7. [Google Scholar]
- Chintalapudi, K.K.; Govindan, R. Localized edge detection in sensor fields. Ad Hoc Netw. 2003, 1, 273–291. [Google Scholar] [CrossRef]
- Welsh, M.; Mainland, G. Programming Sensor Networks Using Abstract Regions. In Proceedings of the NSDI, San Francisco, CA, USA, 29–31 March 2004; Volume 4, p. 3. [Google Scholar]
- Ye, J.; McKeever, S.; Coyle, L.; Neely, S.; Dobson, S. Resolving Uncertainty in Context Integration and Abstraction: Context Integration and Abstraction. In Proceedings of the 5th International Conference on Pervasive Services, Sorrento, Italy, 6–10 July 2008; ACM: New York, NY, USA, 2008; pp. 131–140. [Google Scholar]
- Jin, G.; Nittel, S. Efficient tracking of 2D objects with spatiotemporal properties in wireless sensor networks. Distrib. Parallel Databases 2010, 29, 3–30. [Google Scholar] [CrossRef]
- Francisque, A.; Rodriguez, M.J.; Sadiq, R.; Miranda, L.F.; Proulx, F. Prioritizing monitoring locations in a water distribution network: A fuzzy risk approach. J. Water Supply Res. Technol. AQUA 2009, 58, 488–509. [Google Scholar] [CrossRef]
- Guan, L.-J.; Duckham, M. Decentralized computing of topological relationships between heterogeneous regions. In Proceedings of the 10th International Conference on GeoComputation, Sydney, Australia, 30 November–2 December 2009. [Google Scholar]
- Guan, L.-J.; Duckham, M. Decentralized Reasoning about Gradual Changes of Topological Relationships between Continuously Evolving Regions. Spat. Inf. Theory 2011, 6899, 126–147. [Google Scholar] [CrossRef]
- Saukh, O.; Sauter, R.; Gauger, M.; Marrón, P.J. On Boundary Recognition without Location Information in Wireless Sensor Networks. ACM Trans. Sens. Netw. 2010, 6, 1–35. [Google Scholar] [CrossRef]
- Jitendra, R.R.; Girija, G.; Shanthakumar, N. Theory of Data Fusion. In Multi-Sensor Data Fusion with Matlab; Raol, J.R., Ed.; Taylor and Francis Group, LLC (CRC): Boca Raton, FL, USA, 2010; pp. 1–231. ISBN 9781439800034. [Google Scholar]
- Dunn, P.F. Measurements and Data Analysis for Engineering and Science, 2nd ed.; Taylor and Francis Group, LLC (CRC): Boca Raton, FL, USA, 2010; ISBN 9781439825686. [Google Scholar]
- Fonseca, F.; Egenhofer, M.; Davis, C.; Câmara, G. Semantic granularity in ontology-driven geographic information systems. Ann. Math. Artif. Intell. 2002, 36, 121–151. [Google Scholar] [CrossRef]
- Bleisch, S.; Duckham, M. Sensor network data analysis at different levels of granularity. In Proceedings of the AGILE 2013, Leuven, Belgium, 14–17 May 2013; p. 2. [Google Scholar]
- Kavouras, M.; Kokla, M. Theories of Geographic Concepts: Ontological Approaches to Semantic Integration; Taylor and Francis, Group, CRC Press: Boca Raton, FL, USA, 2008; ISBN 9780849330896. [Google Scholar]
- Pauly, A.; Schneider, M. VASA: An algebra for vague spatial data in databases. Inf. Syst. 2010, 35, 111–138. [Google Scholar] [CrossRef]
- Cheng, T. Fuzzy objects: Their changes and uncertainties. Photogramm. Eng. Remote Sens. 2002, 68, 41–49. [Google Scholar]
- Tang, X.; Kainz, W.; Wang, H. Topological relations between fuzzy regions in a fuzzy topological space. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, S151–S165. [Google Scholar] [CrossRef]
- Wei, W.; Barnaghi, P. Semantic Annotation and Reasoning for Sensor Data. In Smart Sensing and Context SE-6; Barnaghi, P., Moessner, K., Presser, M., Meissner, S., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2009; Volume 5741, pp. 66–76. ISBN 978-3-642-04470-0. [Google Scholar]
- Balazinska, M.; Deshpande, A.; Franklin, M.J.; Gibbons, P.B.; Gray, J.; Nath, S.; Hansen, M.; Liebhold, M.; Szalay, A.; Tao, V. Data Management in the Worldwide Sensor Web. Pervasive Comput. IEEE 2007, 6, 30–40. [Google Scholar] [CrossRef]
- Liu, C.; Wu, K.; Pei, J. An Energy-Efficient Data Collection Framework for Wireless Sensor Networks by Exploiting Spatiotemporal Correlation. Parallel Distrib. Syst. IEEE Trans. 2007, 18, 1010–1023. [Google Scholar] [CrossRef]
- Beal, J.; Schantz, R. A spatial computing approach to distributed algorithms. In Proceedings of the 45th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 6–9 November 2011; pp. 1–5. [Google Scholar]
- Mardkheh, A.J.; Mostafavi, M.A.; Bédard, Y.; Shahriari, K. Spatial Representation of Coastal Risk: A Fuzzy Approach to Deal with Uncertainty. ISPRS Int. J. Geo-Inf. 2014, 3, 1077–1100. [Google Scholar] [CrossRef]
- Zadeh, L.A. Fuzzy sets. Inf. Control 1965, 8, 338–353. [Google Scholar] [CrossRef]
- Mardkheh, A.J.; Mostafavi, M.; Bédard, Y.; Long, B.; Grenier, E. Using geospatial business intelligence paradigm to design a multidimensional conceptual model for efficient coastal erosion risk assessment. J. Coast. Conserv. 2013, 17, 527–543. [Google Scholar] [CrossRef]
- Haller, A.; Janowicz, K.; Cox, S.J.D.; Lefrançois, M.; Taylor, K.; Le Phuoc, D.; Lieberman, J.; García-Castro, R.; Atkinson, R.; Stadler, C. The modular SSN ontology: A joint W3C and OGC standard specifying the semantics of sensors, observations, sampling, and actuation. Semant. Web 2018, 10, 9–32. [Google Scholar] [CrossRef]
- Gruber, T.R. Toward principles for the design of ontologies used for knowledge sharing? Int. J. Hum. Comput. Stud. 1995, 43, 907–928. [Google Scholar] [CrossRef]
- Euzenat, J.; Shvaiko, P. Ontology Matching; Springer: Berlin/Heidelberg, Germany, 2007; ISBN 978-3-642-38721-0. [Google Scholar]
- Noy, N.F. Semantic integration: A survey of ontology-based approaches. ACM Sigmod Rec. 2004, 33, 65–70. [Google Scholar] [CrossRef]
- Kalfoglou, Y.; Schorlemmer, M. Ontology mapping: The state of the art. Knowl. Eng. Rev. 2003, 18, 1–31. [Google Scholar] [CrossRef]
- Cardell-Oliver, R.; Huebner, C.; Foeller-Nord, M. WebSense: A lightweight and configurable application for publishing sensor network data. In Proceedings of the 2011 Seventh International Conference on Intelligent Sensors, Sensor Networks and Information Processing (ISSNIP), Adelaide, SA, Australia, 6–9 December 2011; pp. 235–240. [Google Scholar]
- Wang, X.H.; Zhang, D.Q.; Gu, T.; Pung, H.K. Ontology based context modeling and reasoning using OWL. In Proceedings of the 2004 Second IEEE Annual Conference on IEEE Pervasive Computing and Communications Workshops, Orlando, FL, USA, 14–17 March 2004; pp. 18–22. [Google Scholar]
- Yazici, A.; Zhu, Q.; Sun, N. Semantic data modeling of spatiotemporal database applications. Int. J. Intell. Syst. 2001, 16, 881–904. [Google Scholar] [CrossRef]
- Jitendra, R.R. Multi-Sensor Data Fusion with MATLAB; Taylor and Francis Group, LLC (CRC): Boca Raton, FL, USA, 2010; ISBN 9781439800034. [Google Scholar]
- Ntankouo Njila, C.R.; Mostafavi, M.A.; Brodeur, J. Modelling Vague Shape Dynamic Phenomena from Sensor Network data using a Decentralized Fuzzy Rule-Based Approach. In Proceedings of the International Conference on GIScience Short Paper Proceedings, Montreal, QC, Canada, 27–30 September 2016; Volume 1. [Google Scholar]
- Mardkheh, A.J. Towards Development of Fuzzy Spatial Datacubes: Erosion Risk Assessment and Representation. Ph.D. Thesis, Laval University, Quebec City, QC, Canada, 2014. [Google Scholar]
- Gaber, M.M. Data Stream Processing in Sensor Networks. In Learning from Data Streams: Processing Techniques in Sensor Networks; Gama, J., Gaber, M.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 41–48. ISBN 9783540736783. [Google Scholar]
- Ross, T.J. Fuzzy Logic with Engineering Applications, 3rd ed.; John Wiley and Sons: Hoboken, NJ, USA, 2010; ISBN 0470748516. [Google Scholar]
- Kröller, A.; Fekete, S.P.; Pfisterer, D.; Fischer, S. Deterministic Boundary Recognition and Topology Extraction for Large Sensor Networks. In Proceedings of the Seventeenth Annual ACM-SIAM Symposium on Discrete Algorithm, Miami, FL, USA, 22–24 January 2006; ACM: New York, NY, USA, 2006; pp. 1000–1009. [Google Scholar]
- Guan, L.-J.; Duckham, M. Decentralized Reasoning about Gradual Changes of Topological Relationships between Continuously Evolving Regions. In Spatial Information Theory SE-8; Egenhofer, M., Giudice, N., Moratz, R., Worboys, M., Eds.; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6899, pp. 126–147. ISBN 978-3-642-23195-7. [Google Scholar]
- Pauly, A.; Schneider, M. Vague spatial data types. In Encyclopedia of GIS SE-1434; Springer: Boston, MA, USA, 2008; pp. 1213–1217. ISBN 978-0-387-30858-6. [Google Scholar]
- Bejaoui, L.; Pinet, F.; Bedard, Y.; Schneider, M. Qualified topological relations between spatial objects with possible vague shape. Int. J. Geogr. Inf. Sci. 2009, 23, 877–921. [Google Scholar] [CrossRef]
- Zhao, F.; Guibas, L.J. Wireless Sensor Networks: An Information Processing Approach; Clark, D., Ed.; Elsevier-Morgan Kaufmann: Amsterdam, The Netherlands, 2004; ISBN 1558609148. [Google Scholar]
- Schneider, M. Design and implementation of finite resolution crisp and fuzzy spatial objects. Data Knowl. Eng. 2003, 44, 81–108. [Google Scholar] [CrossRef]
- Egenhofer, M.J.; Franzosa, R.D. Point-set topological spatial relations. Int. J. Geogr. Inf. Syst. 1991, 5, 161–174. [Google Scholar] [CrossRef]
- Guennebaud, G.; Gross, M. Algebraic point set surfaces. Proceedings of IGGRAPH07: Special Interest Group on Computer Graphics and Interactive Techniques Conference: ACM, San Diego, CA, USA, 5–9 August 2007; Volume 26, p. 23. [Google Scholar]
- Murgante, B.; Scorza, F. Ontology and spatial planning. In Proceedings of the Lecture Notes in Computer Science (International Conference on Computational Science and Its Applications), Santander, Spain, 2–23 June 2011; Murgante, B., Gervasi, O., Iglesias, A., Taniar, D., Apduhan, B.O., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6783 LNCS, pp. 255–264. [Google Scholar]
- Kaur, J.; Kumar, A. An Introduction to Fuzzy Linear Programming Problems: Theory, Methods and Applications; Kacprzyk, J., Ed.; Springer Publishing Company, Incorporated: Cham, Switzerland, 2016; ISBN 9783319312736. [Google Scholar]
- Canadian-Transportation-Agency. Railway Noise Measurement and Reporting Methodology; Minister of Public Works and Government Services: Ottawa, ON, Canada, 2011. [Google Scholar]
- Oliveira, M.P.G.; Medeiros, E.B.; Davis, C.A., Jr. Planning the acoustic urban environment: A GIS-centered approach. In Proceedings of the 7th ACM International Symposium on Advances in Geographic Information Systems, Kansas City, MO, USA, 5–6 November 1999; ACM: New York, NY, USA, 1999; pp. 128–133. [Google Scholar]
- Argany, M.; Mostafavi, M.-A. Develop a GIS-Based Context-Aware Sensors Network Deployment Algorithm to Optimize Sensor Coverage in an Urban Area. In Proceedings of the Information Fusion and Intelligent Geographic Information Systems. Advances in Geographic Information Science, Karlsruhe, Germany, 10–12 October 2018; Popovich, V., Thill, J.-C., Schrenk, M., Claramunt, C., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 179–191. [Google Scholar] [CrossRef]
- Wilensky, U. NetLogo 4.0. 2 User Manual; Center for Connected Learning and Computer Based Modeling, Northwest University: Evanston, IL, USA, 2007. [Google Scholar]

| Membership Value and Logic Rules | Truth Value | Spatial Meaning of Sensor Measurement | |
|---|---|---|---|
| 1 | 1|True | Kernel position | (2) |
| 2|May-be | Conjecture | broad boundary position | ||
| 0|False | Outside position |
| Phenomenon Part Detection | Type of Query or Answer Received | Relative Position |
|---|---|---|
| Kernel | Only KQuery | Kernel-inner |
| Kernel | Even one CQuery or one answer from Outer node | Inner-Kernel-boundary |
| Conjecture/Outside | Even one KQuery | Outer-Kernel-boundary |
| Conjecture | Only CQuery | Conjecture-Inner |
| Conjecture | Receiving answer from an Outer node | Inner-Conjecture-boundary |
| Outside | Even one CQuery | Outer-Conjecture-boundary |
| Outside | No query | Outer |
| Kernel Boundary Nodes and Communication Link | Location | Membership Value | Vertex Inference | |||
|---|---|---|---|---|---|---|
| Approximation Method | Rules | |||||
| Inner_node |  | lower | (3) | |||
| communication link | )) | weighted | ||||
| Outer_node | upper | |||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ntankouo Njila, R.C.; Mostafavi, M.A.; Brodeur, J. A Decentralized Semantic Reasoning Approach for the Detection and Representation of Continuous Spatial Dynamic Phenomena in Wireless Sensor Networks. ISPRS Int. J. Geo-Inf. 2021, 10, 182. https://doi.org/10.3390/ijgi10030182
Ntankouo Njila RC, Mostafavi MA, Brodeur J. A Decentralized Semantic Reasoning Approach for the Detection and Representation of Continuous Spatial Dynamic Phenomena in Wireless Sensor Networks. ISPRS International Journal of Geo-Information. 2021; 10(3):182. https://doi.org/10.3390/ijgi10030182
Chicago/Turabian StyleNtankouo Njila, Roger Cesarié, Mir Abolfazl Mostafavi, and Jean Brodeur. 2021. "A Decentralized Semantic Reasoning Approach for the Detection and Representation of Continuous Spatial Dynamic Phenomena in Wireless Sensor Networks" ISPRS International Journal of Geo-Information 10, no. 3: 182. https://doi.org/10.3390/ijgi10030182
APA StyleNtankouo Njila, R. C., Mostafavi, M. A., & Brodeur, J. (2021). A Decentralized Semantic Reasoning Approach for the Detection and Representation of Continuous Spatial Dynamic Phenomena in Wireless Sensor Networks. ISPRS International Journal of Geo-Information, 10(3), 182. https://doi.org/10.3390/ijgi10030182







