2.1. Model Specification
In brief, the simulation of bicycle mobility in the presented model consists of several steps: the generation of environment and residential population, the dynamic assignment of activities, and the simulation of trips. Activity assignment includes decisions about activity type, starting time, duration of an activity, mode, speed, target location, and route. As a result, system-level traffic flows of cyclists emerge from complex decision making and spatial reasoning of every individual resident in regard to their mobility behavior.
We use the model of Wallentin and Loidl [
28] as the conceptual basis and add complexity. We extend the model through the generation of a more heterogeneous population that includes all residents of the study area. The simulated persons are not grouped into specific categories but rather have different socio-demographical characteristics and mobility preferences. Another advancement is in the dynamic scheduling of activities. Moreover, destination locations are selected within reasonable distances to be reached by modes. A modal split is extended to six transportation modes: bicycle, walk, car, car-passenger, public transport, and other transport, thus, daily schedules include bicycle and non-bicycle trips.
The GAMA RC1.8 platform was selected as the programming environment available on Windows, Mac OS, and Ubuntu operating systems [
32]. It exhibits extensive functionalities to work with data models in spatially explicit simulations. Moreover, the improved computational capacity of the platform allows for the simulation of large and complex systems, such as a regional transportation system. The model code is implemented in a high-level, intuitive GAMA modeling language (GAML), provided by the platform. The source code of the model is published in the ComSES Net model library (
https://www.comses.net/ (accessed on 19 February 2021)) under the open CC-BY-NC-SA-3.0 license [
33]. Running the model code requires a minimum of 4 GB of random-access memory (RAM).
The detailed model specification below follows the standard overview, design concepts, and details (ODD) protocol [
34]. The protocol is designed to communicate agent-based models in a standard and reproducible way. It describes the model’s purpose, components of a simulated transportation system, spatial and temporal extents, behavioral rules of agents, and scheduling of processes.
2.1.1. Purpose
The bicycle model aims to generate bicycle traffic flows of one day by executing the trips of self-ruling persons within a regional transportation system. The resulting dynamics of bicycle traffic are an estimation of the transportation system’s overall performance. The model can be used to run scenarios to observe the impact of policy interventions, infrastructure design, and other urban planning strategies.
2.1.2. Entities, State Variables, and Scales
Several entities constitute the system of the model: persons, facilities, roads, intersections, and counting stations. Persons are heterogeneous by demographic attributes. Distinctions include age, gender, and employment status. Age ranges between 6 and 100 years. In terms of employment, there are employed, unemployed, students, pupils, pensioners, and inactive persons.
Roads and facilities represent the built environment that constrains the movements of persons and defines the areas of attraction. Roads are characterized by the number of traversed cyclists, restriction level, safety index, and weight attributes. For cycling, there are restricted, partially restricted, and unrestricted roads. On partially restricted pedestrian roads, cyclists are only allowed to push their bicycles. The safety index as proposed by Loidl and Zagel [
35] describes how comfortable a road for safe cycling is according to its category and quality. Roads are weighted for routing. Weights can represent perimeters or safety indices depending on the type of routing, such as shortest and safest paths, respectively. Road intersections are also modeled to characterize the selected routes of persons as additional trip information.
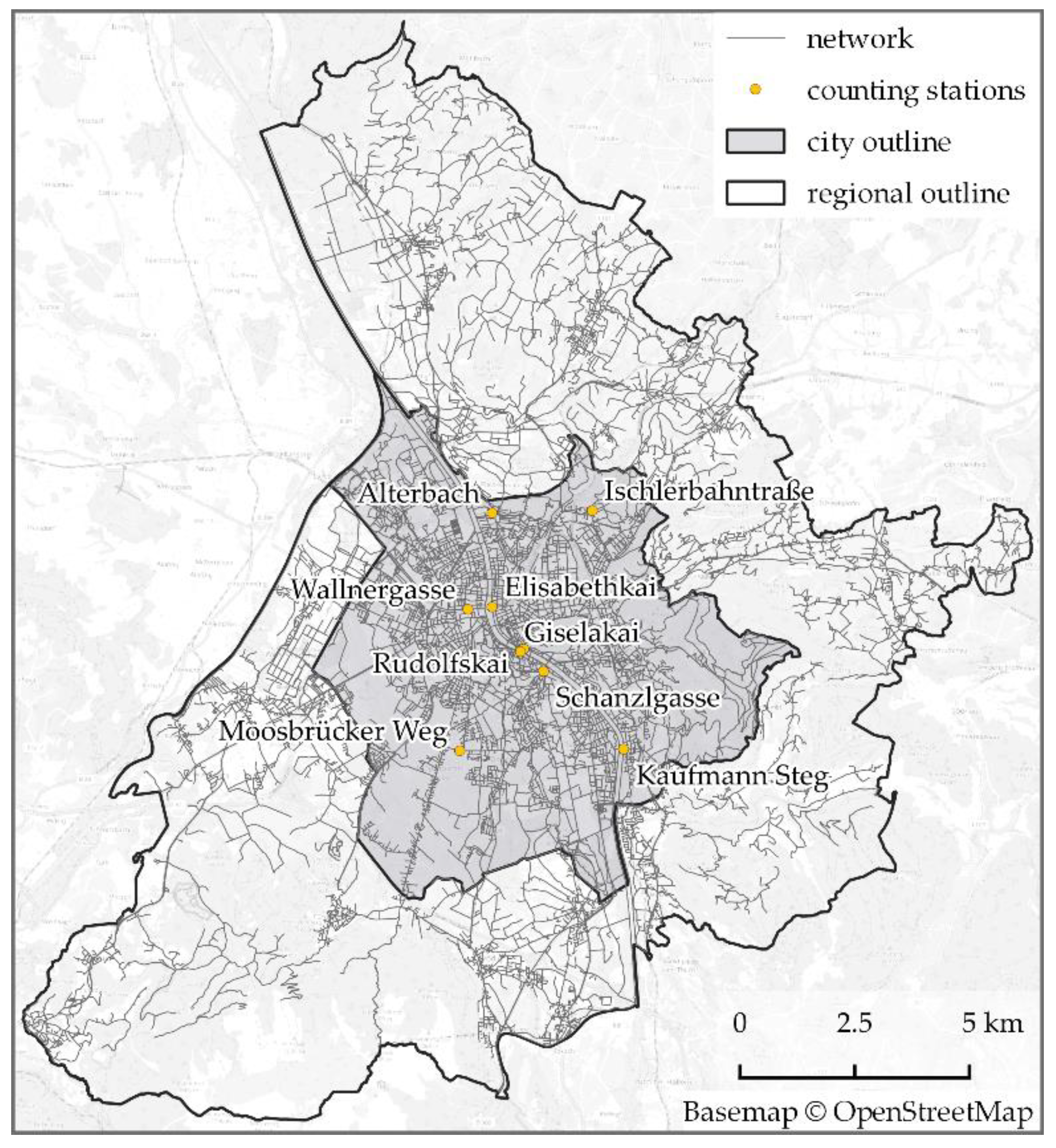
Various facilities serve as locations for specific activities and are classified into ten types. These are workplaces, schools, universities, kindergartens, authorities, doctors, shops, recreation places, and residents’ homes. Facilities do not have a limiting factor to attract visitors, except for workplaces that are characterized by the number of employees. Persons traveling to work select target locations depending on this information. Lastly, a name, position, and the number of passing cyclists characterize counting stations. We use the latter component for verification and validation purposes.
Throughout a simulation, the model collects several high-level state variables that describe a simulated world and its dynamics. There are population-level aggregates that describe a demographic content, such as an age split or distribution by employment. The total number of cyclists actively traveling through a simulated space interprets the traffic dynamics. The model additionally detects active cyclists by trip purposes.
The environment of the model covers the extent of Salzburg city and adjacent municipalities, except one on the Bavarian side of the national border (
Figure 1). The selected extent facilitates the inclusion of commuting trips from areas outside the city and prevents edge effects in the area of interest (City of Salzburg). The temporal extent of the simulation is an average day in October–November. The day was determined by the time frame of the statistical data that underlie behavioral rules. The time-step of the simulation is one minute.
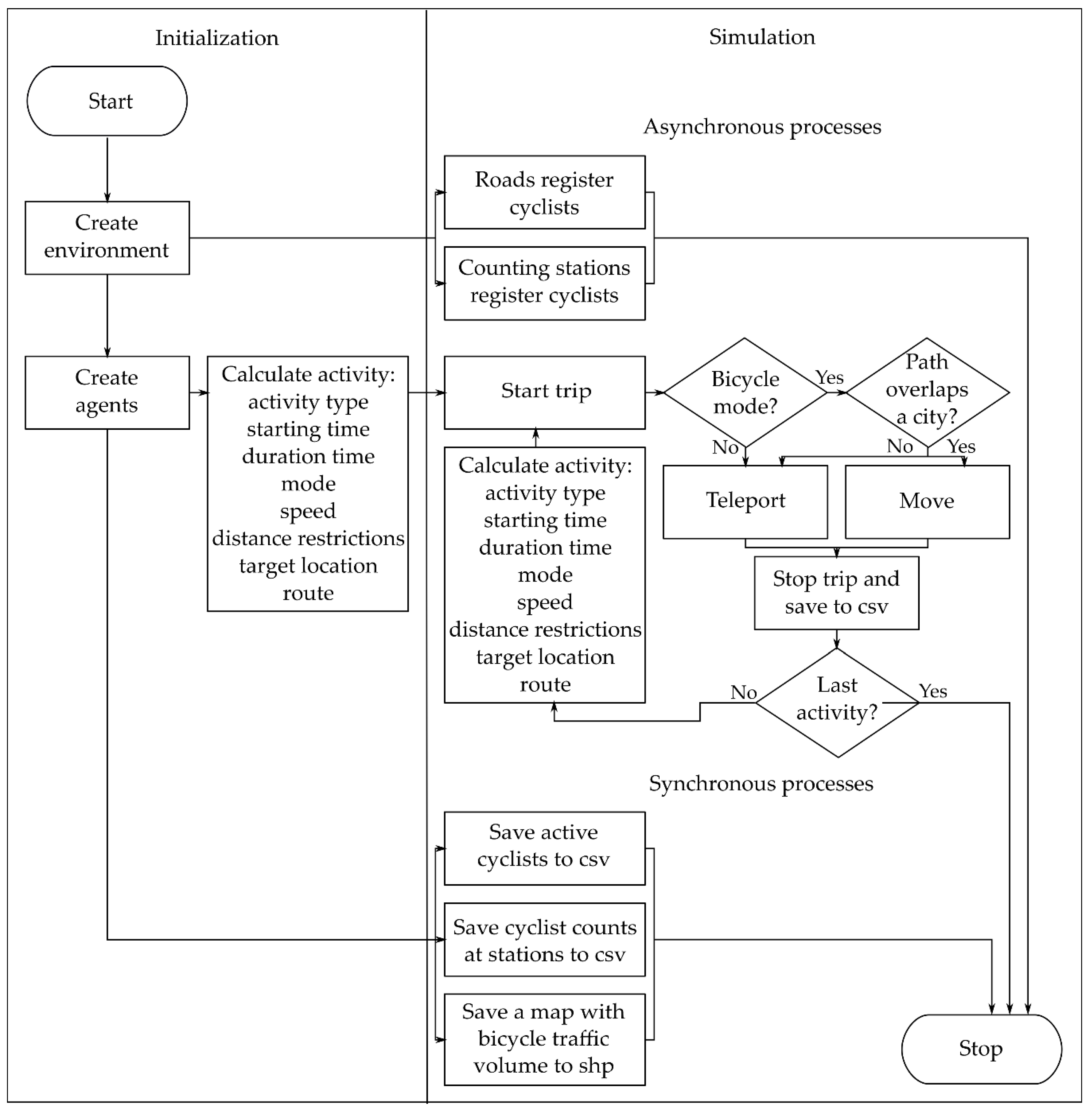
2.1.3. Process Overview and Scheduling
Figure 2 illustrates the key processes that are reenacted in the model every cycle or when conditions are met. Throughout the simulation, persons act asynchronously. They iteratively choose and accomplish desired activities by traveling to facilities by different transportation modes. A person does not have an initial activity chain for the whole day but complements it by assigning a new activity at the end of the current one. The selection of the last activity is integrated as a probability during the activity assignment. Thus, the total amount of activities that a person can undertake depends on the derivatives from the mobility survey. The maximum is eight activities per day.
During the process of activity assignment, behavioral rules determine several activity attributes, such as type, starting time, duration, mode, distance restrictions, speed, and target location. A rule is represented in the form of a probability distribution and characterizes the likelihood of a particular option to be selected. After activity selection, only cyclists that cross a city area travel along a network and register themselves at traversed counting stations and roads. The rest of the persons transfer themselves directly to their destinations, due to the model’s focus is on a bicycle traffic pattern. At the end of each trip, trip-related data, such as synthetic trajectory, distance, travel time, etc., are saved in the “trips” dataset.
Three synchronous processes collect data about traveling cyclists at user-defined time intervals. The “active cyclists” dataset stores the aggregate totals of cyclists traveling around a simulated world according to their trip purposes. Counting stations and a network register the amounts of traversing cyclists into datasets named “counting data” and “traffic volume heatmap”, respectively.
2.1.4. Design Concepts
Several design concepts that define agent-based models were implemented in the bicycle model. The emergence of bicycle traffic flows over space and time is given by the complexity of persons’ diverse mobility behavior, but—at this stage of the model development—not by interactions with each other. Nevertheless, heterogeneity of agents and the probabilistic nature of behavioral rules that govern agents’ decision making make the prediction of traffic volumes emergent. Fitness-seeking behavior is incorporated in the route selection, as persons optimize their paths by safety and distance preferences.
Sensing as the notion of agent awareness of itself and an environment is also implemented in the model. Persons reason about choice options available to them based on the knowledge about their age, gender, and employment. They sense the network quality when navigating to their destinations according to their preferences. Stochasticity is present in the distribution of a population by demographic attributes. Moreover, the modeled rules of activity assignment are based on probability distributions adding the uncertainty of human behavior.
Observation includes monitoring and storing model output for testing and analysis. Active cyclists, traversed cyclists at counting stations, and a network are monitored for verification and validation purposes. For model analysis, trips’ information and roads’ bicycle volumes were collected.
2.1.5. Initialization
During the initialization, the model creates a world with persons and a built environment. The spatial distribution of persons by age, gender, and employment status is calculated from real-world estimates in residential data. For example, if a grid cell has a registered number of female residents aged between 20 and 24, the model will create that number of female persons and assign age randomly within that range.
The model requires a topologically correct network of links for routing operations. Thus, simulated roads connect to a coherent bidirectional network with one-way roads, two-way roads, and restrictions. The network is weighted with a safety index to provide safety-oriented cycling. The adopted calculation of an index follows the indicator-based assessment [
35]. Several road indicators are incorporated into the safety index calculation. These are road category, presence of bicycle infrastructure and established cycling routes, vehicle restrictions, gradient, pavement, and maximum motorized speed from the network shapefile.
Counting stations and network intersections are also initialized directly from shapefiles with no additional computation. Next, the model imports probabilities of activity types, modes, and starting and duration times from comma-separated values (CSV) files. Before the simulation day starts, persons are distributed to the initial activity locations.
2.1.6. Submodels
Activity type choice. There are several activity options: staying at home, working, shopping, recreation activity, business-related activity, visiting authorities, visiting doctor, accompanying people, and staying at other places. The probabilities of these options are different for every individual; firstly, because they vary depending on the position of activity in an activity chain (0–7). In
Table 1, every column represents the probability distribution of activity types based on the numerical order of a calculated next activity, i.e., activity position. Secondly, an individual’s employment status restricts activity options. For example, a pupil below a certain age can travel to school but cannot go to work. At the beginning of a simulation, every person calculates an initial activity by taking a probability distribution where an activity position is null.
Starting and duration time choices. The process of activity assignment continues with the selection of temporal characteristics. The probability of every activity’s starting time depends on the activity’s type and position in an activity chain.
Table A1 in
Appendix A shows an example of probabilities for work activity. Throughout a simulated day, passed hours are eliminated from the probability distributions. There are simplified assumptions for school and university activities. Departure time for school is calculated between 7:00 and 8:00, for university, between 8:00 and 18:00. Furthermore, activity types are restricted to possible durations a person can spend at an activity location. In the case of work activity, the duration varies by gender. Moreover, pupils stay at school depending on age. Additional information about duration values can be found in
Appendix A (
Table A2,
Table A3 and
Table A4).
Mode choice. There are six available modes, such as walking, bicycle, car, car passenger, public transport, and other transport (
Table 2). For the sake of simplification, we assume that a person can only change their mode of transportation at home. The probability distributions of modes vary for every activity type. Moreover, there is a difference between modal splits for region-based and city-based trips.
Distance and speed choice. Another assumption is that modes have different travel distance capacities and speeds. There is a 71% chance a walking trip is shorter than 1 km, and a 29% chance it is between 1 to 5 km. Similar probabilities are given to bicycle trips: distance restrictions can be up to 2 km and 2–8 km with probabilities of 73 and 27%, respectively. Other modes are not restricted by distances. Speed also varies by mode. Walking speed is in the range of 0.7–2.0 m/s, bicycle speed is given 1.6–5.5 m/s. Car, car passenger, and public transport all travel 4.9–14.9 m/s. Other undefined transport has a speed of 2.4–13.6 m/s.
Target choice. A person selects a target location from an available number of relevant facilities that fulfill distance restrictions. The calculation of a suitable workplace has an additional constraint. It takes into account the number of employees every workplace is characterized by. Throughout an activity assignment, a person might not select any activity type or starting time. In such a case, a person returns home and does not travel anymore.
Route choice. The safest and shortest routing options characterize the movement of cyclists and non-cyclists, respectively. The safest routes are calculated using the Dijkstra algorithm and the safety index as impedance. For the shortest routes, the same algorithm uses distance as impedance.
Move. Cyclists whose routes overlap a city area start traveling at calculated departure times along a network toward destinations. The movements are performed according to routing preferences and speed values calculated in prior steps. Non-cyclists and cyclists with trips outside a city do not physically move through a simulated space. They teleport directly to their destinations, and travel times are calculated to represent the real time they would spend on traveling.
2.2. Data
In the proposed agent-based model, we make use of extensive geospatial data sets to define the population, environment, and decision-making rules. Several datasets in
Table 3 were acquired to parameterize the bicycle model. The residential data from Statistik Austria [
36] provides the basis for modeling the socio-demographic heterogeneity of the underlying population. The data of residency by age, gender, and employment status consists of grid cells with a spatial resolution of 250 m.
The mobility survey data of the province of Salzburg [
37] defines behavioral rules. Around 40,000 respondents from the province reported their daily trips. The trips of respondents are ordered in activity chains. Every trip includes attributive information, such as activity ID (sequential number of activity in an activity chain), activity type, timing, distance, and transport mode. The derived distributions of trips by each attribute form probabilistic rules concerning activity types, starting times, modes, distances to a target, and speeds. Furthermore, every simulated activity is characterized by duration time. The corresponding probabilities are inferred from the guidelines and reports of research institutions [
38,
39,
40]. All probability distributions are assembled into separate CSV files for use by the simulation model.
The built environment is represented in the model by an authoritative road network graph [
41] and points of interest (POI) from Open Street Map and authoritative sources [
42,
43,
44,
45,
46]. The workplace facilities are defined by the workplace census information provided by Statistik Austria [
47], where employment values are represented as the number of employees per 100 m grid cell. The city’s and region’s outlines are gathered from the official dataset of administrative boundaries in Austria [
48]. Lastly, the dataset with existing locations of counting sites in Salzburg [
49,
50,
51] is used to create counting stations in the model.
2.3. Design of Experiments
Given the stochastic nature of probability distributions incorporated in the decision making of agents, a model’s response may vary and include an experimental error [
52]. It is recommended to run one simulation several times to achieve meaningful results. The required number of runs is distinct to every model. In order to obtain it, the mean and variability of response values for an increasing number of runs are calculated and analyzed. A response variable can be any record of the model’s non-deterministic output. Lorscheid et al. [
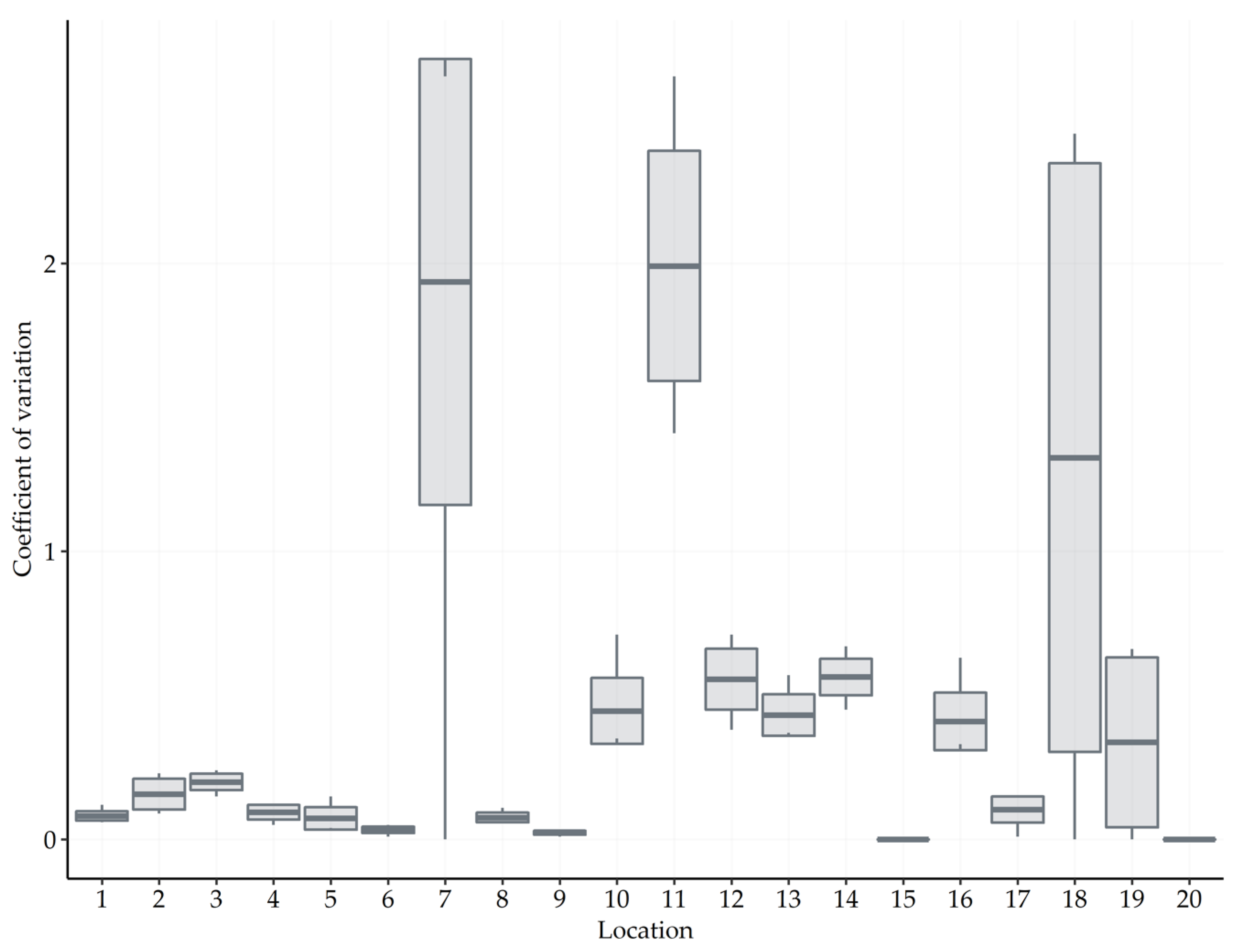
52] propose to use the coefficient of variation as an accuracy measure of the mean and standard deviation. To define it, the standard deviation is divided by the mean value. The coefficients of variation fluctuate according to the number of runs until they stabilize, meaning that additional runs do not minimize an error considerably.
In our model, the average execution time of one simulation run is around 40 min. Such an amount of time impedes a 1000-times repetition. A much higher repetition of simulations would be extremely time consuming and just lead to pseudo-accuracy, given the structural model uncertainty due to assumptions. We, thus, consider one simulation run sufficient for the purpose of the model if experimental errors for low simulation runs stay small.
We carry out an analysis to check the variability of errors in model results depending on the increasing number of runs. Restricted by the cost-benefit factor, we limit the maximum number of simulation runs to 10. We choose the daily bicycle volume as a response variable and record it at 20 random locations. At every step, we raise the number of simulation runs and calculate the mean of daily bicycle volumes at single locations as well as the coefficient of variation. The variability of coefficients, such as standard deviation, can then show how the number of additional runs changes the variation in response variables.
2.4. Verification and Validation
Following the common practice in ABM research, the modeling process consists of designing a conceptual model proceeded by formalizing it into an executable program. Wilensky and Rand [
23] emphasize the principle of ABM design to progressively implement agents and rules in a model. Thus, at every step of additional complexity, we check if it improves the model according to its stated purpose. This process is coined with monitoring state variables to verify that the model is built correctly. The verification testing is done by displaying the dynamic content of a simulation output on charts and a map within the platform interface. A map displaying the entire environment and moving agents is used to demonstrate that all components of a transportation system are present and responsive as expected. To verify that agents move, some graphs demonstrate temporal distributions of traveling cyclists.
Patterns observed in a real system can facilitate the design and validation of its simplified representation. They often express the structure and underlying processes. The pattern-oriented modeling (POM) framework suggests using patterns to define a model in terms of its components and processes, test its internal organization, and validate results [
53]. We use multiple patterns, such as spatial and temporal distributions of cyclists over the study area and their relative frequencies from observed datasets, to indicate the validity of model output.
For the validation, we consider conceptual and operational validities [
54]. Conceptual validity tests cause–effect relationships of underlying model concepts using scenario analysis. This step is similar to the POM’s strategy to test how well the alternative theories of decision-making processes reproduce some patterns [
53]. We formulate four alternative scenarios (
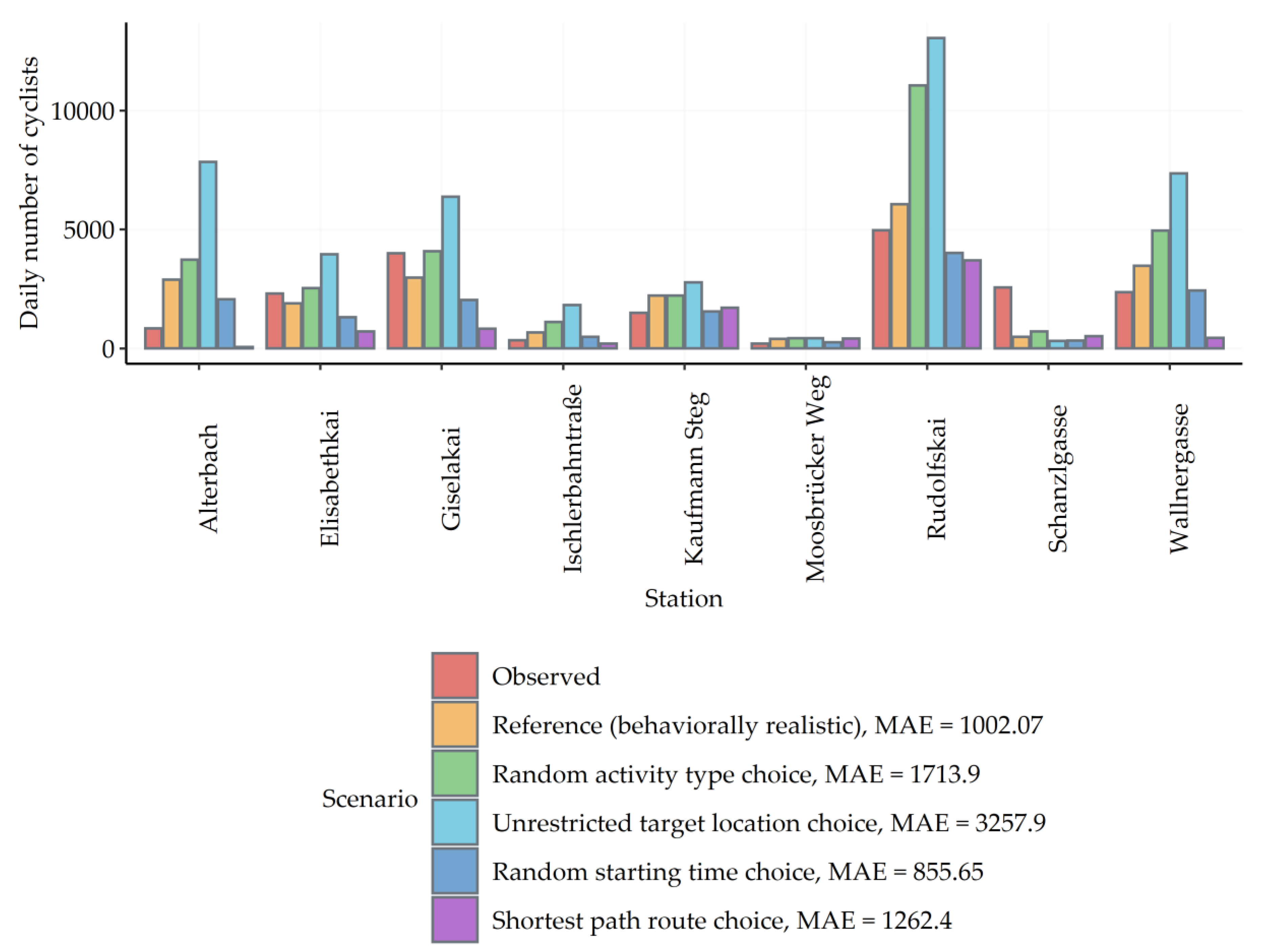
Table 4) to test the impact of the behavioral concepts in our model (behaviorally realistic reference scenario) against the respective null models: activity type choice, target location choice, and starting time choice are tested against random selections, and multi-criteria route choice is tested against the shortest path calculation as its null model.
The comparison of the scenarios is done by investigating the operational validities of their results. Operational validity checks whether the bicycle model and four alternative scenarios are acceptable for the intended purpose. It examines how well model results imitate observed data. According to Kang and Aldstadt [
55], validating the output of a spatially explicit model at different spatio-temporal scales increases its reliability. Such validation eliminates the risk of faulty generative mechanisms when a model reproduces patterns either on a macro scale or a micro scale.
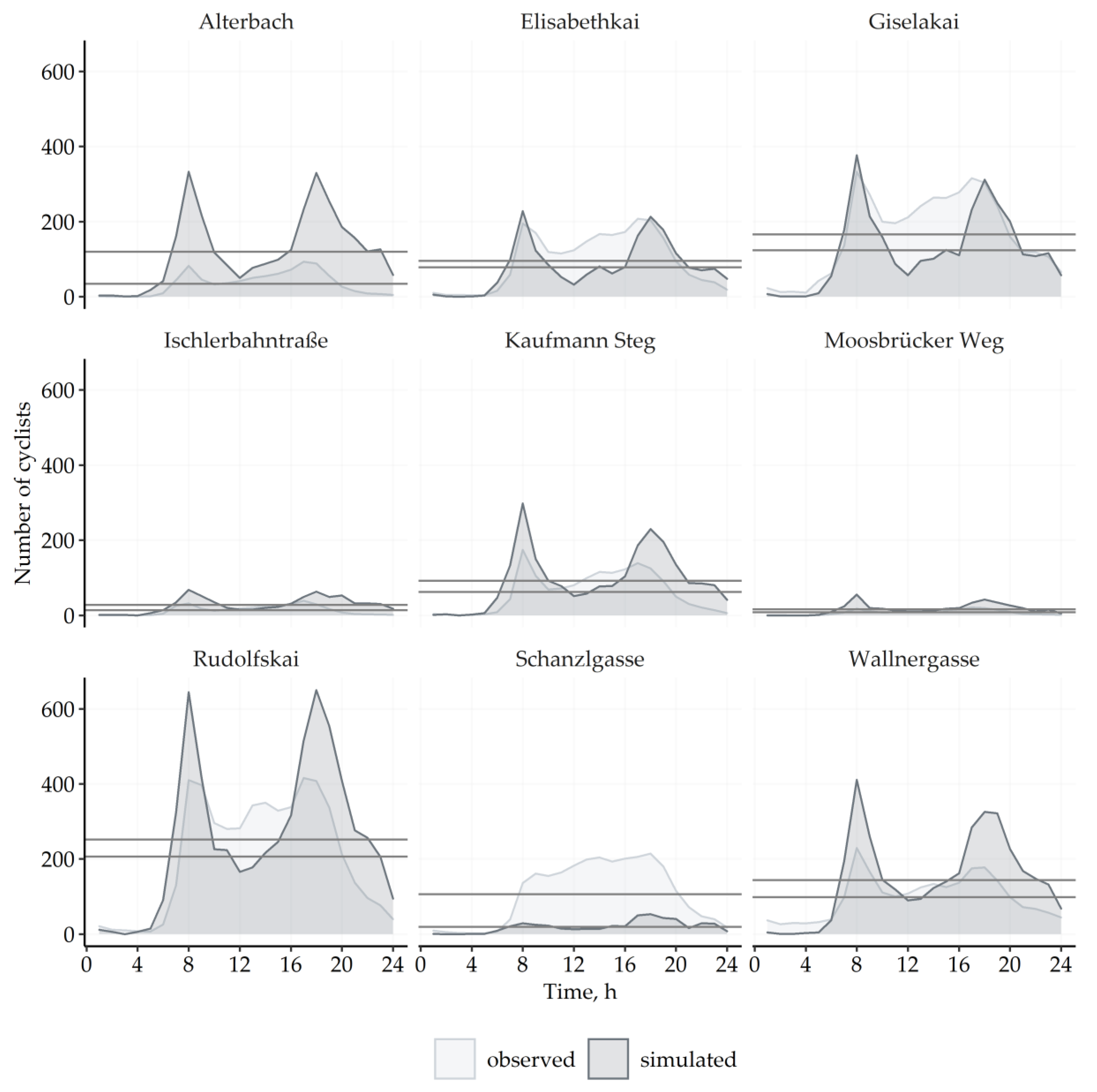
Validation data were acquired from the stationary and mobile sensors that captured the movements of cyclists in the region during October–November. The patterns derived from the data serve as validation criteria at different spatial and temporal scales. The acquired counting data represent counts of cyclists at nine stations between 2012 and 2019 [
49,
50,
51]. The minimum temporal granularity is 15 min. The first criterion is the total amount of traversed cyclists at counting stations over a day. The selected pattern is at a spatially local and temporarily long-term scale. The mean absolute error is used as a comparison method. The absolute error is the difference between simulated and observed daily counts at one station. The average of absolute errors at all stations comprises the mean absolute error. This measure of error demonstrates the magnitude of inaccuracy in model results. The second criterion at a spatially local and temporarily short-term scale is the hourly number of traversed cyclists at counting stations throughout the day. Pearson’s correlation analysis is used to show the strength of the association between observed and simulated hourly values.
The two mobile applications that collected spatio-temporal bicycling data are Bike Citizens and Strava [
56,
57]. Both datasets were spatially matched to the network used in the model. The derived daily totals of traffic volumes per network link are the third validation criterion. The pattern is at spatially local and temporarily long-term scale. Again, Pearson’s correlation analysis is employed.
Finally, validation examines the patterns of relative frequencies in the observed and simulated bicycle traffic at counting stations. Mobility can be influenced by the spatial distribution of attractions and the landscape of a city. Therefore, we inspect the ratio of cyclists between two sides of the city divided by the river Salzach. The next pattern is the ratio of cyclists traversing stations in the city center vs. on the outskirts. At last, we use the morning and afternoon peak ratio to validate bicycle traffic at stations.