A Data Cube Metamodel for Geographic Analysis Involving Heterogeneous Dimensions
Abstract
1. Introduction
2. Background
2.1. Economic Geography Analysis
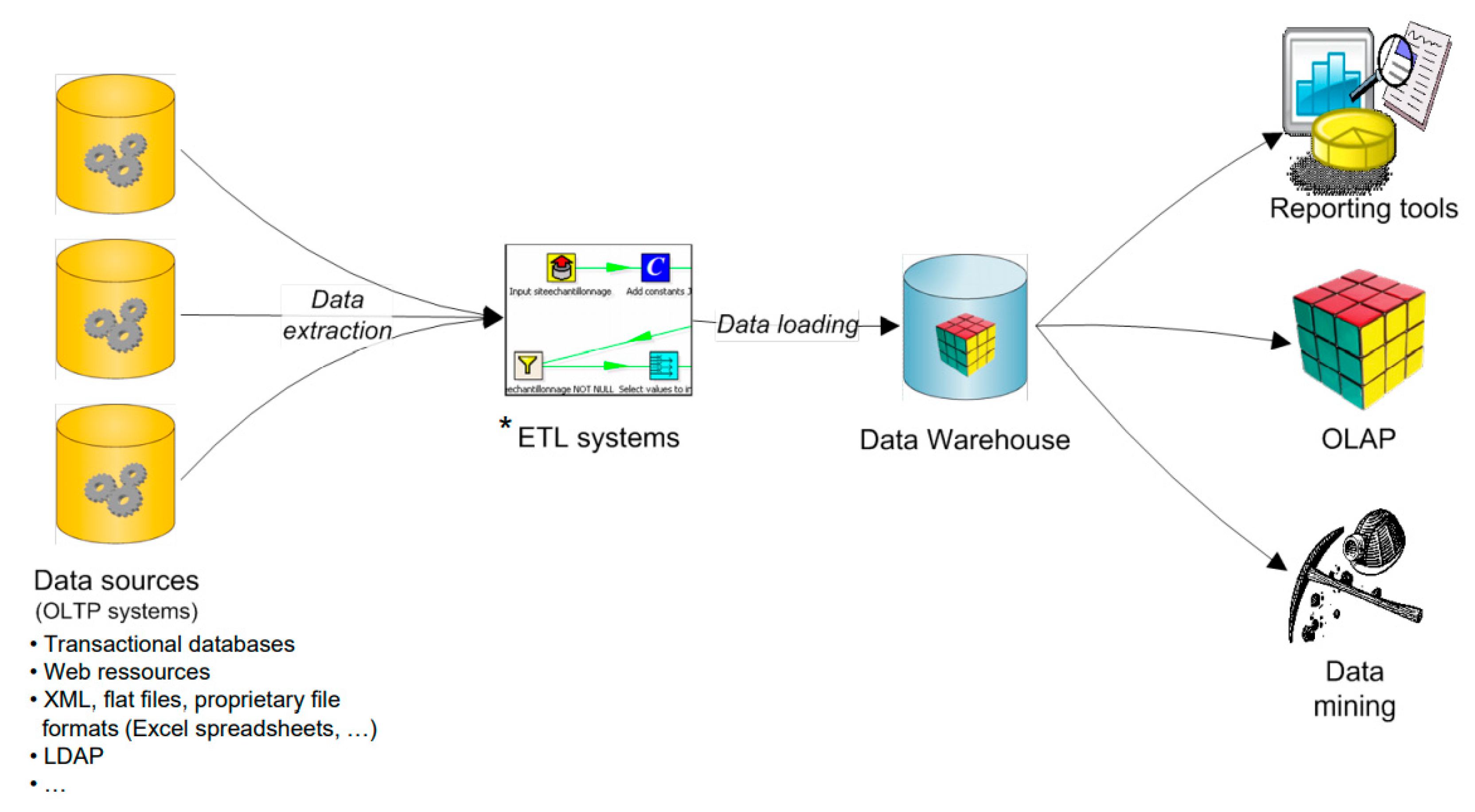
2.2. Business Intelligence and Online Analytical Processing (OLAP)
- respectively allocating dimensions to the rows and columns of a pivot table [13];
- allocating a measure to the cells of a pivot table;
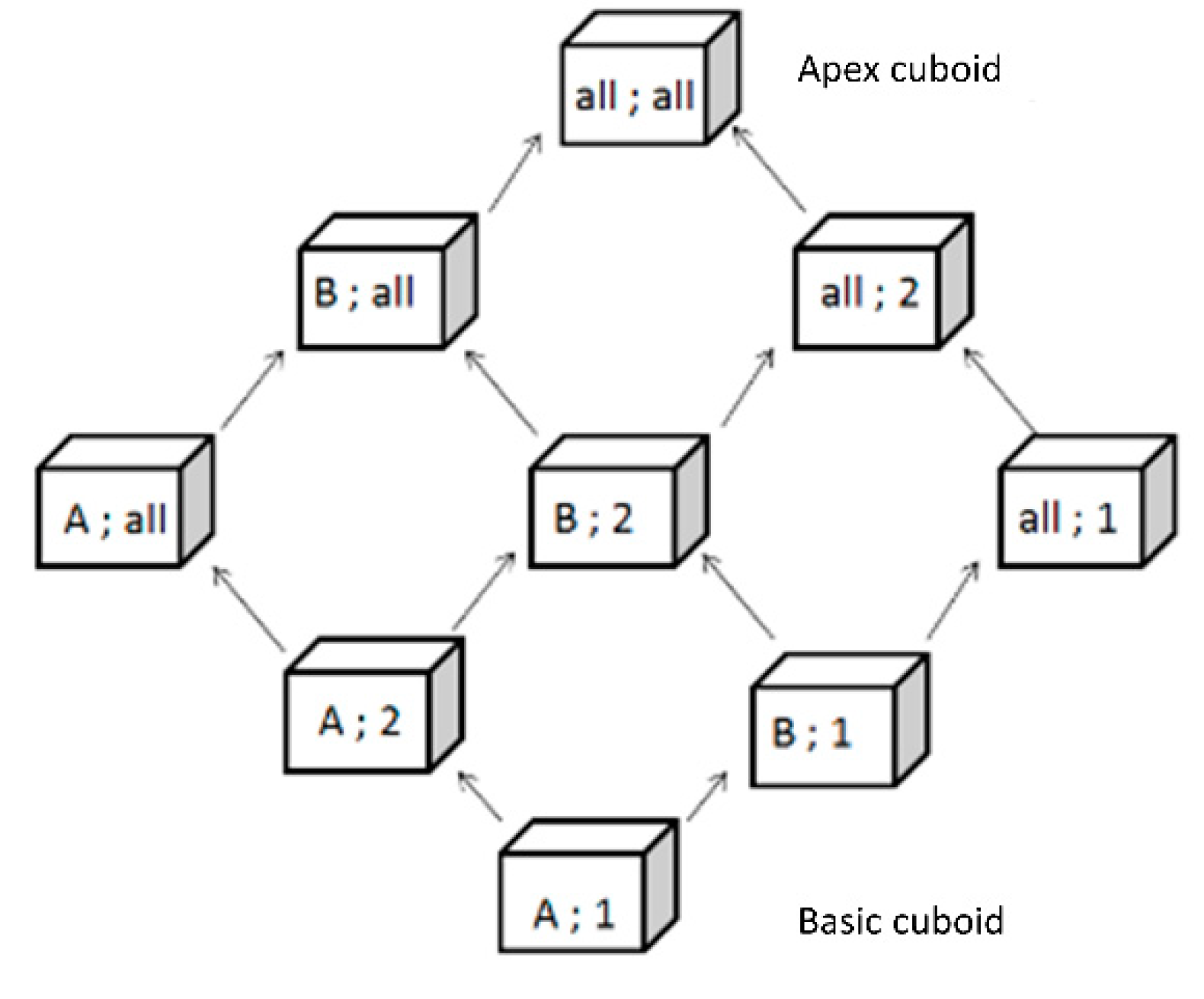
- roll up/drill down in a dimension hierarchy (e.g., switching between levels “year” and “month” of a time dimension) and consequently aggregate measures;
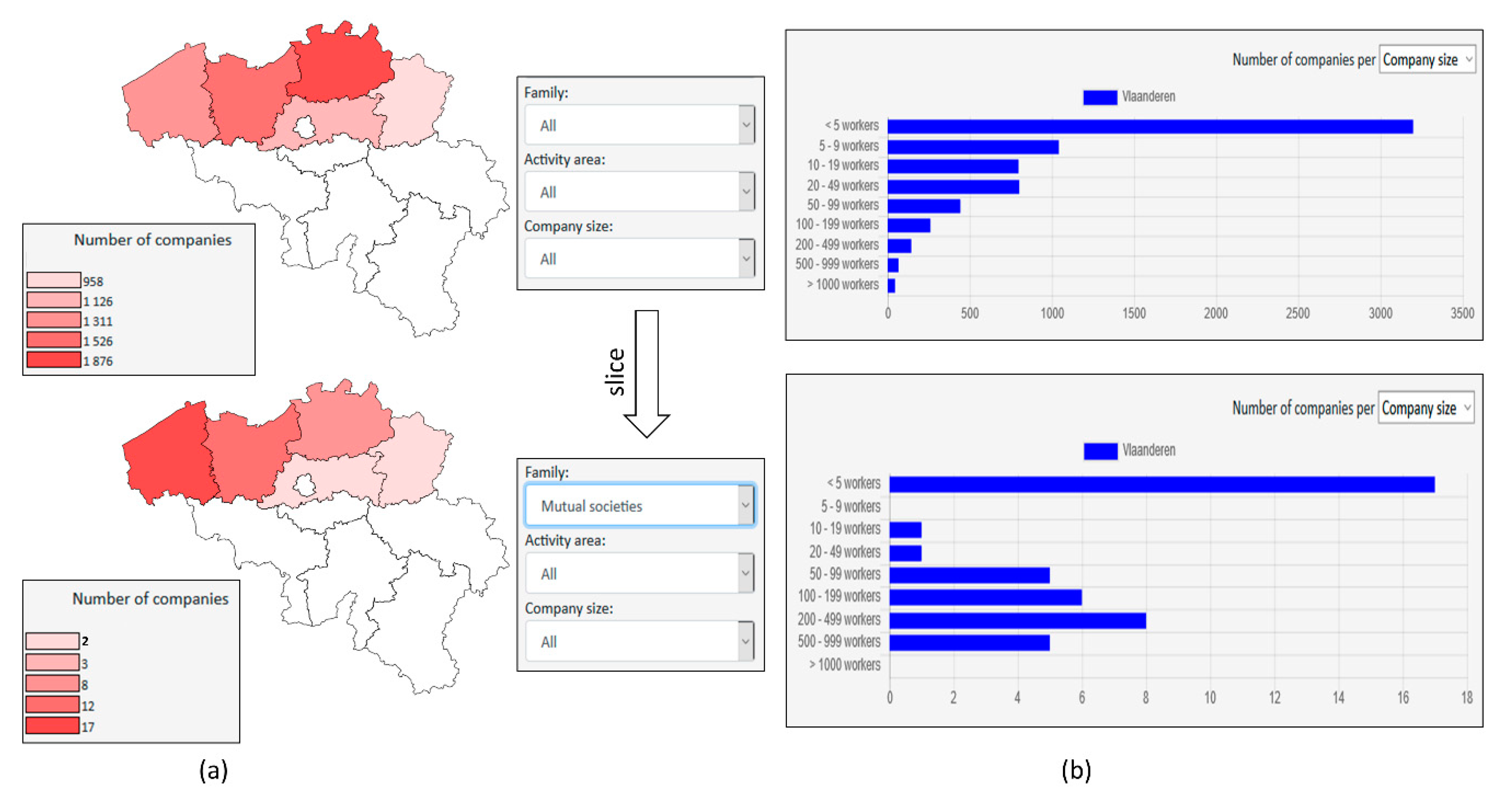
- slice a dimension (e.g., only consider measures attached to month “November 2020” of time dimension).
2.3. Spatial Online Analytical Processing (SOLAP)
2.4. OLAP Implementation
2.5. OLAP Modeling
3. Related Work
3.1. OLAP Constellations and Heterogeneous Dimensions
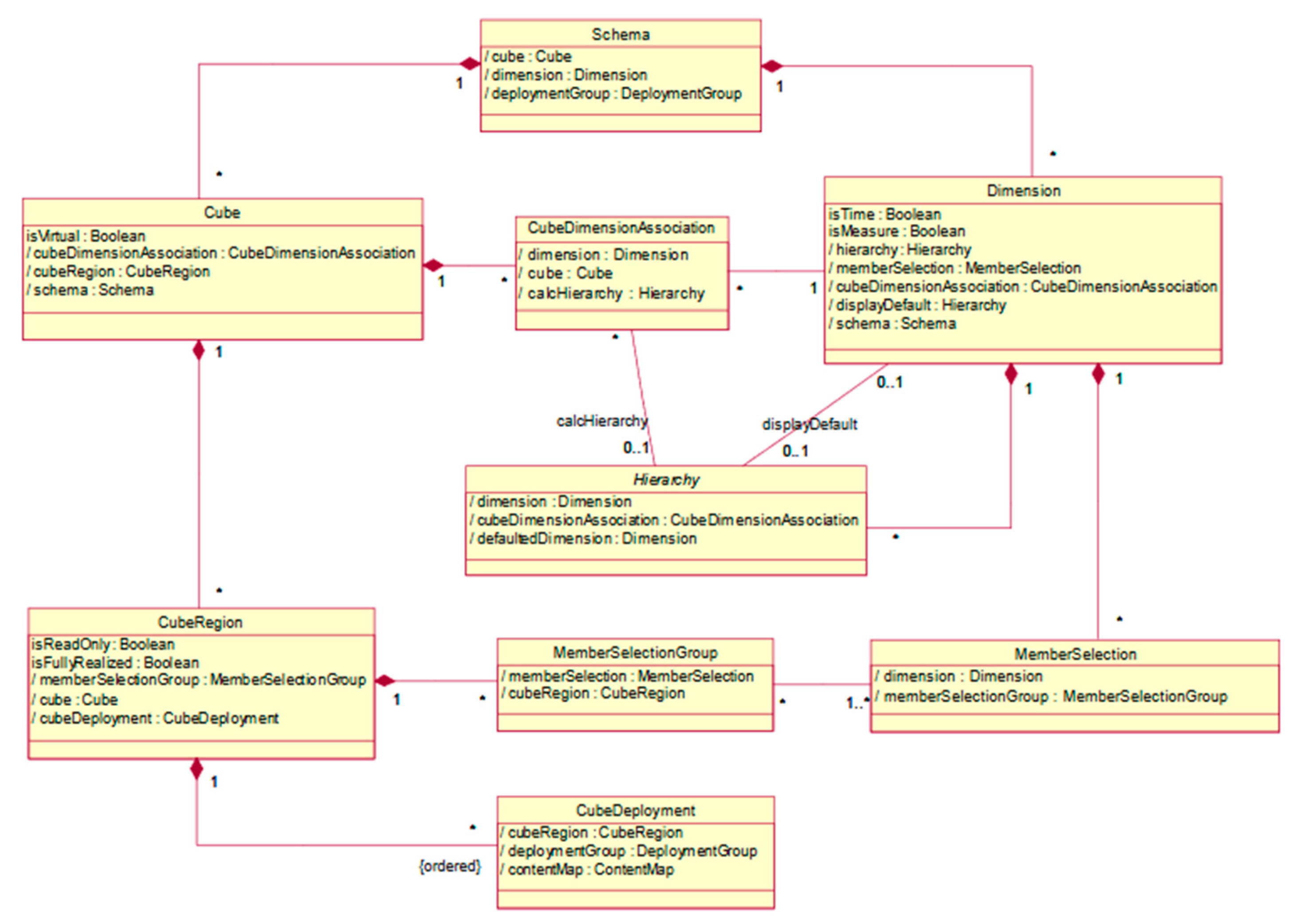
3.2. Data Cube Metamodels
3.3. Synthesis
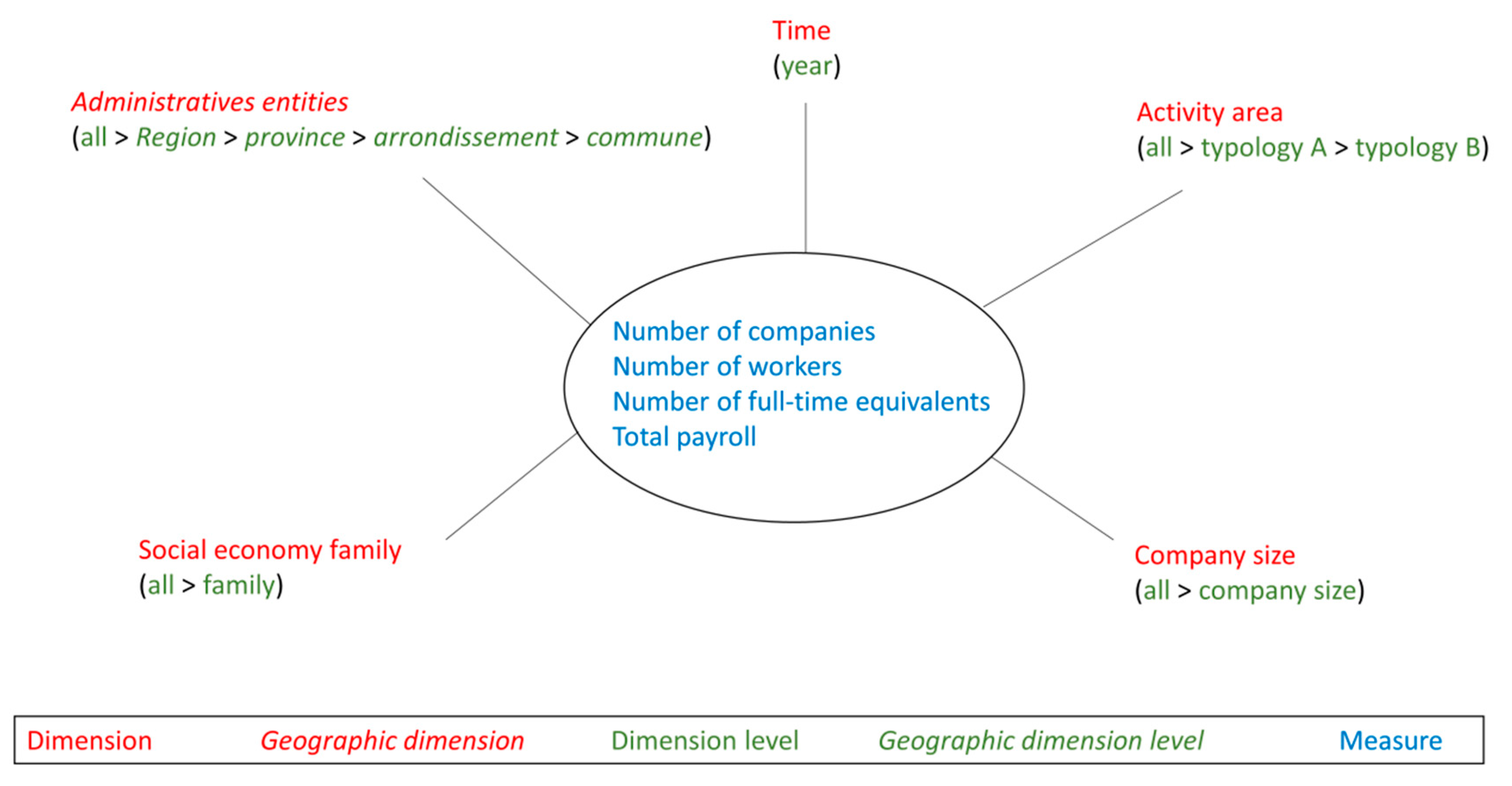
4. Social Economy Case Study and Research Hypothesis
4.1. Social Economy Case Study
- company size (e.g., less than 5 workers, from 5 to 10 workers),
- activity area (e.g., agriculture, human health),
- social economy family (e.g., association, cooperative, foundation, mutual society),
- time (year),
- administrative entity (e.g., Liège province, Paris department).
- sex,
- age,
- socio-professional category (e.g., employee, worker).
4.2. Research Hypothesis
- Multidimensional analysis of heterogeneous data.
- Geographic analysis involving multiscale analysis, multi-territories analysis and time analysis which are likely to change other dimensions definitions (due to heterogeneous data semantics).
- Independence of end-users from IT specialists regarding data exploration and integration.
5. Metamodel
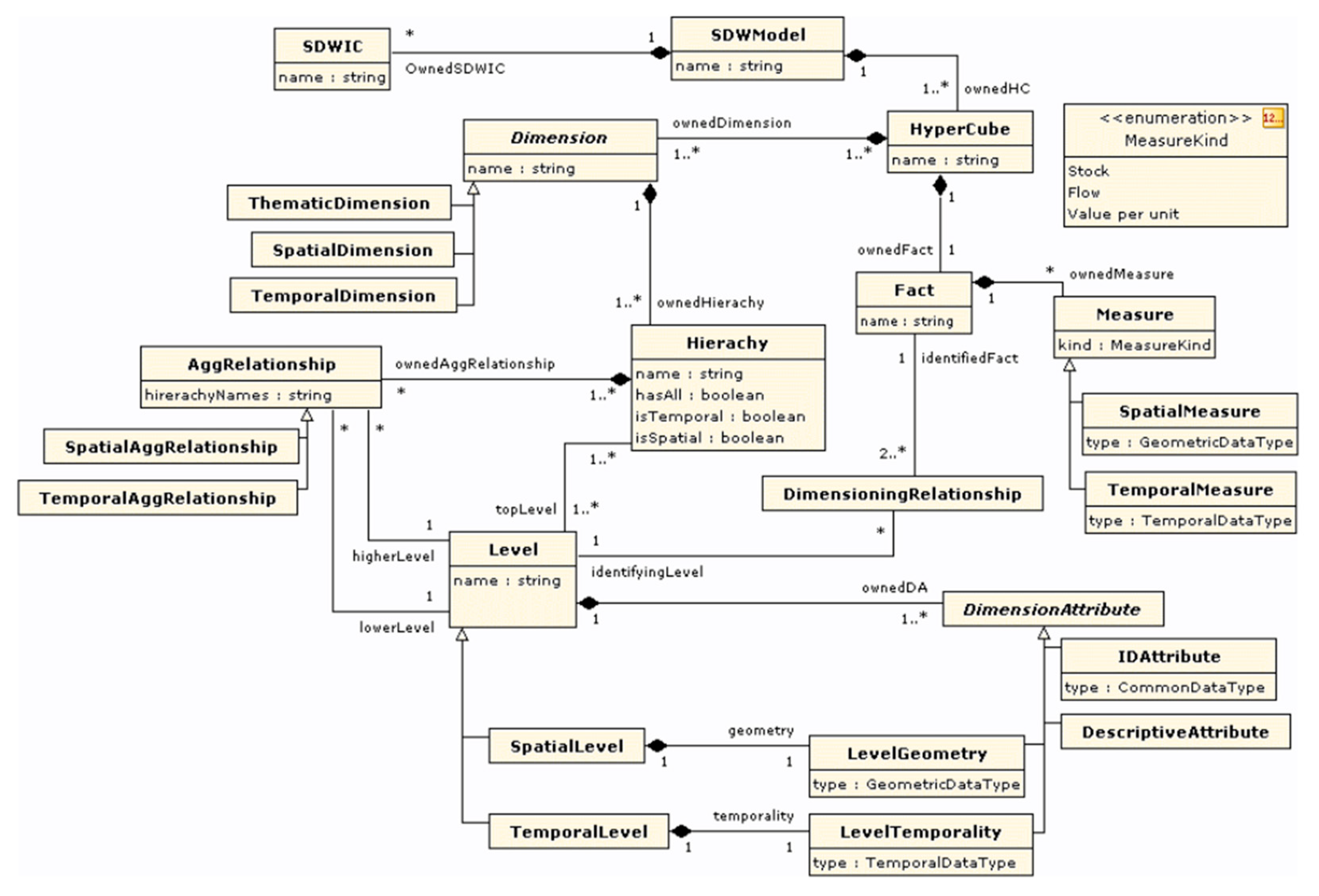
5.1. SOLAP Concepts
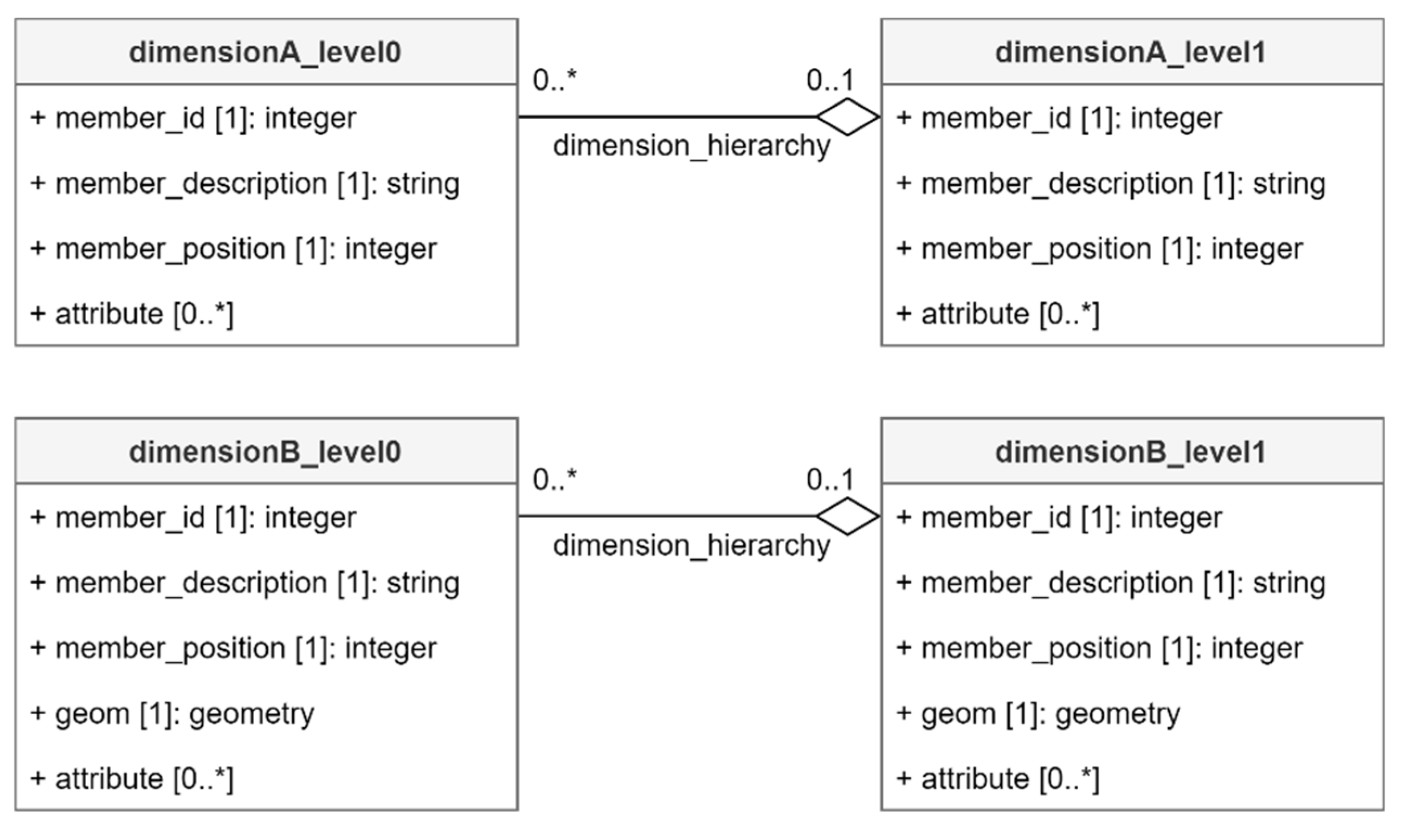
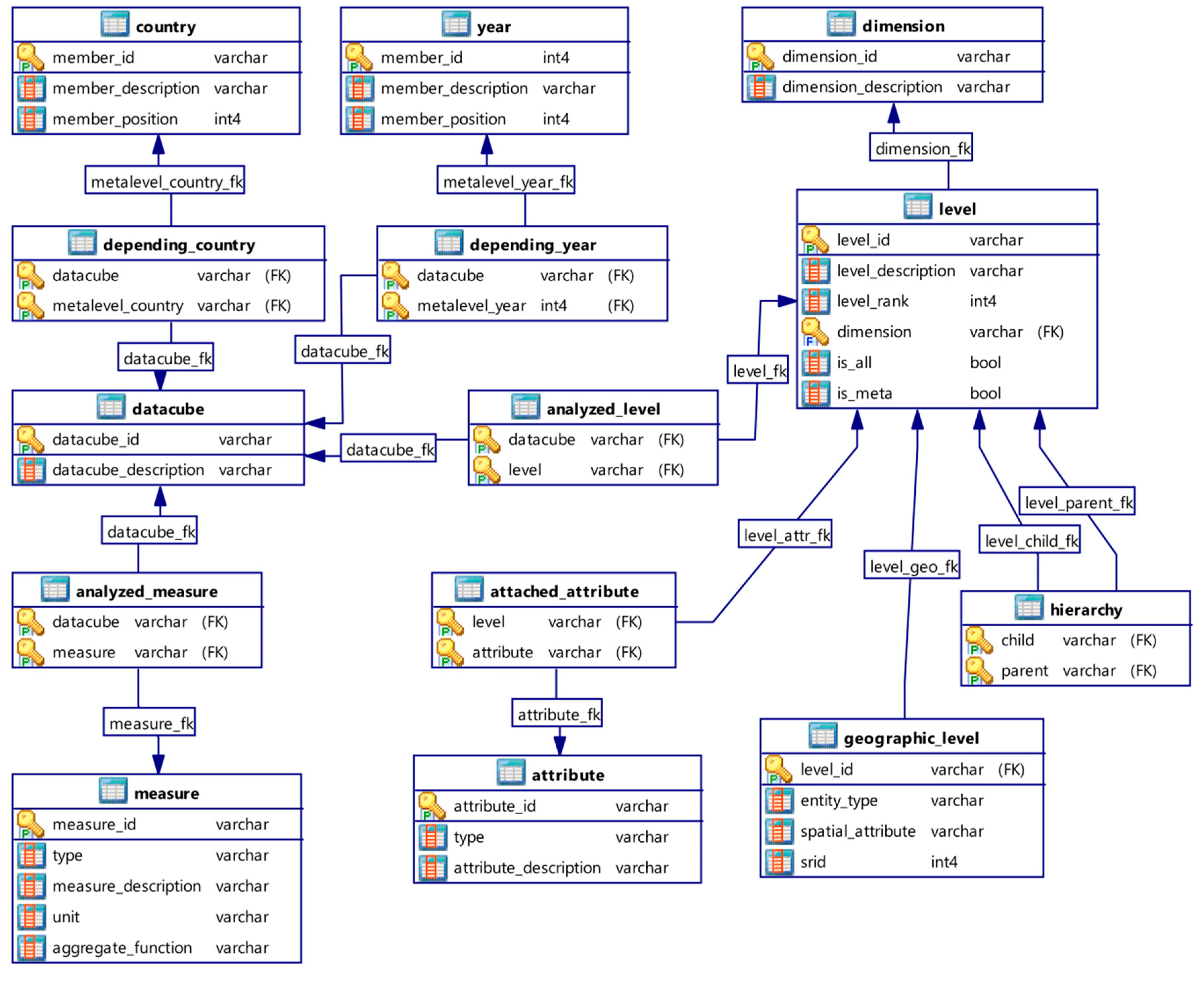
5.2. Data Cube Metamodel
- In most of UML metamodels proposed in literature, data cubes are associated to dimensions. Our metamodel follows a different approach: data cubes are directly associated to dimension levels. This allows navigation between different data cubes through roll up and drill down operations. Indeed, multiscale analysis must consider changes in non-geographic dimensions depending on geographic dimension levels.
- Unlike multiscale analysis involving changes depending on dimension level, our two other objectives, i.e., multi-territories and time analysis, must consider changes depending on dimension members, i.e., time members for time analysis and geographic members for multi-territories analysis. This aspect is managed through a metadimension concept explained in Section 5.4.
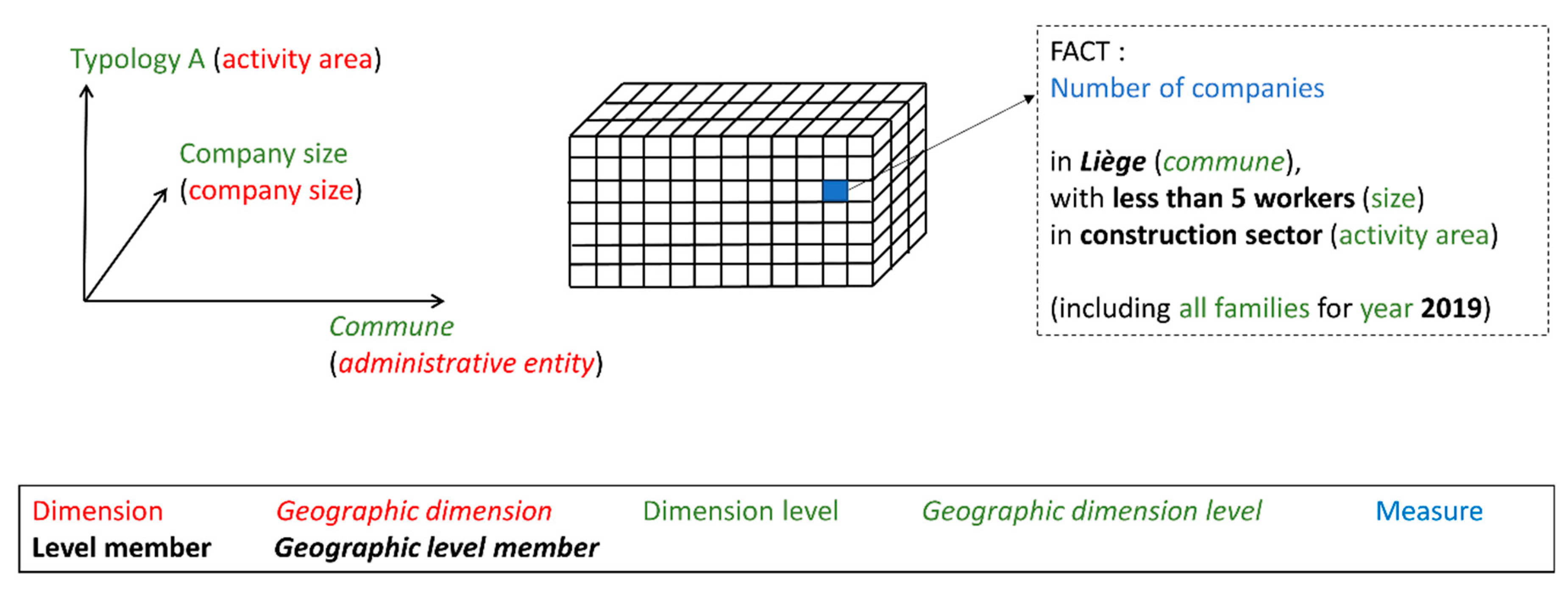
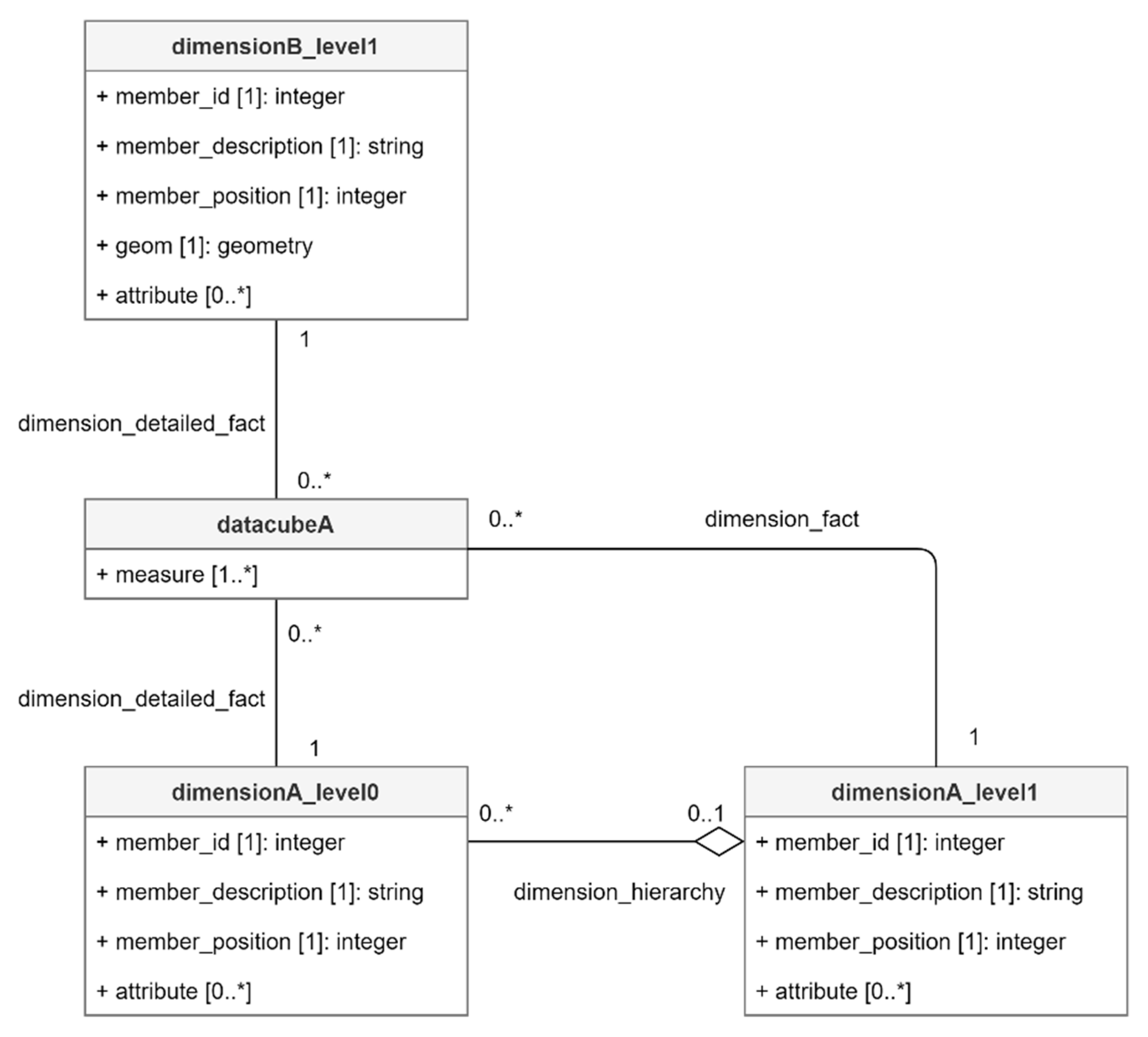
5.3. Instantiated Data Cube Model Example
- a data cube identified as “datacubeA” (property datacube_id in metamodel);
- two dimensions respectively identified as “dimensionA” and “dimensionB” (property dimension_id in metamodel);
- “dimensionA” includes two levels respectively identified as “dimensionA_level0” and “dimensonA_level1” (property level_id in metamodel);
- “dimensionB” includes two geographic levels respectively identified as “dimensionB_level0” and “dimensonB_level1” (property level_id in metamodel);
- “datacubeA” includes the whole dimension “dimensionA”;
- “datacubeA” only includes level “dimension_level1” of dimension “dimensionB”.
- a geographic dimension for SOLAP;
- a data cube depending on a whole dimension and thus enabling drill down and roll up through cuboids;
- a data cube depending on a specific dimension level for heterogeneous data management and thus enabling inter-stellar drill down and roll up through data cubes of a constellation (due to semantic changes depending on analysis scales).
5.4. Metadimension
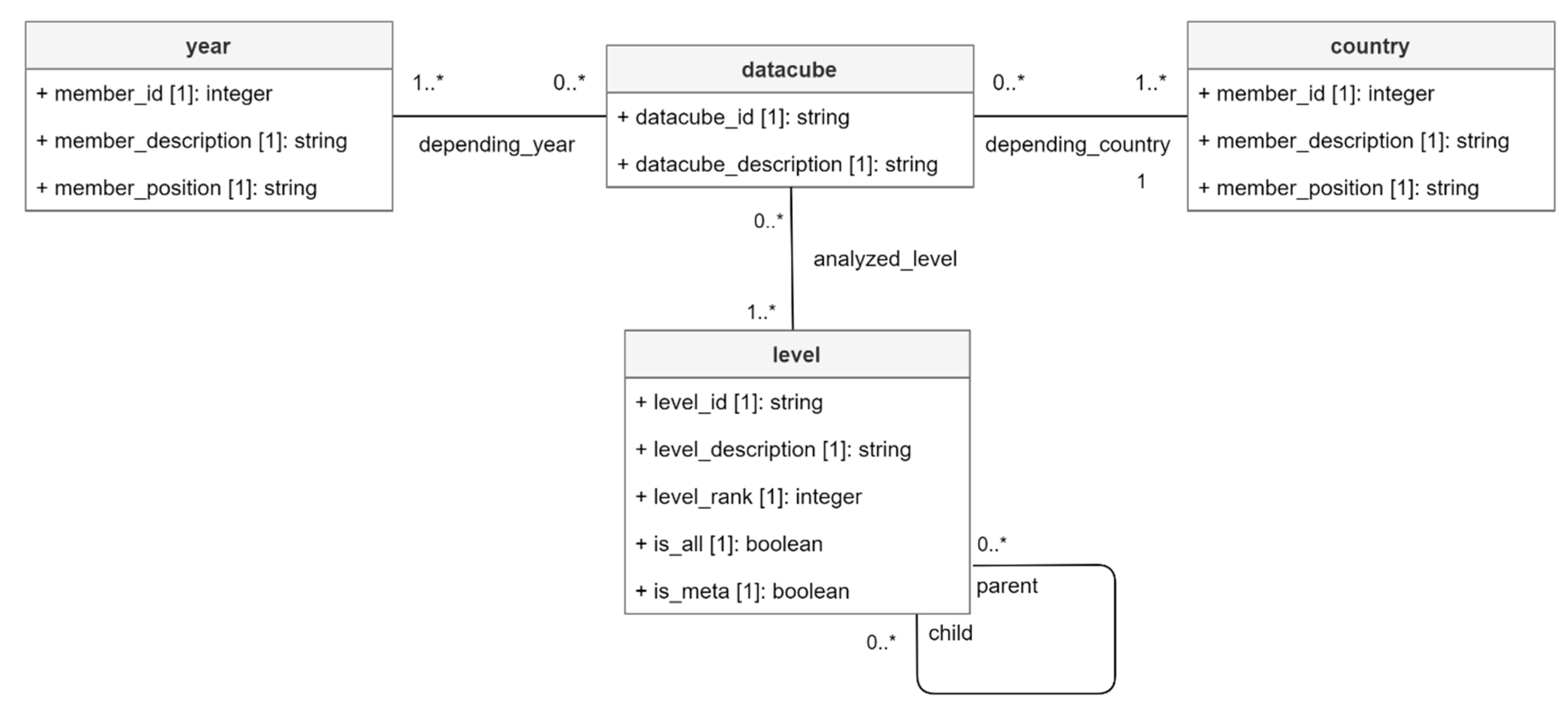
6. Relational Implementation
6.1. Logical Metamodel
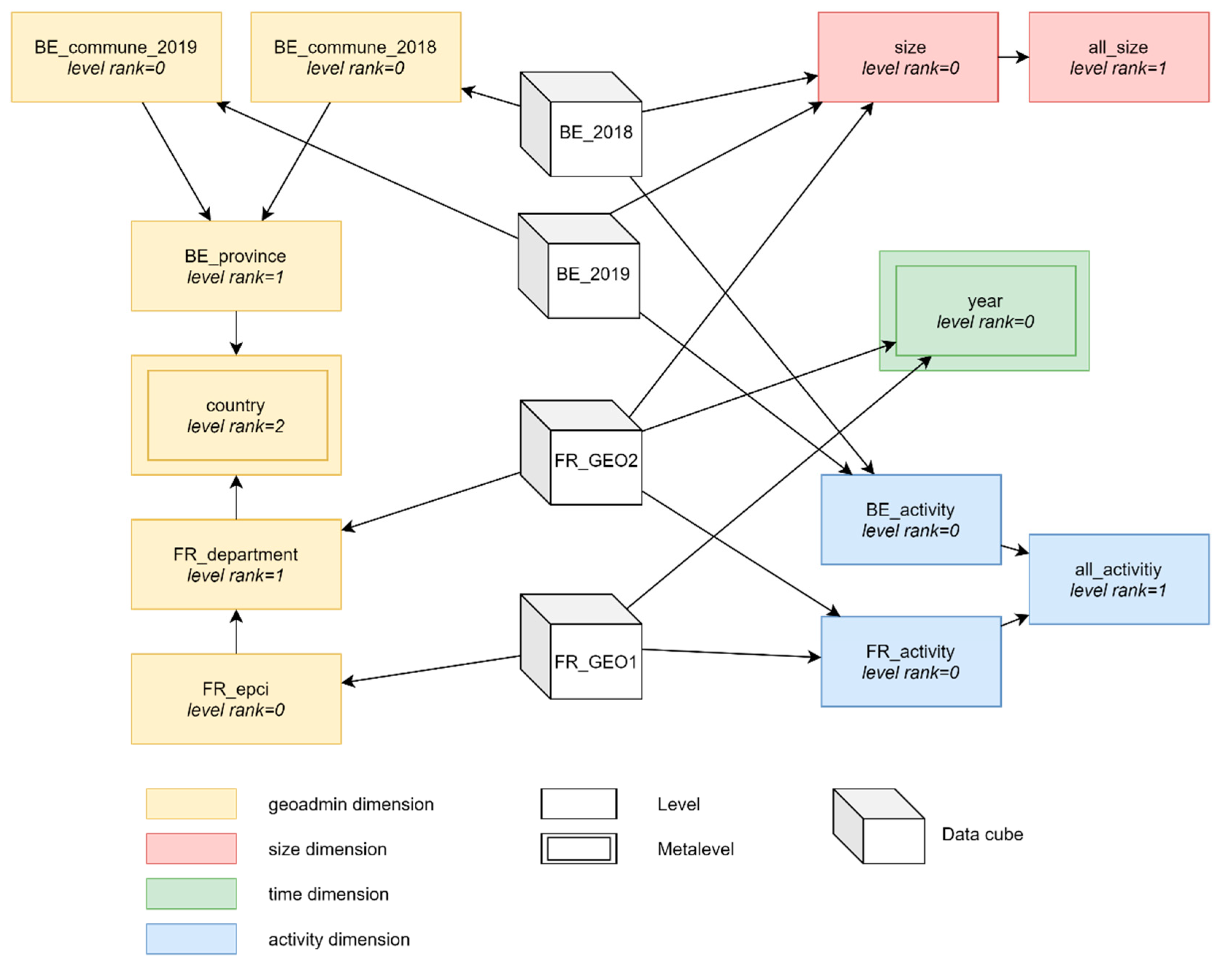
6.2. Constellation Example
- A data cube (cube representation) is a set of facts possibly organized in cuboids depending on the implementation strategy (stored cuboids or not);
- A level (rectangle representation) is a set of dimension members;
- Levels of the same dimension are grouped by color;
- Metalevels (levels belonging to a metadimension) are represented by a double rectangle;
- Arrows represent associations between data cubes and levels (relation analyzed_level in logical metamodel) as well as dimension levels hierarchies;
- A data cube associated to a detailed level of dimension is implicitly associated to other connected levels (e.g., data cube BE_2018 is associated to level size and implicitly associated to level all_size);
6.3. SQL Exploration of Constellations
- CREATE OR REPLACE VIEW datacube_FR_2018 AS
- SELECT datacube_id, datacube_description
- FROM datacube
- INNER JOIN depending_year ON datacube.datacube_id=depending_year.datacube
- INNER JOIN depending_country ON datacube.datacube_id=depending_country.datacube
- AND metalevel_country=’FR’ AND metalevel_year=2018
- SELECT DISTINCT datacube_id, datacube_description
- FROM datacube_FR_2018
- INNER JOIN analyzed_level ON analyzed_level.datacube=datacube_FR_2018.datacube_id
- INNER JOIN level ON level.level_id=analyzed_level.level
- WHERE level.dimension=’size’
- SELECT dimension_id, dimension_description, level_id, level_description, level_rank, is_all
- FROM datacube
- INNER JOIN analyzed_level ON analyzed_level.datacube=datacube.datacube_id
- INNER JOIN level ON level.level_id=analyzed_level.level
- INNER JOIN dimension ON dimension.dimension_id=level.dimension
- WHERE datacube_id=’FR_GEO2’
- ORDER BY dimension_id, level_rank
- SELECT datacube_id, datacube_description
- FROM datacube_FR_2018
- INNER JOIN analyzed_level on datacube_FR_2018.datacube_id=analyzed_level.datacube
- INNER JOIN level on level.level_id=analyzed_level.level
- INNER JOIN hierarchy on hierarchy.child=level.level_id
- AND parent=’fr_department’
- SELECT datacube_id, datacube_description
- FROM datacube
- INNER JOIN depending_year ON datacube_id=depending_year.datacube
- INNER JOIN depending_country ON datacube_id=depending_country.datacube
- INNER JOIN analyzed_level ON datacube_id=analyzed_level.datacube
- INNER JOIN level ON analyzed_level.level=level.level_id
- INNER JOIN dimension ON level.dimension = dimension.dimension_id
- WHERE datacube_id=depending_year.datacube
- AND datacube_id=depending_country.datacube
- AND metalevel_country=’BE’ AND metalevel_year=2018
- AND level_rank=0 AND dimension=’geoadmin’
- Compared geographic levels have the same rank
- Non-represented common dimensions can only be aggregated at their common levels
- Non-common dimensions are aggregated at their “all” level
- Non-represented metadimensions are sliced by common metamembers
- SELECT dimension_id, level_id
- FROM dimension
- INNER JOIN level on dimension = dimension_id
- INNER JOIN analyzed_level on level = level_id
- INNER JOIN datacube on datacube=datacube_id
- WHERE datacube_id=’BE_2018’
- INTERSECT
- SELECT dimension_id, level_id
- FROM dimension
- INNER JOIN level on dimension = dimension_id
- INNER JOIN analyzed_level on level = level_id
- INNER JOIN datacube on datacube=datacube_id
- WHERE datacube_id=’FR_GEO1’
- SELECT DISTINCT dimension_id
- FROM dimension
- INNER JOIN level on dimension = dimension_id
- INNER JOIN analyzed_level on level = level_id
- INNER JOIN datacube on datacube=datacube_id
- WHERE datacube_id=’BE_2018’ AND is_meta=false
- SYMETRICDIFFERENCE
- SELECT DISTINCT dimension_id
- FROM dimension
- INNER JOIN level on dimension = dimension_id
- INNER JOIN analyzed_level on level = level_id
- INNER JOIN datacube on datacube=datacube_id
- WHERE datacube_id=’FR_GEO1’ AND is_meta=false
- SELECT member_id
- FROM year
- INNER JOIN depending_year on metalevel_year=member_id
- INNER JOIN datacube on datacube_id=datacube
- WHERE datacube_id=’FR_GEO1’
- INTERSECT
- SELECT member_id
- FROM year
- INNER JOIN depending_year on metalevel_year=member_id
- INNER JOIN datacube on datacube_id=datacube
- WHERE datacube_id=’BE_2018’
7. Validation
7.1. Overall Architecture
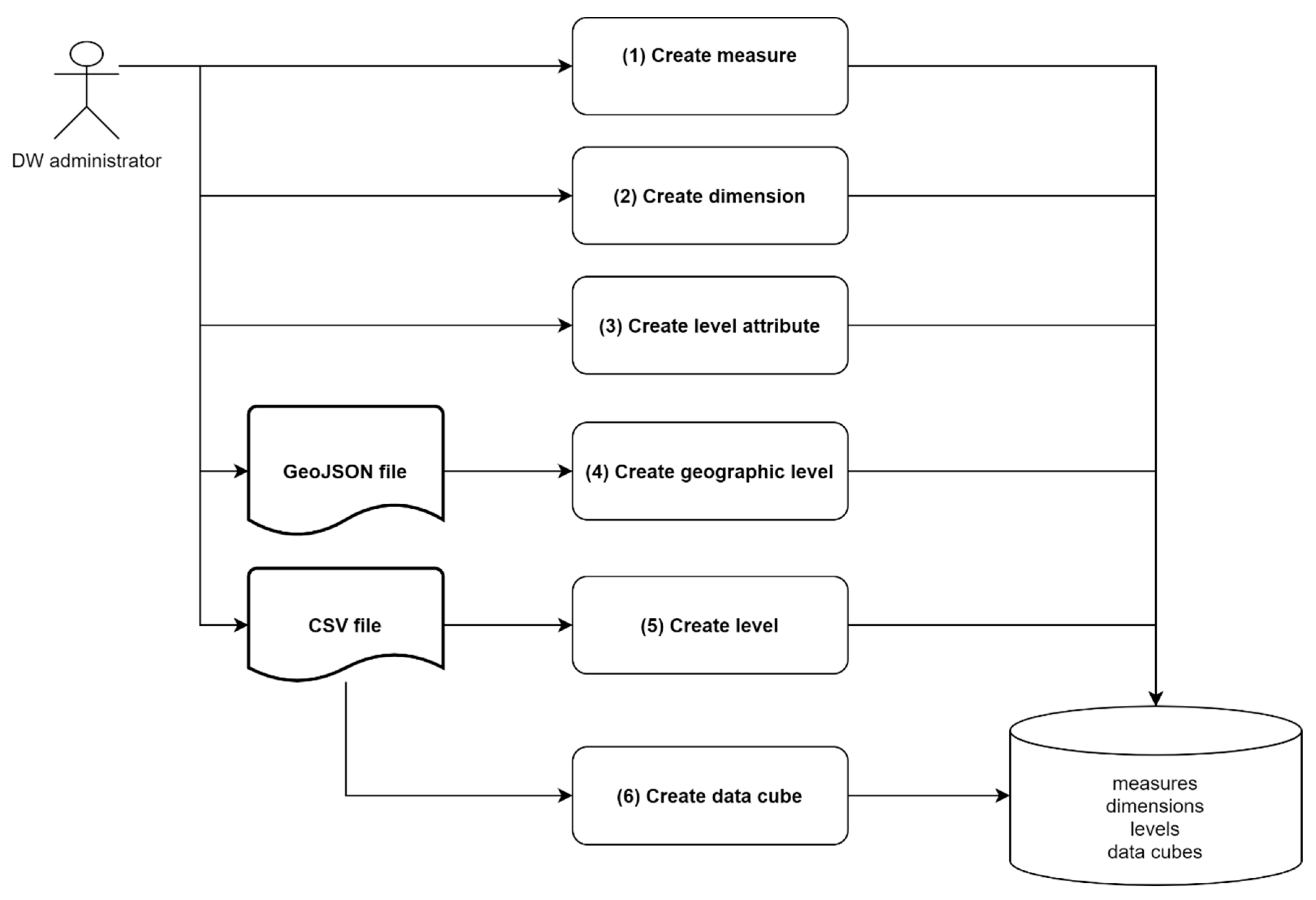
7.2. Data Cubes Administration Module
- Create measure: measures are created by defining parameters required by metamodel like measure_id, type, measure_description, etc.
- Create dimension: dimensions are created by defining parameters dimension_id and dimension_description.
- Create level attribute: attributes are created by defining parameters attribute_id, type and attribute_description.
- Create geographic level: geographic levels of dimensions are created based on a GeoJSON (geo javascript object notation) file including members identifiers, members descriptions (e.g., names of Belgian communes), members geometries according to [16], members identifiers of superior level previously created (e.g., Belgian province) and any other attributes previously created in step 3 (e.g., population of a commune). In addition to this, the administrator defines coordinate reference system in parameter srid according to class geographic_level of the metamodel. Parameters entity_type and spatial_attribute are not needed in “Racines” because geographic levels always include polygons defined in a PostGIS spatial attribute named “geom”. Finally, the administrator defines all parameters belonging to class level of metamodel (level_id, level_rank, etc) as well as level dimension previously defined in step 2.
- Create level: based on a CSV (comma-separated values) file containing cuboid data, a non-geographic level can be created in a way similar to step 4 without the spatial aspect.
- Create data cube: Finally, a data cube can be created if all its measures and dimension levels to associate are already stored in the DW (remember that data cubes can share common dimension levels and measures in order to store constellations in the DW). After the definition of parameters datacube_id, datacube_description and related metadimension metamembers (country and year), data related to cuboids are imported from a CSV file.
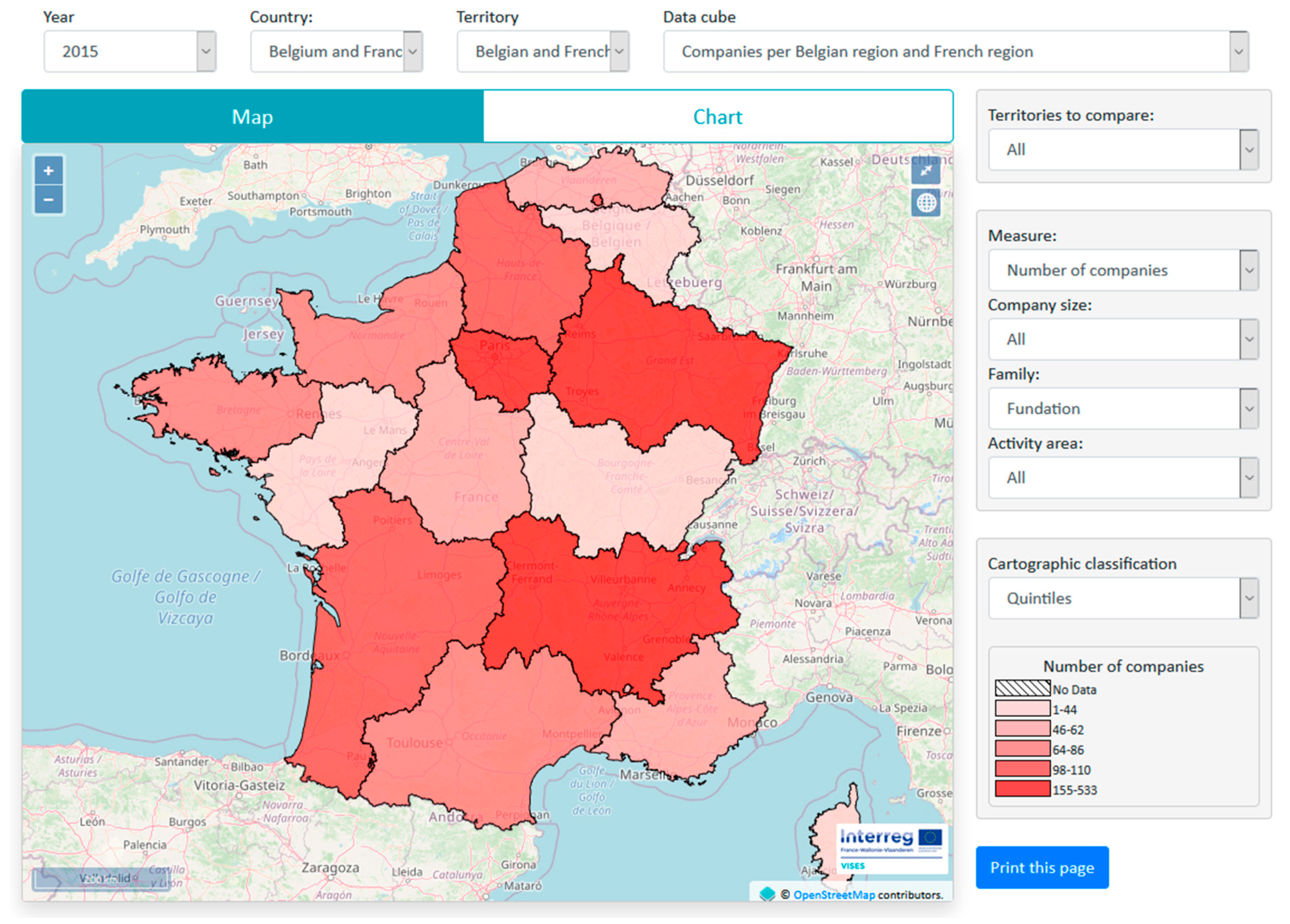
7.3. SOLAP Module
- Companies depending on year, country, administrative entity, activity area, size and social economy family.
- Workers depending on year, country, administrative entity, activity area, social economy family, sex and age.
7.4. Reporting Module
- Population (attribute of dimension level),
- Population density (idem),
- Total numbers of companies, employers and total payroll (data cube measures),
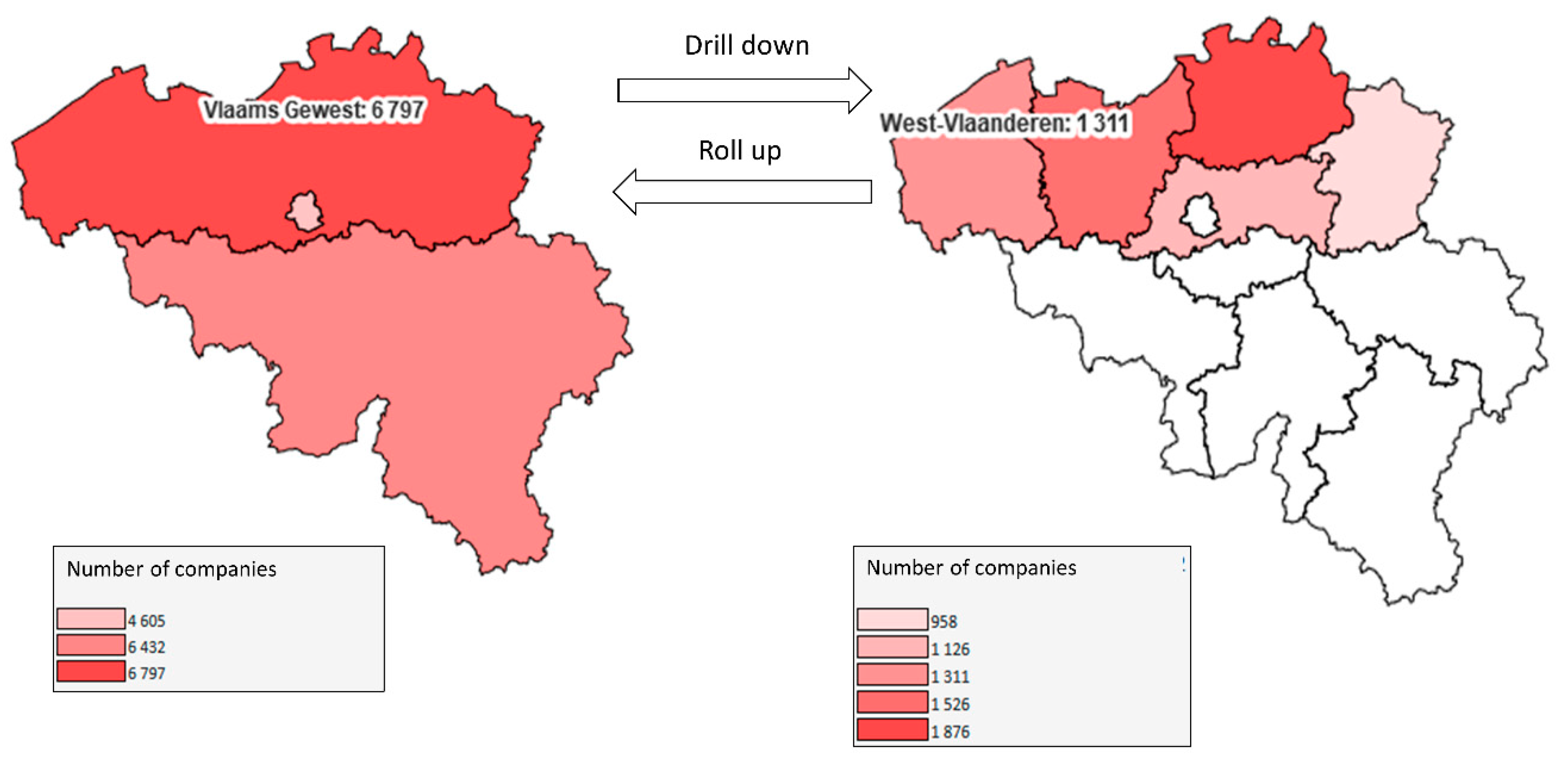
- Maps showing number of companies and workers for same level entities belonging to the administrative entity of superior level, e.g., all provinces belonging to Belgian region “Wallonie” if province “Liège” was chosen (Spatial roll up).
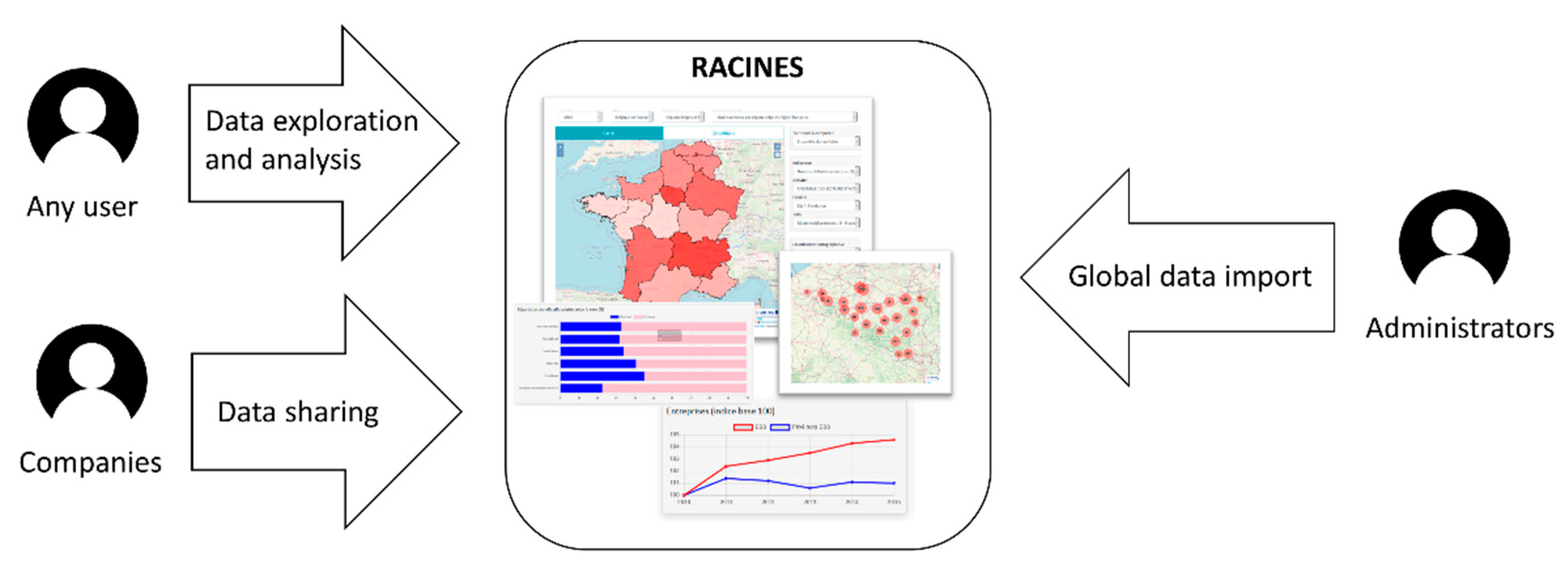
7.5. Product Experience
8. Conclusions
- a data cube administration module for easy integration of heterogeneous data in data cube constellations;
- a SOLAP module for data exploration in dynamic maps (including cross-border maps) and charts;
- a reporting module showing static representation of data depending on hierarchized administrative entities.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Franklin, C.; Hane, P. An introduction to geographic information systems: Linking maps to databases and maps for the rest of us: Affordable and fun. Database 1992, 15, 12–15. [Google Scholar]
- Castells, M. The Rise of the Network Society, 2nd ed.; Wiley-Blackwell: Chichester, UK; Malden, MA, USA, 2010. [Google Scholar]
- Ter Wal, A.L.; Boschma, R.A. Applying social network analysis in economic geography: Framing some key analytic issues. Ann. Reg. Sci. 2009, 43, 739–756. [Google Scholar] [CrossRef]
- Glückler, J.; Doreian, P. Editorial: Social network analysis and economic geography—Positional, evolutionary and multi-level approaches. J. Econ. Geogr. 2016. [Google Scholar] [CrossRef]
- Jones, A.; Murphy, J.T. Theorizing practice in economic geography: Foundations, challenges, and possibilities. Prog. Hum. Geogr. 2011, 35, 366–392. [Google Scholar] [CrossRef]
- Boschma, R.A.; Martin, R. (Eds.) The Handbook of Evolutionary Economic Geography; Edward Elgar: Cheltenham, UK; Northampton, MA, USA, 2010. [Google Scholar]
- Bathelt, H.; Glückler, J. Relational Research Design in Economic Geography; Oxford University Press: Oxford, UK, 2018; Volume 1. [Google Scholar]
- Negash, S.; Gray, P. Business intelligence. In Handbook on Decision Support. Systems 2; Springer: Berlin/Heidelberg, Germany, 2008; pp. 175–193. [Google Scholar]
- Badard, T.; Dubé, E.; Diallo, B.; Mathieu, J.; Ouattara, M. Open Source Geospatial Business Intelligence (BI) in Action, Presented at the OGRS, Nantes. 2009. Available online: https://docplayer.net/10340377-Open-source-geospatial-business-intelligence-bi-in-action.html (accessed on 20 November 2019).
- Katal, A.; Wazid, M.; Goudar, R.H. Big data: Issues, challenges, tools and good practices. In Proceedings of the 2013 Sixth International Conference on Contemporary Computing (IC3), Noida, India, 8–10 August 2013; pp. 404–409. [Google Scholar] [CrossRef]
- Kimball, R.; Ross, M. The Data Warehouse Toolkit: The Definitive Guide to Dimensional Modeling, 3rd ed.; John Wiley & Sons, Inc.: Indianapolis, IN, USA, 2013. [Google Scholar]
- Proulx, M.-J.; Bédard, Y. Comparaison de L’approche Transactionnelle des SIG Avec L’approche Multidimensionnelle pour L’analyse de Données Spatio-Temporelles’. Presented at the Colloque Géomatique 2004—Un Choix Stratégique! Montreal, QC, Canada, 27–28 October 2004; Available online: http://yvanbedard.scg.ulaval.ca/wp-content/documents/publications/359.pdf (accessed on 30 November 2020).
- Gao, B.; Zhang, S.; Yao, N. A multidimensional pivot table model based on MVVM pattern for rich internet application. In Proceedings of the 2012 International Symposium on Computer, Consumer and Control, Taichung, Taiwan, 4–6 June 2012; pp. 24–27. [Google Scholar] [CrossRef]
- Aufaure, M.-A.; Kuchmann-Beauger, N.; Marcel, P.; Rizzi, S.; Vanrompay, Y. Predicting your next OLAP query based on recent analytical sessions. In Data Warehousing and Knowledge Discovery; Bellatreche, L., Mohania, M.K., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8057, pp. 134–145. [Google Scholar]
- Bédard, Y.; Han, J. Fundamentals of spatial data warehousing for geographic knowledge discovery. In Geographic Data Mining and Knowledge Discovery Edition, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2009; pp. 45–67. [Google Scholar]
- Open Geospatial Consortium Inc. OpenGIS® Implementation Standard for Geographic Information—Simple Feature Access—Part 1: Common Architecture. John, R. Herring. 28 May 2011. Available online: https://www.ogc.org/standards/sfa (accessed on 20 November 2006).
- Bimonte, S.; Tchounikine, A.; Miquel, M.; Pinet, F. When spatial analysis meets OLAP: Multidimensional model and operators. Int. J. Data Warehous. Min. 2010, 6, 33–60. [Google Scholar] [CrossRef][Green Version]
- Bimonte, S. Intégration de L’information Géographique dans les Entrepôts de Données et L’analyse en Ligne: De la Modélisation à la Visualisation. Ph.D. Thesis, Institut National des Sciences Appliquées de Lyon, Villeurbanne, France, 2007. [Google Scholar]
- Kasprzyk, J.-P.; Donnay, J.-P. A Raster SOLAP for the visualization of crime data fields. In GEOProcessing 2016; IARIA: Venice, Italy, 2016; pp. 109–117. [Google Scholar]
- Kasprzyk, J.-P.; Donnay, J.-P. A raster SOLAP designed for the emergency services of Brussels agglomeration. In CLOUD COMPUTING 2017; IARIA: Athens, Greece, 2017; pp. 32–38. [Google Scholar]
- Vaisman, A.; Zimányi, E. Mobility data warehouses. IJGI 2019, 8, 170. [Google Scholar] [CrossRef]
- Miquel, M.; Bédard, Y.; Brisebois, A. Conception d’entrepôts de données géospatiales à partir de sources hétérogènes Exemple d’application en foresterie. ISI 2002, 7, 89–111. [Google Scholar] [CrossRef]
- Rocha, G.M.; Capelo, P.L.; Ciferri, C.D.A. Healthcare decision-making over a geographic, socioeconomic, and image data warehouse. In ADBIS, TPDL and EDA 2020 Common Workshops and Doctoral Consortium; Bellatreche, L., Bieliková, M., Boussaïd, O., Catania, B., Darmont, J., Demidova, E., Duchateau, F., Hall, M., Merčun, T., Eds.; Springer International Publishing: Cham, Switzerland, 2020; Volume 1260, pp. 85–97. [Google Scholar]
- Agapito, G.; Zucco, C.; Cannataro, M. COVID-warehouse: A data warehouse of Italian COVID-19, pollution, and climate data. Int. J. Environ. Res. Public Health 2020, 17, 5596. [Google Scholar] [CrossRef]
- Bimonte, S.; Kang, M.-A. Towards a model for the multidimensional analysis of field data. In Advances in Databases and Information Systems; Catania, B., Ivanović, M., Thalheim, B., Eds.; Springer: Berlin/Heidelberg, Germany, 2010; Volume 6295, pp. 58–72. [Google Scholar]
- Vassiliadis, P.; Sellis, T. A survey of logical models for OLAP databases. SIGMOD Rec. 1999, 28, 64–69. [Google Scholar] [CrossRef]
- Pentaho, Mondrian. 2017. Available online: https://mondrian.pentaho.com/documentation/olap.php (accessed on 21 November 2020).
- Microsoft, PowerBI. 2020. Available online: https://powerbi.microsoft.com (accessed on 1 December 2020).
- PostGIS. 2020. Available online: https://postgis.net (accessed on 1 December 2020).
- Ferro, M.; Fragoso, R.; Fidalgo, R. Document-oriented geospatial data warehouse: An experimental evaluation of SOLAP queries. In Proceedings of the 2019 IEEE 21st Conference on Business Informatics (CBI), Moscow, Russia, 15–17 July 2019; pp. 47–56. [Google Scholar] [CrossRef]
- Scabora, L.C.; Brito, J.J.; Ciferri, R.R.; Ciferri, C.D.D. Physical data warehouse design on NoSQL databases—OLAP query processing over HBase. In Proceedings of the 18th International Conference on Enterprise Information Systems, Rome, Italy, 25–28 April 2016; pp. 111–118. [Google Scholar] [CrossRef]
- Gür, N.; Pedersen, T.B.; Hose, K.; Midtgaard, M. Multidimensional enrichment of spatial RDF data for SOLAP—Full version. arXiv 2020, arXiv:2002.06608. [Google Scholar]
- Leite, D.F.B.; Baptista, C.D.S.; Amorim, B.D.S.P. An exploratory SOLAP tool for linked open data. IJBIS 2019, 31, 391. [Google Scholar] [CrossRef]
- Brito, J.J.; Siqueira, T.L.L.; Times, V.C.; Ciferri, R.R.; de Ciferri, C.D. Efficient Processing of drill-across queries over geographic data warehouses. In Data Warehousing and Knowledge Discovery; Cuzzocrea, A., Dayal, U., Eds.; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6862, pp. 152–166. [Google Scholar]
- Malinowski, E.; Zimányi, E. OLAP hierarchies: A conceptual perspective. In Active Flow and Combustion Control. 2018; King, R., Ed.; Springer International Publishing: Cham, Switzerland, 2004; Volume 141, pp. 477–491. [Google Scholar]
- Trujillo, J.; Lujan-Mora, S.; Song, I.-Y. Applying UML and XML for designing and interchanging information for data warehouses and OLAP applications. J. Database Manag. 2004, 15, 41–72. [Google Scholar] [CrossRef]
- Boulil, K.; Bimonte, S.; Pinet, F. Conceptual model for spatial data cubes: A UML profile and its automatic implementation. Comput. Stand. Interfaces 2015, 38, 113–132. [Google Scholar] [CrossRef]
- Babar, M.; Khattak, A.; Arif, F.; Tariq, M. An improved framework for modelling data warehouse systems using UML profile. IAJIT 2020, 17, 562–571. [Google Scholar] [CrossRef]
- Ravat, F.; Song, J. A unified approach to multisource data analyses. Fundam. Inform. 2018, 162, 311–359. [Google Scholar] [CrossRef]
- Erraissi, A.; Belangour, A. Meta-modeling of big data visualization layer using On-Line Analytical Processing (OLAP). IJATCSE 2019, 8, 990–998. [Google Scholar] [CrossRef]
- Boulil, K.; Bimonte, S.; Pinet, F. Un modèle UML et des contraintes OCL pour les entrepôts de données spatiales. De la représentation conceptuelle à l’implémentation. Ingénierie des Systèmes d’Information 2011, 16, 11–39. [Google Scholar] [CrossRef]
- Pedersen, T.; Jensen, C.; Dyreson, C. A foundation for capturing and querying complex multidimensional data. Inf. Syst. 2001, 26, 383–423. [Google Scholar] [CrossRef]
- Garani, G.; Eren, C. Comparison of different temporal data warehouses approaches. Online J. Sci. Technol. 2017, 7, 17–27. [Google Scholar]
- Eder, J.; Koncilia, C.; Morzy, T. The COMET metamodel for temporal data warehouses. In Proceedings of the 14th International Conference on Advanced Information Systems Engineering, Berlin, Heidelberg, 27–31 May 2002; pp. 83–99. [Google Scholar]
- Golfarelli, M.; Maio, D.; Rizzi, S. The dimensional fact model: A conceptual model for data warehouses. Int. J. Coop. Inf. Syst. 1998, 7, 215–247. [Google Scholar] [CrossRef]
- Ravat, F.; Teste, O.; Tournier, R.; Zurfluh, G. Algebraic and graphic languages for OLAP manipulations. Int. J. Data Wareh. Min. 2008, 4, 17–46. [Google Scholar] [CrossRef]
- Abelló, A.; Samos, J.; Soler, F.E.S. Multi-Star Conceptual Schemas for OLAP Systems; UPC Universitat Politècnica de Catalunya BarcelonaTech: Barcelona, Spain, 2001. [Google Scholar]
- Abelló, A.; Samos, J.; Saltor, F. Implementing operations to navigate semantic star schemas. In Proceedings of the 6th ACM International Workshop on Data Warehousing and OLAP—DOLAP ’03, New Orleans, LA, USA, 7 November 2003; p. 56. [Google Scholar] [CrossRef]
- Object Management Group (OMG). Common Warehouse Metamodel (CWM) Specification v 1.1’. 2003. Available online: https://www.omg.org/spec/CWM/1.1/PDF (accessed on 11 January 2021).
- Medina, E.; Trujillo, J. A standard for representing multidimensional properties: The Common Warehouse Metamodel (CWM). In Advances in Databases and Information Systems; Manolopoulos, Y., Návrat, P., Eds.; Springer: Berlin/Heidelberg, Germany, 2002; Volume 2435, pp. 232–247. [Google Scholar]
- Cuzzocrea, A.; Fidalgo, R. SDWM: An enhanced spatial data warehouse metamodel. CEUR Workshop Proc. 2012, 855, 32–39. [Google Scholar]
- Letrache, K.; El Beggar, O.; Ramdani, M. The automatic creation of OLAP cube using an MDA approach. Softw. Pract. Exper. 2017, 47, 1887–1903. [Google Scholar] [CrossRef]
- VISES Project. 2020. Available online: http://www.projetvisesproject.eu/ (accessed on 23 November 2020).
- Cress HDF. 2020. Available online: https://www.cresshdf.org/ (accessed on 23 November 2020).
- Concertes. 2020. Available online: https://concertes.be/ (accessed on 23 November 2020).
- Design and representation of the time dimension in enterprise data warehouses—A business related practical approach. In Proceedings of the 4th International Workshop on Pattern Recognition in Information Systems, Porto, Portugal, 13–14 April 2004; pp. 416–424. [CrossRef]
- Mann, S.; Phogat, A.K. Dynamic construction of lattice of cuboids in data warehouse. J. Stat. Manag. Syst. 2020, 23, 971–982. [Google Scholar] [CrossRef]
- Pedersen, T.; Jensen, C.S. Multidimensional data modeling for complex data. In Proceedings of the 15th International Conference on Data Engineering, Sydney, Australia, 23–16 March 1999; pp. 336–345. [Google Scholar]
- Racines—L’Economie Sociale et Solidaire en Belgique et en Région Hauts-de-France. 2020. Available online: http://racines.projetvisesproject.eu/ (accessed on 28 November 2020).
- Nys, G.-A.; Kasprzyk, J.-P.; Hallot, P.; Billen, R. A semantic retrieval system in remote sensing web platforms. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 1593–1599. [Google Scholar] [CrossRef]
- Tardío, R.; Maté, A.; Trujillo, J. A new big data benchmark for OLAP cube design using data pre-aggregation techniques. Appl. Sci. 2020, 10, 8674. [Google Scholar] [CrossRef]



| Dimension_id | Dimension_Description | Level_id | Level_Description | Level_Rank | Is_All |
|---|---|---|---|---|---|
| activity | Activity Area | fr_activity | French activity area | 0 | False |
| activity | Activity Area | all_activity | All activity areas | 1 | True |
| geoadmin | Administrative entity | fr_department | French Department | 1 | False |
| geoadmin | Administrative entity | country | Country | 2 | False |
| size | Company Size | size | Company Size | 0 | False |
| size | Company Size | all_size | All company sizes | 1 | True |
| time | Time | year | Year | 0 | False |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kasprzyk, J.-P.; Devillet, G. A Data Cube Metamodel for Geographic Analysis Involving Heterogeneous Dimensions. ISPRS Int. J. Geo-Inf. 2021, 10, 87. https://doi.org/10.3390/ijgi10020087
Kasprzyk J-P, Devillet G. A Data Cube Metamodel for Geographic Analysis Involving Heterogeneous Dimensions. ISPRS International Journal of Geo-Information. 2021; 10(2):87. https://doi.org/10.3390/ijgi10020087
Chicago/Turabian StyleKasprzyk, Jean-Paul, and Guénaël Devillet. 2021. "A Data Cube Metamodel for Geographic Analysis Involving Heterogeneous Dimensions" ISPRS International Journal of Geo-Information 10, no. 2: 87. https://doi.org/10.3390/ijgi10020087
APA StyleKasprzyk, J.-P., & Devillet, G. (2021). A Data Cube Metamodel for Geographic Analysis Involving Heterogeneous Dimensions. ISPRS International Journal of Geo-Information, 10(2), 87. https://doi.org/10.3390/ijgi10020087







