New Insight on Soil Loss Estimation in the Northwestern Region of the Zagros Fold and Thrust Belt
Abstract
1. Introduction
2. Materials and Methods
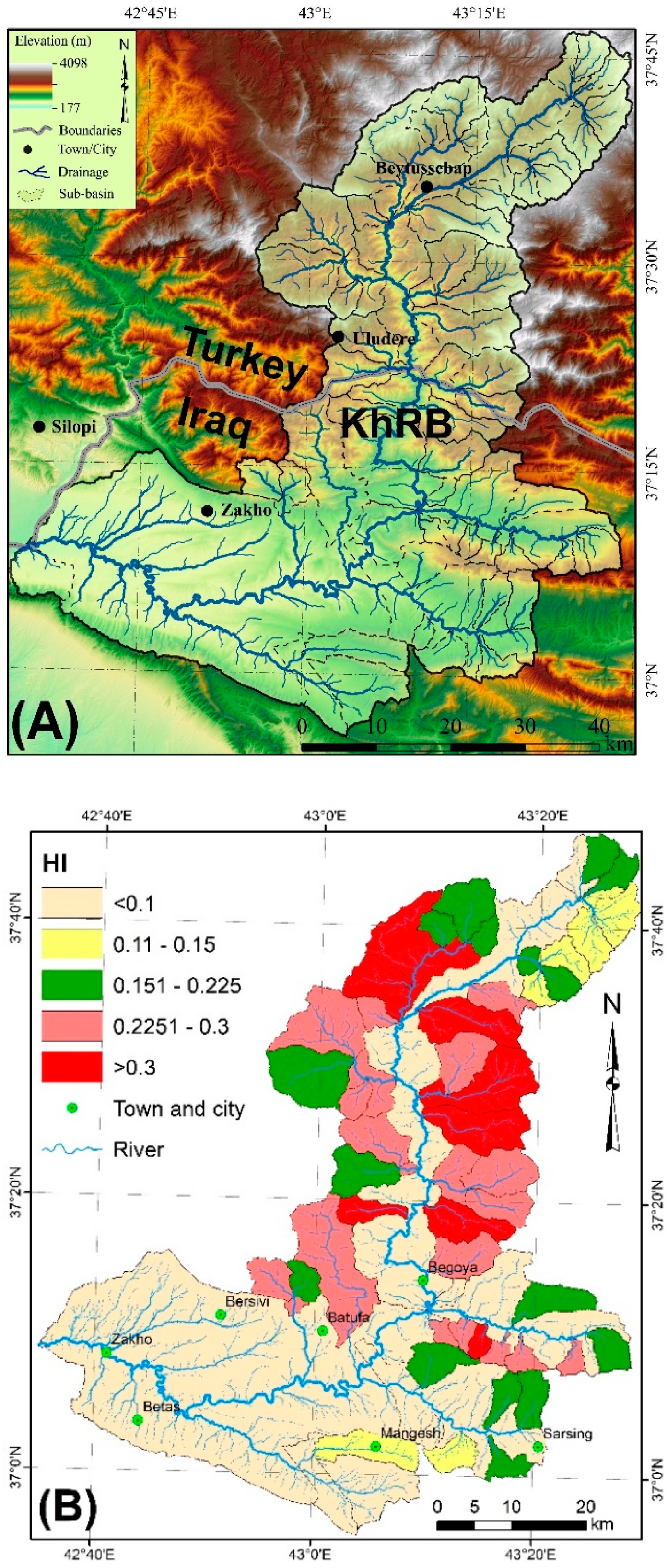
2.1. Study Area
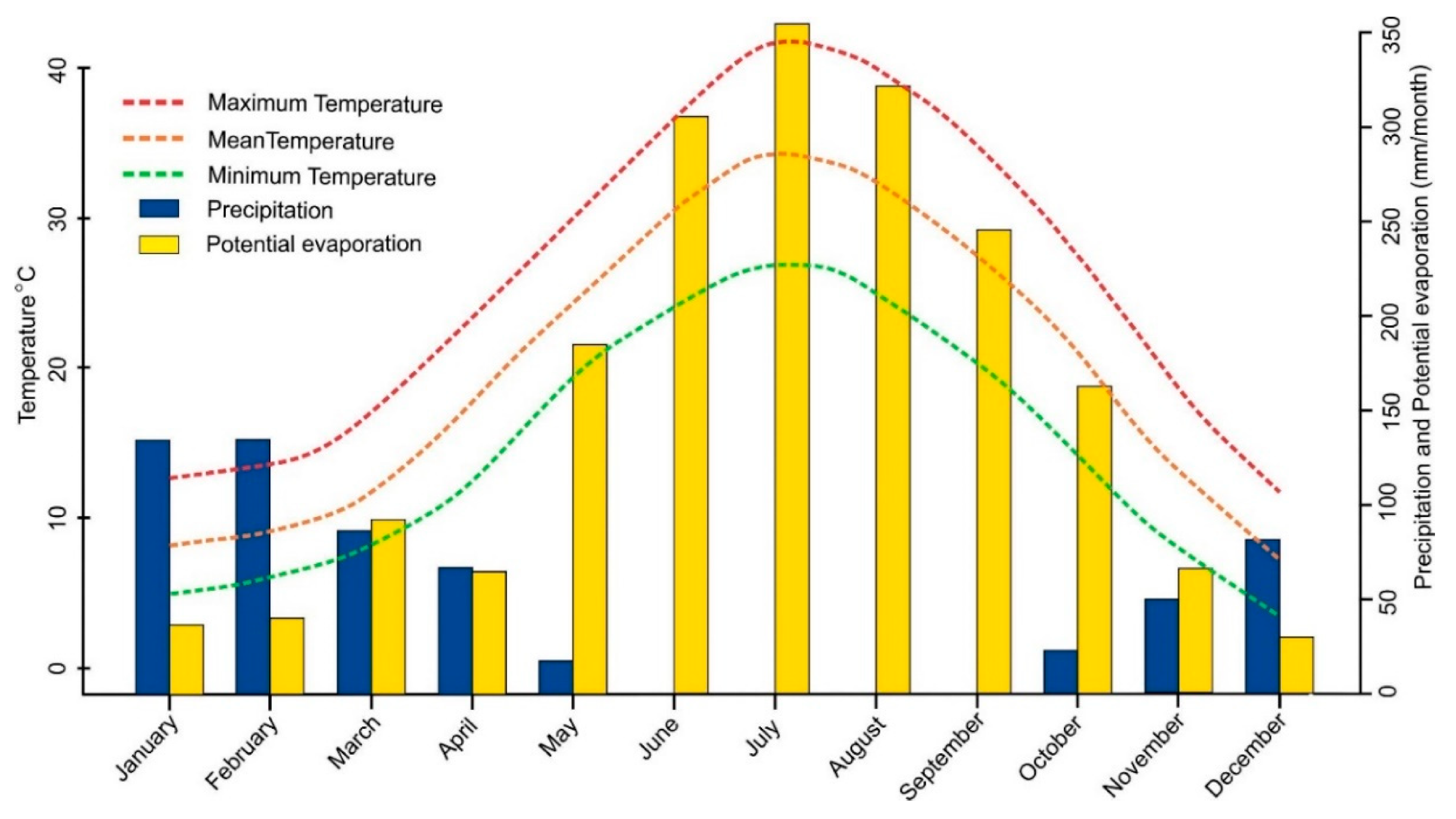
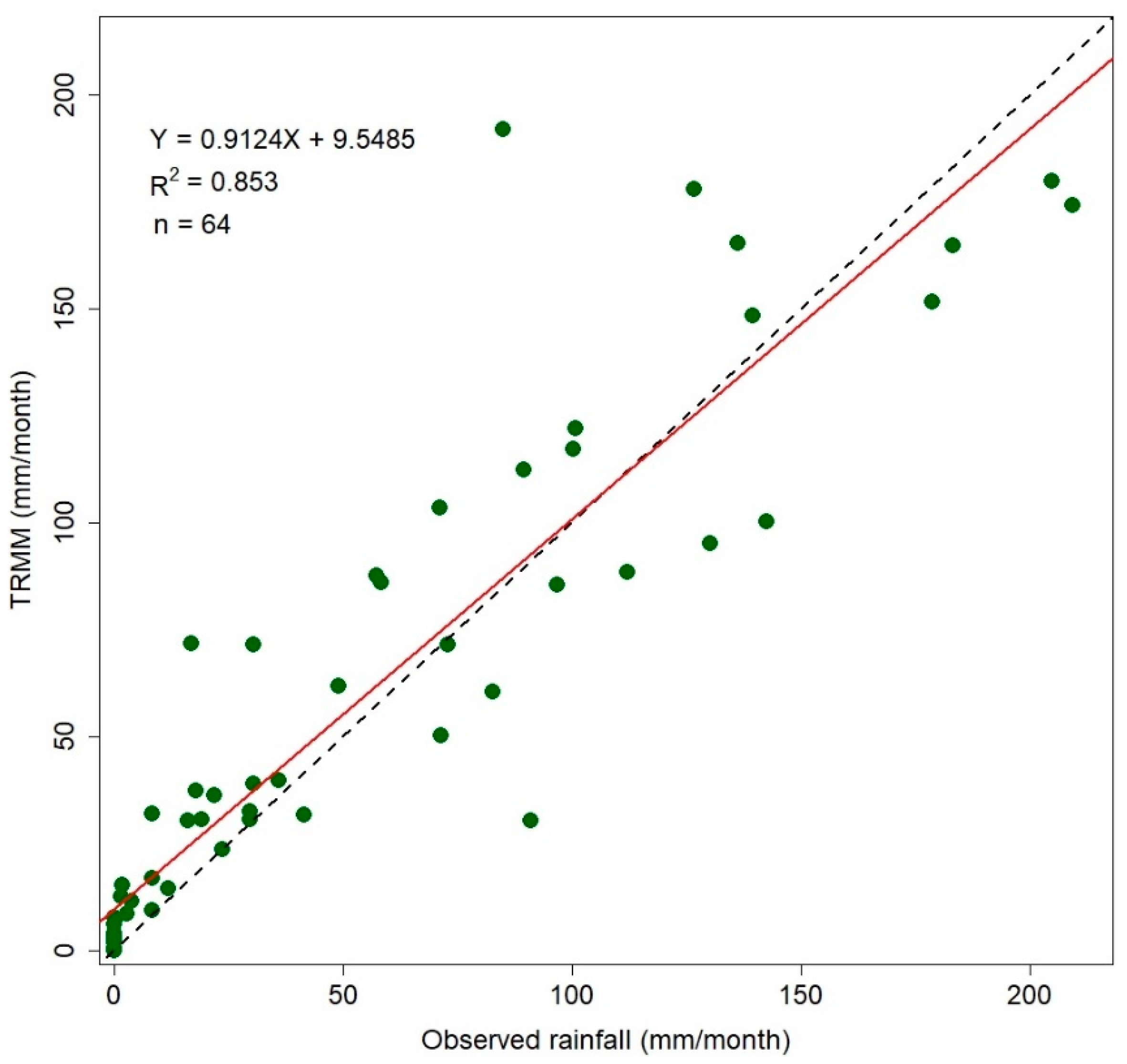
2.2. Data and Software
2.3. Hypsometric Integral (HI)
2.4. RUSLE Model Description
- AE is the actual erosion (yearly rate of the soil loss (t.ha−1.y−1));
- R rainfall and runoff erosivity factor (MJ.mm.ha−1.h−1.y−1);
- K, soil erodibility factor (t.ha.h.ha−1.MJ−1.mm−1);
- LS, the slope length and slope steepness factor;
- C, the cover management factor;
- P, the support practice factor;
- LS, C, and P factors are dimensionless.
2.4.1. Rainfall and Runoff Erosivity (R factor)
2.4.2. Soil Erodibility (K) Factor
2.4.3. Slope Length and Slope-Steepness Factor (LS factor)
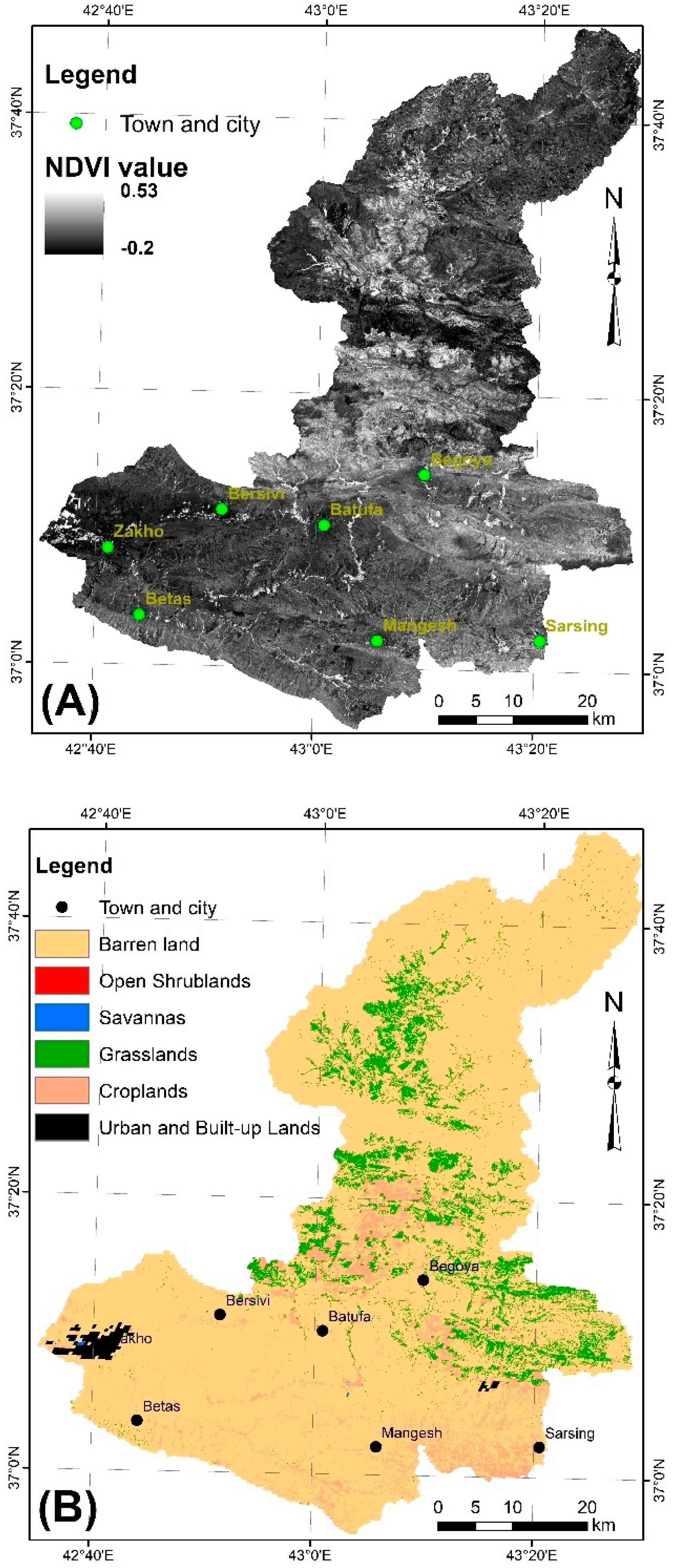
2.4.4. Cover and Management Factor (C factor)
2.4.5. Support Practice Factor Related to Slope Direction (P)
2.5. Sediment Yield (SY)
2.6. Work Procedure
3. Results
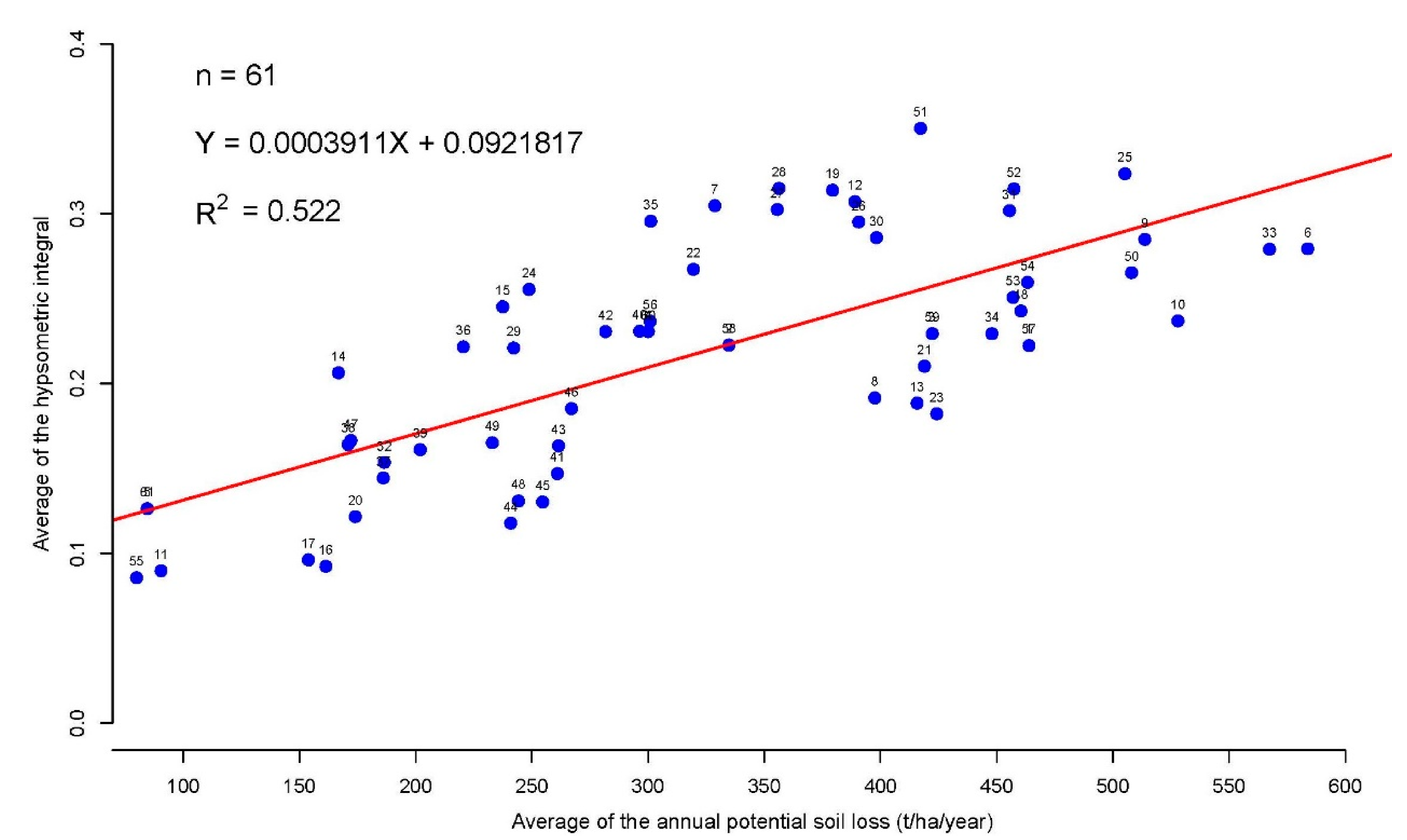
3.1. The Hypsometric Integral (HI)
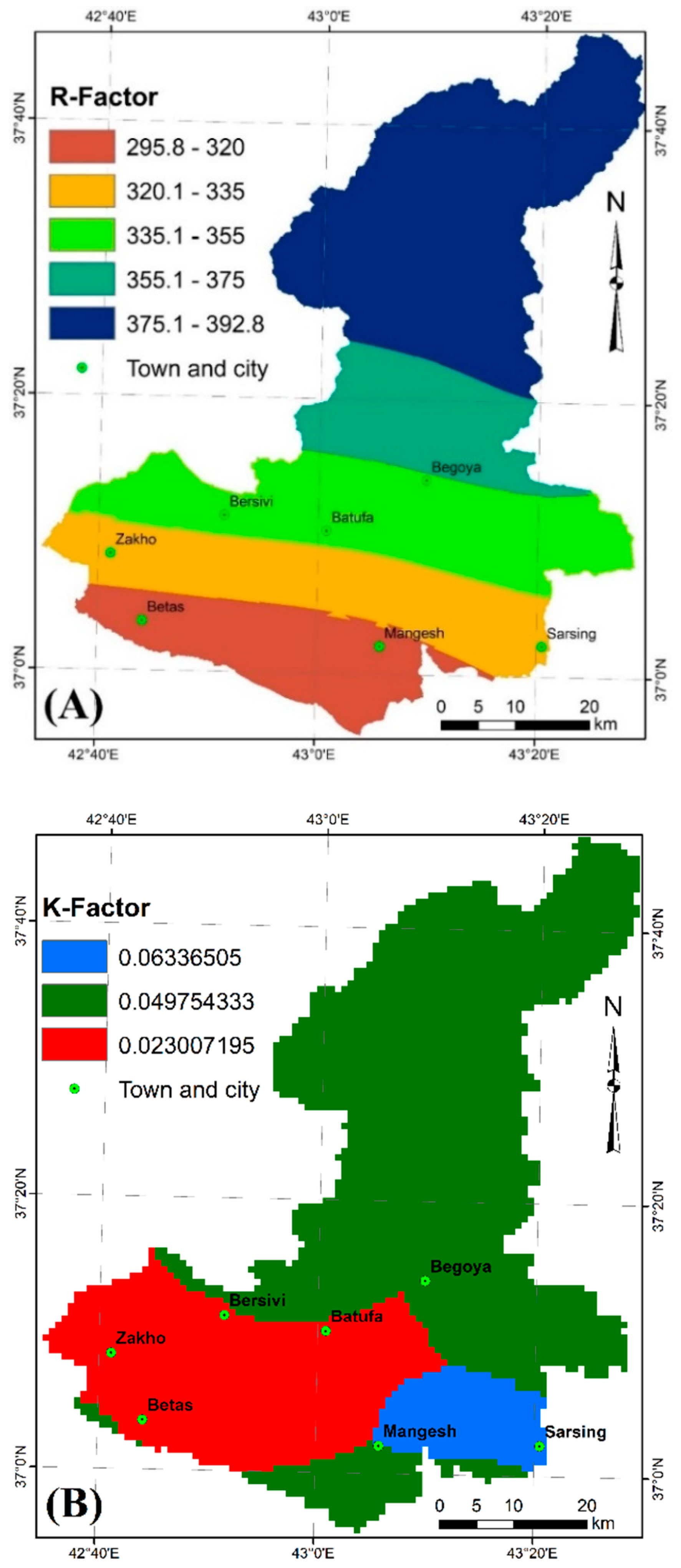
3.2. The R Factor
3.3. K Factor
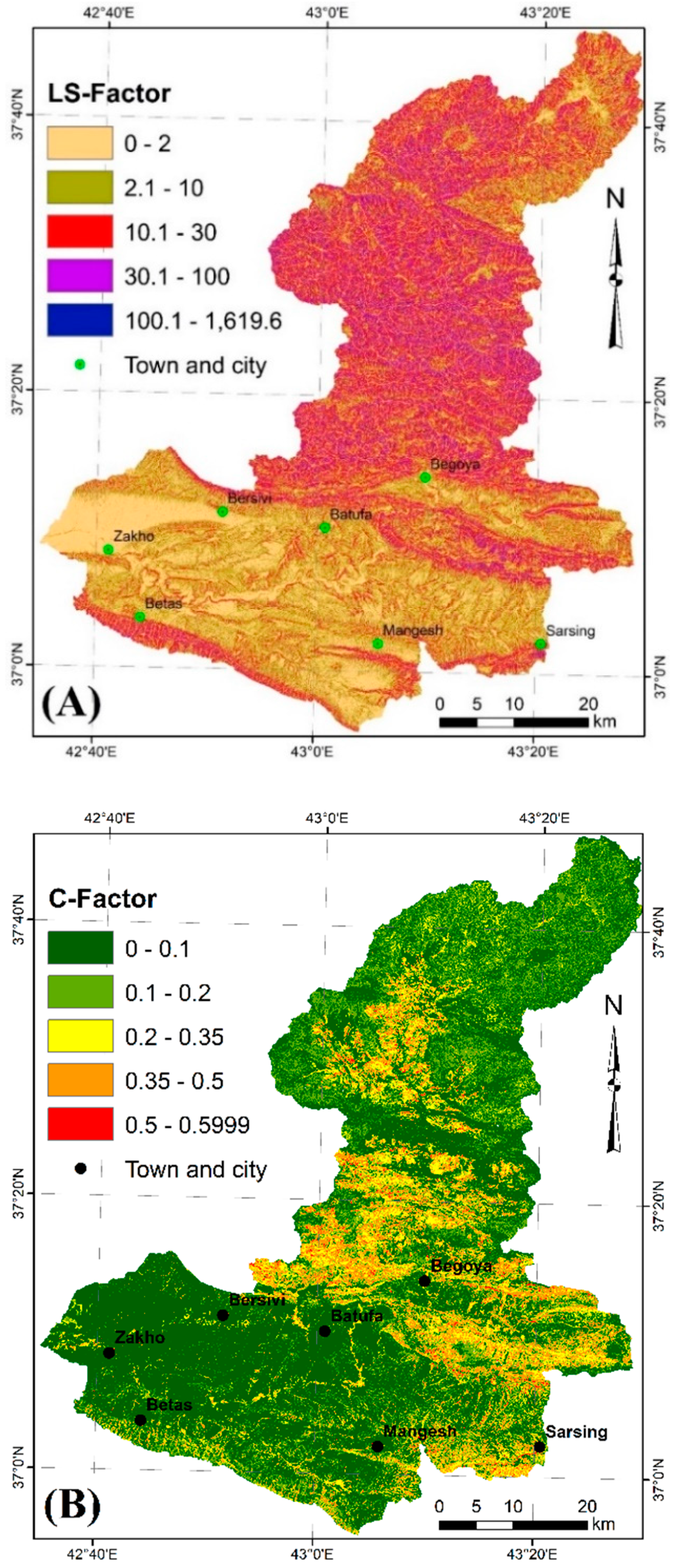
3.4. The LS Factor
3.5. The C Factor
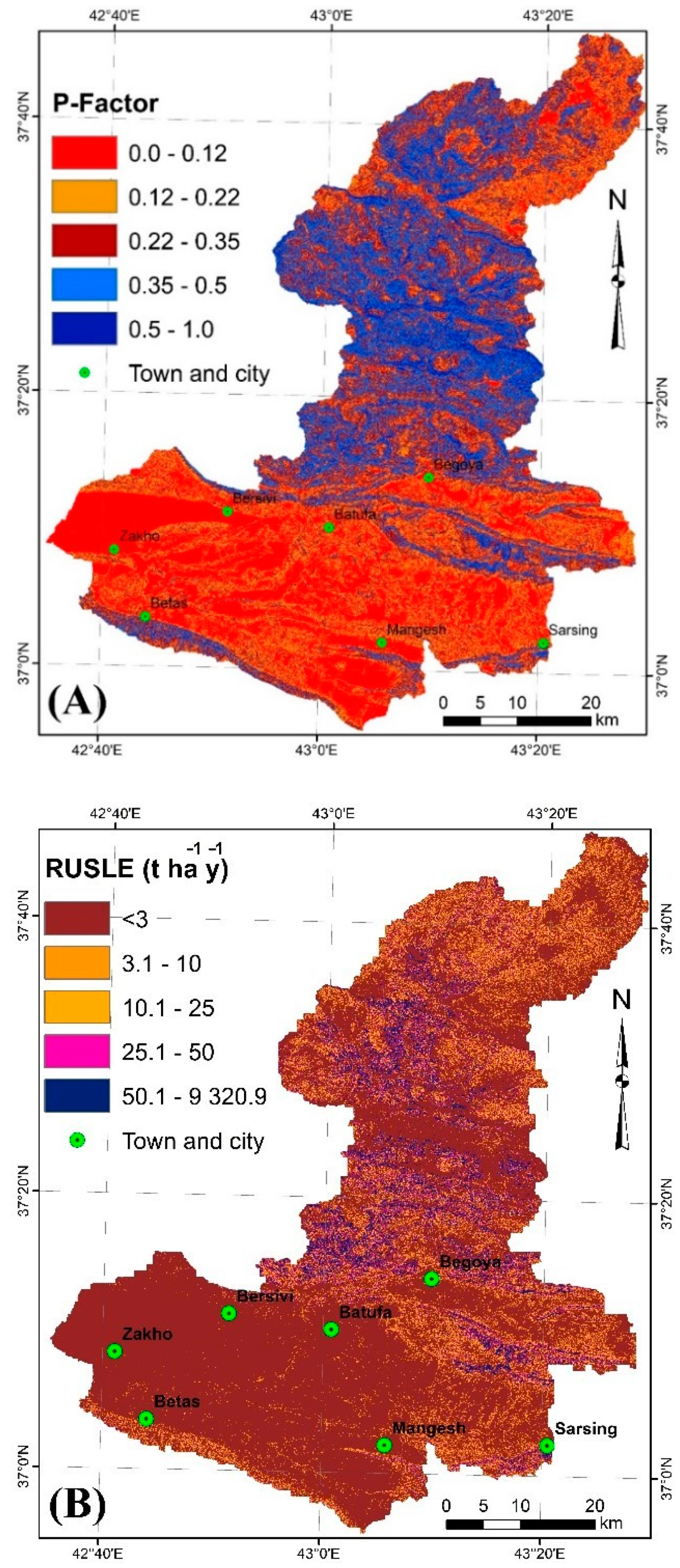
3.6. The P Factor
3.7. Estimation of Soil Loss
3.8. Relationship of PE to RUSLE and the HI
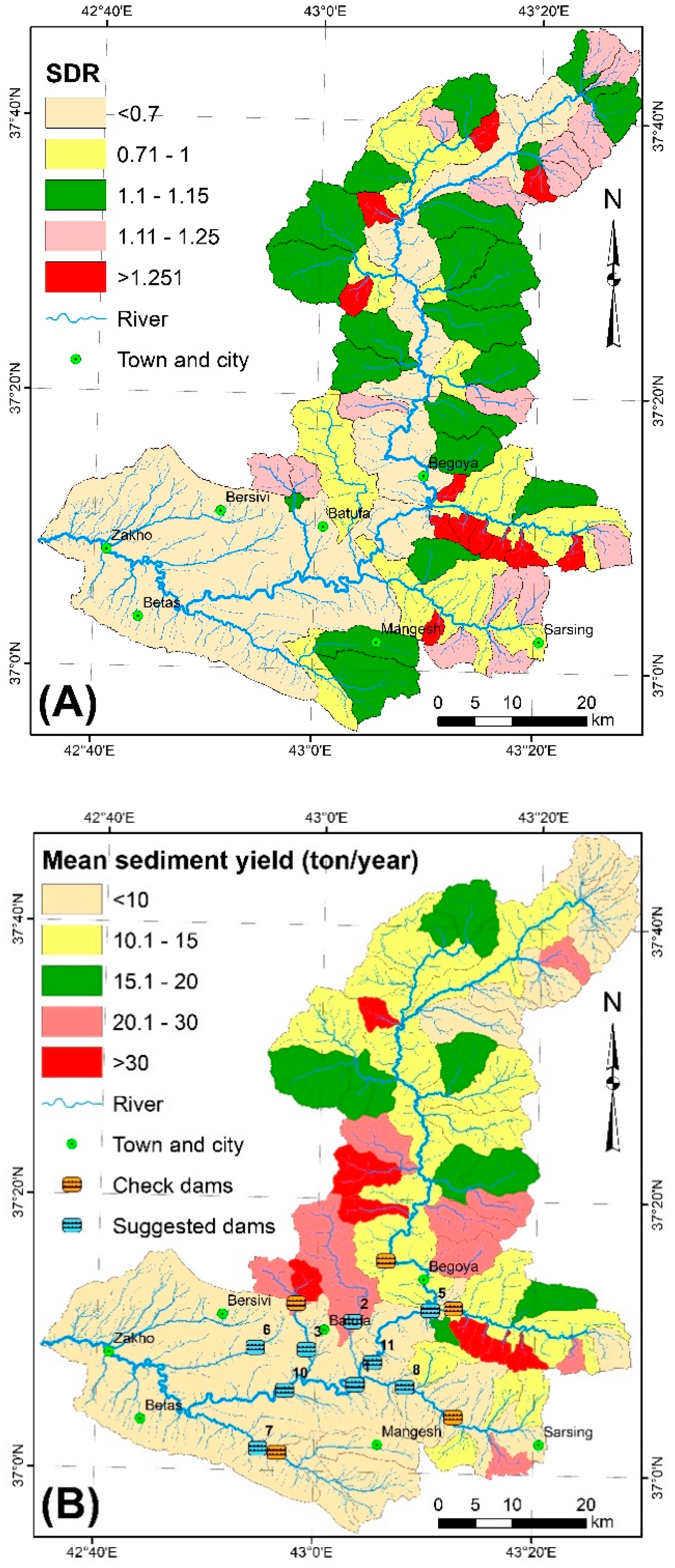
3.9. Estimation the Sediment Yield
4. Discussion
Estimation of the Dam Siltation in the KhRB
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- García-Ruiz, J.M.; Beguería, S.; Nadal-Romero, E.; González-Hidalgo, J.C.; Lana-Renault, N.; Sanjuán, Y. A meta-analysis of soil erosion rates across the world. Geomorphology 2015, 239, 160–173. [Google Scholar] [CrossRef]
- Pimentel, D.; Terhune, E.C.; Dyson-Hudson, R.; Rochereau, S.; Samis, R.; Smith, E.A.; Denman, D.; Reifschneider, D.; Shepard, M. Land degradation: Effects on food and energy resources. Science 1976, 194, 149–155. [Google Scholar] [CrossRef] [PubMed]
- Othman, A.A. Improving Remote Sensing Based Landslide Investigations and Lithological Mapping Using Morphological Features: A Case Study in NE-Iraq and W-Iran; Technische Universität Bergakademie: Freiberg, Germany, 2015. [Google Scholar]
- Kuzucuoğlu, C.; Çiner, A.; Kazancı, N. (Eds.) The Geomorphological Regions of Turkey BT. In Landscapes and Landforms of Turkey; Springer International Publishing: Cham, Switzerland, 2019; pp. 41–178. ISBN 978-3-030-03515-0. [Google Scholar]
- Carretier, S.; Regard, V.; Vassallo, R.; Aguilar, G.; Martinod, J.; Riquelme, R.; Pepin, E.; Charrier, R.; Hérail, G.; Farías, M.; et al. Slope and climate variability control of erosion in the Andes of central Chile. Geology 2013, 41, 195–198. [Google Scholar] [CrossRef]
- Al-Saady, Y.; Al-Suhail, Q.; Al-Tawash, B.; Othman, A. Drainage network extraction and morphometric analysis using remote sensing and GIS mapping techniques (Lesser Zab River Basin, Iraq and Iran). Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
- Othman, A.A.; Al-Maamar, A.F.; Al-Manmi, D.A.M.; Liesenberg, V.; Hasan, S.; Al-Saady, Y.I.; Shihab, A.T.; Khwedim, K. Application of DInSAR-PSI Technology for Deformation Monitoring of the Mosul Dam, Iraq. Remote Sens. 2019, 11, 2632. [Google Scholar] [CrossRef]
- Thornes, J.B. Modelling Soil Erosion by Grazing: Recent Developments and New Approaches. Geogr. Res. 2007, 45, 13–26. [Google Scholar] [CrossRef]
- Obaid, A.K.; Allen, M.B. Landscape expressions of tectonics in the Zagros fold-and-thrust belt. Tectonophysics 2019. [Google Scholar] [CrossRef]
- Allen, M.B.; Talebian, M. Structural variation along the Zagros and the nature of the Dezful Embayment. Geol. Mag. 2011, 148, 911–924. [Google Scholar] [CrossRef]
- Langbein, W.B. Topographic Characteristics of Drainage Basins; US Department of Interior: Tulsa, OK, USA, 1947. [Google Scholar]
- Strahler, A.N. Hypsometric (area-altitude) analysis of erosional topography. Geol. Soc. Am. Bull. 1952, 63, 1117–1142. [Google Scholar] [CrossRef]
- Schumm, S.A. Evolution of drainage systems and slopes in badlands at Perth Amboy, New Jersey. Geol. Soc. Am. Bull. 1956, 67, 597–646. [Google Scholar] [CrossRef]
- Keller, E.A.; Pinter, N. Active Tectonics: Earthquakes, Uplift, and Landscape; Prentice Hall: Upper Saddle River, NJ, USA, 2002. [Google Scholar]
- Li, L.; Du, S.; Wu, L.; Liu, G. An overview of soil loss tolerance. Catena 2009, 78, 93–99. [Google Scholar] [CrossRef]
- Montanarella, L.; Pennock, D.; McKenzie, N.; Badraoui, M.; Chude, V.; Baptista, I.; Mamo, T.; Yemefack, M.; Aulakh, M.; Yagi, K.; et al. World’s soils are under threat. Soil 2016, 2. [Google Scholar] [CrossRef]
- Blanco-Canqui, H.; Lal, R. Principles of Soil Conservation and Management; Springer: Dordrecht, The Netherlands, 2008; ISBN 9781402087097. [Google Scholar]
- Toy, T.J.; Foster, G.R.; Renard, K.G. Soil Erosion: Processes, Prediction, Measurement, and Control; Wiley: Hoboken, NJ, USA, 2002; ISBN 9780471383697. [Google Scholar]
- Laflen, J.M.; Lane, L.J.; Foster, G.R. WEPP: A new generation of erosion prediction technology. J. Soil Water Conserv. 1991, 46, 34–38. [Google Scholar]
- Yu, B.; Rose, C.W.; Ciesiolka, C.A.A.; Coughlan, K.J.; Fentie, B. Toward a framework for runoff and soil loss prediction using GUEST technology. Soil Res. 1997, 35, 1191–1212. [Google Scholar] [CrossRef]
- Viney, N.R.; Sivapalan, M. A conceptual model of sediment transport: Application to the Avon River Basin in Western Australia. Hydrol. Process. 1999, 13, 727–743. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall Erosion Losses: A Guide to Conservation Planning; Science and Education Administration, US Department of Agriculture: Washington, DC, USA, 1978.
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; McCool, D.K.; Yoder, D.C. Predicting Soil Erosion by Water: A Guide to Conservation Planning with the Revised Universal Soil Loss Equation (RUSLE); United States Department of Agriculture: Washington, DC, USA, 1997; Volume 703.
- Nearing, M.A.; Yin, S.; Borrelli, P.; Polyakov, V.O. Rainfall erosivity: An historical review. Catena 2017, 157, 357–362. [Google Scholar] [CrossRef]
- Nearing, M.A.; Govers, G.; Norton, L.D. Variability in Soil Erosion Data from Replicated Plots. Soil Sci. Soc. Am. J. 1999, 63, 1829–1835. [Google Scholar] [CrossRef]
- Boardman, J. Soil erosion science: Reflections on the limitations of current approaches. Catena 2006, 68, 73–86. [Google Scholar] [CrossRef]
- Qiwei, C.; Kangning, X.; Rong, Z. Assessment on erosion risk based on GIS in typical Karst region of Southwest China. Eur. J. Remote Sens. 2020, 1–12. [Google Scholar] [CrossRef]
- Gianinetto, M.; Aiello, M.; Polinelli, F.; Frassy, F.; Rulli, M.C.; Ravazzani, G.; Bocchiola, D.; Chiarelli, D.D.; Soncini, A.; Vezzoli, R. D-RUSLE: A dynamic model to estimate potential soil erosion with satellite time series in the Italian Alps. Eur. J. Remote Sens. 2019, 52, 34–53. [Google Scholar] [CrossRef]
- Saygın, S.D.; Ozcan, A.U.; Basaran, M.; Timur, O.B.; Dolarslan, M.; Yılman, F.E.; Erpul, G. The combined RUSLE/SDR approach integrated with GIS and geostatistics to estimate annual sediment flux rates in the semi-arid catchment, Turkey. Environ. Earth Sci. 2014, 71, 1605–1618. [Google Scholar] [CrossRef]
- Phinzi, K.; Ngetar, N.S. The assessment of water-borne erosion at catchment level using GIS-based RUSLE and remote sensing: A review. Int. Soil Water Conserv. Res. 2019, 7, 27–46. [Google Scholar] [CrossRef]
- Ganasri, B.P.; Ramesh, H. Assessment of soil erosion by RUSLE model using remote sensing and GIS—A case study of Nethravathi Basin. Geosci. Front. 2016, 7, 953–961. [Google Scholar] [CrossRef]
- Thomas, J.; Joseph, S.; Thrivikramji, K.P. Assessment of soil erosion in a tropical mountain river basin of the southern Western Ghats, India using RUSLE and GIS. Geosci. Front. 2018, 9, 893–906. [Google Scholar] [CrossRef]
- Terranova, O.; Antronico, L.; Coscarelli, R.; Iaquinta, P. Soil erosion risk scenarios in the Mediterranean environment using RUSLE and GIS: An application model for Calabria (southern Italy). Geomorphology 2009, 112, 228–245. [Google Scholar] [CrossRef]
- Nasir, N.; Selvakumar, R. Influence of land use changes on spatial erosion pattern, a time series analysis using RUSLE and GIS: The cases of Ambuliyar sub-basin, India. Acta Geophys. 2018, 66, 1121–1130. [Google Scholar] [CrossRef]
- Farhan, Y.; Zregat, D.D.; Farhan, I. Spatial Estimation of Soil Erosion Risk Using RUSLE Approach, RS, and GIS Techniques: A Case Study of Kufranja Watershed, Northern Jordan. J. Water Resour. Prot. 2013, 5, 1247–1261. [Google Scholar] [CrossRef]
- Zerihun, M.; Mohammedyasin, M.S.; Sewnet, D.; Adem, A.A.; Lakew, M. Assessment of soil erosion using RUSLE, GIS and remote sensing in NW Ethiopia. Geoderma Reg. 2018, 12, 83–90. [Google Scholar] [CrossRef]
- Fu, B.J.; Zhao, W.W.; Chen, L.D.; Zhang, Q.J.; Lü, Y.H.; Gulinck, H.; Poesen, J. Assessment of soil erosion at large watershed scale using RUSLE and GIS: A case study in the Loess Plateau of China. Land Degrad. Dev. 2005, 16, 73–85. [Google Scholar] [CrossRef]
- Bircher, P.; Liniger, H.P.; Prasuhn, V. Comparing different multiple flow algorithms to calculate RUSLE factors of slope length (L) and slope steepness (S) in Switzerland. Geomorphology 2019, 346, 106850. [Google Scholar] [CrossRef]
- Ghosal, K.; Das Bhattacharya, S. A Review of RUSLE Model. J. Indian Soc. Remote Sens. 2020, 48, 689–707. [Google Scholar] [CrossRef]
- Chen, T.; Niu, R.; Li, P.; Zhang, L.; Du, B. Regional soil erosion risk mapping using RUSLE, GIS, and remote sensing: A case study in Miyun Watershed, North China. Environ. Earth Sci. 2011, 63, 533–541. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; Porter, J.P. RUSLE: Revised universal soil loss equation. J. Soil Water Conserv. 1991, 46, 30–33. [Google Scholar]
- Chuenchum, P.; Xu, M.; Tang, W. Estimation of Soil Erosion and Sediment Yield in the Lancang–Mekong River Using the Modified Revised Universal Soil Loss Equation and GIS Techniques. Water 2020, 12, 135. [Google Scholar] [CrossRef]
- Samad, N.; Hamid, M.; Muhammad, C.; Saleem, M.; Hamid, Q.; Babar, U.; Tariq, H.; Farid, M.S. Sediment yield assessment and identification of check dam sites for Rawal Dam catchment. Arab. J. Geosci. 2016, 9, 1–14. [Google Scholar] [CrossRef]
- Dutta, S. Soil erosion, sediment yield and sedimentation of reservoir: A review. Model. Earth Syst. Environ. 2016, 2, 1–18. [Google Scholar] [CrossRef]
- Bagherzadeh, A.; Daneshvar, M.R.M. Evaluation of sediment yield and soil loss by the MPSIAC model using GIS at Golestan watershed, northeast of Iran. Arab. J. Geosci. 2013, 6, 3349–3362. [Google Scholar] [CrossRef]
- Zhou, Q.; Yang, S.; Zhao, C.; Cai, M.; Ya, L. A soil erosion assessment of the upper mekong river in yunnan province, China. Mt. Res. Dev. 2014, 34, 36–47. [Google Scholar] [CrossRef]
- Eroğlu, H.; Çakir, G.; Sivrikaya, F.; Akay, A.E. Using high resolution images and elevation data in classifying erosion risks of bare soil areas in the Hatila Valley Natural Protected Area, Turkey. Stoch. Environ. Res. Risk Assess. 2010, 24, 699–704. [Google Scholar] [CrossRef]
- Othman, A.A.; Al-Maamar, A.F.; Al-Manmi, D.A.M.; Veraldo, L.; Hasan, S.E.; Obaid, A.K.; Al-Quraishi, A.M.F. GIS-based modeling for selection of dam sites in the Kurdistan Region, Iraq. ISPRS Int. J. Geo-Inf. 2020, 9, 244. [Google Scholar] [CrossRef]
- Mehri, A.; Salmanmahiny, A.; Tabrizi, A.R.M.; Mirkarimi, S.H.; Sadoddin, A. Investigation of likely effects of land use planning on reduction of soil erosion rate in river basins: Case study of the Gharesoo River Basin. Catena 2018, 167, 116–129. [Google Scholar] [CrossRef]
- Ahmadi Mirghaed, F.; Souri, B.; Mohammadzadeh, M.; Salmanmahiny, A.; Mirkarimi, S.H. Evaluation of the relationship between soil erosion and landscape metrics across Gorgan Watershed in northern Iran. Environ. Monit. Assess. 2018, 190. [Google Scholar] [CrossRef] [PubMed]
- Sheikh, V.; Kornejady, A.; Ownegh, M. Application of the coupled TOPSIS–Mahalanobis distance for multi-hazard-based management of the target districts of the Golestan Province, Iran. Nat. Hazards 2019, 96, 1335–1365. [Google Scholar] [CrossRef]
- Zakeri, E.; Mousavi, S.A.; Karimzadeh, H. Scenario-based modelling of soil conservation function by rangeland vegetation cover in northeastern Iran. Environ. Earth Sci. 2020, 79. [Google Scholar] [CrossRef]
- Zare, M.; Nazari Samani, A.A.; Mohammady, M.; Teimurian, T.; Bazrafshan, J. Simulation of soil erosion under the influence of climate change scenarios. Environ. Earth Sci. 2016, 75. [Google Scholar] [CrossRef]
- Arekhi, S.; Niazi, Y.; Kalteh, A.M. Soil erosion and sediment yield modeling using RS and GIS techniques: A. case study, Iran. Arab. J. Geosci. 2012, 5, 285–296. [Google Scholar] [CrossRef]
- Ebrahimzadeh, S.; Motagh, M.; Mahboub, V.; Mirdar Harijani, F. An improved RUSLE/SDR model for the evaluation of soil erosion. Environ. Earth Sci. 2018, 77, 1–7. [Google Scholar] [CrossRef]
- Demirci, A.; Karaburun, A. Estimation of soil erosion using RUSLE in a GIS framework: A case study in the Buyukcekmece Lake watershed, northwest Turkey. Environ. Earth Sci. 2012, 66, 903–913. [Google Scholar] [CrossRef]
- Imamoglu, A.; Dengiz, O. Determination of soil erosion risk using RUSLE model and soil organic carbon loss in Alaca catchment (Central Black Sea region, Turkey). Rend. Lincei 2017, 28, 11–23. [Google Scholar] [CrossRef]
- Özalp, M.; Yüksel, E.E.; Yıldırımer, S. Subdividing large mountainous watersheds into smaller hydrological units to predict soil loss and sediment yield using the GeoWEPP model. Polish J. Environ. Stud. 2017, 26, 2135–2146. [Google Scholar] [CrossRef]
- Issa, I. Sedimentological and Hydrological Investigation of Mosul Dam Reservoir. Ph.D. Thesis, Lulea University of Technology, Luleå, Sweden, 2015. [Google Scholar]
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission—A new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- GSFC DAAC. Tropical Rainfall Measurement Mission Project (TRMM;3B43 V7). Available online: http://disc.gsfc.nasa.gov/datacollection/TRMM_3B42_daily_V6.shtml (accessed on 10 April 2020).
- Kummerow, C.; Barnes, W.; Kozu, T.; Shiue, J.; Simpson, J. The Tropical Rainfall Measuring Mission (TRMM) sensor package. J. Atmos. Ocean. Technol. 1998, 15, 809–817. [Google Scholar] [CrossRef]
- Nachtergaele, F.; Van Velthuizen, H.; Van Engelen, V.; Fischer, G.; Jones, A.; Montanarella, L.; Petri, M.; Prieler, S.; Teixeira, E.; Shi, X. Harmonized World Soil Database (Version 1.2); FAO: Rome, Italy; IIASA: Laxenburg, Austria, 2012; pp. 1–50. [Google Scholar]
- Akintorinwa, O.J.; Okoro, O. V Combine electrical resistivity method and multi-criteria GIS-based modeling for landfill site selection in the Southwestern Nigeria. Environ. Earth Sci. 2019, 78. [Google Scholar] [CrossRef]
- Shahzad, F.; Gloaguen, R. TecDEM: A MATLAB based toolbox for tectonic geomorphology, Part 2: Surface dynamics and basin analysis. Comput. Geosci. 2011, 37, 261–271. [Google Scholar] [CrossRef]
- Shahzad, F.; Gloaguen, R. TecDEM: A MATLAB based toolbox for tectonic geomorphology, Part 1: Drainage network preprocessing and stream profile analysis. Comput. Geosci. 2011, 37, 250–260. [Google Scholar] [CrossRef]
- ESRI (Environmental Systems Research Institute). ArcGIS Desktop: Release 10.3; ESRI: Redlands, CA, USA, 2015. [Google Scholar]
- Zhang, L.; Liang, S.; Yang, X.; Gan, W. Landscape evolution of the Eastern Himalayan Syntaxis based on basin hypsometry and modern crustal deformation. Geomorphology 2020, 355, 107085. [Google Scholar] [CrossRef]
- Pérez-Peña, J.V.; Azañón, J.M.; Azor, A. CalHypso: An ArcGIS extension to calculate hypsometric curves and their statistical moments. Applications to drainage basin analysis in SE Spain. Comput. Geosci. 2009, 35, 1214–1223. [Google Scholar] [CrossRef]
- Obaid, A.K.; Allen, M.B. Landscape maturity, fold growth sequence and structural style in the Kirkuk Embayment of the Zagros, northern Iraq. Tectonophysics 2017, 717, 27–40. [Google Scholar] [CrossRef]
- Othman, A.A.; Gloaguen, R. River Courses Affected by Landslides and Implications for Hazard Assessment: A High Resolution Remote Sensing Case Study in NE Iraq–W Iran. Remote Sens. 2013, 5, 1024–1044. [Google Scholar] [CrossRef]
- Othman, A.A.; Gloaguen, R.; Andreani, L.; Rahnama, M. Improving landslide susceptibility mapping using morphometric features in the Mawat area, Kurdistan Region, NE Iraq: Comparison of different statistical models. Geomorphology 2018, 319, 147–160. [Google Scholar] [CrossRef]
- Pike, R.J.; Wilson, S.E. Elevation-relief ratio, hypsometric integral, and geomorphic area-altitude analysis. Bull. Geol. Soc. Am. 1971, 82, 1079–1084. [Google Scholar] [CrossRef]
- Zeng, C.; Wang, S.; Bai, X.; Li, Y.; Tian, Y.; Li, Y.; Wu, L.; Luo, G. Soil erosion evolution and spatial correlation analysis in a typical karst geomorphology using RUSLE with GIS. Solid Earth 2017, 8, 721–736. [Google Scholar] [CrossRef]
- Kayet, N.; Pathak, K.; Chakrabarty, A.; Sahoo, S. Evaluation of soil loss estimation using the RUSLE model and SCS-CN method in hillslope mining areas. Int. Soil Water Conserv. Res. 2018, 6, 31–42. [Google Scholar] [CrossRef]
- Ma, X.; He, Y.; Xu, J.; Noordwijk, M.; Lu, X. Spatial and temporal variation in rainfall erosivity in a Himalayan watershed. Catena 2014, 121, 248–259. [Google Scholar] [CrossRef]
- Karan, S.K.; Ghosh, S.; Samadder, S.R. Identification of spatially distributed hotspots for soil loss and erosion potential in mining areas of Upper Damodar Basin—India. Catena 2019, 182, 104144. [Google Scholar] [CrossRef]
- Thomas, J. (Ed.) Frontispiece BT. In Nineteenth-Century Illustration and the Digital: Studies in Word and Image; Springer International Publishing: Cham, Switzerland, 2017; pp. 1–14. ISBN 978-3-319-58148-4. [Google Scholar]
- Panagos, P.; Meusburger, K.; Ballabio, C.; Borrelli, P.; Alewell, C. Soil erodibility in Europe: A high-resolution dataset based on LUCAS. Sci. Total Environ. 2014, 479, 189–200. [Google Scholar] [CrossRef]
- Kerven, G.L.; Menzies, N.W.; Geyer, M.D. Analytical methods and quality assurance. Commun. Soil Sci. Plant Anal. 2000, 31, 1935–1939. [Google Scholar] [CrossRef]
- Pribyl, D.W. A critical review of the conventional SOC to SOM conversion factor. Geoderma 2010, 156, 75–83. [Google Scholar] [CrossRef]
- Waksman, S.A.; Stevens, K.R. A critical study of the methods for determining the nature and abundance of soil organic matter. Soil Sci. 1930, 30, 97–116. [Google Scholar] [CrossRef]
- Desmet, P.J.J.; Govers, G. A GIS procedure for automatically calculating the USLE LS factor on topographically complex landscape units. J. Soil Water Conserv. 1996, 51, 427–433. [Google Scholar]
- Mitasova, H.; Hofierka, J.; Zlocha, M.; Iverson, L.R. Modelling topographic potential for erosion and deposition using GIS. Int. J. Geogr. Inf. Syst. 1996, 10, 629–641. [Google Scholar] [CrossRef]
- Moore, I.D.; Burch, G.J. Physical Basis of the Length-slope Factor in the Universal Soil Loss Equation1. Soil Sci. Soc. Am. J. 1986, 50, 1294–1298. [Google Scholar] [CrossRef]
- Wilson, J.P.; Gallant, J.C. Terrain Analysis: Principles and Applications; Wiley: Hoboken, NJ, USA, 2000; Volume 4, p. 479. [Google Scholar]
- Li, Y.; Qi, S.; Liang, B.; Ma, J.; Cheng, B.; Ma, C.; Qiu, Y.; Chen, Q. Dangerous degree forecast of soil loss on highway slopes in mountainous areas of the Yunnan–Guizhou Plateau (China) using the Revised Universal Soil Loss Equation. Nat. Hazards Earth Syst. Sci. 2019, 19, 757–774. [Google Scholar] [CrossRef]
- Pal, S.C.; Chakrabortty, R. Simulating the impact of climate change on soil erosion in sub-tropical monsoon dominated watershed based on RUSLE, SCS runoff and MIROC5 climatic model. Adv. Space Res. 2019, 64, 352–377. [Google Scholar] [CrossRef]
- Abrams, M.; Hook, S. ASTER User Handbook. Version 2; Jet Propulsion Laboratory/California Institute of Technology: Pasadena, CA, USA, 2002. [Google Scholar]
- Felde, G.W.; Anderson, G.P.; Cooley, T.W.; Matthew, M.W.; Adler-Golden, S.M.; Berk, A.; Lee, J. Analysis of Hyperion data with the FLAASH atmospheric correction algorithm. In 2003 IEEE International Geoscience and Remote Sensing Symposium; IEEE International: New York, NY, USA, 2003; Volume 1, pp. 90–92. [Google Scholar]
- Liesenberg, V.; Gloaguen, R. Evaluating SAR polarization modes at L-band for forest classification purposes in Eastern Amazon, Brazil. Int. J. Appl. Earth Obs. Geoinf. 2013, 21, 122–135. [Google Scholar] [CrossRef]
- Othman, A.A.; Gloaguen, R. Integration of spectral, spatial and morphometric data into lithological mapping: A comparison of different Machine Learning Algorithms in the Kurdistan Region, NE Iraq. J. Asian Earth Sci. 2017. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schelle, J.A.; Deering, D.W. Monitoring the Vernal Advancement or Retrogradation of Natural Vegetation; NASA/GSFC: Greenbelt, MD, USA, 1974.
- Chandramani, L.; Oinam, B. Soil Loss Assessment in Imphal River Watershed, Manipur, North-East India: A Spatio-Temporal Approach BT. In Advances in Water Resources Engineering and Management; Al Khaddar, R., Singh, R.K., Dutta, S., Kumari, M., Eds.; Springer: Singapore, 2020; pp. 81–101. [Google Scholar]
- Durigon, V.L.; Carvalho, D.F.; Antunes, M.A.H.; Oliveira, P.T.S.; Fernandes, M.M. NDVI time series for monitoring RUSLE cover management factor in a tropical watershed. Int. J. Remote Sens. 2014, 35, 441–453. [Google Scholar] [CrossRef]
- Nyesheja, E.M.; Chen, X.; El-Tantawi, A.M.; Karamage, F.; Mupenzi, C.; Nsengiyumva, J.B. Soil erosion assessment using RUSLE model in the Congo Nile Ridge region of Rwanda. Phys. Geogr. 2019, 40, 339–360. [Google Scholar] [CrossRef]
- Prasannakumar, V.; Vijith, H.; Abinod, S.; Geetha, N. Estimation of soil erosion risk within a small mountainous sub-watershed in Kerala, India, using Revised Universal Soil Loss Equation (RUSLE) and geo-information technology. Geosci. Front. 2012, 3, 209–215. [Google Scholar] [CrossRef]
- Lufafa, A.; Tenywa, M.M.; Isabirye, M.; Majaliwa, M.J.G.; Woomer, P.L. Prediction of soil erosion in a Lake Victoria basin catchment using a GIS-based Universal Soil Loss model. Agric. Syst. 2003, 76, 883–894. [Google Scholar] [CrossRef]
- Sharda, V.N.; Ojasvi, P.R. A revised soil erosion budget for India: Role of reservoir sedimentation and land-use protection measures. Earth Surf. Process. Landforms 2016, 41, 2007–2023. [Google Scholar] [CrossRef]
- Jenks, G.F. The Data Model Concept in Statistical Mapping. Int. Yearb. Cartogr. 1967, 7, 186–190. [Google Scholar]
- Sulla-Menashe, D.; Friedl, M.A. User Guide to Collection 6 MODIS Land Cover (MCD12Q1 and MCD12C1) Product; NASA EOSDIS Land Processes DAAC: Sioux Falls, SD, USA, 2018.
- Bouguerra, H.; Bouanani, A.; Khanchoul, K.; Derdous, O.; Tachi, S.E. Mapping erosion prone areas in the Bouhamdane watershed (Algeria) using the Revised Universal Soil Loss Equation through GIS. J. Water L. Dev. 2017, 32, 13–23. [Google Scholar] [CrossRef]
- Kumar, S.; Kushwaha, S.P.S. Modelling soil erosion risk based on RUSLE-3D using GIS in a Shivalik sub-watershed. J. Earth Syst. Sci. 2013, 122, 389–398. [Google Scholar] [CrossRef]
- Renard, K.G.; Yoder, D.C.; Lightle, D.T.; Dabney, S.M. Universal Soil Loss Equation and Revised Universal Soil Loss Equation. Handb. Eros. Model. 2011, 135–167. [Google Scholar] [CrossRef]
- Toy, T.J.; Foster, G.R.; Renard, K.G. RUSLE for mining, construction and reclamation lands. J. Soil Water Conserv. 1999, 54, 462–467. [Google Scholar]
- Olorunfemi, I.E.; Komolafe, A.A.; Fasinmirin, J.T.; Olufayo, A.A.; Akande, S.O. A GIS-based assessment of the potential soil erosion and flood hazard zones in Ekiti State, Southwestern Nigeria using integrated RUSLE and HAND models. Catena 2020, 194, 104725. [Google Scholar] [CrossRef]
- Alexakis, D.D.; Hadjimitsis, D.G.; Agapiou, A. Integrated use of remote sensing, GIS and precipitation data for the assessment of soil erosion rate in the catchment area of “Yialias” in Cyprus. Atmos. Res. 2013, 131, 108–124. [Google Scholar] [CrossRef]
- Assouline, S.; Ben-Hur, M. Effects of rainfall intensity and slope gradient on the dynamics of interrill erosion during soil surface sealing. Catena 2006, 66, 211–220. [Google Scholar] [CrossRef]
- Al-Ruzouq, R.; Shanableh, A.; Yilmaz, A.; Idris, A.; Mukherjee, S.; Khalil, M.; Barakat, M.; Gibril, M.B.A. Dam Site Suitability Mapping and Analysis Using an Integrated GIS and Machine Learning Approach. Water 2019, 11, 1880. [Google Scholar] [CrossRef]
- Mohammed, A.; Pradhan, B.; Mahmood, Q. Dam site suitability assessment at the Greater Zab River in northern Iraq using remote sensing data and GIS. J. Hydrol. 2019, 574, 964–979. [Google Scholar] [CrossRef]
- Ramakrishnan, D.; Bandyopadhyay, A.; Kusuma, K.N. SCS-CN and GIS-based approach for identifying potential water harvesting sites in the Kali Watershed, Mahi River Basin, India. J. Earth Syst. Sci. 2009, 118, 355–368. [Google Scholar] [CrossRef]

| Date | ID | Quality | Cloud Cover |
|---|---|---|---|
| 23 June 2019 | LC08_L1TP_170034_20190623_20200827_02_T1 | 9 | 0.55% |
| 26 August 2019 | LC08_L1TP_170034_20190826_20200826_02_T1 | 9 | 0.02% |
| 27 October 2019 | LC08_L1TP_170034_20191013_20200825_02_T1 | 9 | 0.05% |
| 16 December 2019 | LC08_L1TP_170034_20191216_20201023_02_T1 | 9 | 12.40% |
| Structure Class (s) | Soil Database |
|---|---|
| 1 (very fine granular: 1–2 mm) | G (good) |
| 2 (fine granular: 2–5 mm) | N (normal) |
| 3 (medium or coarse granular: 5–10 mm) | P (poor) |
| 4 (blocky, platy or massive: >10 mm) | H (peaty top soil) |
| Permeability Class (p) | Texture | Saturated Hydraulic Conductivity, mm h−1 |
|---|---|---|
| 1 (fast and very fast) | Sand | >61.0 |
| 2 (moderate fast) | Loamy sand, sandy loam | 20.3–61.0 |
| 3 (moderate) | Loam, silty loam | 5.1–20.3 |
| 4 (moderate low) | Sandy clay loam, clay loam | 2.0–5.1 |
| 5 (slow) | Silty clay loam, sand clay | 1.0–2.0 |
| 6 (very slow) | Silty clay, clay | >1.0 |
| Type of Soil | Texture Class | Sand% | Silt% | Clay% | OC% | OM | K Factor |
|---|---|---|---|---|---|---|---|
| Lithosols | Loam | 43 | 34 | 23 | 1.4 | 2.4136 | 0.049754 |
| Calcic Xerosols | Clay loam | 40 | 37 | 23 | 0.56 | 0.96544 | 0.063365 |
| Chromic Vertisols | Clay | 16 | 29 | 55 | 0.75 | 1.293 | 0.023007 |
| Dam No. | Dam Width (m) | Lake Area (km2) | Volume (m3) | Basin Area (km2) | Soil Loss (m3) | X-Coordinate | Y-Coordinate | Nv |
|---|---|---|---|---|---|---|---|---|
| 1 | 1109.9 | 8.61 | 226,654,026 | 2420.5 | 336,547,265.4 | 43.061066 | 37.10736 | 8 |
| 2 | 509.6 | 1.31 | 37,026,508 | 103.8 | 18,905,137.1 | 43.05568 | 37.18427 | 1 |
| 3 | 850.0 | 2.35 | 53,640,739 | 74.3 | 7,383,939.5 | 42.98572 | 37.14923 | 4 |
| 5 | 667.0 | 5.34 | 421,706,403 | 266.9 | 21,822,711.4 | 43.208654 | 37.20219 | 2 |
| 6 | 443.0 | 0.46 | 5,769,178 | 26.3 | 458,963.8 | 42.907832 | 37.15043 | 0 |
| 7 | 817.0 | 4.39 | 191,423,581 | 219.9 | 4,950,075.4 | 42.914868 | 37.02736 | 1 |
| 8 | 1367.0 | 14.86 | 1,182,091,212 | 276.9 | 13,890,242.6 | 43.136919 | 37.10535 | 0 |
| 10 | 372.0 | 1. 60 | 55,823,171 | 35.6 | 301,711.7 | 42.953957 | 37.09876 | 0 |
| 11 | 737.0 | 6.04 | 199,256,701 | 1963.5 | 313,212,044.7 | 43.08669 | 37.13489 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Othman, A.A.; Obaid, A.K.; Al-Manmi, D.A.M.A.; Al-Maamar, A.F.; Hasan, S.E.; Liesenberg, V.; Shihab, A.T.; Al-Saady, Y.I. New Insight on Soil Loss Estimation in the Northwestern Region of the Zagros Fold and Thrust Belt. ISPRS Int. J. Geo-Inf. 2021, 10, 59. https://doi.org/10.3390/ijgi10020059
Othman AA, Obaid AK, Al-Manmi DAMA, Al-Maamar AF, Hasan SE, Liesenberg V, Shihab AT, Al-Saady YI. New Insight on Soil Loss Estimation in the Northwestern Region of the Zagros Fold and Thrust Belt. ISPRS International Journal of Geo-Information. 2021; 10(2):59. https://doi.org/10.3390/ijgi10020059
Chicago/Turabian StyleOthman, Arsalan Ahmed, Ahmed K. Obaid, Diary Ali Mohammed Amin Al-Manmi, Ahmed F. Al-Maamar, Syed E. Hasan, Veraldo Liesenberg, Ahmed T. Shihab, and Younus I. Al-Saady. 2021. "New Insight on Soil Loss Estimation in the Northwestern Region of the Zagros Fold and Thrust Belt" ISPRS International Journal of Geo-Information 10, no. 2: 59. https://doi.org/10.3390/ijgi10020059
APA StyleOthman, A. A., Obaid, A. K., Al-Manmi, D. A. M. A., Al-Maamar, A. F., Hasan, S. E., Liesenberg, V., Shihab, A. T., & Al-Saady, Y. I. (2021). New Insight on Soil Loss Estimation in the Northwestern Region of the Zagros Fold and Thrust Belt. ISPRS International Journal of Geo-Information, 10(2), 59. https://doi.org/10.3390/ijgi10020059






