An Analysis of Joint Assembly Geometric Errors Affecting End-Effector for Six-Axis Robots
Abstract
1. Introduction
2. Mathematic Error Model of Industrial Robots
2.1. Robot Kinematic Model
2.2. Geometric Error Model
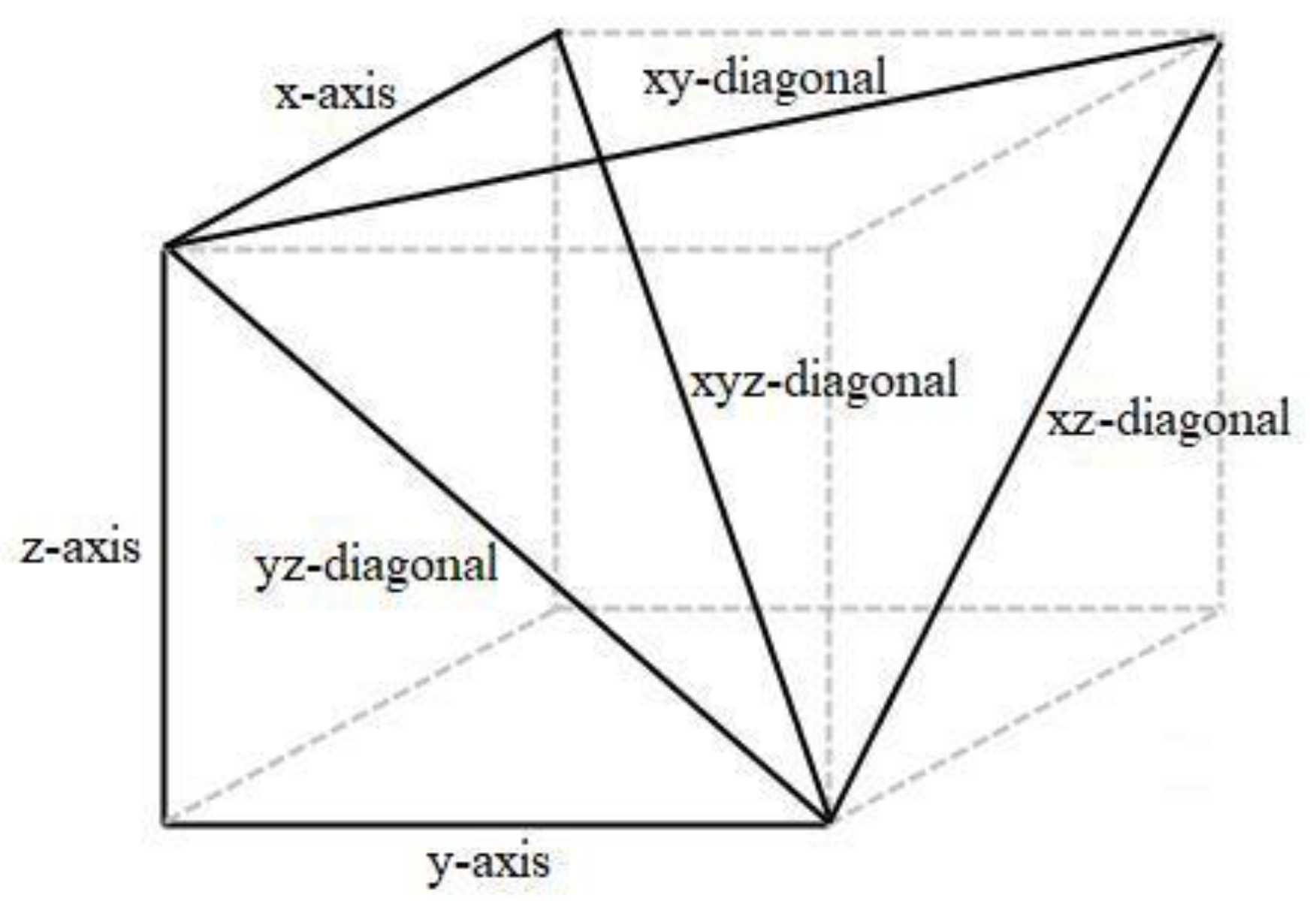
2.3. Tolerancing Analysis
3. Experimental and Analysis
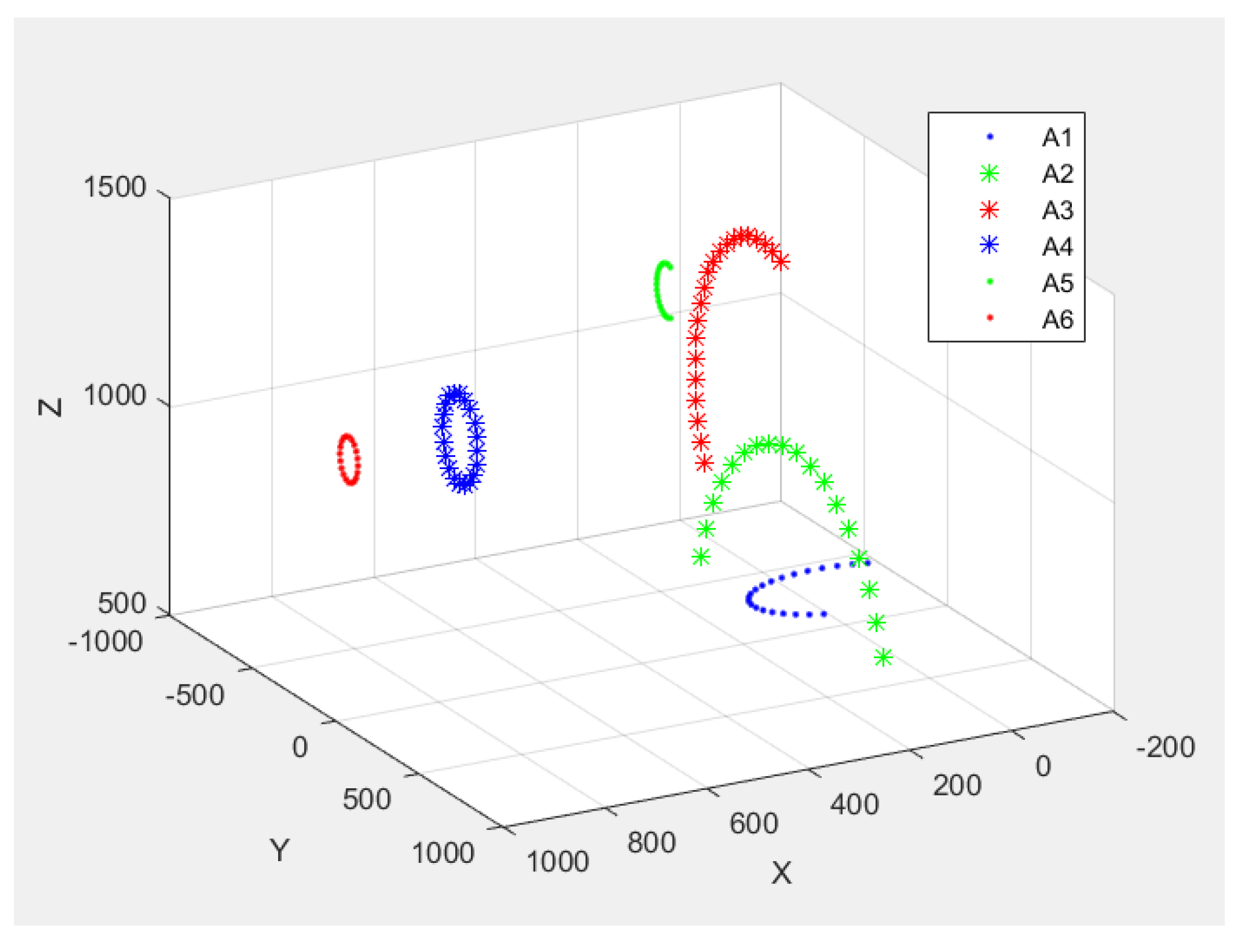
3.1. Experimental Setup
3.2. Experimental Data Analysis
- 2.
- Using the Rodrigues rotation to project the mean center point onto the fitting plane in new 2D coordinates [28].
- 3.
- Using the method of the least mean squares, fit a circle in the new 2D coordinates and get the circle center. The circle’s equation in 2D for a circle with center can be written aswhere the vector for unknown parameters. Applied to all points, it yields to a system of liner equations , where
- 4.
- Transform the circle center back to 3D coordinates by the Rodrigues rotation, as in step (2), but the angle in this step is measured from the new 2D normal vector to the original 3D normal vector, and vector k is the axis of the rotation vector as a cross product between the 2D normal vector and the 3D normal vector. Thus, .
4. Results of the Experiment
4.1. Geometric Error Calculated
4.2. A Comparison of Kinematic Model Calculation and Real Measurement
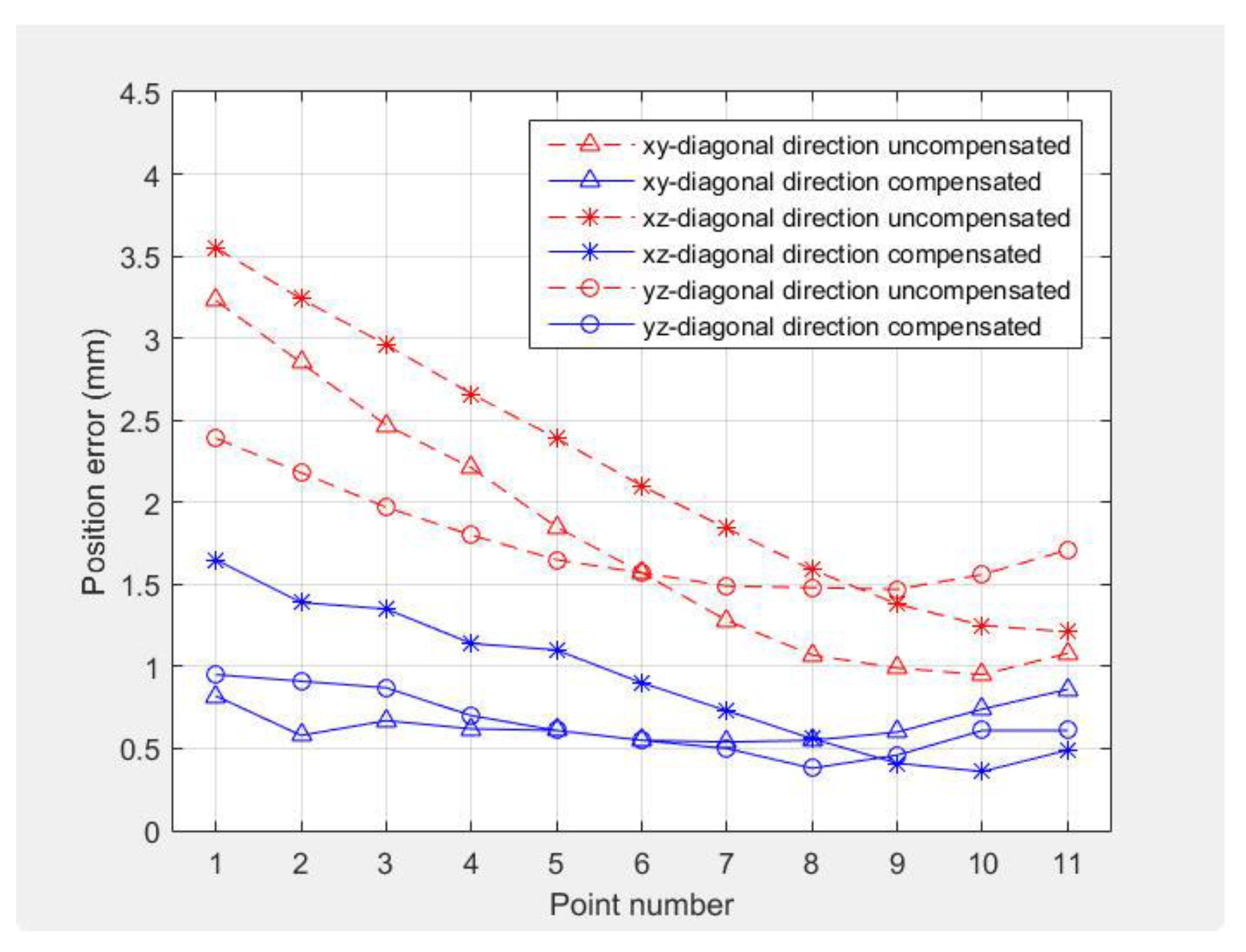
4.3. Tolerancing of Geometric Errors
4.4. Kinematic Error Compensation
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gong, C.; Yuan, J.; Ni, J. Nongeometric error identification and compensation for robotic system by inverse calibration. Int. J. Mach. Tools Manuf. 2000, 40, 2119–2137. [Google Scholar] [CrossRef]
- Meggiolaro, M.A.; Dubowsky, A.; Mavroidis, C. Geometric and elastic error calibration of a high accuracy patient positioning system. Mech. Mach. Theory 2005, 40, 415–427. [Google Scholar] [CrossRef]
- Jang, J.H.; Kim, S.H.; Kwak, Y.K. Calibration of geometric and non-geometric errors of an industrial Robot. Robotica 2001, 19, 311–321. [Google Scholar] [CrossRef]
- Weidong, Z.; Guanhua, L.; Huiyue, D.; Yinglin, K. Positioning error compensation on two-dimensional manifold for robotic machining. Robot. Comput. Integr. Manuf. 2019, 59, 394–405. [Google Scholar]
- Mohnke, C.; Reinkober, S.; Uhlmann, E. Constructive methods to reduce thermal influences on the accuracy of industrial robots. Procedia Manuf. 2019, 33, 19–26. [Google Scholar] [CrossRef]
- Li, R.; Zhao, Y. Dynamic error compensation for industrial robot based on thermal effect model. Measurement 2016, 88, 113–120. [Google Scholar] [CrossRef]
- Barakat, N.A.; Elestawi, M.A.; Spence, A.D. Kinematic and geometric error compensation of a coordinate measuring machine. Int. J. Mach. Tools Manuf. 2000, 40, 833–850. [Google Scholar] [CrossRef]
- Ramesh, R.; Mannan, M.A.; Poo, A.N. Error compensation in machine tools—A review: Part I: Geometric, cutting-force induced and fixture-dependent errors. Int. J. Mach. Tools Manuf. 2000, 9, 1235–1256. [Google Scholar] [CrossRef]
- Okafor, A.C.; Ertekin, Y.M. Derivation of machine tool error models and error compensation procedure for three axes vertical machining center using rigid body kinematics. Int. J. Mach. Tools Manuf. 2000, 8, 1199–1213. [Google Scholar] [CrossRef]
- Chanal, H.; Duc, E.; Ray, P.; Hascoet, J.Y. A new approach for the geometrical calibration of parallel kinematics machines tools based on the machining of a dedicated part. Int. J. Mach. Tools Manuf. 2007, 47, 1151–1163. [Google Scholar] [CrossRef]
- Cetinkunt, S.; Tsai, R.L. Position error compensation of robotic contour end-milling. Int. J. Mach. Tools Manuf. 1990, 30, 613–627. [Google Scholar] [CrossRef]
- OH, Y. Study of Orientation Error on Robot End Effector and Volumetric Error of Articulated Robot. Appl. Sci. 2019, 9, 5149. [Google Scholar] [CrossRef]
- Chen, J.X.; Lin, S.W.; Zhou, X.L. A comprehensive error analysis method for the geometric error of multi-axis machine tool. Int. J. Mach. Tools Manuf. 2016, 106, 56–66. [Google Scholar] [CrossRef]
- Chen, J.; Chao, L.M. Positioning error analysis for robot manipulators with all rotary joints. IEEE J. Robot. Autom. 1987, 3, 539–545. [Google Scholar] [CrossRef]
- Zeng, Y.; Tian, W.; Liao, W. Positional error similarity analysis for error compensation of industrial robots. Robot. Comput. Integr. Manuf. 2016, 42, 113–120. [Google Scholar] [CrossRef]
- Zhu, S.; Ding, G.; Qin, S.; Lei, J.; Zhuang, L.; Yan, K. Integrated geometric error modeling, identification and compensation of CNC machine tools. Int. J. Mach. Tools Manuf. 2012, 52, 24–29. [Google Scholar] [CrossRef]
- Nguyen, H.N.; Zhou, J.; Kang, H.J. A new full pose measurement method for robot calibration. Sensors 2013, 13, 9132–9147. [Google Scholar] [CrossRef]
- Mavroidis, C.; Dubowsky, S.; Drouet, P.; Hintersteiner, J.; Flanz, J. A systemtic error analysis of robotic manipulator: Application to a high performance medical robot. In Proceedings of the International Conference on Robotics and Automation, Albuquerque, NM, USA, 20–25 April 1997; pp. 980–985. [Google Scholar]
- Raksiri, C.; Parnicjkun, M. Geometric and force errors compensation in 3-axis CNC milling machine. Int. J. Mach. Tools Manuf. 2004, 44, 1283–1291. [Google Scholar] [CrossRef]
- Wan, A.; Song, L.; Xu, J.; Liu, S.; Chen, K. Calibration and compensation of machine tool volumetric error using a laser tracker. Int. J. Mach. Tools Manuf. 2018, 124, 126–133. [Google Scholar] [CrossRef]
- Cao, C.T.; Do, V.P.; Lee, B.R. A Novel Indirect Calibration Approach for Robot Positioning Error Compensation Based on Neural Network and Hand-Eye Vision. Appl. Sci. 2019, 9, 1940. [Google Scholar] [CrossRef]
- Nubiola, A.; Bonev, I.A. Absolute calibration of an ABB IRB 1600 robot using a laser tracker. Robot. Comput. Integr. Manuf. 2013, 29, 236–245. [Google Scholar] [CrossRef]
- Li, C.; Liu, X.; Li, R.; Song, H. Geometric Error Identification and Analysis of Rotary Axes on Five-Axis Machine Tool Based on Precision Balls. Appl. Sci. 2020, 10, 100. [Google Scholar] [CrossRef]
- Santolaris, J.; Gines, M. Uncertainty estimation in robot kinematic calibration. Robot. Comput. Integr. Manuf. 2013, 29, 370–384. [Google Scholar] [CrossRef]
- Niku, S.B. Introduction to Robotics Analysis, Systems, Applications; Prentice Hall: New Jersey, NJ, USA, 2001. [Google Scholar]
- Pechard, P.Y.; Tournier, C.; Lartigue, C.; Lugarin, J.P. Geometrical deviations versus smoothness in 5-axis high-speed flank millings. Int. J. Mach. Tools Manuf. 2009, 49, 454–461. [Google Scholar] [CrossRef][Green Version]
- Hayat, A.A.; Body, R.A.; Saha, S.K. A geometric approach for kinematic identification of an industrial robot using a monocular camera. Robot. Comput. Integr. Manuf. 2019, 57, 329–346. [Google Scholar] [CrossRef]
- Enferad, J.; Shahi, A. On the position analysis of a new spherical parallel robot with orientation applications. Robot. Comput. Integr. Manuf. 2016, 37, 151–161. [Google Scholar] [CrossRef]
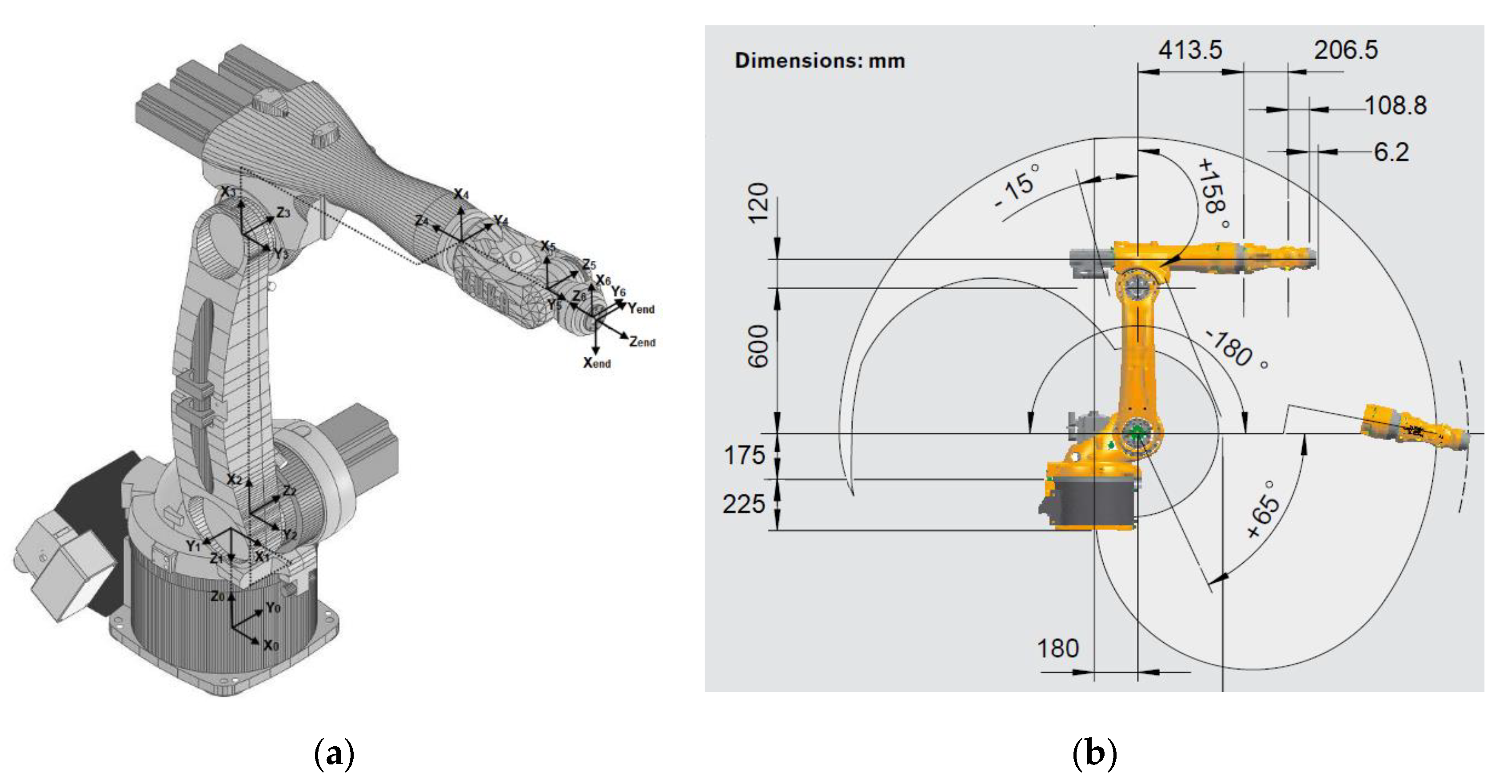







| Link | Rotation (°) | Translation (mm) | θ (°) |
|---|---|---|---|
| 1 | About x 180 | Along z 225 | − |
| 2 | About x 90 | Along x 180, y 120, z −175 | θ1 |
| 3 | About z −90 | Along x 600, z −15 | θ2 |
| 4 | About x 90 | Along x 120, y 413.5, z 135 | θ3 |
| 5 | About x −90 | Along z −206.5 | θ4 |
| 6 | About x 90 | Along y 108.8 | θ5 |
| 7 | About y 180 | Along z −6.2 | θ6 |
| Joint | Interval (°) | Increment (°) | Pose (°) |
|---|---|---|---|
| 1 | −54 to 126 | 9 | − |
| 2 | −160 to −24 | 8 | A1 −90 |
| 3 | 0 to 140 | 7 | A1 90, A2 −90 |
| 4 | −180 to 180 | 18 | A1 0, A2 −90, A3 90 |
| 5 | −108 to 108 | 12 | A1 90, A2 −90, A3 90, A4 0 |
| 6 | −180 to 180 | 18 | A1 0, A2 −90, A3 90, A4 0, A5 0 |
| Joint | |||||
|---|---|---|---|---|---|
| 1 | −0.0331 | 0.0218 | −0.3702 | −0.7174 | −0.0005 |
| 2 | 0.1813 | 0.0068 | −0.4168 | 0.3069 | 0.0014 |
| 3 | −0.0069 | 0.0034 | 0.9521 | 0.5143 | 0.0001 |
| 4 | −0.0295 | 0.0031 | 0.3414 | −0.2313 | 0.0002 |
| 5 | −0.0198 | 0.0361 | 0.4848 | 0.3526 | 0.0004 |
| 6 | −0.0129 | 0.0772 | −0.4767 | −0.4767 | 0.0007 |
| Joint | Perpendicularity or Parallelism | Position | ||
|---|---|---|---|---|
| δ (mm) | x | y | z | |
| 1 | 0.0346 | −0.3702 | −0.7174 | −0.0005 |
| 2 | 0.1742 | −0.4168 | 0.3069 | 0.0014 |
| 3 | 0.0013 | 0.9521 | 0.5143 | 0.0001 |
| 4 | 0.0145 | 0.3414 | −0.2313 | 0.0002 |
| 5 | 0.0086 | 0.4848 | 0.3526 | 0.0004 |
| 6 | 0.0164 | −0.4767 | −0.4767 | 0.0007 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Raksiri, C.; Pa-im, K.; Rodkwan, S. An Analysis of Joint Assembly Geometric Errors Affecting End-Effector for Six-Axis Robots. Robotics 2020, 9, 27. https://doi.org/10.3390/robotics9020027
Raksiri C, Pa-im K, Rodkwan S. An Analysis of Joint Assembly Geometric Errors Affecting End-Effector for Six-Axis Robots. Robotics. 2020; 9(2):27. https://doi.org/10.3390/robotics9020027
Chicago/Turabian StyleRaksiri, Chana, Krittiya Pa-im, and Supasit Rodkwan. 2020. "An Analysis of Joint Assembly Geometric Errors Affecting End-Effector for Six-Axis Robots" Robotics 9, no. 2: 27. https://doi.org/10.3390/robotics9020027
APA StyleRaksiri, C., Pa-im, K., & Rodkwan, S. (2020). An Analysis of Joint Assembly Geometric Errors Affecting End-Effector for Six-Axis Robots. Robotics, 9(2), 27. https://doi.org/10.3390/robotics9020027






