MallARD: An Autonomous Aquatic Surface Vehicle for Inspection and Monitoring of Wet Nuclear Storage Facilities
Abstract
1. Introduction
1.1. Environment
1.2. Application
1.2.1. Deployment of an Improved Cerenkov Viewing Device
1.2.2. Radiation Monitoring of Pool Walls
1.2.3. General Requirements
1.3. Review of Existing ASVs
1.4. Contributions
- An analysis of a range of localisation technologies that are applicable to an autonomous aquatic surface vehicle operating in a confined environment.
- Detail of the mechanical and software design of a uniquely capable autonomous aquatic surface vehicle.
- Experimental work proving that the ASV is capable of meeting the requirements of two example applications: Straight path tracking and position holding.
2. Localisation Technologies
2.1. Analysis of Relevant Localisation Technologies
2.2. Technology Selection
3. Hardware Design
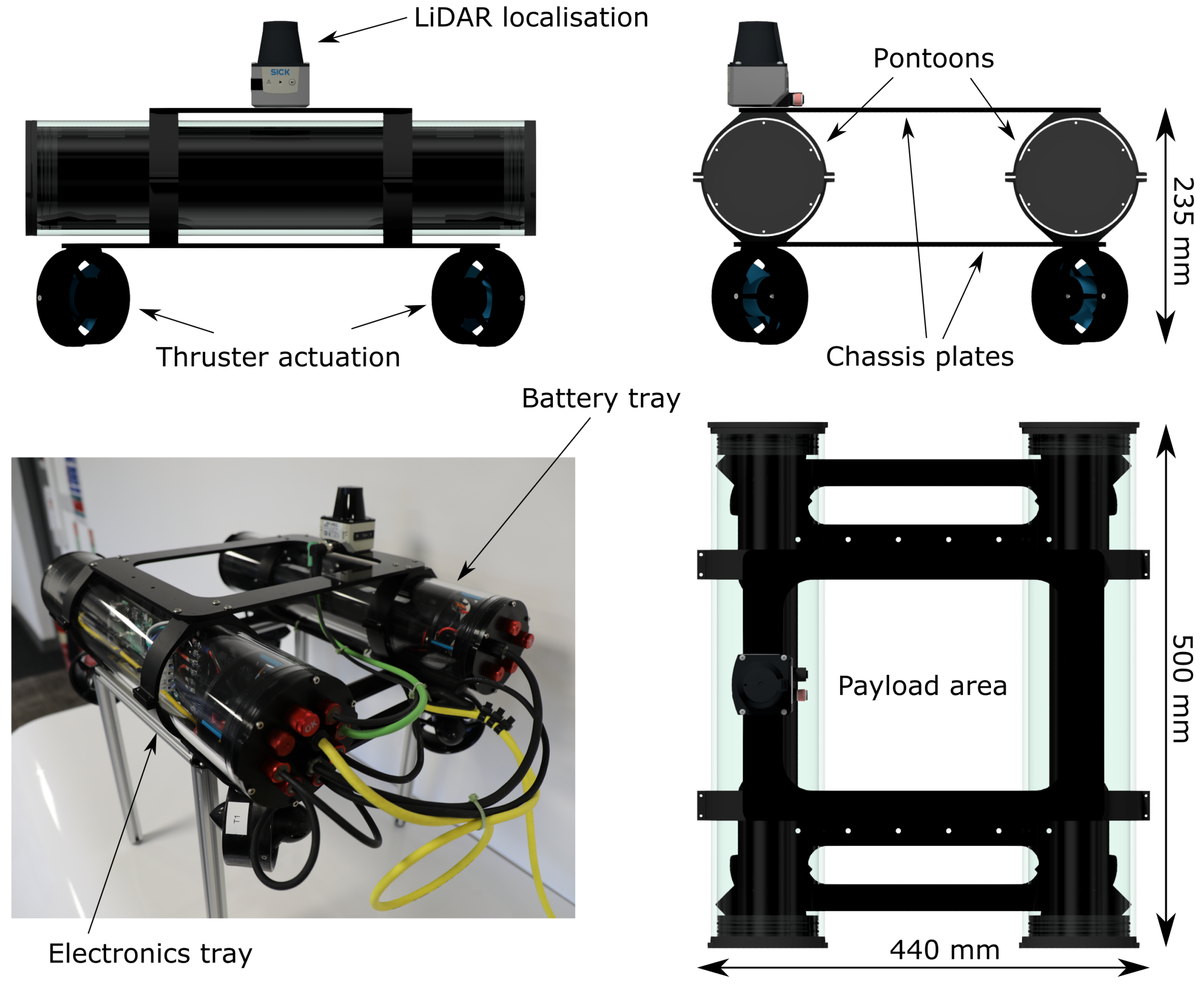
3.1. Mechanical and Propulsion
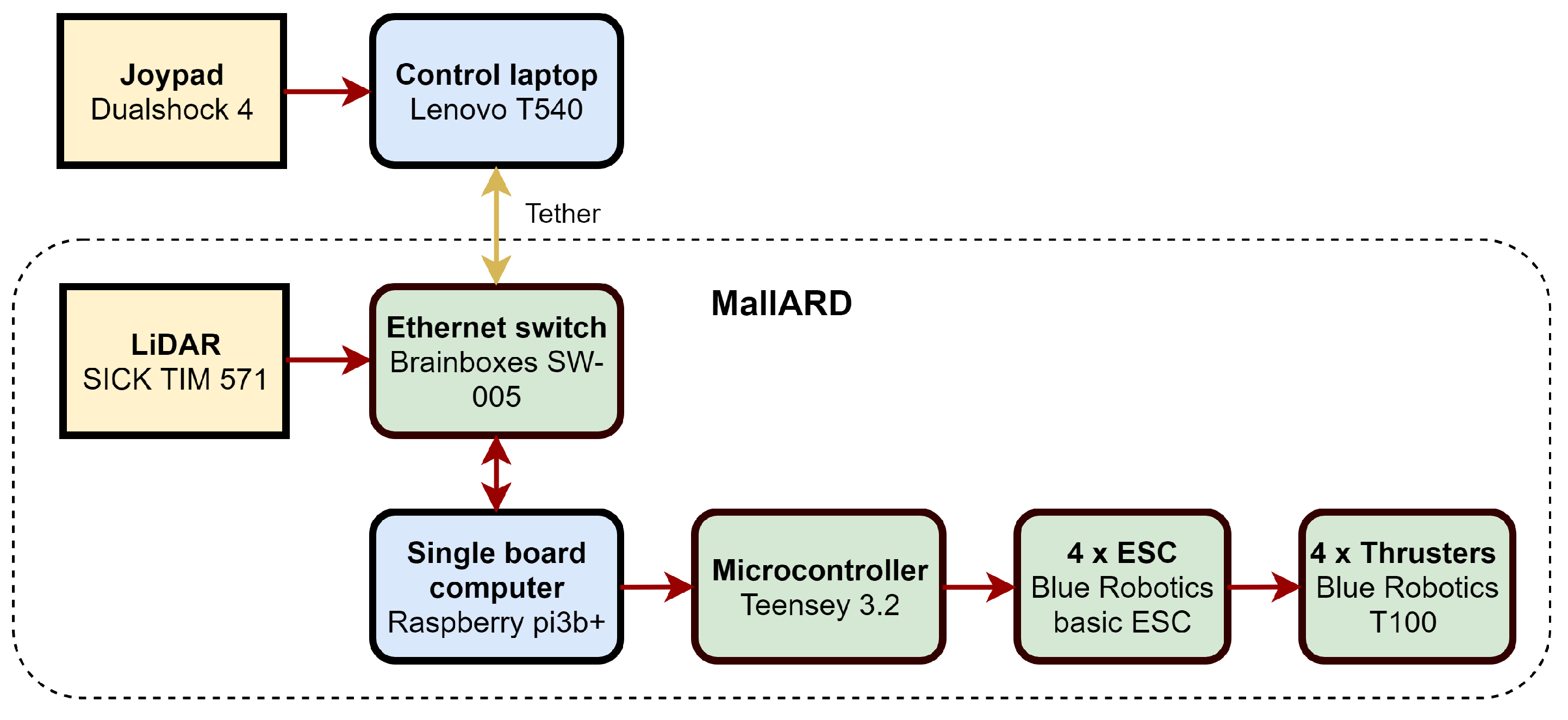
3.2. Electronic
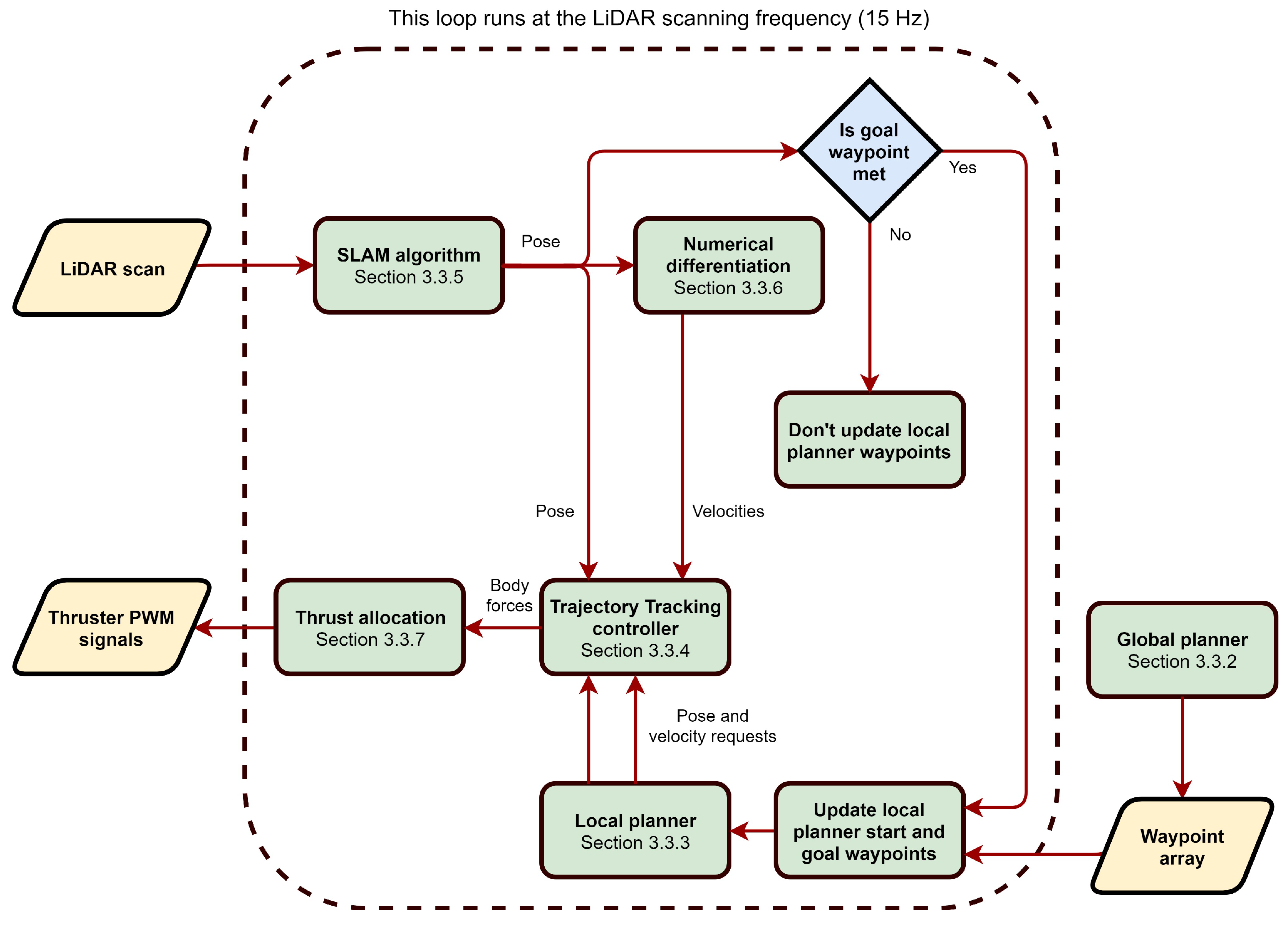
3.3. Localisation and Navigation System
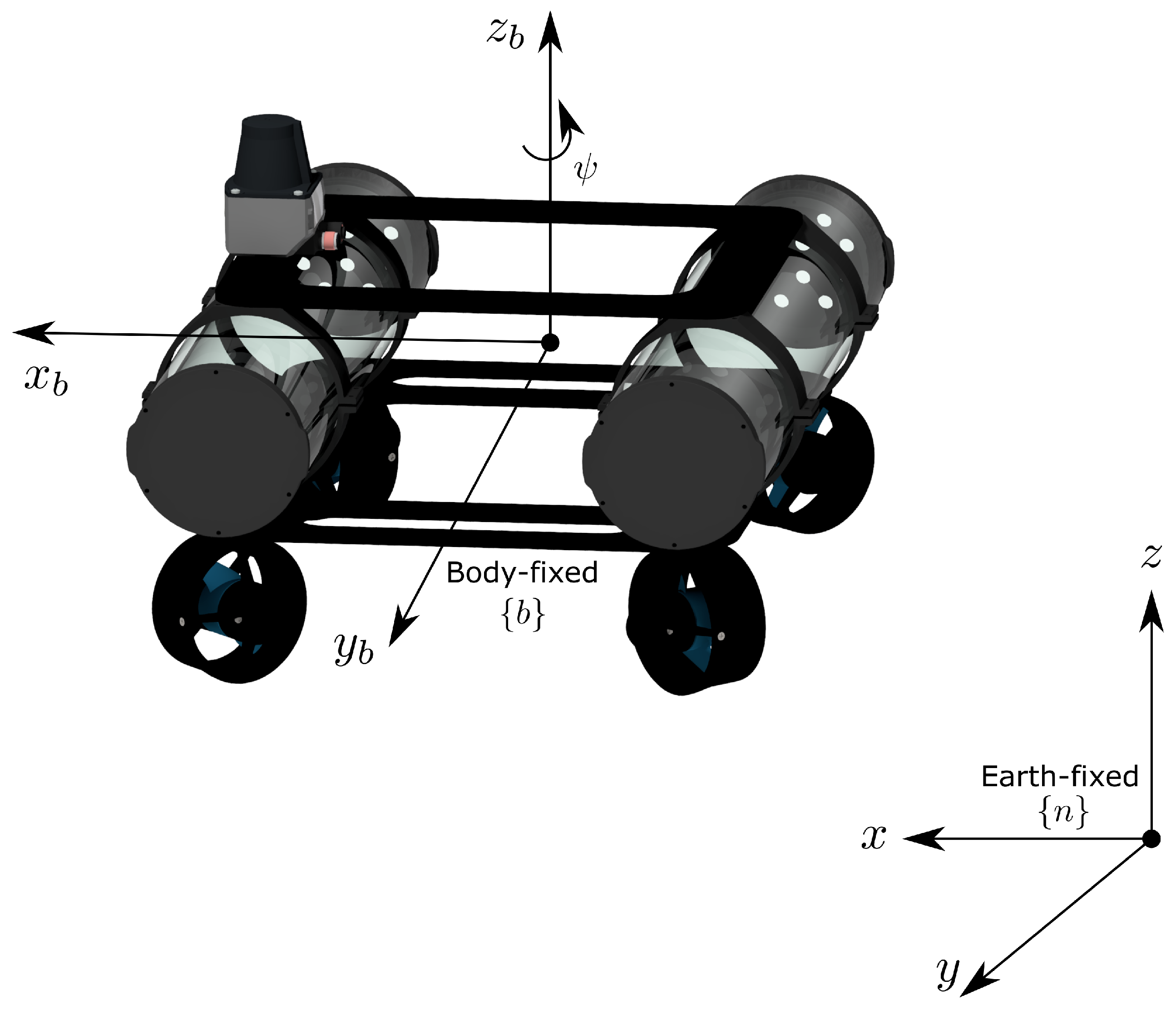
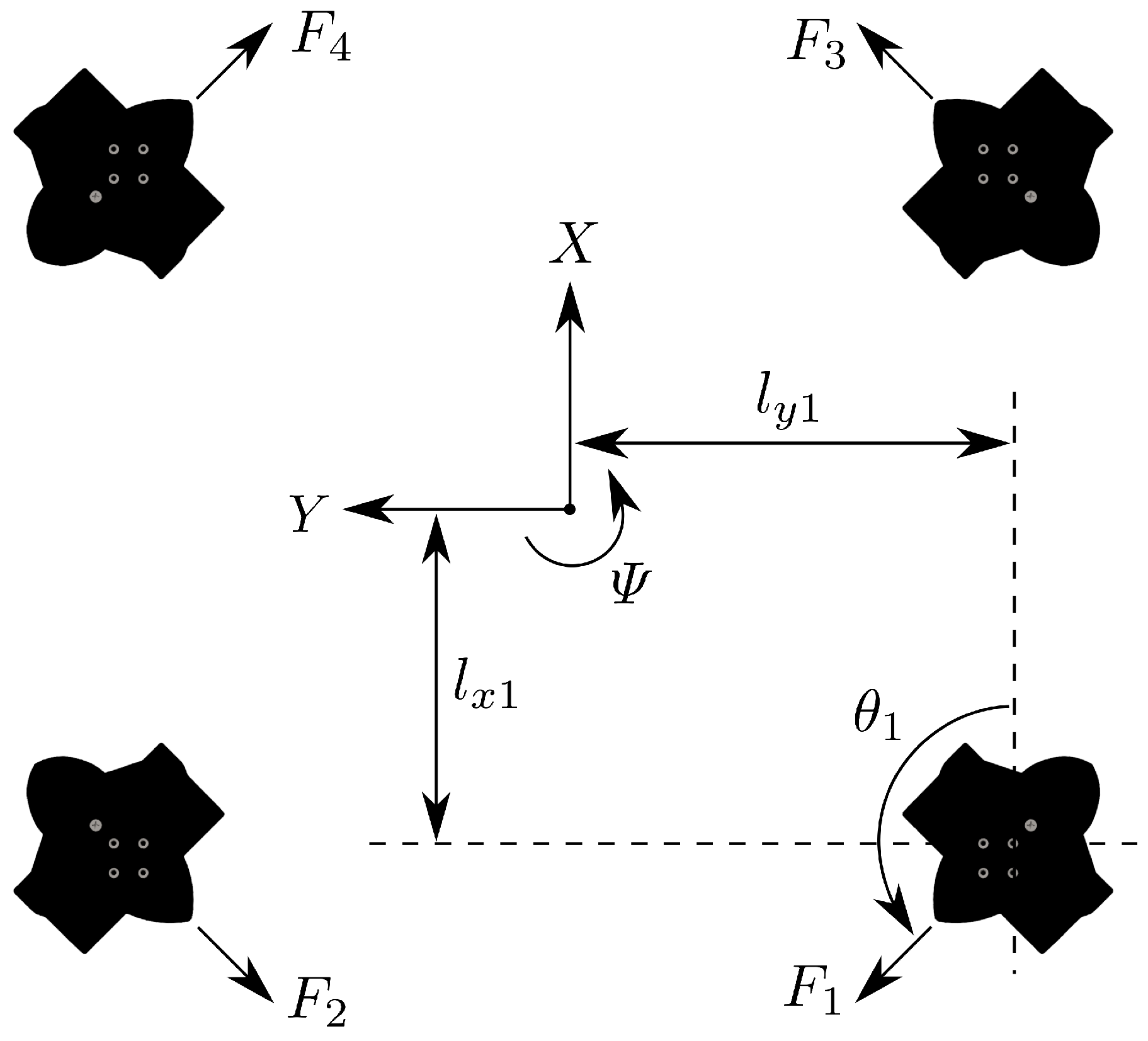
3.3.1. Coordinate System and Conventions
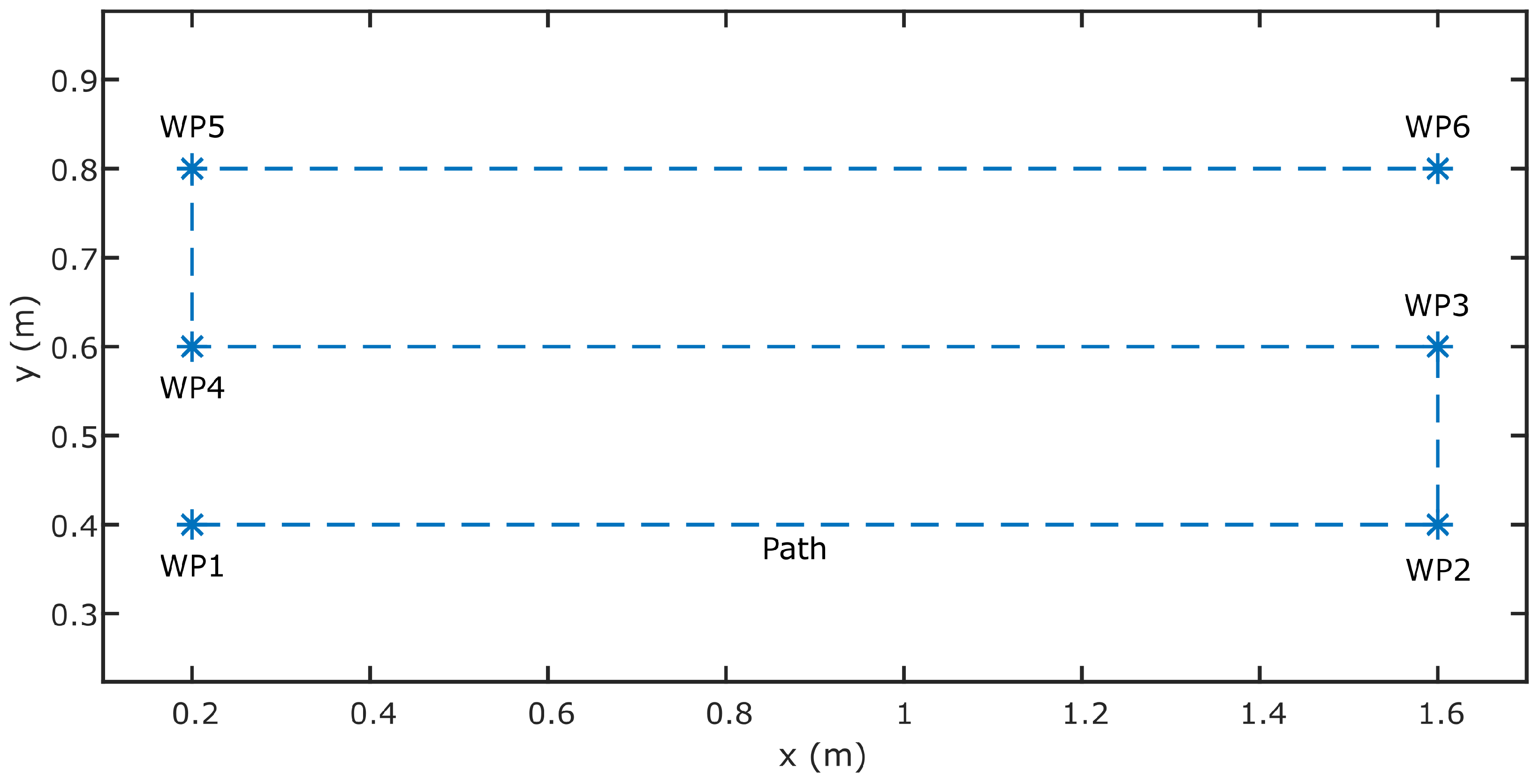
3.3.2. Global Planner
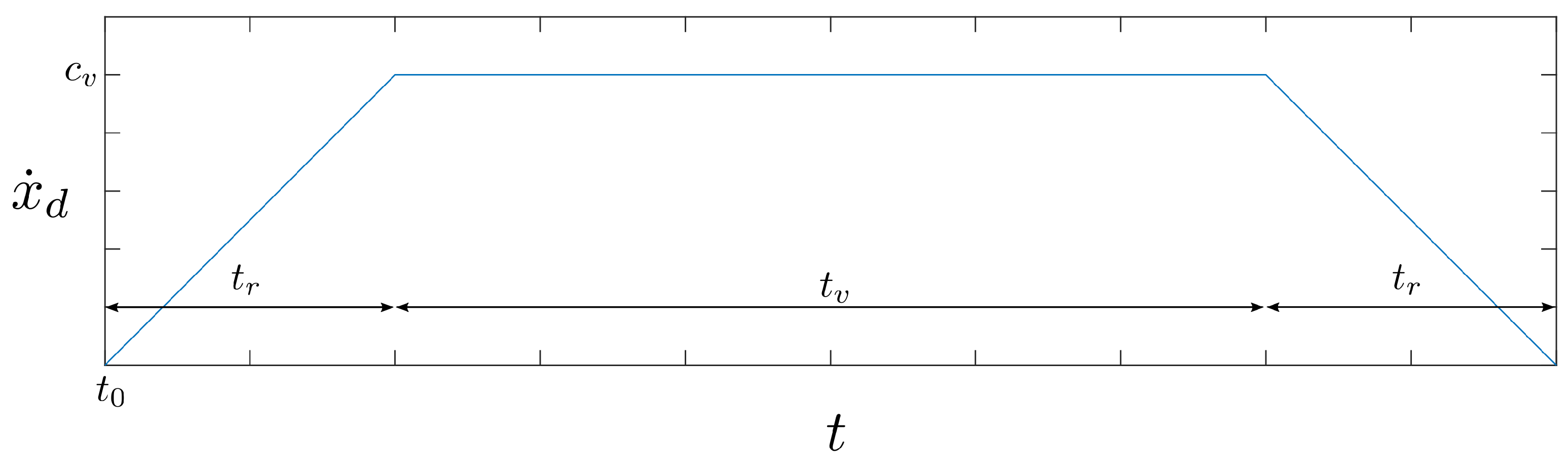
3.3.3. Local Planner
3.3.4. Trajectory Tracking Controller
3.3.5. Localisation and Mapping
3.3.6. Numerical Differentiation
3.3.7. Thrust Allocation
4. Experiments and Deployments
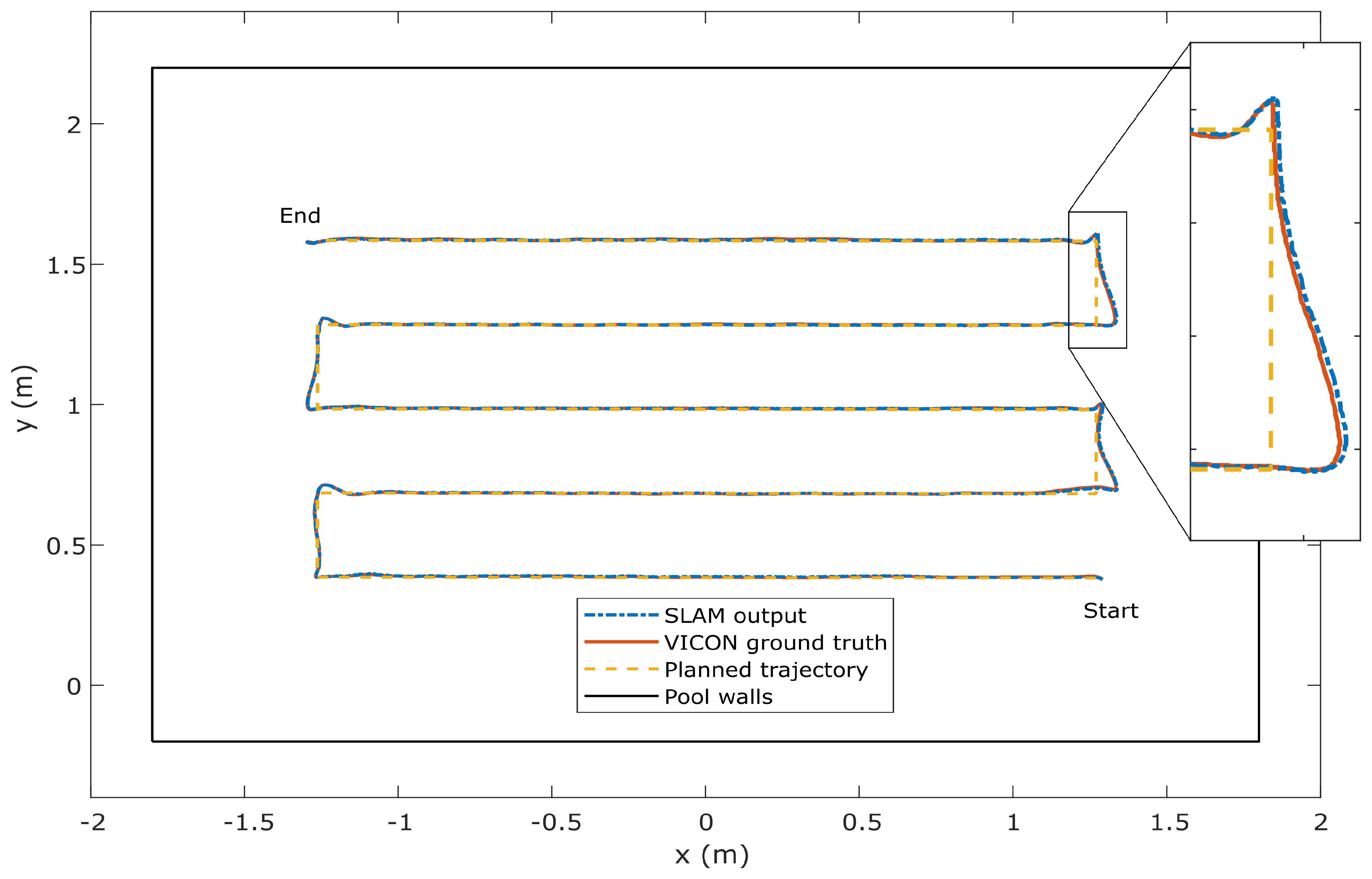
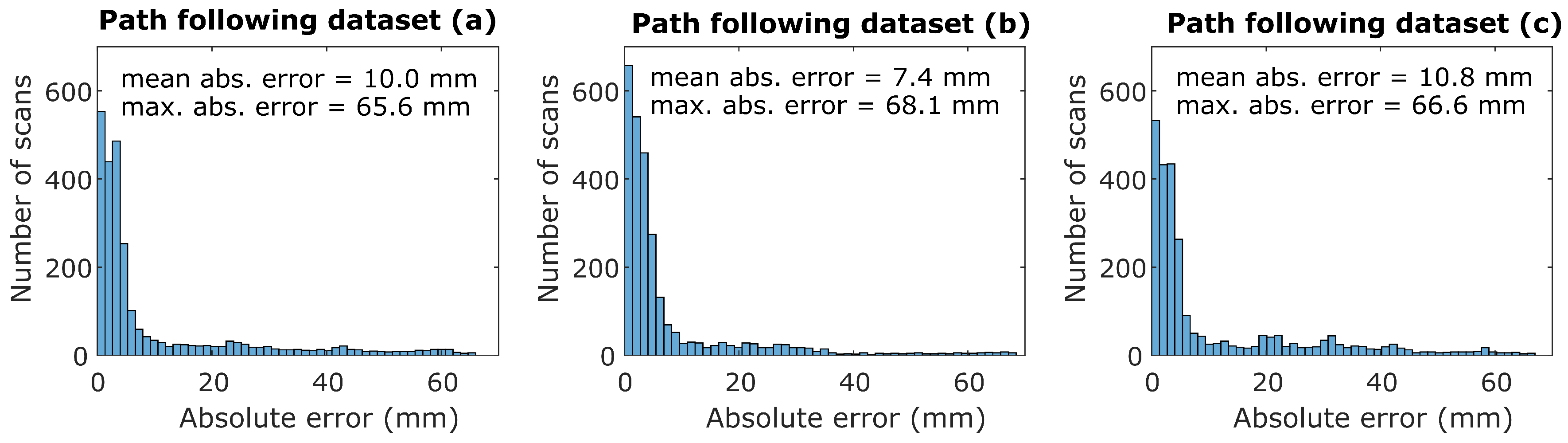
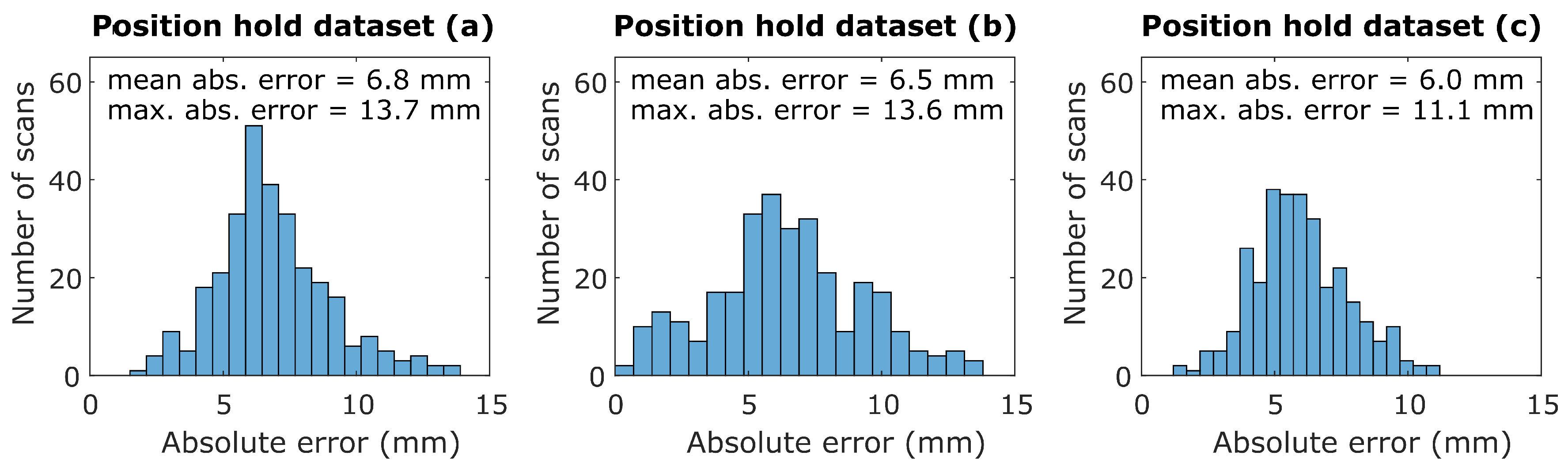
4.1. Experiment Setup
4.2. Results
4.3. Deployments
5. Discussion and Future Work
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Joyce, M. Nuclear Engineering: A Conceptual Introduction to Nuclear Power; Butterworth-Heinemann: Oxford, UK, 2017. [Google Scholar]
- IAEA. Safeguards Techniques and Equipment; Number 1 (Rev. 2) in International Nuclear Verification Series; International Atomic Energy Agency: Vienna, Austria, 2011. [Google Scholar]
- Peehs, M.; Fleisch, J. LWR Spent Fuel Storage Behaviour. J. Nucl. Mater. 1986, 137, 190–202. [Google Scholar] [CrossRef]
- Mallios, A.; Ridao, P.; Ribas, D.; Hernandez, E. Scan matching SLAM in underwater environments. Auton. Robot. 2014, 36, 181–198. [Google Scholar] [CrossRef]
- Yacout, A. Nuclear Fuel; Technical Report; Argonne National Laboratory: Lemont, IL, USA, 2011.
- Balbuena, J.; Quiroz, D.; Song, R.; Bucknall, R.; Cuellar, F. Design and implementation of an USV for large bodies of fresh waters at the highlands of Peru. In Proceedings of the OCEANS 2017-Anchorage, Anchorage, AK, USA, 18–21 September 2017; pp. 1–8. [Google Scholar]
- Dunbabin, M.; Grinham, A. Experimental evaluation of an autonomous surface vehicle for water quality and greenhouse gas emission monitoring. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Anchorage, AK, USA, 3–7 May 2010; pp. 5268–5274. [Google Scholar]
- Melo, M.; Mota, F.; Albuquerque, V.; Alexandria, A. Development of a robotic airboat for online water quality monitoring in lakes. Robotics 2019, 8, 19. [Google Scholar] [CrossRef]
- Griffith, S.; Pradalier, C. Survey Registration for Long-Term Natural Environment Monitoring. J. Field Robot. 2016, 34, 188–208. [Google Scholar] [CrossRef]
- Conte, G.; De Capua, G.P.; Scaradozzi, D. Modeling and control of a low-cost ASV. IFAC Proc. Vol. 2012, 45, 429–434. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y.; Yu, X.; Yuan, C. Unmanned surface vehicles: An overview of developments and challenges. Annu. Rev. Control 2016, 41, 71–93. [Google Scholar] [CrossRef]
- Monteiro, L.S.; Moore, T.; Hill, C. What is the accuracy of DGPS? J. Navig. 2005, 58, 207–225. [Google Scholar] [CrossRef]
- Ramezani, M.; Khoshelham, K.; Fraser, C. Pose estimation by Omnidirectional Visual-Inertial Odometry. Robot. Auton. Syst. 2018, 105, 26–37. [Google Scholar] [CrossRef]
- Munguía, R.; Urzua, S.; Bolea, Y.; Grau, A. Vision-based SLAM system for unmanned aerial vehicles. Sensors 2016, 16, 372. [Google Scholar] [CrossRef]
- Fuentes-Pacheco, J.; Ruiz-Ascencio, J.; Rendón-Mancha, J.M. Visual Simultaneous Localization and Mapping: A Survey. Artif. Intell. Rev. 2015, 43, 55–81. [Google Scholar] [CrossRef]
- Bristeau, P.J.; Callou, F.; Vissiere, D.; Petit, N. The navigation and control technology inside the ar. drone micro uav. IFAC Proc. Vol. 2011, 44, 1477–1484. [Google Scholar] [CrossRef]
- Niu, X.; Yu, T.; Tang, J.; Chang, L. An Online Solution of LiDAR Scan Matching Aided Inertial Navigation System for Indoor Mobile Mapping. Mob. Inf. Syst. 2017, 2017, 4802159. [Google Scholar] [CrossRef]
- Massot-Campos, M.; Oliver-Codina, G. Optical sensors and methods for underwater 3D reconstruction. Sensors 2015, 15, 31525–31557. [Google Scholar] [CrossRef] [PubMed]
- Ryu, J.H.; Gankhuyag, G.; Chong, K.T. Navigation system heading and position accuracy improvement through GPS and INS data fusion. J. Sens. 2016, 2016, 7942963. [Google Scholar] [CrossRef]
- Tang, J.; Chen, Y.; Niu, X.; Wang, L.; Chen, L.; Liu, J.; Shi, C.; Hyyppa. LiDAR scan matching aided inertial navigation system in GNSS-denied environments. Sensors 2015, 15, 16710–16728. [Google Scholar] [CrossRef] [PubMed]
- Travis, W.; Simmons, A.T.; Bevly, D.M. Corridor navigation with a LiDAR/INS Kalman filter solution. In Proceedings of the Intelligent Vehicles Symposium, Las Vegas, NV, USA, 6–8 June 2005; pp. 343–348. [Google Scholar]
- Alonge, F.; D’Ippolito, F.; Garraffa, G.; Sferlazza, A. A hybrid observer for localization of mobile vehicles with asynchronous measurements. Asian J. Control 2019. [Google Scholar] [CrossRef]
- Mallios, A. Sonar Scan Matching for Simultaneous Localization and Mapping in Confined Underwater Environments. Ph.D. Thesis, University of Girona, Girona, Spain, 2014. [Google Scholar]
- Newman, P.; Leonard, J.J.; Rikoski, R. Towards constant-time SLAM on an autonomous underwater vehicle using synthetic aperture sonar. In Proceedings of the International Symposyum of Robotics Research (ISRR03), Siena, Italy, 19–22 October 2003. [Google Scholar]
- Mallios, A.; Ridao, P.; Ribas, D.; Maurelli, F.; Petillot, Y. EKF-SLAM for AUV navigation under probabilistic sonar scan-matching. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 4404–4411. [Google Scholar]
- Ribas, D.; Ridao, P.; Tardós, J.D.; Neira, J. Underwater SLAM in man-made structured environments. J. Field Robot. 2008, 25, 898–921. [Google Scholar] [CrossRef]
- Arnold, S.; Medagoda, L. Robust Model-Aided Inertial Localization for Autonomous Underwater Vehicles. In Proceedings of the 2018 IEEE International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 21–26 May 2018. [Google Scholar]
- Hegrenaes, O.; Hallingstad, O. Model-aided INS with sea current estimation for robust underwater navigation. IEEE J. Ocean. Eng. 2011, 36, 316–337. [Google Scholar] [CrossRef]
- Kohlbrecher, S. Hector Slam; Technical Report; Open Source Robotics Foundation: Mountain View, CA, USA, 2016. [Google Scholar]
- Lennox, C.; Groves, K.; Hondru, V.; Arvin, F.; Gornicki, K.; Lennox, B. Embodiment of an Aquatic Surface Vehicle in an Omnidirectional Ground Robot. In Proceedings of the 2019 IEEE International Conference on Mechatronics (ICM), Ilmenau, Germany, 18–20 March 2019. [Google Scholar]
- Foote, T.; Purvis, M. REP 103 Standard Units of Measure and Coordinate Conventions; Technical Report; Open Source Robotics Foundation: Mountain View, CA, USA, 2014. [Google Scholar]
- Fossen, T.I. Guidance and Control of Ocean Vehicles; Wiley: New York, NY, USA, 1994. [Google Scholar]
- Ferguson, D.; Stentz, A. Field D*: An Interpolation-Based Path Planner and Replanner. In Robotics Research; Thrun, S., Brooks, R., Durrant-Whyte, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2007; pp. 239–253. [Google Scholar]
- Choset, H.; Pignon, P. Coverage path planning: The boustrophedon cellular decomposition. In Field and Service Robotics; Springer: Berlin, Germany, 1998; pp. 203–209. [Google Scholar]
- Marin-Plaza, P.; Hussein, A.; Martin, D.; Escalera, A.d.l. Global and local path planning study in a ros-based research platform for autonomous vehicles. J. Adv. Transp. 2018, 2018, 6392697. [Google Scholar] [CrossRef]
- Yang, Y.; Du, J.; Liu, H.; Guo, C.; Abraham, A. A trajectory tracking robust controller of surface vessels with disturbance uncertainties. IEEE Trans. Control Syst. Technol. 2013, 22, 1511–1518. [Google Scholar] [CrossRef]
- Hoffmann, G.; Waslander, S.; Tomlin, C. Quadrotor helicopter trajectory tracking control. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008; p. 7410. [Google Scholar]
- Merriaux, P.; Dupuis, Y.; Boutteau, R.; Vasseur, P.; Savatier, X. A study of vicon system positioning performance. Sensors 2017, 17, 1591. [Google Scholar] [CrossRef] [PubMed]


| Technology | Scope | Mean Error | Refresh Rate | Environmental Influence |
|---|---|---|---|---|
| GNSS | Absolute localisation | ≈1 m [12] | 20–50 Hz | Only available outdoors |
| Computer vision | Absolute localisation or odometry | - | - | Highly sensitive to environment |
| LiDAR SLAM | Absolute localisation | 3–6 mm [20] | ≈10–50 Hz | Requires local features |
| 6-axis IMU | Fuse with absolute localisation | - | ≈50–200 Hz | Almost unaffected |
| sonar SLAM | Absolute localisation | 1.9 m | ≈1–10 Hz | Only available below surface |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Groves, K.; West, A.; Gornicki, K.; Watson, S.; Carrasco, J.; Lennox, B. MallARD: An Autonomous Aquatic Surface Vehicle for Inspection and Monitoring of Wet Nuclear Storage Facilities. Robotics 2019, 8, 47. https://doi.org/10.3390/robotics8020047
Groves K, West A, Gornicki K, Watson S, Carrasco J, Lennox B. MallARD: An Autonomous Aquatic Surface Vehicle for Inspection and Monitoring of Wet Nuclear Storage Facilities. Robotics. 2019; 8(2):47. https://doi.org/10.3390/robotics8020047
Chicago/Turabian StyleGroves, Keir, Andrew West, Konrad Gornicki, Simon Watson, Joaquin Carrasco, and Barry Lennox. 2019. "MallARD: An Autonomous Aquatic Surface Vehicle for Inspection and Monitoring of Wet Nuclear Storage Facilities" Robotics 8, no. 2: 47. https://doi.org/10.3390/robotics8020047
APA StyleGroves, K., West, A., Gornicki, K., Watson, S., Carrasco, J., & Lennox, B. (2019). MallARD: An Autonomous Aquatic Surface Vehicle for Inspection and Monitoring of Wet Nuclear Storage Facilities. Robotics, 8(2), 47. https://doi.org/10.3390/robotics8020047






