Abstract
Space-based manipulators have traditionally been tasked with robotic on-orbit servicing or assembly functions, but active debris removal has become a more urgent application. We present a much-needed tutorial review of many of the robotics aspects of active debris removal informed by activities in on-orbit servicing. We begin with a cursory review of on-orbit servicing manipulators followed by a short review on the space debris problem. Following brief consideration of the time delay problems in teleoperation, the meat of the paper explores the field of space robotics regarding the kinematics, dynamics and control of manipulators mounted onto spacecraft. The core of the issue concerns the spacecraft mounting which reacts in response to the motion of the manipulator. We favour the implementation of spacecraft attitude stabilisation to ease some of the computational issues that will become critical as increasing level of autonomy are implemented. We review issues concerned with physical manipulation and the problem of multiple arm operations. We conclude that space robotics is well-developed and sufficiently mature to tackling tasks such as active debris removal.
1. Introduction
Space-based manipulators have traditionally been tasked with robotic on-orbit servicing functions, but despite several decades of development since the 1980s, this has yet to come to pass. A new application of space manipulators has emerged—active debris removal—and this need has become urgent. Much of the technological development in space robotics over this period is directly applicable to this new task and indeed, given that the more challenging aspects of on-orbit servicing are not required (namely, servicing tasks), the prospect of active debris removal can be met. All the kinematic, dynamic and control issues are identical—this includes the requirement for grappling the target and passivating it. This will require robotic clamps or grippers. Indeed, once a grapple hold has been attained on capture of the target, it may be necessary to adjust the grip configuration to secure it for transport. Relocating the grip may require robotic fingers for stable grip-to-grip transitions, but securing the grip will require robotic latching mechanisms. Servicing tasks typically have involved the deployment of power tools for bolt manipulation and the use of specialised tools for more challenging tasks such as cutting, taping and resealing thermal blankets. For the most part, this will not be required for active debris removal if the robot is latched to the target. However, the attachment of a propulsive stage to the target for disposal will require basic servicing capability including power tooling for bolt handling (ensuring that said bolts remain secure and not become further sources of debris). It is envisaged that the more difficult manipulations involving invasive servicing procedures will not be necessary.
We first consider a brief schematic of recent on-orbit space manipulators employed by the International Space Station (ISS), and thence proceed to describe the rise and fall of robotic on-orbit servicing missions. We then provide a comprehensive review of the growing space debris crisis and proposed solutions. The freeflyer sporting two or more manipulators is the solution of choice to remove large debris pieces. To that end, the bulk of the paper reviews the kinematics, dynamics and control of space manipulators. We pay particular attention to the grappling task. Hence, our interest here is to provide a schematic of on-orbit servicing robotics that can be applied to space debris removal. Since the comprehensive review in [1], there have been many modern developments in space manipulator robotics. Some excellent more modern reviews include [2] which highlights challenges in servicing non-cooperative satellites and [3,4] which emphasise kinematic and dynamic issues. Here, we are more selective and present a tutorial approach. We take an unusual stance in viewing space manipulators from the perspective of their deployment for space debris mitigation of which on-orbit servicing is in fact a part. Rather than aiming at comprehension, our tutorial review should increase the appeal of the paper to a wider audience.
2. On-Orbit Space Manipulators
Space manipulator robotics has played a significant role on the ISS, which has installed on it three manipulator systems: the Canadian Mobile Servicing System (MSS), the Japanese Experiment Module Remote Manipulator System (JEMRMS), and the European Robotic Arm (ERA) [5]. The MSS includes the 17 m long 7 degree-of-freedom Space Station Remote Manipulator System (SSRMS) with its relocatable base (Table 1), which is comparable to the 11 m long 7 degree-of-freedom ERA with its relocatable base in contrast to the 10 m long 6 degree-of-freedom JEMRMS fixed to the JEM. Both SSRMS and ERA are symmetric about their elbows, with latching end effectors at the end of each three degree-of-freedom wrist enabling hand-over-hand relocatability. Both were designed for assembly and servicing, while JEMRMS was designed for experiment payload manipulation from a fixed location.

Table 1.
Denavit-Hartenburg kinematic parameters for the SSRMS manipulator (adapted from Ref. [5]).
If we compare SSRMS with its predecessor the Shuttle remote manipulator system (SRMS) (Table 2), the improvement in performance is evident.

Table 2.
SRMS and SSRMS physical and performance parameters (adapted from Ref. [5]).
The special purpose dextrous manipulator (SPDM) is a bolt-on dual-arm fine manipulation system to the SSRMS comprising two 3.4 m long 7 degree-of-freedom arms with a positioning accuracy of 2 mm. Their joints are similarly configured with three shoulder joints (roll, pitch and yaw), an elbow pitch joint and three wrist joints (roll, pitch and yaw). Lighted cameras are mounted onto each forearm boom and at each end effector. These robot manipulators and their predecessor, the Shuttle RMS (SRMS), have been deployed for human servicing tasks in providing mobile but stable footings for astronauts and, latterly, more sophisticated manipulation tasks, primarily orbital replacement unit (ORU) exchange on the ISS.
One of the most sophisticated space robot platforms is the 150 kg Robonaut, which was delivered to the ISS as an intravehicular manipulator system in 2011 [6]. It is a teleoperated anthropomorphic design to impart astronaut extravehicular activity (EVA)-equivalence in a package that is similar in size to an EVA-suited astronaut with a reach of 0.7 m. It comprises two 7 degree-of-freedom arms with shoulder, elbow and wrist which mount two five-fingered hands, a head mounted onto a pan-tilt-verge orientable neck, a torso and a 6 degree of freedom (DOF) grappling leg. Robonaut’s hand comprises 14 DOF including a forearm, a 2 DOF wrist and a 12 DOF hand (2 × 3 DOF fingers, 1 × 3 DOF thumb, 2 × 1 DOF fingers plus a 1 DOF palm) mounted onto a 5 DOF arm. Each finger possesses a six-axis force sensor and force sensors at each joint to detect applied forces. Robonaut implements 16 sensors per joint and the forearm mounts 14 motors/harmonic drives, 12 circuit boards and the wiring harness. Its vision system mounted within the head comprises two binocular stereocameras with a fixed verge at arm’s length mounted onto a pan-tilt-verge neck with a pitch axis below the camera frame to permit forward translation of the neck. The payload capacity of each arm is modest at under 10 kg. In total, it has 350 sensors and 42 DOF. Robonaut uses a telepresence-based interface—a full immersion telepresence testbed—to allow it to perform EVA-type tasks such as target tracking, peg-in-hole tasks, tether hook securing, power tool handling, connector mate/demating, etc. [7]. The teleoperator wears cybergloves that measure displacement and bending of the operator’s fingers, a tracker to measure the position of the operator’s hand, arms and head relative to a fixed transmitter, and a head-mounted display to display remote camera views as 3D visual graphical overlays and digital force/torque measurement data. Voice commands are used to freeze and re-index Robonaut’s limbs to avoid drift. A 6 DOF force reflecting hand controller within a joystick provides force feedback to the operator. The Robonaut haptic sensor is mounted at several positions in the cyberglove that mirrors the remote tool stiffness/forces—it is based on an electrorheological fluid actuator which alters its viscosity under an electric field [8].
3. Robotic On-Orbit Servicing
Although astronaut on-orbit servicing (OOS) has progressed in leaps and bounds since the Solar Maximum Repair Mission (1984), it nevertheless was foundational in illustrating the difference between the designed-for-servicing ORU exchange and the not-designed-for-servicing main electronics box (MEB) exchange. Robotic on-orbit servicing has not made such advances in comparison to astronaut EVA capabilities. Robotic OOS is a class of mission in which a robotic servicer (chaser) spacecraft intercepts and performs servicing tasks on a client (target) spacecraft. This potentially involves a range of complexity of servicing tasks from observing the state of the target to translating the target into a new orbital state to direct robotic manipulation of the target to repair or upgrade it. A particularly relevant aspect of OOS is its implications for military space situational awareness from ground telescopes [9,10]. In all these cases that we consider, the targets have been cooperative, differentiating them from the targets from active debris removal which will be uncooperative.
There have been several technology demonstrator missions beginning with the foundational ETS-VII mission. The Japanese Experimental Test Satellite, ETS-VII (1997), successfully tested a 6 DOF 2 m long robotic manipulator with a three-fingered hand teleoperated from the ground under a time delay of 5–7 s (introduced by a TDRSS—tracking and data relay satellite system—relay) to demonstrate r-bar and v-bar automated rendezvous and docking tasks of a 248 kg chaser (Hikoboshi) to a 380 kg target (Orihime) followed by taskboard experiments including general peg-in-hole and ORU exchange-type tasks [11]. The DLR GETEX (German Technology Experiment) software that formed the backbone of the teleoperation tasks was based on task-level programming to upload motion sequences for autonomous execution [12]. It supplemented its 2 Hz video frame rate cameras with proximity rangefinders and implemented force feedback control. ETS-VII successfully demonstrated several on-orbit tasks: (i) remote observation; (ii) autonomous target chase and capture; (iii) ORU exchange including bolt fastening and target berthing; (iv) ORU electrical and fluid interfacing; (v) peg-in-hole insertion task based on wrist force/torque sensing; (vi) model-based predictive teleoperation with a 5–7 s time delay: (vii) flexible object handling, mating/demating of electrical connectors, truss joint connections, tightening of latches, etc.
In 2005, DART (demonstration of autonomous rendezvous technology) attempted to rendezvous and dock with another satellite, but its defective autonomous navigation system caused critical propellant consumption invoking an abort to the mission. This failure was followed by a success, Orbital Express (2007) demonstrated a suite of on-orbit tasks, including freeflying capture, ORU exchange and refuelling by an autonomous servicing satellite (ASTRO) that mounted a 6 degree-of-freedom revolute manipulator that performed tasks on a serviceable satellite (NextSat) [13,14]. While the manipulator arm was in motion, ASTRO operated in free drift with a free-floating base. It corrected its attitude once arm motion was complete, so attitude and manipulator control were implemented independently in time. This was similar to the approach adopted on the preceding ETS-VII servicing mission demonstrator. This is a rather cumbersome approach. Once the compliant grapple fixture on NextSat was captured by the manipulator, the join was rigidised and arm controller parameters adjusted to accommodate the new high inertia payload. Repeated demonstrations of autonomous rendezvous and docking, autonomous propellant transfer and changeout of batteries and onboard computers were performed. ASTRO used both visual and LIDAR tracking to compute relative position and velocity. It demonstrated the use of proximity station-keeping and the use of a robotic arm to grapple the target to minimise interaction forces that would be imposed by positive docking.
Geostationary equatorial orbit (GEO) is the most heavily populated orbit for commercial spacecraft—their orbital altitudes are identical and offering 24 h ground-spacecraft communications links. An example of a promising (subsequently cancelled) servicing capability was Europe’s SMART-OLEV (orbital life extension vehicle) to implement life extension to GEO communications satellites [15]. It comprised a spacecraft based on the SMART-1 bus to mechanically latch onto a client satellite at the apogee engine nozzle to provide orbit transfer and/or station-keeping functions using electric propulsion—it required no interfacing with the client spacecraft which operates normally other than the mechanical dock with its apogee engine capture tool. It had heritage from the earlier cancelled ConeXpress [16] (formerly SLES [17]), a service module to provide 12 years of extended life support to aging geostationary satellites. Using Hall thrusters, it would dock with the target satellite until the capture tool on a retractable boom was inserted into the thrust cone of the inert apogee kick engine without the use of robotic manipulators. The apogee engine nozzle—common to almost all GEO satellites for circularising into GEO orbit from elliptical geosynchronous transfer orbit—is used as a docking port by inserting and locking a DLR-type capture probe in the nozzle’s throat and then retracting the probe until the two spacecraft are locked together. The DLR capture tool includes six sensors for feedback on the relationship between the capture tool and the apogee motor volume and locks when fully inserted using a set of spreading pins. An alternative is the launch adapter ring as the sturdiest part of most spacecraft with which to grapple the spacecraft with manipulators and tooling. The American experience has been similar to the European experience in cancelled robotic OOS missions, the most notable being the Ranger Robotic Satellite Servicer. The next robotic servicing mission is to be Robotic Servicer for Geosynchronous Satellites (RSGS), currently slated for launch in 2021 (private communication 2018).
The chief hindrance to the adoption of the OOS philosophy in spaceflight has been the reluctance to implement widespread adoption of modular and serviceable spacecraft designs with standardised interfaces capable of sustaining kick loads imposed by servicing tasks and amenable to modular repair or simple disassembly. Design for servicing requires ORUs, which are modular boxes with standardised grapple fixtures and connectors that serve as containment packages for functional subsystems—wholesale module replacement is much cheaper than entire satellite replacement and easier than complex repair tasks. Typical servicing tasks involve the exchange of ORUs units through simple mechanical procedures afforded by the standardised interfaces. Indeed, SSRMS itself comprises ORUs of two booms joined by an elbow pitch joint. Each end has identical roll-pitch-yaw wrists mounting identical latching end effectors. Similarly, SPDM bolts onto the SSRMS using only four bolts. SPDM’s standard end effector is an ORU/tool changeout mechanism (OTCM) which incorporates a retractable 7/16th socket wrench. Pistol-grip EVA power tools for astronauts were designed to transfer kick loads from the client to the servicer—Robonaut hands are also designed to handle the same EVA power tools as the astronaut. However, for the final grapple, emphasis in space rendezvous and docking has been in latching. A lightweight quick-change mechanism with a novel locking mechanism with high repeatability, reliability and adaptability is described in [18]. The most representative example of a serviceable spacecraft design is the Multimission Modular Spacecraft (MMS) which was the basis of the Solar Maximum Mission spacecraft (1980), Landsat 4 (1982), Landsat 5 (1984), the Upper Atmosphere Research Satellite (1991) and the Extreme Ultraviolet Explorer (1992). Although the functional subsystems were encapsulated into ORUs, the wiring harness and certain electronics boxes beneath thermal blankets were not designed for serviceability. The Hubble Space Telescope (1990) was also designed for serviceability though it was not based on the MMS platform. As HST has amply demonstrated with five servicing missions, serviceability provides not only repair capability but also upgradability with superior instruments. Nevertheless, no serviceable spacecraft have been designed and launched subsequently to 1980s. The trend has been towards throwaway cubesats, but large spacecraft remain, and spacecraft keep failing [19]. Furthermore, each satellite failure diminishes the space environment by introducing either irreparable junk or a spacecraft of diminished capacity or longevity that must be replaced early.
OOS appears to have reached an impasse—much of the robotics technology has been developed, but there has been little in the way of commercial development. However, active debris removal has emerged as another application of the same technology which could potentially provide the final leverage to OOS as a space infrastructure capability. OOS itself also acts as a debris mitigation strategy—refuelling and servicing spacecraft at end-of-life will reduce the rate of creation of space junk using freeflyer tankers in the geostationary ring (perhaps supplying LH/LOX extracted from lunar water). Defunct parts may be replaced and/or upgraded, although this requires supply from Earth (though supply from lunar in situ resources remains an intriguing future possibility [20]). Still-functional parts such as antennas may also be salvaged from irreparable spacecraft and installed on reparable ones. Re-usable infrastructure hardware in the form of serviceable multi-purpose platforms may similarly be serviced and leased for on-orbit services (communications, navigation or remote sensing). However, here we are considering the direct application of space manipulators to active debris removal. Indeed, this scenario eases some of the more complex manipulations, such as the handling of thermal blankets and tape, which are considered the most difficult of manipulations, but these are not required for debris handling. Nevertheless, the requirement for interception, robust grappling, passivation and attachment of de-orbit devices remains.
4. Space Debris Mitigation
The space debris problem has provided an urgent impetus to space manipulator-based missions that have traditionally focussed on on-orbit servicing of satellites. There have been around 5000 successful rocket launches from Earth into orbit and beyond since the dawn of the space age in 1957 (most launchers carry more than one spacecraft). There are currently 1382 active spacecraft in orbit (of which 340 reside in or near GEO) around Earth (446 American, 135 Russian, 132 Chinese and the rest others). Of the additional 15,888 (2015) pieces of orbital debris larger than 10 cm in size (dominantly in LEO), 2682 are defunct spacecraft, 1907 are spent upper stages, and 11,299 are other fragments [21]. This does not include the estimated 500,000 untrackable debris pieces in the range 1–10 cm (similar to or larger than the calibre of many infantry weapons) and a further 108 pieces down to 1 mm in size from paint chips to solid droplets, 98% of which is artificial space debris [22]. Most of the debris has been caused by the first spacefaring nations—predominantly the USA and USSR. In LEO alone, there are an estimated 150 million fragments of human-created junk less than 1 mm in size, all travelling at 8–12 km/s (for comparison, a rifle bullet travels at only 1.2 km/s). Smaller debris ~1 mm in size can be protected against through Whipple shields though at the cost of mass suitable only for large and human-rated spacecraft. However, larger debris ~2–3 mm in size or larger cannot be shielded against. The most debris-polluted orbits reside at 800–1000 km altitude beyond where natural clearing by atmospheric-induced orbital decay can operate. It is estimated that there are also 31 non-operational nuclear reactors which used NaK coolant between 700–1500 km in altitude from Russian radar ocean reconnaissance satellites (RORSAT) launched in 1967–1988. In 1977, the Cosmos-954 reconnaissance satellite, carrying an onboard nuclear reactor supplied with 50 kg of uranium-235, began behaving erratically and re-entered Earth’s atmosphere without ejecting its reactor into a safe orbit as intended and scattered radioactive debris over a 600 km track in northern Canada. Although no injuries resulted, the cost of the subsequent clean-up operation was considerable. Although the probability of injury from re-entered debris is very small, in 1997, a piece of a spent Delta rocket struck a woman in Tulsa Oklahoma (though without injuring her) demonstrating that physical injury on Earth from space debris is plausible if remote. In LEO, the probability that a 10 m2 satellite will be impacted by trackable debris is 1 × 10−4/y, which increases to 2 × 10−3/y for smaller untrackable debris. The estimated risk of a single debris collision in GEO between tracked objects is around 3% over a 30-year mission lifetime. As debris collides with satellites, they fragment into clouds of further debris. The orbital debris population is tracked and mapped by the US Space Surveillance Network—detectable objects are larger than 10 cm in LEO and larger than 1 m in GEO though new telescopes being constructed will reduce these limits significantly.
It has become common operational practice to implement manoeuvres of active spacecraft to avoid collision with debris—for example, the ISS was manoeuvred into a 1 km higher orbit in 2001 to avoid collision with a Russian SL-8 upper stage (launched in 1971), and since then has had to be manoeuvred on average twice every year. In 1996, the boom of the French satellite Cerise was struck by debris from an exploded Ariane launcher shroud, although the mission was recovered through software workarounds. Indeed, NASA has developed a collision risk assessment process for its all high-value robotic spacecraft to prevent loss by collision with debris [23]. Satellite operators are being forced to undertake evasive manoeuvres on an increasingly frequent basis at the cost of scarce fuel—the defunct Telstar 401 and Galaxy 15 satellites have threatened operational satellites on several occasions.
Although there is a natural atmospheric cleansing process operating in LEO below 800 km altitude, it is the LEO population at 800–1000 km sun-synchronous polar orbits around 86–110° inclination that are close to the Kessler limit, which is expected to be reached by 2055. The Kessler limit is the point beyond which the debris population becomes self-perpetuating and grows uncontrollably [24]. The average growth rate of debris over the past 50 years has been around 300 objects/year but this is accelerating. Even if no further satellites were launched, the number of objects larger than 10 cm in the most populous ring (900–1000 km) will treble over the next 200 years due to debris-debris collision, increasing the collision rate by 10 times. The primary culprits for accelerating attainment of the Kessler limit were two specific events, one accidental and the other deliberate:
- (i)
- In 2007, a Chinese anti-satellite test on its defunct meteorological satellite Fengyun FY-1C generated 2400 debris pieces larger than 10 cm and 35,000 pieces below the resolution limit at 860 km altitude—too high for natural atmospheric cleaning—increasing the space debris population by 30%. By contrast, a US ship-mounted Aegis ballistic missile was launched in 2008 in response, destroying one of its ailing spy satellites USA 193 at a low altitude of 250 km to prevent uncontrolled re-entry to Earth and to maximise the rate of atmospheric sweeping and so minimise debris.
- (ii)
- In 2009, a 10 km/s collision occurred at inclination 72° N between the operational Iridium 33 satellite (at 86° inclination) and the decommissioned Cosmos 2251 (at 74° inclination). This generated two clouds of debris, (598 Iridium fragments and 1603 Cosmos fragments larger than 10 cm) at 790 km altitude.
Russian debris also collided with and terminated the mission of Ecuador’s first and only satellite, Pegasus, in 2013. Large objects can collide generating large amounts of debris—such breakups are estimated to occur at around 4–5 fragmentation events per year. If a 10 cm3 debris fragment collides with a 1200 kg spacecraft, ~106 fragments of ~mm size can be produced. Similarly, discarded rocket stages with residual fuel can explode generating large numbers of debris fragments. The collisional cascading effect of the Kessler syndrome will soon cause entrapment of the Earth.
Space debris has become a significant problem at all satellite-populated orbits, including GEO (Table 3). The primary source of debris resides in GTO (geostationary transfer orbit) within which some 239 objects intersect into the GEO ring. Within GEO itself which represents the greatest collision hazard, there are 1036 large tracked objects, only 340 of which are operational. However, a significant debris population of some 2000 small-scale objects greater than 10 cm size has been detected in GEO and GTO, in addition to the 1036 large objects presumably generated by fuel explosions of spent upper stages [25]. The most heavily spacecraft-populated longitudinal slots are around 75° East longitude (over India) and 105° West longitude (over the Pacific), primarily for telecommunications. The chief problem is that uncontrolled GEO platforms drift to these stable regions due to solar and lunar gravitational forces: between 1997–2003, 34 satellites were abandoned (mostly Russian), of which 22 librate over India and 10 over the Pacific. The probability of collision is given by [26]:
where ρ = spatial density (n/km3), vrel = relative collision velocity (km/s), A = collision cross-section of satellite (km2) and Δt = temporal duration of risk. Unlike at LEO, there is no natural cleansing mechanism at GEO.

Table 3.
Debris population in different utility orbits.
The UN General Assembly COPUOS (Committee on the Peaceful Uses of Outer Space) recommend guidelines to minimize further debris generation [27]. The primary means for debris mitigation must be the prevention of on-orbit breakup and de-orbit or re-orbit of dysfunctional satellites. There are three strategies for the mitigation of space debris [28]: (i) prevent on-orbit breakup; (ii) reduction of object creation during the mission; (iii) removal of objects after mission completion. It is the last option that concerns us here for which there are four further options [29]: (i) built-in self-disposal into graveyard orbits; (ii) robotic sweepers to remove small debris; (iii) retrieval of large objects such as spacecraft and spent stages; (iv) re-use of spent hardware (on-orbit servicing). To minimise debris in GEO, it is recommended by the International Telecommunications Union (ITU) that space assets are self-disposable and manoeuvred into a graveyard orbit at a minimum altitude h above GEO given by:
where CR = solar radiation pressure coefficient, A = spacecraft cross sectional area and m = spacecraft mass. This equates to an altitude range of 300–500 km higher than GEO, which equates to approximately 3 months of income-generating mission operations. With GEO satellites, there is a high compliance rate of 80% of 160 EOL satellites being boosted into disposal orbits close to 300 km above GEO despite there being no legislation [30]. However, early mortality can prevent such boosting, e.g., Skynet 4b was boosted into 150 km altitude above GEO. The GSV (geostationary servicing vehicle) was a proposed service concept for the disposal of spent satellites into graveyard orbits 245–435 km above GEO [31]. However, the current GEO graveyard will not be sustainable as its population grows. It has been proposed the GEO satellites might be delivered to a “Necropolis” at 36,386 km altitude (600 km above GEO) where would reside an 8 tonne truss-based stack (terminus) with a 12 m tower to which dead comsats are transported and attached by a 2.4 tonne ion engine-propelled tug spacecraft (hunter) with 0.5 tonnes xenon propellant [32,33]. End-of-life comsats would inject themselves into this new graveyard orbit, but failed comsats would be ferried. To prevent the explosions in upper stages that generate large numbers of fragments, a European code of conduct recommends that European launcher upper stage tanks be fully vented [34].
To minimise debris in LEO, it is recommended, but not mandatory, to ensure that space assets are removed within 25 years of EOL (only 14% and 8% of LEO spacecraft complied with this recommendation in 2010 and 2014 respectively). Perhaps even a 50-year removal timescale might suffice if it were observed [35], but this has never been realised. There have been recent proposals for large constellations of thousands of small satellites such as up to 12,000 for SpaceX. Existing de-orbiting strategies will require much more aggressive solutions than the current 25-year rule. DAMAGE (debris analysis and monitoring architecture to the geosynchronous environment) indicates that there is a nonlinear increase in the number of catastrophic collisions with constellation size [36]. An increase in cross section from 1 m2 to 6 m2 resulted in a much higher collision rate, but extension of satellite lifetime from 3 to 10 years reduced debris generation by 30%. If the strategy of satellite removal within 25 years were enacted in large constellations in LEO, it would obviate the mitigation effects of this strategy, and the prospects for extending it appear bleak [37]. Hence, self-disposal appears to be ineffective at LEO.
Removal of debris is the only effective solution, but small-scale removal of debris will likely be ineffective [38]. Debris sweeper concepts are based on the use of large vanes rotating like a windmill, but such solutions require very large areas. The only effective solution is the active removal of large space debris by deorbiting, especially in critical sun-synchronous orbits, to prevent them from collisionally fragmenting [39]. It has been determined that it would suffice to remove 5–10 large pieces of debris per year to prevent debris population growth in LEO [40]—these could begin with the large 26 m long Envisat spacecraft and 20 Zenith upper stages, especially in polar orbits close to 1000 km altitude [41]. In addition, some 295 identical SL-8/Kosmos upper stages reside in near circular orbits clustered around 760 km/74°, 970 km/83° and 1570 km/74°. This strategy is sensitive to several conditions such as launch rates, compliance with debris mitigation measures, etc. [42]. A strategy that includes both post-mission disposal and active debris removal offers the best approach—a reduction of disposal timescale by one year reduces the annual number of collisions by 0.53 and the removal of one object reduces the annual number of collisions by 2.94 when employed synergistically, i.e., one active debris removal equates to a reduction in post-mission disposal of 5.5 years [43].
Issues that must be addressed during close proximity operations include minimisation of breakup and debris generation during debris removal. The robotic scenario comprises several well-defined phases: (i) approach—chaser acquires position around 10–25 m away aligned to the target with manipulators stowed; (ii) deployment—manipulators are deployed to capture the target by specific grapple points; (iii) grasp—manipulators engage the target at the grapple points; (iv) post-grasp—manipulators are locked and detumbling manoeuvres performed; (v) de-orbit—apogee engine kit is attached for de-orbit manoeuvre to drop perigee to <650 km altitude and engaged (for a 25 year decay by atmospheric drag). A representative scenario has been described in [44]. H-bar approach and approach along orbit motion is passively unsafe, favouring an approach against orbital motion [45]. Passive approaches to de-orbiting debris exploit perturbing forces such as aerodynamic surfaces, electrodynamic tether, etc. A passive strategy that exploits solar radiation pressure and Earth’s oblateness could be adopted for MEO spacecraft such as global navigation satellites but requires high area-to-mass ratios except for satellites in Molniya orbits [46]. A chaser satellite mounting a robotic arm, robotic tentacles, a harpoon or a deployable net have been the commonest proposals for debris removal. The robotic arm and harpoon require precise targeting and the robotic arm and tentacles require close proximity to the target. ROGER (Robotic Geostationary Orbit Restorer) was a net-based concept for GEO satellite recovery to reduce the incidence of large space debris [47]. Two potential capture mechanisms were envisaged—a net capture or tether-based gripper with the former favoured—to stabilise and dampen its relative rotation to zero. The expandable net capture system is based on the deployment of four flying weights to pull out the net. The tether gripper system is a tether deployed free flyer system front end. ESA’s e.Deorbit project before its cancellation was to involve robotic arms to capture its target [48] while the EC’s removeDEBRIS project will explore harpoons and nets for de-orbiting at LEO. Tethered harpoons with conical tips have been proposed for attaching a chaser to debris with a safe standoff distance with perforation energy given by De Marre’s formula: where k = 37 × 107 for aluminium, d = cone base diameter, b = target thickness. Harpoon tests at low temperature indicate brittle fracture in the target but without spallation or fragmentation into the internal space [49]. Tethered nets on the other hand can cause damage to appendages on spacecraft releasing debris. Harpoons and nets are the most likely capture mechanisms to cause breakage and the creation of more debris. Furthermore, both are remote capture mechanisms that are not compatible with tumbling spacecraft targets. Towing with flexible tethers introduces problems with employing thrusters to accelerate/decelerate. A mechanical tether may be employed to re-orbit debris into disposal orbits [50,51] but they are impractically long. This suggests that the e.Deorbit approach was more versatile than that of removeDEBRIS.
Debris mitigation is a role to which robotic on-orbit servicers can naturally adapt themselves. Robotic capture is the most controllable approach in which the debris is captured, manoeuvred to a lower orbit (at LEO) or graveyard orbit (at GEO) and/or a de-orbit device attached (such as propulsive units, tethers, sails or ballutes). Capture requires that the robotic spacecraft control its orbit and attitude to reduce the relative motion between the chaser and the target. A Kalman filter algorithm must estimate the target motion in order to plan the gripper trajectories for grappling with minimum impact [52]. Many of the critical dynamic parameters—specifically kinematic variables—of the target can be obtained by estimation through the Kalman filter based on visual data. CAD models can provide accurate estimates of mass and moment of inertia, but it is feasible to estimate these values if only approximately if shape has been determined visually and assuming a generic spacecraft model with assumptions regarding mass distribution—for a common launch shroud, this should be feasible. Critical to robotic capture is the implementation of force/torque control to acquire and brake the debris target. It has been proposed that electrostatic torques may be employed to detumble the target without physical contact to <1°/s from the typical 30°/s tumbling [53]. This involves controlling the servicer’s electrostatic potential using an electron gun to beam charges to the closest feature on the rotating target. However, the feasibility of this approach has yet to demonstrated. An extendible brush of PTFE bristles at the tips of the robotic fingers may be employed to contact and tap the surface of the target to reduce high rotation rates to a manageable level for robotic capture [54]. The frictional force for a bristle model is defined by:
where where δ(t) = bristle displacement, , k = bristle stiffness, = relative tangential velocity, δmax = maximum bristle displacement, μ = surface friction. During braking, joint error control may be based on impedance control:
where FB = braking force on target, θi = joint angle, = joint stiffness, JT = Jacobian transpose, which relates stiffness at the end effector to stiffness at joints. During capture, an active compliance control law is given by:
where Ii = joint i inertia, τi = measured joint torque, bi = joint viscosity coefficient. It has been determined that for handling and stabilising upper stages during de-orbit, the appropriate clamping points are at the payload fairing adaptor ring, which is designed to tolerate clamping forces and torques [55]. Two or three manipulators permit distribution of grappling forces/torques equally around the ring. For example, the DLR arm can capture a 7-tonne satellite spinning at 4°/s without exceeding its maximum torque limit of 120 Nm. Post-capture detumbling can exploit the kinematic redundancy of the spacecraft-mounted manipulator [56].
Active de-orbiting of debris requires propulsive capabilities attached to the target to ensure disposal. Re-entry may be controlled or passive—controlled direct re-entry is more efficient than passive uncontrolled re-entry, but the latter is simpler. Controlled de-orbiting is essential to remove larger pieces of debris ~500–1000 kg which could potentially survive re-entry. Nominally, this requires robotic attachment of a propulsion stage to the debris to de-orbit it. Contactless methods of disposing of debris include ion beam shepherding. This involves generating a beam of ions from two sets of ion engines along the same axis by pointing in opposite directions. The chaser directs one ion beam onto the debris to generate thrust on it. The reaction thrust on the chaser is cancelled by the other engine, generating an opposing thrust to maintain a constant distance to the debris. Solar concentrators have been proposed to deflect asteroids by inducing thrust from ablated material, a technique that may be adapted to active debris disposal [57] but requires dynamic stability. Electrodynamic propulsion offers a potentially propellantless option for debris transport [58]. A 1–5 km long conducting electrodynamic tether which mounts solar panels rotating at 6–8 times every orbit generates current which interacts with the Earth’s magnetic field. Electrodynamic thrust is generated when current flows through a conductor in the Earth’s geomagnetic field. The conductor must close the current loop through the ambient plasma by electron emission through hollow cathodes and electron collection to the bare conducting cable. The tether is attached to the debris and uses electrodynamic drag generated by Lorentz JxB forces to remove debris from low Earth orbit [59]. Lorenz forces allow it to manoeuvre by altering the current to match the orbit of the target to be captured by a robotic hand or net. ElectroDynamic Debris Eliminator (EDDE) uses a long conducting tether to manoeuvre in the Earth’s magnetic field powered by solar arrays but consuming no propellant. Small nets at either end of the tether with solar arrays attached at the middle catch debris in the nets and release them at lower altitude to increase the rate of orbital decay. A dozen 100 kg electrodynamic debris eliminators (EDDE) mounted onto one launch adaptor ring can remove 80% of all 2 kg + objects in LEO (concentrating on 71–74°, 81–83° and sun synchronous orbits) in 7 years (1000 tonnes in total). The electrodynamic tether linking the chaser and the target debris captured by a compliant grappling end effector at the end of the tether is a variation on the concept [60]. However, electrodynamic tethers are still subject to a significant probability of being severed by debris, though this be can partially obviated through double line tethers [61]. A deployable large-area drag-sail or ballute may be used to de-orbit debris from LEO below 1000 km altitude [62]. SSTL’s TechDemo-Sat-1 was launched in 2014 fitted with a deployable de-orbit sail acting as a drag brake to orient the satellite target for de-orbiting and re-entry disposal. However, deployed drag devices introduce the potential for further collision in crossing multiple orbits with a wide area membrane while rocket apogee engines impose a prohibitive propellant and mass requirement.
Nevertheless, the most plausible solution for de-orbiting is to either attach a dedicated propulsive stage to de-orbit the debris sacrificially or to employ a reusable, refuellable robotic system that acquires the debris and releases it in a disposal orbit. It has been determined that a single 2000 kg robotic spacecraft (of which 1400 kg is propellant) could remove 35 upper stage rocket bodies from 700–900 km polar orbit using solid rocket de-orbit kits over 7 years with 8 resupply missions [63]. This is similar to the ATLAS concept introduced later (Figure 1). Scheduling of consecutive debris removal operations is an NP-hard travelling salesman problem which has a branch-and-bound solution to minimise the propellant cost and manoeuvre time that is tractable for 5 removals but not for 10 [64]. A branch-and-prune strategy using low-thrust propulsion may be more efficient [65]. A multi-servicer approach invites ant colony optimisation routing and coordination through auction bidding [66]. In GEO orbit, the optimal schedule is to manoeuvre in an anti-orbit direction for minimum Δv [67]. Approximately, 400–500 m/s manoeuvres are required to acquire each target and 250 m/s is required for de-orbiting the upper stage rocket body. It appears that the robotic servicer concept with mounted manipulators is the most viable for active debris removal.

Figure 1.
Dual manipulator servicer ATLAS (advanced telerobotic actuation system) concept.
5. Space Manipulator Operations—Evolution from Teleoperation to Autonomy
All robotic systems employ cameras for visual feedback, and there are several common camera configurations. The camera configuration for a space robot typically comprises at least one mast-mounted binocular camera mounted onto the spacecraft for a global view of the workspace and another camera mounted onto the elbow and/or wrist (eye-in-hand) for close-up observation of manipulation tasks. For example, SRMS mounted one pan-tilt camera at the elbow and another at the end-effector; similarly, SSRMS mounted one pan-tilt camera at each side of the elbow and one pan-tilt camera at each end-effector. Vision-based relative navigation for inspecting uncooperative satellites have been addressed using a stereocamera and three-axis gyroscopes [68]. On-orbit servicing manipulation requires more complex vision processing under variable illumination conditions, however. One plausible assumption on servicing satellite targets is that partial cooperation with attitude control may be available but no visual markers are likely to be discernible [69]. The vision system will have to employ template recognition methods derived from CAD files. However, an unscented Kalman filter can estimate shape and relative attitude, position and velocity of a satellite target by building a 3D map of points from features detected by a monocular camera and LIDAR on the chaser [70]. This suggests that template-matching with a priori data may be dispensed with, but a priori model data does yield superior accuracy [71]. There are multiple transforms between coordinate frames to convert between cameras, pan-tilt units and the end effector [72]. Pose-based visual servoing provides closed-loop feedback control from the error between desired and actual poses in images of the 3D workspace. Pose-based visual servoing is based on the image Jacobian that relates the 3D object pose to the 2D image. The target coordinates (xt,yt,zt) are related to equivalent camera coordinates (xc,yc,zc) by a 3 × 3 rotation (direction cosine) matrix. A pinhole camera model relates 3D camera coordinates (xc,yc,zc) to image projection coordinates (x,y):
where f = camera focal length. To compensate for jittering and other perturbations, an extended Kalman filter may be employed using the pin-hole camera model [73]. In image-based visual servoing, only image coordinates are computed. Feature-based servoing is the most common form of visual servoing [74]. Features begin with object image definition—the “snake” (active contour model) is a deformable curve that extracts object shape by shrink wrapping around object contours on an image based on energy minimisation [75]. The energy minimum lies on the edges of the object image and requires the computation of gradient masks. Feature matching may be achieved through the principle of maximum entropy. To robustify image-based visual servoing, the extended Kalman filter may be employed to estimate feature motion in images [76]. Kalman filters are suited to visual object tracking [77] and an adaptive extended Kalman filter has been applied visual servoing of non-cooperative satellite targets for manipulator capture [78]. Intensity-based servoing offers robustness without the need for feature extraction or pose estimation [79]. Generalised angle representation which is translation, rotation and scale invariant offers a rapid means of computing shape [80]. Laser scanning offers a means to supplement vision with range-finding uncorrupted by scene illumination [81]. The photonic mixer device (PMD) camera exploits phase shift measurements (rather than intensity) to extract range and generate 3D images making them ideal for spacecraft pose estimation at short range during capture [82].
Careful attention must be paid to human-computer interfacing (HCI) technologies for robotic servicer missions [83]. HCI defines the nature of ground station support to the servicer and is critical to the function of the robotic spacecraft. In teleoperative mode, the ground operator controls the remote robot directly through bilateral reflection of operator movements, e.g., Lunakhods 1 and 2 on the moon. End-effector (egocentric) referenced control gives enhanced performance over fixed world (exocentric) referenced control [84]. A minimum time of 20 min is required to capture a tumbling target—this will require more than one ground station for LEO operations which typically has an 8-min ground contact window. Alternatively, a GEO relay such as TDRSS may be used, but this introduces significant signal time delays. There are several challenges to teleoperative on-orbit servicing missions—time delay and jitter [85]. Time delays in teleoperation of a slave manipulator at a remote site by a human operator (master) invoke move-and-wait behaviours in which human input is followed by waiting for the response before initiating further corrective inputs. This is inefficient. PID controllers are sensitive to time delays due to the integral term as it reacts too quickly to errors. The Smith predictor is a model-based predictive controller [86]. It feeds back the predicted response immediately and the prediction error once the real response has been measured after the time delay. There are two feedback loops—a normal outer feedback loop that feeds the output of the plant back to the input subject to time delay and an inner feedback loop which predicts the current unobserved output of the plant. The Smith predictor at the master (operator) side in relation to the slave (remote) side is given by:
where Δt = two-way time delay, = delayed plant, = predicted plant model without delay, τ = plant time constant. Stability requires an accurate model of dynamics to minimise prediction errors and stability is not guaranteed unless model errors are zero. The Smith predictor compensates for known constant time delays of short duration. It is sensitive to mismatches between the actual Gs(s) and estimated . A Kalman filter may be employed to reduce the estimation error. The most common approach to overcoming the problem of time delays is to employ predictive graphical displays [87,88]. Predictive displays involve graphical models of the slave robot and its environment which project its predicted behaviour to compensate for time delays. The higher the fidelity of the model to reality the better the prediction but this has computational costs. It has been demonstrated with the ETS-VII satellite that 7 s time delays in the ground teleoperation control loop can be accommodated readily through predictive graphics based on environmental models [89]. However, this assumes an environment that exhibits only very low-speed dynamic behaviour and is highly predictable. ETS-VII’s environment was a controlled target, but this will not be so for active debris removal. Reduction of the 5–7 s time delay in GEO-based teleoperation may be achieved through dedicated high-capacity lines from the ground station directly connected to the antenna (rather than across traditional internet routing and protocol overheads), which can reduce round trip time delays to GEO to <1 s. There will still be time delays however for LEO operation and beyond through TDRSS. Time delays between the transmission of the commanding signal to the remote robot and the return of feedback to the operator beyond 1–2 s introduce stability issues.
The implementation of force/tactile/haptic feedback control introduces further significant instability difficulties inherent in such time delays. Direct bilateral force teleoperation is based on haptic feedback from the remote robot (slave) to the human operator (master) [90]. A haptic interface is a bidirectional device that permits the human operator to experience the applied forces at the remote site at high update rate. Transparency requires that the impedance from the remote site Ze must be transmitted to the human operator Zt without distortion such that where fm,s = master/slave forces, vm = master/slave velocities. However, perfect transparency requires zero inertia and infinite bandwidth through instantaneous channels. Direct bilateral force-reflecting feedback is a major problem for time-delayed teleoperated systems in generating instability due to mismatched dynamics. Time delays in transmitting force feedback from the slave to the master generate instabilities particularly beyond 500 msec corresponding to human reaction speed. Any latent time delays beyond this tend to increase task error rates and completion times due to move-and-wait strategies being adopted by the human operator. The robust H∞ controller with μ-synthesis can provide stability for prespecified short time delays only [91]. In this case, the use of calibrated 3D graphical predictive displays overlying the actual view of the remote robot permits the operator to interact with the models in real-time [88]. High model dynamics fidelity and accurate least squares calibration is essential. Impedance control has been proposed for bilateral force reflection in teleoperation [92]. Short time delays of up 100 msec have the effect of increasing effective impedance during capture operations while reliable capture favours minimising manipulator impedance to minimise the manipulator contact force [93]. A real-time teleoperative link with telepresence requires a very low latency of ~50 msec or less for effective force reflection. Nevertheless, force feedback of remote forces with a PD feedback controller may be used under significant time delays ~1–2 s and beyond, albeit at much reduced task performance rates. Force reflecting hand controllers can utilise attractive and repulsive potential fields of virtual forces at the remote end effector to form virtual corridors that output predictive forces at the hand controller to indicate the desired motion required by the operator [94,95].
The main approaches to dealing with stable teleoperation with constant time delay are [96]: (a) passivity theory; (b) hybrid compliance control/impedance matching control; (c) model predictive control; and (d) adaptive control. Shared compliant control involves autonomously closing the feedback loop at the robot (slave) side which also employs a passively compliant hand the response of which was fed back to the human operator [97]. It involves reducing the force reflection signal by reducing the error between the master and delayed slave positions. Model predictive controllers which implement learned models will possess similar advantages to predictive graphics. Passivity-based approaches do not require models of the environment, unlike predictive approaches. Passivity theory dictates the transfer of velocity and force information between master and slave [98]. A system is passive if the power of the system is either stored or dissipated:
If power dissipation is positive, the system is passive. Adding a dissipative term to both master and slave PD controllers introduces passivity to guarantee stability [99]:
where = master position error, = master velocity error, = slave position error, = slave velocity error, kd = Δtkp = dissipative gain, Δkd = additional damping, Δt = time delay. There is also a considerably more complex adaptive version of passivity stable to positional drift between master and slave [100]. The master/slave joint torques are determined by the adaptive regressor and synchronised coordinating joint torques and for master and slave arms respectively:
where , , = reference position tracking, Yl(.) = known dynamic parameters, = estimated unknown dynamic parameters, l = master or slave, λ = scale constant > 0, K = gain constant > 0. Adaptive bilateral hybrid position/force control synchronisation of master-slave teleoperation may be enforced through the imposition of holonomic constraints [101]. These schemes require a constant time delay Δt.
For varying time delays, wave variables compute energy flows to determine excess energy and eliminate force reflection waves between the remote and operator robotic devices by matching their characteristic impedances [102,103]. Velocity and force at the master and slave are encoded into time-delay robust wave variables which are subsequently transmitted between master and slave manipulators:
where Z = wave impedance, which tunes the degree of stiffness/compliance. Wave-based communications occurs at a natural frequency , where Δt = time delay. As wave variables encode velocity and force, so wave integrals encode position x and momentum p:
Wave variables automatically exhibit passivity. Wave variables can be combined with Smith predictors to impart stability to the Smith predictor. More recent approaches have incorporated sliding mode controllers and generalised predictive controllers [104].
It has been suggested that passivity-based methods offer guaranteed stability to time delays over shared compliance control which can only tolerate maximum time delays of the order of human reaction speed of ~0.1–0.2 s, but experimental results dispute this limitation [105]. The tele-impedance approach is an alternative to bilateral force-reflecting teleoperation which combines position reference with a stiffness reference, the latter being determined from non-intrusive EMG (electromyographic) measurements from the human operator’s arm [106]. Spring-like compliance at the remote end effector in contact-and-grasp tasks on hard environmental objects dramatically improves teleoperation performance and alleviates the problem of rapid buildup of transient forces on collision [107,108]. Specific applications of teleoperation with time delays of 5–10 s are discussed in [109], which concludes that predictive simulation is essential in time-delayed teleoperation. The implementation of predictors and simulators introduces aspects of autonomy—this is the telerobotic mode. In telerobotic mode, the ground operator uploads designated waypoints which the robot implements locally by autonomously planning and executing a global path while avoiding obstacles, e.g., Sojourner on Mars. The evolution toward autonomy is important for several reasons, but mostly because it requires considerable computational resources onboard. This places a premium on solving manipulator control problems as low down the control hierarchy as is feasible.
6. Freeflyer Manipulator Kinematics
In rendezvous and docking (RVD) manoeuvres, the chaser moves to a proximity position ~100–300 m from the target before manoeuvring a series of inspection flyarounds culminating in a V-bar dock [110]. V-bar involves manoeuvring the chaser horizontally along the same orbital velocity vector of the target; R-bar involves manoeuvring the chaser radially along the radial vector from a different orbit than the target. The relative (circular) orbits of the chaser spacecraft and the target spacecraft are described by the Clohessy-Wilshire version of the Hill equations with respect to the target satellite. The Clohessy-Wiltshire equations describe the phasing manoeuvres for a rendezvous between the chaser and the target. In approaching a tumbling satellite, the chaser matches its angular velocity with the line of sight rotation of the target before grappling. Our concern here is primarily with the subsequent phases of a servicing missions.
A spacecraft mounting one or more manipulators comprises a chain of multiple bodies of n + 1 rigid bodies connected by n single degree of freedom joints. The first body i = 0 is the spacecraft mount, from which n serial links emanate (plus payload n + 1). The dynamics of this multibody system are based on the conservation of momentum. The barycentric approach to multibody dynamics also locates the system centre of mass. The mounting point of a spacecraft-mounted manipulator is not fixed inertially (unlike in a ground-based manipulator). Furthermore, the system operates under zero-gravity conditions. Inertial coordinates are defined with respect to the system centre of mass which is invariant (i.e., a locally inertial coordinate), and spacecraft base coordinates are defined with respect to the centre of mass (centroid) of the spacecraft base. There are two types of dynamic situation: (i) freefloating systems in which the manipulators are the only actuators, so spacecraft attitude is nominally uncontrolled (with six joint actuators controlling a 12 degree of freedom system, this is an underactuated (redundant) system [111]); (ii) freeflying systems in which the manipulators are controlled by manipulator actuators while spacecraft attitude is controlled by attitude actuators. Due to dynamic coupling, motion of the manipulator affects the position and attitude of the spacecraft base in both cases. Manipulator joints incorporate spinning motors which act like gyroscopes on rotating levers with strong Coriolis and centrifugal forces [112]. For example, SRMS had motor gear ratios of 749:1 to 1842:1, so the motors were spinning up to 2000 times the link rotation, enabling high torque amplification at the manipulator joints, but with a significant effect on attitude stabilisation. In freeflyers, the spacecraft base is attitude controlled. While translational control requires the expenditure of propellant, attitude control does not necessarily require fuel expenditure. Although it is possible to stabilise the spacecraft position as well as attitude, this would require the expenditure of propellant thereby limiting the viability of such a spacecraft. Spacecraft position must therefore be uncontrolled in both freeflying and freefloating conditions. Currently, robotic manipulators are operated in free-floating mode with uncontrolled attitude. However, this requires constant adjustment on behalf of the ground operator. For example, the ETS-VII mission employed resolved rate control using the generalised Jacobian computed on the ground, so the attitude control system was switched off [113]. This caused the end effector pitch error to increase rapidly at 0.5–1° over several minutes until compensated for at the end of the motion by reaction wheels. Hence, the generalised Jacobian did not implement effective attitude control due to deficiencies in the available hardware (not the algorithm itself). Gravity gradient torques acting on the ETS-VII spacecraft over short timescales generated free drift of the spacecraft. Given that accuracies of 0.01–0.1° are required for grasping during the final target approach, attitude should be controlled. The control of attitude is also essential to maintain pointing requirements of solar panels to the sun and antennae to the Earth. Active attitude control is desirable particularly under conditions of higher levels of autonomy. A dedicated attitude control system will be required when the manipulators are not in operation, and indeed, all spacecraft possess attitude control systems to compensate for attitude perturbations. Both the SRMS and SPDM had limited angular position accuracy of 1° compared with <0.1° for reaction wheels. The spacecraft base attitude may be controlled using internal angular momentum management devices such as reaction wheels, momentum wheels and/or control moment gyroscopes. The wheels or gimbals are mounted in orthogonal directions often with a fourth skewed wheel for redundancy. The strawman robotic servicer that we have adopted is the ATLAS (advanced telerobotic actuation system) concept for LEO servicing with a wet mass of 1425 kg (of which 476 kg is propellant) (Figure 1). It is configured with two identical manipulators with a mass of 45 kg each (with a similar kinematic structure as the PUMA 560/600 but with inline outboard joints from the shoulder), including grappling end effector but excluding payload (assumed to be a 225 kg ORU typical of MMS design). We consider initially that one manipulator remains stowed to emulate single-manipulator operation and it employs control moment gyroscopes for three-axis stabilisation.
Lie groups is an alternative representation of kinematics that uses the product of exponentials formulation [114,115], but we have adopted the more familiar and more intuitive Denavit-Hartenburg matrix representation. Manipulator kinematics define the relationship between the manipulator joint angles, link geometry and the end effector position and orientation. For ground-mounted manipulators, they are given by:
where q = cartesian generalised position/orientation of end effector, = cartesian generalised velocities of end effector, = cartesian generalised accelerations of end effector, v = translational cartesian end effector velocity, w = angular cartesian end effector velocity, θ = manipulator joint angles, = manipulator joint velocities, = manipulator joint accelerations, f(θ) = cumulative Denavit-Hartenburg transform, J = manipulator Jacobian, = differential of Jacobian. For control purposes, these need to be inverted to yield joint kinematic parameters in terms of cartesian kinematic parameters. For a space-based manipulator, the reference body is typically selected to be the mounting spacecraft though it can be any body of the kinematic chain [116] (Figure 2). The situation for space-based manipulators requires the imposition of constraints—conservation of momentum—to yield solutions.
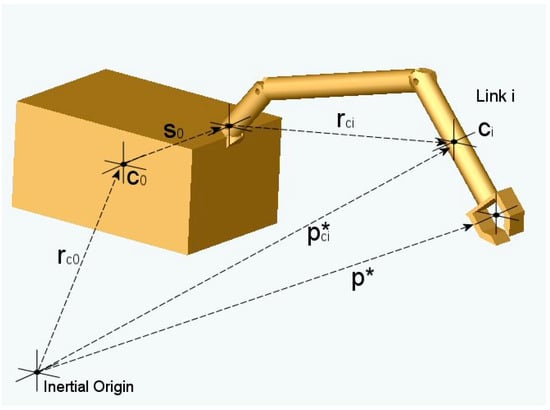
Figure 2.
Kinematic configuration of a single-manipulator mounted spacecraft servicer.
Holonomic systems can be integrated from velocity relations to position relations whereas nonholonomic systems cannot be so integrated. Conservation of linear and angular momentum states:
Conservation of linear momentum as a holonomic system can be integrated into the equilibrium of moments principle:
Conservation of angular momentum is not integrable due to the non-commutativity of rotation and so is a non-holonomic constraint. The non-holonomic character of the freefloating system arises due to the non-integrability of angular momentum. Different end effector paths to the same cartesian end effector position will result in different spacecraft attitudes. Solutions can be obtained through the introduction of manipulator “coning” motion onto the desired manipulator trajectory to maintain attitude stabilisation, but this is a rather ungainly approach, as well as having a high risk of collision. With two arms, one can perform the required task while the other undergoes coning motion to stabilise the base “bucking bronco” style, but the ungainliness, as well as collision hazard, remains. The holonomy/non-holonomy division suggests that separate treatment of linear kinematics and angular kinematics may be warranted. While it is possible to separate the motion of the spacecraft base and the mounted manipulator [117], a more natural separation is between the linear and angular aspects of the system dynamics.
We have adopted a 6-degrees-of-freedom manipulator, but such manipulators can suffer from singular configurations. A singularity occurs when the manipulator Jacobian loses rank, i.e., a degree of freedom. Singular configurations may occur when |JTJ| = 0, but they are predictable from the kinematics. From this, manipulability is defined by . To eliminate singularities, redundant joints may be added. It is often assumed that the spacecraft-mounted manipulator possesses 7 degrees of freedom for kinematic redundancy for greater manipulability, e.g., SSRMS. Kinematic redundancy offers great flexibility of postures for any given task but it requires the Moore-Penrose pseudoinverse of the Jacobian matrix for solution, where = Moore-Penrose pseudoinverse. Several performance conditions can be incorporated:
where represents a projection onto the nullspace of J while z is the nullspace vector. For example, the damped least square inverse Jacobian includes a damping factor for greater smoothness in the neighbourhood of singularities [118,119]: where λ = damping factor. The additional redundant degree of freedom comes at the cost of additional mass imposed by the extra joint and the Moore-Penrose pseudoinverse is more complex to compute compared to the standard Jacobian. Since a freeflying servicing spacecraft provides a re-orientable spacecraft mount for the manipulator, a 6-degrees-of-freedom manipulator may be more appropriate (though the formulation we present is applicable to any kinematic configuration).
We have generalised the approach used for a shuttle-mounted manipulator employing attitude control [120,121] to any kinematic configuration [122,123]. This is the freeflyer approach. For a freeflying manipulator with n links plus a payload n + 1 mounted on a spacecraft of mass m0 employing dedicated attitude control of the spacecraft mount, the Denavit-Hartenburg matrix may be represented as:
where = R = 3 × 3 rotation matrix identical to terrestrial manipulators, n = 3 × 1 normal vector, s = 3 × 1 slide vector, a = 3 × 1 approach vector
= inertial end effector cartesian position
= system centre of mass location (inertially invariant) from equilibrium of moments
= lumped kinematic link parameter, mT = total mass of the system, pci* = inertial position of body i centre of mass, rc0 = vector from inertial coordinates to spacecraft base centre of mass (initially coincident), rn+1 = vector from the end effector to the payload centre of mass (virtual stick), R0 = diag(111) = nominal fixed spacecraft attitude, Ri = rotation matrix for link i with respect to joint i − 1, li = ri + si = length of link i, ri = vector from joint i − 1 to link i centre of mass, si = vector from joint i to link i centre of mass. Our formulation is very similar to that of several others. The connection barycentre defines the location of the centre of mass of each link by weighting joint i by the mass of inboard and outboard links [124]:
The virtual manipulator (VM) approach assumes a serial link chain of zero mass with its base fixed in inertial space at the spacecraft-manipulator system centre of mass (virtual ground) and whose end effector coincides with that of the real manipulator [125,126]. The dynamically equivalent manipulator (DEM) is similar to the VM approach in that it is a virtual manipulator with its base fixed to the centre of mass of the spacecraft-manipulator system. Although the spacecraft base is fixed, the first joint at the manipulator mount is spherical and passive with the end effector coinciding with the real one [127]. According to the dynamically equivalent manipulator model (DEM), the position of the spacecraft mount is given by:
where and
The difference between our formulation and the others is that our formulation maps from joint to joint rather than link centroid to link centroid—this is essential as a step towards driving the joint motors. This permits our formulation to be used directly into the standard terrestrial robotic manipulator algorithms including the Denavit-Hartenburg matrix and Newton-Euler dynamics with only minor changes, namely the link length parameters. Joint trajectories for a space manipulator may be parametrised by polynomials similar to a terrestrial manipulator [128]. The inverse solutions follow from the relative position of the end effector with respect to the manipulator mounting point:
The wrist angles follow from the wrist orientation identically as in the terrestrial manipulator case. We may differentiate our inertial position into velocity:
We retain the general case of a variable attitude permitting derivation of the generalised Jacobian [129,130]:
= manipulator Jacobian
Now,
where Ds = inertia matrix of spacecraft, Dm = inertia matrix of manipulator
Hence,
The generalised Jacobian thus incorporates dynamic as well as kinematic parameters. Its computational complexity can be compared with a traditional Jacobian (Table 4) [131]. For N manipulator arms with n DOF each, the generalised Jacobian has a complexity of (156 + 6N)n + 87 Multiplications and (126 + 6N)n + 6N + 53 additions. The issue of computational complexity becomes acute in the inversion of the Jacobian required for the inverse kinematics. The importance of algorithm development may be illustrated by the replacement of Gaussian elimination (used in Jacobian inversion) with a complexity of O(n3/3) with Levinson’s recursion with a reduced complexity of O(n2 + 2n). The higher computational complexity of the generalised Jacobian favours splitting the computational load between the manipulator control system and a dedicated attitude control system.

Table 4.
Computational complexity of Jacobians.
Singularities in terrestrial manipulators are purely kinematic because the Jacobian is kinematic. Singular joint configurations in freefloaters cannot be mapped into unique points in the cartesian workspace because the generalised Jacobian is a dynamic function rather than a purely kinematic function like the traditional Jacobian. These singularities cannot be predicted from the kinematic configuration alone because they are functions of the history of the end effector path (as a consequence of the non-commutativity of rotations) [132]. The generalised Jacobian suffers from dynamic singularities that are unpredictable [133]. Dynamic singularities are configuration and path dependent making path planning challenging. One approach to combat this is to introduce singular value decomposition to obtain a pseudoinverse of the generalised Jacobian [134,135]. The pseudoinverse has a severe computational cost in making the already complex generalised Jacobian even more complex.
We can simplify the generalised Jacobian formulation by adopting the freeflyer approach, which employs attitude control so that = 0, Js = 0 and w0 = 0 yielding the extended Jacobian:
Since by definition, since s0 is fixed and , because any grasp is invariant:
This extended Jacobian Jm is different to the manipulator Jacobian Jm′ earlier in Equation (35) in that it incorporates parameters related to the spacecraft base. The cross-product formulation of the Jacobian can be derived similarly:
Resolved acceleration follows directly by differentiation:
Whereas the generalised Jacobian suffers from unpredictable dynamic singularities, the extended Jacobian (equivalent to the “dynamic” Jacobian [136]) is dependent on kinematic parameters and masses which are fixed, and so singularities are kinematic in nature and predictable. Hence, the implementation of attitude measurement and control solves the problem of unpredictability of dynamic singularities [119]. Nevertheless, the spacecraft base does translate, but does not rotate:
Due to the desirability of maintaining a stable spacecraft attitude in freefloaters, many efforts have focussed on minimising reaction disturbances from the manipulator to the mounting base, e.g., visual servoing requires stabilisation of spacecraft attitude [137]. The implementation of cycling motion superimposed over the desired trajectory acts equivalently to a set of reaction wheels [138], but this introduces the potential for collision in grasping a target. The reaction null space approach exploited null space to simultaneously control spacecraft attitude and manipulator joint angles by applying a cost function to the pseudoinverse to minimise reaction torques on the spacecraft. [139,140]:
where ζ = null space vector of dimension n − 3. The reactionless approach to satellite capture by a manipulator exploits reaction null space to eliminate attitude movements of the mounting base [141]. To ensure that the robotic arm movements do not affect the base, the coupling momentum must be zero, so the manipulator joint rates are given by:
where Dc = coupling inertia between base and robotic arm, = null space vector of Dc of dimension n − 3. The internal degrees of freedom allow the specification of zero reaction on the base. This is an extremely computationally intensive solution, even more complex than the generalised Jacobian. One means to reduce the computational complexity is to adopt a Jacobian transpose approximation of the form over model-based controllers [142]. For example, the Jacobian transpose can implement a version of the damped least squares inverse [143]:
It trades off accuracy against feasibility through the weighting factor. The enhanced disturbance map (DM) is a path planning algorithm that selects manipulator paths that minimise base attitude disturbances but this approach was also highly complex [144]. A bidirectional approach exploited a Lyapunov function to regulate both manipulator joint angles and spacecraft attitude searching from start-to-goal and from goal-to-start configurations simultaneously, but again at the cost of high computational complexity [145]. It utilises the Moore-Penrose pseudo-inverse of the generalized Jacobian to overcome dynamic singularities using the redundant degrees of freedom. The path-independent workspace is the workspace in which there are no dynamic singularities, but it is smaller than the enclosing path-dependent workspace in which dynamic singularities can occur [146]. The large search spaces invoked by most of these path planning techniques introduce the possibility of using techniques such as genetic algorithms, but they are unsuited to real-time operation. Hence, the computational complexity of these methods renders them unsuitable for space manipulators.
Many of the issues associated with free-floating manipulators vanish with free-flying manipulators with a stabilised spacecraft attitude. Indeed, dedicated attitude control system are employed on all spacecraft. This eases many of the computational complexity problems associated with freefloating systems. The reaction of the robot manipulator dynamics on the mounting spacecraft must be compensated for to maintain a stable attitude.
7. Freeflyer Manipulator Dynamics
The dynamics formulation of robotic manipulators exploits the manipulator kinematics to determine the joint torques. The Lagrange-Euler formulation of manipulator dynamics is given by:
where Dm = manipulator inertia, Cm = manipulator coriolis/centrifugal forces, Fext = external forces, F = friction.
Of particular note, the frictional term in the Lagrange-Euler formulation hides a high degree of complexity. Effective friction compensation requires accurate friction models. The simplest models of friction characterise slip as a combination of static friction, Coulomb (dynamic) friction and viscous friction which varies in proportion to load and opposes motion independent of contact area. Static friction can be reduced below the level of Coulomb friction through the use of lubricants so that stick-slip will be eliminated, e.g., static friction is typically ~0.02 Nm compared with viscous friction of ~0.1 Nm (except in ageing motors). Motor friction is commonly modelled as a nonlinear Stribeck curve, which lumps the effects of backlash, deadzone and velocity-dependent friction together, but it does not model static friction, which yields stick-slip overshoot. Neural networks may be employed to learn manipulator inverse dynamics by storing association patterns which potentially resolve friction difficulties [147]. Although there exist sophisticated friction models such as [148] which has seven parameters, for simplicity, most friction models consider Coulomb friction and viscous friction only additively:
where b = viscous friction coefficient (assumed zero), k = Coulomb friction parameter (assumed zero in most cases). Joint friction is the primary limitation on precision and can lead to stick-slip behaviour or oscillations, especially for low-speed, low-amplitude movements. Torque sensors in the joints can effectively eliminate joint friction (as implemented in DLR manipulator joints). Active force control compensates for unknown friction effects through direct measurement of joint acceleration and forces exploiting a growing/pruning neural network approach [149]. However, self-sensing without the use of specific joint sensors can be achieved by monitoring back EMF generated within the motor (assuming constant field strength) since the back EMF is linearly related to the motor velocity (which may be integrated to give displacement) [150].
Freeflyer dynamics bears some resemblance to the dynamics of mobile manipulators mounted onto rover vehicles [151,152,153]. There are some resemblances of space manipulator dynamics to underwater robotic vehicle dynamics but with added mass forces and moments (additional inertial resistance imposed by fluid), drag and lift forces, and buoyancy forces [154], an example of which may be exploited for the exploration of Europa’s subglacial oceans [155]. However, the space manipulator application is what concerns us here. The Lagrange-Euler formulation of manipulator dynamics is defined by where L = T − U = Lagrangian, T = kinetic energy, U = potential energy = 0 in space. We can express the Lagrangian (equating to kinetic energy) explicitly as a multibody system in space (ignoring any external forces):
The dynamically equivalent manipulator approach yields:
where , ,
The Lagrangian must be converted into a form to yield joint torques. The Lagrange-Euler equation for manipulator torques in space may be expressed as [156]:
This is a highly complex computation. The terrestrial Lagrange-Euler dynamics formulation has a computational complexity of multiplies and additions compared with the equivalent terrestrial Newton-Euler dynamics approach with complexity of 132n multiplies and (111n − 4) additions. A space-based version will be even more complex. The Lagrange-Euler method also does not express constraint equations such as reaction forces between bodies which can be expressed explicitly in the Newton-Euler formulation—this is explicitly required for the compensation of reaction moments on the spacecraft base at the manipulator mount point to stabilise spacecraft attitude. The manipulator may be exploited to identify the spacecraft inertia properties through measurement of both spacecraft acceleration and velocity permitting the use of multibody Newton-Euler equations [157]:
where H0 = initial angular momentum. The Newton-Euler recursive dynamics equations for a manipulator progress from the base to the end effector for the velocity and acceleration for each link and then from the end effector to the base for the forces and torques of each link and joints. The forward recursion loop is given by:
The backward recursion loop is given by:
From this, we can compute the reaction moment on the spacecraft generated by the manipulator which can be fed forward into the spacecraft attitude control system [120,123]:
The term acts as an effective lever arm to the total force and with the total moment comprises the feedforward component to the spacecraft attitude control system to ensure that w0 = 0. Although a six-axis force/torque sensor mounted at the manipulator base can estimate base force/torques at the base from the sum of joint torques [156], we consider this unnecessary. The reaction torques on the mounting spacecraft are considerably in excess of the typical attitude perturbations by gravity gradients, geomagnetic field, atmospheric drag and solar pressure [158].
8. Spacecraft Attitude Stabilisation
The feedforward signal from the robot manipulator to the spacecraft attitude control system is computed as a byproduct of the Newton-Euler manipulator dynamics:
This feedforward signal is input to a three-axis active attitude control system which is torqued to nullify the reaction forces on the spacecraft imposed by the manipulator to maintain a fixed attitude. This approach avoids the dynamic singularities of uncontrolled attitude. The robotic arm transfers angular momentum to the mounting platform where it may be compensated with torqueing wheels within the constraints of these actuators. The torque required by three perpendicular reaction wheels is given by:
where , , ws = satellite angular velocity, Ii = reaction wheel moment of inertia, Ωi = reaction wheel speed. A simple PID controllers may be applied to three-axis spacecraft attitude control [159]:
Optimal control of 6 DOF spacecraft is commonly achieved through LQR-based control algorithms of both position and attitude by virtue of its superiority to PD controllers [160]. There have been explorations in determining optimal PID control gains by minimising augmented integral square error [161], but parameter variations suggest adaptive and/or robust controllers. Adaptive control is concerned with tracking environmental variations while robust control is concerned with disturbance rejection. Nonlinear adaptive control has also been applied to spacecraft attitude control to accommodate parameter uncertainties [162]. Typically, a fourth reaction wheel skewed at angle of rad = 54.7° typically from the other three is employed for redundancy. This requires employing an algorithm that minimises the maximum wheel torque using the pseudo-inverse matrix that transforms the four wheel torques to the three-axis spacecraft torques. This cannot be integrated to yield attitude uniquely because angular momentum is path-dependent. However, minimisation of both maximum wheel torque (angular acceleration) and maximum angular momentum (angular velocity) maximises agility by imposing further constraints to eliminate path-dependence while preventing uneven wheel angular momentum distribution [163].
A simulation of the reaction moments exerted on a spacecraft due to the mounted manipulator are shown in Figure 3 and Figure 4. Figure 3 shows a freespace manipulator movement reacting on the spacecraft mount prior to grasping; Figure 4 shows a force-controlled passivation of the target from the initial grasp. In Figure 3, the six knot points define the free-space manoeuvre from the initial manipulator configuration to its grasp of the target—an acceleration of the end effector from rest over two knot points, a constant velocity coast over two knot points and a deceleration to rest over two knot points. The knot points are defined at cartesian level so are equidistant in time. The reaction moments generated on the spacecraft due to the freespace manipulator motions using ATLAS parameters were ~1–5 Nm (Figure 3). This is consistent with Ranger NBV system simulations which yield typical reaction moments of ~0.25 Nm for freespace position control. However, reaction wheels offer limited torque capability at ~ 0.1–1 Nm, which is insufficient for the agile attitude capability necessary for feedforward compensation. Figure 4 shows the reaction moment trajectory from the instant of target capture of a 225 kg payload (with initial impact force determined by the end effector velocity along the y direction) and then a slightly under-critically damped force controller passivating the target. A PI-based force controller passivated the spacecraft attitude. The problem with reaction wheels is exacerbated during grasping when impact occurs at a relative velocity of 0.1 m/s and 1.0 m/s, the latter generating ~1–5 kNm reaction moments on the spacecraft (the former is more reflective of current docking velocities but still yields up to ~500 Nm reaction moments) (Figure 4). We may compare this with the maximum velocity of SPDM of 0.075 m/s and 2.5 °/s with a payload capability of 500 kg, but we suggest that future servicing missions will proceed at a faster pace under productivity pressures. Clearly, this is far beyond the torqueing capabilities of reaction wheels.
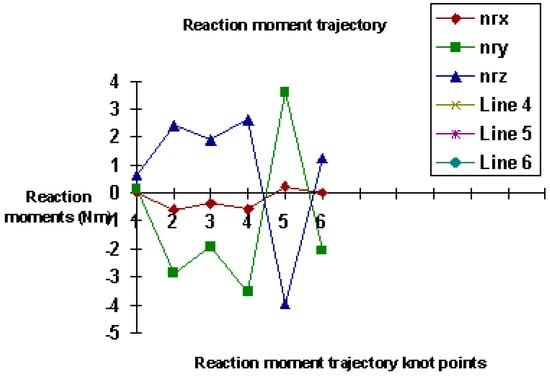
Figure 3.
Reaction moments generated by manipulator on spacecraft during free space motion Nrx, Nry and Nrz—note that the legend artifactually lists lines 4–6 which are not used in the graph.
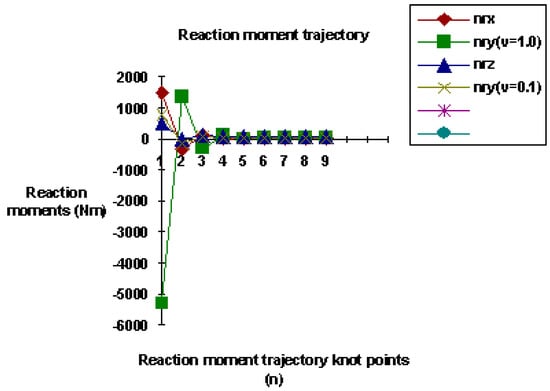
Figure 4.
Reaction moments generated by manipulator on spacecraft during grappling Nrx, Nry and Nrz with Nry at impact velocities 0.1 m/s and 1.0 m/s—note that the legend artifactually shows two additional lines which are not used in the graph.
Control moment gyroscopes (CMG) offer a much higher torque capability as required for force control-based passivation [164]. A control moment gyroscope (CMG) comprises a fixed speed rotor (constant angular momentum) mounted into gimbals so that the angular momentum vector can be altered by driving the gimbals. A small input torque generates a highly amplified output torque on the spacecraft ~100–5000 Nm. In DGCMGs (double gimbal), the rotor is mounted into two gimbals so the rotor angular momentum can be rotated within a sphere (limited only by the gimbal stops). In SGCMGs (single gimbal), the rotor is mounted in a single gimbal so the rotor angular momentum can be rotated in a circle in a plane normal to the gimbal axis. CMGs are driven by a steering law that outputs CMG gimbal rates from spacecraft control torque inputs. DGCMGs have simpler steering laws to SGCMGs but the latter are mechanically much simpler than the former. Any set of n SGCMGs suffers from 2n singular gimbal angles. At singularities, gimbal lock occurs, and control torques cannot be generated to exit the singular condition. We assume that the CMG pyramid lies at the spacecraft centre of mass aligned with the spacecraft principal axes (and so only CMG axial angular momentum is considered). Euler equations for the whole spacecraft with the CMG cluster are given by:
CMG parameters are given by [165]:
where h = axial angular momentum, γi = gimbal angles, δ = pyramid skew angle. This may be differentiated to:
The 3 × n Jacobian J(γ) is under-determined. Hence, gimbal rates are given by:
This is the Moore-Penrose pseudoinverse—if the rank of the cluster gain JJT < 3, the pseudoinverse does not exist (singular state). The pseudoinverse tends to steer the gimbals toward singular states. Null motion may be added into the steering law to avoid singularities—null motion produces no net control torque. The null vector is given by:
The nonzero vector may be chosen to impose constraints such as a gradient-based vector that points toward the singular points:
where . This does not always work, so null motion may be forced to steer towards the desired gimbal angles :
The singularity robust inverse is the generalised version of the pseudoinverse [166]:
Assuming P = I3 and Q = λI4:
where λ = = singularity distance weighting parameter. This is not guaranteed to avoid singularities, but the generalised singularity robust inverse ensures that it approaches and rapidly transits singularities [167]:
A significantly more complex singularity, predictive singularity inverse using a cost function based on a one-step predicted singularity measure, has been proposed [168]. A further method to avoid singularities is to introduce more controllable degrees of freedom to the CMG. One option is to introduce adjustable skew angles to the CMG [169]. Another option is to introduce variable speed to the rotor of the CMG—this is the variable speed CMG (VSCMG). A single gimbal CMG with variable flywheel speed provides the function of both CMG and reaction wheel [170]. They can avoid singularities due to the extra degree of freedom in the angular wheel speed. The VSCMG is nominally operated as a CMG away from singularities to take advantage of its energy efficient torque amplification. As it approaches a singularity, it acts more like a reaction wheel. This is enabled through a weighted pseudoinverse of the form:
where Q = (IRW:ICMG) = composite inertia dyadic, , , . W and μ are design parameters. Suppression of vibration of large structures can be implemented through distributed sets of collocated pairs of CMGs with rate gyroscopes acting as distributed actuators/sensors to active control attitude and vibration simultaneously [171,172]. Viscoelastic damping in CMGs may be implemented using silicone-based rubber mountings [173]. Variable-speed CMGs may be mounted into the links of a space manipulator for simultaneous attitude control and vibration suppression [174,175]. Indeed, such CMGs can significantly reduce reaction torques exerted by the manipulator on the spacecraft base [176]. This is rather a cumbersome solution with a significant hardware cost, particularly if CMGs are paired for CMG singularity avoidance. A more conventional means of vibration isolation is to use active feedback control with LQR and a Kalman state observer [177]. The Kalman filter comprises a model system that acts as a predictor and a measurement system that corrects the prediction. Variable-speed CMGs are also the flywheel of choice for IPACS (integrated power attitude control system) [178]. Electric energy generated by a solar panel drives the motor to spin the rotor which is maintained by the large moment of inertia when the wheel is no longer powered thereby acting as an electromechanical battery [179]. Energy can be dissipated with the rotor acting as an electrical generator. Hence, the adoption of CMGs for dedicated attitude control in freeflying systems offers high torque capability against the reaction moments imposed by the mounted manipulators without the disadvantages of freefloating systems.
9. Freeflyer Manipulator Control Systems
The controller must be cycled at a rate of ~100 Hz in order to provide sufficiently responsive feedback from rapidly changing environments (particularly force sensors during tactile manipulation), while visual frame rates are usually much lower at 5 Hz (though video frame rates are 30 Hz). For comparison, the ETS-VII manipulator arm was controlled using processing on the ground, but the update rates were 4 Hz, limiting it to speeds of 10 mm/s. Similarly, the Shuttle RMS was controlled by the Space Shuttle General Purpose Computer which was limited to a 12.5 Hz update rate limiting it to “fly swatting” operations. By contrast, SSRMS had an update rate of 125 Hz, enabling it to respond more quickly to feedback signals. The constraint of control cycle frequency imposes a computational burden which re-iterates the necessity to solve control problems as low down the control hierarchy as possible. There are several approaches to manipulator control [180]. The computed torque controller employs feedback linearization of manipulator dynamics by employing a nonlinear model to cancel its nonlinear elements. This permits the use of decoupled PID controllers for each motor. The computed torque controller may be regarded as a form of pole cancellation [181] and has the form:
where and . The computed torque controller assumes that the dynamic model is exactly known. The computed torque controller may be supplemented by a fuzzy controller providing a compensator torque to accommodate uncertain parameters and perturbations where = regressor weight matrix as solution to the Riccatti equation , ζ(Φ) = fuzzy manipulator parameters vector, [182]. A model-based computed torque control scheme has been developed to include the dynamics of flexible appendages [183]. Alternatives for vibration suppression generally adopt robust and/or adaptive controllers [184] and the computed torque method may be modified to implement adaptive control gains.
Flexible appendages (with flexible joints and/or links) and fuel sloshing introduce further complications to freeflying dynamics [185,186]. Solar array deployment is a similar multibody dynamics system to the space manipulator control problem [187] and solar panels generally have natural frequencies of 1–5 Hz, which limits attitude control bandwidth to ~0.1 Hz but manipulator update rates must be much higher. However, manipulators themselves are subject to vibration—a considerable fraction of the SRMS operations time was wasted in waiting for vibrations to decay in its graphite-reinforced carbon composite booms of stiffness of ~109 kg/cm2. Flexibility in manipulators will cause the spacecraft to tumble if not addressed [188]. Space manipulators have high load-to-weight ratio of 1:1 (compared with 1:20 for traditional industrial robot arms), making their links flexible. Flexible manipulator links are treated as a Euler-Bernoulli beam with modal displacement given by [189,190,191]:
where EI = flexural stiffness, ρ = linear mass density, k = M/EI = beam curvature, M = beam moment, E = Young’s modulus, I = beam moment of inertia. The solution is the transverse flexural displacement given by:
where = mode shapes and = generalised modal amplitude coordinates, n = number of modes. The Lagrangian dynamics may be partitioned into rigid body and flexural components by [192]:
The model-based computed torque technique is reasonably effective in controlling tip motion by treating flexible link manipulators as perturbations to the rigid manipulator despite there being fewer control actions than degrees of freedom [193]. However, to reduce settling time, active vibration control by feedforward preshaping of the motion is generally required—this involves using two impulses separated by T/2 where T = vibration period [194]. Normal rigid body robotic control systems can be readily adapted to modal control to suppress vibrations by using a “virtual rigid manipulator” approach—this is achieved by replacing actual endpoint kinematic variables by those of a “virtual rigid manipulator” [195]. The virtual rigid manipulator is an assumed rigid manipulator with the same joint angles as the real deformed link manipulator but with coincident end effector positions to the undeformed link manipulator. A modal feedback controller based on LQC observer can estimate modal coordinates:
where , , . Hence, elimination of the C terms linearises the dynamics permitting the adoption of state space representation:
Measurement of link strains give estimates on modal amplitude coordinates. Bending strain energy measure along n + 1 flexible links may be given by:
This allows computation of the additional joint torque components to dampen the modal vibrations. The use of adaptive control approaches with high controller gains can stiffen the joints. However, control of flexible appendages is difficult as sensors and actuators at the joints are not co-located with the beam shape unless mode shapes between tip and actuators are detected using embedded strain gauges. Hence, vibration suppression of flexible multi-link manipulators may be implemented through distributed arrays of piezoelectric sensor/actuators which alter the stiffness of the structure [196]. Similar approaches have been proposed for vibration suppression in large space structures [197] which can be induced by flexible space manipulators which typically have fundamental vibration eigenfrequencies of around 1 Hz depending on the payload. Flexible joints are the dominant flexible element of space manipulators due to the high ratio gearboxes and/or flexsplines of harmonic drives [198]. Joint elasticity is generally modelled as torsional springs with a characteristic stiffness ~104–105 Nm/rad which is dominant over link elasticity. This may be approximated as a linear gearbox spring by:
where k = joint stiffness, Δθ = difference between motor and link angles. However, the gearbox stiffness may not be linear—the flexspline stiffness is typically sigmoidal. Simple PD controllers may be applied to elastic joints inherent in harmonic drive systems to provide stability to fast dynamics [199]. The harmonic drive is characterized by nonlinear compliance with hysteresis and nonlinear damping. The addition of an integral controller to form a PID controller that follows a rigid model may be employed to ensure robustness. The Shuttle RMS’ high inertia with low viscous damping generated a lightly damped mode at the resonant frequency of 70 rad/s when unloaded which required slow speed movement, typically 0.004 rad/s. Robust adaptive control used for rigid manipulators may be generalized to apply to flexible joint manipulators using a reduced order dynamic model by adding an extra corrected control signal to compensate for the effects of flexibility to force the flexible manipulator to behave similarly to a rigid manipulator [200,201], such as global linearisation into passivity through structural damping [202].
Electric motors require a variety of techniques for feedback control to cope with nonlinear dynamics, unobserved states and parameter uncertainties [203]. Suitable techniques include exact linearization using computed torque methods, state estimation using Kalman filtering, error tolerance through robust control and parameter identification through adaptive control techniques. Robust controllers however adopt fixed parameters such as high gain that are tolerant of error to maintain consistent behaviour. Robust controllers include H∞ control [204] and sliding mode (variable structure) controller, the latter being common for underwater robotic vehicles [154] and robotic manipulators [205]. The sliding mode controller drives the system state onto a pre-designed switching surface in state space—the sliding surface = 0 when e → 0 as t → ∞ and where and . The sliding mode controller then maintains the system in the vicinity of the sliding surface through the control law—this renders it robust. The control input is given by:
Unfortunately, the discontinuous sliding mode control law generates high-frequency switching through the sliding surface—chattering—due to finite time delays. This can excite unmodelled high-frequency dynamics into mechanical oscillation—this is particularly problematic for space manipulators where there is no damping medium unlike in submersible-based manipulators. One means to reduce chattering is to replace the discontinuous controller with a continuous saturation function:
Sliding mode controllers have also been married to fuzzy controllers and neural network controllers to compensate for their noise sensitivity close to the sliding surface introduced by the saturation function. Adaptive controllers adjust unknown parameters online on the basis of performance. For example, the SSRMS shoulder yaw joint experienced the significant moment of inertia variations of up to 3.0 kgm2, which can be accommodated using adaptive control. There are several adaptive control schemes applied to manipulators—examples include model predictive control [206], passivity-based adaptive control [207] such as using Jacobian transpose [208] and neural networks. The model reference adaptive control is based on the MIT rule of the form . For example, the computed torque controller decouples the manipulator into a set of linear PD control laws for each motor of the form: where , = effective motor and gear inertia, = effective motor and gear viscous damping, , kp = proportional gain, kv = damping gain. The gains can be adapted using the MIT rule so that the motor output torque tracks the desired behaviour of the linear mass-damper reference model parameters given by:
Most adaptive controllers however are based on segmenting all uncertain parameters into a regressor matrix of the form [209,210]:
where Y = regressor matrix of known parameters, = vector of unknown physical parameters, P = predicted estimate gain, , K = upper bound on P, λ = forgetting factor. Passivity through the Jacobian transpose takes the following form:
where = sliding surface. Adaptive controllers have been employed in space manipulators to deal with parameter variations such as inertial or payload parameters [211,212]. An adaptive control model with a regressor matrix was investigated for a free-floating space-based manipulator [213]. The problem of formulating the regressor matrix lies in linearising the dynamics in inertial space when dealing with an unknown payload which cannot be decoupled dynamically from known manipulator dynamic parameters for a free-floating manipulator [214]. The primary problem with adaptive computed torque controllers is the requirement for measurements of joint velocity and acceleration which are difficult and/or corrupted by noise. A robust adaptive computed torque controller uses joint position measurements and input torques in an extended Kalman filter to estimate joint position, velocities and accelerations [215]. The Kalman filter is a Bayesian technique where the posterior probability p(x|z) of state x is given by the prior probability p(x) of the state x determined by the model combined with the measurement z of state x and conditional probability p(z|x) through Bayes’ rule. The state vector and input u(t) = τ+w(t) yields a nonlinear model with process noise w given by:
To apply the extended Kalman filter, the system must be linearised through a first order Taylor expansion with respect to a reference trajectory:
Hence, the EKF process model is given by:
The measurement model with measurement noise v(t) is given by:
H(t) models the fact that a sensor measures the target state x indirectly and incompletely. Both process and measurement noise are independent Gaussian functions with zero mean and covariances given by: Q(t) = cov(w(t),w(τ)) and R = cov(v(t),v(τ)) respectively. The Kalman-Bucy continuous time filter yields optimal estimates of the state x(t) and the error variance P(t):
Hence, estimated parameters are employed in a PD control law:
The extended Kalman filter is an approach which offers adaptability to structural uncertainties in space manipulators assuming that parameters vary slowly with time [216]. Stable adaptive control methods may be applied directly to a PID control law for a space-based manipulator employing attitude control however [217]. More advanced robust adaptive control uses a weighted bank of extended Kalman filters as a mixture-of-experts [218]. Reinforcement learning may also be used to implement adaptive controllers to respond to changes in payload [219]. SSRMS used fixed control gains rather than adaptive gains due to the latter’s computational complexity.
10. Space Manipulator Force Control
We must now consider external forces and moment acting at the end effector. The equation of motion for freefloating/freeflying robotic servicers including forces exerted by a payload may be given by the Lagrange-Euler formulation:
where Ds = spacecraft inertia, Dm = manipulator inertia matrix, Dc = coupling inertia matrix, Cs = spacecraft nonlinear velocity terms, Cm = manipulator Coriolis and centrifugal terms, Fs = spacecraft wrenches (column vector for forces and torques), τm = manipulator torques, Js = spacecraft Jacobian, Jm = manipulator Jacobian, Fext = external wrenches. Typical servicing manipulator performance parameters are ~1 mm and 0.1° positioning accuracy and 150–200 N and 20–30 Nm applied end-effector forces/torques. The spacecraft component is given by:
The manipulator dynamics component is given by the Lagrange-Euler formulation (Equation (49)):
Integration of the spacecraft component yields total momentum conservation of the system:
Spacecraft motion is given by:
If attitude is controlled, ws = 0. Robotic manipulator regimes of servicing operations may be divided into four phases: (i) free-space manipulator motion to grasp the target using position control; (ii) transitional contact dynamics between manipulator and target; (iii) transitional passivation of target using force control; (iv) servicing operations such as peg-in-hole tasks using hybrid position/force control. The incidence of contact on grasping the target alters the dynamics of the system—prior to contact, the manipulator is in free space mode; on contact and thereafter, the manipulator experiences an external force/moment in acquiring a new payload. This requires re-initialisation of the dynamics of the system. Real-time detection of collision of a manipulator with obstacles may be achieved without explicit force sensors—a collision may treated as a fault in the actuation system [220]. It is dependent on accurate joint torque measurements to generate the residual against the model based on conservation of generalized momentum—a non-zero residual above a threshold indicates collision. However, we assume that force sensors have been adopted.
On impact between the end effector and the target, there is an impact transition in which energy is transferred between the chaser and the target spacecraft. We assume that the contact is frictionless (Hertzian) and that contact is made with the target using robotic fingers. The contacting bodies deform over a finite elliptical contact area—Hertzian contact relates the radius of the contact area A to the normal load F [221]:
where c = constant depending material properties and fingertip geometry, 0 < γ ≤ 1/3 depending on fingertip materials (elastic material has γ = 1/3). The vertical depth of depression of a fingertip with a radius of fingertip curvature r0 is given by:
Contact stiffness of a compliant finger is given by:
Hence, contact stiffness is nonlinear and increases quickly with higher contact force. Impact dynamics are determined by the law of conservation of momentum. Impulse is defined as the integral of the impact force between two bodies:
Energy loss during impulse is given by:
where q = deformation. Hertzian contact assumes an elastic indentation on impact at low velocity but some plastic deformation may occur even under nominally Hertzian conditions. There is a loss of energy accompanying any impact due to deformation that is quantified by the coefficient of restitution e [222,223]—it relates relative velocities between impactors before and after impact:
where (perfectly plastic) 0 < e < 1 (perfectly elastic). Impedance control implies end effector behaviour of which yields a penetration depth given by:
where = damped oscillation frequency, , = natural frequency of oscillation, k = stiffness coefficient of impactor, b = damping coefficient of impactor, mi = mass of impactor, mt = mass of target, , , . This may be differentiated thus:
Duration of contact is equated to a half oscillation period:
Hence, the coefficient of restitution may be expressed as:
When critically damped, ζ = 1, e = 0. Hence, coefficient of restitution can be controlled. Rather than the inaccurate Hertzian linear spring-damper model of impact contact, nonlinear viscoelastic force is given by the Hunt-Crossley expression for impact force [224]:
where γ = constant = 0.25–0.5, K = stiffness coefficient, = damping coefficient, q = deformation. The collisional force may be controlled with an integrated force and damping control law of the form [225]:
where fimp = impact force. Alternatively, an integral controller on the force error may be implemented which stabilizes a PD controller with high contact stiffness [226]. Once the transient impact phase is completed, physical attachment of the manipulator(s) to the target must be error-tolerant, robust and stable. V-grooves may be employed as physical guides to ensure correct alignment prior to latching. A standardised grappling system comprises a motorised spring-loaded pantograph that mounts a probe which is inserted into a probe receptacle with guide rails mounted on the target [227]. On docking, the pantograph is compressed retracting the docking probe for a secured dock with aligned electrical and fluid connections (the latter are not required for active debris removal). This is the basis of the ESA mechanical latch which requires a target capture pin [228]. However, these types of docking mechanism require that the target spacecraft has been designed for servicing and provides a pre-existing interface mechanism for debris removal. This will not, in general, be the case. The issue of a secure latch on an uncooperative target has yet to be solved (this is the rationale behind harpoons and nets), as most latch designs assume a benign target. This suggests that the versatility of grippers renders them the most likely of solutions.
Once contact has occurred, there are interaction forces between the manipulator and the target that must be controlled. The environment stiffness is typically high ke~105–106 N/m and produces little damping so high natural frequency responses are generated with frequency:
where = manipulator compliance, mw = wrist mass. This oscillation will be persistent and will generate contact-make/contact-break cycles. If , the system is stable, so stiff environments must be met with low stiffness manipulation. Hence, force sensing requires high sample rates ~100+ Hz. On grasping, hybrid position/force control and impedance control are the most popular methods of force control. Hybrid position/force control is based on separating movement from force exertion; impedance control is based on the interaction between the manipulator and the environment in which force equates to both stiffness and viscosity. Twist is defined as the 6 × 1 generalised velocity vector indicating free space motion, while wrench is defined as the 6 × 1 generalised force vector indicating constrained motion, . Impedance control ()) is a generalisation of compliance control ( where kp = stiffness gain) and admittance control ( where kv = damping gain) that controls the mechanical impedance at the end effector in contact with a rigid environment [229,230,231]. Admittance control incorporates an outer force feedback controller that generates position commands to an inner position controller. Unfortunately, it is stable only in non-rigid environments. During manipulator-environment interaction, one side must behave as an impedance and the other as an admittance—since the environment generally presents admittances, the manipulator must act as an impedance through impedance control. Indirect force control such as impedance control does not require explicit measurement of force rather it employs motion control. Impedance of the manipulator involves controlling contact forces through stiffness and damping control, i.e., a PD control scheme. Impedance control relates force to motion through mechanical impedance—the manipulator is modelled as a mass-springer-damper. Impedance control converts position error into force and eliminates the problem of instabilities in direct force feedback. Impedance control lacks positional accuracy compared with hybrid position/force control but requires no switching on contact. Physical contact between the manipulator and the target during grappling introduces external forces and torques to the manipulator(s). Initial impact generates transient contact dynamics which in the simplest analysis may be modelled as pre- and post-impact momentum depending on the coefficient of restitution. Contact forces are typically computed from a Hertz model. Impedance control may be employed to provide mass-spring-damper behaviour at the contact between the manipulator and the target to absorb impact energy [232]. Impedance control of the manipulator on contacting the target is given by:
where , Mi, Bi and Ki are impedance control matrices. This translates to a joint torque given by:
Impedance control during transient impact cannot be employed due to time delays—this requires zero-delay physical compliance. Impedance control with a compliant wrist (such as the remote centre compliance device [233]) is one option [234]. The remote centre compliance is a generalised spring with three linear springs connecting two equilateral triangles.
Direct force control requires explicit force feedback from a force/torque sensor typically mounted onto the wrist of the manipulator. Hybrid position/force control partitions the control task into two orthogonal task subspaces [235]: (i) free-space motion of the manipulator under control of position; (ii) constrained interaction of the manipulator with physical surfaces under control of force. A selection matrix S = diag(s1…sn) separates the position-controlled directions from the (I-S) force-controlled directions in cartesian space which may be cast into the equivalent joint space (where si = 1 for force control and si = 0 for position control). The S-matrix defines tasks such as the peg-in-hole task—there are two position-controlled degrees of freedom and four force-controlled degrees of freedom, i.e., S = diag(110110) for the peg-in-hole task. The hybrid position/force control scheme may be cast into joint coordinates through the compliance matrix C = J−1SJ:
A mixed mode of position and force control was implemented in the teleoperated ETS VII space manipulator [236]. The hybrid position/force control scheme based on the geometric orthogonality of free twists and constrained wrenches has been criticized as fallacious [237], but this is unfounded [238]. The chief challenge is that the position-controlled directions require high stiffness but the force-controlled directions require low stiffness—in impedance control, high stiffness implies high impedance and low stiffness implies low impedance. One potential solution is to use explicit force control in the force control directions by converting force into position/velocity using stiffness/damping relationships. Indeed, impedance control does precisely this in indirectly regulating force via position feedback. However, this imposes sluggish behaviour, which favours hybrid position/force control. On the other hand, the selection matrix in hybrid position/force control is unique to a specific task and dynamic task changes require dynamic switching between selection matrices as a task sequence proceeds (this may not be applicable during grappling for active debris removal). It has been proposed to eliminate the selection matrix altogether and resolving conflicts between position and force control through a rule-based priority strategy favouring the force control loop [239]. This is the parallel force/position control scheme, which eliminates the selection matrix and adopts a priority strategy with force control taking priority:
where e = qd − q and ef = Fd − F. Particularly along a stiff surface, the integral force controller gain should be high. Alternatively, an acceleration-based controller allows implementation of a force constrained position controller without a selection matrix [240]. Control is implemented using position control for small external forces but using force control for large external forces. Hybrid impedance control combines hybrid position/force control with impedance control [241]. If effort (force equates to voltage) and flow (velocity equates to current) provide the basis for electrical/mechanical analogy, resistance is damping , capacitance is stiffness , inertia is inductance . Impedance is defined as . Norton circuit comprises an impedance in parallel with a flow source, i.e., capacitance; Thevenin circuit comprises an impedance in series with an effort source, i.e., inertia. Capacitative environments require a force-controlled manipulator; inertial environments require a position-controlled manipulator; resistive environments permit either a position or force-controlled manipulator.
It is commonly proposed that wrenches on the spacecraft base should be minimised to ensure attitude control—this is essential to ensure that the spacecraft base does not move to break contact for impedance control to operate [242]. Zero base angular momentum disturbance can be implemented through the angular null space allowing transfer of impact momentum at the end effector to the spacecraft base [243]. However, there are simpler solutions presented here that stabilise the attitude of the spacecraft base through reaction moment compensation which achieves the same thing.
11. Dual-Manipulator Control
The use of multiple (most commonly, dual) manipulator arms offers significant advantages over a single arm. More than two cooperative manipulators with load distribution has been addressed using a virtual linkage model [244]. A second arm can move to compensate for reactions imposed by the first by maintaining the spacecraft’s inertial position [245], though this would be a wasteful use of an additional arm and ungainly. Multiple arms can share heavier loads, have larger workspace and can perform functions that cannot be performed with a single arm. Other tasks will require cooperative dual tasking, such as coupler mating or common object manipulation. Indeed, dual arms can perform human-like tasks [246]. In particular, a division of labour might be apportioned in which one arm performs a task (manipulate a peg), while the other arm fixes the task location (positioning the hole). In a closed chain configuration, dual arms offer increased rigidity yet retaining flexibility of movement of the grasped object. For dual manipulators, there are several control approaches:
- (i)
- fully decentralised, in which each manipulator is decoupled and controlled independently;
- (ii)
- partially decentralised master/slave approach, in which a master manipulator is controlled to which the slave manipulator has a fixed relative position. In handling a common object, the two robots form a closed kinematic chain with two holonomic constraints [247]:where rm = virtual stick from the end effector to the object centroid
= relative orientation=constant
Differentiating yields:
- (iii)
- centralised approach, in which force control is administered at the common object such as the operational space formulation. The six-degree-of-freedom wrench in cartesian coordinates may be defined by the operational space dynamic model of a manipulator [248]:where = operational space inertia, = wrench including nonlinear terms, = end effector wrench, D(θ) = joint space inertia, = Coriolis and centrifugal parameters, τ = joint torques. Force control in operational space is given by:
In terms of null space projection [249,250]:
Hybrid position/force control can be readily applied to the control of two arms simultaneously [251]. Similarly, impedance control of dual arms can be applied both centralised and decentralised [252]. There are several forms of cooperative arm control: (i) position-controlled master arm with a force-controlled slave arm which does not distribute loads effectively; (ii) dual-arm hybrid position/force control; (iii) dynamic cooperation in which the computed torque controller incorporates manipulator and object dynamics to nullify internal forces. During such dual-manipulator tasks, both arms apply forces which either generate movement of the object (motion forces) or generate internal forces (squeeze forces). This will require compliant control to control the object motion and the internal stresses, e.g., Dual-Arm Generalised Compliant Motion (DAGCM) [253]. An example of a cooperative task is the use of multiple mobile platforms, each mounting a manipulator—this requires a combination of vehicle-manipulator coordination and multiple manipulator coordination for which the operational space formulation, virtual null space internal forces, and a multi-manipulator object grasp matrix have been combined to yield solutions [250]. A similar space application example involves multiple (minimum of three to provide full control of an object) spacecraft with single manipulators handling a common object for assembly tasks, in this case involving coordination between the manipulators and thrusters [254]. Although there are similarities, these are different to the case of multi-manipulators on a single spacecraft that concerns us here [255]. Post grappling, a closed kinematic chain reduces the number of DOF so the excess actuators permit minimisation of a weighted function of actuator torques while a fifth order polynomial reference trajectory for manipulator motions reduces reaction forces on the spacecraft [256]. Multiple arms on a spacecraft comes at a cost of vastly increased computational complexity of coordination. The Jacobian for a dual manipulator system is an 18 × 18 matrix assuming 6 DOF manipulators because, unlike terrestrial dual manipulators, they are coupled dynamically through the base. For closed chain configurations, constraints may be applied kinematically through the Jacobians [257]. Nevertheless, dual arms introduce greater challenges in avoiding dynamic singularities [258]. This reinforces the necessity of simplifying controllers for space-based manipulators using dedicated attitude control permitting decoupling of linear and angular momentum aspects [259]. The use of dual or more arms introduces considerable complexities to path planning, particularly for cooperative tasks. The potential field method is particularly promising in this regard to prevent collisions. Nevertheless, there are several simplifying assumptions that can be imposed: (i) during grappling, the arms exhibit mirroring motion through the bisecting plane; (ii) during grappling and subsequent to grappling, objects may be passed between arms while ensuring that no manipulator crosses the bisecting midplane (Zambesi bridge configuration); (iii) a fixed arm can maintain docking with the target while the other performs servicing tasks. Multiple manipulators grappling a single object are characterised by the grasp matrix which defines the object internal forces [260]:
Each manipulator grip is defined by its own grasp submatrix. Internal grasp forces defined by the constraint polygon formed by the fingers determine the stability of the grasp. For two manipulators grasping one object, the grasp matrix defines the transformation of forces at the grasp points (gi) to the centre of mass (o):
where O3 = 3 × 3 null matrix, I3 = 3 × 3 identity matrix, poci = position vector from grasp point gi to o (virtual stick), S = cross product matrix. Hybrid position/force control of dual arms afford direct control of internal forces with cooperative load distribution. Adaptive versions using derivatives of position and force are feasible. For soft contact, impedance control and passivity-based control are suitable. An observer-based approach to impedance control in compliant capture of a spacecraft has been explored [261].
Adequate grasping requires the maximisation of the contact area between the robotic hand and the target to minimise the force required to maintain a stable grip. There are two main types of grasp—power grasp (chuck grip) using the entire hand in an enveloping configuration involving contact with the palm and precision grasp (key grip) using fingers tips and distal phalanges for contact with the object [262]—though there are variations such as the hook grip for large extended objects (where gravity is exploited). Both require different approaches to grasp planning involving determining the hand pose relative to the target object [263]. The application of a hybrid position/force control selection matrix allows selection of those degrees of freedom which are motion controlled and those which are force controlled in each finger. If force control is dominant, we have a power grasp which is poor at motion control. If motion control is dominant, we have a precision grasp which is poor at rejecting disturbance forces. We may define a grasp performance measure of the form [264]: where γ > 0.5 indicates motion-oriented grip and γ < 0.5 indicates force-oriented grip. Maximisation of the performance measure suggests for optimal force stability and motion manipulability. In grasp mechanics, there are three relevant frames of reference: object frame, contact frame and joint frames [265]. The mapping between finger joint torques and the handled object is generally non-linear making it amenable to modelling by artificial neural networks to optimise the contact forces [266]. The grasp matrix defines the kinematic relationship between applied and internal forces at the contact points on the object being handled and those at the centre of mass of the object. There are three types of contact point which define rolling, sliding and sticking contact motion [267]: (i) frictionless (sliding/rolling) contact in which force is exerted only normal to the surface; (ii) frictional (hard) contact based on Coulomb’s law in which tangential friction force is proportional to normal applied force; (iii) soft contact due to viscoelastic deformation. An object may be grasped at N points of contact: if frictionless, applied forces are normal to the contact point; if frictional, applied forces are both normal and tangential; if a soft contact, a torsional component may be also applied. Coulomb’s law models friction as and . The contact positions and normals define the grip Jacobian matrix which transforms contact forces into object frame wrenches.
There are many different types of end-effector ranging from specialised tools to dual-fingered grippers to multi-fingered hands. While dual fingered jaws may suffice for fixturing workpieces, dextrous manipulation requires multifingered hands with multiple grasp configurations, equilibrium of internal grasping forces, zero slippage, stability of grasp to disturbances and dynamic tactility. The more sides that the polygonal shape possesses (i.e., the closer approximation to circular geometry), the greater the appropriateness for a three fingered grip rather than a two-fingered grip. A three-fingered gripper with three-jointed elastic fingers, a palm joint and soft fingertips allows robust grasping around arbitrary objects, including curling, bending and rotation in three axes [268]. For stability, the three fingertips should have a minimum of three finger contact points. An example is Graspar, a three-fingered gripper capable of grasping complex shapes, adjusting its grasp during slip and yet utilising only a simple binary grasp/release command vocabulary [269]. The two fingers have three joints, while the opposing thumb has two joints, each finger is actuated by a single motorised pair of agonist/antagonist tendons routed over pulleys at the joints and idlers at the centre of each phalange to conform to the object shape. The joints are differentially coupled such that the torque exerted is distributed through the joints according to its moment. Simple contact switches on the grasping surface of each phalange provide simple feedback to ensure simplicity of design and operation yet robust grasping. Another example of a typical illustrative robotic hand developed for space manipulation is the DLR Hand II with four fingers, each with three degrees of freedom plus a base joint (for reconfigurability), capable of both power and precision grip (though there are newer, more advanced hands) [270]. Power grasping involved parallel alignment of the second, third and fourth fingers exerting up to 30 N each, while precision grasping involved the opposition of the first finger and thumb with intersection of the other fingers. A robotic hand requires force and slip sensors on the fingertips and a force sensor in the palm in the simplest arrangement. If tip force sensors are activated, a precision grip may be adopted, while if palm force sensors are activated, a power grip may be adopted. If slippage is detected by the slip sensors, the hand automatically tightens its grip until the sliding is terminated—this a reflex. The DLR Hand II possessed rotary position and torque sensors in each joint and each fingertip exhibited a small force/torque sensor (range of 10–40 N each) for hybrid position/force control.
12. The Nature of Dexterity and Tactility
We suggest that the technologies in the preceding sections are all essential components of a robust approach to the robotics capabilities necessary for active debris removal. We consider in this last section a few more sophisticated capabilities related to dexterity and tactility. Compliance is an essential feature of fine manipulation inherent in hand grasping [265]. Compliant fingertips offer damping and can be a partially effective method for suppressing vibrations [271]. There are several dexterity measures based on the grasp Jacobian matrix G that defines the kinematic geometry of grasping at contact i with respect to object coordinates [272]:
where , p = position vector contact point i, = orientation of contact point i, fi = wrenches at contact point i, fobj = (fT nT)T = wrench on object, Fext = ()T. To control grasping forces, the inversion of the grasp matrix is required which invokes the Moore-Penrose pseudo-inverse of G as it is non-square:
where G+ = Moore-Penrose pseudo-inverse, = internal forces, λ = Lagrange multiplier. The internal forces do not contribute to the motion of the object so should be close to zero. The squeeze forces within the nullspace of the grasp Jacobian allow minimization of slippage to zero, i.e., force closure. The stability of the object is determined by the shape of the potential well about the equilibrium position generated by the grasp configuration. The grasp manipulatability index quantifies how far the grasp configuration is from a singular configuration: while the condition number nc quantifies the distribution of effort between fingers for optimal distribution. Distribution of forces between fingers is given by: subject to the force ellipsoid and where J=hand Jacobian for torque minimisation. To accommodate grasp dynamics, the grasp manipulability index may be adapted to where D(θ) = grasp inertia matrix. Grasp equilibrium requires that the sum of all applied wrenches on the object are zero, . Minimisation of the squared wrench to zero is given by [273]:
where = wrench. This is the force closure condition in which any arbitrary external force can be exerted on an object with frictional contacts while internal forces are generated in the nullspace of the grasp matrix G. Form closure is force closure under frictionless contacts. Dextrous manipulation requires pure rolling in the contact plane with maintenance of contact (vz = 0), no sliding (vx = vy = 0) and no twisting around the contact normal (wz = 0) [274]. To firmly grasp an object, normal contact force must be positive and resolution of tangential and normal contact forces fc must lie within the friction cone. When the tangential force/moment lie within the friction limit surface, there is no sliding between the fingertip and object. While slippage on Earth is usually due to gravitational effects, slippage can occur in space due to inertial effects. To prevent slippage, the contact force must remain within the friction cone, i.e., tangential contact forces do not exceed the normal friction force: where μ = coulomb friction coefficient = 0.4–0.8 typically (0.65 for aluminium), fz = normal contact force > 0 [275,276]. From this, a critical finger measure may be defined as a grasp stability metric based on the fingertip “distance” from its friction limit [277]:
Similarly, a similar potential function-based progression-to-slip measure may be defined [278]:
Slip prevention may require that internal forces to be generated in the null space of the grasp matrix. A significant facet of grasping is that it involves planning with small mid-range movements over extreme angle movements [279] Regrasping, finger gaiting (sequence of regrasps) and finger sliding/rolling provide sophisticated mechanisms for altering grasp configuration [280]. Grasp stability can be maintained if fingertip impedances can be controlled with positive stiffness gains on frictionless contacts [281]. There are several approaches to learning grasp configurations, including modelling mirror neurons acting as hand state-object state association schemas and learning grasp-object shape pattern matching [282]. Grasped object shapes may be modelled as superquadratics:
where εI = shape parameters, and ai = scaling factors. The superquadratic is fitted to the grasp data. For rectangular objects, ε1 and ε2 ≈ 0.1 while for cylindrical objects, ε1 ≈ 1 and ε2 ≈ 0.1. These superquadratic models can be used to estimate orientation and axes and guide further contour following exploration to generate further grasp data. Complex objects may be constructed from generalised cylinders generated through superquadratics. Clearly, although fine manipulation may not be required during grappling for active debris removal, the problem of grasping without slippage is highly relevant to this application—it may be also be considered that regrasping and finger gaiting during transport may also be advantageous but we consider that secure latching would be a simpler approach.
Tactile sensing is more complex than force/torque sensing—although dominated by static and dynamic force/pressure measurement, it is supplemented by temperature, vibration, stretch and texture measurements. Vibration sensing exploits the fact that slip generates low frequency ~10–100 Hz vibrations. Haptic exploration involves rolling/sliding fingers to determine surface features such as texture [283]. Texture comprises two major dimensions—roughness and softness—which can be detected by tactile micropressure sensor arrays [284]. Capacitative, piezoresistive, piezoelectric, inductive and optical measurements are superior to thermoresistive, inductive and magnetic measurements [285]. Example tactile sensors include [286,287,288,289]. PZT tactile sensors in conjunction with pressure sensors with a feedback circuit can provide sensitive tactile measurements including differentiating between hard and soft objects [290]. The theory of elasticity provides the basis for determining physical contact parameters from tactile sensor measurements [291]. The four basic human skin sensations of pressure, texture, temperature and pain have been replicated for teleoperation [292]. Piezoelectric film can detect only dynamically changing forces and slip similar to Pacinian corpuscles in human skin; to measure static forces, resistive or capacitative measurements are required. Force sensing provides information on pressure for shape and hardness determination, piezoelectric dynamic vibration sensors provides information on texture and slip, while fast response thermocouples provides information on thermal conductivity. Pain was recorded as an overload in all three sensors. Thermal feedback was provided through a Peltier effect heat pump, texture/slip and pressure feedback was provided by increasing temperatures towards the thermal design limit of 50 °C. The system revealed that operators gave 90% correct identification of surfaces after only 10 min of training. Active touch sensing using multifingered hands may be used to acquire 3D scene information by manipulating and detecting changes in the environment [293]. Complete haptic feedback for handling compliant and slippery material requires force feedback for pressure information and tactile imaging for the extraction of shape [273]. Conductive silicone rubber impregnated by carbon particles may be employed as a tactile sensor in measuring applied force through resistance change. Slippage direction and extraction of shape from an array of such tactile “taxels” may be enabled by neural networks. This can provide the basis for elastomeric artificial skin. Artificial skin comprising 2D arrays of taxels affords highly sophisticated robotic control strategies [294] including the implementation of tactile maps [295]. Active tactile sensing with multiple fingers mounted with arrays of tactels enables the construction of 3D scenes of the touched surface [293]. Superquadratics can be fitted to the grasp shape through the shape parameters. Electronic skin with embedded pressure and temperature sensors may be based on flexible organic thin-film transistors which can stretch without altering the substrate’s conductive properties [296]. Inkjet printing can apply circuitry patterns of conducting thin films—nanowires—with organic transistor-based amplifiers onto a substrate.
Tactility is inherently multisensory which invites consideration of multisensory fusion. Multiple sensor data affords greater accuracy than single sensor data but measurement data between sensors must be correlated. Bayesian inferencing provides a principled means for combining multisensory data probabilistically. Bayes’ rule computes a posteriori probability of a hypothesis given its a priori probability and the conditional probability of an observation given that hypothesis. Dempster-Shafer theory of evidential reasoning extends Bayesian probability by overcoming some of its shortcomings at the cost of higher computational complexity. We can assume that for a robot manipulator and its finger configuration, tracking its changing pose is of paramount importance and multiple sensors provide indirect measurements of this changing pose. We are not aware of any work examining sensor fusion of multiple sensor modalities relating to tactility but propose that it is an area that should be developed. Assuming that tactility fusion is a variation on robot pose fusion, a discrete linear system model with state x(k) of pose, input u(k) with process noise w(k) and measurement output z(k) with measurement noise v(k) has a state space form:
Process and measurement noise are independent and Gaussian with covariance Q(k) and R(k) respectively. In the case of multiple sensors, there is more than one measurement equation. The Kalman filter is a recursive Bayesian method that generates an optimal solution to mean square error in the presence of Gaussian noise [297]. The Kalman filter has been the most commonly used approach on spacecraft for merging attitude determination sensors for spacecraft attitude estimation so it has an extensive space pedigree. The linear Kalman filter comprises two parts:
(i) the prediction part estimates a posteriori state and its covariance P(k) from the process model:
(ii) the correction part updates the previous estimate based on measurements z(k):
The primary problem in multisensory fusion is in uncertainty, which may be implemented through Bayesian probability, Dempster-Shafer evidence or fuzzy sets [298]. These types of capabilities will require high computational capabilities for rapid sensor fusion in real time, imposing severe computational burdens—a high-speed hardware sensor fusion system comprising massively parallel multiprocessors has achieved rapid 1 msec visual/force feedback rates [299]. The question is whether this degree of sophistication in tactility involving artificial skins and sensor fusion is necessary for active debris removal. The short answer is almost certainly “no” for grappling and securing the target debris but if thermal blanket handling or salvaging of potentially useful or valuable parts (essentially a form of space mining) becomes necessary then the answer will be “yes” if that eventuality arises. Nevertheless, dextrous grasping involves the combination of visual imaging and tactile sensing—grasp planning requires visual contour extraction to determine finger placements [300]. It is clear that a form of multisensory fusion might be valuable for active debris removal suggesting that some of these more sophisticated methods will add value to these new tasks.
13. Conclusions
We have reviewed many of the technological aspects of space robotics that have direct implications for active debris removal in a tutorial fashion. Although servicing will not be required during active debris removal, many of the tactile aspects are relevant both on grappling to acquire the target and potentially on re-grappling to maintain secure docking during transport. We have favoured the implementation of spacecraft attitude control systems on the chaser spacecraft (in particular, control moment gyroscopes) to ease the control problem of employing one or more manipulators mounted onto the spacecraft. It is hoped that this tutorial review will provide a useful stepping off point to equip the reader with the implications and issues that must be addressed in tackling this severe and timely problem of active debris removal. It is also hoped that we have presented good news—that we have the technological sophistication to implement active debris removal now. If we do not, we run the risk of becoming entombed on our planet. However, technology is not the barrier.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ellery, A. Introduction to Space Robotics; Springer: London, UK, 2000. [Google Scholar]
- Flores-Abad, A.; Ma, O.; Pham, K.; Ulrich, S. A review of space robotics technologies for on-orbit servicing. Prog. Aerosp. Sci. 2014, 68, 1–26. [Google Scholar] [CrossRef]
- Moosavian, S.A.A.; Papadopoulos, E. Free-flying robots in space: An overview of dynamics modeling, planning and control. Robotica 2007, 25, 537–547. [Google Scholar] [CrossRef]
- Xu, W.; Liang, B.; Xu, Y. Survey of modeling, planning, and ground verification of space robotic systems. Acta Astronaut. 2011, 68, 1629–1649. [Google Scholar] [CrossRef]
- Laryssa, P.; Lindsay, E.; Layi, O.; Marius, O.; Nara, K.; Aris, L.; Ed, T. International space station robotics: A comparative study of ERA, JEMRMS and MSS. In Proceedings of the 7th ESA Workshop on Advanced Space Technologies for Robotics and Automation, Noordwijk, The Netherlands, 19–21 November 2002. [Google Scholar]
- Ambrose, R.; Aldridge, H.; Askew, R.; Burridge, R.; Bluethmann, W.; Diftler, M.; Lovchik, C.; Magruder, D.; Rehnmark, F. Robonaut: NASA’s space humanoid. IEEE Intell. Syst. 2000, 15, 57–62. [Google Scholar] [CrossRef]
- Goza, S.; Clarke, J.-P.; Rochlis, J. Space Station telerobotics—Designing a human-robot interface. In Proceedings of the 2001 Conference and Exhibit on International Space Station Utilization, Cape Canaveral, FL, USA, 15–18 October 2001. [Google Scholar]
- Mavroidis, C.; Pfeiffer, C.; Lennon, J.; Paljic, A.; Celestino, J.; Bar-Cohen, Y. Modelling and design of an electrorheological fluid based haptic system for teleoperation of space robots. In Proceedings of the ROBOTICS 2000 Conference: The 4th International Conference and Exposition/Demonstration on Robotics for Challenging Situations and Environments, Albuquerque, NM, USA, 27 February–2 March 2000. [Google Scholar]
- Scott, R.; Ellery, A. An approach to ground based space surveillance of geostationary on-orbit servicing operations. Acta Astronaut. 2015, 112, 56–68. [Google Scholar] [CrossRef]
- Scott, R.; Ellery, A. Speckle imaging for optical tracking of on-orbit servicing in geostationary orbit. J. Spacecr. Rocket. 2016, 53, 433–447. [Google Scholar] [CrossRef]
- Yoshida, K. Achievements in space robotics. IEEE Robot. Autom. Mag. 2009, 16, 20–28. [Google Scholar] [CrossRef]
- Hirzinger, G. Multisensory shared autonomy and tele-sensor programming—Key issues in space robotics. Robot. Auton. Syst. 1993, 11, 141–162. [Google Scholar] [CrossRef]
- Ogilvie, A.; Allport, J.; Hannah, M.; Lymer, J. Autonomous satellite servicing using the Orbital Express demonstration manipulator system. In Proceedings of the 9th International Symposium on Artificial Intelligence, Robotics and Automation in Space, Universal City, LA, USA, 26–29 February 2008. [Google Scholar]
- Mulder, T. Orbital Express autonomous rendezvous and capture flight operations: Part 1 of 2—Mission description, AR&C exercises 1, 2 and 3. Adv. Astronaut. Sci. 2008, 130, 649–651. [Google Scholar]
- Kaiser, C.; Sjöberg, F.; Delcura, J.M.; Eilertsen, B. SMART-OLEV—An orbital life extension vehicle for servicing commercial spacecrafts in GEO. Acta Astronaut. 2008, 63, 400–410. [Google Scholar] [CrossRef]
- Caswell, D.; Visentin, G.; Ortega, G.; de Kam, J.; Nugteren, P.; Scholten, H. ConeXpress orbital life extension vehicle. ESA Bull. 2006, 127, 54–61. [Google Scholar]
- Wingo, D. Orbital Recovery’s responsive commercial space tug for life extension. In Proceedings of the AIAA 2nd Responsive Space Conference, Los Angeles, CA, USA, 19–22 April 2004. [Google Scholar]
- Meghdari, A.; Barazandeh, F. Design and fabrication of a novel quick-change mechanism. Mechatronics 2000, 10, 809–818. [Google Scholar] [CrossRef]
- Ellery, A.; Kreisel, J.; Sommer, B. The case for robotic on-orbit servicing of spacecraft: Spacecraft reliability is a myth. Acta Astronaut. 2008, 63, 632–648. [Google Scholar] [CrossRef]
- Ellery, A. Extraterrestrial 3D printing and in-situ resource utilisation to sidestep launch costs. J. Br. Interplanet. Soc. 2018, 70, 337–343. [Google Scholar]
- Ashurbeyli, I. Urbocop: Saving planet Earth. Room Space J. 2016, 3, 9. Available online: https://room.eu.com/article/urbocop/saving-planet-earth (accessed on 25 April 2019).
- Mehrholz, D.; Leuschacke, L.; Flury, W.; Jehn, R.; Klinkrad, H.; Landgraf, M. Detecting, tracking and imaging space debris. ESA Bull. 2002, 109, 128–133. [Google Scholar]
- Newman, K. NASA robotic conjunction assessment process: Overview and operational experiences. Acta Astronaut. 2010, 66, 1253–1261. [Google Scholar] [CrossRef][Green Version]
- Kessler, D.J.; Cour-Palais, B.G.; Cour-Palais, B.G. Collision frequency of artificial satellites: The creation of a debris belt. J. Geophys. Res. Biogeosci. 1978, 83, 2637. [Google Scholar] [CrossRef]
- Schildknecht, T.; Musci, R.; Ploner, M.; Beutler, G.; Flury, W.; Kuusela, J.; Cruz, J.D.L.; Palmero, L.D.F.D. Optical observations of space debris in GEO and in highly-eccentric orbits. Adv. Space Res. 2004, 34, 901–911. [Google Scholar] [CrossRef]
- McKnight, D.S.; Di Pentino, F.R. New insights on the orbital debris collision hazard at GEO. Acta Astronaut. 2013, 85, 73–82. [Google Scholar] [CrossRef]
- COPUOS. Progress Report of the Working Group on Space Debris. UN General Assembly COPUOS Document A/AC.105/C1/L284. Available online: http://www.unoosa.org/pdf/limited/c1/AC105_C1_L284E.pdf (accessed on 25 April 2019).
- Ailor, W.; Krag, H. Space debris and space safety: Looking forward. J. Br. Interplanet. Soc. 2009, 62, 261–264. [Google Scholar]
- Petro, A.J. Techniques for orbital debris control. J. Spacecr. Rocket. 1992, 29, 260–263. [Google Scholar] [CrossRef]
- Johnson, N. New look at the GEO and neat-GEO regimes: Operations, disposals and debris. Acta Astronaut. 2012, 80, 82–88. [Google Scholar] [CrossRef][Green Version]
- Yasaka, T.; Ashford, E. GSV: An approach toward space system servicing. Earth Space Rev. 1996, 5, 9–17. [Google Scholar]
- Longstaff, R.; Hempsell, M.; Alexandra, S. Study into the sustainable disposal of end of life GEO satellites. J. Br. Interplanet. Soc. 2016, 69, 429–438. [Google Scholar]
- Grasset, P.; Parkinson, B. Retrieval strategies for dead comsats for the Necropolis system mission. J. Br. Interplanet. Soc. 2017, 70, 261–304. [Google Scholar]
- Bonnal, C.; Gigou, J.; Aubin, D. Space debris mitigation measures applied to European launchers. Acta Astronaut. 2009, 65, 1679–1688. [Google Scholar] [CrossRef]
- Walker, R.; Martin, C.; Stokes, P.; Wilkinson, J.; Klinkrad, H. Analysis of the effectiveness of space debris mitigation measures using the delta model. Adv. Space Res. 2001, 28, 1437–1445. [Google Scholar] [CrossRef]
- Lewis, H.; Radtke, J.; Beck, J.; Oswakld, M.; Anderson, P.; Virgili, B.; Krag, H. Sensitivity of the space debris environment to large constellations and small satellites. J. Br. Interplanet. Soc. 2017, 70, 105–117. [Google Scholar]
- Virgili, B.B.; Dolado, J.; Lewis, H.; Radtke, J.; Krag, H.; Revelin, B.; Cazaux, C.; Colombo, C.; Crowther, R.; Metz, M. Risk to space sustainability from large constellations of satellites. Acta Astronaut. 2016, 126, 154–162. [Google Scholar] [CrossRef]
- Ornes, S. Bringing down the trash. Phys. World 2012, 6, 28–32. [Google Scholar] [CrossRef]
- Liou, J.C.; Johnson, N. Risks in space from orbiting debris. Science 2006, 311, 340–341. [Google Scholar] [CrossRef]
- Liou, J.-C.; Johnson, N.; Hill, N. Controlling the growth of future LEO debris populations with active debris removal. Acta Astronaut. 2010, 66, 648–653. [Google Scholar] [CrossRef]
- Bonnal, C.; Ruault, J.-M.; Desjean, M.-C. Active debris removal: Recent progress and current trends. Acta Astronaut. 2013, 85, 51–60. [Google Scholar] [CrossRef]
- White, A.E.; Lewis, H.G. The many futures of active debris removal. Acta Astronaut. 2014, 95, 189–197. [Google Scholar] [CrossRef]
- Lewis, H.G.; White, A.E.; Crowther, R.; Stokes, H. Synergy of debris mitigation and removal. Acta Astronaut. 2012, 81, 62–68. [Google Scholar] [CrossRef]
- Peters, S.; Pirzkall, C.; Fiedler, H.; Förstner, R. Mission concept and autonomy considerations for active Debris removal. Acta Astronaut. 2016, 129, 410–418. [Google Scholar] [CrossRef]
- Deloo, J.; Mooij, E. Active debris removal: Aspects of trajectories, communication and illumination during final approach. Acta Astronaut. 2015, 117, 277–295. [Google Scholar] [CrossRef]
- Lücking, C.; Colombo, C.; McInnes, C.R. A passive satellite deorbiting strategy for medium earth orbit using solar radiation pressure and the J2 effect. Acta Astronaut. 2012, 77, 197–206. [Google Scholar] [CrossRef]
- ROGER Team. ROGER—Phase A Study Final Report Executive Summary. EADS Space Transportation Report ROG-SIBRE-EXS. 2003. Available online: https://gsp.esa.int/documents/10192/43064675/C15678ExS.pdf/d4c58fae-33ab-4820-bc47-a66ca843093b (accessed on 25 April 2019).
- Biesbroek, R.; Innocenti, L.; Wolahan, A.; Serrano, M.E. Deorbit—ESA’s active debris removal mission. J. Br. Interplanet. Soc. 2017, 70, 143–151. [Google Scholar]
- Dudziak, R.; Tuttle, S.; Barraclough, S. Harpoon technology development for the active removal of space debris. Adv. Space Res. 2015, 56, 509–527. [Google Scholar] [CrossRef]
- Huang, P.; Zhang, F.; Meng, Z.; Liu, Z. Adaptive control for space debris removal with uncertain kinematics, dynamics and states. Acta Astronaut. 2016, 128, 416–430. [Google Scholar] [CrossRef]
- Chobotov, V.; Melamed, N.; Ailor, W.H.; Campbell, W.S. Ground assisted rendezvous with geosynchronous satellites for the disposal of space debris by means of Earth-oriented tethers. Acta Astronaut. 2009, 64, 946–951. [Google Scholar] [CrossRef]
- Nagamatsu, H.; Kubota, T.; Nakatani, I. Capture strategy for retrieval of a tumbling satellite by a space robotic manipulator. In Proceedings of the IEEE International Conference on Robotics and Automation, Minneapolis, MN, USA, 22–28 April 1996. [Google Scholar]
- Bennett, T.; Stevenson, D.; Hogan, E.; Schaub, H. Prospects and challenges of touchless electrostatic detumbling of small bodies. Adv. Space Res. 2015, 56, 557–568. [Google Scholar] [CrossRef]
- Nishida, S.I.; Kawamoto, S. Strategy for capturing tumbling space debris. Acta Astronaut. 2011, 68, 113–120. [Google Scholar] [CrossRef]
- Felicetti, L.; Gasbarri, P.; Pisculli, A.; Sabatini, M.; Palmerini, G.B. Design of robotic manipulators for orbit removal of spent launchers’ stages. Acta Astronaut. 2016, 119, 118–130. [Google Scholar] [CrossRef]
- Wang, M.; Luo, J.; Yuan, J.; Walter, U. Detumbling control for kinematically redundant space manipulator post-grasping a rotational satellite. Acta Astronaut. 2017, 141, 98–109. [Google Scholar] [CrossRef]
- Vasile, M.; Maddock, C.; Saunders, C. Orbital debris removal with solar concentrators. In Proceedings of the 61st International Astronautical Congress, Prague, Czech Republic, 27 September–1 October 2010. [Google Scholar]
- Levin, E.; Pearson, J.; Carroll, J. Wholesale debris removal from LEO. Acta Astronaut. 2012, 73, 100–108. [Google Scholar] [CrossRef]
- Hoyt, R.; Forward, R. Terminator Tether: Autonomous Deorbit of LEO Spacecraft for Space Debris Mitigation. AIAA 00-0329. 2000. Available online: http://www.tethers.com/papers/TTReno00.pdf (accessed on 25 April 2019).
- Nishida, S.-I.; Kawamoto, S.; Okawa, Y.; Terui, F.; Kitamura, S. Space debris removal system using a small satellite. Acta Astronaut. 2009, 65, 95–102. [Google Scholar] [CrossRef]
- Pardini, C.; Hanada, T.; Krisko, P.H.; Anselmo, L.; Hirayama, H. Are de-orbiting missions possible using electrodynamic tethers? Task review from the space debris perspective. Acta Astronaut. 2007, 60, 916–929. [Google Scholar] [CrossRef]
- Visagie, L.; Lappas, V.; Erb, S. Drag sails for space debris mitigation. Acta Astronaut. 2015, 109, 65–75. [Google Scholar] [CrossRef]
- Castronuovo, M.M. Active space debris removal—A preliminary mission analysis and design. Acta Astronaut. 2011, 69, 848–859. [Google Scholar] [CrossRef]
- Madakat, D.; Morio, J.; Vanderpooten, D. Biobjective planning of an active debris removal mission. Acta Astronaut. 2013, 84, 182–188. [Google Scholar] [CrossRef]
- Olympio, J.; Frouvelle, N. Space debris selection and optimal guidance for removal in the SSO with low-thrust propulsion. Acta Astronaut. 2014, 99, 263–275. [Google Scholar] [CrossRef]
- Stuart, J.; Howell, K.; Wilson, R. Application of multi-agent coordination methods to the design of space debris mitigation tours. Adv. Space Res. 2016, 57, 1680–1697. [Google Scholar] [CrossRef]
- Yu, J.; Chen, X.-Q.; Chen, L.-H.; Hao, D. Optimal scheduling of GEO debris removing based on hybrid optimal control theory. Acta Astronaut. 2014, 93, 400–409. [Google Scholar] [CrossRef]
- Fourie, D.; Tweddle, B.E.; Ulrich, S.; Saenz-Otero, A. Flight Results of Vision-Based Navigation for Autonomous Spacecraft Inspection of Unknown Objects. J. Spacecr. Rocket. 2014, 51, 2016–2026. [Google Scholar] [CrossRef]
- Oumer, N.; Panin, G.; Mulbauer, Q.; Tseneklidou, A. Vision-based localisation for on-orbit servicing of a partially cooperative satellite. Acta Astronaut. 2015, 117, 19–37. [Google Scholar] [CrossRef]
- Volpe, R.; Palmerini, G.; Sabatini, M. Passive camera-based determination of a non-cooperative and unknown satellite’s pose and shape. Acta Astronaut. 2018, 151, 805–817. [Google Scholar] [CrossRef]
- Capuano, V.; Kim, K.; Hu, J.; Harvard, A.; Chung, S.J. Monocular-based pose determination of uncooperative known and unknown space objects. In Proceedings of the 68th nternational Astronautical Congress, Bremen, Germany, 1–5 October 2018. [Google Scholar]
- Stieber, M.; Vukovich, G.; Petriu, E.; McKay, M. Vision-based sensing and control for space robotics applications. IEEE Trans. Instrum. Meas. 1999, 48, 807–812. [Google Scholar] [CrossRef][Green Version]
- Dong, G.; Zhu, Z.H. Position-based visual servo control of autonomous robotic manipulators. Acta Astronaut. 2015, 115, 291–302. [Google Scholar] [CrossRef]
- Drummond, T.; Cipolla, R. Real-time visual tracking of complex structures. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 932–946. [Google Scholar] [CrossRef]
- Kass, M.; Witkin, A.; Terzopoulos, T. Snakes: Active contour models. Int. J. Comput. 1988, 1, 321–331. [Google Scholar] [CrossRef]
- Sabatini, M.; Monti, R.; Gasbarri, P.; Palmerini, G.B. Adaptive and robust algorithms and tests for visual-based navigation of a space robotic manipulator. Acta Astronaut. 2013, 83, 65–84. [Google Scholar] [CrossRef]
- Chen, S.Y. Kalman Filter for Robot Vision: A Survey. IEEE Trans. Ind. Electron. 2012, 59, 4409–4420. [Google Scholar] [CrossRef]
- Dong, G.; Zhu, Z.H. Autonomous robotic capture of non-cooperative target by adaptive extended Kalman filter based visual servo. Acta Astronaut. 2016, 122, 209–218. [Google Scholar] [CrossRef]
- Silveirra, G. On intensity-based 3D visual servoing. Robot. Autonom. Syst. 2014, 62, 1636–1645. [Google Scholar] [CrossRef]
- Ozen, S.; Bouganis, A.; Shanahan, M. A fast evaluation criterion for the recognition of occluded shapes. Robot. Auton. Syst. 2007, 55, 741–749. [Google Scholar] [CrossRef]
- Reymann, C.; Lacroix, S. Improving LiDAR point cloud classification using intensities and multiple echoes. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 5122–5128. [Google Scholar]
- Tzschichholz, T.; Ma, L.; Schilling, K. Model-based spacecraft pose estimation and motion prediction using a photonic mixer device camera. Acta Astronaut. 2011, 68, 1156–1167. [Google Scholar] [CrossRef]
- Ianni, J.; Repperger, D.; Baker, R.W.; Williams, R.L. Human interfaces for robotic satellite servicing. High-Power Lasers Appl. 2002, 4632, 95–104. [Google Scholar]
- Lamb, P.; Owen, D. Human performance in space telerobotic manipulation. In Proceedings of the ACM Symposium on Virtual Reality Software and Technology, Monterey, CA, USA, 7–9 November 2005. [Google Scholar]
- Sellmaier, F.; Boge, T.; Spurmann, J.; Gully, S.; Rupp, T.; Huber, F. On-orbit servicing missions: Challenges and solutions for spacecraft operations. In Proceedings of the SpaceOps 2010 Conference, Huntsville, Alabama, 25–30 April 2010. [Google Scholar]
- Abe, N.; Yamanaka, K. Smith predictor control and internal model control—A tutorial. In Proceedings of the SICE 2003 Annual Conference, Fukai, Japan, 4–6 August 2003; pp. 1383–1387. [Google Scholar]
- Backes, P.; Beahan, J.; Long, M.; Steele, R.; Bon, B.; Zimmerman, W. Ground-remote control for space station telerobotics with time delay. In Proceedings of the AAS Guidance & Control Conference, Keystone, CO, USA, 8–12 February 1992; pp. 285–303. [Google Scholar]
- Kim, W.; Bejczy, A. Demonstration of a high-fidelity predictive/preview display technique for telerobotic servicing in space. IEEE Trans. Robot. Autom. 1993, 9, 698–702. [Google Scholar] [CrossRef]
- Imaida, T.; Yokokohji, Y.; Doi, T.; Oda, M.; Yoshikawa, T. Ground–Space Bilateral Teleoperation of ETS-VII Robot Arm by Direct Bilateral Coupling Under 7-s Time Delay Condition. IEEE Trans. Robot. Autom. 2004, 20, 499–511. [Google Scholar] [CrossRef]
- Hokayem, P.F.; Spong, M.W. Bilateral teleoperation: An historical survey. Automatica 2006, 42, 2035–2057. [Google Scholar] [CrossRef]
- Leung, G.; Francis, B.; Apkarian, J. Bilateral controller for teleoperators with time delay via μ-synthesis. IEEE Trans. Robot. Autom. 1995, 11, 105–116. [Google Scholar] [CrossRef]
- Lawrence, D.; Chapel, J.; Depkovitch, T. Issues, concerns and initial implementation results for space based telerobotic control. In Proceedings of the Goddard Conference on Space Applications of Artificial Intelligence & Robotics, Greenbelt, MD, USA, 13–14 May 1987. [Google Scholar]
- Nakanishi, H.; Kodama, M.; Yoshida, K. Influence of Control Time Delay on the Dynamics of Satellite Capture. Trans. Soc. Aeronaut. Space Sci. Space Technol. 2009, 7, 29–34. [Google Scholar] [CrossRef]
- Penin, L.; Matsumoto, K.; Wakabayashi, S. ETS-VII space robot teleoperation through virtual force reflection. In Proceedings of the 5th International Symposium on Artificial Intelligence Robotics & Automation in Space (ESA SP-440), Noordwijk, The Netherlands, 1–3 June 1999; pp. 389–396. [Google Scholar]
- Penin, L.; Wakabayashi, S.; Matsumoto, K. Force reflection for ground control of Space robots. IEEE Robot. Autom. Mag. 2000, 7, 50–63. [Google Scholar] [CrossRef]
- Arcaca, P.; Melchiorri, C. Control schemes for teleoperation with time delay: A comparative study. Robot. Autonom. Syst. 2002, 38, 49–64. [Google Scholar] [CrossRef]
- Kim, W.; Hannaford, B.; Bejczy, A. Force reflection and shared compliant control in operating telemanipulators with time delay. IEEE Trans Robot. Autom. 1992, 8, 176–185. [Google Scholar] [CrossRef]
- Muradore, R.; Fiorini, P. Review of bilateral teleoperation algorithms. Acta Polytech. Hungar. 2010, 13, 191–208. [Google Scholar]
- Anderson, R.; Spong, M. Bilateral control of teleoperators with time delay. IEEE Trans. Autom. 1989, 34, 494–501. [Google Scholar] [CrossRef]
- Chopra, N.; Spong, M.; Lozano, R. Synchronisation of bilateral teleoperators with time delay. Automatica 2008, 44, 2142–2148. [Google Scholar] [CrossRef]
- Li, Z.; Cao, X.; Tang, Y.; Li, R.; Ye, W. Bilateral Teleoperation of Holonomic Constrained Robotic Systems with Time-Varying Delays. IEEE Trans. Instrum. Meas. 2013, 62, 752–765. [Google Scholar] [CrossRef]
- Niemeyer, G.; Slotine, J.J. Stable adaptive teleoperation. IEEE J. Ocean. Eng. 1991, 16, 152–162. [Google Scholar] [CrossRef]
- Niemayer, G.; Slotine, J.J. Telemanipulation with time delays. Int J Robot. Res. 2004, 23, 873–890. [Google Scholar] [CrossRef]
- Várkonyi, T.A.; Rudas, I.J.; Pausits, P.; Haidegger, T. Survey on the control of time delay teleoperation systems. In Proceedings of the 2014 18th International Conference on Intelligent Engineering Systems (INES), Tihany, Hungary, 3–5 July 2014; pp. 89–94. [Google Scholar]
- Eusebi, A.; Melchiorri, C. Force reflecting telemanipulators with time delay: Stability analysis and control design. IEEE Trans Robot. Autom. 1998, 14, 635–640. [Google Scholar] [CrossRef]
- Ajoudani, A.; Tsagarakis, N.; Bicchi, A. Tele-impedance: Teleoperation with impedance regulation using a body–machine interface. Int. J. Robot. 2012, 31, 1642–1656. [Google Scholar] [CrossRef]
- Sheridan, T. Space teleoperation through time delay: Review and prognosis. IEEE Trans. Robot. Autom. 1993, 9, 592–606. [Google Scholar] [CrossRef]
- Sheridan, T.B.; Ottensmeyer, M.; Kim, S. Human-computer cooperation and intervention in telesurgery. Robot. Auton. Syst. 1996, 18, 127–134. [Google Scholar] [CrossRef]
- Penin, L. Teleoperation with time delay: A survey and its use in space robotics. In Proceedings of the ESA Workshop on Advanced Space Technologies for Robotics & Automation, ESTEC, Noordwijk, The Netherlands, 5–7 December 2000. [Google Scholar]
- Arantes, G.; Rocco, M.; da Fonseca, I.; Theil, S. Far and proximity manoeuvres of a constellation of service satellites and autonomous pose estimation of customer satellite using machine vision. Acta Astronaut. 2010, 66, 1493–1505. [Google Scholar] [CrossRef]
- Tortopidis, I.; Papadopoulos, E. On point-to-point motion planning for underactuated space manipulator systems. Robot. Autonom. Syst. 2007, 55, 122–131. [Google Scholar] [CrossRef]
- Murphy, S.; Wen, J. Analysis of active manipulator elements in space manipulation. IEEE Trans. Robot. Autom. 1993, 9, 544–552. [Google Scholar] [CrossRef]
- Yoshida, K. Engineering Test Satellite VII Flight Experiments for Space Robot Dynamics and Control: Theories on Laboratory Test Beds Ten Years Ago, Now in Orbit. Int. J. Robot. 2003, 22, 321–335. [Google Scholar] [CrossRef]
- From, P.J.; Pettersen, K.Y.; Gravdahl, J.T. Singularity-free dynamic equations of spacecraft-manipulator systems. Acta Astronaut. 2011, 69, 1057–1065. [Google Scholar] [CrossRef]
- Muller, A. Screw and Lie group theory in multibody kinematics: Motion representation and recursive kinematics of tree topology systems. Multibody Syst. Dyn. 2017, 42, 219–248. [Google Scholar] [CrossRef]
- Saha, S. A unified approach to Space robot kinematics. IEEE Trans. Robot. Autom. 1996, 12, 401–405. [Google Scholar] [CrossRef]
- Nagashima, F.; Nakaruma, Y. Efficient computation scheme for the kinematics and inverse dynamics of a satellite-based manipulator. In Proceedings of the 1992 IEEE International Conference on Robotics and Automation, Nice, France, 12–14 May 1992; pp. 905–912. [Google Scholar]
- Siciliano, B. Kinematic control of redundant robot manipulators: A tutorial. J. Intell. Robot. Syst. 1990, 3, 201–212. [Google Scholar] [CrossRef]
- Xu, W.; Liang, B.; Xu, Y. Practical approaches to handle the singularities of a wrist-partitioned space manipulator. Acta Astronaut. 2011, 68, 269–300. [Google Scholar] [CrossRef]
- Longman, R.; Lindberg, R.; Zedd, M. Satellite-mounted robot manipulators—New kinematics and reaction compensation. Int. J. Robot. Res. 1986, 6, 87–103. [Google Scholar] [CrossRef]
- Lindberg, R.; Longman, R.; Zedd, M. Kinematic and dynamic properties of an elbow manipulator mounted on a satellite. J. Astronaut. Sci. 1990, 38, 397–421. [Google Scholar]
- Ellery, A. Resolved motion control of space manipulators. In Proceedings of the 45th International Astronautics Congress, Jerusalem, Israel, 9–14 October 1994. [Google Scholar]
- Ellery, A. An engineering approach to the dynamic control of space robotic on-orbit servicers. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2004, 218, 79–98. [Google Scholar] [CrossRef]
- Hooker, W.; Margulies, G. Dynamical attitude equations for n-body satellite. J. Astronaut. Sci. 1965, 12, 123–128. [Google Scholar]
- Vafa, Z.; Dubowsky, S. The Kinematics and Dynamics of Space Manipulators: The Virtual Manipulator Approach. Int. J. Robot. 1990, 9, 3–21. [Google Scholar] [CrossRef]
- Vafa, Z.; Dubowsky, S. On the dynamics of space manipulators using the virtual manipulator with applications to path planning. J. Astronaut. Sci. 1990, 36, 441–472. [Google Scholar]
- Liang, B.; Xu, Y.; Bergerman, M. Mapping a Space Manipulator to a Dynamically Equivalent Manipulator; CMU-RI-TR-96-33; Robotics Institute, Carnegie Mellon University: Pittsburgh, PA, USA, 1996. [Google Scholar]
- Xu, Y.; Xu, W.; Liang, B.; Li, C.; Qiang, W. Path Planning of Free-Floating Robot in Cartesian Space Using Direct Kinematics. Int. J. Adv. Robot. Syst. 2007, 4, 4. [Google Scholar] [CrossRef]
- Umetani, Y.; Yoshida, K. Resolved motion rate control of space manipulators using a generalised Jacobian. IEEE Trans. Robot. Autom. 1989, 5, 303–314. [Google Scholar] [CrossRef]
- Xu, W.; Liu, Y.; Liang, B.; Xu, Y.; Qiang, W. Autonomous path planning and experiment study of free-floating space robot for target capturing. J. Intell. Robot. Syst. 2008, 51, 303–331. [Google Scholar] [CrossRef]
- Yokokohji, Y.; Toyoshima, T.; Yoshikawa, T. Efficient computational algorithms for trajectory control of free-flying space robots with multiple arms. IEEE Trans. Robot. Autom. 1993, 9, 571–580. [Google Scholar] [CrossRef]
- Dubowsky, S.; Papadopoulos, E. The kinematics, dynamics, and control of free-flying and free-floating space robotic systems. IEEE Trans. Robot. Autom. 1993, 9, 531–543. [Google Scholar] [CrossRef]
- Nanos, K.; Papadopoulos, E. On cartesian motions with singularities avoidance for free-floating space robots. In Proceedings of the 2012 IEEE International Conference on Robotics and Automation, St. Paul, MN, USA, 14–18 May 2012; pp. 5398–5403. [Google Scholar]
- Cocuzza, S.; Pretto, I.; Debei, S. Reaction torque control of redundant space robotic systems for orbital maintenance and simulated microgravity tests. Acta Astronaut. 2010, 67, 285–295. [Google Scholar] [CrossRef]
- Cocuzza, S.; Pretto, I.; Debei, S. Novel reaction control techniques for redundant space manipulators: Theory and simulated microgravity tests. Acta Astronaut. 2011, 68, 1712–1721. [Google Scholar] [CrossRef]
- Wee, L.B.; Walker, M. On the dynamics of contact between space robots and configuration control for impact minimization. IEEE Trans. Robot. Autom. 1993, 9, 581–591. [Google Scholar]
- Hafez, A.A.; Anurag, V.; Shah, S.; Krishna, K.M.; Jawahar, C. Reactionless visual servoing of a dual-arm space robot. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–5 June 2014; pp. 4475–4480. [Google Scholar]
- Longman, R. Kinetics and Workspace of Robot Mounted on Satellite that Is Free to Rotate and Translate; AIAA 88-4097-CP; Springer: Boston, MA, USA, 1988. [Google Scholar]
- Nenchev, D.N.; Yoshida, K.; Vichitkulsawat, P.; Uchiyama, M. Reaction null-space control of flexible structure mounted manipulator systems. IEEE Trans. Robot. Autom. 1999, 15, 1011–1023. [Google Scholar] [CrossRef]
- Yoshida, K.; Nenchev, D. Reactionless manipulations and proposal to ETS-VII onboard experiments. In Proceedings of the Fifth International Symposium on Artificial Intelligence Robotics & Automation in Space (ESA SP-440), Noordwijk, The Netherlands, 1–3 June 1999; pp. 415–420. [Google Scholar]
- Piersigilli, P.; Sharf, I.; Misra, A. Reactionless capture of a satellite by a two degree-of-freedom manipulator. Acta Astronaut. 2010, 66, 183–192. [Google Scholar] [CrossRef]
- Papadopoulos, E.; Moosavian, S.A.A. Dynamics and control of space free-flyers with multiple manipulators. Adv. Robot. 1994, 9, 603–624. [Google Scholar] [CrossRef]
- Ciaverini, S.; Siciliano, B.; Egeland, O. Review of the damped least-squares inverse kinematics with experiments on an industrial robot manipulator. IEEE Trans. Control Syst. Technol. 1994, 2, 123–134. [Google Scholar] [CrossRef]
- Torres, M.; Dubowsky, S. Minimising spacecraft attitude disturbances in space manipulator systems. AIAA J. Guid. Control Dyn. 1992, 15, 1010–1017. [Google Scholar] [CrossRef]
- Nakumra, Y.; Mukherjee, R. Nonholonomic path planning of space robots via the bidirectional approach. IEEE Trans. Robot. Autom. 1989, 9, 531–543. [Google Scholar] [CrossRef]
- Papadopoulos, E.; Dubowsky, S. On the nature of control algorithms for free-floating space manipulators. IEEE Trans. Robot. Autom. 1991, 7, 750–758. [Google Scholar] [CrossRef]
- Hirzinger, G.; Brunner, B.; Landzettel, K.; Schott, J. Preparing a new generation of space robots—A survey of research at DLR. Robot. Auton. Syst. 1998, 23, 99–106. [Google Scholar] [CrossRef]
- Armstrong-Hélouvry, B.; Dupont, P.; De Wit, C.C. A survey of models, analysis tools and compensation methods for the control of machines with friction. Automatica 1994, 30, 1083–1138. [Google Scholar] [CrossRef]
- Loo, C.K.; Mandava, R.; Rao, M.V.C. A Hybrid Intelligent Active Force Controller for Articulated Robot Arms Using Dynamic Structure Neural Network. J. Intell. Robot. Syst. 2004, 40, 113–145. [Google Scholar] [CrossRef]
- Hanson, B.; Leveseley, M. Self-sensing applications for electromagnetic actuators. Sens. Actuators 2004, 116, 345–351. [Google Scholar] [CrossRef]
- Seraji, H. Configuration control of rover-mounted manipulators. In Proceedings of the 1995 IEEE International Conference on Robotics and Automation, Nagoya, Japan, 21–27 May 1995. [Google Scholar]
- Gardner, J.F.; Velinsky, S.A. Kinematics of mobile manipulators and implications for design. J. Robot. Syst. 2000, 17, 309–320. [Google Scholar] [CrossRef]
- Papadimitriou, I.; Papadopoulos, E.; Poulakakis, I. On Path Planning and Obstacle Avoidance for Nonholonomic Platforms with Manipulators: A Polynomial Approach. Int. J. Robot. 2002, 21, 367–383. [Google Scholar]
- Yuh, J. Design and Control of Autonomous Underwater Robots: A Survey. Auton. Robot. 2000, 8, 7–24. [Google Scholar] [CrossRef]
- Lynch, B.; Ellery, A. Efficient control of an AUV vehicle-manipulator system: An application for the exploration of Europa. IEEE J. Ocean. Eng. 2014, 39, 552–570. [Google Scholar] [CrossRef]
- Iagnemma, K.; Morel, G.; Dubowsky, S. The precise control of manipulators with high joint-friction using base force/torque sensing. Automatica 2000, 36, 931–941. [Google Scholar]
- Ma, O.; Dan, H. On-Orbit Identification of Inertia Properties of Spacecraft Using Robotics Technology; Final Technical Report 20070426205; New Mexico State University: Las Cruces, NM, USA, 2006. [Google Scholar]
- Xu, W.; Liu, Y.; Liang, B.; Wang, X.; Xu, Y. Unified multi-domain modelling and simulation of space robot for capturing a moving target. Multibody Syst. Dyn. 2010, 23, 293–331. [Google Scholar] [CrossRef]
- Li, C.; Teo, K.; Li, B.; Ma, G. Constrained optimal PID-like controller design for spacecraft attitude stabilization. Acta Astronaut. 2012, 74, 131–140. [Google Scholar] [CrossRef]
- Guarnaccia, L.; Bevilacqua, R.; Pastorelli, S.P. Suboptimal LQR-based spacecraft full motion control: Theory and experimentation. Acta Astronaut. 2016, 122, 114–136. [Google Scholar] [CrossRef]
- Li, X.; Yu, H.; Yuan, M. Design of optimal PID controller with ε-Routh stability for different processes. Math. Probl. Eng. 2013, 2013, 582879. [Google Scholar]
- Shi, J.F.; Ulrich, S.; Allen, A. Spacecraft adaptive attitude control with application to space station free-flyer robotic capture. In Proceedings of the AIAA Guidance, Navigation & Control Conference, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar]
- Sugita, M. Torque distribution algorithm for effective use of reaction wheel torques and angular momentums. Acta Astronaut. 2017, 139, 18–23. [Google Scholar] [CrossRef]
- Ellery, A. Robotic in-orbit servicers—The need for control moment gyroscopes for attitude control. Aeronaut. J. 2004, 108, 207–214. [Google Scholar] [CrossRef]
- Vadali, S.R.; Walker, S.R.; Oh, H.-S. Preferred gimbal angles for single gimbal control moment gyros. J. Guid. Control. Dyn. 1990, 13, 1090–1095. [Google Scholar] [CrossRef]
- Bedrossian, N.S.; Paradiso, J.; Bergmann, E.V.; Rowell, D. Steering law design for redundant single-gimbal control moment gyroscopes. J. Guid. Control. Dyn. 1990, 13, 1083–1089. [Google Scholar] [CrossRef]
- Wie, B.; Bailey, D.; Heiberg, C. Singularity Robust Steering Logic for Redundant Single-Gimbal Control Moment Gyros. J. Guid. Control. Dyn. 2001, 24, 865–872. [Google Scholar] [CrossRef]
- Leeghim, H.; Bang, H.; Park, J.-O. Singularity avoidance of control moment gyros by one-step ahead singularity index. Acta Astronaut. 2009, 64, 935–945. [Google Scholar] [CrossRef]
- Kojima, H. Singularity analysis and steering control laws for adaptive skew pyramid-type control moment gyroscopes. Acta Astronaut. 2013, 85, 120–137. [Google Scholar] [CrossRef]
- Schaub, H.; Vadali, S.; Junkins, J. Feedback control law for variable speed control moment gyros. J. Astronaut. Sci. 1998, 46, 307–328. [Google Scholar]
- Hu, Q.; Jia, Y.; Xu, S. Dynamics and vibration suppression of space structures with control moment gyroscopes. Acta Astronaut. 2014, 96, 232–245. [Google Scholar] [CrossRef]
- Hu, Q.; Guo, C.; Zhang, J. Singularity and steering logic for control moment gyros on flexible space structures. Acta Astronaut. 2017, 137, 261–273. [Google Scholar] [CrossRef]
- Kawak, B. Development of a low-cost, low micro-vibration CMG for small agile satellite applications. Acta Astronaut. 2017, 131, 113–122. [Google Scholar] [CrossRef]
- Jia, Y.; Misra, A.K. Robust trajectory tracking control of a dual-arm space robot actuated by control moment gyroscopes. Acta Astronaut. 2017, 137, 287–301. [Google Scholar] [CrossRef]
- Hu, Q.; Zhang, J. Maneouvre and vibration control of flexible manipulators using variable speed control moment gyroscopes. Acta Astronaut. 2015, 113, 105–119. [Google Scholar] [CrossRef]
- Carpenter, M.; Peck, M. Reducing Base Reactions with Gyroscopic Actuation of Space-Robotic Systems. IEEE Trans. Robot. 2009, 25, 1262–1270. [Google Scholar] [CrossRef]
- Beker, M.G.; Bertolini, A.; Brand, J.F.J.V.D.; Bulten, H.J.; Hennes, E.; Rabeling, D.S. State observers and Kalman filtering for high performance vibration isolation systems. Sci. Instrum. 2014, 85, 034501. [Google Scholar] [CrossRef] [PubMed]
- Richie, D.J.; Lappas, V.J.; Prassinos, G. A practical small satellite variable-speed control moment gyroscope for combined energy storage and attitude control. Acta Astronaut. 2009, 65, 1745–1764. [Google Scholar] [CrossRef]
- Swarup, B. Energy storage takes off. Phys. World 2007, 7, 42–45. [Google Scholar] [CrossRef]
- Ajwad, S.A.; Iqbal, J.; Ullah, M.I.; Mehmood, A. A systematic review of current and emergent manipulator control approaches. Front. Mech. Eng. 2015, 10, 198–210. [Google Scholar] [CrossRef]
- Freund, E. Fast Nonlinear Control with Arbitrary Pole-Placement for Industrial Robots and Manipulators. Int. J. Robot. 1982, 1, 65–78. [Google Scholar] [CrossRef]
- Song, Z.; Yi, J.; Zhao, D.; Li, X. A computed torque controller for uncertain robotic manipulator systems: Fuzzy approach. Fuzzy Sets Syst. 2005, 154, 208–226. [Google Scholar] [CrossRef]
- Meng, Q.; Zhang, T.; Li, D.-C.; Liang, J.-M.; Liu, B.; Song, J.-Y. Fault Tolerant Attitude Control for Flexible Satellite with Uncertainties and Actuator Saturation. Int. J. Adv. Robot. Syst. 2013, 10, 262. [Google Scholar] [CrossRef]
- Azadi, M.; Fazelzadeh, S.; Eghtesad, M.; Azadi, E. Vibration suppression and adaptive-robust control of a smart flexible satellite with three axes maneouvering. Acta Astronaut. 2011, 69, 307–322. [Google Scholar] [CrossRef]
- Lampariello, R.; Oumer, N.; Artigas, J.; Rackl, W.; Panin, G.; Purschke, R.; Harder, J.; Walter, U.; Frickel, J.; Masic, I.; et al. FORROST: Advances in on-orbit robotic technologies. In Proceedings of the 2015 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2015. [Google Scholar]
- Nanos, K.; Papadopoulos, E.G. On the dynamics and control of flexible joint space manipulators. Eng. Pract. 2015, 45, 230–243. [Google Scholar] [CrossRef]
- Ge, X.-S.; Chen, L.-Q.; Yan-Zhu, L. Optimal control of the deployment process of solar wings on spacecraft. Acta Astronaut. 2007, 60, 684–690. [Google Scholar] [CrossRef]
- Longman, R. Attitude tumbling due to flexibility in satellite-mounted robots. J. Astronaut. Sci. 1990, 36, 4096. [Google Scholar]
- Toglia, C.; Sabatini, M.; Gasbarri, P.; Palmerini, G.B. Optimal target grasping of a flexible space manipulator for a class of objectives. Acta Astronaut. 2011, 68, 1031–1041. [Google Scholar] [CrossRef]
- Sabatini, M.; Gasbarri, P.; Monti, R.; Palmerini, G.B. Vibration control of a flexible space manipulator during on orbit operations. Acta Astronaut. 2012, 73, 109–121. [Google Scholar] [CrossRef]
- Chebbi, J.; Dubanchet, V.; Gonzalez, P.; Alazard, D. Linear dynamics of flexible multibody systems. Multibody Syst. Dyn. 2017, 41, 75–100. [Google Scholar] [CrossRef]
- Cetinkunt, S.; Book, W. Flexibility effects on the control system performance of large-scale robotic manipulators. J. Astronaut. Sci. 1990, 36, 531–556. [Google Scholar]
- Ge, S.S.; Lee, T.; Zhu, G. Energy-based robust controller design for multi-link flexible robots. Mechatronics 1996, 6, 779–798. [Google Scholar] [CrossRef]
- Book, W. Structural flexibility of motion systems in the space environment. IEEE Trans. Robot. Autom. 1993, 9, 524–530. [Google Scholar] [CrossRef]
- Murotsu, Y.; Tsujio, S.; Senda, K.; Hayashi, M. Trajectory control of flexible manipulators on a free-flying space robot. IEEE Syst. 1992, 12, 51–57. [Google Scholar]
- Halim, D.; Luo, X.; Trivailo, P. Decentralised vibration control of a multi-link flexible robotic manipulator using smart piezoelectric transducers. Acta Astronaut. 2014, 104, 186–196. [Google Scholar] [CrossRef]
- Karray, F.; Modi, V.; Chan, J. Path planning with obstacle avoidance as applied to a class of space based flexible manipulators. Acta Astronaut. 1995, 37, 69–86. [Google Scholar] [CrossRef]
- Ozgoli, S.; Taghirad, H. Survey on the control of flexible joint robots. Asian J. Control 2006, 8, 332–344. [Google Scholar] [CrossRef]
- Tomei, P. A simple PD controller for robots with elastic joints. IEEE Trans. Autom. 1991, 36, 1208–1213. [Google Scholar] [CrossRef]
- Khorasani, K. Adaptive control of flexible-joint robots. IEEE Trans. Robot. Autom. 1992, 8, 250–267. [Google Scholar] [CrossRef]
- Lozano, R.; Brogliato, B. Adaptive control of robot manipulators with flexible joints. IEEE Trans. Autom. Control 1992, 37, 174–181. [Google Scholar] [CrossRef]
- Brogliato, B.; Ortega, R.; Lozano, R. Global tracking controllers for flexible-joint manipulators: A comparative study. Automatica 1995, 31, 941–956. [Google Scholar] [CrossRef]
- Taylor, G. Nonlinear control of electric machines: An overview. IEEE Control Syst. 1994, 14, 41–51. [Google Scholar]
- Pazelli, T.F.; Terra, M.H.; Siqueira, A.A. Experimental investigation on adaptive robust controller designs applied to a free-floating space manipulator. Eng. Pract. 2011, 19, 395–408. [Google Scholar] [CrossRef]
- Piltan, F.; Sulaiman, N. Review of sliding mode control of robotic manipulator. World Appl. Sci. J. 2012, 18, 1855–1869. [Google Scholar]
- Wang, M.; Luo, J.; Walter, U. A non-linear model predictive controller with obstacle avoidance for a space robot. Adv. Space Res. 2016, 57, 1737–1746. [Google Scholar] [CrossRef]
- Tang, Y.; Arteage, M. Adaptive control of robot manipulators based on passivity. IEEE Trans. Autom. Control 1994, 39, 1871–1875. [Google Scholar] [CrossRef]
- Wang, H.; Xie, Y. Passivity based adaptive Jacobian tracking for free-floating space manipulators without using spacecraft acceleration. Automatica 2009, 45, 1510–1517. [Google Scholar] [CrossRef]
- Wang, H.; Xie, Y. On the recursive adaptive control for free-floating space manipulators. J. Intell. Robot. Syst. 2012, 66, 443–461. [Google Scholar] [CrossRef]
- Wang, H.; Xie, Y. Prediction Error Based Adaptive Jacobian Tracking for Free-Floating Space Manipulators. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3207–3221. [Google Scholar] [CrossRef]
- Walker, M.; Wee, L.-B. Adaptive control of space-based robot manipulators. IEEE Trans. Robot. Autom. 1991, 7, 828–835. [Google Scholar] [CrossRef][Green Version]
- Zhang, F.; Qu, J.; Fu, Y.; Wang, S. Robust Adaptive Control of a Free-Floating Space Robot System in Cartesian Space. Int. J. Adv. Robot. Syst. 2015, 12, 157. [Google Scholar] [CrossRef]
- Parlaktuna, O.; Ozkan, M. Adaptive control of free-floating space manipulators using dynamically equivalent manipulator model. Robot. Auton. Syst. 2004, 46, 185–193. [Google Scholar] [CrossRef]
- Xu, Y.; Shum, H.-Y.; Kanade, T.; Lee, J.J. Parametrisation and adaptive control of space robot systems. IEEE Trans. Aerosp. Electron. Syst. 1994, 30, 435–451. [Google Scholar]
- Gourdeau, R.; Schwartz, H.M. Adaptive Control of Robotic Manipulators Using an Extended Kalman Filter. J. Syst. Meas. 1993, 115, 203–208. [Google Scholar] [CrossRef]
- Ehrenwald, L.; Guelman, M. Stability and convergence of integrated adaptive control for space manipulators. Acta Astronaut. 1997, 39, 623–629. [Google Scholar] [CrossRef]
- Xu, Y.; Shum, H.-Y.; Lee, J.J.; Kanade, T. Adaptive Control of Space Robot System with an Attitude-Controlled Base; CMU-RI-TR-91-14; Robotics Institute, Carnegie Mellon University: Pittsburgh, PN, USA, 1991. [Google Scholar]
- Fekri, S.; Athans, M.; Pascoal, A. Issues, progress and new results in robust adaptive control. Int. J. Adapt. Control Signal Process. 2006, 20, 519–579. [Google Scholar] [CrossRef]
- Pradhan, S.K.; Subudhi, B. Real-Time Adaptive Control of a Flexible Manipulator Using Reinforcement Learning. IEEE Trans. Autom. Sci. Eng. 2012, 9, 237–249. [Google Scholar] [CrossRef]
- De Luca, A.; Mattone, R. Sensorless robot collision detection and hybrid force/motion control. In Proceedings of the IEEE International Conference on Robotics & Automation, Barcelona, Spain, 18–22 April 2005; pp. 999–1004. [Google Scholar]
- Kao, I.; Yang, F. Stiffness and contact mechanics for soft fingers in grasping and manipulation. IEEE Trans. Robot. Autom. 2004, 20, 132–135. [Google Scholar] [CrossRef]
- Faik, S.; Witteman, H. Modelling of Impact Dynamics: A Literature Survey. 2000. Available online: https://pdfs.semanticscholar.org/7e01/984665b818fc26c45c7377201d574691879a.pdf (accessed on 25 April 2019).
- Gilardi, G.; Sharf, I. Literature survey of contact dynamics modelling. Mech. Mach. Theory 2002, 37, 1213–1239. [Google Scholar] [CrossRef]
- Haddadi, A.; Hashtrudi-Zaad, K. Real-Time Identification of Hunt–Crossley Dynamic Models of Contact Environments. IEEE Trans. Robot. 2012, 28, 555–566. [Google Scholar] [CrossRef]
- Shoji, Y.; Inaba, M.; Fukuda, T. Impact control of grasping. IEEE Trans. Ind. Electron. 1991, 38, 187–194. [Google Scholar] [CrossRef]
- Rocco, P.; Ferretti, G.; Magnani, G. Implicit force control for industrial robots in contact with stiff surfaces. Automatica 1997, 33, 2041–2047. [Google Scholar] [CrossRef]
- Medina, A.; Tomassini, A.; Suatoni, M.; Aviles, M.; Solway, N.; Coxhill, I.; Paraskevas, I.; Rekleitis, G.; Papadiopoulos, E.; Krenn, R.; et al. Towards a standardised grasping and refulelling on-orbit servicing for GEO spacecraft. Acta Astronaut. 2017, 134, 1–10. [Google Scholar] [CrossRef]
- Panin, J. New latching mechanism. ESA J. 1992, 16, 363–378. [Google Scholar]
- Hogan, N. Impedance Control: An Approach to Manipulation: Part I—Theory. J. Syst. Meas. 1985, 107, 1–7. [Google Scholar] [CrossRef]
- Hogan, N. Impedance Control: An Approach to Manipulation: Part II—Implementation. J. Syst. Meas. 1985, 107, 8–16. [Google Scholar] [CrossRef]
- Hogan, N. Impedance Control: An Approach to Manipulation: Part III—Applications. J. Syst. Meas. 1985, 107, 17–24. [Google Scholar] [CrossRef]
- Stolfi, A.; Gasbarri, P.; Sabatini, M. A combined impedance-PD approach for controlling a dual-arm space manipulator in the capture of a non-cooperative target. Acta Astronaut. 2017, 139, 243–253. [Google Scholar] [CrossRef]
- Nevins, J.; Whitney, D. Assembly research. Automatica 1980, 16, 595–613. [Google Scholar] [CrossRef]
- Uyama, N.; Nakanishi, H.; Nagaoka, K.; Yoshida, K. Impedance-based contact control of a free-flying space robot with a compliant wrist for non-cooperative satellite capture. In Proceedings of the 2012 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vilamoura, Algarve, 7–12 October 2012; pp. 4477–4482. [Google Scholar]
- Raibert, M.; Craig, J. Hybrid position/force control of manipulators. ASME Trans. Energy Res. Technol. 1981, 102, 126–133. [Google Scholar] [CrossRef]
- Yoon, W.-K.; Goshozono, T.; Kawabe, H.; Kinami, M.; Tsumaki, Y.; Uchiyama, M.; Oda, M.; Doi, T. Model-Based Space Robot Teleoperation of ETS-VII Manipulator. IEEE Trans. Robot. Autom. 2004, 20, 602–612. [Google Scholar] [CrossRef]
- Duffy, J. The fallacy of modern hybrid control theory that is based on “orthogonal complements” of twist and wrench spaces. J. Robot. Syst. 1990, 7, 139–144. [Google Scholar] [CrossRef]
- Vukobratović, M.; Stojić, R. Historical perspective of hybrid control in robotics: Beginnings, evolution, criticism and trends. Mech. Mach. Theory 1995, 30, 519–532. [Google Scholar] [CrossRef]
- Chiaverini, S.; Sciavicco, L. The parallel approach to force/position control of robotic manipulators. IEEE Trans. Robot. Autom. 1993, 9, 361–373. [Google Scholar] [CrossRef]
- Takahashi, T.; Tsuboi, T.; Kishida, T.; Kawanami, Y.; Shimizu, S.; Iribe, M.; Fukushima, T.; Fujita, M. Adaptive grasping by multifingered hand with tactile sensor based on robust force and position control. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008; pp. 264–271. [Google Scholar]
- Anderson, R.; Spong, M. Hybrid impedance control of robotic manipulators. IEEE J. Robot. Autom. 1988, 4, 549–556. [Google Scholar] [CrossRef]
- Nakanishi, H.; Yoshida, K. Impedance Control for Free-flying Space Robots Basic Equations and Applications. In Proceedings of the 2006 IEEE/RSJ International Conference on Intelligent Robots and Systems, Beijing, China, 9–15 October 2006. [Google Scholar]
- Nenchev, D.; Yoshida, K. Impact analysis and post-impact motion control issues of a free-floating Space robot subject to a force impulse. IEEE Trans. Robot. Autom. 1999, 15, 548–557. [Google Scholar] [CrossRef]
- Rastegari, R.; Moosavian, S.A.A. Multiple impedance control of space free-flying robots via virtual linkages. Acta Astronaut. 2010, 66, 748–759. [Google Scholar] [CrossRef]
- Agrawal, S.K.; Shirumalla, S. Planning motions of a dual-arm free-floating manipulator keeping the base inertially fixed. Mech. Mach. Theory 1995, 30, 59–70. [Google Scholar] [CrossRef]
- Smith, C.; Karayiannidis, Y.; Napantidis, L.; Garat, X.; Qi, P.; Dimarogonas, D.; Kragie, D. Dual arm manipulation—A survey. Robot. Autonom. Syst. 2012, 60, 1340–1353. [Google Scholar] [CrossRef]
- Luh, J.; Zheng, Y. Constrained Relations between Two Coordinated Industrial Robots for Motion Control. Int. J. Robot. 1987, 6, 60–70. [Google Scholar] [CrossRef]
- Khatib, O. Inertial Properties in Robotic Manipulation: An Object-Level Framework. Int. J. Robot. 1995, 14, 19–36. [Google Scholar] [CrossRef]
- Khatib, O.; Yokoi, K.; Chang, K.; Ruspini, D.; Holmberg, R.; Casal, A. Vehicle/arm coordination and multiple mobile manipulator decentralised cooperation. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems, Osaka, Japan, 4–8 November 1996; pp. 546–553. [Google Scholar]
- Khatib, O.; Yokooi, K.; Chang, K.; Ruspini, D.; Holmberg, R.; Casai, A. Coordination and decentralised cooperation of multiple mobile manipulators. J. Robot. Syst. 1996, 13, 755–764. [Google Scholar] [CrossRef]
- Uchiyama, M.; Dauchez, P. Symmetric hybrid position/force control scheme for the coordination of two robots. In Proceedings of the 1988 IEEE International Conference on Robotics and Automation, Philadelphia, PA, USA, 24–29 April 1988; pp. 351–356. [Google Scholar]
- Caccavale, F.; Chiacchio, P.; Marino, A.; Villani, L. Six-DOF Impedance Control of Dual-Arm Cooperative Manipulators. IEEE/ASME Trans. Mechatron. 2008, 13, 576–586. [Google Scholar] [CrossRef]
- Backes, P. Dual-arm supervisory and shared control space servicing task experiments. In Proceedings of the Space Programs and Technologies Conference, Huntsville, AL, USA, 24–27 March 1992. [Google Scholar]
- Rekleitis, G.; Papadopoulos, E. On on-orbit passive object handling by cooperating space robotic servicers. In Proceedings of the 2011 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2011), San Francisco, CA, USA, 25–30 September 2011; pp. 595–600. [Google Scholar]
- Swain, A.K.; Morris, A.S. Dynamic control of multi-arm co-operating manipulator systems. Robotica 2004, 22, 271–283. [Google Scholar] [CrossRef]
- Yale, G.E.; Agrawal, B.N. Lyapunov Controller for Cooperative Space Manipulators. J. Guid. Control. Dyn. 1998, 21, 477–484. [Google Scholar] [CrossRef][Green Version]
- Lampariello, R.; Abiko, S.; Hirzinger, G. Dynamics modelling of structure-varying kinematic chains. In Proceedings of the 2008 IEEE International Conference on Robotics and Automation, Pasadena, CA, USA, 19–23 May 2008. [Google Scholar]
- Mithun, P.; Anurag, V.V.; Bhardwaj, M.; Shah, S.V. Real-time dynamic singularity avoidance while visual servoing of a dual-arm space robot. In Proceedings of the 2015 Conference on Advances in Robotics, Goa, India, 2–4 July 2015. [Google Scholar]
- Xu, W.; Liu, Y.; Xu, Y. Coordinated motion planning of a dual-arm space robot for target capturing. Robotica 2012, 30, 755–771. [Google Scholar] [CrossRef]
- Bonitz, R.; Hsia, T. Internal force-based impedance control for cooperating manipulators. IEEE Trans. Robot. Autom. 1996, 12, 78–89. [Google Scholar] [CrossRef]
- Crain, A.; Ulrich, S. Disturbance observer-based impedance control for a compliant capture of an object in space. In Proceedings of the 2018 AIAA Guidance, Navigation, and Control Conference, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Cutkosky, M. On grasp choice, grasp models, and the design of hands for manufacturing. IEEE Trans. Robot. Autom. 1989, 5, 269–279. [Google Scholar] [CrossRef]
- Kang, S.B.; Ikeuchi, K. Toward automatic robot instruction from perception-mapping human grasps to manipulator grasps. IEEE Trans. Robot. Autom. 1997, 13, 81–95. [Google Scholar] [CrossRef]
- Li, Z.; Hsu, P.; Sastry, S. Grasping and Coordinated Manipulation by a Multifingered Robot Hand. Int. J. Robot. 1989, 8, 33–50. [Google Scholar]
- Cutkosky, M.; Kao, I. Computing and controlling the compliance of a robotic hand. IEEE Trans. Robot. Autom. 1989, 5, 151–165. [Google Scholar] [CrossRef]
- Xiong, C.; Xiong, Y. Neural network-based force planning for multi-fingered grasp. Robot. Autonom. Syst. 1997, 21, 365–375. [Google Scholar] [CrossRef]
- Chan, J.; Liu, Y. Dynamic simulation of multi-fingered robot hands based on a unified model. Robot. Autonom. Syst. 2000, 32, 185–201. [Google Scholar] [CrossRef]
- Francois, C.; Ikeuchi, K.; Hebert, M. Three-fingered gripper for manipulation in unstructured environments. In Proceedings of the 1991 IEEE International Conference on Robotics and Automation, Sacramento, CA, USA, 9–11 April 1991; pp. 2251–2266. [Google Scholar]
- Crisman, J.; Kanojia, C.; Zeid, I. Graspar: A flexible, easily controllable robotic hand. IEEE Robot. Autom. Mag. 1996, 3, 32–38. [Google Scholar] [CrossRef]
- Hirzinger, G.; Butterfass, J.; Grebenstein, M.; Hahnle, M.; Schafer, I.; Sporer, N. Robonauts need lightweight arms and articulated hands. In Proceedings of the 6th Advanced Space Technologies for Robotics & Automation (ASTRA 2000), Noordwijk, The Netherlands, 5–7 December 2000. [Google Scholar]
- Xue, Y.; Kao, I. Dextrous sliding manipulating using soft fingertips. In Proceedings of the 1994 IEEE International Conference on Robotics & Automation, San Diego, CA, USA, 8–13 May 1994; pp. 3397–3402. [Google Scholar]
- Shimoga, K. Robot Grasp Synthesis Algorithms: A Survey. Int. J. Robot. 1996, 15, 230–266. [Google Scholar] [CrossRef]
- Coelho JPiater, J.; Grupen, R. Developing haptic and visual perceptual categories for reaching and grasping with a humanoid robot. Robot. Autonom. Syst. 2001, 37, 195–218. [Google Scholar] [CrossRef]
- Okamura, A.; Smaby, N.; Cutkosky, M. Overview of dexterous manipulation. In Proceedings of the IEEE International Conference on Robotics & Automation, San Francisco, CA, USA, 24–28 April 2000. [Google Scholar]
- Kerr, J.; Roth, B. Analysis of multifingered hands. Int. J. Robot. Res. 1986, 4, 3–17. [Google Scholar] [CrossRef]
- Melchiorri, C. Slip detection and control using tactile and force sensors. IEEE/ASME Trans. Mech. 2000, 5, 235–243. [Google Scholar] [CrossRef]
- Kao, I.; Cutkosky, M.; Johansson, R. Robotic stiffness control and calibration as applied to human grasping tasks. IEEE Trans. Robot. Autom. 1997, 13, 557–566. [Google Scholar] [CrossRef]
- Kao, I. Stiffness control and calibration of robotic and human hands and fingers. In Proceedings of the 1994 IEEE International Conference on Robotics and Automation, San Diego, CA, USA, 8–13 May 1994; pp. 399–405. [Google Scholar]
- Rosenbaum, D.; Herbort, O.; van der Wel, R.; Weiss, D. What’s in a grasp? Am. Sci. 2014, 102, 366–376. [Google Scholar]
- Bicchi, A. Hands for dextrous manipulation and robust grasping: A difficult road toward simplicity. IEEE Trans. Robot. Autom. 2000, 16, 652–662. [Google Scholar] [CrossRef]
- Bicchi, A.; Kumar, V. Robotic grasping and contact: A review. In Proceedings of the IEEE International Conference on Robotics & Automation, San Francisco, CA, USA, 24–28 April 2000; pp. 348–353. [Google Scholar]
- Sahbani, A.; El-Khoury, S.; Bidaud, P. An overview of 3D object grasp synthesis algorithms. Robot. Auton. Syst. 2012, 60, 326–336. [Google Scholar] [CrossRef]
- Okamura, A.; Turner, M.; Cutkosky, M. Haptic exploration of objects with rolling and sliding. In Proceedings of the IEEE International Conference on Robotics & Automation, Monterey, CA, USA, 10–11 July 1997; pp. 2485–2490. [Google Scholar]
- Oddo, C.M.; Controzzi, M.; Beccai, L.; Cipriani, C.; Carrozza, M.C. Roughness Encoding for Discrimination of Surfaces in Artificial Active-Touch. IEEE Trans. Robot. 2011, 27, 522–533. [Google Scholar] [CrossRef]
- Tiwana, M.I.; Redmond, S.J.; Lovell, N.H. A review of tactile sensing technologies with applications in biomedical engineering. Sens. Actuators A: Phys. 2012, 179, 17–31. [Google Scholar] [CrossRef]
- Someya, T.; Sekitani, T.; Iba, S.; Kato, Y.; Kawaguchi, H.; Sakurai, T. A large-area, flexible pressure sensor matrix with organic field-effect transistors for artificial skin applications. Proc. Acad. Sci. 2004, 101, 9966–9970. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.; Gu, Y.; Fei, P.; Mai, W.; Gai, Y.; Yang, R.; Bao, G.; Wang, Z. Flexible piezotronic strain sensor. Nano Lett. 2008, 8, 3035–3040. [Google Scholar] [CrossRef]
- Park, Y.-L.; Chen, B.-R.; Wood, R.J. Design and Fabrication of Soft Artificial Skin Using Embedded Microchannels and Liquid Conductors. IEEE Sens. J. 2012, 12, 2711–2718. [Google Scholar] [CrossRef]
- Dahiya, R.S.; Cattin, D.; Adami, A.; Collini, C.; Barboni, L.; Valle, M.; Lorenzelli, L.; Oboe, R.; Metta, G.; Brunetti, F. Towards Tactile Sensing System on Chip for Robotic Applications. IEEE Sens. J. 2011, 11, 3216–3226. [Google Scholar] [CrossRef]
- Omata, S.; Murayama, Y.; Constantinou, C.E. Real time robotic tactile sensor system for the determination of the physical properties of biomaterials. Sens. Actuators A Phys. 2004, 112, 278–285. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, N. Control of contact via tactile sensing. IEEE Trans. Robot. Autom. 2000, 16, 482–495. [Google Scholar] [CrossRef]
- Caldwell, D.; Lawthor, S.; Wardle, A. Tactile perception and its application to the design of multi-modal cutaneous feedback systems. In Proceedings of the IEEE International Conference on Robotics & Automation, Minneapolis, MN, USA, 22–28 April 1996; pp. 3215–3221. [Google Scholar]
- Allen, P.K.; Michelman, P. Acquisition and interpretation of 3-D sensor data from touch. IEEE Trans. Robot. Autom. 1990, 6, 397–404. [Google Scholar] [CrossRef]
- Silvera-Tawil, D.; Rye, D.; Velonaki, M. Artificial skin and tactile sensing for socially interactive robots: A review. Robot. Auton. Syst. 2015, 63, 230–243. [Google Scholar] [CrossRef]
- Denei, S.; Mastrogiovanni, F.; Cannata, G. Towards the creation of tactile maps for robots and their use in robot contact motion control. Robot. Auton. Syst. 2015, 63, 293–308. [Google Scholar] [CrossRef]
- Someya, T. Building bionic skin: How flexible electronics can provide e-skin for humans. IEEE Spectrum. 2013, 50, 51–56. [Google Scholar] [CrossRef]
- Luo, R.; Yih, C.-C.; Su, K.L. Multisensor fusion and integration: Approaches, applications, and future research directions. IEEE Sens. J. 2002, 2, 107–119. [Google Scholar] [CrossRef]
- Khaleghi, B.; Khamis, A.; Karray, F.O.; Razavi, S.N. Multisensor data fusion: A review of the state-of-the-art. Inf. Fusion 2013, 14, 28–44. [Google Scholar] [CrossRef]
- Namiki, A.; Nakabo, Y.; Ishii, I.; Ishikawa, M. 1ms sensory-motor fusion system. IEEE/ASME Trans. Mech. 2000, 5, 244. [Google Scholar] [CrossRef]
- Seitz, M. Towards autonomous robotic servicing: Using an integrated hand-arm-eye system for manipulating unknown objects. Robot. Auton. Syst. 1999, 26, 23–42. [Google Scholar] [CrossRef]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).