Laban-Inspired Task-Constrained Variable Motion Generation on Expressive Aerial Robots

Abstract

This paper presents a method for creating expressive aerial robots through an algorithmic procedure for creating variable motion under given task constraints. This work is informed by the close study of the Laban/Bartenieff movement system, and movement observation from this discipline will provide important analysis of the method, offering descriptive words and fitting contexts—a choreographic frame—for the motion styles produced. User studies that use utilize this qualitative analysis then validate that the method can be used to generate appropriate motion in in-home contexts. The accuracy of an individual descriptive word for the developed motion is up to 77% and context accuracy is up to 83%. A capacity for state discernment from motion profile is essential in the context of projects working toward developing in-home robots.

1. Introduction

Robots are increasingly used in human-facing public and private environments. The movement of such agents will inherently change the experience of these environments for any human in them. Our project draws particular inspiration from an in-home, elderly population who may feel unsafe in direct proximity to the type of motion generated by minimum energy flight paths of UAVs, for example. In such a context, a well-designed robotic system should communicate with people in a manner befitting the environment, matching that of their human counterparts and transmitting information about the system’s internal state. That is, appropriate movement needs to be choreographed to befit context.

Robotic platforms can communicate with people through variations in language, visual displays, sound, and motion. This latter method is more immediate and can be carried out in parallel with other functions. This is analogous to how people use complex gestures or postural changes for everyday interactions [1]. Such a channel has been used for symbolic communication between mobile robots and human users through gestures [2] and facial expressions [3]. Robots that communicate well through these channels may be termed expressive. Examples of service robots are AMIGO [4], designed to carry out tasks like serving patients in the hospital and ROBOSEM [5], used as a telepresent English tutor in an educational setting. Robots are also used in domestic environments to assist with housework, have social interactions, and provide in-home care for the elderly [6,7,8]. There, a high number of degrees of freedom create redundant options in motion patterns in order to communicate urgency or calmness in the state of the robot, but how do we leverage the movement of low degree of freedom, non-humanlike robots, like UAVs or UGVs shown in Figure 1 during assigned tasks?

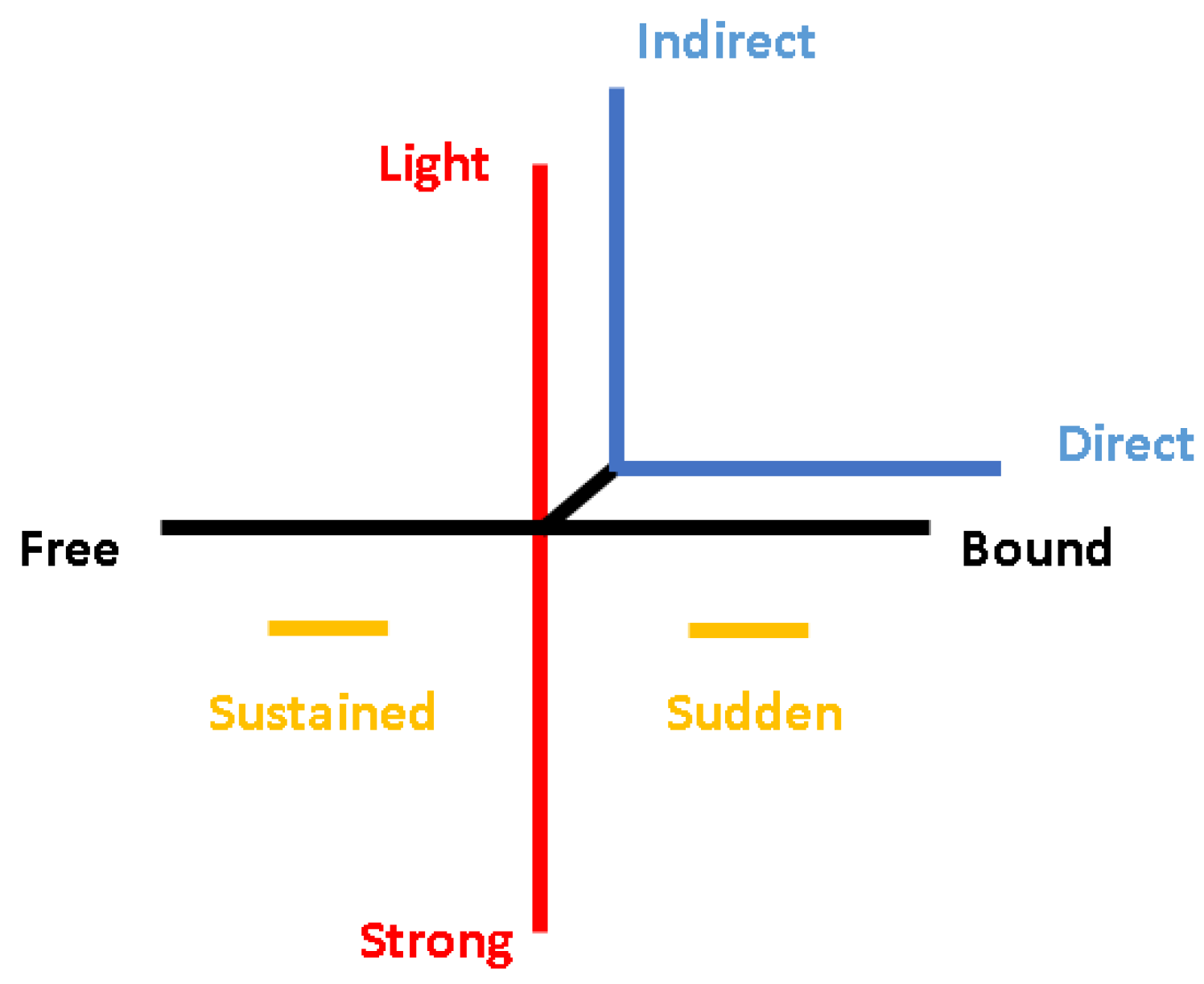
Laban movement analysis (LMA) is a method and language to observe, describe, notate, and interpret varieties of human movement, part of a larger system called the Laban/Bartenieff movement system (LBMS). Effort is an LMA component that deals with dynamic qualities of the movement, and the inner attitude or intent behind a movement [9]. In this section, we will present how we’ve adapted the LMA component of Effort into our method to generate variable, and thus expressive, robotic motion. We will capitalize words which are being used in the LMA taxonomy to distinguish them from colloquial use. The pedagogy used to teach Effort utilizes word banks for movers to develop personal inroads to their perception and experience of movement. This technique may also be used to develop a descriptive set of words that can be used to evaluate the perception of generated motion profiles on general users. In this paper, we will use a master teacher affiliated with the Laban/Bartenieff Institute of Movement Studies (LIMS) who is a certified movement analyst (CMA), the credential provided by LIMS, to provide analysis of the method presented in this section, creating fodder for the development of lay user studies, which will also be presented. This descriptive analysis by a CMA will help sharpen a method for choreographing robotic motion.

Several prior efforts have leveraged LMA, in particular the notion of movement quality defined in the system, Effort [10,11,12,13,14]. For example, previous research has used an LMA-trained performer to create flying robot trajectories using Effort [15] and in [12] real arm movements performed by a CMA were studied. A thorough comparison to [15], which is closest to the work presented here, is provided in Section 5.1. In [11] relaxed terminal conditions were used in the method. This will not work in our context, where a team of robots needs to meet functional tasks in a spatial environment—determined by a human user. The work in [13] maps Laban’s four Effort parameters to low degree of freedom robots for emotive expression. Others have focused on the development of expressive tools for choreography on quadrotors [16]. This work relates to a growing community of work to create expressive robotic systems [17,18,19,20,21]. Further, many of these works assign an emotive characterization on their variable motion. Our position is that emotive models will be limited in application and soon be outmoded. Like the use of language, which evolves as new slang creeps in, and art, which reflects the period and place in which it was created, movement is something inherently expressive with subjective, contextual interpretation [22,23].

Here we note the many differences between the articulated human mover and the simple UAVs we are working with, which do not have any articulation. We work directly with a CMA in direct observation of a parametric method for generating variable motion, correlated with Effort parameters. The resulting method is then evaluated in context by lay (non-expert) individuals. Thus, our task is to (a) create high-level motion parameters to control mobile robot motion behaviors, (b) translate these parameters to a trajectory that satisfies given task constraints, (c) evaluate robotic motions generated with a CMA, and (d) guide evaluation by 18 lay viewers with context based on CMA motion observation and our application area. In this work we will leverage the theory of Affinities between Effort and Space (another component of LMA) in creating expressive robots. Laban observed and described the relationship of dynamic movement (Effort) to the space in which the movement occurred (Space) [24,25,26]. This will allow us to create a perceived experience of the motion of the UAV in appropriate relationship to its task. Then, we will ask an expert movement analyst to evaluate the use of the LMA terminology. Finally, user studies will further evaluate our method. 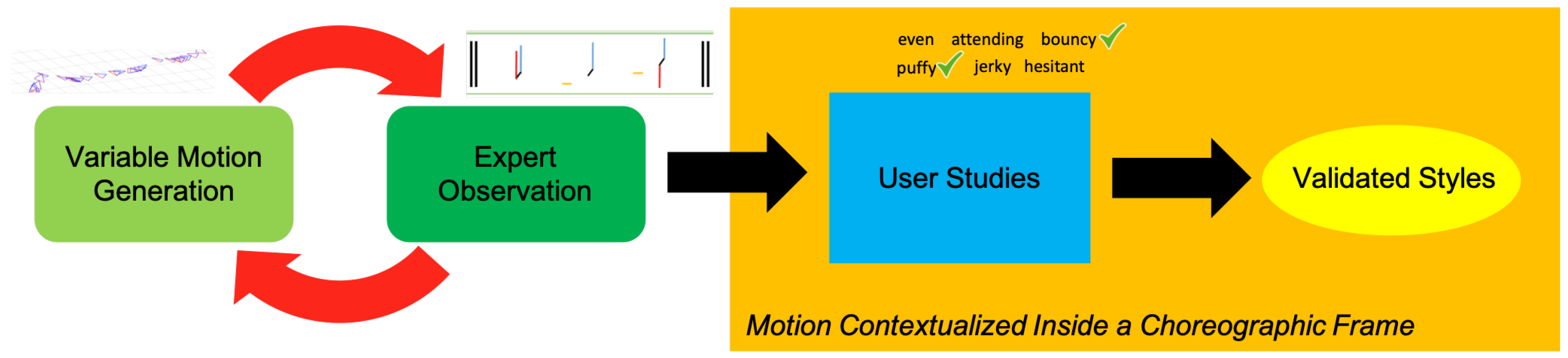An overview of the work is presented in Figure 2.

The rest of the paper is structured as follows: Section 2 reviews Effort and goes over the steps of our method for creating and running robotic motions in simulation for a flying robot. In Section 3, we conduct evaluations of the robotic motions generated by having a CMA watch the flying robot motion simulation videos and provide analysis that is leveraged in lay user studies. In Section 4, we present the result of these user studies. In Section 5, we discuss future applications of this method. In the future, we are particularly interested in crafting increased levels of perceived safety in user populations such as the elderly, who may be assisted by a team of mobile robots to provide prolonged, increased independence.

2. Methods: LMA-Inspired Motion Generation

This section presents the technique used to produce variable motion alongside theory from LMA that guides the design of this system (the first, green block on the left of the overview in Figure 2). We do not suppose that these are the only ways to implement variable motion parameters, but we hope that our method aligns with the existing features named in LMA. First, we assumed that the task is defined as a series of way points with a desired motion completion time. Our work is motivated by the idea that another system architecture sends these way points and timing information; perhaps they are determined by an in-home monitoring system. Our job, then, was to be able to complete the task with various qualities that will be interpreted by the user as different, allowing for the system to blend in harmoniously in a private home setting and to share internal system information to be shared with a user through motion profile.

2.1. Problem Definition

Let a task be defined by n given task way points $p_i={[x_i,y_i,z_i]}^T\in P$ and task time $t_i\in T$, where $[x_i,y_i,z_i]$ is the position coordinate of an inertia world frame in 3D space, and $i=1,2,\dots ,n$. Let a task be given by a set of way points in space $p_i$ and corresponding times $t_i$ the platform needs to visit them. Then a task is the set $\mathcal{T}$:

$$\mathcal{T}=\{(p_1,t_1),(p_2,t_2),(p_3,t_3),\dots ,(p_n,t_n)\}.$$

(1)

Given a task, we wanted to apply Weight Effort ${\gamma }_w$, Time Effort ${\gamma }_t$ and Space Effort ${\gamma }_s$ on the input set, $\mathcal{T}$, to get the desired motion $\omega \left(t\right)$ shown in Figure 3.

2.2. Adapting the LMA Component of Effort

Laban names four Motion Factors, Time, Weight, Space, and Flow, where each Motion Factor has two opposing extremes, defining a mover’s attitude towards its motion [24,25,26]. Movements are described and distinguished by the qualities of these Motion Factors. A labeled and color-coded Effort graph is constructed by these four Motion Factors and the two opposing extremes of each factor are shown in Figure 4. In our method, the priority is for the robot to satisfy the required finite robot task states in the given necessary times. These required finite robot task states are modeled as given task way points. We then added to this base requirement parameters that simulated a notion of Weight, Time, and Space—three of the four factors identified by Laban.

It is possible that, given the low-degree of freedom of these platforms, they cannot reproduce the complex behavior created by articulated human beings, which Laban was studying. Flow Effort, as the underpinning from which all Effort expression emerges, has no use of space and as such is not included in the Affinities of Effort and Space that is being utilized to create an appropriate perceived experience in the UAV motion. Thus, we neglected Flow Effort in our method. This should allow for more discernment in the final evaluation and may produce more repeatable evaluation of the method.

2.2.1. Weight Effort (Strong–Light)

Weight Effort reflects a mover’s attitude toward their relationship to gravity. For our method Weight Effort is recreated by varying the altitude of the robot—as a proxy for how the robot’s simulated attitude might be about gravity during a motion. The Strong Weight Effort will be simulated by creating a pathway, between our way point constraints, with an overall lower altitude. The Light Weight Effort will be simulated by creating a pathway with overall higher altitude. The value of Weight Effort ${\gamma }_w$ indicates these changes over robot pathway which is shown below.

$${\gamma }_w=\left\{\begin{array}{cc}0,\hfill & \mathrm{no}\mathrm{Weight}\mathrm{Effort}\hfill \\ >0,\hfill & \mathrm{Strong}\mathrm{Effort}\hfill \\ <0,\hfill & \mathrm{Light}\mathrm{Effort}\hfill \end{array}\right.$$

We applied the Weight Effort ${\gamma }_w$ on the task set $\mathcal{T}$ to generate weighted task set ${\mathcal{T}}_w$ which augmented the given and weighted task way points. Every weighted way point $w{p}_i$ is calculated by the given task way point $p_i={[x_i,y_i,z_i]}^T$ and $p_{i+1}={[x_{i+1},y_{i+1},z_{i+1}]}^T$. The center point $p{c}_i={[x{c}_i,y{c}_i,z{c}_i]}^T$ between $p_i$ and $p_{i+1}$ is given by

$$p{c}_i={[\frac{x_i+x_{i+1}}{2},\frac{y_i+y_{i+1}}{2},\frac{z_i+z_{i+1}}{2}]}^T.$$

(2)

Then, we calculated weighted way point $w{p}_i={[w{x}_i,w{y}_i,w{z}_i]}^T$ which is located in the vertical plane constructed by $p_i$, $p_i^{\prime }$, $p_{i+1}^{\prime }$ and $p_{i+1}$ shown in Figure 5. The distance $l_i$ between the weighted way point $w{p}_i$ and $p{c}_i$ is given in Equation (3), where ${\gamma }_w$ is the value of Weight Effort. The line connecting $w{p}_i$ and $p{c}_i$ must be perpendicular to the line that connects $p_i$ and $p_{i+1}$.

$$l_i={\gamma }_w\sqrt{{(x_{i+1}-x_i)}^2+{(y_{i+1}-y_i)}^2+{(z_{i+1}-z_i)}^2}$$

(3)

We got two new points located at each side of the line connecting $p_i$ and $p_{i+1}$ in the vertical plane. If ${\gamma }_w>0$, we chose the weighted point which was located under the line that connects $p_i$ and $p_{i+1}$. If ${\gamma }_w<0$, we chose the weighted point above that line. If ${\gamma }_w=0$, no Weight effort is applied and the weighted point $w{p}_i$ is exactly $p{c}_i$. Then, the weighted task set ${\mathcal{T}}_w$ is defined in Equation (4). Next, let the linear interpolations between the sequence of points $p_1,w{p}_1,p_2,w{p}_2,\dots ,w{p}_{n-1},p_n$ be the raw, discrete reference translation trajectory $raw\_{\omega }_{trans}\left(t\right)$ (the red dashed line in Figure 5), which we used to generate Time effort ${\gamma }_t$ later.

$${\mathcal{T}}_w=\{(p_1,t_1),(w{p}_1,t_2),(p_2,t_3),\dots ,(p_n,t_{2n-1})\}.$$

(4)

2.2.2. Time Effort (Sudden–Sustained)

The value of Time Effort ${\gamma }_t$, defines features of the velocity profile of a motion and simulates the robot’s attitude toward time during that task. We changed the robot’s velocity profile to show different qualities of Time Effort. Sudden Time Effort is simulated when the robot moves towards the next immediate target point with more velocity changes. Sustained Time Effort will be simulated by fewer changes in the robot’s velocity profile. In our definition, ${\gamma }_t$, which will be our Time Effort parameter, is the number of total local extremas on the velocity’s profile along with the linear-interpolated flight path created in Section 2.2.1. That is, ${\gamma }_t$ shows how frequently the velocity changes with respect to time. In other words, if we set a value of ${\gamma }_t$, the velocity’s profile had exactly ${\gamma }_t$ local extremas. A high ${\gamma }_t$ means more changes in the combined velocity which means a more “sudden” behavior.

Given a value ${\gamma }_t$, task time $T_{task}$ in seconds and raw reference translation trajectory $raw\_{\omega }_{trans}\left(t\right)$, we can calculate the final translation trajectory ${\omega }_{trans}\left(t\right)$. If we enforce ${\gamma }_t$ local extremas on the velocity profile, then we have m maximas and $(m-1)$ minimas, where ${\gamma }_t=2m-1$ and m is a positive integer. Next, we evenly sampled the indexes of these local extremas on $raw\_{\omega }_{trans}\left(t\right)$, then computed the accelerated translation trajectory from a local minima’s index i to its next local maxima’s index j with acceleration a, and compute the decelerated translation trajectory from a local maxima’s index j to its next local minima’s index i with acceleration $-a$, where a is defined in Equation (5).

$$a=\frac{2|i-j|{({\gamma }_t-1)}^2}{T_{task}^2}.$$

(5)

After calculating each accelerated translation trajectory from every local minima to its next local maxima and each decelerated translation trajectory from every local maxima to its next local minima, we can get the final translation trajectory ${\omega }_{trans}\left(t\right)=[P_1,P_2,P_3,\dots ,P_k]$, and its timing sequence $t_1,t_2,t_3,\dots ,t_k$, where $P_i={[x_i,y_i,z_i]}^T$, $i=1,2,3,\dots ,k$ and k is the number of the final way points.

2.2.3. Space Effort (Direct–Indirect)

The value of Space Effort ${\gamma }_s$ shows the robot’s simulated attitude toward its target point while moving in 3D space. Direct Space Effort means the robot will move towards the next immediate target point with fewer or no changes in heading angle (yaw), instead heading directly to the next immediate target point. Indirect Space Effort requires, on the other hand, the robot to show more changes on yaw motions of its heading with different ranges while it moves towards the next immediate target point.

The value of ${\gamma }_s$ is used to calculated the yaw motion’s range $ya{w}_{range}\in [-r,r]$ as shown in Equation (6). If ${\gamma }_s=0$, then no Space Effort, and, thus, no yaw choreography, is applied on the aerial robot. Given the final translation trajectory ${\omega }_{trans}\left(t\right)$ and its timing sequence $t_1,t_2,t_3,\dots ,t_k$, we can compute the rotation trajectory ${\omega }_{rot}\left(t\right)={[{\theta }_1,{\theta }_2,{\theta }_3,\dots ,{\theta }_k]}^T$ by calculating every rotation vector ${\theta }_i={[\theta x_i,\theta y_i,\theta z_i]}^T$, where $i=1,2,3,\dots ,k$, in its own body frame along with the translation trajectory timing sequence.

$$r=\frac{180°\ast {\gamma }_s}{2}$$

(6)

To calculate every rotation vector ${\theta }_i={[\theta x_i,\theta y_i,\theta z_i]}^T$ with timing sequence $t_1,t_2,t_3,\dots ,t_k$. We kept all $\theta x_i$ and $\theta y_i$ to be 0 and compute every yaw angle $\theta z_i$. We assigned the initial value of yaw angle to be 0, let it increase by e between every timing index until it reaches the positive yaw range r, then let it decrease by e between every timing index until it reaches the negative yaw range $-r$, go back and forth until assigning all the yaw angles from $\theta z_1$ to $\theta z_k$ is finished, e is a user-defined minimum change in angle for the yaw, which may be tuned to platform controller capabilities.

After computing all the yaw angles $\theta z_i$, we kept all the values of roll angles $\theta x_i$ and pitch angles $\theta y_i$ to be 0, because due to the definition the Space Effort is only related to the yaw motion. However, at the way points $p_1,w{p}_1,p_2,\dots$, we still needed to set the corresponding rotation angels of $\theta x_i$ and $\theta y_i$ in order to adjust the orientation of the flying robot to the new flight path shown in Figure 5. In order to achieve this, we assigned new orientations to the flying robot directly at those way points. Then we got the final rotation trajectory ${\omega }_{rot}\left(t\right)$ along with the time sequence $t_1,t_2,t_3,\dots ,t_k$.

2.3. Simulation of the Entire Motion Trajectory

Thus, we associated the weight value of ${\gamma }_w$ to the Laban’s Weight Effort, ${\gamma }_t$ with Time Effort, and ${\gamma }_s$ with Space Effort. These values represent the quality of each motion factor as follows:

$${\gamma }_w\sim Strong$$

$${\gamma }_t\sim Sudden$$

$${\gamma }_s\sim Indirect,$$

where the opposite of the Effort qualities listed, Light Weight Effort, Sustained Time Effort, and Direct Space Effort, require relatively small values of ${\gamma }_w$, ${\gamma }_t$, and ${\gamma }_s$.

Given a task set $\mathcal{T}$ defined in Equation (1), and our motion parameters, namely Weight Effort ${\gamma }_w$, Time Effort ${\gamma }_t$, and Space Effort ${\gamma }_s$, we can calculate the final translation trajectory ${\omega }_{trans}\left(t\right)$ and the final rotation trajectory ${\omega }_{rot}\left(t\right)$ by applying our method from Section 2.2.1, Section 2.2.2 and Section 2.2.3. In summary, the equation that produces each quality of motion is described by three parameters, ${\gamma }_w$, ${\gamma }_t$, and ${\gamma }_s$. The final trajectory is determined by the numerically generated waypoints $\left[P_k\right]$ and headings $\left[{\theta }_k\right]$, which occur at associated times $t_k$. This discrete set of waypoints is much more finely distributed than the original set of task waypoints and effectively produces motion that looks continuous. Thus, we have

$$\omega \left(t\right)=\left[\begin{array}{c}{\omega }_{trans}\left(t\right)\\ {\omega }_{rot}\left(t\right)\end{array}\right]=\left[\begin{array}{c}f(P_k,t_k)\\ f({\theta }_k,t_k)\end{array}\right].$$

(7)

2.4. Example Motion Generation

First, all the task states or constraints are predefined by users and stored in a task file so that the data can be loaded directly into the simulator. Here we defined the task constraints to be the given task way points and task time. Thus, after loading all the given task constraints, we set the total task time $T_{task}$. Next, we set the values of our three motion parameters, which define the particular variety of Effort-inspired motion. For example, in Figure 6, Figure 7, Figure 8 and Figure 9, we set $T_{task}=4$, Weight Effort ${\gamma }_w=0.1$, Time Effort ${\gamma }_t=20$, and Space Effort ${\gamma }_s=0.2$. The yaw resolution, e, is set to be 1° in our simulator.

From a given $({\gamma }_w,{\gamma }_t,{\gamma }_s)$, first we calculated the weighted task set ${\mathcal{T}}_w$ defined in Equation (4), then created linear interpolations between the sequence of points in ${\mathcal{T}}_w$. An example of the discrete reference translation trajectory $raw\_{\omega }_{trans}\left(t\right)$ is shown in Figure 6 in red dashed lines. Then, Time Effort ${\gamma }_t$ is applied to $raw\_{\omega }_{trans}\left(t\right)$ and Space Effort ${\gamma }_s$ to ${\theta }_z$ to get the final translation trajectory ${\omega }_{trans}\left(t\right)$ and final rotation trajectory ${\omega }_{rot}\left(t\right)$, respectively.

The final translation trajectory ${\omega }_{trans}\left(t\right)$ and rotation trajectory ${\omega }_{rot}\left(t\right)$ define the flying robot’s translation and rotation behaviors respectively. The plot in Figure 7 shows an example of the flying robot’s translation behavior in 3D space, namely the changes of its translational velocity and acceleration with respect to time on the interpolated weighted flight path. The plot in Figure 8 shows an example of the robot’s rotation (orientation) behavior, which are the changes of its angular velocity and acceleration with respect to its own body frame.

In the simulation, the flying robot is represented as a triangle. Figure 9 shows all the poses of the flying robot with corresponding positions and orientations in the timing sequence; thus, we can see the detailed motion changes of the UAV with respect to time in 3D space as needed for evaluation (which will be done using videos from these angles).

3. Methods: Expert Evaluation and Development of Motion Description

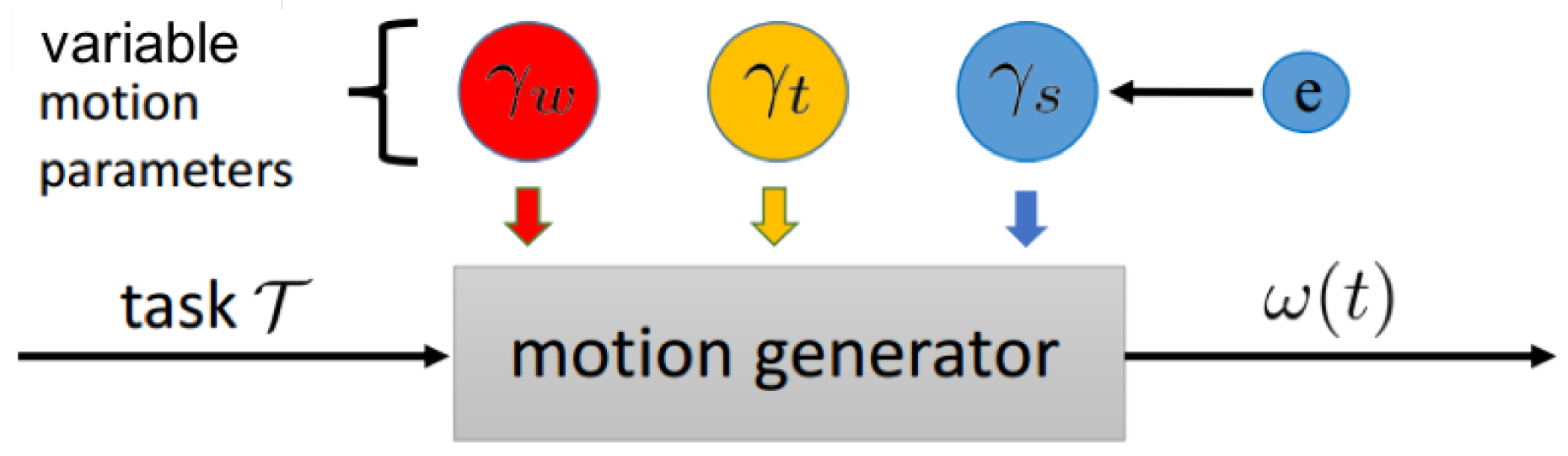
In order to evaluate our method and develop descriptions to be validated by lay viewers, we simulated 10 distinct motion styles. The 10 configurations used and the corresponding motion parameter values of ${\gamma }_w$, ${\gamma }_t$, and ${\gamma }_s$ are shown in

Table 1. Effort configuration labels and parameter settings.

Motions	Weight Effort	${\mathit{\gamma }}_{\mathit{w}}$	Time Effort	${\mathit{\gamma }}_{\mathit{t}}$	Space Effort	${\mathit{\gamma }}_{\mathit{s}}$	Task Time
01	None	0	None	0	Most Direct	0	4
02	None	0	Less Sudden	6	Less Direct	0.1	4
03	Less Strong	0.1	Less Sustained	4	Most Direct	0	4
04	Less Strong	0.1	None	0	Less Indirect	0.2	4
05	Less Strong	0.1	Sustained	3	Less Indirect	0.2	4
06	Less Strong	0.1	Sudden	20	Less Indirect	0.2	4
07	Less Light	−0.1	Less Sudden	6	More Direct	0.05	4
08	Less Light	−0.1	Less Sudden	6	Indirect	0.4	4
09	Light	−0.2	Less Sudden	6	Less Direct	0.1	4
10	Strong	0.2	Less Sudden	6	Less Direct	0.1	4

. Then, we used the Effort component of LMA (This observation was provided by the second co-author who received their CMA in 1984 and has been working actively in the field since, while the method in the previous section was developed under the guidance of the third author who is also a CMA, certified in 2016.) to observe these 10 videos, performing a comprehensive motion analysis, including writing down the general movement patterns in the LMA framework and providing descriptive words for each movement observed (the second to the left, dark green block in Figure 2). From these words, descriptive contexts for the home environment were established that are utilized in lay viewer user studies in the next section.

The purpose of this structure is to leverage the expertise of a dancer and choreographer in creating a choreographic frame for the varied motions generated. What we have found in prior work is that context modifies the meaning of motion, breaking down the use of emotive or affective labels [27]; this is commonly known in the dance community, e.g., discussed through the lens of culture here [28], and may be thought of as creating a choreographic frame such that the intent of an artistic piece is clear. Thus, here, descriptive (rather than emotive) labels, which may seem initially odd placed next to movement, e.g., labels like “clear” and “puffy”, are used. These are words used in LMA to create connection between movement variation and situated human experience; for example, “puffy” describes the kind of light, indirect movement that is evoked from running a hand across a fluffy, puffy wad of cotton candy or tulle. The role of this expert observation was to use an eye that has both a wealth of experience in creating meaning through motion in choreographic practice. Thus, this CMA expert provided a channel between objective variation in movement and subjective human experience. Moreover, this co-author was not familiar with the details of the motion generation, providing a more objective eye on the movement; just as has been shown in prior work, familiarity with motion structure changes how it is seen [29].

In Table 1, we list a subset of possible Effort configurations that were used for the validation of the method. Each configuration was used to generate motion trajectories subject to the same task $\mathcal{T}$. For the motion generated in Video 01 we keep all the values of motion parameters to be 0. In other words, we do not apply any Weight and Time Effort and set Space Effort as “most” Direct. From there, each motion example is generated from a representative sampling of possible configurations. The CMA evaluator was given two views of the robot motion without any knowledge of the method producing them. A multi-frame capture of these videos is shown in Figure 9.

3.1. Results

The results of the CMA’s observations are shown in Figure 10 and

Table 2. Certified movement analyst (CMA) descriptions of motion profiles.

Motions	Descriptive Words	Descriptive Contexts
01	even, steady, directed, clear, calm	Monotonously patrolling an empty backyard.
02	hurried, scanning, pondering, surging	Efficiently picking up a messy bedroom.
03	cautious, considering, fluffy, buoyant	Happily decorating for a birthday party in the living room.
04	even, attending, noticing, watching, smooth	Calmly monitoring a child playing with a toy in the living room.
05	puffy, cautious, available, attending, easy	Cautiously searching for a light switch in the dark in the bedroom.
06	guarded, controlled, attending, even	Anxiously clean up a spilled bowl of cereal in the living room.
07	jerky, hesitant, choppy, rough	Nervously cook a new recipe in the kitchen.
08	floating, meandering, pondering, considering, pausing	Carefully search for a lost toy in the backyard.
09	sighing, wandering, wispy, unsure	Lightly answering the door to invite company into the foyer.
10	chaotic, zig-zag, uncertain, floating	Gently dancing around to get blood going in the exercise room.

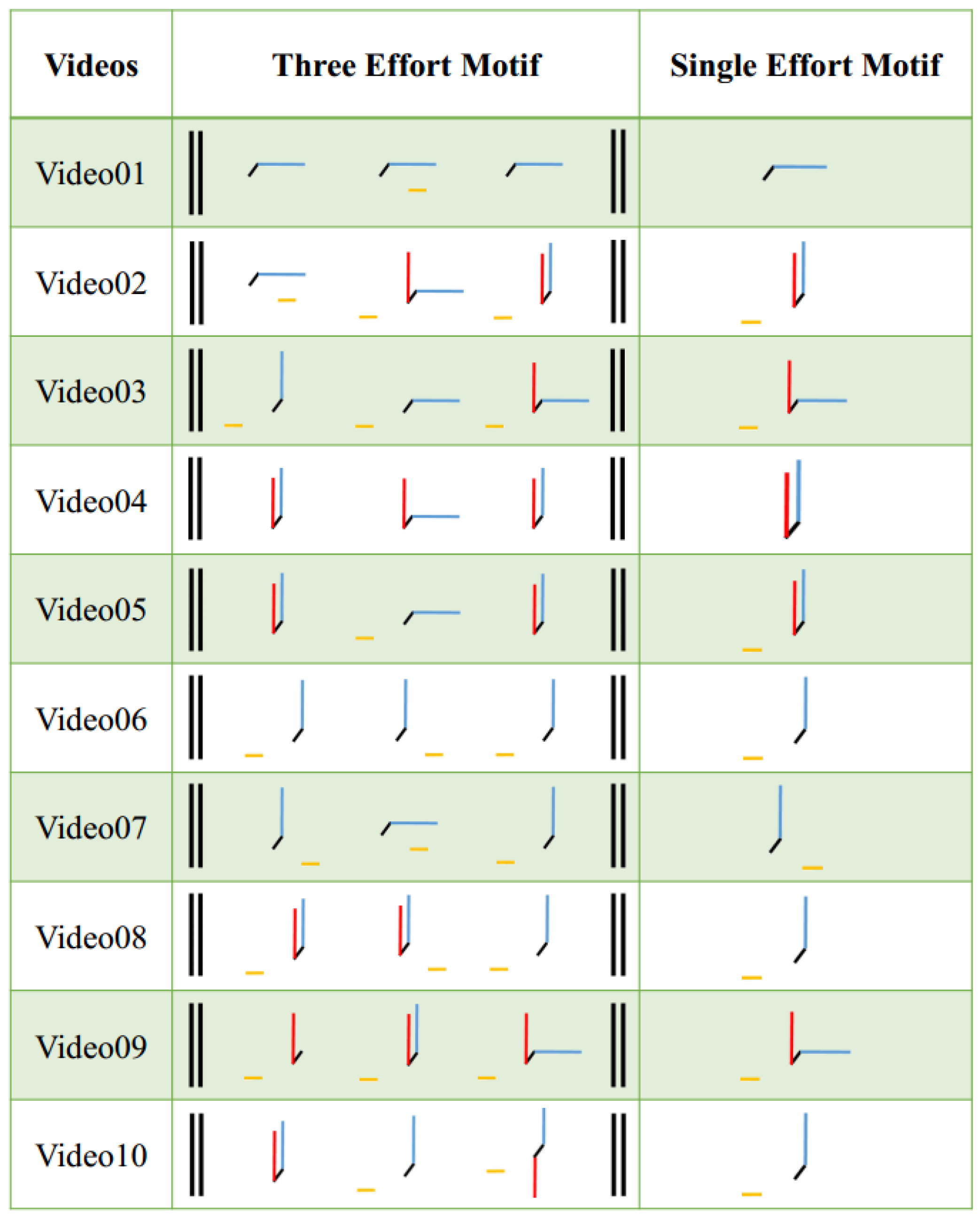
. In Figure 10 the observed motion patterns are described by Motifs, an LBMS tool used to represent the essential components of movement patterns and sequences. These Motifs consisted of three separate Effort configurations, which means the CMA perceived more dynamism in the profiles than we expected. The single Effort configuration was selected after we requested the CMA to choose just one. Given that each motion profile was generated with just one set of three parameters, this was a better fit to the generation method; however, in future work, we would like to explore this perceived variation over time.

Given the analysis in this format, we can say that each three-Effort Motif (the middle column in Figure 10) shows the perceived progression in time. For example, for Video 04, the first Effort combination was Light and Direct, the second Effort combination was Light and Indirect, and the third Effort combination was Light and Direct again. The whole movement pattern, when restricted, can be described in a single Effort Motif in rightmost column of Figure 4 as Light and Direct.

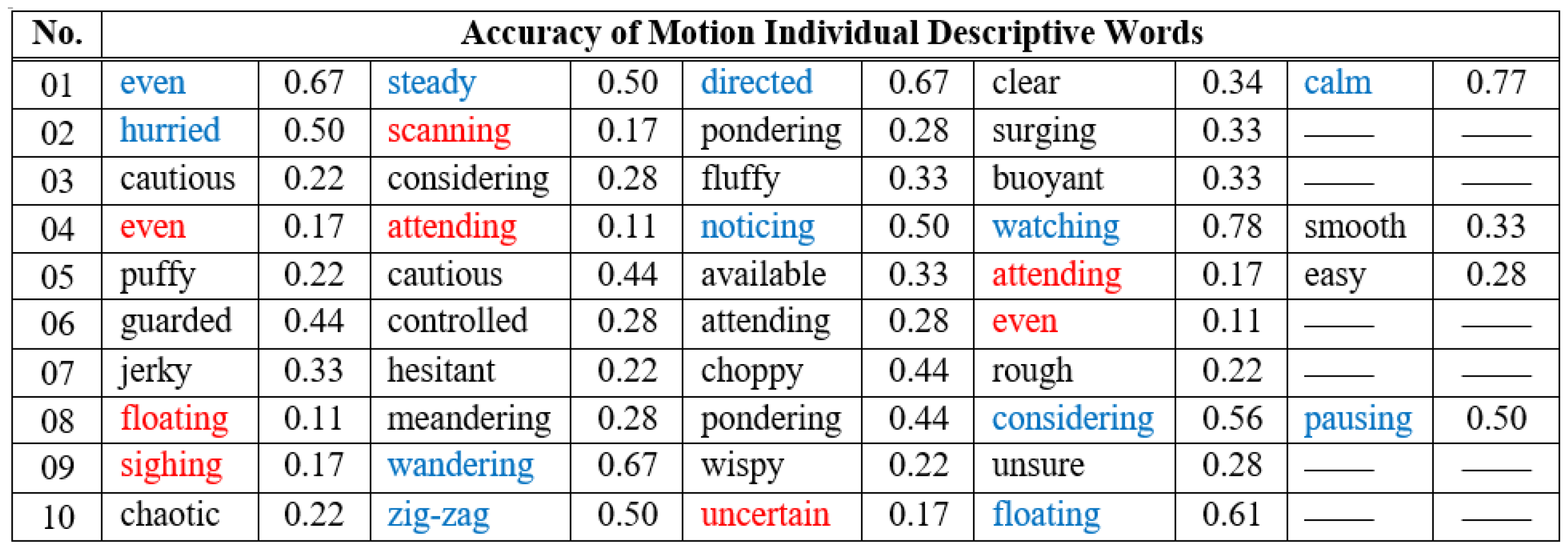
Because lay users will not be familiar with the meaning of these Motifs, we also established a set of descriptive words and our corresponding contexts for each flying robot motion simulation which are given in Table 2. These contexts were selected to be in a “home” environment due to the nature of our sponsored research; by giving some context, we created a more meaningful (if imagined) scenario within which users can evaluate motion.

Thus, in Table 2, every flying robot motion simulation is described by a set of words. For example, for the motion simulation in Video 04, it is described by “attending, even, noticing, watching, smooth” which was related to the values of the motion parameters, where ${\gamma }_w=0.1$, ${\gamma }_t=0$, and ${\gamma }_s=0.2$. In other words, according to our analysis, the above motion parameter settings can be used to generate a motion that is reasonably described by the corresponding descriptive words. In a home context, we may expect to find such movements in a watchful mother attending to her child (hence the context provided in Table 2).

From the movement analysis given by the CMA, we can summarize that our method can be used to generate motion that is expressive for even low degree of freedom robots. Another anticipated result of the flying robot motion analysis is that the motion simulation in Video 01 gives the observer an impression of neutral, plain movement as described by words “even, steady, direct, clear, and calm”. We first establish the parameter setting of ${\gamma }_w={\gamma }_t={\gamma }_s=0$ shown in Table 1. Moreover, from a technical point of view, this direct, linear interpolation between way points is the minimum distance to traverse and thus corresponds to a traditional planning method. Thus, this “default” behavior is like traditional motion planners, which we used as a benchmarking comparison for our method, which creates deviations in this linear path to create different modes of motion. We labeled this setting “none” (or neutral) in Weight and Time Effort quality but “most” Direct in Space Effort in Table 1 of Video 01 due to the direct path taken by these traditional techniques.

In Video 03, we set the Space Effort ${\gamma }_s=0$ which aims to generate a Direct motion for the UAV. The motion analysis results shown in Table 2 also verify this, the descriptive words “Cautious” and “Considering” show the directness of the motion of the flying robot in the simulation. What’s more, the Effort Motifs in Figure 10 of Video 3 also show Direct Space Effort as well as Sustained Time Effort feature, correlating with a small value for ${\gamma }_t$.

3.2. Discussion

In observing the videos, the CMA noticed a correlation of her perception of Weight Effort to a change in the Vertical Dimension. This observation is consistent with the theory of Affinities of Effort and Space in which Laban observed that Light Weight Effort tends to be expressed in the space of up, while Strong Weight Effort tends to be expressed in the space of down. The CMA observed the use of spatial affinities as a substitute for true Weight Effort which is probably generated in humans through a change in muscle tonus and dynamic. In particular, the quality of Light Weight Effort was very clear, but Strong Weight Effort was more diminished and observable only via a shift in spatial pathway.

For Space Effort, the CMA noted the use of simulated robot pose as an effective inroad to Direct and Indirect Space Effort. This is seen in human movers through the use of “open” or “closed” body pose with respect to the midline. The CMA felt this was the most successfully recreated factor with regard to finding both polarities: a meandering pathway indicated attention to the whole environment while a steady yaw heading produced a very clear spatial attention toward a single point. For Time Effort, the CMA observed that Sudden Time Effort was quite visible, giving the impression of hurried or even rushed movement patterns. Sustained Time Effort was visible more as a “hovering”, which is not precisely the same as in human movers, where luxurious indulgence in attitude toward time is seen more readily. Finally, the CMA agreed that Flow Effort was not present in any of the videos.

This poses several important questions for future iterations of such work. How can the practice of changing muscle tonus, as found in Weight Effort in human movers—an important perceptual cue to movement’s intent—be approximated or simulated in robotic agents? This will inherently require additional degrees of freedom on a platform, but could be created through some artificial convention (as lights in a stoplight have conventionally accepted meanings). This capability is important for the recreation of Strong Weight Effort. Secondly, how does a machine appear to indulge in time—creating Sustained Time Effort? Movement efficiency is something that has come to be expected from machines, however, in human-facing, care-taking scenarios, such efficiency could become exhausting to a human viewer (at least, this is the case in choreography). A balance that finds hold in prior associations and creates new, more relaxed interaction paradigms may be needed in these scenarios.

Finally, the neglected Flow Motion Factor is one that has proven difficult to capture in robotic systems. According to the LMA taxonomy, this is also one that could help bring a more “life-like” sense to robotic motion. For low-degree of freedom robots, this may not be possible to achieve without extra expression modalities such as light and sound. Thus, this section provides an initial validation of our method and directions for improvement in the future. Furthermore, we have constructed accessible descriptive words and contexts, which will be used in the next section to offer untrained viewers descriptive options with which to evaluate these movements. Again, we emphasize that these motions cannot convey an absolute emotional state like ‘happy’ or ‘sad’ but may be associated with certain, we could say textures, which may be appropriate in the listed in-home contexts.

4. Results: Contextual Evaluation by Lay Viewers

Based on the results from the CMA, we created 20 questions to conduct a further study for general untrained users on motion simulation videos generated by our algorithms (this the blue square in Figure 2). We recruited 18 participants from our university (eight male and 10 female, aged 18–30 years). These participants were reimbursed with a $15 gift card for their time. The surveys took about one hour. The participants watched the same videos as the CMA did and answered two questions for each video.

The first question asked each participant to choose the descriptive word or words (from a group of nine with space to write in a tenth) that best matched the corresponding aerial robot motions in the video. The second question was to choose a single context out of three options which best described the overall motion. The ‘correct’ answers were those given by the CMA and the ‘incorrect’ options were randomly sampled from the whole bank of descriptive words and contexts, respectively.

Two issues with the experiment should be mentioned here. Firstly, the researchers failed to provide all the “correct” answers for the first question on Video 01. To address this, the first eight participants were required to do this question again. Secondly, the pool of participants ended up being entirely native Chinese speakers. While this was not intended, it may have influenced the results positively by removing the variable of cultural differences of interpretation. However, researchers found that participants needed to check the meaning of the descriptive words in the dictionary when they were taking the surveys.

4.1. Results

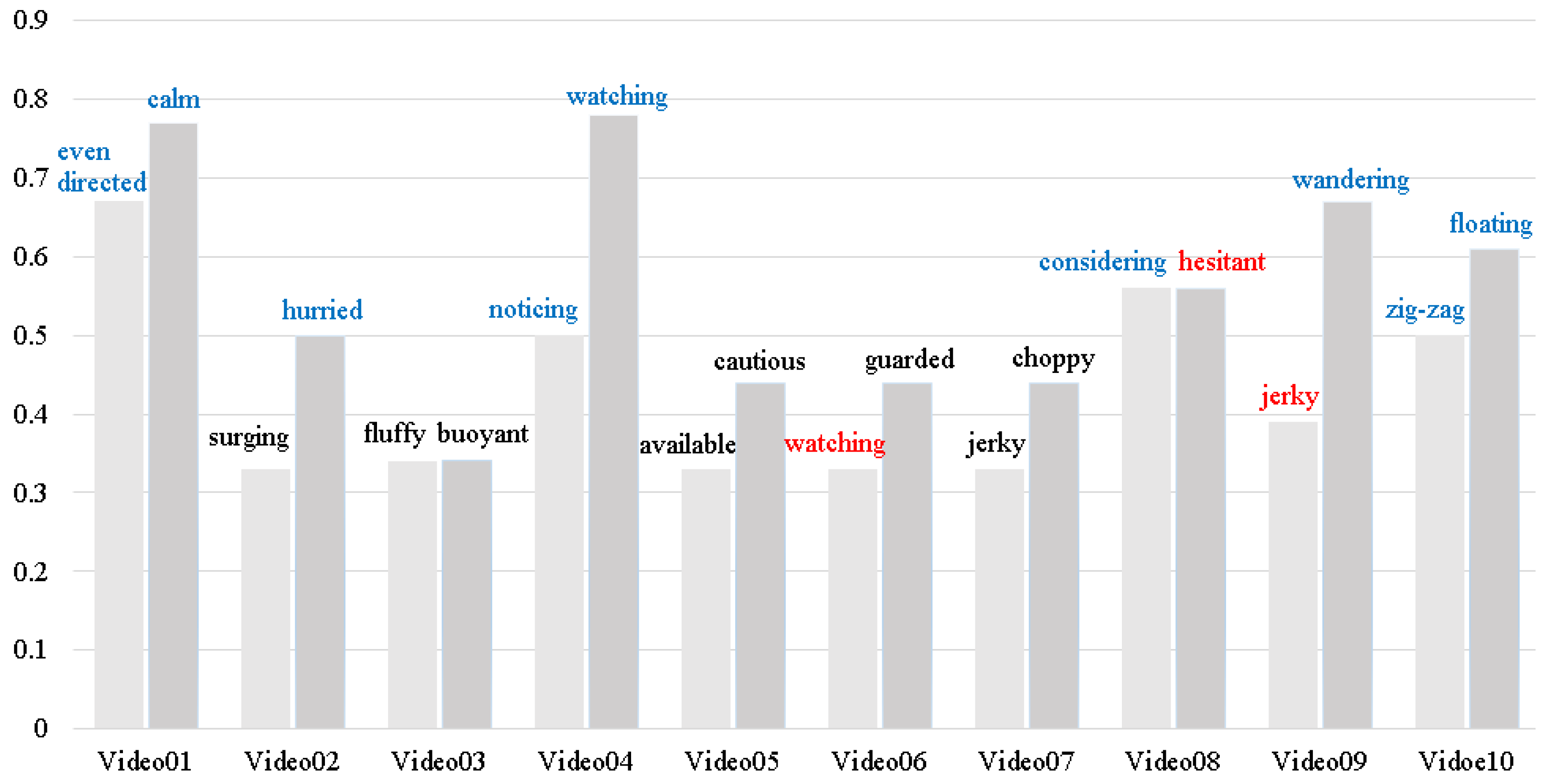
The results from the untrained participants are given in Figure 11 and Figure 12. Figure 11 gives the accuracy of the individual descriptive word for each flying robot motion simulation. The accuracy of individual descriptive word for each question was defined as the percentage of participants that identified it correctly when viewing the video associated with it. Figure 12 gives the overall accuracy for both the descriptive words and the contexts. The overall accuracy of descriptive words for each question was defined as the average of individual word accuracy for all ‘correct’ words for the given video. Participants were not especially good at identifying the correct descriptive words, although several videos had consistency in the top words chosen (see Figure 13). Participants were $50\%$ accurate or more on eight of the 10 videos with respect to their expected context. These results confirm the scaling suggested in Section 2 and suggest thresholds for the quantitative parameters used to generated the motion profiles. These are summarized in

Table 3. Suggested thresholds for ${\gamma }_w$, ${\gamma }_t$, and ${\gamma }_s$.

${\gamma }_w$	${\gamma }_w>0$ Strong Effort	${\gamma }_w=0$ Neutral	${\gamma }_w<0$ Light Effort
${\gamma }_t$	${\gamma }_t>6$ Sudden Effort	${\gamma }_t=6$ Neutral	${\gamma }_t<6$ Sustained Effort
${\gamma }_s$	${\gamma }_t>0.1$ Indirect Effort	${\gamma }_s=0.1$ Neutral	${\gamma }_t<0.1$ Direct Effort

, which shows the suggested threshold for each motion parameter, namely ${\gamma }_w$, ${\gamma }_t$, and ${\gamma }_s$.

4.2. Discussion

In general, participants only picked two to three choices in descriptive word questions and offered no word of their own in the free response field. We believe there was a significant language barrier for participants in this part of the task. Further, it is unusual for untrained viewers to describe motions with words like “choppy” and participants commented on that after the exercise. From Figure 12, we can see all the overall accuracy for each video is $25\%$, which means our results are within the range of users selecting randomly (for two to three words out of nine, random choice is 22–33% accurate). However, in several cases, there was a dominating descriptive word, such as “watching” in Video 04, “wandering” in Video 09, and “floating” in Video 10, meaning some words were well-suited descriptors to untrained participants. On the other hand, incorrect answers such as “watching” in Video 06, “hesitant" in Video 08, and “jerky" in Video 09 were also found.

For motion context questions, the results show that for all context except one users were more likely to select the expected, pre-labeled context than others. As shown in Figure 12, our results are better than random choice, which is around $33\%$ (only one video was labeled with its context with lower frequency). This indicates that the overall motion of the aerial robot can still give participants a strong, consistent sense of its intended motion quality. Further, even though users did not resonate with the descriptive words, they proved useful in generating the contexts that were meaningful for users. This produces artificial motion on a simulated aerial robot that is validated with meaningful description and context, shown in the yellow oval in Figure 2.

5. Conclusions: Toward Expressive Aerial Robots

We have presented a novel method for generating expressive, variable robotic motion. We have compared our method to prior methods that use LMA as a guidepost for creating similarly expressive motions. In particular, we have contrasted our restraint in giving emotive labeling and our inclusion of context explicitly in evaluation of our method. From work with a CMA observer, we have shown that our algorithm can be effectively used for generating distinct variety of movement. From the results of the user study, when framed with context, we successfully showed that even for general, untrained users, the motions performed by a simulated aerial robot via our method give participants different impressions.

5.1. Comparison to Prior Work with Expressive Aerial Robots

Here, we provide an extended comparison of the work presented here to prior work [15] that has also implemented a model of Laban’s Effort framework on aerial robots. In this work, an artist was hired to “author” motion on a robotic platform. This produced eight captured movements that were implemented on hardware and evaluated using the Circumplex Model of Affect [30]. In our work, we have generated a task-sensitive parameterization of Effort that can be used to generate more than eight motions; while 10 are presented here, more can be created through the framework with different values of ${\gamma }_w$, ${\gamma }_t$, and ${\gamma }_s$ or through different “tasks” $\mathcal{T}$. Moreover, we have pioneered a descriptive validation based on describing movement quality (rather than evaluating its perceived affect) through descriptive words and situating generated motion inside choreographic context through established motion contexts. Finally, it should be noticed that in this process, we leverage and explicate the intellectual contribution of an artist and this is recognized through co-authorship.

5.2. Future Direction

The advantage of this method is that we can extend the motion analysis provided here to further query population specific groups not familiar with the LMA taxonomy, such as members of a particular generation, like the baby boomers, whose shared generational context may produce a population-specific interpretation of motion. Future work will run more evaluations with groups of users both in virtual reality and on real robot platforms in order to explore the communication channel between humans and aerial robots.

For our desired application of in-home robotic assistants, there are many related fields of work that need to be completed. It is envisioned that, as in the fairytale Cinderella, where woodland creatures work together to aid this character in her daily chores, that teams of relatively simple robots may be able to assist elderly people. As it is, our work is in simulation and not implementable on hardware. Moreover, we need some subsystem for manipulation to aid in many common tasks of daily living. The larger vision of this project is described in [31].

Motion expressiveness, as created by the ability to vary motion profiles within some task-constraints, will play an increasingly important role in robot applications. These variable motion behaviors should reflect the robot’s task states and modulate according to context. As more research is done in this area and corroborated methods emerge, artificial agents may communicate with human counterparts not just with language-based channels but also with nonverbal channels. These behaviors will be context and population specific and can be choreographed by experts and artists through established taxonomies.