Trajectory Design for Energy Savings in Redundant Robotic Cells †
Abstract
:1. Introduction
2. Energy Consumption Estimation
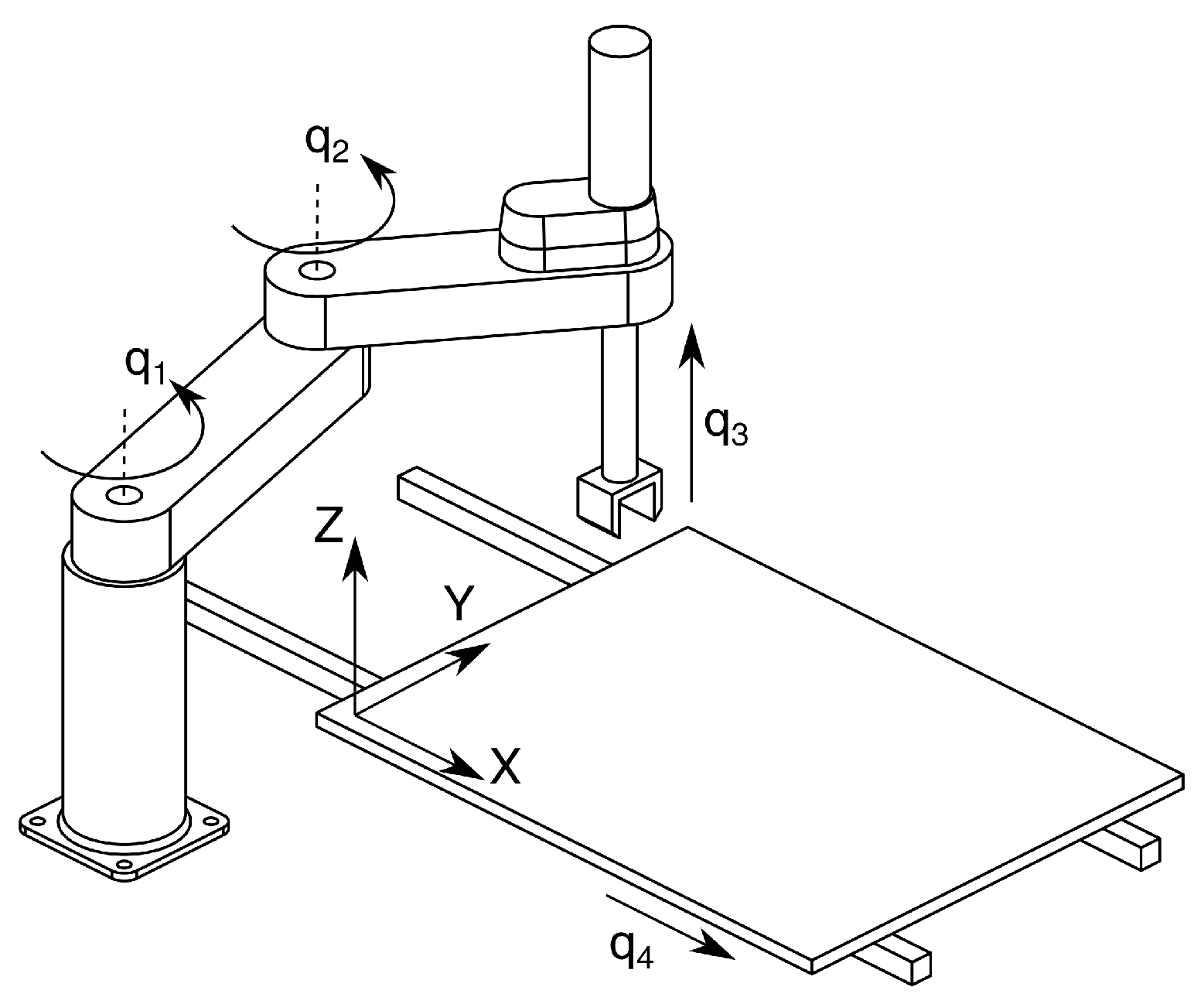
2.1. SCARA Robot
2.2. Linear Unit
3. Energy Optimization
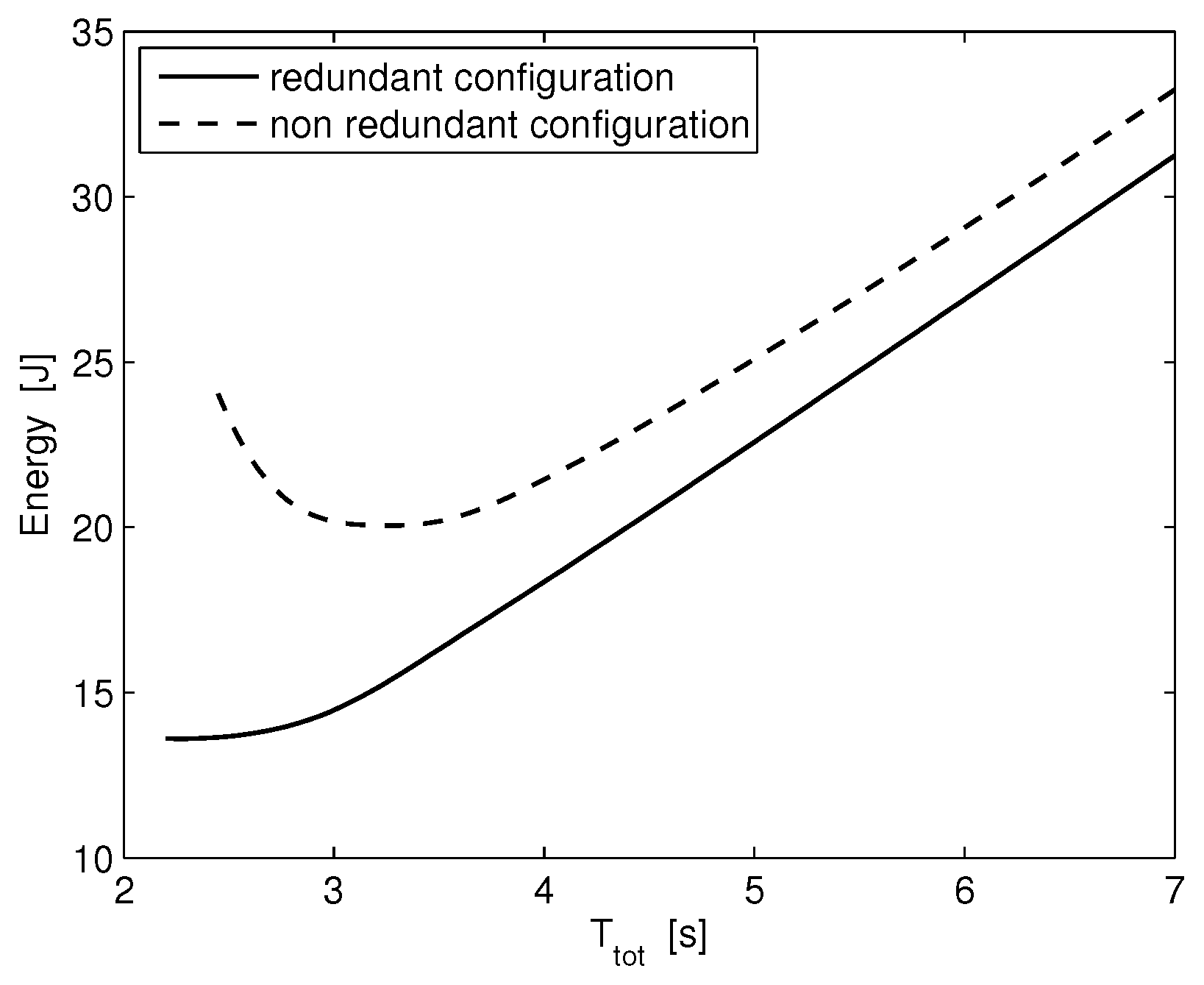
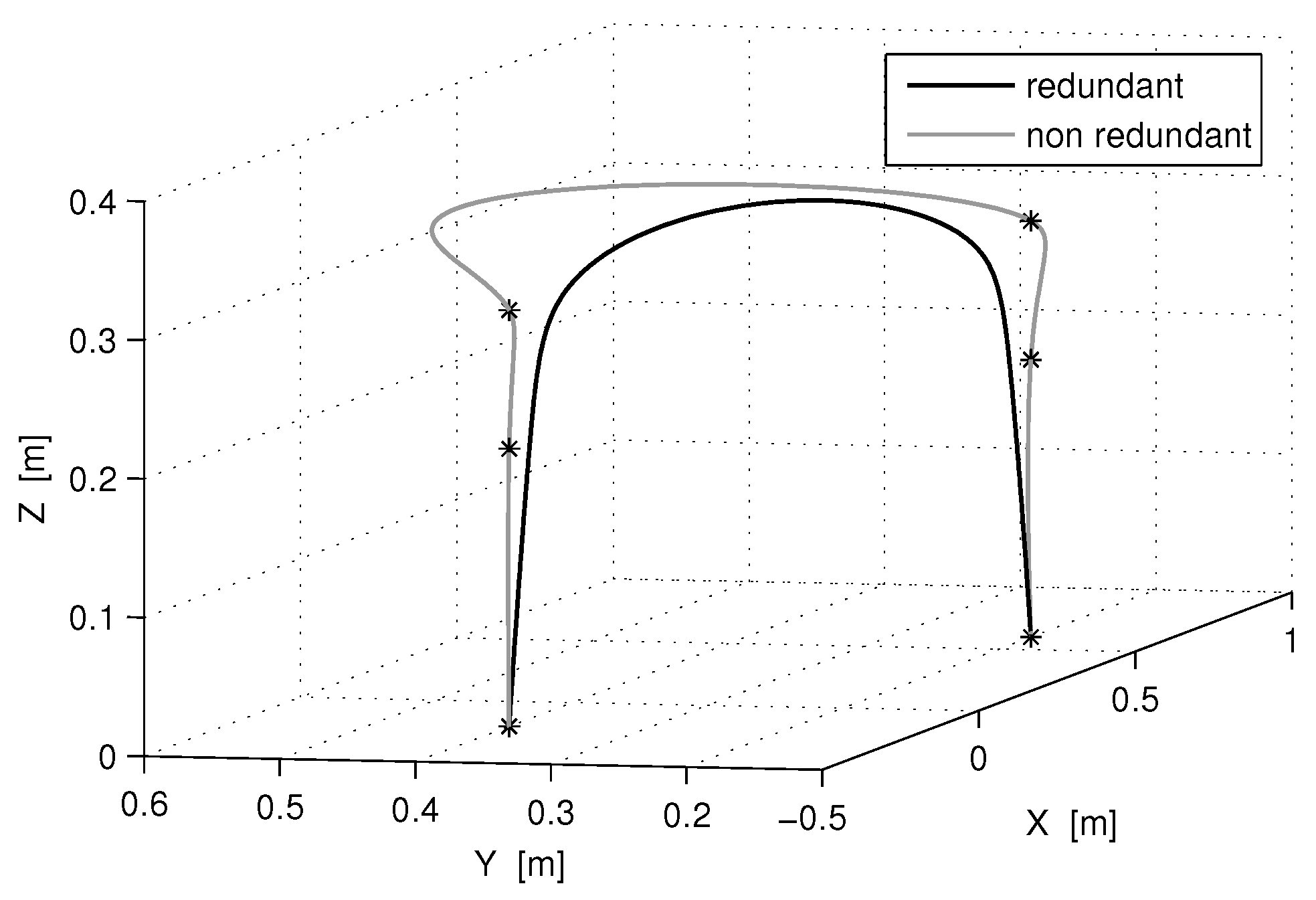
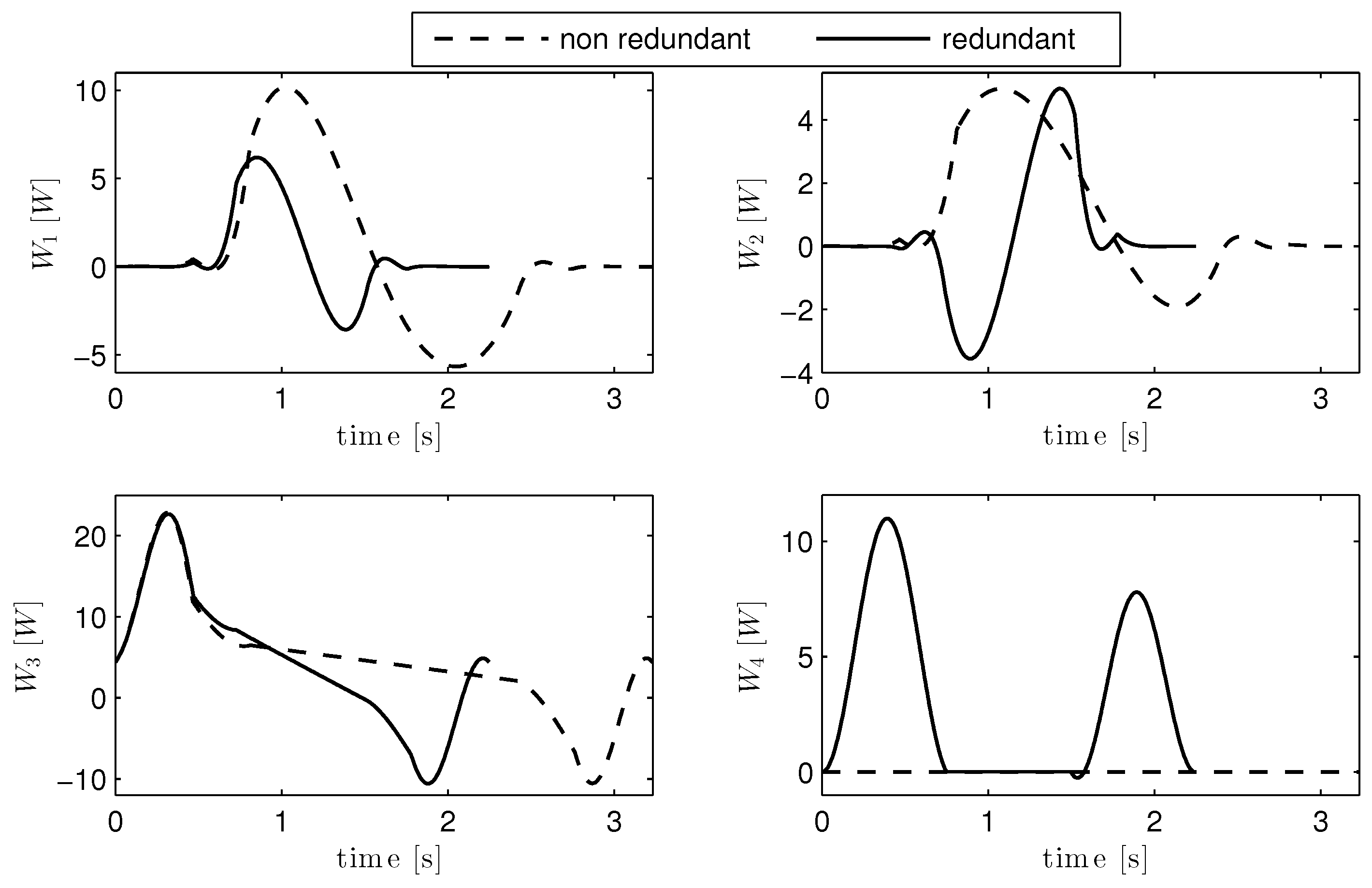
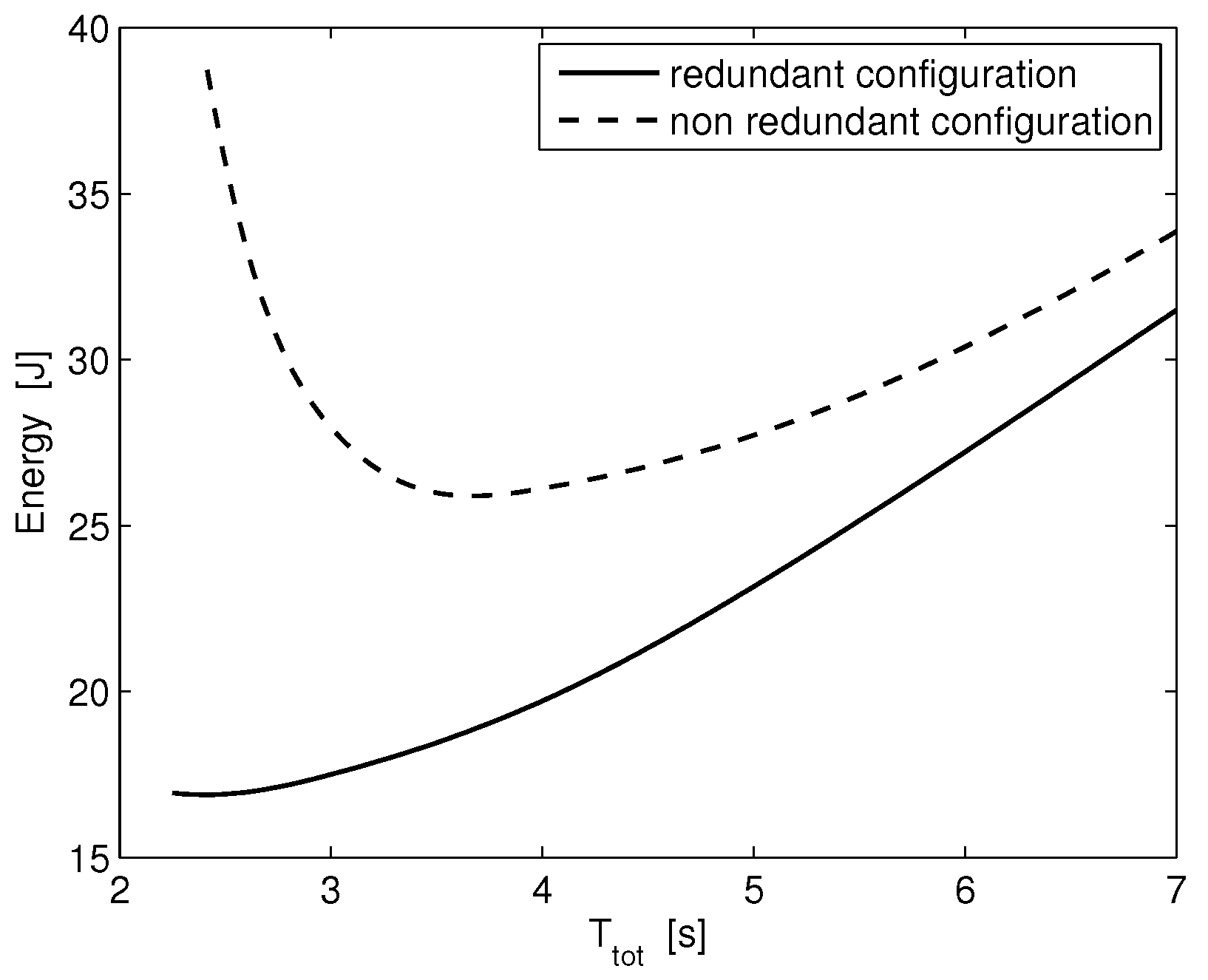
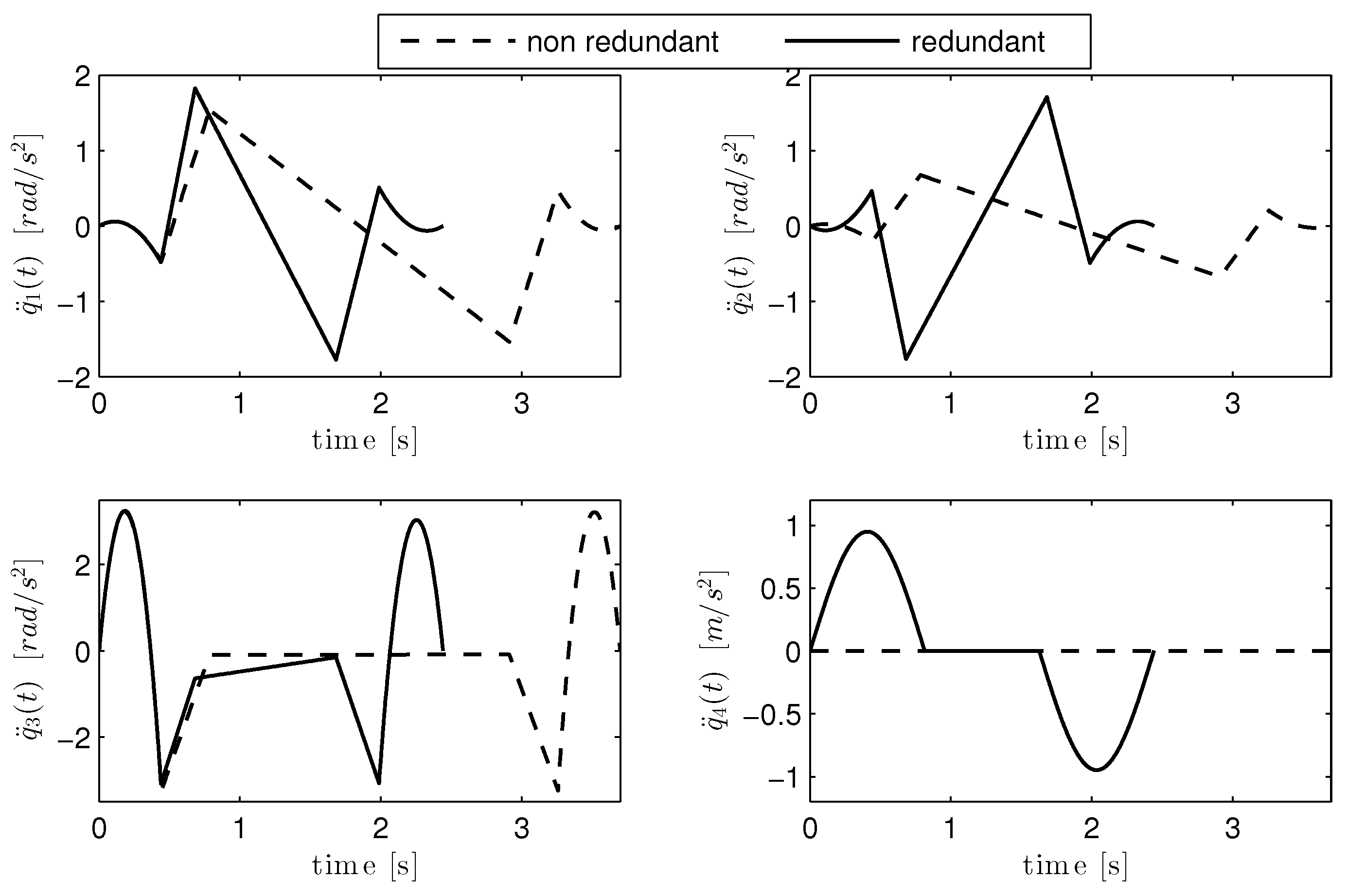
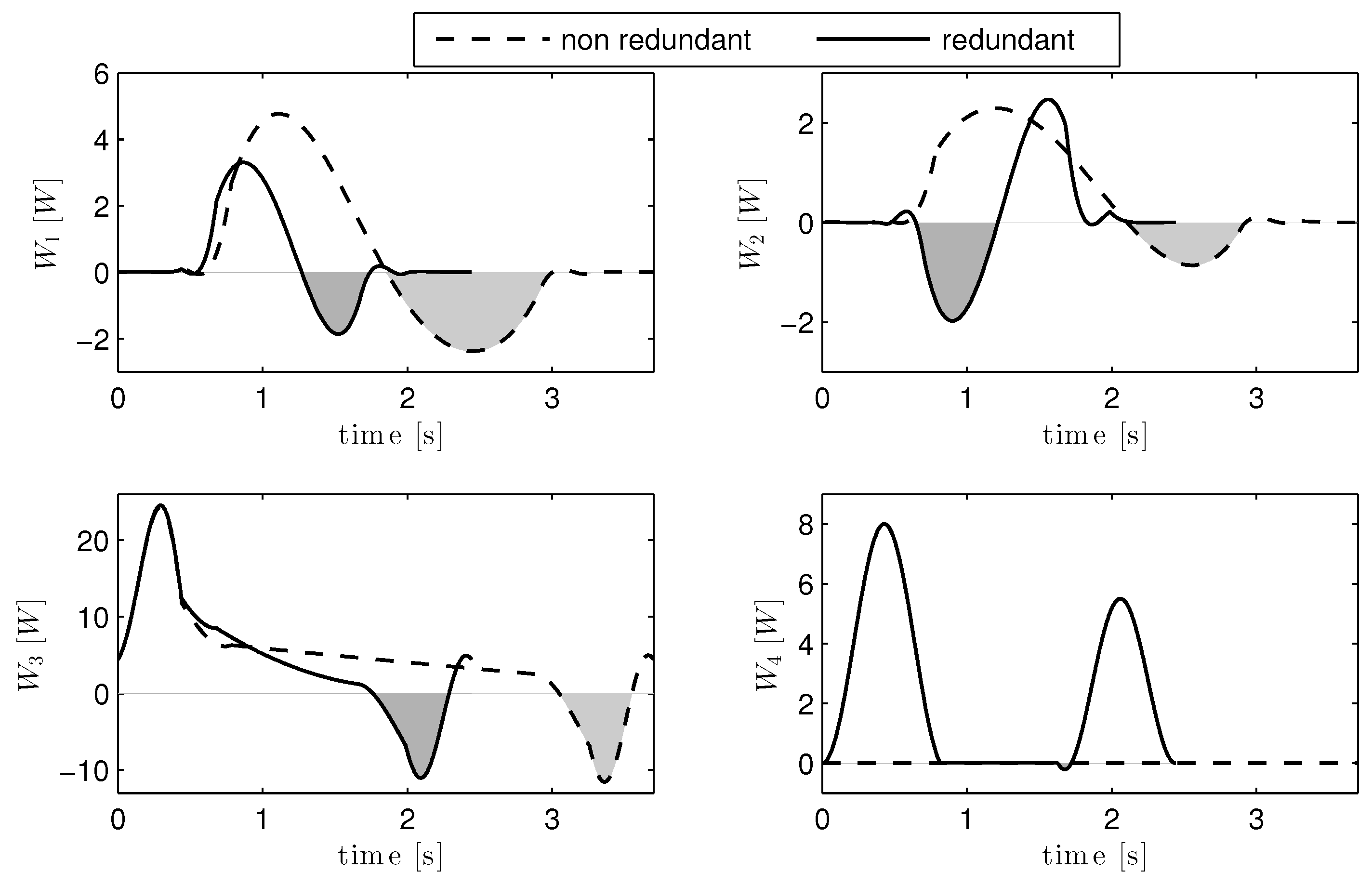
3.1. Trajectory Optimization with Electric Power Regeneration
3.2. Trajectory Optimization Without Regeneration
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Helm, D. The European framework for energy and climate policies. Energy Policy 2014, 64, 29–35. [Google Scholar] [CrossRef]
- Tanaka, K. Review of policies and measures for energy efficiency in industry sector. Energy policy 2011, 39, 6532–6550. [Google Scholar] [CrossRef]
- Carabin, G.; Wehrle, E.; Vidoni, R. A review on energy-saving optimization methods for robotic and automatic systems. Robotics 2017, 6, 39. [Google Scholar] [CrossRef]
- Hansen, C.; Eggers, K.; Kotlarski, J.; Ortmaier, T. Comparative evaluation of energy storage application in multi-axis servo systems. In Proceedings of the 14th IFToMM world congress, Taipei, Taiwan, 25–30 October 2015; pp. 201–210. [Google Scholar]
- Meike, D.; Ribickis, L. Energy efficient use of robotics in the automobile industry. In Proceedings of the 15th International Conference on Advanced Robotics (ICAR), Tallinn, Estonia, 20–23 June 2011; pp. 507–511. [Google Scholar]
- Kim, Y.J. Design of low inertia manipulator with high stiffness and strength using tension amplifying mechanisms. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 28 September–2 October 2015; pp. 5850–5856. [Google Scholar]
- Aziz, M.A.; Zhanibek, M.; Elsayed, A.S.; AbdulRazic, M.O.; Yahya, S.; Almurib, H.A.; Moghavvemi, M. Design and analysis of a proposed light weight three DOF planar industrial manipulator. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Portland, OR, USA, 2–6 October 2016; pp. 1–7. [Google Scholar]
- Li, Y.; Bone, G.M. Are parallel manipulators more energy efficient? In Proceedings of the 2001 IEEE International Symposium on Computational Intelligence in Robotics and Automation, Banff, AB, Canada, 29 July–1 August 2001; 41–46; pp. 41–46. [Google Scholar]
- Abe, A. An effective trajectory planning method for simultaneously suppressing residual vibration and energy consumption of flexible structures. Case Stud. Mech. Syst. Signal Process. 2016, 4, 19–27. [Google Scholar] [CrossRef]
- Brossog, M.; Kohl, J.; Merhof, J.; Spreng, S.; Franke, J. Energy consumption and dynamic behavior analysis of a six-axis industrial robot in an assembly system. Procedia CIRP 2014, 23, 131–136. [Google Scholar]
- Recoskie, S.; Lanteigne, E.; Gueaieb, W. A High-Fidelity Energy Efficient Path Planner for Unmanned Airships. Robotics 2017, 6, 28. [Google Scholar] [CrossRef]
- Alajlan, A.; Elleithy, K.; Almasri, M.; Sobh, T. An Optimal and Energy Efficient Multi-Sensor Collision-Free Path Planning Algorithm for a Mobile Robot in Dynamic Environments. Robotics 2017, 6, 7. [Google Scholar] [CrossRef]
- Stuart, S. DC Motors, Speed Controls, Servo Systems: An Engineering Handbook, 3rd ed.; Pergamon Press: Oxford, UK, 1972. [Google Scholar]
- Inoue, K.; Ogata, K.; Kato, T. An efficient power regeneration and drive method of an induction motor by means of an optimal torque derived by variational method. IEEE Trans. Ind. Appl. 2008, 128, 1098–1105. [Google Scholar] [CrossRef]
- Hansen, C.; Öltjen, J.; Meike, D.; Ortmaier, T. Enhanced approach for energy-efficient trajectory generation of industrial robots. In Proceedings of the IEEE International Conference on Automation Science and Engineering (CASE), Seoul, Korea, 20–24 August 2012; pp. 1–7. [Google Scholar]
- Hansen, C.; Kotlarski, J.; Ortmaier, T. Experimental validation of advanced minimum energy robot trajectory optimization. In Proceedings of the 16th International Conference on Advanced Robotics (ICAR), Montevideo, Uruguay, 25–29 Novomber 2013; pp. 1–8. [Google Scholar]
- Halevi, Y.; Carpanzano, E.; Montalbano, G. Minimum energy control of redundant linear manipulators. J. Dyn. Syst. Meas. Contr. 2014, 136, 051016. [Google Scholar] [CrossRef]
- Ruiz, A.G.; Fontes, J.V.; da Silva, M.M. The influence of kinematic redundancies in the energy efficiency of planar parallel manipulators. In Proceedings of the ASME 2015 International Mechanical Engineering Congress and Exposition. American Society of Mechanical Engineers, Houston, TX, USA, 13–19 November 2015; p. V04AT04A010. [Google Scholar]
- Ruiz, A.G.; Santos, J.C.; Croes, J.; Desmet, W.; da Silva, M.M. On redundancy resolution and energy consumption of kinematically redundant planar parallel manipulators. Robotica 2018, 36, 809–821. [Google Scholar] [CrossRef]
- Lee, G.; Sul, S.K.; Kim, J. Energy-saving method of parallel mechanism by redundant actuation. Int. J. Precis. Eng. Manuf.-Green Technol. 2015, 2, 345–351. [Google Scholar] [CrossRef]
- Lee, J.; Lee, G.; Oh, Y. Energy-efficient robotic leg design using redundantly actuated parallel mechanism. In Proceedings of the IEEE International Conference on Advanced Intelligent Mechatronics (AIM), Munich, Germany, 3–7 July 2017; pp. 1203–1208. [Google Scholar]
- Hansen, C.; Kotlarski, J.; Ortmaier, T. A concurrent optimization approach for energy efficient multiple axis positioning tasks. J. Control Decis. 2016, 3, 223–247. [Google Scholar] [CrossRef]
- Sayed-Ahmed, A.; Wei, L.; Seibel, B. Industrial regenerative motor-drive systems. In Proceedings of the Twenty-Seventh Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Orlando, FL, USA, 5–9 Febebruary 2012; pp. 1555–1561. [Google Scholar]
- Richiedei, D.; Trevisani, A. Analytical computation of the energy-efficient optimal planning in rest-to-rest motion of constant inertia systems. Mechatronics 2016, 39, 147–159. [Google Scholar] [CrossRef]
- Biagiotti, L.; Melchiorri, C. Trajectory Panning for Automatic Machines and Robots; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Ata, A.A. Optimal trajectory planning of manipulators: A review. J. Eng. Sci. Technol. 2007, 2, 32–54. [Google Scholar]
- Cook, C.; Ho, C. The application of spline functions to trajectory generation for computer-controlled manipulators. In Computing Techniques for Robots; Springer: Berlin, Germany, 1984; pp. 101–110. [Google Scholar]
- Boscariol, P.; Gasparetto, A.; Vidoni, R. Planning continuous-jerk trajectories for industrial manipulators. In Proceedings of the ASME 2012 11th Biennial Conference on Engineering Systems Design and Analysis. American Society of Mechanical Engineers, Nantes, France, 2–4 July 2012; pp. 127–136. [Google Scholar]

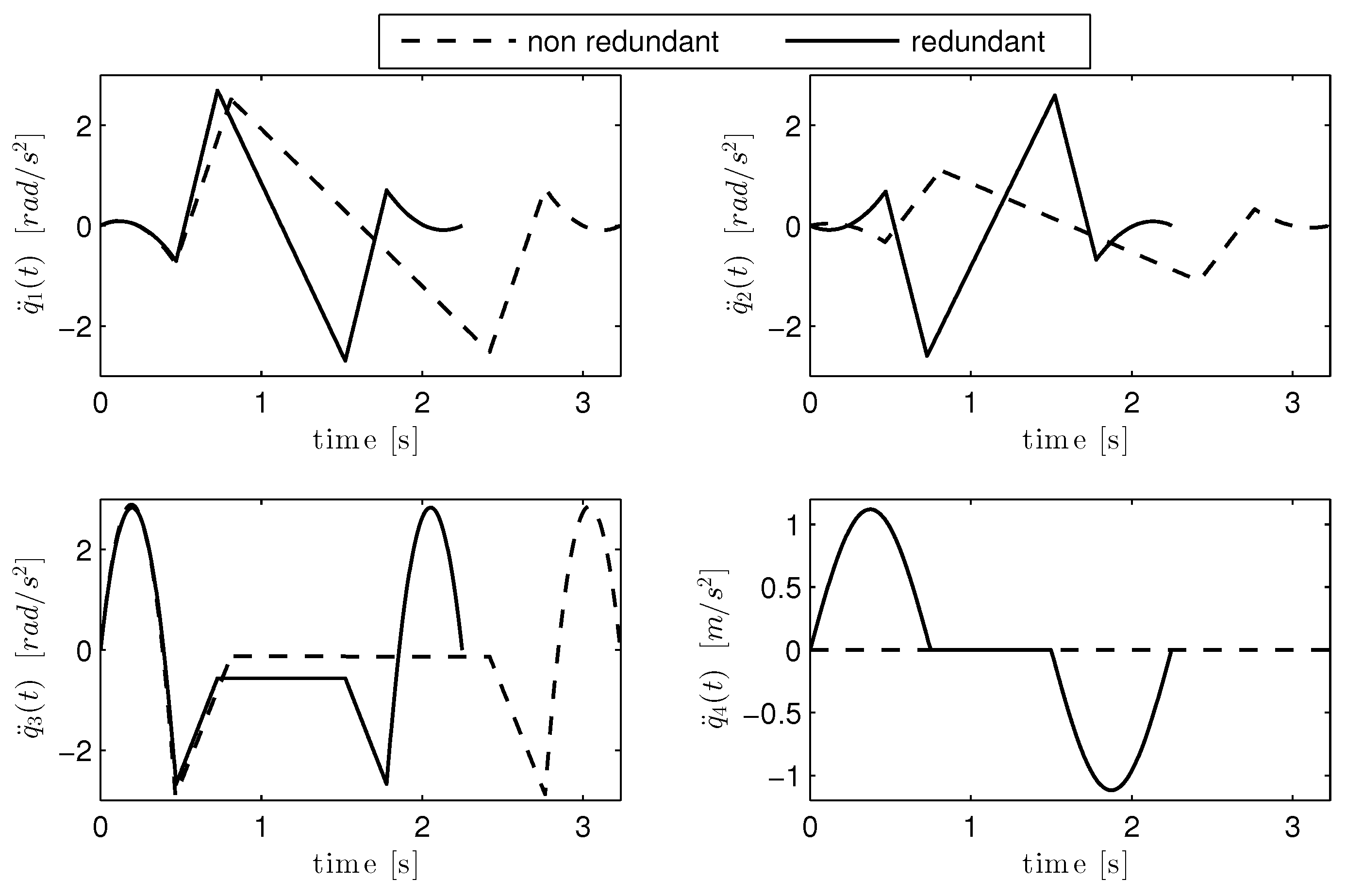

| Parameter | Joint 1 | Joint 2 | Joint 3 |
|---|---|---|---|
| Link length | 0.45 m | 0.35 m | - |
| Link mass | 14 kg | 18 kg | 2 kg |
| Gear ratio | |||
| Motor inertia | kg m2 | kg m2 | kg m2 |
| Viscous friction coefficient | 0.001 Nm s/rad | 0.001 Nm s/rad | 0.001 Nm s / rad |
| Coulomb friction force | Nm | Nm | Nm |
| Motor winding resistance | 3 Ω | 3 Ω | 3.5 Ω |
| Motor back-emf constant | 0.6 Vs/rad | 0.6 Vs/rad | 0.6 Vs/rad |
| Motor torque constant | 0.6 Nm/A | 0.6 Nm/A | 0.6 Nm/A |
| Peak motor torque | 2.5 N | 2.5 N | 1.5 N |
| Peak motor power | 75 W | 75 W | 50 W |
| Parameter | Value |
|---|---|
| Moving mass | 5.18 kg |
| Viscous friction coefficient | Ns/m |
| Coulomb friction force | N |
| Back-emf constant | 3.1 Vs/m |
| Torque constant | 3.12 N/A |
| Via-point | X [m] | Y [m] | Z [m] |
|---|---|---|---|
| 1 | 0.6 | 0.2 | 0 |
| 2 | 0.6 | 0.2 | 0.2 |
| 3 | 0.6 | 0.2 | 0.3 |
| 4 | −0.2 | 0.4 | 0.3 |
| 5 | −0.2 | 0.4 | 0.2 |
| 6 | −0.2 | 0.4 | 0 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boscariol, P.; Richiedei, D. Trajectory Design for Energy Savings in Redundant Robotic Cells. Robotics 2019, 8, 15. https://doi.org/10.3390/robotics8010015
Boscariol P, Richiedei D. Trajectory Design for Energy Savings in Redundant Robotic Cells. Robotics. 2019; 8(1):15. https://doi.org/10.3390/robotics8010015
Chicago/Turabian StyleBoscariol, Paolo, and Dario Richiedei. 2019. "Trajectory Design for Energy Savings in Redundant Robotic Cells" Robotics 8, no. 1: 15. https://doi.org/10.3390/robotics8010015
APA StyleBoscariol, P., & Richiedei, D. (2019). Trajectory Design for Energy Savings in Redundant Robotic Cells. Robotics, 8(1), 15. https://doi.org/10.3390/robotics8010015






