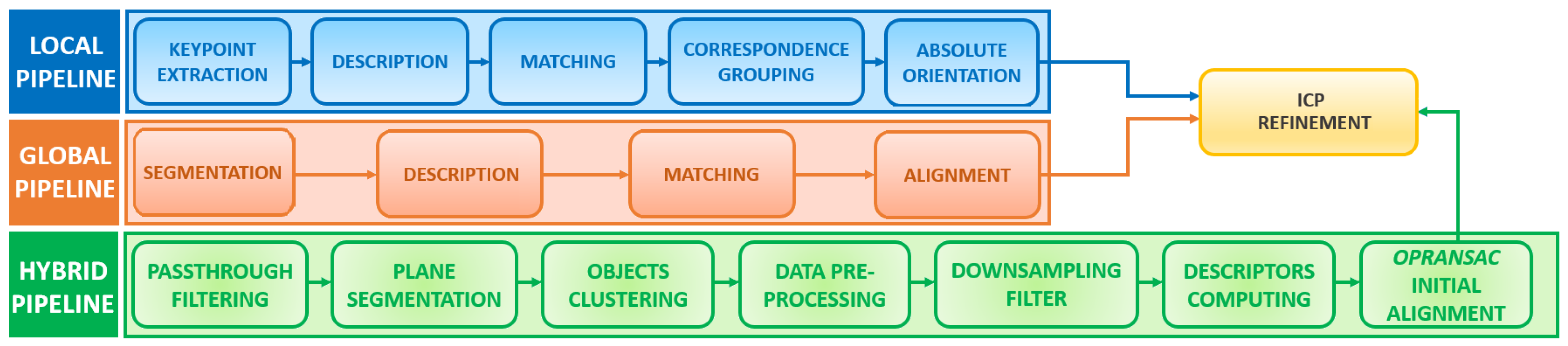
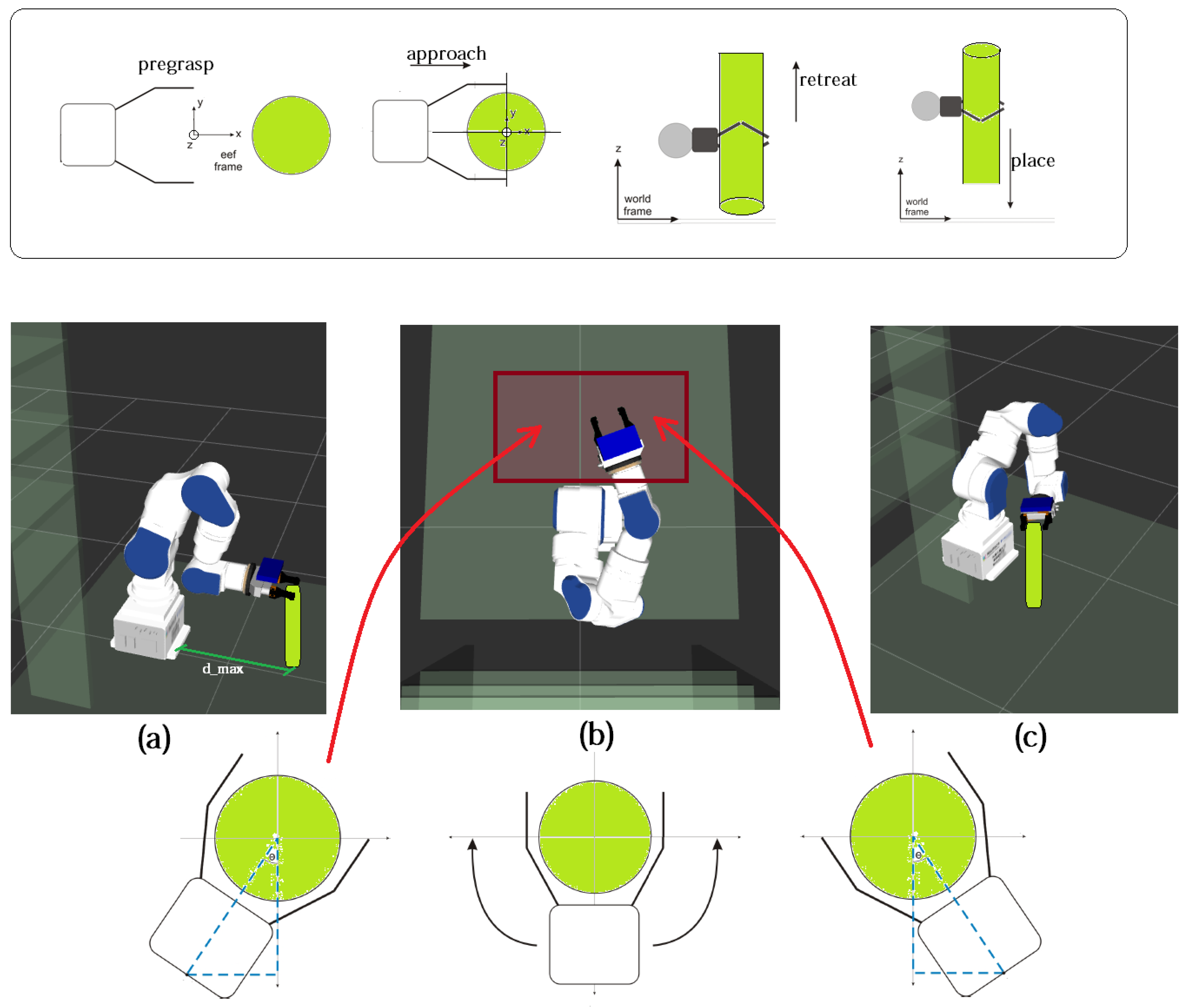
2.3.3. Hybrid Pipeline
In this specific application, the objects can be distinguished only by geometric information, without any kind of visual features (e.g., barcodes). The scene is usually large and affected by partial occlusions and similar objects in proximity. Standard recognition approaches proved to be unsuitable because of the limitations discussed above. The algorithm proposed in this paper extracts the most generalizable steps of each SoA pipeline and merges both the global segmentation and the local descriptor robustness, as shown in
Figure 4. Moreover, a new approach is introduced based on the RANSAC method [
13]: unlike the SoA pipeline that provides the matching phase and the alignment phase as two separated steps, the proposed algorithm performs the two phases in one step. It optimizes a critical parameter to be more efficient and robust than the traditional RANSAC approach (see
Section 2.3.4). This step was called Optimized RANSAC (OPRANSAC) to underline the optimization process. The initial coarse alignment provided by OPRANSAC is finally refined by the Iterative Closest Point (ICP) method [
18]. After the recognition, the algorithm output is the 6D localized pose. The hybrid pipeline is divided into eight steps:
1. PassThrough filtering. Undesirable data on the input scene are reduced by applying a series of PCL filters. Identifying the portion of the scene of interest and removing the rest can be a good way to simplify the recognition process from the beginning.
2. Plane segmentation. PCL provides Sample Consensus Segmentation (SCS), a very useful component which executes a segmentation algorithm based on normal analysis. The main problem is the choice of the right value of the parameter
k, which is the number of neighbors around a point used to compute the normal vector. The RANSAC method is a randomized algorithm for robust model fitting, and SCS uses it to estimate the parameters of the mathematical plane model of the given scene. RANSAC divides point data between inliers (the points which satisfy the plane equation) and outliers (all other points) by providing a vector of
model coefficients. Note that extracting the plane strongly depends on the quality of the surface normals, as shown in
Figure 5. The image on top-left of
Figure 6 illustrates the outcome of this step.
3. Object clustering. The process is based on Euclidean Cluster Extraction (ECE) approach, which uses a Kd-tree structure to find the nearest neighbors. The method uses a fixed minimum distance threshold,
.
Figure 6 shows the results.
4. Data preprocessing. Before the description analysis, each cluster and the given PC-model are passed through the Moving Least Square (MLS) filter. Overlapping areas, small registration errors, and holes are smoothed to improve the quality of the geometric descriptors.
5. VoxelGrid filter downsampling. As seen in
Section 2.2, the PC-model and scene can be provided by different data sources. This means that their descriptors can be very different, and this affects the correspondence step. To improve this aspect, a simple downsampling step through a Voxelized Grid approach was used so that all point clouds have almost the same density.
6. FPFH descriptors. The FPFH local descriptor was finally selected for its robustness after carrying out several experiments with different local and global descriptors. The main limitation of global descriptors, e.g., VFH, is that they are not suitable for complex scenarios: in the case study, there are many objects on the tray which are similar and close to each other, and very often they are occluded. FPFH features, on the other hand, represent the surface normals and the curvature of the objects, as shown in
Figure 7. FPFH turned out to be the descriptor which was least influenced by the complexity of the task in most of the experimental scenarios, as described in
Section 2.3.4.
7. Point cloud initial alignment: OPRANSAC. In order to compare two generic
Ssource and
Starget point clouds in 3D space, they need to be aligned. The OPRANSAC step in
Figure 4 is crucial because it must calculate the rigid geometric transformation to be applied to
Ssource to align it to
Starget. The hybrid pipeline proposes an initial alignment obtained by following the approach in [
19], i.e., by using the
Prerejective RANSAC method and without having previous knowledge about the object pose. This method uses the two analyzed point clouds, the respective local FPFH descriptors, and a series of setting parameters to tune the consensus function. The alignment process was performed through the class
SampleConsensusPrerejective, which implements an efficient RANSAC pose estimation loop.
The following difficulties were encountered during this phase: in some similar scenes in which the objects on the table were slightly moved, the SoA algorithm did not correctly recognize the target object, often confusing it with objects of different geometry. When it recognized the target object, the correspondence rates were very different from one scene to another or similar for different objects. So, the results obtained by these common techniques did not meet the supermarket scenario requirements. This is why a careful analysis of this crucial step was carried out: to identify only the most sensitive input parameters that affect the algorithm result. The parameter that was identified as the most critical is the
number of nearest features to use (
): small changes generate very different outputs. Trying to select a single value of this parameter for every observed scene and for every PC-model was impossible. The adopted solution is the maximization of the following fitness function over
:
where
is the cardinality of the set
I of inlier points between the two point clouds
and
after the
alignment calculated by using the current value of
, and
H is the 4 × 4 homogenous transformation matrix to perform such alignment. The transformation matrix
is extracted directly from
H.
In order to assign a label to the PC-model input, a classifier was not used, but a brute force search method was adopted by selecting the label corresponding to the highest value of the fitness function. However, the fitness function value of each cluster is computed by optimizing it with respect to an algorithm parameter. To maximize the fitness function, two nested loops were implemented. The inner loop computes the best value of by increasing it each time by a fixed step (i.e., ). This loop represents the optimization step, and it is the core of the approach since the choice of is crucial for the success of the algorithm. The external loop is just a brute force search; it executes this operation for each target cluster labeled in the specific scene, i.e., with j from 1 to the number of clusters identified in the scene. Finally, the best result is chosen: the corresponding homogeneous transformation matrix and the labeled cluster are selected. The pseudo-code is reported in Algorithm 1.
| Algorithm 1 OPRANSAC initial alignment. |
- 1:
input: - 2:
- 3:
- 4:
- 5:
- 6:
- 7:
- 8:
- 9:
procedurePerform Alignment - 10:
- 11:
- 12:
- 13:
for to do - 14:
- 15:
for to N do - 16:
- 17:
- 18:
if then - 19:
- 20:
- 21:
- 22:
end if - 23:
- 24:
end for - 25:
end for - 26:
end procedure
|
The maximum fitness value, which is equal to 1, is obtained when all the points have a near distance below the fixed
threshold. The partiality of the views (clusters) and therefore of the point clouds makes unlikely a high level of fitness, although over 70% matching in the experimental tests was found. The definition of the similarity parameter, therefore, enables the comparison between incomplete object clusters and PC-models, but also it enables the definition of optimization heuristics based on the cardinality of the point clouds.
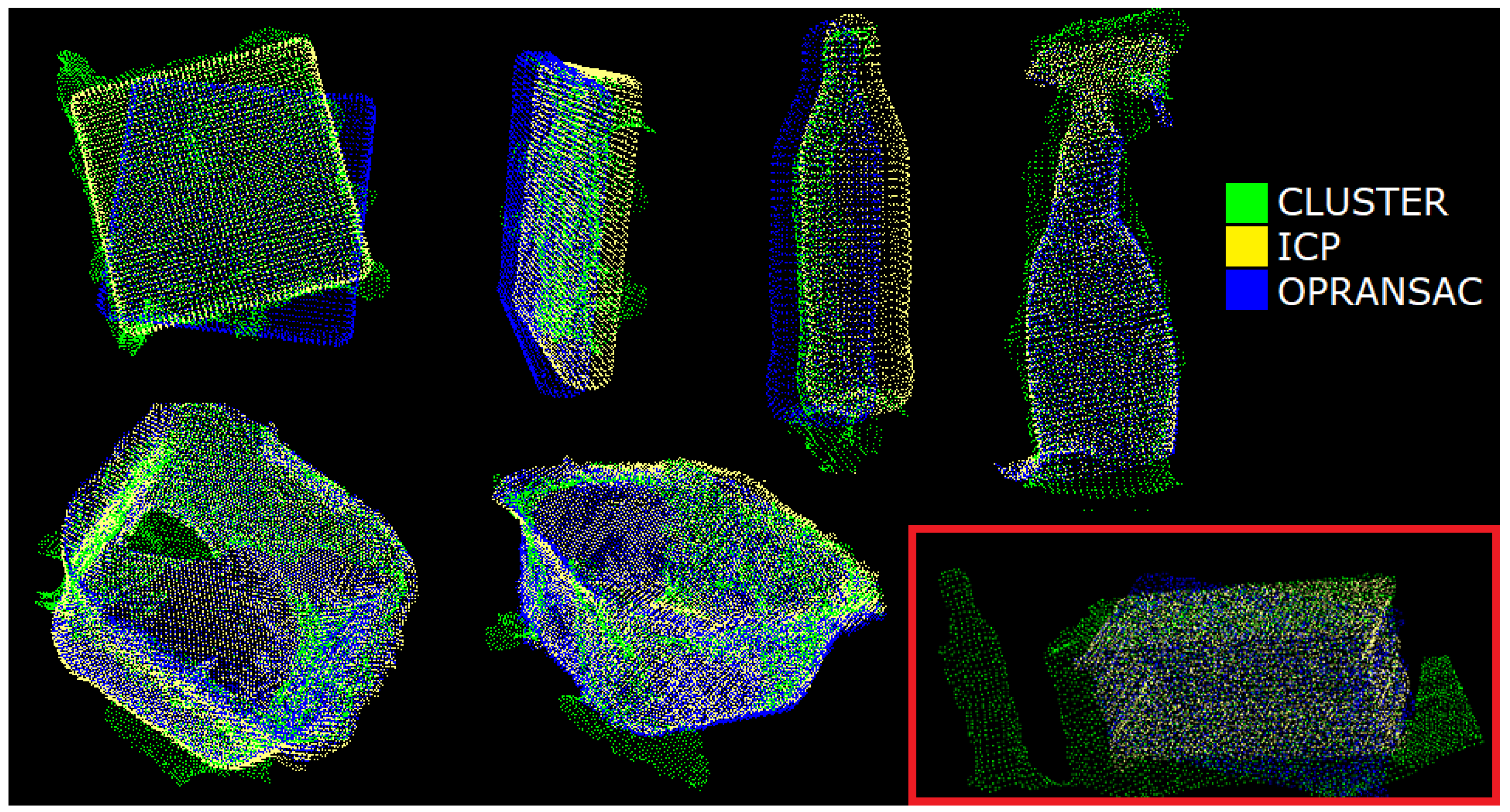
Figure 8 shows some (blue) PC-models coarsely aligned to their respective (green) clusters.
8. ICP The last step of the hybrid pipeline is the ICP algorithm.
is refined to better estimate the 6D object pose. The output is the transformation matrix
.
Figure 8 illustrates the final result.
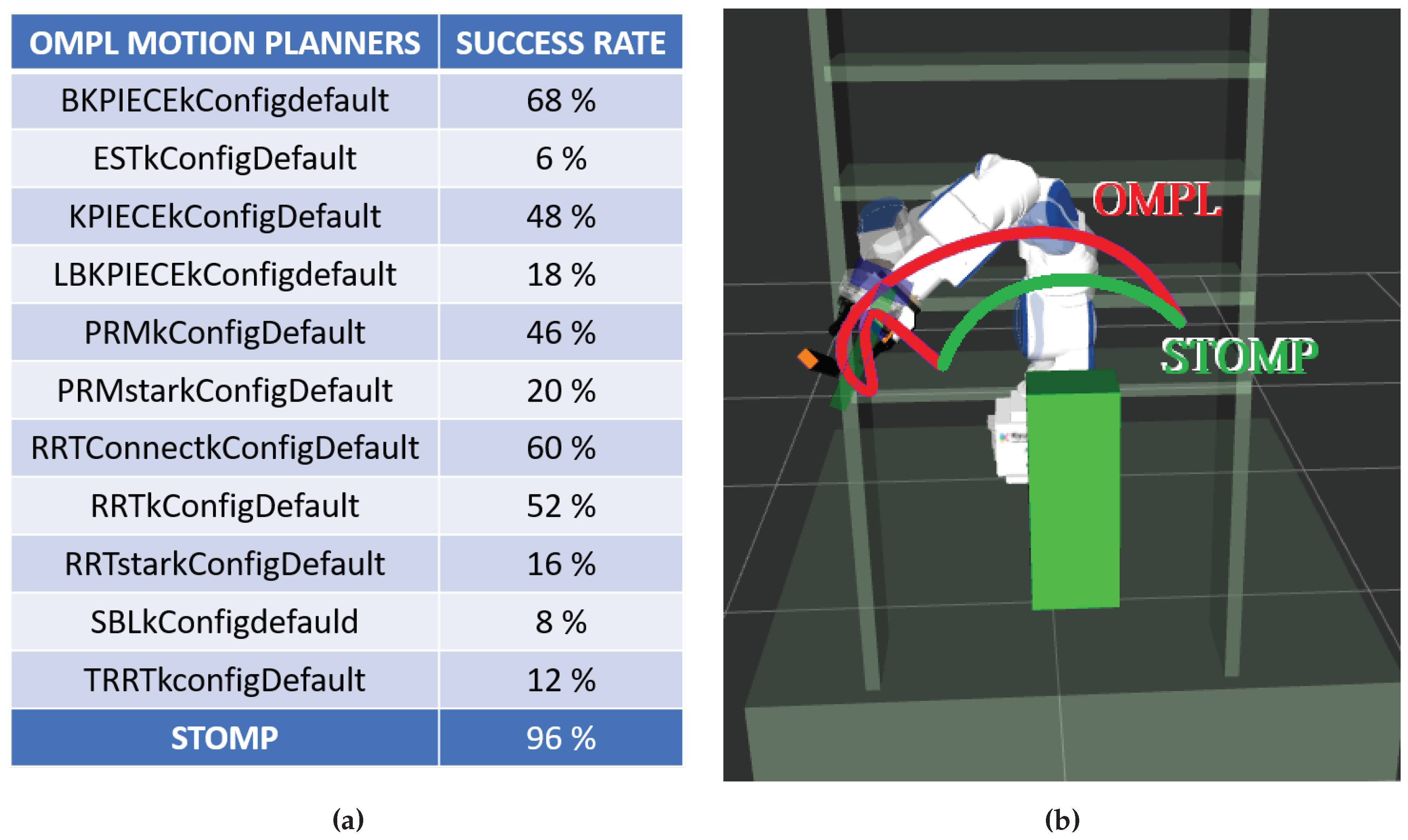
2.3.4. Tests and Performance Assessment
This subsection discusses the most interesting results obtained during preliminary tests carried out before the implementation of the proposed algorithm.
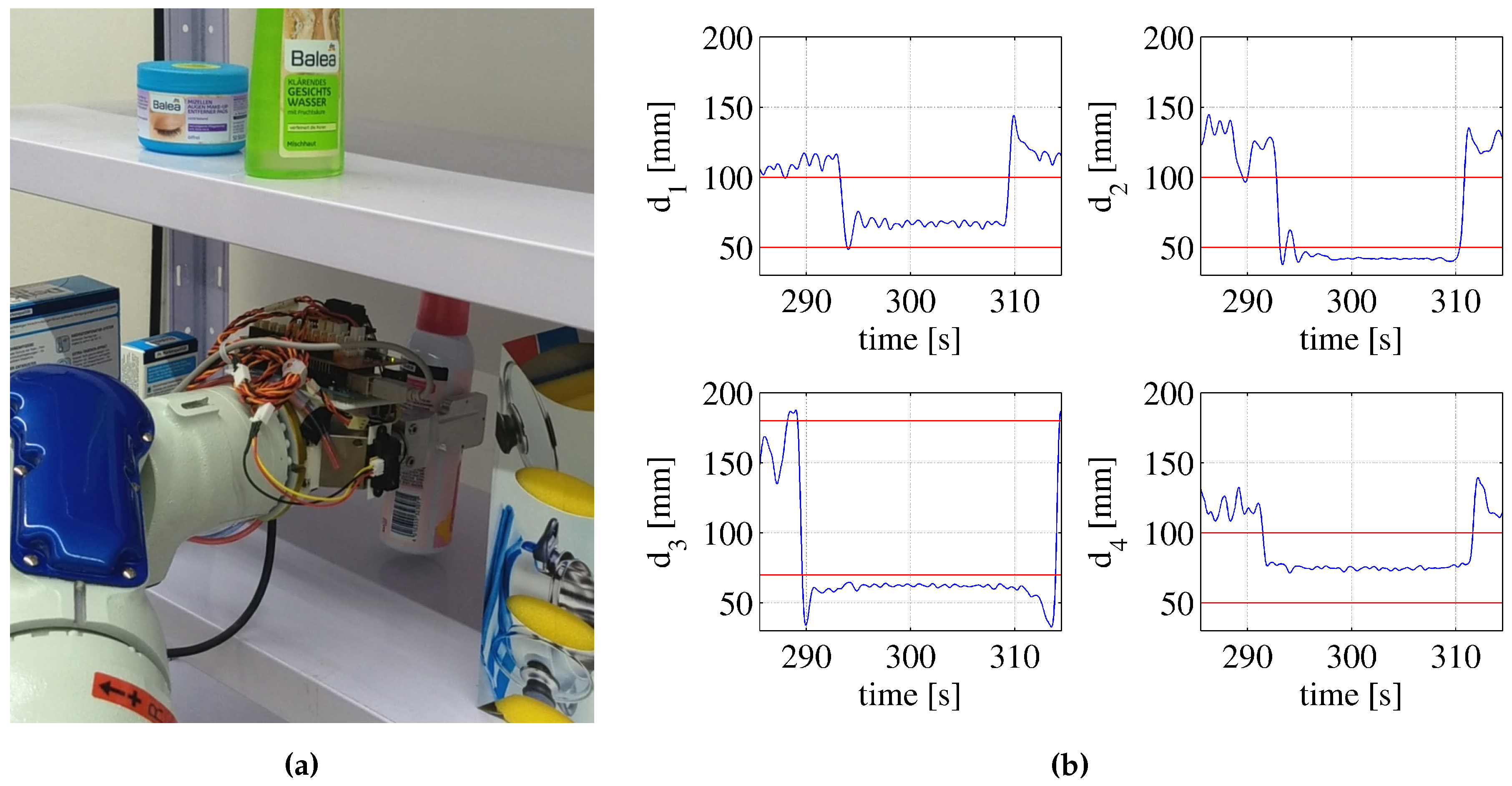
Camera placement. Camera placement influences the results of many recognition phases, e.g., the plane segmentation and the object clustering. When the camera is placed in a high position with respect to the object tray, the plane segmentation is good because the normals estimation is accurate. However, the clustering process becomes worse because the object front view is lost. The dimensions of both the clusters and the captured scene are influenced by the camera distance from the observed scene. The larger the distance, the smaller the object clusters, and the corresponding point clouds have fewer points. On the other hand, to frame as many objects as possible, the distance should be large enough. Finally, the distance should be high enough to let the camera stay out of the robot workspace so as to avoid an additional obstacle for the pick and place task. As a trade-off between the discussed constraints, the camera was placed such that the closest object is at about 0.3 m and the furthest one is at about 0.9 m.
Object placement. In this work, objects are assumed to be randomly placed but all upright on the tray and at a minimum distance of 0.3 m. This value was chosen to allow the robot to grasp an object without colliding with other close objects (see
Section 3.3) and also to guarantee a correct clustering of the scene. With reference to the red box in
Figure 8, if the objects are closer than 0.3 m, the clustering algorithm may generate a cluster with two objects. Nevertheless, their final alignment can be still successful: the (yellow) PC-model is aligned to the correct portion of the incorrect (green) cluster.
Key-point extraction tests. The first experimental tests followed step-by-step the SoA techniques based on the local pipeline applied to the first data set (
Figure 2a). Referring to [
20], the Normal Aligned Radial Features (NARF) algorithm deals with both the detection and the description of key-points. To the best of our knowledge, NARF is the most up-to-date and best-performing available algorithm. This method is based on two principles:
a key-point must be placed where the surface is stable to provide a robust normal estimation, and there are also sufficient changes in the neighbors;
if there is a partial view of the scene (like in the considered scenarios), it can focus on the edges of an object: the boundary of a foreground object will be quite unique and it can be used to extract points of interest.
In this context, three types of interesting points can be defined, as shown in
Figure 9: the
Object edges, which are outer points that belong to the object, the
Shaded edges, which are the background points on the boundary with occlusions, and the
Veil points, which are the points interpolated between the object edges and the shadow points.
While shadow points are not useful, veil detection is required because these points should not be used during the feature extraction. There are several indicators that may be useful for edge extraction, such as critical changes of normals. NARF uses the change in the average distance of neighbors to the point, which is a very robust indicator of noise and resolution changes. This means that a good key-point needs to have significant changes in the surface around itself in order to be detected in the same place even though viewed in different perspectives.
The experimental results showed that objects that have a complex geometry (e.g., the spray bottle) give a lot of key-points (e.g., on the handle): it is possible that a detailed tuning algorithm could converge to good results. On the contrary, for the objects which have more regular geometries (e.g., the boxes), it is more difficult because too few key-points are extracted and, therefore, the percentage of failure dramatically increases when searching for model–scene correspondences.
The natural solution would be to decrease the exploration radius of the algorithm, but this alternative soon becomes a bottleneck because it extracts a greater number of key-points than the previous cases; however, many of them are fake edges. This effect is absolutely a disadvantage because the algorithm finds a number of possible combinations when it compares the PC-model and the scene, as shown in
Figure 10. Choosing the right correspondence is difficult because all of them have similar matches.
A careful analysis underlines that these results also depend on other factors. For the successful adoption of a local pipeline to recognize objects, the PC-model and the scene should have the same precision, cardinality, accuracy, resolution, and scales. All of these limitations do not allow for the generalization of the use of this algorithm, especially when using PC-models extrapolated directly from some online existing databases. That is why the key-point extraction method was completely discarded.
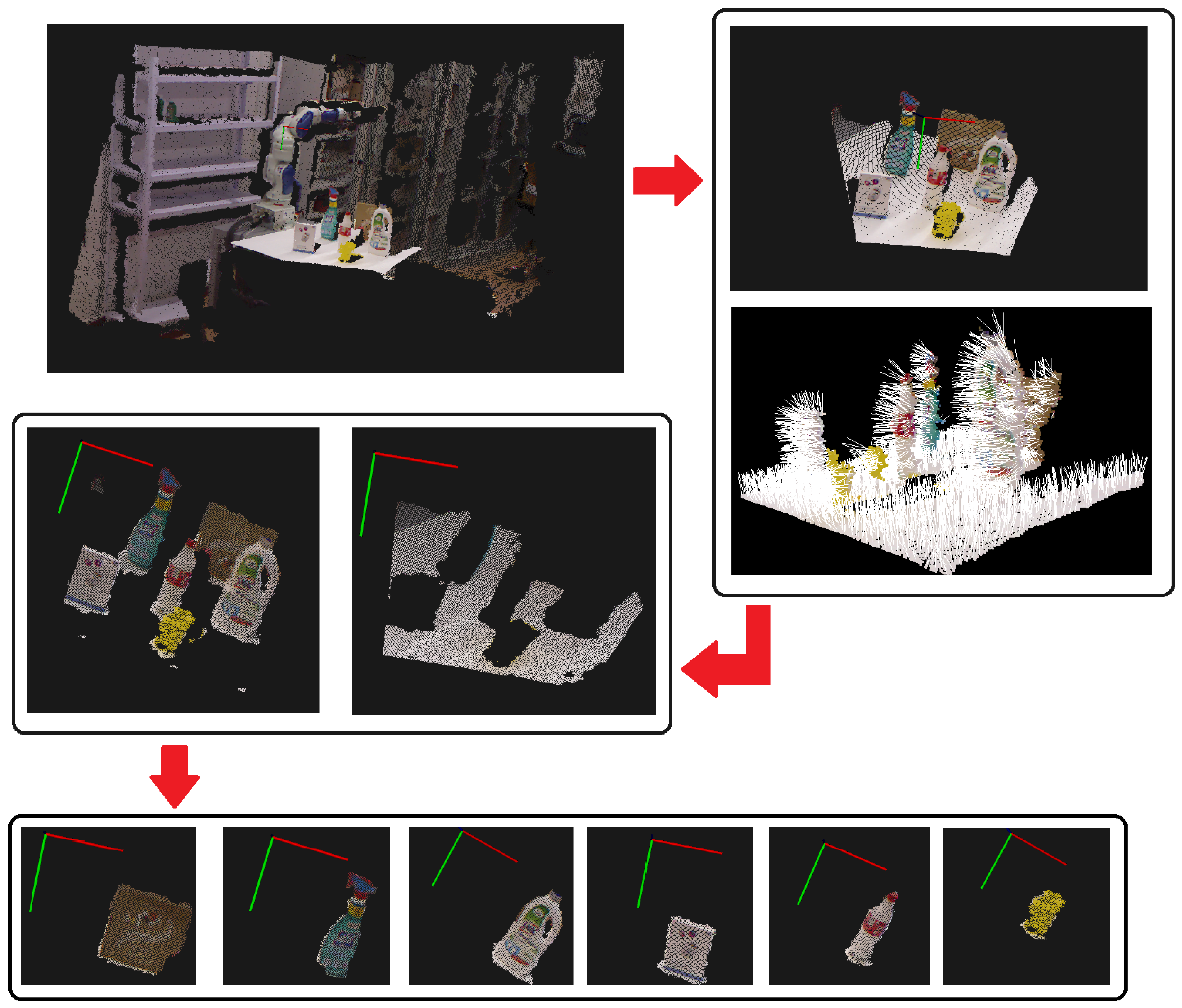
Hybrid pipeline applied to the first data set. To evaluate the general behavior of the proposed pipeline in terms of its precision and reliability, an extensive test was initially executed on 50 different scenes containing objects of the first data set (
Figure 2a).
Some testing objects were reconstructed using the ReconstructMe software. Despite the rough modeling of some parts (e.g., holes in the basin or the absence of the green cap of the soap bottle), the corresponding PC-models, for a size ranging from 100 kB to 200 kB, were directly used and processed in the proposed pipeline, showing its convenience.
As seen in
Figure 4, the PassThrough filter removes the points outside the interesting range. On the remaining point cloud, the estimation of the normal surface vectors is performed to determine the support plane. The clustering step closes the segmentation phase and provides data to the more specific description phase. The entire step-by-step segmentation process is illustrated in
Figure 11.
The data preprocessing step uses an MLS filter and VoxelGrid filter to obtain an improved version of both the models and the cluster point clouds (see
Figure 12).
The quality of the object recognition results is assessed through a manual check of the algorithm decisions: for each new scene, all the identified clusters are labeled, leading to the experimental data reported below.
Table 1 contains the average of the best fitness scores obtained by comparing each PC-model (row) with each cluster (column).
The objects with the most extensive surfaces (1 and 6) have a higher matching value with their respective clusters than the others. Consequently, the expected percentage of failure during recognition is low. In fact, their point cloud’s clusters have obviously more samples than those of the other objects and, therefore, their features will certainly have greater information content. On the opposite side, the clusters which represent the yellow glass (7) have fewer samples because of its small size. Moreover, the noise introduced through the sensor system makes very coarse and distorted clusters, which is why the feature’s precision and, therefore, the resulting fitness value are really compromised. The curvatures of the glass are not well defined in the clusters and that is why even the filtering techniques used are not enough to represent it better. So, the result is the low fitness value between the glass PC-model and the glass clusters. This result means that very often the glass PC-model can be confused with incorrect clusters, such as the small box (2) of similar height or the bottom part of the spray bottle (5) of similar geometry, as well as the coke bottle (3). The same difficulties could be encountered with object 4, because its geometry should be primarily defined by its handle, which should distinguish the corresponding cluster from the others. However, the detail may be unclear if the bottle is not frontally located or if it is too far from the camera.
Table 2 counts how many times the PC-model is recognized with the specific cluster, regardless of its fitness value. By aggregating the data, there are 307 true positive and 43 false positives, which corresponds to a correct recognition in the 87.71% of the cases and a wrong recognition in the remaining 12.29%. Generalizing these results, it is possible to construct a confusion matrix (
Table 3), which indicates the quality of the algorithm and estimates its accuracy. Ideally, it should be an identity matrix, but due to false negatives of the tests, it is a bit deformed.
Finally, the ICP algorithm refines the initial coarse alignment provided by OPRANSAC.
Figure 8 shows clear cases of convergence and the typical results.
Robustness analysis. A further interesting test was performed to evaluate the algorithm robustness. Three limit cases were studied:
scenarios with objects partially occluded, as in
Figure 13a,c;
scenarios with objects outside the data set, i.e., the purple container in
Figure 13b,c;
scenarios with more similar objects, e.g., two coke bottles as in
Figure 13b,c.
Table 4 shows the matrix of the fitness values obtained at the end of the experiment in
Figure 13a. By aligning a given PC-model (Arabic number labels) to the found clusters (Roman number labels), the computed fitness values underline how the partial occlusion of the red basin does not affect the performance of the algorithm.
Table 5 and
Table 6, on the other hand, refer to the experiments in
Figure 13b,c, respectively. In these scenarios, two difficulties are introduced: the purple container, which does not belong to the data set, and two similar coke bottles. The clustering process correctly produces two different clusters for the similar objects (labeled
IIIa and
IIIb in the table) and a cluster for the unknown object (labeled
Distraction). Even in this case, the two bottles get the highest fitness values compared to the PC-model and, on the contrary, the cluster of the object outside the data set has the lowest fitness value.
Analysis of the execution time. Twenty experimental tests were done with the second data set (
Figure 2b). In order to measure the execution time of the alignment step of the algorithm, the main parameters were set as in
Table 7, and 20 scenes with 11 objects were prepared. The results, expressed in seconds, are reported in
Table 8. Note that the OPRANSAC step requires more computational time due to the introduction of the N-loop for each cluster. The refinement ICP phase shows a constant trend of around 700 ms, which is negligible.
Confusion matrix. Another interesting test was performed to deeply evaluate the algorithm robustness. The confusion matrix reported in
Table 9 refers to the second data set. It is important to remark that without a criterion to exclude uncertain recognitions, objects are always recognized, and this can produce a high rate of false positives. A simple way to reduce this phenomenon is to fix a threshold,
, to exclude the cases of poor likeness. This alternative method improves also the execution time of the algorithm because the expected loop can be interrupted if the average model–cluster correspondence is lower than
. For each test, the algorithm is invoked, taking the PC-model of the object to be recognized as input. The algorithm output is a selected cluster with a fitness value,
fitness. By comparing
fitness with
, it is possible to choose whether the correspondence is acceptable or not: if
, the model–cluster association is valid (1); otherwise, no (0). By repeating this test for all object PC-models in the same scene and for 20 different scenarios, it is possible to report the percentage results in
Table 9. The values in the last column represent the unrecognition rates (
).
The C, D, and F boxes have a higher number of hits because their fitness match values are always the highest for their respective clusters than that with the other clusters, and so the percentage of failure, when the aim is to recognize these objects, is low. However, they are the objects with simpler geometry and larger surface extension, and this means that their point cloud clusters have obviously more samples than those of the others objects. On the other hand, the clusters of the G, H, I, and J objects have fewer points because they are small items and also their distance from the camera causes very coarse and distorted clusters. This limits the fitness values and therefore the success of the algorithm. The curvatures of the smaller objects are not well defined in the clusters, and even the filtering is not enough to represent them better. So, the result is a low fitness value implying that the desired target object is often confused with an incorrect cluster.
By aggregating the data, 220 tests were carried out: the algorithm produced 156 true positive and 52 false positives, which correspond to a correct recognition in 71% of the cases and a wrong recognition in 23%, while the remaining 6% of the considered cases did not produce any association at least equal to , i.e., unrecognized objects (UR).