Abstract
GT-style rubber-fiberglass (RF) timing belts are designed to effectively transfer rotational motion from pulleys to linear motion in robots, small machines, and other important mechatronic systems. One of the characteristics of belts under this type of loading condition is that the length between load and pulleys changes during operation, thereby changing their effective stiffness. It has been shown that the effective stiffness of such a belt is a function of a “nominal stiffness” and the real-time belt section lengths. However, this nominal stiffness is not necessarily constant; it is common to assume linear proportional stiffness, but this often results in system modeling error. This technical note describes a brief study where the nominal stiffness of two lengths ( and ) of GT-2 RF timing belt was tested up to breaking point; regression analysis was performed on the results to best model the observed stiffness. The experiments were performed three times, providing a total of six stiffness curves. It was found that cubic regression mod els () were the best fit, but that quadratic and linear models still provided acceptable representations of the whole dataset with values above .
1. Introduction
Timing belts are a common means of motion transfer between rotating motors/shafts in a machine or mechatronic system. Many small-to-medium sized mechatronic systems such as 3D printers [1], robots [2,3], desktop computer numerical control (CNC) machines [4], and positioners [5] use such belts, typically in the GT-style [6,7]. GT-style belts are specifically designed to effectively translate rotating motion from pulleys into linear motion with minimal deformation, slippage, and backlash. One of the fundamental characteristics of such a motion transfer system is that the length of the belts changes with time, causing time-variant stiffnesses in the belts which must be considered in dynamic system modeling and design. Note that the "stiffness" in the belt is considered only in the tension direction of the belt for this work, resulting in a stiffness that can be described as a single value or function instead of the full stiffness matrix [8,9].
When analyzing and designing any robotic and other mechatronic systems, it is vital that a good dynamic model of the system be developed and used. Since such systems often use some kind of flexible belts for motion transfer, the belt stiffness is a very important parameter in a system model. In cases where the length of the belt is constant (e.g., running between two fixed pulleys), the stiffness k of the belt can be modeled as a spring where ; therefore, the stiffness of the belt is a function of its deflection x under load. In effect, this constant-length stiffness of the belt is its “nominal” design stiffness. However, in cases where the belt changes length during use, the effective length of these belt is a function of time and, therefore, its stiffness is also time-variant; this time-variant stiffness is the “effective” or apparent stiffness of the belt at some time t. It has been shown that the effective stiffness of the length-changing belts can be directly calculated as a function of the nominal stiffness value, the belt width, and the real-time length of the belt [10] such that:
where is the effective stiffness as a function of time, is the nominal stiffness, b is the belt width, and is the length of the belt section at time t. For any case where the length remains constant, the effective and nominal stiffnesses are equal since the value of is a constant. Note that the value of may be a constant or function of material properties for different belt materials; it cannot be considered a function of time the way that the length of the belt is. The most commonly-used GT-style belt is the GT-2; Figure 1 shows the fundamental geometry and specifications for this type of belt.
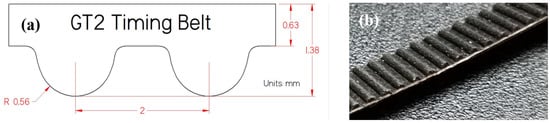
Figure 1.
GT-2 belt (a) specifications and (b) basic geometry.
Figure 2 shows a common application, where a GT-style belt is used to transfer motion from a stepper motor to drive a linear positioning system. Also shown is a 2D dynamic model representation of such a system (Figure 2b), where the differences in effective stiffness, based on belt length, in the belt sections are clearly evident. The sections and change in effective stiffness as a function of time, while section stays constant during use [11,12] so the effective and nominal stiffnesses are equal.
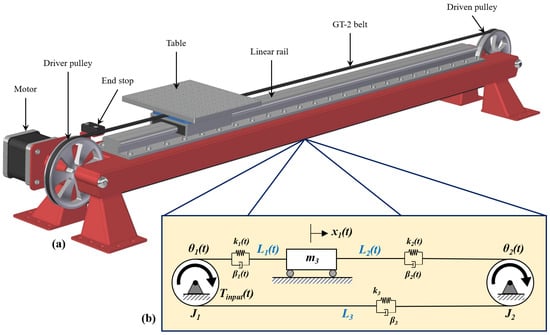
Figure 2.
(a) simple positioning system that utilizes a GT-type belt to drive the table and (b) its representative dynamic model.
The work described in this note explored the nominal stiffness and the best way to model it in dynamic systems where belt length is not constant. Several previous studies have assumed that rubber-based timing belts have a linear nominal stiffness [5,11,12,13,14,15,16,17,18]. However, it is vital for designers and engineers working with dynamic systems which use belts for energy transfer to understand the true effects of the belt stiffness [19,20]. Therefore, experimental data was collected and used to derive conclusions on the true stiffness behavior of the GT-2 belts during use. The collected data was subjected to regression analysis to see which type of model best fit, allowing the comparison of models for the same dataset. The information in this study will prove useful, both in choosing k stiffness values for dynamic models and for judging expected model error if linear stiffness assumptions are used.
2. Procedure and Results
Two lengths of new GT-2 belts, 400 mm and 760 mm, were subjected to a simple tensile test until they ruptured. The test apparatus was a custom-built, screw-driven manual desktop test stand set up for tensile testing with capability and a travel rate of (1.6 mm) per screw revolution. The screw drive was rotated at a constant rate of revolutions per second (0.8 mm/s), a reading being taken every revolution of the screw or every 1.6 mm. Since the length measurement was based on a count of the threads during travel, the uncertainty in length was too small to quantify; the digital readout for the unit used a load cell with a given uncertainty of 100 gram-force or . It was necessary to use this kind of manual tensile testing machine as none of the available standard machines were sensitive enough to measure the force-deflection behavior of these kinds of belts [21]. In addition, the discrete time measurement ensured a reasonably-sized dataset for curve-fitting. This was replicated twice to obtain a set of six different curves, three from each length. The ruptured belts were observed to fail suddenly and to show tearing of the glass fibers inside, as shown in Figure 3. The GT-2 belts used were a composite of neoprene (synthetic rubber) [22] and glass fibers, where the fibers appeared to drive the failure point of the belts.

Figure 3.
Belt break interface, showing broken fibers.
The collected data, in terms of force-deflection curves, are shown in Figure 4a, while the equivalent stress–strain curves for the tests are shown in Figure 4b. The length of the belts clearly had an effect on the force-deflection curves, but this largely disappeared when the length was accounted for in the stress–strain curves. Note that most of the curves show hyper-elastic behavior, i.e., there is no region in the curve where the stiffness is constant.
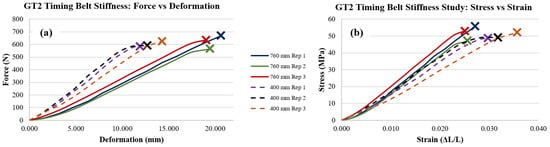
Figure 4.
Belt stiffness curves: (a) force-deflection curve and (b) stress–strain curve.
As the nominal compliance of the belts was clearly found to be nonlinear, a regression analysis was performed to model the curves and find the level of unexplained variance in these curves. One of the most common polynomial regression models [23,24] used for hyper-elastic materials is the cubic polynomial. The basic model used for this study began with the following polynomial model:
where a cubic model includes all of the variables, a quadratic model can be generated by setting , and a linear model can be used with . These curve fits, completed using Microsoft Excel™ (Microsoft Corp, Redmond, WA, USA) are shown in Figure 5a, and the fits for each of the variable and the resulting values are shown in the first six cases in Table 1.
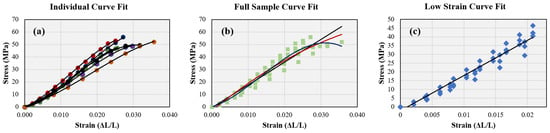
Figure 5.
Curve fits for (a) individual belts (cubic model); (b) full sample curve fit (cubic, quadratic, and linear models); and (c) low-strain linear curve fit.

Table 1.
Belt stiffness model curve fit data.
After fitting the cubic models to each of the six sets of experimental data, the cubic model, a quadratic model, and a linear model were then fit to the entire set at once, as shown in Figure 5b. A significant drop in the value was noted for all of the models fit to the dataset, but differences between the cubic, quadratic, and linear models were observed to be small, as shown in Table 1.
It was observed that the low-strain region of the dataset (Figure 5b,c) conforms better to a linear model when the entire dataset is used. In actual use, it is most likely that the belts will not reach more than 20–30% of the belt breaking strength during normal use [14,25,26], so this is a valid assumption for many systems; this will, of course, need to be determined by the modeler or designer before using a linear belt model. If the low-strain assumption can be used, then the data fit a linear model with a slightly greater value than a quadratic model for the entire dataset and is certainly superior to a linear model for the entire dataset. The linear model for this case is shown in the last row of Table 1.
3. Recommendations for Use and Applications
In cases where a time-variant belt length is used in a dynamic system model, the time-dependent stiffness of the belt must be considered, even when a mix of time-variant and time-invariant belt lengths are used. In practice, it is recommended that the modeler follow a three-step procedure:
- Identify the nominal stiffness of each belt type used in the system (e.g., if two thicknesses of belts are used, two different nominal stiffnesses will be present). This information may be collected from manufacturer datasheets or from tests on each belt type, similar to the tests done in this technical report.
- Decide if a linear or nonlinear nominal stiffness model will be used for each belt type. The primary driving force for this decision will be the computational cost for analyzing the system; for a simple system, it may be practical to use a nonlinear nominal stiffness model, but a linear model would be more feasible in a system with several elements. However, the importance of the model accuracy is a serious consideration and may justify a high computational cost if high accuracy is required.
- Based on the configuration of the system and the decisions made in the first two steps, the effective stiffness k can take one of four forms:
- (a)
- If the belt length is constant and a linear model is used for , the effective stiffness in the equations of motion will be constant and described by
- (b)
- If the belt length is constant and a nonlinear model is used to find , the nominal stiffness will be a function derived form a force-deflection curve. The effective stiffness in that belt section will be described bywhere is a continuous function of x.
- (c)
- If the belt length is time-variant and a linear model is used for , the effective stiffness in the equations of motion will be time-variant and described by
- (d)
- If the belt length is time-variant and a nonlinear model is used to find , the nominal stiffness will be a function derived form a force-deflection curve. In this case, the effective belt section stiffness will be described bywhere is a continuous function of x and the belt length is a function of time. Therefore, the effective stiffness will be dependent on both the length of the belt and the amount of force placed on the belt.
When modeling these dynamic systems, it is recommended that the simplest model of the belt stiffness which gives acceptable accuracy be used in order to balance computational cost with extreme accuracy in the model. In most cases, the uncertainty in the material properties of the belt and the common use of linearization in dynamic models would erase any advantage to using an extremely high-fidelity belt model.
4. Conclusions
This short technical note presents the results of a brief exploratory study on modeling the nominal stiffness of GT-2 timing belts; this information can be used to more accurately model the true, time-variant, stiffness behavior of common GT-2 belts when the effective length of belt sections changes with time. It was observed that these belts do not behave in a linear way, as expected for belts with a hyper-elastic base material, but that a linear model can provide a reasonable approximation of the behavior under some conditions, particularly low-strain conditions. When possible, the cubic stiffness model should be used, but this would often be impractical for dynamic systems with many components, as it can cause a simple model to become nonlinear in more than one variable. When practical and necessary for problem tractability, a linear model may be used with a reasonable degree of accuracy. The modeler or designer should keep in mind that some uncertainty will exist with any belt model and should choose the model that best balances accuracy with computational cost.
Author Contributions
B.W. and A.E.P. conceived and designed the study. All authors helped to set up the experiments, collect data, perform the regression analyses, and write the report.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest. No external funding was used to perform the work described in this study. Opinions and conclusions presented in this work are solely those of the authors.
Nomenclature
- b = Belt width (m)
- = Belt section i damping coefficient
- = Nominal belt stiffness (N/m)
- = Effective (true) belt section i stiffness (N/m)
- = Belt section i length (m)
- = Mass of block i (kg)
- = Pulley i angle (degrees)
References
- Laureto, J.; Pearce, J. Open Source Multi-Head 3D Printer for Polymer-Metal Composite Component Manufacturing. Technologies 2017, 5, 36. [Google Scholar] [CrossRef]
- Krahn, J.; Liu, Y.; Sadeghi, A.; Menon, C. A tailless timing belt climbing platform utilizing dry adhesives with mushroom caps. Smart Mater. Struct. 2011, 20, 115021. [Google Scholar] [CrossRef]
- Parietti, F.; Chan, K.; Asada, H.H. Bracing the human body with supernumerary Robotic Limbs for physical assistance and load reduction. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–7 June 2014. [Google Scholar]
- Choudhary, R.; Sambhav; Titus, S.D.; Akshaya, P.; Mathew, J.A.; Balaji, N. CNC PCB milling and wood engraving machine. In Proceedings of the International Conference On Smart Technologies For Smart Nation (SmartTechCon), Bangalore, India, 17–19 August 2017. [Google Scholar] [CrossRef]
- Sollmann, K.; Jouaneh, M.; Lavender, D. Dynamic Modeling of a Two-Axis, Parallel, H-Frame-Type XY Positioning System. IEEE/ASME Trans. Mechatron. 2010, 15, 280–290. [Google Scholar] [CrossRef]
- York Industries. York Timing Belt Catalog: 2mm GT2 Pitch (pp. 16). Available online: http://www.york-ind.com/print_cat/york_2mmGT2.pdf (accessed on 13 June 2018).
- SDP/SI. Handbook of Timing Belts, Pulleys, Chains, and Sprockets. Available online: www.sdp-si.com/PDFS/Technical-Section-Timing.pdf (accessed on 13 June 2018).
- Huang, J.L.; Clement, R.; Sun, Z.H.; Wang, J.Z.; Zhang, W.J. Global stiffness and natural frequency analysis of distributed compliant mechanisms with embedded actuators with a general-purpose finite element system. Int. J. Adv. Manuf. Technol. 2012, 65, 1111–1124. [Google Scholar] [CrossRef]
- Barker, C.R.; Oliver, L.R.; Breig, W.F. Dynamic Analysis of Belt Drive Tension Forces During Rapid Engine Acceleration; SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 1991. [Google Scholar]
- Gates-Mectrol. Technical Manual: Timing Belt Theory. Available online: http://www.gatesmectrol.com/mectrol/downloads/download_common.cfm?file=Belt_Theory06sm.pdf&folder=brochure (accessed on 13 June 2018).
- Hace, A.; Jezernik, K.; Sabanovic, A. SMC With Disturbance Observer for a Linear Belt Drive. IEEE Trans. Ind. Electron. 2007, 54, 3402–3412. [Google Scholar] [CrossRef]
- Johannesson, T.; Distner, M. Dynamic Loading of Synchronous Belts. J. Mech. Des. 2002, 124, 79. [Google Scholar] [CrossRef]
- Childs, T.H.C.; Dalgarno, K.W.; Hojjati, M.H.; Tutt, M.J.; Day, A.J. The meshing of timing belt teeth in pulley grooves. Proc. Inst. Mech. Eng. D 1997, 211, 205–218. [Google Scholar] [CrossRef]
- Callegari, M.; Cannella, F.; Ferri, G. Multi-body modelling of timing belt dynamics. Proc. Inst. Mech. Eng. K 2003, 217, 63–75. [Google Scholar] [CrossRef]
- Leamy, M.J.; Wasfy, T.M. Time-accurate finite element modelling of the transient, steady-state, and frequency responses of serpentine and timing belt-drives. Int. J. Veh. Des. 2005, 39, 272. [Google Scholar] [CrossRef]
- Feng, X.; Shangguan, W.B.; Deng, J.; Jing, X.; Ahmed, W. Modelling of the rotational vibrations of the engine front-end accessory drive system: a generic method. Proc. Inst. Mech. Eng. D 2017, 231, 1780–1795. [Google Scholar] [CrossRef]
- Rodriguez, J.; Keribar, R.; Wang, J. A Comprehensive and Efficient Model of Belt-Drive Systems; SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2010. [Google Scholar]
- Cepon, G.; Boltezar, M. An Advanced Numerical Model for Dynamic Simulations of Automotive Belt-Drives; SAE Technical Paper Series; SAE International: Warrendale, PA, USA, 2010. [Google Scholar]
- Tai, H.M.; Sung, C.K. Effects of Belt Flexural Rigidity on the Transmission Error of a Carriage-driving System. J. Mech. Des. 2000, 122, 213. [Google Scholar] [CrossRef]
- Zhang, L.; Zu, J.W.; Hou, Z. Complex Modal Analysis of Non-Self-Adjoint Hybrid Serpentine Belt Drive Systems. J. Vib. Acoust. 2001, 123, 150. [Google Scholar] [CrossRef]
- Materials Testing Guide; ADMET: Norwood, MA, USA, 2013.
- Kumar, D.; Sarangi, S. Data on the viscoelastic behavior of neoprene rubber. Data Brief. 2018, 21, 943–947. [Google Scholar] [CrossRef] [PubMed]
- Mansouri, M.; Darijani, H. Constitutive modeling of isotropic hyperelastic materials in an exponential framework using a self-contained approach. Int. J. Solids Struct. 2014, 51, 4316–4326. [Google Scholar] [CrossRef]
- Shahzad, M.; Kamran, A.; Siddiqui, M.Z.; Farhan, M. Mechanical Characterization and FE Modelling of a Hyperelastic Material. Mater. Res. 2015, 18, 918–924. [Google Scholar] [CrossRef]
- Tokoro, H. Analysis of transverse vibration in engine timing belt. JSAE Rev. 1997, 18, 33–38. [Google Scholar] [CrossRef]
- Gerbert, G.; Jnsson, H.; Persson, U.; Stensson, G. Load Distribution in Timing Belts. J. Mech. Des. 1978, 100, 208. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).