Intent Understanding Using an Activation Spreading Architecture

Abstract

In this paper, we propose a new approach for recognizing intentions of humans by observing their activities with a color plus depth (RGB-D) camera. Activities and goals are modeled as a distributed network of inter-connected nodes in an Activation Spreading Network (ASN). Inspired by a formalism in hierarchical task networks, the structure of the network captures the hierarchical relationship between high-level goals and low-level activities that realize these goals. Our approach can detect intentions before they are realized and it can work in real-time. We also extend the formalism of ASNs to incorporate contextual information into intent recognition. We further augment the ASN formalism with special nodes and synaptic connections to model ordering constraints between actions, in order to represent and handle partial-order plans in our ASN. A fully functioning system is developed for experimental evaluation. We implemented a robotic system that uses our intent recognition to naturally interact with the user. Our ASN based intent recognizer is tested against three different scenarios involving everyday activities performed by a subject, and our results show that the proposed approach is able to detect low-level activities and recognize high-level intentions effectively in real-time. Further analysis shows that contextual and partial-order ASNs are able to discriminate between otherwise ambiguous goals.

1. Introduction

Intent understanding is the problem of recognizing people’s goals by passively observing them perform some activities and predicting their future actions [1]. This is a crucial capability of an artificial intelligent system which helps provide a proper level of social behaviors, when interacting with other intelligent agents, including humans. Intent recognition is very similar to the problem of plan/activity recognition, which has been extensively studied [1,2,3]. Plan recognition is the process of selecting the most suitable plan that an agent is undertaking, based on an observed sequence of atomic actions [4]. Intent recognition aims to predict a high-level activity or goal well before it is realized, in contrast with plan/activity recognition, which addresses the problem of recognizing activities after they are finished. Due to the prediction aspect, a natural requirement of intent recognition systems is to work in real-time. This is especially true for vision-based systems, which have to recognize intentions by analyzing a video stream of a person performing some activities in real-time. Such a capability would be very valuable in many application domains including surveillance, learning by observation and human-robot interaction (HRI).

A plan is normally defined as a set of low-level actions with a partial order constraint to represent ordering of actions [5]. Actions that precede another action should be performed prior to that action in order to satisfy their pre-conditions. Actions that have no ordering constraints with respect to each other can be performed in any arbitrary order. The observable evidence for a plan recognizer is one of many possible linearizations of the plan that satisfies the existing partial ordering constraints. Plan/activity recognizers are generally not designed to predict future activities and require observing the whole or a large part of a sequence of low-level actions to robustly recognize the plan. However, early detection is a key requirement for intent recognition systems and this is usually ignored in previous research on plan recognition. Any automatic system for intent recognition should process incoming sensory data and recognize the goal/intention in real-time to support early detection. The mainstream approach in plan recognition is based on searching in a plan library to find a match with the observed evidence [1]. A recent theoretical analysis on the complexity of this problem [6] shows that single-agent plan recognition with a library of known plans and an evaluation function is in class P and multi-agent plan recognition is NP-complete. This suggests that the running time requirement of single-agent plan recognizers is related to the size of the plan library; therefore any such system cannot perform in real-time if the plan library is large enough.

Intent understanding is also related to spatiotemporal pattern classification. Hidden Markov Models (HMMs) and their extensions are widely used for classification of activities in many applications, including vision-based systems, such as [7]. Evidence is usually encoded as observable random variables and activities are represented as the hidden states of a Markov process, which models the behavior of the observed agent. However, most vision-based previous work on activity recognition is centered on detecting a particular activity in a specific scenario. Simple activities, such as “moving an object” or “waving the hand”, which usually have a very short time-span, have been the focus of study in prior work [8]. Such activities are normally considered as atomic actions in the planning literature, since they are short and simple enough for the entire system to execute without breaking them down into even simpler actions. Understanding high-level activities and detecting intentions are, however, more challenging problems. Representing high-level activities as hidden states in an HMM is not trivial because they usually consist of several low-level actions and have a long time-span resulting in long and complex temporal patterns that are hard to recognize with Bayesian-based approaches like HMMs.

A vision-based intent recognition system is introduced in this paper, to address the problems mentioned above. We assume that domain knowledge about how certain activities are performed is available as an HTN. The central idea of the proposed approach is to model intentions, high-level activities and low-level actions in a distributed network of inter-connected nodes where activation spreads in the network via synaptic connections. A low-level activity is a basic action with a short time span, such as grabbing an object. A high-level activity/intention, such as making tea, is a more complex activity with longer time span and is usually a composite of low-level actions. We show that Activation Spreading Networks (ASN) are suitable for intent recognition, because their graph-based representation can naturally model the hierarchical relationship between high-level, low-level activities and goals/intentions. Inference in ASNs is done with spreading activation through the network, which is inherently a distributed task. This feature makes ASNs particularly suitable for real-time intent recognition. Intuitively, nodes represent activities and different edges represent different relationships between activities such as decomposition of high-level intentions into low-level actions and partial order constraints between actions. These edges are designed to spread activation messages from low-level actions to high-level intentions. Activation values show the likelihood of each intention. Our approach brings together several key contributions: (I) early detection of intentions/high-level activities before they are realized; (II) processing of RGB-D video streams in real-time to detect and track objects, as well as the subject and its skeleton joint positions in 3D, which are used as basic features in our recognition network; (III) introducing an ASN-based approach to model hierarchical activities similar to the formalism used in Hierarchical Task Networks (HTNs); (IV) extending the formalism of ASNs to incorporate contextual information into intent recognition; (V) further augmenting the ASN formalism with special nodes and synaptic connections to model ordering constraints between actions, in order to represent and handle partial-order plans in our ASN. The effect of using contextual information and ordering constraints to distinguish between similar intentions has been experimentally tested and the results show that incorporating contextual and ordering information in the network significantly helps in identifying the correct intentions. We incorporated 16 nodes representing high-level intentions and 80 nodes representing different instances of low-level actions in our ASN to show that our approach is scalable in the number of nodes in the ASN and the number of intentions it can detect.

The rest of this paper is organized as follows: the next section presents an overview of previous work in intent recognition. Section 3 introduces our video parser that is responsible for extracting vision-based features, and Section 4 describes our ASN-based intent recognition approach. Section 5 presents our experimental evaluation results. Finally, Section 6 provides the conclusion and a discussion on possible future work.

2. Previous Work

In this section, we briefly present prior work related to intent recognition by considering symbolic approaches and probabilistic frameworks, and we discuss how our ASN-based approach handles the limitations of these previous methods.

2.1. Symbolic Approaches

Symbolic approaches to goal or behavior recognition are based on abductive reasoning, which –unlike deduction—cannot guarantee a conclusion. Abduction is the process of generating a hypothesis that best explains the observed evidence [9]. This problem has been well studied in multi-agent domains and in applications such as cooperative systems, opponent modeling and agent programming paradigms. In [10], a general framework for plan recognition in the Belief/Desire/Intention (BDI) [11] paradigm is introduced. The authors use a general logical abstraction of plans and Answer Set Programming (ASP) [12] techniques to formalize a non-monotonic reasoning scheme for abduction. In a similar work [13], the same authors formalized incomplete observations to expand the mental state abduction framework in the presence of incomplete or missing information. Another similar work [14] uses situation-sensitive Causal Bayesian Networks (CBNs) for intent recognition in the care of the elderly. Graphical representations of CBNs are translated into a special form of declarative language. Abduction and probabilistic reasoning are combined by using ASP on logical terms obtained from CBNs and probabilistic analysis on CBNs. In a recent work [15], authors use predicate logic to encode a knowledge base containing a set of decomposition rules describing domain knowledge with Hierarchical Task Networks (HTN). A bottom-up abductive reasoning scheme tries to match the observed sequence of actions with corresponding tasks and methods, resulting in recognition of a plan that best describes the evidence. A theoretical study in ASP [16] shows that finding a stable model for a logic program is NP-complete. This suggests such logic programming-based and abductive methods are not a good candidate for real-time analysis. In addition, the significant challenge of relating predicates to sensory data makes such symbolic systems of limited use in real-world applications, as they remain mostly theoretical and not appropriate for the robotics and particularly computer vision domains.

2.2. Probabilistic Approaches

A large body of work uses HMMs to perform temporal inference for action recognition. For example, in [17] Hidden Markov Models are used to represent and recognize strategic behaviors of robotic agents in a game of soccer. After training HMMs corresponding to different actions, it is possible to determine the likelihood that a given sequence of observations was produced from a model. In the scope of that work, intent recognition is only performed in the context of a very controlled environment, where there are few agents and a very limited number of possible actions. [18,19] also utilize the HMM-based framework presented in [17]. In these approaches, however, intent recognition is performed in far less structured environments. The authors show that this method can work for recognizing the intentions of a human agent towards objects in a scene, or of two human agents towards each other or towards other objects, using only observable variables from basic sensor information. More complex models, such as parameterized-HMM [20], entropic-HMM [21], variable-length HMM [22], coupled-HMM [23], and hierarchical-HMM [24] have been used to recognize more complex activities. In [25], the authors use stochastic context-free grammars to compute the probability of a temporally consistent sequence of primitive actions recognized by HMMs. Brand and Kettnaker [21] introduce an entropic-HMM approach to organize the observed video activities (such as office activity and outdoor traffic) into meaningful states. In [26], a Bayesian network is used to model intentions, with the highest level node representing the overall intention and the lower level nodes representing sub-actions that contribute to that intention. In [27], authors use a Bayesian network and propose a two-stage inference process to predict the next activity features and its label in the context of a smart room.

There are many other recent efforts using more complex Bayesian net approaches for recognizing human activities [28,29,30,31,32]. In [33], a probabilistic framework for activity recognition from partially observed videos is introduced. Sparse coding is used to estimate posterior probabilities with bag of visual words representation. In another similar approach [34], object affordances and trajectories are used in a temporal conditional random field. Activity recognition is done with a probabilistic inference in a set of particles framework in which each particle is a conditional random field. Bayesian nets and specifically HMMs are shown to be working very well for recognizing activities that are simple and short. However, they tend to suffer from overfitting training data if they are used to recognize complex and long activities. There has been little research on real-time probabilistic and specifically Bayesian-based intent recognition systems in a hierarchical manner. Probabilistic approaches usually have difficulties recognizing complex, long spatiotemporal patterns. It is not straightforward to model hierarchical relationships between low-level actions and high-level intentions in such systems. Additionally, it is not easy to incorporate domain knowledge into such frameworks and they rely on extensive datasets for training. Our proposed ASN-based intent recognition approach addresses these shortcomings by explicitly modeling different relationships between actions and intentions in the network. The structure of the network is determined by conversion algorithms that create ASNs from domain knowledge given as HTNs.

3. Vision-Based Capabilities

In order to detect human intentions, we process a video stream from a scene where a person is performing various activities, including both short and long time span actions in accordance to high-level intentions. This data stream is fed into a video parser to extract useful features for intent recognition. The scene is observed with a Microsoft Kinect camera, which provides both depth and RGB frames for the scene. In addition, we use the Microsoft Kinect skeleton-tracking package available in the Microsoft Kinect SDK for Windows [35]. The camera position and orientation does not change during recording. Table 1 shows the properties of the different Kinect streams used in our experiments.

Table 1. Kinect camera stream properties.

Stream	Properties
RGB Frame	640 × 480 pixels, 30 fps
Depth Frame	640 × 480 pixels. Format = 13 bit depth in mm + 3 bit player index. Min 8 cm max 4 m
Skeleton	20 joints. Format = (x, y, z) metric 3D joint position in the camera coordinate system

Table 1. Kinect camera stream properties.

Stream	Properties
RGB Frame	640 × 480 pixels, 30 fps
Depth Frame	640 × 480 pixels. Format = 13 bit depth in mm + 3 bit player index. Min 8 cm max 4 m
Skeleton	20 joints. Format = (x, y, z) metric 3D joint position in the camera coordinate system

The basic features that we use for intent recognition are the human pose and object locations in the 3D metric camera coordinate system. Obviously, detecting more features (such as object pose) can help the recognition system, but estimating these more complex features requires more processing time and they are not usually as robust as the simpler ones. Human joint locations are obtained in real-time with the skeleton-tracking package from Microsoft. In order to robustly estimate object locations we developed a processing pipeline that works on RGB and depth frames in real-time and estimates object locations in 3D. Figure 1 shows the overall architecture of the video parser. We describe the individual stages of the pipeline in the following subsections.

Figure 1. Video parser architecture.

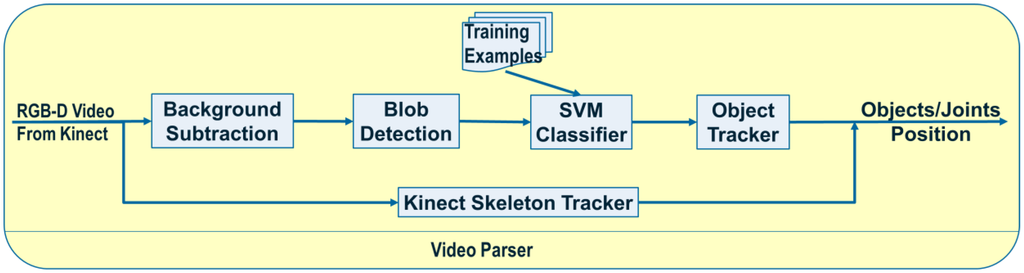
Figure 1. Video parser architecture.

3.1. Background Subtraction

As the first step in our video parser, background subtraction helps reduce the computation time significantly in later stages. By taking advantage of the fixed camera assumption in our scenarios, we probabilistically model the background and use foreground regions for object detection. Figure 2 shows the steps for background subtraction in our system. We use both RGB and depth frames to build a robust background subtraction module with no sensitivity to aperture changes in the RGB camera. We use the Codebook background modeling [36] on RGB frames and a Mixture of Gaussians (MoG) background modeling [37] on depth frames to independently build two background models in RGB and depth space, and consequently determine two foreground masks. An aggregated mask is obtained by applying a bitwise and operation between the two separate foreground masks. Finally, to remove small pixel-level noise in the foreground mask, we use a contour-based segmentation algorithm to refine foreground regions by filling out small holes and removing isolated pixels. We used the OpenCV library in most parts of our video parser.

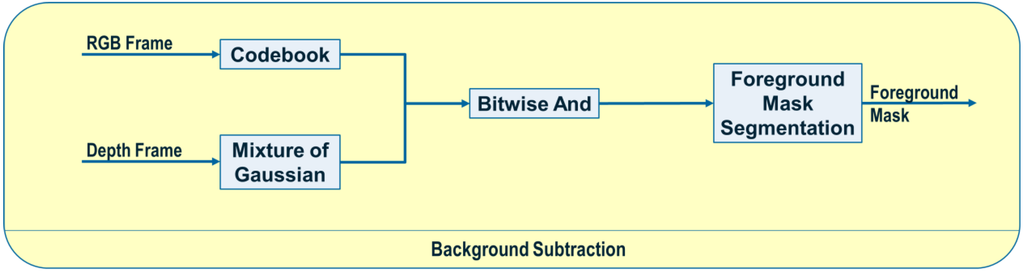
Figure 2. Background subtraction module.

Figure 2. Background subtraction module.

3.2. Blob Detection

The output of the background subtraction stage is a binary foreground mask. In blob detection, we detect individual candidate blobs in the foreground mask that contain foreground objects, by finding connected components in the mask. The connectivity is simply defined by neighboring pixels with the same binary value in the foreground mask. It is important that blobs contain only a single foreground object before initializing the object tracker, since we are using a holistic object descriptor for detection. We assume that the foreground objects do no overlap in the RGB image when they initially appear in the scene. This is no longer required after initializing the object tracker. An additional issue is caused by the foreground regions corresponding to people in the scene, rather than objects. We use the human body segmentation information provided by Microsoft Kinect (on the depth image) to discard foreground regions that overlap with the segmented body, in order to avoid considering them as candidate blobs for object detection.

3.3. Object Detection

We use the detected blobs in the foreground as inputs to a multi-class Support Vector Machine (SVM) [38] classifier, which was trained using images for objects of interest in our scenarios. Since real-time processing is a crucial feature of video-based intent recognition, we decided to use normalized color histograms as features for classification, which are significantly faster to compute compared to more sophisticated features, such as Scale-Invariant Feature Transform (SIFT) [39]. Since color histograms are holistic properties, a segmentation of objects in the RGB space is required, and the blob detection module discussed in Section 3.2 provides the segmentation we need. We used 8 bins for hue and 8 different quantized values for saturation in each bin. The distance measurement used for the classification of color histograms is the Bhattacharyya distance [40]; if the minimum distance of a blob’s color histogram from any of the training color histograms is above a threshold, then no class will be assigned to that blob, showing no known object is present in that region.

3.4. Object Tracking

After detecting an object in one of the blobs for several consecutive frames, we start tracking the object in the scene and remove the corresponding class from the classifier in the object detector to reduce the computational requirements of the system, since running the object detector on every blob in every frame is a time-consuming process. To track objects we use the Continuously Adaptive Meanshift (Camshift) [41] algorithm. For simplicity, we assume that no objects would leave the scene once they are detected. This makes tracking easier, avoiding the need to stop or re-initialize the tracker when objects leave the field of view and then re-enter. The output of the object tracker is a region in the RGB frame corresponding to each detected object. We use the centroid of that region and the depth information from the depth image to estimate the location of the objects in the 3D camera coordinate system.

4. Intent Recognition with Activation Spreading Networks

In this section we formally define our ASN-based approach to intent recognition from RGB-D videos. Activation Spreading Networks provide a parallel, distributed and fast search mechanism for intent recognition. Through spreading activation messages to other nodes in the network and accumulating activation by receiving messages from neighbor nodes, we can robustly detect the intention of a subject of interest and the corresponding plan that the subject is following to realize that intention. We can predict a set of future activities of the subject based on the detected plan. These capabilities depend on designing an activation-spreading network that captures the real structure of activities, plans and intentions related to the system. This is the domain knowledge, which (in different forms) is incorporated in every planning system. One of the most widely used forms of representing planning knowledge is Hierarchical Task Networks (HTN) [42]. The main idea behind HTNs is to store mini-plans to achieve common goals in a database of reusable methods, and to use them while planning—for fast processing. Theoretical studies [43] show that HTNs in their unrestricted form are actually more complex than Partial Order Planning (POP) [5]. Only after enforcing some limitations on the expressivity of HTNs, this form of planning becomes tractable. In the following subsections we formally define ASN and HTN, provide an algorithm to build an ASN from an HTN, and describe an inference algorithm based on ASN for intent recognition.

4.1. Preliminaries

We adapt the definition of HTNs from SHOP² [44], which is a well-known HTN planner.

Operator: an operator $R\left(v_1,\dots v_n\right)=\left(name\left(R\right),pre\left(R\right),add\left(R\right),del\left(R\right)\right)$ is a parameterized strips-like atomic action where $v_1,\dots ,v_n$ are variables used in precondition, add and delete lists. Each variable $v_i$ has a set of all possible substitutions or domain $D\left(v_i\right)$.

Task: A task $T\left(x_1,\dots ,x_m\right)$ is either a primitive or a compound task where $T$ is task symbol along with a list of terms $x_1,\dots ,x_m$ as arguments. If task $T\left(x_1,\dots ,x_m\right)$ is primitive then $T$ is an operator name and the task arguments are used as the operator parameters.

Method: A method $M=\left(name\left(M\right), task\left(M\right), pre\left(M\right), subtasks\left(M\right)\right)$ is a possible expansion of the non-primitive task $task\left(M\right)$ and it is only applicable in situations satisfying the precondition $pre\left(M\right)$. Intuitively, a method represents a particular way of achieving a given task.

Task Network: a task network $N$ is a tuple of the form $(U,<)$ where $U$ is a set of tasks and $<$ is a partial order constraint on $U$. If $U$ contains only primitive tasks, it is called a primitive task network otherwise it is called non-primitive task network.

Hierarchical Task Network: a hierarchical task network is a set of operators, methods, task networks and tasks. Intuitively, a hierarchical task network is a representation of the planning domain knowledge.

The ultimate goal in HTN planning is to complete a task. Usually the goal task is compound and the planner should choose a suitable method from the set of available methods to break down the goal task into smaller tasks. This recursive procedure continues until all tasks in the network are primitive. HTN planners are equivalent to context-free grammars in their set of possible solutions [43], but to simplify our intent recognition problem, we restrict the HTN formalism to avoid recursion in the methods. Put differently, we assume that no compound task can be a member of the subtasks of itself. The intention of completing a compound task is the focus of our intent recognition system. From now on, when we mention “detecting a task”, we implicitly mean detecting the intention to complete a task before its completion. Next, we formally define an activation-spreading network.

Activation Spreading Network: An activation spreading network $G=\left(V,E_S,E_M, cl, F, d\right)$ is a directed acyclic graph.

• $V$ is the set of nodes. Each node $v\in V$ has an activation value $ac\left(v\right)$ that is a positive real number.
• $E_S$ is the set of sum edges connecting nodes in the graph. Each sum edge $e\in E_S$ has a weight $w\left(e\right)\le 1$. A sum edge is an edge through which activation messages spread in the network and the receiving node processes it by updating its activation value with a summation.
• $E_M$ is the set of max edges connecting nodes in the graph. A max edge is another type of edge through which activation messages spread in the network and the receiving node processes it by updating its activation value with a maximum value selection.
• $cl$ is the internal clock sending periodic signals to all nodes in the graph.
• $F$ is a firing threshold.
• $d$ is a decay factor that is a real number between 0 and 1.

A node updates its activation value by multiplying it with the decay factor $d$ on every clock tick. Upon receiving an activation message, a node updates its activation value by summing the activation message multiplied by the edge weight, with its own activation value if the message was received via a sum edge. A node updates its activation value by choosing the maximum activation message on all ingoing max edges. Upon receiving a tick from the clock, a node sends activation messages equal to its activation value on outgoing edges, if its activation value is above $F$. Algorithm 1 shows the algorithm of processing activation messages in the ASN. This procedure is called for a node upon receiving an activation message. Algorithm 2 shows the algorithm of activation spreading in the network. This procedure is called for a node upon receiving a periodic signal from the clock.

Algorithm 1 Activation message processing algorithm in ASN

let v∈V be the node receiving activation message from s

let S_max={n|(n,v)∈E_M and n sent message to v in recent clock signal}

if S_max≠∅

ac(v)=max┬(v'∈S_max ) ac(v^' )

else

ac(v)=ac(v)+ac(s)×w((s,v))

Algorithm 1 Activation message processing algorithm in ASN

let v∈V be the node receiving activation message from s

let S_max={n|(n,v)∈E_M and n sent message to v in recent clock signal}

if S_max≠∅

ac(v)=max┬(v'∈S_max ) ac(v^' )

else

ac(v)=ac(v)+ac(s)×w((s,v))

Algorithm 2 Activation spreading algorithm in ASN.

let $v\in V$ be the node receiving periodic signal from$cl$

let $ac\left(v\right)=ac\left(v\right)\times d$

if $ac\left(v\right)>F$

send activation messages to all nodes $v\text{'}$ in which $\left(v,v^{\prime }\right)\in E_S{{\displaystyle \cup }}^{\text{}}{E}_M$

Algorithm 2 Activation spreading algorithm in ASN.

let $v\in V$ be the node receiving periodic signal from$cl$

let $ac\left(v\right)=ac\left(v\right)\times d$

if $ac\left(v\right)>F$

send activation messages to all nodes $v\text{'}$ in which $\left(v,v^{\prime }\right)\in E_S{{\displaystyle \cup }}^{\text{}}{E}_M$

4.2. From Hierarchical Task Network to Activation Spreading Network

We define an activation-spreading network as an acyclic graph to simplify the design by avoiding recurrent ASNs. This is in line with our simplifying assumption about not having recursions in the HTN formalism that we adapted for our work. Each task in HTN can be seen as a potential intention. Tasks in an HTN form a hierarchy according to the definition of methods. Intuitively, this means that intentions can be sub-goals for a higher-level intention. Different methods of the same task describe different ways of achieving the goal. We now describe how to instantiate an ASN from the domain knowledge represented as an HTN. Algorithm 3 shows the conversion algorithm.

Algorithm 3 HTN to ASN conversion algorithm

for every operator $R\left(v_1,\dots v_n\right)$ in HTN

for every substitution $\left(va{l}_1,\dots va{l}_n\right)$ in the domain of $D\left(v_1\right)\times \dots D\left(v_n\right)$

add node $R\left(va{l}_1,\dots va{l}_n\right)$ to the ASN

for every compound task $T\left(x_1,\dots ,x_m\right)$ in HTN

for every substitution $\left(va{l}_1,\dots va{l}_m\right)$ of $\left(x_1,\dots ,x_m\right)$

add node $T\left(va{l}_1,\dots va{l}_m\right)$ to the ASN if not already present

for every method $M\in methods\left(T\right)$ and $\left(va{l}_1,\dots va{l}_m\right)⊢pre\left(M\right)$

add node $T^M\left(va{l}_1,\dots va{l}_m\right)$ to the ASN

add a max edge from $T^M\left(va{l}_1,\dots va{l}_m\right)$ to $T\left(va{l}_1,\dots va{l}_m\right)$

for every task $T\prime \left(x{\prime }_1,\dots ,x{\prime }_{m\prime }\right)$ in $subtasks\left(M\right)$

let $\left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ be a substitution for $\left(x{\prime }_1,\dots ,x{\prime }_{m\prime }\right)$

agreement with $\left(va{l}_1,\dots va{l}_m\right)$

if $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ is compound then

add $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ if not already present

add a sum edge from $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ to $T^M\left(va{l}_1,\dots va{l}_m\right)$ with

$\frac{1}{\left|subtasks\left(M\right)\right|}$ as weight

else if $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ is primitive then

let $R$ be the operator corresponding to $T\prime$

add a sum edge from $R\left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ to $T^M\left(va{l}_1,\dots va{l}_m\right)$ with

$\frac{1}{\left|subtasks\left(M\right)\right|}$ as weight

Algorithm 3 HTN to ASN conversion algorithm

for every operator $R\left(v_1,\dots v_n\right)$ in HTN

for every substitution $\left(va{l}_1,\dots va{l}_n\right)$ in the domain of $D\left(v_1\right)\times \dots D\left(v_n\right)$

add node $R\left(va{l}_1,\dots va{l}_n\right)$ to the ASN

for every compound task $T\left(x_1,\dots ,x_m\right)$ in HTN

for every substitution $\left(va{l}_1,\dots va{l}_m\right)$ of $\left(x_1,\dots ,x_m\right)$

add node $T\left(va{l}_1,\dots va{l}_m\right)$ to the ASN if not already present

for every method $M\in methods\left(T\right)$ and $\left(va{l}_1,\dots va{l}_m\right)⊢pre\left(M\right)$

add node $T^M\left(va{l}_1,\dots va{l}_m\right)$ to the ASN

add a max edge from $T^M\left(va{l}_1,\dots va{l}_m\right)$ to $T\left(va{l}_1,\dots va{l}_m\right)$

for every task $T\prime \left(x{\prime }_1,\dots ,x{\prime }_{m\prime }\right)$ in $subtasks\left(M\right)$

let $\left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ be a substitution for $\left(x{\prime }_1,\dots ,x{\prime }_{m\prime }\right)$

agreement with $\left(va{l}_1,\dots va{l}_m\right)$

if $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ is compound then

add $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ if not already present

add a sum edge from $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ to $T^M\left(va{l}_1,\dots va{l}_m\right)$ with

$\frac{1}{\left|subtasks\left(M\right)\right|}$ as weight

else if $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ is primitive then

let $R$ be the operator corresponding to $T\prime$

add a sum edge from $R\left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ to $T^M\left(va{l}_1,\dots va{l}_m\right)$ with

$\frac{1}{\left|subtasks\left(M\right)\right|}$ as weight

The conversion algorithm first adds all possible instantiations of operators in the HTN as nodes $R\left(va{l}_1,\dots va{l}_n\right)$ in the ASN. These nodes will be the leaves of the hierarchical structure of the obtained ASN. With a similar procedure, we also add new nodes $T\left(va{l}_1,\dots va{l}_m\right)$ to the network for each unique instantiation of compound tasks. Each instance of a compound task can be realized in different ways represented by a set of methods. To capture this property of HTNs in our network, we add additional nodes such as $T^M\left(va{l}_1,\dots va{l}_m\right)$ for each method $M$ and connect these nodes to the parent node $T\left(va{l}_1,\dots va{l}_m\right)$ with max edges. With this configuration, the activation value of node $T\left(va{l}_1,\dots va{l}_m\right)$ would be the maximum activation value among all of its methods. Activation values of nodes in the ASN provide a comparative measure for the likelihood of their corresponding tasks happening in the scene and are used for inference. Sum edges are not a suitable choice for connecting method nodes to task nodes because several methods with low activations should not accumulate a high activation in the task node, since the likelihood of a high-level task happening in the scene is only as high as the maximum likelihood of its methods.

Any method $M$ in our HTN, breaks down a high-level task into lower-level tasks (either compound or primitive). This is captured in our ASN by connecting nodes of lower-level tasks to their parent node corresponding to the method, which in turn is connected to the high-level task. A method should have a higher likelihood if a larger number of its subtasks have higher activation values. For instance, a method with only a single subtask node with activation value greater than zero is less probable than another method with two or more subtasks with the same activation values. This is why we chose to use sum edges to connect subtasks to their parent method. The edge weights are $\frac{1}{\left|subtasks\left(M\right)\right|}$. This is a normalization factor and it makes the activation values in method nodes comparable to each other, regardless of their subtask size. A sample ASN created with this conversion algorithm is shown in Figure 3. It is important to note that the algorithm in Algorithm 3 does not use the partial order relation. At this stage, we simply ignore the ordering constraints between tasks and cannot distinguish between methods (perhaps not even for the same high-level task) that have exactly the same subtasks but in different orders. We will extend our ASN approach to handle partial order constraints in Section 4.5.

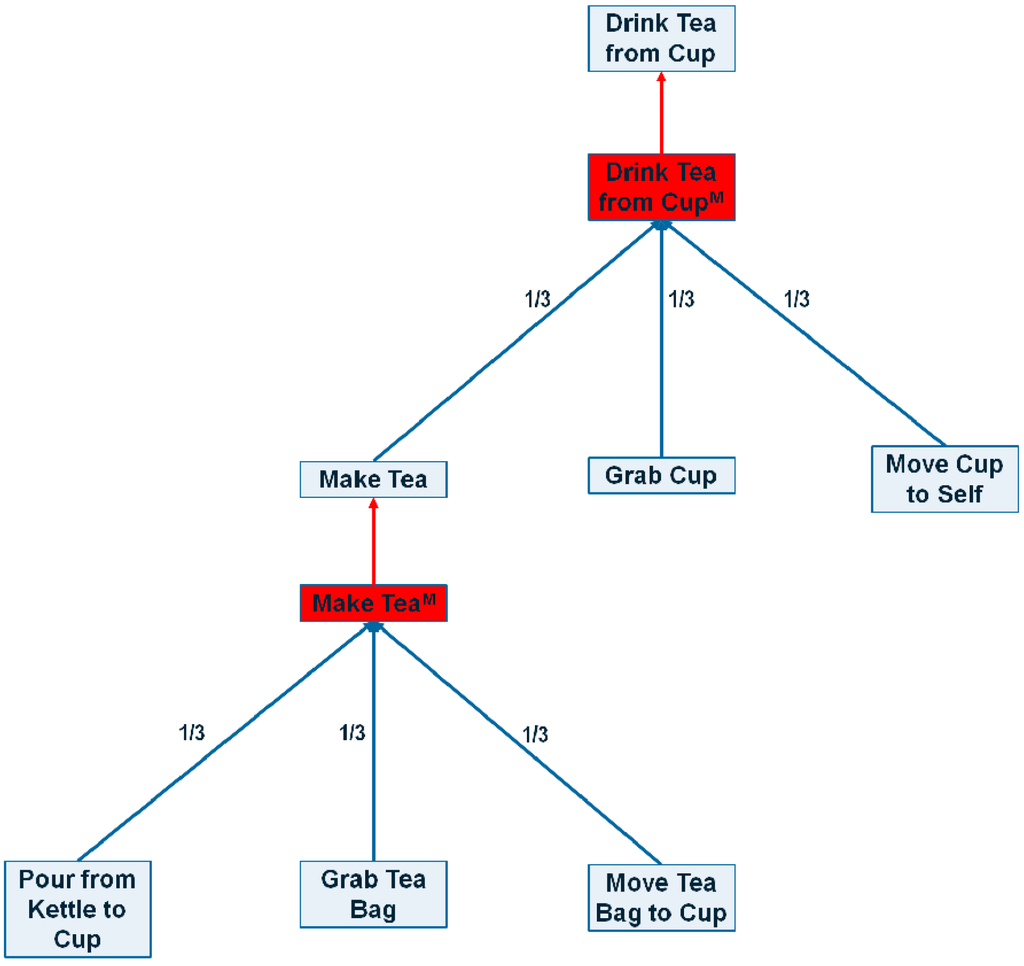
Figure 3. A sample portion of the ASN generated from an HTN. Red edges are max edges, blue edges represent sum edges and red boxes represents method nodes.

Figure 3. A sample portion of the ASN generated from an HTN. Red edges are max edges, blue edges represent sum edges and red boxes represents method nodes.

4.3. Intent Recognition in Activation Spreading Networks

As explained in Section 4.2, the activation values are a comparative measure for selecting the most probable intention based on the observed evidence. The hierarchical structure of tasks in HTN suggests that at any given time, a subject is actively pursuing a set of intentions that are in agreement with each other but are at different levels in the hierarchy. Lower-level tasks that normally correspond to short time span activities that are a part of a larger and longer activity. This hierarchical structure is preserved in the process of converting HTN to ASN in its connected nodes. We use this hierarchical structure and the activation values of the nodes in the network to robustly detect the intention of completing a set of tasks but at different levels in the hierarchy. More precisely, we start the search from the highest-level nodes corresponding to the highest level intentions and choose the one with the largest activation value above a threshold. If none of the nodes have activation values greater than the threshold, then the system detects the idle state for the subject. We then continue our search by only considering the children of that node. The highest activation value is chosen at each stage iteratively until we reach the lowest level, containing only operators. To disregard very low activation values, any node with activation below a threshold cannot be chosen even if it has the highest activation. The intent recognition algorithm is presented in Algorithm 4.

It is important to note that activation values of nodes are only comparable if they are on the same level. Nodes in higher levels usually have smaller activation values, since they only receive activation values from lower-level nodes and edges have weights less than one, which reduces the activation values. This is why we only compare nodes at the same level in each stage of the recognition process. It is also possible that the node with the highest activation value in a lower level conflicts with the node with the highest activation in a higher level. The lower level node might belong to a task that does not contribute to the higher-level task with the largest activation value. To have a coherent recognition of intentions on different levels, at each stage of the process we limit our search space to nodes that are the children of the selected higher-level task.

Algorithm 4 Intent recognition algorithm in ASN

let $s=\left\{v|v is a node in ASN and has no outgoing arrow\right\}$

repeat until $s=\varnothing$

let $v_{max}=\underset{v\in s}{\text{argmax}}ac\left(v\right)$

add $v_{max}$ to the set of recognized intentions if $ac\left(v\right)>F$

$s=\left\{v|v is a node in ASN and has outgoing arrow to v_{max}\right\}$

Algorithm 4 Intent recognition algorithm in ASN

let $s=\left\{v|v is a node in ASN and has no outgoing arrow\right\}$

repeat until $s=\varnothing$

let $v_{max}=\underset{v\in s}{\text{argmax}}ac\left(v\right)$

add $v_{max}$ to the set of recognized intentions if $ac\left(v\right)>F$

$s=\left\{v|v is a node in ASN and has outgoing arrow to v_{max}\right\}$

Since the network is acyclic, an external stimulus (i.e., observation of a low-level activity) starts the activation spreading process in the network. Low-level activities correspond to operator nodes in the network. These nodes are leaves in the network, and they can propagate activation values up in the hierarchy, but no other nodes can send activation messages to them. We use simple formulas to compute the activation values for the operator nodes, based on the features extracted by the video parser. This part of the system will be defined in Section 5.2.

4.4. Context-Based Intent Recognition

The precondition properties of operators and methods in HTN allow us to choose suitable methods to reduce a task network to a fully formed plan. These preconditions describe a context or situation in which that operator or method is suitable for achieving a goal. Planning approaches usually need to know about preconditions to successfully develop a plan suitable for the current circumstances by choosing suitable methods and operators. Similarly for intent recognition, we also face the problem of choosing the hypothesis that best describes the observed evidence. This suggests that having some information about the actual context of the observed scene can help in intent recognition, by analyzing what method or task is more probable for the subject to undertake, given the known circumstances. Unlike preconditions in planning, which model the required conditions, contextual information for intent recognition in our framework works as a favoring mechanism that makes some tasks more probable, and others less probable.

In order to incorporate contextual information in our intent recognition system, we modify the definition of ASN to include another type of nodes to represent contextual information and two special types of edge to connect contextual information to the relevant task nodes in the network. The formal definition of a contextual ASN (CASN) is as follows:

Contextual Activation Spreading Network: A CASN is an ASN with an additional set of:

• Context nodes $V_C$ representing different contextual information. A context node $v_c\in V_C$ has an activation value $ac\left(v_c\right)$ representing the level of certainty for that context.
• Positive context edges $E_{C+}$ connecting nodes in $V_C$ to nodes in $V$.
• Negative context edges $E_{C-}$ connecting nodes in $V_C$ to nodes in $V$.

Nodes in $V_C$ represent contextual information and their activation values represent the level of certainty about that information. It is important to note that the activation values do not represent probabilities and should not be interpreted as such. Nodes in $V_C$ do not have any ingoing edges of any type and cannot send activation messages to any other nodes. Nodes in $V_C$ cannot have activation values greater than 1. Nodes in $V_C$ do not decay by clock ticks. Upon receiving activation messages, the receiving node $v$ would update its activation value by first applying the procedure in Algorithm 1 and then multiplying the activation value by $\left({\displaystyle \sum }_{(v_c,v)\in E_{C+}}\frac{\left(1+ac\left(v_c\right)\right)}{\left|\left\{(v_c,v)\in E_{C+}\right\}\right|}-{\displaystyle \sum }_{(v_c,v)\in E_{C-}}\frac{\left(1-ac\left(v_c\right)\right)}{\left|\right\{(v_c,v)\in E_{C-}\left\}\right|}\right)$. Algorithm 5 shows the algorithm for processing activation messages in the CASN.

Edges in $E_{C+}$ and $E_{C-}$ show the positive and negative effect of contextual information on the tasks. Having additional contextual information about the subject or the environment being observed by the system should not increase or decrease the activation value of any tasks, unless we are observing some activities in the scene. In other words, we should not detect any intentions when no activity is being observed, even if all contextual information is in favor of a particular activity. That is why we chose the above formula to update activation values. If no contextual information is available, then the activation values of nodes in $V_C$ are zero and the multiplication factor is one. If contextual information in favor of a task is stronger than contextual information against a task, then the multiplication factor would be greater than 1, and it will be less than 1 otherwise. A sample of CASN is shown in Figure 4.

Algorithm 5 Activation message processing algorithm in CASN

let $v$ be the node receiving activation message from $s$

let $S_{max}=\left\{n|\left(n,v\right)\in E_M and n sent message to v in recent clock signal\right\}$

if $S_{max}\ne \varnothing$

$ac\left(v\right)=\underset{v\prime \in S_{\max }}{\max }ac\left(v^{\prime }\right)$

else

$ac\left(v\right)=ac\left(v\right)+ac\left(s\right)\times w\left(\left(s,v\right)\right)$

$c\left(v\right)=ac\left(v\right)\times \left({\displaystyle \sum }_{(v_c,v)\in E_{C+}}\frac{\left(1+ac\left(v_c\right)\right)}{\left|\left\{(v_c,v)\in E_{C+}\right\}\right|}-{\displaystyle \sum }_{(v_c,v)\in E_{C-}}\frac{\left(1-ac\left(v_c\right)\right)}{\left|\right\{(v_c,v)\in E_{C-}\left\}\right|}\right)$

The text in blue represents modifications to the original procedure for ASN presented in Algorithm 1.

Algorithm 5 Activation message processing algorithm in CASN

let $v$ be the node receiving activation message from $s$

let $S_{max}=\left\{n|\left(n,v\right)\in E_M and n sent message to v in recent clock signal\right\}$

if $S_{max}\ne \varnothing$

$ac\left(v\right)=\underset{v\prime \in S_{\max }}{\max }ac\left(v^{\prime }\right)$

else

$ac\left(v\right)=ac\left(v\right)+ac\left(s\right)\times w\left(\left(s,v\right)\right)$

$c\left(v\right)=ac\left(v\right)\times \left({\displaystyle \sum }_{(v_c,v)\in E_{C+}}\frac{\left(1+ac\left(v_c\right)\right)}{\left|\left\{(v_c,v)\in E_{C+}\right\}\right|}-{\displaystyle \sum }_{(v_c,v)\in E_{C-}}\frac{\left(1-ac\left(v_c\right)\right)}{\left|\right\{(v_c,v)\in E_{C-}\left\}\right|}\right)$

The text in blue represents modifications to the original procedure for ASN presented in Algorithm 1.

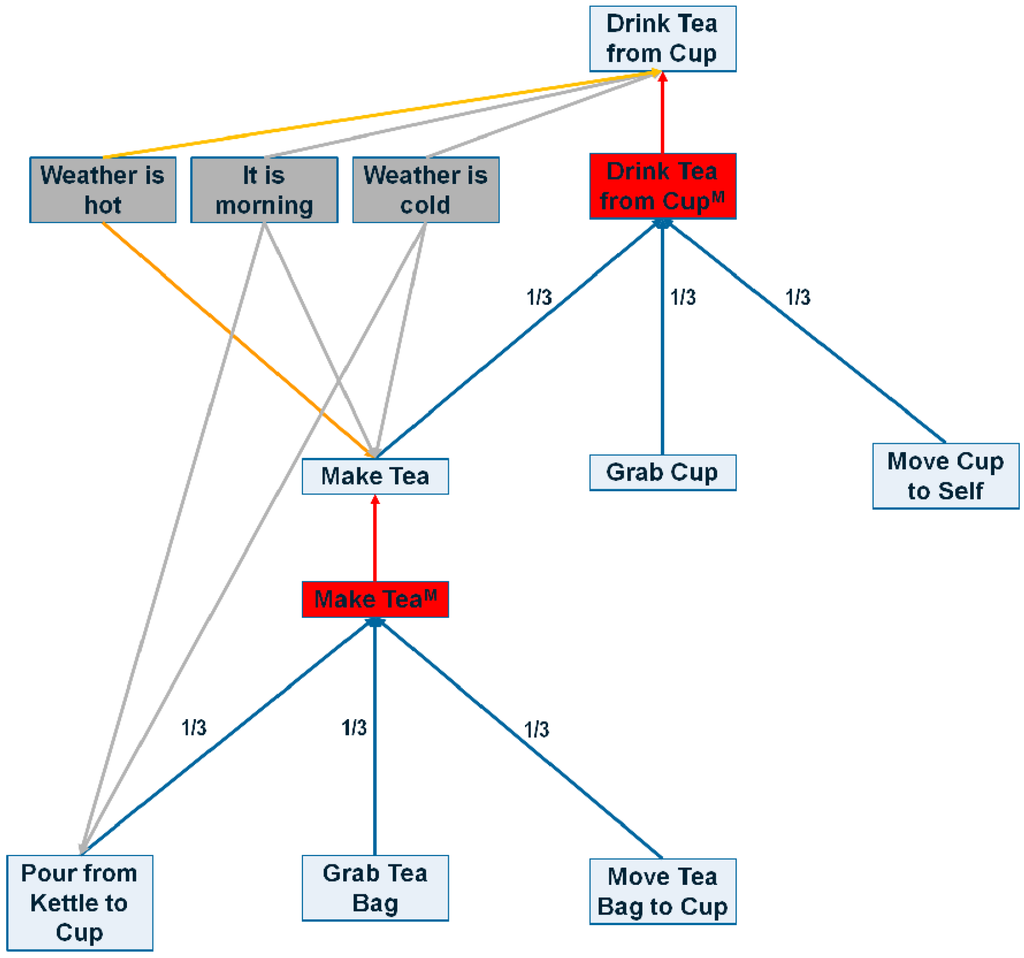
Figure 4. A sample portion of the CASN. Red edges are max edges, blue edges represent sum edges, grey lines show positive context edges and orange represents negative context edges. Red boxes represents method nodes and grey boxes show context nodes.

Figure 4. A sample portion of the CASN. Red edges are max edges, blue edges represent sum edges, grey lines show positive context edges and orange represents negative context edges. Red boxes represents method nodes and grey boxes show context nodes.

4.5. Partial-Order Modeling in Activation Spreading Networks

As previously discussed in Section 4.2, the ASN and CASN cannot model partial-order constraints in the hierarchical task network formalism, and the intent recognition procedure in ASN and CASN cannot distinguish between methods of two different tasks that are only different in their partial-order constraints. We now propose an extension to ASN in order to model partial-order constraints by allowing edges to receive activation messages and defining a special type of edge (ordering edges) to connect nodes to other edges in the network.

Partial-Order Contextual Activation Spreading Network: A Partial-Order Contextual Activation Spreading Network (POCASN) is a CASN with an additional set of:

• Ordering edges $E_{PO}$, connecting nodes in $V$ to edges in $E_S$. Every sum edge $e\in E_S$ has an activation value $ac\left(e\right)$ in addition to its weight $w\left(e\right)$ and can receive activation messages from ordering edges in $E_{PO}$.
• Min edges $E_m$, connecting nodes in $V$ to each other. A min edge is another type of edge in which activation messages spreads in the network and the receiving node processes it by updating its activation value with a minimum value selection.

Upon receiving an activation message from node $n$, a sum edge $e\in E_S$ updates its activation value with $ac\left(e\right)=\max \left\{ac\left(e\right)+ac\left(n\right), 1-w\left(e\right)\right\}$. With every clock tick, activation values of all sum edges like $e\in E_S$ decays according to: $ac\left(e\right)=ac\left(e\right)\times d.$. Upon receiving an activation message, a node updates its activation value by summing the activation message multiplied by the edge weight plus the edge activation value, with its own activation value if the message was received via a sum edge. A node would update its activation value by choosing the minimum activation message on all ingoing min edges. Algorithm 6 shows the algorithm of processing activation messages in the POCASN.

The main idea behind POCASN is to allow nodes to strengthen edges that connect subsequent tasks (in the task partial ordering) to the common parent node, by sending activation messages to those edges. If a task receives high activation values (showing a detection of that task), it cannot significantly affect its parent node, unless the preceding task in the partial-order has been detected and strengthened the edge connecting that task to its parent. The procedure of activation spreading in POCASN suppresses spreading of activation among nodes, if the order of observed tasks is not in agreement with the partial order constraints. The edges in $E_{PO}$ connect task nodes to edges from the subsequent task nodes in the partial order to their common parent. The reason behind defining min edges is to model tasks that have no ordering constraints with respect to each other. For such tasks there is no requirement on their order of execution. However, these tasks can all be the immediate prerequisite of another set of tasks. All the prerequisite tasks should have been detected (have high activation values) to strengthen edges on the subsequent set of tasks. We use min edges to connect all unrelated nodes to an extra node, which, in turn, is connected to the edges of the subsequent set of tasks. This ensures that all prerequisite tasks are detected before expecting to observe the subsequent tasks in the task network. We limit the activation value of edges in $E_S$ to $1-w\left(e\right)$, mainly because any activation values more than that would amplify the activation value of the sender node by multiplying it with a number greater than 1, which is not desirable.

We now introduce the algorithm to convert HTN to POCASN by modifying the original conversion algorithm presented in Algorithm 3. The new conversion algorithm that creates a POCASN from an HTN is shown in Algorithm 7.

Algorithm 6 Activation message processing procedure in POCASN

let $v$ be the node receiving activation message from $s$

let $S_{max}=\left\{n|\left(n,v\right)\in E_M and n sent message to v in recent clock signal\right\}$

$\text{let}\hspace{0.17em}{S}_{min}=\left\{n|\left(n,v\right)\in E_m and n sent message to v in recent clock signal\right\}$

if $S_{max}\ne \varnothing$

$ac\left(v\right)=\underset{v\prime \in S_{\max }}{\max }ac\left(v^{\prime }\right)$

$\text{else}\hspace{0.17em}if\hspace{0.17em}{S}_{min}\ne \varnothing$

$ac\left(v\right)=\underset{v\prime \in S_{\min }}{\min }ac\left(v^{\prime }\right)$

else

$ac\left(v\right)=ac\left(v\right)+ac\left(s\right)\times \left(w\left(\left(s,v\right)\right)+ac\left(\left(s,v\right)\right)\right)$

$ac\left(v\right)=ac\left(v\right)\times \left({\displaystyle \sum }_{(v_c,v)\in E_{C+}}\frac{\left(1+ac\left(v_c\right)\right)}{\left|\left\{(v_c,v)\in \right\}\right|}-{\displaystyle \sum }_{(v_c,v)\in E_{C-}}\frac{\left(1-ac\left(v_c\right)\right)}{\left|\right\{(v_c,v)\in E_{C-}\left\}\right|}\right)$

The text in blue represents modifications to the original procedure for CASN presented in Algorithm 5.

Algorithm 6 Activation message processing procedure in POCASN

let $v$ be the node receiving activation message from $s$

let $S_{max}=\left\{n|\left(n,v\right)\in E_M and n sent message to v in recent clock signal\right\}$

$\text{let}\hspace{0.17em}{S}_{min}=\left\{n|\left(n,v\right)\in E_m and n sent message to v in recent clock signal\right\}$

if $S_{max}\ne \varnothing$

$ac\left(v\right)=\underset{v\prime \in S_{\max }}{\max }ac\left(v^{\prime }\right)$

$\text{else}\hspace{0.17em}if\hspace{0.17em}{S}_{min}\ne \varnothing$

$ac\left(v\right)=\underset{v\prime \in S_{\min }}{\min }ac\left(v^{\prime }\right)$

else

$ac\left(v\right)=ac\left(v\right)+ac\left(s\right)\times \left(w\left(\left(s,v\right)\right)+ac\left(\left(s,v\right)\right)\right)$

$ac\left(v\right)=ac\left(v\right)\times \left({\displaystyle \sum }_{(v_c,v)\in E_{C+}}\frac{\left(1+ac\left(v_c\right)\right)}{\left|\left\{(v_c,v)\in \right\}\right|}-{\displaystyle \sum }_{(v_c,v)\in E_{C-}}\frac{\left(1-ac\left(v_c\right)\right)}{\left|\right\{(v_c,v)\in E_{C-}\left\}\right|}\right)$

The text in blue represents modifications to the original procedure for CASN presented in Algorithm 5.

The conversion procedure is similar to the original algorithm in Algorithm 3 with some modifications. Recall that partial-order constraints in HTN are a part of a task network which itself is the body of a method for accomplishing a compound task. While processing different methods for a compound task, we first need to topologically sort the set of tasks in the method body, according to their partial-order constraints. While processing each task $T^{\prime }$ in the body of a method, we first find a chain containing that particular task to find out all the immediate prerequisite tasks $pre\left(T\prime \right)$. Then we add a dummy node to the network for collecting activation values of all tasks in the $pre\left(T\prime \right)$ via min edges. This dummy node in turn spreads activation to the sum edge from $T\prime$ to the method, in order to model sequencing.

Algorithm 7 HTN to POCASN conversion algorithm

for every operator $R\left(v_1,\dots v_n\right)$ in HTN

for every substitution $\left(va{l}_1,\dots va{l}_n\right)$ in the domain of $D\left(v_1\right)\times \dots D\left(v_n\right)$

add node $R\left(va{l}_1,\dots va{l}_n\right)$ to the ASN

for every compound task $T\left(x_1,\dots ,x_m\right)$ in HTN

for every substitution $\left(va{l}_1,\dots va{l}_m\right)$ of $\left(x_1,\dots ,x_m\right)$

add node $T\left(va{l}_1,\dots va{l}_m\right)$ to the ASN if not already present

for every method $M\in methods\left(T\right)$ and $\left(va{l}_1,\dots va{l}_m\right)⊢pre\left(M\right)$

add node $T^M\left(va{l}_1,\dots va{l}_m\right)$ to the ASN

add a max edge from $T^M\left(va{l}_1,\dots va{l}_m\right)$ to $T\left(va{l}_1,\dots va{l}_m\right)$

$\text{let}\hspace{0.17em}sorted\left(M\right)\hspace{0.17em}\text{be}\hspace{0.17em}\text{an}\hspace{0.17em}\text{topological}\hspace{0.17em}\text{sort}\hspace{0.17em}\text{of}\hspace{0.17em}subtasks\left(M\right)$

for every task $T\prime \left(x{\prime }_1,\dots ,x{\prime }_{m\prime }\right)$ in $sorted\left(M\right)$

let $\left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ be a substitution for $\left(x{\prime }_1,\dots ,x{\prime }_{m\prime }\right)$ in

agreement with $\left(va{l}_1,\dots va{l}_m\right)$

$\text{let}\hspace{0.17em}chain\left(T^{\prime }\right)\hspace{0.17em}\text{be}\hspace{0.17em}\text{the}\hspace{0.17em}\text{longest}\hspace{0.17em}\text{chain}\hspace{0.17em}\text{containing}\hspace{0.17em}T’\hspace{0.17em}\text{and}\hspace{0.17em}pos\left(T\prime \right)\hspace{0.17em}\text{be}$

$\text{the}\hspace{0.17em}\text{position}\hspace{0.17em}\text{of}\hspace{0.17em}{T}^{\prime }\hspace{0.17em}\text{in}\hspace{0.17em}chain\left(T^{\prime }\right)$

$\text{let}\hspace{0.17em}pre\left(T\prime \right)=\left\{task|task<T^{\prime }and \nexists tas{k}^{\prime }:\left(task<tas{k}^{\prime }and tas{k}^{\prime }<T\prime \right)\right\}$

$\text{add}\hspace{0.17em}\text{node}\hspace{0.17em}pre\left(T\prime \right)\hspace{0.17em}\text{to}\hspace{0.17em}\text{ASN}\hspace{0.17em}\text{if}\hspace{0.17em}\text{not}\hspace{0.17em}\text{exists}\hspace{0.17em}\text{and}\hspace{0.17em}pre\left(T\prime \right)\ne \varnothing$

$\text{add}\hspace{0.17em}\text{min}\hspace{0.17em}\text{edges}\hspace{0.17em}\text{from}\hspace{0.17em}\text{every}\hspace{0.17em}\text{node}\hspace{0.17em}n\in pre\left(T^{\prime }\right)\hspace{0.17em}\text{to}\hspace{0.17em}\text{node}\hspace{0.17em}pre\left(T\prime \right)$

if $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ is compound then

add node $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ if not already present

add a sum edge from $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ to $T^M\left(va{l}_1,\dots va{l}_m\right)$ with

$\frac{1}{\left|subtasks\left(M\right)\right|\times pos\left(T\prime \right)}$ as weight

$\text{add}\hspace{0.17em}\text{ordering}\hspace{0.17em}\text{edge}\hspace{0.17em}\text{from}\hspace{0.17em}pre\left(T\prime \right)\hspace{0.17em}\text{to}\hspace{0.17em}\text{edge}\hspace{0.17em}\left(T\prime ,T^M\right)\hspace{0.17em}\text{if}\hspace{0.17em}pre\left(T\prime \right)\ne \varnothing$

else if $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ is primitive then

let $R$ be the operator corresponding to $T\prime$

add a sum edge from $R\left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ to $T^M\left(va{l}_1,\dots va{l}_m\right)$ with

$\frac{1}{\left|subtasks\left(M\right)\right|\times pos\left(T\prime \right)}$ as weight

$\text{add}\hspace{0.17em}\text{ordering}\hspace{0.17em}\text{edge}\hspace{0.17em}\text{from}\hspace{0.17em}pre\left(T\prime \right)\hspace{0.17em}\text{to}\hspace{0.17em}\text{edge}\hspace{0.17em}\left(R,T^M\right)\hspace{0.17em}\text{if}\hspace{0.17em}pre\left(T\prime \right)\ne \varnothing$

The text in blue represents modifications to the original algorithm for ASN presented in Algorithm 3.

Algorithm 7 HTN to POCASN conversion algorithm

for every operator $R\left(v_1,\dots v_n\right)$ in HTN

for every substitution $\left(va{l}_1,\dots va{l}_n\right)$ in the domain of $D\left(v_1\right)\times \dots D\left(v_n\right)$

add node $R\left(va{l}_1,\dots va{l}_n\right)$ to the ASN

for every compound task $T\left(x_1,\dots ,x_m\right)$ in HTN

for every substitution $\left(va{l}_1,\dots va{l}_m\right)$ of $\left(x_1,\dots ,x_m\right)$

add node $T\left(va{l}_1,\dots va{l}_m\right)$ to the ASN if not already present

for every method $M\in methods\left(T\right)$ and $\left(va{l}_1,\dots va{l}_m\right)⊢pre\left(M\right)$

add node $T^M\left(va{l}_1,\dots va{l}_m\right)$ to the ASN

add a max edge from $T^M\left(va{l}_1,\dots va{l}_m\right)$ to $T\left(va{l}_1,\dots va{l}_m\right)$

$\text{let}\hspace{0.17em}sorted\left(M\right)\hspace{0.17em}\text{be}\hspace{0.17em}\text{an}\hspace{0.17em}\text{topological}\hspace{0.17em}\text{sort}\hspace{0.17em}\text{of}\hspace{0.17em}subtasks\left(M\right)$

for every task $T\prime \left(x{\prime }_1,\dots ,x{\prime }_{m\prime }\right)$ in $sorted\left(M\right)$

let $\left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ be a substitution for $\left(x{\prime }_1,\dots ,x{\prime }_{m\prime }\right)$ in

agreement with $\left(va{l}_1,\dots va{l}_m\right)$

$\text{let}\hspace{0.17em}chain\left(T^{\prime }\right)\hspace{0.17em}\text{be}\hspace{0.17em}\text{the}\hspace{0.17em}\text{longest}\hspace{0.17em}\text{chain}\hspace{0.17em}\text{containing}\hspace{0.17em}T’\hspace{0.17em}\text{and}\hspace{0.17em}pos\left(T\prime \right)\hspace{0.17em}\text{be}$

$\text{the}\hspace{0.17em}\text{position}\hspace{0.17em}\text{of}\hspace{0.17em}{T}^{\prime }\hspace{0.17em}\text{in}\hspace{0.17em}chain\left(T^{\prime }\right)$

$\text{let}\hspace{0.17em}pre\left(T\prime \right)=\left\{task|task<T^{\prime }and \nexists tas{k}^{\prime }:\left(task<tas{k}^{\prime }and tas{k}^{\prime }<T\prime \right)\right\}$

$\text{add}\hspace{0.17em}\text{node}\hspace{0.17em}pre\left(T\prime \right)\hspace{0.17em}\text{to}\hspace{0.17em}\text{ASN}\hspace{0.17em}\text{if}\hspace{0.17em}\text{not}\hspace{0.17em}\text{exists}\hspace{0.17em}\text{and}\hspace{0.17em}pre\left(T\prime \right)\ne \varnothing$

$\text{add}\hspace{0.17em}\text{min}\hspace{0.17em}\text{edges}\hspace{0.17em}\text{from}\hspace{0.17em}\text{every}\hspace{0.17em}\text{node}\hspace{0.17em}n\in pre\left(T^{\prime }\right)\hspace{0.17em}\text{to}\hspace{0.17em}\text{node}\hspace{0.17em}pre\left(T\prime \right)$

if $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ is compound then

add node $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ if not already present

add a sum edge from $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ to $T^M\left(va{l}_1,\dots va{l}_m\right)$ with

$\frac{1}{\left|subtasks\left(M\right)\right|\times pos\left(T\prime \right)}$ as weight

$\text{add}\hspace{0.17em}\text{ordering}\hspace{0.17em}\text{edge}\hspace{0.17em}\text{from}\hspace{0.17em}pre\left(T\prime \right)\hspace{0.17em}\text{to}\hspace{0.17em}\text{edge}\hspace{0.17em}\left(T\prime ,T^M\right)\hspace{0.17em}\text{if}\hspace{0.17em}pre\left(T\prime \right)\ne \varnothing$

else if $T\prime \left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ is primitive then

let $R$ be the operator corresponding to $T\prime$

add a sum edge from $R\left(val{\prime }_1,\dots val{\prime }_{m\prime }\right)$ to $T^M\left(va{l}_1,\dots va{l}_m\right)$ with

$\frac{1}{\left|subtasks\left(M\right)\right|\times pos\left(T\prime \right)}$ as weight

$\text{add}\hspace{0.17em}\text{ordering}\hspace{0.17em}\text{edge}\hspace{0.17em}\text{from}\hspace{0.17em}pre\left(T\prime \right)\hspace{0.17em}\text{to}\hspace{0.17em}\text{edge}\hspace{0.17em}\left(R,T^M\right)\hspace{0.17em}\text{if}\hspace{0.17em}pre\left(T\prime \right)\ne \varnothing$

The text in blue represents modifications to the original algorithm for ASN presented in Algorithm 3.

Weights of sum edges in POCASN represent a minimum effective value for the edges, since they can receive activation values from ordering edges to make them stronger. Unlike the original ASN in which sum edges would connect task nodes to method nodes in the network with a shared normalization weight of $\frac{1}{\left|subtasks\left(M\right)\right|}$, in POCASN we need to assign smaller weights to outgoing edges from tasks that come after other tasks in the chain. This is because observing a task that comes after another task in the chain, should not be sufficient for detecting the intention by itself. This observation is only important if we previously detected preceding tasks (high activation values for preceding tasks). Weights of sum edges should be normalized by the size of the subtasks in order for different methods on the same level to have comparable activation values. $\frac{1}{\left|subtasks\left(M\right)\right|\times pos\left(T\prime \right)}$ was chosen as the weight of sum edge connecting node $T\prime$ to its parent. $\frac{1}{\left|subtasks\left(M\right)\right|}$ is the normalization factor for a method and $\frac{1}{pos\left(T\prime \right)}$ is the effect of ordering of task $T\prime$ among other tasks in the network. A sample POCASN is shown in Figure 5.

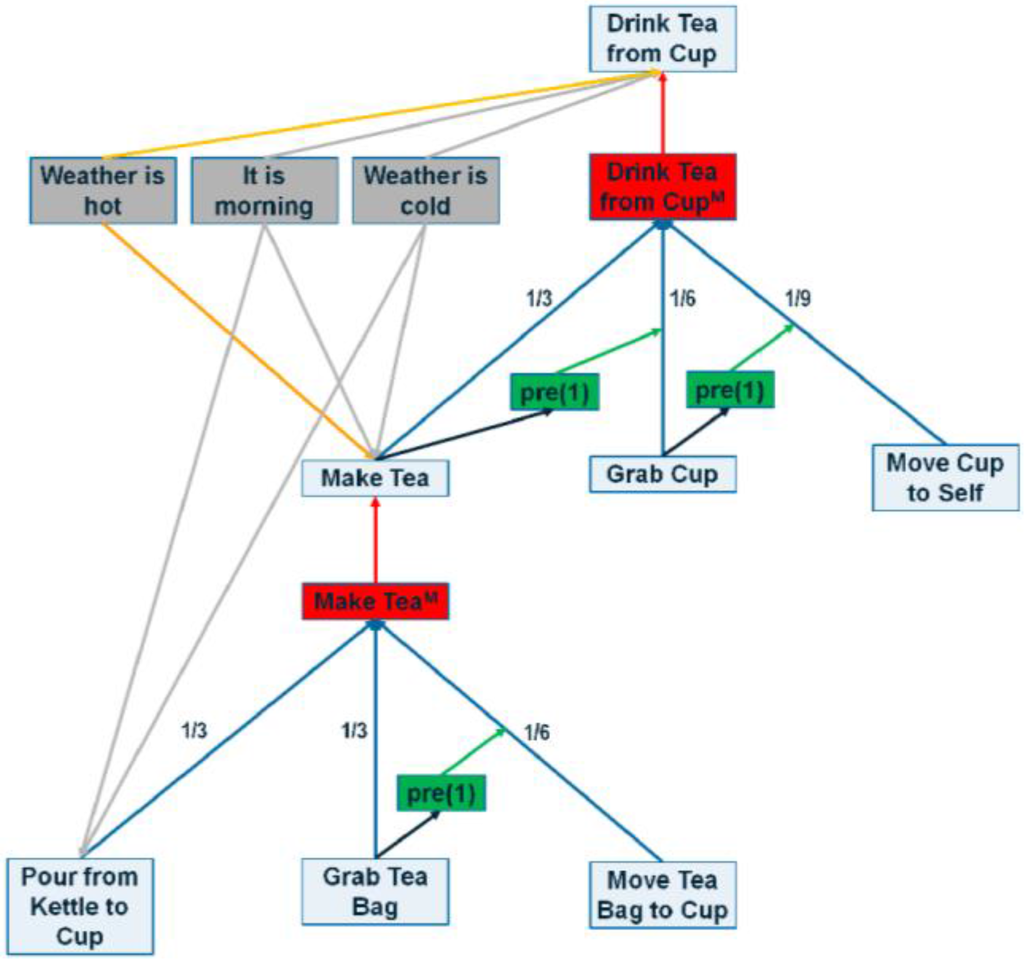
Figure 5. A sample portion of the POCASN. Red edges are max edges, green lines are ordering edges, black lines are min edges, blue edges represent sum edges, grey lines show positive context edges and orange represents negative context edges. Red boxes represents method nodes, grey boxes show context nodes and green boxes represent dummy nodes used to connect ordering edges to sum edges.

Figure 5. A sample portion of the POCASN. Red edges are max edges, green lines are ordering edges, black lines are min edges, blue edges represent sum edges, grey lines show positive context edges and orange represents negative context edges. Red boxes represents method nodes, grey boxes show context nodes and green boxes represent dummy nodes used to connect ordering edges to sum edges.

5. Experimental Evaluation

In this section we describe our implemented system and introduce the experiment domain, the HTN domain knowledge we used for experiments, the contextual information incorporated in the system, the resulting ASN, CASN and POCASN and the experimental results in three different tested scenarios.

5.1. Experiment Domain

The domain chosen for the experiments consists of 16 high-level daily activities and 2 different low-level activities. All these activities are defined upon 8 different objects. Book, cup, bowl, kettle, lettuce, tea bag, bottle and instant coffee are the objects of interest in our intent recognition system. Figure 6 shows our training images for the video parser. We developed our real-time intent recognition system in C++ using Microsoft Kinect SDK and OpenCV as our two main software tools. The system captures live feed from a Kinect camera and outputs the results of intent recognition as activation values for the important task nodes in our network. For a more natural interaction, we also used a NAO robot (by Aldebaran Robotics) to provide audio feedback to the user to inform him/her about the detected intention. The robot controller is designed to interpret detected intentions from our intent recognition system and make the robot behave appropriately by having a real-time interaction with the user. Figure 7 shows a captured screen-shot of the developed software.

Figure 6. Training images used for the object detector in the video parser module.

Figure 6. Training images used for the object detector in the video parser module.

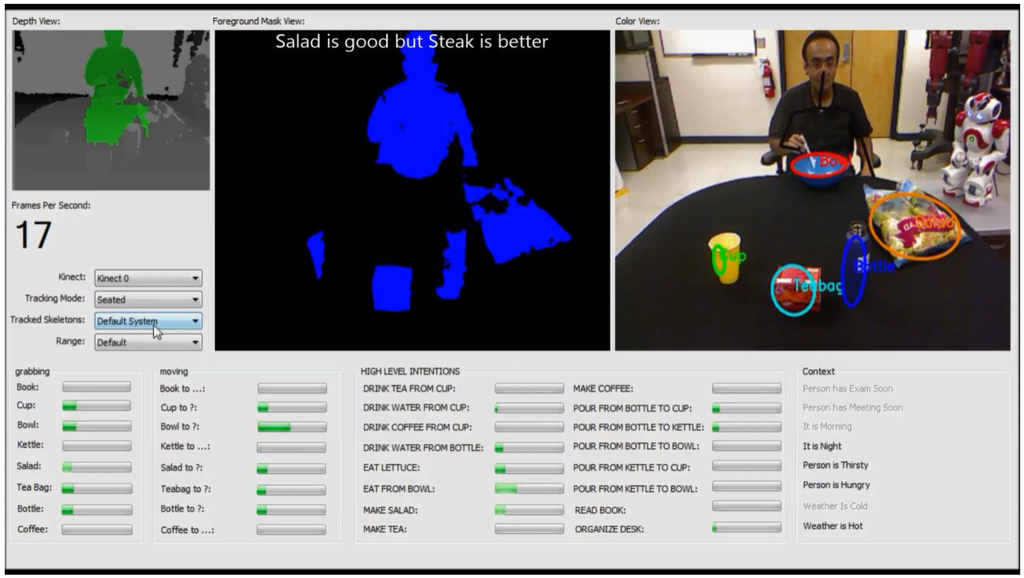
Figure 7. Screenshot of our intent recognition system.

Figure 7. Screenshot of our intent recognition system.

Our low-level activities (corresponding to operators in the HTN formalism) are grabbing and moving. The high-level activities (corresponding to compound tasks in the HTN formalism) are drink [what] from [where] in which [what]={tea, water, coffee} and [where]={cup, bottle}, eat from bowl, pour from [src] to [dest] in which [src]={kettle, bottle} and [dest]={cup, bowl, kettle}, make salad, organize desk, make tea, make coffee, read book and eat lettuce. The set of all contextual information about the scene contains 8 different items: person has exam soon, person has meeting soon, it is morning, it is night, person is thirsty, person is hungry, weather is cold, and weather is hot. We use two different states for contextual information, and we do not use the full spectrum of activation values of contextual nodes. We either know a particular context is true, or it is either false or unknown. If it is known, then the activation value is set to 0.2, otherwise it is set to 0. The effect of this contextual information on the compound tasks is shown in Table 2.

Table 2. The effect of contextual information on compound tasks.

Compound Task	Positive Context	Negative Context
drink tea from cup	weather is cold, it is morning	weather is hot
drink water from cup	person is thirsty, weather is hot	-
drink coffee from cup	it is morning, weather is cold	weather is hot, it is night
drink water from bottle	person is thirsty, weather is hot	-
eat from bowl	person is hungry	-
pour from kettle to cup	weather is cold, it is morning	-
pour from kettle to bowl	-	-
make salad	-	-
organize desk	person has meeting soon	-
make tea	weather is cold, it is morning	weather is hot
make coffee	weather is cold, it is morning	weather is hot, it is night
pour from bottle to kettle	weather is cold	-
pour from bottle to cup	person is thirsty	-
pour from bottle to bowl	-	-
read book	person has exam soon	-
eat lettuce	person is hungry	-

Table 2. The effect of contextual information on compound tasks.

Compound Task	Positive Context	Negative Context
drink tea from cup	weather is cold, it is morning	weather is hot
drink water from cup	person is thirsty, weather is hot	-
drink coffee from cup	it is morning, weather is cold	weather is hot, it is night
drink water from bottle	person is thirsty, weather is hot	-
eat from bowl	person is hungry	-
pour from kettle to cup	weather is cold, it is morning	-
pour from kettle to bowl	-	-
make salad	-	-
organize desk	person has meeting soon	-
make tea	weather is cold, it is morning	weather is hot
make coffee	weather is cold, it is morning	weather is hot, it is night
pour from bottle to kettle	weather is cold	-
pour from bottle to cup	person is thirsty	-
pour from bottle to bowl	-	-
read book	person has exam soon	-
eat lettuce	person is hungry	-

Table 3 shows the HTN-based representation of high-level tasks and their decomposition into lower-level tasks and operators. The operator grab has a single parameter with the domain containing all possible objects, and the operator move has two parameters: the first parameter is the object with the domain containing all objects; the second parameter is the destination and it can be an object, a special value self (the person is moving the object towards him/herself), or another special value not known. Compound tasks do not have parameters for instantiation and have a single method of decomposition.

Table 3. A summary of domain knowledge as an HTN

Compound Task	Method Decomposition
drink tea from cup	make tea < grab cup < move cup to self
drink water from cup	pour from bottle to cup < grab cup < move cup to self
drink coffee from cup	make coffee < grab cup < move cup to self
drink water from bottle	grab bottle < move bottle to self
eat from bowl	grab bowl < move bowl to self
pour from kettle to cup	grab kettle < move kettle to cup
pour from kettle to bowl	grab kettle < move kettle to bowl
make salad	grab lettuce < move lettuce to bowl
organize desk	grab object x < move object x to object y (for all possible x, y where x≠y)
make tea	pour from kettle to cup, grab tea bag < move tea bag to cup
make coffee	pour from kettle to cup, grab coffee < move coffee to cup
pour from bottle to kettle	grab bottle < move bottle to kettle
pour from bottle to cup	grab bottle < move bottle to cup
pour from bottle to bowl	grab bottle < move bottle to bowl
read book	grab book < move book to self
eat lettuce	grab lettuce < move lettuce to self

Table 3. A summary of domain knowledge as an HTN

Compound Task	Method Decomposition
drink tea from cup	make tea < grab cup < move cup to self
drink water from cup	pour from bottle to cup < grab cup < move cup to self
drink coffee from cup	make coffee < grab cup < move cup to self
drink water from bottle	grab bottle < move bottle to self
eat from bowl	grab bowl < move bowl to self
pour from kettle to cup	grab kettle < move kettle to cup
pour from kettle to bowl	grab kettle < move kettle to bowl
make salad	grab lettuce < move lettuce to bowl
organize desk	grab object x < move object x to object y (for all possible x, y where x≠y)
make tea	pour from kettle to cup, grab tea bag < move tea bag to cup
make coffee	pour from kettle to cup, grab coffee < move coffee to cup
pour from bottle to kettle	grab bottle < move bottle to kettle
pour from bottle to cup	grab bottle < move bottle to cup
pour from bottle to bowl	grab bottle < move bottle to bowl
read book	grab book < move book to self
eat lettuce	grab lettuce < move lettuce to self

5.2. Activation Spreading Networks

The HTN introduced in Section 5.1 can be converted to an ASN. After instantiating all operators, we have 80 operator nodes in the network. Figure 5 shows a portion of the resulting POCASN without all the operators and context nodes for simplicity. The network contains 80 different operator nodes accounting for all possible instantiations of grab and move. The clock in our ASN increments with receiving a new frame from the camera, therefore the clock frequency is equal to the frame rate (25 to 30 fps for our configuration). We chose 0.98 as the decay factor in our network and the firing threshold is set to zero for simplicity.

To determine the activation value of operators, we used simple formulas that can be directly computed from the features extracted by the video parser. The activation value of move nodes is computed with Equation (1) and the activation value of grab nodes is computed with Equation (2).

$$ac\left(R\right)=\min \left\{\begin{array}{c}\left(-\frac{distance\hspace{0.17em}change\hspace{0.17em}between\hspace{0.17em}objec\mathrm{t}\hspace{0.17em}and\hspace{0.17em}destination}{0.2}\right)\\ \left(\frac{0.4}{actual\hspace{0.17em}distance\hspace{0.17em}between\hspace{0.17em}objec\mathrm{t}\hspace{0.17em}and\hspace{0.17em}destination}\right)\end{array}\right\}$$

(1)

$$ac\left(R\right)=\min \left\{\begin{array}{c}\left(-\frac{distance\hspace{0.17em}change\hspace{0.17em}between\hspace{0.17em}hands\hspace{0.17em}and\hspace{0.17em}the\hspace{0.17em}objec\mathrm{t}}{0.2}\right)\\ \left(\frac{0.4}{actual\hspace{0.17em}distance\hspace{0.17em}between\hspace{0.17em}hands\hspace{0.17em}and\hspace{0.17em}the\hspace{0.17em}objec\mathrm{t}}\right)\end{array}\right\}$$

(2)

5.3. Scenarios

For experimental evaluation we performed three different scenarios, during which the intent recognition system was running and the robot in the scene was interacting with the subject at runtime. These scenes are also recorded and can later be fed into our system as a live stream to simulate the situation where the program is actually processing frames as they stream in. This is useful for repeating the same experiments given different contextual situations. The first scenario (eating) consists of a person eating salad (lettuce) and then drinking water from a bottle. It is 60 s long and lettuce, bowl, bottle, tea bag and cup are present in the scene. The second scenario (reading) consists of a person reading a book, then making tea and finally drinking tea from a cup. Tea bag, coffee, book, kettle and cup are visible in this scene and the video is 65 s long. In the final scenario (drinking) the subject makes tea and drinks tea from the cup. Kettle, tea bag, cup and coffee are present in the scene. The drinking scenario is 36 s long. We manually segmented the videos into partitions for different high-level intentions and used that as the ground truth. We experimented with ASN, CASN and POCASN to see how well they can handle these three scenarios. We also investigated the effect of considering contextual information and partial-order constraints on the system performance. Section 5.4 provides a discussion of the results obtained during the experimental evaluation.

5.4. Experiments

A relevant performance metric for intent recognition is how early the system is able to detect an intention reliably. Recall that for intent recognition we compare activation values of nodes at the same level in the hierarchical structure of the network, in order to choose the node with largest activation value as the recognized intention. The difference between the highest and the second highest activation values represents the level of confidence for recognition. For a quantitative analysis of the intent recognition with ASNs, we used two metrics:

Early detection rate: $\frac{t_i^{*}}{t_i}$ where $t_i$ is the total runtime of the segment for intention $i$ in a scenario, and $t_i^{*}$ is the earliest time (from the start of the segment) at which the correct intention was recognized consistently until the end of segment for intention $i$.

Confidence of detection: $\frac{ac\left(i\right)}{ac\left(max-1\right)}$ where $ac\left(i\right)$ is the activation value of the correct intention $i$ at any given time and $ac\left(max-1\right)$ is the second highest activation value of the nodes in the same level as $i$.

For effective intent recognition we want the early detection rate to be close to 0, which means that the system was able to detect that intention immediately. An average of early detection rate for a scenario is simply computed over all intentions present in that scenario. For the confidence of detection, larger values show a better (more confident) recognition of intentions. Any values greater than 1 show a correct recognition at that particular time. An average confidence of detection for an intention in a scenario is computed over all time-steps in a scenario in the intention’s ground truth segment.

5.4.1. Eating Scenario

Figure 8 shows the activation values of high-level (compound) tasks in our CASN. Figure 9 shows the same results but with ASN. In the full context version, we assumed the system knows the following: it is hot, it is night, the person is hungry and person is thirsty. We annotated the graph with how the robot responded during each case. We also show the ground truth segmentation of intentions.

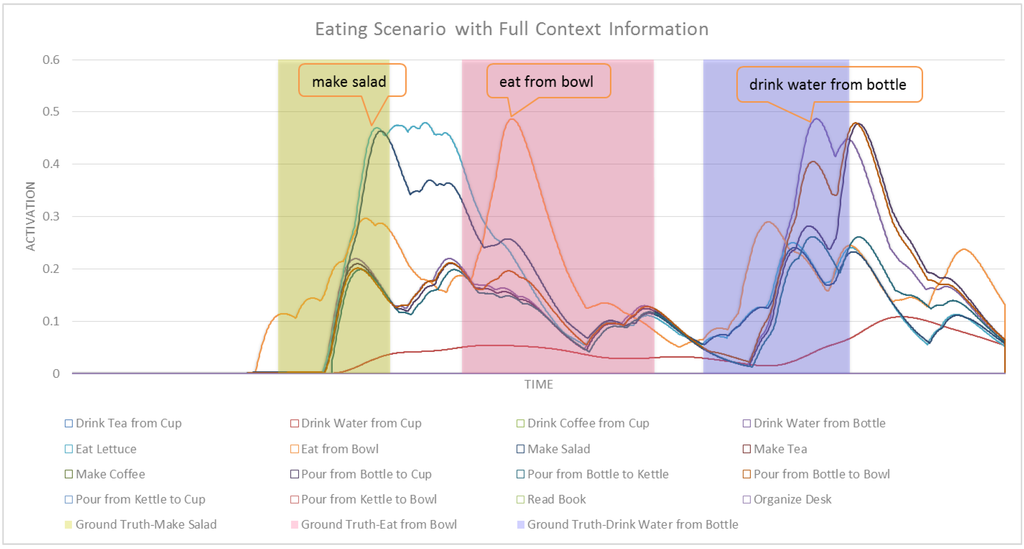
Figure 8. Activation values for the eating scenario with CASN.

Figure 8. Activation values for the eating scenario with CASN.

Figure 9. Activation values for the eating scenario with ASN

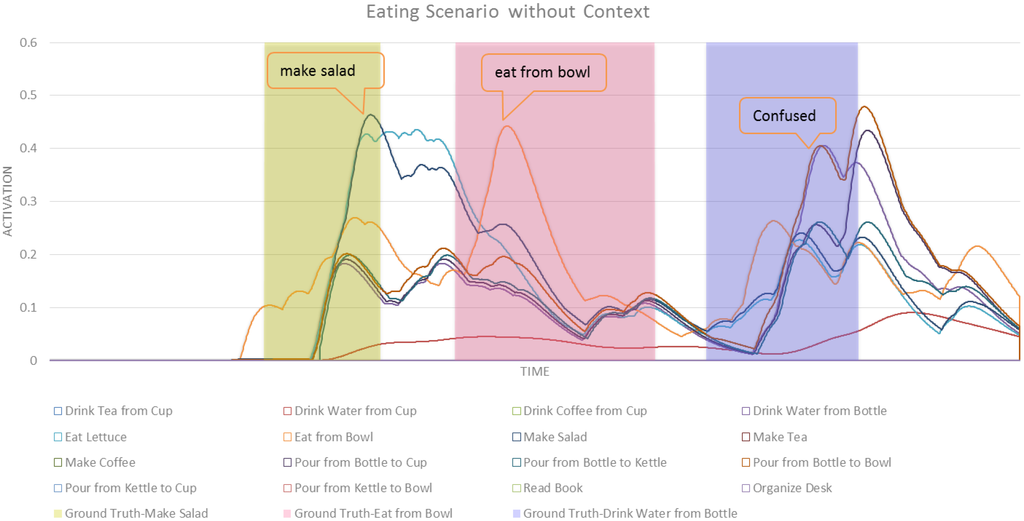
Figure 9. Activation values for the eating scenario with ASN

A comparison of Figure 8 with Figure 9 shows how CASN can distinguish between similar activities better than the ASN. To highlight this improvement, Figure 10 and Figure 11 show a subset of related tasks for these two networks. These activities are at the same level in the structure of the network, therefore their activation values are comparable. In Figure 10, we can see a significant disambiguation of similar activities including drinking water from bottle, pouring from bottle to cup and pouring from bottle to bowl. The ASN was not able to choose the correct intention among these very similar tasks. Figure 11 shows how the activation values of these three activities are very close, which makes a reasonable detection impossible. The early detection results and average confidence of detections for this scenario in CASN and ASN are shown in Table 4. CASN improves ASN by correctly detecting drink water from bottle with 51.12% early detection rate, compared to no detection in ASN. The confidence of detection is also improved for eat from bowl and drink water from bottle tasks. However ASN worked slightly better for make salad, because in CASN contextual nodes are strengthening the eat from bowl task, which has the second highest activation value in the make salad segment of this scenario.

Table 4. Early detection rates and average confidence of detections for eating scenario

Intention		Early Detection Rate	Average Confidence of Detection
CASN	make salad	62.25%	1.02
	eat from bowl	4.85%	1.60
	drink water from bottle	51.12%	0.80
ASN	make salad	57.84%	1.08
	eat from bowl	5.42%	1.39
	drink water from bottle	no detection	0.68

Table 4. Early detection rates and average confidence of detections for eating scenario

Intention		Early Detection Rate	Average Confidence of Detection
CASN	make salad	62.25%	1.02
	eat from bowl	4.85%	1.60
	drink water from bottle	51.12%	0.80
ASN	make salad	57.84%	1.08
	eat from bowl	5.42%	1.39
	drink water from bottle	no detection	0.68

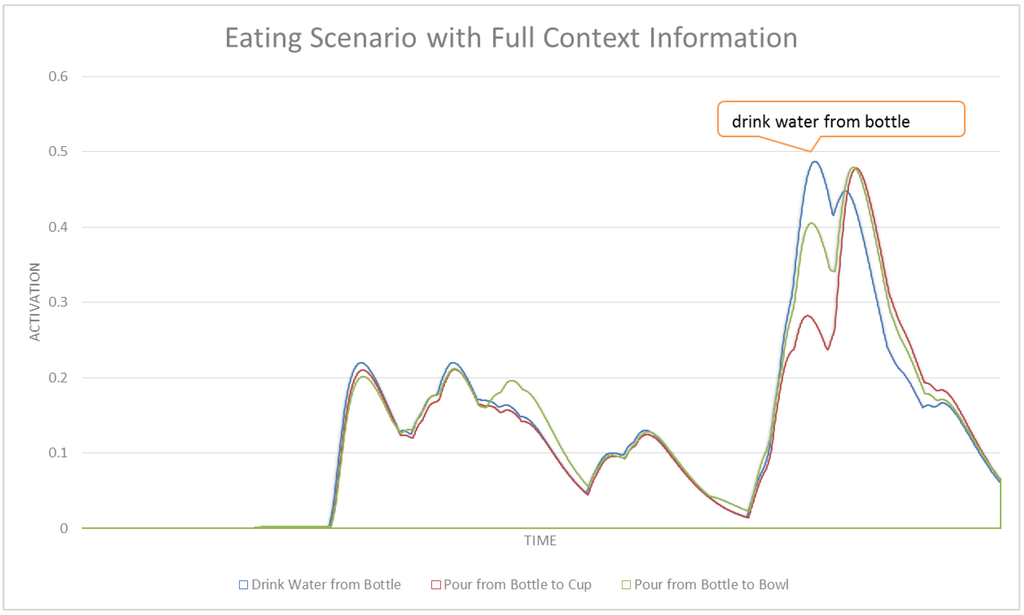
Figure 10. A subset of activities for the eating scenario with CASN.

Figure 10. A subset of activities for the eating scenario with CASN.

Figure 11. A subset of activities for the eating scenario with ASN.

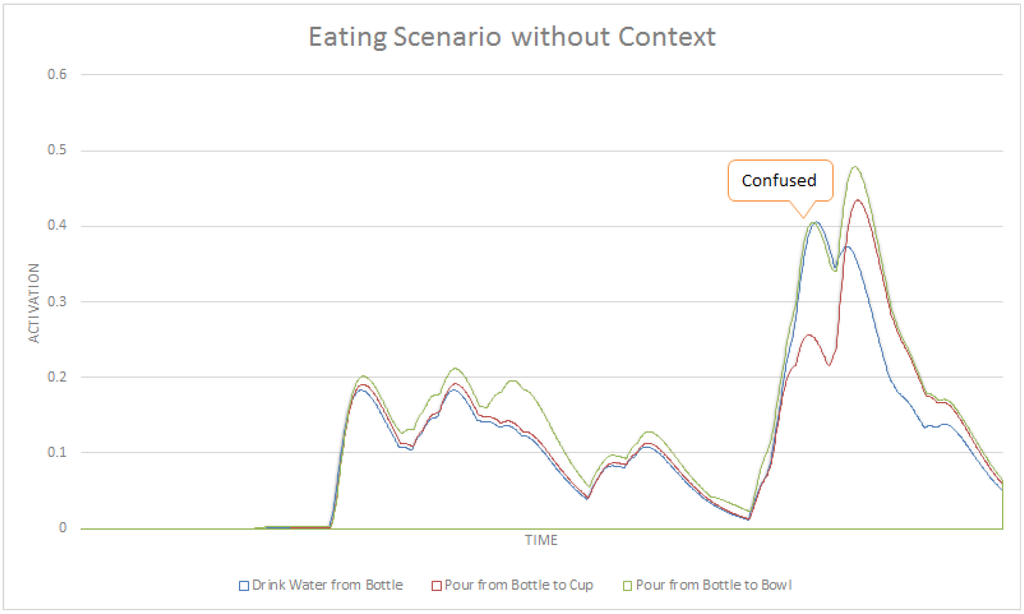
Figure 11. A subset of activities for the eating scenario with ASN.

5.4.2. Reading Scenario

Figure 12 shows the activation values of high-level (compound) tasks in our CASN. Figure 13 shows the same results but with ASN. In the full context version, we assumed the system knows the following: person has exam soon, it is morning and weather is cold.

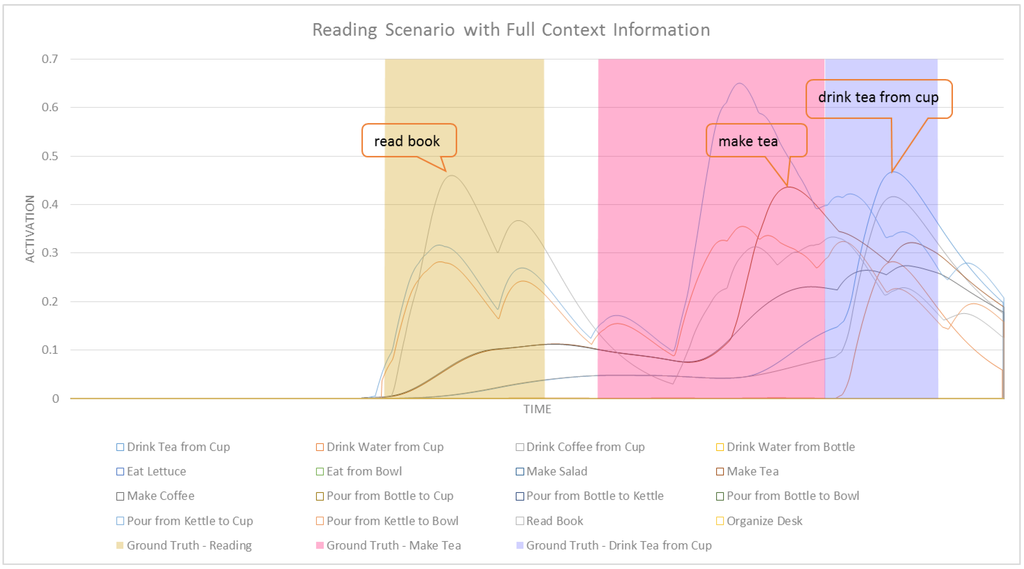
Figure 12. Activation values for the reading scenario with CASN.

Figure 12. Activation values for the reading scenario with CASN.

Figure 13. Activation values for the reading scenario with ASN.

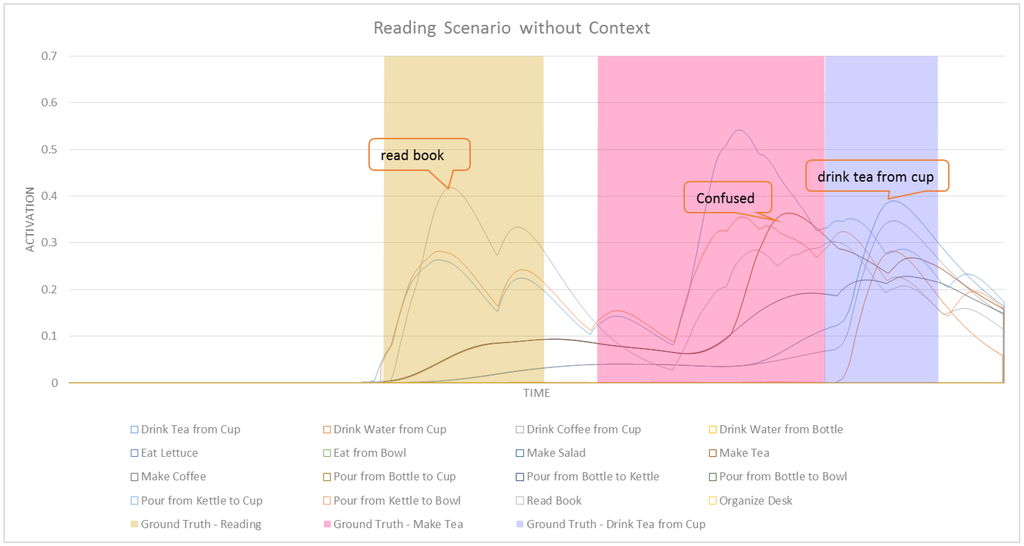
Figure 13. Activation values for the reading scenario with ASN.

A comparison of Figure 12 with Figure 13 shows that nodes in CASN accumulate higher activation values. This is expected since contextual information can have positive effects on the activation values of some task nodes in the network. In CASN, we would have no activation values spreading from context nodes. This is visible in Figure 12, since we have no activation values at the beginning of this graph. Context would only amplify the effect of activation spreading in the network in favor of some related tasks. Figure 14 and Figure 15 show a subset of related tasks for these two networks. As shown in these figures, ASN is not able to detect the make tea intention. The early detection results and average confidence of detections for this scenario in CASN and ASN are shown in Table 5. It is clear that CASN is performing better than ASN for this scenario by detecting make tea with 58.80% early detection rate compared to no reliable detection of this intention in ASN. No detection for this task does not imply that it was not recognized in any time-step. This means that the network could not correctly recognize that intention at the last time-step of its ground truth time segment. However, make tea had the highest activation values for the most parts of the ground truth. An interesting property of our ASN is shown in this experiment. Although the system was not able to detect make tea reliably (not until the end of ground truth segment) it could correctly recognize the next task drink tea from cup. This shows that our ASN-based intent recognition is able to recover from detection errors in the previous time-steps. The use of context also improved the early detection rate for drink tea from cup by 16%.

Table 5. Early detection rates and average confidence of detections for reading scenario.

Intention		Early Detection Rate	Average Confidence of Detection
CASN	read a book	21.22%	1.23
	make tea	58.80%	1.31
	drink tea from cup	22.66%	1.24
ASN	read a book	23.58%	1.24
	make tea	no detection	1.18
	drink tea from cup	38.66%	1.23

Table 5. Early detection rates and average confidence of detections for reading scenario.

Intention		Early Detection Rate	Average Confidence of Detection
CASN	read a book	21.22%	1.23
	make tea	58.80%	1.31
	drink tea from cup	22.66%	1.24
ASN	read a book	23.58%	1.24
	make tea	no detection	1.18
	drink tea from cup	38.66%	1.23

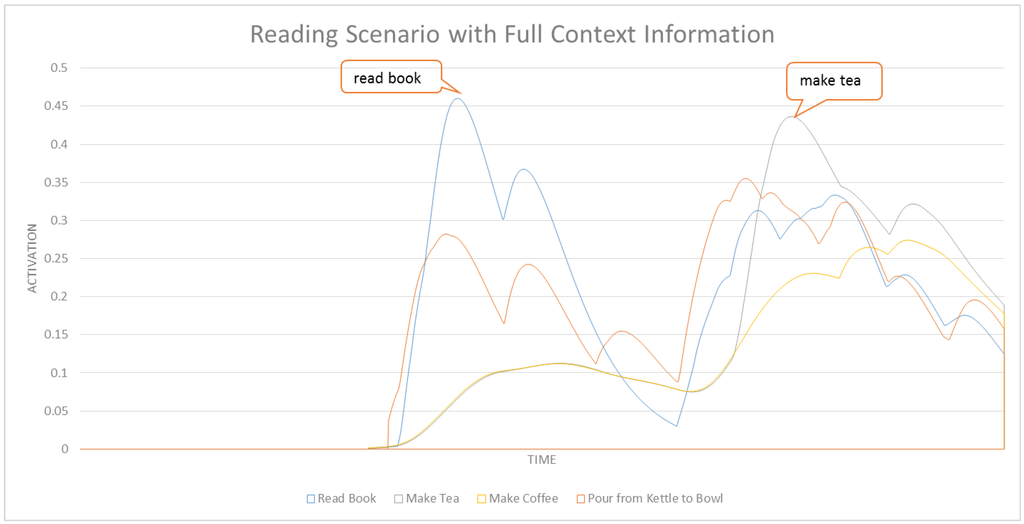
Figure 14. A subset of activities for the reading scenario with CASN.

Figure 14. A subset of activities for the reading scenario with CASN.

Figure 15. A subset of activities for the reading scenario with ASN.

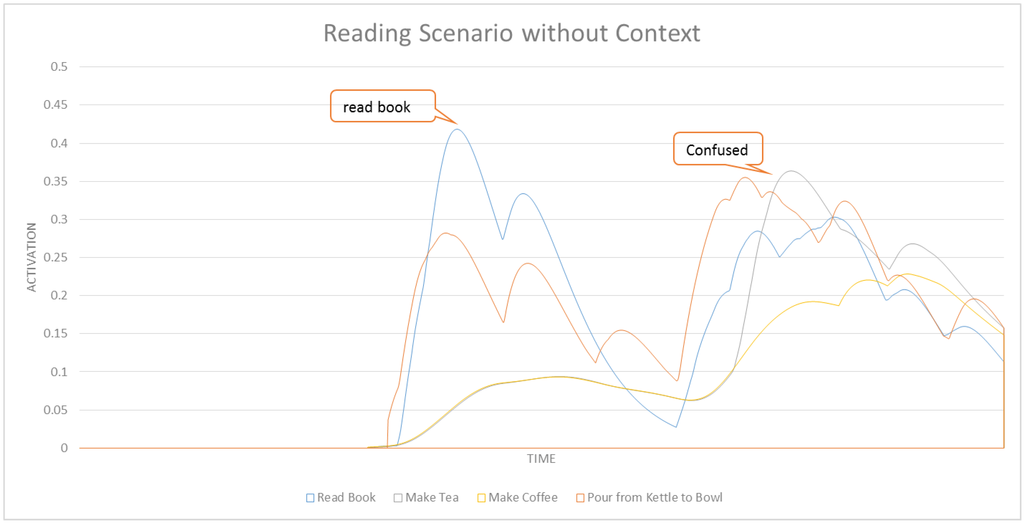
Figure 15. A subset of activities for the reading scenario with ASN.

5.4.3. Drinking Scenario

Figure 16 shows the activation values of high-level (compound) tasks in our POCASN. Figure 17 shows the same results but with ASN. The drinking scenario is designed to evaluate the performance of POCASN and its comparison with the original ASN. No contextual information is used in POCASN, in order to see the effect of partial-order modeling for intent recognition. The first major difference between POCASN and the original ASN is that in POCASN, activation values are much higher. This is because of spreading activation values to edges in addition to nodes. A node corresponding to a previous task would strengthen the edges of the next task, and this results in a higher spreading of activation to the parent method node. Drink Tea from Cup and Drink Coffee from Cup are similar tasks in our network, with only a difference on grabbing and moving coffee instead of tea. In the reading scenario we could detect this activity with the help of contextual information, which here is absent. POCASN is able to detect this intention reliably, as shown in Figure 18. A similar graph for ASN in Figure 19 shows that ASN cannot disambiguate between these two tasks. Table 6 shows detection rates and average confidence of detection for the drinking scenario, for both POCASN and ASN. In POCASN, the network is expecting to observe the next correct task—the edges connecting the expected task to its method node are already strengthened, which greatly helps decrease the early detection rate. Even for drink tea from cup, the accumulated activation values received from make tea are enough for a detection of that intention. The 0% early detection rate for drink tea from cup in POCASN illustrates this situation.

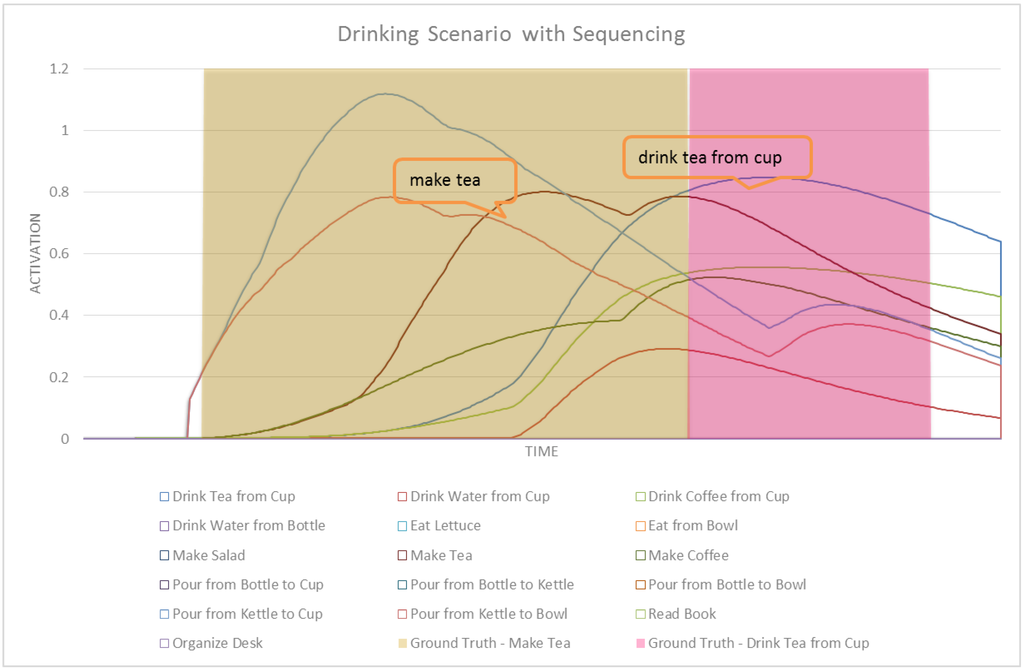
Figure 16. Activation values for the drinking scenario with POCASN.

Figure 16. Activation values for the drinking scenario with POCASN.

Figure 17. Activation values for the drinking scenario with ASN.

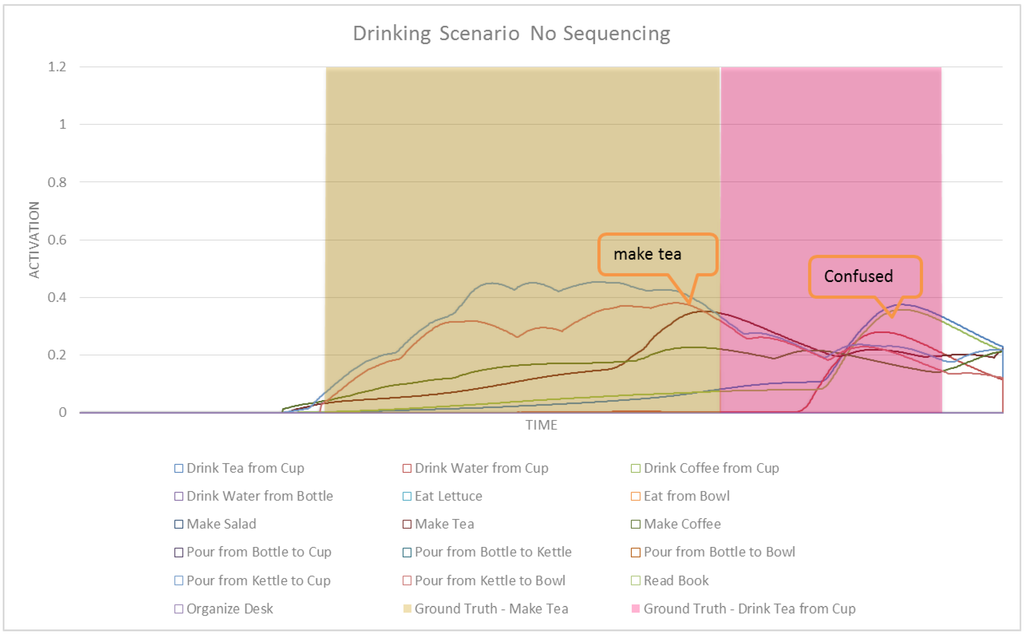
Figure 17. Activation values for the drinking scenario with ASN.

Table 6. Early detection rates and average confidence of detections for drinking scenario

Intention		Early Detection Rate	Average Confidence of Detection
POCASN	make tea	31.84%	1.63
	drink tea from cup	0%	1.50
ASN	make tea	76.01%	1.09
	drink tea from cup	no detection	1.06

Table 6. Early detection rates and average confidence of detections for drinking scenario

Intention		Early Detection Rate	Average Confidence of Detection
POCASN	make tea	31.84%	1.63
	drink tea from cup	0%	1.50
ASN	make tea	76.01%	1.09
	drink tea from cup	no detection	1.06

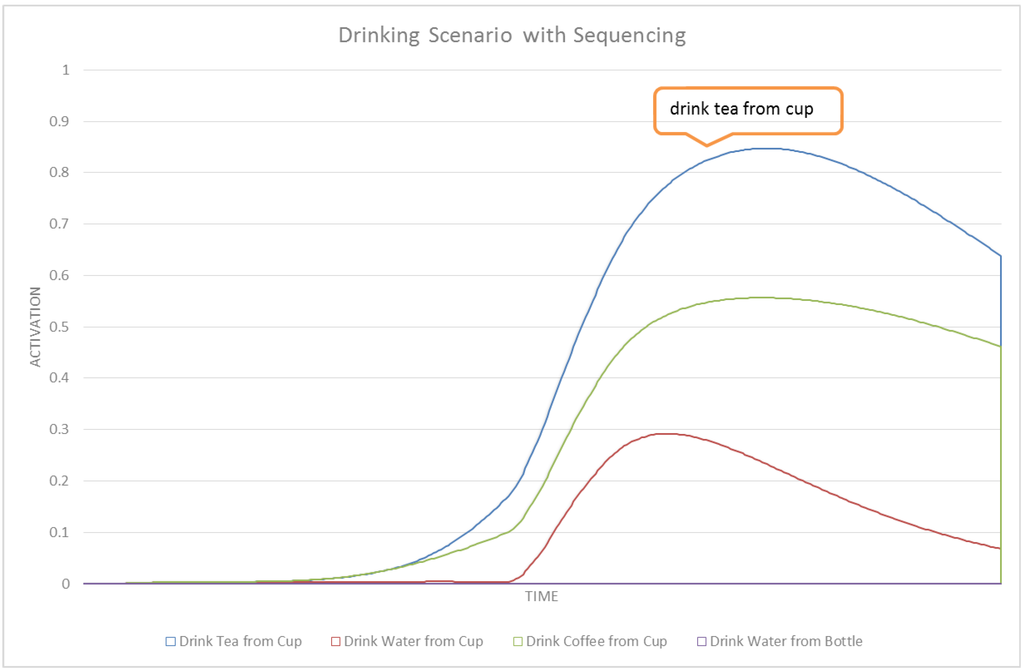
Figure 18. A subset of activities for the drinking scenario with POCASN.

Figure 18. A subset of activities for the drinking scenario with POCASN.

Figure 19. A subset of activities for the drinking scenario with ASN.

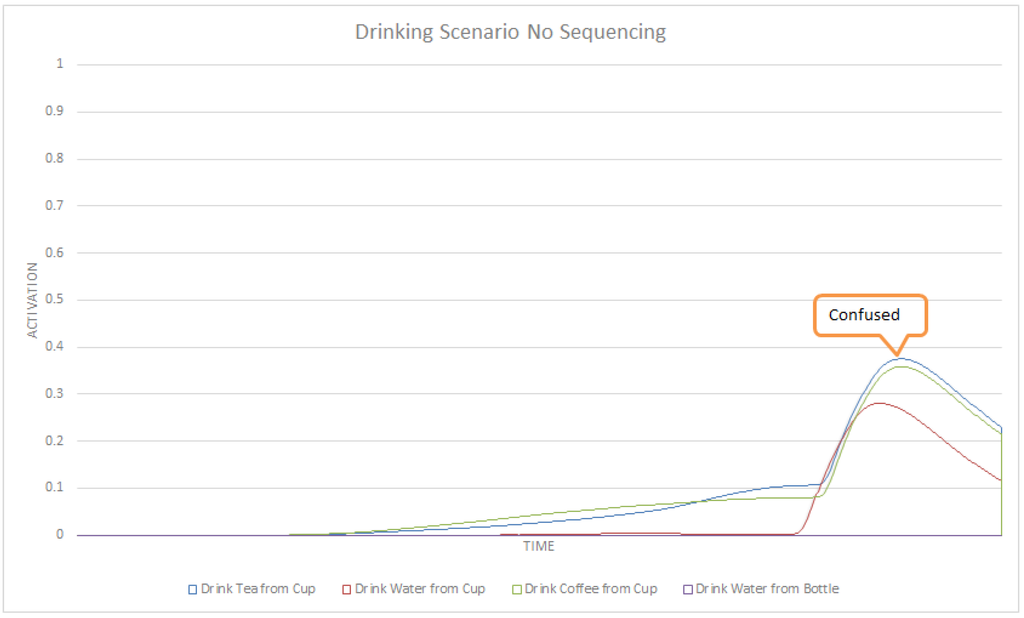
Figure 19. A subset of activities for the drinking scenario with ASN.

6. Conclusions

In this paper we propose a novel real-time vision-based intent recognition system based on Activation Spreading Networks (ASNs). The key idea behind employing ASNs for intent recognition is to use a distributed network of connected nodes to robustly recognize the intention according to the activation values accumulated on the nodes in the network. We formally defined ASNs and showed how we can create a hierarchical ASN from Hierarchical Task Networks (HTNs). We then described an algorithm for intent recognition with ASNs by selecting the maximum activation value from sets of comparable nodes in the network. We extended this ASN formalism to handle contextual information. We formally defined how to modify the original ASN to obtain a Contextual ASN (CASN) and to process this type of information, and we showed how to relate context to different tasks. Finally, we extended the ASN formalism to model partial-order constraints in the HTN to obtain a Partial-Order CASN (POCASN). We implemented all three ASN, CASN and POCASN approaches in a fully functioning system. The resulting system can process RGB-D video streams in real-time to detect, recognize and track objects, extract features from video, and recognize intentions while observing a person performing daily tasks. Our experiments showed that the system is able to efficiently and reliably recognize intentions, even before activities are finished. In our experiments we also compared ASN, CASN and POCASN and showed how CASN and POCASN can improve the performance of the original ASN.

As future work, we plan to extend our ASN-based approach in order to learn the structure of the network by analyzing a training set of observed activities. For now, our system relies on having an HTN-based description of the domain knowledge to detect intentions. We plan to investigate how this kind of domain knowledge could be extracted by machine learning techniques. Another direction of future work is related to handling missing information, which is frequent in real-world problems due to partial observability of the environment (e.g., occlusion) or failing sensors. Furthermore, we plan to analyze how well our approach is able to recover from errors in different modules of the system, especially the video parser.