Abstract
Learning and planning are powerful AI methods that exhibit complementary strengths. While planning allows goal-directed actions to be computed when a reliable forward model is known, learning allows such models to be obtained autonomously. In this paper we describe how both methods can be combined using an expressive qualitative knowledge representation. We argue that the crucial step in this integration is to employ a representation based on a well-defined semantics. This article proposes the qualitative spatial logic QSL, a representation that combines qualitative abstraction with linear temporal logic, allowing us to represent relevant information about the learning task, possible actions, and their consequences. Doing so, we empower reasoning processes to enhance learning performance beyond the positive effects of learning in abstract state spaces. Proof-of-concept experiments in two simulation environments show that this approach can help to improve learning-based robotics by quicker convergence and leads to more reliable action planning.
1. Motivation
Robotic applications have evolved considerably, yet they still lack the efficiency, flexibility and adaptability that is needed to improve our everyday life as versatile service robots. Planning and learning are the two major paradigms employed to make a robot act intelligently. Planning is a form of symbolic reasoning applied on various levels of abstraction. Planning is effective whenever reliable forward models of the robot and its environment are available. Learning is a powerful method to generate such models from data. However, it requires carefully handcrafted state space representations to converge to high-quality models in reasonable time. Neither planning nor learning on their own suffice to meet the demands of versatile service robots. By integrating both paradigms one can benefit from their respective strengths. So far, a true integration of learning and planning has not been achieved that allows a robot to acquire new skills efficiently in a truly autonomous way.
Our work is motivated by this basic question of how to integrate learning and planning, leveraging their individual strengths to produce reliable and versatile robot behavior. We propose a qualitative reasoning framework as the glue between those two paradigms. Qualitative reasoning lifts information, e.g., obtained by perception, to a knowledge level, enabling us to integrate it with common sense knowledge and to use available reasoning techniques [1,2,3]. The qualitative representation serves two purposes: (1) to make a planning or action selection process with learned models more efficient; and (2) to control selection of learning samples in order to make a learning process more reliable and to obtain high-quality models with little manual design effort. We present two experimental studies in simulation for a specific robot task: to throw an object to a specific destination. The results indicate that qualitative reasoning can serve the intended purposes and thus serve as an interface to integrate planning and learning. This exemplified study is intended to show the feasibility and promising characteristics of the approach as a whole, paving the way for in-depth investigations on individual aspects.
1.1. Scenario
In this study we consider a household robot learning how to throw objects, for example to throw waste into a dustbin (see Figure 1). We have chosen this instance as a representative of a wide range of manipulation tasks for which no reliable kinematic forward models are available due to unobservable physical parameters such as inertia.

Figure 1.
Simulated PR2 robot gathering data on the effect of throwing objects.
We use two simulated setups: a physics simulation that gives access to a direct manipulation of the velocity and direction of the throw, and a more realistic simulation of a complete robot where the parameters of the throw result indirectly from the movement of the robot arm.
Abstract common sense knowledge is readily available for this scenario, for example in form of a description of the positive correlation of initial impulse and throwing distance achieved. This knowledge is specific to the throwing scenario and has to be adapted to other applications as needed—developing such background models of everyday tasks is subject to research in the area of qualitative reasoning.
Ideally, our approach will help to shift the workload from tweaking state space representations and finding search heuristics to a clean knowledge representation of a particular task. Along this idea, our main goal is to demonstrate the principle of combining planning and learning with qualitative representations rather than providing a particularly polished solution to the throwing task.
The term “planning” is used in different contexts in AI, from symbolic action planning to motion planning. In all cases it denotes a search procedure in a specified state space. The most simple form of search is sampling, i.e., considering random states until one with the desired properties is found. As in other lower-level robotics tasks [4] we use sampling here as a simple form of planning. As we will show, our qualitative models reduce the set of states to be considered in the sampling process. The same technique can be applied to other search techniques. In this paper we use the term “sampling” as a specific (albeit simple) instantiation of “planning”.
1.2. Approach and Contribution
Figure 2 shows an overview of our approach. The control strategy of both learning and action planning is jointly based on a qualitative task description. Additionally, the planning component exploits common sense rules about the problem domain. Task descriptions on the qualitative level characterize classes of concrete tasks. In this paper we are concerned with the class of throwing any object to any position in front of the robot. Technically, we develop a qualitative spatio-temporal logic with well-defined semantics to link the quantitative level of observation and control values with an abstract symbolic representation. Qualitative representations of space as studied in the field of qualitative spatial and temporal reasoning (QSTR) are partially motivated by the aim to grasp the semantics of the catalog of human cognitive concepts [5] and should thus contribute to making specifications intuitive.
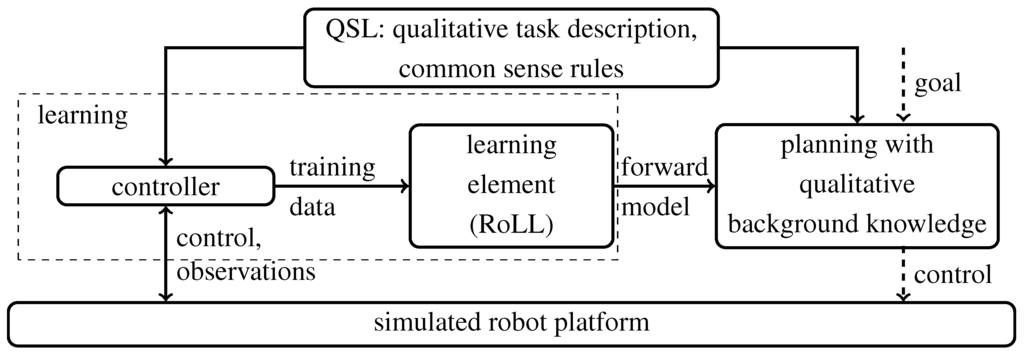
Figure 2.
Integrating learning and planning with qualitative task knowledge.
The aim of the learning component is to generate the initially unknown forward model of the manipulation task from the robot’s own observations. We use the Robot Learning Language (RoLL) [6] to specify all aspects of learning tasks declaratively: how to gather training data, which learning algorithm to use and the specification of the function to be learned. This declarative framework allows us to smoothly integrate the qualitative concepts. To gather data, we use the idea of motor babbling by randomly choosing robot actions and observing the effect. In contrast to classical motor babbling, observations are matched against the task description in order to identify whether the observation matches the task at hand. For learning the forward model of throwing an object to the front we thus only collect robot control values that lead to throwing the object forward.
Once sufficient training data has been collected, a forward model is learned and automatically integrated into the control program by RoLL. As learning algorithm we use the model tree learner M5’ from the WEKA learning toolbox [7]. The resulting model is then used for planning, given a concrete goal (e.g., the coordinates of a dust bin to throw into). A common technique in robotics for exploiting such models is unbiased sampling in the space of parameters. The knowledge representation language described in this paper allows the programmer to augment a task specification with coarse commonsense rules, which are then exploited to guide and accelerate the sampling process.
The contribution of this work is to demonstrate how qualitative knowledge representations can be used to integrate learning and planning based on a declarative problem description. To this end, we introduce qualitative spatial logic (QSL). We further identify two beneficial characteristics of this approach. First, we show how QSL-based task specifications help to identify those observations of a robot that are useful for a given learning problem. Second, we show how the general idea of exploiting abstract common sense rules to solve everyday tasks—which is a basic motivation of the qualitative reasoning community (see [3])—can be implemented in context learning manipulation tasks using QSL. Both characteristics are demonstrated by empirical evaluation in simulations, ranging from pure physical computations with the Bullet physics engine (http://bulletphysics.org) to a realistic simulation of a PR2 robot in a household environment (Figure 1 and Figure 16) with the MORSE (https://www.openrobots.org) [8,9] simulator.
2. Qualitative Representation of Manipulation Tasks with Qualitative Spatial Logic (QSL)
We propose a spatial logic based on qualitative relations to represent knowledge for manipulation tasks. Defining a representation with clear semantics that builds on components developed in the area of symbolic knowledge representation and reasoning, we obtain a representation that we can reason about using methods developed in the artificial intelligence community.
State spaces in manipulation tasks are essentially characterized by the spatial structure of the environment, developing a qualitative representation for manipulation is thus tightly related to qualitative spatial representation and reasoning (see [10] for a recent overview). Moreover, manipulation is dynamic and thus the spatial representation needs to be augmented to capture change over time. While there exist purely qualitative approaches addressing dynamic aspects, these approaches are specialized to a single aspect of dynamics, for example the change of distance between objects over time. By contrast, we require a more universal approach that allows us to represent changes with respect to the entire spatial representation. For example, we dare to represent a learning task declaratively by saying that a start configuration (e.g., can on desk) should be changed to obtain some desired end configuration (e.g., can in dustbin). Sequences of such statements are also called snapshot-based spatio-temporal models [11]. In its generality, the question of combining a qualitative spatial representation with a temporal representation is tackled in the contemporary field of spatial logics [11] which comprises several demanding research questions. As our approach does not depend on specific reasoning properties, we opt for a straightforward combination of linear temporal logic (LTL) with a qualitative spatial representation. This enables us to compose declarative statements about actions and their effects on a coarse level of abstraction.
QSL can be seen as a toolbox which enables us to flexibly combine the qualitative representations deemed helpful for representing a learning task at hand. We use QSL for two purposes: (1) to guide the planning process (Section 3 and Section 4); and (2) to control selection of learning samples in order to make the learning process more reliable (Section 5).
2.1. Qualitative Representation of Space
Qualitative spatial representations stand out from general qualitative representations, as space exhibits rich structures. In contrast to space, ordinary physical dimensions like, for example, weight or temperature, give rise to few meaningful distinctions only, for example heavier vs. lighter, colder vs. warmer. Such concepts can be captured by comparing values using the usual ordering relations , which in qualitative reasoning are referred to as the point calculus [12], illustrated in Figure 3a. In case of comparing intervals rather than points, Allen [13] describes a representation and reasoning technique based on 13 interval relations. Seven relations are shown in Figure 3b, the remaining six are obtained by considering the inverses of all relations shown except for equality. By contrast, already two-dimensional space can be described in a multitude of ways. A straightforward generalization of the one-dimensional case is based on projecting connected regions onto the two coordinate axes. The projections are intervals and their relation can be described using Allen’s interval relations. This approach is known as the block algebra [14] and illustrated in Figure 4. Moreover, there are several useful binary relations to describe point locations in two-dimensional space. For example, binary relations can describe relative positions with respect to a global coordinate system using the Star relations [15], relative position with respect to points augmented with an orientation using StarVars relations [16], or ternary relations that jointly capture distance and direction information using tpcc relations [17]. See Figure 5 for an illustration of these relations.
Although the representations mentioned so far address two-dimensional space only, their respective partition scheme can be extended to three dimensions in a straightforward manner. In case of the block algebra, the generalization is obtained by projecting objects on X, Y, and Z axis and describing the three interval relations obtained. Three-dimensional block algebra relations are thus 3-tuples of Allen’s interval relations. By combining two independent cone-like relations shown in Figure 5, one applied to the X/Y plane and the other to the Y/Z plane, a three-dimensional cone with rectangular cross-section is obtained.
Due to the complex interdependencies occurring in qualitative spatial relations, defining relations is only the first step in designing a qualitative representation. The difficult step is then to identify reasoning algorithms that can process these relations symbolically, most importantly to identify relations only given implicitly and to recognize potential conflicts. For example, in the context of Allen’s interval relations consider the two facts that intervals X and Y stand in relation o (overlaps) and intervals Y and Z stand in the relation o too. From these facts it follows that X and Z either stand in relation b, m, or o as can be verified graphically. This knowledge is captured in the so-called qualitative calculus [18,19], an algebraic construct that is induced by a set of qualitative relations. We note that qualitative spatial representations are always constructed in a way such that there are finitely many relations that are jointly exhaustive and pairwise disjoint [19] as this eases technicalities of the representation. For example, this allows negation of a fact (e.g., the can is not on the desk) to be rewritten as disjunction over all alternatives. Disjunction can be understood as set union in a relation-based representation: relations are sets of domain values and set operations are thus applicable. Clearly, the statement or holds if and only if with holds. We adopt the usual notion in qualitative spatial reasoning to write disjunctions as sets, i.e., instead of writing we write . In this paper we are primarily concerned with representation, but we point out that analysis of the underlying qualitative calculus is necessary to reveal applicable rules for symbolic manipulation of knowledge and reasoning algorithms. To this end, we only employ relations that have previously been investigated.
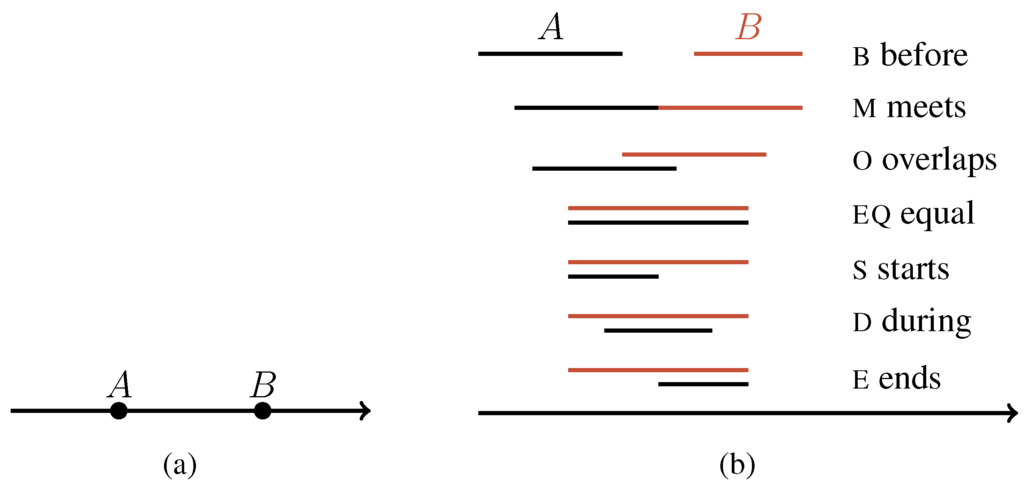
Figure 3.
Qualitative calculi capturing basic ordering knowledge for comparing values and constructing spatial relations. (a) Point calculus [12] with relations , it holds ; (b) Allen’s interval relations [13], for every relation except EQ there exists an inverse relation suffixed by “i”, e.g., .
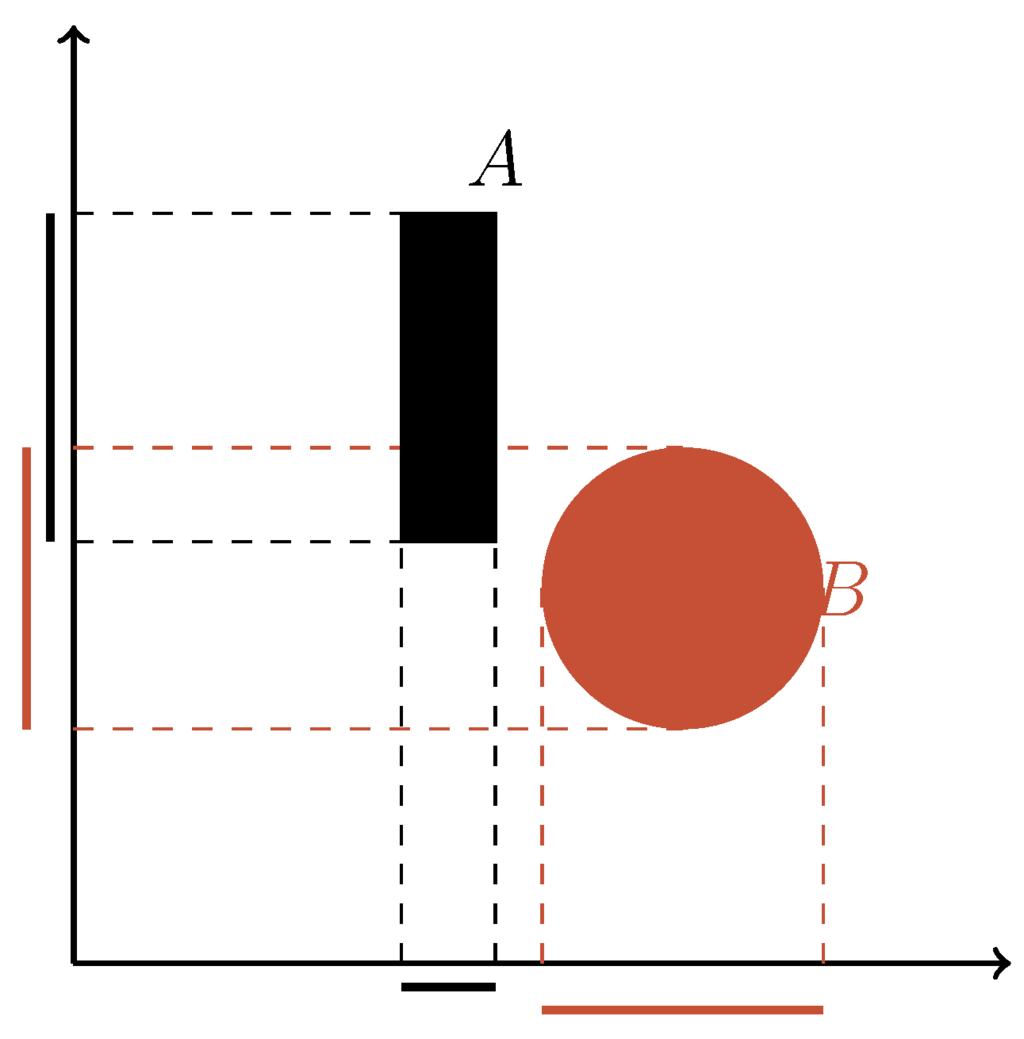
Figure 4.
Spatial relations in the block algebra [14] constructed from Allen’s interval relations shown in Figure 3b, it holds .
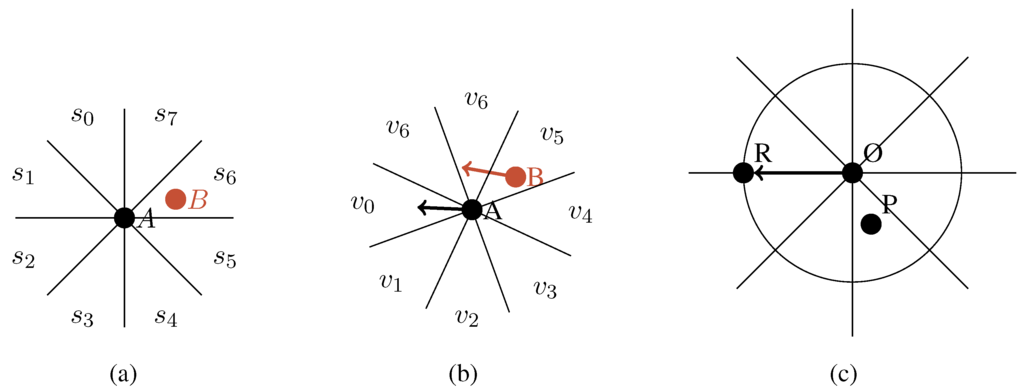
Figure 5.
Qualitative spatial calculi for representing and reasoning about point locations in two-dimensional space. (a) Cardinal relations in star4 [15], it holds s6(A,B); (b) Directional relations in StarVars [16], arrows represent orientation. It holds v5(A,B); (c) Ternary tpcc [17] relations, P is in relation “close back left” with respect to origin O and reference R.
Qualitative relations can be regarded as constraints over variables, for example the relation restricts the position of “can” and “desk” such that “can” is atop the “desk” and in contact. Qualitative reasoning is thus widely considered as a form of constraint-based reasoning. In this case, the elements of a qualitative representation are constraints:
Definition 1.
Let r be a (binary) qualitative relation and be either variables representing spatial entities or constants. A formula is then called a qualitative constraint. We say that a qualitative constraint is satisfiable if values for all variables involved can be chosen such that they stand in relation r. Similarly, we say that a constraint is satisfied for concrete entities (constants) and , if holds. The mapping (also called interpretation) is then called a model of the formula .
Since it is intuitive, we use r to describe the relation of domain values as well as a symbolic label to write down statements. Hence, on represents a spatial relationship between objects in a scene and on is used to compose declarative statements too. Given a spatial scene, we describe the scene by the set of qualitative constraints satisfied by the domain objects. For a fixed repertoire of relations, we use the conjunctive formula of all satisfied constraints to describe a spatial configuration.
Example 1.
Consider the scene shown in Figure 6 and the block-algebra relations shown in Figure 4. For readability we introduce shorthand notations of important block-algebra relations, recalling that stands for and thus captures disjunction with qualitative relations:
The semantics of relation above is thus that in a projection of objects to the Y axis one object occurs before the other, whereas there are no constrains with respect to the X axis. Then, the scene depicted in Figure 6 can be described as follows:
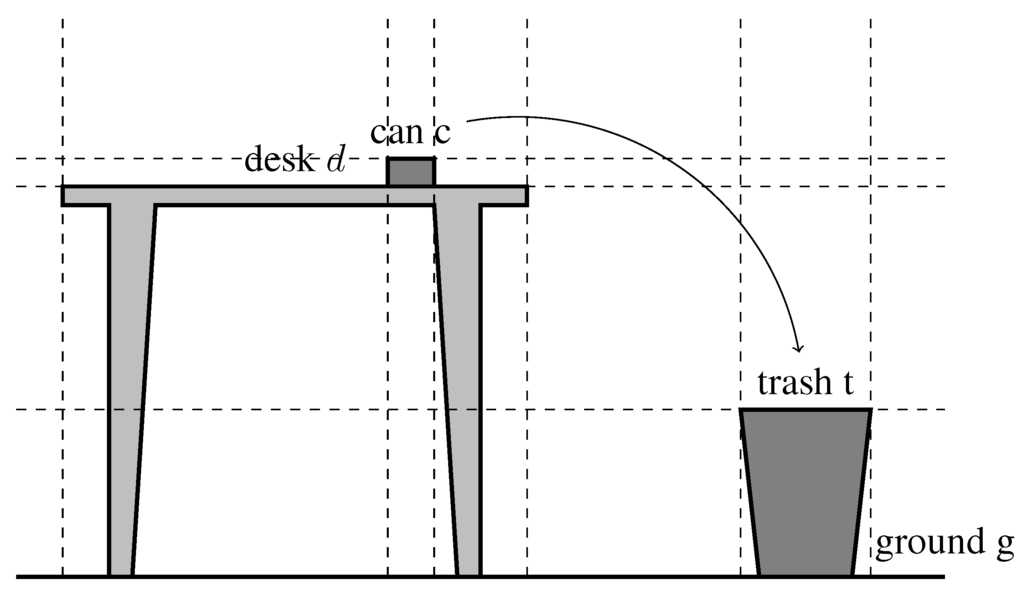
Figure 6.
Example task configuration with partitioning of qualitative relations according to the block algebra.
Not all constraints given in Equation (1) are necessary to describe the scene unequivocally to the level of abstraction of the block algebra, for example the fact is derivable from knowing the can to be positioned above the table and the table to be positioned above ground. Qualitative reasoning techniques allow such inferences to be performed by identifying that a statement logically follows from another.
In our work we assume that any qualitative description provided during programming is automatically supplemented to include all derivable facts by means of qualitative reasoning. For the relations described here except for the ternary tpcc relations, qualitative reasoning can be realized by efficient Linear Programming techniques as described in [20]. This is due to the fact that these relations represent regions which can be described as linear inequalities, for example the block algebra relation can be described by the inequality , where stands for the maximum value of the bounding box of desk d and for the respective minimum value.
2.2. Spatial Logic of Manipulation Tasks
Our approach of representing the development of qualitative spatial knowledge over time is based on linear temporal logic (LTL) [21]. LTL extends propositional logic by interpreting propositional formulas not only with respect to one assignment of symbols to truth values, but with respect to an infinite linear sequence of assignments, called worlds. A statement may hold in one world, and it may be false in another. LTL is widely used in software engineering and program verification, but it has also received attention from the autonomous robotics community since the 1990s—see [22]. So far, LTL has been applied to declarative specification and synthesis of controllers from a high-level specification [23] and it is also applied for motion planning [24,25,26]. Similar to the approach described in this paper, Kreutzmann et al. [27] apply LTL to specify processes in logistics declaratively.
In the following we describe the spatial logic underlying our approach as a straightforward combination of LTL and qualitative constraints as introduced in Definition 1. In short, we use plain LTL but replace all propositional symbols with qualitative constraints. Details of LTL are not important for this paper, so we only give a rather intuitive account of the logic—a comprehensive introduction to LTL may be found in [28].
2.2.1. Syntax and Semantics of Qualitative Spatial Logic (QSL)
A well-formed formula ϕ in QSL is defined by the following grammar rule:
Here, C denotes a qualitative constraint as defined in Definition 1. For brevity, we only define a minimal set of operations. Other Boolean operations can easily be expressed by term rewriting, e.g., . In the following we assume such rewriting to be performed whenever required and make use of all usual operators and conjuncts. Semantics of LTL can be defined using a Kripke structure : The interpretation function I assigns truth values to the constraints independently for all time points . Technically, maps a constraint to the set of time points at which it is satisfied.
Example 2.
Consider the two snapshots shown in Figure 7. At time , the constraint touches(b, g) is not satisfied, at time it is. A Kripke model representing this development of the world would interpret touches(b, g) to be false at time , so we have (touches(b, g)), but (touches(b, g)). If we imagine the ball to be bouncing off three times, we would have (touches(b, g)) .
Using to refer to a subsequence of , the semantics are defined as follows.
With this definition, some frequently used and useful temporal operators can be defined. Table 1 summarizes the common temporal operators.
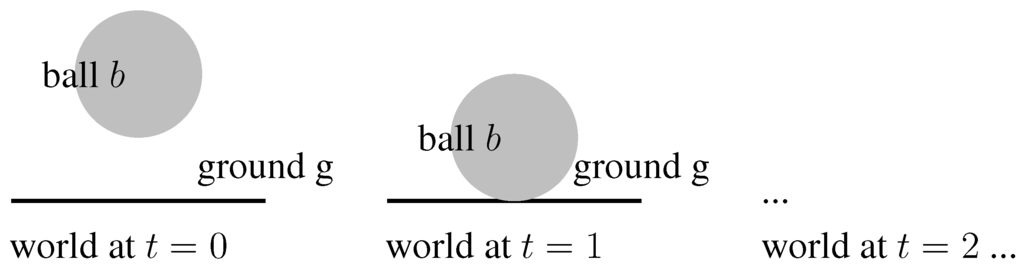
Figure 7.
Two snapshots of a scene.

Table 1.
Temporal operators in LTL and QSL.
| ∘ | next | holds in next world |
| ⋄ | eventually | |
| □ | always | |
| until | ϕ holds until ψ holds at some point in future | |
| release | ϕ released ψ, if ψ stops to hold at some future point, ϕ will hold, |
2.3. Reasoning with QSL
Given an interpretation of spatial constraints for all worlds, the task of deciding whether a sub-sequence of the world is a satisfying assignment of a given formula is called model checking. In our application we apply model checking for instance to identify whether an observed process suits a declarative description of the task to be performed. The interpretation of the constraints is thus determined by the observation. A constraint is is considered to be true, if the relation r between the objects referred to by variables X and Y is observed.
Beyond knowing that a sequence of observations constitutes a model for a formula, we are also interested in identifying when the formula gets true. For example, by model checking the formula we seek to identify the first time point at which ball and ground get into contact. To this end, we adapt the notion of model checking to our needs:
Definition 2.
The model checking problem in qualitative spatial logic is the task to compute for a given formula ϕ and a Kripke model such that t is the smallest number such that . If no such time point exists, the value ∞ is returned.
Example 3.
Suppose, S is the formula given in Equation (1) from Example 1 and G is constructed the same way, but saying that the can is inside the trash. Then we can describe the task of getting the can from start configuration S to goal configuration G simply as . We may be interested to analyze an action sequence performed by the robot in order to identify whether it matches the task . Similarly, we may be interested in model checking the action performed against the formula in order to identify whether the robot has been throwing too short since the can is still left of the trash at the first time it touches the ground.
Model checking with LTL is due to its PSPACE-completeness computationally demanding, even in case of bounded models. Several approaches explore the computational properties of model checking and several algorithmic subclasses have been identified that are characterized by which (modal) operators are employed [29]. Model checking of manipulation tasks specified in the LTL-like logic QSL benefits from two characteristics:
- Task specifications gain their expressivity from the rich set of spatial primitives that can be employed, not from the complex temporal interrelationships which makes model checking hard.
- Tasks are of short duration and models derived from observing the process are thus small. For example, throwing a ball takes few seconds only, which if observed at 100 Hz rate only leads to a few thousand worlds.
In our application a simple search turns out to be sufficient—in a more complex setting an optimized implementation may be advantageous, which can be obtained automatically as described by Gebser et al. [30]. Alternatively, a potential computational bottleneck in practical applications could be tackled with efficient randomized approaches such as Monte Carlo model checking [31]. For illustration we determine computation times of model checking with variations of the formula from the example above, using nested until-terms to represent hitting the ground i times and bouncing off it in-between:
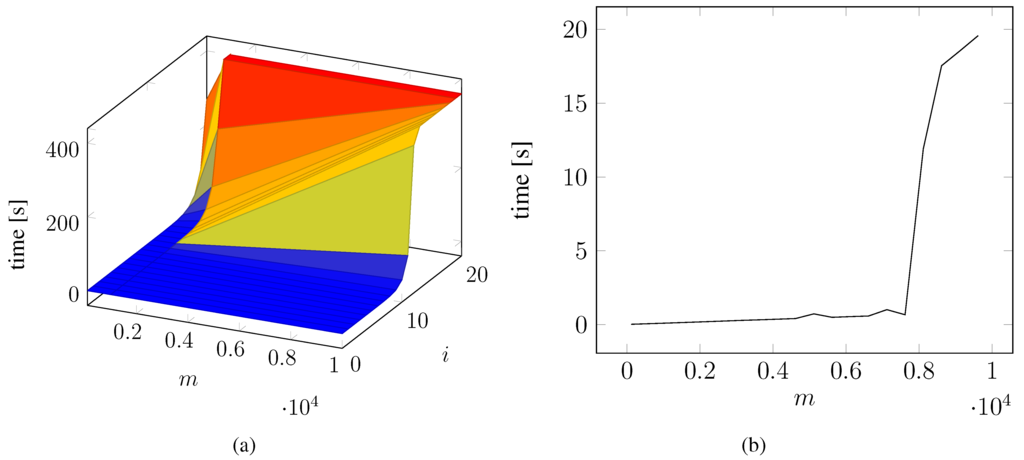
Figure 8.
Computing time of model checking against a model of size m. (a) Computing time by model size and formula complexity, capped at 400 s; (b) Computing time for by model size.
We apply model checking for several , using states grounded in the physical simulation of a ball hitting the ground and bouncing off again repeatedly. Additionally, we vary the size of the model by changing the sample rate. For evaluation we used a single core on an Intel i7 processor running at 2.3 Ghz, yet we are only concerned with a qualitative analysis here. In Figure 8 we present the computing times of a naive model checking implementation that recursively checks whether the input formula is satisfied in a world using linear iterative search. Figure 8a shows a 3d plot of computing time against model size () and formula complexity (), capping computing time at 400 s. The combinatorial explosion occurring with model checking can be nicely seen, but it occurs even in our naive implementation after a nesting depth of 10 existentially quantified modal operators which is significantly more complex than typical task specifications of a single learning task. To provide a closer look at the times, Figure 8b presents the computing time of model checking against the total model size. As can be seen, for model sizes below 6000 data points (which would correspond to 60 s of real time if data points are collected at 100 Hz), computing time is significantly below 1s. The sudden rise in computing time at around 8000 may be due to poor memory handling in our implementation. This exemplifies that computing times of model checking a typical task specification against observation is indeed feasible.
3. Qualitative Spatial Logic in Learning and Planning
We use QSL to represent tasks and common sense rules representing background knowledge. By reasoning about observations using QSL we provide control to learning and planning.
3.1. Determining and Classifying Instances for Learning
In order to generate training data we generate random control parameters and observe their effects using the robot simulator. We assume that observations grant access to object parameters referred to in the task description such as position in space, direction of movement, etc. This is usually accomplished by interpreting sensor data and not in the scope of this work. We regard observations as time-stamped sequences of mappings from object properties to concrete values. These mappings induce an interpretation function and thus Kripke model in the sense of QSL. We define the interpretation function I to assign truth to a qualitative constraint with relation r holding between between objects at time point t, mathematically , if the constraint is satisfied by the observation at the respective time point.
In order to specify which data from the sequence of observations is to be used as training data alongside the control parameters, we perform model checking. We write a logic formula to specify the time step from which data is to be obtained and denote the respective object properties. Since the model of a formula may cover several time points in the observation we mark the part of the sub-formula which designates the time point we are interested in.
Example 4.
As training data we seek to collect the position of an object o thrown by the robot at the first time o hits the ground g. We represent this objective as a pair where ϕ is formula with a marked sub-formula that describes ‘hitting the ground for the first time’ and P the set of properties to retrieve. In our example we would have
Here, is a qualitative relation from the block algebra that describes contact in the dimension “height” (object is “met by” the ground, see Figure 3b. Model checking the entire formula would identify a model that covers all time points until finally holds. Therefore, gets marked (denoted here by an underline) to say that we are interested in the time point of the model at which becomes true.
The RobotLearningLanguage supports a generative and an analytical mode to use these models. For the generative mode, RoLL checks for an observed data point whether the specification is satisfied and only if it is, the data is stored in a database to be potentially used for learning later. In the analytical mode, the data in the database is later analyzed by model checking. In this way, different specifications can be applied to the same data, generating different sets of learning data, leading to different forward models. This flexibility in the language principally opens up the possibility to generate constraint sets automatically and test them in a meta-learning cycle, i.e., RoLL could employ several alternative specifications of the task for learning in parallel, automatically selecting the specification which leads to the best learning performance.
3.2. Enhancing Efficiency of Action Planning by Reasoning
The aim of planning is to determine a control action that makes the robot achieve a concrete goal. Planning relies on the forward model determined by the learning element. Mathematically speaking, we aim to minimize where f is the forward model, a a control action, and g the goal to achieve. A common approach to solve this problem is to sample the space of control actions until a parameter is found that is sufficiently close to the goal. Sampling-based methods have the advantage of being independent of the characteristics of the forward model. For instance, they are not susceptible to local minima as approaches relying on local search. The disadvantage of sampling is, however, that it may require many iterations until a suitable parameter is sampled, in particular if only a small fraction of the parameter space is mapped by the forward model sufficiently close to the goal.
In our approach we adopt the general schema of sampling the space of control actions, but we employ reasoning to steer sampling towards the areas of the search space that are more likely to contain the desired solution. At this point, background knowledge comes into play. Due to its nature, background knowledge may oversimplify and thus may lead to wrong consequences for a problem at hand if it gets applied in a strict manner. A sampling-based approach counter-acts this problem as it only leads to avoiding parts of the search space—it will never ignore a part of the search space completely.
Technically we proceed as follows. At the start of planning, a function , is initialized that ranges over the space of control actions A. The idea is that d captures the probability goal , d is not a probability density function in the mathematical sense as we do not require . But there exists a bijective mapping to a probability density function with with an appropriate scaling factor α. Therefore we say that d represents a probability distribution. We do not require to be satisfied, simply for the benefit of easing presentation and implementation.
In order to determine a random action we sample according to the distribution represented by d. To this end we discretize A, which may be a high-dimensional space, into discrete cells and perform for each cell numerical integration over d, obtaining values . In our implementation we fix . The sum of all cells gives the area of the graph d, i.e., . By uniformly sampling x from we identity cell with and then sample uniformly from the parameter space represented by cell . This approximates sampling according to arbitrary distribution d.
Key of our approach is to modify d given knowledge about previous control action a and the resulting effect according to the forward model. In a way we learn a suitable distribution by reasoning. To this end, we represent inference rules from which we can derive a suitable update of d.
Definition 3.
We call an inference rule if Φ, called the premises, and Ψ, called the conclusion, are QSL formulas without temporal modal operators, i.e., both are Boolean constraint formulas. Additionally, Ψ contains free variables that represent action parameters.
The idea underlying this definition is that a premises describes a specific class of outcomes as predicted by the forward model if action is performed. Typically, a premises captures a class of failed attempts to solve the task at hand. Since we are only concerned with achieving a static goal situation, no temporal modal operators are involved. The corresponding conclusion then describes how a future attempt to solve the task should relate to a. In other words, conclusions describe where in the space of control actions a suitable action parameter can be found, given the premises was satisfied. A premises is said to be satisfied if the formula evaluates to true, interpreting truth values of the qualitative constraints according to and goal g. Mathematically speaking, goal g and constitute a model of the premises and we can thus employ our standard model checking procedure with goal g and defining the interpretation I of the only one world in this model.
Example 5.
Suppose we have trained a forward model to predict the position at which object o will hit the ground if it is thrown with single control action , where a gives the impulse delivered to the object. For simplicity, we only consider a one-dimensional space of control actions in this example. The description of the goal identifies the target position and the position of the robot . A suitable common sense rule is the following, expressed using a relation from the star calculus (see Section 2.1 and Figure 5a):
Given , the expected landing position can be determined by the forward model. The premise says that if the robot has to throw in direction , but the object will land in with respect to the goal, it has thrown too far. Therefore, the conclusion constrains the impulse of future attempts to values smaller than a.
We apply conclusions by modifying distribution d according to the qualitative relation described by the conclusion. It is a task of qualitative reasoning to identify the parts of the control space A that satisfy the solution, we write to refer to the region of A in which satisfies the conclusion. Since our qualitative relations are expressible using linear inequalities, this task is simply a matter of hyper-plane intersections. We then determine a modifier to update d. This function decreases from the border of if moving farther outside :
Finally, we update d by setting . Re-using the discretization of A employed for sampling, this task can easily be solved in a discrete manner.
Example 6.
Continuing the previous example, assume we are confronted with an action that satisfies the premises, i.e., the robot was throwing too far. In the case of we would conclude and obtain the modification function shown in Figure 9a. The desired action is of course unknown to the robot but is marked in the graph for illustration too. After three attempts of throwing either too far and not far enough (assuming a corresponding rule analogous to the one described before given), the function shown in Figure 9b is obtained. It can be seen that the graph of this function concentrates around the desired action , steering sampling towards retrieving a suitable action.
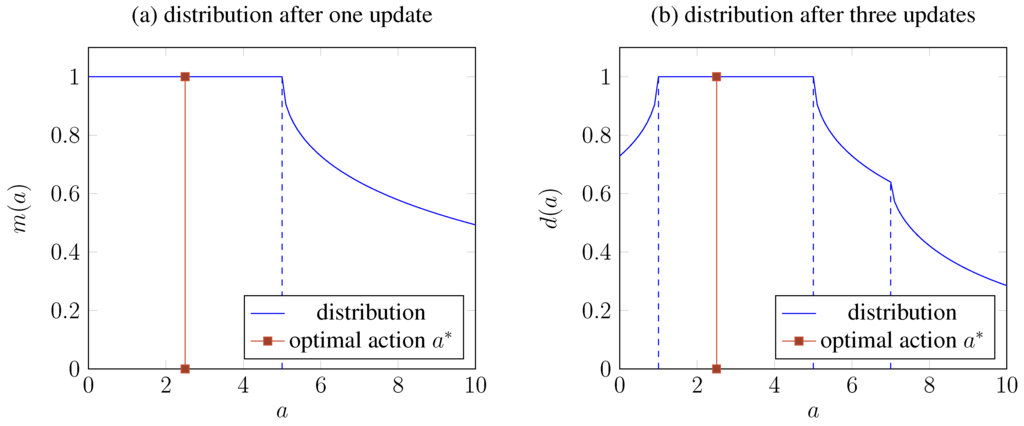
Figure 9.
Updating the representation of a distribution based on sampled actions and qualitative inference leads to a concentration around the desired but unknown action . (a) after evaluating action ; (b) after evaluating actions 5, 1, and 7.
4. Evaluation of QSL-based Reasoning for Planning
We implemented knowledge representation and reasoning with QSL in LISP as an extension of the Robot Learning Language (RoLL) [6] which provides integration with a robotic platform or simulation thereof as well as with the WEKA library [32] for machine learning.
For this part of the analysis we focus on the effect of QSL-based reasoning. We thus need to eliminate effects caused by the learning element and a potential bias of the forward models learned. To this end, we isolate the physical simulation from the robot simulation environment. We compare the performance of our QSL-based approach to planning with pure sampling, varying between idealized and realistic conditions for the learning component.
4.1. Experimental Setup
Physical simulation in MORSE is based on the popular Bullet physics engine (http://bulletphysics.org) and we have written a simple simulator in C++ using Bullet to simulate ball throwing, linking it directly with our RoLL program. Our environment contains a ball of 10 cm diameter and 1 kg mass in an empty world with an infinite ground plane and natural gravity. Since a robot arm essentially controls where an object is released and at which direction and speed, we directly utilize these parameters as control actions. The robot is positioned at the origin.
- height of release over ground between 0.5 m and 1.5 m
- vertical velocity between −1.0 m and 3.0 m/s
- horizontal velocity between 0.0 m and 3.0 m/s (negative values would be symmetrical)
Additionally, the simulation can be configured to apply random forces to the ball. If enabled, we apply a force drawn from a normal distribution with unit size Newton every cycle of the simulation, leading to scattered landing positions as shown in Figure 10.
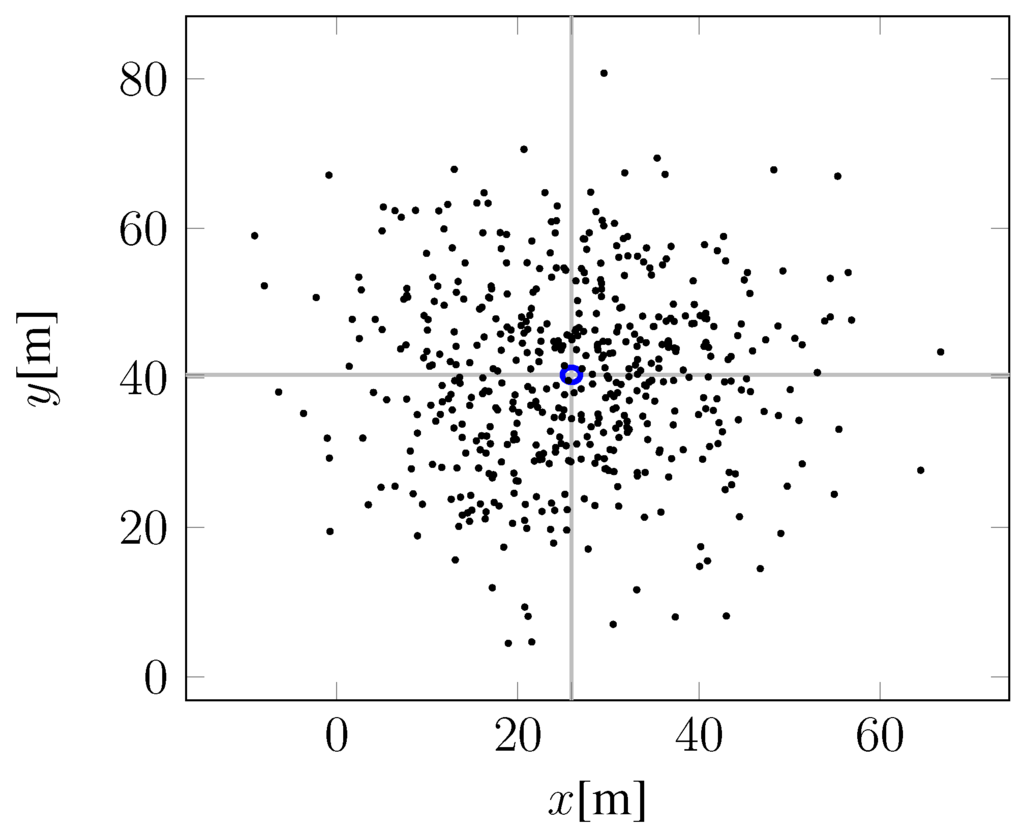
Figure 10.
Landing positions in simulation with added noise, the position obtained with no noise is marked blue.
4.2. Learning the Forward Model
We determine four distinct forward models from training data sets of different characteristics. Training data is computed by systematically varying the possible input parameters, and invoking the physical simulation to determine the throwing distance achieved. To this end, we discretize heights with step size of 0.2 m, vertical and horizontal velocities with 0.3 m/s each. In total this results in 6 (heights) × 14 (vert. vel.) × 11 (hor. vel.) = 924 possible data points and their respective throwing distances achieved. These 924 data points are determined once with noise added and once without. The idea of considering noise-free data is to enable comparison with an idealized input to learning. In the same spirit, the 924 data point evenly distribute over the parameter space to provide an idealized unbiased input to the learning module. For the realistic use case, we create another data set by randomly choosing about 10% of the full data set. We draw a random number between 0 and 1 for each data point, only including it when the random number was below 0.1. Because of this procedure, the resulting data sets do not have exactly the same size.
For each data set we learned a model tree using the M5’ algorithm from the WEKA toolbox [7]. Table 2 lists the four data sets and shows the respective error ratings obtained in the cross validation by WEKA. We observe similar absolute errors in the following experiments (cmp. Figure 12). The table also shows the minimum and maximum throwing distances from each data set to provide a rough overview of the learning data.

Table 2.
Overview of learned models with their underlying data and the obtained errors reported by WEKA for cross-validation. MAE: mean absolute error, RMSE: root mean squared error
| Noise in | Number of | Observed Distances | Learning Errors | ||
|---|---|---|---|---|---|
| Environment | Training Instances | Max | Min | MAE | RMSE |
| no noise | 924 | 0.0149 | 2.57376 | 0.0 | 0.0205 |
| no noise | 73 | 0.0594 | 1.88315 | 0.0 | 0.079 |
| noise | 924 | 0.1466 | 3.01778 | –0.32156 | 0.1939 |
| noise | 89 | 0.1943 | 2.8557 | –0.32156 | 0.258 |
4.3. QSL-Based Reasoning for Planning
We use the method described in Section 3.2 to plan by sampling from a distribution over possible actions, updating the distribution after some attempts. The common sense rule we use in the experiments is simple: increase velocity in horizontal and vertical direction if you wish to throw farther, reduce to throw less far. This is captured by the following two rules that are similar to Equation (4) in Example 5, but exploit the fact that only parameters to achieve distance d are to be determined:
Here, g stands for the desired goal distance and d for the distance achieved by the attempt using and as action parameter for horizontal and vertical velocity. The variables and represent parameter values to be used in future attempts as described in Section 3.2.
These rules are applied every four steps in the sampling procedure, updating the distribution according to the rules applied to the best action sampled with the last 4 steps as input to the reasoner. The motivation of only updating every fourth step is that sampling regularly generates outliers that if used with reasoning do not lead to significant change of the distribution.
4.4. Determining the Iteration Cutoff
In a first experiment we wish to identify a suitable limit of the number of iterations necessary for planning. By fixing a reasonable limit we can eliminate this parameter from further experiments. To this end we vary the maximum number of iterations from 10 to 100. For each value we randomly generate 100 goal distances within the range of observed distances in the full-sized noise-free data set and run the pure sampling as well as the QSL-based method, recording the average deviation from the desired goal distance. This result is shown in Figure 11.
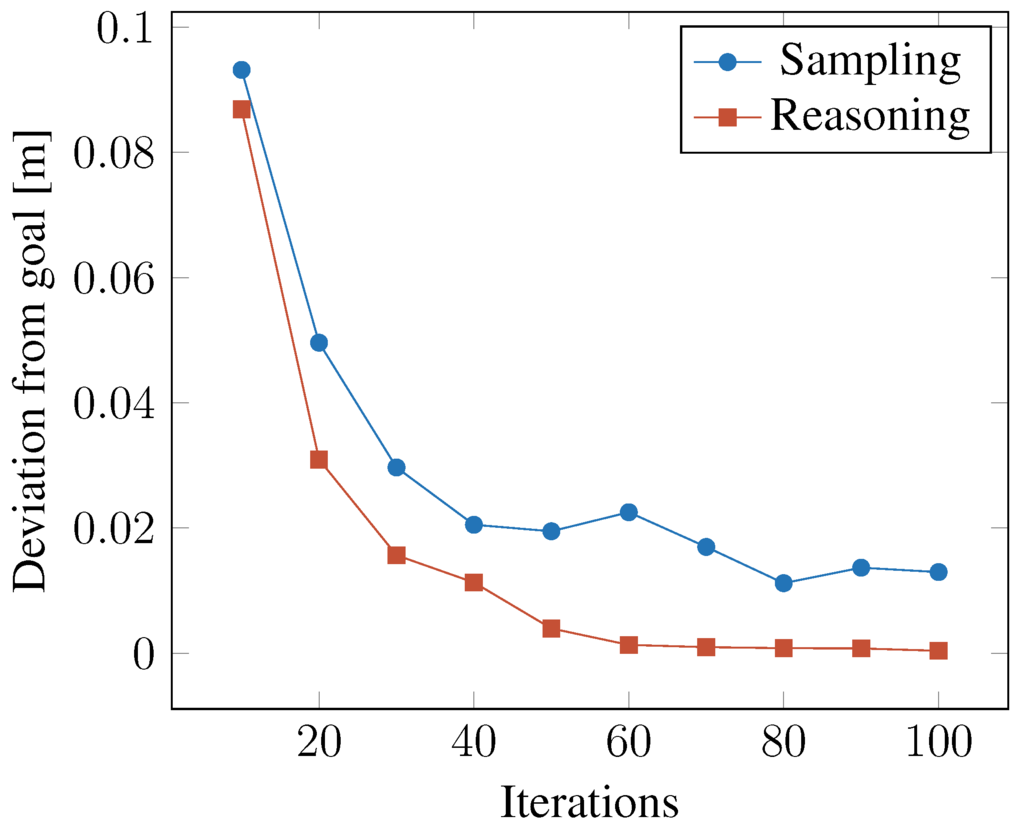
Figure 11.
Accuracy of search procedures with model no-noise, all data.
Figure 11 shows that the QSL-based method finds parameters that—according to the learned forward model—would produce better parameters for the throw than with uninformed sampling. Most importantly at this point, the deviation from a desired goal value does not significantly improve with more than 50 iterations. For the following experiments, we therefore set the number of maximum iterations for the planning process to 50.
4.5. Planning Quality
Next, we ran 100 trials with random goal distances for each combination of the four forward models listed in Table 2 and the two planning options. The trials were always performed in the same environment (no-noise vs. noise) as in the environment, in which the learning data was observed.
Figure 12 confirms the training error from Table 2 on the test sets. The box plots depict the median error values as a line, the box boundaries show the upper and lower quartiles. Because the data shows a long tail towards high error values, we chose the whiskers to extend twice as long as is usually done in boxplots. Even with this adjustment, there are many outlier points towards higher errors. A Student’s t-test shows that the loss in prediction quality from the reduction in data is statistically significant both for the no-noise data () and even more pronounced for the noisy data (). The effect size after Cohen shows a small effect () for the artificial data without noise, and a medium effect () for the more realistic noisy data.
Figure 13 shows the deviation from the goal, i.e., the resulting difference of the predicted throwing distance and the target distance. As in Figure 11, the QSL-based method exploiting qualitative reasoning lowers the error on average (, ), but also reduces the spread of the results (, ). The difference is statistically significant (). The results thus confirm the first experiment and also generalizes it to all data sets considered. Still, in all cases, the computed actions are predicted to be very close to the target distance.
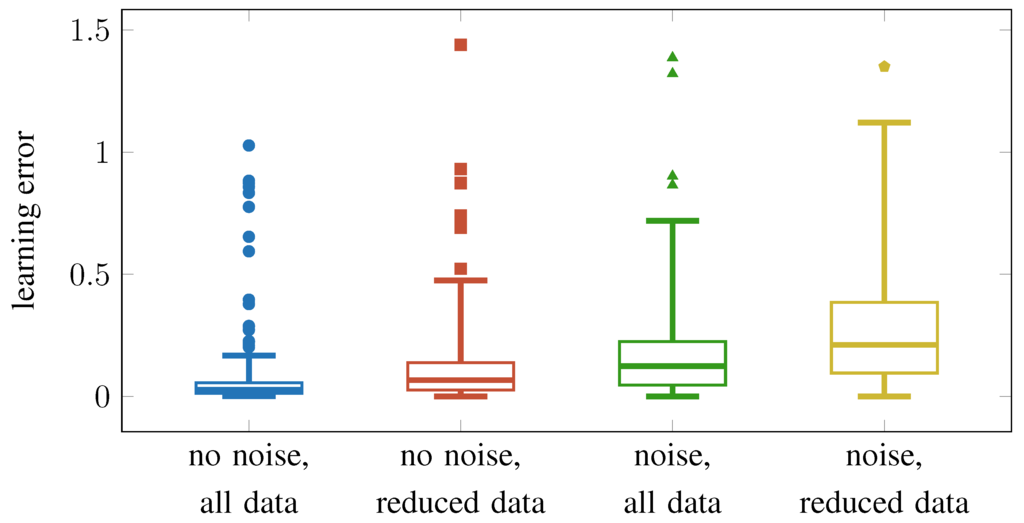
Figure 12.
Prediction error measured in 200 test tasks, depending on the data used in the learning process. Values outside of 3 inter-quartile ranges are considered outliers.
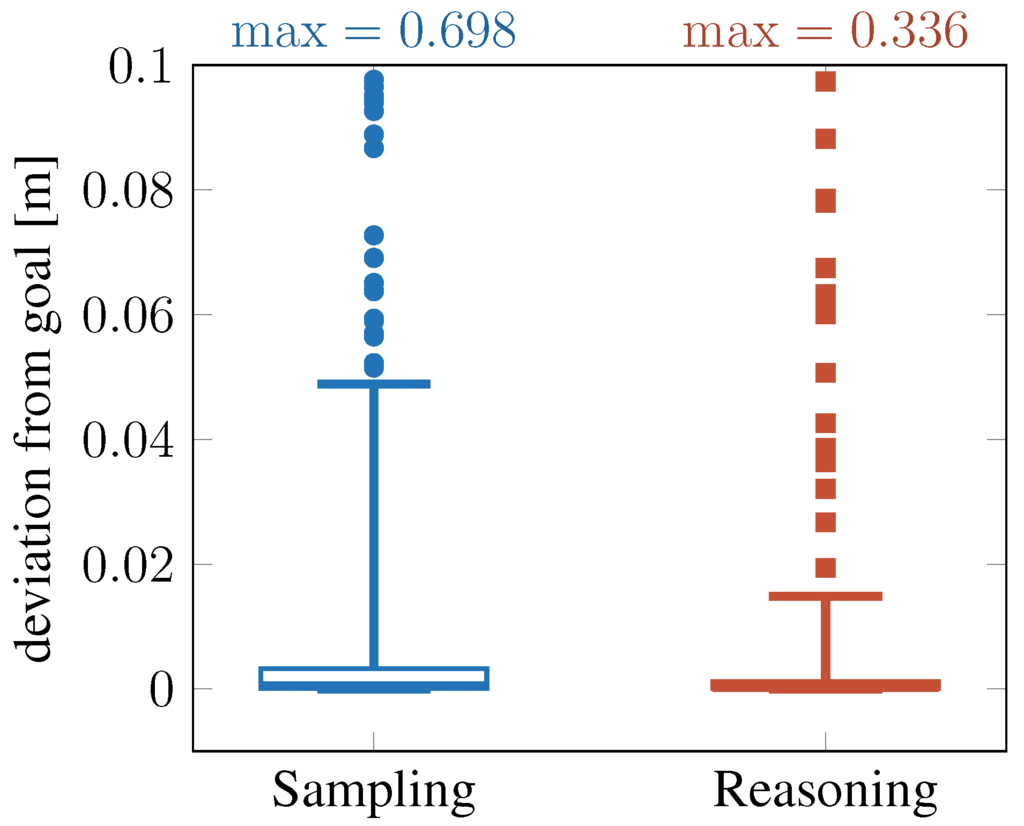
Figure 13.
Planning error measured in 400 test tasks, depending on method. Values outside of 30 inter-quartile ranges are considered outliers, not all outliers are shown.
Figure 14 shows the total error of our learning-and-planning approach. The resulting error is mostly due to the learning inaccuracies. As shown before, the reduction of data usually results in significantly worse results (except for the data of the no-noise condition with sampling with , for all other pairs of all-data/reduced-data ). Reasoning lowers the average error significantly with all data sets () except the no-noise, reduced-data set () Also reasoning results generally in a lower spread of the results, thus making the process more reliable.
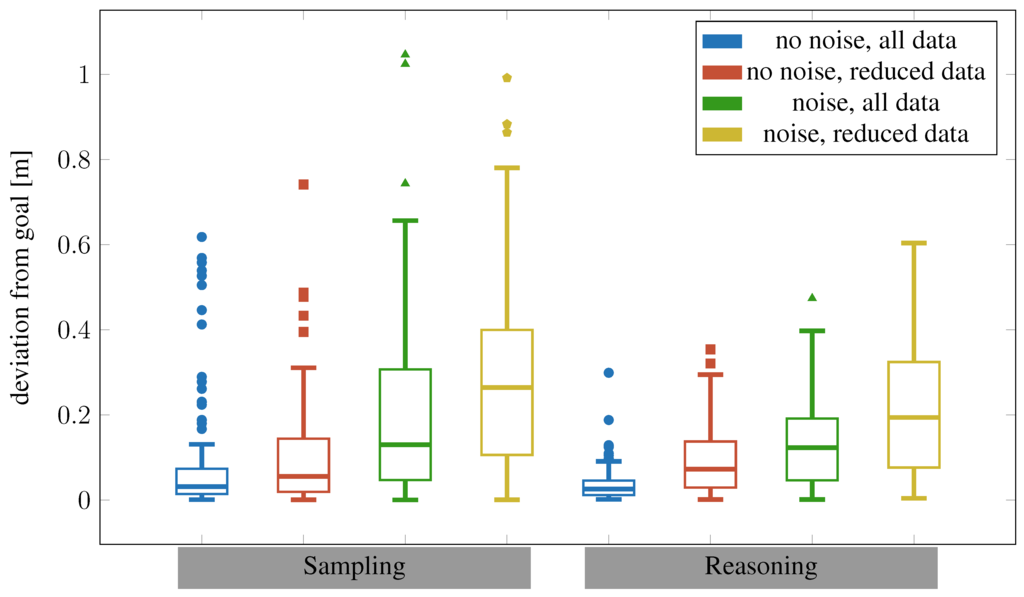
Figure 14.
Total error measured in 100 test tasks with different models and search models. Values outside of 1.5 inter-quartile ranges are considered outliers. All models are tested in the environment in which they were learned.
4.6. Transfer of Planning
It is generally a lot easier to gather learning data in simplified simulations than in realistic simulations, let alone with real robots. This is why we were interested, if models learned in a simplified environment might still be useful in more complex, noisy environments. We therefore use the models learned from no-noise training sets with planning in the noisy environment. Again, we randomly generated 100 test tasks. Figure 15 shows the results of the overall learning-and-planning procedure. The values for the noise-models are identical to those in Figure 14, we only included them for a better comparison.
Interestingly, the model learned from the reduced data set is even slightly better when used with reasoning than the one with the full data, but the effect is not statistically significant (). This may be due to the different complexities of the learned models in context of a simple physical relationship. While the model tree learned with the full data set has a depth of 6 and contains 52 leaf nodes, the model learned from the reduced data set only has depth 2 with 3 leaf nodes. Assuming that in real-world settings it is only possible to gather small data sets (which corresponds to the noise, all data condition), the use of possibly larger data sets gathered in a simulation without noise is a promising approach. The improvement of using the full data set gathered under idealized conditions over the reduced noisy data set is statistically significant for the sampling approach (), but not for the reasoning approach (). In the latter case, the improvement of using the reduced idealized data set as compared to the noisy reduced data set is statistically significant () with a significance level of . So a reduction in data may be beneficial, especially when this reduction is not random, as we will see in Section 5.
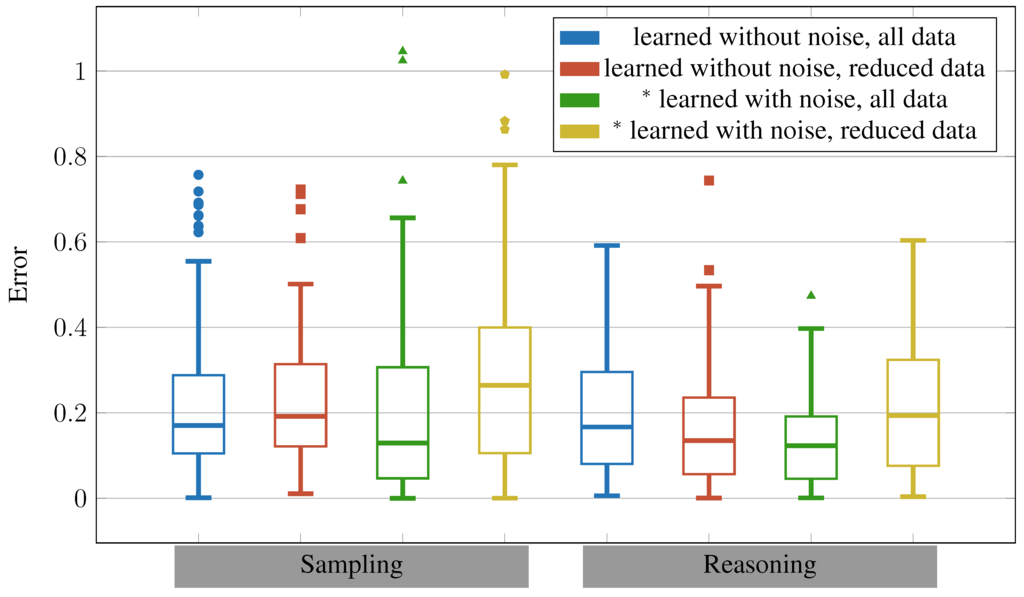
Figure 15.
Total error measured in 100 test tasks. All models noise are applied in the environment with noise (the results for models that were learned with noisy data are identical to the ones in Figure 14, they are marked * and shown here for better comparison). Values outside of 1.5 inter-quartile ranges are considered outliers.
4.7. Discussion of the Results
Already the first experiment on the number of iterations necessary for planning shows that QSL-based reasoning outperforms pure sampling in terms of deviation and in terms of the number of iterations necessary to determine a control action of specific quality (see Figure 11).
Figure 13 shows the deviation from the goal, i.e., the resulting difference of the predicted throwing distance and the target distance. As in Figure 11, the QSL-based method exploiting qualitative reasoning lowers the error on average, but also the spread of the results. The results thus confirm the first experiment and also generalizes it to all data sets considered. Still, in all cases, the computed actions are predicted to be very close to the target distance.
The experiment on transferability from simplified simulation to realistic conditions is particular interesting as it addresses a typical use case in robot software engineering: learning in simulation but application on the real platform. The results show that the proposed method can handle this situation, the QSL-based approach degrading less than the sampling-based method.
In summary, the evaluation of planning shows that employing the QSL-based method outperforms in all cases a pure sampling-based planning method. The results on transferability indicate further that models from a simplified environment can well be applied to more complex environments using the proposed method.
5. Evaluation of Reasoning for Learning
In the previous section we generated data with the Bullet simulation engine by specifying the velocity and direction of the ball at the moment of throwing. Neither humans nor robots can throw objects in this way, directly controlling launch parameters: they have to move joints in a specific order with specific timing. Another simplification of the Bullet simulation is that it happens in an open space with no objects around other than the ground and without any embodiment of an agent. In a real throwing situation, the object can bounce off other objects or the robot itself. Because of the indirect control of the throwing parameters and obstacles in the world, the data in a more realistic setup gets much more noisy. In particular, objects may not fly in the intended direction, but may land behind the robot (for example, if the arm is moved to vigorously) or at any place by bouncing off. In the following we show in a more realistic setup, how a QSL-based specification of the task can be used to remove outliers from the observed data and how this helps to improve the learning result. In the previous section we saw that a random reduction of data leads to poorer predictions. Here we want to show that a goal-directed filtering of the data is necessary in more realistic setups.
In the following we first present the more complex experimental setup with a realistic robot simulation. Then we describe the qualitative models used in this experiment to remove outliers from the gathered data. Finally we show the results of learning the prediction models with data sets filtered with different qualitative models.
5.1. Experimental Setup
For overall simulation of a sophisticated platform we employ MORSE [8,9], a versatile simulator for complex robot interaction scenarios, to simulate a Willow Garage PR2 robot in a kitchen environment shown in Figure 1. We chose MORSE because it uses the Bullet physics engine and because it provided a realistic household environment and a fully modeled state-of-the art robot. For throwing objects in outdoor scenarios, additional parameters such as air drag and turbulence could be important. But in this paper we are not concerned with finding the perfect throwing algorithm, but rather use this task to demonstrate our reasoning-and-learning approach.
MORSE is configured to connect to the robot operating system ROS (http://www.ros.org) [33] as middleware. The learning and planning procedures implemented in RoLL then connect to ROS in order to control the robot or to retrieve observations. Neither the PR2 robot nor its control architecture with the ROS middleware are designed for throwing objects. To make the robot throw an object (in our case an empty jar), we first move the elbow and wrist joints of the right arm to a low position. Then the robot moves the two joints to a new position, with a specified time to perform the movement. After half the time that the movement should last, the robot lets go of the object. In this way, our throw can be determined by five variables:
- elbow joint at start/end configuration
- wrist joint at start/end configuration
- time in which the action is to be performed
In order to avoid problems related to gripping and releasing objects, the simulator is extended to attach and release objects to the manipulator (see Figure 1 left).
A full trial consists of the robot (1) moving to a pre-specified relative position in front of the object; (2) grasping the object with a predefined arm movement; (3) turning 90 degrees to the left; (4) throwing the object with the given parameters of lower and upper position and the total throw duration. With this procedure, uncertainties in realistic manipulation tasks are captured to some degree, like the orientation of the robot. But there are still parameters in real situations that are not modeled, for example the exact grasping point or the possibility of losing the object while turning to the throwing position. This choice was a compromise between a realistic setup and the efficiency of gathering data.
For the task of throwing an object into the trash, it would be most convenient to throw in a frontal direction, as we did in the Bullet simulation of Section 4. As a direct measure to achieve this, we only use the elbow and wrist joints of the PR2 robot, which move along the robot’s orientation axis. Depending on the specific throwing parameters, the robot can thus be expected to throw an object along its orientation axis, either in a frontal or backward position. But due to nondeterminism in the simulation (caused by small delays in the middleware and slightly different initial positions) and the presence of objects from which the thrown object can bounce off, the landing positions divert to other directions. Figure 16 gives an impression of typical outcomes in the data gathering process. To model this additional variation, we now learned two forward models: one that returns the expected throwing distance given the five input variables above (comparable to the model learned in Section 4) and one that returns the angular 2D deviation from a straight throw, also given the five input variables.
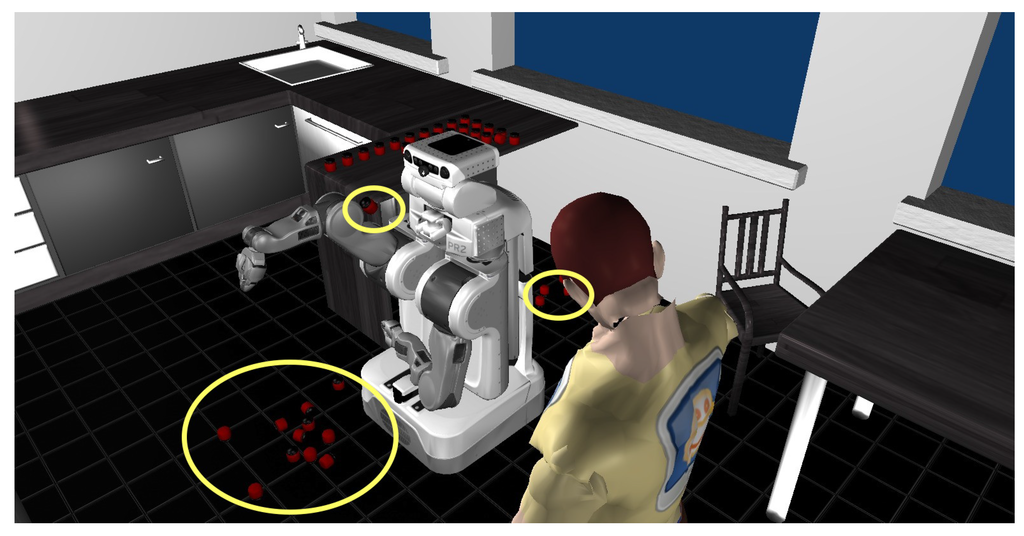
Figure 16.
Result from a data gathering run, showing highlighted landing positions on the floor behind the robot, on the robot, and the desired samples on the floor in front of the robot. Objects cannot bounce off the simulated human as he is modeled as a non-solid object. Its presence just simplified the positioning of the camera in the scene.
For gathering the data, random values of the input variables were generated. As with a real robot, data acquisition in the MORSE simulator is more painful than in the Bullet simulation. On the one hand, each throw needs a lot more time, because the robot first has to grasp an object, turn into a position without too many obstacles in front of it, and perform the arm movements. On the other hand, having several ROS nodes and the complex simulator running can lead to deadlocks and inexplicable crashes.
In total we collected 158 data points. They include runs, where the object landed behind or on top of the robot.
5.2. QSL-Based Task Specification for Filtering
The qualitative models in Section 4 served for guiding the reasoning process with the learned models. In the more realistic experimental setup with the MORSE simulator, we now have the additional problem that the observed data contains many outliers. Learning algorithms can deal with outliers to some extent, but a preprocessing step of the data to make it fit the goals of the learning task is often necessary when using real-world data [34]. To make this step explicit and based on explicit reasoning mechanisms, we define two qualitative formulas that describe our expectations of a frontal throw, and then use model checking for filtering the learning data. The StarVars formalisms is especially well-suited for this example, as it is primarily concerned with modeling directions.
5.2.1. Proper Throw
We specify that throwing is the process of the robot r holding an object o (body of the robot and body of the object are touching) until it is released once and forever. Finally the object lands on the ground g. Additionally, we demand that the object was thrown at least 0.5 m away from the robot’s center as otherwise it would have landed on the robot’s body. To this end, we introduce a point directly in front the robot’s base, 0.5 m off its center position. This yields the following formula:
Relation touch is written as disjunction of block-algebra relations in 3D, requiring the objects involved to overlap or meet in any dimension, i.e., b, bi are not allowed as relation (cp. Figure 3b).
Relation overlaps can be modeled with tpcc relations (cp. Figure 5 on page 259) by using the combination of all relations representing sectors within the circular close sector. In the labeling of Figure 5, the robot’s position r would be used as origin O, the front point would serve as reference point R. An object landing at the position marked with P in Figure 5 (close back left) would be regarded overlapping with the robot. In our implementation, however, we directly determine the distance to the robot and compare it against a constant value of 0.5 using point calculus relation “<”. Doing so we only have to deal with linear inequalities.
5.2.2. Throwing to the Front
We specify that a successful throw makes an object land in a 60 angle in front of the robot. This can be accomplished using StarVars relations (see Figure 5b on page 259) to describe positions in the X/Y plane (abstracting from height over ground). We use the variant of this calculus that uses 10 sectors in total, the constraint is captured by the following formula in QSL where r refers to the robot and o to the object thrown:
In fact, Formula (10) does not even allow the object to leave the front-sector temporarily, but this does not make a difference in our setup.
5.3. Learning Performance
We apply filtering by model checking the observations from an attempt against the task description as explained in Section 3.1.
The remaining training instances are used to learn the forward model for distance and direction respectively. Table 3 and Table 4 show the sizes of the resulting data sets and the learning performance.

Table 3.
Learning performance of distance model. MAE: mean absolute error, RMSE: root mean squared error.
| Used | Number of | Learning Errors | |
|---|---|---|---|
| Filter | Training Instances | MAE | RMSE |
| none | 158 | 0.2092 | 0.2565 |
| radius (Equation (8)) | 88 | 0.1021 | 0.1457 |
| frontal (Equation (9)) | 125 | 0.2217 | 0.2677 |
| radius + frontal | 80 | 0.0939 | 0.136 |

Table 4.
Learning performance of direction model. MAE: mean absolute error, RMSE: root mean squared error.
| Used | Number of | Learning Errors | |
|---|---|---|---|
| Filter | Training Instances | MAE | RMSE |
| none | 158 | 0.8058 | 1.431 |
| radius (Equation (8)) | 88 | 0.4164 | 1.1046 |
| frontal (Equation (9)) | 125 | 0.0156 | 0.0279 |
| radius + frontal | 80 | 0.0103 | 0.0178 |
The radius filter removes such samples where the object bounced off the robot body. Because of the non-determinism we get from slightly varying initial throwing positions (resulting from the robot’s own grasping and movement to the throw-off position), even the same throwing action can result in very different landing positions, depending on whether the object dropped directly or bounced off the robot’s arm. In many cases the object landed on top of the robot, getting stuck on the upper arm or between the arms (as shown in Figure 16). This constraint, however, does not filter for collisions with other objects, for example the refrigerator in front of the robot (see Figure 1). These bounces could be filtered with another rule, but as they happened rarely, we chose to leave them in the training set.
The frontal filter removes all instances with landing positions next to or behind the robot, the latter constituting the vast majority of cases. Only in the rare cases when the object bounced off pieces of furniture did the object land next to the robot.
For both forward models, the two filters improve learning performance, the order with respect to learning errors being identical for mean absolute error and root mean squared error. For the distance model the radius filter is most effective, while for the angular deviation model, the reduction to frontal throws shows the largest effect. This is not surprising since reduction to the front sector simplifies this prediction problem. The combination of both filters leads to the best results in both cases, reducing the mean absolute learning error for the distance model by –55.1% (–47.0% for the root mean squared error) and for the direction model by –98.7% (–98.8% for the root mean squared error).
6. Discussion
The experiments have shown that the overall performance of a robot employing the basic architecture of learning and planning can be improved in two regards. First, learning of forward models can be improved with respect to the resulting learning error by matching observations during training against a declarative task description of the task that shall be learned. In principle this approach allows a complex task to be decomposed into several subtasks which are easier to learn. A robot can then decide by qualitative reasoning which of the subtasks learned matches a concrete task at hand. This approach is however counteracted by the problem that filtering out too much training data for achieving many subtasks may also worsen the learning performance, because every filter removes data and a mere reduction of data without a limitation of the state space is usually harmful.
Second, planning with the learned forward models can be improved by reasoning about failed attempts. In our experiments the reasoning-based approach to planning either requires less iterations to achieve the same performance with respect to deviation from the desired goal or better performance in the same number of iterations (see Figure 11 and Figure 13). While the median only improves modestly, the considerable long error tail in sampling-based planning is reduced significantly (see Figure 14), thereby improving robustness of planning. The small improvement in the median is likely caused by the rather simple problem to be solved in combination with only one common sense rule as background knowledge.
6.1. Discussion of Related Approaches
The idea of exploiting a symbolic representation to improve robot architectures based on learning and planning has been considered previously.
In context of learning robot navigation, Frommberger [35] shows that a qualitative state space representation leads to quicker learning and better performance of the learned strategy. While Frommberger’s contribution to task representation is to identify suitable qualitative spatial relations for learning collision-free navigation, we propose a general approach that can be used with different qualitative relations, but which also captures temporal relationships and thus allows tasks to be described. Current approaches to learning show that symbol semantics useful for robot manipulation like the qualitative relations used in our representation can also be acquired by means of learning [36]. So far, most systems rely on hand-coded symbols (e.g., [37]) though. On the level of basic spatial relations we also use predefined relations in order to be informed of qualitative reasoning techniques applicable. In context of QSL we can then combine these basic relations with logic composition to specify important relations declaratively.
High-level task descriptions related to our approach are also considered in the RoboEarth framework [38] to represent manipulation tasks. However, their approach assumes a suitable grounding of concepts such as “handle” or “opening a door” to be given. By contrast, our approach using QSL exactly aims at defining such complex motion primitives declaratively in order to allow the robot to learn them. Tenorth et al. [39] use (primarily numeric) constraints to describe movements of robots and manipulators to determine action sequences in a pancake cooking scenario. This has the disadvantage over a logic with clear semantics like QSL that no standard reasoning procedures like model checking are applicable, but all inference mechanisms have to be hand-coded.
Previously, logics in robotics have mostly used on a high level of abstraction, not aiming to connect high-level task knowledge all the way to observations and actions in a uniform framework. For example, approaches based on the popular family of Golog languages [40,41] provide a logic-based, universal declarative programming environment that seamlessly integrates with symbolic planning, but relies on the basic actions to be preprogrammed. Thus, our work can be regarded to extend existing logic-based approaches in robotics down to less abstract, task-specific knowledge, enabling learning and action planning to be integrated with a knowledge representation that can be used like a programming language.
Achieving this integration of programming and learning has been identified by Mitchell as one of the central long-term research questions for machine learning [42]. While our approach is realized in the context of the Robot Learning Language (RoLL) [43], there have been other approaches to integrate learning into robot control programs. Thrun [44] has proposed the language CES offering the possibility to leave “gaps” in the code that can be closed by learned functions. CES only uses one specific gradient descent algorithm and doesn’t offer explicit possibilities to integrate other learning algorithms. Besides, the training examples have to be provided by the programmer, experience acquisition is not supported on the language level [45]. Andre and Russell [46,47] propose a language with the same idea as CES of leaving some parts of the program open to be filled in through learning, in this case reinforcement learning.
7. Conclusions
We propose qualitative spatial logic QSL as a qualitative knowledge representation to represent knowledge about manipulation tasks. Our representation is essentially based on qualitative relations among domain level entities or control parameters, employing representations developed in the qualitative spatial reasoning community, a sub-field of artificial intelligence (AI) in general and knowledge representation in particular. Since background knowledge available to programmers is on an abstract level, a qualitative representation is well-suited. However, not until we embed these concepts in a temporal logic we gain the ability to describe some general patterns and principles underlying a learning tasks. Doing so, our approach also presents another use case of linear temporal logic LTL in robotics. The logic framework we describe allows us to tackle tasks in learning and planning with standard reasoning tasks, in particular model checking. This is an important step towards automating the application of learning in robot software engineering as our approach mainly requires a declarative description of the task to be solved, possibly augmented with background knowledge. By exploiting AI techniques to improve robot performance this work contributes to the field of AI robotics that seeks to exploit AI techniques in robotics.
While this study serves to demonstrate the principal utility of QSL as a representation and reasoning mechanism for learning-based robotics in a fully controllable evaluation environment, future work aims at demonstrating the ability to push ahead the state of the art of tasks that can be mastered with learning. In more challenging manipulation settings we propose to also study the computational cost of employing logic-level reasoning that was not noticeable in the study described here. Also, we propose to integrate the learning and planning component in a bootstrapping fashion in order to investigate whether this allows the learning performance to be improved further. After learning a first forward model from a small amount of data, the planning component can be used in conjunction with the qualitative partitioning of the problem space to generate further training instances that more evenly distribute over the whole problem space.
Acknowledgments
Alexandra Kirsch acknowledges support of the Bavarian Academy of Sciences and Humanities, Diedrich Wolter acknowledges financial support of Technogieallianz Oberfranken (TAO).
Author Contributions
Both authors contributed equally to this work.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Williams, B.C.; de Kleer, J. Qualitative Reasoning About Physical Systems—A Return to Roots. Artif. Intell. 1991, 51, 1–9. [Google Scholar] [CrossRef]
- Bredeweg, B.; Struss, P. Current topics in qualitative reasoning. AI Mag. 2003, 24, 13–16. [Google Scholar]
- Davis, E. Representations of Commonsense Knowledge; Morgan Kaufmann Series in Representation and Reasoning; Morgan Kaufmann Publishers: San Mateo, CA, USA, 1990. [Google Scholar]
- Mösenlechner, L.; Beetz, M. Parameterizing Actions to have the Appropriate Effects. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), San Francisco, CA, USA, 25–30 September 2011.
- Knauff, M.; Strube, G.; Jola, C.; Rauh, R.; Schlieder, C. The Psychological Validity of Qualitative Spatial Reasoning in One Dimension. Spat. Cogn. Comput. 2004, 4, 167–188. [Google Scholar] [CrossRef]
- Kirsch, A. Robot Learning Language—Integrating Programming and Learning for Cognitive Systems. Robot. Auton. Syst. J. 2009, 57, 943–954. [Google Scholar] [CrossRef]
- Hall, M.; Frank, E.; Holmes, G.; Pfahringer, B.; Reutemann, P.; Witten, I.H. The WEKA Data Mining Software: An Update. SIGKDD Explor. 2009, 11, 10–18. [Google Scholar] [CrossRef]
- Echeverria, G.; Lassabe, N.; Degroote, A.; Lemaignan, S. Modular openrobots simulation engine: MORSE. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 9–13 May 2011.
- Lemaignan, S.; Echeverria, G.; Karg, M.; Mainprice, M.; Kirsch, A.; Alami, R. Human-Robot Interaction in the MORSE Simulator. In Proceedings of the 2012 7th ACM/IEEE International Conference on Human-Robot Interaction Conference (Late Breaking Report), Boston, MA, USA, 5–8 March 2012.
- Cohn, A.G.; Renz, J. Qualitative Spatial Representation and Reasoning. Chapter 13: Foundations of Artificial Intelligence. In Handbook of Knowledge Representation; Van Harmelen, F., Lifschitz, V., Porter, B., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; Volume 3, pp. 551–596. [Google Scholar]
- Kontchakov, R.; Kurucz, A.; Wolter, F.; Zakharyaschev, M. Spatial Logic + Temporal Logic = ? In Handbook of Spatial Logics; Aiello, M., Pratt-Hartmann, I.E., van Benthem, J.F., Eds.; Springer: Dordrecht, The Netherlands, 2007; pp. 497–564. [Google Scholar]
- Vilain, M.B.; Kautz, H.A. Constraint propagation algorithms for temporal reasoning. In Proceedings of the 5th National Conference of the 13 American Association for Artificial Intelligence (AAAI-86), Philadelphia, PA, USA, 11–15 August 1986; pp. 377–382.
- Allen, J.F. Maintaining knowledge about temporal intervals. Commun. ACM 1983, 26, 832–843. [Google Scholar] [CrossRef]
- Balbiani, P.; Condotta, J.; Fariñas del Cerro, L. Tractability Results in the Block Algebra. J. Logic Comput. 2002, 12, 885–909. [Google Scholar] [CrossRef]
- Renz, J.; Mitra, D. Qualitative Direction Calculi with Arbitrary Granularity. In Proceedings of the 8th Pacific Rim International Conference on Artificial Intelligence (PRICAI-04), Auckland, New Zealand, 9–13 August 2004; Volume 3157, pp. 65–74.
- Lee, J.H.; Renz, J.; Wolter, D. StarVars—Effective Reasoning about Relative Directions. In Proceedings of the Internatoinal Joint Conference on Artificial Intelligence (IJCAI), Beijing, China, 3–9 August 2013; Rossi, F., Ed.; AAAI Press: Palo Alto, California, 2013; pp. 976–982. [Google Scholar]
- Moratz, R.; Ragni, M. Qualitative spatial reasoning about relative point position. J. Vis. Lang. Comput. 2008, 19, 75–98. [Google Scholar] [CrossRef]
- Ligozat, G.; Renz, J. What Is a Qualitative Calculus? A General Framework. In Proceedings of the 8th Pacific Rim International Conference on Artificial Intelligence (PRICAI-04), Auckland, New Zealand, 9–13 August 2004; Zhang, C., Guesgen, H., Yeap, W., Eds.; Volume 3157, pp. 53–64.
- Dylla, F.; Mossakowski, T.; Schneider, T.; Wolter, D. Algebraic Properties of Qualitative Spatio-temporal Calculi. In Proceedings of the 11th International Conference on COSIT, Scarborough, UK, 2–6 September 2013; Volume 8116, pp. 516–536.
- Kreutzmann, A.; Wolter, D. Qualitative Spatial and Temporal Reasoning with AND/OR Linear Programming. In Proceedings of the 21st European Conference on Artificial Intelligence (ECAI), Prague, Czech, 17–22 August 2014.
- Pnueli, A. The temporal logic of programs. In Proceedings of the 18th Annual Symposium on Foundations of Computer Science (FOCS), Providence, RI, USA, 31 October–2 November 1977; pp. 46–57.
- Antoniotti, M.; Mishra, B. Discrete event models + temporal logic = supervisory controller: Automatic synthesis of locomotion controllers. In Proceedings of the IEEE Conference on Robotics and Automation (ICRA), Nagoya, Japan, 21–27 May 1995; Volume 2, pp. 1441–1446.
- Kress-Gazit, H.; Wongpiromsarn, T.; Topcu, U. Correct, Reactive Robot Control from Abstraction and Temporal Logic Specifications. Spec. Issue IEEE Robot. Autom. Mag. Form. Methods Robot. Autom. 2011, 18, 65–74. [Google Scholar] [CrossRef]
- Kloetzer, M.; Belta, C. LTL planning for groups of robots. In Proceedings of the IEEE International Conference on Networking, Sensing and Control (ICNSC), Ft. Lauderdale, FL, USA, 23–25 April 2006; pp. 578–583.
- Smith, S.L.; Tůmová, J.; Belta, C.; Rus, D. Optimal path planning under temporal logic constraints. In Proceeding of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Taipei, Taiwan, 18–22 October 2010; pp. 3288–3293.
- Kloetzer, M.; Belta, C. Automatic deployment of distributed teams of robots from temporal logic motion specifications. IEEE Trans. Robot. 2010, 26, 48–61. [Google Scholar] [CrossRef]
- Kreutzmann, A.; Colonius, I.; Wolter, D.; Dylla, F.; Frommberger, L.; Freksa, C. Temporal logic for process specification and recognition. Intell. Serv. Robot. 2013, 6, 5–18. [Google Scholar] [CrossRef]
- Kröger, F.; Merz, S. Temporal Logic and State Systems; Texts in Theoretical Computer Science; Springer: Berlin Heidelberg, 2008. [Google Scholar]
- Bauland, M.; Mundhenk, M.; Schneider, T.; Schnoor, H.; Schnoor, I.; Vollmer, H. The tractability of model checking for LTL: The good, the bad, and the ugly fragments. Electron. Notes Theor. Comput. Sci. 2009, 231, 277–292. [Google Scholar] [CrossRef]
- Gebser, M.; Grote, T.; Schaub, T. Coala: A Compiler from Action Languages to ASP. In Lecture Notes in Computer Science In Proceedings of the 12th European Conference on Logics in Artificial Intelligence (JELIA), Helsinki, Finland, 13–15 September 2010; Volume 6341, pp. 360–364.
- Grosu, R.; Smolka, S.A. Monte Carlo Model Checking. In Tools and Algorithms for the Construction and Analysis of Systems; Springer: Berlin Heidelberg, 2005; Volume 3440, pp. 271–286. [Google Scholar]
- Witten, I.H.; Frank, E. Data Mining: Practical Machine Learning Tools and Techniques, 2nd ed.; Morgan Kaufmann: San Francisco, CA, USA, 2005. [Google Scholar]
- Quigley, M.; Conley, K.; Gerkey, B.; Faust, J.; Foote, T.; Leibs, J.; Wheeler, R.; Ng, A.Y. ROS: An open-source Robot Operating System. In Proceedings of the ICRA Workshop on Open Source Software, Kobe, Japan, 17 May 2009.
- Kirsch, A.; Schweitzer, M.; Beetz, M. Making Robot Learning Controllable: A Case Study in Robot Navigation. In Proceedings of the ICAPS Workshop on Plan Execution: A Reality Check, Monterey, CA, USA, 5–10 June 2005.
- Frommberger, L. Learning to Behave in Space: A Qualitative Spatial Representation for Robot Navigation with Reinforcement Learning. Int. J. Artif. Intell. Tools (IJAIT) 2008, 17, 465–482. [Google Scholar] [CrossRef]
- Kulick, J.; Toussaint, M.; Lang, T.; Lopes, M. Active Learning for Teaching a Robot Grounded Relational Symbols. In Proceedings of the International Joint Conference on Artificial Intelligence, IJCAI, Beijing, China, 3–9 August 2013.
- Beetz, M.; Mösenlechner, L.; Tenorth, M. CRAM—A Cognitive Robot Abstract Machine for Everyday Manipulation in Human Environments. In Proceedings of the International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 1012–1017.
- Tenorth, M.; Perzylo, A.C.; Lafrenz, R.; Beetz, M. Representation and Exchange of Knowledge about Actions, Objects, and Environments in the RoboEarth Framework. IEEE Trans. Autom. Sci. Eng. (T-ASE) 2013, 10, 643–651. [Google Scholar] [CrossRef]
- Tenorth, M.; Bartels, G.; Beetz, M. Knowledge-based Specification of Robot Motions. In Proceedings of the 21st European Conference on Artificial Intelligence (ECAI 2014), Prague, Czech, 18–22 August 2014.
- Levesque, H.J.; Reiter, R.; Lespérance, Y.; Lin, F.; Scherl, R.B. Golog: A logic programming language for dynamic domains. J. Logic Program. 1997, 31, 59–83. [Google Scholar] [CrossRef]
- Levesque, H.; Lakemeyer, G. Cognitive robotics. In Handbook of Knowledge Representation; Lifschitz, V., van Harmelen, F., Porter, F., Eds.; Elsevier: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Mitchell, T. The Discipline of Machine Learning; Technical Report CMU-ML-06-108; Carnegie Mellon University: Pittsburgh, PA, USA, 2006. [Google Scholar]
- Kirsch, A. Integration of Programming and Learning in a Control Language for Autonomous Robots Performing Everyday Activities. Ph.D. Thesis, Technische Universität München, Munich, Germany, 2008. [Google Scholar]
- Thrun, S. Towards programming tools for robots that integrate probabilistic computation and learning. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), San Francisco, CA, USA, 24–28 April 2000.
- Thrun, S. A Framework for Programming Embedded Systems: Initial Design and Results; Technical Report CMU-CS-98-142; Carnegie Mellon University, Computer Science Department: Pittsburgh, PA, USA, 1998. [Google Scholar]
- Andre, D.; Russell, S. Programmable Reinforcement Learning Agents. In Proceedings of the 13th Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 3–8 December 2001; MIT Press: Cambridge, MA, USA, 2001; pp. 1019–1025. [Google Scholar]
- Andre, D. Programmable Reinforcement Learning Agents. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2003. [Google Scholar]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).