A Spatial Queuing-Based Algorithm for Multi-Robot Task Allocation

Abstract

Multi-robot task allocation (MRTA) is an important area of research in autonomous multi-robot systems. The main problem in MRTA is to allocate a set of tasks to a set of robots so that the tasks can be completed by the robots while ensuring that a certain metric, such as the time required to complete all tasks, or the distance traveled, or the energy expended by the robots is reduced. We consider a scenario where tasks can appear dynamically and a task needs to be performed by multiple robots to be completed. We propose a new algorithm called SQ-MRTA (Spatial Queueing-MRTA) that uses a spatial queue-based model to allocate tasks between robots in a distributed manner. We have implemented the SQ-MRTA algorithm on accurately simulated models of Corobot robots within the Webots simulator for different numbers of robots and tasks and compared its performance with other state-of-the-art MRTA algorithms. Our results show that the SQ-MRTA algorithm is able to scale up with the number of tasks and robots in the environment, and it either outperforms or performs comparably with respect to other distributed MRTA algorithms.

1. Introduction

Multi-robot task allocation (MRTA) is an important aspect of multi-robot systems, where robots have to autonomously perform tasks that are distributed spatially and temporally within an environment. MRTA is used in numerous applications of robotic systems, including reconnaissance [1], unmanned search and rescue operations [2,3], cooperative transportation [4,5,6] and autonomous exploration [7,8]. The fundamental problem addressed in MRTA is the following: Given a set of robots and a set of tasks that need to be performed by the robots, what is a suitable assignment of robots to tasks so that a global objective, such as the time to complete the tasks, or the distance traveled, or the energy expended by the robots is reduced. The MRTA problem is known to be an NP-hard problem [9], and finding the optimal solution to the problem is not feasible beyond very trivial scenarios.

Over the past decade, researchers have proposed several solutions to the MRTA problem. These solutions include both centralized MRTA techniques that can guarantee optimal or near-optimal solutions and decentralized or distributed approaches that rely on local computations on each robot and communication between robots to solve the MRTA problem in a coordinated manner. Popular methods for distributed MRTA are to partition the environment into logical regions [1,10] and to use market-based techniques, such as auctions, to enable robots to select tasks to perform [11]. Many MRTA algorithms usually consider that only one robot is required to complete a task, that the information about the task is available a priori and that the task information does not change over time as robots operate in the environment. However, in many real-life scenarios, a single task might require operations from multiple robots to be completed. Static allocation of tasks to robots might not be valid in scenarios where multiple robots are required to complete a task, as the availability of a task to a robot can change dynamically as other robots perform operations on the task. To handle MRTA efficiently in such scenarios, it makes sense to investigate techniques that will allow robots to select tasks while considering their individual preferences, as well as the current task availabilities.

To address these issues, we propose an MRTA algorithm called SQ-MRTA (Spatial Queueing-MRTA) based on the concept of spatial queues [12]. The SQ-MRTA algorithm locally builds a queue of preferred tasks for each robot based on calculations that take into account the robot’s location and its distance to the available tasks within the environment. An auction-based mechanism is then used as a coordination mechanism to enable robots to avoid conflicts between tasks they select to perform and to choose the most suitable task at the current instant. Combined together, these two aspects enable robots to quickly select tasks in a distributed manner while allowing for dynamic changes, such as new tasks getting added to the environment or existing tasks getting completed by other robots. We have evaluated our proposed MRTA algorithm using an accurately-simulated model of the Coroware Corobot robot within the Webots robot simulator and compared its performance with three other state-of-the-art MRTA algorithms. Our experimental results show that the SQ-MRTA algorithm is able to scale up in terms of the time taken to complete tasks and the distance traveled by the robots as the number of robots and tasks increases. Our algorithm also outperforms an optimal, but centralized assignment technique and a distributed, but greedy heuristic and performs comparably with another distributed MRTA technique.

The remainder of this paper is structured as follows: The next section introduces related works on MRTA. Section 3 provides a formalization of the problem studied in this paper and presents our MRTA algorithm called SQ-MRTA. Section 4 lays out our experimental setup, describes the algorithms chosen for comparison and reports the results and analysis of our algorithm with respect to the compared algorithms. The last section summarizes conclusions drawn from our research and points to ongoing and future directions of this work. An earlier version of this work has appeared in [13]. This paper significantly extends [13] by formalizing our spatial queue technique for MRTA, implementing three additional MRTA techniques for comparison and reporting a detailed analysis of the performance of the SQ-MRTA algorithm for different task and robot distributions.

2. Related Work

Multi-robot task allocation (MRTA) has been an active area of research in robotics over the past decade, and several researchers have proposed techniques based on constrained optimization techniques, local heuristics, market-based algorithms, etc., to solve the MRTA problem. MRTA algorithms can generally be divided into two categories: centralized and decentralized or distributed. In centralized MRTA algorithms, a single entity, usually a central controller station, has a global view of the system [14]. This offers the advantage of reducing the complexity of the algorithm by diminishing the amount of inter-robot communication and coordination, but it also adversely affects the scalability and robustness of the algorithm, as the central station has to handle more computation as the number of robots or tasks increase, and the failure of the central station could stop the operation of all of the robots. To address the deficiency of centralized MRTA algorithms, researchers have proposed decentralized and distributed algorithm.

For distributed MRTA, Gerkey and Mataric [9] described a formal taxonomy using three problem features: robots can either be single-task (ST) or multi-task (MT), signifying whether or not the robots are capable of executing more than one task at a time. The second feature consists of single-robot (SR) or multi-robot tasks (MR), wherein a task requires either one robot (SR) or more than one robot (MR) to get completed. The third feature relates to the flow of tasks into the robots environment: instantaneous assignment (IA) refers to a static scenario, where the assignment of tasks to robots is finalized at the beginning of the robots’ operations and future changes to the assignments are not allowed; conversely time-extended assignment (TA) implies a dynamic setting in which allocations may change or additional tasks enter the system over time. In [4], the same authors have utilized this classification to minimize resource usage, task completion time and communication overhead for an MRTA algorithm using a fitness-based auction technique with negotiation and task commitment. In [15], Gerkey’s taxonomy was extended to include more complex dependencies and constraints between robots and tasks. For performing MRTA with task constraints, Zlot and Stentz [16] have proposed an auction-based algorithm. Gil Jones et al. [7] focus on MRTA methods for forming ad hoc teams of heterogeneous robots in short notice, such as for emergency scenarios. The robots are assumed to have little a priori knowledge about tasks, about other robots and their capabilities or about their environment and use auction-based algorithms enhanced with learning mechanisms for MRTA [2] followed by clustering techniques and genetic algorithms for further improvements [3]. Other auction-based MRTA algorithms have been described in [17,18].

Liu and Shell focus on a large-scale online MRTA algorithm in [10] that mixes both centralized and decentralized approaches in order to take advantage of spatial and temporal efficiencies, while reducing overall global communication. Their algorithm identifies clusters, or partitions, of strongly-connected robot-task pairs and operates on these clusters in parallel. The same authors introduce the interval Hungarian algorithm in [19], which focuses on measuring the effects of uncertainty on the outcome of task allocation. This algorithm assigns robots to tasks in a one-to-one ratio, but also calculates an interval representing the tolerance of the assignment to outside forces modeled as a probability distribution, which may disrupt or invalidate the value of the assignment. In [20,21], the authors propose an incremental allocation system based on the Hungarian algorithm, which can produce an optimal solution with increasingly efficient feasible solutions at each intermediate step.

Another work, focusing on uncertainty, is Sucan and Kavraki’s simultaneous task and motion planning (STAMP) in [22]. They argue that motion planning cannot be decoupled from task planning, as any infeasibility in executing physical motions renders the task planning useless. They use their concept of a task motion multigraph (TMM) to encode hardware capabilities into the task graph and then implement a Markov decision process to guide the robot by incorporating feasibility probabilities into the decision-making process.

The MRTA problem has also been studied recently in the context of multi-vehicle routing. In [23], the authors investigate a scenario much like a time-extended version of our environment: routing policies for multiple vehicles servicing tasks with multiple classes of demands (priorities). Seow, Dang and Lee apply task allocation to the real-world taxi dispatch system of Singapore in [6]. Using the infrastructure of the centralized system currently in place, they propose a distributed model, whereby the on-board computers act as agents on behalf of the drivers. The environment is partitioned into logical regions, grouping taxis within those regions who then negotiate concurrent assignments of pending requests with a focus on the group average, resulting in reduced average customer wait time and reduced empty taxi cruising time. In a similar vein, Lim and Rus test their stochastic path planning solution against a Singapore road network incorporating historical traffic and travel data in [5]. Dasgupta describes a cooperative foraging scenario with shared task execution using pheromones to denote a task progress in [8]. Four heuristic-based algorithms with increasing levels of efficiency are then proposed to solve the MRTA problem. Celik and Modiano have framed MRTA within a mobile data collecting network in [1] with policies for single and multiple collector scenarios with and without possible interference between assigned sectors and frequency bands. Zhang, Collins and Barbu build on stochastic clustering auction research in [24], which uses simulated annealing to explore an allocation space. Luo generalizes the competitive analysis of the online weighted bipartite matching problem for groups of tasks in [25].

In contrast to the works above, our spatial queuing approach considers the inter-dependencies between tasks. It takes advantage of the knowledge that tasks require multiple inspections and grades each task based on its overall proximity to all other known tasks. Between two tasks that are equidistant from a robot’s current location, the task that is closer to a third task will be selected by the robot to perform first. This will ensure that the robot will have the opportunity to efficiently visit multiple tasks in one sortie. Our intuition is that this consideration for future assignments should reduce the time and distance required to complete all task demands when compared to an approach that is only concerned with finding a task schedule that allocates tasks individually.

3. Multi-Robot Task Allocation Using Spatial Queuing

To motivate our MRTA problem, we consider an automated landmine detection scenario where a set of robots are deployed within a bounded 2D environment with potential landmines. The location of the landmines is not known a priori. Robots are equipped with sensors that are capable of detecting landmine-like objects, albeit within a certain level of uncertainty due to sensor noise. Robots initially explore the environment, and when a robot finds an object of interest that could potentially be a landmine, it requests other robots, possibly with different sensor types, to visit the location of the detection and to confirm the object on their sensors. Within this scenario, the following points summarize the setting for our MRTA problem:

• A task corresponds to a set of robots visiting the location of an object of interest and recording the object’s characteristics such as its magnetic signature on their sensors. For legibility, we have referred to each robot’s visit to the object’s location and taking its reading as the robot performing its portion of the task.
• Tasks are homogeneous, and the order of performing the tasks does not affect the outcome of performing the tasks.
• Robots can perform a task asynchronously by performing their portion of the task at different times.
• A task is considered to be complete when the desired number of robots have performed their portion of the task.
• Tasks can arrive dynamically: when a robot finds an object of interest (e.g., a potential landmine), it records the location of the object and broadcasts it to other robots in the system.
• Robot and task positions are initially shared between robots and assumed to be common knowledge.
• Finally, we assume that the time required to perform a task, e.g., to analyze a potential landmine with a robot’s sensor, is nominal as compared to the time required by robots to navigate between tasks.

Within the aforementioned context, the MRTA problem corresponds to finding a suitable allocation of tasks to robots, so that the total time required to complete the tasks is reduced. Because the time to perform tasks by robots is considered to be much less than robot navigation times between tasks, our MRTA problem attempts to find an allocation or ordering of tasks for each robot that minimizes robots’ inter-task navigation times. The MRTA problem described above corresponds to the MR-ST-TA setting [9], where MR (multi-robot task) denotes that multiple robots are required to complete a task, ST (single-task robot) denotes each robot can perform a single task at a time and TA (time-extended assignment) denotes that each robot can determine and update its schedule or order of tasks to perform over a finite time window, as opposed to determining the task schedule instantaneously.

Formally, we consider a set of mobile robots $R=\{r_i:i=1,2,...,m\}$ that are deployed within a bounded environment $E\subset {\mathcal{R}}^2$. We assume that each robot is capable of localizing itself with respect to the environment, and its pose at any instant is given by ${\rho }_{r_i}$. The environment also contains a set of tasks $T=\{{\tau }_i:i=1,2,...,n\}$ that are distributed arbitrarily within the environment; the location of task ${\tau }_i$ is denoted by ${\rho }_{{\tau }_i}$. Following the task setting described above, the objective of the robots is to visit the location of each task and to perform certain operations related to the task. We assume that task ${\tau }_i$ requires operations to be performed by $d_{{\tau }_i}\le \left|R\right|$ distinct robots to be completed. Because the focus of this paper is on the task allocation algorithm, we assume that techniques for appropriately positioning and localizing robots to perform operations at the locations of the tasks are already available. The distance between two tasks, ${\tau }_i$ and ${\tau }_j$, is denoted by $d_{ij}=\parallel {\rho }_{{\tau }_i}-{\rho }_{{\tau }_j}\parallel$, while the distance between robot $r_i$ and task ${\tau }_j$ is denoted by ${\widehat{d}}_{ij}=\parallel {\rho }_{r_i}-{\rho }_{{\tau }_j}\parallel$. Furthermore, we let ${\rho }_i^0$ denote the initial position of robot $r_i$ and ${\tau }_{r_i^1}$ denote the first task selected by robot $r_i$. Within this setting, the MRTA problem can be formally defined as the following:

Definition: Multi-robot task allocation. Given a set of robots R and a set of tasks T, find a suitable allocation $A:2^R\to T$ such that:

$${\displaystyle min\sum _{r_i\in R}\left(\parallel {\rho }_{r_i}^0-{\rho }_{{\tau }_{r_i^1}}\parallel +\sum _{({\tau }_j,{\tau }_k)\in A\left(\mathcal{R}\right)}\parallel {\rho }_{{\tau }_j}-{\rho }_{{\tau }_k}\parallel \right),\forall \mathcal{R}\subseteq R:r_i\in \mathcal{R}}$$

subject to:

$$\begin{array}{cc}\hfill {\tau }_j\ne {\tau }_k& \forall ({\tau }_j,{\tau }_k)\in A\left(\mathcal{R}\right),\forall \mathcal{R}\subseteq R:r_i\in \mathcal{R},\forall r_i\hfill \\ \hfill \left|A\left(\mathcal{R}\right)\right|=d_{{\tau }_i}& A\left(\mathcal{R}\right)={\tau }_i,\mathcal{R}\subseteq R,\forall {\tau }_i\hfill \end{array}$$

The above formulation of the MRTA problem attempts to find an allocation for each robot, such that the distances traveled by the robots to perform the tasks are minimized. The two constraints of the problem ensure that the same task does not get allocated to the same robot more than once, and the total number of robots allocated to perform a task equals the demand for the task.

The solution to the MRTA problem has been shown to be an instance of the dynamic traveling salesman problem and proven to be NP-hard [8]. In this paper, we propose a spatial queue-based [12] MRTA solution technique that attempts to solve the MRTA problem using a heuristic that represents the distances between robots and tasks as an ordered queue based on the robots’ locations and inter-task distances. To achieve this in a systematic manner, each robot utilizes the following four mathematical constructs:

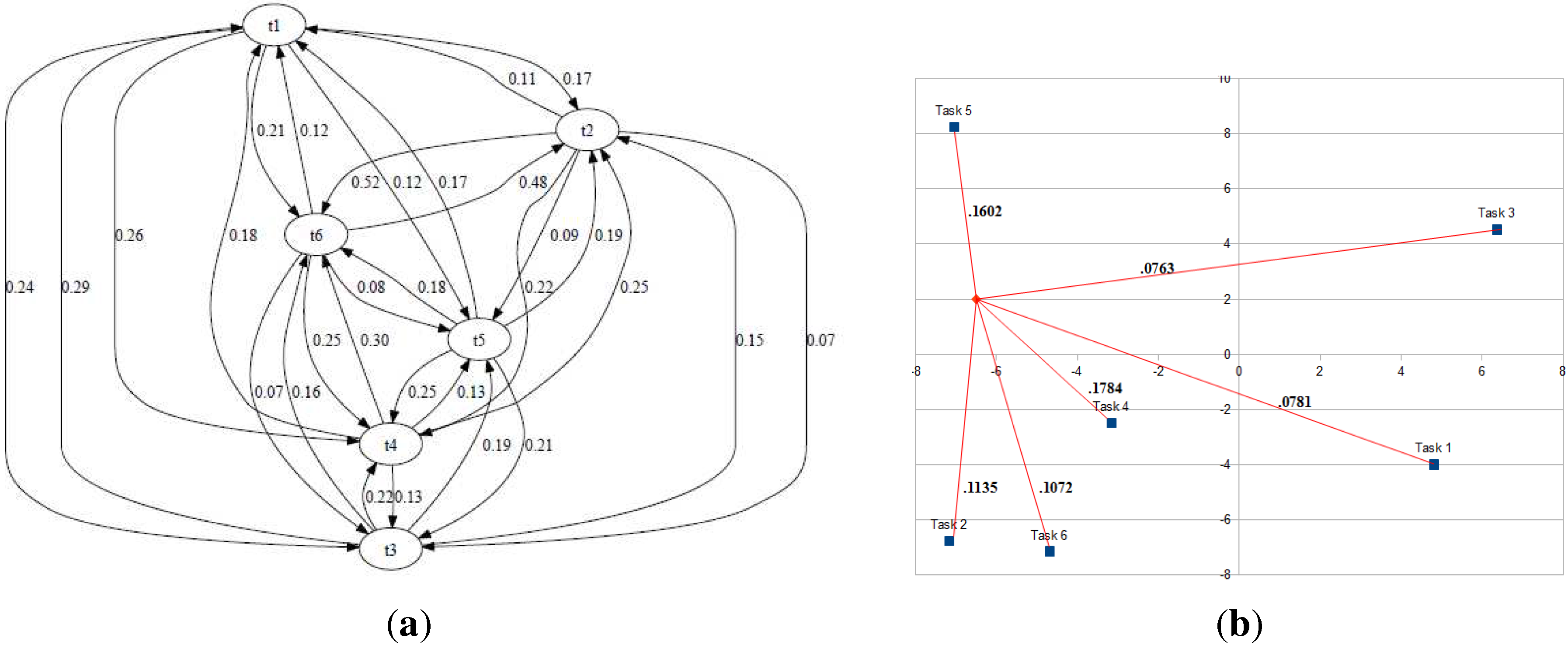
• Inter-task transition matrix: Inter-task distances form the basis of our method, as the objective of the MRTA technique is to enable robots to find a suitable schedule or order of navigating between tasks, so that the total distance traveled by them is reduced. The inter-task distances are represented as a transition matrix. The transition matrix at time-step t is denoted by $M\left(t\right)$ and given by the normalized inverse Euclidean distances between every task pair, as shown in Equation (1):

  $$M\left(t\right)=\left[\begin{array}{cccc}{\pi }_{11}& {\pi }_{12}& ...& {\pi }_{1n}\\ {\pi }_{21}& {\pi }_{22}& ...& {\pi }_{2n}\\ & ...\\ {\pi }_{n1}& {\pi }_{n2}& ...& {\pi }_{nn}\end{array}\right]$$

  (1)

  where ${\pi }_{i,j}=\frac{\frac{1}{d_{i,j}}}{{\sum }_{j\ne i}\frac{1}{d_{i,j}}}$.
  Each entry ${\pi }_{ij}$ of $M\left(t\right)$ represents the probability of a robot to select task ${\tau }_j$ following ${\tau }_i$, based on the distance between the tasks’ locations. Note that ${\pi }_{ii}=0$, and therefore, the diagonal elements of the matrix are zeros. The transition matrix values are calculated independently by all robots. Initially, the transition matrix is computed for all task pairs, but as time proceeds, each robot recalculates the matrix when it completes a task or when it receives information that a task has been completed by other robots. The transition probabilities of completed tasks are set to zero, and the probability values in $M\left(t\right)$ are re-normalized. Figure 1a shows an example of initial transition matrix values for six tasks in a $20\times 20$ m${}^2$ environment.

Figure 1. (a) A representation of an environment with six tasks and the corresponding inter-task transition probabilities; (b) a visual representation of a robot’s state vector from its initial deployment position in the same environment.

Figure 1. (a) A representation of an environment with six tasks and the corresponding inter-task transition probabilities; (b) a visual representation of a robot’s state vector from its initial deployment position in the same environment.

2.

Robot state vector: The state vector of a robot is comprised of the inverse Euclidean distances between the robot and each task in the environment. The state vector for robot i, $V_{r_i}$ at time-step t is given by:

$$V_{r_i}\left(t\right)=(\widehat{{\pi }_{i1}}\left(t\right),\widehat{{\pi }_{i2}}\left(t\right),...,\widehat{{\pi }_{in}}\left(t\right))where\widehat{{\pi }_{ij}}\left(t\right)=\frac{1}{{\widehat{d}}_{i,j}\left(t\right)}$$

(2)

where ${\widehat{d}}_{i,j}\left(t\right)$ is the distance between robot $r_i$ and task ${\tau }_j$ at time-step t. Figure 1b illustrates an example of the state vector values for a robot with six tasks.

3.

Task proximity vector: The task proximity vector of a robot $r_i$ represents its preference for each task ${\tau }_j$ in the environment based on performing task ${\tau }_j$ first, followed by the remaining tasks. It is calculated as the product of the robot $r_i$’s state vector and the inter-task transition matrix. The task proximity vector for robot $r_i$ at time-step t, ${\acute{V}}_{r_i}\left(t\right)$, is given by:

$${\acute{V}}_{r_i}\left(t\right)=V_{r_i}\left(t\right)\times M\left(t\right)$$

(3)

4.

Robot spatial task queue: The spatial task queue of a robot denotes the order in which the robot plans to perform the tasks in the environment. It is calculated by removing all tasks from the task proximity vector that are either occupied or completed and sorting the remaining tasks in descending order based on their proximity vector values. The task queue for robot $r_i$ at time-step t, $Q_{r_i}\left(t\right)$, is given by:

$$Q_{r_i}\left(t\right)=\{q_1,q_2,...,q_n:q_k\ge q_{k+1}\forall k,q_k\in {\acute{V}}_{r_i}\left(t\right)\}$$

(4)

The SQ-MRTA algorithm used by a robot $r_i$ to select a task using its spatial task queue is shown in Algorithm 1. The algorithm is fully distributed, and each robot decides to select and perform a task at each time-step based on a bid that it submits representing the distance to the most suitable task calculated using the spatial queue equations described above. The algorithm takes as input the set of tasks T and corresponding locations. Robot $r_i$ first checks if there are tasks that it is eligible to perform; tasks that are not yet complete and that have not been performed by itself (Line 4). If robot $r_i$ has not submitted a bid in the current time-step, then it selects a task using the spatial queue equations (Lines 6–9) and submits a bid for the task at the head of its spatial queue by broadcasting a bid message to other robots (Lines 16–17). However, because other robots are simultaneously and asynchronously selecting tasks using the SQ-MRTA algorithm, there might be no task available for robot $r_i$ (Line 10). In such a scenario, robot i waits to receive a message from another robot signaling that it finished performing its operations for a certain task. Once a performed task signal is received, robot $r_i$ checks to see if the task that was just performed also got completed, and if the task was completed, robot $r_i$ rebuilds the transition matrix, removing the recently completed task (Lines 11–14). If robot $r_i$ has already submitted a bid for a certain task, it waits until it receives competing bids for the task from all other robots. If $r_i$ is the highest bidder, it accepts the task and broadcasts the acceptance information to all other robots. It then starts to navigate towards the location of the task to perform its operations on the task and, after performing the task, rebuilds the transition matrix (Lines 21–25). On the other hand, if it is not the highest bidder, it selects the next available task in its spatial queue. If there is no task in the spatial queue, it waits for a task to become available by waiting for a performed task signal from another robot, as before (Lines 27–35). When there are no more eligible tasks, robot $r_i$ infers that all tasks have been completed, and it terminates its task allocation algorithm.

Algorithm 1 Spatial queuing multi-robot task allocation.

1: Input: T = { ${\tau }_i$ : 1 ≤ i ≤ n }

2: Build transition matrix M${}_t$ as shown in Equation 1

3: bid ← 0

4: while an eligible task remains do

5: If I have not bid in this time-step then

6:  Calculate state vector as shown in Equation 2

7:  Generate task proximity vector using Equation 3

8:  Remove proximity vector entries for tasks completed by me or occupied by other robots

9:  Sort remaining proximity vector values in descending order and insert into queue Q

10:  if Q is empty then

11:   wait until task-performed signal received from another robot

12:   if a performed task is now complete then

13:    Rebuild transition matrix Mt

14:   end if

15:  else

16:   bid ← queue[head]       ▹ = value of most preferred task

17:   sendBroadcast(BID, bid)

18:  end if

19: else

20:  wait until competing bids received from all other robots

21:  if I am the highest bidder for my preferred task then

22:   if If task I have bid on is still available then

23:    sendBroadcast(ACCEPT, task)

24:    Execute task

25:    Rebuild transition matrix Mt

26:   else

27:    Move to next entry in queue

28:    if there is a task available in the queue then

29:     bid ← queue[head]

30:      sendBroadcast(BID, bid)

31:    else

32:      wait until task-performed signal received from any active robot

33:     bid ← 0

34:     if a performed task is now complete then

35:       Rebuild transition matrix Mt

36:     end if

37:    end if

38:   end if

39:  end if

40: end if

41: end while

4. Experimental Setup and Results

We have verified the performance of the SQ-MRTA algorithm using simulated Corobot robots on the Webots Version $6.3.0$ simulator. Webots is a fully-integrated design and coding platform, allowing for both virtual robot and environment design. Robot controllers can be written in a high-level programming language and can interact with the sensors and actuators of the simulated robot. The robot prototype utilized in all of our simulations is the Coroware Corobot robot, an indoor, four-wheeled, skid-steer robot. The footprint of the robot measures 40 cm $\times 30$ cm. Each robot also has a unique, integer-based identifier. For detecting obstacles, the robot is equipped with four infra-red (IR)-based distance sensors, one on each side, oriented at ${60}^{\circ }$ from the front of the vehicle, and two cross beam IR sensors mounted on the front bumper. The robot also includes an emitter-receiver pair for bidirectional Wi-Fi communication with other robots. An indoor localization device, called a Hagisonic Stargazer, with a localization accuracy of $\pm 2$ cm, was added to the robot. On the simulated robot, a GPS and a compass node were used to emulate the behavior of the localization device. The errors introduced by noise in the different sensors and actuators of the physical robot were also included in the simulated robot, following the noise vs. range characteristics of the IR sensors (Sharp GP2Y0D21YK) on the physical Corobot robot; the IR sensors on the simulated Corobot had a $5\%$ error due to noise for readings taken at ranges of 0.1–0.8 m, and $50\%$ error for ranges beyond $0.8$ m. Each wheel of the simulated Corobot robot had a maximum and frictional force of 10 and $2.26$ units, respectively, in correspondence to the physical Corobot robot; wheel slip noise was set to zero by observing the amount of wheel slippage of the robot within a test arena. Finally, the communication noise (packet loss) was set to zero, while observing average communication packet loss in the WiFi network setup between the robots. A photograph of the Corobot robot is shown in Figure 2a, and the simulated robot within Webots is shown in Figure 2b.

Figure 2. (a) Photograph of a Corobot robot; (b) simulated Corobot robot with visible distance sensor rays used for simulations within Webots; (c) screenshot of the 20 m $\times 20$ m arena within Webots with 10 Corobot robots deployed.

Figure 2. (a) Photograph of a Corobot robot; (b) simulated Corobot robot with visible distance sensor rays used for simulations within Webots; (c) screenshot of the 20 m $\times 20$ m arena within Webots with 10 Corobot robots deployed.

Collision avoidance and navigation: For avoiding static obstacles, like walls, in the environment, the robot uses a Braitenberg vehicle-like controller [26]. Using this controller, when the robot encounters an obstacle, it attempts motion after adjusting its orientation randomly to between between ${30}^{\circ }$ and ${90}^{\circ }$, in both negative and positive sense of its original orientation. For avoiding mobile obstacles, like other robots, robots communicate the coordinates of their current location and heading intermittently with each other. If two robots’ paths intersect within a range of three meters of their current locations, they adjust their courses by temporarily changing their orientation to ${10}^{\circ }$ of their original orientation if their headings are exactly opposite of each other or giving ‘right-of-way’ to the robot with the lower-ID, as described in [27].

Each robot’s navigation is controlled using a subsumption architecture [28], as shown in Figure 3. A subsumption architecture works by directing sensor inputs to encapsulated control units representing the internal processes responsible for controlling outward behavior. The outputs of these units either feed into more complex functions or, ultimately, result in actionable vectors in response to the stimuli provided. These control units are organized into layers based on the level of complexity associated with the behavior. All of the tiers for a specific behavior converge to one point; therefore, the architecture must specify which outputs have priority, overriding lower priority directives. In our system, the robot’s primary directive is to move towards a goal point generated by the task allocation system. However, other sensory data may override this directive by adjusting wheel speeds in order to avoid an obstacle or to prevent collision with another robot (mobile obstacles) in the vicinity.

Figure 3. Generic subsumption architecture for a Corobot.

Figure 3. Generic subsumption architecture for a Corobot.

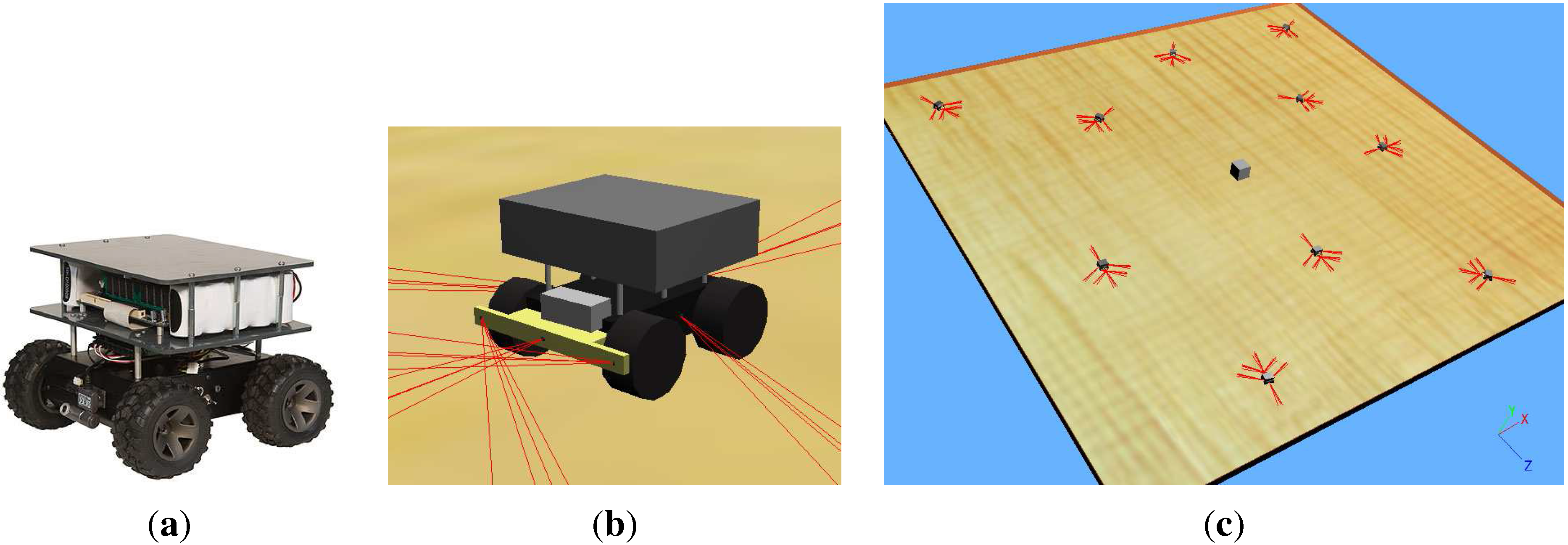
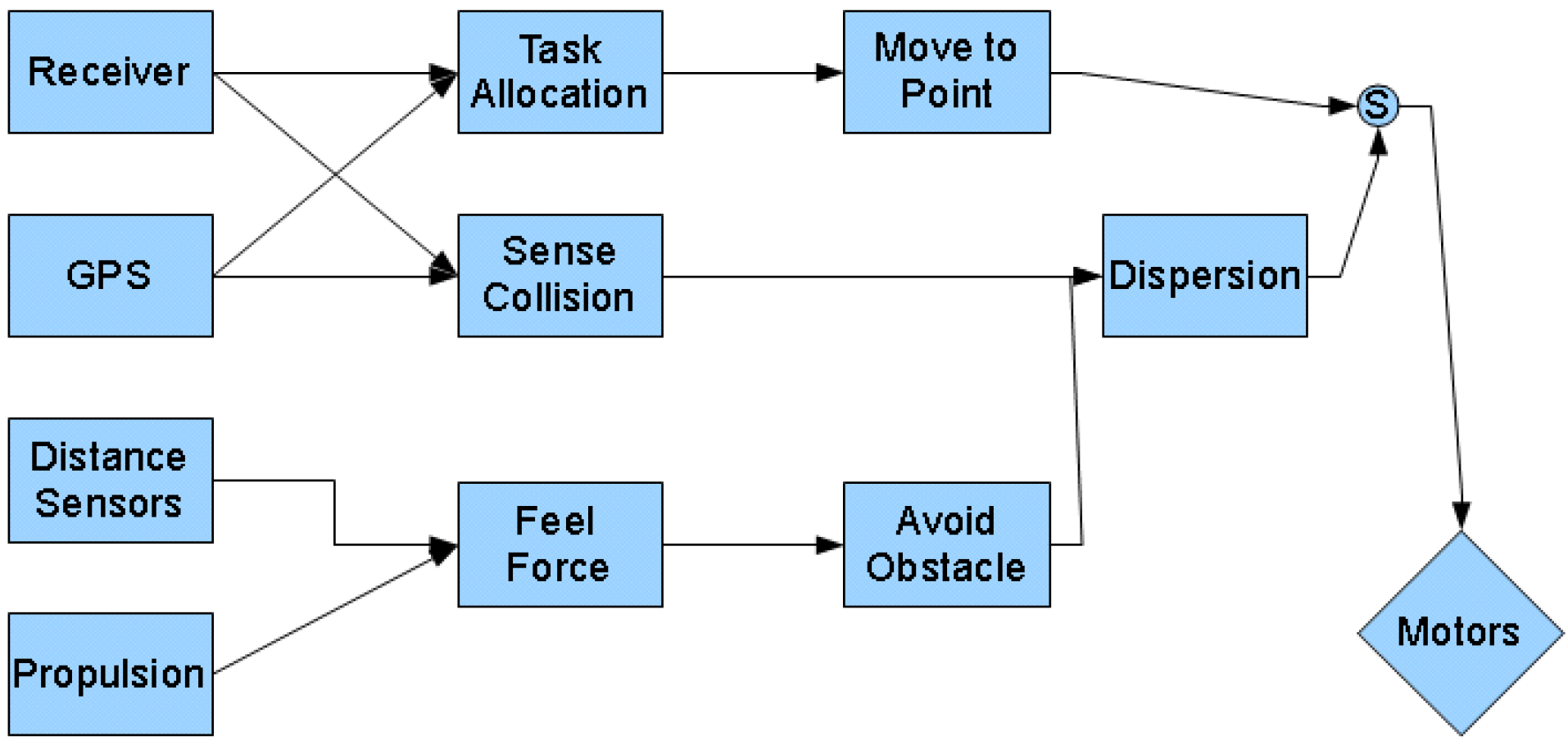
4.1. Algorithms Compared

We have compared the performance of our proposed SQ-MRTA algorithm with three other state-of-the-art MRTA algorithms, as described below:

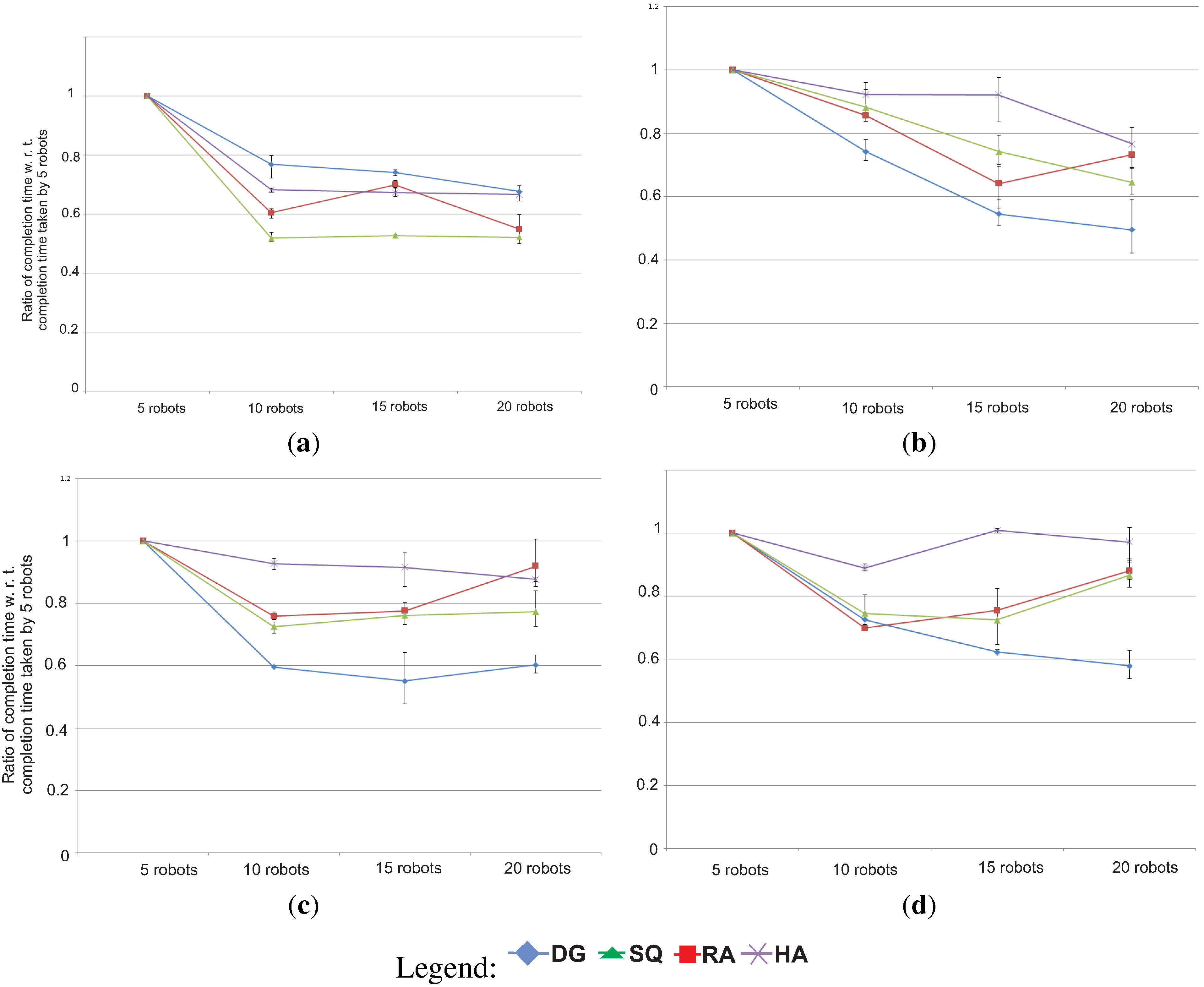
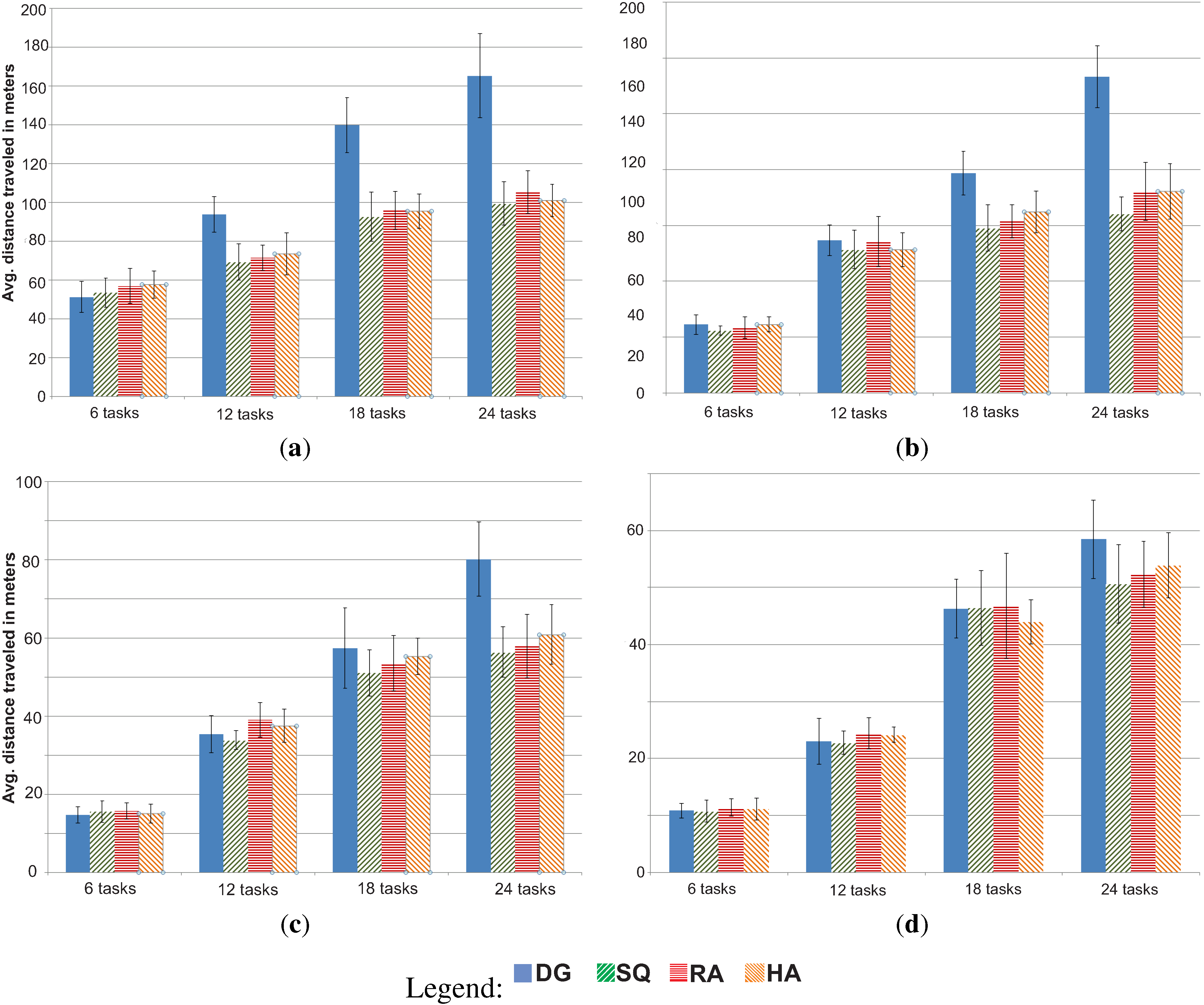
• Hungarian algorithm (HA): The Hungarian algorithm (HA) [29], is a classic algorithm for task assignment under constraints. The algorithm takes as input the locations of the tasks and the initial locations of the robots and outputs a feasible assignment of tasks to robots that minimizes the distance traveled by each robot. The Hungarian algorithm is an offline algorithm, and it works with a static view of the environment; it does not take into account dynamic attributes, such as delays arising due to collision avoidance between robots or when tasks become temporarily unavailable due to ongoing operations by a robot. In our setting, because the number of tasks (number of tasks × demanded for each task = $n\times d_{{\tau }_i}$) is greater than the number of robots (m), we applied the Hungarian algorithm iteratively for sets of tasks equal to the number of robots. In each iteration, a subset of m tasks, ordered by a task identifier, are allocated to m robots using the Hungarian method. In the final iteration, if there are less than m tasks remaining, dummy tasks are introduced to get the number of tasks passed to the Hungarian algorithm to m.
• Decentralized greedy algorithm (DG): In the decentralized greedy (DG) algorithm, each robot uses a contract net-like protocol [30] to select tasks. The information about task locations is common knowledge to all robots, but robots are not aware of each other’s locations. Each robot broadcasts a bid corresponding to the distance to its closest task and also receives bids from other robots for their respective closest tasks. If a robot has the lowest bid on a certain task, it selects to perform the task and broadcasts its selection to other robots. A robot that did not submit the lowest bid on a task then bids on its next closest task. The protocol continues until each task has been selected (visited) by the number of robots corresponding to the task’s demand. In the DG algorithm, all robots are either allocated to a task or, if all tasks are already selected by some robot, the remaining robots must sit idle and await the completion of some task, so that it may again submit a bid. The pseudo-code of the DG algorithm used in our simulations is shown in Algorithm 2.
• Repeated auctions algorithm (RA): The repeated auctions (RA) algorithm [25] treats groups of tasks in a time-extended manner with the condition that all tasks in one group must be satisfied or performed before allocating the next group of tasks. We have adapted the repeated auction algorithm, so that as tasks become available, new auctions begin immediately in order to allocate free tasks to idle robots. Our repeated auction algorithm works as follows: each robot determines the utility of every task by subtracting their private value of the task from the current maximum price of that task (set to zero initially). The private value of a robot for a task is simply the inverse Euclidean distance between the robot’s position and the location of the task. A bid is then formed by finding the difference of the two highest utilities, adding a small offset and adding this result to the current price. As this is a distributed model, each robot must track these prices individually via broadcast communication. If a robot is outbid, this process is repeated until the maximum utility value is negative, at which point the robot has nothing to gain and will remain idle and wait for the next auction. When a stable allocation is determined, a round of the auction terminates, and the winning robots proceed to perform their tasks. The pseudo-code for our RA algorithm is given in Algorithm 3.

Experimental setup: The simulations were run in a bounded two-dimensional environment with three different environment sizes: $5\times 5$ m${}^2$, $10\times 10$ m${}^2$ and $20\times 20$ m${}^2$. Results are reported for the $20\times 20$ m${}^2$ environment that is shown in Figure 2c. The number of robots was varied over $5,10,15$ and 20 robots, while the number of tasks was varied over $6,12,18$ and 24 tasks. Task locations were generated randomly while ensuring that that tasks must be at least 1 m from the walls of the environment and that inter-task distances were at least 2 m. The required number of robot visits (task demand) to complete a task was varied between 3 and 5. For each robot-task pair, 10 environments with different task locations and initial robot locations were generated. Results were averaged over 10 simulation runs. To enable a systematic comparison of the performance of the algorithms, the initial locations of the robots and tasks were the same for each algorithm.

4.2. Experimental Results

For our simulation results, we measured the performance of the SQ-MRTA algorithm along the following metrics: the time required to complete all tasks while varying both the number of robots and tasks separately, the distance traveled by robots to perform tasks and the total idle time during which robots were waiting for other robots to perform tasks, so that tasks become available. The data were extracted from each robot, for each of the 10 environments, over all combinations of tasks and robots and then averaged first at the environment level and then again at the robot-task pair level, resulting in 16 robot-task combinations for each of the four algorithms compared.

Algorithm 2 Decentralized greedy task allocation using the contract-net protocol.

1: Input: T = { ${\tau }_i$ : 1 ≤ i ≤ n }

2: while an incomplete task exists do

3: Set bid as the distance to the closest available task

4: Set task to the task number of the closest task

5: If an available task was found then

6:  sendBroadcast(BID, bid)

7: else

8:  wait until task-performed signal received

9: end if

10: wait until competing bids received

11: if my bid is the global minimum then

12:  sendBroadcast(ACCEPT, task)

13:  Execute task

14: else

15:  wait for ACCEPT signal

16: end if

17: end while

Algorithm 3 Repeated greedy auctions for online MRTA.

1: Input: T = { ${\tau }_i$ : 1 ≤ i ≤ n }

2: while an incomplete task exists do

3: for all unoccupied tasks do

4:  Set value ← the inverse distance from my position and the task

5:  Set utility ← the difference between value and the task’s current price

6:  Store task IDs and utilities for the highest and second highest utility values

7: end for

8: if an available task was found then

9:  bid ← price + (highest - second + ϵ) ▹ ϵ is a small constant to ensure the bid price increases

10:  sendBroadcast(BID, highestID, bid)

11: else

12:  wait until task-complete signal received

13: end if

14: wait until competing bids received

15: if I am the high bidder then

16:  sendBroadcast(ACCEPT, highestID)

17:  Increment price by: highest - second + ϵ

18:  Execute highestID

19: end if

20: end while

The completion time for all tasks is measured as the number of seconds elapsed when all of the tasks are completed. Figure 4a–d show completion times for each of the four algorithms that are compared while keeping the number of robots fixed and varying the total number of tasks in the environment. In terms of completion times, the SQ-MRTA algorithm closely matches the results of the repeated auctions algorithm. In contrast, the performance of the Hungarian and decentralized greedy approaches diminishes consistently as the number of robots increases.

Figure 4. Completion times with robot levels fixed for 6, 12, 18 and 24 tasks with: (a) five robots; (b) 10 robots; (c) 15 robots; and (d) 20 robots.

Figure 4. Completion times with robot levels fixed for 6, 12, 18 and 24 tasks with: (a) five robots; (b) 10 robots; (c) 15 robots; and (d) 20 robots.

Studying these results illuminates a couple of interesting conclusions, the first being that the decentralized greedy approach is very inefficient when the number of tasks greatly outweighs the number of robots. In Figure 4a, where the robot count is five, the decentralized greedy approach gets progressively worse as more tasks are introduced to the system. As the task to robot ratio grows, a greedy approach becomes ineffective, because it cannot cope with the number of possible trajectories available for completing all outstanding task requirements; by definition, it can only superficially select the best allocation for the immediate iteration and the constraints therein. It is only by adding more robots to the environment that this approach mirrors the efficiency displayed by the repeated auction and spatial queuing methods. In Figure 4d, when the robot count is 20, there is little statistical difference between these three methods. However, the opposite can be said for the Hungarian method: at first, it is producing results very similar to the repeated auction and spatial queuing algorithms, but as additional robots are introduced, it performs poorly. This can be attributed to the fact that the Hungarian method calculates the schedule off-line, and therefore, the algorithm has little ability to adapt to changes occurring dynamically during run time, such as incorporating collision avoidance times when the number of robots in the environment increases.

The inefficiency of the decentralized greedy system with five Corobots can be seen clearly in Figure 5a, which graphs the ratio of completion times as more tasks are added to the environment, starting with six tasks. With five available robots, the decentralized greedy algorithm nearly triples in running time with a task load of 24. In contrast, the other three methods accomplish the same task load at slightly over 1.5-times the time taken for six tasks. Similar performance is obtained for $10,15$ and 20 robots. As observed in Figure 4, overall completion time increases as the task load increases; similarly, the opposite is expected when the number of tasks is fixed, but additional robots are added to the system. This is precisely what Figure 6a–d convey via charts of completion time from the perspective of task load. Generally, we can observe from these results that the increase from five up to 10 robots offers the most improvement in efficiency, after which path interference (collision avoidance) overhead introduced by additional robots limits the gains or even decreases the system efficiency. In Figure 6a (six tasks), an average decrease in execution time of $35\%$ is visible when the number of robots increases from five up to 10. However, 15 and 20 robots offer almost no advantage, and the growth is almost flat ($\pm 4\%$). At 12 tasks, Figure 6c shows that performance gains are visible with 10 and 15 robots. The average decrease in execution time nearly doubles from 15% with 10 robots to 29% with 15 robots; an additional decrease of 5% accompanies an increase to 20 robots. Conversely, with task loads of 18 (Figure 6c) and 24 (Figure 6d), growth is flat or negative when 15 or 20 robots are present. With 18 tasks, the completion time decreases by 25% on average when jumping from five up to 10 robots; 15 robots offers no advantage, and 20 robots actually performs worse by 4%. A task load of 24 is completed 24% faster by 10 robots than five; 15 robots complete this same task load 2% slower than with 10, and 20 robots slip another 4% as compared to 15 robots. A possible explanation for this anomaly is the ideal localization of tasks with respect to robot deployment points; it should be noted that task groups are not super- or sub-sets of one another, each grouping being unique and independent.

It should also be noted that both our spatial queuing algorithm and repeated auctions show their worth by outperforming the greedy heuristic in scenarios that require multi-stage path planning in order to visit all of the tasks. This happens when the ratio of robots to tasks is less than one. As the ratio of robots to tasks approaches one and beyond, the greedy algorithm closes the gap and produces similar results. At a ratio of one or more, every task can be assigned to the closest robot, and there is less efficiency to be gained through decision making to select tasks using the SQ-MRTA or repeated auctions algorithm. Examples of the benefits of this decision making are visible in Figure 6b, 12 tasks and five robots (23%), Figure 6c, 18 tasks, with five and 10 robots (31% and 14%, respectively), and Figure 6a, 24 tasks, with 5, 10 and 15 robots (37%, 38% and 26%, respectively) by calculating the average improvement in completion time using the greedy results as a baseline. The Hungarian algorithm, as mentioned before, cannot respond to change and, therefore, performs poorly.

The ratios for the completion time of 10, 15 and 20 robots (as compared to a baseline of five robots for each method) are shown in Figure 7. These results show that, except for six tasks where the number of robots greatly outnumbers the tasks, the decentralized greedy heuristic improves the most with more robots (an average overall gain in efficiency of 35%), while at the same time, the Hungarian algorithm improves the least (15%).

Figure 5. Ratio of completion times of 12, 18 and 24 tasks as compared to six tasks with: (a) five robots; (b) 10 robots; (c) 15 robots; and (d) 20 robots.

Figure 5. Ratio of completion times of 12, 18 and 24 tasks as compared to six tasks with: (a) five robots; (b) 10 robots; (c) 15 robots; and (d) 20 robots.

The average distance traveled per robot is another key metric when analyzing overall MRTA performance. Minimizing the distance traveled in turn decreases the usage of a robot’s power source, which is a valuable resource in practical settings. Figure 8a–d show the average total distance traveled per robot, with 5, 10, 15 and 20 robots, as the task load increases from 6 to 24. The average total distance traveled per robot is directly proportional to the number of tasks and inversely proportional to the number of robots, or in other words, distance increases with task load and decreases with the number or robots. The data show quite clearly that the repeated auction, SQ-MRTA and Hungarian algorithms perform comparably in all scenarios (overall average distance of 50 m for the repeated auction method and 53 m for both spatial queuing and Hungarian). The greedy algorithm, however, operates less efficiently, as the task load is increased, culminating in a gap of approximately 60 m in the worst case (five robots, 24 tasks). Its overall average distance traveled was 65 m. As we witnessed with task completion times, the greedy algorithm does improve with the addition of more robots, and this can be seen in Figure 8d, where its performance is comparable to the other methods, barring a slight increase of about $12\%$ in the 24-task case. As observed in Figure 8, in terms of average distances traveled by robots, the SQ-MRTA algorithm performs comparably (within $1\%$ lesser distance traveled) to the RA algorithm. In general, the SQ-MRTA algorithm can be used as a complementary mechanism to the RA algorithm for MRTA.

Figure 6. Completion times with task load fixed for 5, 10, 15 and 20 robots for: (a)six robots; (b) 12 robots; (c) 18 robots; and (d) 24 tasks.

Figure 6. Completion times with task load fixed for 5, 10, 15 and 20 robots for: (a)six robots; (b) 12 robots; (c) 18 robots; and (d) 24 tasks.

Finally, another important performance metric for MRTA algorithms is the time for which robots remain idle while waiting for tasks to become available. The idle time denotes wasted energy by robots, and lower idle times correspond to better MRTA algorithm performance. Instead of reporting the idle time or the time for which a robot is waiting for available tasks, we have reported the average simulation time, which is the time for which a robot is active as a fraction of the total time required to completed all tasks. Since the robots using the Hungarian method are following a schedule calculated offline, they can terminate their operations immediately upon completing their assigned tasks; they do not need to remain idle waiting for performing more tasks on demand. Therefore, we have used the average simulation time for the Hungarian method as a benchmark for comparing the performance of the remaining three algorithms in terms of simulation time. Their average simulation times will be some multiple of the simulation time taken by the Hungarian method. Figure 9 graphs the evolution of the simulation time for all 16 combinations of robots and tasks. Again, we see that the decentralized greedy algorithm cannot compete in many situations that benefit from path planning. Its overall average simulation time ratio is $1.47$, whereas the simulation time ratios with repeated auction and spatial queuing algorithms are $1.25$ and $1.27$, respectively. However, its performance improves as the robot to task ratio approaches one. We also notice that there are sharp increases in the ratio of simulation times for 15 robot-six tasks ($1.86$) and for 20 robot-six tasks ($1.97$), as compared to an average ratio of $1.24$ for all other scenarios. These sharp increases can be explained by the fact that many robots sit idle, never winning any tasks in the spatial queuing, decentralized greedy and repeated auctions algorithms, while these same robots terminate immediately in the Hungarian case as soon as their schedule of initially assigned tasks is performed. Apart from these two spikes, spatial queuing and repeated auctions maintain a simulation time ratio just above one (Hungarian algorithm baseline). For scenarios with 15 robots-six tasks and for scenarios with 20 robots, the ratio increases considerably, giving an average of 1.57 and reaching two in two cases, as compared to a composite average of 1.25 for the 5-, 10- and 15-robot environments, respectively. The reason for this increase is that as the number of robots grows, the congestion in the environment also increases, and more time is spent by robots, both to reach task locations and to wait for tasks to become available.

Figure 7. Ratio of completion times as robots are added to the simulation: (a) six tasks; (b) 12 tasks; (c) 18 tasks; and (d) 24 tasks.

Figure 7. Ratio of completion times as robots are added to the simulation: (a) six tasks; (b) 12 tasks; (c) 18 tasks; and (d) 24 tasks.

Figure 8. Overall distance traveled in meters with: (a) five robots; (b) 10 robots; (c) 15 robots; and (d) 20 robots.

Figure 8. Overall distance traveled in meters with: (a) five robots; (b) 10 robots; (c) 15 robots; and (d) 20 robots.

Figure 9. Ratio of simulation times of different methods with respect to the simulation time of the Hungarian method as the baseline.

Figure 9. Ratio of simulation times of different methods with respect to the simulation time of the Hungarian method as the baseline.

Figure 10a–d report the scalability of the SQ-MRTA algorithm as the number of robots increases from 5–30, with $6,12,18$ and 24 tasks. Figure 10a,b show that the average distances traveled by each robot increase linearly as the number of tasks increases, for different numbers of robots. A similar, linear scalability trend is observed for the completion times of all tasks as the number of tasks increases, with a different number of robots. These results indicate that the SQ-MRTA algorithm has linear scalability in the number of robots and tasks: when the number of tasks or robots increases, the algorithm performs the additional computation within a time that is linearly proportional to the number of tasks or robots added, and each additional robot does not impose any extra overhead on the computation done by the remaining robots.

Figure 10. Average distance traveled by each robot for different numbers of robots between five and 30 for $6,12,18$ and 24 tasks grouped by robots (a) and grouped by tasks (b). Completion times of all tasks for different numbers of robots between five and 30 for $6,12,18$ and 24 tasks grouped by robots (c) and grouped by tasks (d).

Figure 10. Average distance traveled by each robot for different numbers of robots between five and 30 for $6,12,18$ and 24 tasks grouped by robots (a) and grouped by tasks (b). Completion times of all tasks for different numbers of robots between five and 30 for $6,12,18$ and 24 tasks grouped by robots (c) and grouped by tasks (d).

Overall, our simulation results show that our proposed spatial queuing algorithm for MRTA achieves a suitable task allocation for robots that performs comparably to other algorithms in terms of task completion times and distances traveled by the robots for different combinations of numbers of robots and tasks. The relative performance of each algorithm is susceptible to several parameters, including the number of robots, the number of tasks and environment features, such as the size and number of obstacles. The specific MRTA algorithm that will guarantee the best performance in terms of task completion time, distance traveled by robots and robot waiting times can be selected in accordance to these parameters.

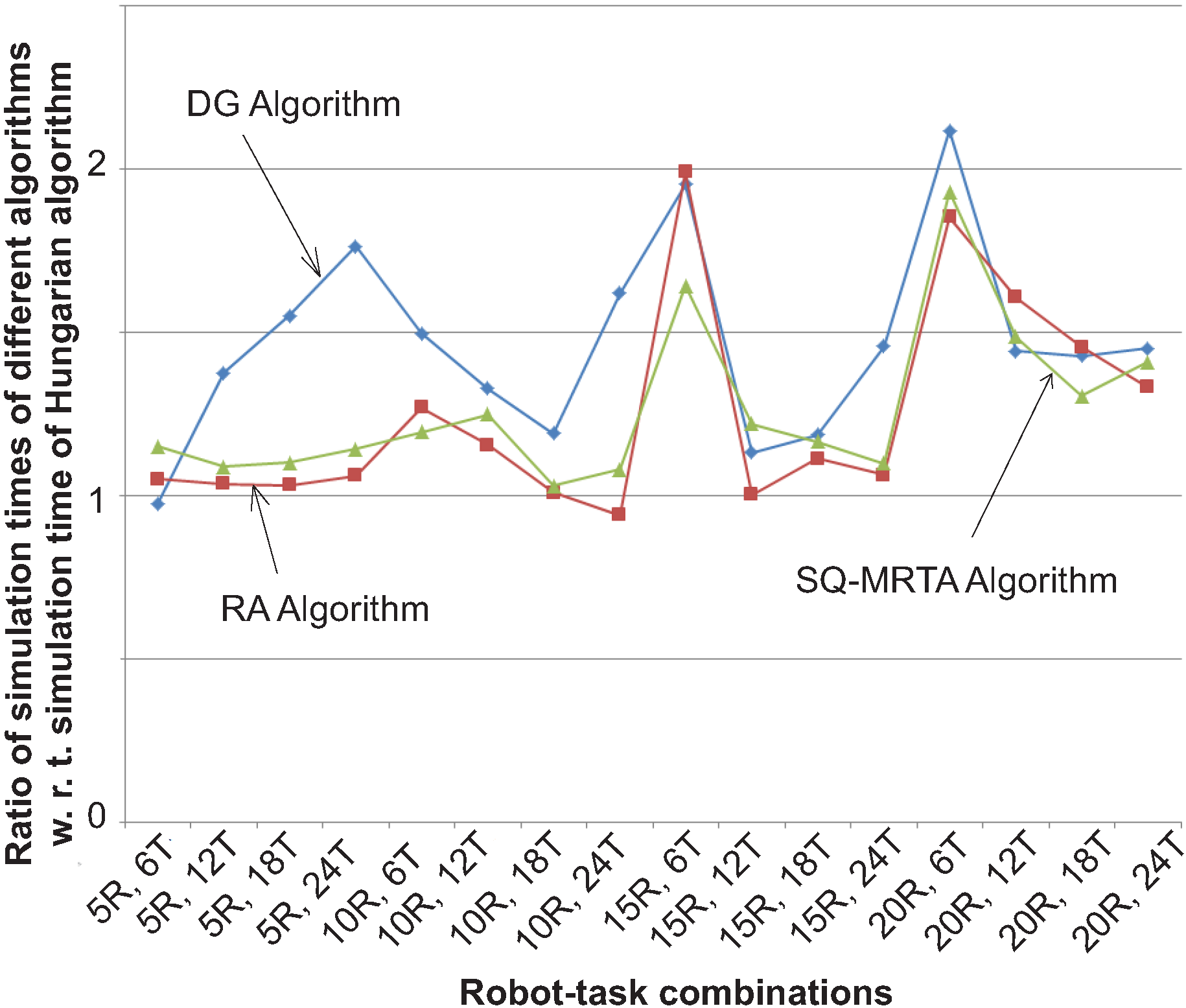
5. Communication Complexity

Estimating the amount of communication among the members of a multi-robot system for performing common tasks is crucial for designing reliable MRTA algorithms. In this section, we analyze the cost of communicating our system using the SQ-MRTA algorithm based on common metrics.

The communication network created by our system can be represented by a connected graph where robots are represented as the edges and their interconnections as the vertexes. The topology of this network is a full mesh structure or complete graph where robots are able to communicate to each other, as illustrated in Figure 11. This is a redundant network with a redundancy level equal to $m-1$, which for all our test systems is bigger than three, a level considered as a highly-robust network [31].

Figure 11. Network topology required by the SQ-MRTA (Spatial Queueing-Multi Robot Task Allocation) algorithm.

Figure 11. Network topology required by the SQ-MRTA (Spatial Queueing-Multi Robot Task Allocation) algorithm.

Now, concerning the cost of communication, the problem of finding efficient allocations using auctions has been classified as a demand queries’ problem that is known to be exponential when based on combinatorial allocations [32]. Blumrosen and Nisan [33] have analyzed more in detail the computational power of the mechanism of demand queries, and they have proven that it can be efficient with an approximate polynomial cost when considerations, such as weaker types of queries, can be done in the system and that, in general, the communication cost for allocation problems is exponentially lower than the cost needed in traditional bundle-price auctions.

In our case, the set of robots R, where $\left|R\right|=m$, represents the bidders in a combinatorial auction scheme and the set of tasks T, where $\left|T\right|=n$, represents the items to be sold. The task queue for robot $r_i$ at time-step t, $Q_{r_i}\left(t\right)$, given in Formula (4), plays the role of the valuation function commonly defined in price and combinatorial auctions settings. $Q_{r_i}\left(t\right)$ is effectively the function to find an allocation of k subsets of tasks $({\mathcal{T}}_1,...,{\mathcal{T}}_k)$. The goal is to calculate an allocation of tasks that maximizes the global benefit of the multi-robot system: ${\sum }_i\left(Q_{r_i}\left({\mathcal{T}}_i\right)\right)$. For that, an upper bound estimated on the number of bids four one round is at most $n\times m$. If at each round of $n\times m$ consecutive rounds, only one task is allocated, the upper bound based on the exchange of queries-bids is $O(n^2{m}^2$). However, the number of tasks does not remain constant in our domain, since any task can be allocated to one robot only once. Hence, the lower bound based on the exchanges of queries-bids is $O\left(nlogm\right)$.

6. Conclusions and Future Work

In this paper, we proposed a spatial queuing algorithm for the multi-robot task allocation problem. We verified the performance of our proposed algorithm on accurate models of the Corobot robot simulated on the Webots simulator for different combinations of numbers of robots and tasks. We also compared its performance with three different state-of-the-art algorithms for MRTA, namely a decentralized greedy algorithm, a repeated auction algorithm and an optimized offline schedule based on the Hungarian algorithm. Our results show that the offline schedule calculated by the Hungarian algorithm, while optimal in theory, does not necessarily translate to a real-world scenario where small changes in the environment, such as collision avoidance time incurred by robots and wait times for robots for tasks to become available, can significantly affect the performance of the algorithm. In addition, the results clearly indicate that a greedy allocation heuristic is inefficient in situations that require managing a small set of robots with a large number of tasks; only when the number of robots approaches the number of tasks does the greedy algorithm match the performance of repeated auctions or of the spatial queuing algorithm. Our spatial queuing method performed well in all scenarios and was comparable to the performance of the repeated auctions algorithm in all scenarios.

There are several directions in which this work is being extended currently. We are working on implementing the SQ-MRTA algorithm on physical robots. There are many simplifying assumptions in a simulated environment, such as communication reliability and accurate localization of the robots based on a simulated GPS receiver that needs to be relaxed in a physical environment. Yet another direction we are investigating is to use a set of heterogeneous robots instead of the homogeneous set of robots assumed in this paper. It may be beneficial to include robots with varying operational and sensor capabilities, especially when the primary goal is to detect buried objects, such as landmines. As such, the confidence levels of performing a task, such as landmine detection by a particular robot, may need to be graded and would necessitate the inclusion of priorities based on these confidence levels. Lower confidence levels may require supplemental inspections, possibly by specific sensor types, and higher confidence levels may change the priority of a task, so that it attracts fewer other robots and directs robots towards regions with higher priority tasks.

Further directions that we plan to investigate are to introduce a minimum number of tasks to allocate at one time, at least within some limited window of time, and also exploring the option of augmenting the transition matrix used in the spatial queue formation with data discovered during run time. With the current settings, the time-step, or intervals at which the robot checks for new tasks in the SQ-MRTA algorithm, is determined manually. A more sophisticated method that adjusts the time-step based on feedback from the robots about the current completion time for tasks could improve the time performance of the algorithm. In this paper, all tasks have been assumed to be of the same priority. For further generalization of the SQ-MRTA algorithm, task priorities could be integrated into the matrix by weighting the combination of distance and task priority. In this work, we have assumed that tasks are homogeneous and that the order of performing the tasks does not affect the outcome of performing the tasks. This assumption is valid for the example domain of multi-robot landmine detection used in the paper, as well as for similar domains that involve detection tasks that do not have hard completion deadlines. Another future direction we are investigating to generalize our approach is to relax this assumption to introduce task deadlines and to consider temporal constraints between tasks.

In this paper, we have provided a novel, fully-decentralized algorithm for MRTA based on a spatial queueing model. We envisage that further investigation of queuing models for the MRTA problem can lead to improved solutions that will enable multiple robots to perform spatially-distributed tasks in an efficient manner.