Multi-Objective Intelligent Industrial Robot Calibration Using Meta-Heuristic Optimization Approaches

Abstract

Precision component displacement, processing, and manipulation in an industrial environment require the high-precision positioning and orientation of industrial robots. However, industrial robots’ positioning includes uncertainties due to assembly and manufacturing tolerances. It is therefore required to use calibration techniques for industrial robot parameters. One of the major sources of uncertainty is the one associated with industrial robot geometrical parameter values. In this paper, using multi-objective meta-heuristic optimization approaches and optical metrology measurements, more accurate Denavit–Hartenberg (DH) geometrical parameters of an industrial robot are estimated. The sensor data used to perform this calibration are the absolute 3D position readings using a highly accurate laser tracker (LT) and industrial robot joint angle readings. Other than position accuracy, the mean absolute deviation of the DH parameters from the manufacturer’s given parameters is considered as the second objective function. Therefore, the optimization problem investigated in this paper is a multi-objective one. The solution to the multi-objective optimization problem is obtained using different evolutionary and swarm optimization approaches. The evolutionary optimization approaches are nondominated sorting genetic algorithms and a multi-objective evolutionary algorithm based on decomposition. The swarm optimization approach considered in this paper is multi-objective particle swarm optimization. It is observed that NSGAII outperforms the other two optimization algorithms in terms of a more diverse Pareto front and the function corresponding to the positional accuracy. It is further observed that through using NSGAII for calibration purposes, the root mean squared for positional error has been improved significantly compared with nominal values.

1. Introduction

The total number of annual industrial robot installations worldwide in industry is increasing [1]. This is mainly due to their capability to perform highly repetitive and dexterous industrial tasks with high precision on a factory floor for high-performance manipulations and object handling. This property contributes to the flexibility and productivity of the factory environment. Industrial robots’ position and orientation control requires a mathematical model to establish their dynamic behavior and forward kinematics (FKs) [2]. However, the position and orientations of an industrial robot contain errors. These errors are mainly caused by manufacturing tolerances, the wear and tear of the industrial robot, irregularities in industrial robot geometry, and the resolution of encoders. To alleviate the problem caused by parameter and geometrical uncertainties in an industrial robot, offline calibration is essential [3].

Using FKs equations, the six-dimensional position and orientations of an industrial robot end-effector is calculated as a function of its joint angle values. The motion of an industrial robot can be either developed in terms of position and orientation or end-effector velocity. On the other hand, the relationship between robot joint values as a function of industrial robot end-effector position and orientation is defined by the inverse kinematics of the industrial robot. Both the FKs and inverse kinematics equations include the Denavit–Hartenberg (DH) parameters of the industrial robot [4,5]. Manufacturing tolerances, wear and tear, environmental effects, and assembly tolerances in an industrial robot may cause deviations in the DH parameters that may cause uncertainties in its FKs [6]. Therefore, the calibration of an industrial robot’s DH parameters is required to increase its motion precision.

Calibrations of industrial robots are performed at three different levels including joint angle encoders, FKs calibration including geometrical dimensions of the industrial robot, and non-kinematic calibration [7,8,9,10]. For the joint encoder calibration, level I calibration, a mathematical correcting formula is computed which acts on the measured values of the joint encoders and results in a more accurate joint angle value. Zero offset calibration may also be required in some industrial robots which benefit from incremental encoders [11,12,13]. For level II calibration, the accuracy of the geometrical parameters of the industrial robot are increased using precision measurement equipment resulting in more accurate forward kinematics. Finally, calibration on level III includes compensation for flexibility and dynamic error within FKs equations. In this paper, calibration at level II is considered, in which by using the measurements from a laser tracker (LT), more accurate values for the DH parameters of the industrial robot are given.

Neural networks [14,15], deep neural networks [16], and a fuzzy interpolation approach [17,18,19] are among the non-parametric approaches for calibration. An adaptive fuzzy inference system investigated in [17] uses this intelligent structure for non-parametric calibration purposes. The fuzzy interpolation approach for error compensation used in [18,19] considers model-based FKs for the industrial robot and the residual error corresponding to these FKs is compensated based on the position errors of neighboring grid points around the desired point. Different non-contact metrology equipment has already been used within calibration applications. For instance, LTs of different types are utilized for the calibration of different industrial robots and collaborative industrial robots [20,21,22]. Calibration approaches using LTs are considered in [20,23] for the calibration purposes of heavy-duty industrial robots. The approaches using deep neural networks are among the more advanced artificial intelligence approaches to calibrate different industrial robots using LTs [24,25]. A model free positional error compensation approach is investigated in [26] where improved kriging interpolation is used to improve the positional accuracy of industrial robots [26]. A detailed list of the calibration approaches including metrological equipment details and industrial robot details are listed in

Table 1. Different industrial robot calibration approaches.

Ref. No.	Main Calibration Approach	Industrial Robot	Metrology Equipment and Brand
[14]	Extended Kalman filter and an artificial neural network	Stewart Platform	Digital indicators
[15]	Extreme learning machine neural network	GSK RB03 robot	Nokov’s MARS 2H
[16]	Deep neural networks	KUKA KR300 R2500 ULTRA	Leica LT800 LT
[17]	Adaptive neuro-fuzzy inference system (ANFIS)	2-DOF five-bar parallel robot	Digital indicators
[19]	Fuzzy interpolation method	PUMA 560 robot model	Single-beam LT system
[20]	Nonlinear least squares	PA10 robot arm	Leica SMART310 LT
[21]	Least squares support vector regression with radial basis function kernel	IRB1410	Leica AT960
[24]	Deep neural networks	KUKA KR500	API Radian LT
[25]	Convolutional neural network	SRA166	LT manufactured by IHI Scube

. In this paper a parametric robot calibration that provides in-depth information about the geometrical dimension of the industrial robot is utilized. In [7] several meta-heuristic approaches are used to calibrate industrial robots. These methods include the evolutionary optimization approach of differential evolution, the swarm intelligence approach of particle swarm optimization and artificial bee colony, and the physics-inspired optimization method of gravitational search algorithms. Meta-heuristic approaches are the preferred choice when the cost function is defined implicitly, and/or it is not differentiable. Moreover, since meta-heuristic approaches start their search from multiple initial points, they may suffer less from local minimum problems. However, single-objective optimization approaches are investigated in [7], and the only objective function considered is positioning error.

In this paper, the mean absolute deviations in DH parameter values with respect to the manufacturer’s given ones is an additional objective function. Hence, the obtained solutions not only minimize the positioning error, but also minimize the deviation of the DH parameter values with respect to the original parameter values given by the manufacturer. This is a clear improvement of the proposed approach over the previously investigated approaches which solely consider the positioning accuracy of the industrial robots. The DH parameter values given by manufacturers are obtained as a result of different tests and measurements during the manufacturing process and quality control phase. These robots are usually used within different industrial disciplines, making their corresponding FKs highly reliable due to heavy usage within industrial environments. A report published in February 2025 states that the Universal Robots company, a manufacturer established in 2005 and headquartered in Odense, Denmark, has been successful in selling a total of 100,000 industrial robots capable of lifting up to 30 kg load [27]. To benefit from the test results obtained by the manufacturer, the optimization settings in this paper are designed such that the obtained DH parameter values do not fall far from the manufacturer’s given parameter values. A high deviation from the manufacturer’s given parameter values may be rejected in the implementation phase due to reliability concerns. Therefore, the proposed approach is a multi-objective calibration approach which not only deals with minimizing the positioning error but also minimizes the mean absolute deviation of the obtained parameters from the manufacturer’s given parameters. This makes the obtained DH parameter values as close as possible to the manufacturer’s given parameters. The multi-objective meta-heuristic calibration of the DH parameters of industrial robots using LTs which may contribute to more reliable FKs model is the main novelty of this paper. To the best of the author’s knowledge, minimizing the intervention of the calibration approach in the manufacturer’s given parameters has never been investigated in the literature. To perform multi-objective optimization using a dominance approach is preferred over an aggregation approach, which aggregates all objective functions to reduce the number of objective functions in a multi-objective optimization problem to one. The nondominated sorting genetic algorithm (NSGAII) [28] and a multi-objective evolutionary algorithm based on decomposition (MOEA/D) are the two evolutionary optimization algorithms used in this paper. On the other hand, multi-objective particle swarm optimization (MOPSO) is a swarm intelligence approach to handle multiple objective functions. Therefore, NSGAII, MOEA/D, and MOPSO are the three chosen algorithms to handle this problem. The experimental setup includes an LT and an industrial robot. The Pareto front obtained from the three meta-heuristic optimization approaches are tested in terms of the diversity of solutions and their minimality. A comparison between the three optimization algorithms suggests that the Pareto front obtained from NSGAII is the most diverse solution. Using the Pareto front obtained from NSGAII, it is possible to have a wide range of solutions for different mean absolute deviations from the manufacturer’s given parameters. Finally, the comparison results between the positional accuracy of two points with respect to the manufacturer’s given parameter values demonstrated a significant improvement in the positional accuracy.

This structure of this paper is as follows. In Section 2, the multi-objective optimization problem is formulated. A summary of the optimization algorithms is given in Section 3. The setup used for implementing the proposed multi-objective optimization approach for the calibration purpose of industrial robots is explained in Section 4. The results of the optimization are given in Section 5. The concluding remarks, acknowledgements, and references are the last sections.

2. Problem Formulation

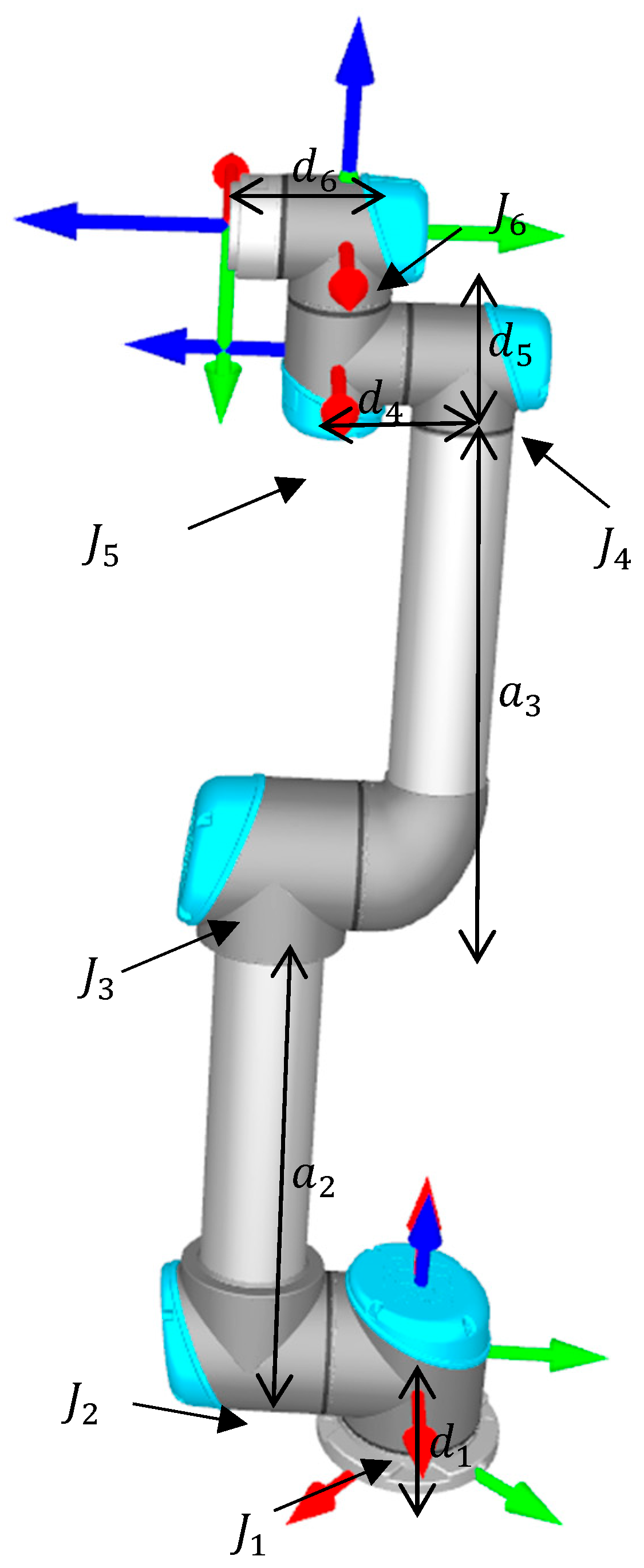
2.1. Industrial Robot DH Parameters

FKs return the Cartesian position and orientation of the desired joint including the industrial robot end-effector in terms of a transformation matrix with respect to a frame including the base joint. A frequently used approach to identify the FKs for a n-degrees of freedom (n-DOF) serial manipulator with n + 1 links is a DH system. The DH parameters of an industrial robot consist of four types of parameters which are used to uniquely describe the industrial robot geometry. These parameters are then used within the industrial robot FKs formulation to find the Cartesian position and orientation for the desired joint. In this paper the following notations are used:

• Joint angle ${\theta }_i$: This parameter is one of the DH parameters of the industrial robot which is usually measured online using joint encoders and it is defined as the angle between $x_{i-1}$ and $x_i$ axes about the $z_{i-1}$ axis, where $x_i$, and $z_i$ are the x-axis and the z-axis of the i-th joint;
• Link offset $d_i$: This parameter is the second DH parameter of the industrial robot which is defined as the distance from the origin of frame $(i-1)$ to the $x_i$ axis along the $z_{i-1}$ axis;
• Link length $a_i:$ This parameter is the third DH parameter of the industrial robot which is defined as the distance between the $z_{i-1}$ and $z_{i-1}$ axis along the $x_i$ axis, where the intersecting axis is parallel to $z_{i-1}\times z_i$;
• Link twist ${\alpha }_i:$ This parameter is the last parameter in the DH parameter list which is defined as the angle between the $z_{i-1}$ and $z_i$ axes about the $x_i$ axis.

2.2. Forward Kinematics of UR5

The precision of an industrial robot’s position and orientation is affected by its FKs which refers to the process of computing the position and orientation coordinates as a function of its DH parameters [7]. FKs equations are usually defined in matrix form to define the spatial formulation between consecutive link coordinate frames.

$${}_i{}^{i-1}T=\left[\begin{array}{cccc}{cq}_i& -{c{\alpha }_{i}sq}_i& {s{\alpha }_{i}sq}_i& {a_{i}cq}_i\\ {sq}_i& c{\alpha }_i{cq}_i& -s{\alpha }_i{cq}_i& {a_{i}sq}_i\\ 0& s{\alpha }_i& c{\alpha }_i& d_i\\ 0& 0& 0& 1\end{array}\right]$$

(1)

where ${}_i{}^{i-1}T$ is the link transformation matrix from the link $i$−1 to the link $i$. Furthermore, $q_i\prime s, i=1,\dots ,6$ represent the joint angle $i$, ${\alpha }_i\prime s, i=1,\dots ,6$, $a_i\prime s, i=1,\dots ,6$, and $d_i, i=1,\dots ,6$ represent the other DH parameters of the robot. For the sake of brevity, the mathematical functions are also presented in a short form such that ${cq}_i, {sq}_i, c{\alpha }_i, \mathrm{a}\mathrm{n}\mathrm{d} s{\alpha }_i , i=1,...6$ represent ${cos(q}_i),$ ${sin(q}_i),$ $c{os\alpha }_i,$ and $sin\left({\alpha }_i\right),i=1,...,6$, respectively. The forward kinematics of the industrial robot end-effector in base coordinates is obtained by a matrix multiplication of all consecutive transformation matrices [29,30].

$$T_e={}_6{}^{0}T={}_1{}^{0}T{}_2{}^{1}T{}_3{}^{2}T{}_4{}^{3}T{}_5{}^{4}T{}_6{}^{5}T.$$

(2)

The last column of $T_e$ represents the three-dimensional coordinates of the industrial robot end-effector and the rotational matrix embedded within $T_e$ demonstrates its orientations.

The nominal values of the DH parameters of UR5 given by Universal Robot, the manufacturer of the UR5, are as follows (see Figure 1)—https://www.universal-robots.com/articles/ur/application-installation/dh-parameters-for-calculations-of-kinematics-and-dynamics/ (accessed on 1 May 2022):

$$\begin{array}{c}{d}_1=0.08916m,a_2=-0.425m,a_3=-0.392m,d_4=0.1092m,\\ d_5=0.0947m,d_6=0.0823m+d\end{array}$$

(3)

where $d$ is the distance between the center of the laser target and the center of the robot end-effector (see Figure 3). The mounting for the laser target is in the direction of the robot’s last link and its value is added to $d_6$. The measured value of $d$ is equal to $0.1695 m$. Moreover, $d_2=d_3=0$, and $a_i=0,i=\mathrm{1,4},\mathrm{5,6}$. The robot, within the experiments performed in this paper, is considered in its downward orientation with its tool center point (TCP) axis rotation vector equal to $\left(\begin{array}{ccc}\pi & 0& 0\end{array}\right)$.

2.3. Multi-Objective Calibration

To calibrate the industrial robot, the two objective functions considered are the mean absolute deviation from manufacturer parameters (MADMP) and the root mean squared value of error in the three axes. While optimizing the root mean squared error (RMSE) results in having an overall least squares solution, the deviation of the estimated DH parameter values from the manufacturer’s given DH parameter values may be high. To avoid such a phenomenon, it is required to optimize both objective functions simultaneously to deliver optimal dimensions while minimizing the RMSE and avoiding a large deviation from the manufacturer’s given DH parameter values. The manufacturer’s given DH parameter values are given as a result of accurate measurements during the manufacturing and quality control process by the manufacturer. Therefore, the manufacturer’s given DH parameter values are highly reliable parameter values. Although we use precision measurements using an LT in this paper, it is expected to have more accurate DH parameter values; a large deviation from the manufacturer’s given parameter values is undesirable. To have more accurate FKs with their DH parameter values close to the manufacturer’s given parameter values, MAMDP is taken as the second objective function. Therefore, the cost function evaluates the accuracy of the FKs of the industrial robot using DH parameters generated during optimization using the multi-objective optimization techniques of NSGAII, MOPSO, and MOEA/D [31]. First, the given parameters are used within the FKs as in (1) to find the positions within the industrial robot coordinate frame. The positions are then transformed into LT coordinates and are evaluated through precision positions read from the LT to compute the RMSE value. The positions associated with the industrial robot positions need to be computed within LT coordinates utilizing a transformation matrix.

$${\left[\begin{array}{ccc}{x}_{rl}& y_{rl}& z_{rl}\end{array}\right]}^T={Tr}_{rl}{\left[\begin{array}{cc}\begin{array}{cc}{x}_{rr}& y_{rr}\end{array}& \begin{array}{cc}{z}_{rr}& 1\end{array}\end{array}\right]}^T$$

(4)

where $x_{rl}$, $y_{rl}$, and $z_{rl}$ are the laser target positions attached to the robot end-effector measured using LT in LT coordinates, $\left(x_{rr}^i,y_{rr}^i,z_{rr}^i\right),i=1,\dots ,N$, are the robot end-effector positions using its FKs within its own coordinates, and ${Tr}_{rl}$ is the transformation matrix from the robot base coordinate system to the coordinate system of the LT. To calculate the transformation matrix ${Tr}_{rl}$, a least square operator is implemented for all measurements. To do so, the coordinate transformation equation of (14) is rewritten as follows:

$$\underset{D}{\underbrace{\left[\begin{array}{cc}\begin{array}{ccc}\begin{array}{c}{x}_{rl}^1\\ y_{rl}^1\\ z_{rl}^1\end{array}& \dots & \begin{array}{c}{x}_{rl}^i\\ y_{rl}^i\\ z_{rl}^i\end{array}\end{array}& \begin{array}{cc}\dots & \begin{array}{c}{x}_{rl}^N\\ y_{rl}^N\\ z_{rl}^N\end{array}\end{array}\end{array}\right]}}={Tr}_{rl}\underset{R}{\underbrace{\left[\begin{array}{cc}\begin{array}{ccc}\begin{array}{c}{x}_{rr}^1\\ y_{rr}^1\\ \begin{array}{c}{z}_{rr}^1\\ 1\end{array}\end{array}& \begin{array}{c}\\ \dots \\ \begin{array}{c}\\ \dots \end{array}\end{array}& \begin{array}{c}{x}_{rr}^i\\ y_{rr}^i\\ \begin{array}{c}{z}_{rr}^i\\ 1\end{array}\end{array}\end{array}& \begin{array}{cc}\begin{array}{c}\\ \dots \\ \begin{array}{c}\\ \dots \end{array}\end{array}& \begin{array}{c}{x}_{rr}^N\\ y_{rr}^N\\ \begin{array}{c}{z}_{rr}^N\\ 1\end{array}\end{array}\end{array}\end{array}\right]}}$$

(5)

The transformation matrix ${Tr}_{rl}$ is calculated as follows:

$${Tr}_{rl}=D{R}^{†}$$

(6)

where $R^{†}$ presents the Moore–Penrose pseudoinverse of $R$. The transformation matrix ${Tr}_{rl}$ which is the result of (6) can then be applied to the end-effector positions in industrial robot coordinates as follows:

$$\left[\begin{array}{c}{x\prime }_{rl}\\ {y\prime }_{rl}\\ {z\prime }_{rl}\end{array}\right]={Tr}_{rl}\left[\begin{array}{c}\begin{array}{c}{x}_{rr}\\ y_{rr}\end{array}\\ \begin{array}{c}{z}_{rr}\\ 1\end{array}\end{array}\right]$$

(7)

where ${x\prime }_{rl}$, ${y\prime }_{rl}$, and ${z\prime }_{rl}$ represent the robot end-effector position in the x-, y-, and z-axis using robot joint encoders in LT coordinates. The position errors ($er$) are calculated as follows:

$${er}_1^i=\left|{x^{\prime }}_{rl}^i-x_{rl}^i\right|,{er}_2^i=\left|{y^{\prime }}_{rl}^i-y_{rl}^i\right|,{er}_3^i=\left|{z^{\prime }}_{rl}^i-z_{rl}^i\right|,i=1,\dots ,N$$

(8)

The first multi-objective function is defined as the mean absolute deviation of the given parameters with respect to the manufacturer’s given parameter values.

$$f_1={\displaystyle \frac{1}{6}}\left(\sum _{i=\mathrm{1,4},\mathrm{5,6}}\left|d_{io}-d_i\right|+\sum _{i=\mathrm{2,3}}\left|a_{io}-a_i\right|\right)$$

(9)

where the $d_{io},i=\mathrm{1,4},\mathrm{5,6}$, and $a_{io},i=\mathrm{2,3}$ parameters are the parameters obtained during the optimization process using the meta-heuristic optimization approaches, and $d_i,i=\mathrm{1,4},\mathrm{5,6}$, and $a_i,i=\mathrm{2,3}$ are given in (3). The second objective function within this multi-objective problem is defined as follows:

$$f_2=\sqrt{\sum _{i=1}^{NP}\sum _{j=1}^3{{\displaystyle \frac{1}{3NP}}\left({er}_j^i\right)}^2}$$

(10)

where $NP$ is the total number of experimental points.

Figure 1. DH parameters. Green arrows refer to x-axis, red arrows refer to y-axis, and blue arrows refer to z-axis corresponding to each joint frame.

Figure 1. DH parameters. Green arrows refer to x-axis, red arrows refer to y-axis, and blue arrows refer to z-axis corresponding to each joint frame.

3. Multi-Objective Optimization Approaches

3.1. Nondominated Sorting Genetic Algorithm

The nondominated sorting genetic algorithm II, NSGAII, is an evolutionary multi-objective algorithm designed by Deb [32,33]. According to domination principles, solution A dominates solution B if and only if its associated cost function in all dimensions is better or equal to solution B. A Pareto front is a collection of solutions which do not dominate another member of the Pareto front but dominate the rest of the solutions. NSGAII operates using Pareto front principles. In this algorithm, N chromosomes are randomly initialized and using genetic algorithm operators of crossover and mutation, N offspring are generated. The generated offspring as well as the current chromosomes are combined to have 2N number of chromosomes. The selection operator works based on the dominance principles. To perform the selection process, the first Pareto front is extracted from the available solutions. The solutions in the first Pareto front are automatically selected for the next generation. By eliminating the members of the first Pareto front, the next Pareto front is obtained which is selected to survive for the next generation. This procedure is continued until all available Pareto solutions are selected. However, when selecting the last Pareto front, it is possible that if all members of Pareto are selected, the number of individuals for the next generation will be more than N. To avoid this issue, from the last Pareto front, chromosomes which preserve diversity are preferred. At the next iteration, the N number of chromosomes selected using this selection procedure are then evolved and the Pareto selection procedure is applied to them. This algorithm iterates for a few times before the stop condition is met. The pseudo code of this algorithm is summarized as follows:

(1)

Randomly initialize n-dimensional ${Pop}_i,i=1,\dots ,N$ with in feasible space.

(2)

Apply a selection algorithm on the population and choose parents.

(3)

Apply genetic algorithm operators of crossover and mutations to the selected parents.

(4)

Combine the old population and the offspring and evaluate the whole population.

(5)

Apply nondominated sorting to the overall population.

(6)

Select N number of the population from the first Pareto fronts. For the last Pareto front, if selecting all members of the Pareto front, make the number of next generations more than N, apply a crowding distance measurement algorithm, and choose the individuals with the highest crowding distance index to maximize the diversity within the next generation.

(7)

If the STOP condition is not met GOTO 2, otherwise STOP the procedure.

3.2. Multi-Objective Particle Swarm Optimization Algorithm

Particle swarm optimization imitates the unpredictable and chaotic movement of fish with a school of fish to perform optimization [34]. In this algorithm, the solutions are represented by particle positions which move within n-dimensional search space to perform optimization [35]. Each particle records its best position, and the overall best position of the whole swarm is recorded as well. A velocity vector is used to update the position of each member of the swarm [36]. The value of the velocity vector is calculated as the vectoral sum of the direction towards the best personal experiment and the direction of the vector to the global experiment of the swarm. Another component of the velocity vector is an inertia term to maintain the last velocity direction. The velocity vector is added to the particle position vector to update the new particle positions. Multi-objective particle swarm optimization is the multi-objective version of particle swarm optimization which works based on dominance principles to handle the multiple objective cost functions [31,37]. This algorithm benefits from a repository from which the overall best position for each particle is selected using a hypercubic partitioning approach. The pseudo code for this algorithm is as follows:

(1)

Randomly initialize n-dimensional ${Pop}_i,i=1,\dots ,N$ with in feasible space.

(2)

Initialize n-dimensional ${Vel}_i, i=1,\dots ,N$ to zero vector.

(3)

Calculate the multi-objective cost function associated with each member of the swarm.

(4)

Construct the swarm repository $({Rep}_j,j=1,\dots ,M)$ out of nondominated solutions within the swarm.

(5)

Generate hypercubes out of particles in the repository in the objective function space. Locate particles in the repository in their respective hypercube.

(6)

Initialize the best experience ${PBest}_i,i=1,\dots ,N$ for each particle by using their initial multi-objective cost function.

(7)

Compute the velocity matrix using the following equation: ${Vel}_i=w{Vel}_i+r_1{c}_1{PBest}_i-{Pop}_i+r_2{c}_2{Rep}_h-{Pop}_i$.

• where $r_1, r_2\in [0, 1]$ are random numbers and $c_1, c_2\in [0, 2]$ are fixed and user-defined parameters. The parameter $w$ is the inertia parameter. A comparison study in [38] on the inertia parameter recommends the following linearly decreasing function for this parameter [39,40].

$$w=w_{max}-{\displaystyle \frac{w_{max}-w_{min}}{Maxiter}}\times it$$

(11)

where $Maxiter$ is the maximum number of iterations, $it$ is the current number of iterations, $w_{min}$ is a constant parameter, and $w_{max}$ is another constant parameter. The recommended value for $w_{min}$ is 0.4 and the recommended value for $w_{max}$ is 0.9. Inspired by the results obtained in that paper, this type of inertia weight is used in this paper. The choice of the particle from the repository is completed using a hypercubic approach. First the hypercubes are chosen from the objective space for the repository particles. Then particles are assigned to the respective hypercube. A roulette wheel selection mechanism is then applied to the hypercube proportional to the number of particles within the hypercube. After selecting the hypercube, a member of the repository within the hypercube (${Rep}_h$) is selected and the velocity vector (${Vel}_i$) is updated.

(8)

The position vector is then updated as ${Pop}_i={Pop}_i+{Vel}_i$.

However, in a case where values corresponding to the particle in each dimension exceed the boundary, one may use the boundary value as the new value for ${Pop}_i$ in the corresponding dimension or multiply ${Vel}_i$ by $-1$ and add it to ${Pop}_i$.

(9)

Evaluate the new values of ${Pop}_i$ and update ${PBest}_i,i=1,\dots ,N,$ and $({Rep}_j,j=1,\dots ,M)$ with newly generated nondominated solutions.

(10)

GOTO (7) and iterate the algorithm until the STOP condition is met.

3.3. Multi-Objective Evolutionary Algorithm Based on Decomposition

The multi-objective evolutionary algorithm based on decomposition (MOEA/D) is a multi-objective dominance type of algorithm rather than an aggregation algorithm which selects the parents for reproduction based on the closest neighborhood [41]. In this algorithm, the closest neighborhood with a specific number of members is assigned to each individual [42,43]. Then two members from each neighborhood are selected randomly for an evolutionary operation. The repository is updated by choosing the overall nondominated members of the repository and the newly generated individuals as a result of evolutionary operations. The neighborhood is constructed upon repository members. The algorithm iterates a few times until the stop condition is met.

(1)

Randomly initialize n-dimensional ${Pop}_i,i=1,\dots ,N$ within feasible space.

(2)

Evaluate the randomly generated population and initialize the repository by adding the nondominated ones to the repository. Initialize $z_i$ ’s as the best solution obtained so far for the objective function $f_i$ ’s.

(3)

Find $T$ closest neighbors for each individual in terms of Euclidean distance within generated population ${Pop}_i,i=1,\dots ,N$: $B_i=\{{Pop}_1,{Pop}_2,\dots ,{Pop}_T\}$.

(4)

For each individual ${Pop}_i,i=1,\dots ,N$ select two parents from their associated neighborhood $B_i$ and apply evolutionary operations to generate new offspring.

(5)

Update $z_i$ ’s as the best solution obtained so far in the case that a better $z_i$ is found.

(6)

Evaluate the new individuals if they dominate the repository members; update the repository by adding them and removing the dominated ones.

(7)

Update neighborhoods according to the newly obtained $z_i$’s.

(8)

If STOP criteria are not met, GOTO 4.

4. Experimental Setup

The experimental setup includes an LT for position measurements and an industrial robot which are specified in detail in this section. To mount the laser target for position measurements, the required fixtures are 3D printed.

4.1. Laser Tracker

A high-precision LT is used to perform the positioning task [44]. The LT used in these experiments is a Leica LT model AT960-MR from Hexagon Metrology Limited, Shropshire, UK. It is a favorite positioning equipment for critical distance, location, shape, and surface measurements [45] (see Figure 2). This piece of measurement equipment measures the 3D position of the laser target attached to the end-effector. The laser target mounted using a 3D-printed fixture to the end-effector is a precision 1.5 in red ring reflector which benefits from perpendicular mirrors detectable through the LT. The LT is connected via Wi-Fi to a PC which operates Windows 10 and has Spatial Analyzer^® software version 2019.05.16 as the operating software for LT. The LT performs measurements at 10 Hz and its maximum operational measurement distance is 60 m. The precision of the LT is $3 \mu m/m$. This equipment benefits from a class II laser source and can operate within different environmental conditions, and its environmental rating is IP54.

4.2. Industrial Robot

A collaborative industrial robot is utilized, which is manufactured by Universal Robot and can handle 5 Kg of load at a maximum no-load angular velocity of $180°/sec$. The robotic operating system (ROS) is an open-source robust communication environment for communicating with robots [46]. The UR5 is operated from a Linux 18.04-operated PC with ROS melodic. Using this software interface, time, joint angle values, angular velocities of the joint, and joint motor currents are gathered through a single ROStopic. The sampling time of the industrial robot is slightly variable, but its mean value is $8 msec$.

The data collected through the LT is sampled at 10Hz which is different from the sample time associated with the industrial robot. Shift and resampling operators are therefore required to be performed to synchronize position data collected from the LT and the data collected from UR5. The data points collected from UR5 are associated with robot angular velocities of less than 0.0548 rad/sec. Calibration is therefore performed during static and near-static robot movement with the total number of collected points being equal to 92. The measurements are recorded 2.8 m away from the industrial robot’s base. The communications diagram between equipment within the experimental setup are demonstrated in Figure 2.

5. Experimental Results

The experimental setup for performing this experiment is demonstrated in Figure 3. The three multi-objective optimization algorithms applied to the optimization problem are NSGAII, MOPSO, and MOEA/D. The number of individuals taken for the three optimization algorithms is equal to 200. The number of repository members for MOPSO and MOEA/D which benefit from a repository is equal to 100. The total number of generations for the three algorithms is taken as equal to 1000. Figure 4 demonstrates the Pareto front obtained from the three optimization algorithms. The statistics associated with the three Pareto fronts obtained from the three optimization algorithms are summarized within

Table 2. Mean squared error for position using the three optimization algorithms.

		NSGAII	MOPSO	MOEAD
Cost function #1	Min (mm)	0.0094031	0.17594	0.84645
	Max (mm)	19.0	0.80271	1.5
	Range (mm)	19.0	0.62677	0.60869
	Standard deviation (mm)	5.8	0.21223	0.11697
	Mean (mm)	9.3	0.42292	0.87284
	Median (mm)	9.1	0.33401	0.84645
Cost function #2	Min (µm)	70.713	74.603	74.824
	Max (µm)	98.631	93.189	119.08
	Range (µm)	27.917	18.586	44.259
	Standard deviation (µm)	4.9674	6.1017	9.2482
	Mean (µm)	73.377	79.639	116.87
	Median (µm)	72.357	78.450	119.08

. The range value associated with cost function #1 obtained for NSGAII is the largest value among the three investigated approaches. Therefore, the best results in terms of the diversity of the solutions for cost function #1 are obtained from NSGAII.

This indicates that this algorithm has the most diverse solution set which covers a wide range of values for mean intervention in the DH parameters of the industrial robot. It is therefore easy to study the calibration errors associated with different values of MADMP from the Pareto front obtained from NSGAII. Moreover, although MOPSO has some points which dominate the solutions in the Pareto front given by NSGAII (see Figure 4b), the best solutions in terms of RMSE accuracy exist in the Pareto front given in NSGAII.

A further study on the members of the Pareto fronts for NSGAII is given. From the Pareto front obtained using NSGAII, two points of A and B are selected (see Figure 4). The first point is point (A), in which the best positional accuracy regardless of MADMP is obtained. The second point is point (B), in which MADMP is kept less than 1 cm. The RMSE for the positional error in all three dimensions over the training data points corresponding to this point is equal to 72.187 μm. Using the parameters corresponding to points A and B, the positional accuracies are obtained as in

Table 3. Mean squared error for position corresponding to selected points from Pareto.

		Point A DH Parameters	Point B DH Parameters	Manufacturer’s Given Parameters
Train set	MAE (µm)	55.025	56.290	70.221
	RMSE (µm)	70.713	72.187	97.924
	MDMP (mm)	19	10	0
Test set	MAE (µm)	60.842	61.370	75.381
	RMSE (µm)	75.856	76.349	100.55
	MDMP (mm)	19	10	0

. To test the generalization of the obtained parameters to the test data, 20 random new data and unvisited points are used, and the generalization performance of the DH parameters for the test measurements are given. As can be seen from this table, the results for point A are the best obtained results. This validates the results of optimization. As can be seen from the table, the DH parameter values corresponding to both points A and B result in more precise positioning than that of the original DH parameter values given by the manufacturer. Moreover, it is observed that the positional accuracies corresponding to point A are better than point B. The overall RMSE values for the test dataset corresponding to points A and B demonstrate 27.79% and 26.28% improvements over the RMSE values for the same dataset corresponding to the manufacturer’s given parameters, respectively. The distance between the 3D robot positions corresponding to the DH parameter value selected from the Pareto front and the LT measurements, and the manufacturer’s given DH parameter values and from the positions measured from the LT in the x-y plane and x-z plane are given in Figure 5a,b. As can be observed from these figures, the positions corresponding to point A and point B are closer to the positions given by the laser tracker than the positions corresponding to manufacturer’s given parameters.

Moreover, the positional errors in the x and y dimensions are depicted in Figure 6a,b. As can be seen from these figures, the positional error corresponding to the DH parameter of points A and B are less than the ones for the manufacturer’s given DH parameter values in the x- and y-axis.

6. Conclusions and Future Work

Geometrical dimension measurement error is one of the major sources of uncertainty for an industrial robot’s FKs. To deal with such an uncertainty, multi-objective level II calibration is utilized to identify the DH parameters of an industrial robot within this paper. Other than finding more precise DH parameters for the purpose of increasing generalization capabilities, the mean absolute deviation of the DH parameters with respect to the manufacturer’s given parameters is considered. To perform the calibration, positional measurements are provided by a highly accurate LT, namely Leica AT960, which is capable of measurements with a precision up to 3 µm/m. After identifying the DH parameters of the industrial robot, they will be used within its FK structure; therefore, the proposed approach is a parametric one, and the estimated parameters have real physical meaning. The meta-heuristic optimization approaches of NSGAII, MOEA/D, and MOPSO, which operate based on the dominance principle rather than an aggregation approach, are the preferred choices for the optimization problem investigated in this paper. Using these meta-heuristic optimization approaches, three Pareto fronts are obtained for the multi-objective optimization problem. However, the Pareto front found by NSGAII is the most diverse Pareto front. Furthermore, this algorithm provides the best results in terms of positional accuracy among the three investigated multi-objective optimization approaches. Using the Pareto front obtained from NSGAII, it is possible to further analyze the obtained results to choose the desired parameter values for the industrial robot DH parameters. Finally, two points out of NSGAII Pareto front are investigated in more detail. One of the points is selected as the point with the minimum positional error and high parameter deviation from the manufacturer’s given parameters. For the other selected point, the mean parameter deviation from the manufacturer’s given parameters is restricted to 1 cm. It is observed that when using the parameter set A, the RMSE of the position error in terms of test data improved by 27.79% compared with the positional accuracy corresponding to the manufacturer’s given parameter values. On the other hand, for parameter B, the RMSE of the position error for the test data improved by 26.28%.

An analysis of the unified error and calibrated parameters during the machining process has been investigated using the Lie theory for a KUKA KR500 industrial robot [47]. As a future study, an analysis of errors during machining for an industrial robot during the machining process will be investigated.